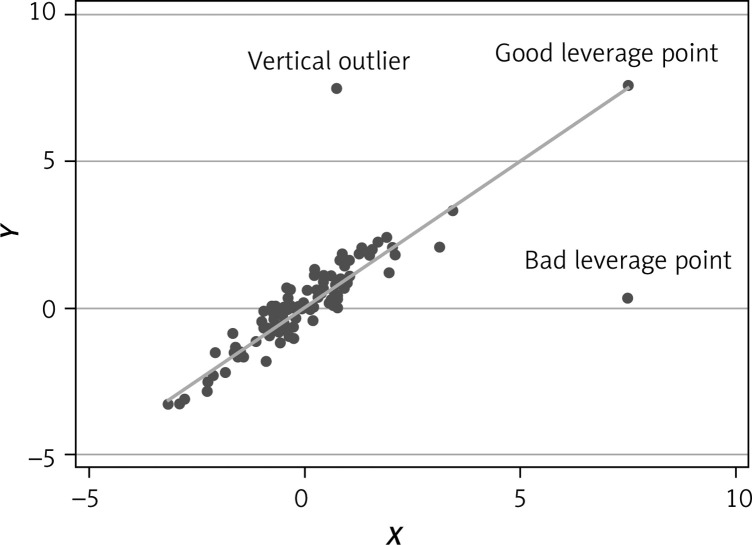
It is a fact that most real-world datasets in biomedical research contain outliers and leverage points. To define what an outlier and a leverage point is, let us assume a Y\X regression model where Y is the outcome variable and X the independent covariate(s). Outliers are Y outcome observations that are distant from the majority of the other observations (in terms of the y-axis). Outliers can sometimes be influential, meaning they can substantially impact the results of a regression analysis, i.e., the estimated b-coefficients and, consequently, the predicted outcome y variable. However, at this point we have to distinguish between (a) “non-influential” outliers i.e., those that have a minimal impact on the estimated regression model but will still lead to an overestimation of the standard error and (b) the “influential” outliers which seriously impact the estimated model because they “pull” the regression line towards themselves [1]. The influential points can be removed from the modelling process, but only when substantive reasons are present, e.g., if these observations have been mis-recorded. In any other case they should be retain in the model as they are true observations and the results should be interpreted with caution. In contrast an inlier is an “unusual” observation that lies in the interior of a dataset making it difficult to distinguish from the other values. Leverage points are X observations (i.e., independent covariates) that are distant from the majority of other observations (in terms of the x-axis), regardless of their effect on the Y outcome. For example, let assume that we want to estimate a Y\X regression model of systolic blood pressure (SBP, y, outcome) levels based on age, body mass, salt consumption and physical activity status of n individuals. An outlier is an observation (individual) that has quite distant SBP levels from the majority of the other individuals, although its age, body mass, salt consumption and physical activity levels are within the range of the other cases. On the other hand, a leverage point is an observation (individual) that has quite distant age, and/or body mass, salt consumption and physical activity (x, covariates) levels compared to the majority of the other cases, regardless of the SBP levels. Leverage points are characterised as “good” when they do not influence the regression line and “bad” when they influence the regression line (like the outliers). In Figure 1 differences between (vertical) outliers and (good/bad) leverage values for a simple linear regression model are illustrated [2].
Figure 1.
Outliers and leverage points in a simple regression analysis Y\X
It is well known that the ordinary least squares (OLS) method – the one that is commonly used in linear regression model fitting – is highly sensitive (i.e., not robust) and provides poor estimates for the b-coefficients when influential observations (outliers and/or bad leverage points) are present. Moreover, the classical linear regression assumes a Gaussian distribution of the residuals (and consequently the outcome variable), which is often violated due to the influential observations. However, regression analysis can still be applied in the presence of outliers and/or leverage points using the robust regression approach. In this article four robust regression techniques that combine high breakdown points and high efficiency are presented. The breakdown point is a global measure of robustness, giving the highest proportion of outliers found in the data before the estimator goes over all bounds. The maximum acceptable breakdown point is 50%. For example, the MM-estimator has a 0.5 break point, meaning that the MM-estimator resists contamination of up to 50% of outliers. Statistical efficiency is the number of sampling procedures needed to achieve a given accuracy. Generally speaking, the efficiency of an estimator is a ratio of variances at a fixed sample size, comparing the “gold standard” estimator. For example, the MM-estimator has 95% efficiency. Moreover, the presented robust regression techniques are also used in order to handle small sample sizes (e.g., n < 100) (e.g., the distance-constrained maximum likelihood (DCML) estimator) and techniques that are used when more than 50% of the values are considered as influential points (e.g., the shooting S-estimator and the MM-estimator). It should be noted here that the robust regression methods are not widely understood and used in biomedical sciences, although their application seems essential in many model fitting problems.
Detection of influential observations: At first, we have to detect influential points. Wilcox [3] compared five commonly used methods to allocate leverage points and concluded that no single method always performs better than the others. Specifically, Wilcox reported that the minimum generalized variance (MGV) method and the projection methods performed relatively well in identifying leverage points when the number of covariates was not higher than nine [3]. The projection method is more flexible since it projects all points into a line, passing through a given point and the centre of the data cloud; no particular shape is assumed for capturing points that are not leverage observations. As regards the detection of outliers, the minimum covariance determinant (MCD) and the minimum volume ellipsoid (MVE) have also been proposed [4]. They both use the Mahalanobis distance but with a measure of location and scatter that has a high breakdown point. That is, they are not over-influenced by outliers, which is important given the goal of avoiding masking. Using the usual mean values and the covariance matrix can result in masking.
Properties of robust regression techniques: Several investigators have different opinions on which properties are more important for a robust regression estimator. At least fourteen robust regression estimators exist nowadays [5]. We will try to prioritize the most important properties for a robust regression estimator. So, a robust estimator should: (a) be practical to compute, (b) have large sample theory for a fairly large class of distributions, (c) have high asymptotic efficiency and (d) have high outlier resistance for several common types of outliers, e.g., to be high breakdown.
The case of small sample size: In several studies, especially in small clinical trials or experimental studies, researchers have to work with relatively small sample sizes (i.e., n < 100), whereas the data are often contaminated by influential points. In these cases, it has been recommended to use 3 robust estimators. The MM-estimator and the τ-estimator can guarantee an acceptable compromise between high breakdown (i.e., 50%) and very high efficiency (i.e., 95%) [6]. Moreover, for inference and prediction of the outcome values, the fast-robust bootstrap (FRB) method can be used for calculating the MM and the τ-estimators [5]. The third robust estimator is the distance-constrained maximum likelihood (DCML) estimator, which is recommended in the case of very small sample sizes [7]. Moreover, there is a new family of robust regression estimators called bounded residual scale estimators (BRS estimators), and they are simultaneously highly robust and efficient for very small sample sizes [8], but their properties have not been well studied yet. Among all the aforementioned estimators, the DCML estimator is the one most commonly recommended by many investigators due to the following reasons: inference is better justified (i.e., more robust confidence intervals); Maronna and Yohai [7] have proposed a Monte Carlo-based method to compute confidence and prediction intervals. Moreover, it can be computed faster, and has a simpler and more intuitive definition.
The case of large proportion of influential points in the data: Another important issue arises of which estimator to use when the outliers and/or the leverage points exceed a substantial proportion of the data, i.e., 50%. If outliers and/or bad leverage points are present in more than 50% of the cases, the cellwise robust estimators such as the shooting S-estimator or the shooting MM-estimator [9] have been proposed. However, in this case a problem arises since a large amount of information is thrown away [10].
In conclusion, it is a true that in several biomedical analyses researchers frequently encounter variables with the presence of influential outliers and bad leverage points. Robust regression estimators are favoured in all the aforementioned cases, since they can prevent the entire results and thus avoid erroneous interpretations and conclusions.
Conflict of interest
The authors declare no conflict of interest.
References
- 1.Gschwandtner M, Filzmoser P. Computing robust regression estimators: developments since dutter (1977) Austrian J Stat. 2012;41:45–58. [Google Scholar]
- 2.Verardi V, Croux C. Robust regression in stata. Stata J. 2009;9:439–53. [Google Scholar]
- 3.Wilcox RR. Some small-sample properties of some recently proposed multivariate outlier detection techniques. J Stat Comput Simul. 2008;78:701–12. [Google Scholar]
- 4.Rousseeuw PJ, Van Zomeren BC. Unmasking multivariate outliers and leverage points. J Am Stat Assoc. 1990;85:633–9. [Google Scholar]
- 5.Salibian-Barrera M, Van Aelst S, Yohai VJ. Robust tests for linear regression models based on τ-estimates. Comput Stat Data An. 2016;93:436–55. [Google Scholar]
- 6.Yohai VJ. High breakdown-point and high efficiency robust estimates for regression. Ann Statist. 1987;15:642–56. [Google Scholar]
- 7.Maronna RA, Yohai VJ. High finite-sample efficiency and robustness based on distance-constrained maximum likelihood. Comput Stat Data An. 2015;83:262–74. [Google Scholar]
- 8.Smucler E, Yohai VJ. Highly robust and highly finite sample efficient estimators for the linear model. In: Nordhausen K, Taskinen S, editors. Modern Nonparametric, Robust and Multivariate Methods: Festschrift in Honour of Hannu Oja. 1st ed. New York: Springer; 2015. pp. 91–108. [Google Scholar]
- 9.Oellerer V, Alfons A, Croux C. The shooting S-estimator for robust regression. Comput Stat. 2016;31:829. [Google Scholar]
- 10.Leung A, Yohai VJ, Zamar RH. Multivariate location and scatter matrix estimation under cellwise and casewise contamination. Comput Stat Data An. 2017;111:59–76. [Google Scholar]