Stimulus-frequency-dependent dominance of sound localization cues across the cochleotopic map of the inferior colliculus

Abstract

The horizontal direction of a sound source (i.e., azimuth) is perceptually determined in a frequency-dependent manner: low- and high-frequency sounds are localized via differences in the arrival time and intensity of the sound at the two ears, respectively, called interaural time and level differences (ITDs and ILDs). In the central auditory system, these binaural cues to direction are thought to be separately encoded by neurons tuned to low and high characteristic frequencies (CFs). However, at high sound levels a neuron often responds to frequencies far from its CF, raising the possibility that individual neurons may encode the azimuths of both low- and high-frequency sounds using both binaural cues. We tested this possibility by measuring auditory-driven single-unit responses in the central nucleus of the inferior colliculus (ICC) of unanesthetized female Dutch Belted rabbits with a multitetrode drive. At 70 dB SPL, ICC neurons across the cochleotopic map transmitted information in their firing rates about the direction of both low- and high-frequency noise stimuli. We independently manipulated ITD and ILD cues in virtual acoustic space and found that sensitivity to ITD and ILD, respectively, shaped the directional sensitivity of ICC neurons to low (<1.5 kHz)- and high (>3 kHz)-pass stimuli, regardless of the neuron’s CF. We also found evidence that high-CF neurons transmit information about both the fine-structure and envelope ITD of low-frequency sound. Our results indicate that at conversational sound levels the majority of the cochleotopic map is engaged in transmitting directional information, even for sources with narrowband spectra.

NEW & NOTEWORTHY A “division of labor” has previously been assumed in which the directions of low- and high-frequency sound sources are thought to be encoded by neurons preferentially sensitive to low and high frequencies, respectively. Contrary to this, we found that auditory midbrain neurons encode the directions of both low- and high-frequency sounds regardless of their preferred frequencies. Neural responses were shaped by different sound localization cues depending on the stimulus spectrum—even within the same neuron.

INTRODUCTION

A hallmark of the central auditory system is the topographic representation of frequency selectivity within each auditory brain area, mimicking that along the receptor surface in the cochlea. Neural frequency preference is usually defined by the characteristic frequency (CF), the tone frequency for which a neuron’s response can be evoked at the lowest sound level. In the central nucleus of the inferior colliculus (ICC), a major brain area along the mammalian subcortical auditory pathway, neurons are arranged into a stack of laminar sheets (Oliver and Morest 1984). Neurons within the same lamina share CFs within a common, narrow frequency band, whereas those of neighboring laminae have CFs shifted by ~0.3 oct, leading to a stepwise tonotopy (Chen et al. 2012; Malmierca et al. 2008; Schreiner and Langner 1997). This tonotopic clustering of neurons has led to the hypothesis that auditory signal processing in the ICC (including binaural processing) occurs within distinct frequency channels (Schreiner and Langner 1997).

At sound levels near hearing threshold, ICC neurons are only activated by tone frequencies near their CFs; therefore, auditory signal processing necessarily occurs in narrow frequency channels. However, as sound level increases, most ICC neurons become excited by a broad range of tone frequencies about the CF (Ehret and Merzenich 1988; Palmer et al. 2013). This raises the possibility that a large extent of the cochleotopic map may be involved in processing auditory stimuli at relatively high sound levels, even stimuli with narrow frequency spectra. On the other hand, Yu and Young (2013) derived frequency tuning of ICC neurons with a reverse correlation technique operating on average firing rates to a set of broadband stimuli and found that tuning bandwidth did not broaden at high sound levels. This implies that auditory processing to stimuli with complex spectra occurs within narrow frequency channels at all sound levels.

In the present study, we answer the following question about basic auditory signal processing in the brain: Do neurons with CFs that do not overlap with the spectrum of a sound source (“off-CF” neurons) contribute information about the direction of the source? The potential for off-CF neural contributions to sound localization coding is of particular interest because the perception of the azimuths of sound sources with low- and high-frequency spectra are respectively dominated by interaural time and level differences (ITDs and ILDs), known as the “duplex” theory of sound localization (Macpherson and Middlebrooks 2002; Strutt 1907; Wightman and Kistler 1992). We previously reported that low- and high-CF ICC neurons have directional sensitivity to broadband stimuli that is respectively dominated by ITD and ILD (Day et al. 2012; Day and Delgutte 2013), consistent with both the duplex theory and the hypothesis that neurons process frequency components of an auditory signal near their CFs (i.e., narrow frequency channels). However, these data were measured at relatively low sound levels where tonal frequency tuning is narrow. Furthermore, a broadband stimulus contains energy at all frequencies and therefore provides neurons with both on-CF and off-CF stimulation. If off-CF neurons do provide information about sound source direction at high sound levels, the question remains as to whether the directional sensitivity of individual neurons is shaped by the same or different binaural cues for low- and high-frequency stimuli.

To answer the above questions, we recorded from ICC neurons in awake Dutch Belted rabbits—a species with a hearing range that spans ITD- and ILD-dominated frequencies (Heffner and Masterton 1980). We measured azimuth tuning curves in virtual acoustic space in response to stimuli that systematically varied in frequency spectra and sound level. Furthermore, we independently manipulated the ITD and ILD cues of low- and high-frequency stimuli to determine which cue dominated directional sensitivity.

MATERIALS AND METHODS

Data were collected from two female Dutch Belted rabbits (Covance) over a period from 6 to 29 mo of age. Both rabbits had normal auditory brain stem response thresholds. All experimental procedures were approved by the Ohio University Institutional Animal Care and Use Committee.

Experimental procedures.

Rabbits underwent an original surgery under anesthesia to affix a lightweight three-dimensional (3D)-printed aluminum headbar with attached microdrive slot (Laurel H. Carney, University of Rochester) to the skull with dental acrylic. Subsequent surgeries were performed to drill a hole in the skull for guide tube entry and microdrive mounting (Neuralynx 9 Drive) and to replace the microdrive as needed. The craniotomy hole (3-mm diameter) was centered at various locations within an area approximately 8–11 mm caudal to the bregma suture and 2–5 mm lateral to the midline suture. The microdrive was inserted into the slot on the headbar, which oriented guide tubes at an angle ~68° below the tooth-orbit line. After insertion, the space between brain and microdrive was filled with silicone elastomer (Kwik-Sil; World Precision Instruments).

Each microdrive was loaded with four independently drivable tetrodes, which exited the drive through 28-gauge stainless steel guide tubes (Eagle Stainless) packed in an equilateral triangular pattern (1 center and 3 corners). Each tetrode was handmade from four insulated microwires twisted and heat-bonded together (18-µm diameter, 90% platinum-10% iridium with HML insulation and VG bond coat; California Fine Wire). The upper region of each tetrode was ensheathed in polyimide tubing (Neuralynx) and the lower region stiffened with cyanoacrylate glue. Tetrode tips were electroplated (0.1-µA anodal current, 90 s; Plexon nanoZ) under sonication in platinum black solution (Neuralynx) until impedances in saline were between 0.1 and 0.5 MΩ. Immediately after microdrive insertion, tetrodes were advanced their full extent, passing through occipital cortex and inferior colliculus (IC). Single-unit data were collected over a period of many days as the tetrodes were gradually retracted, usually in 63-µm steps. Microdrives were periodically replaced to target different regions within the ICC, including both sides of the brain.

Data were collected during daily 2.5-h awake recording sessions within a double-walled, sound-attenuated chamber (ETS-Lindgren Acoustic Systems). Rabbits were loosely secured in a custom-made “chair,” head-fixed via headbar, fitted with ear molds for sound presentation (Reprosil; Dentsply), and monitored by video throughout the session. Before the first session, rabbits were gradually acclimated to the setup over 1.5 wk.

Stimulus presentation and data acquisition.

Stimulus presentation and data acquisition were controlled by custom software in MATLAB (MathWorks) interfacing with LabVIEW [National Instruments (NI)] and RPvdsEx and OpenEx [Tucker-Davis Technologies (TDT)]. Acoustic signals were handled by a NI PXIe-1082 chassis. Acoustic stimuli were created digitally, converted to analog signals at 50-kHz sampling rate with 24-bit resolution (NI PXI-4461), and amplified (TDT SA1) to drive insert earphones (Etymotic ER-2). The sound tubes of the earphone and a probe microphone were embedded in the ear mold to position their ends at the entrance of the ear canal. Sound was therefore presented in closed field. The probe microphone (Etymotic ER-7C) was used to calibrate the acoustic assembly via a chirp stimulus. Measured acoustic signals were digitized at 100-kHz sampling rate (NI PXI-4461). The probe microphone was itself calibrated periodically to ensure fidelity and extend calibrated frequency range up to 16 kHz. The probe microphone was calibrated with a 1/4-in. pressure microphone (PCB Piezotronics 378C10) coupled together by a 3-mL syringe (Rasetshwane and Neely 2011). Sensitivity of the pressure microphone was checked for consistency with a sound-level calibrator (Larson Davis CAL200).

Neural signals were handled by a TDT RZ5D BioAmp processor. Electrical potentials between tetrode tips and ground (guide tubes) were buffered by a headstage (TDT ZC32), digitized at 25-kHz sampling rate with 28-bit resolution, and filtered between 0.4 Hz and 11.25 kHz (TDT PZ5-32) before being stored on disk by the RZ5D. Spikes were sorted online (TDT OpenEx) for guidance during recording sessions but off-line (Plexon Offline Sorter) for reported data. Voltage traces were filtered between 1 and 5 or 10 kHz. Spike thresholds were manually chosen for each electrode within a tetrode. For each threshold-crossing event on any electrode within a tetrode, a 0.25-ms window of the voltage trace was captured on each electrode, centered such that one-third of the window was before the time of threshold crossing (Fig. 1A). A subsequent threshold-crossing event was not allowed to be triggered until 0.25 ms after the last (“dead time”). For all threshold-crossing events, peak voltage amplitudes of each electrode within a tetrode were plotted against each other in two-dimensional (2D) (Fig. 1, B and C) or 3D scatterplots, the latter of which could be rotated to find the 2D projection that best separated data clusters. For our data, automated cluster separation algorithms within the Offline Sorter software were often erroneous, including those based on principal components analysis. Therefore, single-unit clusters were circled manually in the 2D or 3D scatterplots that yielded best cluster separation. Spike data were considered single unit if they 1) formed a complete cluster separate from others and 2) had <2% submillisecond interspike intervals. Only single-unit data are reported.

Fig. 1.

Spike sorting. A: example of voltage trace windows simultaneously captured across electrodes A–D within a tetrode in response to a threshold-crossing event. B and C: 2-dimensional histograms of the peak voltage amplitudes of threshold-crossing events for 2 electrodes within a tetrode. Data in B and C are from different experimental sessions (labels at top right). Grayscale indicates number of occurrences, with white being the greatest. Multiunit clusters are at bottom left. The color white was set to a value lower than the maximum number of occurrences so that the smaller single-unit clusters could be visualized.

Figure 1B shows an example spike-sorting scatterplot with a large multiunit cluster (Fig. 1B, bottom left) and two single-unit clusters, the latter two above and below the diagonal having separation from the multiunit cluster that we considered borderline and decent, respectively. The cluster above the diagonal had better separation when viewed in the appropriate projection plane of a 3D scatterplot (not shown). Figure 1C shows another example with a well-separated, single-unit cluster (upper). In this case, the multiunit cluster (lower) overlapped substantially with a putative single-unit cluster bleeding out of the right-hand side; this putative cluster did not meet our criterion of separability.

Stimuli.

For each neuron the following were measured: 1) the frequency-level response area (FRA); 2) azimuth tuning curves in response to low- and high-pass noise under four different binaural cue conditions; 3) azimuth tuning curves in response to narrowband noise at four different center frequencies and at two different sound levels; and for neurons recorded later in the study 4) ITD tuning curves in response to low-pass noise with same and opposite left/right polarity. For each measurement, the order of stimulus parameters was varied randomly across 15 repetitions, except the FRA (2 repetitions). Stimuli were either tone pips (100 ms on, 5-ms on/off sin² ramps, 200 ms off) or frozen noise bursts (300 ms on, 5-ms on/off sin² ramps, 300 ms off). Noise stimuli were created to have energy only within a chosen passband by first assembling a conjugate symmetrical Fourier transform with magnitude of 1 and random phase (uniform distribution) within the passband and zero magnitude and phase outside the passband (“brick-wall” filtering) and then taking the inverse Fourier transform to create the waveform in the time domain. Low- and high-pass noise bursts had energy within 0.1–1.5 and 3–16 kHz, respectively. Narrowband noise bursts had 2/3-oct bandwidth geometrically centered about center frequencies of 1, 2, 4, and 8 kHz.

Acoustic waveforms presented over earphones were made directional by filtering with left and right directional transfer functions (DTFs) specific to each azimuth within the front horizontal plane (from Day et al. 2012). As described previously, DTFs were simplified from head-related transfer functions measured from a cadaver rabbit using principal components analysis to remove idiosyncratic spectral features while keeping frequency-specific ITD and ILD appropriate for rabbits (Fig. 2). For all azimuth tuning curves, stimuli were presented at azimuths between −90° and +90° (ipsilateral and contralateral to the recording site, respectively) in 15° steps where 0° was directly in front of the rabbit. Low- and high-pass noise bursts were alternatively filtered with 1) normal DTFs (congruent binaural cues; “ITD+ILD”), 2) and 3) two alternate DTFs augmented to manipulate ITD and ILD independently (incongruent binaural cues; “ITD-only” and “ILD-only”), and 4) normal DTFs with sound only in the contralateral ear (monaural; “contra-only”). ITD-only DTFs had left and right magnitude spectra fixed to 1, which fixed ILD to that at 0° while allowing ITD to vary naturally with azimuth. ILD-only DTFs had left and right phase spectra set to 0, which fixed ITD to that at 0° while allowing ILD to vary naturally with azimuth.

Fig. 2.

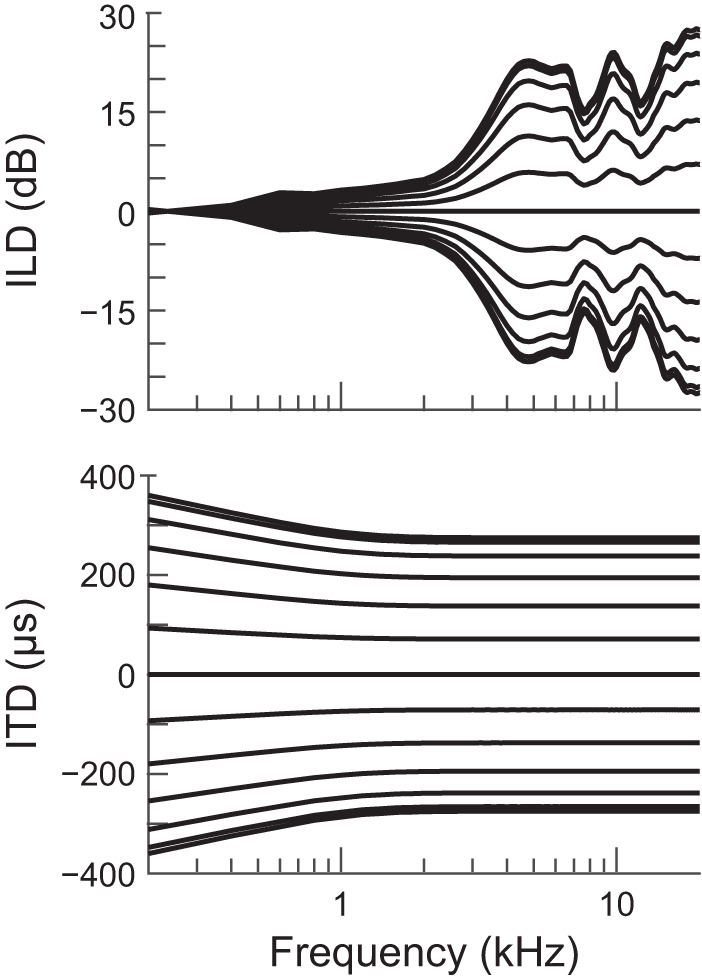
Binaural cues of the directional transfer functions used to make stimuli directional in virtual acoustic space. Each curve is the interaural level difference (ILD; top) or interaural time difference (ITD; bottom) vs. frequency for 1 azimuth in the horizontal plane. Curves in each plot are ordered −90° to 90° from bottom to top. Positive azimuths, ILDs, and ITDs indicate directions contralateral to the recording site.

For FRA measurement, tone pips were presented at frequencies from 0.1 to 16 kHz in 1/4-oct steps and at sound levels from 5 to 70 dB SPL in 5-dB steps. For ITD tuning curves, ITD was varied from −1,000 to +1,000 µs (ipsilateral to contralateral leading, respectively) in 50-µs steps. In the “opposite-polarity” condition, the waveform in one ear was inverted. All azimuth and ITD tuning curves were measured at 70 dB SPL, except for azimuth tuning curves in response to narrowband noise, which were additionally measured at 35 dB SPL. These sound levels were well below the maximum undistorted output of the insert earphones, which was 105–110 dB SPL.

Data analysis.

Stimulus trials that contained artifacts due to infrequent rabbit movements were omitted from analysis. Stimulus-evoked and spontaneous spike counts were made in the stimulus window and last 100 ms of the 300-ms silent period of each trial, respectively.

The FRA (average firing rate as a function of both log frequency and level) was upsampled by a factor of 2 and then smoothed with a 2D filter made of a Gaussian frequency window (SD = 1/16 oct) and a triangular level window (Palmer et al. 2013). CF was determined by visual observation of the FRA as the frequency that elicited a response at the lowest sound level, where the response was an increase or decrease of the firing rate from the spontaneous rate. Multiunit FRAs were measured at every tetrode depth regardless of the presence of single units. At a certain depth within the IC, multiunit FRAs transformed from a diffuse shape characteristic of the dorsal cortex to a “V” shape with low CF characteristic of the ICC (see Fig. 6A). As depth increased, CF increased in frequency and then reached a depth where the FRA returned to a diffuse shape. This tonotopic region of tuned multiunit FRAs was consistent with the ICC (Aitkin et al. 1972; Hind et al. 1963; Merzenich and Reid 1974). Single units found within this region were considered to be within the ICC. Only single units deemed to be within the ICC are reported.

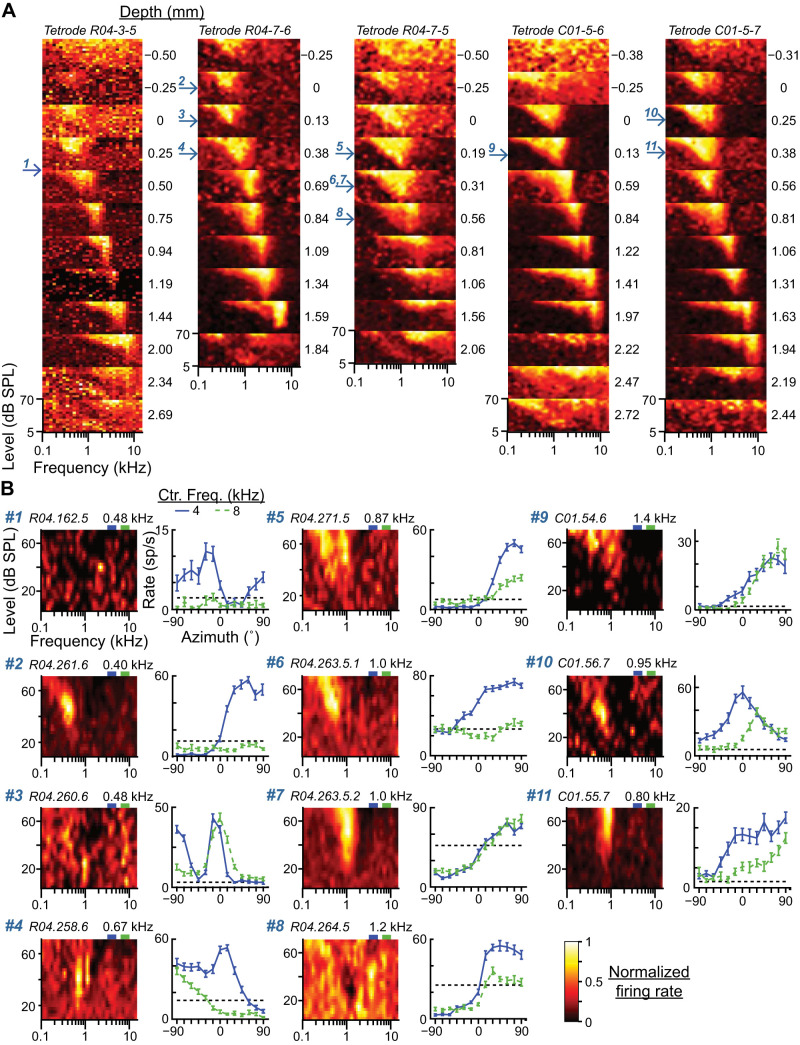
Fig. 6.

Cochleotopic locations of low-characteristic frequency (CF) neurons. A: multiunit frequency-level response area (FRAs) recorded from 5 different tetrodes (columns) at 10–12 different depths (plots within each column). Depth relative to the approximate dorsal border of the central nucleus of the inferior colliculus (ICC) is indicated on right of each plot. Tuning to frequency within the ICC systematically increases with depth. Arrows on left of panels indicate depths at which low-CF neurons were recorded, with numbers matched to the data in B. B: FRAs (left) and azimuth tuning curves in responses to narrowband noise at 4- and 8-kHz center frequencies (right) for each of the 11 low-CF neurons whose depths are indicated by arrows in A (corresponding number at top left). Dashed black lines in azimuth tuning plots indicate spontaneous rates. Neuron ID and CF are at top left and top right, respectively, of each FRA plot. Green and purple rectangles above each FRA indicate low and high passbands, respectively.

Multiunit FRAs always had a V shape, enabling easy estimation of CF, whereas some single units had complex FRAs that were either diffuse or suggested excitatory and inhibitory subregions. For single units with complex FRAs, CF was determined as that of the multiunit FRA at the same tetrode site. Furthermore, for ventral sites where the lower-frequency FRA tail was visible but the upper-frequency tip exceeded the range of tone frequencies presented, the single-unit CF was assigned a value of 20 kHz. CF was always compared to the progression of multiunit frequency tuning at different depths within the same tetrode, such as in Fig. 6A, to ensure that lower-frequency tails of high-CF neurons were not misclassified as low-CF neurons.

For azimuth tuning curves, an estimate of the mutual information (MI; Cover and Thomas 2006) between spike count, n, and stimulus azimuth, θ, was computed: $\widehat{\text{MI}}\left(n;\theta \right)={\displaystyle {\sum }_n{\displaystyle {\sum }_{\theta }P(n|\theta )P\left(\theta \right){\log }_2\frac{P(n|\theta )}{P\left(n\right)}}}$. The conditional spike count distribution, P(n|θ), was assumed to be a Poisson distribution with mean equal to the mean spike count at azimuth θ. The marginal distribution, P(θ), was a uniform distribution of the M = 13 stimulus azimuths, $P\left(\theta \right)=\frac{1}{M}=\frac{1}{13}$. The other marginal distribution, P(n), was computed as $P\left(n\right)={\displaystyle {\sum }_{\theta }P(n|\theta )P\left(\theta \right)}$. A bootstrap procedure was used to correct for bias in the MI estimate (Chase and Young 2005). Spike count data were resampled with replacement, and then MI was computed on the resampled data (MI_boot). The bias was estimated as $\text{Bias}={\overline{\text{M}\text{I}}}_{\text{boot}}-\widehat{\text{M}\text{I}}$, where ${\overline{\text{M}\text{I}}}_{\text{boot}}$ was the average over 500 bootstrap-resampled data sets. Debiased MI was $\text{MI}=\widehat{\text{M}\text{I}}-\text{Bias}$. Finally, normalized MI (MI_norm) was computed by dividing MI by the entropy of the stimulus azimuth, ${\log }_{2}M={\log }_{2}13$, which is the largest value MI may take.

To assess the validity of the assumption that spike count distributions are Poisson, we examined the relationship between mean and variance of spike counts for every sample set in our data except those used to measure the FRA (N = 11,372 sample sets with usually 15 counts per sample). For a Poisson distribution, the mean is equal to the variance. Figure 3A shows a plot of variance vs. mean for sample sets grouped within equally log-spaced bins of mean count (black curve); also plotted are simulated data in which spike counts were drawn randomly from Poisson distributions with means and number of trials equal to those of the experimental sample sets (gray curve). The spread of simulated data along the unity line is due to the limited number of trials in the estimation of mean and variance. Below a firing rate of 25 sp/s the relationship of mean and variance of experimental data was matched to that of Poisson distributions, but at and above this rate the variances spread to values lower than those expected from simple estimation error, likely because of the variance-narrowing effect of the spike refractory period at higher driven rates. Therefore, MI may be underestimated in some cases when the neuron was driven at a higher rate; in such cases there may be less actual overlap of spike count distributions in response to different stimuli than that assumed for Poisson distributions. Moreover, although Fig. 3A shows that the relationship between mean and variance is reasonably close to unity on average across experimental data, individual neurons may deviate. Nonetheless, potential underestimation of MI was likely mild because the deviation of the variance at highest driven rates from that of a Poisson distribution was small, as is depicted in Fig. 3B.

Fig. 3.

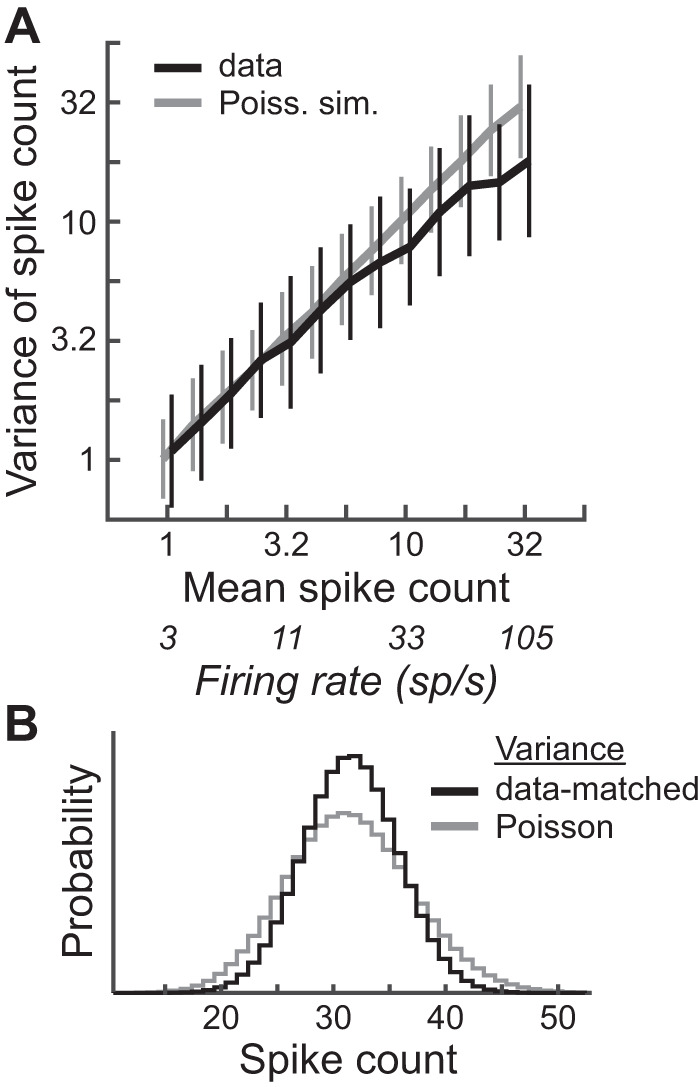
Comparison of spike count distributions to Poisson distributions. A: log sample variance (mean ± SD) vs. log sample mean for all spike count sample sets in the data except those used to measure frequency-level response areas, binned within equally log-spaced bins of mean spike count (black curve; N is between 354 and 1,222 within each bin) and same plot for simulated spike count data drawn randomly from Poisson distributions with means and number of trials matched to those in the experimental sample sets (gray curve). Unbiased estimates of log sample variance were computed by adding log₁₀e/(m − 1) to the log₁₀ sample variance, where m is the number of trials (Gershon et al. 1998). Curves are shifted horizontally for visibility. B: theoretical spike count distributions, each with means of 32, the highest mean count in the data (rate = 105 sp/s): Poisson distribution (gray curve) and discretized, normal distribution with variance set to the average of that of experimental data at a mean of 32 (black curve).

Population decoding.

A maximum-likelihood decoder was implemented to estimate stimulus azimuth from the pattern of spike counts across neurons during a single stimulus presentation (Day and Delgutte 2013, 2016; Jazayeri and Movshon 2006). Under the assumptions that spike counts of different neurons 1) are conditionally independent of each other and 2) come from Poisson distributions, the log-likelihood function takes the form

$$\log \mathcal{L}(\theta |\left\{n_i\right\})={\displaystyle \sum }_{i=1}^N{n}_i\log f_i\left(\theta \right)-{\displaystyle \sum }_{i=1}^N{f}_i\left(\theta \right)-{\displaystyle \sum }_{i=1}^N\log \left(n_i!\right)$$

where n_i is the spike count of the ith neuron in a single trial, {n_i} is the set of spike counts across neurons in a single trial, N is the number of neurons, and f_i(θ) is the mean spike count of the ith neuron as a function of azimuth (i.e., the azimuth tuning curve). For a given {n_i}, stimulus azimuth was estimated as the θ that maximized the log-likelihood function. The parameters of the decoder, f_i(θ), were estimated from measured spike count data in the ITD+ILD condition. In practice, f_i(θ) was given a floor value of 0.001 to prevent occurrences of log(0). Test spike counts in a single trial, {n_i}, were selected randomly with replacement from the sample of spike counts of each neuron in response to azimuth θ*. For each θ*, {n_i} was generated for 1,000 trials. As explained in results, {n_i} was separately generated from data measured under ITD+ILD, ITD-only, and ILD-only conditions. When {n_i} was generated from the ITD+ILD condition, those spike counts were removed from the data used to estimate the f_i(θ) so that the decoder was not trained and tested on the same data.

The above log-likelihood equation is based on an assumption of conditional independence of spike counts between different neurons, which is consistent with a reported lack of noise correlation in paired recordings of ICC neurons in anesthetized animals (Belliveau et al. 2014; Garcia-Lazaro et al. 2013). Our use of tetrodes also allowed the possibility of measuring noise correlation between single units recorded simultaneously. However, the number of trials measured in our data lacked the statistical power necessary to assess the existence of weak noise correlations. The log-likelihood equation also assumes Poisson spike count distributions, which is not strictly true for our data (Fig. 3A). Therefore, the performance of the decoder will be suboptimal.

Experimental design and statistical analysis.

Data came from 32 ICC neurons in one female rabbit and 27 ICC neurons in the other, although single-unit isolation was not always maintained for every stimulus listed above. CFs of neurons in each rabbit spanned the cochleotopic map. FRAs and azimuth tuning curves were heterogeneous but not obviously different between individual rabbits; therefore data were pooled. Many additional neurons were not reported because of either spike waveforms not meeting single-unit classification criteria or determination that the neuron was outside the ICC after completion of the tetrode track.

The number of stimulus repetitions (15) was chosen to exceed a criterion of accuracy of firing rate estimation. Under the assumption that the distribution of spike counts in response to a fixed stimulus follows a Poisson distribution (Fig. 3A), at least 13 stimulus repetitions are necessary to estimate a mean firing rate of 100 sp/s within a 300-ms window with a 95% confidence interval of ±10 sp/s. The same repetitions would estimate mean firing rates of 50 and 20 sp/s with 95% confidence intervals of ±7 and ±4.4 sp/s, respectively.

All statistical tests were performed in MATLAB. Differences between azimuth tuning curves from the same neuron measured under different binaural-cue conditions, or between ITD tuning curves measured with same versus opposite left/right polarity, were assessed with multiple Wald tests and corrected for multiple comparisons with the Benjamini–Hochberg procedure (Wasserman 2004). Significance levels for azimuth and ITD tuning curves were set at 0.01 and 0.05, respectively. The Wald statistic was

$$W_{\theta }=\frac{{\overline{n}}_1\left(\theta \right)-{\overline{n}}_2\left(\theta \right)}{\sqrt{\frac{s_1^2\left(\theta \right)}{m_1}+\frac{s_2^2\left(\theta \right)}{m_2}}}$$

where ${\overline{n}}_1\left(\theta \right)$ and ${\overline{n}}_2\left(\theta \right)$ are the mean spike counts at azimuth (or ITD) θ under conditions 1 and 2, respectively, $s_1^2\left(\theta \right)$ and $s_2^2\left(\theta \right)$ are the spike count sample variances, and m₁ and m₂ are the number of repetitions. Effect size was defined as the sum of the absolute value of Wald statistics over all azimuths (or ITDs): $W={\displaystyle {\sum }_{\theta }\left|W_{\theta }\right|}$. For ITD tuning curves, the effect of ITD on spike count was assessed with a Kruskal–Wallis test with significance level of 0.01.

RESULTS

Low- and high-CF neurons can each transmit directional information about low- and high-frequency stimuli.

We measured the firing rates of ICC neurons in response to a 70-dB SPL noise burst spanning either low (0.1–1.5 kHz) or high (3–16 kHz) frequencies and presented from each of 13 equally spaced azimuths in the front horizontal plane. The ranges of frequencies within the low- and high-pass bands are thought to be localized via ITDs and ILDs, respectively (Macpherson and Middlebrooks 2002; Strutt 1907; Wightman and Kistler 1992). We quantified the information an individual neuron transmits about the azimuth of a stimulus as the MI between neural firing rate and stimulus azimuth, normalized by the maximum possible MI (MI_norm). A MI_norm of 0 indicates a flat azimuth tuning curve, which provides no information about azimuth, and a MI_norm of 1 indicates that the azimuth of the stimulus can be exactly predicted by observing the firing rate.

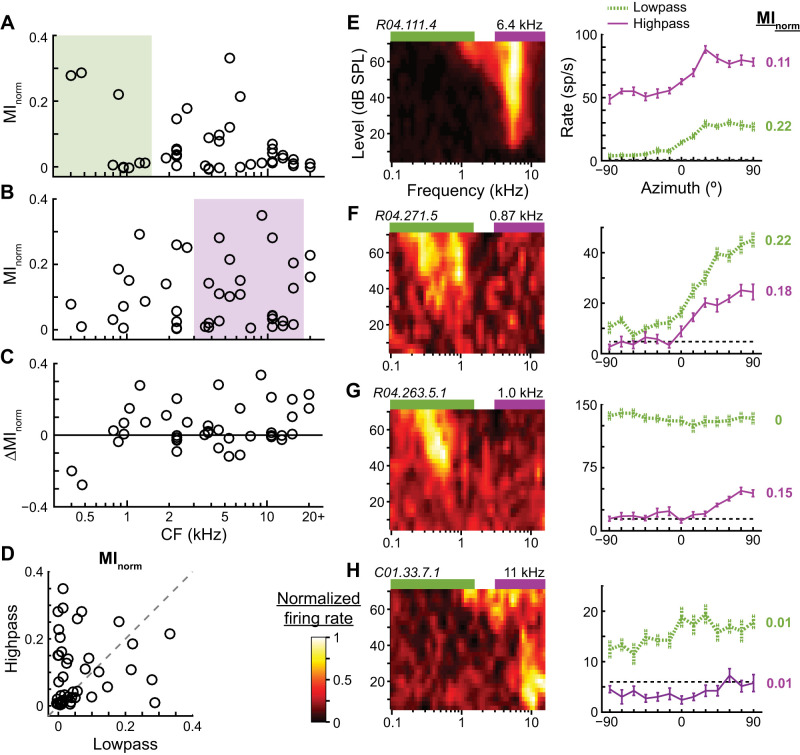
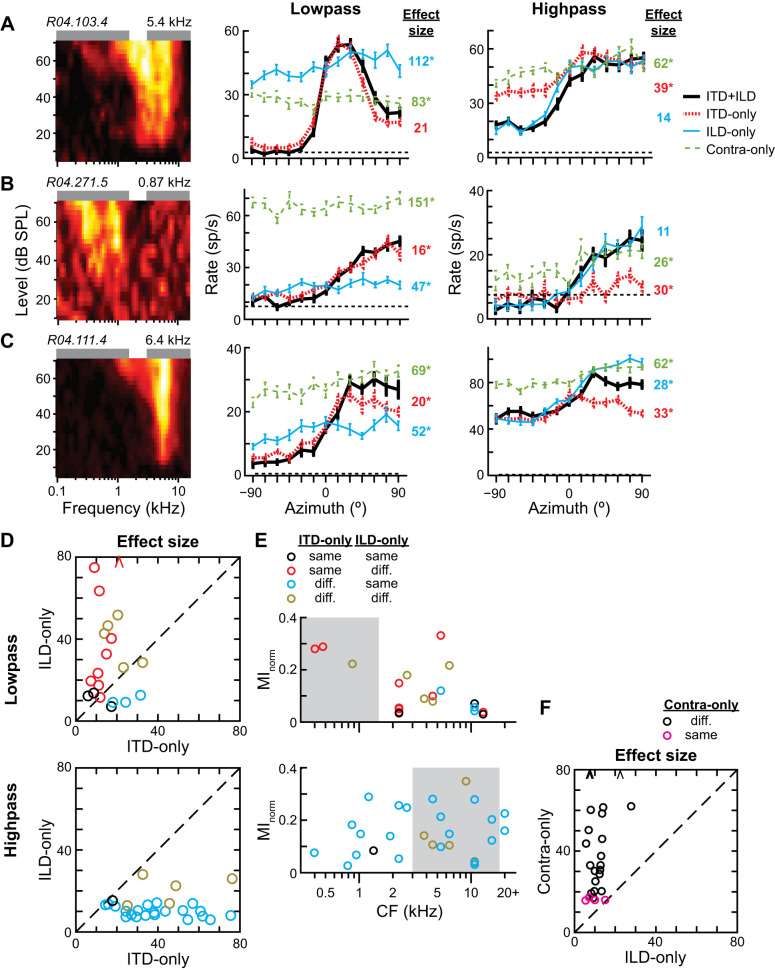
In response to low-pass noise, a subset of neurons in our sample transmitted relatively high information about azimuth, including neurons with CFs both within and above the passband (Fig. 4A). The potential to transmit directional information is expected for neurons with CFs within the stimulus passband but not necessarily for those with CFs far from the passband. Figure 4E shows data from an ICC neuron that had a CF of 6.4 kHz, well above the low passband. Its FRA clearly overlapped the high passband, and the neuron was directionally sensitive to high-pass noise. However, the tail of its FRA overlapped the low passband at high sound levels, and it also was directionally sensitive to low-pass noise. The ability of high-CF neurons to transmit directional information about low-pass noise was therefore generally consistent with the stimulus exciting the low-frequency tails of their FRAs.

Fig. 4.

Directional sensitivity to low- and high-pass noise across the cochleotopic map of the central nucleus of the inferior colliculus (ICC). A and B: normalized mutual information (MI_norm) vs. the characteristic frequency (CF) of each neuron in response to low (A; 0.1–1.5 kHz)- and high (B; 3–16 kHz)-pass noise at 70 dB SPL (n = 42). Colored rectangles indicate noise passbands. C: difference (Δ) of MI_norm between high- and low-pass noise (high − low) vs. CF. D: MI_norm of each neuron for low- vs. high-pass noise. Dashed line is unity line. E–H: frequency-level response areas (FRAs; left) and azimuth tuning curves (right) for 4 different ICC neurons. In each FRA, the color associated with firing rate is normalized to highest (white) and lowest (black) rates. Neuron ID and CF are at top left and top right, respectively, of each FRA. Green and purple rectangles above each FRA indicate low and high passbands, respectively. Azimuth tuning curves (mean ± SE) are shown in response to low- and high-pass noises. Dashed black lines indicate spontaneous rates. Normalized MI is shown on right of each curve, with color matched to curve.

Another subset of neurons in the same sample transmitted relatively high information about the azimuth of high-pass noise, including neurons with CFs within and well below the passband (Fig. 4B). Figure 4F shows data from a neuron with a CF of 0.87 kHz; its FRA clearly had an excitatory region that overlapped the low passband flanked by an inhibitory region ending at the lower edge of the high passband. Although there was no clear overlap of its FRA with the high passband, it was nonetheless directionally sensitive to high-pass noise.

Figure 4C shows the within-neuron difference of MI_norm for high- and low-pass noises, where positive indicates better encoding of the direction of the high-pass noise. ICC neurons in our sample tended to transmit more information about the azimuth of high- than low-pass noise, including low-CF neurons. Whether a neuron was directionally sensitive to a stimulus could not be reliably predicted from the extent of overlap of its pure-tone-derived FRA with the passband. For example, the neuron in Fig. 4G had an excitatory region of its FRA overlap with the low passband, but its firing rate to low-pass noise was saturated across azimuth, yielding no directional information. It is possible that this neuron may have transmitted directional information about the low-pass stimulus at lower sound levels where the firing rate would not be saturated. On the other hand, the neuron in Fig. 4H had an excitatory region of its FRA overlap with the high passband, but its firing rate in response to high-pass noise was mostly flat across azimuth and slightly suppressed below its spontaneous rate. Many neurons in our sample transmitted no or weak directional information for low- and high-pass noises (Fig. 4D, bottom left data points). However, these directionally insensitive or weakly sensitive neurons were all responsive to sound (such as in Fig. 4H), and their inability to transmit directional information specifically about the band-pass stimuli at 70 dB SPL does not necessarily preclude their ability to transmit directional information about stimuli with other spectra or at other sound levels.

Localized vs. widespread transmission of directional information across the cochleotopic map.

The above results show that at the moderately loud sound level of 70 dB SPL, ICC neurons across nearly the whole extent of the cochleotopic map can transmit directional information about stimuli with either low- or high-frequency spectra. FRAs tend to narrow with decreasing sound level, meaning a smaller range of tone frequencies evoke a response from each neuron at lower sound levels. We therefore hypothesized that at lower sound levels ICC neurons are only directionally sensitive to stimuli with spectra overlapping or near their CFs. To test this, we measured azimuth tuning curves at 35 and 70 dB SPL in response to narrowband noise bursts (2/3 oct) centered at 1, 2, 4, and 8 kHz. Together, these stimuli spanned a 3.67-oct range but left a 1/3-oct gap between each passband.

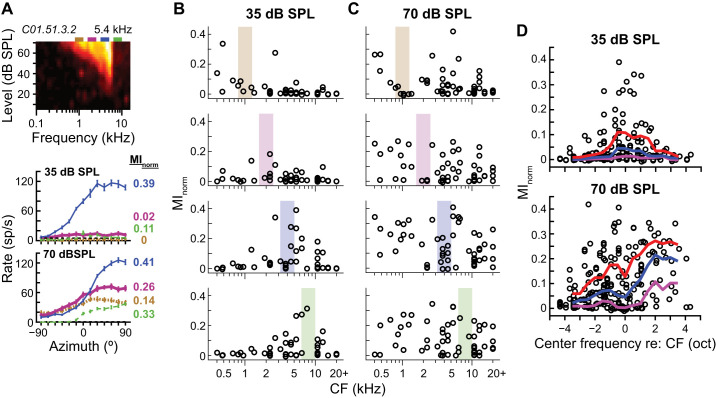
Figure 5A shows narrowband azimuth tuning curves measured from a high-CF ICC neuron. At 35 dB SPL, only the 4-kHz passband overlapped with the neuron’s FRA; correspondingly, the neuron was mostly directionally sensitive to the 4-kHz stimulus. At 70 dB SPL the neuron’s FRA widened and overlapped fully or partially with all of the stimulus passbands. At this higher sound level, the neuron was directionally sensitive to all stimuli.

Fig. 5.

Localized vs. widespread transmission of directional information across the cochleotopic map. A: frequency-level response area (FRA; top) and azimuth tuning curves in response to narrowband noise (2/3 oct wide) at each of 4 center frequencies at 35 (middle) and 70 (bottom) dB SPL for 1 central nucleus of the inferior colliculus (ICC) neuron. Line type and color of azimuth tuning curve indicate center frequency: 1 (dotted tan), 2 (thick magenta), 4 (thin blue), and 8 (dashed green) kHz. Rectangles above the FRA indicate noise passbands, color-matched to the azimuth tuning curves. Normalized mutual information (MI_norm) values indicated on right of each curve. B and C: MI_norm vs. characteristic frequency (CF) of each neuron in response to narrowband noises with center frequencies of 1, 2, 4, and 8 kHz (top to bottom) at 35 (B; n = 46) and 70 (C; n = 54) dB SPL. Colored boxes indicate noise passbands. D: MI_norm vs. narrowband center frequency relative to each neuron’s CF for 35 (top) and 70 (bottom) dB SPL. Data pooled over all center frequencies. Positive frequency values indicate that the noise band was higher than the neuron’s CF. Octave-wide, roving 25th, 50th. and 75th percentiles of the data indicated by purple, blue, and red curves, respectively.

At 35 dB SPL neurons in our sample that had CFs far from the passband tended to transmit little directional information about the stimulus (Fig. 5B), whereas at 70 dB SPL neurons that had CFs either near or far from the passband could transmit relatively high directional information (Fig. 5C). In Fig. 5D, we pooled data across center frequencies and plotted normalized MI vs. stimulus center frequency relative to neural CF. Plotted in this way it is clear that at 35 dB SPL neurons transmitted high directional information only for stimuli with center frequencies within approximately ±2 oct of their CFs. At 70 dB SPL, high directional information was transmitted by neurons for stimuli with center frequencies within ±4 oct of their CFs, and there was a tendency to transmit more directional information for stimuli that had spectra above the CFs. The data were consistent with our hypothesis that at low sound levels ICC neurons are only directionally sensitive to stimuli with spectra near their CFs, although at 35 dB SPL this region of the cochleotopic map with high directional sensitivity was still 4 oct wide.

Previous studies have reported high-CF neurons sensitive to ITD of low-frequency stimuli (D’Angelo et al. 2005; Fitzpatrick et al. 2002; Kuwada et al. 2006); therefore our finding that high-CF ICC neurons are directionally sensitive to stimuli several octaves below CF was somewhat expected. However, our finding that low-CF ICC neurons are directionally sensitive to stimuli several octaves above CF was surprising (elaborated on in discussion) and deserves further scrutiny. We focused on the 11 ICC neurons with CFs below 1.5 kHz for which we collected narrowband azimuth tuning data. All of these low-CF neurons had high normalized MI in response to narrowband noise with center frequencies of 4 and/or 8 kHz (Fig. 5C). These 11 neurons were measured from five tetrodes; Fig. 6A shows multiunit FRAs at different tetrode depths for each of the five tetrodes. The depths of each of the 11 neurons are indicated by arrows to the left of the panels (single-unit data were recorded in the same session as the corresponding multiunit FRA). The locations of all low-CF neurons were squarely within the range of depths exhibiting V-shaped FRAs indicative of the ICC, and clearly in the low-frequency region of the cochleotopic map. Figure 6B shows FRAs and narrowband azimuth tuning curves for each of the 11 low-CF neurons. FRAs were heterogeneous and often complex. In some cases the 4- and 8-kHz passbands appeared to overlap with inhibitory subregions of the FRA (e.g., neurons 4, 6, and 7), whereas in others the passbands appeared to be outside of the receptive field (neurons 9 and 11). The response of a neuron to narrowband noise could not be predicted from its FRA. However, we note that each stimulus within the FRA was only repeated twice, so small deviations from spontaneous rate may be masked by measurement noise. Azimuth tuning curves of the low-CF neurons were also heterogeneous. Some neurons had firing rates that were exclusively facilitated above spontaneous rate (neurons 3, 9, 10, and 11), but most had firing rates that were facilitated at some azimuths and suppressed at others.

Dependence of azimuth tuning curve shape on stimulus spectrum.

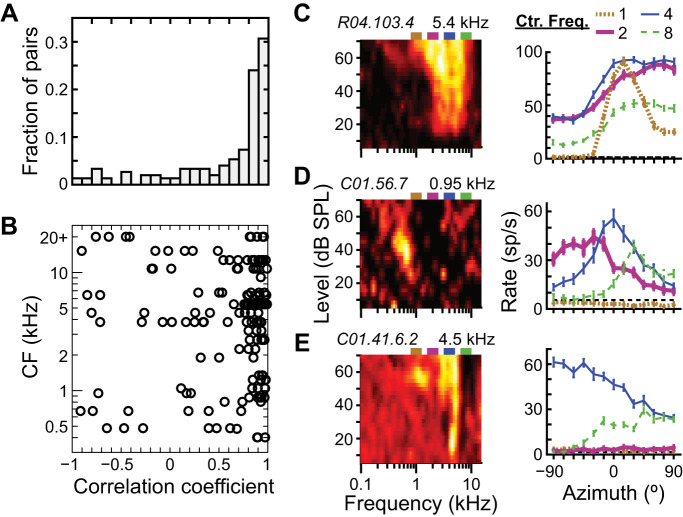
The ICC neuron in Fig. 5A had narrowband azimuth tuning curves at 70 dB SPL that were all similar in shape across different center frequencies. Specifically, the Pearson’s correlation coefficients between tuning curves ranged from 0.83 to 0.97 across all possible pairs of center frequencies. Figure 7A shows a histogram of correlation coefficients of all within-neuron pairs of narrowband azimuth tuning curves at 70 dB SPL. We restricted our correlation analysis to those azimuth tuning curves that were directionally sensitive; data were only included for pairs of tuning curves for which both had MI_norm > 0.03. [This criterion MI_norm was chosen arbitrarily, but overall results were the same for a criterion value of 0.05. See Fig. 4H (both curves) and Fig. 8C (high-pass ITD-only curve) for examples of tuning curves just below (0.01) and just above (0.05) the criterion, respectively.] Although 55% of tuning curve pairs had correlation coefficients of 0.80 or more, implying similarly shaped tuning curves like those in Fig. 5A, 45% had correlation coefficients from −1 to 0.80, implying tuning curves with different shapes in response to stimuli with different spectra. Those neurons with pairs of tuning curves that had correlation coefficients < 0.80 were distributed across the cochleotopic map (Fig. 7B).

Fig. 7.

Dissimilar azimuth tuning curve shapes in response to different narrowband spectra. A: histogram of within-neuron correlation coefficients between azimuth tuning curves measured in response to 2 different narrowband center frequencies at 70 dB SPL. Data only included for pairs in which both tuning curves had normalized mutual information > 0.03 (N = 150 pairs from 44 neurons). B: correlation coefficients of tuning curve pairs vs. the characteristic frequency (CF) of the corresponding neuron. C–E: frequency-level response areas (FRAs; left) and azimuth tuning curves in response to each narrowband stimulus at 70 dB SPL (right) for 3 different central nucleus of inferior colliculus (ICC) neurons that have stimulus-dependent tuning curve shapes. Different center frequencies are indicated by azimuth tuning curves with different line type and color: 1 (dotted tan), 2 (thick magenta), 4 (thin blue), and 8 (dashed green) kHz.

Fig. 8.

Interaural time difference (ITD) and interaural level difference (ILD) sensitivity primarily shape azimuth tuning curves in response to low- and high-pass noise, respectively. A–C: frequency-level response areas FRAs; left) and azimuth tuning curves in response to low-pass (center) and high-pass (right) noise at 70 dB SPL for 3 different central nucleus of inferior colliculus (ICC) neurons with strong directional sensitivity to both stimuli. Curves with different line types and color indicate binaural cue condition in virtual acoustic space: ITD+ILD, ITD-only, ILD-only, and contralateral-ear-only (contra-only). Effect sizes of Wald tests for differences between the ITD+ILD curve and each of the other curves are listed on right, color-matched to each binaural cue condition. *Statistically significant differences (Wald tests with correction for multiple comparisons, P < 0.01). D: plots of the effect size between ITD-only and ITD+ILD curves vs. the effect size between ILD-only and ITD+ILD curves within the same neuron for low-pass (top; n = 20) and high-pass (bottom; n = 27) noise at 70 dB SPL. Small effect size indicates that tuning curves were similar. Data only included for ITD+ILD curves with normalized mutual information (MI_norm) > 0.03. Statistically significant differences between the ITD+ILD curve and either of the ITD-only or ILD-only curves indicated by circle color: neither different (black), only ILD-only different (red), only ITD-only different (cyan), both different (tan). Arrowhead data points indicate values beyond the axis. Dashed line is the unity line. E: MI_norm vs. characteristic frequency (CF) of each neuron for azimuth tuning curves in response to low-pass (top) and high-pass (bottom) noise, color-coded to display significant differences between binaural cue conditions. Same data as in Fig. 4, A and B, except without values of MI_norm < 0.03. F: plot of the effect size between ILD-only and ITD+ILD curves vs. the effect size between contralateral-ear-only and ITD+ILD curves within the same neuron for high-pass noise at 70 dB SPL (n = 27). Data only included for ITD+ILD curves with MI_norm > 0.03. Statistically significant difference between the ITD+ILD curve and contralateral-ear-only curve indicated by circle color: difference (black), no difference (magenta).

Figure 7, C–E, show examples of neurons with dissimilar azimuth tuning curves for different stimulus passbands: the neuron in Fig. 7C had azimuth tuning curves with a similar, contralaterally maximal, sigmoid shape for center frequencies of 2, 4, and 8 kHz (r = 0.96 to 0.98, all pairs of 2, 4, and 8 kHz) and a peaked shape at 15° for 1-kHz center frequency (r = 0.65 to 0.78, 1 kHz vs. others); that in Fig. 7D had approximately peaked azimuth tuning curves at −30°, 0°, and 30° for 2-, 4-, and 8-kHz center frequencies, respectively (r = −0.74 to 0.21, all pairs of 2, 4, and 8 kHz), and no directional sensitivity to the 1-kHz center frequency (MI_norm = 0); that in Fig. 7E had sigmoid-shaped azimuth tuning curves that were maximally excited for ipsilateral and contralateral azimuths for 4- and 8-kHz center frequencies, respectively (r = −0.80) and no response to 1- or 2-kHz center frequencies. Of the 44 neurons that had at least two narrowband azimuth tuning curves with MI_norm > 0.03, 28 (64%) had at least one tuning curve pair that was correlated <0.80. In other words, most ICC neurons showed evidence of dissimilarity in the shapes of their azimuth tuning curves for some stimuli.

ITD and ILD shape directional sensitivity to low- and high-pass noises, respectively.

We previously reported that directional sensitivity of low- and high-CF ICC neurons in response to broadband noise is dominated by ITD and ILD, respectively (Day et al. 2012; Day and Delgutte 2013). On the other hand, our results above show that low- and high-CF neurons can be directionally sensitive to either low- or high-pass stimuli or both, stimuli whose directional perception is thought to be respectively shaped by ITD and ILD. The question remains as to whether the directional sensitivity of an individual ICC neuron is shaped either by one binaural cue for any stimulus (low or high frequency) or by different binaural cues for different stimuli. We addressed this by measuring azimuth tuning curves to low- and high-pass stimuli under three incongruent binaural cue conditions: ITD-only (with ILD fixed to that at 0°), ILD-only (with ITD fixed to that at 0°), and contralateral-ear-only (or “contra-only,” to disambiguate between binaural and monaural directional sensitivity). These data were compared to those measured under the congruent binaural cue condition, ITD+ILD, where both ITD and ILD varied naturally with azimuth (i.e., the condition for data in Fig. 4).

Few ICC neurons in our sample were strongly directionally sensitive to both low- and high-pass noises at 70 dB SPL (Fig. 4D, top right data points); Fig. 8, A–C, show data from three neurons that were. Figure 8A shows data from a high-CF neuron 1) whose low-pass ITD+ILD tuning curve was significantly different from the ILD-only and contra-only but not ITD-only tuning curves (Wald tests with correction for multiple comparisons, P < 0.01) and 2) whose high-pass ITD+ILD tuning curve was significantly different from the ITD-only and contra-only but not ILD-only tuning curves. This indicates that the neuron’s directional sensitivity was determined by sensitivity to ITD and ILD for low- and high-pass noises, respectively. The effect size of the statistical test for significant difference between tuning curves is indicated to the right of each incongruent-cue tuning curve. A small effect size for this statistical test indicates that the ITD+ILD tuning curve was similar to the incongruent-cue tuning curve, or, in other words, the cue that was allowed to vary with azimuth in the incongruent-cue condition was sufficient to reproduce the azimuth tuning under the ITD+ILD condition. Figure 8B shows data from a low-CF neuron whose spectrum-specific pattern of binaural cue dominance mimicked that in Fig. 8A. [However, for this neuron the low-pass ITD+ILD tuning curve was also significantly different from the ITD-only tuning curve because of a single small but statistically significant difference between firing rates at −60° (P = 6 × 10⁻⁵)]. Figure 8C shows a different spectrum-specific pattern of binaural cue dominance. This high-CF neuron had both low- and high-pass ITD+ILD tuning curves that were significantly different from ITD-only, ILD-only, and contra-only tuning curves. The ITD+ILD tuning curve overlapped the ITD-only and ILD-only tuning curves for low- and high-pass stimuli, respectively, only for ipsilateral but not contralateral directions. This indicates that the neuron’s contralateral directional sensitivity was determined by the combination of ITD and ILD cues for both low- and high-pass stimuli but with different relative weighting of the two cues in the two frequency bands.

We restricted our analysis of binaural cue dominance to directionally sensitive ITD+ILD tuning curves (MI_norm > 0.03). Again, overall results did not change if a higher criterion MI_norm was used. In general, low-pass ITD+ILD tuning curves were more similar to ITD-only than ILD-only tuning curves, whereas high-pass ITD+ILD tuning curves were more similar to ILD-only than ITD-only tuning curves (Fig. 8D). Of the 20 directionally sensitive low-pass ITD+ILD tuning curves, 12 were not significantly different from their ITD-only tuning curves; the rest had relatively small but significant differences. Together, these indicate dominance of ITD in shaping low-pass azimuth tuning. Conversely, of the 27 directionally sensitive high-pass ITD+ILD tuning curves, 22 were not significantly different from their ILD-only tuning curves; again, the rest had relatively small but significant differences. Together, these indicate dominance of ILD in shaping azimuth tuning. Figure 8E shows the directional information transmitted by neurons in the ITD+ILD condition versus their CF, the same data as in Fig. 4, A and B, except limited to directionally sensitive neurons and color-coded to indicate significant difference from the ITD-only and/or ILD-only tuning curves. High-CF neurons that transmitted relatively high directional information about low-pass noise did so mostly because of their sensitivity to ITD (Fig. 8E, top). Conversely, low-CF neurons that transmitted relatively high directional information about high-pass noise did so because of their sensitivity to ILD (Fig. 8E, bottom). Our data therefore indicate that directional sensitivity of ICC neurons is driven by different binaural cues for low- and high-pass stimuli, even in the same neuron.

We included the contralateral-ear-only condition to disambiguate binaural versus monaural sensitivity. Since the sound level in each ear changes with the azimuth of the source, neurons that are only sensitive to the sound level in one ear may have firing rates that modulate with azimuth due to purely monaural sensitivity. Truly binaural neurons should have different ITD+ILD and contra-only tuning curves. Of the 27 directionally sensitive high-pass ITD+ILD tuning curves, 23 (85%) were significantly different from their corresponding contra-only tuning curves (Fig. 8F), indicating that most directional sensitivity to the high-pass stimulus was due to binaural interaction. Over all 42 neurons whose low- and high-pass azimuth tuning curves were measured, only 6 (14%) had contra-only tuning curves that were not significantly different from either their low- or high-pass ITD+ILD tuning curves, i.e., no evidence of binaural sensitivity for either stimulus. None of these six putative monaural neurons was directionally sensitive to the stimuli (MI_norm < 0.02), except for one (MI_norm = 0.23 for high-pass stimulus).

Performance of maximum-likelihood decoder is consistent with the duplex theory of sound localization.

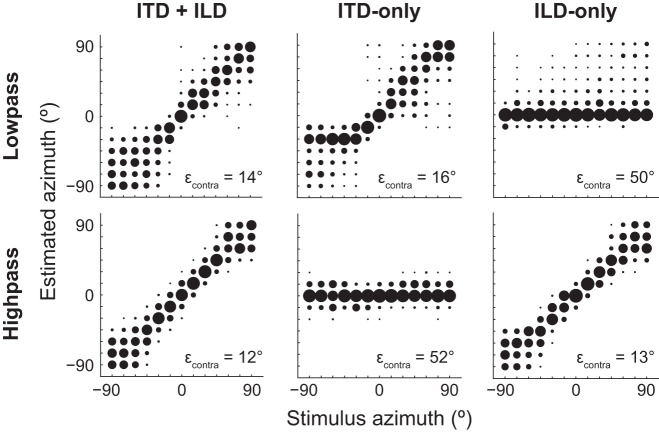
Psychophysical studies using independent manipulation of binaural cues in virtual acoustic space have found that ITD and ILD, respectively, dominate human directional perception of low- and high-pass sound (Macpherson and Middlebrooks 2002; Wightman and Kistler 1992). Since low- and high-pass ITD+ILD tuning curves in our data set were most similar to ITD-only and ILD-only tuning curves, respectively, we predicted that the performance of a maximum-likelihood decoder of stimulus azimuth operating on the population neural response would exhibit the same spectrum-specific pattern of binaural cue dominance as that of human psychophysical data. Our decoder operated on the pattern of spike counts across the neural sample within a single stimulus trial and estimated stimulus azimuth as that with maximum likelihood for the observed population response. We trained the decoder on data from the ITD+ILD condition and then tested it on data from the same condition as well as the ITD-only and ILD-only conditions, separately for responses to low- and high-pass noise. For both low- and high-pass noises, the decoder accurately estimated contralateral azimuths when tested on data in the ITD+ILD condition, indicating that the number of neurons in our sample was sufficient to decode azimuth (Fig. 9, left). In the lower right corner of each panel of Fig. 9, we list the root mean square (RMS) localization error over all contralateral azimuths since output of the ICC on one side of the brain is necessary and sufficient to perceptually localize sources on the opposite side of space (Jenkins and Masterton 1982). The decoder estimated contralateral azimuths of high-pass noise with slightly greater accuracy than low-pass noise; it was unclear whether or not this difference was simply due to sample size.

Fig. 9.

Maximum-likelihood estimate of stimulus azimuth from the neural population response is consistent with duplex theory. In each panel the maximum-likelihood decoder was trained on population responses from the interaural time difference (ITD)+interaural level difference (ILD) condition to low-pass (top) and high-pass (bottom) noise at 70 dB SPL (n = 42 neurons). The decoder was tested on population responses to either low- or high-pass noise in the ITD+ILD (left), ITD-only (center), and ILD-only (right) conditions. Bubble diameter indicates fraction of estimated azimuths over 1,000 trials of each stimulus azimuth. Root mean square (RMS) localization error (ε_contra) over all contralateral azimuths (0° to 90°) indicated at bottom right of each plot. The decoder accurately estimated contralateral azimuths of low- and high-pass noise under ITD-only and ILD-only cue conditions, respectively.

For low-pass noise, the decoder accurately localized contralateral sources when tested on data in the ITD-only but not ILD-only conditions (Fig. 9, top). When tested on the ILD-only condition, azimuth was usually estimated as 0° for all stimulus azimuths, consistent with the ITD cue fixed to that at 0°. Conversely, for high-pass noise the decoder accurately localized sources when tested on data in the ILD-only but not ITD-only conditions (Fig. 9, bottom). When tested on the ITD-only condition, azimuth was usually estimated as 0° for all stimulus azimuths, this time consistent with the ILD cue fixed to that at 0°. For neither low- nor high-pass noises did the decoder localize as accurately in the incongruent-cue as in the congruent-cue condition. However, our decoder analysis indicates that the pattern of neural activity across our ICC sample 1) in response to low-pass noise was similar enough between ITD+ILD and ITD-only conditions to accurately decode azimuth from only ITD cues and 2) in response to high-pass noise was similar enough between ITD+ILD and ILD-only conditions to accurately decode azimuth from only ILD cues.

High-CF neurons sensitive to fine-structure ITD.

Neural sensitivity to ITD comes in two varieties, that of either the time-varying amplitude envelope or the fine structure of the cochlear-filtered acoustic waveform. Sensitivity to fine-structure ITD can be assessed by measuring ITD tuning curves separately for conditions where the left- and right-ear acoustic pressure waveforms are either the same or inverted (Joris 2003). When left- and right-ear polarities switch from same to opposite the acoustic fine structure is inverted between the two ears while the envelope remains the same. Therefore, neurons that are specifically sensitive to envelope ITD have identical same- and opposite-polarity ITD tuning curves; differences between the two indicate additional or exclusive sensitivity to fine-structure ITD. In response to low-level, broadband noise, high-CF ICC neurons are only sensitive to envelope ITD (Devore and Delgutte 2010; Joris 2003). Whether high-CF ICC neurons can be sensitive to fine-structure ITD for stimuli other than broadband noise is unknown.

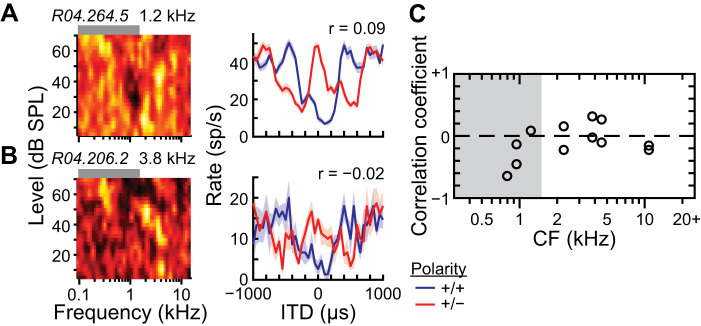
We measured ITD tuning curves to low-pass noise at 70 dB SPL under same- and opposite-polarity conditions for a subset of ICC neurons. Figure 10, A and B, show data from low- and high-CF neurons, respectively, where the peaks and troughs were flipped between same- and opposite-polarity ITD tuning curves as expected from partial sensitivity to fine-structure ITD. We restricted our analysis of ITD tuning to those neurons within the subset whose firing rates were modulated by changes in the ITD of low-pass noise (Kruskal–Wallis test, P < 0.01). Of the 12 neurons that were ITD sensitive to low-pass noise, all had significant differences between same- and opposite-polarity ITD tuning curves (Wald tests with correction for multiple comparisons, P < 0.05), indicating some sensitivity to fine-structure ITD, and had CFs between 0.8 and 11 kHz. The degree of similarity of same- and opposite-polarity ITD tuning curves can be captured by the Pearson’s correlation coefficient: pure envelope and pure fine-structure ITD sensitivities yield coefficients near +1 and −1, respectively, and coefficients between these values indicate sensitivity to both. For example, the ITD tuning curves in Fig. 10, A and B, had coefficients near zero, indicating sensitivity to both types of ITD. Correlation coefficients in our sample (including high-CF neurons) were between −0.64 and 0.31, indicating sensitivity to both fine-structure and envelope ITD of low-pass noise (Fig. 10C).

Fig. 10.

Sensitivity of high-characteristic frequency (CF) central nucleus of inferior colliculus (ICC) neurons to fine-structure interaural time difference (ITD) of low-pass noise. A and B: frequency-level response areas (FRAs; left) and ITD tuning curves in response to low-pass noise at 70 dB SPL (right; mean ± SE) for 2 different ICC neurons. Polarity of the left and right acoustic waveforms during measurement of ITD tuning indicated by different colored curves: same polarity (blue), opposite polarity (red). Correlation coefficient (r) between same- and opposite-polarity ITD tuning curves indicated at top right of each plot. C: correlation between same- and opposite-polarity ITD tuning curves vs. CF of each neuron (n = 12). Data only included for neurons with significant same-polarity ITD tuning (Kruskal–Wallis test, P < 0.01). Dashed line indicates zero correlation.

The two neurons in Fig. 10, A and B, had firing rates that were suppressed at zero ITD compared with the rates at large ITDs; at large ITDs the same- and opposite-polarity curves converged, indicating that the left- and right-ear signals were largely uncorrelated with each other. Firing rate suppression suggests a coincidence mechanism based on the interaction of excitatory and inhibitory inputs from the two ears, e.g., coincident excitation and inhibition leads to a smaller firing rate than that for uncorrelated excitation and inhibition. Alternatively, firing rates facilitated near zero ITD compared with those at large ITDs suggest a coincidence mechanism based on the interaction of excitatory inputs from both ears. In our small sample of neurons sensitive to ITD of low-pass noise, we found equal numbers of neurons exhibiting firing rate facilitation and suppression, and examples of each were found for CFs below and above 1.5 kHz (data not shown).

DISCUSSION

We found that at a sound level of 70 dB SPL ICC neurons across the cochleotopic map transmitted information in their firing rates about the direction of both low- and high-pass stimuli. At 35 and 70 dB SPL, neurons transmitted directional information about narrowband noise with center frequencies within approximately ±2 and ±4 oct about their CFs, respectively, consistent with frequency tuning being typically narrower at 35 dB SPL and broader at 70 dB SPL (Ehret and Merzenich 1988; Palmer et al. 2013). The binaural cues that shaped directional sensitivity for low- and high-pass stimuli were not neuron specific but stimulus specific: ITD and ILD, respectively, shaped directional sensitivity for low- and high-pass stimuli regardless of whether the neuron had a low or high CF. Furthermore, the directional sensitivity of high-CF neurons to low-pass stimuli was at least partially due to sensitivity to fine-structure ITD as opposed to strictly envelope ITD. Using a maximum-likelihood decoder on the neural population response to estimate sound source azimuth, we found that the firing rates of neurons to independently varied ITD and ILD cues were necessary and sufficient to accurately estimate the azimuth of low- and high-pass stimuli, respectively, consistent with the “duplex” psychophysical theory of sound localization (Macpherson and Middlebrooks 2002; Wightman and Kistler 1992). Finally, we found that most ICC neurons had azimuth tuning curve shapes that were not consistently similar for different narrowband stimulus spectra.

Directional sensitivity to low- and high-frequency stimuli.

It has long been known that neurons within the ICC are sensitive to sound source azimuth (e.g., Semple et al. 1983; Sterbing et al. 2003) and specifically ITD and ILD (e.g., Geisler et al. 1969; Rose et al. 1966). Stimuli used to measure azimuth, ITD, or ILD tuning curves in the ICC have traditionally been pure tones at the CF of the neuron or broadband noise. The same is true for measurements made in the primary binaural nuclei of the auditory pathway, the medial and lateral superior olives (MSO and LSO, respectively) (e.g., Boudreau and Tsuchitani 1968; Bremen and Joris 2013; Goldberg and Brown 1969; Tollin and Yin 2002a), as well as auditory thalamus and cortex (e.g., Clarey et al. 1995; Middlebrooks and Pettigrew 1981; Phillips and Irvine 1981). Neither pure tones at CF nor broadband noise reveals the ability of neurons to transmit directional information about stimuli with spectra far from the CF. Some studies additionally measured ITD, or sometimes ILD, tuning curves in response to tones with frequencies other than the CF, but these frequencies were often within 1 or 2 oct of the CF and restricted to either ITD- or ILD-dominated ranges, i.e., low frequencies (≤2 kHz) for low-CF neurons and high frequencies (>4 kHz) for high-CF neurons (Day and Semple 2011; Irvine and Gago 1990; Kitzes 2008; Yin and Chan 1990; Yin and Kuwada 1983). Delgutte et al. (1995) measured azimuth tuning curves of ICC neurons in response to high-pass noise (2–35 kHz) but only reported data from high-CF neurons (≥2 kHz). Chan et al. (1987) measured ITD tuning curves of ICC neurons to noise stimuli with different band-pass spectra up to a maximum frequency of 4 kHz but only reported data from low-CF neurons (<2.5 kHz). To the best of our knowledge, the only studies that have reported binaural sensitivity to stimuli with spectra far from CF have been by Kuwada et al.; they found high-CF neurons within the dorsal nucleus of the lateral lemniscus and the ICC that were sensitive to the ITD of low-frequency tones, indicating binaural sensitivity in the frequency tuning tail region (D’Angelo et al. 2005; Fitzpatrick et al. 2002; Kuwada et al. 2006). Our findings in the present study provide both a confirmation and an extension of the work by Kuwada et al. We not only find ITD sensitivity to low-frequency stimuli of high-CF neurons but, using virtual acoustic space, show that under natural binaural conditions (i.e., ITD+ILD) this ITD sensitivity allows high-CF ICC neurons to transmit amounts of directional information about low-frequency stimuli similar to those they transmit about high-frequency stimuli using ILD sensitivity. On the other hand, our finding that low-CF neurons can transmit directional information about high-pass stimuli appears to be novel. That this has not been previously reported is perhaps not surprising given that stimuli with energy several octaves away from the CF of a neuron are either not expected to drive a neuron or must be presented at high intensities to evoke a response. However, the sound level we used to evoke off-CF responses (70 dB SPL) was not abnormally loud but that of normal human conversation (Olsen 1998).

We found that directional information about narrowband noise stimuli at 70 dB SPL was transmitted by ICC neurons across the cochleotopic map (Fig. 5C), inconsistent with the hypothesis that frequency components of an auditory signal are only processed within matched frequency channels (or more accurately, “cochleotopic channels”) of the ICC (Schreiner and Langner 1997). Our finding was consistent with the well-known broadening of FRAs in most ICC neurons at high sound levels (Ehret and Merzenich 1988; Palmer et al. 2013). However, it is important to distinguish between frequency tuning to individual tones (i.e., the FRA) and frequency weighting within an auditory filter, where the simultaneous frequency components of a complex signal are differentially weighted by the neuron. At high sound levels, far-off-CF tones may evoke a response from a neuron, but the same frequency component may not contribute much weight to the response in the presence of simultaneous stimulus energy at components nearer to the CF. Several studies have reported that auditory filtering by ICC neurons (as well as auditory brain stem and AN fibers) in response to broadband stimuli is relatively narrow about the CF and level independent (Koka and Tollin 2014; Mc Laughlin et al. 2007; Young and Calhoun 2005; Yu and Young 2013). Signal processing in the ICC may be accurately modeled by level-independent, overlapping band-pass filters in response to broadband sounds, but in response to band-limited sounds neurons stimulated in their upper- or lower-frequency “tails” may contribute as much directional information about a sound source as neurons with CFs centered on the stimulus (Fig. 5D).

Previous studies independently manipulating ITD and ILD in virtual acoustic space have reported that directional sensitivity of low- and high-CF binaural neurons is respectively dominated by sensitivity to ITD and ILD (Day et al. 2012; Delgutte et al. 1995; Slee and Young 2011; Tollin and Yin 2002b). These studies used a broadband noise stimulus with sound level fixed at 20 dB re: threshold, likely positioning the stimulus within the “tip” region of each neuron’s FRA where frequency tuning is relatively narrow. Whether the pairing of low- and high-CF neurons with ITD and ILD dominance, respectively, remains at high sound levels (such as 70 dB SPL) in response to broadband noise is unknown. In the present study, we found that the dominance of either binaural cue in the directional sensitivity of a neuron was not specific to the CF of the neuron but the spectrum of the stimulus—both low- and high-CF neurons could exhibit dominance to ITD or ILD cues. Our results raise the interesting possibility that the MSO and LSO, being major, binaurally sensitive inputs to the ICC, could potentially exhibit the same stimulus-frequency-dependent dominance of binaural cues at high sound levels, e.g., low-CF MSO neurons dominated by ILD cues in high-frequency stimuli or high-CF LSO neurons dominated by ITD cues in low-frequency stimuli. Alternatively, MSO and LSO neurons could retain specific sensitivities to ITD and ILD, respectively, and the stimulus-dependent dominance of binaural cues seen in the ICC could potentially result from a convergence of MSO and LSO inputs onto the same neuron.

It is well known that high-CF neurons (starting at the level of the auditory nerve) respond to high-intensity, low-frequency tones in the tails of their FRAs (Kiang and Moxon 1974). This responsiveness follows from cochlear mechanics: the traveling wave along the basilar membrane in response to a low-frequency tone must pass through the basal, high-CF region before maximally displacing the apical, low-CF region. At high sound levels, the displacement of the basilar membrane in the basal, high-CF region is large enough to trigger action potentials in corresponding high-CF AN fibers. These action potentials are phase-locked to low-frequency tones (Joris et al. 1994; Kiang and Moxon 1974) or, in the case of the low-pass noise stimulus of the present study, temporally locked to specific spectrotemporal features in the noise waveform. Phase-locking in the frequency tuning tails of high-CF anteroventral cochlear nucleus (AVCN) neurons, which receive input from AN fibers, has been shown to be even greater than that in the AN (Joris et al. 1994). ITD-sensitive responses then arise in the MSO via coincidence detection of phase-locked inputs from the left and right AVCN. Therefore, ITD sensitivity of high-CF ICC neurons in response to low-pass noise can likely be explained simply by the phase-locking of high-CF AN fibers to low-frequency stimuli. That ITD and not ILD dominates the directional sensitivity of high-CF ICC neurons to low-pass noise is likely due to the small range of free-field ILDs available at low frequencies (Fig. 2). Following this logic, we predict that firing rates in response to low-frequency stimuli of high-CF neurons in the MSO, and perhaps LSO, are also directionally sensitive and shaped by ITD cues. For example, Fig. 10B shows the ITD tuning curve of a high-CF neuron with “trough-type” characteristics suggestive of LSO origin. In this neuron, ITDs near zero led to a suppression of firing rate (same-polarity curve), which would occur with the coincidence of an excitatory input from one ear and an inhibitory input from the other, as in the LSO.

Our finding that low-CF ICC neurons can be directionally sensitive to high-frequency stimuli at moderately high sound levels is surprising because such sensitivity does not follow from responses at the periphery. For high-frequency tones, the traveling wave reaches its maximal displacement in the basal, high-CF region of the basilar membrane, then sharply decays before reaching the apical, low-CF region. Low-CF AN fibers respond to high-intensity tones only up to ∼1 oct above CF (Temchin et al. 2008) and cannot account for responses 4 oct above CF, such as those in Fig. 5, C and D. Sensitivity of low-CF ICC neurons to high-frequency sounds may suggest inputs from high-CF neurons onto low-CF neurons. However, anatomical studies consistently show that projections to the ICC are matched in CF and intracollicular projections largely remain within the same lamina (see for review Oliver 2005). Neurons at single cochleotopic locations in the dorsal and ventral cochlear nuclei have been shown to project to the ICC over an area encompassing several adjacent laminae (Malmierca et al. 2005), but these would not account for sensitivity to stimuli 4 oct higher than the CF.

It is important to note that our finding that low-CF ICC neurons respond to moderately-high-intensity, high-frequency noise stimuli is surprising not because other studies have used similar stimuli and reached an opposite conclusion but because we found responsiveness where it was not expected and, to the best of our knowledge, has not been previously examined. In light of our unexpected finding, we offer two other possible explanations. First, our low-CF neurons may have come from the shell region surrounding the ICC, where neurons have broad, irregular frequency tuning (Aitkin et al. 1972). Figure 6A shows that our low-CF neurons were squarely within the cochleotopic region of the IC, but we do not know how close they were to the medial, lateral, rostral, or caudal borders of the ICC. Several pieces of evidence make this explanation less likely: 1) low-CF neurons were recorded along multiple tetrode tracks in both rabbits, decreasing the likelihood that the low-CF region of ICC was missed every time, and 2) all of the low-CF neurons encountered responded to both narrowband noises centered at 4 and 8 kHz (Fig. 6B), and at the very least some of these were likely within the ICC. Second, responses to high-frequency noise stimuli may have been driven by low-frequency distortion produced naturally within the cochlea. Distortion products occur in response to stimuli with energy at multiple frequency components and can be indirectly measured by otoacoustic emissions. In a recent study, we measured the distortion product otoacoustic emissions (DPOAEs) of Dutch Belted rabbits, including the two in the present study, in response to two primary tones, f₁ and f₂, with a frequency ratio of f₂/f₁ = 1.2 (Haragopal et al. 2020). At high levels of the primary tones, the 2f₁ − f₂ and 3f₁ − 2f₂ DPOAEs were prominent in both rabbits of the present study (these frequencies are always lower than that of the primary tones; see Fig. 1C of Haragopal et al. 2020). Although we used a fixed f₂/f₁ of 1.2, distortion products may be maximum within a range of f₂/f₁ from 1.1 to 1.4 for different primary frequencies (Allen and Fahey 1993; Whitehead et al. 1992). Taking this range of f₂/f₁, we estimated that the lowest maximum distortion product possible between frequency components within our narrowband noise stimulus centered at 8 kHz was 1.3 and 3.8 kHz for the 3f₁ − 2f₂ and 2f₁ − f₂ distortion products, respectively. Therefore, low-frequency distortion products from our high-frequency noise stimuli could potentially overlap with the FRAs of low-CF neurons.

Implications for decoding sound source direction.

At some point downstream in the central auditory pathway, sound source direction must be decoded from the responses of auditory neurons upstream. A major issue that must be overcome in any decoding scheme is that the spiking activity of upstream neurons (say in the ICC) varies not only with the parameter of interest but also with other parameters such as intensity and spectrotemporal modulation (Benichoux et al. 2017). The neural computation for decoding direction may be more efficient if the azimuth tuning curve of each neuron is consistent across changes in other stimulus parameters. For example, we previously found that the shapes of broadband-noise-derived azimuth tuning curves of individual ICC neurons were correlated across different sound levels; a maximum-likelihood decoder of direction could be made more efficient by exploiting tuning similarity across level (Day and Delgutte 2016). In the present study, we found that most ICC neurons had azimuth tuning curves that were inconsistent in shape for some narrowband stimulus spectra. Therefore, the same simplifying computation we used to control for tuning curve differences due to sound level cannot be used for differences due to sound spectra. Our results indicate that direction-decoding computations in the brain must compensate for stimulus-dependent variation in the shapes of azimuth tuning curves of individual neurons.

GRANTS

This research was supported by the National Institute on Deafness and Other Communication Disorders of the National Institutes of Health under award numbers R03 DC-013388 and R15 DC-017616 (M.L.D.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.L.D. conceived and designed research; R.D., G.A.W., T.R.W., N.C.S., and M.L.D. performed experiments; R.D., G.A.W., T.R.W., N.C.S., and M.L.D. analyzed data; M.L.D. interpreted results of experiments; M.L.D. prepared figures; M.L.D. drafted manuscript; M.L.D. edited and revised manuscript; R.D., K.E.H., G.A.W., T.R.W., N.C.S., and M.L.D. approved final version of manuscript.