To the Editor:
Identifying optimal testing strategies for severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in long-term care facilities (LTCFs) is a public health priority.1 Asymptomatic surveillance is necessary to detect asymptomatic and presymptomatic carriers to prevent widespread coronavirus disease 2019 (COVID-19) outbreaks in LTCFs. In the context of test availability, costs, and acceptability constraints, the trade-offs between testing intensity and potential benefits are currently unknown for LTCFs.1 Unique features of COVID-19 transmission dynamics within LTCFs and communities need to be considered when implementing an optimal surveillance strategy. Using a dynamic model of COVID-19 transmission in a LTCF setting, we estimated the impact of several SARS-CoV-2 surveillance strategies varying in test frequency and sampling on the time to diagnosis and the cumulative number of cases at first diagnosis.
Methods
We developed an agent-based model2 of SARS-CoV-2 transmission among (n = 280) residents and staff members of a hypothetical LTCF (Appendix, Supplementary Methods). Briefly, 1 infectious case is imported into the LTCF during the first 2 weeks of simulation, with all individuals susceptible at baseline. Individual status is tracked daily until a first case is diagnosed. Individuals can acquire SARS-CoV-2 from the community at a daily probability matching the definition of moderate community transmission (50 cases/100,000 people/14 days).3 The daily probability of being infected inside the LTCF varies with the number of infectious individuals, the basic reproductive number (R 0 = 3),4 and the duration of infectiousness (D I = 7 days).5 Individuals test positive for SARS-CoV-2 for 14 days postinfection, with a test sensitivity of 0.9. Seven strategies (S) were modeled with 1000 iterations each, testing: S1. 100% of individuals every 14 days; S2. 50% every 7 days; S3. 100% every 7 days; S4. 50% twice a week; S5. 20% every weekday; S6. 14% every day; and S7. 100% twice a week.
Strategies were evaluated by the number of days to first diagnosis, the cumulative number of infected cases at the time of first diagnosis, and the number of tests used. We conducted sensitivity analyses accounting for uncertainty around model parameter values (Appendix, Supplementary Methods).
Results
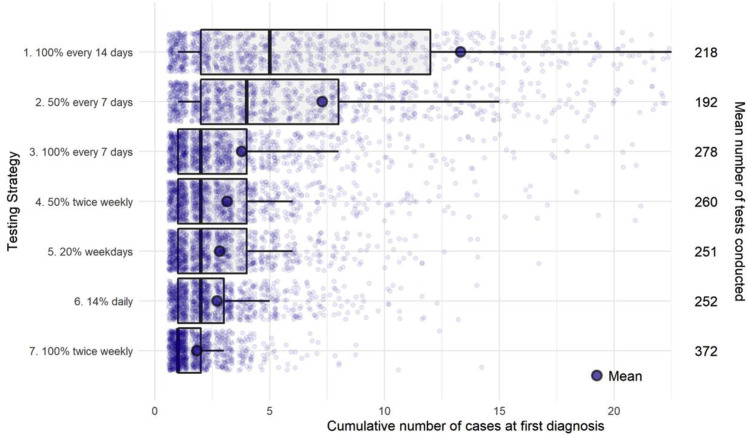
Table 1 reports the delay to first diagnosis and cumulative cases by testing strategy. S1 was less optimal than S2 with longer delay to diagnosis (7.9 vs 6.6 days), more cases at first diagnosis (13.3 vs 7.3), and more tests to detect the first case (218 vs 192). Comparing S3 to S2, delay to diagnosis was shortened to 4.0 days and the number of cases decreased to 3.8, using 86 extra tests (25/case averted). S3 to S6 had similar results, with a slight benefit in spreading the tests over 7 days. S7 produced the most favorable clinical outcomes (delay = 1.7 days, cases = 1.8), yet required additional tests (33/case averted compared with S2, 47/case averted compared with S3).
Table 1.
Delay to First Diagnosis, Number of Cumulative Cases at First Diagnosis, and Number of Tests Conducted to Diagnose a First Case, by Testing Strategy, in the Context of a Simulation of a SARS-CoV-2 Outbreak in a LTCF
| Testing Strategy∗ | Delay to First Diagnosis, Mean d (Median, IQR) | Cumulative Cases at First Diagnosis, Mean (Median, IQR) | Number of Tests Conducted, Mean |
|---|---|---|---|
| 1. Test 100% every 14 d | 7.9 (7.0, 8.0) | 13.3 (5.0, 9.0) | 218 |
| 2. Test 50% every 7 d | 6.6 (6.0, 6.0) | 7.3 (4.0, 5.0) | 192 |
| 3. Test 100% every 7 d | 4.0 (3.5, 4.0) | 3.8 (2.0, 3.0) | 278 |
| 4. Test 50% twice a wk | 3.5 (3.0, 4.0) | 3.2 (2.0, 3.0) | 260 |
| 5. Test 20% on weekdays | 3.3 (3.0, 4.0) | 2.8 (2.0, 3.0) | 251 |
| 6. Test 14% daily | 3.3 (3.0, 4.0) | 2.7 (2.0, 2.0) | 252 |
| 7. Test 100% twice a wk | 1.7 (1.0, 1.0) | 1.8 (1.0, 1.0) | 372 |
All individuals are susceptible at baseline, 1 infectious case is imported randomly in the first 2 weeks of simulation, and the model tracks individual disease status daily until a first case is diagnosed. Results for 1000 iterations.
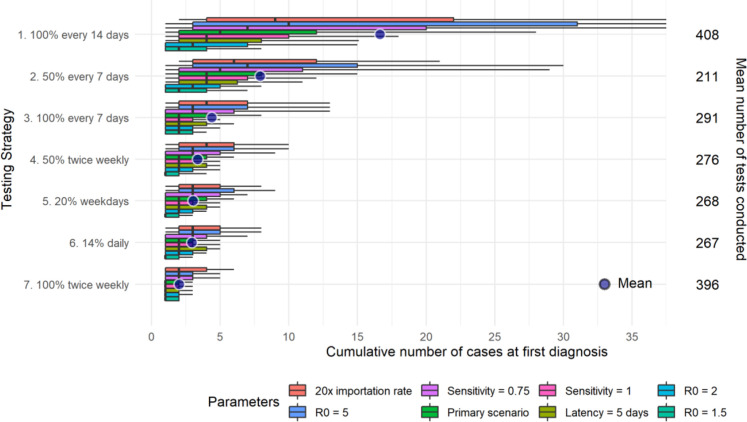
Results of the sensitivity analyses were concordant with our primary scenarios. Incremental benefits associated with more frequent testing increased with the high community importation rate, high infectiousness, and low-test sensitivity scenarios (Appendix, Supplementary Results).
Discussion
Our simulation of 7 SARS-Cov-2 testing strategies varying frequency and sampling suggests that the optimal strategy is informed by the level of community transmission and the basic reproduction number within the LTCF. We recommend testing at least 50% of people weekly in the context of a low probability of infectiousness (R 0 < 2), and 100% of people weekly when the probability of transmission is higher (R 0 = 3 and community importation rate = 3.6 ∗ 10−5). Testing 100% of people twice a week may be beneficial when the risk is very high (R 0 = 5 or importation rate = 7.14 ∗ 10−4). Once a case is diagnosed, more comprehensive testing should follow.6
R 0 may not be directly quantifiable as it depends on modifiable (handwashing, mask wearing, physical distancing) and nonmodifiable factors (occupancy, physical crowding). As modifiable factors are less easily intervenable in LTCFs,7 more frequent testing may guard against widespread transmission and allow less stringent confinement measures. The differences in number of cases averted between scenarios are clinically significant considering the high fatality rates observed in LTCFs and the challenges to control outbreaks in closed environments.1 Substantial incremental benefits were associated with increased testing, and the current development of rapid low-cost viral tests8 suggests that frequent testing could be cost-effective.
Our recommendations support emerging modeling evidence that testing frequency has a stronger effect on SARS-Cov-2 transmission than test sensitivity9 , 10 and provides further insights in the context of LTCFs. Nevertheless, our simulation begins when a first case is introduced, and a conventional cost-effectiveness analysis should acknowledge that when community transmission is low, more tests will need to be conducted before a first diagnosis.
Conclusions and Implications
With low transmission rates, weekly testing of 50% of residents and staff should be implemented as a minimal surveillance strategy to prevent widespread outbreaks. Weekly testing of 100% of residents and staff provides added benefit in higher infectiousness contexts. These results can be instrumental in developing timely surveillance of SARS-CoV-2 transmission among a population severely impacted by the COVID-19 pandemic.
Acknowledgments
C.L.D. received a PhD trainee fellowship from the Canadian Network on Hepatitis C. The Canadian Network on Hepatitis C is funded by a joint initiative of the Canadian Institutes of Health Research (NHC-142832) and the Public Health Agency of Canada. C.L.D. also received a doctoral training award from the Fond de Recherche du Québec – Santé. S.S. received post-doctoral fellowships from the Fond de Recherche du Québec – Santé and the Canadian Institutes of Health Research. Q.D.N. received a doctoral training award from the Fond de Recherche du Québec – Santé and from the Canadian Institutes of Health Research.
Footnotes
The authors have no conflict of interest to disclose.
This research did not receive any funding from agencies in the public, commercial, or not-for-profit sectors.
Supplementary Methods
Detailed model structure
We developed a stochastic, agent-based model of SARS-CoV-2 transmission among (n = 280) residents and staff members of a hypothetical LTCF. Four disease states are modeled: (1) susceptible to infection; (2) infected – latent phase; (3) infected – infectious phase; and (4) post-infection (recovered or deceased). All individuals are susceptible at baseline, and 1 infectious case of SARS-CoV-2 is randomly imported into the LTCF as an exogeneous shock during the first 2 weeks of simulation to seed the outbreak. Individuals are assumed to mix randomly and can acquire SARS-CoV-2 at a daily probability of p(t) = p out(t) + p ins(t), with p out(t) the probability of acquisition from an individual outside of the LTCF (eg, through visitors or staff members in contact with the community), and p ins the probability of acquisition from an individual inside the LTCF. p ins(t) varies as a function of the number of infectious individuals at time t, the basic reproductive number within the LTCF R 0, and the duration of infectiousness D I. Following infection, individuals enter a latent phase of duration D L, followed by an infectious phase of duration D I, before transitioning to the postinfection phase. The model tracks individual disease status daily (with fixed time steps) until a first case is diagnosed. We assumed that individuals can test positive for SARS-CoV-2 up to 14 days after the day of infection, with sn the sensitivity of the reverse transcription polymerase chain reaction (RT-PCR) test. For each strategy, 1000 iterations were performed. Simulations were run using R version 4.0.0 (R Core Team, Vienna, Austria), and the code is available on https://github.com/quocdnguyen/test-strategy.
Sensitivity analyses
Since the probability of acquiring SARS-CoV-2 could vary among LTCFs we compared a range of R 0 values (1.5, 2, and 5) to reflect diverse transmission conditions. In addition, uncertainty subsists around the viral dynamics of SARS-CoV-2 and the sensitivity of viral tests. We, therefore, conducted secondary analyses using varying values for p out(t) (7.14 ∗ 10−4, 20 times moderate community transmission), R 0 (1.5, 2, and 5), D L (5 days), and sn (0.75 and 1.00).
Supplementary Results
Supplementary Fig. 1.
Distributions of cumulative cases at time of first diagnosis by testing strategy for the primary scenarios. The left vertical axis shows 1 of the 7 testing strategies. The horizontal axis (truncated) indicates the cumulative number of cases at first diagnosis for all simulations [boxplot of the distribution (0.1, 0.25, 0.5, 0.75, and 0.9 percentiles) and mean]. Each point represents the result for 1 iteration. The right vertical axis shows the average number of tests conducted to diagnose the first case.
Supplementary Fig. 2.
Distributions of cumulative cases at time of first diagnosis by testing strategy for the secondary scenarios (varying importation rate, R0, test sensitivity, and latency). The left vertical axis represents each 1 of the 7 testing strategies. The horizontal axis (truncated) indicates the cumulative number of cases at first diagnosis for all simulations [boxplots of the distribution (0.1, 0.25, 0.5, 0.75, and 0.9 percentiles) and mean]. The right vertical axis shows the average number of tests conducted to diagnose the first case. Each color displays a sensitivity analysis varying one parameter value from the primary scenario.
References
- 1.Pillemer K., Subramanian L., Hupert N. The Importance of long-term care populations in models of COVID-19. JAMA. 2020;324:25–26. doi: 10.1001/jama.2020.9540. [DOI] [PubMed] [Google Scholar]
- 2.Luke D.A., Stamatakis K.A. Systems science methods in public health: Dynamics, networks, and agents. Annu Rev Public Health. 2012;33:357–376. doi: 10.1146/annurev-publhealth-031210-101222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.US Department of Health Human Services Centers for Disease Control and Prevention . Centers for Disease Control and Prevention; Atlanta: 2020. CDC activities and initiatives supporting the COVID-19 response and the president's plan for opening America up again. [Google Scholar]
- 4.He W., Yi G.Y., Zhu Y. Estimation of the basic reproduction number, average incubation time, asymptomatic infection rate, and case fatality rate for COVID-19: Meta-analysis and sensitivity analysis. J Med Virol. 2020 doi: 10.1002/jmv.26041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bullard J., Dust K., Funk D. Predicting infectious SARS-CoV-2 from diagnostic samples. Clin Infect Dis. 2020 doi: 10.1093/cid/ciaa638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Centers for Disease Control and Prevention . Centers for Disease Control and Prevention; Atlanta: 2020. Testing guidelines for nursing homes. Interim SARS-CoV-2 testing guidelines for nursing home residents and healthcare personnel. [Google Scholar]
- 7.Dosa D., Jump R.L., LaPlante K., Gravenstein S. Long-term care facilities and the coronavirus epidemic: Practical guidelines for a population at highest risk. J Am Med Dir Assoc. 2020;21:569–571. doi: 10.1016/j.jamda.2020.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Guglielmi G. The explosion of new coronavirus tests that could help to end the pandemic. Nature. 2020;583:506–509. doi: 10.1038/d41586-020-02140-8. [DOI] [PubMed] [Google Scholar]
- 9.Paltiel A.D., Zheng A., Walensky R.P. Assessment of SARS-CoV-2 screening strategies to permit the safe reopening of college campuses in the United States. JAMA Netw Open. 2020;3 doi: 10.1001/jamanetworkopen.2020.16818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Larremore D.B., Wilder B., Lester E. Test sensitivity is secondary to frequency and turnaround time for COVID-19 surveillance. medRxiv. 2020 doi: 10.1126/sciadv.abd5393. [DOI] [PMC free article] [PubMed] [Google Scholar]