Nonlinear time series and principal component analyses: Potential diagnostic tools for COVID-19 auscultation

Highlights

• •Development of a potential diagnostic tool for COVID-19 auscultation.
• •Proposes cost-effective digital auscultation based on mathematical techniques.
• •Investigates spectral features of normal – vesicular and bronchial breath sounds.
• •Nonlinear time series and fractal analyses unwrap airflow dynamics in lungs.
• •The principal component analysis helps in classifying the lung sounds.

Abstract

The development of novel digital auscultation techniques has become highly significant in the context of the outburst of the pandemic COVID 19. The present work reports the spectral, nonlinear time series, fractal, and complexity analysis of vesicular (VB) and bronchial (BB) breath signals. The analysis is carried out with 37 breath sound signals. The spectral analysis brings out the signatures of VB and BB through the power spectral density plot and wavelet scalogram. The dynamics of airflow through the respiratory tract during VB and BB are investigated using the nonlinear time series and complexity analyses in terms of the phase portrait, fractal dimension, Hurst exponent, and sample entropy. The higher degree of chaoticity in BB relative to VB is unwrapped through the maximal Lyapunov exponent. The principal component analysis helps in classifying VB and BB sound signals through the feature extraction from the power spectral density data. The method proposed in the present work is simple, cost-effective, and sensitive, with a far-reaching potential of addressing and diagnosing the current issue of COVID 19 through lung auscultation.

1. Introduction

Our respiratory organ lung is the primary infection area for pandemic disease-causing viruses like coronavirus, influenza, and others due to its constant exposure to viruses, bacteria, chemicals, and particles in the atmosphere [1,2]. Disability-Adjusted Life Year (DALY) is a statistical term coined by the World Health Organization (WHO) such that one DALY is equivalent to one lost year of healthy life due to the burden of disease. The Global Burden of Disease Study published in 2017 reports that the DALYs per year from 1990 to 2017 due to chronic respiratory diseases lies between 97.2 to 112.3 million [3]. Among the thirty most common causes of death, five are respiratory-related diseases [4]. Therefore, proper monitoring, diagnosis, and treatment of respiratory-related diseases are crucial for the healthy being of humankind. Auscultation is the primary procedure employed by the physicians to investigate or diagnose the respiratory condition of a patient through the lung sounds [5]. The lung sounds at different positions contain information about lung conditions. The lung sounds are produced (1) by the friction caused by the turbulent flow of air through the airway walls in the respiratory tract, (2) while the air moves to a broader space from narrower during the respiration and (3) from the glottis [6]. The pathological condition of lungs gets reflected through the sound having some signature features, which helps in diagnosis [7].

Normal and adventitious breath sounds are the two classes of breath sounds [8]. Vesicular breath (VB) and Bronchial breath (BB) are the normal breath sounds. Wheezing, crackles, pleural rub, stridor, and rhonchi sounds are examples of adventitious breath sounds [9]. The adventitious breath sounds indicate lung problems such as infection, inflammation, obstruction, fluid in the lungs, asthma, and others. The normal breath sounds VB, and BB carries information about the ordinary working condition of the lungs. The VB sounds are soft non-musical low pitch sounds, which became softer during the expiration. In VB sounds, the duration of the inspiration is about three times longer than the expiration. The VB sounds can be auscultated from most areas of the lungs, especially from the bases and periphery. Unlike VB sounds, BB sounds are high pitched and louder, like tubular or hollow sounds. The duration of inspiration and expiration cycle in BB sounds are almost similar that are auscultated over the trachea [10], [11], [12]. The BB sounds are considered abnormal if they are auscultated over the periphery of the lungs. This abnormality arises due to the presence of consolidated tissue in the lung airway, which is caused by pneumonia and fibrosis [13]. Pneumonia and fibrosis due to the presence of consolidated tissue in the lung airway leads to the abnormal breath sound. Therefore, a study focussing on the signature characteristics of VB and BB sounds is necessary to diagnose and classify normal and abnormal lung sounds, especially in the case of a disease like COVID 19, affecting the lungs severely.

The conventional auscultation procedure using the stethoscopes for the diagnosing of respiratory-related diseases have inherent shortcoming like inter-listener variability. The electronic auscultation and automated classifications helps in preventing such shortcomings. Several computer-aided techniques like Fourier transform, wavelet transform, nonlinear time series analysis, principal component analysis, and others are used for the analysis of breath sounds [7,12,14]. The digital data of auscultation is a time-domain data, which is a superposition of various frequency components. Transformation of the signal from the time domain to the frequency domain, employing Fourier transform technique, gives information about the frequency components. The Fourier series decomposes the time domain signal as the superposition of various sine and cosine waves with different frequencies. The Fourier transform is an effective tool for breath sound analysis because of the distinct spectral characteristics of different breath sounds. The Fourier transform tells us only about the presence and magnitude of a particular frequency component, and it doesn't give information about the instant at which a particular frequency occurs. The temporal information of the occurrence and duration of a frequency component can be studied using the wavelet analysis. Wavelet analysis uses specific short duration wavelet functions called mother wavelets like Morse, Morlet, Haar, and others to bring out the temporal information of the frequency components. Wavelet analysis helps in studying the sudden frequency changes in conditions like crackles. Breath sounds are time-series data formed by the dynamics of airflow through the bronchial tubes and bronchioles, in the lungs and trachea, make the lung a dynamical system [7,15].

The dynamical systems in nature do not unveil all its dependent parameters. From most of the systems, we get only the change of one of the parameters with time as time-series data. Powerful nonlinear time series analysis can bring out the hidden information of the dynamical system. Nonlinear time series analysis finds applications in various fields such as signal processing, biomedical, weather forecasting, economics, and applied physics [16], [17], [18]. The phase portrait in the phase plane is the geometrical representation of the change in the state of the system with time. The nonlinear time series analysis could reconstruct the phase portrait of the system from the time series, utilizing the Method of delays by estimating the time lag, l, and embedding dimension, m. The time lag is the time separation between the adjacent uncorrelated points, while the embedding dimension is the number of dependent variables required to specify the system completely. Fractal dimension (D), Hurst exponent (H) and sample entropy (S) are the parameters that help to analyze the complexity of the time-series signals [19].

Fractal structures are omnipresent in this universe [20], [21], [22], [23]. Analyzing the fractal nature and quantifying its complexity by fractal dimension is an interdisciplinary field with wide applications. The study of self-affine nature and complexity gives the fractal behavior of a time series. Methods like walker divider, epsilon bracket, power spectrum, box-counting, and other methods gives an estimation of fractal dimension, among which the box-counting method is the simple and effective one [24]. Another critical term for classification of the complexity of a time series is the Hurst exponent. The value of H indicates the extent of correlation between the elements of a time series. For the signals with the value of H between 0 and 0.5, there is a low correlation between the adjacent values indicating its antipersistent nature. The low correlation of antipersistent signals suggests a very complex and random nature. When the value of H is close to 0.5, the signal is termed as Brownian time series, as it does not contain information about the future values, and when the H value is between 0.5 and 1 the signal is called persistent time series as there is a short term positive correlation among the data. Hence, there is a possibility of prediction in persistent time-series signals [25]. Sample entropy is another statistical tool based on information theory that measures the uncertainty in a time series. It can quantify the randomness of a time series without the previous information about its source. Sample entropy, which is a measure of the speed at which new information is produced in time-series data, is extensively used in medical and experimental signal analysis [19,26].

One of the important objectives of the present study is the computer-aided automated classification of VB and BB sounds. Principal component analysis (PCA) is an effective tool for grouping data sets with similar characteristics. PCA identifies the directions called principal components, along which there is a maximum variation in dataset, and neglecting the unwanted dimensionalities. PCA could compress a data set by extracting only the most crucial information from it. Groups with almost the same properties have almost the same principal component values, which helps in grouping similar datasets. The present work attempts a detailed analysis of VB and BB sound signals through spectral, nonlinear time series and complexity analysis to extend to COVID 19 auscultation. Principle component analysis is also employed to separate the VB and BB sound signals for computer-aided automated detection [27].

2. Materials and methods

Nowadays, digitization and automation of the medical field employing computer-aided techniques have made the diagnosis accurate and quick. In the present work, digital audio signals of 37 respiratory cycles (one inspiration and expiration) of vesicular (18) and bronchial (19) breath sounds from various databases are analyzed by spectral, nonlinear time series, and complexity analyses [28], [29], [30], [31], [32]. The signals during inspiration and expiration are also investigated.

2.1. Spectral analysis

Lung sound signals are the variation of sound intensity in the time domain. Fourier transform brings out the spectral information hidden in the time domain signals. Simple and effective Fast Fourier transform (FFT) algorithm converts the time domain signal into the frequency domain. The Fourier transformed complex signal X(f) of time-domain signal ‘x(t)’ is defined as [7],

$$X\left(f\right)=\int x\left(t\right)e^{i2\pi ft}dt,$$ (1)

where f and t are the frequency and time, respectively. The real-valued power spectral density (PSD) function, which gives the distribution of power of the signal over the frequency range , can be computed from the FFT signal using the equation,

$$\mathit{PSD}=\frac{{\left|X\left(f\right)\right|}^2}{N},$$ (2)

where ‘N’ is the length of the original signal. The dominant frequency of the signal and other frequency components can be estimated using PSD. The PSD function helps in the classification of signals based on their spectral signatures. The temporal evolution of the frequency components in a signal helps in understanding the temporal evolution of the system under study. The wavelet analysis paves the path for such an investigation.

The translation of a fixed-function called mother wavelet (φ) through the continuous signal generates wavelets [7]. In the present study, Morse wavelet is chosen as the mother wavelet function, which is useful for analyzing the time-varying frequency and amplitude signals. The wavelet transform of the signal (x(t)) for a scale parameter - s and translation parameter τ is given by,

$$W_{c}f(s,\tau )=\underset{-\infty }{\stackrel{\infty }{\int }}x\left(t\right).s^{-1/2}\phi \left(\frac{t-\tau }{s}\right)\mathit{dt}.$$ (3)

2.2. Nonlinear time series analysis

Nonlinear time series analysis is a potential tool to extract valuable information about the system from time-series data. The phase portrait analysis unveils the whole dynamics of a system. The reconstruction of the phase portrait of a dynamical system from a univariate time series is done by using the ‘Method of delay’ employing the time lag l and embedding dimension m as parameters. A reconstructed vector in the phase plane in terms of l and m can be formulated as,

$${\mathbf{x}}_{\mathbf{n}}=(x_{n-(m-1)l},x_{(n-(m-2)l)},\cdots \cdots ,x_n).$$ (4)

For a good one to one correspondence and similarity between the reconstructed phase portrait and actual attractor, the time lag and embedding dimension must by optimum. The time lag can be calculated by employing the mutual information function. The mutual information function, which takes account of the nonlinearity of data points, is the best method available for getting time lag. The embedding dimension, which is the number of dependent parameters of the system, is calculated by using Cao's method [19,33].

The Lyapunov exponent λ is a measure of divergence rate of trajectories in a chaotic system [34]. The distance between two Takens vectors in the phase space δ(t) and δ(0) at time t and t = 0 are related as given in Eq. (5).

$$\delta \left(\mathrm{t}\right)=\delta \left(0\right)·\text{exp}\left(\lambda ·\mathrm{t}\right)$$ (5)

The slope of the log (δ(t)/ δ(0)) vs t plot gives the value of the Lyapunov exponent λ [19].

2.3. Complexity analysis

Fractal dimension, Hurst exponent, and sample entropy are the quantities used to quantify and classify the complexities of a time series. The fractal dimension quantifies the intricate patterns in a time series. The box-counting method is a simple and effective technique for finding the fractal dimension. Box counting method estimates the fractal dimension by superimposing the signal with grids of varying dimension ‘ε’ and counting the number of grids N(ε) required to cover the signal [24]. The value of N(ε) and ε follow a fractal power law with the fractal dimension D as given by Eq. (6).

$$\mathrm{N}\left(\epsilon \right)\propto {\epsilon }^{-D}$$ (6)

The fractal dimension D appears as the slope of logN( ∈ ) vs $\log \left(\frac{1}{\in }\right)$ graph, from which the value of Hurst exponent H can be calculated using Eq. (7).

$$\mathrm{H}=2-\mathrm{D}$$ (7)

0 ≤ H<0.5 – Antipersistent, H = 0.5 – Brownian and 0.5<H ≤ 1 – Persistent, give the classification of time series based on the value of H [25].

The uncertainty in a time-series signal can be estimated through the sample entropy from the correlation sum C(r) of dimension m and m + 1 for a radius r using Eq. (8) [35]. The value of sample entropy at a particular embedding dimension is the average of sample entropy value for different values of r.

$$Sampleentropy\left(m,r\right)=\text{ln}\left(\frac{C^m\left(r\right)}{C^{m+1}\left(r\right)}\right)$$ (8)

2.4. Principal component analysis

The principal component analysis is a robust classification scheme for grouping data having identical features like P, S, H, and D. Among these, the value of P at different frequencies suits best for representing time-series signals. The power spectral density data is large, which makes the principal component analysis tedious. Hence the method of feature extraction from power spectral density data helps in overcoming the difficulty. For this, the frequency data range 100 – 1000 Hz is divided into 26 segments, and the mean value of P of each segment is taken as the representative variable for carrying out principal component analysis using the R software.

3. Results and discussion

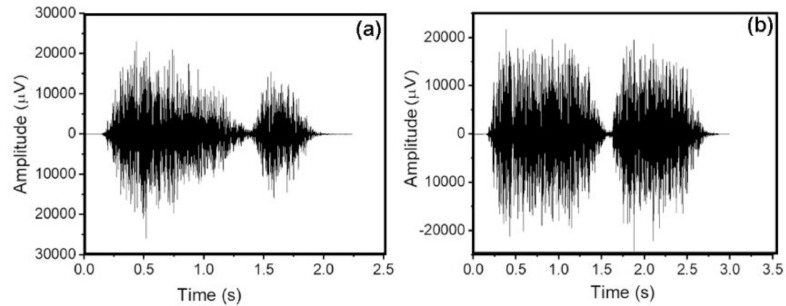
The analysis of lung sounds for clinical diagnosis begins with the invention of the stethoscope by the famous French physician Rene Laennec, the father of clinical auscultation. The basic properties of the VB and BB breath sounds are understood by analyzing 37-time spectra, and a representative time spectrum is given in Fig. 1 . Fig. 1 shows that, in VB sound signals, the duration and magnitude of the inspiration (INS) are higher than that of expiration (EXP), which is in agreement with the literature report [8]. This difference shows that the mechanism of origin of VB sounds for inspiration and expiration is different. There is a clear pause between the inspiratory and expiratory phases for both VB and BB signals. The duration of expiration and inspiration for BB signals are almost similar. The spectral features of both signals are understood from the Fourier transform and wavelet analyses.

Fig. 1.

The time spectrum of (a) VB and (b) BB sound signals.

3.1. Spectral analysis

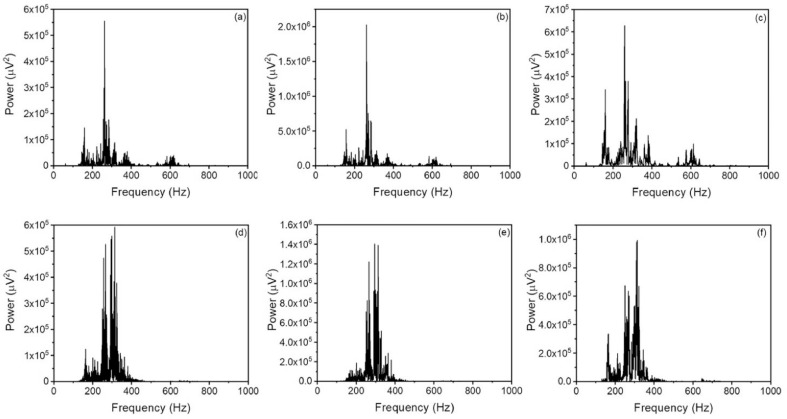
The spectral features can be extracted by analyzing the PSD of VB and BB, along with their inspiration and expiration signals, as shown in the representative plot Fig. 2 . From the PSD of VB shown in Fig. 2(a), it can be seen that the signal contains a high-intensity peak between 200 and 300 Hz. It is worth to note that the frequency of the VB sound is almost confined to a single frequency. The VB sound signal originates from the lobar and segmental airways during inspiration and expiration. As this involves the airflow through segmental and lobar bronchi of diameters 0.56 cm and 0.83 cm respectively, all passages of air through these produce a sound signal of the nearly same frequency, which is responsible for the appearance of a high-intensity sound signal at a nearly single frequency as shown in Fig. 2(b). The VB signal during expiration is more from the central airways besides the lobar and segmental bronchi, which is responsible for the appearance of more frequency components in Fig. 2(c), the PSD plot of VB expiration. Fig. 2(a) to 2(c) also displays the harmonic components of the fundamental around 600 Hz.

Fig. 2.

Power spectral density plot for VB signals - (a) respiration (b) inspiration, (c) expiration and for BB signals - (d) respiration (e) inspiration, (f) expiration.

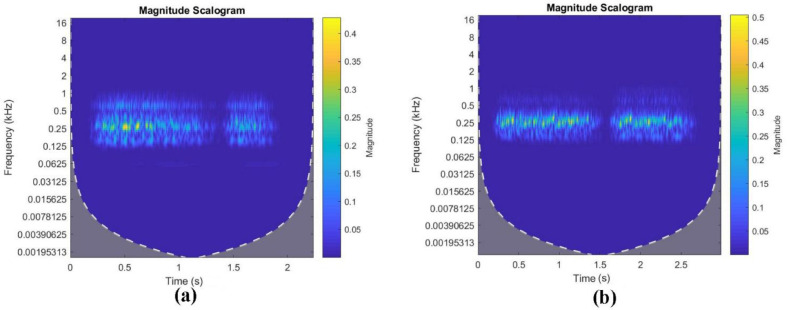
The PSD of the BB signal displayed in Fig. 2(d) shows a greater frequency spread with a large number of frequency components (between 250 and 400 Hz) of higher intensity. The presence of a large number of frequency components can be viewed as due to the flow of air through the trachea and main stem bronchi of diameters 1.8 cm and 1.22 cm, respectively [36]. The airflow during inspiration and expiration through tubes of different diameters generates sound signals of different frequencies. The time duration of expiration in BB is slightly less than inspiration, while in VB, the duration of inspiration to expiration is in 3:1 ratio, as shown in the wavelet scalogram Fig. 3 . From Fig. 3(a), it can be seen that the frequency component of higher intensity lasts only for a short duration during expiration than during inspiration. The observation is in agreement with the PSD plot shown in Fig 2(b) and 2(c). The wavelet scalogram of BB, shown in Fig. 3(b) agrees with the literature reports of a slightly higher duration of inspiration than expiration. Unlike Fig. 3(a) of VB, Fig. 3(b) shows the persistence of frequency components of larger intensities almost during the entire duration of inspiration and expiration. This persistence nature helps in differentiating BB from VB. The scalogram, Fig. 3 also shows the presence of larger frequency components of very low intensities, as observed in the PSD plot.

Fig. 3.

Wavelet scalogram of (a) VB and (b) BB signals.

3.2. Nonlinear time series analysis

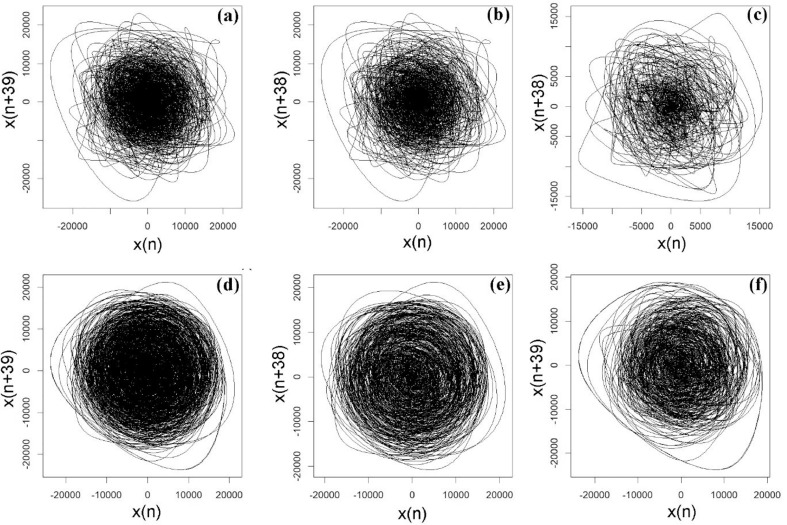
Nonlinear time series is a powerful tool for studying the dynamics of a system. The breath, being a time-varying signal embedded with conditions of lungs and the airways, it is subjected to nonlinear time series analysis using the R software. The geometrical representation of the dynamical system through phase portrait analysis is done by estimating the time lag using the function “timeLag” in the nonlinearTseries package in the R software. The optimum time lag is selected as the time lag at which the average mutual information becomes a minimum. The embedding dimension is estimated by using the “estimatingEmbeddingDim” function in the nonlinearTseries package employing the algorithm proposed by Cao. The function “buildTakens” is used to generate the coordinates for the phase portrait, according to Eq. (4) [19]. A representative phase portrait of VB and BB sound with its inspiration and expiration signal is shown in Fig. 4 . The phase portrait of the BB signal (Fig. 4(d)) seems to be much more complicated than the VB signal (Fig. 4(a)). The degree of freedom for the air molecules is different in VB and BB, which accounts for the variation in the complexity. The air molecules pass through lobar and segmental bronchi of smaller diameters 0.83 cm and 0.56 cm [36], respectively, in VB, compared to the airways trachea and bronchi of diameter 1.8 cm and 1.22 cm, respectively in BB. Greater the diameter of the airways, the higher is the degree of freedom and entropy. This higher degree of freedom is reflected in the phase portrait as an increase in complexity, as evidenced through Fig. 4. The difference in the duration of inspiration and expiration, as displayed in Fig. 1 can also be seen in the corresponding phase portraits as a varying number of phase points. The lower expiration time in VB appears as a comparatively less complex phase portrait (Fig. 4(c)) than that of inspiration (Fig. 4(b)). The nearly equal inspiration and expiration time appear as phase portraits of nearly equal complexities, as displayed in Fig. 4(e) and 4(f).

Fig. 4.

Phase portrait for VB signals - (a) respiration (b) inspiration, (c) expiration and for BB signals - (d) respiration (e) inspiration, (f) expiration.

The maximal Lyapunov exponent (λ) is a measure of unpredictability and one of the indications of the presence of chaotic nature in the time series [37]. Fig. 5 shows the box plot of λ for the VB and BB signals along with the inspiration and expiration. It is evident from Fig. 5 that all the signals have a positive value of λ, which is one of the conditions for chaoticity and unpredictability. From the box plot of λ shown in Fig. 5(a), it is clear that the mean value of the λ of BB signals is higher than that of the VB signals. The larger value of λ of BB signals is because of the formation of vortices while the air flows turbulently through the trachea and bronchi of the respiratory tract. This higher value of λ is in agreement with the results obtained in the phase portrait analysis. The value of λ of the BB signal is found to be higher than VB during inspiration and expiration, and the box plots comparing the D values are shown in Fig. 5(b) and 5(c).

Fig. 5.

Maximum Lyapunov exponent (λ) for BB and VB signals of (a) respiration (b) inspiration, and (c) expiration.

3.3. Complexity analysis

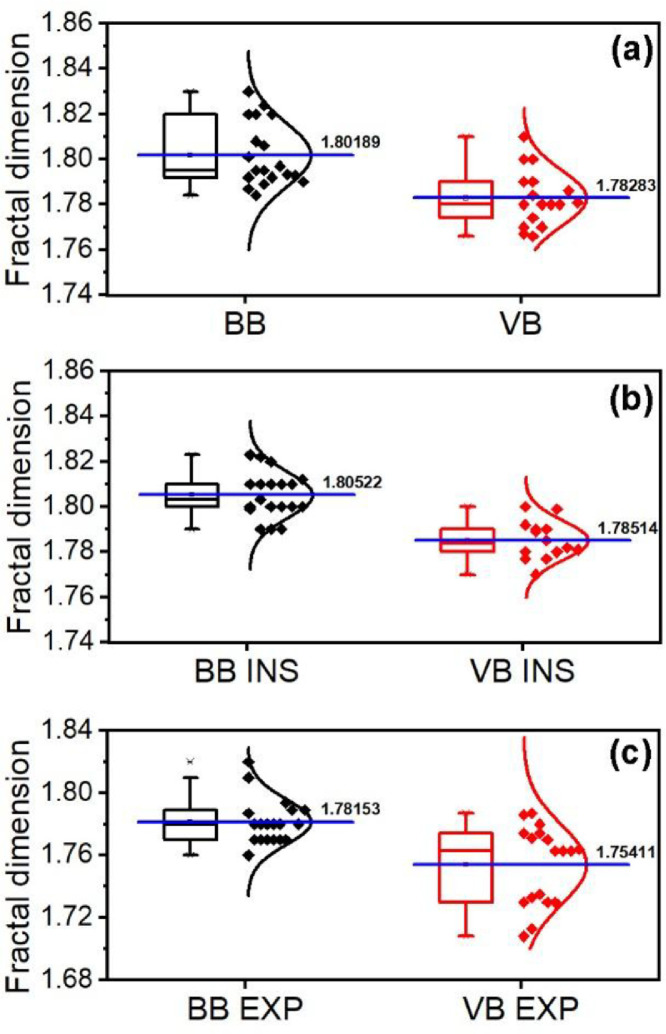
The quantification of the complexity of a time series can be done by estimating its fractal dimension. The box-counting dimension of the signals are calculated using the ‘fd.estim.boxcount’ function in the ‘fractaldim’ package of R software and are shown as a box plot in Fig. 6 (a). The mean fractal dimension of the BB signal greater than that of the VB signal indicates its higher degree of complexity. This higher complexity of BB is in agreement with the phase portrait analysis. The higher complexity of the BB signal compared to the VB signal can be attributed to the persistence of high intense frequency components throughout the inspiration and expiration, as evidenced by Fig. 3. The fractal dimension of the BB signal is found to be higher than VB during inspiration and expiration, and the box plots comparing the D values are shown in Fig. 6(b) and 6(c).

Fig. 6.

Fractal dimension (D) for BB and VB signals of (a) respiration (b) inspiration, and (c) expiration.

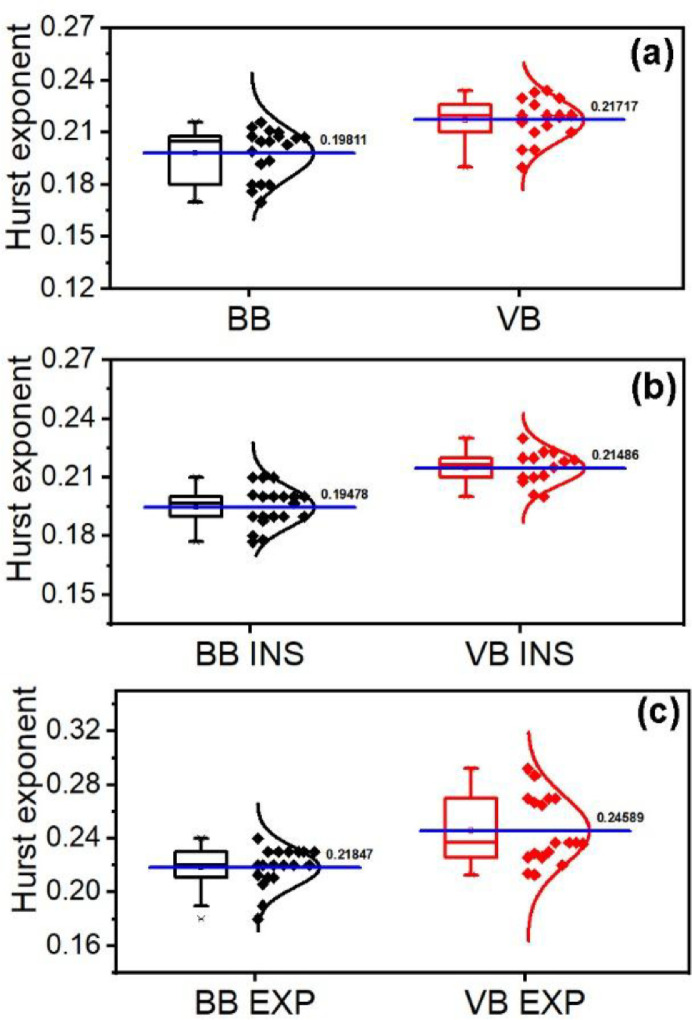
The classification of the signals based on the complexity can also be done by analyzing the Hurst exponent (H) calculated using Eq. (7). The box plot of the H values of BB and VB during inspiration and expiration is given in Fig. 7 . Fig. 7 shows that all the breath signals have the Hurst exponent value between 0 and 0.5, which shows its antipersistent nature. This antipersistent nature suggests a very low correlation between the elements in the time series and the highly complex nature of the breath sound signals. The mean value of Hurst exponent for the BB signal is less than that of the VB signal, which suggests high complexity of the BB signal compared to the VB signal, as explained earlier. The value of Hurst exponent of inspiration (Fig. 7(b)) is also less than that of expiration (Fig. 7(c)).

Fig. 7.

Hurst exponent (H) for BB and VB signals of (a) respiration (b) inspiration, and (c) expiration.

Breathing involves the flow of air molecules inward or outward, the dynamics of the molecules of which are capable of giving information about the airways. Any blockage in the airways affects the nature of the flow, which is getting reflected in the PSD, wavelet, phase portrait, D, and H values. Sample entropy is another parameter that tells the degree of disorder involved in the airflow, during inspiration and expiration through the respiratory tract, introduced by obstructions of different nature. The sample entropy of the breath signals is estimated using the ‘sampleEntropy’ function in the R software and is shown as a box plot in Fig. 8 . From the figure, it can be seen that the mean value of sample entropy of BB signals is higher than the VB signals. The higher value of sample entropy for BB signals is due to the increased complexity and the presence of high intensity persistent multiple frequency components, as evidenced by the phase portrait, PSD, and wavelet analysis. The sample entropy for inspiration and expiration in both VB and BB also exhibits a similar variation.

Fig. 8.

Sample entropy for BB and VB signals of (a) respiration (b) inspiration, and (c) expiration.

3.4. Principal component analysis

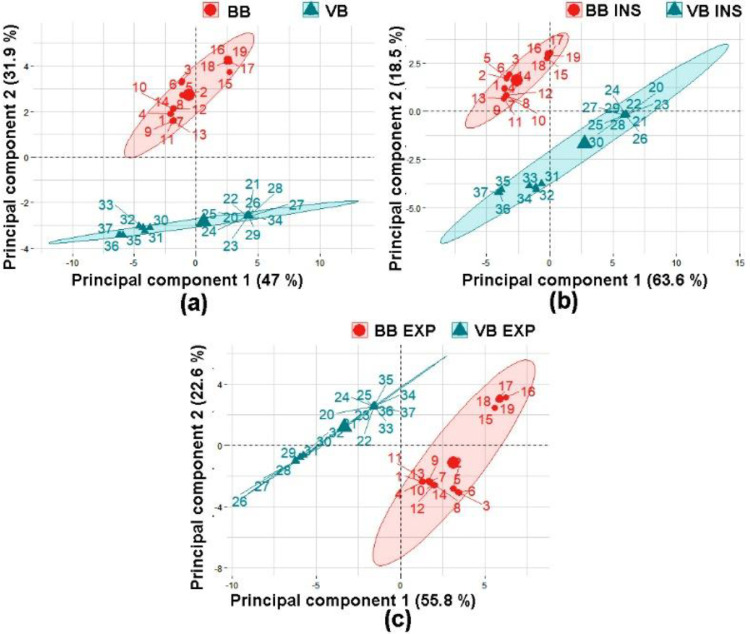
The principal component analysis is a powerful tool for grouping datasets with similar characteristics. In the present work, the power spectral data is used for the feature extraction and principal component analysis. Initially, the 26 power spectral features are extracted from the data as detailed earlier. The 26 power spectral features of each signal are used in R software to compute the principal component analysis. The projection of the dataset in the main two principal components is shown in Fig. 9 (a). The first two principal components cover about 78.9% of the total variance of the original data set. Fig. 9 suggests the possibility of classifying VB and BB sound signals based on their spectral features. From Fig. 9(b) and 9(c), the distinction between inspiration and expiration breath signals of VB and BB, are also evident. The distinctiveness among the parameters derived from the analysis of VB and BB signals opens the possibility of application to a wider spectrum of auscultation in pulmonology.

Fig. 9.

Principal component analysis of VB and BB (a) respiration, (b) inspiration and (c) expiration.

4. Conclusion

Auscultation is one of the oldest methodologies of diagnosis that is in practice with the aid of stethoscope and other modern equipment. The modern lifestyle, together with environmental pollution, leads to different types of pulmonary diseases affecting the lungs. The World Health Organization considers five respiratory-related diseases among the thirty most common causes of death, which necessitate the development of novel, simple, and cost-effective methods for auscultation. The work reported in the paper elucidates the potential of nonlinear time series and fractal analyses in the auscultation of lung-related diseases by investigating 37 vesicular and bronchial breath signals together with different spectral analysis tools like PSD and wavelet. The spectral analysis reveals the distinction between VB and BB in terms of the number of frequency components. When VB shows a nearly single high intense frequency component, BB shows many frequency components of high intensity. The wavelet scalogram of VB and BB reveals the duration of persistence of the high intense frequency component during inspiration and expiration, which accounts for the turbulent flow of air through the respiratory tract. The dynamics of air molecules in the airways during the respiration is unveiled through the nonlinear time series analysis of VB and BB signals. The difference in the degree of freedom of air molecules due to the difference in the diameter of the airways in VB and BB accounts for the difference in the complexity, which is reflected through phase portrait, sample entropy, fractal dimension, and Hurst exponent. The maximal Lyapunov exponent for BB higher than VB suggests that BB is more chaotic than VB. The principal component analysis carried out by the feature extraction of PSD data suggests the possibility and sensitivity of classifying the VB and BB signals. The distinctiveness among the spectral parameters and the chaoticity parameters H, S, D, and λ derived from the analysis of VB and BB signals opens the possibility of application to a broader spectrum of auscultation in pulmonology. The method can be employed as a promising, simple, and low-cost tool for addressing the current issue of the pandemic COVID 19 for understanding the lung condition by analyzing the inspiration and expiration breath signals. However, due to the unavailability of a credible database, we could not investigate with the sound signal of respiration of COVID 19 patients.

Author contributions

All authors have contributed equally in data collection, program development, and analysis.

Declaration of Competing Interest

None