Abstract
There is strong evidence that short-run fluctuations in air pollution negatively impact infant health and contemporaneous adult health, but there is less evidence on the causal link between long-term exposure to air pollution and increased adult mortality. This project estimates the impact of long-term exposure to air pollution on mortality by leveraging quasi-random variation in pollution levels generated by wind patterns near major highways. I combine geocoded data on the residence of every decedent in Los Angeles over three years, high-frequency wind data, and Census short form data. Using these data, I estimate the effect of downwind exposure to highway-generated pollutants on the age-specific mortality rate by using orientation to the nearest major highway as an instrument for pollution exposure. I find that doubling the percentage of time spent downwind of a highway increases mortality among individuals 75 or older by 3.8%–6.5%. These estimates are robust and imply significant loss of life years.
1. Introduction
The effect of air pollution on premature mortality is a fundamental parameter for environmental regulation. For example, the United States Environmental Protection Agency (US EPA) estimates that the 1990 Clean Air Act Amendments (CAAA) will generate $12 trillion in gross benefits from 1990 to 2020, with 92% of these benefits accruing in the form of avoided mortality (US EPA 2011, Chap. 7, p. 8). In the past decade, researchers have employed quasi-experimental designs with great success to estimate the effects of air pollution on fetal and infant health (Chay and Greenstone 2003; Currie and Neidell 2005; Currie, Neidell, and Schmieder 2009; Jayachandran 2009; Currie and Walker 2011; Arceo-Gomez, Hanna, and Oliva 2016; Knittel, Miller, and Sanders 2016). There is also strong evidence that short-term fluctuations in air pollution negatively impact contemporaneous pediatric and adult health (Ransom and Pope 1995; Pope et al. 1999; Friedman et al. 2001; Moretti and Neidell 2011; Schlenker and Walker 2016). In comparison, however, there is a shortage of quasi-experimental evidence linking long-term exposure to air pollution to increased adult mortality. This effect is of great policy interest because the goal of most air quality regulations, such as the CAAA, is to achieve long-term reductions in ambient pollution levels.
Estimating the effects of long-term exposure to air pollution is challenging for two reasons. First, it is difficult to identify quasi-random variation in long-term air pollution levels across geographic areas. Second, even if pollution were randomly assigned, individuals may endogenously migrate in response to pollution (Banzhaf and Walsh 2008). The identifying variation in air pollution thus needs to be cross-sectional in nature (or a very long panel), exogenous, and yet subtle enough not to induce migration.
I exploit quasi-random variation in pollution levels generated by wind patterns near major Los Angeles highways to estimate the effect of long-term exposure to air pollution on mortality rates. Relative to other major California metropolitan areas, the Los Angeles Basin has consistent, predictable wind patterns. The atmospheric sciences literature has established that certain pollutants, and especially ultrafine particles (UFPs), are found at elevated levels up to 600 m downwind of major highways. In contrast, pollution levels rapidly decline within 100 m on the upwind or parallel wind sides of highways. This pattern suggests the use of location relative to highways as a proxy for pollution exposure.
My research design compares mortality rates for individuals who live within 600 m of highways but on different sides, one predominantly upwind and the other predominantly downwind. This comparison should isolate variation in long-term pollution exposure—the median household in my analytic sample has lived at the same address for over two decades—that is uncorrelated with other factors affecting mortality. In particular, after controlling for distance from highway and a fine set of spatial fixed effects, there is little reason to believe that individuals who live downwind of highways differ from individuals who live upwind of highways, unless people move in response to the pollution itself. Such a response seems unlikely because the pollutants in question, UFPs, nitrogen oxides, and carbon monoxide (CO), are measurable with scientific equipment but not readily perceived by the human senses at the concentrations found near highways (and atmospheric research suggests that coarser particles, which are more readily sensed, do not disperse as far). Furthermore, I demonstrate that property values are not lower downwind of highways, which would be the natural consequence of endogenous migration in response to perceived pollution.
I find a statistically and economically significant relationship between downwind exposure in the Los Angeles Basin and mortality rates among the elderly. For individuals over the age of 75—the most vulnerable group—a one standard deviation increase in share of time spent downwind of a highway increases mortality by 3%–5%. When instrumenting for percentage of time downwind using orientation (e.g., north, south, east, or west) to the highway, my estimates imply that a one standard deviation increase in time spent downwind of a highway increases mortality by 6%. These effects persist across a range of elderly or near-elderly age groups (e.g., individuals over 65 or over 70) and spatial bandwidths. My estimates are somewhat larger in magnitude than those from studies that estimate the high-frequency time-series relationship between daily mortality rates and daily particulate levels. They are smaller than existing cross-sectional estimates, but they remain economically significant, implying over 300,000 life years lost in the Los Angeles Basin alone. There is little evidence that households are currently aware of the potential risks of downwind exposure; property values are balanced across the highways. This fact suggests that residential sorting behavior, development patterns, and adaptation measures are suboptimal. The health damages also imply substantial benefits from regulating UFPs and other near-highway pollutants. They represent, to the best of my knowledge, the first quasi-experimental evidence on the effects of long-term exposure to fine or ultrafine particulate pollution on adult mortality.
2. Background
Dozens of studies establish that daily or weekly fluctuations in air pollution have negative impacts on contemporaneous adult health, including mortality (Pope et al. 1999). Extrapolating the effects of short-term fluctuations to long-term exposure, however, is problematic for two reasons. First, the effects of exposure may accumulate over time, so that the cumulative effect of long-term exposure is greater than the implied effect of the sum of repeated short-term exposure coefficients. Second, over short time horizons, the “harvesting” effect—the possibility that short-term insults to health “harvest” sick individuals who were about to die anyway—may underlie some of the contemporaneous relationship between pollution shocks and adult mortality. If so, then the effect of cumulative exposure to pollution may be smaller than suggested by short-term estimates. In summary, for adults it is difficult to bound the effects of long-term pollution exposure in either direction using estimates from short-run pollution fluctuations.1
2.1. Particulates and Health
Particulate pollution has been a focus of air quality regulations since the 1970 CAAA. In 1971, the EPA issued CAA standards focusing on total suspended particles (TSPs), or particles of approximately 100 μm in diameter or less. In 1987, they revised the standards to focus on PM10 (particles 10 μm in diameter or less), and in 1997 they issued standards targeting PM2.5 (particles 2.5 μm in diameter or less). The clear trend in regulation is toward finer particles over time, and the current research focus on the health effects of particulates is on fine particulates (PM2.5) and UFPs (particles 0.1 μm in diameter or less).
The most heavily cited evidence linking long-term exposure to air pollution and premature adult mortality comes from cross-sectional epidemiological studies. The seminal paper in this series is the “Six City study” (Dockery et al. 1993), which documents a significant relationship between mortality risk and air pollution across six cities. The mortality rate in the most polluted city in that study was 26% higher than the mortality rate in the least polluted city, with the strongest association observed for fine particulates (PM2.5). This finding was replicated in a follow-up study covering all US metropolitan areas with available pollution data (Pope et al. 2002), and a similar relationship exists for cardiovascular events and PM2.5 (Miller et al. 2007). Pope, Ezzati, and Dockery (2009) use two repeated cross-sections and demonstrate that long-differenced (20-year) changes in PM2.5 correlate significantly with changes in city-level life expectancy. The EPA applies results from this literature when evaluating the CAAA (US EPA 2011), but it is unclear whether the observed relationships reflect a causal effect of air pollution on mortality or whether they reflect the role of unobserved confounding factors that correlate with air pollution levels across cities.
A small number of papers have employed quasi-experimental methods to estimate the effect of long-term pollution exposure on adult mortality. Chay, Greenstone, and Dobkin (2003) use variation in the long-run reduction in TSP pollution induced by the CAAA of 1970. They find that counties with the largest decreases in TSPs (i.e., the most polluted counties prior to 1970) did not experience greater reductions in adult or elderly mortality than counties with smaller decreases in TSPs. However, they urge caution in interpreting these results “due to the imprecision of the estimated effects and evidence of significant problems with the research design” (Chay, Greenstone, and Dobkin 2003, p. 299). Chen et al. (2013) exploit a policy in China that provides coal-fired heat to all cities north of the Huai River. Using a regression discontinuity (RD) design, they estimate that TSPs are 55% higher north of the river and that life expectancies are 5.5 years lower. These results imply large effects of air pollution on mortality. The implications for regulation in the United States and other developed countries are unclear, however, because pollution levels are much higher in China.
The other evidence linking particulates and health comes from laboratory or biomarker studies with animals and humans. Elder et al. (2004, 2007) exposed laboratory rats to UFP levels mimicking urban roadside environments and found negative effects on white blood cell counts and heart rate. Vinzents et al. (2005) and Brauner et al. (2007) document significant relationships between personal exposure to UFPs over several hours and oxidative DNA damage in humans. Frampton et al. (2006) exposed human subjects to UFPs and found negative effects on blood leukocytes (white blood cells); Brook et al. (2009) exposed human subjects to PM2.5 and found adverse effects on blood pressure. Of relevance to this study, both Frampton et al. (2006) and Oberdörster et al. (2009) found that UFPs reduced pulmonary diffusing capacity for CO, suggesting a negative interaction effect between two of the main pollutants from motor vehicles (UFP and CO).
2.2. Pollution Dispersion Near Highways
Understanding the dispersal of pollutants from highways is critical for implementing my identification strategy and interpreting my results. Karner, Eisinger, and Niemeier (2010) synthesize results from 41 atmospheric science studies on near-roadway air quality. These studies measure pollutant levels at varying distances from busy highways in the upwind, downwind, and parallel wind directions. Several clear patterns emerge from this meta-analysis that inform my research design.
First, pollutant levels are consistently higher downwind of highways than upwind of highways. This implies that the percentage of time spent downwind of highways should affect pollutant exposure. Second, although many pollutants decay to near-background levels within 200 m downwind, several do not. Most significant among these are UFPs, which have demonstrated adverse health effects in laboratory studies, nitrogen oxides (NO and NO2, or NOx), and to a lesser degree CO. UFPs decay to background levels by 570 to 910 m downwind, and nitrogen oxides decay to background levels by 550 to 570 m downwind. Notable pollutants whose plumes do not extend beyond 100 to 200 meters downwind, or whose concentrations do not seem to be strongly affected by wind direction, include coarse and fine particulates (PM10 and PM2.5) and ozone (a secondary pollutant). In practical terms, by 300 m the only pollutants with levels that are at least 15% higher than background levels are UFPs (150% higher), NO (70% higher), and CO (25% higher) (Karner, Eisinger, and Niemeier 2010, p. 5337). Dispersion of up to 500 m is important because the spatial resolution of my data, although high, becomes imprecise for coding at radii of less than 100 m. Noise is an additional “pollutant” that decays with distance from the highway, but recent research reveals that noise levels do not vary strongly with wind direction and thus are unlikely to affect my research design (Shu, Yang, and Zhu 2014).
An additional study, conducted after the Karner et al. meta-analysis, is particularly relevant to my research design. Quiros et al. (2013) measure UFP concentrations before, during, and after a 36-hour shutdown of the I-405 highway in Los Angeles. This July 2011 event, locally known as “Carmageddon”, was scheduled to accommodate a major highway improvement project. During the closure, particle number concentrations—which are determined by UFP counts—were 83% lower 50 to 300 m downwind of I-405 than during comparable non-closure days. There were no substantial trends in particles upwind of the freeway.2 These results corroborate the effects of downwind exposure on pollution concentrations in the area included in this study.
Elevated outdoor UFP levels may have limited health effects if the particles do not penetrate indoors. Jamriska et al. (1999), Palmgren et al. (2003), and Morawska et al. (2009) study the relationship between outdoor and indoor levels of traffic-generated particle emissions in a variety of contexts. They find that UFPs have high penetration efficiency into buildings unless mitigated with a high-efficiency filtration system, which most residential buildings lack.
In summary, the only pollutants that consistently reach levels high enough to generate a meaningful first stage several hundred meters from the highway are UFPs, nitrogen oxides, and CO.3 These pollutants are either colorless and odorless (UFPs and CO) or are found at concentrations too low to be perceptible to the human senses (the odor threshold for NO2 is 0.12 ppm, which is above the 99.9 percentile of NO2 measurements at near-highway pollution monitors in the study area; Nagata and Takeuchi 2003, p. 122). It is thus unlikely that individuals will move in response to downwind frequency.
In terms of health impacts, the clearest hazard is UFPs, since they are the most elevated relative to background levels and have been shown to have negative impacts in laboratory studies. CO is also dangerous (Currie and Neidell 2005; Currie, Neidell, and Schmieder 2009), and may negatively interact with UFPs, but its plume decays much more rapidly. Nitrogen oxides are a criteria pollutant in part because they interact with volatile organic compounds (VOCs) to form ozone. Since the Los Angeles Basin is VOC-limited (South Coast Air Quality Management District 2014), and has been for many years (Milford, Russell, and McRae 1989), additional nitrogen oxides will not increase ground-level ozone concentrations. Nevertheless, there is some evidence that sustained exposure to low levels of nitrogen oxides, like those found in the study area, may have negative health impacts. Complicating inference is the fact that in almost all contexts there is strong colinearity between fine particles and nitrogen oxides (Committee on the Medical Effects of Air Pollutants 2015). A cautious interpretation of my results is that I estimate the reduced form effect of an increase in several near-roadway air pollutants—UFPs, NO2, and CO—on mortality.
A final strand of literature directly related to this research estimates the relationship between roadway proximity and health. Hoek et al. (2002) examine data in the Netherlands and find that the risk of mortality is 41% higher for individuals living within 100 m of major roads or freeways. Gauderman et al. (2007) find that children living within 500 m of California freeways had depressed lung development relative to children living more than 1500 m from freeways. Currie and Walker (2011) exploit a natural experiment arising from the introduction of electronic tolling and find that reductions in traffic congestion near toll plazas reduce the incidence of prematurity and low birth weight among mothers living within 2000 m of the plazas. Rosenbloom et al. (2012) find that all-cause mortality among individuals who have previously suffered from heart attacks is 13%–27% higher when living within 1000 m of a major roadway.
3. Data
This study estimates the effect of downwind exposure from highways in the Los Angeles Basin (the area of Los Angeles County that lies northwest of the Pacific Ocean and southeast of the mountains). The Los Angeles Basin is an ideal study area for several reasons. First, it contains a large population (approximately 5 million in 2000). Second, there are many major highways. Third, there are consistent, predictable wind patterns across the Basin. This is helpful in assigning wind directions to census blocks—the unit of analysis—because weather stations are much sparser than census blocks. Finally, I have detailed data on Los Angeles real estate transactions. This enables property-value based falsification tests.
The data underlying my estimates come from four distinct sources. The primary outcome is the census block age-specific mortality rate. To compute this rate, I combine two data sets. The first is the California Death Address File. These data contain information on every death in California from 1999 to 2001, including the residential address of each decedent. Key variables include age and cause of death. The second data set is the GeoLytics CensusCD 2000 Short Form. These data contain 2000 Census short form data, aggregated and geocoded at the census block level. Key variables include population by age group, gender, and race. Note that no data beyond these basic demographic variables exist at the census block level because the Census long form is only distributed to one in six households and is not available below the block group level, which is much too coarse a geographic unit for this analysis (United States Census Bureau 2016).
In Los Angeles, each census block generally corresponds to a city block and averages 150 to 300 m on each side. I geocoded the Death Address File addresses for the entire Los Angeles area and assigned each address to a census block. I then computed three-year census block mortality rates for various census age groups, including ≥65, ≥70, and ≥75 years of age.4 For each census block, I calculated the distance and angle (orientation) to the nearest major highway, as defined by ESRI ArcGIS.
The independent variable of interest is downwind frequency, or the fraction of time spent downwind of a major highway. I define a census block as downwind at a moment in time if the wind direction is within 45 degrees of a perpendicular ray running from the highway to the Census Block.5 If the wind blows in any other direction or if there is no wind, then the census block is not downwind. Note that if the wind blows approximately parallel to the highway (i.e., within 45 degrees of the highway's direction), then neither side of the highway is downwind. In Section 6.1, I experiment with an alternative definition of downwind that weights exposure by the cosine of the difference in angles between the wind direction and a perpendicular ray from the highway to the census block and find similar results. I omit a very small number of populated census blocks that are near the intersections of two highways, as the downwind direction for these blocks is ambiguous.
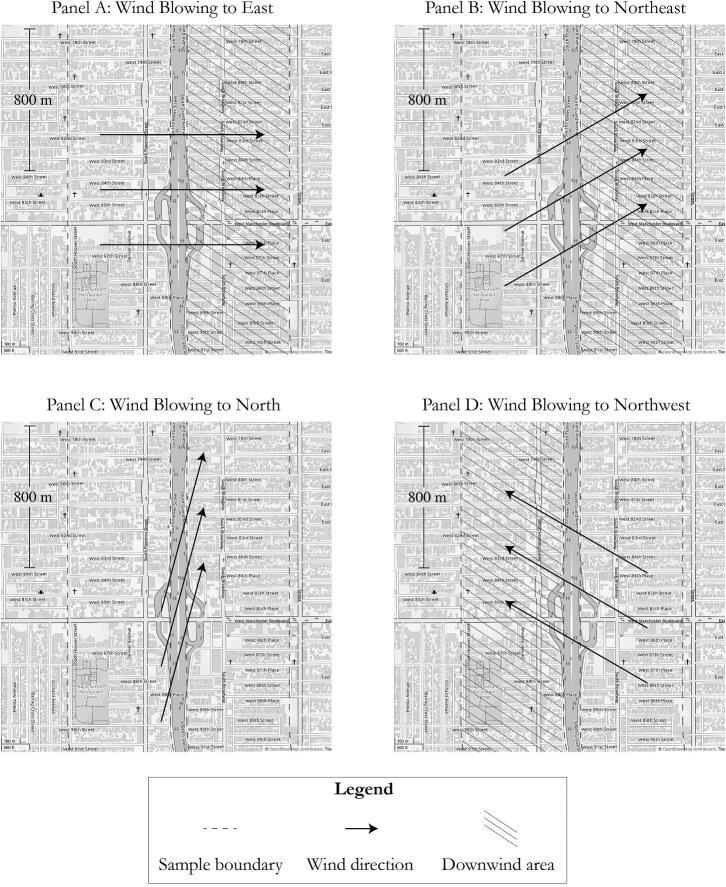
Figure 1 depicts four scenarios with different wind directions. The figure overlays a short segment of Interstate 110, which runs north–south in the Los Angeles Basin. Dashed lines mark the analytic sample boundaries, which include the area between 50 and 600 m from the highway. Solid arrows represent the wind direction.
Figure 1.
Stylized wind direction scenarios. Panels depict a segment of Interstate 110, which runs north–south in the sample area. Wind direction varies by panel. Map tiles from OpenStreetMap, www.openstreetmap.org/copyright.
Panel A presents the downwind area when the wind blows east. This is a straightforward scenario, as the wind direction is perpendicular to the north–south highway, and the eastern side of the highway is downwind. Panel B presents the downwind area as the wind shifts to blowing northeast. Since the angle between a perpendicular ray from the highway and the wind direction is still less than 45 degrees, the downwind area remains unchanged. Panel C presents the downwind area as the wind shifts to blowing almost north. The angle between a perpendicular ray from the highway and the wind direction is now more than 45 degrees, so the wind is almost parallel to the highway. Neither side is now downwind. Finally, Panel D presents the downwind area as the wind shifts to blowing northwest. The western side of the highway is now downwind.
In addition to demonstrating the underlying geometry, Figure 1 also highlights the spatial scale of the study. The outer dashed lines mark 600-m limits from the center of the highway. These limits encompass less than 1.5 city blocks on either side. The inner dashed lines represent 50-m limits from the center of the highway, the minimum distance for a census block to be included in the analytic sample. There is also an 800-m length marked in the figure to represent the radius of the highway segment spatial fixed effects discussed in Section 4.
To measure wind direction and speed I collected one year of wind data for 20 available Los Angeles Basin weather stations from MesoWest. I matched each census block to its nearest weather station and assigned wind directions and wind speeds using this match. The average distance to the nearest weather station in the analytic sample is 4.9 km, with a standard deviation of 2.1 km and a maximum distance of 11.1 km. I verify the accuracy of these data by predicting the measured downwind frequency at census blocks within 500 m of a weather station using data from the next nearest weather station. The correlation coefficient between predicted downwind frequency and actual downwind frequency is 0.87 (N = 64). However, this figure understates the accuracy of the predictions because the average distance to the next nearest weather station is higher than the average distance to the nearest weather station. If I limit the sample to census blocks where the next nearest weather station is less than 7.4 km away, the average distance to the next nearest weather station (5.0 km) becomes similar to the average distance to the nearest weather station in the analytic sample (4.9 km). In this restricted sample, the correlation between predicted downwind frequency and actual downwind frequency is 0.96 (N = 32).
The last data set is data on property sales. I use these data to conduct falsification tests using property values and to make inferences about the frequency at which households in the sample move. These data come from DataQuick and represent the universe of real estate transactions involving single-family homes in Los Angeles County between 1990 and 1998. The data include address, date of transaction, transaction price, and square footage.
Table 1 presents summary statistics for key variables. There are 27,908 census blocks in the overall sample (the Los Angeles Basin), but only 9,027 lie in the analytic sample (i.e., between 50 and 600 m from a major highway). In both samples, the three-year mortality rate among individuals 75 or older is approximately 0.16, with two thirds of that due to cardio-respiratory causes and under 20% due to cancer. The average block is downwind of the closest highway 15% of the time, and the winds do not blow at all 42% of the time. The average block contains 167 individuals, 7 of whom are over the age of 75. Approximately half of all households in both samples own their own homes. The share of black individuals is lower in the analytic sample (12%) than in the full sample (14%).
Table 1.
Summary statistics.
| Full sample | Analytic sample | |||||
|---|---|---|---|---|---|---|
| Mean | Range | N | Mean | Range | N | |
| 3-yr mortality rate among | ||||||
| 75± year olds from: | ||||||
| All causes | 0.157 | 0.000–0.857 | 27,908 | 0.155 | 0.000–0.833 | 9027 |
| (0.178) | (0.181) | |||||
| Cardio-respiratory | 0.103 | 0.000–0.800 | 27,908 | 0.103 | 0.000–0.800 | 9027 |
| (0.145) | (0.148) | |||||
| Cancer | 0.029 | 0.000–0.667 | 27,908 | 0.029 | 0.000–0.667 | 9027 |
| (0.076) | (0.078) | |||||
| External causes | 0.002 | 0.000–0.500 | 27,908 | 0.002 | 0.000–0.500 | 9027 |
| (0.019) | (0.020) | |||||
| Other variables | ||||||
| Frequency downwind | 0.150 | 0.003–0.490 | 27,908 | 0.152 | 0.003–0.490 | 9027 |
| of major highway | (0.130) | (0.129) | ||||
| Frequency dead wind | 0.423 | 0.101–0.660 | 27,908 | 0.421 | 0.101–0.660 | 9027 |
| (0.135) | (0.131) | |||||
| Population | 164.8 | 1–6375 | 27,908 | 166.9 | 1–2215 | 9027 |
| (180.2) | (167.6) | |||||
| Population aged 75+ | 8.5 | 1–542 | 27,908 | 6.7 | 1–154 | 9027 |
| (15.1) | (7.3) | |||||
| Distance to highway | 1182 | 0–7666 | 27,908 | 313 | 50–600 | 9027 |
| (meters) | (1035) | (158) | ||||
| Share owner occupied | 0.548 | 0–1 | 27,869 | 0.518 | 0–1 | 9022 |
| (0.323) | (0.315) | |||||
| Share black | 0.143 | 0–1 | 27,908 | 0.119 | 0–1 | 9027 |
| (0.240) | (0.202) | |||||
| Share aged 75+ | 0.064 | 0–1 | 27,908 | 0.053 | 0–1 | 9027 |
| (0.071) | (0.058) | |||||
Notes: The observation is the census block. Parentheses contain standard deviations. The analytic sample is limited to census blocks with centroids between 50 and 600 m from major highways.
Figure 2 overlays the entire analytic sample on a map of the Los Angeles Basin. The census blocks in the sample are tightly clustered around highways. In a few cases—for example, just below the exact center of the map—the distribution of census blocks appears asymmetric, with a much higher density of blocks on one side of the highway. This occurs when one side of the highway is primarily residential, whereas the other side is primarily industrial or commercial. To ensure that this type of imbalance does not bias the research design, I employ a spatial fixed effects strategy, discussed in Section 4, that limits comparisons to areas in which I have residential census blocks on both sides of the highway.6
Figure 2.
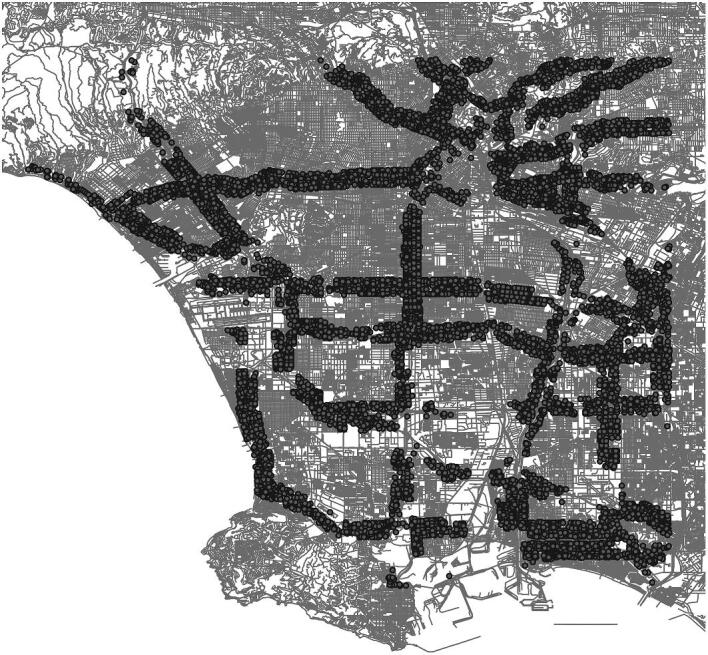
Analytic sample census blocks.
A critical question for the research design is how long the average individual in the sample has lived near the highway. If mobility is high in the sample, then the average length of exposure to elevated pollution levels will be short. The Census short form does not have a question on how long a household has lived at the current location, but the Census long form, which is available at the census tract level, does. The median individual over 75 living in one of the analytic sample's census tracts has lived at the current location for 25 years, and 78% of them have lived at the current location for over 10 years.7 Thus, the vast majority of “downwind” individuals in the sample have been exposed to elevated pollution levels for over a decade, and many for over two decades.
4. Empirical Strategy
My empirical strategy compares census blocks that are close together but differ in downwind exposure from highways. Because downwind exposure changes discontinuously at the highway, and because I limit comparisons to households that are spatially proximate (see Figure 1), the strategy shares features with a boundary discontinuity design. In a typical boundary discontinuity design, identification relies on the assumption that housing supply and demand are smooth across the boundary (in this case, the highway). That assumption may not hold for a single highway segment, because highways often form dividing lines between neighborhoods. However, in this case there are at least eight highways and over two dozen highway segments (where a segment refers to a multimile stretch of highway that does not intersect any other highways). Thus, identification relies on the assumption that, if there are discontinuous changes in housing supply or demand at highways, these changes are not consistently related to the prevailing wind directions. In Section 6.2, I test for failures in this assumption by examining the relationship between downwind exposure and household characteristics or property values.
To implement my strategy, I trim the sample along the dimension that is orthogonal to the highway. I then generate spatial fixed effects along the dimension that is parallel to the highway, which I refer to as “highway segment fixed effects”. I estimate two sets of regressions using these data. First, I estimate ordinary least squares (OLS) regressions of census block mortality rates on percentage of time spent downwind of a highway, controlling for distance to the highway and highway segment fixed effects. Later, I estimate two stage least squares (2SLS) regressions in which time spent downwind of a highway is the endogenous regressor and orientation to the highway is the instrument.
The analytic sample consists of census blocks with centroids located between 50 and 600 m from major highways in the Los Angeles Basin. I set a minimum distance from the highway because the geocoding of residential addresses to census blocks and census blocks to highways is only accurate to within 50 to 100 m. This inaccuracy occurs for several reasons. First, the GeoLytics Census Block boundaries are inexact. In theory, they should precisely overlay the road network, which is the primary delineator of census blocks in the Los Angeles Basin, but in practice I observe some slippage. Second, as demonstrated in Figure 1, Los Angeles highways are wide—often 75 m or more—so their network representation in the ArcGIS shape file is not exact. Third, the mapping of addresses to coordinates is only approximate in many cases. The ArcGIS shape file assigns each road segment an address range, and addresses within that range are linearly interpolated. For example, in a road segment assigned an address range of 101 through 109, the geocoder assumes that the address of 105 lies at the midpoint of that road segment. All of these issues combine to generate measurement error in the assignment of addresses to census blocks. Further from the highway, this generates noise in the dependent variable (census block mortality rates) but not the independent variable (downwind exposure to the highway), since a census block that is far from the highway should have the same downwind exposure as its neighbor. Adjacent to the highway, however, the measurement error affects the independent variable as well, causing attenuation bias. I thus set a minimum distance of 50 m to the highway in selecting the analytic sample. This minimum distance threshold is analogous to a “donut RD” in the regression discontinuity framework (Barreca et al. 2011).
I take the maximum distance from the highway of 600 m from the atmospheric sciences literature summarized in Karner, Eisinger, and Niemeier (2010). This literature finds elevated UFP levels out to 570 m when normalizing concentrations against those found upwind of highways.8 The 600-m figure lies near the middle of the range of spatial bandwidths used in existing studies of roadway proximity and health (see Section 2.2). I test the sensitivity of the results to different maximum (and minimum) distances in Section 6.
I generate highway segment fixed effects after trimming the sample on distance from the highway. The highway segment fixed effects are similar to the spatial fixed effects (SFEs) that have appeared in other spatial analyses (Goldstein and Udry 2008; Magruder 2012). The SFE estimator is analogous to a standard fixed effects estimator in that it demeans each observation i relative to other nearby observations. It then estimates the regression 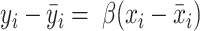 , where
, where 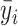 and
and 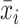 represent the mean values for observations within a radius r of observation i. Unlike a standard fixed effects estimator, however, SFEs cannot be represented as a set of dummy variables, because the relevant comparison group changes continuously as we move through space.
represent the mean values for observations within a radius r of observation i. Unlike a standard fixed effects estimator, however, SFEs cannot be represented as a set of dummy variables, because the relevant comparison group changes continuously as we move through space.
The highway segment fixed effects modify the SFE estimator to demean observation i relative to observations lying within a radius r along the dimension parallel to the highway.9 I implement highway segment fixed effects rather than standard spatial fixed effects because they allow me to independently control the spatial bandwidth along two orthogonal dimensions: distance from the highway and distance along the highway. For example, suppose that r = 800 m and that observation i lies 400 m south of an east–west highway. Observation i is compared to all other observations on that highway that are within 800 m in the east–west direction. This includes observations over 400 m north of the highway, even though these observations are more than 800 m away from observation i in two-dimensional space. With standard spatial fixed effects, it is impossible to assess the sensitivity of the results to decreasing the radius of the SFE without also decreasing the bandwidth around the highway. Independent manipulation of both bandwidths is important because the highway segment fixed effects are meant to control omitted variables bias, whereas the bandwidth around the highway determines the composition of the sample (and potentially the average treatment effect).
Figure 3 presents a stylized example of the near-highway bandwidth and highway segment fixed effects when applied to a highway running east–west. Consider block S0, lying directly south of the highway. When calculating 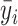 and
and 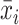 for S0, I include all blocks whose centroids are within a radius r in the east–west direction, regardless of which side of the highway they are on. This cut represents the highway segment fixed effect. In the north–south direction I include all blocks with centroids within 600 m of the highway. This cut represents the near-highway bandwidth. Thus, if the reference block is S0, then blocks S−1, S0, S1, N−1, N0, N1, N3, N4, and N5 all enter the calculation of
for S0, I include all blocks whose centroids are within a radius r in the east–west direction, regardless of which side of the highway they are on. This cut represents the highway segment fixed effect. In the north–south direction I include all blocks with centroids within 600 m of the highway. This cut represents the near-highway bandwidth. Thus, if the reference block is S0, then blocks S−1, S0, S1, N−1, N0, N1, N3, N4, and N5 all enter the calculation of 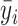 and
and 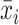 . Blocks S−2, S2, N−2, and N2 are excluded because they are more than r meters from S0 in the east–west direction, and block N6 is excluded because it is more than 600 m from the highway (and therefore not in the analytic sample at all).
. Blocks S−2, S2, N−2, and N2 are excluded because they are more than r meters from S0 in the east–west direction, and block N6 is excluded because it is more than 600 m from the highway (and therefore not in the analytic sample at all).
Figure 3.
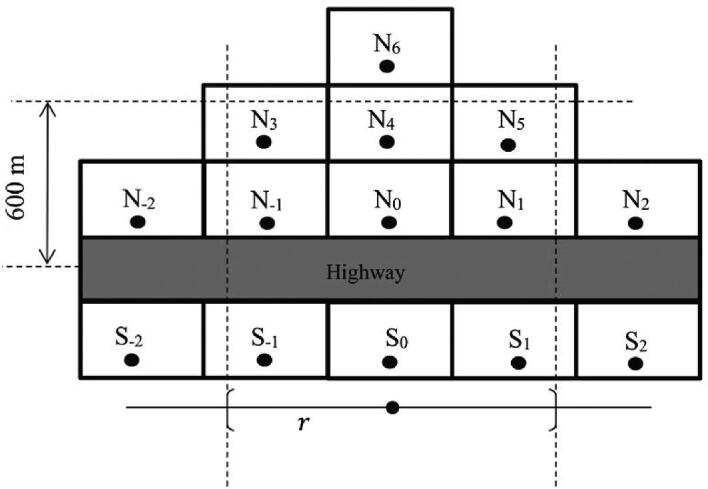
Stylized example of highway segment fixed effects.
After trimming the sample to census blocks located between 50 and 600 m and transforming the data with highway segment fixed effects, I estimate OLS regressions of the form
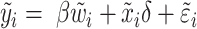 |
(1) |
where yi represents the three-year mortality rate in census block i among individuals 75 or older, 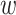 i represents the fraction of time that census block i is downwind of a highway, and xi represents other covariates. I define the transformation
i represents the fraction of time that census block i is downwind of a highway, and xi represents other covariates. I define the transformation 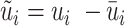 , where
, where 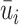 is the mean of observations lying within r meters of observation i along a line parallel to the highway. I set a default highway segment fixed effect bandwidth of r = 800 m but test the results’ robustness to different bandwidths. Covariates in the vector xi include distance to the highway, weather station fixed effects, race, and age distribution.
is the mean of observations lying within r meters of observation i along a line parallel to the highway. I set a default highway segment fixed effect bandwidth of r = 800 m but test the results’ robustness to different bandwidths. Covariates in the vector xi include distance to the highway, weather station fixed effects, race, and age distribution.
I augment the OLS estimates with 2SLS estimates that employ the orientation of the census block to the highway as an instrument for downwind exposure. Orientations of 0, 90, 180, or 270 degrees imply, respectively, that the highway lies north, east, south, or west of the census block. The identifying variation for the 2SLS estimates is broadly similar to the OLS identifying variation. Nevertheless, 2SLS estimates have two potential advantages over OLS estimates. First, the 2SLS estimates should be less sensitive to the exclusion of spatial fixed effects because the relative position of census blocks to the nearest highway is evenly distributed throughout the Los Angeles Basin. In contrast, even if housing is evenly distributed across both sides of all highways, downwind exposure could be higher in certain areas of Los Angeles simply because winds might blow more consistently in those areas. Second, the 2SLS estimates should reduce the measurement error in downwind frequency that arises because most census blocks do not contain weather stations. Because the measurement error will likely attenuate the OLS estimates, I expect—and find—that the 2SLS estimates exceed the OLS estimates in magnitude.
I parameterize the instrument, orientation to the nearest major highway, as a set of seven dummy variables. Each dummy variable represents a 45-degree range (e.g., 22.5 degrees to 67.5 degrees, 67.5 degrees to 112.5 degrees, etc.). The excluded category is north (337.5 degrees to 22.5 degrees). The first stage regression is thus
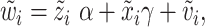 |
(2) |
where zi represents the set of 45-degree range dummy variables, and 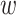 i, xi, and the transformation
i, xi, and the transformation 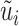 are as defined previously. The second stage estimates the equation:
are as defined previously. The second stage estimates the equation:
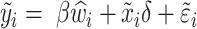 |
(3) |
where 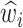 are the fitted values from the first-stage results.
are the fitted values from the first-stage results.
In all regressions (OLS and 2SLS), I compute standard errors that are robust to spatial dependence, following Conley (1999). I employ a uniform kernel and a spatial bandwidth of 3200 m (2 mi) in computing the standard errors. Their size is insensitive to reasonable variations in this bandwidth or alternative kernel choices. All regressions are weighted by the unit of analysis (the census block); Section 6.1 discusses population-weighted estimates as well.
5. Results
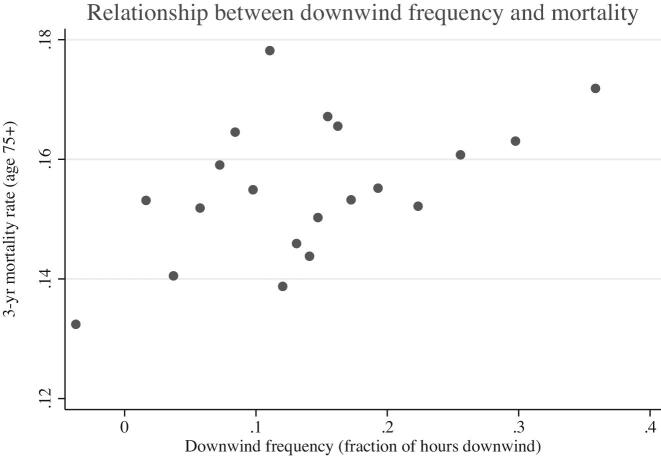
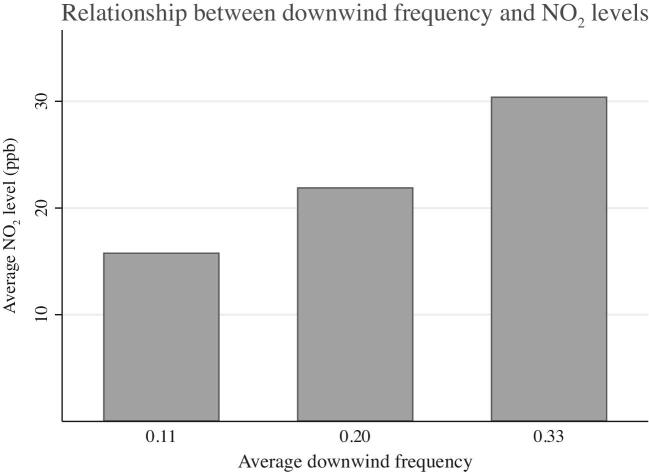
I begin with a graphical analysis of the relationship between downwind exposure and mortality. Figure 4 presents a bin scatterplot of the three-year mortality rate among individuals 75 or older against the frequency of downwind exposure to a major highway. In this figure, both mortality rates and downwind exposure are residualized with respect to 800-m highway segment fixed effects; downwind frequency is thus negative for a small number of census blocks. Figure 4 reveals that census blocks with a high frequency of downwind exposure have higher mortality rates than census blocks with a low frequency of downwind exposure.
Figure 4.
Relationship between downwind frequency and mortality. This figure plots a bin scatterplot of the three-year mortality rate for 75+ year olds against downwind frequency. Variables are residualized with respect to 800-m highway segment fixed effects. Each bin contains approximately 500 observations.
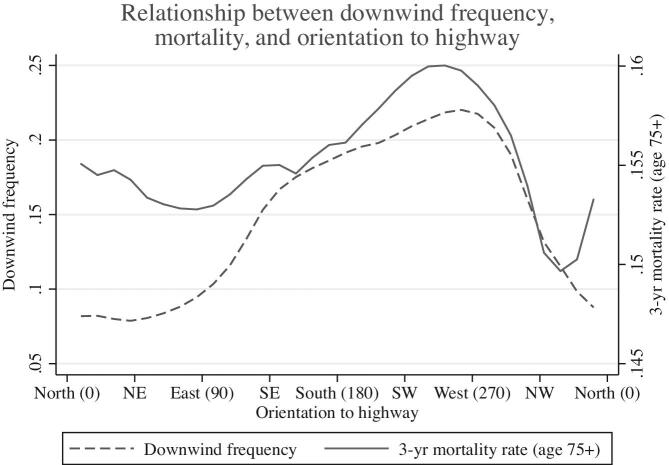
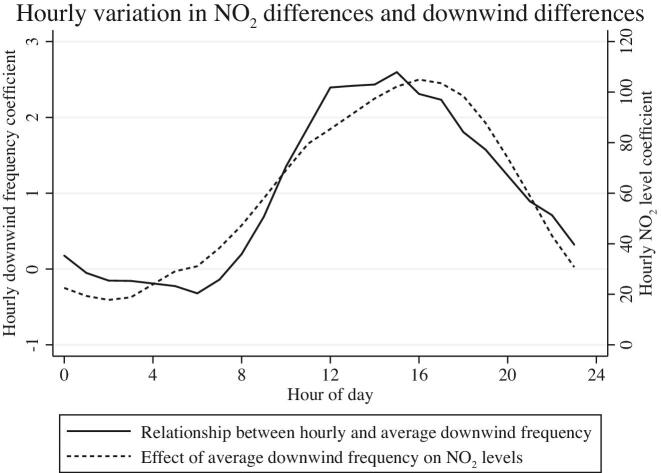
Figure 5 presents the instrumental variables analog of Figure 4. Figure 5 plots the relationships of two variables with respect to orientation to the highway (the instrument) using local polynomial regressions.10 The first plot—the dashed line—is the relationship between downwind frequency and orientation to the highway. This plot is the graphical analog of the first-stage regression. It reveals that when the highway lies south or west of a census block, the block is downwind much more often than when the highway lies north or east. The second plot—the solid line—is the relationship between the three-year mortality rate among individuals 75 or older and orientation to the highway. This plot is the graphical equivalent of the reduced-form regression. It reveals that when the highway lies south or west of a census block, the mortality rate is higher than when the highway lies north or east. The visible correlation between the dashed line and the solid line suggests a relationship between downwind frequency and mortality, consistent with Figure 4.
Figure 5.
Relationship between downwind frequency, mortality, and orientation to highway. This figure plots local polynomial regressions of downwind frequency or the three-year mortality rate for 75+ year olds on orientation to highway in degrees (bandwidths of 15 and 30 degrees, respectively, Epanechnikov kernel). Variables are residualized with respect to 800-m highway segment fixed effects. On the x-axis each tick mark is separated by 45 degrees, and parentheses contain orientation in degrees.
The results tables report the coefficient on downwind frequency, which ranges from 0 to 1. However, the raw coefficient is not directly relevant because a change in downwind frequency from 0 to 1 represents a shift of almost eight standard deviations and is far outside the support of the data. In the text, I thus refer to effects of a one standard deviation (0.13 unit) change in downwind frequency; by coincidence, this is approximately equivalent to doubling downwind frequency from its average level of 0.154 units.
Table 2 presents results from estimating equation (1) via least squares. Column (1) regresses the three-year mortality rate among individuals 75 or older on frequency downwind, plus controls for distance to the highway, weather station fixed effects, race, and age distribution. It does not transform the data using highway segment fixed effects, instead including flexible controls for latitude and longitude (quintics in latitude and longitude, plus first and second order interactions between latitude and longitude). A one standard deviation (or 0.13 unit) increase in downwind frequency is associated with a 0.5 percentage point (or 3%) increase in the all-cause mortality rate. This result is statistically significant (t = 2.5). Column (2) transforms the data using highway segment fixed effects and corresponds to equation (1); this is my preferred OLS specification. The effect of a one standard deviation change in downwind frequency increases to 0.8 percentage points (5%) and becomes highly significant (t = 3.6).
Table 2.
OLS effects of frequency downwind of highways.
| 3-year mortality rate for 75± year olds from: | ||||||||
|---|---|---|---|---|---|---|---|---|
| Dependent variable: | All causes | Cardio-respiratory | Lung cancer | Other cancer | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Frequency downwind | 0.039 | 0.064 | 0.021 | 0.044 | 0.002 | 0.006 | 0.008 | 0.005 |
| (0.016) | (0.018) | (0.013) | (0.014) | (0.003) | (0.004) | (0.007) | (0.009) | |
| Effect of 1 SD change in frequency downwind | 0.005 | 0.008 | 0.003 | 0.006 | 0.000 | 0.001 | 0.001 | 0.001 |
| Highway segment FE | Yes | Yes | Yes | Yes | ||||
| Dependent variable mean | 0.155 | 0.155 | 0.103 | 0.103 | 0.006 | 0.006 | 0.022 | 0.022 |
| N | 9027 | 9027 | 9027 | 9027 | 9027 | 9027 | 9027 | 9027 |
Notes: Each column represents a separate regression of the dependent variable on the percentage of time spent downwind of a major highway. The observation is the census block, and the sample is limited to census blocks with centroids between 50 and 600 m from major highways. Parentheses contain spatial standard errors with a 3200 m bandwidth. All regressions include controls for distance to highway, weather station fixed effects, share African-American, and share over ages 50, 55, 60, 65, 70, and 75. Regressions without highway segment fixed effects include quintics in latitude and longitude and first- and second-order interactions between latitude and longitude. Regressions with highway segment fixed effects include highway segments fixed effects with an 800 m bandwidth.
Columns (3) through (8) in Table 2 report results for mortality from specific causes. Columns (3) and (4) report effects on cardio-respiratory-related mortality using the same regressions as columns (1) and (2), respectively. Previous epidemiological studies, as well as laboratory studies, suggest that air pollution should have pronounced impacts on cardiovascular health. Columns (3) and (4) reveal that over half the effect on overall mortality is due to deaths from cardio-respiratory diseases, and the specification with highway segment fixed effects achieves statistical significance (t = 3.1). Columns (5) and (6) report effects on lung cancer deaths, and columns (7) and (8) report effects on deaths from other cancers. In all cases, the effects are positive but statistically insignificant.
Table 3 presents results from the first-stage regression of downwind frequency on orientation to the nearest highway. Column (1) estimates the relationship with the default set of controls plus flexible controls for latitude and longitude, and column (2) implements highway segment fixed effects. The coefficients in both columns are similar and confirm the visual relationship in Figure 5; census blocks with a highway to the west or south are downwind at a higher frequency than census blocks with a highway to the east or north. Since I parameterize orientation to the nearest highway as seven indicator variables, the possibility of many weak instruments is a concern. However, the F-statistic on the instruments ranges from 26.5 to 30.4, which are well above the suggested critical values for first-stage F-statistics in Stock, Wright, and Yogo (2002). Furthermore, the partial R2 for the instruments exceeds 0.55 in both columns.11
Table 3.
First-stage relationship between orientation to highway and frequency downwind.
| Dependent variable: | Frequency downwind | |
|---|---|---|
| (1) | (2) | |
| Highway northeast | 0.005 | −0.025 |
| (0.010) | (0.009) | |
| Highway east | 0.031 | −0.025 |
| (0.016) | (0.024) | |
| Highway southeast | 0.071 | 0.053 |
| (0.014) | (0.012) | |
| Highway south | 0.109 | 0.109 |
| (0.013) | (0.013) | |
| Highway southwest | 0.221 | 0.194 |
| (0.026) | (0.024) | |
| Highway west | 0.242 | 0.187 |
| (0.036) | (0.034) | |
| Highway northwest | 0.029 | 0.024 |
| (0.028) | (0.022) | |
| F-statistic | 30.4 | 26.5 |
| Partial R2 | 0.551 | 0.653 |
| Highway segment FE | Yes | |
| N | 9027 | 9027 |
Notes: Each column represents a separate regression of the frequency downwind on seven indicators summarizing orientation to the nearest major highway. The omitted category is north. The observation is the census block, and the sample is limited to census blocks with centroids between 50 and 600 m from major highways. Parentheses contain standard errors clustered on a spatial grid with a width of 0.05 degrees longitude or latitude in each cell. All regressions include controls for distance to highway, weather station fixed effects, share African-American, and share over ages 50, 55, 60, 65, 70, and 75. Regressions without highway segment fixed effects include quintics in latitude and longitude and first- and second-order interactions between latitude and longitude. Regressions with highway segment fixed effects include highway segment fixed effects with an 800 m bandwidth. The F-statistic tests the hypothesis that all seven orientation indicators equal zero; the partial R2 is the R2 generated by these seven orientation indicators after partialing out controls.
Table 4 reports 2SLS estimates of the effect of downwind exposure to highways on mortality. Columns (1) and (2) present the effects on overall mortality among 75+ year olds. The first column includes the default controls and flexible functions of latitude and longitude but no highway segment fixed effects, whereas the second column adds highway segment fixed effects and is my preferred 2SLS specification. The estimated effect on mortality rates of a one standard deviation increase in downwind exposure is 0.9 percentage points (6%) with or without highway segment fixed effects. Both estimates are highly significant (t = 3.0 and t = 2.8). The 2SLS estimates are less sensitive than the OLS estimates to the use of highway segment fixed effects, presumably because orientation to the highway is more balanced across space than is downwind frequency.
Table 4.
2SLS effects of frequency downwind of highways.
| 3-year mortality rate for 75± year olds from: | ||||||||
|---|---|---|---|---|---|---|---|---|
| Dependent variable: | All causes | Cardio-respiratory | Lung cancer | Other cancer | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Frequency downwind | 0.067 | 0.066 | 0.035 | 0.036 | 0.003 | 0.009 | 0.015 | 0.015 |
| (0.022) | (0.024) | (0.018) | (0.019) | (0.004) | (0.005) | (0.009) | (0.010) | |
| Effect of 1 SD change in frequency downwind | 0.009 | 0.009 | 0.005 | 0.005 | 0.000 | 0.001 | 0.002 | 0.002 |
| Highway segment FE | Yes | Yes | Yes | Yes | ||||
| Dependent variable mean | 0.155 | 0.155 | 0.103 | 0.103 | 0.006 | 0.006 | 0.022 | 0.022 |
| N | 9027 | 9027 | 9027 | 9027 | 9027 | 9027 | 9027 | 9027 |
Notes: Each column represents a separate 2SLS regression of the dependent variable on the instrumented percentage of time spent downwind of a major highway. The observation is the census block, and the sample is limited to census blocks with centroids between 50 and 600 m from major highways. The instruments are a set of seven indicator variables summarizing orientation to the nearest major highway. Parentheses contain spatial standard errors with a 3200 m bandwidth. All regressions include controls for distance to highway, weather station fixed effects, share African-American, and share over ages 50, 55, 60, 65, 70, and 75. Regressions without highway segment fixed effects include quintics in latitude and longitude and first and second order interactions between latitude and longitude. Regressions with highway segment fixed effects include highway segments fixed effects with an 800 m bandwidth.
Columns (3) and (4) report 2SLS estimates of the effects on cardio-respiratory mortality. As with the OLS estimates, the effect on cardio-respiratory mortality accounts for the majority of the overall mortality effect. A one standard deviation increase in downwind frequency raises the cardio-respiratory mortality rate by 0.5 percentage points. Both estimates are marginally significant (t = 2.0 and t = 1.9). Columns (5) through (8) report 2SLS estimates of the effects on mortality from lung cancer and other cancers. All point estimates are positive, but most are statistically insignificant. The one exception occurs for lung cancer, which achieves marginal significance in column (6) (t = 1.9); the point estimate implies that a one standard deviation increase in downwind exposure increases lung cancer mortality by 0.1 percentage points (20%).
I next explore whether effects appear for younger age groups. Previous cross-sectional studies have found that the relationship between air pollution and negative health events increases with age in both proportional and absolute terms (Miller et al. 2007), but there may be detectable effects for younger age groups. Table 5 reports estimates from the preferred OLS and 2SLS specifications for two younger age groups. The sample size grows for the younger age groups because the likelihood of a census block containing a positive number of people in a given age group grows with the size of the age group. Columns (1) through (4) report effects on all-cause mortality and cardio-respiratory mortality for 65–74 year olds. The effects are close to zero and statistically insignificant. Columns (5) through (8) report effects on all-cause mortality and cardio-respiratory mortality for 50–64 year olds. The point estimates are again close to zero and statistically insignificant. These results suggest either that the negative health impacts of air pollution are primarily distributed among the oldest age groups, or that cumulative exposure to air pollution tends to shorten lives by years rather than decades.12
Table 5.
Effects of frequency downwind for different age groups.
| 3-yr mortality rate for | 3-yr mortality rate for | |||||||
|---|---|---|---|---|---|---|---|---|
| 65–74 year olds: | 50–64 year olds from: | |||||||
| Dependent variable: | All causes | Cardio-respiratory | All causes | Cardio-respiratory | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Estimation method: | OLS | 2SLS | OLS | 2SLS | OLS | 2SLS | OLS | 2SLS |
| Frequency downwind | 0.005 | 0.004 | 0.009 | 0.009 | −0.003 | −0.002 | −0.002 | −0.004 |
| (0.010) | (0.014) | (0.008) | (0.010) | (0.005) | (0.006) | (0.003) | (0.004) | |
| Effect of 1 SD change in frequency downwind | 0.001 | 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | −0.001 |
| Dependent variable mean | 0.058 | 0.058 | 0.030 | 0.030 | 0.022 | 0.022 | 0.009 | 0.009 |
| N | 9796 | 9796 | 9796 | 9796 | 10,659 | 10,659 | 10,659 | 10,659 |
Notes: Each cell represents a separate regression of the dependent variable on the percentage of time spent downwind of a major highway (OLS) or instrumented percentage of time spent downwind of a major highway (2SLS). The observation is the census block, and the sample is limited to census blocks with centroids between a minimum of 50 m and a maximum of 600 m from major highways. The instruments are a set of seven indicator variables summarizing orientation to the nearest major highway. Parentheses contain spatial standard errors with a 3200 m bandwidth. All regressions include controls for distance to highway, weather station fixed effects, 800 m highway segment fixed effects, share African-American, and share over ages 50, 55, 60, 65, 70, and 75.
Finally I present evidence on whether the mortality effects appear to be the result of cumulative exposure to pollution or contemporaneous exposure to pollution. Either mechanism is plausible, but the policy implications may differ by mechanism. For example, if contemporaneous exposure drives the effects, then minimizing exposure during the most vulnerable periods of life—the youngest and oldest ages—may be sufficient to minimize damages. To discriminate between these mechanisms I estimate effects separately by month of year. Underlying this estimation strategy is the fact that winds blow more often during the summer months than the winter months in the Los Angeles Basin. Thus, if the effects are driven primarily by contemporaneous exposure, one should expect larger effects during the summer months than the winter months because the downwind distinction is more meaningful during summer. In short, there should be a seasonal pattern in the mortality coefficients that matches the seasonal pattern in wind activity.
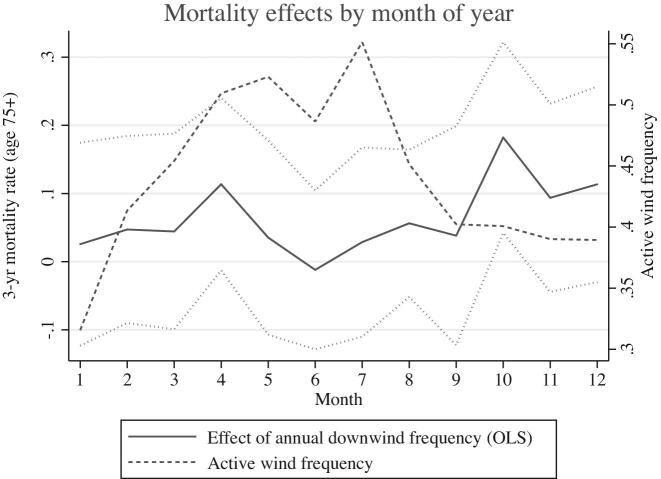
To exploit seasonal variation in wind patterns I proceed in two steps. First, I estimate the fraction of time during which the winds blow for each month of the year. Then I estimate the preferred OLS regression specification by month of year. Figure 6 presents the results of this exercise. The dashed line plots the “first-stage” coefficients for each month. It reveals that winds are much more likely to blow during the summer. During the peak month, July, the wind blows almost twice as often in the sample area as during the nadir month, January.
Figure 6.
Mortality effects by month of year. This figure plots regression coefficients or means estimated by month of year. The solid line plots coefficients from a regression of monthly mortality rates on overall downwind frequency, controlling for distance to highway, weather station fixed effects, highway segment fixed effects, share African-American, and share over ages 50, 55, 60, 65, 70, and 75. The dashed line plots the sample-weighted share of month during which wind blows at under 1 mph.
The solid line in Figure 6 plots coefficients from the regression of monthly mortality rates on (overall) downwind frequency. The seasonal pattern is more muted than the seasonal pattern in wind activity, and the correlation between the two patterns appears, if anything, negative. In particular, the largest mortality coefficient occurs near the winter (October), and the smallest mortality coefficient occurs during the summer (June). This pattern is the opposite of what one might expect if the effects were driven primarily by contemporaneous exposure.
Nevertheless, precision is an issue when stratifying by month of year. The dotted lines plot confidence intervals for the monthly mortality effects, and in many months the confidence interval includes both zero and the largest mortality effect. Thus, although the evidence in Figure 6 suggests that the observed mortality effects represent cumulative exposure rather than contemporaneous exposure, it is not conclusive.
6. Robustness and Falsification Tests
The estimated effects of downwind exposure on mortality are conditional on choices about the affected population and the appropriate spatial bandwidths. In this section, I explore the estimates’ sensitivity to these choices and conduct a series of falsification exercises to test whether the relationship between mortality and downwind exposure could be due to residential sorting.
6.1. Robustness to Parameter Choices and Weights
The regressions estimate the effect of downwind exposure on mortality rates among a specific population: 75+ year olds living 50 to 600 m from highways. As I describe in Section 4, data limitations dictate the minimum distance from a highway (50 m), and the results from the atmospheric sciences literature inform the maximum distance from a highway (600 m). I use a radius of 800 m for the spatial fixed effects because it corresponds to one half mile and is close in magnitude to the 600-m radius that I apply around the highways. Finally, for simplicity, I define “downwind” to mean that the wind direction is within 45 degrees of a perpendicular ray running from the highway to the census block. Table 6 examines how the estimates change with respect to these parameter choices.
Table 6.
Robustness of effects to different spatial parameters.
| 3-year mortality rate for 75± year olds from: | |||||
|---|---|---|---|---|---|
| Dependent variable: | All causes | Cardio-respiratory | |||
| (1) | (2) | (3) | (4) | N | |
| Estimation method: | OLS | 2SLS | OLS | 2SLS | |
| Baseline estimate | 0.064 | 0.066 | 0.044 | 0.036 | 9027 |
| (0.018) | (0.024) | (0.014) | (0.019) | ||
| Effect of 1 SD change in frequency downwind | 0.008 | 0.009 | 0.006 | 0.005 | |
| Modification: | |||||
| Cosine-weighted downwind frequency | 0.059 | 0.057 | 0.039 | 0.032 | 9027 |
| (0.017) | (0.022) | (0.014) | (0.018) | ||
| Effect of 1 SD change in frequency downwind | 0.008 | 0.007 | 0.005 | 0.004 | |
| 400 m highway segment FE | 0.073 | 0.070 | 0.054 | 0.038 | 9027 |
| (0.018) | (0.025) | (0.015) | (0.020) | ||
| Effect of 1 SD change in frequency downwind | 0.010 | 0.009 | 0.007 | 0.005 | |
| 1600 m highway segment FE | 0.057 | 0.066 | 0.039 | 0.038 | 9027 |
| (0.017) | (0.023) | (0.014) | (0.018) | ||
| Effect of 1 SD change in frequency downwind | 0.007 | 0.009 | 0.005 | 0.005 | |
| 25 m “donut” around highway | 0.054 | 0.050 | 0.034 | 0.023 | 9307 |
| (0.019) | (0.025) | (0.015) | (0.019) | ||
| Effect of 1 SD change in frequency downwind | 0.007 | 0.007 | 0.004 | 0.003 | |
| 100 m “donut” around highway | 0.081 | 0.083 | 0.050 | 0.045 | 8193 |
| (0.021) | (0.026) | (0.016) | (0.020) | ||
| Effect of 1 SD change in frequency downwind | 0.010 | 0.011 | 0.007 | 0.006 | |
| Within 400 m of highway | 0.051 | 0.054 | 0.037 | 0.035 | 6039 |
| (0.020) | (0.028) | (0.018) | (0.023) | ||
| Effect of 1 SD change in freq downwind | 0.007 | 0.007 | 0.005 | 0.005 | |
| Within 800 m of highway | 0.061 | 0.056 | 0.034 | 0.022 | 11,839 |
| (0.015) | (0.021) | (0.012) | (0.017) | ||
| Effect of 1 SD change in frequency downwind | 0.008 | 0.007 | 0.004 | 0.003 | |
Notes: Each cell represents a separate regression of the dependent variable on the percentage of time spent downwind of a major highway (OLS) or instrumented percentage of time spent downwind of a major highway (2SLS). The observation is the census block, and the sample is limited to census blocks with centroids between a minimum of 25/50/100 m (50 m is the baseline) and a maximum of 400/600/800 m from major highways (600 m is the baseline). The instruments are a set of seven indicator variables summarizing orientation to the nearest major highway. Parentheses contain spatial standard errors with a 3200 m bandwidth. All regressions include controls for distance to highway, weather station fixed effects, highway segment fixed effects, share African-American, and share over ages 50, 55, 60, 65, 70, and 75.
Table 6 reports estimates from the preferred OLS and 2SLS specifications for a variety of spatial bandwidths. Each coefficient represents a separate regression. Columns (1) and (2) report effects of downwind exposure on all-cause mortality, and columns (3) and (4) report effects of downwind exposure on cardio-respiratory mortality. The top set of rows reproduces the baseline OLS and 2SLS estimates, taken from Tables 2 and 4, for comparison purposes.
The first set of rows (following the top set) presents results from regressions that change the definition of downwind frequency. The alternative definition of downwind frequency weights exposure by the cosine of the difference in angles between the wind direction and a perpendicular ray from the highway to the census block. Formally, the weight is 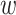 = cos(θ − 90), where θ is the angle between the wind direction and the highway. This implies
= cos(θ − 90), where θ is the angle between the wind direction and the highway. This implies 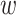 = 1 when the wind blows perpendicular to the highway,
= 1 when the wind blows perpendicular to the highway, 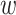 = 0.71 when the wind blows at a 45-degree angle to the highway, and
= 0.71 when the wind blows at a 45-degree angle to the highway, and 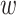 = 0 when the wind blows parallel to the highway. I set a zero lower bound on
= 0 when the wind blows parallel to the highway. I set a zero lower bound on 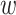 so that it does not become negative when a census block is upwind. With this alternative definition, census blocks receive some downwind exposure even when the wind blows at angles between 0 and 45 degrees to the highway. Using this alternative definition, I find estimates that are slightly smaller in magnitude than the baseline estimates but remain highly significant.
so that it does not become negative when a census block is upwind. With this alternative definition, census blocks receive some downwind exposure even when the wind blows at angles between 0 and 45 degrees to the highway. Using this alternative definition, I find estimates that are slightly smaller in magnitude than the baseline estimates but remain highly significant.
The next two sets of rows present estimates that apply spatial fixed effects with radii of 400 m (one quarter mile) and 1600 m (one mile). In all columns, the estimates are reasonably close to the baseline estimates, implying that the results are not very sensitive to changes in the radius of the spatial fixed effects. The subsequent two sets of rows present estimates that change the “donut size”, or minimum distance from a highway, to 25 m or 100 m. Reducing the donut size to 25 m—which Figure 1 makes clear is too small—decreases the OLS (2SLS) effects on all-cause mortality by 16% (24%). The OLS (2SLS) effects on cardio-respiratory mortality drop by 23% (36%). Increasing the donut size to 100 m has the opposite effect, with effect sizes increasing by approximately 25%, except in column (3), where they increase by 14%. These patterns are consistent with the fact that measurement error in a census block's location relative to the highway becomes more severe as the donut size shrinks.
The bottom two sets of rows present estimates that change the maximum distance from a highway to 400 m or 800 m. Reducing the maximum distance to 400 m has the largest impact of any spatial bandwidth modification; the OLS effect on all-cause mortality drops by 20%, though it remains statistically significant (t = 2.6). The 2SLS drops by 18%. The effects on cardio-respiratory mortality are also less impacted, dropping by 3%–16%. Increasing the maximum distance to 800 m has modest impacts on most estimates except the 2SLS effect on cardio-respiratory mortality, which decreases by 39% and loses statistical significance. Overall, although the estimates do vary with some spatial bandwidths, both the OLS and 2SLS effects on all-cause mortality are consistently positive and statistically significant.
The results in all main tables are weighted by the unit of analysis (the census block). Table A.2 in Online Appendix A reports alternative population-weighted estimates. Population-weighting can make the estimates more representative of the Los Angeles population but less representative of Los Angeles geography. It also has ambiguous impacts on precision.
The first set of rows in Table A.2 in Online Appendix A reproduces the baseline (census block–weighted) estimates. Subsequent sets of rows report estimates weighted by actual census block population, predicted census block population over age 75+, actual census block population age 50–74, and actual census block population age 75+, respectively.13 Age 75+ population weights should make the estimates more representative of the Los Angeles population circa 2000, whereas age 50–74 population weights should make them more representative of the Los Angeles population today.
Weighted OLS results, reported in columns (1) and (3) for all-cause and cardio-respiratory mortality, respectively, are generally smaller in magnitude than unweighted results. The effect of a one standard deviation change in downwind frequency on all-cause mortality ranges from 0.6 to 0.8 percentage points (compared to an unweighted effect of 0.8 percentage points), and the effect on cardio-respiratory mortality ranges from 0.3 to 0.7 percentage points (compared to an unweighted effect of 0.6 percentage points). Nevertheless, in all cases the results remain statistically significant.
Weighted 2SLS results, reported in columns (2) and (4) for all-cause and cardio-respiratory mortality, respectively, are more sensitive to the choice of weights. In all but one case—all-cause mortality weighted by actual age 75+ population—the weighted 2SLS coefficients are smaller in magnitude than the weighted OLS coefficients. Furthermore, weighting generally increases the 2SLS standard errors, despite decreasing the OLS standard errors. As a result the weighted 2SLS coefficient estimates are statistically insignificant in all cases except when examining all-cause mortality weighted by actual age 75+ population (t = 2.0). To understand the sensitivity of the 2SLS estimates I re-estimated the first-stage regression using each set of population weights. The first-stage F-statistic in the unweighted regression is approximately 60% larger than the ones in the weighted regressions (26.5 vs. 16.5). Thus, the instrument is not as strong when populating weighting.14
6.2. Falsification Tests
Identification in this study hinges on the assumption that an individual's orientation to the nearest highway is “as good as randomly assigned”. There are two ways in which this assumption could fail. One would be if there were discrete changes in housing supply or demand at highways that were unrelated to winds but consistently occurred in the direction of prevailing winds. In practice, this would entail northern and eastern sides of highways being consistently poorer than southern and western sides. The second would be if households moved in response to the wind-driven pollution. Previous work, for example, has found that changes in ozone pollution are capitalized into Southern California property values (Sieg et al. 2004). In this context movement is less likely since UFP and CO pollution is undetectable to human senses. Furthermore, any movement in response to illness would attenuate the effects rather than inflate them. In either scenario, however, I would expect demographic characteristics and property values to vary with downwind exposure. Tables 7 and 8 thus estimate the relationships between these characteristics and downwind exposure.
Table 7.
Effects of frequency downwind on placebo measures.
| Share of population: | External-cause mortality rate among: | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dependent variable: | Over 75 | Over 65 | Owning residence | African-American | 75+ year olds | All residents | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | |
| Estimation method: | OLS | 2SLS | OLS | 2SLS | OLS | 2SLS | OLS | 2SLS | OLS | 2SLS | OLS | 2SLS |
| Frequency downwind | 0.012 | 0.016 | 0.019 | 0.029 | 0.073 | 0.078 | −0.010 | −0.035 | −0.0007 | −0.0010 | −0.0015 | −0.0022 |
| (0.009) | (0.013) | (0.015) | (0.023) | (0.071) | (0.074) | (0.028) | (0.036) | (0.0018) | (0.0024) | (0.0009) | (0.0015) | |
| Effect of 1 SD change in frequency downwind | 0.002 | 0.002 | 0.002 | 0.004 | 0.010 | 0.010 | −0.001 | −0.005 | 0.000 | 0.000 | 0.000 | 0.000 |
| Dependent variable mean | 0.053 | 0.053 | 0.109 | 0.109 | 0.518 | 0.518 | 0.119 | 0.119 | 0.0020 | 0.0020 | 0.0012 | 0.0012 |
| N | 9027 | 9027 | 9027 | 9027 | 9022 | 9022 | 9027 | 9027 | 9027 | 9027 | 9027 | 9027 |
Notes: Each cell represents a separate regression of the dependent variable on the percentage of time spent downwind of a major highway (OLS) or instrumented percentage of time spent downwind of a major highway (2SLS). The observation is the census block, and the sample is limited to census blocks with centroids between a minimum of 50 m and a maximum of 600 m from major highways. The instruments are a set of seven indicator variables summarizing orientation to the nearest major highway. Parentheses contain spatial standard errors with a 3200 m bandwidth. All regressions include controls for distance to highway, weather station fixed effects, 800 m highway segment fixed effects, share African-American, and share over ages 50, 55, 60, 65, 70, and 75.
Table 8.
Effects of frequency downwind on property values.
| Dependent variable: | Log price | Square feet | ||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Estimation method: | OLS | 2SLS | OLS | 2SLS | OLS | 2SLS |
| Panel A: 1990–2000 sales | ||||||
| Frequency downwind | 0.017 | −0.112 | −0.037 | −0.140 | 208.5 | 124.7 |
| (0.078) | (0.173) | (0.049) | (0.094) | (186.3) | (351.3) | |
| Effect of 1 SD change in frequency downwind | 0.002 | −0.015 | −0.005 | −0.018 | 27.1 | 16.2 |
| Control for log sq. ft and date sold | Yes | Yes | ||||
| Dependent variable mean | 11.961 | 11.961 | 11.961 | 11.961 | 1311.2 | 1311.2 |
| N | 21,455 | 21,455 | 21,455 | 21,455 | 21,455 | 21,455 |
| Panel B: 2006–2010 sales | ||||||
| Frequency downwind | 0.017 | −0.026 | −0.069 | −0.091 | 162.3 | 97.1 |
| (0.094) | (0.103) | (0.058) | (0.065) | (138.5) | (144.5) | |
| Effect of 1 SD change in frequency downwind | 0.002 | −0.003 | −0.009 | −0.012 | 21.1 | 12.6 |
| Control for log sq. ft and date sold | Yes | Yes | ||||
| Dependent variable mean | 13.029 | 13.029 | 13.029 | 13.029 | 1385.1 | 1385.1 |
| N | 21,713 | 21,713 | 21,713 | 21,713 | 21,713 | 21,713 |
Notes: Each cell represents a separate regression of the dependent variable on the percentage of time spent downwind of a major highway (OLS) or instrumented percentage of time spent downwind of a major highway (2SLS). The observation is a housing sale, and the sample is limited to sales in census blocks with centroids between a minimum of 50 m and a maximum of 600 m from major highways. The instruments are a set of seven indicator variables summarizing orientation to the nearest major highway. Parentheses contain spatial standard errors with a 3200 m bandwidth. All regressions include controls for distance to highway, weather station fixed effects, 800 m highway segment fixed effects, share African-American, and share over ages 50, 55, 60, 65, 70, and 75. Regressions in columns (3) and (4) include controls for log square footage and a cubic in time of sale (measured at the daily frequency).
Table 7 presents results from OLS and 2SLS regressions in which the dependent variable is a measure that should be unrelated to downwind exposure if my research design is valid. Columns (1) through (4) estimate OLS and 2SLS regressions in which the dependent variable is the share of the census block population over 75 or 65 years of age. The coefficients in all four columns are statistically insignificant. Columns (5) and (6) estimate OLS and 2SLS regressions in which the dependent variable is the share of households that own their own home. The coefficients are statistically insignificant, and the point estimates imply that downwind census blocks have higher rates of home ownership, contrary to what one might expect if residential sorting were occurring. In either column, I can reject the hypothesis that a one standard deviation increase in downwind exposure correlates with a greater than 0.6 percentage point (1.1%) decline in home ownership rates. Columns (7) and (8) estimate regressions in which the dependent variable is the share of individuals who are African-American. The coefficients are statistically insignificant, and the point estimates imply that downwind census blocks are less likely to contain African-Americans. Columns (9) through (12) estimate regressions in which the dependent variable is the external-cause mortality rate—that is, deaths from accidents, homicide, or suicide—among 75+ year olds (the ninth and tenth columns) or among all individuals (the eleventh and twelfth columns). In all cases, the coefficients are statistically insignificant, although in general they are imprecisely estimated relative to the mean because external-cause mortality is a rare outcome.
Ideally I would test whether household income and education vary with downwind exposure as well, but these measures are not on the Census short form and thus are not available below the block group level. As an alternative, I test whether property values vary with downwind exposure. Table 8 presents results from OLS and 2SLS regressions in which the dependent variables are housing prices or housing characteristics. The unit of observation is a house or condominium sale, and I match each sale to a census block from the analytic sample to assign downwind frequency. These regressions represent a strong test of the research design in that any large-scale residential sorting should manifest itself in housing prices. The data for these regressions come from DataQuick (1990 to 2000 sales) or the Los Angeles County Assessor's Office (2006 to 2010 sales). The DataQuick data's date range fits the study period better, but they only include sales of single-family homes and only cover the City of Los Angeles (which does not contain the entire Los Angeles Basin). The Assessor's Office data cover sales of all residential units in the entire Los Angeles Basin, but the date range is somewhat later than my study's data. Given these limitations, I present estimates for each data source separately.
Column (1) of Table 8 reports results from OLS regressions of log price on downwind frequency, as well as the standard controls. Panel A reports estimates on the 1990 to 2000 sales sample (DataQuick), and Panel B reports estimates from the 2006 to 2010 sales sample (Assessor's Office). A one standard deviation (0.13 unit) increase in downwind exposure is associated with a statistically insignificant 0.2% increase in property values in either data set. Column (2) reports analogous estimates from 2SLS regressions, and the effects are negative but statistically and economically insignificant. For example, the largest coefficient (–0.112 in Column (2) of Panel A) implies that a one standard deviation increase in downwind frequency is associated with a statistically insignificant 1.5% decrease in property values. Columns (3) and (4) estimate the same regressions as Columns (1) and (2) but include log square footage and a cubic in date sold as controls to increase precision. The standard errors fall by 37%–46%, but all coefficients remain statistically and economically insignificant. Columns (5) and (6) estimate OLS and 2SLS regressions in which the dependent variable is square footage to check that square footage is not endogenously determined by downwind frequency. A one standard deviation increase in downwind frequency is associated with a statistically insignificant 16 to 27 square foot increase in house size.
When considering the potential for omitted variables bias it is instructive to directly compare the magnitudes of the coefficients from the property value regressions with those from the mortality rate regressions. The largest coefficient in the price regressions in Table 8, –0.140 in column (4) of Panel A, implies that a one standard deviation increase in downwind frequency is associated with a statistically insignificant 1.8% decrease in property values. The comparable mortality rate regression coefficient in Table 4 implies that a one standard deviation increase in downwind frequency causes a 5.8% increase in mortality rates. In the Los Angeles Basin I find a cross-sectional elasticity of mortality rates with respect to property values of approximately 0.05. This implies that a 1.8% decrease in property values is associated with a 0.09% increase in mortality rates, a figure that is almost two orders of magnitude less than the estimated effect of 5.8%. It is thus unlikely that the mortality coefficients simply represent neighborhood differences between upwind and downwind census blocks, unless these neighborhood differences are somehow not capitalized into property values.
7. Discussion
The results imply that living downwind of highways increases mortality rates among the elderly. However, it is difficult to interpret the magnitude of the “reduced-form” estimates without a “first stage” relating downwind frequency to pollution. Estimating this first-stage relationship is challenging because air quality monitors are sparsely located and do not measure UFPs, the pollutant I expect the instrument to affect most strongly.15
7.1. “First-Stage” Estimates
As a proxy for UFPs, and as a relevant pollutant itself, I consider measurements of NO2. Vehicles are the primary source of NO2 in Los Angeles, accounting for 85% of nitrogen oxide emissions (US EPA 2014). Furthermore, the near-roadway dispersion pattern of NO2 mimics UFPs more closely than other pollutants mimic UFPs (Karner, Eisinger, and Niemeier 2010). I calculate the downwind frequency of air pollution monitors near highways in the Los Angeles Basin, and estimate a first-stage relationship between downwind frequency and NO2 concentrations. I compare these first-stage estimates to results from the atmospheric sciences literature and apply them in interpreting the reduced-form results.
Four air pollution monitors in the Los Angeles Basin are close to highways: the West Los Angeles-Veterans Administration (VA) Hospital monitor near Santa Monica, the Los Angeles-Westchester Parkway monitor near Los Angeles International Airport (LAX), the North Long Beach monitor, and the Lynwood monitor. For the first two, the highway lies northeast of the monitor, and thus they are primarily upwind. For the latter two, the highway lies southwest of the monitor, and thus they are primarily downwind. I collected hourly NO2 measurements from these monitors from 1995 to 2009.16
Figure 7 charts average hourly NO2 concentration against downwind frequency for three groups of monitors. Two monitors have downwind frequencies of 0.11, one has a downwind frequency of 0.20, and one has a downwind frequency of 0.33. Table 9 presents estimates from regressions of hourly NO2 concentrations on monitor downwind frequency. Column (1) reveals that a one standard deviation (0.13 unit) increase in downwind frequency is associated with a 9.2 part per billion (ppb) increase in NO2 concentrations, or 33% of the mean level. Column (2) adds day-of-sample fixed effects to increase precision and eliminate bias from any imbalance in sample periods across monitors. A one standard deviation increase in downwind frequency is associated with a 7.9 ppb increase in NO2 concentrations (29% of the mean level).
Figure 7.
Relationship between downwind frequency and NO2 levels. This figure plots average NO2 concentration against average downwind frequency for air pollution monitors located near highways in the Los Angeles Basin. The 0.11 bin contains two monitors, and other bins contain one monitor each.
Table 9.
Relationship between NO2 and frequency downwind of highways.
| Dependent variable: | NO2 concentration (ppb) | |
|---|---|---|
| (1) | (2) | |
| Frequency downwind | 70.5 | 61.1 |
| (2.1) | (1.6) | |
| Effect of 1 SD change in frequency downwind | 9.2 | 7.9 |
| Day-of-sample FE | Yes | |
| Dependent variable mean | 27.4 | 27.4 |
| N | 400,218 | 400,218 |
Notes: Each column represents a separate OLS regression of the dependent variable on the percentage of time spent downwind of a major highway. The observation is the hour-by-site. Parentheses contain standard errors clustered by month of sample.
A primary concern in interpreting these estimates is that I cannot control for monitor-specific characteristics. For example, one upwind monitor is near LAX, and one downwind monitor is near the Port of Long Beach. An idealized research design would include highway segment spatial fixed effects to control for any local factors that might affect NO2 concentrations at a monitor, but I lack sufficient monitors for this design. Stated another way, I would like to cluster at the monitor level, but it is infeasible to do so with only four monitors. As an alternative robustness check, Figure 8 plots coefficients from two sets of regressions, each estimated separately by hour of day. The first set of regressions—the solid line—regresses hourly downwind frequency on average downwind frequency (which is fixed within a monitor). The relationship between these two variables is close to zero from midnight until 8 a.m., and then becomes strongly positive from 10 a.m. until 8 p.m. This pattern reveals that most of the downwind exposure at downwind monitors accrues during daylight hours when the winds blow consistently. It also implies that I should expect the relationship between NO2 levels and average downwind frequency to be stronger during the day than during the night. The second set of regressions—the dashed line—regresses NO2 concentrations (which vary by hour) on average downwind frequency. This reveals that the relationship between NO2 concentrations and average downwind frequency is strong during the day, when downwind monitors are actually downwind, and weak during the night, when they are not. These patterns are consistent with the hypothesis that downwind exposure generates the observed differences in NO2 concentrations across monitors and are inconsistent with the hypothesis that monitor-specific characteristics generate the observed differences in NO2 concentrations across monitors. If the latter were true, I would expect NO2 concentrations to be consistently higher throughout the day at downwind monitors, contrary to Figure 8. For completeness, I note that the small NO2 coefficients during nighttime hours are not the result of an absence of NO2 during these hours; NO2 concentrations from midnight to 8 a.m. are nearly identical to the overall average.
Figure 8.
Hourly variation in NO2 differences and downwind differences. This figure plots regression coefficients from regressions of hourly downwind frequency on average downwind frequency (solid line) or regressions of NO2 concentrations on average downwind frequency (dashed line). Each regression is limited to a single hour of day, and in all regressions the unit of observation is a single pollution reading at one monitor.
The first-stage estimates are broadly consistent with the results in the atmospheric sciences literature. Karner, Eisinger, and Niemeier (2010) report that, across 11 studies, NO2 concentrations are on average 1.7 to 2.2 times higher than ambient levels on the prevailing downwind side of the highway. The preferred estimate (column (2) of Table 9) implies that average NO2 concentrations at the two downwind monitors are 2.1 times higher than ambient levels.17 This 2.1-times figure is also consistent with the results from Quiros et al. (2013) following the shutdown of I-405 in Los Angeles. Quiros et al. find that NO levels are approximately twice as high on the downwind side of I-405 when it is open relative to when it is closed.18
I combine the first-stage estimates with the reduced-form results to generate a back-of-the-envelope estimate of the elasticity of mortality with respect to pollution. The first-stage estimates imply that moving from the upwind side to the downwind side increases downwind frequency by 15.5 percentage points and average pollution levels by 43%,19 and the reduced-form estimates imply that a 15.5 percentage point increase in downwind frequency raises mortality rates by 3.9%–6.7%. The “IV” estimate thus suggests an elasticity of mortality rates (among 75+ year olds) with respect to near-roadway pollution in the range of 0.10 to 0.18.
7.2. Comparisons of Estimates
A natural question is how the estimates compare to estimates from the existing literature. I consider several relevant comparisons from the existing literature: time-series estimates of the effects of short-run exposure; long-difference estimates from Pope, Ezzati, and Dockery (2009); cross-sectional estimates from Dockery et al. (1993) (the “Six City study”); and RD estimates from Chen et al. (2013). Making these comparisons requires some transformation of the results.
Pope et al. (1999) summarize an extensive literature estimating the mortality effects of short-run exposure to particulates using daily time-series data. They find consistent estimates of a 0.5%–1.5% increase in mortality rates in response to a 10 μg/m3 increase in particulate pollution. Lipfert and Wyzga (1995) translate these effects into elasticities in a meta-analysis and find an average elasticity of daily adult mortality rates to fine particulate pollution of 0.039. Most studies do not separately estimate effects for the elderly and non-elderly, but among those that do, the mortality effects appear concentrated among the elderly. To compare short-term exposure results against mine, I construct a life table using observed mortality rates in census tracts within 1 km of Los Angeles Basin highways. I compare the projected effects of a 10% increase in pollution using my estimates with the projected effects of the same increase using estimates from studies examining short-term exposure. Specifically, I compare the effect of a mortality elasticity of 0.14 for 75+ year olds (my average estimate) to the effect of a mortality elasticity of 0.039 for all adults (the average estimate from short-term exposure studies).
Using the life table, and assuming the estimated mortality effects occur only at age 75 and beyond, I compute that a 10% change in near-roadway air pollution changes life expectancy at birth by 0.05 years.20 In comparison, a mortality elasticity of 0.039 for all adults implies that a 10% change in pollution changes life expectancy at birth by 0.036 years. Thus my estimates are approximately 40% larger in magnitude than the implied effects from short-term exposure studies. This pattern suggests that any harvesting issues that may inflate long-run projections from daily exposure studies are more than offset by the negative impacts of cumulative long-run exposure to pollutants.
In contrast to short-term exposure studies, Pope et al. estimate that a 10% (2 μg/m3) decrease in PM2.5 over 20 years in the United States increases life expectancy by 0.12 years. My estimate that a 10% change in near-roadway air pollution changes life expectancy at birth by 0.05 years is approximately 60% smaller than the estimate from Pope et al. Thus my estimates are larger than those from daily-exposure studies but smaller than those estimated off long-run trends.21
Dockery et al. find an elasticity of mortality rates with respect to fine particle pollution (PM2.5) of approximately 0.2 when using cross-sectional data. However, their outcome is the 15-year mortality rate amongst individuals from age 25 to 74 at baseline. To compare my estimates, I compute the effect of an increase in mortality rates amongst 75+ year olds on overall mortality rates for a cohort of 25 to 74 year olds followed over 15 years. The result is an elasticity of mortality rates amongst 25 to 74 year olds with respect to near-roadway pollution of approximately 0.03,22 which is approximately seven times smaller than the cross-sectional estimate from Dockery et al.
Finally, Chen et al. estimate that a 55% increase in TSPs in China reduces life expectancy at birth by 5.5 years. Using my life table, and assuming that mortality effects occur only at age 75 and beyond, I compute that a 55% increase in near-roadway air pollution reduces life expectancy at birth by 0.24 years.23 This is approximately 23 times smaller than the estimate from Chen et al. Pollution levels in China, however, are much higher than in the US; average TSP levels in the United States were about 60 μg/m3 in 1990 (Chay and Greenstone 2003), whereas Chen et al. report average Chinese TSP levels of 350 to 550 μg/m3 (six to nine times higher).
Table 10 summarizes the findings across studies of different types. To aid in comparisons, I compute the implied effect of a 10% increase in air pollution for each study.24 The table reveals that my estimates are somewhat larger than estimates from daily time-series studies, but notably smaller than estimates from cross-sectional or long-differences studies.
Table 10.
Life expectancy estimates from existing literature.
| Effect of 10% | ||
|---|---|---|
| Study | Research design | pollution increase |
| Lipfert and Wyzga (1995) | Daily time-series analysis | 0.04 years |
| Pope, Ezzati, and Dockery (2009) | 20-year long difference | 0.12 years |
| Dockery et al. (1993) | Cross-sectional analysis | 0.22 years |
| Chen et al. (2013) | Single boundary discontinuity | 1 year |
| This study | Multiple boundary discontinuities | 0.05 years |
Notes: Effect sizes represent the implied effect of a 10% increase in pollution on life expectancy.
When reconciling my results with the existing literature, several factors are important to consider. First, the relevant particulates differ across papers. I focus on UFPs, and to a lesser degree nitrogen oxides and CO. Lipfert and Wyzga, Dockery et al., and Pope et al. focus on coarser PM2.5 (and, implicitly, other pollutants that correlate with fine particulates), and Chen et al. focus on still coarser TSPs. Second, Dockery et al. and, to a lesser degree, Pope et al. do not employ quasi-experimental research designs, so their estimates may reflect some degree of selection bias. Third, even when comparing different “long-term exposure” papers, the pollution exposure period may differ. Although the median 75 year old in my study has lived at the same location for over 25 years, younger individuals have shorter occupancy durations. The median 45–54 -year old in my study area, for example, has lived in the same location for only eight years. An eight-year exposure period is roughly comparable to the implicit exposure period in Pope et al. but is shorter than the exposure periods in Dockery et al. and Chen et al. The briefer exposure period for younger individuals could contribute to the null effects I observe on those younger than 75. Finally, the sparsity of pollution monitors and lack of UFP monitoring affect the reliability of my “first-stage” estimates. If I have overestimated the first stage, then I will underestimate the IV coefficient.
The overall trend that emerges from these comparisons is that, within the United States, studies leveraging more plausibly exogenous pollution variation appear to find smaller elasticities of mortality with respect to pollution. The largest elasticities arise in cross-sectional studies such as Dockery et al. (1993) and Pope et al. (2002). Pope, Ezzati, and Dockery (2009) employ a long-differencing strategy across cities and find elasticities that are smaller than the cross-sectional studies but larger than the ones reported here. My estimates are somewhat larger than results from papers examining the daily response of mortality rates to fluctuations in air pollution, however, suggesting that in this case the inability to account for cumulative effects outweighs the potential bias from harvesting when making long-run extrapolations from high-frequency studies.
7.3. Policy Implications
I consider the implications of my results for two relevant policies: congestion pricing and adoption of zero-emission vehicles (ZEVs). Recent work in the European context has demonstrated that congestion pricing schemes can reduce pollution levels. For example, Gibson and Carnovale (2015) estimate the pollution impacts of road pricing in Milan, Italy. They find particulate matter decreases of between 6 and 17%. I consider the effects of a generic congestion pricing policy that reduces pollution levels by 10%.
In the previous section I find that a 10% reduction in pollution increases life expectancy at birth by 0.05 years. This increase equates to an additional 78,000 life years gained across the 1.55 million individuals in my analytic sample. The economic value of this life-expectancy gain totals $7.8 billion when valuing each life year at $100,000 (Neumann, Cohen, and Weinstein 2014), or approximately $100 million for the cohort born each year in my sample area. This compares to a benefit of $257 million in reduced traveltime costs if the policy were to reduce congestion by 50% in my sample area.25 For a congestion pricing policy, the economic benefits of decreased premature mortality could be equivalent to approximately 40% of the primary time-savings benefits.
To gauge the potential benefits from regulating mobile-source pollution, I consider a policy in which I replace all cars on Los Angeles-area highways with ZEVs. To calculate the impact of this policy, I construct a counterfactual scenario in which no census blocks are ever downwind of a highway. In this scenario, applying my 2SLS estimates to the life table reveals a 0.22-year increase in life expectancy at birth. This increase equates to an additional 341,000 life years gained across the 1.55 million individuals in my analytic sample, or $34.1 billion when valuing each life year at $100,000. I do not attempt to calculate the exact cost of replacing every car in the Los Angeles Basin with a ZEV over several decades. Nevertheless, I note that there are approximately 2.9 million cars in the Los Angeles Basin, and the value of applying the federal electric vehicle tax credit to all of these vehicles equates to $21.8 billion.26 In that sense, the local air pollution benefits alone may justify a significant fraction of the current electric vehicle credit, at least in dense urban areas.27
Finally, although they are beyond the scope of this paper, it is instructive to consider other potential costs from air pollution. I measure only effects on mortality; additional effects on morbidity or medical expenditures could increase the total economic impacts of mobile-source pollution. Avoidance behavior—for example, remaining inside to try to avoid pollution—could generate further economic costs. The lack of any evidence of residential sorting with regard to downwind exposure in Tables 7 and 8 suggests that individuals are unlikely to engage in more avoidance behavior downwind of highways than they do upwind of highways. Nevertheless, avoidance behavior in the vicinity of highways could be a general equilibrium effect of mobile-source air pollution that neither my outcome nor research design would detect.
8. Conclusion
I find statistically and economically significant effects of exposure to near-roadway pollution on mortality amongst the elderly. I find no evidence of selection bias or residential sorting—both demographic characteristics and property values appear unrelated to downwind exposure—suggesting that households are generally unaware of the invisible pollution gradient.
This lack of awareness regarding the potential risks has welfare implications for sorting, adaptation, and regulation. Sorting behavior is suboptimal in that downwind households face similar prices as upwind households despite increased risk. With complete information, the relative price of downwind housing should be lower than that of upwind housing. How additional information changes the absolute prices of upwind and downwind housing depends on current household beliefs, however. If households already view highway proximity as inherently dangerous due to near-roadway pollution, then additional information on wind direction and pollutant dispersion should increase upwind prices and decrease downwind prices. But if households are unaware of the risks of near-roadway pollution, then additional information could decrease both upwind and downwind prices, with a greater effect downwind.
The ZEV simulation suggests a plausible estimate of individual willingness to pay (WTP) to avoid near-highway pollution exposure is $22,000 in the average downwind block, or approximately $66,000 per household. With an average home price of $369,000 in my analytic sample, this implies that a price difference of 15%–20% between upwind and downwind areas—corresponding to a price elasticity with respect to pollution of –0.35 to –0.47—would not be unreasonable.28 This magnitude is at the upper end of the range in Chay and Greenstone (2005), who find an elasticity of housing prices with respect to total suspended particulates of –0.2 to –0.35. The implicit price drop is not sufficiently large to suggest that it is optimal to leave downwind blocks undeveloped, but it could induce re-sorting based on risk aversion and, on the margin, encourage higher density development upwind than downwind. Adaptation is another margin of adjustment. Air filtration units cost an order of magnitude less than the implied WTP to avoid downwind areas, and they could be effective in reducing indoor exposure.29
Finally, regulation of UFPs has the potential to reduce the marginal damages of mobile-source emissions. Since UFPs are not a criteria pollutant, it is unclear how effective current automotive emission control systems are in reducing them, or what the potential for improvement is. Increasing the prevalence of ZEVs, however, would reduce UFP emissions, as well as emissions of any other relevant pollutant (e.g., CO). The ZEV policy simulation suggests that the “hyperlocal” health benefits of ZEVs may be substantial. In aggregate my estimates imply that near-highway pollution generates damages totaling tens of billions of dollars in the Los Angeles area alone. Given that over 70% of the US population lives in urbanized areas (US Census Bureau 2015), the potential nationwide impacts of near-highway pollution are considerably larger and worth considering from both research and regulatory perspectives.
Supplementary Material
Acknowledgements
The editor in charge of this paper was M. Daniele Paserman.
Acknowledgments: I thank Reed Walker, Richard Carson, Olivier Deschenes, Mark Jacobsen, and Jeremy Magruder, and seminar participants at the University of Oregon, UCSD, University of Arizona, University of Washington, Uppsala University, Lund University, University of Toronto, Hong Kong University of Science and Technology, and Georgia State University for valuable suggestions. Allison Lassiter and Sikandra Christian provided excellent research assistance. Funding for this research was provided under NIA Grant 5P30AG012839 and by the National Institute of Food and Agriculture, U.S. Department of Agriculture, under Project No. CA-B-AEC-7785-H. Any errors in the paper are the author's. Anderson is a Research Associate at NBER.
Footnotes
The issues discussed are less problematic for infants. Because infants are very young, a short-term fluctuation in pollution can represent a large change in total lifetime pollution exposure.
Quiros et al. also compared downwind weekday particle number concentrations in 2011 to concentrations from the same area in 2001 (taken from an earlier study). They found that concentrations fell 60% from 2001 to 2011, suggesting that the effects of being downwind from freeways may have declined during this period.
As noted previously, all other pollutants decay to within 15% of background levels or less by 300 m. Since the difference in average downwind frequency between an “upwind” and a “downwind” block is only of the order of 15 to 20 percentage points, the actual difference in average pollution exposure between upwind and downwind blocks would only be a maximum of 2%–3% for these other pollutants. These differences in pollution would be too small to generate a detectable effect on mortality in my data, unless the mortality effect were of a clinically implausible magnitude.
I define the three-year mortality rate for the ≥75 years of age group in census block i as follows. The numerator is the number of deaths in census block i from 1999 to 2001 among people who would be 75 years or older in 2000. The denominator is the imputed number of people living in Census Block i in 1999 who would be 75 years or older in 2000. The imputed number of people living in census block i in 1999 is the actual number of people living in census block i on 1 April 2000, plus the number of people who died between 1 January 1999 and 31 March 2000. A few blocks achieve mortality rates in excess of 1, so I drop blocks with extreme values (e.g., mortality rates greater than 1.0 or in excess of four standard deviations of what would be predicted from their population of 75+ year olds).
“Wind direction” in this case refers to the direction toward which the wind blows. However, in meteorological data, “wind direction” refers to the direction from which the wind blows.
Areas that lack residential census blocks on one side of the highway have no variation in downwind exposure within a small spatial radius. Thus, these areas do not contribute to my estimates when employing the spatial fixed effects design. Areas with a few residential census blocks on one side of the highway do contribute to my estimates, but the implicit weight they receive is very low because they have little variation in downwind exposure within a small spatial radius.
To calculate these figures, I match each census block from the analytic sample to its census tract and calculate the statistics across matched census tracts, weighting each census tract by the number of matched census blocks. If I expand the focus to all individuals over age 65, the median individual has lived at the current location for 25 years, and 73% of them have lived at the current location for at least 10 years.
Karner et al. report that elevated UFP concentrations persist out to 910 m downwind of highways when normalized against background concentrations far from highways. However, given my research design, normalizing against upwind levels is more relevant than normalizing against concentrations in areas with no highways.
 |
As in Figure 4, all variables in Figure 5 are residualized with respect to 800 meter highway segment fixed effects.
Estimating the effects using Limited Information Maximum Likelihood (LIML), whose median is generally close to the population parameter to be estimated even in cases with many instruments, generates estimates that are nearly identical to the 2SLS estimates.
To ensure that the main results are robust to the exact age cutoff used in defining the oldest age group, Table A.1 in Online Appendix A explores their sensitivity to using different age cutoffs. Columns (1) through (4) report effects on all-cause mortality and cardio-respiratory mortality for 70+ year olds. The effects are 11%–36% smaller in absolute magnitude than for 75+ year olds, but statistical significance remains unchanged. Columns (5) through (8) report effects on all-cause mortality and cardio-respiratory mortality for 65+ year olds. The effects diminish further but, with the exception of the 2SLS coefficient for cardio-respiratory mortality, remain statistically significant. Columns (9) through (12) report effects for a much younger age group, 50+ year olds. The coefficients are close to zero and reveal no significant effects for this much younger cutoff. In summary, the effects decrease for younger age groups, but persist when expanding the population to include 70–74 year olds and, in most cases, 65–69 year olds.
To predict the census block population over age 74, I use the fitted values from a regression of actual population over age 74 on a third-order polynomial of actual population age 50–74. One reason to use predicted population over age 74 instead of actual population over age 74 is that with actual population the weights are endogenous since they appear in the denominator of the dependent variable, the census block's 75+ mortality rate. Weighting by population over age 74 also raises the question of whether long-term care homes could cause clustering of elderly population in certain census blocks. I could not find any long-term care homes located next to freeways in the Los Angeles Basin, but to be cautious I also dropped any blocks with extreme values of population over age 74 (e.g., greater than 15% or 50 individuals).
This could occur if certain high-population areas (e.g., neighborhoods near downtown) are also places in which the wind does not blow as consistently or frequently.
The absence of UFP monitoring is not surprising since UFPs are not currently a regulated pollutant.
One monitor started collecting data in 2004, and another stopped collecting data in 2008. To ensure that an imbalance in sample periods across monitors does not affect my results, I estimate first-stage regressions with day-of-sample fixed effects.
On average, the two downwind monitors are downwind 26.8% of the time. The intercept for the regression in column (2) of Table 9 is 15.0, so the implied average NO2 concentration at the downwind monitors is 15.0 + 61.1 * 0.268 = 31.4. This figure is 2.1 times higher than the intercept of 15.0 (i.e., a theoretical monitor that is never downwind of the highway).
Quiros et al. take measurements at several distances on the eastern (downwind) side of I-405, but, past 150 m, the NO concentrations on operational days stabilize at double the concentrations of the closure day.
On average, the two downwind monitors are downwind 26.8% of the time, whereas the two upwind monitors are downwind 11.3% of the time. The intercept for the regression in Column (2) of Table 9 is 15.0, so the implied average NO2 concentration at the downwind monitors is 15.0 + 61.1 * 0.268 = 31.4, and the implied average NO2 concentration at the upwind monitors is 15.0 + 61.1 * 0.113 = 21.9. The proportional increase in average NO2 concentration from moving from upwind to downwind is thus 31.4/21.9 = 1.43.
My smallest estimate (OLS with no highway segment FE) generates an effect on life expectancy of 0.035 years, and my largest estimate (2SLS with highway segment FE) generates an effect on life expectancy of 0.064 years.
One concern in comparing effect magnitudes is that restricting mortality effects to 75+ year olds in my simulations may attenuate the predicted impacts if the true effects extend to younger age groups as well. However, if I apply my largest estimate for 65+ year olds (reported in Table A.1 in Online Appendix A) to individuals of age 65 and above in the life table, I compute that a 10% change in near-roadway pollution changes life expectancy at birth by 0.06 years, which is within the range of my predictions above (see Footnote 20). Even when applying the insignificant coefficients for 50+ year olds from Table A.1 in Online Appendix A and adding one standard error to these coefficients, I only project that a 10% change in near-roadway pollution changes life expectancy at birth by 0.05 to 0.08 years.
My smallest estimate (OLS with no highway segment FE) generates an elasticity of 0.02, and my largest estimate (2SLS with highway segment FE) generates an elasticity of 0.04.
My smallest estimate (OLS with no highway segment FE) generates an effect on life expectancy of 0.18 years, and my largest estimate (2SLS with highway segment FE) generates an effect on life expectancy of 0.30 years.
In the case of Dockery et al. (1993), this computation requires a life table. I use my Los Angeles life table, which is likely a reasonable approximation for the United States.
Schrank, Lomax, and Eisele (2015) report 44.1 hours of traffic delay per capita in Los Angeles in 2000. Setting the value of time at half the Los Angeles MSA median wage in 2000 implies an annual delay cost of $325 per capita (U.S. Department of Labor 2001; Parry and Small 2009), or $504 million across 1.55 million individuals in my sample area. A 50% reduction translates to $257 million.
Los Angeles County contained approximately 5.9 million registered automobiles in 2008 (California Department of Finance 2009), and the Los Angeles Basin contains approximately half the population of Los Angeles County. The federal electric vehicle tax credit is $7,500, so $7,500 * 2.9 million = $21.8 billion.
Complicating the comparison is the fact that both the costs and benefits evolve dynamically. The benefits figure does not take into account the fact that the “treated” population will include future cohorts not yet born, whereas the costs figure does not take into account that even low-maintenance electric vehicles will need replacement after two or three decades. The purpose of the comparison is thus not to conduct a precise benefit–cost analysis but to establish that the value of the life-expectancy gains and the electric vehicle credit are of the same order of magnitude.
The equilibrium effect on property values would depend on the degree of heterogeneity in WTP as well as the relative supply of upwind and downwind properties. See, for example, Sieg et al. (2004) and Kuminoff and Pope (2014).
Since UFPs are 0.1 microns or less, current air filters would need to be tested for effectiveness in reducing UFPs. High-efficiency particulate air (HEPA) filters are currently tested to remove particles greater than 0.3 microns.
References
- Arceo-Gomez Eva O., Hanna Rema, Oliva Paulina (2016). “Does the Effect of Pollution on Infant Mortality Differ between Developing and Developed Countries? Evidence from Mexico City.” Economic Journal, 126(591), 257–280. [Google Scholar]
- Banzhaf H. Spencer, Walsh Randall P. (2008). “Do People Vote with Their Feet? An Empirical Test of Tiebout's Mechanism.” American Economic Review, 98(3), 843–863. [Google Scholar]
- Barreca Alan I., Guldi Melanie, Lindo Jason M., Waddell Glen R. (2011). “Saving Babies? Revisiting the Effect of Very Low Birth Weight Classification.” The Quarterly Journal of Economics, 126, 2117–2123. [DOI] [PubMed] [Google Scholar]
- Brauner Elvira Vaclavik, Forchhammer Lykke, Møller Peter, Simonsen Jacob, Glasius Marianne, Wåhlin Peter, Raaschou-Nielsen Ole, Loft Steffen (2007). “Exposure to Ultrafine Particles from Ambient Air and Oxidative Stress-Induced DNA Damage.” Environmental Health Perspectives, 115, 1177–1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brook Robert D., Urch Bruce, Dvonch J. Timothy, Bard Robert L., Speck Mary, Keeler Gerald, Morishita Masako, Kaciroti Niko, Harkema Jack, Corey Paul, Silverman Frances, Wellenius Greg, Mittleman Murray A., Rajagopalan Sanjay, Brook Jeffrey R. (2009). “Insights Into the Mechanisms and Mediators of the Effects of Air Pollution Exposure on Blood Pressure and Vascular Function in Healthy Humans.” Hypertension, 54, 659–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- California Department of Finance (2009). 2008 California Statistical Abstract. Sacramento, CA. [Google Scholar]
- Chay Kenneth, Dobkin Carlos, Greenstone Michael (2003). “The Clean Air Act of 1970 and Adult Mortality.” Journal of Risk and Uncertainty, 27, 279–300. [Google Scholar]
- Chay Kenneth Y., Greenstone Michael (2003) “The Impact of Air Pollution on Infant Mortality: Evidence from Geographic Variation in Pollution Shocks Induced by a Recession.” The Quarterly Journal of Economics, 118, 1121–1167. [Google Scholar]
- Chay Kenneth Y., Greenstone Michael (2005). “Does Air Quality Matter? Evidence from the Housing Market.” Journal of Political Economy, 113, 376–424. [Google Scholar]
- Chen Yuyu, Ebenstein Avraham, Greenstone Michael, Li Hongbin (2013). “Evidence on the Impact of Sustained Exposure to Air Pollution on Life Expectancy from China's Huai River Policy.” Proceedings of the National Academy of Sciences, 110, 12936–12941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Committee on the Medical Effects of Air Pollutants (2015). Interim Statement on Quantifying the Association of Long-Term Average Concentrations of Nitrogen Dioxide and Mortality. Public Health England, London; https://www.gov.uk/government/publications/nitrogen-dioxide-interim-view-on-long-term-average-concentrations-and-mortality, retrieved 22 February, 2016. [Google Scholar]
- Conley Timothy G. (1999). “GMM Estimation with Cross Sectional Dependence.” Journal of Econometrics, 92, 1–45. [Google Scholar]
- Currie Janet, Neidell Matthew (2005). “Air Pollution and Infant Health: What Can We Learn from California's Recent Experience?” The Quarterly Journal of Economics, 120, 1003–1030. [Google Scholar]
- Currie Janet, Neidell Matthew, Schmieder Johannes F. (2009). “Air Pollution and Infant Health: Lessons from New Jersey.” Journal of Health Economics, 28, 688–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currie Janet, Walker Reed (2011). “Traffic Congestion and Infant Health: Evidence from E-ZPass.” American Economic Journal: Applied Economics, 3, 65–90. [Google Scholar]
- Dockery Douglas W., Pope C. Arden, Xu Xiping, Spengler John D., Ware James H., Fay Martha E., Ferris Benjamin G., Speizer Frank E. (1993). “An Association between Air Pollution and Mortality in Six US Cities.” New England Journal of Medicine, 329, 1753–1759. [DOI] [PubMed] [Google Scholar]
- Elder Alison, Couderc Jean-Philippe, Gelein Robert, Eberly Shirley, Cox Christopher, Xia Xiaojuang, Zareba Wojciech, Hopke Philip, Watts Winthrop, Kittelson David, Frampton Mark, Utell, Mark, Oberdörster Günter (2007). “Effects of On-Road Highway Aerosol Exposures on Autonomic Responses in Aged, Spontaneously Hypertensive Rats.” Inhalation Toxicology, 19, 1–12. [DOI] [PubMed] [Google Scholar]
- Elder Alison C. P., Gelein Robert, Azadniv Mitra, Frampton Mark, Finkelstein Jack, Oberdörster Günter (2004). “Systemic Effects of Inhaled Ultrafine Particles in Two Compromised, Aged Rat Strains.” Inhalation Toxicology, 16, 461–471. [DOI] [PubMed] [Google Scholar]
- Frampton Mark W., Stewart Judith C., Oberdörster Günter, Morrow Paul E., Chalupa David, Pietropaoli Anthony P., Frasier Lauren M., Speers Donna M., Cox Christopher, Huang Li-Shan, Utell Mark J. (2006). “Inhalation of Ultrafine Particles Alters Blood Leukocyte Expression of Adhesion Molecules in Humans.” Environmental Health Perspectives, 114, 51–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman Michael S., Powell Kenneth E., Hutwagner Lori, Graham LeRoy M., Teague W. Gerald (2001). “Impact of Changes in Transportation and Commuting Behaviors during the 1996 Summer Olympic Games in Atlanta on Air Quality and Childhood Asthma.” JAMA, 285, 897–905. [DOI] [PubMed] [Google Scholar]
- Gauderman W. James, Vora Hita, McConnell Rob, Berhane Kiros, Gilliland Frank, Thomas Duncan, Lurmann Fred, Avol Edward, Kunzli Nino, Jerrett Michael, Peters John(2007). “Effect of Exposure to Traffic on Lung Development from 10 to 18 Years of Age: A Cohort Study.” The Lancet, 369, 571–577. [DOI] [PubMed] [Google Scholar]
- Gibson Matthew, Carnovale Maria (2015). “The Effects of Road Pricing on Driver Behavior and Air Pollution.” Journal of Urban Economics, 89, 62–73. [Google Scholar]
- Goldstein Markus, Udry Christopher (2008). “The Profits of Power: Land Rights and Agricultural Investment in Ghana.” Journal of Political Economy, 116, 981–1022. [Google Scholar]
- Hoek Gerard, Brunekreef Bert, Goldbohm Sandra, Fischer Paul, van den Brandt Piet A. (2002). “Association between Mortality and Indicators of Traffic-Related Air Pollution in the Netherlands: A Cohort Study.” The Lancet, 360(9341), 1203–1209. [DOI] [PubMed] [Google Scholar]
- Jamriska Milan, Thomas S., Morawska Lidia, Clark B. A. (1999). “Relation between Indoor and Outdoor Exposure to Fine Particles near a Busy Arterial Road.” Indoor Air, 9, 75–84. [DOI] [PubMed] [Google Scholar]
- Jayachandran Seema. (2009). “Air Quality and Early-Life Mortality Evidence from Indonesia's Wildfires.” Journal of Human Resources, 44, 916–954. [Google Scholar]
- Karner Alex A., Eisinger Douglas S., Niemeier Deb A. (2010). “Near-Roadway Air Quality: Synthesizing the Findings from Real-World Data.” Environmental Science & Technology, 44, 5334–5344. [DOI] [PubMed] [Google Scholar]
- Knittel Christopher R., Miller Douglas L., Sanders Nicholas J.. (2016). “Caution, Drivers! Children Present: Traffic, Pollution, and Infant Health.” Review of Economics and Statistics, 98(2), 350–366. [Google Scholar]
- Kuminoff Nicolai V., Pope Jaren C. (2014). “Do ‘Capitalization Effects’ for Public Goods Reveal the Public's Willingness to Pay?” International Economic Review, 55, 1227–1250. [Google Scholar]
- Lipfert Frederick W., Wyzga Ronald E. (1995). “Air Pollution and Mortality: Issues and Uncertainties.” Journal of the Air & Waste Management Association, 45, 949–966. [DOI] [PubMed] [Google Scholar]
- Magruder Jeremy R. (2012). “High Unemployment Yet Few Small Firms: The Role of Centralized Bargaining in South Africa.” American Economic Journal: Applied Economics, 4, 138–166. [Google Scholar]
- Milford Jana B., Russell Armistead G., McRae Gregory J. (1989). “A New Approach to Photochemical Pollution Control: Implications of Spatial Patterns in Pollutant Responses to Reductions in Nitrogen Oxides and Reactive Organic Gas Emissions.” Environmental Science & Technology, 23, 1290–1301. [Google Scholar]
- Miller Kristin A., Siscovick David S., Sheppard Lianne, Shepherd Kristen, Sullivan Jeffrey H., Anderson Garnet L., Kaufman Joel D. (2007). “Long-Term Exposure to Air Pollution and Incidence of Cardiovascular Events in Women.” New England Journal of Medicine, 356, 447–458. [DOI] [PubMed] [Google Scholar]
- Morawska Lidia, Jamriska M., Guo H., Jayaratne E. R., Cao M., Summerville S. (2009). “Variation in Indoor Particle Number and PM2.5 Concentrations in a Radio Station Surrounded by Busy Roads before and after an Upgrade of the HVAC System.” Building and Environment, 44, 76–84. [Google Scholar]
- Moretti Enrico, Neidell Matthew (2011). “Pollution, Health, and Avoidance Behavior Evidence from the Ports of Los Angeles.” Journal of Human Resources, 46, 154–175. [Google Scholar]
- Nagata Yoshio, Takeuchi N. (2003). “Measurement of Odor Threshold by Triangle Odor Bag Method.” Odor Measurement Review. Office of Odor, Noise and Vibration Environmental Management Bureau, Ministry of the Environment, Government of Japan, Tokyo, Japan, pp. 118–127.
- Neumann Peter J., Cohen Joshua T., Weinstein Milton C. (2014). “Updating Cost-Effectiveness — the Curious Resilience of the $50,000-per-QALY Threshold.” New England Journal of Medicine, 371, 796–797. [DOI] [PubMed] [Google Scholar]
- Oberdörster Günter et al. (2009). “Assessment of Ambient UFP Health Effects: Linking Sources to Exposure and Responses in Extrapulmonary Organs.” Rochester PM Center Report, 1–35. [Google Scholar]
- Palmgren Finn, Wåhlin Peter, Kildesø Jan, Afshari Alireza, Fogh Christian L. (2003). “Characterisation of Particle Emissions from the Driving Car Fleet and the Contribution to Ambient and Indoor Particle Concentrations.” Physics and Chemistry of the Earth, Parts A/B/C, 28, 327–334. [Google Scholar]
- Parry Ian W. H., Small Kenneth A. (2009). “Should Urban Transit Subsidies Be Reduced?” American Economic Review, 99(3), 700–724. [Google Scholar]
- Pope C. Arden III et al. (1999). “Epidemiology of Particle Effects.” In Air Pollution and Health. Academic Press, San Diego, pp. 673–705. [Google Scholar]
- Pope C. Arden III, Ezzati Majid, Dockery Douglas W. (2009). “Fine-Particulate Air Pollution and Life Expectancy in the United States.” New England Journal of Medicine, 360, 376–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pope C. Arden III, Burnett RT, Thun MJ, Calle Eugenia E., Krewski Daniel, Ito Kazuhiko, Thurston George D. (2002). “Lung Cancer, Cardiopulmonary Mortality, and Long-Term Exposure to Fine Particulate Air Pollution.” JAMA, 287, 1132–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiros David C., Quiros David C., Zhang Qunfang, Choi Wonsik, He Meilu, Paulson Suzanne E., Winer Arthur M., Wang Rui, Zhu Yifang (2013). “Air Quality Impacts of a Scheduled 36-h Closure of a Major Highway.” Atmospheric Environment, 67, 404–414. [Google Scholar]
- Ransom Michael R., Pope C. Arden III (1995). “External Health Costs of a Steel Mill.” Contemporary Economic Policy, 13, 86–97. [Google Scholar]
- Rosenbloom Joshua I., Wilker Elissa H., Mukamal Kenneth J., Schwartz Joel, Mittleman Murray A. (2012). “Residential Proximity to Major Roadway and 10-Year All-Cause Mortality after Myocardial Infarction.” Circulation, 125, 2197–2203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlenker Wolfram, Reed Walker W.. (2016). “Airports, Air Pollution, and Contemporaneous Health.” Review of Economics Studies, 83(2), 768–809. [Google Scholar]
- Schrank David, Lomax Tim, Eisele Bill (2015). 2015 Urban Mobility Scorecard. Texas Transportation Institute, College Station, TX: http://mobility.tamu.edu. [Google Scholar]
- Shu Shi, Yang Pu, Zhu Yifang (2014). “Correlation of Noise Levels and Particulate Matter Concentrations near Two Major Freeways in Los Angeles, California.” Environmental Pollution, 193, 130–137. [DOI] [PubMed] [Google Scholar]
- Sieg Holger, Kerry Smith V., Spencer Banzhaf H., Walsh Randy (2004). “Estimating the General Equilibrium Benefits of Large Changes in Spatially Delineated Public Goods*.” International Economic Review, 45, 1047–1077. [Google Scholar]
- South Coast Air Quality Management District (2014) “VOC White Paper.” Presented at the Diamond Bar, CA. http://www.aqmd.gov/docs/default-source/Agendas/aqmp/white-paper-working-groups/voc-white-paper-draft-presentation-final-(080114).pdf?sfvrsn=2, retrieved 22 February, 2016.
- Stock James H, Wright Jonathan H, Yogo Motohiro (2002). “A Survey of Weak Instruments and Weak Identification in Generalized Method of Moments.” Journal of Business & Economic Statistics, 20, 518–529. [Google Scholar]
- United States Census Bureau (2015). “2010 Census Urban and Rural Classification and Urban Area Criteria.” http://www.census.gov/geo/reference/ua/urban-rural-(2010).html, retrieved 2 July 2015.
- ——— (2016). “Census Data API.” http://api.census.gov/data/2000/sf3.html, retrieved 5 February 2016.
- United States Environmental Protection Agency (2011). “The Benefits and Costs of the Clean Air Act from 1990 to (2020).”
- ——— (2014). “State and County Emission Summaries | Air Emission Sources | US EPA.”
- US Department of Labor (2001). Los Angeles–Riverside–Orange County, CA National Compensation Survey April 2000. Washington, DC. [Google Scholar]
- Vinzents Peter S., Møller Peter, Sørensen Mette, Knudsen Lisbeth E., Hertel Ole, Jensen Finn Palmgren, Schibye Bente, Loft Steffen(2005). “Personal Exposure to Ultrafine Particles and Oxidative DNA Damage.” Environmental Health Perspectives, 113, 1485–1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.