A healthcare logistic network considering stochastic emission of contamination: Bi-objective model and solution algorithm

Highlights

• •A novel healthcare waste location-routing problem is developed with a new perspective in healthcare logistics networks.
• •A stochastic essence for the emission of contamination is considered.
• •The management of medical wastes in Coronavirus Disease 2019 is focused.
• •A real case study is modeled to manage the logistics of infectious and non-infectious healthcare wastes.
• •A Multi-Objective Water-Flow like Algorithm with novel operators is developed and compared with the others.

Abstract

This paper presents a novel healthcare waste location-routing problem by concentrating on a new perspective in healthcare logistics networks. In this problem, there are healthcare, treatment, and disposal centers. Locations of healthcare centers are known, however, it is required to select appropriate locations for treatment, recycling, and disposal centers. Healthcare wastes are divided into infectious and non-infectious wastes. Since a great volume of healthcare wastes are infectious, the emission of contamination can have obnoxious impacts on the environment. The proposed problem considers a stochastic essence for the emission of contamination which depends on the transferring times. In this respect, transferring times between healthcare and treatment centers have been considered as normal random variables. As transferring time increases, it is more likely for the contamination to spread. Having visited a treatment center, infectious wastes are sterilized and they will no longer be harmful to the environment. This research develops a bi-objective mixed-integer mathematical formulation to tackle this problem. The objectives of this model are minimization of total costs and emission of contamination, simultaneously. Complexity of the proposed problem led the researchers to another contribution. This study also develops a Multi-Objective Water-Flow like Algorithm (MOWFA), which is a meta-heuristic, to solve the problem. This algorithm uses a procedure based on the Analytical Hierarchy Process (AHP) to rank the non-dominated solutions in the archive set. By means of a developed mating operator, the MOWFA utilizes the best ranked solutions of the archive in order to obtain high quality offspring. Two neighborhood operators have been designed for the MOWFA as the local search methods. Extensive computational experiments have been conducted to evaluate the effectiveness of the MOWFA on several test problems compared with other meta-heuristics, namely the Multi-Objective Imperialist Competitive Algorithm (MOICA) and Multi-Objective Simulated Annealing (MOSA). These experiments also include a real healthcare waste logistic network in Iran. The computational experiments demonstrate that our proposed algorithm prevails these algorithms in terms of some well-known performance evaluation measures.

1. Introduction

Industrialization and population growth have led the world to rapid increase of waste generation (Dehghani et al., 2019). Among different types of wastes, managing healthcare wastes has always been a crucial environmental concern for human beings. In developing countries, healthcare waste generation is increasing rapidly since the access to medical services has been improved, and therefore more individuals go to healthcare centers to undergo medical procedures (Windfeld and Brooks, 2015). The amount of medical wastes generated in each country depends on its medical situations. Lee et al. (2004) summarized the generation rate of medical wastes in different countries. Inappropriate handling of healthcare wastes can be a threat to public health (Alagöz and Kocasoy, 2008). For providing healthcare services to the growing population, the number of healthcare institutions has been increased in the whole world. As the number of healthcare centers increases, the amount of healthcare wastes grows remarkably. However, if the healthcare wastes are not tackled properly, it may have detrimental effects on the environment. Healthcare wastes are produced because of medical treatment, scientific experiments, and health protection. These wastes can be categorized into infectious and non-infectious wastes. Infectious wastes are defined as hazardous materials that are suspected of having pathogens in sufficient amounts to impose disease on susceptible preys. Living organisms are affected and diseased by the toxins of these viable microorganisms. Parasites, bacteria, viruses, and fungi are examples of pathogens. The following materials are considered as infectious wastes: (1) infectious materials used in autopsies, surgeries, and laboratory works on the individuals with contagious diseases, (2) infected bodies of animals undergoing experiments in laboratories, (3) infectious materials collected from the patients which have been isolated in specific wards. These materials include body fluids, clothes, swabs, glassware substances, gloves used in surgeries, or bandages stained by infected wounds, feces, sputum, etc., and (4) other substances that were in touch with infected individuals. There are several sources that produce healthcare wastes such as hospitals, animal research centers, nursing homes, ambulance service providers, mortuaries, laboratories, wards of drug addicts, dental clinics, etc. All these establishments in this study have been considered as healthcare centers. Non-infectious wastes are non-hazardous substances that are not toxic, genotoxic, flammable, corrosive, etc. (Marinković et al., 2008). This type of wastes poses no health risk and there is no need for a particular method to disinfect them. Expired drugs, blister packs, and plasters are examples of non-infectious wastes.

Despite the existence of considerable number of studies on the healthcare waste management, many modifications can be applied to this field in order to capture practical aspects of this problem. One of the most important concepts that can be added to the logistic network of healthcare wastes is the emission of contamination when these wastes are transported from healthcare centers to the treatment centers. Therefore, one of the contributions of this study is to incorporate the concept of releasing hazardous emissions to the environment. The World Health Organization (WHO, 2014) has offered a handbook on safe management of healthcare wastes. In this handbook, the WHO offers some advice for preventing and handling spillages that proves the possibility of hazardous emissions to the surroundings during transportation. To see this handbook, please visit “https://www.who.int/news-room/fact-sheets/detail/health-care-waste” and “https://www.who.int/water_sanitation_health/publications/wastemanag/en/”. Moreover, the WHO discussed various key factors on sound management of healthcare wastes. This means that managing healthcare wastes is a challenging and worldwide issue in real life. Therefore, different aspects of healthcare waste management such as transportation of these wastes should be tackled more accurately. According to the aforementioned reasons, the motivation of the current study is justified. In the proposed logistic network of this study, the infectious wastes are transferred to the treatment centers, while the non-infectious substances are required to be treated in recycling centers. Therefore, it is vital to separate the infectious wastes from the non-infectious materials in the healthcare centers. Since the infectious wastes are not neutralized properly or thoroughly in healthcare centers, risks are inevitable for the workers and the environment. The emission of contamination has a stochastic essence since it depends on various factors such as the length of transferring times. Hence, it is significant to consider the probability of hazardous emissions in designing a logistic network for healthcare wastes. An example which intensifies the importance of this research is the pandemic of the Coronavirus Disease 2019 (COVID-19) that generates considerable volume of medical wastes in each day. Therefore, there is a necessity for safe management of such wastes especially when these wastes are moved off-site. More information can be found at the WHO guidance, “Safe management of wastes from health-care activities” (WHO, 2014).

As another contribution, this research proposes a bi-objective model for the healthcare waste location-routing problem. Due to transportation of infectious wastes in the healthcare logistic network, it is possible that the emissions grow larger as the transportation time increases, and therefore the surrounding environment will be at risk. In the proposed model, transferring times between healthcare and treatment centers have been considered as normal random variables. In this research, the transferring times have been acquired from a real-life case study and they are proven to have normal distribution by conducting normality test. To integrate the stochastic essence of the emissions to the problem, the emission values are treated as random variables as well. The fleet of vehicles is heterogeneous, and there are time windows for visiting healthcare centers. The objectives of the model are to minimize total costs and release of contamination, concurrently. The location-routing problem is NP-hard because of its high intricacy (Nagy and Salhi, 2007, Samanlioglu, 2013). Therefore, the complexity of this problem convinced the authors to use multi-objective meta-heuristics in order to find high quality solutions within reasonable running times. The researchers have extended the contribution of this study by developing a Multi-Objective Water-Flow like Algorithm (MOWFA) to optimize the objectives. The MOWFA uses a heuristic based on a Multi-Attribute Decision Making (MADM) approach to rank non-dominated solutions so as to generate more appropriate offspring from the best ranked individuals. For the local search of the proposed algorithm, we designed two new neighborhood operators to find new solutions with respect to the solution representation and solution space of the problem. A dataset consisting of 45 test problems has been generated. To assess the performance of the proposed algorithm, two other methods have been utilized to solve the problem. A comprehensive set of experiments has been conducted and the results from implementation of all methods have been discussed.

The rest of this research is formed as follows: Section 2 discusses the literature and elaborates on the research gap which has been tackled in this study. Section 3 details the problem and the proposed mathematical model is presented. Section 4 develops a new algorithm based on the classical version of the water-flow like algorithm (Yang and Wang, 2007) to solve the problem. Experimental comparisons are made between the proposed method and two other meta-heuristics in Section 5. Section 5 also introduces a large-size real case study in Iran to demonstrate the practicality of our model and prove the efficacy of the proposed algorithm in providing diverse scenarios for decision makers. This paper has been concluded in Section 6 and some suggestions for future studies are provided in this section as well.

2. Related works

Nowadays, the production of medical wastes, along with its environmental and economic difficulties, has challenged urban management systems regarding collection, treatment, recycling, and disposal of these wastes. A great share of waste management costs is associated with waste collection, transportation, treatment, and recycling. In this respect, focusing on assessment and optimization of waste management systems can lead to reduction of issues (Babaee Tirkolaee et al., 2019). The problem of medical waste collection is a variant of the Vehicle Routing Problem (VRP). The VRP has a widespread practicality in well-known problems such as supply chain management, transportation, communications, etc. Because of detrimental threat of medical wastes to human health and environment, we have seen a growing interest in waste collection problems (Nolz et al., 2014). Since there are many influential factors that affect a healthcare waste network, there exists significant research gaps that should be tackled to provide more realistic solutions for real-life networks. A healthcare waste network comprises different factors such as treatment, recycling, and disposal centers. Treatment centers are set up to decrease or sterilize hazards of wastes. The process of treatment is supposed to disinfect wastes such that there will be no danger for subsequent disposal or recycling. For treating wastes, there are several available technologies that can be used to neutralize infectious wastes: (1) Incineration of wastes: through incinerating wastes, pathogens will be destroyed and turned into ashes. Pyrolysis and gasification are alternative thermal-based treatment technologies, (2) Autoclave devices: these devices utilize steam along with pressure to lessen the amount of microbiological entities in infectious wastes to a safe level at which these wastes can be recycled or dumped without high risk. Autoclaves are common tools which are usually used for disinfecting biomedical wastes, (3) Microwave irradiation: this technology operates based on non-contact heating infectious materials. Microwave irradiation requires less cycle time comparing to some other technologies, (4) Ethylene Oxide (EO) sterilization: In the EO technology, the sterilization process is carried out via a low temperature gas. In this method, the surface of materials are sterilized by a vacuum-based process. Since the EO uses low temperature gas, it is suitable for a wide range of materials. Through the EO sterilization, the cellular metabolism and reproduction of microorganisms are prevented.

Other than treating wastes, the process of recycling these materials is a factor of high importance as well. Recycling can be considered as a waste removal strategy in the healthcare industry. By recycling healthcare wastes, the consumption of raw materials will be decreased, and consequently the amount of wastes that must be dumped in a disposal site will be lessened as well.

Another main factor in the healthcare waste chain is the disposal centers. If the disposal centers are not appropriately constructed, the untreated medical wastes can contaminate potable, surface, and ground waters. Absence of proper waste disposal systems is a major issue associated with healthcare wastes. To investigate whether the previous studies have considered these important factors in their proposed healthcare networks or not, the authors have decided to extract these elements from the existing researches and provide a summary of literature in Table 1 . Moreover, the details of the most relevant studies have been reviewed as well: Shih and Chang (2001) designed a computer system for the infectious waste collection problem. This computer system has been used to: (1) determine routes for the collection vehicles, and (2) assign routes to each day of the week. Sheng et al. (2006) used the fuzzy measure method, weighting approach, and compromised programming method to solve the vehicle routing problem for transferring hospital materials. Nuortio et al. (2006) presented a conceptual model for the waste collection problem and applied it in a real-case study in Eastern Finland. They also developed a Guided Variable Neighborhood Thresholding (GVNT) algorithm. A mixed-integer mathematical model has been developed by Alumur and Kara (2007) for the hazardous location-routing problem. Alagöz and Kocasoy (2008) evaluated the optimum routes by means of software programs such as MapInfo and Roadnet for collecting healthcare wastes in Istanbul, Turkey. A geographic information-based system has been developed by Shanmugasundaram et al. (2012) for the healthcare waste management problem. Samanlioglu (2013) presented a multi-objective model for the location-routing problem which has been used for managing industrial hazardous wastes in the Marmara region of Turkey. The proposed model aimed to minimize total costs, transportation risk, and total risk for the population existing around the disposal and treatment sites. Hachicha et al. (2014) modeled the off-site transportation of infectious healthcare wastes as a Capacitated Vehicle Routing Problem (CVRP). Nolz et al. (2014) focused on an inventory routing problem and they applied it for the collection of infectious medical materials. Zhao et al. (2016) developed improved approaches for the network design problem that has been applied in a hazardous waste management system. They have used three multi-objective optimization methods including: (1) Weighted-Sum Method (WSM), (2) Augmented Weighted Tchebycheff Method (AWTM), and (3) Augmented ε-constraint Method (AECM) to solve the proposed problem. Naji-Azimi et al. (2016) focused on the Multi-Trip Vehicle Routing Problem (MT-VRP) for transportation of biomedical samples. They considered a time window for each request and tried to desynchronize the arrivals of biomedical samples through managing: (1) routes ordering, and (2) departure times of vehicles. The researchers developed a multi-start heuristic to solve the model. A grey-AHP approach has been proposed by Thakur and Ramesh (2017) for selecting a healthcare waste disposal strategy in Uttarakhand, Northern State of India. An optimization model has been proposed by Mantzaras and Voudrias (2017) for collection, transportation, treatment, and disposal of healthcare wastes. Hajar et al. (2018) studied the on-site medical waste collection problem and modeled it as a vehicle routing problem with time windows. Rabbani et al. (2018a) proposed a multi-objective model for collection of hazardous wastes. Their proposed model targeted to minimize: (1) transportation and construction costs, (2) population and environmental risks. They developed an augmented $\epsilon$-constraint method to solve the problem. In another study, Rabbani et al. (2018b) developed a new model for the industrial hazardous waste locating-routing problem, where there are compatibility restrictions between some types of wastes. To find solutions to their model, they used two meta-heuristics, namely the Non-dominated Sorting Genetic Algorithm II (NSGA-II) and Multi-Objective Particle Swarm Optimization (MOPSO) algorithm. Wichapa and Khokhajaikiat (2018) focused on the location routing problem for the disposal of infectious wastes. They developed a hybrid approach consisting of the AHP, Genetic Algorithm (GA), and Goal Programming (GP) method. Baradaran et al. (2019) studied the stochastic vehicle routing problem, where the fleet of collection vehicles is heterogeneous and there are several prioritized time windows for visiting demand nodes. They developed an Artificial Bee Colony (ABC) method to solve the problem. Babaee Tirkolaee et al. (2019) proposed a mixed-integer linear programming (MILP) model for the multi-trip VRP with time windows in an urban waste collection network. They developed a Simulated Annealing (SA) method to solve the proposed model. Khoukhi et al. (2019) developed a genetic algorithm for the multi-trip VRP with time windows and concurrent pickup and delivery, where a fleet of homogeneous vehicles is used to service a set of hospitals. Ghaderi and Burdett (2019) proposed a two-stage stochastic programming model as an integrated location and routing approach for hazardous materials transportation in multi-modal transportation systems. In the first stage, strategic decisions are made concerning the location of transfer yards and in the second stage, hazmat routing is performed.

Table 1.

Summary of the most related studies.

Research	Problem														Algorithm
	Multi-objective		Recycling center		Treatment center		Time windows		Heterogeneous fleet		Emissions		Healthcare
	Yes	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes	No
Shih and Chang (2001)		*		*		*		*		*		*	*		LINGO
Sheng et al. (2006)	*			*		*		*		*		*	*		Compromised programming method + Fuzzy measure method + Weighting method
Nuortio et al. (2006)		*		*		*	*		*			*		*	GVNT
Alumur and Kara (2007)	*		*		*			*		*		*		*	CPLEX
Alagöz and Kocasoy (2008)	*			*	*			*	*			*	*		MapInfo + Roadnet
Samanlioglu (2013)	*		*		*			*		*	*			*	Lexicographic weighted Tchebycheff
Hachicha et al. (2014)		*		*		*		*		*		*	*		CPLEX
Nolz et al. (2014)		*		*		*		*		*		*	*		Sampling method + Adaptive large neighborhood search
Zhao et al. (2016)	*		*		*			*		*		*		*	WSM, AECM, AWTM
Naji-Azimi et al. (2016)		*		*		*	*			*		*	*		Multi-start heuristic
Mantzaras and Voudrias (2017)		*		*	*			*	*			*	*		GA + Monte Carlo simulation
Hajar et al. (2018)	*			*		*	*			*		*	*		CPLEX
Rabbani et al. (2018a)	*		*		*			*		*	*			*	AECM
Rabbani et al. (2018b)	*		*		*			*	*			*		*	NSGA-II, MOPSO
Wichapa and Khokhajaikiat (2018)	*			*	*			*		*		*	*		AHP + GP + GA
Baradaran et al. (2019)	*			*		*	*		*			*		*	ABC
Babaee Tirkolaee et al. (2019)		*		*		*	*		*			*		*	SA
Khoukhi et al. (2019)		*		*		*	*			*		*		*	GA
This paper	*		*		*		*		*		*		*		MOWFA + MOICA + MOSA

By reviewing the literature, it has become clear for the authors that the emission of contamination along with other real-life constraints in healthcare logistics transportation can be an interesting topic to focus on. Having reviewed the previous studies, this paper offers the following contributions to the literature:

• 1.According to the summary of previous studies shown in Table 1, it is obvious that there is still a need for considering emission of contamination in a healthcare logistic network. Therefore, a mixed-integer mathematical model has been proposed for the healthcare waste location-routing problem considering stochastic transferring times and emission of contamination.
• 2.To the best of the authors’ knowledge, the performance of a water-flow like algorithm has not been investigated on a healthcare waste location-routing problem. Hence, a modified version of this method is developed for the proposed problem. Evaluating the performance of a modified water-flow like algorithm in solving a healthcare transportation problem with the mentioned features was a challenge for the authors that has been tackled in this research. The effectiveness of the proposed algorithm has been demonstrated by means of computational experiments.
• 3.The proposed algorithm utilizes an MADM-based procedure for generating proper offspring.
• 4.Two neighborhood operators have been devised for the MOWFA for finding better solutions.

3. Problem statement

3.1. Problem description and notations

This study tries to provide a new mathematical formulation for the healthcare waste location-routing problem. The concern regarding the emission of hazardous contamination during transportation of infectious wastes persuaded us to incorporate this concept into the proposed formulation. The developed model has been designed for two types of wastes which are known as infectious and non-infectious wastes. Both infectious and non-infectious wastes are generated at healthcare centers. Infectious and non-infectious wastes are separated from each other in healthcare centers by trained employees. A heterogeneous fleet of vehicles has been considered to collect infectious and non-infectious wastes, separately. Hence, any interaction between these two types of wastes is avoided. Collection vehicles have limited capacity. The number of available vehicles is predefined and fixed. There are some standards for containers of the vehicles used for collection of infectious wastes. The vehicles for collecting infectious wastes are usually equipped with rigid, tamper-proof, and puncture-resistant containers. These containers are impermeable and made of high-density plastics or metals that maintain the wastes safely and prevent any liquid leakage (WHO, 2014). However, these standards are not met in all countries due to high costs and unavailability of the containers with the aforementioned specifications. In the absence of these standards, there is a possibility of emission of contamination to the surroundings. Hence, the proposed model of this paper has incorporated this possibility to minimize the risk of exposure to contamination. In the proposed model, it is not allowed to collect the wastes of a healthcare center partially. The whole amount of each waste type produced at a healthcare center cannot be more than the capacity of the vehicle that is assigned for collection of that type of waste. To collect each type of waste, each healthcare center is visited precisely once by merely one vehicle.

The proposed network consists of four main elements: a set of healthcare centers, and three sets of facilities including treatment, recycling, and disposal centers (Rabbani et al., 2018b). Treatment, recycling, and disposal centers are capacitated. The locations of healthcare centers are known and predefined. However, the locations of treatment, recycling, and disposal centers are determined by the proposed model. A limited number of treatment, recycling, and disposal centers can be established. After visiting a set of healthcare centers, a collection vehicle has two options to drop off its load: (1) if its load is infectious, the vehicle moves to a treatment center, and (2) if its load is non-infectious, the vehicle will visit a recycling center. After treating the infectious wastes, the residues can be either recyclable or non-recyclable. Recyclable wastes are moved to recycling centers, while the others are transferred to disposal centers. Waste residues that are generated by the recycling process will also be transported to disposal centers. The technologies used in treatment centers to treat infectious wastes are not the same. Each treatment center can be established with at most one treatment technology. Time windows are considered for collecting infectious and non-infectious wastes from healthcare centers. Violating a time window will cost a penalty on the network. The time-lapse between generation and treatment of wastes must not exceed 72 h in winter and 48 h in summer. However, due to limitation of space in healthcare centers, both types of wastes must be collected on daily basis. All amounts of infectious and non-infectious wastes must be collected from healthcare centers. All parameters are deterministic except for the traveling times between the healthcare and treatment centers. Graphical display of this network has been depicted in Fig. 1 .

Fig. 1.

Graphical display of the proposed network.

The notations used to formulate the proposed model are introduced below:

Sets:
$\mathit{IW}:$	Set of infectious wastes ($\mathit{iw}=1,2,\cdots ,I)$.
$\mathit{NW}:$	Set of non-infectious wastes ($\mathit{nw}=1,2,\cdots ,NI)$.
$\mathrm{\Lambda }:$	Set of healthcare centers ($h,\stackrel{´}{h}=1,2,\cdots ,H)$.
$\mathrm{\Theta }:$	Set of treatment centers ($\mathit{tc}=1,2,\cdots ,TC)$.
$\mathrm{\Gamma }:$	Set of recycling centers ($\mathit{rc}=1,2,\cdots ,RC)$.
$\mathrm{Y}:$	Set of disposal centers ($\mathit{dc}=1,2,\cdots ,DC)$.
$\mathrm{\Psi }:$	Set of treatment technologies ($\mathit{tt}=1,2,\cdots ,TT$).
$\mathrm{\Omega }:$	Set of vehicles for collection of infectious wastes ($\mathit{vi}=1,2,\cdots ,VI$).
$\mathrm{\Delta }:$	Set of vehicles for collection of non-infectious wastes ($\mathit{vn}=1,2,\cdots ,VN$).
Parameters:
${\mathit{CTC}}_{\mathit{tc},tt}:$	Cost of setting up the treatment center $\mathit{tc}$ with the technology$\mathit{tt}$.
${\mathit{CRC}}_{\mathit{rc}}:$	Cost of setting up the recycling center$\mathit{rc}$.
${\mathit{CDC}}_{\mathit{dc}}:$	Cost of setting up the disposal center$\mathit{dc}$.
$\mathit{COF}:$	Cost of fuel (per unit).
${\mathit{CIV}}_{\mathit{vi}}:$	Fixed cost of utilizing the vehicle $\mathit{vi}$ to collect infectious wastes.
${\mathit{CNV}}_{\mathit{vn}}:$	Fixed cost of utilizing the vehicle $\mathit{vn}$ to collect non-infectious wastes.
${\mathit{CTI}}_{\mathit{iw},tc,tt}:$	Treatment cost of the infectious waste $\mathit{iw}$ in the treatment center $\mathit{tc}$ with the technology$\mathit{tt}$.
${\mathit{CRI}}_{\mathit{iw},rc}:$	Recycling cost of the infectious waste $\mathit{iw}$ in the recycling center$\mathit{rc}$.
${\mathit{CDI}}_{\mathit{iw},dc}:$	Disposal cost of the infectious waste $\mathit{iw}$ in the disposal center$\mathit{dc}$.
${\mathit{CRN}}_{\mathit{nw},rc}:$	Recycling cost of the non-infectious waste $\mathit{nw}$ in the recycling center$\mathit{rc}$.
${\mathit{CDN}}_{\mathit{nw},dc}:$	Disposal cost of the non-infectious waste $\mathit{nw}$ in the disposal center$\mathit{dc}$.
${\mathit{TIHT}}_{\mathit{iw},h,tc}:$	Per unit cost of transferring the infectious waste $\mathit{iw}$ from the healthcare center $h$ to the treatment center$\mathit{tc}$.
${\mathit{TITR}}_{\mathit{iw},tc,rc}:$	Per unit cost of transferring the infectious waste $\mathit{iw}$ from the treatment center $\mathit{tc}$ to the recycling center$\mathit{rc}$.
${\mathit{TITD}}_{\mathit{iw},tc,dc}:$	Per unit cost of transferring the infectious waste $\mathit{iw}$ from the treatment center $\mathit{tc}$ to the disposal center$\mathit{dc}$.
${\mathit{TIRD}}_{\mathit{iw},rc,dc}:$	Per unit cost of transferring the infectious waste $\mathit{iw}$ from the recycling center $\mathit{rc}$ to the disposal center$\mathit{dc}$.
${\mathit{TNHR}}_{\mathit{nw},h,rc}:$	Per unit cost of transferring the non-infectious waste $\mathit{nw}$ from the healthcare center $h$ to the recycling center$\mathit{rc}$.
${\mathit{TNTD}}_{\mathit{nw},rc,dc}:$	Per unit cost of transferring the non-infectious waste $\mathit{nw}$ from the recycling center $\mathit{rc}$ to the disposal center$\mathit{dc}$.
${\mathit{DH}}_{h,\stackrel{´}{h}}:$	Distance between the healthcare centers $h$ and $\stackrel{´}{h}$ ($h\ne \stackrel{´}{h}$).
${\mathit{DT}}_{h,tc}:$	Distance between the healthcare center $h$ and the treatment center$\mathit{tc}$.
${\mathit{DR}}_{h,rc}:$	Distance between the healthcare center $h$ and the recycling center$\mathit{rc}$.
${\mathit{DTR}}_{\mathit{tc},rc}:$	Distance between the treatment center $\mathit{tc}$ and the recycling center$\mathit{rc}$.
${\mathit{DTD}}_{\mathit{tc},dc}:$	Distance between the treatment center $\mathit{tc}$ and the disposal center$\mathit{dc}$.
${\mathit{DRD}}_{\mathit{rc},dc}:$	Distance between the recycling center $\mathit{rc}$ and the disposal center$\mathit{dc}$.
${\mathit{TBH}}_{h,\stackrel{´}{h}}:$	Transferring time between the healthcare centers $h$ and $\stackrel{´}{h}$ ($h\ne \stackrel{´}{h}$).
${\mathit{THTC}}_{h,tc}:$	Transferring time between the healthcare center $h$ and the treatment center$\mathit{tc}$.
${\mathit{ACI}}_{\mathit{vi}}:$	Available capacity of the vehicle $\mathit{vi}$ for collection of infectious wastes.
${\mathit{ACN}}_{\mathit{vn}}:$	Available capacity of the vehicle $\mathit{vn}$ for collection of non-infectious wastes.
${\mathit{ACTC}}_{\mathit{tc}}:$	Available capacity of the treatment center$\mathit{tc}$.
${\mathit{ACRC}}_{\mathit{rc}}:$	Available capacity of the recycling center$\mathit{rc}$.
${\mathit{ACDC}}_{\mathit{dc}}:$	Available capacity of the disposal center$\mathit{dc}$.
${\mathit{LBI}}_h:$	Lower bound of the time window considered for collection of infectious wastes from the healthcare center$h$.
${\mathit{UBI}}_h:$	Upper bound of the time window considered for collection of infectious wastes from the healthcare center$h$.
${\mathit{LBN}}_h:$	Lower bound of the time window considered for collection of non-infectious wastes from the healthcare center$h$.
${\mathit{UBN}}_h:$	Upper bound of the time window considered for collection of non-infectious wastes from the healthcare center$h$.
${\mathit{QI}}_{\mathit{iw},h}:$	Quantity of the infectious waste $\mathit{iw}$ generated by the healthcare center$h$.
${\mathit{QN}}_{\mathit{nw},h}:$	Quantity of the non-infectious waste $\mathit{nw}$ generated by the healthcare center$h$.
$\mathit{MNT}:$	Maximum number of treatment centers.
$\mathit{MNR}:$	Maximum number of recycling centers.
$\mathit{MND}:$	Maximum number of disposal centers.
${\mathit{RRI}}_{\mathit{iw},tc,tt}:$	Rate of recyclable infectious waste $\mathit{iw}$ in the treatment center $\mathit{tc}$ with the treatment technology$\mathit{tt}$.
${\mathit{RCI}}_{\mathit{iw},rc}:$	Rate of recyclable infectious waste $\mathit{iw}$ in the recycling center$\mathit{rc}$.
${\mathit{RCN}}_{\mathit{nw},rc}:$	Rate of recyclable non-infectious waste $\mathit{nw}$ in the recycling center$\mathit{rc}$.
${\alpha }_{\mathit{iw}}:$	Emission coefficient of the infectious waste$\mathit{iw}$ (${\alpha }_{\mathit{iw}}\in (0,1])$.
$\mathit{pen}:$	Penalty cost imposed on the network if a time window is violated.
$M:$	A considerably large number.
${\mathit{TECH}}_{\mathit{tc},tt}:$	=1, if the treatment center $\mathit{tc}$ has the treatment technology$\mathit{tt}$; otherwise, =0.
${\mathit{ICT}}_{\mathit{iw},tt}:$	=1, if the infectious waste $\mathit{iw}$ can be treated by the technology$\mathit{tt}$; otherwise, =0.
Decision variables:
${\mathit{ATI}}_{\mathit{vi},h}:$	Amount of time violated by the vehicle $\mathit{vi}$ in visiting the healthcare center$h$ for collecting infectious wastes.
${\mathit{ATN}}_{\mathit{vn},h}:$	Amount of time violated by the vehicle $\mathit{vn}$ in visiting the healthcare center$h$ for collecting non-infectious wastes.
${\mathit{AITH}}_{\mathit{iw},tc,h,vi}:$	Amount of the infectious waste $\mathit{iw}$ received by the treatment center $\mathit{tc}$ from the healthcare center $h$ using the vehicle$\mathit{vi}$.
${\mathit{AIRT}}_{\mathit{iw},rc,tc,vi}:$	Amount of the infectious waste $\mathit{iw}$ received by the recycling center $\mathit{rc}$ from treatment center $\mathit{tc}$ using the vehicle$\mathit{vi}$.
${\mathit{AIDT}}_{\mathit{iw},dc,tc,vi}:$	Amount of the infectious waste $\mathit{iw}$ received by the disposal center $\mathit{dc}$ from the treatment center $\mathit{tc}$ using the vehicle$\mathit{vi}$.
${\mathit{AIDR}}_{\mathit{iw},dc,rc,vi}:$	Amount of the infectious waste $\mathit{iw}$ received by the disposal center $\mathit{dc}$ from the recycling center $\mathit{rc}$ using the vehicle$\mathit{vi}$.
${\mathit{ANRH}}_{\mathit{nw},rc,h,vn}:$	Amount of the non-infectious waste $\mathit{nw}$ received by the recycling center $\mathit{rc}$ from the healthcare center $h$ using the vehicle$\mathit{vn}$.
${\mathit{ANDR}}_{\mathit{nw},dc,rc,vn}:$	Amount of the non-infectious waste $\mathit{nw}$ received by the disposal center $\mathit{dc}$ from the recycling center $\mathit{rc}$ using the vehicle$\mathit{vn}$.
${\mathit{ETI}}_{\mathit{vi},h}:$	Entrance time of the vehicle $\mathit{vi}$ in the healthcare center $h$ (For collecting infectious wastes).
${\mathit{ETN}}_{\mathit{vn},h}:$	Entrance time of the vehicle $\mathit{vn}$ in the healthcare center $h$ (For collecting non-infectious wastes).
${\mathit{Cont}}_{\mathit{iw}}:$	Amount of emission of contamination while transferring the infectious waste$\mathit{iw}$.
$Z_1:$	First objective function (total costs of the network).
$Z_2:$	Second objective function (total emission of contamination).
${\mathit{TCE}}_{\mathit{tc},tt}:$	=1, if the treatment center $\mathit{tc}$ is established with the technology$\mathit{tt}$; otherwise, =0.
${\mathit{RCE}}_{\mathit{rc}}:$	=1, if the recycling center $\mathit{rc}$ is established; otherwise, =0.
${\mathit{DCE}}_{\mathit{dc}}:$	=1, if the disposal center $\mathit{dc}$ is established; otherwise, =0.
${\mathit{VIW}}_{\mathit{vi}}:$	=1, if the vehicle $\mathit{vi}$ is used for collection of infectious wastes; otherwise, =0.
${\mathit{VN}}_{\mathit{vn}}:$	=1, if the vehicle $\mathit{vn}$ is used for collection of non-infectious wastes; otherwise, =0.
${\mathit{VITC}}_{\mathit{vi},tc}:$	=1, if the vehicle $\mathit{vi}$ is allocated to the treatment center$\mathit{tc}$; otherwise, =0 (For infectious wastes).
${\mathit{VIRC}}_{\mathit{vi},rc}:$	=1, if the vehicle $\mathit{vi}$ is allocated to the recycling center$\mathit{rc}$; otherwise, =0 (For infectious wastes).
${\mathit{VNRC}}_{\mathit{vn},rc}:$	=1, if the vehicle $\mathit{vn}$ is allocated to the recycling center$\mathit{rc}$; otherwise, =0 (For non-infectious wastes).
${\mathit{VIDC}}_{\mathit{vi},dc}:$	=1, if the vehicle $\mathit{vi}$ is allocated to the disposal center$\mathit{dc}$; otherwise, =0 (For infectious wastes).
${\mathit{VNDC}}_{\mathit{vn},dc}:$	=1, if the vehicle $\mathit{vn}$ is allocated to the disposal center$\mathit{dc}$; otherwise, =0 (For non-infectious wastes).
${\mathit{VIH}}_{\mathit{vi},h,\stackrel{´}{h}}:$	=1, if the vehicle $\mathit{vi}$ is selected to travel from the healthcare center $h$ to the healthcare center$\stackrel{´}{h}$; otherwise, =0 (For infectious wastes).
${\mathit{VNH}}_{\mathit{vn},h,\stackrel{´}{h}}:$	=1, if the vehicle $\mathit{vn}$ is selected to travel from the healthcare center $h$ to the healthcare center$\stackrel{´}{h}$; otherwise, =0 (For non-infectious wastes).
${\mathit{TCO}}_{\mathit{tc},tt,iw}:$	=1, if the treatment center $\mathit{tc}$ has used the technology $\mathit{tt}$ to treat the infectious waste$\mathit{iw}$; otherwise, =0.
${\mathit{VHT}}_{\mathit{vi},h,tc}:$	=1, if the vehicle $\mathit{vi}$ carries infectious wastes from the healthcare center $h$ to the treatment center$\mathit{tc}$; otherwise, =0.
${\mathit{VHR}}_{\mathit{vn},h,rc}:$	=1, if the vehicle $\mathit{vn}$ carries non-infectious wastes from the healthcare center $h$ to the recycling center$\mathit{rc}$; otherwise, =0.

3.2. Mathematical formulation

Based on the assumptions mentioned in Section 3.1, a bi-objective mixed-integer programming model is proposed for the healthcare waste location-routing problem that aims to: (1) determine the routes of vehicles for collecting infectious and non-infectious wastes, (2) Specify the technology that is used by each treatment center, (3) determine the locations of treatment, recycling, and disposal centers, (4) estimate the costs of this network, (5) estimate the amount of emission that will be released to the environment. The formulation of the proposed model is as follows:

$$\mathit{Minimize}{Z}_1=\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{tt}=1}^{\mathit{TT}}\mathit{CT}{C}_{\mathit{tc},tt}\times TC{E}_{\mathit{tc},tt}+\sum _{\mathit{rc}=1}^{\mathit{RC}}\mathit{CR}{C}_{\mathit{rc}}\times RC{E}_{\mathit{rc}}+\sum _{\mathit{dc}=1}^{\mathit{DC}}\mathit{CD}{C}_{\mathit{dc}}\times DC{E}_{\mathit{dc}}$$ (1.a)

Eq. (1) is the first objective function of the model that targets to minimize the total costs of the network. The first objective function is formulated by summing Eqs. (1.a), (1.b), (1.c), (1.d), (1.e), (1.f), (1.g), (1.h), (1.i). Eq. (1.a) is associated with the costs of establishing facilities.

$$+\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{CI}{V}_{\mathit{vi}}\times VI{W}_{\mathit{vi}}+\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{CN}{V}_{\mathit{vn}}\times V{N}_{\mathit{vn}}$$ (1.b)

Eq. (1.b) formulates the fixed costs of utilizing collection vehicles.

$$+\sum _{\mathit{iw}=1}^I\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{tt}=1}^{\mathit{TT}}\sum _{h=1}^H\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{CT}{I}_{\mathit{iw},tc,tt}\times AIT{H}_{\mathit{iw},tc,h,vi}$$ (1.c)

Eq. (1.c) obtains the costs of treating infectious wastes.

$$\begin{array}{c}+\sum _{\mathit{iw}=1}^I\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{CR}{I}_{\mathit{iw},rc}\times AIR{T}_{\mathit{iw},rc,tc,vi}\\ +\sum _{\mathit{nw}=1}^{\mathit{NI}}\sum _{h=1}^H\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{CR}{N}_{\mathit{nw},rc}\times ANR{H}_{\mathit{nw},rc,h,vn}\end{array}$$ (1.d)

Recycling costs of both types of wastes are formulated in Eq. (1.d).

$$\begin{array}{c}+\sum _{\mathit{iw}=1}^I\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{CD}{I}_{\mathit{iw},dc}\times AID{T}_{\mathit{iw},dc,tc,vi}\\ +\sum _{\mathit{nw}=1}^{\mathit{NI}}\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{CD}{N}_{\mathit{nw},dc}\times AND{R}_{\mathit{nw},dc,rc,vn}\end{array}$$ (1.e)

Eq. (1.e) computes the costs of disposing of both infectious and non-infectious wastes.

$$\begin{array}{c}+\sum _{\mathit{iw}=1}^I\sum _{h=1}^H\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{TIH}{T}_{\mathit{iw},h,tc}\times AIT{H}_{\mathit{iw},tc,h,vi}\\ +\sum _{\mathit{iw}=1}^I\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{TIT}{R}_{\mathit{iw},tc,rc}\times AIR{T}_{\mathit{iw},rc,tc,vi}\\ +\sum _{\mathit{iw}=1}^I\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{TIT}{D}_{\mathit{iw},tc,dc}\times AID{T}_{\mathit{iw},dc,tc,vi}\\ +\sum _{\mathit{iw}=1}^I\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{TIR}{D}_{\mathit{iw},rc,dc}\times AID{R}_{\mathit{iw},dc,rc,vi}\end{array}$$ (1.f)

Eq. (1.f) formulates the costs of transferring infectious wastes.

$$\begin{array}{c}+\sum _{\mathit{nw}=1}^{\mathit{NI}}\sum _{h=1}^H\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{TNH}{R}_{\mathit{nw},h,rc}\times ANR{H}_{\mathit{nw},rc,h,vn}\\ +\sum _{\mathit{nw}=1}^{\mathit{NI}}\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{TNT}{D}_{\mathit{nw},rc,dc}\times AND{R}_{\mathit{nw},dc,rc,vn}\end{array}$$ (1.g)

The costs of transferring non-infectious wastes have been formulated in Eq. (1.g).

$$+pen(\sum _{h=1}^H\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{AT}{I}_{\mathit{vi},h}\times VI{W}_{\mathit{vi}}+\sum _{h=1}^H\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{AT}{N}_{\mathit{vn},h}\times V{N}_{\mathit{vn}})$$ (1.h)

Eq. (1.h) obtains the costs of violating time windows.

$$\begin{array}{c}+COF(\sum _{h=1}^H\sum _{h^{\prime }=1}^H\sum _{\mathit{vi}=1}^{\mathit{VI}}D{H}_{h,h^{\prime }}\times VI{H}_{\mathit{vi},h,h^{\prime }}+\sum _{h=1}^H\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}D{T}_{h,tc}\times VIT{C}_{\mathit{vi},tc}\\ +\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{DT}{R}_{\mathit{tc},rc}\times VIR{C}_{\mathit{vi},rc}+\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{DT}{D}_{\mathit{tc},dc}\times VID{C}_{\mathit{vi},dc}\\ +\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{DR}{D}_{\mathit{rc},dc}\times VID{C}_{\mathit{vi},dc}+\sum _{h=1}^H\sum _{h^{\prime }=1}^H\sum _{\mathit{vn}=1}^{\mathit{VN}}D{H}_{h,h^{\prime }}\times VN{H}_{\mathit{vn},h,h^{\prime }}\\ +\sum _{h=1}^H\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{vn}=1}^{\mathit{VN}}D{R}_{h,rc}\times VNR{C}_{\mathit{vn},rc}+\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{DR}{D}_{\mathit{rc},dc}\times VND{C}_{\mathit{vn},dc})\end{array}$$ (1.i)

Eq. (1.i) calculates the costs of fuel for the utilized vehicles.

$$\mathit{Minimize}{Z}_2=\sum _{\mathit{iw}=1}^I{\mu }_{\mathit{Con}{t}_{\mathit{iw}}}$$ (2)

The second objective function is formulated in Eq. (2) that minimizes the emission of contamination to the environment.

Subject to:

$$\sum _{\mathit{iw}=1}^I\sum _{\mathit{vi}=1}^{\mathit{VI}}\sum _{h=1}^H\mathit{AIT}{H}_{\mathit{iw},tc,h,vi}\times VIT{C}_{\mathit{vi},tc}⩽ACT{C}_{\mathit{tc}}\times TC{E}_{\mathit{tc},tt}\forall tc,\forall tt$$ (3)

Constraint (3) implies that the amount of infectious wastes received by a treatment center cannot exceed the capacity of that treatment center.

$$\begin{array}{c}{\sum }_{\mathit{iw}=1}^I{\sum }_{\mathit{tc}=1}^{\mathit{TC}}{\sum }_{\mathit{vi}=1}^{\mathit{VI}}\mathit{AIR}{T}_{\mathit{iw},rc,tc,vi}\times VIR{C}_{\mathit{vi},rc}+\\ {\sum }_{\mathit{nw}=1}^{\mathit{NI}}{\sum }_{h=1}^H{\sum }_{\mathit{vn}=1}^{\mathit{VN}}\mathit{ANR}{H}_{\mathit{nw},rc,h,vn}\times VNR{C}_{\mathit{vn},rc}⩽ACR{C}_{\mathit{rc}}\times RC{E}_{\mathit{rc}}\end{array}\forall rc$$ (4)

Constraint (4) ensures that the amount of wastes (infectious and non-infectious) received by a recycling center cannot be more than its capacity.

$$\begin{array}{c}{\sum }_{\mathit{iw}=1}^I{\sum }_{\mathit{tc}=1}^{\mathit{TC}}{\sum }_{\mathit{vi}=1}^{\mathit{VI}}\mathit{AID}{T}_{\mathit{iw},dc,tc,vi}\times VID{C}_{\mathit{vi},dc}+\\ \begin{array}{c}{\sum }_{\mathit{iw}=1}^I{\sum }_{\mathit{rc}=1}^{\mathit{RC}}{\sum }_{\mathit{vi}=1}^{\mathit{VI}}\mathit{AID}{R}_{\mathit{iw},dc,rc,vi}\times VID{C}_{\mathit{vi},dc}+\\ {\sum }_{\mathit{nw}=1}^{\mathit{NI}}{\sum }_{\mathit{rc}=1}^{\mathit{RC}}{\sum }_{\mathit{vn}=1}^{\mathit{VN}}\mathit{AND}{R}_{\mathit{nw},dc,rc,vn}\times VND{C}_{\mathit{vn},dc}⩽ACD{C}_{\mathit{dc}}\times DC{E}_{\mathit{dc}}\end{array}\end{array}\forall dc$$ (5)

Constraint (5) guarantees that all amounts of wastes collected by a disposal center cannot exceed its capacity.

$$\sum _{\mathit{vi}=1}^{\mathit{VI}}\sum _{\mathit{tc}=1}^{\mathit{TC}}\mathit{AIT}{H}_{\mathit{iw},tc,h,vi}⩾Q{I}_{\mathit{iw},h}\forall iw,\forall h$$ (6)

$$\sum _{\mathit{vn}=1}^{\mathit{VN}}\sum _{\mathit{rc}=1}^{\mathit{RC}}\mathit{ANR}{H}_{\mathit{nw},rc,h,vn}⩾Q{N}_{\mathit{nw},h}\forall nw,\forall h$$ (7)

Constraints (6), (7) guarantee that all available wastes in this network are collected from healthcare centers.

$$\begin{array}{c}{\sum }_{\mathit{vi}=1}^{\mathit{VI}}{\sum }_{h=1}^H\mathit{AIT}{H}_{\mathit{iw},tc,h,vi}={\sum }_{\mathit{vi}=1}^{\mathit{VI}}{\sum }_{\mathit{rc}=1}^{\mathit{RC}}\mathit{AIR}{T}_{\mathit{iw},rc,tc,vi}+\\ {\sum }_{\mathit{vi}=1}^{\mathit{VI}}{\sum }_{\mathit{dc}=1}^{\mathit{DC}}\mathit{AID}{T}_{\mathit{iw},dc,tc,vi}\end{array};\forall iw,\forall tc$$ (8)

$$\sum _{h^{\prime }=1}^H\mathit{VI}{H}_{\mathit{vi},h^{\prime },h}=\sum _{h^{\prime }=1}^H\mathit{VI}{H}_{\mathit{vi},h,h^{\prime }};\forall vi,\forall h$$ (9)

$$\sum _{h^{\prime }=1}^H\mathit{VN}{H}_{\mathit{vn},h^{\prime },h}=\sum _{h^{\prime }=1}^H\mathit{VN}{H}_{\mathit{vn},h,h^{\prime }};\forall vn,\forall h$$ (10)

Constraints (8), (9), (10) indicate that a vehicle must leave the corresponding node of a healthcare center after completion of its service.

$$\sum _{\mathit{iw}=1}^I\sum _{h=1}^H\mathit{AIT}{H}_{\mathit{iw},tc,h,vi}\times VI{W}_{\mathit{vi}}⩽AC{I}_{\mathit{vi}};\forall vi,\forall tc$$ (11)

$$\sum _{\mathit{iw}=1}^I\sum _{\mathit{tc}=1}^{\mathit{TC}}\mathit{AIR}{T}_{\mathit{iw},rc,tc,vi}\times VI{W}_{\mathit{vi}}⩽AC{I}_{\mathit{vi}};\forall vi,\forall rc$$ (12)

$$\sum _{\mathit{iw}=1}^I\sum _{\mathit{tc}=1}^{\mathit{TC}}\mathit{AID}{T}_{\mathit{iw},dc,tc,vi}\times VI{W}_{\mathit{vi}}⩽AC{I}_{\mathit{vi}};\forall vi,\forall dc$$ (13)

$$\sum _{\mathit{iw}=1}^I\sum _{\mathit{rc}=1}^{\mathit{RC}}\mathit{AID}{R}_{\mathit{iw},dc,rc,vi}\times VI{W}_{\mathit{vi}}⩽AC{I}_{\mathit{vi}};\forall vi,\forall dc$$ (14)

$$\sum _{\mathit{nw}=1}^{\mathit{NI}}\sum _{h=1}^H\mathit{ANR}{H}_{\mathit{nw},rc,h,vn}\times V{N}_{\mathit{vn}}⩽AC{N}_{\mathit{vn}};\forall vn,\forall rc$$ (15)

$$\sum _{\mathit{nw}=1}^{\mathit{NI}}\sum _{\mathit{rc}=1}^{\mathit{RC}}\mathit{AND}{R}_{\mathit{nw},dc,rc,vn}\times V{N}_{\mathit{vn}}⩽AC{N}_{\mathit{vn}};\forall vn,\forall dc$$ (16)

Constraints (11), (12), (13), (14), (15), (16) ensure that the vehicles do not carry more than their capacities.

$$\mathit{TC}{O}_{\mathit{tc},tt,iw}⩽TEC{H}_{\mathit{tc},tt};\forall iw,\forall tc,\forall tt$$ (17)

Constraint (17) ensures that the required technology is available in treatment centers for infectious wastes.

$$\sum _{h=1}^H\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{VI}{H}_{\mathit{vi},h,h^{\prime }}\times VI{W}_{\mathit{vi}}=1;\forall h^{\prime }$$ (18)

$$\sum _{h=1}^H\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{VN}{H}_{\mathit{vn},h,h^{\prime }}\times V{N}_{\mathit{vn}}=1;\forall h^{\prime }$$ (19)

Equations (18), (19) guarantee that each healthcare center is visited exactly once.

$$\sum _{\mathit{tt}=1}^{\mathit{TT}}\mathit{TC}{E}_{\mathit{tc},tt}⩽1;\forall tc$$ (20)

Constraint (20) implies that each treatment center can be established with at most one treatment technology.

$$\sum _{\mathit{tc}=1}^{\mathit{TC}}\mathit{VIT}{C}_{\mathit{vi},tc}\times VI{W}_{\mathit{vi}}=1;\forall vi$$ (21)

$$\sum _{\mathit{rc}=1}^{\mathit{RC}}\mathit{VIR}{C}_{\mathit{vi},rc}\times VI{W}_{\mathit{vi}}=1;\forall vi$$ (22)

$$\sum _{\mathit{dc}=1}^{\mathit{DC}}\mathit{VID}{C}_{\mathit{vi},dc}\times VI{W}_{\mathit{vi}}=1;\forall vi$$ (23)

$$\sum _{\mathit{rc}=1}^{\mathit{RC}}\mathit{VNR}{C}_{\mathit{vn},rc}\times V{N}_{\mathit{vn}}=1$$ (24)

$$\sum _{\mathit{dc}=1}^{\mathit{DC}}\mathit{VND}{C}_{\mathit{vn},dc}\times V{N}_{\mathit{vn}}=1;\forall vn$$ (25)

Constraint (21), (22), (23), (24), (25) state that the vehicles must be assigned to a facility.

$$\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{VH}{T}_{\mathit{vi},h,tc}=1;\forall h,\forall tc$$ (26)

$$\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{VH}{R}_{\mathit{vn},h,rc}=1;\forall h,\forall rc$$ (27)

Constraints (26), (27) state that only one vehicle is assigned to the route between healthcare and treatment / recycling centers.

$$\mathit{ET}{I}_{\mathit{vi},h}\times \sum _{h^{\prime }=1}^H\mathit{VI}{H}_{\mathit{vi},h^{\prime },h}\times VI{W}_{\mathit{vi}}⩾LB{I}_h;\forall h,\forall vi$$ (28)

$$\mathit{ET}{I}_{\mathit{vi},h}\times \sum _{h^{\prime }=1}^H\mathit{VI}{H}_{\mathit{vi},h^{\prime },h}\times VI{W}_{\mathit{vi}}-AT{I}_{\mathit{vi},h}⩽UB{I}_h;\forall h,\forall vi$$ (29)

$$\mathit{ET}{N}_{\mathit{vn},h}\times \sum _{h^{\prime }=1}^H\mathit{VN}{H}_{\mathit{vn},h^{\prime },h}\times V{N}_{\mathit{vn}}⩾LB{N}_h;\forall h,\forall vn$$ (30)

$$\mathit{ET}{N}_{\mathit{vn},h}\times \sum _{h^{\prime }=1}^H\mathit{VN}{H}_{\mathit{vn},h^{\prime },h}\times V{N}_{\mathit{vn}}-AT{N}_{\mathit{vn},h}⩽UB{N}_h;\forall h,\forall vn$$ (31)

Violations of time windows have been obtained in Constraints (28), (29), (30), (31).

$$\mathit{Con}{t}_{\mathit{iw}}=\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{h=1}^H\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{THT}{C}_{h,tc}\times VH{T}_{\mathit{vi},h,tc}\times {\alpha }_{\mathit{iw}};\forall iw$$ (32)

Eq. (32) computes the amount of contamination that is released to the environment during transferring the infectious waste $\mathit{iw}$ to treatment centers.

$$\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{tt}=1}^{\mathit{TT}}\mathit{TC}{E}_{\mathit{tc},tt}⩽MNT$$ (33)

$$\sum _{\mathit{rc}=1}^{\mathit{RC}}\mathit{RC}{E}_{\mathit{rc}}⩽MNR$$ (34)

$$\sum _{\mathit{dc}=1}^{\mathit{DC}}\mathit{DC}{E}_{\mathit{dc}}⩽MND$$ (35)

Constraints (33), (34), (35) satisfy the limitations on the number of facilities.

$$\mathit{VIT}{C}_{\mathit{vi},tc}⩽\sum _{\mathit{iw}=1}^I\sum _{\mathit{tt}=1}^{\mathit{TT}}\mathit{IC}{T}_{\mathit{iw},tt}\times TC{E}_{\mathit{tc},tt};\forall vi,\forall tc;\forall vi,\forall tc$$ (36)

Constraint (36) secures that each collection vehicle which has been assigned to carry infectious wastes must drop its load at a treatment center with the compatible treatment technology.

$$\mathit{ET}{I}_{\mathit{vi},h}+\left(1-VI{H}_{\mathit{vi},h,h^{\prime }}\right)\times M⩾ET{I}_{\mathit{vi},h^{\prime }}+TB{H}_{h,h^{\prime }};\forall vi,\forall h,h^{\prime }>1$$ (37)

$$\mathit{ET}{N}_{\mathit{vn},h}+\left(1-VN{H}_{\mathit{vn},h,h^{\prime }}\right)\times M⩾ET{N}_{\mathit{vn},h^{\prime }}+TB{H}_{h,h^{\prime }};\forall vn,\forall h,h^{\prime }>1$$ (38)

Constraints (37), (38) secure the evasion of sub-tours.

$$\sum _{\mathit{rc}=1}^{\mathit{RC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{AIR}{T}_{\mathit{iw},rc,tc,vi}=\sum _{h=1}^H\sum _{\mathit{vi}=1}^{\mathit{VI}}\sum _{\mathit{tt}=1}^{\mathit{TT}}\mathit{RR}{I}_{\mathit{iw},tc,tt}\times AIT{H}_{\mathit{iw},tc,h,vi};\forall iw,\forall tc$$ (39)

$$\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{AID}{T}_{\mathit{iw},dc,tc,vi}=\sum _{h=1}^H\sum _{\mathit{vi}=1}^{\mathit{VI}}\sum _{\mathit{tt}=1}^{\mathit{TT}}(1-RR{I}_{\mathit{iw},tc,tt})\times AIT{H}_{\mathit{iw},tc,h,vi};\forall iw,\forall tc$$ (40)

$$\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\mathit{AID}{R}_{\mathit{iw},dc,rc,vi}=\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}\left(1-RC{I}_{\mathit{iw},rc}\right)\times AIR{T}_{\mathit{iw},rc,tc,vi};\forall iw,\forall rc$$ (41)

$$\sum _{\mathit{dc}=1}^{\mathit{DC}}\sum _{\mathit{vn}=1}^{\mathit{VN}}\mathit{AND}{R}_{\mathit{nw},dc,rc,vn}=\sum _{h=1}^H\sum _{\mathit{vn}=1}^{\mathit{VN}}\left(1-RC{N}_{\mathit{nw},rc}\right)\times ANR{H}_{\mathit{nw},rc,h,vn};\forall nw,\forall rc$$ (42)

Equations (39), (40), (41), (42) imply the flow balance between facilities.

$$\begin{array}{c}\forall h,\forall tc,\forall rc,\forall dcAT{I}_{\mathit{vi},h},AT{N}_{\mathit{vn},h},AIT{H}_{\mathit{iw},tc,h,vi},AIR{T}_{\mathit{iw},rc,tc,vi},AID{T}_{\mathit{iw},dc,tc,vi},...\\ \mathit{AID}{R}_{\mathit{iw},dc,rc,vi},ANR{H}_{\mathit{nw},rc,h,vn},AND{R}_{\mathit{nw},dc,rc,vn},ET{I}_{\mathit{vi},h},...\\ \mathit{ET}{N}_{\mathit{vn},h},Con{t}_{\mathit{iw}},Z_1,Z_2⩾0\end{array};\forall iw,\forall nw,\forall vi,\forall vn,$$

4. (43)

$$\begin{array}{c}\mathit{TC}{E}_{\mathit{tc},tt},RC{E}_{\mathit{rc}},DC{E}_{\mathit{dc}},VI{W}_{\mathit{vi}},V{N}_{\mathit{vn}},VIT{C}_{\mathit{vi},tc},...\\ \mathit{VIR}{C}_{\mathit{vi},rc},VNR{C}_{\mathit{vn},rc},VID{C}_{\mathit{vi},dc},VND{C}_{\mathit{vn},dc},...\\ \begin{array}{c}\mathit{VI}{H}_{\mathit{vi},h,h^{\prime }},VN{H}_{\mathit{vn},h,h^{\prime }},TC{O}_{\mathit{tc},tt,iw},VH{T}_{\mathit{vi},h,tc},...\\ \mathit{VH}{R}_{\mathit{vn},h,rc}\in \{0,1\}\end{array}\end{array};\begin{array}{c}\forall iw,\forall nw,\forall vi,\\ \forall vn,\forall h,\forall tc,\forall rc\\ \forall dc,\forall tt\end{array}$$ (44)

Finally, Constraints (43) and (44) show positive and binary variables, respectively

Lemma.

This lemma is presented to deliver better understanding for calculating the second objective function values. In the proposed model, the travel times between healthcare and treatment centers are normal random variables as ${\mathit{THTC}}_{h,tc}N({\mu }_{{\mathit{THTC}}_{h,tc}},{\sigma }_{{\mathit{THTC}}_{h,tc}}^2)$ . Therefore, we have ${\mathit{Cont}}_{\mathit{iw}}~N({\mu }_{{\mathit{Cont}}_{\mathit{iw}}},{\sigma }_{{\mathit{Cont}}_{\mathit{iw}}}^2$), where it is possible to obtain ${\mu }_{{\mathit{Cont}}_{\mathit{iw}}}$ and ${\sigma }_{{\mathit{Cont}}_{\mathit{iw}}}^2$ by the Equations (45), (46) , respectively.

$${\mu }_{\mathit{Con}{t}_{\mathit{iw}}}=\sum _{h=1}^H\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}{\mu }_{\mathit{THT}{C}_{h,tc}}\times VH{T}_{\mathit{vi},h,tc}\times {\alpha }_{\mathit{iw}};\forall iw$$ (45)

$${\sigma }_{\mathit{Con}{t}_{\mathit{iw}}}^2=\sum _{h=1}^H\sum _{\mathit{tc}=1}^{\mathit{TC}}\sum _{\mathit{vi}=1}^{\mathit{VI}}{\sigma }_{\mathit{THT}{C}_{h,tc}}^2\times VH{T}_{\mathit{vi},h,tc}\times {\alpha }_{\mathit{iw}}^2;\forall iw$$ (46)

Proof.

Let assume that $(iw=1,h=1,tc=1)$, therefore, ${\mathit{Cont}}_1$ is obtained as ${\alpha }_1\times {\mathit{THTC}}_{1,1}\times {\sum }_{\mathit{vi}=1}^{\mathit{VI}}{\mathit{VHT}}_{\mathit{vi},1,1}$. According to Eq. (26), we have ${\sum }_{\mathit{vi}=1}^{\mathit{VI}}{\mathit{VHT}}_{\mathit{vi},1,1}$ = 1. Hence, ${\mu }_{{\mathit{Cont}}_1}={\alpha }_1\times {\mu }_{{\mathit{THTC}}_{1,1}}\times {\sum }_{\mathit{vi}=1}^{\mathit{VI}}{\mathit{VHT}}_{\mathit{vi},1,1}$ and ${\sigma }_{{\mathit{Cont}}_1}^2={\alpha }_1^2\times {\sigma }_{{\mathit{THTC}}_{1,1}}^2\times {\sum }_{\mathit{vi}=1}^{\mathit{VI}}{\mathit{VHT}}_{\mathit{vi},1,1}$. The generalized perspective for all infectious wastes proves this lemma.

5. Solution methodology

The location-routing problem is known to have an NP-hard nature, which implies that it is complicated to find optimal solutions for large-sized problems (Yildiz et al., 2013). Besides, the proposed model in this research has a non-linear essence, and therefore it is justifiable to use multi-objective meta-heuristics for solving this problem. Hence, this paper employs two multi-objective meta-heuristic algorithms to tackle the problem. In addition to these methods, we have developed a hybrid version of the WFA that differs from the classical version of this method in several perspectives. All employed algorithms are capable of searching for the solution space of the proposed problem in order to find a set of non-dominated solutions for the decision maker to choose from.

5.1. Representation scheme of solutions

One of the remarkable factors that influences the complexity and required computational time of evolutionary methods is the representation scheme of solutions (Chen et al., 2013). Using a proper solution representation may lead the algorithm to all possible candidate solutions (Rabbani et al., 2018b). To encode the potential solutions of the problem tackled in this paper, we have used the order-based representation scheme which has been used widely in the literature. In this encoding scheme, each solution is a ($\mathit{WT}+NF)\times NSN$ matrix, where WT, NF, and NSN represent the number of waste types, centers, and demand nodes, respectively. The first WT rows of a solution are permutations whose elements are in the range $[1,NSN]$. The other rows are dedicated to the order of treatment, recycling, and disposal centers. It is possible that these rows have empty cells (Rabbani et al., 2018b). Suppose that there is a logistic network with dimension $(10/5/4/3)$, which means that this network consists of ten healthcare centers, five treatment centers, four recycling centers, and three disposal centers, respectively. An illustrated example of a solution for this network has been depicted in Fig. 2 .

Fig. 2.

An illustrated example of the solution representation scheme.

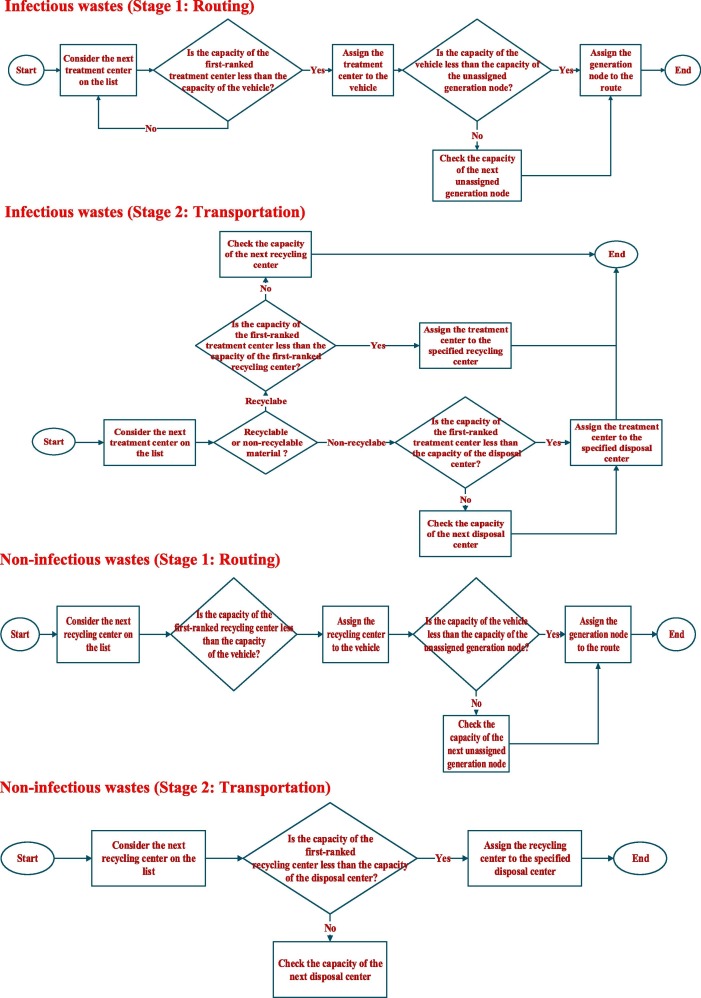
A two-stage decoding procedure is required to transform this representation scheme into meaningful solutions and obtain the objective function values. The first stage is dedicated to the routing dimension of the problem, while the second stage tackles the transportation aspect of the problem. In the first stage, feasible routes for collection vehicles are determined based on their destination nodes. The destination node of a collection vehicle is considered as a treatment, recycling, or disposal center that its remaining capacity is equal to or greater than the capacity of the corresponding vehicle. Having determined the proper center for unloading a vehicle, its collection route will be determined. Hence, an assignment procedure is needed to determine the routes of vehicles. This procedure starts with assigning the first-ranked unassigned node to the route and it continues until no more generation nodes can be added to the route considering the limitations of vehicles. The second stage of the decoding procedure is dedicated to determining the amount of waste residues that should be transferred between different centers. The second stage starts with assigning the residues of the first-ranked treatment center to the first-ranked recycling and disposal centers. This process continues with the rest of the treatment centers according to the ordered list until the remaining capacity of the recycling and disposal centers cannot embrace residues of other treatment centers. The same procedure is applied to transfer non-recyclable wastes from recycling centers to disposal centers (Rabbani et al., 2018b). Fig. 3 displays the flowchart of the two-stage decoding procedure. Each vehicle passes through these steps regarding the type of its waste.

Fig. 3.

Flowchart of the decoding procedure.

5.2. Water-Flow like algorithm (WFA)

Yang and Wang (2007) have been motivated by the water-flow behavior in traveling through different terrains to introduce a meta-heuristic, namely the Water-Flow like Algorithm (WFA) for optimization problems. In the WFA, water-flows and terrains are considered as solutions and search space, respectively. The WFA operates based on several procedures (Yang and Wang, 2007, Nourmohammadi et al., 2019): (1) Splitting and moving procedures, (2) Merging, (3) Evaporation, and (4) Precipitation. In order to save space, the procedures of the classical WFA have been explained in Appendix A.

5.3. Multi-Objective Water-Flow like algorithm (MOWFA)

This section introduces the modifications offered in this research for the water-flow like algorithm. One of these modifications has occurred in the splitting and moving procedures of the WFA. In the proposed algorithm, for each original flow, a real random number (RRN) on the interval $[0,1]$ is generated. Each original flow is substituted by its sub-flows if: (1) the original flow is dominated by at least one of its sub-flows, or (2) the random number RRN is equal to or more than 0.5. Otherwise, the sub-flows are neglected and the original flow is used once again to produce NOSF number of new sub-flows. This procedure forces the MOWFA to find better solutions and enhances the quality and diversity of non-dominated solutions, simultaneously. The first condition helps to detect more appropriate solutions in terms of quality, while the second condition enables the MOWFA to find more diverse solutions. Similar to many other multi-objective optimization methods, the non-dominated solutions found in each iteration of the MOWFA are stored in an archive set.

To find the non-dominated solutions of each iteration, the non-dominated sorting technique proposed by Deb et al. (2002) has been used. In this technique, each individual is compared with other individuals of population to determine the first front of non-dominated solutions. A multi-objective optimization problem comprises a set of minimizing or maximizing objectives defined over a solution space. For the proposed model with two minimization objectives, a solution $j$ is dominated by another solution $\stackrel{´}{j}$ if we have ${\mathit{OFV}}_{\mathit{obj}}(\stackrel{´}{j})\le {\mathit{OFV}}_{\mathit{obj}}\left(j\right)(obj=1,2)$ for both objectives and there will be at least one objective such that${\mathit{OFV}}_{\mathit{obj}}(\stackrel{´}{j})<{\mathit{OFV}}_{\mathit{obj}}\left(j\right)$. This means that the solution $\stackrel{´}{j}$ dominates the solution $j$ if the objective values of solution $\stackrel{´}{j}$ are less than or equal to the objective values of solution$j$, and at least one objective value of $\stackrel{´}{j}$ is less than the one assessed at solution$j$.

The newly found non-dominated solutions are compared to the existing solutions of the archive. A newly found solution becomes a member of the archive if it is not dominated by the solutions of the archive. The dominated solutions of the archive will be eliminated from this set. As another modification to the classical WFA, we propose a new procedure based on the Analytical Hierarchy Process (AHP) and the solutions stored in the archive set. The AHP is a well-known Multi-Attribute Decision Making (MADM) approach proposed by Saaty (1987) to determine the weights of criteria and rank the alternatives. Since the solutions existing in the archive set are the best found solutions during the optimization process, the proposed approach is implemented on these solutions so that more proper solutions might be found in their neighborhoods. In each iteration, the AHP method is applied to the solutions of the archive set, and therefore the weights of the criteria are obtained and the solutions are ranked. The hierarchy used in the MOWFA has three different levels: (1) goal, (2) criteria, and (3) alternatives. Fig. 4 shows an illustration of this hierarchy. The objective functions are considered as the criteria in the AHP method and the solutions of the archive set are considered as alternatives. The relative weights of criteria are determined by means of pairwise comparisons. To conduct these comparisons, the judgments of the decision maker is adopted using the 9-point scale. Keeping the 9-point scale in mind, in the MOWFA, the first objective function has been referred to as “equally to moderately importance” over the second objective function. This means that the first objective function is twice as important as the second objective function for the decision maker. To calculate the weights of criteria, the arithmetic mean as an approximation method is used. The exact calculations have not been considered in the proposed algorithm since the complexity will be increased significantly without any necessity. In the next step, the non-dominated solutions existing in the archive set are compared with each other regarding each objective. The overall priority of alternatives are calculated through combining the weights of objectives with the priority weights of non-dominated solutions. Having ranked the solutions of the archive set, the first and the second ranked solutions are selected for mating. A mating operator is applied to the selected solutions, and therefore two new offspring are generated. It is noteworthy that in each iteration, the Consistency Index (CI) is computed to investigate whether the judgments are consistent or not. If the consistency index is determined to be less than 0.1, the solutions of the archive set are ranked and the best found solutions are selected for mating. Otherwise, the AHP procedure in the MOWFA is neglected for the current iteration and the mating procedure is not performed for the respective iteration.

Fig. 4.

Decision hierarchy for ranking solutions in the MOWFA.

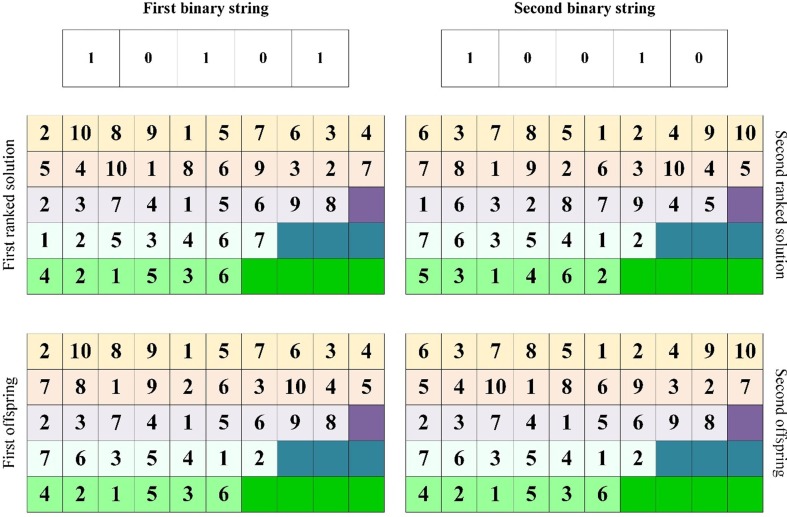
The mating operator generates two binary strings with the length$1\times (WT+NF)$, where WT and NF denote the number of wastes and facilities. Algorithm 1 describes the proposed procedure and the mating operator. Fig. 5 illustrates an example of producing two offspring from the selected solutions. In the next step, two generated offspring are used to update the archive set.

Algorithm 1: Proposed approach for generating new offspring
Notations:
NOR	Number of rows in a solution ($\mathit{nor}=1,2,\cdots ,NOR)$.
${\mathit{E}\mathit{F}\mathit{B}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}$	The ${\mathit{nor}}^{\mathit{th}}$ element on the first random binary string.
${\mathit{E}\mathit{S}\mathit{B}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}$	The ${\mathit{nor}}^{\mathit{th}}$ element on the second random binary string.
${\mathit{F}\mathit{S}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}$	The ${\mathit{nor}}^{\mathit{th}}$ row of the first selected solution.
${\mathit{S}\mathit{S}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}$	The ${\mathit{nor}}^{\mathit{th}}$ row of the second selected solution.
${\mathit{F}\mathit{O}\mathit{F}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}$	The ${\mathit{nor}}^{\mathit{th}}$ row of the first offspring.
${\mathit{S}\mathit{O}\mathit{F}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}$	The ${\mathit{nor}}^{\mathit{th}}$ row of the second offspring.
1.	Generate two random binary strings;
2.	For$\mathit{nor}=1$toNORdo
3.	If${\mathit{EFBS}}_{\mathit{nor}}=1$do
4.	${\mathit{FOFS}}_{\mathit{nor}}\leftarrow {\mathit{FSS}}_{\mathit{nor}};$
5.	Else
6.	${\mathit{FOFS}}_{\mathit{nor}}\leftarrow {\mathit{SSS}}_{\mathit{nor}};$
7.	End if
8.	If${\mathit{ESBS}}_{\mathit{nor}}=1$do
9.	${\mathit{SOFS}}_{\mathit{nor}}\leftarrow {\mathit{SSS}}_{\mathit{nor}};$
10.	Else
11.	${\mathit{SOFS}}_{\mathit{nor}}\leftarrow {\mathit{FSS}}_{\mathit{nor}};$
12.	End if
13.	End for
14.	Update the archive set with the newly generated offspring;
15.	Eliminate the dominated solutions from the archive set;
	Output: An updated archive set.

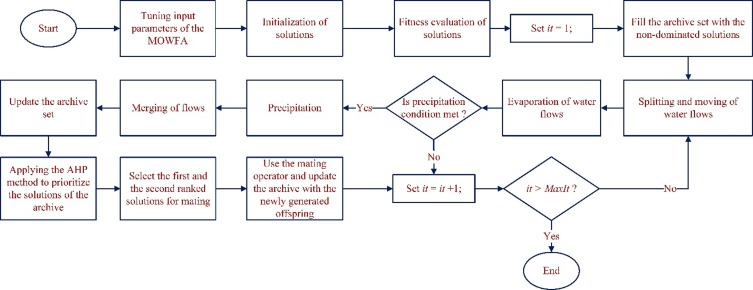
In addition to the aforementioned modifications, the MOWFA uses two novel neighborhood operators (as local search methods in the splitting and moving procedures) to produce new feasible solutions from each water-flow. By using these operators, it is possible to find the solutions in the neighborhood of an existing water-flow. These neighborhood operators are elaborated in the following sub-sections. The MOWFA stops after a maximum number of iterations ($\mathit{MaxIt})$. Fig. 6 shows the flowchart of the proposed algorithm.

Fig. 5.

Two offspring generated by the mating operator.

Fig. 6.

Flowchart of the proposed algorithm.

5.3.1. First neighborhood operator

A random integer number (RAIN) is generated on the interval [$1,NSN]$, where NSN denotes the number of demand nodes. The first RAIN columns of a solution is preserved, and several elements of other columns have to take new positions. In this respect, in each row, several elements existing on the columns $(RAIN+1)$ to NSN are chosen randomly to change their positions. The pseudo-code of this operator is presented in Algorithm 2.

Algorithm 2: First neighborhood operator
Notations:
NSN	Number of demand nodes (Number of columns).
RAIN	A random integer number in the range of$[1,NSN]$.
NOR	Number of rows in a solution ($\mathit{nor}=1,2,\cdots ,NOR)$.
${\mathit{R}\mathit{N}\mathit{P}}_1$	First random position number.
${\mathit{R}\mathit{N}\mathit{P}}_2$	Second random position number (${\mathit{RNP}}_1\ne {\mathit{RNP}}_2)$.
${\mathit{N}\mathit{U}\mathit{C}}_{\mathit{n}\mathit{o}\mathit{r}}$	Number of used (non-empty) cells on the ${\mathit{nor}}^{\mathit{th}}$ row.
${\mathit{V}\mathit{A}\mathit{L}}_{\mathit{n}\mathit{o}\mathit{r}}^{{\mathit{R}\mathit{N}\mathit{P}}_1}$	The value on the ${\mathit{RNP}}_1$ column and $\mathit{nor}$ row.
${\mathit{V}\mathit{A}\mathit{L}}_{\mathit{n}\mathit{o}\mathit{r}}^{{\mathit{R}\mathit{N}\mathit{P}}_2}$	The value on the ${\mathit{RNP}}_2$ column and $\mathit{nor}$ row.
STR	A set to store random numbers.
1.	Generate an integer random number (RAIN) on the $[1,NSN]$;
2.	Preserve the first RAIN columns;
3.	For$\mathit{nor}=1$toNORdo
4.	Empty the set STR;
5.	Choose a random position (${\mathit{RNP}}_1)$ in the range $[RAIN+1,{\mathit{NUC}}_{\mathit{nor}}]$;
6.	Add ${\mathit{RNP}}_1$ to the set STR;
7.	Choose a random position (${\mathit{RNP}}_2)$ in the range $[RAIN+1,{\mathit{NUC}}_{\mathit{nor}}]$;
8.	If${\mathit{RNP}}_2\notin STR$do
9.	Swap the ${\mathit{VAL}}_{\mathit{nor}}^{{\mathit{RNP}}_1}$ and ${\mathit{VAL}}_{\mathit{nor}}^{{\mathit{RNP}}_2}$;
10.	End if
11.	End For
	Output: A new feasible solution.

Fig. 7 shows an example of generating a new solution via the first neighborhood operator. According to this figure, the first four columns of the parent solution are transferred to the new solutions without any changes ($\mathit{RAIN}=4$). Then, the 5th to 10th columns of the solution are subject to changes in order to produce a new solution. In each row, two positions have been selected randomly and their values have been swapped.

Fig. 7.

A new solution generated by the first neighborhood operator.

5.3.2. Second neighborhood operator

To produce a new water-flow, two positions of each row are selected randomly, and the values on these positions are swapped. To select two random positions on each row ($\mathit{nor}=1,\cdots ,NOR$), we generate two random real numbers (${\mathit{RN}}_{\mathit{nor}}^1$and${\mathit{RN}}_{\mathit{nor}}^2$) on the interval$[0,1]$. The numbers ${\mathit{RN}}_{\mathit{nor}}^1$and${\mathit{RN}}_{\mathit{nor}}^2$ are multiplied by the number of non-empty cells (used cells) on the ${\mathit{nor}}^{\mathit{th}}$ row, and the results are rounded up. Therefore, two positions (${\mathit{POS}}_{\mathit{nor}}^1$and${\mathit{POS}}_{\mathit{nor}}^2$) are obtained and the values existing in these positions are substituted with each other. The pseudo-code of the second neighborhood operator is given in Algorithm 3.

Algorithm 3: Second neighborhood operator
Notations:
${\mathit{R}\mathit{N}}_{\mathit{n}\mathit{o}\mathit{r}}^1$	A real random number in the range [0, 1].
${\mathit{R}\mathit{N}}_{\mathit{n}\mathit{o}\mathit{r}}^2$	A real random number in the range [0, 1] (${\mathit{RN}}_{\mathit{nor}}^1\ne {\mathit{RN}}_{\mathit{nor}}^2$).
${\mathit{P}\mathit{O}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}^1$	First selected position on the ${\mathit{nor}}^{\mathit{th}}$ row.
${\mathit{P}\mathit{O}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}^2$	Second selected position on the ${\mathit{nor}}^{\mathit{th}}$ row.
$\mathit{V}\mathit{A}\mathit{L}({\mathit{P}\mathit{O}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}^1)$	The value on the position${\mathit{POS}}_{\mathit{nor}}^1$.
$\mathit{V}\mathit{A}\mathit{L}({\mathit{P}\mathit{O}\mathit{S}}_{\mathit{n}\mathit{o}\mathit{r}}^2)$	The value on the position${\mathit{POS}}_{\mathit{nor}}^2$.
NOR	Number of rows in a solution ($\mathit{nor}=1,2,\cdots ,NOR)$.
${\mathit{S}\mathit{T}\mathit{R}}_{\mathit{n}\mathit{o}\mathit{r}}$	A set to store random numbers for the ${\mathit{nor}}^{\mathit{th}}$ row.
${\mathit{N}\mathit{U}\mathit{C}}_{\mathit{n}\mathit{o}\mathit{r}}$	Number of used (non-empty) cells on the ${\mathit{nor}}^{\mathit{th}}$ row.
1.	For$\mathit{nor}=1$toNORdo
2.	Generate a real random number (${\mathit{RN}}_{\mathit{nor}}^1)$ on the interval $[0,1]$;
3.	${\mathit{POS}}_{\mathit{nor}}^1=\lceil {\mathit{NUC}}_{\mathit{nor}}\times {\mathit{RN}}_{\mathit{nor}}^1\rceil ;$
4.	Add ${\mathit{RN}}_{\mathit{nor}}^1$ to the set ${\mathit{STR}}_{\mathit{nor}}$;
5.	Generate a real random number (${\mathit{RN}}_{\mathit{nor}}^2)$ on the interval $[0,1]$;
6.	If${\mathit{RN}}_{\mathit{nor}}^2\notin {\mathit{STR}}_{\mathit{nor}}$do
7.	${\mathit{POS}}_{\mathit{nor}}^2=\lceil {\mathit{NUC}}_{\mathit{nor}}\times {\mathit{RN}}_{\mathit{nor}}^2\rceil ;$
8.	Swap the $\mathit{VAL}({\mathit{POS}}_{\mathit{nor}}^1)$ and $\mathit{VAL}({\mathit{POS}}_{\mathit{nor}}^2)$;
10.	End if
11.	End for
	Output: A new feasible solution.

Fig. 8 illustrates a sample solution produced by means of the second neighborhood operator. According to the instructions given in Algorithm 3, for each row, two random numbers have been generated in the interval$\left[0,1\right]$. In this respect, we have ${\mathit{RN}}_1^1=0.81,{\mathit{RN}}_1^2=0.90,{\mathit{RN}}_2^1=0.12,{\mathit{RN}}_2^2=0.63,{\mathit{RN}}_3^1=0.27,{\mathit{RN}}_3^2=0.54,{\mathit{RN}}_4^1=0.42,{\mathit{RN}}_4^2=0.79,{\mathit{RN}}_5^1=0.03$, and${\mathit{RN}}_5^2=0.39$. Based on these random numbers, the candidate positions for swapping are obtained as ${\mathit{POS}}_1^1=9,{\mathit{POS}}_1^2=10,{\mathit{POS}}_2^1=2,{\mathit{POS}}_2^2=7,{\mathit{POS}}_3^1=3,{\mathit{POS}}_3^2=5,{\mathit{POS}}_4^1=3,{\mathit{POS}}_4^2=6,{\mathit{POS}}_5^1=1$, and${\mathit{POS}}_5^2=3$. The values on these positions are swapped, and therefore a new solution is generated as shown in Fig. 8.

Fig. 8.

A new solution generated by the second neighborhood operator.

5.4. Other employed algorithms

To investigate the success of the MOWFA in solving the proposed model, we have used two other meta-heuristics namely, the Multi-Objective Imperialist Competitive Algorithm (MOICA), and Multi-Objective Simulated Annealing (MOSA). The reason behind choosing these two well-known methods is that the MOICA and MOSA have been successful in solving various multi-objective problems (Hosseini and Al Khaled, 2014, Fathollahi-Fard et al., 2019)

5.4.1. Description of the MOICA

The imperialist competitive algorithm (ICA), as an evolutionary algorithm, has been inspired by socio-political evolutions. In the MOICA, each solution is considered as a country. Similar to political backgrounds, countries are either imperialist or colonies. Therefore, for each imperialist, there is a set of colonies. The algorithm searches for the best country during the optimization process. The best country has the best possible combination of socio-political features. These socio-political features include economic policy, culture, language, etc (Zandieh et al., 2017). To obtain different Pareto fronts, the MOICA hires the non-dominated sorting technique after producing initial population of countries. This algorithm utilizes the crowding distance metric to rank individuals of each front. For the MOICA, there is an archive set that stores non-dominated individuals of the first Pareto front in each iteration. By using the non-dominated sorting technique and crowding distance metric, the best countries (solutions) are chosen from the population and they are regarded as imperialists. The rest of the countries are considered as colonies. The power of each imperialist should be evaluated to determine its share of the colonies. In other words, the more the power of an imperialist, the greater its share of the colonies that can be allocated to it.

In each iteration of the MOICA, there is an assimilating movement in which the colonies of an imperialist move toward their respective imperialist. Through this movement, the features of colonies will become similar to the features of their corresponding imperialist. Therefore, the colonies of an imperialist are improved. For the MOICA, there is a revolution operator that enhances the exploration ability of the algorithm. This operator selects a random colony with a probability and revolves its position in the search space based on a random manner. Because of assimilation and revolution procedures, if a colony was found to be better than its imperialist, their positions would be exchanged. The imperialists compete with each other by seizing the weakest colonies of one another. The algorithm stops if a predefined termination criterion is met. In this research, an upper bound has been defined for the number of iterations and the algorithm will stop if it reaches this upper bound (Zandieh et al., 2017, Nabipoor Afruzi et al., 2014). The roots and basic concepts of this algorithm can be found in Atashpaz-Gargari and Lucas (2007).

5.4.2. Description of the MOSA

The simulated annealing (SA) is a renowned method inspired by physical annealing process in the field of metallurgy. This method has been developed based on the statistical mechanics concept. In the annealing process, proper low energy state crystallization is achieved by slow cooling of a metal. On the other hand, fast cooling will result in improper crystallization. Gradual reduction of high temperature to low temperature will lead to a crystalline state. Therefore, each temperature must be maintained for a sufficient amount of time so that the crystal will have enough time to reach the minimum energy state. The SA imitates the crystallization process in order to find optimal or near optimal solution.

This research employs the Multi-Objective Simulated Annealing (MOSA) which hires the concepts of dominance and Pareto optimality to converge to the Pareto optimal set. In addition to the convergence behavior, the MOSA utilizes the transition palpability to preserve appropriate spread of the solutions throughout the obtained Pareto front. One of the advantages of the MOSA over evolutionary algorithms is that this method requires no big memory to store the population. Hence, the MOSA can find an approximate Pareto front in a short running time (Zidi et al., 2012). The MOSA encounters two situations in search of the optimal solution. First, the algorithm finds a better solution than the current one. In this case, the better solution is accepted and the current one is discarded. Secondly, the MOSA finds worse solutions that are accepted according to an acceptance probability (Baños et al., 2013). The acceptance probability of new solutions when they are worse than the current solution depends on the temperature. The acceptance probability is low if the temperature is low. Conversely, in case of being worse than the current solution, the probability of accepting a new solution is high when the temperature is also high (Yannibelli and Amandi, 2013). The acceptance probability is determined based on the Boltzmann Probabilistic Distribution (Nino et al., 2012). This acceptance helps the MOSA to dodge the local optimum. The MOSA stores the non-dominated solutions in an unlimited size archive (Zidi et al., 2012). The newly found solution can be added to the archive if it is not dominated by any of the existing solutions in the archive set (Baños et al., 2013). The MOSA continues the optimization process until the temperature cools down below a predefined threshold.

6. Numerical analysis

This section provides several numerical experiments to evaluate the performances of the algorithms. The location-routing problem (LRP) is extremely complex to solve due to the fact that it belongs to the class of NP-hard problems. This complexity increases when the number of demand nodes or the candidates for location facilities are large. Using meta-heuristics for solving the problem is justifiable since the proposed model is more intricate than the classical LRP. Therefore, meta-heuristics are welcome to quickly find feasible solutions to large size instances of this problem (Prodhon and Prins, 2014). We used the MATLAB software (R2015b) to code the algorithms and we ran these methods on an Inter Corei3 personal computer (3.4 GHz CPU) with 8 GB of memory (RAM).

6.1. Generating test problems

To evaluate the MOWFA and compare its performance with the MOICA and MOSA, 45 test problems with different sizes are produced. The test problems 1 to 15 are small-sized problems, while the test problems 16 to 30 are medium-sized problems. The test problems 31 to 45 are considered as large-sized problems. The main parameters of the proposed problem and their ranges have been shown in Table 2 .

Table 2.

Characteristics of test problems.

Parameters	Parameters
${\mathit{CTC}}_{\mathit{tc},tt}U[1.6\times {10}^8,2\times {10}^8]$	${\mathit{TIHT}}_{\mathit{iw},h,tc}U[1.5\times {10}^2,1.7\times {10}^2]$
${\mathit{CRC}}_{\mathit{rc}}U[1\times {10}^8,1.4\times {10}^8]$	${\mathit{TITR}}_{\mathit{iw},tc,rc}U[1.5\times {10}^2,1.7\times {10}^2]$
${\mathit{CDC}}_{\mathit{dc}}U[5\times {10}^7,7\times {10}^7]$	${\mathit{TITD}}_{\mathit{iw},tc,dc}U[1.5\times {10}^2,1.7\times {10}^2]$
$\mathit{COF}U[1\times {10}^3,3\times {10}^3]$	${\mathit{TIRD}}_{\mathit{iw},rc,dc}U[1.5\times {10}^2,1.7\times {10}^2]$
${\mathit{CIV}}_{\mathit{vi}}U[3\times {10}^5,5\times {10}^5]$	${\mathit{TNHR}}_{\mathit{nw},h,rc}U[1.1\times {10}^2,1.3\times {10}^2]$
${\mathit{CNV}}_{\mathit{vn}}U[1\times {10}^5,2\times {10}^5]$	${\mathit{TNTD}}_{\mathit{nw},rc,dc}U[1.1\times {10}^2,1.3\times {10}^2]$
${\mathit{CTI}}_{\mathit{iw},tc,tt}U[1.4\times {10}^3,2\times {10}^3]$	${\mathit{THTC}}_{h,tc}N(60,10)$
${\mathit{CRI}}_{\mathit{iw},rc}U[1\times {10}^3,1.2\times {10}^3]$	${\mathit{RRI}}_{\mathit{iw},tc,tt}U(0.3,0.7)$
${\mathit{CDI}}_{\mathit{iw},dc}U[0.5\times {10}^3,0.8\times {10}^3]$	${\mathit{RCI}}_{\mathit{iw},rc}U(0.3,0.7)$
${\mathit{CRN}}_{\mathit{nw},rc}U[0.8\times {10}^3,1.1\times {10}^3]$	${\mathit{RCN}}_{\mathit{nw},rc}U(0.3,0.7)$
${\mathit{CDN}}_{\mathit{nw},dc}U[0.5\times {10}^3,0.8\times {10}^3]$	$\mathit{pen}U[1\times {10}^3,1.1\times {10}^3]$
${\alpha }_{\mathit{iw}}U(0.2,1]$

* Note: $U$ denotes the uniform distribution, and $N$ represents the normal distribution.

6.2. Calibration of parameters

The performance of a meta-heuristic is affected by the values of its control parameters (Afshar-Nadjafi et al., 2017). Hence, in this section, the control parameters of the MOWFA are calibrated via the Taguchi Method (TM) to improve the efficiency of this algorithm. By using the Taguchi method, a large amount of information is obtained by conducting the least number of experiments (Hasçalık and Çaydas, 2008). In this study, a five-level Taguchi design has been considered for the parameters of the MOWFA. A total objective function (a convex combination of objectives) has been used as a response for the Taguchi designs. To dodge the trap of different measures, the objective function values are normalized. Normalized values of objectives for the $j^{\mathit{th}}$ solution (${\mathit{NORFV}}_j^1$ and${\mathit{NORFV}}_j^2$) are obtained using the following formulas:

$$\mathit{NORF}{V}_j^1=\frac{\mathit{OF}{V}_1^{\ast }}{\mathit{OF}{V}_j^1}$$ (47)

$$\mathit{NORF}{V}_j^2=\frac{\mathit{OF}{V}_2^{\ast }}{\mathit{OF}{V}_j^2}$$ (48)

Where, ${\mathit{OFV}}_j^1$ and ${\mathit{OFV}}_j^2$ denote the values of the first and the second objective functions for the $j^{\mathit{th}}$ solution, respectively. The best acquired values of the first and the second objectives are represented as ${\mathit{OFV}}_1^{\ast }$ and${\mathit{OFV}}_2^{\ast }$, respectively. For the solution$j$, the total objective function (${\mathit{TFV}}_j$) is computed by Eq. (49). $\theta (0\le \theta \le 1)$ represents the relative importance of the objectives.

$$\mathit{TF}{V}_j=\frac{1}{\theta \times NORF{V}_j^1+(1-\theta )\times NORF{V}_j^2}$$ (49)

In the next step, the total objective function values are converted into the Relative Percentage Deviation (RPD) which is computed by the Eq. (50) (Hosseinian and Baradaran, 2019a):

$$\mathit{RPD}=\frac{\left|\mathit{AL}-B\right|}{B}\times 100$$ (50)

Where, $\mathit{AL}$ represents the total objective function value obtained by a hired algorithm, and $B$ is the best value of the total objective function. The levels which have been considered for the parameters are shown in Table 3 . The chosen levels of parameters are reported in Table 4 . Besides, Fig. 9 depicts the average S/N ratio plots for the small, medium, and large size test problems. Other algorithms have been tuned by the same procedure.

Table 3.

Levels of input parameters.

Parameters	Level 1	Level 2	Level 3	Level 4	Level 5
${\mathit{VL}}_0$	10	15	20	25	30
${\mathit{MS}}_0$	10	15	20	25	30
$\mathit{ET}$	10	20	30	40	50
$\mathit{MaxIt}$	100	200	300	400	500

Table 4.

Tuned values of parameters for the MOWFA.

Parameters	Problem size
	Small	Medium	Large
${\mathit{VL}}_0$	30	30	10
${\mathit{MS}}_0$	10	20	30
$\mathit{ET}$	50	20	50
$\mathit{MaxIt}$	500	500	500

Fig. 9.

S/N ratio plots for parameters of the MOWFA: (a) small size problems, (b) medium size problems, and (c) large size problems.

6.3. Performance evaluation metrics

The literature of multi-objective optimization problems provides numerous metrics to evaluate the strengths and weaknesses of multi-objective optimizers. This research hires several comparison metrics to evaluate the performances of the MOWFA, MOICA, and MOSA in obtaining more appropriate solution sets. These metrics are described as follows:

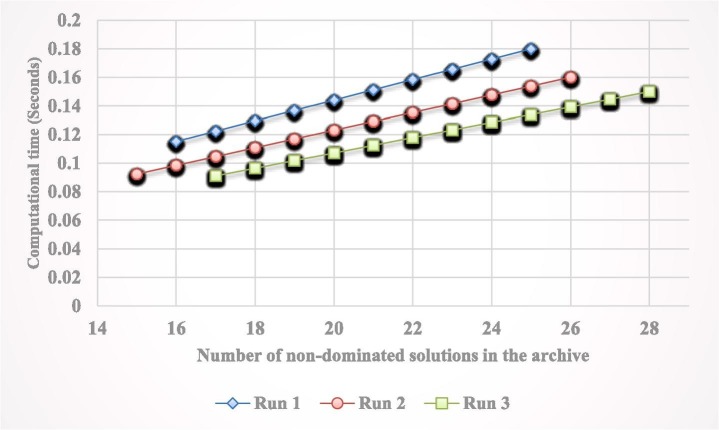
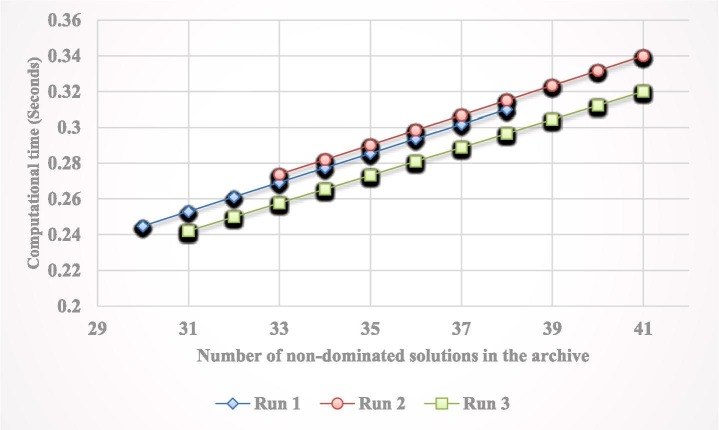
6.3.1. Computational time (CPU time)

We have employed two indexes introduced by Li et al. (2014) to compare the algorithms in terms of computational time. These metrics are denoted as ATO and ATA which represent the average computational time to find one solution, and the average computational time to obtain all solutions, respectively. These criteria are computed using the following formulas:

$$\mathit{ATA}=\frac{{\sum }_{\mathit{rn}=1}^{\mathit{RN}}\mathit{Com}{t}_{\mathit{rn}}}{\mathit{RN}}$$ (51)

$$\mathit{ATO}=\frac{\mathit{ATA}}{{\sum }_{\mathit{rn}=1}^{\mathit{RN}}\frac{\mathit{NSO}{L}_{\mathit{rn}}}{\mathit{RN}}}$$ (52)

Where, ${\mathit{NSOL}}_{\mathit{rn}}$ is the number of obtained solutions in the ${\mathit{rn}}^{\mathit{th}}$ run. RN represents the number of runs and ${\mathit{Comt}}_{\mathit{rn}}$ denotes the computational time in the ${\mathit{rn}}^{\mathit{th}}$ run.

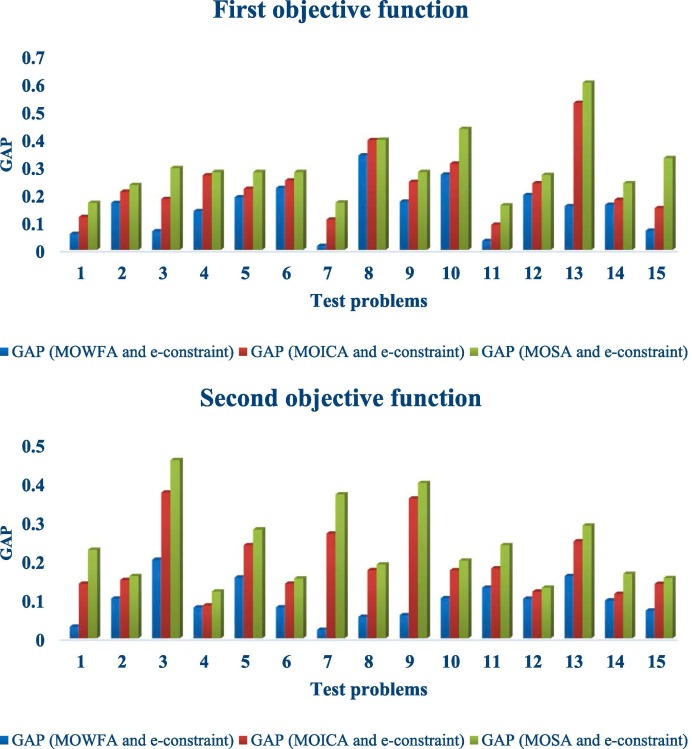
6.3.2. Error ratio (ER)

The error ratio (ER) has been used in many multi-objective optimization studies. The ER is used to measure the non-convergence of an approximation Pareto front found by a multi-objective optimization algorithm towards the Pareto optimal front. This metric is calculated by the following formula (Yazdani et al., 2019):

$$\mathit{ER}=\frac{{\sum }_{j=1}^{\mathit{NODS}}{e}_j}{\mathit{NODS}}$$ (53)

Where, $\mathit{NODS}$ represents the number of non-dominated solutions on the approximation front obtained by an algorithm. $e_j$ is equal to 1 if the $j^{\mathit{th}}$ non-dominated solution found by a given algorithm belongs to the Pareto optimal front. Otherwise, $e_j$ is equal to 0. Smaller ER values indicate better performance of a method (Yazdani et al., 2019, Hosseinian et al., 2019, Veldhuizen, 1999).

6.3.3. Spacing metric (SM)

The spacing metric (SM), developed by Schott (1995), is a diversity-based performance measure that provides information on the distribution of solutions existing in an approximation Pareto front (Rabbani et al., 2018b). In a comparison of two Pareto sets, the approximation front with the lower SM value has a better uniformity of distribution of solutions. The SM is computed by the Eqs. (54), (55), (56) (Yazdani et al., 2019):

$$d_j=\underset{j^{\prime }\in SNDS\wedge j^{\prime }\ne j}{min}\sum _{\mathit{obj}=1}^{\mathit{OBJ}}\left|\mathit{OF}{V}_{\mathit{obj}}^j-OF{V}_{\mathit{obj}}^{j^{\prime }}\right|$$ (54)

$$\overline{d}=\frac{1}{\mathit{NODS}}\sum _{j=1}^{\mathit{NODS}}{d}_j$$ (55)

$$\mathit{SM}=\sqrt{\frac{1}{\mathit{NODS}-1}\sum _{j=1}^{\mathit{NODS}}{\left(d_j-\overline{d}\right)}^2}$$ (56)

Where, $\mathit{SNDS}$ is the set of non-dominated solutions on the Pareto front. $d_j$ denotes the minimum distance between the solution $j$ on the approximation front and other solutions. $\overline{d}$ is the mean of all $d_j$s. $\mathit{OBJ}$ is the number of objective functions in the optimization problem. ${\mathit{OFV}}_{\mathit{obj}}^j$ represents the value of objective function $\mathit{obj}$ for the solution $j$.

6.3.4. Maximum spread (MS)

Zitzler (1999) proposed the maximum spread (MS) metric, known as diversification metric, to measure the spread of the approximation Pareto front. The normalized MS metric is obtained by the Eq. (57) (Zitzler, 1999, Helbig and Engelbrecht, 2013, Yazdani et al., 2019):

$$\mathit{MS}=\sqrt{\frac{1}{\mathit{OBJ}}\sum _{\mathit{obj}=1}^{\mathit{OBJ}}{\left(\frac{\underset{j=1}{\overset{\mathit{NODS}}{max}}OF{V}_{\mathit{obj}}^j-\underset{j=1}{\overset{\mathit{NODS}}{min}}OF{V}_{\mathit{obj}}^j}{\mathit{OF}{V}_{\mathit{obj}}^{max}-OF{V}_{\mathit{obj}}^{min}}\right)}^2}$$ (57)

6.4. Results and discussion

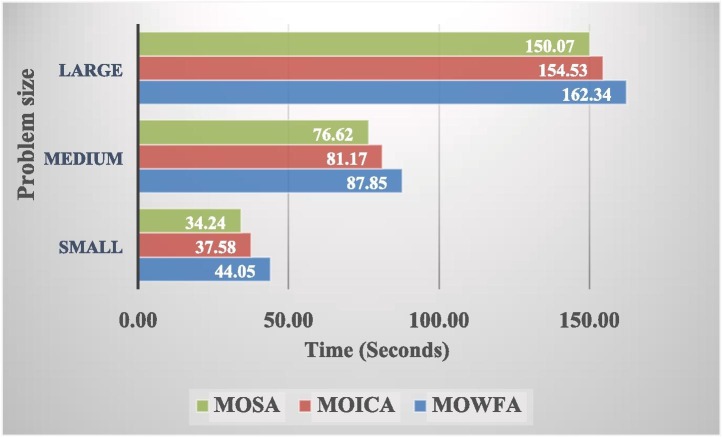
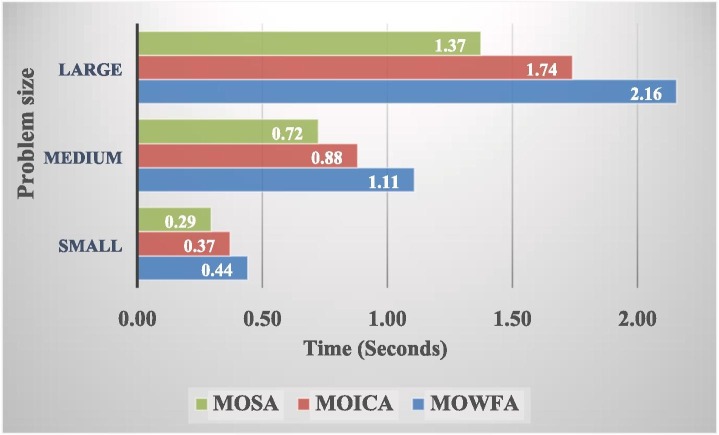
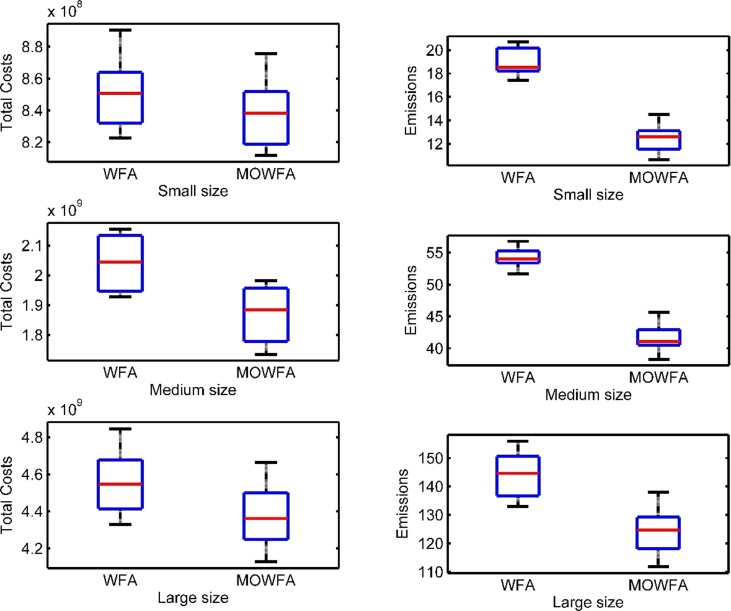
Table 5, Table 6, Table 7 detail the computational results of the MOWFA, MOICA, and MOSA in terms of the ER, SM, and MS metrics. Each algorithm has been run for ten times and the average of the obtained values have been reported in these tables. According to the obtained results, the MOWFA has better convergence than the MOICA and MOSA since the MOWFA acquired fewer ER values. Regarding the uniformity of non-dominated solutions obtained by these three methods, it is inferred that the MOWFA outperformed the other methods with respect to the SM metric. Comparing the MS values indicates that the MOWFA has behaved better in producing more diverse solutions than other methods. The performances of algorithms have been compared in terms of their average computational times in Fig. 10, Fig. 11 . These figures show that the MOSA has the least CPU times in finding one solution (ATO metric) and all solutions (ATA metric). The MOWFA is slower than other methods due to the local search strategies embedded in this algorithm.

Table 5.

Comparison of algorithms in terms of ER, SM, and MS metrics for small size problems.

Problems	ER			SM			MS
	MOWFA	MOICA	MOSA	MOWFA	MOICA	MOSA	MOWFA	MOICA	MOSA
1	0.33	0.54	0.69	1.68	5.49	4.09	0.77	0.59	0.46
2	0.36	0.50	0.63	1.49	4.28	6.10	0.62	0.42	0.31
3	0.05	0.23	0.36	5.78	9.74	9.52	0.96	0.76	0.62
4	0.37	0.57	0.76	8.01	12.08	11.66	0.98	0.75	0.68
5	0.25	0.49	0.66	9.41	13.65	11.84	0.80	0.57	0.45
6	0.04	0.28	0.44	2.17	5.52	6.73	0.80	0.58	0.46
7	0.11	0.29	0.52	6.12	8.37	9.99	0.74	0.55	0.41
8	0.22	0.34	0.53	5.22	7.91	8.27	0.96	0.73	0.63
9	0.38	0.51	0.69	1.11	5.85	4.65	0.75	0.54	0.44
10	0.39	0.52	0.76	4.03	6.49	7.24	0.64	0.46	0.32
11	0.06	0.29	0.43	2.46	6.94	4.69	0.91	0.67	0.56
12	0.39	0.53	0.74	8.15	11.77	10.87	0.76	0.52	0.43
13	0.38	0.61	0.82	3.80	8.79	6.17	0.70	0.49	0.37
14	0.19	0.33	0.49	5.76	7.99	8.31	0.76	0.55	0.45
15	0.32	0.56	0.74	2.49	5.82	5.21	0.64	0.43	0.31
Average	0.26	0.44	0.62	4.51	8.05	7.69	0.78	0.57	0.46

Table 6.

Comparison of algorithms in terms of ER, SM, and MS metrics for medium size problems.

Problems	ER			SM			MS
	MOWFA	MOICA	MOSA	MOWFA	MOICA	MOSA	MOWFA	MOICA	MOSA
16	0.31	0.52	0.75	1.54	6.81	3.93	0.52	0.30	0.16
17	0.17	0.57	0.80	7.14	12.30	9.00	0.78	0.52	0.38
18	0.04	0.42	0.66	1.38	8.51	6.46	0.94	0.72	0.58
19	0.11	0.42	0.66	1.64	5.06	0.11	0.83	0.60	0.48
20	0.06	0.73	0.96	5.69	9.36	6.86	0.60	0.34	0.21
21	0.11	0.27	0.48	1.87	5.74	3.42	0.68	0.46	0.36
22	0.18	0.68	0.89	8.36	13.32	10.20	0.73	0.50	0.38
23	0.21	0.68	0.92	8.36	15.51	12.92	0.99	0.73	0.61
24	0.18	0.63	0.83	7.50	14.52	11.05	0.58	0.35	0.24
25	0.35	0.26	0.48	2.35	5.65	2.63	0.93	0.65	0.54
26	0.21	0.33	0.54	6.94	11.93	7.08	0.82	0.52	0.40
27	0.38	0.41	0.66	5.67	11.30	6.54	0.69	0.42	0.31
28	0.26	0.57	0.81	9.76	14.84	12.68	0.60	0.36	0.23
29	0.38	0.29	0.52	6.84	13.13	8.91	0.71	0.46	0.33
30	0.10	0.61	0.83	8.20	14.34	11.54	0.74	0.53	0.40
Average	0.20	0.49	0.72	5.55	10.82	7.56	0.74	0.50	0.37

Table 7.

Comparison of algorithms in terms of ER, SM, and MS metrics for large size problems.

Problems	ER			SM			MS
	MOWFA	MOICA	MOSA	MOWFA	MOICA	MOSA	MOWFA	MOICA	MOSA
31	0.27	0.61	0.84	2.35	7.56	6.21	0.81	0.53	0.40
32	0.09	0.44	0.62	5.43	11.48	9.15	0.69	0.47	0.34
33	0.33	0.65	0.89	3.35	7.16	5.50	1.00	0.67	0.55
34	0.11	0.44	0.64	2.86	10.46	7.66	0.77	0.52	0.42
35	0.41	0.73	0.92	3.44	8.86	7.62	0.75	0.51	0.37
36	0.12	0.46	0.68	3.03	10.22	7.24	0.67	0.36	0.24
37	0.34	0.68	0.91	3.32	7.59	5.51	0.75	0.55	0.42
38	0.08	0.39	0.64	2.30	9.29	6.88	0.67	0.46	0.32
39	0.13	0.47	0.57	6.45	14.25	11.25	0.83	0.53	0.42
40	0.04	0.39	0.62	3.97	10.51	8.93	0.92	0.63	0.52
41	0.26	0.59	0.78	5.77	12.18	10.35	0.87	0.59	0.46
42	0.31	0.65	0.90	6.87	13.15	11.22	0.68	0.37	0.25
43	0.25	0.58	0.76	5.49	11.56	9.03	0.68	0.37	0.23
44	0.19	0.50	0.67	5.75	10.92	8.28	0.92	0.60	0.46
45	0.29	0.60	0.82	5.12	9.51	8.31	0.97	0.72	0.58
Average	0.22	0.55	0.75	4.37	10.31	8.21	0.80	0.53	0.40

Fig. 10.

Comparison of algorithms in terms of the ATA.

Fig. 11.

Comparison of algorithms in terms of the ATO.

6.4.1. Statistical comparisons

The performances of the three algorithms have been statistically evaluated as well. The statistical comparisons have been implemented using the 2-sample t-test and the following hypotheses. These comparisons have been made in terms of each performance metric at a 95% confidence level. The null hypothesis ($H_0$) assumes the equality of the means of methods regarding a performance measure which implies that there is no significant difference between them. The alternative hypothesis ($H_1$) presents the opposite assumption. Thus, the null hypothesis ($H_0$) is rejected if the p-value is less than 5% (Zandieh et al., 2019).

$H_0$:	The means of a performance measure value obtained by the algorithms are not significantly different.
$H_1$:	The means of a performance measure value obtained by the algorithms are significantly different.

Each algorithm has solved the test problems for ten times. The following sub-sections discuss the statistical comparisons between the algorithms in terms of the performance metrics mentioned in Section 5.3.

• • MOWFA versus MOICA

Table 8 compares the performances of the MOWFA and MOICA. Results reported in Table 8 indicate that the p-values are less than 5% for the ER, SM, and MS performance measures. Hence, the null hypotheses ($H_0$) for these metrics are rejected which means that the superiority of the MOWFA is evident over the MOICA. On the other hand, the p-values for the ATO and ATA metrics are not less than 5%. Therefore, it can be concluded that the MOWFA is not significantly slower than the MOICA.

• • MOWFA versus MOSA

Table 8.

Statistical test results for the MOWFA vs. MOICA.

Problem size	Performance measure	Lower bound	Upper bound	p-Value	Description
Small	ATO	−0.01	0.15	0.10	$H_0$is not rejected.
	ATA	−0.20	13.13	0.057	$H_0$is not rejected.
	ER	−0.28	−0.08	7.03e−004	$H_0$is rejected.
	SM	−5.55	−1.51	0.0013	$H_0$is rejected.
	MS	0.12	0.29	2.22e−005	$H_0$is rejected.
Medium	ATO	0.003	0.45	0.04	$H_0$is rejected.
	ATA	−18.96	32.32	0.59	$H_0$is not rejected.
	ER	−0.39	−0.18	3.85e−006	$H_0$is rejected.
	SM	−7.76	−2.77	1.74e−004	$H_0$is rejected.
	MS	0.14	0.34	3.69e−005	$H_0$is rejected.
Large	ATO	−0.03	0.87	0.07	$H_0$is not rejected.
	ATA	−42.46	58.09	0.75	$H_0$is not rejected.
	ER	−0.41	−0.24	8.12e−009	$H_0$is rejected.
	SM	−7.30	−4.59	9.81e−010	$H_0$is rejected.
	MS	0.19	0.35	2.70e−007	$H_0$is rejected.

The MOWFA and MOSA have been compared statistically, and the results have been summarized in Table 9 . Based on the outputs, the p-values are less than 5% for most of the metrics. Therefore, the null hypotheses for these measures are rejected. This means that the MOWFA significantly overcomes the MOSA regarding the ER, SM, and MS. Moreover, it can be inferred that the MOWFA is significantly slower than the MOSA.

Table 9.

Statistical test results for the MOWFA vs. MOSA.

Problem size	Performance measure	Lower bound	Upper bound	p-Value	Description
Small	ATO	0.05	0.23	0.001	$H_0$ is rejected.
	ATA	3.30	16.30	0.004	$H_0$ is rejected.
	ER	−0.46	−0.25	1.023e−007	$H_0$ is rejected.
	SM	−5.14	−1.20	0.0026	$H_0$ is rejected.
	MS	0.23	0.41	2.78e−008	$H_0$ is rejected.
Medium	ATO	0.15	0.61	0.00	$H_0$is rejected.
	ATA	−14.20	36.66	0.37	$H_0$ is not rejected.
	ER	−0.61	−0.41	6.62e−011	$H_0$ is rejected.
	SM	−4.57	0.56	0.12	$H_0$ is not rejected.
	MS	0.26	0.47	5.52e−008	$H_0$ is rejected.
Large	ATO	0.33	1.22	0.00	$H_0$ is rejected.
	ATA	−37.83	62.38	0.61	$H_0$ is not rejected.
	ER	−0.62	−0.44	6.86e−013	$H_0$ is rejected.
	SM	−5.10	−2.57	9.94e−007	$H_0$ is rejected.
	MS	0.31	0.48	1.49e−010	$H_0$ is rejected.

6.4.2. Ranking solution approaches

In the following, we used a two-phase approach based on the Multi-Attribute Decision Making (MADM) methods to rank the algorithms in terms of their results. The goal of this approach is to find the most efficient algorithm in solving test problems. In this respect, the algorithms and performance evaluation metrics are considered as the alternatives and criteria, respectively. In the first phase of this approach, the weights of the criteria are calculated via the Best-Worst Method (BWM), and the second phase involves prioritizing the algorithms by means of the Simple Additive Weighting (SAW) method. This approach is called the BWM-SAW that has been described in Algorithm 4.

Algorithm 4: BWM-SAW method
Notations:
NC		Number of criteria ($\mathit{nc}=1,2,\cdots ,NC)$.
NA		Number of algorithms (alternatives) ($\mathit{na}=1,2,\cdots ,NA$).
BTO		Best-To-Others vector.
OTW		Others-To-Worst vector.
${\mathit{\omega }}_{\mathit{n}\mathit{c}}^{\mathbf{\ast }}$		Optimal weight of the criterion$\mathit{nc}$ ($\mathit{nc}=1,2,\cdots ,NC)$.
$\mathit{C}\mathit{O}\mathit{N}\mathit{V}$		Consistency value.
${\mathit{D}\mathit{M}}_{(\mathit{N}\mathit{A}\times \mathit{N}\mathit{C})}$		Decision matrix (Rows and columns represent the algorithms and criteria, respectively).
${\mathit{E}\mathit{L}}_{\mathit{n}\mathit{a},\mathit{n}\mathit{c}}$		The element on the ${\mathit{na}}^{\mathit{th}}$ row and ${\mathit{nc}}^{\mathit{th}}$ column of the decision matrix.
${\mathit{N}\mathit{E}}_{\mathit{n}\mathit{a},\mathit{n}\mathit{c}}$		Normalized element on the ${\mathit{na}}^{\mathit{th}}$ row and ${\mathit{nc}}^{\mathit{th}}$ column.
${\mathit{U}\mathit{S}}_{\mathit{n}\mathit{a}}$		Ultimate score of the ${\mathit{na}}^{\mathit{th}}$ algorithm.
Phase 1 (BWM)	1.	Determine the most important (the best) criterion.
	2.	Determine the least important (the worst) criterion.
	3.	Use a number on the interval $\left[1,9\right]$ to show the preference of the most important criterion over the other criteria. Hence, the Best-To-Others vector (BTO) is formed as ${\mathit{BTO}}_B=(o_{B,1},o_{B,2},\cdots ,o_{B,NC})$, where $o_{B,nc}$ denotes the preference of the best criterion B over the criterion$\mathit{nc}$.
	4.	Use a number on the interval $\left[1,9\right]$ to show the preference of all employed criteria over the least important criterion. Therefore, the Others-To-Worst vector (OTW) is obtained as ${\mathit{OTW}}_W={(o_{1,W},o_{2,W},\cdots ,o_{\mathit{NC},W})}^T$, where $o_{\mathit{nc},W}$ is the preference of the criterion $\mathit{nc}$ over the worst criterion W.
	5.	Determine the optimal weights of criteria by solving the following model (Rezaei, 2015):$\mathit{Min}CONV$(58)
		Subject to:
		$\left|\frac{{\omega }_B}{{\omega }_{\mathit{nc}}}-o_{B,nc}\right|⩽CONV\forall nc$(59)
		$\left|\frac{{\omega }_{\mathit{nc}}}{{\omega }_W}-o_{\mathit{nc},W}\right|⩽CONV\forall nc$(60)
		${\sum }_{\mathit{nc}=1}^{\mathit{NC}}{\omega }_{\mathit{nc}}=1$(61)
		${\omega }_{\mathit{nc}}⩾0\forall nc$(62)Where, $\mathit{CONV}$ is the consistency value and its lower values are more desirable.
6.	Create the decision matrix (DM).
Phase 2 (SAW)	7.	Normalize the elements of the DM using Eqs. (63) to (66) (Memariani et al., 2009, Hosseinian and Baradaran, 2019b):$E{L}_{\mathit{nc}}^{\mathit{MAX}}=\underset{1⩽na⩽NA}{\mathit{Max}}(E{L}_{\mathit{na},nc});\forall nc$(63)
		$E{L}_{\mathit{nc}}^{\mathit{MIN}}=\underset{1⩽na⩽NA}{\mathit{Min}}(E{L}_{\mathit{na},nc});\forall nc$(64)
		$N{E}_{\mathit{na},nc}=\frac{E{L}_{\mathit{na},nc}}{E{L}_{\mathit{nc}}^{\mathit{MAX}}};\forall na,\forall nc$(For benefit criteria)(65)
		$N{E}_{\mathit{na},nc}=\frac{E{L}_{\mathit{nc}}^{\mathit{MIN}}}{E{L}_{\mathit{na},nc}};\forall na,\forall nc$(For cost criteria)(66)
	8.	Calculate the ultimate score of each algorithm using Eq. (67) (Memariani et al., 2009, Hosseinian and Baradaran, 2019b):
		$U{S}_{\mathit{na}}={\sum }_{\mathit{nc}}^{\mathit{NC}}{\omega }_{\mathit{nc}}.N{E}_{\mathit{na},nc};\forall na$(67)
	Output: Ranking of algorithms.

Table 10, Table 11 report the results of implementing the BWM-SAW methodology for ranking the algorithms. Based on Table 10, the ER has been identified as the most important criterion, while the ATO has been discovered as the least important attribute. Table 11 clarifies that the MOWFA prevails other methods in all test problems with different sizes. The MOICA and MOSA are placed in the second, and third positions.

Table 10.

Weights of the criteria obtained by the BWM.

Problem size	Performance measures
	ER	SM	MS	ATO	ATA
Small	0.2827	0.2386	0.2712	0.0668	0.1407
Medium	0.2818	0.2130	0.2589	0.0396	0.2068
Large	0.3144	0.2388	0.2769	0.0431	0.1269

Table 11.

Results of the BWM-SAW method.

Problem size	Algorithms	Normalized decision matrix					Ultimate score	Rank
		ER	SM	MS	ATO	ATA
Small	MOWFA	1.00	1.00	1.00	0.67	0.78	*0.95	1
	MOICA	0.59	0.56	0.73	0.80	0.91	0.68	2
	MOSA	0.42	0.59	0.59	1.00	1.00	0.63	3
Medium	MOWFA	1.00	1.00	1.00	0.65	0.87	*0.96	1
	MOICA	0.41	0.51	0.67	0.82	0.94	0.63	2
	MOSA	0.28	0.73	0.50	1.00	1.00	0.61	3
Large	MOWFA	1.00	1.00	1.00	0.64	0.92	*0.97	1
	MOICA	0.39	0.42	0.66	0.79	0.97	0.57	2
	MOSA	0.29	0.53	0.50	1.00	1.00	0.53	3

6.5. Comparisons with an exact method

The $\epsilon$-constraint method (Khodemani-Yazdi et al., 2019) was hired to validate the outputs of the algorithms. This exact algorithm solved the small size problems and its results were compared with the MOWFA, MOICA, and MOSA. Fig. 12 shows that the MOWFA obtains closer results to the $\epsilon$-constraint method. Therefore, it is concluded that the MOWFA can obtain near-optimal solutions.

Fig. 12.

Comparing the $\epsilon$-constraint method with meta-heuristics

6.6. Comparison with the classical WFA

Some experiments have been conducted to assess the performance of the MOWFA in comparison with the classical WFA. Since the WFA is a single-objective method, it has been run twice for each of the test problems. In each run, one of the objectives used in the mathematical model has been optimized by the WFA. Fig. 13 shows boxplots comparing the best objective function values obtained by the MOWFA and WFA for small, medium, and large size test problems. According to Fig. 13, the outcome of the comparisons demonstrates that the MOWFA is more competitive than the classical version of this algorithm.

Fig. 13.

Boxplots on the objective function values

6.7. Analysis of the AHP computations in the MOWFA

As mentioned in Section 4.3, the MOWFA uses the AHP algorithm in each iteration to find the best solutions of the archive for the mating operator. Since the implementation of the AHP requires pairwise comparisons between non-dominated solutions, it is required to assess the impact of using the AHP on the computational times. Therefore, we have conducted an analysis which evaluates the computation efforts with respect to the number of existing non-dominated solutions in the archive set.

Three test instances with different sizes have been selected randomly. From twenty number of runs considered for the MOWFA, we have chosen three runs to investigate the impact of the AHP on the computational time of each iteration. These runs are associated with situations where all judgments are consistent. Fig. 14, Fig. 15, Fig. 16 show the computational times of each iteration for the chosen three test problems in three runs. Each figure is associated with one of the problems. As shown in these figures, the required computational times of each iteration increases as the number of non-dominated solutions in the archive grows. It can be concluded that the size of the archive set considerably increases the computational times of the MOWFA.

Fig. 14.

Impact of the AHP algorithm on computational times of the MOWFA for a small-size problem

Fig. 15.

Impact of the AHP algorithm on computational times of the MOWFA for a medium-size problem

Fig. 16.

Impact of the AHP algorithm on computational times of the MOWFA for a large-size problem

6.8. Applying solution approaches to a real-life network

In this section, a real-life logistic network is considered which consists of 15 healthcare centers in Tehran Province, Iran. There are 5, 5, and 4 potential locations for treatment, recycling, and disposal centers, respectively. The locations of healthcare centers are known and predefined. A private transportation company is responsible for collecting wastes of healthcare centers. A team of planners are working in this company that determine the routes of vehicles considering the network’s constraints. This company must consider the time windows of these centers since the violation of time windows will result in severe penalties. Through waste collection services of this company, the wastes of all healthcare centers are collected and transported to the required facilities. Non-recyclable wastes are carried to municipal authorized dump (landfill) sites. There are two types of vehicles for collecting wastes. The company uses rear-loader and manual side-loader vehicles for collecting infectious and non-infectious wastes, respectively. Both types of vehicles need a crew of one or two workers to operate properly. In most cases, one of the workers drives the vehicle, while the other one monitors and fills the garbage bed. The capacity of vehicles for collection of infectious and non-infectious wastes are approximately 2.5–3.5 and 4.0–5.5 tons, respectively. The vehicles initiate the process of visiting healthcare centers at 9:00 pm. As considered in the proposed model, it is possible to establish a treatment center with one of the following sterilization technologies:

• (1) Autoclaves: These devices are applied for medical purposes to carry out sterilization through elevated temperature and pressure.
• (2) Gamma irradiation machines: Sterilization through gamma irradiation is one of the most well-known ways to neutralize contaminations. Gamma irradiation machines wipe out the pathogens via breaking down bacterial deoxyribonucleic acid (DNA) which leads to inhibition of bacterial division.
• (3) Incineration devices: These machines treat waste materials by combusting organisms to ash. Therefore, all organic elements in biohazard wastes are incinerated and sterilized. In this technique, the volume and weight of wastes are decreased about 90% (Alvim-Ferraz and Afonso, 2003, Manga et al., 2011).
• (4) Ethylene oxide equipment: Ethylene oxide is a poisonous gas for treating infectious wastes in low temperatures. Ethylene oxide sterilizers invade the nucleic acids of microorganisms and cellular proteins. These equipment are usually used for heat/moisture-sensitive wastes.

The costs of applying the aforementioned technologies are different. This network has five types of infectious wastes such as materials used for surgeries and laboratory experiments, clothes and bandages collected from patients, body fluids, etc. Moreover, two non-infectious materials are gathered from healthcare centers such as plasters, blister packs for medicine, expired drugs, etc. These wastes are not hazardous and they do not need any special treatment technology to be disinfected. All types of infectious wastes in this network can be sterilized by the aforementioned treatment technologies. All healthcare centers produce both infectious and non-infectious wastes. Table 12 shows the daily amount of infectious (AIW) and non-infectious (ANW) wastes generated in healthcare centers. To space spaces and avoid repetition of centers’ name, an identification (ID) has been assigned to each healthcare center. In this network comprising 15 healthcare centers, total amounts of infectious and non-infectious wastes are approximately 18 and 27 tons, respectively.

Table 12.

Daily amount of wastes generated in healthcare centers (in tons).

Healthcare center (ID)	AIW$(\mathit{T}\mathit{o}\mathit{n})$	ANW$(\mathit{T}\mathit{o}\mathit{n})$	Healthcare center (ID)	AIW$(\mathit{T}\mathit{o}\mathit{n})$	ANW$(\mathit{T}\mathit{o}\mathit{n})$	Healthcare center (ID)	AIW$(\mathit{T}\mathit{o}\mathit{n})$	ANW$(\mathit{T}\mathit{o}\mathit{n})$
1	1.83	2.75	6	2.66	3.99	11	0.39	0.59
2	1.72	2.58	7	0.57	0.86	12	1.08	1.62
3	0.37	0.55	8	0.66	0.98	13	1.25	1.87
4	1.72	2.58	9	0.79	1.19	14	1.20	1.81
5	1.62	2.42	10	0.28	0.41	15	1.86	2.79
* Note: 1 Ton =${10}^{3}kg$

For the infectious wastes, transferring times between healthcare and treatment centers have been considered as normal random variables (with a mean of 60 min and a standard deviation of 10 min). Through consulting with the experts of the company, the transferring times between healthcare and treatment centers have been extracted and investigated to test whether the acquired data follow the normal distribution or not. To conduct the normality test, the Anderson-Darling statistic has been used at the significance level of 0.05. The null hypothesis of this test assumes that the specified data follow the normal distribution. Therefore, if the P-Value is less than 0.05, it can be inferred that the collected data do not follow the normal distribution. Otherwise, the transferring times have been normally distributed. The normal distribution plot of transferring times between healthcare and treatment centers is shown in Fig. 17 . As shown in Fig. 17, an approximate straight line has been drawn via the plotted points. Since the$P-Value=0.399$, the null hypothesis is not rejected, and therefore we can conclude that the transferring times follow the normal distribution.

Fig. 17.

Normal probability plot of transferring times between healthcare and treatment centers

Distances between facilities have been extracted from Google Earth. According to the discussions held by the experts, the emission coefficients of infectious wastes (${\alpha }_{\mathit{iw}})$ ($\mathit{iw}=1,\cdots ,5)$ range from 0.30 to 0.35. It is possible to establish three treatment centers, two recycling centers, and two disposal centers. Due to large scope of distances between healthcare centers and other facilities, a part of the real-life logistic network has been shown in Fig. 18 .

Fig. 18.

An illustration of the case study network

The proposed model has been applied to this network in order to determine the locations of the treatment, recycling, and disposal centers in addition to determining the order of visiting healthcare centers to collect their wastes. The MOWFA, MOICA, and MOSA have been employed to solve the model considering the conditions of this real-life network. Once again, the performance evaluation metrics have been used to compare these methods. To have a robust comparison, each algorithm was run twenty times and the outputs have been shown in Table 13 . Based on the outputs, it is obvious that the MOWFA has achieved considerably better results regarding the ER, SM, and MS metrics. The MOSA has been the fastest method comparing to other methods.

Table 13.

Results of comparing algorithms in a real-life network.

Performance metric	Algorithms	Best value	Average value	Worst value
ATO	MOWFA	2.01	2.09	2.18
	MOICA	1.70	1.76	1.81
	MOSA	1.41	1.43	1.47
ATA	MOWFA	165.39	167.88	169.98
	MOICA	159.02	162.19	164.77
	MOSA	152.33	153.93	155.47
ER	MOWFA	0.03	0.20	0.27
	MOICA	0.37	0.63	0.75
	MOSA	0.51	0.72	0.87
SM	MOWFA	1.32	3.19	4.35
	MOICA	8.58	17.58	24.15
	MOSA	7.35	13.30	16.33
MS	MOWFA	0.87	0.80	0.72
	MOICA	0.63	0.48	0.35
	MOSA	0.49	0.40	0.32

The performances of the employed algorithms have been statistically compared as well. Table 14 shows the statistical analyses for the real-life network. According to the outputs, the null hypothesis is rejected for the ER, SM, and MS metrics which indicate the significant superiority of the MOWFA over the MOICA and MOSA.

Table 14.

Statistical analyses for the real-life network.

Performance metric	Comparisons	Lower bound	Upper bound	p-Value	Description
ATO	MOWFA vs. MOICA	0.17	0.49	0.0045	$H_0$ is rejected.
	MOWFA vs. MOSA	0.51	0.80	2.29e−004	$H_0$ is rejected.
ATA	MOWFA vs. MOICA	−0.14	11.66	0.0537	$H_0$ is not rejected.
	MOWFA vs. MOSA	9.37	18.30	9.98e−004	$H_0$ is rejected.
ER	MOWFA vs. MOICA	−0.78	−0.04	0.035	$H_0$ is rejected.
	MOWFA vs. MOSA	−0.88	−0.18	0.0135	$H_0$ is rejected.
SM	MOWFA vs. MOICA	−26.58	−1.04	0.0398	$H_0$ is rejected.
	MOWFA vs. MOSA	−17.09	−1.65	0.028	$H_0$ is rejected.
MS	MOWFA vs. MOICA	0.05	0.56	0.027	$H_0$ is rejected.
	MOWFA vs. MOSA	0.21	0.57	0.00	$H_0$ is rejected.

Fig. 19 illustrates the approximate Pareto fronts obtained by these three methods for one of the runs of problem. Comparing to other methods, the solutions of the MOWFA have better qualities (convergence) which implies that the approximate Pareto front of the proposed algorithm strongly dominates the non-dominated solutions of other algorithms. The solutions of the MOWFA have also covered a wider area of the objective space which shows their higher diversity. According to Fig. 19, the uniformity of the MOWFA’s solutions throughout the Pareto front is far better than the uniformity of the Pareto fronts discovered by the MOICA and MOSA. This was expected due to better values of spacing metric.

Fig. 19.

Pareto fronts discovered by the algorithms

As mentioned earlier, the problem has been solved for twenty times and the order of visited healthcare centers acquired by the MOWFA for a single run has been reported in Table 15 . Table 15 also details the capacity of available vehicles and the weights of wastes they carry to their destination. Based on the information provided in Table 15, the company requires 8 and 7 vehicles for collecting infectious and non-infectious wastes, respectively.

Table 15.

Order of visited healthcare centers for a single run.

Infectious wastes
#Vehicle Num	Capacity$(\mathit{T}\mathit{o}\mathit{n})$	Order of visited healthcare centers	Total carried weight$(\mathit{T}\mathit{o}\mathit{n})$
1	2	1	1.83
2	2.2	3–7-8–10	1.87
3	2	4	1.72
4	2.5	12–13	2.33
5	3	6	2.66
6	3.5	2–5	3.34
7	2.5	9–11-14	2.39
8	2	15	1.86
Non-infectious wastes
#Vehicle Num	Capacity$(\mathit{T}\mathit{o}\mathit{n})$	Order of visited healthcare centers	Total carried weight$(\mathit{T}\mathit{o}\mathit{n})$
1	4	8–10-11–3	2.54
2	4.5	6	3.99
3	4.4	7–9-12	3.67
4	5.5	1–2	5.33
5	5.5	4–13	4.45
6	5.5	5–15	5.22
7	4	14	1.81

To validate the results of the proposed algorithm, the Percentage Relative Error (PRE) (in terms of objective values) between the outputs of the MOWFA and experts’ estimations were computed using Eq. (68) (Hosseinian and Baradaran, 2020):

$$\mathit{PR}{E}_{\mathit{rn}}^{\mathit{nc}}=\frac{\mathit{AL}{G}_{\mathit{nc}}^{\mathit{rn}}-Ex{p}_{\mathit{nc}}}{\mathit{Ex}{p}_{\mathit{nc}}}\times 100$$ (68)

Where, ${\mathit{PRE}}_{\mathit{rn}}^{\mathit{nc}}$ represents the percentage relative error between the solutions of the algorithm and experts’ estimation in the ${\mathit{rn}}^{\mathit{th}}$ run for the objective function$\mathit{nc}$. ${\mathit{ALG}}_{\mathit{nc}}^{\mathit{rn}}$ is the value of ${\mathit{nc}}^{\mathit{th}}$ objective function in the run $\mathit{rn}$ by the optimizer. ${\mathit{Exp}}_{\mathit{nc}}$ is the estimation value of ${\mathit{nc}}^{\mathit{th}}$ objective declared by the experts of the company. The values given by the experts of the company have been estimated based on their experiences of similar networks that they have previously encountered. Fig. 20, Fig. 21 depict the gaps for the first and the second objective functions, respectively. According to the PRE values reported in Fig. 20, Fig. 21, it can be inferred that the outputs of the MOWFA is different from the given estimations of experts for less than 10%. This implies the high accuracy of the proposed method and it shows that the MOWFA can offer reliable results for the studied network.

Fig. 20.

Values of $\mathit{PRE}$ metric in terms of first objective function

Fig. 21.

Values of $\mathit{PRE}$ metric in terms of second objective function

Regarding the site selection perspective of the proposed problem, Table 16 summarizes the selected sites for treatment, recycling, and disposal centers. Based on the results in Table 16, the following outlines have been obtained. By providing these outputs to the experts of the company, they approved the order of visited healthcare centers and objective values.

• 1.For most of the runs, the combination of treatment site “5″ and technology “1” has been selected as the best choice. The MOWFA has chosen this combination in 70% of runs. The fifth treatment site along with the first technology is the most frequent selected combination by the MOICA as it has been chosen in 45% of runs. For the MOSA, this combination has been selected for 55% of runs.
• 2.The candidate location “3″ has been chosen as the best site for recycling center selected by all algorithms. This site has been selected as the most appropriate location for more than 60% of runs.
• 3.Regarding the best location for establishing a disposal center, the site “2″ has strongly overcome the other locations since it is the most frequent chosen site by the algorithms. The MOWFA, MOICA, and MOSA have selected this site for 80%, 80%, and 70% of their runs.

Table 16.

Selected sites for treatment, recycling, and disposal centers.

Run	MOWFA				MOICA				MOSA
	tc	tt	rc	dc	tc	tt	rc	dc	tc	tt	rc	dc
1	4	1	3	2	5	1	5	2	5	1	5	2
2	5	1	3	2	5	2	3	2	5	1	3	2
3	3	1	3	2	5	4	5	1	1	1	3	2
4	5	1	3	2	5	1	4	2	5	1	3	2
5	5	1	3	2	5	1	3	2	5	1	3	2
6	5	1	4	2	5	3	5	3	4	4	3	2
7	5	1	3	2	4	1	5	2	5	1	5	2
8	5	1	4	2	5	1	3	2	5	1	1	1
9	1	1	2	2	5	1	3	2	5	1	3	4
10	5	1	3	3	5	2	3	4	5	4	2	1
11	5	1	2	2	2	1	3	2	2	2	3	2
12	5	1	3	2	5	3	3	2	2	1	3	2
13	3	1	1	2	4	1	3	2	5	1	5	2
14	5	1	2	4	5	4	3	4	3	1	3	2
15	5	1	3	2	5	1	3	2	5	3	3	3
16	5	3	3	2	5	1	3	2	2	1	3	4
17	1	3	3	3	5	1	3	2	5	1	2	2
18	5	1	3	2	5	1	3	2	5	1	3	2
19	5	1	3	2	1	1	3	2	5	2	3	2
20	5	1	3	4	5	4	5	2	5	1	3	1

7. Conclusions and future works

This research proposed a bi-objective mixed-integer mathematical model for the healthcare waste location-routing problem. The proposed model concentrates on stochastic emission of contamination during transportation of infectious wastes collected from healthcare centers. This phenomenon that may occur in real-world healthcare logistic networks and other realistic assumptions of the proposed model are the major contributions of this research. The objectives of this model are minimization of total costs and emission of contamination. This study also offers a multi-objective water-flow like algorithm to solve various test instances of this highly intricate problem. These test instances include small, medium, and large size problems. In addition to the proposed algorithm, two other meta-heuristics were hired to solve test problems. The results of all three algorithms were compared based on several performance evaluation metrics. Experimental results demonstrate that the MOWFA is more capable than the MOICA and MOSA in terms of the ER, SM, and MS. The model has been applied to a real healthcare waste logistic network in Iran to show its practicality. All algorithms were used to solve this case study as well. Due to the comparisons made between the algorithms, the MOWFA showed a high level of efficacy in comparison with other state-of-the-art algorithms. The following directions can be considered for future studies:

• 1.Uncertainty in other parameters of the model can also be considered to present a more realistic problem.
• 2.The developed local search operators can be embedded in other optimizers and their results should be compared with the outputs of this research.
• 3.Other performance evaluation metrics such as generalized distance, inverted generalized distance, set coverage, and hyper-volume can be used to assess the efficiency of the proposed method.
• 4.Comparing to single-solution algorithms, the proposed method may need more computation times. Therefore, developing some procedures that reduce the running time of the MOWFA is an opportunity for further studies.
• 5.Considering the occurrence of accidents during transferring infectious wastes and the spread of contaminants is an interesting subject for future studies.
• 6.It is recommended to develop new techniques for expediting the MOWFA in the AHP procedure since the calculation of weights requires more computation efforts as the number of solutions in the archive set increases.

CRediT authorship contribution statement

Mohammad Nikzamir: Data curation, Writing - original draft, Software, Validation, Visualization, Formal analysis, Resources. Vahid Baradaran: Conceptualization, Methodology, Writing - original draft, Supervision, Visualization, Investigation, Data curation, Project administration, Resources.

Appendix A: Procedures of the classical WFA

The classical WFA method uses the following procedures to solve an optimization problem. These procedures continue until a termination condition is reached (Yang and Wang, 2007, Nourmohammadi et al., 2019):

• • Splitting and moving procedures: As the water-flows pass the terrains, they are divided into multiple sub-flows. Then, they tend to flow through lower terrains. These mechanisms are simulated by the splitting and moving procedures in the WFA. Suppose that there is a flow ($F$) that is running with the mass (${\mathit{MS}}_F)$ and the velocity (${\mathit{VL}}_F)$. The splitting procedure is executed for the flow F if (${\mathit{MS}}_F\times {\mathit{VL}}_F)$ exceeds a specific threshold (TR). The number of flows (NOF) starts growing as the splitting procedure carries on. This growth is constrained by defining an upper limit for the number of sub-flows (NOSF) that originated from each flow. The number of sub-flows derived from the flow F is obtained by Eq. (69) (Yang and Wang, 2007, Nourmohammadi et al., 2019):

$$\mathit{NS}{F}_F=Min\left(Max\left(1,int\left(\frac{M{S}_F\times V{L}_F}{\mathit{TR}}\right)\right),NOSF\right)$$ (69)

Where, ${\mathit{NSF}}_F$ represents the number of sub-flows originated from the $F^{\mathit{th}}$ flow. By using the function$\mathit{int}()$, the closest integer number to a value is obtained. Having obtained the number of sub-flows originating from each flow, the positions of the newly generated sub-flows must be determined. This procedure is known as the moving process in the WFA. The moving procedure is implemented by using one or more local search strategies that may lead the algorithm to find more appropriate solutions in the neighborhood. Local search methods are iterated for a certain number of repetitions. It should be noted that when${(MS}_F\times {\mathit{VL}}_F)<TR$, there will be no splitting process and the flow only leads to a feasible neighborhood solution. Having implemented the splitting and moving procedures, the original flow is neglected since it has been substituted by the sub-flows. The mass and the velocity of each sub-flow are calculated by Eqs. (70), (71), respectively (Yang and Wang, 2007, Nourmohammadi et al., 2019):

$$M{S}_{F,ms}=\left(\frac{\mathit{OF}{V}_{\mathit{ms}}}{{\sum }_{\mathit{ms}=1}^{\mathit{NS}{F}_F}\mathit{OF}{V}_{\mathit{ms}}}\right)\times M{S}_F$$ (70)

$$V{L}_{F,ms}=\left\{\begin{array}{cc}\sqrt{V{L}_F^2+2\times \mathrm{\Delta }OF{V}_{F,ms}\times \varsigma };& \mathit{if}(V{L}_F^2+2\times \mathrm{\Delta }OF{V}_{F,ms}\times \varsigma )>0\\ 0;& \mathit{Otherwise}\end{array}\right)$$ (71)

Where, ${\mathit{MS}}_{F,ms}$ and ${\mathit{OFV}}_{\mathit{ms}}$ are the mass and fitness value of the flow$\mathit{ms}$. ${\mathit{VL}}_{F,ms}$ is the velocity of the sub-flow $\mathit{ms}$ streaming from the flow $F$. $\varsigma$ denotes the gravitational acceleration. ${\mathrm{\Delta }OFV}_{F,ms}$ represents the difference between the fitness values of F and $\mathit{ms}$.

• • Merging procedure: There is a possibility that flows revisit each other when they are passing through lower terrains. In this case, these flows will be merged using a merging procedure. Suppose that the flow $F$ encounters the flow $\mathit{ms}$ in the same location which implies that these two flows have the same fitness values. The WFA discards the flow $\mathit{ms}$ and the velocity and mass of this flow are merged with the flow $F$ by using the following equations (Yang and Wang, 2007, Nourmohammadi et al., 2019):

$$M{S}_F=M{S}_F+M{S}_{\mathit{ms}}$$ (72)

$$V{L}_F=\frac{V{L}_F.M{S}_F+V{L}_{\mathit{ms}}.M{S}_{\mathit{ms}}}{M{S}_F+M{S}_{\mathit{ms}}}$$ (73)

• • Evaporation procedure: The water-flows evaporate gradually as they pass the terrains. This characteristic enables the water-flows to develop their search space in order to avoid the local optima trap. To simulate this procedure, the WFA uses an evaporation operator every $\mathit{ET}$ iterations on all flows. By using Eq. (74), a new mass for the flow F after the evaporation process ($\stackrel{´}{{\mathit{MS}}_F)}$is obtained (Yang and Wang, 2007, Nourmohammadi et al., 2019):

$$M{S}_F^{\prime }=\left(1-\frac{1}{\mathit{ET}}\right)\times M{S}_F$$ (74)

• • Precipitation procedure: The WFA applies two sorts of precipitation procedures to simulate the phenomenon of returning the evaporated water to the terrain. These precipitation procedures include regular and irregular precipitations. The WFA implements the regular precipitation along with the evaporation process every $\mathit{ET}$ iterations. In the regular precipitation, the evaporated water will be precipitated and therefore the new flows will have different positions. The mass of the flow $\mathit{ms}$ after the precipitation process ($\stackrel{´}{{\mathit{MS}}_{\mathit{ms}})}$ is obtained as follows (Yang and Wang, 2007, Nourmohammadi et al., 2019):

$$M{S}_{\mathit{ms}}^{\prime }=\frac{M{S}_{\mathit{ms}}}{{\sum }_{F=1}^{\mathit{NOF}}M{S}_F}\times \left(M{S}_0-\sum _{F=1}^{\mathit{NOF}}M{S}_F\right)$$ (75)

• •The irregular precipitation occurs when all flows of the same generation have zero velocity. In this case, all flows are evaporated and then the same number of flows will return to the terrains by means of the rainfall. Therefore, the newly generated flows may dodge local traps by deviating from their origins. The masses of these newly generated flows are calculated as follows (Yang and Wang, 2007, Nourmohammadi et al., 2019):

$$M{S}_F^{\prime }=\left(\frac{M{S}_F}{{\sum }_{F=1}^{\mathit{NOF}}M{S}_F}\right)\times M{S}_0$$ (76)

Where, NOF denotes the current number of flows. The newly generated flows obtained by the regular and irregular precipitations are added to the population of flows. Hence, a remarkable number of flows may have the same fitness values. In this respect, after implementing each precipitation procedure, the merging process is carried out so as to avoid excessive searches.