Sharing the sacrifice, minimizing the pain: Optimal wage reductions

Abstract

Faced with temporary revenue shocks, employers may implement wage reductions — a common response to COVID-19 for U.S. universities. I provide a framework for optimal reductions when labor is inelastic wherein a planner balances “minimizing the pain” and “sharing the sacrifice.” I show that for a broad class of utility functions the optimal schedule includes (1) a cutoff wage below which the reduction is zero and (2) weakly progressive reduction rates above the cutoff wage. I illustrate the results using data from a large U.S. university.

Highlights

• •Many universities and other firms are cutting employee wages in response to COVID-19.
• •I write a framework to determine “optimal” cuts given inelastic labor.
• •Optimal plans are progressive with a cutoff wage below which zero reductions occur.
• •I compare the model’s predictions to the actions taken by a large U.S. university.

1. Introduction

Faced with declining revenues during COVID-19, universities around the country are implementing temporary compensation reductions for faculty and other staff. These cuts may take the form of reduced salaries, furloughs, changes to indirect compensation packages, or any combination of these.2 Speaking of the need for “shared sacrifices”, administrators have announced plans that often feature (1) a threshold wage below which no cuts are implemented, (2) a weakly progressive schedule of cuts which increase in percentage terms as wages increase, and (3) equal application across academic departments and administrative offices.3 Despite these commonalities, plans differ significantly in details, suggesting that decision makers may have different objectives.4

I offer a parsimonious framework for determining the “optimal” wage reduction schedule that generates a given level of cost savings. To incorporate the stated need for “shared sacrifices”, I modify the social welfare function of Miller et al. (2019) — a social planner seeks to minimize the weighted sum of the average of the “pain” experienced by workers and the variance of that pain across workers, similar to the “equal sacrifice” model of Weinzierl (2014). I apply the framework to data from a major U.S. university and show how the optimal schedule of reductions varies with changes to the weight placed on the “shared sacrifice” and the total amount to be raised. I then compare the model’s predictions to the reduction plan announced by the university. For brevity, I present the framework and application without extended discussion — I conclude with commentary on the assumptions of the framework.

2. A framework for shared sacrifice

Consider a firm with $N$ employees indexed by $i$. Each employee supplies labor inelastically and earns wages $w_i$ — I discuss productivity and output below. Suppose the firm must reduce total wages ${\sum }_{i=1}^N{w}_i=W$ by $R$. Let $r_i$ be employee $i$’s reduction. Let $p(w,r)$ measure the disutility (or “pain”) experienced by an individual with wage $w$ who receives a reduction $r$. Let $E_p=\frac{1}{N}{\sum }_{i}p(w_i,r_i)$ be the average pain and let $Var\left(p\right)=\frac{1}{N}{\sum }_i{(p(w_i,r_i)-E_p)}^2$ be the variance in the pain across employees. The planner’s problem is to choose reductions $\left\{r_i\right\}$ that satisfy:

$$\underset{{\left\{r_i\right\}}_{i=1}^N}{min}(1-\alpha )E_p+\alpha Var\left(p\right)\text{s.t.}\sum _{i=1}^N{r}_i=R,\frac{r_i}{w_i}\in [0,1]\forall i.$$ (1)

In this equation, $\alpha \in [0,1]$ represents the weight placed on “shared sacrifice”: the greater is $\alpha$, the less the planner cares about minimizing the average pain, and the more the planner cares about equalizing pain across employees. The first constraint on $\left\{r_i\right\}$ ensures that the schedule achieves the given reductions, and the second constraint ensures that the plan does not increase wages or decrease wages below zero. My theoretical result characterizes the solution to Eq. (1) under certain conditions on $p$ and is summarized in Proposition 1.

Proposition 1

Suppose $p(w,r)$ is continuously differentiable. Let $p(w,w)=\infty$ , $p(w,0)=0$ , and let $p$ be strictly increasing in $r$ for a given $w$ and strictly decreasing in $w$ for a given $r$ . Furthermore, let $\frac{\partial p}{\partial r}$ be strictly increasing in $r$ for all $w$ . Finally, assume the wage distribution is non-degenerate. Then the solution to Eq. (1) , $\left\{r_i^{\ast }\right\}$ , is unique and characterized by a cutoff wage $w^{\ast }\ge 0$ such that $w_i<w^{\ast }\Rightarrow r_i^{\ast }=0$ and a schedule of reductions that are weakly progressive: for $w_i>w^{\ast }$ , if $w_i>w_j$ , $\frac{r_i}{w_i}\ge \frac{r_j}{w_j}$ .

Proof

See Appendix. □

The restrictions on $p$ are easily satisfied: given a smooth and strictly concave utility function $u\left(w\right)$ with $u\left(0\right)=-\infty$, the loss function $p(w,r)=u\left(w\right)-u(w-r)$ satisfies the conditions of Proposition 1. The log form $p(w,r)=ln\left(w\right)-ln(w-r)=-ln(1-\frac{r}{w})$ may be particularly appealing as $p$ is a function of the reduction rate $\frac{r}{w}$. Under this form, when $\alpha =0$ the optimal policy loads the reductions on employees earning the highest wages and when $\alpha =1$ the planner sets $\frac{r_i}{w_i}=\frac{R}{W}\forall i$.

2.1. An example with three employees

Suppose the firm has three employees with $w_1=\$$50,000,w${}_2$ $=$ $150,000, and $w_3=\$$250,000. Let $p(w,r)=ln\left(w\right)-ln(w-r)$. Define $t_i=r_i∕w_i$ as the ‘tax’ rate assessed on each employee’s wages. Table 1 provides optimal rates and the average ‘pain’ as both the total level of reduction and the weight $\alpha$ placed on the “sharing” of the sacrifice varies. The first set of rows shows that when the planner seeks to minimize the average pain alone, reductions occur to the employees earning the highest wages alone — when the level of total reduction is 30%, the post-reduction wages for employees 2 and 3 are equal. As $\alpha$ increases, the rates move closer together though they remain progressive. Even with positive values for $\alpha$, lower earners may not experience a reduction.

Table 1.

An example with three employees.

		Level of total reduction
		10% ($45,000)	20% ($90,000)	30% ($135,000)
$\alpha =0$	$t_1$	0	0	0
	$t_2$	0	0	0.1167
	$t_3$	0.18	0.36	0.47
	$\frac{1}{N}\sum p$	0.0661	0.1488	0.2530
$\alpha =0.25$	$t_1$	0	0	0
	$t_2$	0	0.0690	0.2024
	$t_3$	0.18	0.3186	0.4186
	$\frac{1}{N}\sum p$	0.1985	0.1517	0.2561
$\alpha =0.5$	$t_1$	0	0	0
	$t_2$	0.0126	0.1329	0.2543
	$t_3$	0.1725	0.2802	0.3874
	$\frac{1}{N}\sum p$	0.0673	0.1572	0.2612
$\alpha =0.75$	$t_1$	0	0.0757	0.1912
	$t_2$	0.0648	0.1708	0.2744
	$t_3$	0.1411	0.2424	0.3371
	$\frac{1}{N}\sum p$	0.0730	0.1812	0.3147
$\alpha =0.9$	$t_1$	0.0523	0.1576	0.2629
	$t_2$	0.0867	0.1881	0.2896
	$t_3$	0.1175	0.2156	0.3136
	$\frac{1}{N}\sum p$	0.0898	0.2076	0.3411
$\alpha =0.99$	$t_1$	0.0956	0.1961	0.2966
	$t_2$	0.0987	0.1988	0.2990
	$t_3$	0.1017	0.2015	0.3013
	$\frac{1}{N}\sum p$	0.1039	0.2217	0.3552

Notes: This table reports the optimal reduction rates (as a percentage of wages) and average “pain” experienced by a firm with three employees. For this example, $w_1=\$$50,000, $w_2=\$$150,000, and $w_3=\$$250,000, and $p(w,r)=ln\left(w\right)-ln(w-r)$.

3. An empirical example

I implement the framework on a dataset of employee wages from a U.S. university with more than 20,000 students. I obtain annual wages for each worker employed by the university as of February 2020 (i.e. before the onset of COVID-19-related closures in the U.S.). While the university offers a range of non-salary benefits such as contributions to retirement plans which may be affected by cuts to wages, I abstract away from non-salary compensation for simplicity.5 I drop employees whose primary appointment is in athletics or student housing.6

The resulting dataset consists of 4630 employees with total wages of $311.5 million per year. The median wage is $57,566, and the interquartile range extends from $38,297 to $84,771. The data include 3412 unclassified (i.e. salaried) employees earning a total of $266.9 million with a median wage of $68,323. Of these, 2085 are faculty, earning a total of $157.6 million with a median wage of $68,992. Fig. 1 illustrates the distribution of salaries with four histograms: Panel (a) illustrates the distribution over all employees, Panel (b) focuses on classified (i.e. hourly) employees, Panel (c) focuses on unclassified employees, and Panel (d) illustrates the distribution of faculty wages.

Fig. 1.

Wage distributions by employee type. Notes: These figures present the distribution of effective wages for individuals employed by the sample university as of February, 2020. For Panels (a) and (c), I drop six individuals who earn more than $400,000.

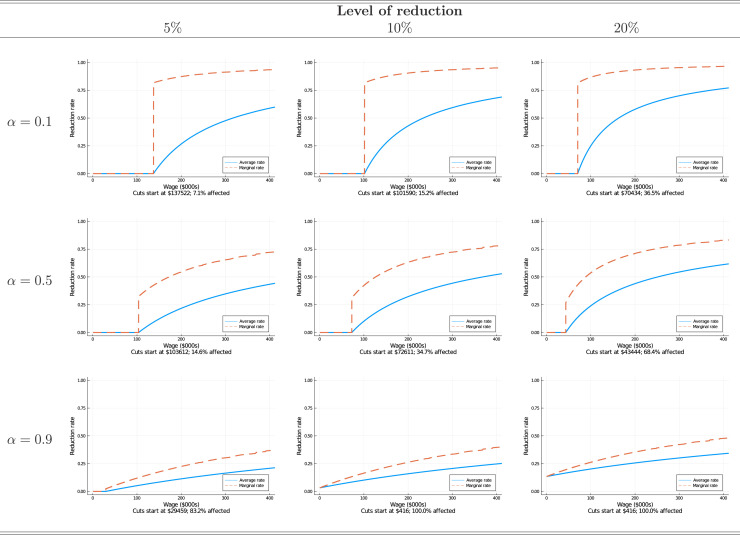
Given this set of wages $w_i$ and the pain function $p(w,r)=ln\left(w\right)-ln(w-r)$ I solve Eq. (1) using numeric optimization techniques described in Appendix.7 The results are shown in Fig. 2. For each total reduction level in $\{5\text{\%},10\text{\%},20\text{\%}\}$, I report optimal policies for $\alpha \in \{0.1,0.5,0.9\}$ and plot the averagereduction rate $t_i=r_i∕w_i$ and the marginal rate $\partial r_i∕\partial w_i$ as well as the cutoff wage and the percentage of employees affected. Given a level of reduction, increasing $\alpha$ reduces the cutoff wage and flattens the reduction rates for those above the cutoff — indeed, when $\alpha =0.1$, marginal rates rise above 90% close to the cutoff wage. Similarly, given an $\alpha$, increasing the level of total reduction decreases the cutoff wage and steepens the post-cutoff reduction rates.

Fig. 2.

Optimal reduction policies under log utility. Notes: These figures depict the results of solving Eq. (1) for the wage distribution shown in Fig. 1(a) when $p(w,r)=ln\left(w\right)-ln(w-r)$. The average rate is $r_i∕w_i$ and the marginal rate is $\partial r_i∕\partial w_i$.

To understand how well this model maps onto the data, I use the model to estimate the $\alpha$ that most closely matches the behavior of the university’s administrators. In August 2020 the university announced policy that is piecewise-linear with respect to the tax rate:

$$\frac{r_i}{w_i}=\left\{\begin{array}{cc}0,\hfill & w_i<45000\hfill \\ 0.12\cdot \frac{w_i-45000}{105000},\hfill & 45000\le w_i<150000\hfill \\ 0.12+0.06\cdot \frac{w_i-150000}{50000},\hfill & 150000\le w_i<200000\hfill \\ 0.18,\hfill & 200000\le w_i\hfill \end{array}\right)$$ (2)

Applied to the data, this plan generates $18.42 million in wage savings for the university, or 5.9% of total salaries. I calibrate $\alpha$ by minimizing the root mean square error between the solutions to Eq. (1) and the rates given by Eq. (2), where the mean is taken across individuals. The best fit occurs at $\alpha \approx 0.842$, where the RMSE is 0.0076. Fig. 3 compares the best-fit optimal plan with this $\alpha$ to the announced plan. The optimal plan begins cuts at $45,729, very close to the university’s plan; both plans affect approximately 66% of workers. I interpret this fraction, combined with the calibrated $\alpha$, as evidence that internal equity considerations are relatively important to this employer.8 Differences occur for high wage earners — the university’s plan calls for slightly higher cuts from salaries of roughly $150,000 to $230,000 and maintains a constant rate above $200,000, whereas the optimal plan continues to increase rates for the highest earners.

Fig. 3.

Announced reduction plan and calibrated optimal plan. Notes: This figure compares the reduction plan announced by the university to the best fit optimal plan according to a root mean square error metric. The announced reductions begin at $45,000; the calibrated optimal plan begins at $45,729. See text for details.

Optimal plans are also driven by the underlying distribution of worker wages. I explore this in Fig. 4 by considering a scenario in which the unclassified and classified worker groups are separately required to take a reduction in total pay of 5.9% (matching the university’s announced cuts), and compare the resulting reduction schedules to the scenario in which all employees are collectively required to take a reduction of 5.9%. I select $\alpha$ to be at and around the level estimated from the announced plan. As classified wages are lower than unclassified wages, separating them from unclassified employees leads to a schedule for the unclassified group with a higher cutoff wage and lower post-cutoff reductions, while the cutoff wage for the classified group decreases and post-cutoff reductions are higher. These results suggest a political economy component to intra-firm negotiations over any reduction policy — low-wage employees benefit from being included in groups with high wage employees to shoulder the burden of reductions.

Fig. 4.

Optimal reduction policies by employee type under log utility and a 5.9% reduction. Notes: These figures depict the results of solving Eq. (1) for the wage distributions shown in Fig. 1 when $p(w,r)=ln\left(w\right)-ln(w-r)$ and the total reduction is set at 5.9% (matching the university’s announced reductions).

4. Discussion

The framework presented above is consistent with the optimal tax literature in the sense of employing a “flexibly utilitarian” measure of welfare: when $\alpha =0$, each individual’s pain is valued equally by the planner (Mirrlees, 1976, Saez, 2001, Mirrlees and Adam, 2010). The pain functions I employ in the empirical analysis are constructed as lost utility relative to an expected baseline, consistent with prospect theory (Kahneman, 1979). There is empirical evidence to support this loss framework, particularly when perceived risk is high (List, 2004, Barberis, 2013). Where my framework departs from most literature is on the issue of labor supply. I assume that labor is supplied inelastically — the employer experiences no loss in productivity as a consequence of implementing temporary wage reductions, no matter the rate (Hannan, 2005). In the long run, depending on the friction in the relevant labor markets, any reduction in wages may incentivize employees to separate from the firm (Parsons, 1986). However, as pay reductions are generally announced as temporary measures (i.e. for a duration over which employees may not easily be able to change their effort) and often occur in response to industry-level shocks (i.e. at times when labor market frictions may be high), this assumption may be reasonable for the purposes of the model (Hall, 2005).

The framework does not consider wage rigidity directly — rather the planners’ disutility of pain is an implicit source of rigidity. In reality, rigidity may be negatively correlated with wages, as low-wage workers may be protected by minimum wage laws or unions and high-wage workers may be compensated in part by performance bonuses or profit-sharing.9 If this correlation is sufficiently strong, the observed wage distribution may automatically respond to revenue decreases in ways that closely follow the predictions of this model. In the face of differential wage rigidity, Eq. (1) could be modified to incorporate the relevant frictions, though the progressiveness result of Proposition 1 would no longer hold.

The framework also departs from the traditional view of firms as profit-maximizers, at least insofar as it takes the level of reduction as given and does not consider layoffs or reductions in output. Indeed, the university considered here chose to layoff some employees in housing and athletics and shuttered many study abroad programs. However, consistent with this analysis, Cajner et al. (2020) analyze the U.S. labor market during the “pandemic recession” through June 2020 and document nominal wage cuts among high wage workers (instead of layoffs); Olafsdottir (2020) examines the 2008–2010 Icelandic recession and finds that 80% of employees experienced wage cuts. The reasons behind this behavior are not yet well understood — Rees (1993) argues that “fairness” plays an important role in setting wages and Krekel et al. (2019) survey analyses of employee moral and find that subjective well-being is linked to profitability.

Finally, the framework assesses pain at the individual level, though tax policies are often analyzed at a household level(Kleven et al., 2009). Individual organizations typically only control the wages of one member of a household. If matching is assortative and the organization is a monopsonistic demander of labor (i.e. a large university in a “college town”), the analysis is likely to be unaffected. If couples are heterogeneously employed, similar reductions could lead to significantly different household-level pain. However, any attempt by a single employer to differentially treat employers based on household income would likely run afoul of the Equal Pay Act.

While I present this framework in part due to timely concerns surrounding revenue uncertainty in U.S. higher education as a consequence of the COVID-19 pandemic, temporary wage reductions or other changes in employment are one of a number of tools used by firms in many sectors to respond to short-term crises. As the world prepares to deal with volatility from a number of sources – climate change, energy shortages, and political transitions come to mind – firms may be forced to adjust their internal structures and incentives. Doing so will require a delicate balancing act which may substantially vary across firms due to the distribution of wages and bargaining power within each.

Appendix. Proof of Proposition 1

Given the assumptions on $p(w,r)$, apply the inverse function theorem to write $r(p,w)$ – the revenue earned by assigning a worker with wage $w$ pain $p$. Re-write Eq. (1) in terms of choosing individual pain and an average pain:

$$\underset{{\left\{p_i\right\}}_{i=1}^N,E_p}{min}(1-\alpha )E_p+\alpha \frac{1}{N}\sum _{i=1}^N{(p_i-E_p)}^2$$$$\text{s.t.}\sum _{i=1}^{N}r(p_i,w_i)=R,\frac{1}{N}\sum _{i=1}^N{p}_i=E_p,r(p_i,w_i)\ge 0\forall i$$ (3)

The solution is characterized by the Karush–Kuhn–Tucker conditions. Let $\frac{1}{N}\lambda$ be the multiplier on the first constraint, $\mu$ be the multiplier on the second constraint, and $\frac{1}{N}{\eta }_i$ be the multiplier on the (set of) third constraint(s). Examine the first-order condition for $E_p$ and plug in the second constraint to obtain

$$0=(1-\alpha )-2\alpha \frac{1}{N}\sum _{i=1}^N(p_i-E_p)-\mu \Rightarrow \mu =1-\alpha .$$

Next examine the first-order condition with respect to $p_i$ to obtain

$$0=2\alpha \frac{1}{N}(p_i-E_p)+\mu \frac{1}{N}+\frac{1}{N}\lambda \frac{\partial r}{\partial p}(p_i,w_i)+\frac{1}{N}{\eta }_i\frac{\partial r}{\partial p}(p_i,w_i)$$

$$0=2\alpha (p_i-E_p)+(1-\alpha )+(\lambda +{\eta }_i)\frac{\partial r}{\partial p}(p_i,w_i).$$ (4)

Suppose that $p_i=E_p$ for all $p_i$. Since $R>0$, so too is $E_p>0$ and therefore $p_i>0$ for all $i$. Therefore, ${\eta }_i=0$ for all $i$, so Eq. (4) implies that $\frac{\partial r}{\partial p}(E_p,w_i)=-\frac{1-\alpha }{\lambda }$, a constant. This is impossible if $w_i$ varies across individuals, as $\frac{\partial r}{\partial p}$ is strictly increasing in $w$ at $E_p$. Therefore, as long as the wage distribution is not degenerate, some individual must have $p_i>E_p$.10 Since $\frac{\partial r}{\partial p}$ is positive for all $p_i$, $\lambda$ must be negative.

Suppose, for a given $i$, that ${\eta }_i=0$. Given $E_p$ and $\lambda$, since $\frac{\partial r}{\partial p}$ is strictly decreasing in $p$ (since $\frac{\partial p}{\partial r}$ is strictly increasing in $r$), there is a unique $p_i^{\ast }(E_p,\lambda ;w_i)$ (which may be negative) that solves Eq. (4). Furthermore, $p_i^{\ast }$ is continuous, increasing in $w_i$, and strictly monotonic in $\{E_p,\lambda \}$. Define $\widetilde{p_i}(E_p,\lambda ;w_i)=max\{p_i^{\ast }(E_p,\lambda ;w_i),0\}$. Since $p^{\ast }$ is unique, $\tilde{p}$ is unique and monotonic, and there is some wage $w^{\ast }$ such that for $w_i<w^{\ast },\tilde{p}\left(\cdot \right)=0$. We can write the remaining conditions as a system of two equations in two unknowns $\{E_p,\lambda \}$:

$$E_p=\frac{1}{N}\sum _{i=1}^N\tilde{p}(E_p,\lambda ;w_i)$$$$R=\sum _{i=1}^{N}r(\tilde{p}(E_p,\lambda ;w_i),w_i)$$ (5)

For any $\lambda <0$, note that if $E_p=0$, $\frac{1}{N}{\sum }_{i=1}^N\tilde{p}(E_p,\lambda ;w_i)>0$ since there must be at least one $p_i>E_p$. Since $\frac{\partial r}{\partial p}\to 0$ as $p\to \infty$, there is some $E_p$ such that $\tilde{p}(E_p,\lambda ;w_i)<E_p\forall i$. Since $\tilde{p}$ is continuous and is strictly monotonic for at least one $i$, for any $\lambda$ there is some unique $E_p^{\ast }\left(\lambda \right)$ that solves the first equation. Given the continuity and monotonicity of $r(p,w)$, the system has a unique solution $\{E_p^{\ast },{\lambda }^{\ast }\}$. The solution to Eq. (3) is given by $\{\tilde{p}(E_p^{\ast },{\lambda }^{\ast }),E_p^{\ast }\}$, which implies there is a unique $r_i^{\ast }=r({\tilde{p}}_i^{\ast },w_i)$ that solves Eq. (1). Since $p(w,r)=0\iff r(p,w)=0$, $r_i^{\ast }$ is characterized by the cutoff wage $w^{\ast }$ such that for $w_i<w^{\ast },r_i=0$. Furthermore, given the monotonicity of ${\tilde{p}}_i^{\ast }$ and the strict convexity of $p(w,r)$ (from $\frac{\partial p}{\partial r}$ strictly increasing in $r$), if $w_i>w_j$, $\frac{r_i}{w_i}\ge \frac{r_j}{w_j}$.  □

I compute solutions to Eq. (1) by following the program suggested by the proof. In an inner loop, given a $E_p$ and $\lambda$, I solve for $p_i^{\ast }$. In an outer loop, I search for $E_P^{\ast }$ and ${\lambda }^{\ast }$ using numeric optimization techniques (Wächter and Biegler, 2006, Mogensen and Riseth, 2018).