Model-Assisted Designs for Early-Phase Clinical Trials: Simplicity Meets Superiority

Abstract

Drug development enterprise is struggling because of prohibitively high costs and slow progress. There is urgent need for adoption of novel adaptive designs to improve the efficiency and success of clinical trials. A major barrier is that many conventional designs are inadequate for modern drug development, yet most novel adaptive designs are difficult to understand, require complicated statistical modeling, demand complex computation, and need expensive infrastructure for implementation. The objective of this article is to introduce and review a class of novel adaptive designs, known as model-assisted designs, to remove this barrier and increase the use of novel adaptive designs. Model-assisted designs enjoy superior performance comparable to more complicated, model-based adaptive designs, but their decision rule can be pretabulated and included in the protocol—thus implemented as simply as the conventional designs. We review state-of-the-art model-assisted designs for phase I clinical trials for single-agent, drug-combination and late-onset toxicity scenarios. We also briefly introduce model-assisted designs for phase II trials to handle binary, coprimary endpoints and delayed response. Freely available user-friendly software and trial examples (trialdesign.org) facilitate the adoption of model-assisted designs.

INTRODUCTION

Despite rapid advancements in the knowledge of biomedicine, current drug development is on an unsustainable path plagued by high costs, slow progress, and a high failure rate.^1,2 A recent survey reports that the estimated average out-of-pocket cost per approved new drug is 2.5 billion US dollars.³ To address this pressing issue, one important approach embraced by the US Food and Drug Administration is to use novel adaptive designs.⁴

Numerous novel adaptive designs have been proposed to improve the efficiency and accuracy of phase I trials to find the maximum-tolerated dose (MTD) and of phase II trials to identify effective treatments.^5-7 Most of these novel designs, however, failed to be translated into clinical trials,^8,9 because they often are difficult to understand and require complicated statistical modeling, demanding computation, and expensive infrastructure for implementation. As a result, conventional designs (eg, the 3 + 3 design) are still dominantly used despite relatively poor performance. There is an urgent need to increase the adoption of novel adaptive designs.

The objective of this article is to introduce and review a class of novel phase I and II designs, known as model-assisted designs,^10-12 to overcome this quandary of simplicity versus performance. Model-assisted designs yield superior performance compared with the conventional algorithm-based designs and are comparable to more complicated (model-based) designs. With the model-assisted designs, the decision rule can be pretabulated and included in the protocol and, thus, implemented in as simple a way as the conventional designs. By increasing the awareness of model-assisted designs, we hope that more practitioners will apply the novel designs to improve the efficiency and success of early-phase trials.

PHASE I TRIAL DESIGNS

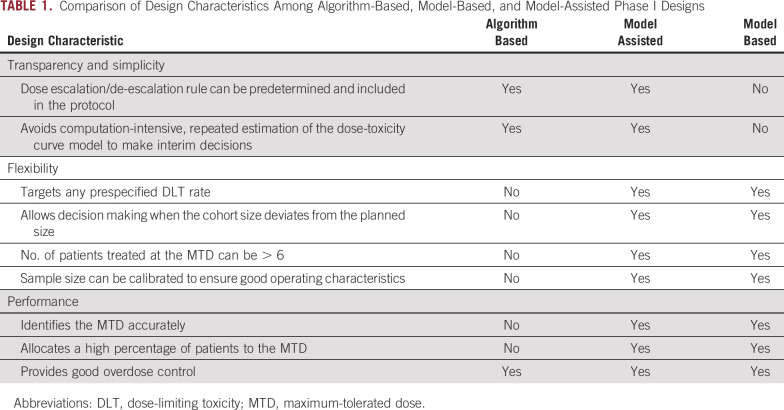
On the basis of their statistical foundation and implementation approach, phase I trial designs can be classified into three types: algorithm-based, model-based, and model-assisted designs.^10-12 Table 1 contrasts the characteristics of these three types of designs.

TABLE 1.

Comparison of Design Characteristics Among Algorithm-Based, Model-Based, and Model-Assisted Phase I Designs

ALGORITHM-BASED DESIGNS

Algorithm-based design is a class of conventional design that uses a set of simple, prespecified rules to determine the dose escalation and de-escalation. Examples include the conventional 3 + 3 design¹³ and its extensions, such as the accelerated titration design¹⁴ and the rolling 6 design.¹⁵ It has long been known that the 3 + 3 design has relatively poor operating characteristics^16,17; for example, it has no specific target dose-limiting toxicity (DLT) rate (but has a range of DLT rates between 17% and 33%), has poor accuracy to identify the MTD, has poor precision to estimate the DLT rate, and has a greater tendency to underdose patients (ie, it treats patients at the doses lower than the MTD). However, because it is simple and easy to implement, the 3 + 3 design is by far the most commonly used phase I design in practice.

CONTEXT

• Key Objective Is there any novel adaptive design that is simple to implement?

• Knowledge Generated This article introduces and reviews a class of novel phase I and II designs, known as model-assisted designs, to provide a state-of-the-art approach to overcome the quandary of simplicity versus performance that hinders the adoption of novel adaptive designs. Model-assisted designs yield superior performance compared with more complicated model-based designs, but the decision rule can be pretabulated and included in the protocol and, thus, implemented in as simple a way as the conventional designs.

• Relevance Model-assisted designs are easy to implement and have great potential to improve the efficiency and success rate of early-phase trials.

MODEL-BASED DESIGNS

Model-based design is a class of novel adaptive designs that uses a statistical model (eg, a logistic model) to describe the dose-toxicity curve and guide dose transition. Examples include the continuous reassessment method (CRM)¹⁷ and its various extensions (eg, dose escalation with overdose control),¹⁸ Bayesian logistic regression model,¹⁹ and Bayesian model averaging CRM.²⁰ As information accrues during the trial, the CRM continuously updates the estimate of the model after each cohort and then uses the updated estimate to determine the dose for the next cohort. Numerous studies have shown that the CRM significantly outperforms the 3 + 3 design,^16,21 with higher accuracy to identify and allocate more patients to the MTD as well as the ability to target any prespecified DLT rates. Despite decades of advocacy by statisticians, the use of the CRM, however, is still limited because of statistical and computational complexity of the design.^8,9 For appropriate use, the CRM requires specialized expertise to choose and calibrate the dose-toxicity model and to re-estimate the model at each decision of dose escalation/de-escalation. It remains a challenge to communicate to clinicians how the design works, which leads them to perceive dose allocations as coming from a black box.

MODEL-ASSISTED DESIGNS

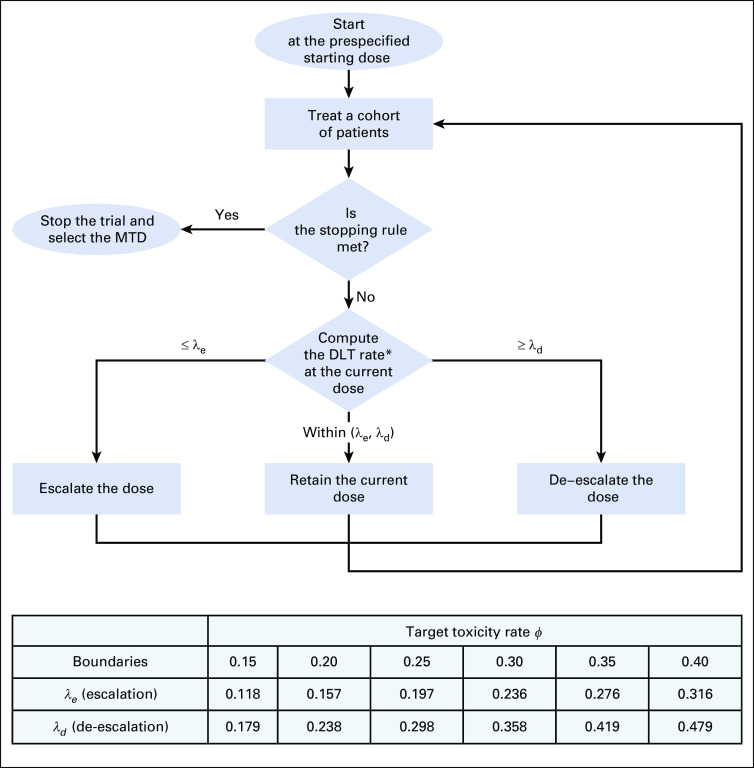
Model-assisted designs were developed to combine the advantages of algorithm-based designs and model-based designs.^10,12,22 Similar to the model-based design, the model-assisted design uses a statistical model (eg, the binomial model) to derive the design for efficient decision making; however, like the algorithm-based design, its dose escalation and de-escalation rule can be predetermined before the onset of the trial and, thus, can be implemented in as simple a way as the algorithm-based designs. Examples of model-assisted designs include the modified toxicity probability interval (mTPI) design²³ and its variation, mTPI-2²⁴; Bayesian optimal interval (BOIN) design^25,26; and keyboard design²² (Fig 1). Zhou et al^11,12 and Ruppert and Shoben²⁷ conducted comprehensive numeric studies to compare the model-assisted designs with the 3 + 3 design and several model-based designs (eg, CRM and escalation with overdose control).¹² The results showed that the model-assisted designs substantially outperformed the 3 + 3 design and yielded a performance comparable to model-based designs on several metrics, including the accuracy of identification of the MTD and allocation of patients to the MTD and the risk of overdosing patients (ie, treatment of a patient at a dose greater than the MTD). Among the model-assisted designs, BOIN stands out; it outperforms the mTPI with higher accuracy identifying the MTD and a lower risk of overdosing patients, and it is simpler and more transparent than the mTPI-2 and keyboard designs.¹² BOIN is also more versatile; it can handle drug-combination trials,²⁸ late-onset toxicity,²⁹ low-grade toxicities,³⁰ and toxicity and efficacy jointly.^31,32 Therefore, in what follows, after a brief review of the mTPI/mTPI-2 and keyboard designs, we use BOIN as an example to illustrate the features and advantages of model-assisted designs.

FIG 1.

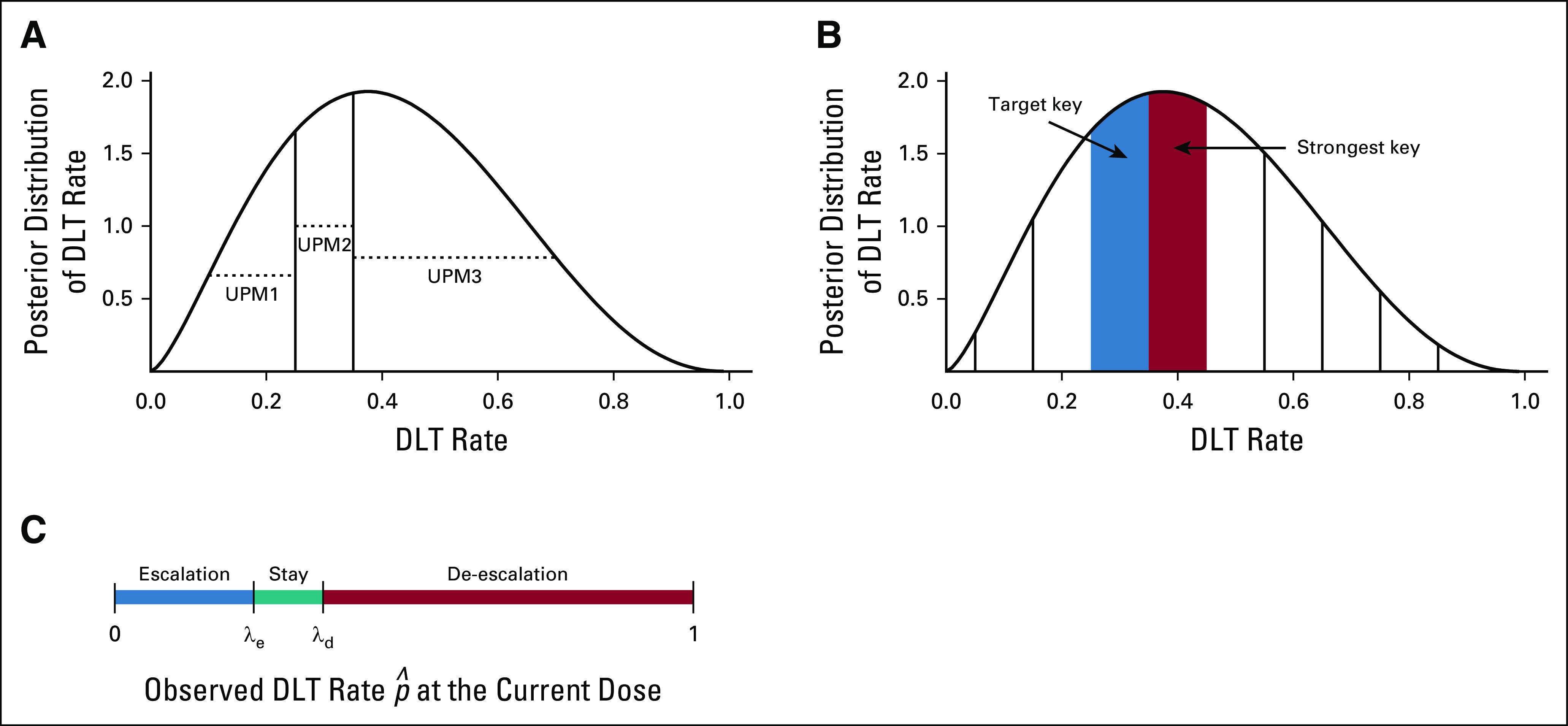
Illustration of the (A) modified toxicity probability interval, (B) keyboard, and (C) Bayesian optimal interval designs. The curves in (A) and (B) are the posterior distributions of the dose-limiting toxicity (DLT) probability at the current dose. To determine the next dose, the modified toxicity probability interval design calculates and compares the values of the three unit probability masses (UPMs), whereas the keyboard design compares the location of the strongest key with respect to the target key. Bayesian optimal interval compares the observed DLT rate at the current dose with the optimized dose escalation boundary, λ_e, and de-escalation boundary, λ_d.

The mTPI design starts with a definition of three toxicity probability intervals: underdosing, proper dosing, and overdosing intervals—for example, (0, 0.2), (0.2, 0.4), and (0.4, 1), respectively. Given the data observed at the current dose, mTPI makes the decision of dose escalation and de-escalation on the basis of the unit probability mass (UPM) of the three intervals. Let p denote the true DLT probability of the current dose. The UPM of an interval is defined as the posterior probability that p is within the interval divided by the length of the interval, calculated according to a statistical model known as the beta-binomial model. If the UPM associated with the underdosing (or overdosing) interval is the largest among the three UPMs, the design escalates (or de-escalates) the dose; otherwise, the dose stays at the current dose. One deficiency of mTPI is that it overly downweighs the overdosing probability, because the overdosing interval is typically wider than the proper dosing interval, which leads to a high risk of overdose of patients (ie, treatment of a high percentage of patients at doses greater than the MTD).²²

The keyboard design addresses the overdosing issue of mTPI by defining a series of equal-width dosing intervals (or keys) to represent the potential locations of p.²² The proper dosing interval is called the target key. The design makes the decision of dose escalation and de-escalation by examining the relative position between the target key and the strongest key, in which the strongest key is defined as the interval that the true DLT is most likely located. The strongest key is identified using the beta-binomial model. If the strongest key is on the left (or right) side of the target key, the observed data suggest that the current dose is most likely underdosing (or overdosing); thus, the design escalates (or de-escalate) the dose; otherwise, the dose stays at the current dose. The keyboard design outperforms the mTPI with substantially lower risk of overdosing patients and better accuracy to identify the MTD.^11,22 The variation of the mTPI (ie, mTPI-2²⁴) adopts the same dose escalation/de-escalation rule as the keyboard design but is less transparent. The mTPI-2 relies on complicated procedures, such as Occam’s razor and model selection.

Compared with the mTPI/mTPI-2 and keyboard designs, the BOIN design is more straightforward and transparent (Fig 1). Let $\hat{p}$ denote the observed DLT rate at the current dose, defined as the number of patients experiencing DLT at the current dose divided by the total number of DLT-evaluable patients treated at the current dose.

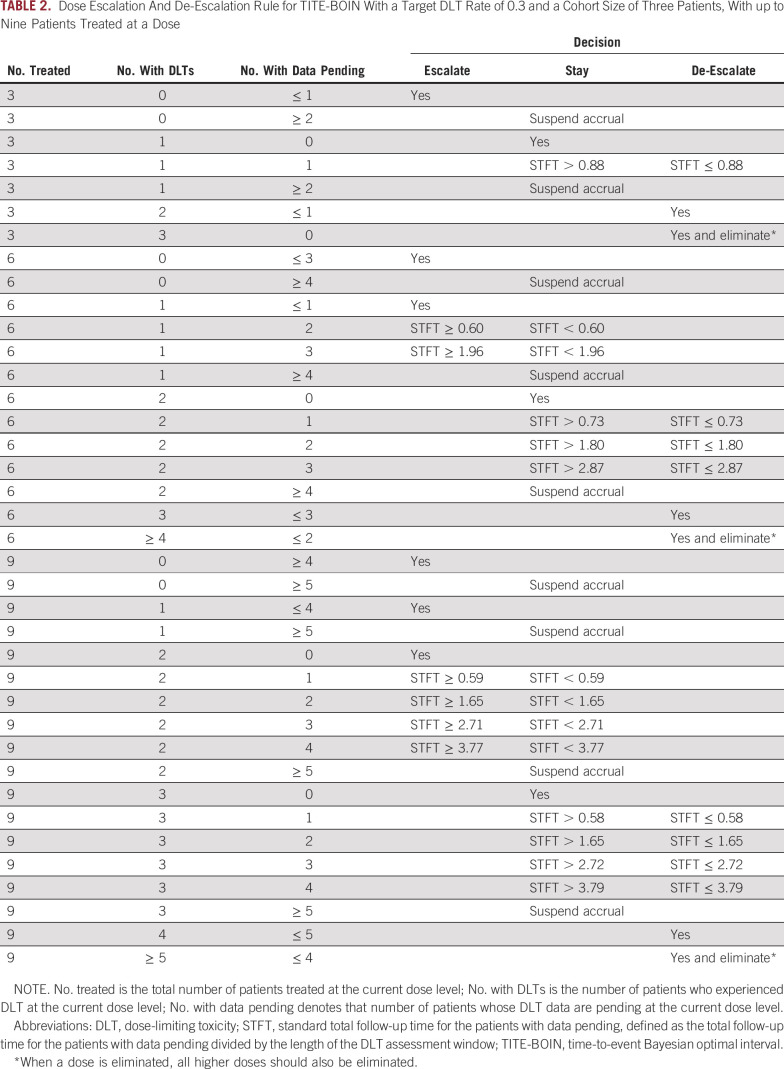
The BOIN design makes dose escalation/de-escalation recommendations simply by comparing $\hat{p}$ with prespecified dose escalation (λ_e) and de-escalation (λ_d) boundaries, as illustrated in Figure 2 and described as follows:

FIG 2.

The flowchart of the Bayesian optimal interval design in which λ_e and λ_d are the dose escalation boundary and the de-escalation boundary, respectively. (*) DLT rate = total number of patients who experienced DLT at the current dose divided by the total number of patients treated at the current dose. MTD, maximum-tolerated dose.

1. Treat the first cohort of patients at the lowest dose, or the clinician-specified starting dose.

2. Assign a dose to the next cohort of patients:

   • If $\hat{p}$ ≤ λ_e, escalate the dose to the next higher level.

   • If $\hat{p}$ ≥ λ_d, de-escalate the dose to the next lower level.

   • Otherwise, stay at the current dose.

3. Repeat step 2 until the prespecified maximum sample size is reached or the number of patients treated on a single level reaches a certain number (eg, 12). At that point, select the MTD as the dose at which the DLT estimate is closest to the target.^25,26

Figure 2 provides the default, optimal dose escalation and de-escalation boundaries (λ_e, λ_d) for commonly used target DLT rates, φ. These boundaries minimize the incorrect decisions of escalating/de-escalating the dose when it actually is greater/lower than the MTD according to a binomial model.²⁶ Given that φ = 0.3, the escalation and de-escalation boundaries are λ_e = 0.236 and λ_d = 0.358, respectively. That is, at the current dose, if the observed DLT rate is less than 0.236 (eg, 0/3 DLT), we escalate the dose; if the observed DLT rate is greater than 0.358 (eg, 2/3 DLTs), we de-escalate the dose; otherwise, the dose stays at the same level (eg, 1/3 DLT). For patient safety, BOIN imposes an overdose control rule: If the observed data indicate that there is more than a 95% chance that the current dose is higher than φ and at least three patients have been treated, the current and higher doses are eliminated from the trial. The trial is terminated if the lowest dose is eliminated.

The simple and intuitive structure of BOIN gives it several unique advantages. Because BOIN guarantees de-escalation of the dose when the observed toxicity rate $\hat{p}$ is higher than the de-escalation boundary λ_d, it is particularly easy for clinicians and regulatory agents to assess the safety of a trial with BOIN. For example, given a target DLT rate of φ = 0.25, we know a priori that a phase I trial using BOIN guarantees de-escalation of the dose if the observed DLT rate is higher than 0.298. Accordingly, BOIN also allows users to easily calibrate the design to satisfy specific safety requirements mandated by regulatory agents by choosing an appropriate target DLT rate. Suppose that, for a phase I trial with a new compound, the regulatory agency mandates that the dose must be de-escalated if the observed toxicity rate is higher than 0.25. We can easily fulfill that requirement by setting the target DLT rate at φ = 0.21, such that BOIN guarantees de-escalation of the dose if the observed toxicity rate of $\hat{p}$ ≥ 0.25. Such flexibility and transparency are the important advantages of BOIN compared with the other model-assisted designs, such as mTPI/mTPI-2 and keyboard designs.

Because model-assisted designs are built upon rigorous statistical theory, like model-based designs, they also enjoy the same flexibility as the model-based designs. For example, BOIN can target any prespecified DLT rate tailored to the trial. For heavily treated patients with recurrent cancer, a target DLT rate of greater than 0.3 may be an acceptable tradeoff to achieve greater treatment efficacy; conversely, for newly diagnosed patients with cancer, a lower target DLT rate (eg, 0.15 or 0.2) may be more appropriate. Similarly, we may tolerate higher rates of reversible DLTs, but drugs with serious irreversible toxicities may mandate lower target rates. In contrast, the 3 + 3 design has no specific target DLT rate, but we must find a dose with the DLT rate between 17% and 33%. In addition, unlike the 3 + 3 design, for which the dose escalation and de-escalation decisions can be made only when we have three or six evaluable patients, BOIN allows decision making with incomplete cohorts in the face of dropouts as a result of DLT inevaluability. This is because BOIN makes decisions on the basis of the observed DLT rate at the current dose, which can be calculated when given any number of observations.

TRIAL EXAMPLES

BOIN design has been used in variety of oncology trials including those for pediatric tumors^33,34 (ClinicalTrials.gov identifier: NCT02354547), adult tumors (ClinicalTrials.gov identifiers: NCT03577704, NCT0302316, NCT02942264, NCT03318900, NCT03600155, NCT0205075, NCT03740256, NCT03330028, NCT03114462, NCT03036904, NCT02705196, NCT02942095, NCT03740256, NCT03784677, and NCT03760081), solid tumors (eg, breast [ClinicalTrials.gov identifier: NCT0302316], brain [ClinicalTrials.gov identifier: NCT02942264], ovarian [ClinicalTrials.gov identifier: NCT03318900], stomach [ClinicalTrials.gov identifier: NCT03330028], neck [ClinicalTrials.gov identifier: NCT03114462], lung [ClinicalTrials.gov identifier: NCT02942095), bladder [ClinicalTrials.gov identifier: NCT03740256], prostate [ClinicalTrials.gov identifier: NCT03784677], and germ cell [ClinicalTrials.gov identifier: NCT03760081]), and liquid tumors (eg, leukemia [ClinicalTrials.gov identifier: NCT03600155], and lymphoma NCT03114462]). BOIN design has been used for various treatment agents, including chemotherapy (ClinicalTrials.gov identifier:NCT02942264), radiotherapy (ClinicalTrials.gov identifier: NCT03114462), checkpoint inhibitor (ClinicalTrials.gov identifier: NCT03600155), monoclonal antibody (ClinicalTrials.gov identifier: NCT03577704), oncolytic virus (ClinicalTrials.gov identifier: NCT02705196), and T-cell immunotherapy (ClinicalTrials.gov identifier: NCT03318900). BOIN also has also been used in nononcology trials, such as stem cell therapy for stroke patients with stroke.³⁵

We used an ongoing National Cancer Institute phase I to II trial (ClinicalTrials.gov identifier: NCT02942264) to illustrate the design. One of the trial’s objectives of was to identify the MTD of TG02, a pyrimidine-based multikinase inhibitor combined with temozolomide in adult patients with recurrent anaplastic astrocytoma or glioblastoma. Because of lack of effective treatments for this patient population, the target DLT rate was set at a relatively high value of 0.35. Four doses (ie, 150, 200, 250, and 300 mg) of TG02 were investigated. The maximum sample size for dose finding was 24 patients, treated in cohorts of three patients each. According to the toxicity profile of TG02 in other patients with cancer, the principal investigator chose 200 mg of TG02 as the starting dose. According to the BOIN design, the dose will be escalated if the observed DLT rate at the current dose is lower than λ_e = 0.276, and it will be deescalated if the observed DLT rate is greater than λ_d = 0.419 (Fig 2). For the purpose of overdose control, if the observed data suggest that there is more than a 95% chance that a dose is greater than the MTD—that is, Pr(p > .35 | data) > 0.95—that dose and higher doses will be eliminated from additional examination. When the lowest dose is eliminated, the trial will be stopped for safety. The 3 + 3 design could not be used to find the MTD appropriately for this trial, because it deemed a DLT rate of 33% or greater to be unacceptably high.

LATE-ONSET TOXICITY

Late-onset toxicity is common in targeted therapies and immunotherapies.^36,37 It causes major logistic difficulty for aforementioned phase I designs, which require that a DLT must be observed soon enough to apply decision rules to choose doses for new patients. For example, if the DLT takes up to 8 weeks to evaluate and the accrual rate is one patient per week, on average, then five new patients could be accrued while investigators wait to evaluate the previous three patients’ outcomes. The question is this: How can new patients receive timely treatment when the previous patients’ outcomes are pending?

A few model-based designs have been proposed to address this logistic issue, including the time-to-event CRM (TITE-CRM)³⁸ and data-argumentation CRM (DA-CRM).³⁹ These designs support continuous accrual and yield superior performance in finding the MTD.^39,40 However, like the CRM, they are statistically and computationally complex and require repeated model fitting after each cohort, which limits their use.

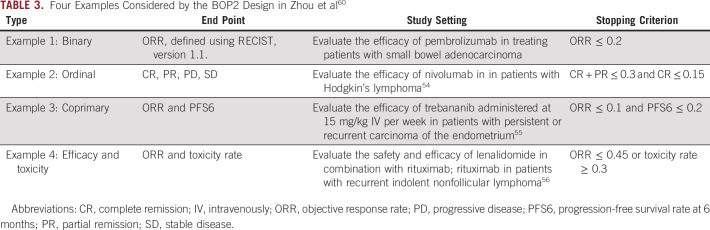
Model-assisted designs, including time-to-event BOIN (TITE-BOIN)²⁹ and time-to-event keyboard (TITE-Keyboard) designs,⁴¹ provide a well-performing and yet easy-to-implement approach to address late-onset toxicity. The TITE-BOIN works by predicting the unobserved, pending DLT data according to a time-to-event model. Thereby, the BOIN dose escalation/de-escalation rule described previously can be applied in real time to choose a dose for new patients. The TITE-BOIN uses a model for prediction, but its decision rule can be pretabulated, similar to the algorithm-based rolling 6 design. Table 2 shows the TITE-BOIN decision rule with a cohort size of three patients, which can be generated easily using the software described in the Software section. During the trial, at the current dose, we counted the number of patients, the number of patients who experienced DLT, and the number of pending patients and their standard total follow-up times (STFT); we then used the table to make the dose escalation/de-escalation decision. The STFT was computed as the sum of the follow-up times for all pending patients at the current dose divided by the DLT assessment window. To illustrate the use of the TITE-BOIN decision table, suppose that three patients have been treated at the current dose: one had a DLT, one had no DLT, and one has DLT data pending. According to Table 2, if the STFT of the pending patient is greater than 0.88, we treat the next cohort at the same dose; otherwise, we de-escalate the dose. Suppose that the next cohort of three patients is treated at the same dose and that, among the six treated patients, one patient had a DLT, two had no DLT, and three have DLT data pending. Given that the DLT assessment window is 3 months and that, at the current dose, three pending patients have been observed for 1, 1.6, and 2.5 months, respectively, the STFT is (1 + 1.6 + 2.5)/3 = 1.7. To treat the next cohort, because the STFT of the three patients with data pending is less than 1.96, we keep the current dose. Numeric study shows that TITE-BOIN yields superior performance compared with model-based designs (eg, TITE-CRM), and outperforms the rolling 6 design with higher accuracy to identify the MTD and allocate more patients to the MTD.²⁹

TABLE 2.

Dose Escalation And De-Escalation Rule for TITE-BOIN With a Target DLT Rate of 0.3 and a Cohort Size of Three Patients, With up to Nine Patients Treated at a Dose

Another model-assisted design that is capable of handling late-onset toxicity is the TITE-Keyboard design.⁴¹ Rather than predicting the pending DLT data, the TITE-Keyboard design takes a different statistical approach by discounting the observed data information, statistically known as the likelihood, to reflect that some observations are pending. Nevertheless, the TITE-Keyboard produces a decision table similar to Table 2 and yields performance that is comparable to that of the TITE-BOIN.

DRUG COMBINATION TRIALS

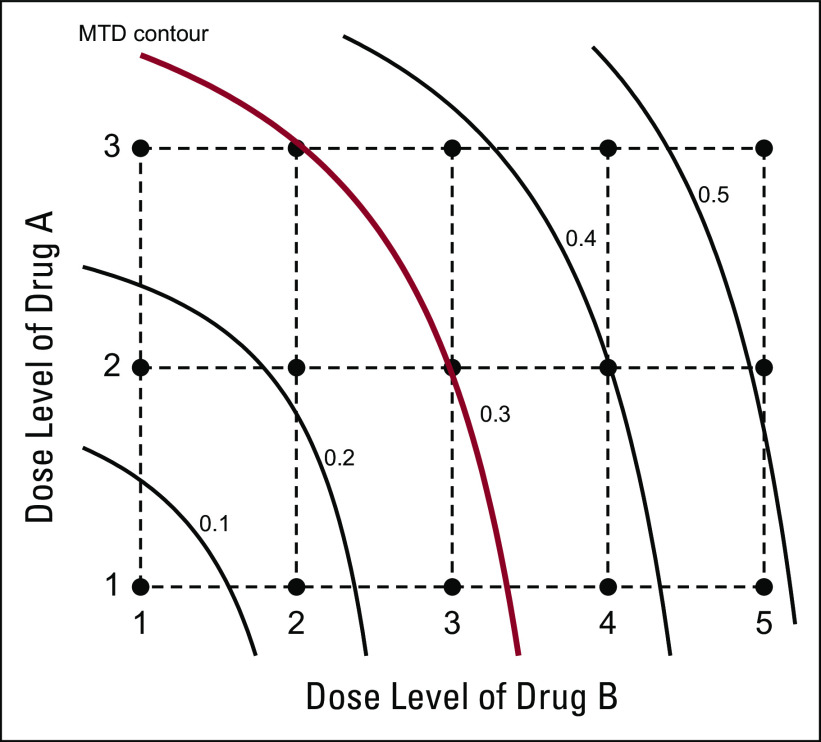
Designing combination trials is more challenging. Unlike single-agent trials with a string of ordered doses, combinations in the dose matrix are only partially ordered in toxicity, and multiple MTDs (ie, the MTD contour) may exist in the dose matrix (Appendix Fig A1). Numerous designs have been proposed to find an MTD or the MTD contour for combination trials.^28,42-52 Almost all are model-based designs using a strategy similar to that of a CRM: devise a model to describe the dose-toxicity surface and then, on the basis of accumulating data, continuously update the model estimate to select a dose for the new patient. Because of their statistical and computational complexity, despite good performance, these model-based designs are rarely used for conducting trials.

Model-assisted designs provide a simple and robust approach to phase I combination trials.⁴³ One example is the BOIN combination design,²⁸ which makes the decision of dose escalation/de-escalation according to the same rule as the single-agent BOIN design described in the Model-Assisted Designs section, and thereby inherits the single-agent design’s simplicity and good performance. The only difference is that, in combination trials, when we decide to escalate or de-escalate the dose, there is more than one neighboring dose to which we can move. For example, when we escalate/de-escalate the dose, we can escalate/de-escalate either the dose of drug A or the dose of drug B. The BOIN combination design makes this choice according to how likely a dose combination is to be located within the acceptable region (λ_e, λ_d) given the observed data.²⁸ Simulation study shows that the BOIN combination design yields competitive performance comparable to more complicated, model-based designs.²⁸ Another model-assisted combination design is the keyboard combination design, which adopts similar dose escalation/de-escalation strategy as the BOIN combination design and yields competitive performance.⁵² Model-assisted designs also were developed to find multiple MTDs (or the MTD contour) for combination trials (eg, the waterfall design).⁵¹

MODEL-ASSISTED PHASE II DESIGNS

The concept of model-assisted design is also applicable to phase II trials. For example, Simon’s optimal (or minimax) two-stage design⁵³ could be classified as a model-assisted design in the sense that it is derived from a statistical model (ie, a binomial model for response), but its go/no-go decision rule can be predetermined when the design parameters are specified. During the trial conduct, users only must evaluate whether the number of responses passes the predetermined stopping boundaries to make go/no-go decisions. Simon’s optimal two-stage designs are appropriate for the simple setting in which the end point is binary and quickly ascertainable, and these designs allow only one interim look.

Phase II trials sometimes are more complicated and have more than one end point. Table 3 provides four trial examples with different types of end points (eg, ordinal end point and coprimary end points).^54-56 In addition, multiple interim looks are useful to improve the flexibility and efficacy of the trial, especially in basket and platform trials.^57-59 The Bayesian optimal phase II (BOP2) design⁶⁰ provides a simple, flexible, and efficient model-assisted design to allow multiple interims and handle different types of phase II trials under a unified framework.

TABLE 3.

Four Examples Considered by the BOP2 Design in Zhou et al⁶⁰

The key feature of BOP2 is that, although the end points in the four examples are clinically different, they all can be represented using a variable Y with K distinct categories, statistically known as a multinomial random variable. For instance, in example 1, Y has K = 2 categories (1 = response and 2 = no response); in example 3, Y has K = 4 categories (ie, 1 = [response, progression-free survival at 6 months {PFS6} > 0.2 met]; 2 = [response, PFS6 not met]; 3 = [no response, PFS6 met]; and 4 = [no response, PFS6 not met]). This unified end point Y is modeled using a Bayesian model, known as the Dirichlet-multinomial model. The BOP2 design allows any arbitrary number of interim looks. At each interim look, the go/no-go decision is made on the basis of the evaluation of Bayesian stopping criteria using posterior probabilities. As an example, consider a treatment that is deemed ineffective if the objective response rate (ORR) is ≤ θ, in which θ is a threshold prespecified by clinicians (eg, θ = 20%). At each interim, the go/no-go decision is made according to the following Bayesian stopping criteria: Stop the trial if Pr(ORR ≤ θ|Data) > C_n; otherwise continue. In the equation, the posterior probability Pr(ORR ≤ θ|Data) represents, given the interim data, how likely the true ORR is to be less than the threshold θ; and C_n is an adaptive probability cutoff that depends on the interim sample size n. Given the response rate deemed ineffective (ie, the null hypothesis) and the response rate deemed desirable (ie, the alternative hypothesis), the value of C_n is chosen such that the type I error rate is controlled at a prespecified level and the statistical power is maximized. (See Zhou et al⁶⁰ for details.) Similar Bayesian stopping criteria can be applied to other types of end points to determine whether the treatment is promising.⁶⁰

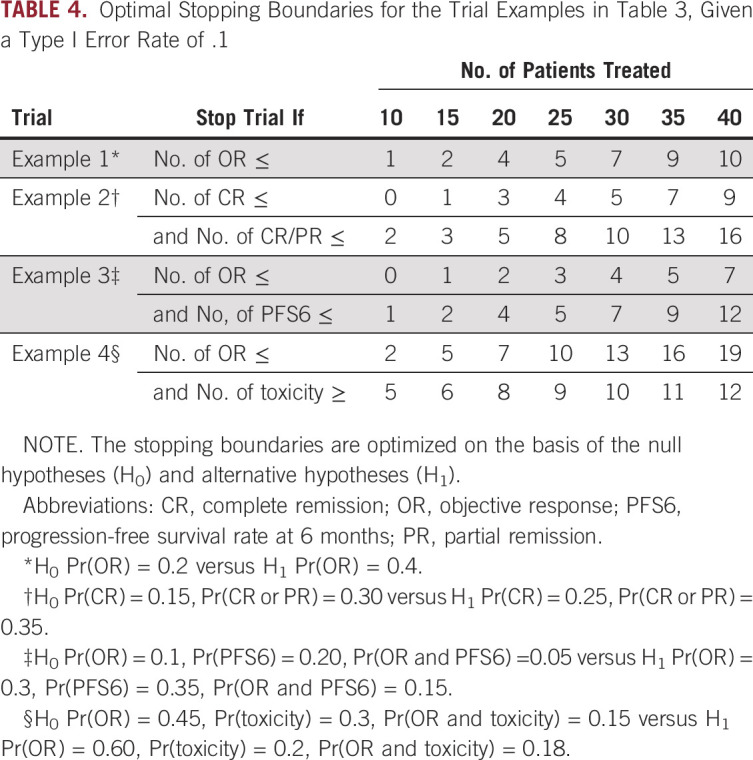
As a model-assisted design, one important advantage of the BOP2 design is that its stopping boundary can be enumerated and included in the trial protocol before the onset of the trial. Table 4 presents the corresponding stopping boundaries for each trial example. When they conduct the trial, clinicians simply count the number of relevant events and make the go/no-go decision according to whether that count exceeds the boundary or not. If the end point requires a long time to be scored, clinicians may have to suspend the accrual and wait for the interim data mature to make interim decisions. This is undesirable and prolongs the trial duration. The time-to-event BOP2 (TOP) design was developed to address this issue and allow real-time interim decision making.⁶¹ The stopping boundaries of the TOP design also can be enumerated and included in the trial protocol.

TABLE 4.

Optimal Stopping Boundaries for the Trial Examples in Table 3, Given a Type I Error Rate of .1

Simon’s two-stage, BOP2, and TOP designs focus on one-arm trials. Brown et al⁶² provide a comprehensive review on phase II trials in oncology, including randomized trials. The research on model-assisted designs for randomized phase II trials has been limited, and the designs warrant additional investigation.

SOFTWARE

The aforementioned model-assisted designs can be easily implemented using a Windows desktop program or online Web applications (freely available at trialdesign.org). Each module has an intuitive graphic user interface and rich documents to help users navigate through the process. A phase I or II trial can be designed easily by the following three steps:

1. Specify the design parameters (eg, sample size, cohort size, target DLT rate).

2. Use the software to produce decision table, design diagram, and operating characteristics of the design. The software also generates sample texts and protocol template to facilitate the protocol write-up.

3. Use the design decision table to conduct the trial and make adaptive decisions (eg, dose escalation/stay/de-escalation or go/no-go).

DISCUSSION

One major barrier for the adaptation of novel adaptive designs is that these designs often are complicated to implement. Model-assisted designs provide an attractive approach to remove this barrier and reconcile the conflict of simplicity versus performance by seizing the best of the two worlds. Model-assisted designs offer the superior performance compared with the more complicated, model-based adaptive designs but, once designed, can be implemented in as simple a way as the conventional designs. Implementation is facilitated even more by freely available user-friendly software. The approach establishes a new KISS principle: keep it simple and smart!

As in all trial designs, the design parameters for model-assisted designs must be carefully chosen to reflect the clinical setting and the study objective. For the BOIN design, the target DLT rate can vary with the type of phase I studies. The maximum sample size must be realistic and attainable. For the BOP2 design, the choice of using a binary end point or coprimary end point, and their null and target rates, depends on which disease type is studied and how effective the standard of care is. The number of interim analyses should account for both design efficiency and the logistic complexity. The choice of designs parameters should be validated and carefully calibrated through extensive computer simulation to ensure that the design has desirable operating characteristics under a variety of scenarios. The design parameters, study conduct boundaries, and operating characteristics must be spelled out and listed in the study protocol.

Appendix

Fig A1.

Maximum-tolerated dose (MTD) contour in drug combination trials. Curved lines indicated the toxicity contours with true toxicity rates of 0.1, 0.2, 0.3, 0.4, and 0.5, respectively. Combinations located along the rows and columns are ordered in toxicity, but, in other directions of the dose matrix (eg, along the diagonals from the upper left corner to the lower right corner), the toxicity order is unknown because of unknown drug-drug interactions.

AUTHOR CONTRIBUTIONS

Conception and design: All authors

Collection and assembly of data: Ying Yuan, J. Jack Lee

Data analysis and interpretation: All authors

Manuscript writing: All authors

Final approval of manuscript: All authors

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or ascopubs.org/po/author-center.

Ying Yuan

Honoraria: Ono Pharmaceutical

Consulting or Advisory Role: Boehringer Ingelheim Pharmaceuticals, Salzman Group, Midas Medical Technologies

J. Jack Lee

Consulting or Advisory Role: AbbVie

No other potential conflicts of interest were reported.