Specifying the True- and False-Positive Rates in Basket Trials

In the clinical evaluation of anticancer therapies, after identification of a recommended dose, investigators typically seek evidence of drug efficacy in populations of patients hypothesized to benefit from it. The purpose of these signal-finding studies is to prioritize additional development and to determine whether drugs should be tested in randomized phase III trials and, if so, in which populations of patients. In studying modern targeted agents, investigators frequently have been able to identify groups of patients with remarkably impressive tumor responses. Because these identified populations usually are small and efficacy often is substantially better than that for available therapies, conclusions from single-arm trials of this nature can be used to inform off-label treatment decisions and sometimes lead to inclusion in treatment guidelines or regulatory approvals. An understanding of the performance characteristics of the novel clinical trial designs commonly used in this setting is critical to avoid inappropriate clinical decision making on the basis of false-positive clinical trial results.

The group of patients in whom a therapy is hypothesized to have activity can be identified in a number of ways, including genomic and proteomic profiles, and activity of the drug can be influenced by histology or the primary tumor site. The combination of a hypothesized mechanism of action and uncertainty around the populations of patients who would likely benefit has encouraged a trend toward more-complex early-phase trials.¹ A major challenge is the desire to study the effects of the drug simultaneously in patients with different primary sites of disease or histologies with the goal of evaluating the efficacy of the drug in these contexts, often referred to as baskets.^2-9 A related recent trend in clinical trial design has been increasing enthusiasm for the use of adaptive designs, whereby design parameters can be changed dynamically as the trial progresses and evidence about efficacy gradually emerges.¹⁰ A final important trend has been the use of Bayesian design as a tool to evaluate the emerging evidence in a formal statistical model.^11-15 Many of these methods are predicated on the underlying expectation of broadly similar efficacy across baskets because the statistical model allows the sharing of information across baskets with the purpose of completing the trial in a shorter time frame with fewer patients than a traditional strategy whereby each basket is regarded as an independent phase II trial. This combination of design complexity with sophisticated statistical modeling has led to situations in which important clinical trials are being launched without a broad understanding of the implications of the novel methods used, an issue that has been identified previously in the context of novel phase I study designs.¹⁶ In this commentary, we examine the properties of a particular Bayesian adaptive design that increasingly is being used in the context of basket trials, and we use the clinical setting of a completed basket trial to demonstrate that the design is heavily tilted toward positive conclusions about the efficacy of the drug.¹⁷

The complexity of these modern methods makes having a clear understanding of the properties of design, characterized by easily interpretable measures, essential when planning a new clinical trial. Although Bayesian statistical analyses generally focus on reporting the probability that an individual drug works (the so-called posterior probability), we believe that the evaluation of properties of designs in terms of the familiar metrics used in the context of clinical trials is important. These properties are the true-positive rate (the probability that a truly effective agent will be shown to be effective [often referred to as power]) and the false-positive rate (the probability that an ineffective agent is erroneously judged to be effective [often referred to as the type I error]). We generally like to keep the false-positive rate low because we do not want to encourage additional study of a drug that does not work, and we want the true-positive rate to be high because we want to be confident that if the drug truly works, its effectiveness will be recognized. In the context of a basket trial, we need to expand these terms to determine the efficacy of the drug in each basket individually. Therefore, to fully understand the implications of these data-sharing methods, we must calculate a more-elaborate set of true- and false-positive rates, specifically when the drug does not work at all, when it only works in one basket, when it only works in two baskets, and so forth.

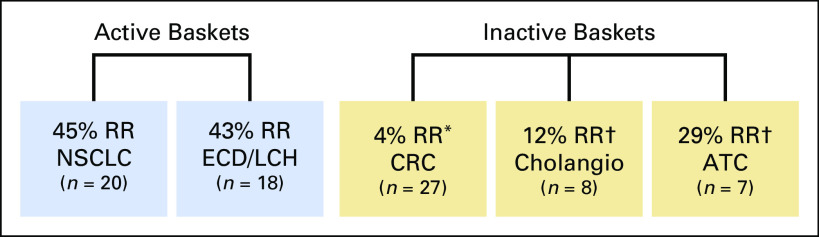
As an illustration of the clinical setting, we refer to the findings of a recent basket trial that investigated the effects of vemurafenib, a selective oral inhibitor of the BRAF kinase.² The trial assessed efficacy in five disease-specific baskets: non–small-cell lung cancer, colorectal cancer, cholangiocarcinoma, Erdheim-Chester disease or Langerhans cell histiocytosis, and anaplastic thyroid cancer. In this study, a response rate of ≤ 15% was considered nonpromising, whereas a response rate of ≥ 45% was considered promising. Figure 1 illustrates the observed response rates in each basket. The investigators concluded that the drug shows promising activity in the non–small-cell lung cancer basket and the Erdheim-Chester disease or Langerhans cell histiocytosis basket but that it is inactive in colorectal cancer. The investigators were unwilling to make definitive conclusions about its effectiveness in cholangiocarcinoma and anaplastic thyroid cancer because of the small sample sizes. Although this trial did not use the Bayesian hierarchical design proposed by Berry et al,¹⁷ we use the clinical setting of the vemurafenib trial to investigate the performance of the Berry design.

Fig 1.

Each basket displays the observed response rate (RR) from the vemurafenib trial for a particular disease (sample sizes in parentheses). (*) Patients received combination therapy (vemurafenib + cetuximab). (†) An RR of 15% was considered inactive, and an RR of 45% was considered active. Activity was considered to be inconclusive as a result of a small number of patients. ATC, anaplastic thyroid cancer; Cholangio, cholangiocarcinoma; CRC, colorectal cancer; ECD/LCH: Erdheim-Chester disease or Langerhans cell histiocytosis; NSCLC, non–small-cell lung cancer.

The Bayesian hierarchical model is structured to capture the correlation between the anticipated efficacies of the drug across various baskets. As the trial progresses and evidence about response rates gradually emerges, the model implicitly shares information among baskets, a concept frequently referred to as information borrowing. The extent to which information is borrowed is determined by the variability among response rates across baskets. This aggregation of evidence is rooted in a key feature of Bayesian methods, the prior distribution of the between-basket variability, an entity that is prespecified by the analyst. In the context of a basket trial, this prior distribution essentially titrates the extent to which emerging evidence of drug efficacy from one basket can be used to bolster the evidence in other baskets. Berry et al¹⁷ recommended a specific prior distribution to reflect “a small amount of heterogeneity across the groups.” They acknowledged that the properties of their method might be sensitive to this choice of prior distribution. However, they presented a sensitivity analysis that concluded that the properties are actually relatively insensitive to this choice.

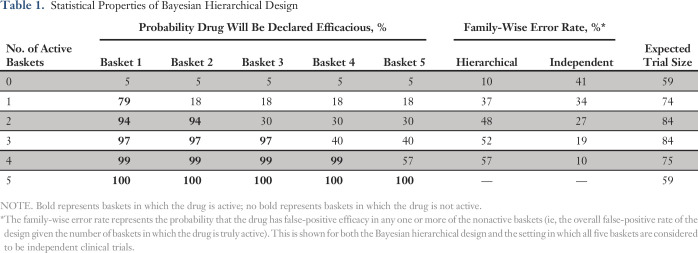
We evaluated the false-positive and false-negative error rates for a hypothetical trial similar in structure to the vemurafenib trial, with five baskets and null and alternative response rates of 15% and 45%, respectively. We simulated trials by following the Bayesian hierarchical design and conducted interim analyses after the first 10 patients were accrued and then after every additional five patients until a maximum of 19 patients per basket were enrolled. Early stopping rules terminated accrual to individual baskets if the basket-specific posterior probability that the true response rate is greater than a midlevel response rate of 30% was < 5% (stop for futility) or > 90% (stop for efficacy) at any interim analysis. At the end of the trial, the treatment was declared efficacious in a basket if the posterior probability that the response rate that exceeded the null value of 15% was > 87%. This final decision rule was calibrated to provide an overall false-positive rate of 10% when the drug was inactive in all baskets. We used throughout the specific prior distribution recommended by Berry et al.¹⁷ The true- and false-positive rates are listed in Table 1. The efficacies of the baskets are in order from left to right. For example, in the second row (one active basket), basket 1 is the one in which the drug is truly active, whereas in baskets 2 to 5, the drug is not active. In this scenario, we see that a 79% chance for observing a true-positive result exists in the active basket, whereas for each nonactive basket, the false-positive rate is 18%. The next column on the right captures the probability that one or more of the nonactive baskets is a false-positive finding, a term usually referred to as the family-wise error rate, a key criterion for evaluating multiple hypotheses in clinical trials.^18,19 We see that this overall false-positive rate is 37% when the drug truly works in only one basket and rises to 57% when the drug does not work in only one basket. The final column lists the expected trial size. Although the maximum trial size was set to 95 patients, the expected trial size ranged from 59 to 84 patients, depending on the true efficacy configuration of the baskets. The table also lists the family-wise error rates for the setting in which each basket is regarded as an entirely independent clinical trial wherein the false-positive rate is 10%. The family-wise error rate is a relatively high 41% when any one of five independent trials can be a false-positive finding (top row) but is the nominal 10% when the drug is truly ineffective in only one basket (four active baskets row).

Table 1.

Statistical Properties of Bayesian Hierarchical Design

Close examination of Table 1 demonstrates two complementary results from using the Bayesian design. First, the false-positive rate is much higher than we would normally expect or desire. Although the targeted overall false-positive rate of 10% has been achieved for the setting in which the drug has no efficacy (ie, the drug works in none of the baskets as shown in the first row), this standard rapidly erodes as we investigate settings in which the drug works in some baskets but not in others. For example, if we look at the two active baskets row of the table, we see a high probability (94%) of declaring each of the two active baskets to be efficacious. This high probability comes at the expense of a 48% chance of incorrectly declaring that the drug works in at least one of the three inactive baskets. Why does this happen? The answer lies in the sharing of evidence embedded in the statistical modeling. Consider the most extreme case (the four active baskets row of the table) where we see that the nonactive basket has a false-positive rate of 57%. In this setting, the evidence typically is dominated by strong positive results from the four baskets in which the drug is truly active, and the imposition of the prior distribution encourages the model to interpret the results from all five baskets as strongly correlated (ie, similar in efficacy), which leads to a high probability that the inactive basket will be classified incorrectly as active. This high false-positive rate can be manipulated with more-stringent decision rules. However, by changing these rules alone, we do not have the flexibility to specify desired true- and false-positive rates. In related work, we explored in depth options for modifying the Bayesian design used in our simulations by examining various choices of prior distributions and of decision rules used, demonstrating that trials can be designed on the basis of hierarchical modeling with much better control of the family-wise error rates.²⁰

We believe that straightforward reporting of the various true- and false-positive rates, as listed in Table 1, are fundamental to understanding the merits of any proposed basket study design. Seemingly innocuous choices, such as the use of a prior distribution that Berry et al¹⁷ characterized as “weak, which allows the data to shape the amount of borrowing,” can actually have a substantial influence on the real risks of obtaining false-positive results. A high false-positive rate that does not accurately reflect the true evidence that emerges from the clinical trial can have important clinical ramifications in that it could lead to a strong incentive to provide the treatment to future patients who have the disease characteristics of the baskets in which the drug is inactive.

We believe strongly that modern basket clinical trials that endeavor to answer multiple objectives by testing several hypotheses can benefit from novel designs that seek to reach conclusions as quickly and efficiently as possible.²¹ This inevitably involves the merging of information from various baskets in one way or another, and alternative designs^22,23 have recently been proposed in the literature, including a design we have advocated that focuses on whether baskets should be aggregated for the purposes of sharing evidence.²⁴ However, regardless of how the study is designed, investigators must have a clear understanding of the properties of the design in terms of familiar key characteristics, such as false-positive and false-negative rates.

AUTHOR CONTRIBUTIONS

Concept and design: All authors

Financial support: Mithat Gönen

Administrative support: Colin B. Begg

Collection and assembly of data: Mithat Gönen

Data analysis and interpretation: Kristen M. Cunanan, Mithat Gönen

Manuscript writing: All authors

Final approval of manuscript: All authors

Accountable for all aspects of the work: All authors

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or po.ascopubs.org/site/ifc.

Kristen M. Cunanan

No relationship to disclose

Alexia Iasonos

No relationship to disclose

Ronglai Shen

No relationship to disclose

David M. Hyman

Consulting or Advisory Role: Atara Biotherapeutics, Chugai Pharmaceutical, CytomX Therapeutics, Boehringer Ingelheim, AstraZeneca

Research Funding: AstraZeneca, Puma Biotechnology, Loxo Oncology

Gregory J. Riely

Consulting or Advisory Role: Genentech

Research Funding: Novartis (Inst), Roche (Inst), Genentech (Inst), Millennium Pharmaceuticals (Inst), GlaxoSmithKline (Inst), Pfizer (Inst), Infinity Pharmaceuticals (Inst), ARIAD Pharmaceuticals (Inst)

Patents, Royalties, Other Intellectual Property: Patent application submitted covering pulsatile use of erlotinib to treat or prevent brain metastases (Inst)

Travel, Accommodations, Expenses: Novartis, Merck Sharp & Dohme

Mithat Gönen

Consulting or Advisory Role: Tesaro

Colin B. Begg

No relationship to disclose