New approximations, and policy implications, from a delayed dynamic model of a fast pandemic

Abstract

We study an SEIQR (Susceptible–Exposed–Infectious–Quarantined–Recovered) model due to Young et al. (2019) for an infectious disease, with time delays for latency and an asymptomatic phase. For fast pandemics where nobody has prior immunity and everyone has immunity after recovery, the SEIQR model decouples into two nonlinear delay differential equations (DDEs) with five parameters. One parameter is set to unity by scaling time. The simple subcase of perfect quarantining and zero self-recovery before quarantine, with two free parameters, is examined first. The method of multiple scales yields a hyperbolic tangent solution; and a long-wave (short delay) approximation yields a first order ordinary differential equation (ODE). With imperfect quarantining and nonzero self-recovery, the long-wave approximation is a second order ODE. These three approximations each capture the full outbreak, from infinitesimal initiation to final saturation. Low-dimensional dynamics in the DDEs is demonstrated using a six state non-delayed reduced order model obtained by Galerkin projection. Numerical solutions from the reduced order model match the DDE over a range of parameter choices and initial conditions. Finally, stability analysis and numerics show how a well executed temporary phase of social distancing can reduce the total number of people affected. The reduction can be by as much as half for a weak pandemic, and is smaller but still substantial for stronger pandemics. An explicit formula for the greatest possible reduction is given.

Highlights

• •A time delayed SEIQR model is specialized to the case of a fast pandemic.
• •Full progression from initial infection to saturation is studied in depth.
• •Multiple scales and long-wave approximations are presented.
• •Low-dimensional dynamics is noted for both constant and time-varying infectivity.
• •Temporary social distancing significantly reduces the total numbers affected.

Nomenclature

$\overline{\beta }$

Infection rate

$m$

Density of contacts

$\beta$

Net infectivity ($\overline{\beta }m$)

${\beta }_n$

Baseline infectivity in a society

${\beta }_l$

Infectivity in the presence of social distancing or lockdown

$\alpha$

Rate of immunity loss

$\gamma$

Self-recovery rate

$p$

Probability of identifying and isolating an infected individual

$\sigma$

Asymptomatic and noninfectious time duration

$\tau$

Asymptomatic but infectious time duration

$\kappa$

Time spent in quarantine

$r$

Disease reproduction number

$S\left(t\right)$

Fraction of susceptible population at time $t$

$E\left(t\right)$

Fraction of exposed population at time $t$

$I\left(t\right)$

Fraction of infectious population at time $t$

$Q\left(t\right)$

Fraction of quarantined population at time $t$

$R\left(t\right)$

Fraction of recovered population at time $t$

$P\left(t\right)$

Integral of $I\left(t\right)$ $\left(\text{i.e.}{\int }_{-\infty }^{t}I\left(\zeta \right)d\zeta \right)$

$S_n\left(\infty \right)$

Steady-state fraction of susceptible population with $\beta ={\beta }_n$

$S_L\left(\infty \right)$

Steady-state fraction of susceptible population with $\beta ={\beta }_l$

$H(t-a)$

Heaviside step function defined as $H(t-a)=\left\{\begin{array}{c}\hfill 1,t\ge a\hfill \\ \hfill 0,t<a\hfill \end{array}\right)$

$T_o$

Time of implementing lockdown or social distancing measures

$T_c$

Time of removing lockdown or social distancing measures

$\overline{p}$

$=p{e}^{-\gamma \tau }$

$\nu$

$=1+\tau$

$\mu$

$=\overline{p}{(1+\tau )}^2-1$

1. Introduction

This work is partially motivated by the global pandemic of COVID-19. Understanding the dynamics of infectious diseases in a population can help in developing strategies to mitigate the spread [1], [2]. This paper presents new mathematical approximations and an asymptotic solution for a specific dynamic model for such infectious diseases. Some policy implications are discussed as well.

Mathematical models for the spread of disease have almost a century old history. In their seminal paper, Kermack and McKendrick [3] proposed a three-state model (popularly known as SIR) governing the evolution of susceptible (S), infected (I), and recovered (R) populations. In their model, the recovered population is assumed to have developed immunity against the infection. The model contains two free parameters, one for infection rate and one for recovery rate. The SIR model is widely used to predict the number of infected people in closed populations. The model has an analytical solution. Over time, the SIR model [4] has been modified to study infections where the recovered population can be reinfected (as with the common cold) and is known as the two-state SIS model. In the classic endemic model [5], for diseases that are active over $10$-$20$ years, information of new births and deaths are included. In another variant of the SIR model known as the four-state MSIR [6] model, passive immunity inherited by newborns from their mothers is included: for example, newborn babies can be immune to measles for some time after their birth, but become susceptible later on. Other modifications have considered the effect of a carrier population [6], which never recovers from the disease but is asymptomatic (relevant to, e.g., tuberculosis). Such people can again suffer from the disease later, or continue to infect others while remaining asymptomatic. In SEIR [7], a four-state model, one of the states (E) represents the exposed population, infected but non-infectious. In the SEIQR model [8], yet another state, representing a quarantined population, is added to the SEIR model. All the models discussed above, including SIR, SIS, MSIR, SEIR, and SEIQR are governed by nonlinear differential equations. More complicated partial differential equation models that include the effect of the age structure [4] of the population and vaccination history are also available [7].

The models mentioned so far need not include time delays. However, the incubation, asymptomatic, and symptomatic phases of a disease can be incorporated as time delays in mathematical models. Including such delays in the differential equation models make them delay differential equations (DDEs), also known as retarded functional differential equations. Researchers have used DDEs [9], [10] to model the spread of infections like Zika [11], HIV [12], influenza [13], and Hepatitis B [14]. Recently, a scalar DDE with one delay (time of recovery) based on a logistic model was used to study the spread of COVID-19 in Italy [15]. Some policy implications based on parameter studies and simulations were reported, but analytical progress on the delayed equation was limited.

We observe that the abovementioned models, with a few states, can be formally developed from underlying network models. Network epidemiological models with a large number of states [16], [17], [18], [19], [20], [21] follow fine details of the spatial and temporal spread of an infection. Their average or overall behavior can be described using what we might call lumped, compartmental, or continuum models.

In a recent article [22], a network of compartmental models, with each model representing an age group was used to study the COVID-19 outbreak in India. Other works that have recently appeared, which study the progression of COVID-19 in different parts of the world, include [23], [24], [25], [26]. These works primarily deal with parameter identification, numerical simulations, and prediction of the number of cases with time, along with some policy implications.

Even with lumped models, if various effects [4] like incubation times, natural birth and death rates, prior immunity, and carrier states are included, then analytical solutions are usually unavailable. However, sometimes difficult problems can be solved approximately using asymptotic methods [27], [28] or related methods, and this paper presents such approximations for a slightly simplified case that is relevant to a fast-spreading pandemic.

In recent work that is directly related to our paper [9], a five-state SEIQR system with delays has been developed as a continuum limit from a network model under quite general conditions. That system has then been examined as a generic model for infectious diseases. The model, even after simplification, has multiple parameters and coupled states, and so analytical progress is difficult. However, several interesting limits, steady states, and stability criteria have been presented [9], along with supporting numerical results and policy implications.

Here we take up a simplified version of that model [9]. Our simplification is only that we ignore the possibility of some past sufferers of the disease eventually losing their immunity, and becoming vulnerable to infection all over again. With this simplification, significant new analytical approximations and insights are possible, and constitute the contribution of this paper. We note that Young et al. [9] say the following (their state of $(1,0,0,0,0)$ is an uninfected population):

“The fact that orbits starting from near $(1,0,0,0,0)$ will approach an endemic equilibrium is difficult to prove; this part of our prediction is supported by numerical simulations”.

In this context, we will present a new asymptotic multiple-scales solution for weak growth in a special case, and two informal long-wave approximations for moderate growth, all three solutions describing the complete evolution from infinitesimal infection to final saturation. These new approximations provide useful new analytical support and understanding that is not included within [9].

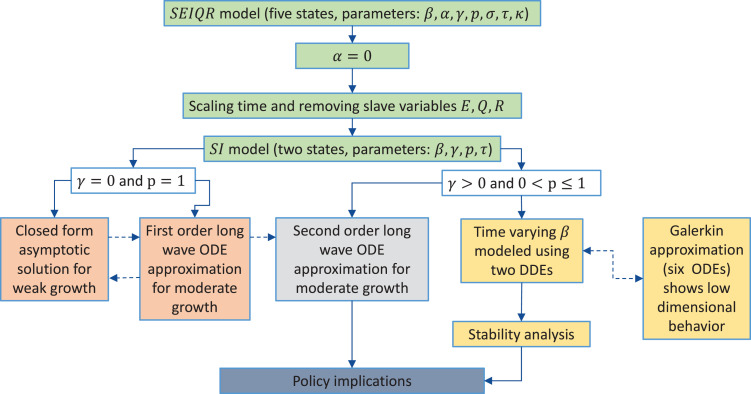
An overview of the paper is depicted in Fig. 1. In Section 2, the five-state SEIQR DDE model of Young et al. [9] is presented. Upon setting $\alpha =0$ (for a fast pandemic), $E$, $Q$, and $R$ become slave variables. An SI DDE model with two-states is obtained.

Fig. 1.

Flow chart showing the overview of the paper.

A further simplified case of $\gamma =0$ and $p=1$ (zero self-recovery and certain quarantine) is considered in Section 3. An asymptotic solution for weak growth using the method of multiple scales (MMS) has been obtained. For moderate growth, a long-wave approximation is considered, which converts the DDE into a first-order scalar ODE.

In Section 4, the general case of $\gamma >0$ and $0<p\le 1$ (nonzero self-recovery and probability of quarantine less than or equal to unity) is discussed. In this case, the long-wave approximation converts the DDE (SI model) into a second-order ODE. Excellent agreement is found between the solution of the ODE and that of the DDE for parameters associated with various diseases.

In Section 5, the two-state SI model of Section 2 is modified to account for time-varying $\beta$. A Galerkin approximation is used to convert the DDE model with time-varying $\beta$ into six first-order ODEs. For both continuous and discontinuous variations in $\beta$, an excellent match is found between the solutions of the ODEs and the DDE. This match verifies the assumed low-order behavior of the DDE model, assumed throughout this paper.

In Section 6, a policy of social distancing that involves piecewise constant variations in $\beta$ in considered. In particular, a policy that uses a low value of $\beta$ for an extended period, followed by a higher “normal” value, is shown to reduce the total fraction affected quite significantly (e.g., from $85\text{\%}$ to $55\text{\%}$ for some parameter choices). An explicit formula for the maximum reduction possible in this way is found. Notably, the reduction depends only on fraction affected, and not on any other system parameters. This provides a key policy implication and is the main practical contribution of the paper.

2. Mathematical model

As mentioned above, our mathematical model is essentially that of Young et al. [9], with one of their small parameters set to zero. Fig. 2, adapted from their paper, shows the lumped model which is itself obtained by them from an underlying network model. In the model there are five subpopulations (actually population fractions) that add up to unity. The general governing equations [9] are:

$$\dot{S}\left(t\right)=-\tilde{\beta }mS\left(t\right)I\left(t\right)+\alpha R\left(t\right)$$ (1)

$$\dot{E}\left(t\right)=\tilde{\beta }m\left[S\left(t\right)I\left(t\right)-S(t-\sigma )I(t-\sigma )\right]$$ (2)

$$\dot{I}\left(t\right)=\tilde{\beta }mS(t-\sigma )I(t-\sigma )-\gamma I\left(t\right)-\tilde{\beta }mp{e}^{-\gamma \tau }\times S(t-\sigma -\tau )I(t-\sigma -\tau )$$ (3)

$$\dot{Q}\left(t\right)=\tilde{\beta }mp{e}^{-\gamma \tau }\left[S(t-\sigma -\tau )I(t-\sigma -\tau )\right)-\left(S(t-\sigma -\tau -\kappa )I(t-\sigma -\tau -\kappa )\right]$$ (4)

$$\dot{R}\left(t\right)=-\alpha R\left(t\right)+\gamma I\left(t\right)+\tilde{\beta }mp{e}^{-\gamma \tau }S(t-\sigma -\tau -\kappa )\times I(t-\sigma -\tau -\kappa )$$ (5)

In the above equations, the free parameters are interpreted as follows: $\tilde{\beta }$ is the infection rate, $m$ is the density of contacts, $\gamma$ is the self-recovery rate, $p$ is the probability of identifying and isolating an infected individual, and $\alpha$ is the rate of immunity loss. We have not introduced any simplifications of our own so far.

Fig. 2.

The SEIQR model with delays. Healthy individuals $S\left(t\right)$ are infected with rate constant $\beta$. Infected individuals $E\left(t\right)$ remain asymptomatic and non-infectious for a time duration $\sigma$. Subsequently, these individuals become infectious and enter population $I\left(t\right)$, but remain asymptomatic for a time duration $\tau$. Upon showing symptoms, they enter population $Q\left(t\right)$ and are quarantined with probability $p$ for a time $\kappa$, beyond which they infect nobody. Some infectious asymptomatic individuals may become non-infectious on their own, with rate $\gamma$. After quarantine, the cured population $R\left(t\right)$ could in principle lose immunity at a small rate $\alpha$, but we take $\alpha =0$ for a fast-spreading pandemic.

We note, first, that $E$ and $Q$ in Eqs. (2), (4) are influenced by $S$ and $I$ along with their delayed values, but $E$ and $Q$ do not themselves influence $S$, $I$ and $R$. In other words, $E$ and $Q$ are slave variables, and we henceforth ignore them.

In the three equations that remain, we can clearly absorb $m$ into $\tilde{\beta }$ or equivalently, write

$$\tilde{\beta }m=\beta .$$ (6)

If social distancing is practiced, then we expect $m$ to decrease and thus $\beta$ to be lower, even though $\tilde{\beta }$ may remain the same. For this reason, in the later portions of this paper, we will consider time-varying $\beta$ while holding other parameters constant.

For a fast-spreading pandemic, we assume $\alpha =0$ for simplicity, which makes $R$ a slave as well, and we need to only retain the equations for $S$ and $I$. Finally, by choice of units of time, we can let $\sigma =1$. This is equivalent to nondimensionalizing $\tau$ which has units of time, as well as $\gamma$ and $\beta$ which have units of 1/time. Our equations now are

$$\dot{S}\left(t\right)=-\beta \left(t\right)S\left(t\right)I\left(t\right)$$ (7)

$$\dot{I}\left(t\right)=\beta (t-1)S(t-1)I(t-1)-\gamma I\left(t\right)-\beta (t-1-\tau )\times p{e}^{-\gamma \tau }S(t-1-\tau )I(t-1-\tau )$$ (8)

In the above, if $\beta$ was constant rather than time-varying, then its $t$-dependence would be dropped. Note that, if $\beta$ varies with time, its variation can be considered externally specified and not a part of the solution. Eqs. (7), (8) make intuitive sense in a lumped-variable setting as follows. Eq. (7) says that the instantaneous rate of new infections is proportional to how infectious the disease is ($\tilde{\beta }$), how much people are meeting each other ($m\left(t\right)$), how many uninfected people there are ($S\left(t\right)$) and how many infectious people are out in public ($I\left(t\right)$). Eq. (8) says that the rate of change in the number of infectious people is equal to previously infected people just exiting the latency phase and entering the infectious phase, minus the rate at which people are recovering on their own, minus also the rate at which people displaying symptoms are being put into quarantine (these quarantined people are slightly diminished in number due to self-recovery, which is good; and due to some people not being quarantined, which is a system inefficiency).

We are interested in near-unity initial conditions for $S(-\infty )=1$ that lead to growth of the infection and eventual saturation. In particular, the net damage done by the disease is represented by $1-S\left(\infty \right)$.

From now onward, until the start of Section 5, we will consider $\beta$ to be a constant parameter. For clarity, therefore, we write the governing equations out with constant $\beta$,

$$\dot{S}\left(t\right)=-\beta S\left(t\right)I\left(t\right)$$ (9)

$$\dot{I}\left(t\right)=\beta S(t-1)I(t-1)-\gamma I\left(t\right)-\beta p{e}^{-\gamma \tau }\times S(t-1-\tau )I(t-1-\tau )$$ (10)

Let

$$P\left(t\right)={\int }_{-\infty }^{t}I\left(\zeta \right)d\zeta ,$$ (11)

where we are interested in the asymptotic initial condition $P(-\infty )=0$ as the limiting case of a tiny level of initial infection. Then Eq. (9) yields

$$S\left(t\right)=e^{-\beta P\left(t\right)}$$ (12)

which incorporates the initial condition of interest, namely $S(-\infty )=1$. Inserting $S\left(t\right)$ from Eq. (12) into Eq. (10), we obtain

$$\ddot{P}\left(t\right)=\beta e^{-\beta P(t-1)}\dot{P}(t-1)-p{e}^{-\gamma \tau }\beta e^{-\beta P(t-1-\tau )}\dot{P}(t-1-\tau )-\gamma \dot{P}\left(t\right).$$ (13)

Integrating both sides with respect to time, and by defining

$$\overline{p}=p{e}^{-\gamma \tau },$$ (14)

we obtain

$$\dot{P}\left(t\right)=\overline{p}{e}^{-\beta P(t-1-\tau )}-e^{-\beta P(t-1)}-\gamma P\left(t\right)+1-\overline{p},$$ (15)

where $1-\overline{p}$ is an integration constant chosen to match initial conditions at $-\infty$. Thus, for constant $\beta$ and with the approximation of $\alpha =0$ for a fast-spreading pandemic, Eqs. (1) through (5) effectively reduce to the single nonlinear delay differential equation shown in (15).

It may be noted that $\dot{P}=0$, i.e., $P$ equals a constant, is allowed by Eq. (15) for $P$ that satisfy

$$(1-\overline{p})\left(1-e^{-\beta P}\right)-\gamma P=0.$$ (16)

Eq. (16) is satisfied by $P=0$ for all parameter values. Additionally, for $\gamma >0$, it has a single strictly positive root if

$$\frac{\beta }{\gamma }\left(1-\overline{p}\right)>1.$$ (17)

If $\gamma =0$ (i.e., there is no self-recovery), and $0\le \overline{p}<1$ (i.e., not everybody is quarantined), then for $\beta >0$, $P=0$ is the only equilibrium solution. This means if $P$ increases from zero, it can grow without bound and $S\left(\infty \right)=0$, i.e., everybody in the population gets infected. The case of $\beta =0$ is not interesting because the infection does not spread. Finally, if $\gamma =0$ and $\overline{p}=1$, then Eq. (16) is identically satisfied for every constant $P$.

Thus, we conclude that a simple yet interesting situation within Eq. (15) occurs when $p=1$ (all infected people display symptoms and are quarantined) and $\gamma =0$ (there is no recovery without displaying symptoms). We will first study this restricted case in some detail, because some analytical progress is possible that provides useful insights.

3. A simple subcase: $p=1$ and $\gamma =0$

For $p=1$ and $\gamma =0$, we have from Eq. (15),

$$\dot{P}\left(t\right)=e^{-\beta P(t-1-\tau )}-e^{-\beta P(t-1)}$$ (18)

As mentioned above, any constant $P$ is an equilibrium, though possibly an unstable one.

3.1. Linear stability analysis for small $P$

In the initial stages $P\left(t\right)$ is small, and Eq. (18) can be linearized to

$$\dot{P}\left(t\right)=\beta P(t-1)-\beta P(t-1-\tau )$$ (19)

Eq. (19) has infinitely many characteristic roots, and has oscillatory solutions which we must disallow because their decreasing portions require negative $I\left(t\right)$. However, monotonic solutions exist as well, and we will examine them. The characteristic equation of Eq. (19) is

$$\lambda =\beta e^{-\lambda }\left(1-e^{-\lambda \tau }\right).$$ (20)

Among the infinitely many roots of the above equation, those with nonnegative real parts are of main interest because they lead to growth of $P\left(t\right)$ from initial tiny values. We note that if the real part of $\lambda$ is assumed nonnegative, then the magnitude of the right hand side is bounded by $2\beta$. This means, for infinitesimal $\beta$, any right half plane roots of Eq. (20) are infinitesimal as well. We also note that $\lambda =0$ is a root regardless of $\beta$.

For non-infinitesimal $\beta$, a criterion for real roots in the right half plane is easily found because $\lambda =0$ is a root of Eq. (20) and the right hand side first increases and then decreases to zero as $\lambda \to \infty$. These conditions imply that a nonzero positive root is assured if the slope of the right hand side at $\lambda =0$ exceeds unity. That condition is

$$\beta \tau >1.$$ (21)

Eq. (21) suggests that the contagion may take hold if $\beta \tau >1$, and perhaps not if $\beta \tau <1$. Note that $\tau$ is fixed by biology but $\beta$ can be lowered by practicing social distancing, which will be discussed towards the end of the paper.

Incidentally, in Young et al. [9], the instability condition including $p\le 1$ and $\gamma >0$ is given as Eq. (17). For $p=1$ and $\gamma \to 0$, Eq. (17) easily reduces to Eq. (21).

3.2. Initial numerical observations

For initial insight, we consider some numerical solutions of Eq. (18) obtained using Matlab’s built-in solver dde23 with specified error tolerances of 10⁻⁷ or better. The initial function used was

$$P\left(t\right)=a\left(1+\frac{t}{1+\tau }\right),t\le 0,$$ (22)

with $a$ small and positive, and mentioned in the figure captions. Once $P\left(t\right)$ is obtained (numerically or, later, analytically), we can calculate $S\left(t\right)$ by using Eq. (12). Results below will therefore be presented only in terms of the original variable $S\left(t\right)$, since the impact of the disease is reflected by $1-S\left(\infty \right)$.

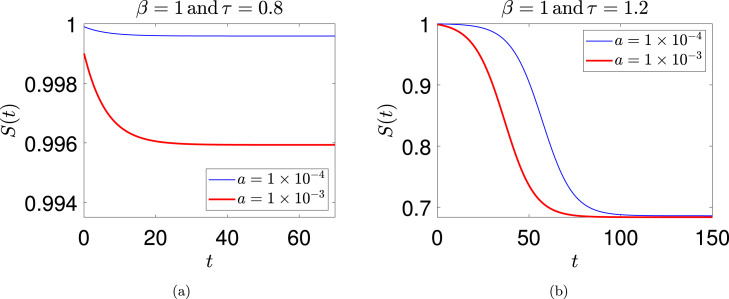
Two solutions for $\beta =1$ and $\tau =0.8$ are shown in Fig. 3(a). It is seen that not much decay occurs; and the solution in each case saturates at a value proportional to the magnitude of the initial function used. This is linear behavior (recall also the discussion following Eq. (21)).

Fig. 3.

Two solutions each for (a) $\beta \tau =0.8<1$ and (b) $\beta \tau =1.2>1$. The initial function used for integrating Eq. (18) was $P\left(t\right)=a\left(1+\frac{t}{1+\tau }\right),t\le 0$. The two solutions in (b) are relatively time-shifted because the underlying system is autonomous, and one solution grows from smaller initial values; see main text for further discussion.

In contrast, two solutions for $\beta =1$ and $\tau =1.2$ are shown in Fig. 3(b). Numerical solutions for two different initial functions show that the rapidly spreading phase of the disease and the saturation value of $S$ are essentially identical, independent of the initial function. It is important to note that the relative time-shift between these two solutions is inconsequential. The underlying dynamical system is autonomous, and the use of asymptotic initial conditions at $-\infty$ leaves a free parameter in the solution that allows time-translations (this will be explicitly clear in the analytical approximations later in the paper). The solution that starts from smaller initial values takes a little longer to climb to larger values, resulting in the time-shift.

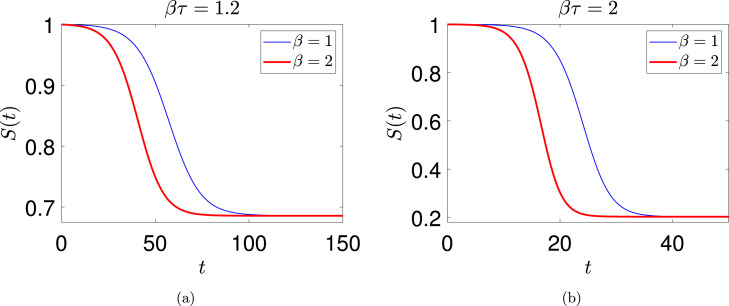
Next, two solutions for $\beta =1$ and $\beta =2$, but with $\beta \tau =1.2$ in each case, and with identical initial functions ($a=0.0001$) are shown in Fig. 4(a).

Fig. 4.

Two solutions for (a) $\beta \tau =1.2>1$ and (b) $\beta \tau =2>1$. The parameters $\beta$ and $\tau$ are individually varied. The initial function used for integrating Eq. (18) was $P\left(t\right)=1\times 10^{-4}\left(1+\frac{t}{1+\tau }\right),t\le 0$.

The limiting or saturation value $S\left(\infty \right)$, which is the population fraction that remains unaffected, appears independent of $\beta$ for $\beta \tau$ held fixed. Similar behavior is seen in the two curves in Fig. 4(b) for $\beta \tau =2$ and identical initial conditions. Again, $S\left(\infty \right)$ appears independent of $\beta$ for $\beta \tau$ held fixed.

3.3. Saturation value of $P$

Prompted by numerics, let

$$P\left(\infty \right)=\frac{C}{\beta }$$ (23)

for some $C$ to be determined. In the solution of interest, $I\left(t\right)$ starts from infinitesimal values, and each individual who is a part of $S\left(t\right)$ stays in the infectious state for exactly $\tau$ units of time. Since the total number of individuals thus affected is exactly $1-S\left(\infty \right)$, we can see that for the solution of interest1

$$P\left(\infty \right)=\left(1-S\left(\infty \right)\right)\tau .$$ (24)

From Eq. (23), we obtain

$$\frac{C}{1-e^{-C}}=\beta \tau$$ (25)

Eq. (25) needs to be solved numerically, but two limits are clear. As $\beta \tau \to 1^{+}$, we have $C\to 0$. A simple calculation shows

$$C\approx 2(\beta \tau -1).$$ (26)

The other limit is for $\beta \tau \gg 1$, where $C\to \beta \tau$.

Numerically, for $\beta \tau =1.2$, we find $C=0.376$ or $S\left(\infty \right)=e^{-0.376}\approx 0.687$, which matches Fig. 3(a); and for $\beta \tau =2$, we find $C=1.594$ or $S\left(\infty \right)=e^{-1.594}\approx 0.203$, which matches Fig. 3(b). The difference between even $\beta \tau =1.2$ and $\beta \tau =2$, though both are unstable, is large in terms of consequences for the population.

3.4. Maximum value of stable $S\left(\infty \right)$

The above results indicate that if $\beta \tau >1$, then a solution that grows asymptotically from a zero value at minus infinity saturates at a value given by Eq. (26). However, all $P$ values are equilibrium values: it is therefore interesting to ask what the minimum value of $P$ is for which the equilibrium is stable. We can find this by considering the corresponding limiting steady value of $S$ to be $S^{\ast }$, writing Eq. (10) for $p=1$ and $\gamma =0$ as

$$\dot{I}\left(t\right)=\beta S^{\ast }I(t-1)-\beta S^{\ast }I(t-1-\tau ),$$

and concluding that the required stability condition is (by adapting Eq. (21))

$$\beta \tau S^{\ast }<1.$$ (27)

For $\beta \tau$ slightly exceeding unity, referring to Eqs. (23), (26), the upper limit of

$$S^{\ast }=\frac{1}{\beta \tau }$$

implied by Eq. (27) corresponds to about half as many people being infected as would be if the asymptotic solution for constant $\beta$ was allowed to run its course all the way from initiation to saturation. This situation will be clearly seen in the multiple scales solution for constant $\beta$ and weak growth starting from zero at $t=-\infty$. We now turn to that solution.

3.5. Multiple scales solution for weak growth

The foregoing results indicate that the $P\left(t\right)$ solution starts asymptotically from zero at $t=-\infty$ and grows monotonically if $\beta \tau >1$, but saturates at a small value when $\beta \tau$ slightly exceeds unity. We can develop an asymptotic solution for the case where

$$\beta =\frac{1}{\tau }+ϵ,0<ϵ\ll 1.$$ (28)

We will use the method of multiple scales [27], [28], [29], [30]. We rewrite Eq. (18) as

$$\dot{P}\left(t\right)=e^{-\left(\frac{1}{\tau }+ϵ\right)P(t-1-\tau )}-e^{-\left(\frac{1}{\tau }+ϵ\right)P(t-1)}$$ (29)

and note that the $ϵ=0$ case is on the stability boundary for $P\left(t\right)=0$. We introduce three time scales for a second order expansion,

$$T_0=t,T_1=ϵt,T_2={ϵ}^{2}t,$$ (30)

think of $P\left(t\right)$ as $P(T_0,T_1,T_2)$ with a slight abuse of notation, and observe that the time derivative is to be interpreted as

$$\dot{P}=\frac{\partial P}{\partial T_0}+ϵ\frac{\partial P}{\partial T_1}+{ϵ}^2\frac{\partial P}{\partial T_2}+\cdots .$$ (31)

Further, a delayed quantity such as $P(t-\Delta )$ is to be interpreted as

$$P(t-\Delta )=P(T_0-\Delta ,T_1-ϵ\Delta ,T_2-{ϵ}^2\Delta ),$$ (32)

where due to the smallness of $ϵ$, Taylor series expansions in $ϵ$ can be used for the second and third arguments, but not the first argument, i.e., 

$$P(t-\Delta )=P(T_0-\Delta ,T_1,T_2)-ϵ\Delta \frac{\partial P(T_0-\Delta ,T_1,T_2)}{\partial T_1}+\frac{{ϵ}^2{\Delta }^2}{2}\frac{{\partial }^{2}P(T_0-\Delta ,T_1,T_2)}{\partial T_1^2}-{ϵ}^2\Delta \frac{\partial P(T_0-\Delta ,T_1,T_2)}{\partial T_2}+\mathcal{O}\left({ϵ}^3\right).$$ (33)

Finally, $P$ itself is to be expanded as

$$P=ϵP_0+{ϵ}^2{P}_1+{ϵ}^3{P}_2+\cdots$$ (34)

where higher order terms in the expansion would require retention of still slower time scales. This much is routine, and yields an equation of the form (using the symbolic computation software Maple; note that the leading order term is $\mathcal{O}\left(ϵ\right)$):

$$\left(\frac{\partial }{\partial T_0}{P}_0\left(T_0,T_1,T_2\right)+\frac{P_0\left(T_0-1-\tau ,T_1,T_2\right)}{\tau }\right)-\left(\frac{P_0\left(T_0-1,T_1,T_2\right)}{\tau }\right)ϵ+L_2{ϵ}^2+L_3{ϵ}^3+\cdots =0,$$ (35)

where two long expressions have been written simply as $L_2$ and $L_3$ (details omitted for brevity). At $\mathcal{O}\left(ϵ\right)$ we have

$$\frac{\partial }{\partial T_0}{P}_0\left(T_0,T_1,T_2\right)+\frac{P_0\left(T_0-1-\tau ,T_1,T_2\right)}{\tau }-\frac{P_0\left(T_0-1,T_1,T_2\right)}{\tau }=0,$$ (36)

for which we adopt the solution (based on previous observations; and also upon rejecting fast-varying exponential decaying terms [29], [30])

$$P_0(T_0,T_1,T_2)=A(T_1,T_2),$$ (37)

i.e., $P_0$ is a constant on the fast or $T_0$ time scale. Inserting Eq. (37) into Eq. (35), we obtain at $\mathcal{O}\left({ϵ}^2\right)$,

$$\frac{\partial }{\partial T_0}{P}_1\left(T_0,T_1,T_2\right)+\frac{P_1\left(T_0-1-\tau ,T_1,T_2\right)}{\tau }-\frac{P_1\left(T_0-1,T_1,T_2\right)}{\tau }=0,$$ (38)

with terms containing $A(T_1,T_2)$ canceling each other out at this order. This means $A(T_1,T_2)$ remains indeterminate at this order, and we are free to choose

$$P_1\left(T_0,T_1,T_2\right)=0,$$ (39)

because it adds nothing new to the already retained $P_0$. Inserting the above into Eq. (35), we obtain at $\mathcal{O}\left({ϵ}^3\right)$,

$$\frac{\partial }{\partial T_0}{P}_2\left(T_0,T_1,T_2\right)+\frac{P_2\left(T_0-1-\tau ,T_1,T_2\right)}{\tau }-\frac{P_2\left(T_0-1,T_1,T_2\right)}{\tau }=L_3,$$ (40)

where $L_3$ is a long expression independent of $T_0$ and containing the function $A(T_1,T_2)$ along with its $T_1$-derivatives only. Now, appealing to the required boundedness of $P_2$ (which corresponds to removal of secular terms, and can also be viewed as a choice that allows the approximation to stay valid for a longer time), we insist that $L_3=0$. Further, since $T_2$ derivatives of $A$ do not appear, we set $A$ back to a function of $T_1$ alone (no contradiction up to this order). In this way, we finally obtain

$$\left(1+\frac{\tau }{2}\right)A^{\prime \prime }-\tau A^{\prime }+\frac{A{A}^{\prime }}{\tau }=0,$$ (41)

where we note that $\tau$ is a positive parameter, $A$ is a function of $T_1$, and primes denote $T_1$-derivatives. The above differential equation is to be solved as a function of $T_1$, with the initial condition $A(-\infty )=0$. The solution turns out to be

$$A={\tau }^2\left\{1+tanh\left(\frac{\tau (T_1-c_0)}{\tau +2}\right)\right\},$$ (42)

where $c_0$ is an indeterminate constant that allows time-shifting (recall Fig. 3(b) and the related discussion). Inserting $T_1=ϵt$, and then (recall Eq. (28))

$$ϵ=\beta -\frac{1}{\tau },$$ (43)

we finally obtain the leading order approximation for the entire solution, for $\beta \tau$ slightly greater than unity, as

$$P\left(t\right)\sim (\beta \tau -1)\tau \left\{1+tanh\left(\frac{(\beta \tau -1)(t-c_1)}{\tau +2}\right)\right\},$$ (44)

where $c_1$ is an undetermined constant. The above solution saturates, as $t\to \infty$, at

$$P\left(\infty \right)\sim 2\tau (\beta \tau -1),$$ (45)

which matches Eq. (26) upon noting that we can replace $\frac{C}{\beta }$ with $C\tau$ with no errors introduced at leading order. At the same order of approximation, we can also write

$$P\left(t\right)\sim \frac{\beta \tau -1}{\beta }\left\{1+tanh\left(\frac{\beta (\beta \tau -1)(t-c_1)}{1+2\beta }\right)\right\},$$ (46)

whence

$$S\left(t\right)\sim e^{-(\beta \tau -1)\left\{1+tanh\left(\frac{\beta (\beta \tau -1)(t-c_1)}{1+2\beta }\right)\right\}},$$ (47)

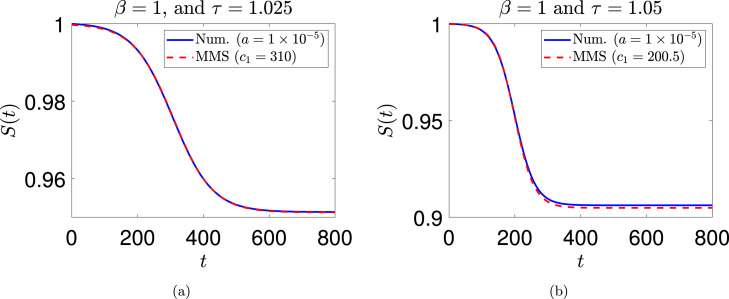
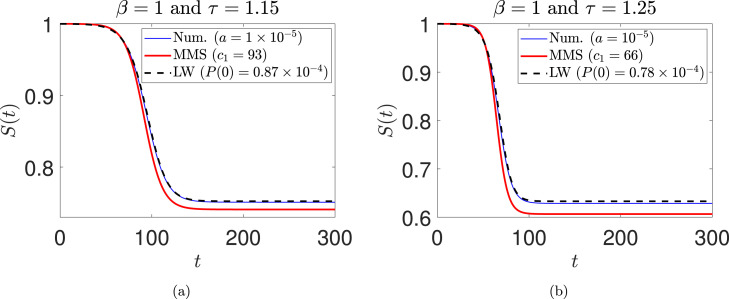
where we have used the ‘$\sim$’ notation because this is an asymptotic approximation. A numerical example is given in Fig. 5 for $\beta \tau =1.025$ ($\beta =1$ and $\tau =1.025$) and $\beta \tau =1.05$ ($\beta =1$ and $\tau =1.05$). The match is good, but deteriorates for larger values of $\beta \tau$.

Fig. 5.

Comparison between numerical solution and asymptotic (method of multiple scales, or MMS) solution for (a) $\beta =1$, $\tau =1.025$, $a=1\times 10^{-5}$ (numerical) and $c_1=310$ (MMS); (b) $\beta =1$, $\tau =1.05$, $a=1\times 10^{-5}$ (numerical) and $c_1=200.5$ (MMS). The initial condition used for integrating Eq. (18) is $P\left(t\right)=a\left(1+\frac{t}{1+\tau }\right),t\le 0$. The arbitrary time-shift $c_1$ of the multiple scales solution (Eq. (47)) is chosen here to obtain a good visual match.

It may be noted that, for such weak growth where only a small fraction of the total population gets infected before the pandemic runs its course, by Eq. (46),

$$S\left(\infty \right)\sim 1-2(\beta \tau -1).$$ (48)

In comparison (recall Eq. (27)), $S$ could in principle be stable at a value as high as

$$S^{\ast }=\frac{1}{\beta \tau }=\frac{1}{1+(\beta \tau -1)}\sim 1-(\beta \tau -1),$$ (49)

i.e., the uncontrolled and constant-$\beta$ solution infects about twice as many people as seems strictly necessary; we will return to this in Section 5.

We will next develop a long-wave approximation that performs better for somewhat larger $\beta \tau$.

3.6. Long-wave approximation for moderate growth

The advantage of using an asymptotic method like the method of multiple scales is that we have formal validity as $ϵ\to 0$. We are reassured that the solution we are seeking does in fact exist, and has approximately the shape obtained as the leading order approximation. However, in the present case, for somewhat larger $ϵ$ the solution is not very accurate; moreover, proceeding to higher orders leads to long expressions that seem difficult to simplify usefully. Therefore, encouraged by our asymptotic solution, we now develop a more informal but more accurate approximation. In particular, we try a long-wave (LW) approximation as follows.

We suppose that there is a “long” scale (technically a time scale, for this problem) which we shall call $L$, such that

$$P\left(t\right)=\hat{P}\left(\frac{t}{L}\right),L\gg 1.$$ (50)

Let

$$\xi =\frac{t}{L}.$$ (51)

Now Eq. (18) becomes

$$\frac{{\hat{P}}^{\prime }\left(\xi \right)}{L}=e^{-\beta \hat{P}\left(\xi -\frac{1+\tau }{L}\right)}-e^{-\beta \hat{P}\left(\xi -\frac{1}{L}\right)}.$$ (52)

Expanding the above in a series for large $L$, retaining terms up to $\mathcal{O}\left(L^{-2}\right)$, and solving for ${\hat{P}}^{\prime \prime }$, we obtain

$${\hat{P}}^{\prime \prime }=\beta {\hat{P}}^{\prime 2}+\frac{2L{\hat{P}}^{\prime }}{\tau +2}\left(1-\frac{e^{\beta \hat{P}}}{\beta \tau }\right).$$ (53)

We note that on the right hand side the second term is dominant because it contains the large parameter $L$, while the first term does not. The left hand side has the highest derivative and cannot be dropped without changing the order of the differential equation. For these reasons, a further approximation to Eq. (53) is

$${\hat{P}}^{\prime \prime }=\frac{2L{\hat{P}}^{\prime }}{\tau +2}\left(1-\frac{e^{\beta \hat{P}}}{\beta \tau }\right).$$ (54)

Eq. (54) is integrable, and yields

$${\hat{P}}^{\prime }=\frac{2L}{\tau +2}\left(\hat{P}-\frac{e^{\beta \hat{P}}}{{\beta }^2\tau }\right)+C_0,$$ (55)

where $C_0$ is an integration constant. The initial condition of interest is ${\hat{P}}^{\prime }=0$ and $\hat{P}=0$ as $\xi \to -\infty$, whence we obtain

$${\hat{P}}^{\prime }=\frac{2L}{\tau +2}\left(\hat{P}-\frac{e^{\beta \hat{P}}}{{\beta }^2\tau }\right)+\frac{2L}{{\beta }^2\tau (\tau +2)}.$$ (56)

We now return to Eq. (53), where we can insert Eq. (56) into the non-dominant term as an approximation. A simple way to do it is to replace the first term on the right hand side with an approximation that is integrable, i.e., 

$$\beta {\hat{P}}^{\prime 2}=\beta {\hat{P}}^{\prime }\left\{\frac{2L}{\tau +2}\left(\hat{P}-\frac{e^{\beta \hat{P}}}{{\beta }^2\tau }\right)+\frac{2L}{{\beta }^2\tau (\tau +2)}\right\}.$$ (57)

This gives

$${\hat{P}}^{\prime \prime }=\beta {\hat{P}}^{\prime }\left\{\frac{2L}{\tau +2}\left(\hat{P}-\frac{e^{\beta \hat{P}}}{{\beta }^2\tau }\right)+\frac{2L}{{\beta }^2\tau (\tau +2)}\right\}+\frac{2L{\hat{P}}^{\prime }}{\tau +2}\left(1-\frac{e^{\beta \hat{P}}}{\beta \tau }\right).$$ (58)

The above is integrable, and after enforcing the initial condition ${\hat{P}}^{\prime }=0$ and $\hat{P}=0$ as $\xi \to -\infty$, setting $L=1$ (it was a bookkeeping parameter all along, helping us keep track of which effects are big and which are small), and dropping the hat, we obtain the informal long-wave approximation

$$\frac{dP}{dt}=\frac{(2+\beta P)P}{\tau +2}+\frac{2P}{\beta \tau (\tau +2)}+\frac{4}{{\beta }^2\tau (\tau +2)}\left(1-e^{\beta P}\right).$$ (59)

We mention that Eq. (59) is indeed a significant simplification, because it replaces a DDE (infinite-dimensional phase space) with a first order ODE (one-dimensional phase space). It also applies to a specific solution, all the way from infinitesimal initiation to final saturation. The freedom in a single initial condition that it offers is equivalent to simply the arbitrary time-shift already noted in the multiple scales solution. While it cannot be solved explicitly in closed form, its solution can be formally expressed in implicit form using an indefinite integral (omitted for brevity).

The qualitative behavior of the approximation in Eq. (59) may be checked easily for small positive $P$ by linearizing the right hand side to obtain

$$\dot{P}=\frac{2(\beta \tau -1)}{\beta \tau (\tau +2)}P,$$ (60)

which is consistent with the earlier result that growth requires $\beta \tau >1$ (inequality (21)). In Fig. 6, numerical solutions for $\beta \tau$ somewhat greater than unity are shown. We consider $\beta \tau =1.15$ (see Fig. 6(a)) and $\beta \tau =1.25$ (see Fig. 6(b)). The numerically obtained long-wave solutions match well with full numerical solutions of the original DDE; in fact, they match significantly better than the multiple scales solution.

Fig. 6.

Comparison between numerical, multiple scales (MMS), and long-wave solutions for (a) $\beta =1$, $\tau =1.15$, $a=1\times 10^{-5}$ (numerical), $c_1=93$ (MMS), and $P\left(0\right)=0.87\times 10^{-4}$ (long-wave); (b) $\beta =1$, $\tau =1.25$, $a=1\times 10^{-5}$ (numerical), $c_1=66$ (MMS), and $P\left(0\right)=0.78\times 10^{-4}$ (long-wave). The initial condition used for integrating Eq. (18) is $P\left(t\right)=a\left(1+\frac{t}{1+\tau }\right),t\le 0$. The initial condition $P\left(0\right)$ is used to integrate the long-wave equation (59). The coefficient $c_1$ is used in the multiple scales solution (see Eq. (47)).

Finally, a direct analytical comparison with the multiple-scales solution can be made by expanding the right hand side of Eq. (59) in a power series for small $P$, retaining up to quadratic terms. That equation can be solved in closed form, and gives a hyperbolic tangent solution as well, which initially looks a little different from the multiple scales solution:

$$P\left(t\right)=\frac{\beta \tau -1}{\beta (2-\beta \tau )}\left\{1+tanh\left(\frac{(\beta \tau -1)(t-c_1)}{\beta \tau (\tau +2)}\right)\right\}.$$ (61)

However, noting that the multiple scales solution was for $\beta \tau$ close to unity, if we replace $(2-\beta \tau )$ with $2-1=1$, and replace $\beta \tau (\tau +2)$ with $1\cdot \left(\frac{1}{\beta }+2\right)$, then we recover Eq. (46). This is not surprising because for $\beta \tau$ slightly greater than unity, the long-wave approximation is asymptotic as well. The approximation is only informal (as opposed to asymptotic) when we use it for arbitrary values of $\beta$ and $\tau$, with $\beta \tau$ not close to unity.

This concludes our study of the $p=1$ and $\lambda =0$ subcase, which is interesting both because it is a reasonable limit and because it permits any constant $P$ as an equilibrium. The latter is not true for general parameter values, to which we turn next. Encouraged by the simplicity of the long-wave approximation as opposed to the multiple scales solution, we try only the former.

4. Long-wave approximation for general parameter values

We now discuss approximating a specific solution. This solution starts from an infinitesimal infection level, changes monotonically but slowly over a long time, then accelerates over a relatively short time, to finally saturate at a finite value as the time goes to infinity. We now take up Eq. (15), reproduced below:

$$\dot{P}\left(t\right)=\overline{p}{e}^{-\beta P(t-1-\tau )}-e^{-\beta P(t-1)}-\gamma P\left(t\right)+1-\overline{p}.$$

Proceeding with the same ansatz as Eq. (50), expanding up to second order, and setting $L$ to unity, we obtain

$$\ddot{P}=\beta {\dot{P}}^2+\frac{2}{\mu }\left(\overline{p}(1+\tau )-1-\frac{e^{\beta P}}{\beta }\right)\dot{P}+\frac{2}{\beta \mu }\left(\overline{p}-1+(1-\overline{p}-\gamma P)e^{\beta P}\right),$$ (62)

where

$$\mu =\overline{p}{(1+\tau )}^2-1.$$ (63)

A few things may be noted here. First, assuming that $\tau$ and $\overline{p}$ are not too small, we assume $\mu >0$ in Eq. (63). Second, we were able to use a trick for the $p=1$ and $\gamma =0$ case to reduce the order of the approximating long-wave differential equation; for those parameter values, the last term on the right hand side in Eq. (62) becomes zero. Here, we have had to retain the second order ordinary differential equation. Third, if there is a nonzero positive $P$ for which Eq. (62) has an equilibrium solution, then that $P$ must satisfy

$$\overline{p}-1+(1-\overline{p}-\gamma P)e^{\beta P}=0,$$ (64)

which is equivalent to Eq. (16). This means the steady state $P$ in this general case will be exactly correct, unlike the previous subcase of $p=1$ and $\gamma =0$. However, note that this unique limiting $P$ is for the specific solution that starts asymptotically at zero, at $t=-\infty$. Since we now have a second order differential equation in the long-wave approximation, trying to approximate what is purportedly a single solution, we have a minor dilemma in interpreting the two degrees of freedom available in initial conditions for Eq. (62). One of those corresponds to an arbitrary time-shift, as noted earlier. That leaves one other initial condition. Since our derivation has not identified what this initial condition should be, we expect that it should be inconsequential. This does turn out to be the case, as seen next.

For small $P$ and small $\dot{P}$, Eq. (62) can be linearized to give

$$\ddot{P}+C_1\dot{P}+C_{2}P=0,$$ (65)

where $C_1$ and $C_2$ are given by

$$C_1=-\frac{2}{\mu }\left(\overline{p}(1+\tau )-1-\frac{1}{\beta }\right),$$ (66)

$$C_2=-\frac{2}{\beta \mu }(\beta (1-\overline{p})-\gamma ).$$ (67)

For stability of $P=0$ we must have $C_1>0$ and $C_2>0$, but this solution is of little interest because the infection does not grow. If $C_1<0$ and $C_2>0$, then growing oscillations are predicted. Such solutions are non-physical for our application, because $P$ must be monotonic.

For monotonic growth with a single unstable growth direction, we require $C_1>0$ and $C_2<0$. We assume that $\mu >0$ (recall Eq. (62) and Eq. (63)) accordingly our conditions become

$$\frac{\beta }{\gamma }(1-\overline{p})>1,$$ (68)

$$\overline{p}(1+\tau )-1-\frac{1}{\beta }<0.$$ (69)

Eq. (68) matches the loss of stability condition of Young et al. [9] as well as our own Eq. (17). In other words, the condition for a solution growing from zero exactly matches the condition for the existence of another equilibrium for strictly positive $P$. This condition, though obtained here from the long-wave approximation, matches the theoretical result exactly because it is near this stability boundary that the long-wave approximation is asymptotic. Note that if $C_1>0$ and $C_2<0$ in Eq. (65), then the two characteristic roots are real: one is positive and one is negative. The positive root leads to the growing solution, which is of primary interest in this paper. The negative root absorbs the apparently free initial condition, contributes an exponentially decaying term that dies soon, and has no influence on the growing solution provided the initial conditions are sufficiently early in the outbreak.

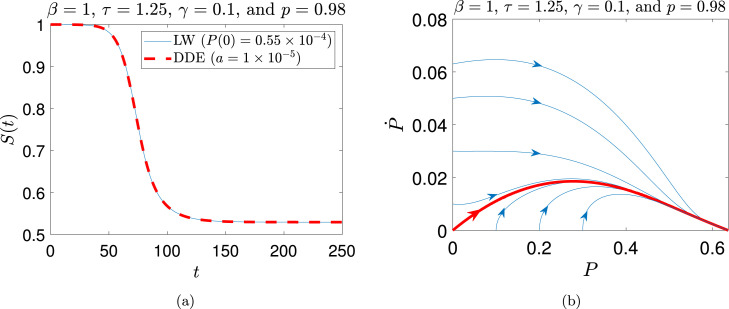
A numerical example is shown in Fig. 7 for the case of $C_1>0$ and $C_2<0$. The parameter $p=0.98$ implies that the probability of detecting infected individuals is not perfect. Further, $\gamma =0.1$ models a small fraction of the infectious population recovering without being quarantined. The Long-wave solution almost perfectly matches the solution from numerical integration of the DDE (Eq. (18)). The phase portrait shown in Fig. 7(b) indicates that the stability properties of the solution of interest (shown in red) are correctly inherited by the long-wave approximation. Nearby solutions are attracted towards the same asymptotic solution starting from infinitesimal initial infection and growing monotonically towards final saturation.

Fig. 7.

Comparison between numerical solution of Eq. (15) and long-wave solutions for (a) $\beta =1$, $\tau =1.25$, $\gamma =0.1$, $p=0.98$, $a=1\times 10^{-5}$ (DDE), and $P\left(0\right)=0.55\times 10^{-4}$ (long-wave); (b) Phase portrait of the long wave Eq. (62), the red thick line is the solution of Eq. (15).

For this specific kind of solution, the long-wave approximation gives a good match to the DDE solution as long as $\mu >0$, $C_1>0$ and $C_2<0$.

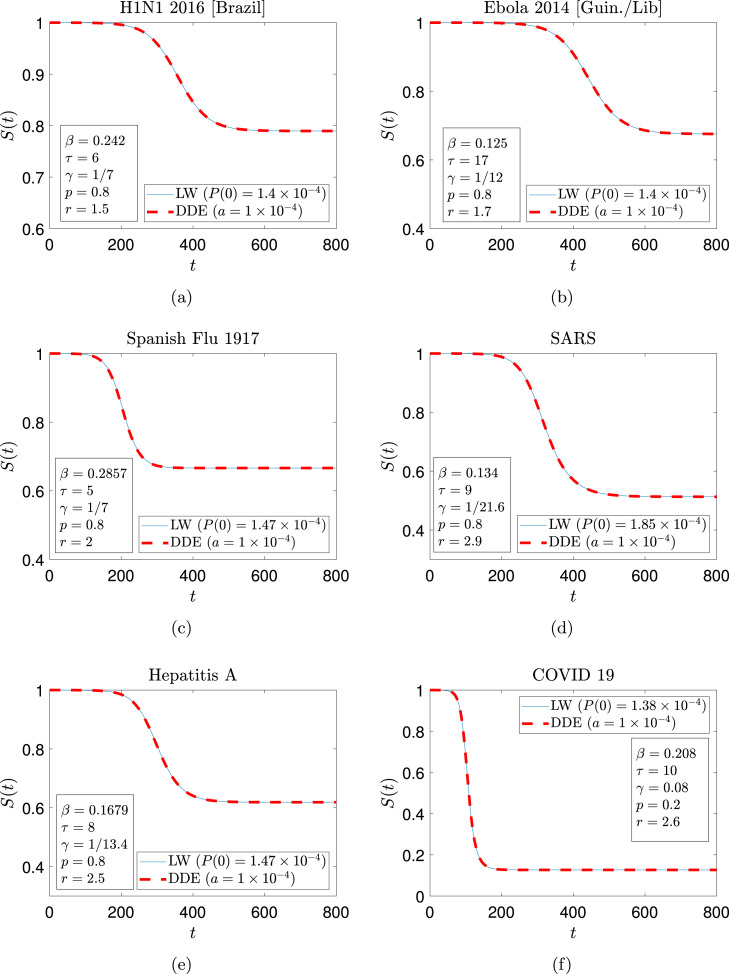
In Fig. 8, we compare the solution of the long-wave ODE (Eq. (62)) and that of the DDE (Eq. (15)) for parameters corresponding to six different diseases. These parameters are reported in Table 1 and are taken from Refs. [9], [31], [32], [33], [34], [35], [36]. In Fig. 8, the long-wave solution captures the disease progression accurately in all cases.

Fig. 8.

Comparison between numerical solution (of the DDE) and long-wave solutions for parameter sets corresponding to six different diseases (a) H1N1 (Brazil) [9] (b) Ebola [31] (c) Spanish Flu 1917 [33] (d) SARS [33] (e) Hepatitis A [33], and (f) COVID-19 [34], [35]. Initial conditions and other parameter values used to generate the results are shown in each figure separately.

Table 1.

Parameters for different infections.

Infection	$r$	$\frac{1}{\gamma }$	$\beta =r\gamma$	$p$	$\tau$
H1N1 2016 (Brazil) [9]	1.7	7	0.242	0.8	6
Ebola 2014 (Guin./Lib) [31]	1.5	12	0.125	0.8	17
Spanish Flu 1917 [32]	2	7	0.2857	0.8	5
SARS [33]	2.9	21.6	0.134	0.8	9
Hepatitis A [33]	2.25	13.4	0.197	0.8	8
COVID-19 [34], [35], [36]	2.6	12.5	0.208	0.2	10

We now consider more general dynamics, starting from less restricted initial conditions, and allowing for a time-varying infection rate $\beta$.

5. Time-varying $\beta$

As a part of its public health policy, based on observed spread of the disease, a government may prescribe temporarily greater social distancing. Social distancing effectively lowers $\beta$. We can then use Eqs. (7) and (8), rewritten here for readability (incorporating $\overline{p}$ from Eq. (14)):

$$\dot{S}\left(t\right)=\beta \left(t\right)S\left(t\right)I\left(t\right),$$ (70)

$$\dot{I}\left(t\right)=\beta (t-1)S(t-1)I(t-1)-\overline{p}\beta (t-1-\tau )\times S(t-1-\tau )I(t-1-\tau )-\gamma I\left(t\right).$$ (71)

It is worthwhile to verify that the system has low dimensional behavior. To this end, in this section we present a six-state Galerkin approximation for Eqs. (70), (71) using Legendre polynomials as basis functions. The ODEs from the Galerkin approximation are shown below (see the appendix for a derivation and [37], [38] for details). Writing $\nu =1+\tau$, ${\alpha }_2=1-\frac{2}{\nu }$ and ${\alpha }_3=\frac{3}{2}{\left(1-\frac{2}{\nu }\right)}^2-\frac{1}{2}$, the reduced order model is

$${\dot{\eta }}_1=\frac{2}{\nu }{\eta }_2,$$ (72)

$${\dot{\eta }}_2=\frac{6}{\nu }{\eta }_3,$$ (73)

$${\dot{\eta }}_3=-\frac{2}{\nu }{\eta }_2-\frac{6}{\nu }{\eta }_3-\beta \left(t\right)\left({\eta }_1+{\eta }_2+{\eta }_3\right)\left({\eta }_4+{\eta }_5+{\eta }_6\right),$$ (74)

$${\dot{\eta }}_4=\frac{2}{\nu }{\eta }_5,$$ (75)

$${\dot{\eta }}_5=\frac{6}{\nu }{\eta }_6,$$ (76)

$${\dot{\eta }}_6=-\frac{2}{\nu }{\eta }_5-\frac{6}{\nu }{\eta }_6+\beta (t-1)\left({\eta }_1+{\alpha }_2{\eta }_2+{\alpha }_3{\eta }_3\right)\times \left({\eta }_4+{\alpha }_2{\eta }_5+{\alpha }_3{\eta }_6\right)-\overline{p}\beta (t-\nu )\left({\eta }_1-{\eta }_2+{\eta }_3\right)\left({\eta }_4-{\eta }_5+{\eta }_6\right)-\gamma \left({\eta }_4+{\eta }_5+{\eta }_6\right).$$ (77)

In the above approximation $S\left(t\right)={\eta }_1\left(t\right)+{\eta }_2\left(t\right)+{\eta }_3\left(t\right)$ and $I\left(t\right)={\eta }_4\left(t\right)+{\eta }_5\left(t\right)+{\eta }_6\left(t\right)$. Here, $\beta \left(t\right)$ is a known function of time and the state variables do not have delays. Note that we approximate the dynamical system here, and not a specific solution as we did with the long wave approximation.

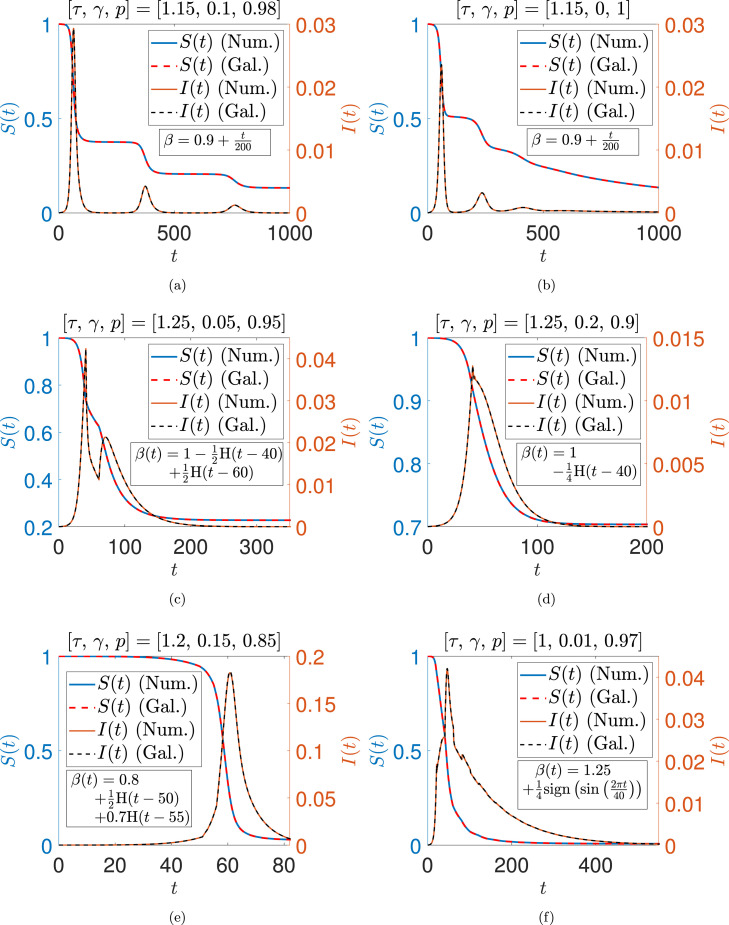
The accuracy of the reduced order model is demonstrated in Fig. 9. For each of several sets of parameters, we find an excellent match between numerical solutions of the DDEs and the Galerkin based ODEs. Both continuous and discontinuous $\beta$’s are considered. The reduced order model shows that our DDEs (Eqs. (70), (71)), though formally infinite-dimensional systems, are effectively finite-dimensional. The remaining dynamics consists of rapidly decaying components that are soon inconsequential.

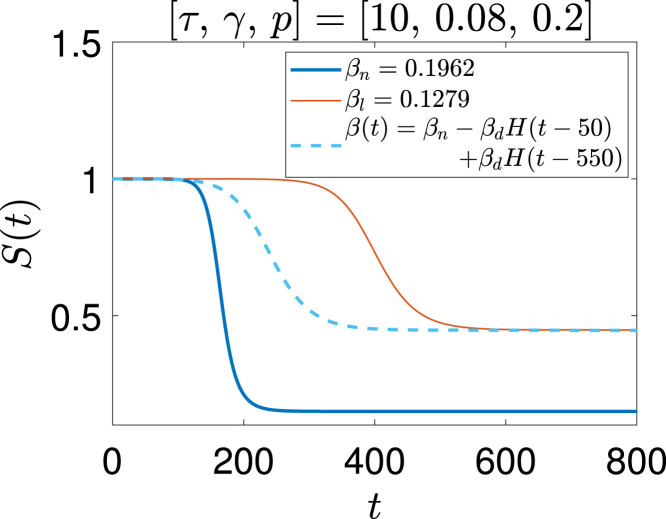
Fig. 9.

Comparison between numerical and Galerkin solutions for various parameters. $H(t-c)=1$ if $t>c$, and is zero otherwise. Initial functions used for Eqs. (70), (71) are $S\left(t\right)=1-10^{-5}\left(1+\frac{t}{1+\tau }\right),t\le 0$ and $I\left(t\right)=10^{-5}\left(1+\frac{t}{1+\tau }\right),t\le 0$. Initial conditions for Eqs. (72)–(77) are fitted by Galerkin projection (see the appendix).

In the next section, we present some policy implications of time-varying $\beta$.

6. Policy implications

Since social distancing lowers $\beta$, we consider the implications of time-varying $\beta$ in the simple case where $\beta$ is set to a low value ${\beta }_l$ early in the pandemic, held at that value for a sufficiently long time, and then set back to its higher, normal value ${\beta }_n$. We emphasize that ${\beta }_n$ is a matter of culture and lifestyle, which people may not like to change permanently; and use of ${\beta }_l<{\beta }_n$ is a temporary measure. We will show that the implications can be significant in terms of reducing the total number of people affected. Moreover, a simple analytical formula for the obtainable benefits will be found.

Consider a country with a constant $\beta ={\beta }_n$ under normal living conditions. If the pandemic runs its course without any social distancing measures, the solutions of Eqs. (70), (71) approach $S\left(t\right)=S_n$ and $I\left(t\right)=0$. To study the stability of these solutions, we substitute $S\left(t\right)=S_n+\xi$ and leave $I$ unaltered, and drop the subscript $n$ from $\beta$, to obtain from Eqs. (70), (71)

$$\dot{\xi }=-\beta S_{n}I,$$ (78)

$$\dot{I}=\beta S_{n}I(t-1)-\gamma I\left(t\right)-\beta S_n\overline{p}I(t-1-\tau ).$$ (79)

The stability of Eq. (79) determines the stability of the system. Substituting $I=e^{\lambda t}$ into Eq. (79), and setting $\lambda =0$ at the bifurcation point, the condition for stability is seen to be

$$\beta S_n(1-\overline{p})\le \gamma .$$ (80)

From Eq. (64), the steady-state value $S_n$ satisfies (note the $n$ subscript on $\beta$)

$$\left(\overline{p}-1\right)S_n+\left(1-\overline{p}+\frac{\gamma log\left(S_n\right)}{{\beta }_n}\right)=0.$$ (81)

It is seen above that if $\gamma >0$ but $\overline{p}=1$, then $S_n=1$. This means that, for large $p$ and small $\tau$, $S_n$ will not be much smaller than unity. However, in practice, $\gamma \tau$ is not very small, and $p$ is not very large. As an example representative of COVID-19 ($\gamma =0.08$, $p=0.2$, $\tau =10$, and ${\beta }_n=0.1962$, and $\overline{p}=p{e}^{-\gamma \tau }$), we find that $S_n=0.15$ from Eq. (81).

The possible advantages of social distancing are now seen from the inequality (80). Substituting ${\beta }_n=0.1962$, $S_n=0.15$, along with the abovementioned values for $\overline{p}$ and $\gamma$, we find the inequality (80) is met by a relatively large margin:

$$0.0268<0.08.$$

In fact, for the same $\beta ={\beta }_n$, stability could potentially be achieved by a significantly larger steady value of $S\left(t\right)$, say

$$S_L=\frac{\gamma }{{\beta }_n(1-\overline{p})},$$ (82)

which works out to 0.45 for the parameter values being considered in this example. In other words, the number of unaffected people could potentially be three times larger, and the number of affected people could be less by about one third (0.55 as opposed to 0.85). The policy implication is that if we hold $\beta$ at a lower value ${\beta }_l$ and let the pandemic run its course and stabilize at $S\left(t\right)=S_L$, then subsequently raising $\beta$ back to ${\beta }_n$ will yield a stable state, and further infections will not grow. Stated another way, if $\beta$ is held at a constant value for all time, the pandemic progresses beyond the point of first herd immunity to a state where more people are affected than necessary. However, with a temporary phase of social distancing, the controlled pandemic can in principle grow to precisely the level where herd immunity just becomes effective for the normal level of interactions, at which point social distancing can be lifted with no further penalties. In this way, while preserving our long term levels of social interactions, we can achieve the smallest possible numbers of people affected.

The precise value of ${\beta }_l$ needed is easy to compute for the present model. We first use our normal parameters in Eq. (82) to compute the best achievable outcome, $S_L$. The corresponding $\beta ={\beta }_l$ is found using Eq. (64), which here becomes

$$\left(\overline{p}-1\right)S_L+\left(1-\overline{p}+\frac{\gamma log\left(S_L\right)}{{\beta }_l}\right)=0,$$ (83)

which for the parameter values of the present example yields ${\beta }_l=0.1279$.

The simple social distancing policy recommendation now is

$$\beta \left(t\right)=\left\{\begin{array}{cc}{\beta }_n\hfill & \text{for}0<t<T_o,\hfill \\ {\beta }_l\hfill & \text{for}{T}_0\le t\le T_c,\hfill \\ {\beta }_n\hfill & \text{for}t>T_c,\hfill \end{array}\right)$$ (84)

where social distancing is imposed at time $T_o$, early in the pandemic when very few people have been affected; and $T_c$ is understood to be sufficiently late such that an intermediate equilibrium at $S_L$ is established. Subsequently, $\beta$ is set back to ${\beta }_n$ and life proceeds as usual.

In Fig. 10, we show the evolution of the pandemic for three cases: (i) $\beta \left(t\right)={\beta }_n=0.1962$ (constant for all time), (ii) $\beta \left(t\right)={\beta }_l=0.1279$ (held constant for all time), and (iii) $\beta \left(t\right)$ given by Eq. (84) with $T_0=50$ and $T_c=550$. In case (i), $85\text{\%}$ of the population is affected. In case (ii), only $55\text{\%}$ of the population is affected. In case (iii), too, only $55\text{\%}$ is affected even though $\beta$ is later increased to the level of case (i).

Fig. 10.

Fraction of susceptible population with $\beta \left(t\right)={\beta }_n=0.1962$, $\beta \left(t\right)={\beta }_l=0.1279$, and $\beta \left(t\right)={\beta }_n-{\beta }_{d}H(t-55)+{\beta }_{d}H(t-550)$. The parameters used for the generating the results are $\gamma =0.08$, $p=0.2$, and $\tau =10$. Here ${\beta }_d={\beta }_n-{\beta }_l$.

The effectiveness of this variable-$\beta$ policy can be expressed using the ratio $\rho <1$, defined by

$$\rho =\frac{1-S_L}{1-S_n}.$$

If $\rho$ is significantly less than unity, then the benefits of adopting the above optimal social distancing policy are high. A simple expression for $\rho$ can be obtained as follows. First, Eq. (82) is solved for ${\beta }_n$, which is inserted into Eq. (81). Simple manipulations then yield

$$\rho =\frac{1}{1-S_n}+\frac{1}{log\left(S_n\right)}.$$ (85)

The above formula is in terms of $S_n$, which is formally a quantity that depends on model parameters $\beta$, $\tau$, $\gamma$ and $p$. However, in terms of interpretation, the dependence on $S_n$ alone is both interesting and useful, because it shows the answer is dependent only on the severity of the pandemic. In particular, for very small $S_n$, $\rho \approx 0.5$. However, even for $S_n=0.15$ (i.e., 85% of the population would normally be affected), we find that $\rho =0.65$, or about two thirds.

In the popular press, the idea is commonly expressed that social distancing spreads the infected people out by flattening the curve, and this gives the medical services of a country more time to respond. Our result shows that the total number affected can be significantly reduced as well.

7. Concluding discussion

In this paper we have taken up a recently presented SEIQR model with delays. For a fast-spreading pandemic, loss of immunity of previously infected and cured people may reasonably be ignored. Under that simplification, the SEIQR model decouples so that only the $S$ and $I$ population equations need to be tackled. It is known for this model that, for fixed parameter values in the unstable regime, an outbreak can occur. An initially small infected population can grow, and a significant portion of the original population can be affected.

We have first studied this model in some detail, seeking useful approximate solutions. For a weakly growing outbreak that affects a small proportion of the total population, and under a further simplification that neglects self-recovery and assumes perfect quarantining, the method of multiple scales yields an analytical expression for the complete progression of the outbreak, from infinitesimal initiation to final saturation. For moderate growth rates, a long wave approximation for the same parameters provides a nonlinear first order ODE for the same progression. With imperfect quarantining and nonzero self-recovery the long wave approximation for the full progression of the outbreak is given by a second order ODE. Finally, although the underlying DDE system is technically infinite dimensional, we have shown that a six-state Galerkin-based reduced order model for the system does an excellent job of capturing a wide range of solutions, i.e., the dynamics is effectively low-dimensional.

Subsequently, we have examined the implications of policy-induced social distancing, incorporated in our model as a time-varying infection rate $\beta \left(t\right)$. Interestingly and promisingly, we have found that an extended period of social distancing, imposed early in the outbreak, followed by an eventual relaxation to usual levels of interaction, can significantly lower the total numbers infected without losing stability of the final state. In the limit of weak growth, the number of infected people is cut in half. For faster growth, the reduction is a smaller but still significant. We have obtained a simple analytical formula for the reduction possible.

The above policy implications seem simple and robust. The intuitive key to understanding this reduction caused by social distancing lies in stability under fresh, but small, infection. Here, stability implies that with a small infected population, the outbreak will not grow very much (recall Fig. 3(a) versus 3(b)). Under identical conditions, a larger infected population could cause the outbreak to grow: the assumption is that once the infected numbers are contained, a fresh large influx of infected people will be avoided. If $\beta$ is set to ${\beta }_l$ with social distancing, the outbreak saturates at a relatively high $S_L$. Subsequently, assuming no large influx of infected people, $\beta$ can be increased back to the normal ${\beta }_n$, and the outbreak does not grow significantly further.

CRediT authorship contribution statement

C.P. Vyasarayani: Data curation, Formal analysis, Visualization, Writing - original draft. Anindya Chatterjee: Conceptualization, Formal analysis, Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Communicated by V.M. Perez-Garcia

Appendix.

Here we outline our Galerkin projection calculation. Readers interested in the theoretical background may see, e.g., the so-called tau method of imposing boundary conditions in [39].

The initial functions for Eqs. (70), (71) are assumed to be $S\left(t\right)=U_1\left(t\right),-\nu \le t\le 0$ and $I\left(t\right)=U_2\left(t\right),-\nu \le t\le 0$. Define $y_1(s,t)=S(t+s)$ and $y_2(s,t)=I(t+s)$. Eqs. (70) and (71) along with their history functions can be equivalently posed as the following partial differential equations with time dependent boundary conditions

$$\frac{\partial y_1}{\partial t}=\frac{\partial y_1}{\partial s},-\nu \le s\le 0,$$ (86)

$$\frac{\partial y_2}{\partial t}=\frac{\partial y_2}{\partial s},-\nu \le s\le 0,$$ (87)

$${\frac{\partial y_1}{\partial t}|}_{s=0}=-\beta \left(t\right)y_1(0,t)y_2(0,t),$$ (88)

$${\frac{\partial y_2}{\partial t}|}_{s=0}=\beta (t-1)y_1(-1,t)y_2(-1,t)-\overline{p}\beta (t-\nu )\times y_1(-\nu ,t)y_2(-\nu ,t)-\gamma y_2(0,t).$$ (89)

Now, we assume a solution for $y_1(s,t)$ and $y_2(s,t)$ as follows

$$y_1(s,t)={\varphi }_1\left(s\right){\eta }_1\left(t\right)+{\varphi }_2\left(s\right){\eta }_2\left(t\right)+{\varphi }_3\left(s\right){\eta }_3\left(t\right)$$ (90)

$$y_2(s,t)={\varphi }_1\left(s\right){\eta }_4\left(t\right)+{\varphi }_2\left(s\right){\eta }_5\left(t\right)+{\varphi }_3\left(s\right){\eta }_6\left(t\right)$$ (91)

The basis functions ${\varphi }_1\left(s\right)=1$, ${\varphi }_2\left(s\right)=1+\frac{2s}{\nu }$, and ${\varphi }_3\left(s\right)=\frac{3}{2}{\left(1+\frac{2s}{\nu }\right)}^2-\frac{1}{2}$ are shifted Legendre polynomials defined on the domain $-\nu \le s\le 0$. Substitute (90) into (86), (91) into (87). Premultiplying each equation with ${\varphi }_1\left(s\right)$ and then by ${\varphi }_2\left(s\right)$ and integrating over the domain $-\nu \le s\le 0$ each time, we obtain

$${\dot{\eta }}_1=\frac{2}{\nu }{\eta }_2,\text{ and }{\dot{\eta }}_2=\frac{6}{\nu }{\eta }_3.$$ (92)

$${\dot{\eta }}_4=\frac{2}{\nu }{\eta }_5,\text{ and }{\dot{\eta }}_5=\frac{6}{\nu }{\eta }_6.$$ (93)

The inner products with ${\varphi }_3\left(s\right)$ are not taken. Instead, we substitute (90), (91) in the boundary conditions (88), (89). There, we have $y_1(0,t)={\eta }_1+{\eta }_2+{\eta }_3$  , $y_2(0,t)={\eta }_4+{\eta }_5+{\eta }_6$  , $y_1(-1,t)={\eta }_1+{\varphi }_2(-1){\eta }_2+{\varphi }_3(-1){\eta }_3$  , $y_1(-\nu ,t)={\eta }_1-{\eta }_2+{\eta }_3$  , $y_2(-1,t)={\eta }_4+{\varphi }_2(-1){\eta }_5+{\varphi }_3(-1){\eta }_6$  , and $y_2(-\nu ,t)={\eta }_4-{\eta }_5+{\eta }_6$. Eqs. (88), (89) become

$${\dot{\eta }}_1+{\dot{\eta }}_2+{\dot{\eta }}_3=-\beta \left(t\right)\left({\eta }_1+{\eta }_2+{\eta }_3\right)\left({\eta }_4+{\eta }_5+{\eta }_6\right),$$ (94)

$${\dot{\eta }}_4+{\dot{\eta }}_5+{\dot{\eta }}_6=\beta (t-1)\left({\eta }_1+{\alpha }_2{\eta }_2+{\alpha }_3{\eta }_3\right)\left({\eta }_4+{\alpha }_2{\eta }_5+{\alpha }_3{\eta }_6\right)-\overline{p}\beta (t-\nu )\left({\eta }_1-{\eta }_2+{\eta }_3\right)\left({\eta }_4-{\eta }_5+{\eta }_6\right)-\gamma \left({\eta }_4+{\eta }_5+{\eta }_6\right),$$ (95)

giving us six ODEs for the six states, equivalent to Eqs. (72)–(77). The initial conditions for our ODEs can be obtained from history functions as ${\eta }_k\left(0\right)=\frac{2k-1}{\nu }{\int }_{-\nu }^0{U}_1\left(s\right){\varphi }_k\left(s\right)ds,k=1,2,3$ and ${\eta }_r\left(0\right)=\frac{2(r-3)-1}{\nu }{\int }_{-\nu }^0{U}_2\left(s\right){\varphi }_{r-3}\left(s\right)ds,r=4,5,6$.