A water balance based, spatiotemporal evaluation of terrestrial evapotranspiration products across the contiguous United States

Abstract

Accurate gridded estimates of evapotranspiration (ET) are essential to the analysis of terrestrial water budgets. In this study, ET estimates from three gridded energy-balance based products (ET_EB) with independent model formations and data forcings are evaluated for their ability to capture long term climatology and inter-annual variability in ET derived from a terrestrial water budget (ET_WB) for 671 gaged basins across the CONUS. All three ET_EB products have low spatial bias and accurately capture inter-annual variability of ET_WB in the central US, where ET_EB and ancillary estimates of change in total surface water storage (ΔTWS) from the GRACE satellite project appear to close terrestrial water budgets. In humid regions, ET_EB products exhibit higher long-term bias, and the covariability of ET_EB and ET_WB decreases significantly. Several factors related to either failure of ET_WB, such as errors in ΔTWS and precipitation, or failure of ET_EB, such as treatment of snowfall and horizontal heat advection, explain some of these discrepancies. These results mirror and build on conclusions from other studies: on inter-annual timescales, ΔTWS and error in precipitation estimates are non-negligible uncertainties in ET estimates based on a terrestrial water budget, and this confounds their comparison to energy balance ET models. However, there is also evidence that in at least some regions, climate and landscape features may also influence the accuracy and long-term bias of ET estimates from energy balance models, and these potential errors should be considered when using these gridded products in hydrologic applications.

1. INTRODUCTION

After precipitation, evapotranspiration (ET) is the largest term in the terrestrial surface hydrologic budget (Haddeland et al. 2011). Virtually all water taken up by vegetation is evapotranspired, and as the largest anthropogenic use of surface and groundwater is the irrigation of cropland (Shiklomanov 2000, Döll et al., 2012), characterization of ET has important implications for managing human water consumption. The importance of ET for surface hydrologic budgets and agricultural water use motivates the need for continuous observation-based data sources that can characterize the spatial and temporal variability of ET at a level of detail that can help resolve key aspects of the terrestrial hydrologic cycle.

Surface energy budget based models of ET have substantially enhanced the availability of spatially and temporally continuous ET estimates. Remotely sensed data have also been integrated into surface energy models (Kalma et al. 2008, Li et al. 2009, Glenn et al. 2011), including land surface models (LSMs, Lo et al. 2015), to further increase the accuracy of energy budget based ET estimates. Several methods for integrating remotely sensed observations into energy budget based ET estimates are available, ranging from using remotely sensed data to increase resolution of vegetation parameters in surface energy models (Mu et al., 2011) to utilization of direct measurements of surface energy fluxes (Kustas et al., 2011).

Regardless of whether remotely sensed data are used, most gridded ET products derived from surface energy budget models (hereafter referred to as ET_EB products) still require ancillary data on surface meteorological conditions, including but not limited to incident and reflected short wave radiation, near-surface air temperature, vapor pressure, and wind speed (Kalma et al. 2008, Glenn et al. 2011). Because of differences in modeling approaches with regards to remotely sensed and meteorological data inputs, different ET_EB products show unique patterns of space-time bias which are related to propagation of errors in forcing data (Ferguson et al. 2010, Vinukollu et al. 2011, Cai et al. 2014), conditions under which models are not well calibrated (Hain et al. 2015, Ferguson et al. 2010, French et al. 2005, Jiménez et al. 2011, Velpuri et al. 2013, Vinukollu et al. 2011), and to climatic conditions where model assumptions fail (Anderson et al. 2012, Choi et al. 2009, Kustas et al. 2012).

Because of a lack of spatially continuous ground-based measurements of ET, ET_EB products are difficult to validate at large spatial scales. One of the most common approaches to validate ET_EB estimates is to evaluate their consistency with empirical estimates of ET based on a terrestrial water budget (ET_WB), calculated for individual basins as:

$$\text{ET}=\text{P}+\text{G}-\text{Q}-\mathrm{\Delta }\text{TWS}$$ Eq. 1.1

where ET (mm) is the mean basin ET, P (mm) is mean basin precipitation, G (mm) accounts for net inter-basin groundwater flux, Q (mm) is basin runoff (normalized by drainage area), and ΔTWS (mm) is the change in basin total water storage between the current and previous time step (where total water storage is the total water stored in soil, surface water, groundwater, and vegetation). Inter-basin groundwater flux is often assumed to be zero, especially in basins with limited anthropogenic withdrawals. In gaged basins, Q is known with high accuracy. If estimates of basin P are also available, then a water-budget based estimate of ET (ET_WB) can be developed by assuming ΔTWS is zero:

$${\text{ET}}_{\text{WB}}=\text{P}-\text{Q}$$ Eq. 1.2

The approximation in Eq. 1.2 has conventionally been accepted if all terms are evaluated over a sufficiently long time period (annual or longer) to support the assumption that ΔTWS=0 (Twine et al. 2004).

There has been consensus that ET_EB products fail to close long-term (Sheffield et al. 2009, Gao et al. 2009) and inter-annual (Zhang et al. 2012, Zeng et al. 2014, Velpurri et al. 2013, Han et al. 2015, Liu et al. 2016) terrestrial water budgets (i.e., ET_EB ≠ ET_WB in many regions in the contiguous U.S. (CONUS). Long-term non-closure errors ($\overline{{\mathrm{\epsilon }}_{\text{NC}}}=\overline{{\text{ET}}_{\text{EB}}}-\overline{{\text{ET}}_{\text{WB}}}$, with over-bars indicating multi-year averages) follow distinct spatial and climatic gradients, with arid regions exhibiting substantially lower long-term bias than humid regions (Sheffield et al. 2009, Gao et al. 2009). Similarly, most ET_EB estimates appear better suited to estimate both multi-year trends and inter-annual variability in arid regions than in humid regions (Zhang et al. 2012, Zeng et al. 2014, Velpurri et al. 2013). As such, interannual non-closure errors (ε_NC = ET_EB − ET_WB) exhibit similar regional patterns as long-term bias $(\overline{{\mathrm{\epsilon }}_{\text{NC}}})$.

The spatial characterization of long term and inter-annual non-closure errors provides insight into the accuracy of different ET_EB products for different regions, providing valuable guidance for how such products can be used in different hydrologic applications. Unfortunately, these error estimates are confounded by potential error embedded in ET_WB. For instance, basin-average P can exhibit long-term mean bias if estimated from a sparse gaging network, particularly in basins with stark topographic gradients (Prat et al. 2015). The inter-annual variance of basin-average P can also be biased if the variance of precipitation at the gages used to develop the basin-averaged estimate is a poor representation of the true precipitation variability across the basin. Most likely, the variance of basin-average P will be too high because variances of true areal averages should be lower than individual point estimates, but there are limited numbers of gages available to estimate the areal averages. In addition to precipitation biases, recent studies that have incorporated changes to ΔTWS derived from the Gravity Recovery and Climate Experiment (GRACE) satellites indicate that inter-annual variability in ΔTWS may be an important component of the annual terrestrial water budget in many regions (Rodell and Famiglietti 2001, Rodell et al. 2004, Sahoo et al., 2011, Zeng et al. 2012, Han et al. 2015). Therefore, non-closure errors between ET_WB and ET_EB are difficult to disentangle from uncertainty in basin P and ΔTWS. There have been attempts to disentangle these terms using sensitivity analyses to elucidate regions where ε_NC is significantly influenced by precipitation uncertainty (Ferguson et al., 2009; Sheffield et al. 2009; Gao et al., 2009; Hain et al., 2014), or GRACE Tellus based measures of ΔTWS (Sheffield et al. 2009; Gao et al., 2010), with results generally showing that precipitation uncertainty is an important component of ε_NC.

A key question underscoring these efforts is whether non-closure errors are caused by bias in the mean or variance of components used to estimate ET_WB (e.g., P, ΔTWS), or if the model formulations that underscore different ET_EB products fail to capture fundamental processes that drive ET variability. In this study, we seek to advance the evaluation of ET_EB across the CONUS, building on recent work exploring the accuracy of ET_EB estimates at different spatial and temporal scales (Zhang et al., 2012; Han et al., 2015). Han et al. (2015) explored evidence of hydrologic consistency between ET_WB and two very different ET_EB products: the NOAH land surface model (Chen et al., 1996) and the ALEXI model (Anderson et al. 1997). In that study, the authors hypothesized that inter-annual non-closure errors in NOAH ET estimates $\left({\text{ET}}_{\text{EB}}^{\text{NOAH}}\right)$ were not due to failure of the model as previously argued (Zhang et al., 2012), but rather were linked to errors in estimated values of ET_WB. They found a marked improvement in correlation between ET_WB and ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ over a 10 year period in the Mississippi River Basin, particularly in the Ohio and Upper Mississippi sub-basins, when they included GRACE Tellus ΔTWS in the ET_WB approximation in Eq. 1.1 (assuming G to equal zero). Further, they found that the inter-annual correlation between ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ and ALEXI ET estimates $\left({\text{ET}}_{\text{EB}}^{\text{ALEXI}}\right)$ was high across 15 different basins in the central U.S., although the magnitude of inter-annual variability of ET from both products was low compared to the inter-annual variability of ET_WB. They concluded that higher inter-annual variability in ET_WB over ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ and ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$ is an artifact of erroneously excluding ΔTWS from the ET_WB estimate. The results supported the argument that the NOAH land surface model could provide accurate estimates of inter-annual ET variability in humid basins, in contrast to the conclusions of Zhang et al. (2012).

The work in Han et al. (2015) showed the importance of possible errors in ET_WB when assessing ET_EB estimates. However, their conclusions were limited to the Mississippi River basin and based on 10 years of data, which limits the conclusions that can be made for ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ in humid basins across the CONUS. In addition, the study used consistency between ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ and ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$ as evidence that ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ estimates were correct, which ignores the possibility that both products could exhibit similar errors despite their different estimation approaches. We also note that comparisons between ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ and spatially interpolated ET estimates from a network of eddy covariance towers (Jung et al. 2009) in the Ohio Basin were poor (correlation coefficient of ~0.4, Han et al. 2015), somewhat countering the claim that discrepancies between ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ and ET_WB in the Ohio were due to errors in ET_WB. Finally, error in P has been shown to be a potentially large source of uncertainty in ET_WB as well as in land surface model ET (Hain et al. 2015), yet annual ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ was the only ET estimate compared directly to ET_WB. Since ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ and ET_WB used in that study had the same P forcing (from NLDAS-2), basin level correlation between these two ET estimates could have been influenced by correlated errors in P.

In this study, we revisit the results of Han et al. (2015) using an expanded analysis to address some of the limitations of the original analysis. Specifically, we consider the following additions:

1. In addition to using ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ and ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$, we include an ET product that uses a similar model formulation to NOAH, but which uses different information on local moisture anomalies and real-time remotely sensed vegetation indices from the MODIS platform to force moisture based reductions in ET (${\text{ET}}_{\text{EB}}^{\text{MOD}16}$, Mu et al. 2011).

2. We compare all 3 ET products (${\text{ET}}_{\text{EB}}^{\text{NOAH}}$, ${\text{ET}}_{\text{EB}}^{\text{MOD}16}$, ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$) directly to ET_WB, expanding the study area to include 671 basins with substantial coverage over the CONUS.

3. We examine both long-term bias between ET_WB and ET_EB and inter-annual anomalies between ET_WB and ET_EB after accounting for long-term bias. By contrasting ET_EB performance across products, comparing long term and inter-annual non-closure errors between ET_EB and ET_WB, and relating these non-closure errors to watershed characteristics, we characterize regional variability in ET_EB performance.

4. We integrate a new ΔTWS product derived from the GRACE satellite data (GRACE Mascon, Wiese 2015) to evaluate hydrologic consistency between ET_EB and ET_WB, and assess the ability to combine ET_EB with both GRACE Tellus and Mascon ΔTWS to describe the difference between precipitation and runoff across the CONUS. Regional variability in the importance of ΔTWS for annual water budgets across the CONUS is discussed.

5. To further diagnose the cause of non-closure errors, we assess regional relationships between non-closure errors and other atmospheric and meteorological proxies besides ΔTWS (e.g., precipitation, horizontal heat advection, snow cover) that could be a source of error in either ET_EB or ET_WB estimates.

2. METHODS

2.1. ET Data Overview

2.1.1. Water balance ET (ET_WB)

ET_WB. was calculated for the 671 watersheds included in the large-sample basin scale hydrometerological dataset developed by Newman et al. (2015) from the Hydro-Climatic Data Network (HCDN) 1988 dataset (marked “HCDN 2009” in the GAGES-II dataset, Falcone et al. 2010). The selection of these small to mid-sized gaged watersheds (median area 336 km²) was based on criteria for minimal human disturbance (Falcone et al. 2010) and data quality (including basin-level density of precipitation gages) and continuity. As an additional screening, we validated that basins included in the database had minimal irrigation by calculating the percent irrigated area using the MODIS Irrigated Agriculture Dataset for the United States (MIrAD, Pervez et al. 2010). The vast majority of basins had negligible irrigated area.

Annual water year (October-September) discharge for each gage was calculated between 2003–2015 and converted to annual runoff (Q, mm) by dividing by drainage area. Precipitation data were taken from the National Land Data Assimilation System 2 (NLDAS-2, Xia et al. 2012) primary forcing dataset. Basin-average P was calculated for water years 2003–2015 by averaging all NLDAS grid cells whose centers are located within the basin (Hijmans 2014). For each basin for each year, annual ET_WB was calculated using Equation 1.2, as was the 13-year mean $\left(\overline{{\text{ET}}_{\text{WB}}}\right)$. Basins with any ET_WB values less than zero were eliminated from the analysis.

2.1.2. Energy Balance Based ET Products (ET_EB)

In addition to the water budget approach, ET can be characterized using a surface energy budget as follows:

$$\text{Rn}=\text{H}+\text{LE}+\text{G}$$ Eq. 2

where Rn (net radiation, generally expressed as W m⁻²) is partitioned to sensible heat flux (H, W m⁻²), latent heat flux (LE, W m⁻²), and ground heat flux (G, W m⁻²), with the partitioning dependent on surface and atmospheric characteristics and conditions. ET_EB (mm) can then be derived from LE by dividing by the latent heat of vaporization of water.

When there is unlimited water available for evapotranspiration, the partitioning of Rn between H, G, and LE can be modeled using a variety of physically-based or empirical methods, where G is generally assumed to be constant (often zero) on a daily or greater time step, and the relative partitioning of energy to H and LE is dependent on surface meteorological conditions, including air temperature, relative humidity, wind speed, and vegetation cover.

While numerous surface energy budget based ET_EB exist (see Kalma et al. 2008 for a review), for the purposes of this study, we consider two basic classes:

1. Penman-Monteith based ET (${\text{ET}}_{\text{EB}}^{\text{NOAH}}$, ${\text{ET}}_{\text{EB}}^{\text{MOD}16}$): Potential Evapotranspiration (PET) is calculated from daily surface meteorological variables (reanalysis data) using a modified Penman-Monteith equation, with spatially variable vegetation indices used to estimate surface emissivity and resistance. PET is scaled to ET using time varying estimates of moisture availability.

   1. ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$(Chen et al., 1996): NLDAS-2 Noah LSM ET output is calculated by the National Centers for Environmental Prediction (NCEP) using North American Regional Reanalysis (NARR) surface meteorological data fields, with NARR downward shortwave radiation bias-corrected to the University of Maryland Surface Radiation Budget (SRB) (Pinker et al. 2003), which uses data from the GOES-8 satellite. Resistance terms are applied to Penman-based PET for four separate terrestrial surface types (canopy transpiration, canopy evaporation of intercepted precipitation, soil evaporation, sublimation). Resistance terms are modified by the underlying soil moisture, which is forced by NLDAS-2 P (Xia et al. 2012, Xia et al. 2015, Peters-Lidard et al. 2011).
   2. ${\text{ET}}_{\text{EB}}^{\text{MOD}16}$(Mu et al. 2011): The ${\text{ET}}_{\text{EB}}^{\text{MOD}16}$ product developed by the University of Montana uses Global Modeling and Assimilation Office (GMAO) Modern-Era Retrospective analysis for Research and Applications (MERRA, Rienecker et al., 2011) data, in conjunction with 8-day data inputs from the MODIS platform of the AVHRR satellite (leaf area index, enhanced vegetation index, and albedo) to calculate PET. As vegetation growth is primarily limited by water availability, real-time updates of local vegetation conditions from MODIS data are used to capture water limited ET (Cleugh et al. 2007). Mu et al. (2007) updated this algorithm to scale evaporation by relative humidity and scale transpiration by vapor pressure deficit, used as a proxy indicator of soil moisture limitations

2. Remotely-sensed thermal infra-red ET (${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$, Anderson et al. 1997, Kustas et al., 2011): H is calculated from a time-differential linear model of atmospheric boundary layer (ABL) development which is forced with two measurements of radiometric surface temperature taken in the morning from GOES satellites, an initial estimate of ABL height from early morning sounding data, and wind speed to give an estimate of instantaneous H flux at 1.5 hour prior to solar noon. Instantaneous LE is then calculated using Equation 2, and is converted to daily cumulative LE using ancillary estimates of daily cumulative insolation assuming a diurnally constant value of (LE/Sdn), where Sdn is instantaneous solar radiation.

2.2. Long-term Non-Closure Error

To examine long-term non-closure errors, the period of record bias was calculated as:

$$\overline{{\mathrm{\epsilon }}_{\text{NC}}}=\overline{{\text{ET}}_{\text{EB}}}-\overline{{\text{ET}}_{\text{WB}}}$$ Eq.3

where the overbar indicates the 2003–2015 mean, and ET_EB is based on either NOAH, MOD16, or ALEXI estimates. We first evaluate and compare the distribution and spatial patterns of $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ across the three energy-balance models.

We then calculate the rank correlation between $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ and a variety of watershed characteristics to determine the potential drivers of long-term bias. The majority of these watershed characteristics were extracted from the Geospatial Attributes of Gages for Evaluating Streamflow, version II (GAGES II) database (Falcone et al 2010), with several exceptions. For example, percent (%) irrigated area in each basin, a potential source of anthropogenic decoupling of true ET from ET_WB, was taken as the basin mean value for the MIrAD-US dataset (Pervez and Brown 2010). Mean horizontal heat advection ($\overline{{\text{H}}_{HORIZ}}$, a possible error source in ET_EB) was calculated as the basin mean of the square root of the sum of squared northward and eastward components of vertically integrated sensible heat flux for June, July, and August (JJA) for the years 2003–2015 from the ERA-Interim reanalysis product (Dee et al., 2011). For potential long-term water balance errors, mean ΔTWS for each basin was calculated using the method in Landerer and Swenson (2012) from 2003–2015 for the GRACE Tellus (Swenson, 2012) and the newer GRACE Mascon (Save et al. 2016) data products (see Supplemental Text 1 for more detail). Since both ${\text{ET}}_{\text{EB}}^{\text{MOD}16}$ and ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$ depend on remotely sensed data that may not be available on certain days (e.g., because of cloud cover), estimates depend on gap-filling procedures that could degrade their accuracy. Therefore, we used the average percent of pixel-days with missing values per basin per year (mean % NA pixel-days) from the direct retrievals from GOES thermal imagery in the ALEXI product as a proxy for obstructive cloud cover.

Finally, to ensure that the results are not sensitive to the NLDAS-2 precipitation product used in the calculation of $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$, we reevaluate the distribution of $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ with $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ calculated from several different precipitation datasets (see Supplemental Text 2).

2.3. Inter-annual Non-Closure Error

Inter-annual non-closure errors can arise from a variety of error sources in ET_EB or ET_WB. In the case that these errors are caused by bias in the mean or variance of ET_EB or ET_WB, it may still be possible to show hydrologic consistency in the direction of inter-annual change between ET_EB and ET_WB if the data are first mean adjusted and scaled. Therefore, we center both variables to remove long-term mean biases (with prime indicating annual departure from the mean, ${\text{ET}}^{\prime }=\text{ET}-\overline{\text{ET}}$), and also produce a scaled version of these data by dividing by the standard deviation (denoted $s{\text{ET}}^{\prime }=\frac{(\text{ET}-\overline{\text{ET}})}{sd(\text{ET})}$). We then use geographically weighted regression (GWR) to explore how the relationship between ET_WB and ET_EB varies across space. GWR is a localized regression method that uses a kernel function and spatial bandwidth to pool data at nearby sites in the estimation of a regression linking response and predictor variables (Brunsdon et al. 1998). The resulting regression exhibits smooth variations in the coefficient estimates at different sites across space. GWR provides a compromise between calculating a single regression coefficient on the global dataset, which would eliminate spatial variability in the process, or calculating individual regression estimates for each point in the study area, which could result in unstable coefficient estimates with high standard errors due to low sample size. In this analysis, GWR models were built to explore the spatial variability in how well ${\text{ET}}_{\text{EB}}^{\prime }$ tracks inter-annual variability in ${\text{ET}}_{\text{WB}}^{\prime }$.

For each ET_EB product, two GWR models were built:

$${\mathrm{sET}}_{{\text{EB}}^{\text{,i,t}}}^{\prime }={\mathrm{\beta }}_{\text{i}}{\text{sET}}_{{\text{WB}}^{\text{,i,t}}}^{\prime }+{\mathrm{\epsilon }}_{\text{i},\text{t}}$$ (Eq. 3.1)

$${\text{ET}}_{{\text{EB}}^{\text{,i,t}}}^{\prime }={\mathrm{\beta }}_{\text{i}}{\text{ET}}_{{\text{WB}}^{\text{,i,t}}}^{\prime }+{\mathrm{\epsilon }}_{\text{i},\text{t}}$$ (Eq. 3.2)

where t indicates the year and i indicates the i^th basin. β_i is allowed to smoothly vary across the CONUS by pooling nearby basins using a Gaussian kernel function with optimal bandwidth selected via cross validation (Bivand and Yu, 2017). The first model (Eq. 3.1) explores whether ${\text{sET}}_{\text{EB}}^{\prime }$ exhibits hydrologic consistency with ${\text{sET}}_{\text{WB}}^{\prime }$ after accounting for the potential of both mean and variance biases in all water and energy balance terms The second model (Eq. 3.2) explores the ability of ${\text{ET}}_{\text{EB}}^{\prime }$ to close inter-annual terrestrial water budgets in an absolute sense (less any mean biases in either ET_EB or ET_WB). In particular, β_𝑖 from Eq. 3.2 not only reflects the strength of the relationship between ${\text{ET}}_{\text{EB}}^{\prime }$ and ${\text{ET}}_{\text{WB}}^{\prime }$, but also the difference in magnitude of inter-annual fluctuations between energy-balance and water-balance ET (i.e., variance bias).

To better understand the distribution of errors exhibited by the GWR, we also examine the distribution of scaled, inter-annual non-closure errors, calculated as the difference between the scaled, annual anomalies:

$${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\text{NC}}=s{\text{ET}}_{EB}^{\prime }-s{\text{ET}}_{WB}^{\prime }$$ (Eq. 4)

For a particular region, any clustering in _sε_NC in certain years and not others would suggest that characteristics of specific climate events contribute substantially to discrepancies between $s{\text{ET}}_{EB}^{\prime }$ and $s{\text{ET}}_{WB}^{\prime }$. These discrepancies could arise from errors in both energy-balance and water-balance based models. Likely sources of error in annual estimates of ET_WB include errors in estimates of basin P or violations in the assumption that changes in basin surface water storage (ΔTWS) are negligible on an annual time-step. Energy balance models were not originally designed to operate at the continental scale, where horizontal fluxes of energy can lead to violations of the assumption of daily local conservation of energy (Trenberth et al. 2009). In addition, these models have parameterizations of sublimation that have been previously questioned (Wang et al. 2015). Therefore, we explore clustering in _sε_NC by product and year, and then correlate _sε_NC to several variables on an annual scale, including basin-average P, ΔTWS for both GRACE Tellus (ΔTWS_T) and GRACE Mason (ΔTWS_M) data products, % of precipitation as snow from the ERA-Interim monthly data, and JJA horizontally advected sensible heat flux (H_HORIZ).

3.1. Long-term non-closure error

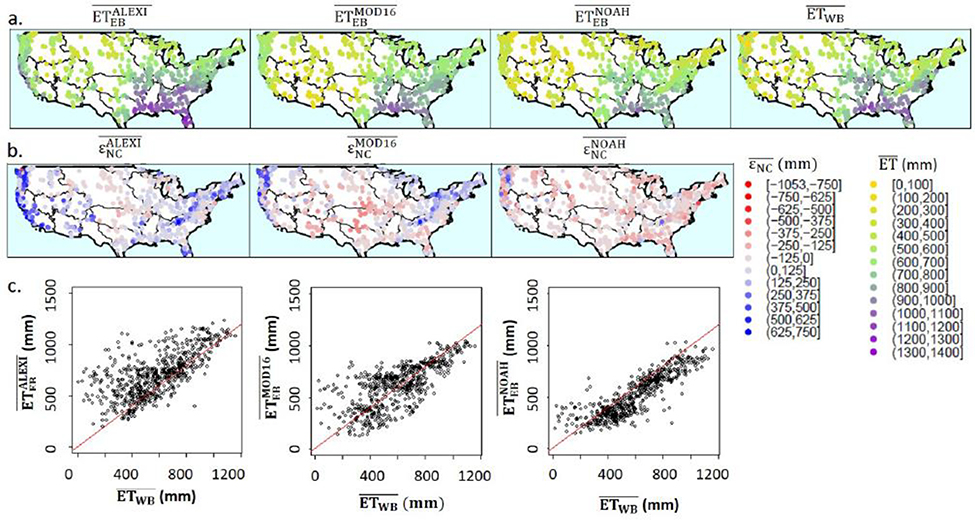
The mean annual estimates for all water and energy balance models ($\overline{{\mathrm{ET}}_{\mathrm{WB}}}$, $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$, $\overline{{\text{ET}}_{\text{EB}}^{\text{NOAH}}}$, and $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$) show similar spatial patterns, with the highest and lowest mean annual ET estimates seen in the Southeast and Southwest and western continental interior, respectively (Figure 1a). However, ET_EB models exhibit several areas of disagreement in estimates of long-term mean annual ET with respect to ET_WB, as well as with each other (Figure 1b). For example, in basins to the west of the Rockies along the California coast, $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ predicts higher ET values compared to $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ and $\overline{{\text{ET}}_{\text{EB}}^{\text{NOAH}}}$, which are similar to those seen in the ET_WB model. Over the entire CONUS, $\overline{{\text{ET}}_{\text{EB}}^{\text{NOAH}}}$ tends to predict lower annual ET compared to the other three models. $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ and $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ tend to be higher than $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ in the Pacific Northwest and in basins along the Appalachian Mountain Chain, while $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ is higher than all other ET estimates along the Gulf Coast and through Florida, and $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ is lower than all other models in the central U.S. The range (maximum-minimum) of ET estimates across the CONUS is smaller for $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ (924 mm) and $\overline{{\text{ET}}_{\text{EB}}^{\text{NOAH}}}$ (881mm) compared to $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ (1060 mm), which is more similar to that of $\overline{{\text{ET}}_{\text{WB}}}$ (1136 mm). In general, spatial consistency between the long-term means established by the four ET models appears to be lowest in the eastern third of the country and along the western coastline.

Figure 1:

a: Spatial distribution of long-term mean annual ET from terrestrial water balance and energy balance models. Color scale is in units of mm/year. Each point represents a streamflow gaging station. b: $\overline{{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{NOAH}}}$, $\overline{{\mathrm{\epsilon }}_{\mathrm{NC}}^{\text{MOD}16}}$, and $\overline{{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{ALEXI}}}$ in mm/year, where positive $\overline{{\mathrm{\epsilon }}_{\mathrm{NC}}}$ (blue) indicates that $\overline{\mathrm{E}{\mathrm{T}}_{\mathrm{EB}}}$ overpredicts relative to $\overline{\mathrm{E}{\mathrm{T}}_{\mathrm{WB}}}$. c: Scatterplot of $\overline{\mathrm{E}{\mathrm{T}}_{\mathrm{EB}}}$ versus $\overline{\mathrm{E}{\mathrm{T}}_{\mathrm{WB}}}$ with 1-to-1 line shown. Regular and square brackets represent inclusive and exclusive bounds of the interval, respectively.

When analyzing Figure 1, we note that errors in long-term basin-average P (and thus $\overline{{\text{ET}}_{\text{WB}}}$) are expected for any particular basin, for example due to gage location within basin topography. It is less likely, however, that long-term error in orographically-adjusted basin-averaged P would be biased in the same direction across the 671 basins, although this possibility cannot be precluded due to documented undercatch of gage precipitation linked to surface winds (Adam and Lettenmaier 2003, Yang et al. 2005) and/or potential systematic errors in data processing. However, the latter issue can be controlled for through the comparison of multiple products in the calculation of $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$. Further, if the mean of the distribution of $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ is significantly above zero for some ET_EB products and below zero for others, we argue that one or more of these ET_EB products are systematically biased compared to the true (and unknown) long-term ET.

In this context, we examine the distribution of $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ for each of the three energy balance models in Figure 1c. The mean of $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ is relatively unbiased relative to $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$, with a mean bias of about 4% above $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$. The mean ALEXI-based ET estimates are approximately 120 mm/year higher than mean $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ on average, suggesting that $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ has a positive mean bias of 21% across CONUS. However the majority of the basins with the highest values of $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{ALEXI}}}$ are in mountainous regions (i.e. along the Cascades, Sierra Nevada, Rockies, and Appalachian Mountains), where topographic (slope and aspect) effects on the assumed net radiation (Rn in Eq. 2) will impact the information content of remotely sensed data inputs. Removing basins with average slopes above 15% from the analysis (Supplemental Figure S1) reduces the positive mean bias of $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ to approximately 49 mm/year (or 9%) above mean $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$.

While the ALEXI and MOD16 products produce slightly higher long-term ET estimates on average than the water balance based estimate, which is potentially consistent with undercatch in the NLDAS-2 precipitation product, the mean $\overline{{\text{ET}}_{\text{EB}}^{\text{NOAH}}}$ is about 80 mm/year lower than mean $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ on average (negative mean bias of about 13%). Importantly, since both $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ and $\overline{{\text{ET}}_{\text{EB}}^{\text{NOAH}}}$ are based on the same NLDAS-2 precipitation dataset, it is unlikely that this discrepancy is linked to systematic bias in the precipitation field. Further, the results are very similar if the scatterplots in Figure 1c are replicated for $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ calculated with three additional gridded precipitation products (Supplemental Text 2, Figure S2). A notable exception occurs when using the less accurate NLDAS-2 secondary precipitation forcing, which is based on the NARR reanalysis and is thus likely to be less accurate than gaged data. In this case, the NOAH model exhibits the least long-term bias compared to ET_WB. Assuming that any systematic, long-term bias in $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ across the majority of basins would be a downward bias associated with undercatch, the results in Figure 1 indicate that ALEXI and MOD16 models are more likely to be relatively unbiased with respect to the true, long-term ET across the CONUS, particularly in regions of mild terrain. Under this same assumption, Figure 1 also suggests that there may be moderate negative biases in the mean long-term annual ET estimated by the NOAH model.

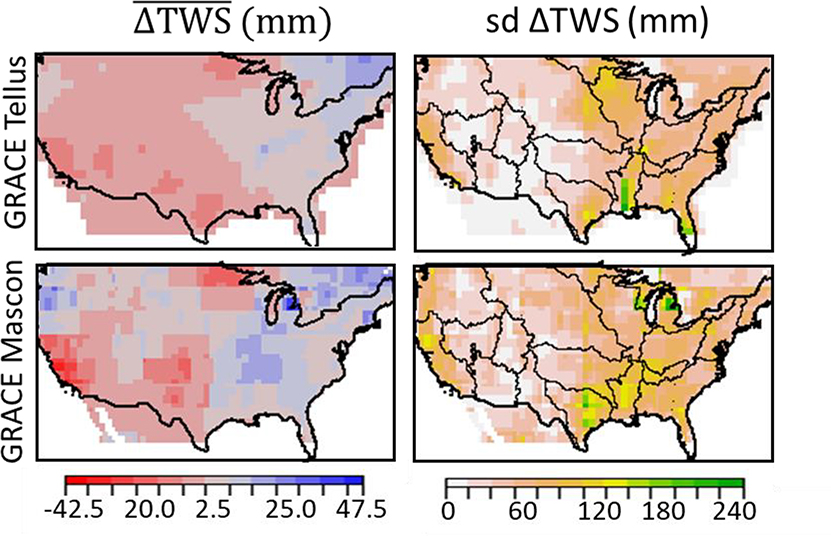
The assessment above does not consider ΔTWS as a potential source of error in ET_WB but this error should be minimized in the long-term average $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ because it is unlikely that there would be large changes in basin storage in basins with relatively little anthropogenic influences over a decadal period (i.e., $\overline{\mathrm{\Delta }\text{TWS}}$ should be near zero). To validate this assumption, 2003–2015 $\overline{\mathrm{\Delta }\text{TWS}}$ was calculated using the GRACE Tellus $\left({\overline{\mathrm{\Delta }\text{TWS}}}_{\text{T}}\right)$ and GRACE Mascon $\left({\overline{\mathrm{\Delta }\text{TWS}}}_{\text{M}}\right)$ products (Figure 2, left column). We found that for most regions in the CONUS, $\overline{\mathrm{\Delta }\text{TWS}}$ was very close to zero, with an interquartile range across basins of −1.5 – 6.4 mm for ${\overline{\mathrm{\Delta }\text{TWS}}}_{\text{T}}$ and 0.1–11.8 mm for ${\overline{\mathrm{\Delta }\text{TWS}}}_{\text{M}}$. It should be noted, however, that the standard deviations of $\overline{\mathrm{\Delta }\text{TWS}}$ (Figure 2, right column) suggests that inter-annual variability in ΔTWS may be important in some regions, and estimates are higher for ${\overline{\mathrm{\Delta }\text{TWS}}}_{\text{M}}$ than for ${\overline{\mathrm{\Delta }\text{TWS}}}_{\text{T}}$. ${\overline{\mathrm{\Delta }\text{TWS}}}_{\text{M}}$ indicates that the highly irrigated regions of southern California and near the Ogallala Aquifer are losing between approximately 20–30mm of TWS per water year, and that TWS in the Midwest may be increasing by about 10–20 mm per year. However, large $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ values for all of the energy balance products are found in regions where the absolute magnitudes of $\overline{\mathrm{\Delta }\text{TWS}}$ are negligible, and even in regions with high-magnitude $\overline{\mathrm{\Delta }\text{TWS}}$, these values are still several times smaller than $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ (Figure S3). Further, changes in basin storage linked to irrigated water withdrawn from hydraulically disconnected groundwater sources (e.g., Ogallala Aquifer) should not substantially affect the ET in relatively natural basins without much irrigation. Therefore, it does not seem likely that $\overline{\mathrm{\Delta }\text{TWS}}$ plays a large role in the long-term biases between ET_WB and ET_EB estimates.

Figure 2:

Left column: 2003–2015 mean Δ𝑇WS (in mm) calculated using GRACE Tellus (top) and GRACE Mascon (bottom) data products. Non-zero values indicate long term change in Sep-Oct annual water storage, with positive (blue) values indicating net gain in ΔTWS and negative (red) values indicating net loss in $\overline{\mathrm{\Delta TWS}}$. Right column: standard deviation of 2003–2015 ΔTWS (in mm) calculated using GRACE Tellus (top) and GRACE Mason (bottom) data products.

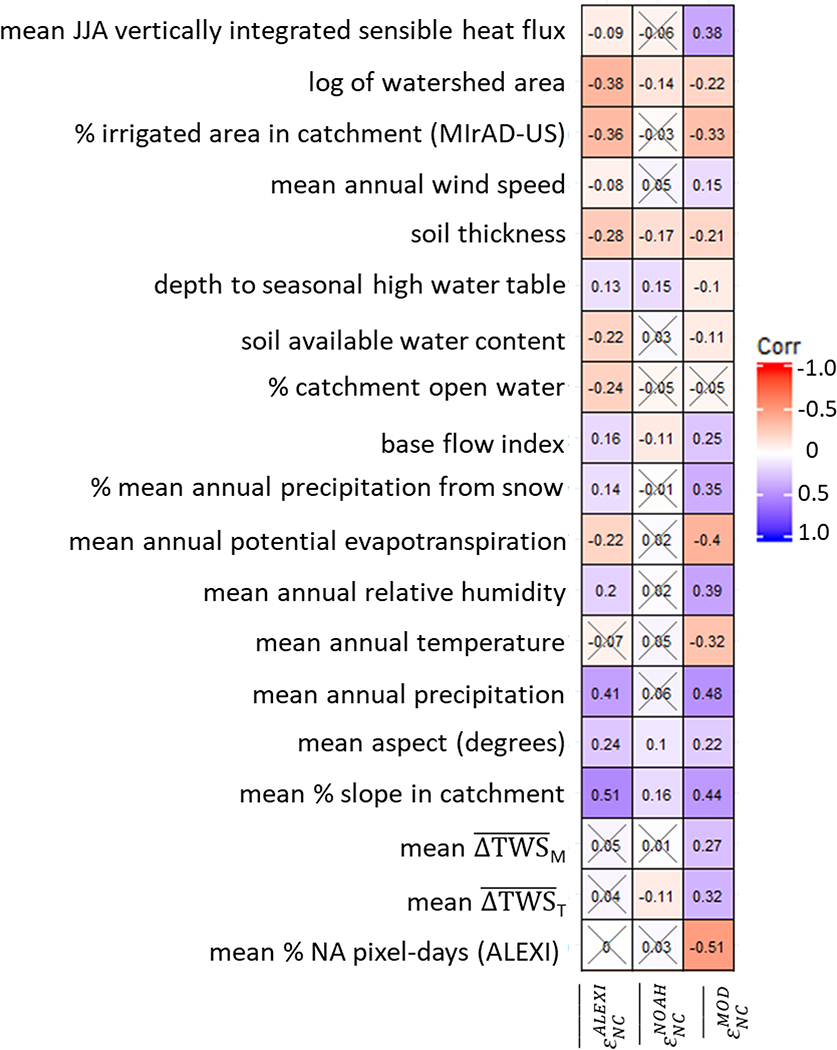
To identify regional characteristics that could explain long-term non-closure error $(\overline{{\mathrm{\epsilon }}_{\text{NC}}})$, we evaluated the Spearman correlation between $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ and physical and meteorological characteristics associated with each watershed (Figure 3). We note that absolute correlation coefficients above 0.08 are statistically significant (α = 0.05) in a sample of 671 basins, but we focus on stronger relationships with absolute correlation coefficients above 0.4–0.6 that indicate potentially more important relationships between watershed characteristics and $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$. Since many watershed characteristics are collinear, we interpret large correlations between $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ and these characteristics as indicative of a strong association, but not necessarily a causal relationship.

Figure 3:

Spearman’s correlation coefficient between $\overline{{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{ALEXI}}}$ (left column), $\overline{{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{NOAH}}}$(center column) and $\overline{{\mathrm{\epsilon }}_{\mathrm{NC}}^{\text{MOD}16}}$ (right column) and watershed characteristics. Color scale represents strength of negative (red) or positive (blue) correlation between non-closure error and watershed characteristic. Correlation coefficients which were not significant at α =0.05 are indicated with an X.

One of the most notable results of the correlation analysis is that $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{ALEXI}}}$ and $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{MOD}16}}$ are strongly and positively correlated with mean annual P. In contrast, $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{NOAH}}}$, which is forced with the same NLDAS-2 P used to calculate $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$, shows no significant correlation with mean annual P. This result suggests that long-term bias in NLDAS-2 P (and thus $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$) for each basin may be a leading driver of long-term non-closure error for the ALEXI and MOD16 models, but not for the NOAH model because it is based on the same precipitation dataset. This conclusion is consistent with the smaller variance in the scatter of Figure 1c for the NOAH model compared to the ALEXI and MOD16 models.

Another notable result is that both $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{ALEXI}}}$ and $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{MOD}16}}$ show significant positive correlation with increasing mean percent slope in the basin, a result that may indicate degradation of remotely sensed information in basins with complex terrain (also see Figure S1). Alternatively, correlation between $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{ALEXI}}}$ and $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{MOD}16}}$ and % SLOPE may be further evidence that NLDAS-2 P, and therefore $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$, are negatively biased in regions with complex terrain. Though cloud cover has been associated with degraded performance of $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ at shorter time scales, mean % NA pixel-days over each basin was not significantly correlated to $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{ALEXI}}}$, suggesting that cloudiness does not contribute to long-term model bias. However, $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{MOD}16}}$ was significantly and negatively correlated to mean % NA pixel-days, suggesting that $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ may be more likely to underestimate ET in cloudier basins. This discrepancy may be explained by the different ways that the ALEXI and MOD16 models gap-fill remotely sensed data.

Many of the remaining correlation coefficients are small, suggesting these relationships have little biophysical importance, though some are interesting to observe in the context of contrasting model formulation. For example, mean JJA horizontal heat advection $\left(\overline{{\text{H}}_{\text{HORIZ}}}\right)$ showed significant correlation with $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{MOD}16}}$, but not $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{ALEXI}}}$. This is interesting, as an increase in $\overline{{\text{H}}_{\text{HORIZ}}}$ (i.e., large-scale heat advection) would be associated with an increase in estimation of LE and ET in the MOD16 model, whereas increasing $\overline{{\text{H}}_{\text{HORIZ}}}$ would be associated with a direct decrease in estimates of LE and ET (and an increase in estimates of H) in the ALEXI model.. Also, weak correlations between $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ and $\overline{\mathrm{\Delta }{\text{TWS}}_{\text{M}}}$ and $\overline{\mathrm{\Delta }{\text{TWS}}_{\text{T}}}$, particularly for $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{ALEXI}}}$ and $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\mathrm{NOAH}}}$, further suggest that changes in basin storage are not driving discrepancies between water-budget and energy-budget based estimates of average annual ET (also see Figure S3)

3.2. Inter-annual non-closure error

We first evaluate the relationship between annual ET_EB and ET_WB estimates for water years 2003–2015 over the CONUS using GWRs. By contrasting the β estimates for NOAH, ALEXI, and MOD16 products and looking for regional coherence and discordance in these estimates, we hope to elucidate regions where hydrologic inconsistency is caused by annual errors in either ET_EB or ET_WB. In particular, hydrologic consistency between ET_WB and ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ would be expected to be higher than hydrologic consistency between ET_WB and both ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$ or ${\text{ET}}_{\text{EB}}^{\text{MOD}16}$ in basins where annual error in basin-level estimates from NLDAS-2 P were of sufficient magnitude to lead to correlated errors in ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ and ET_WB estimates.

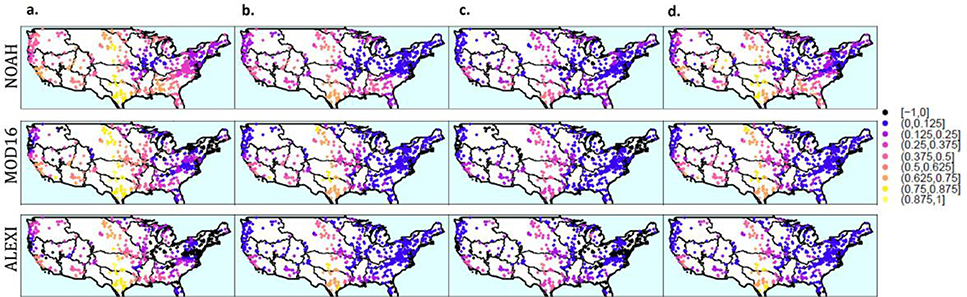
Figure 4 shows the spatial distribution of β (4a) and R² (4b) for the GWR on scaled data (i.e., ${\text{sET}}_{\text{WB}}^{\prime }$ against ${\text{sET}}_{\text{EB}}^{\prime }$, Equation 3.1). These spatial patterns are validated with location-specific regressions and Pearson correlation coefficients (see Supplemental Figure S4) to ensure that results are not an artifact of the spatial bandwidth chosen in the GWR models (Wheeler and Tiefelsdorf, 2005). Several patterns emerge when looking at the spatial distributions in Figure 4 a,b. First, the eastern portions of the Missouri, Arkansas White-Red, and Texas-Gulf River basins have β values that approach one, suggesting that for all three products, ET_WB and ET_EB track each other very closely. For all three models, β values are also moderately high for basins in the Lower Mississippi River, Lower Colorado, and the southern part of the California basin. However, in all other regions of the CONUS, the variability in ET_EB relative to ET_WB diverges, and this divergence varies by energy balance model. For all ET_EB estimates, β values are lower in the east than in the continental interior and southwest coast. In addition, β and R² values are higher for ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$ than for ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$ and ${\text{ET}}_{\text{EB}}^{\text{MOD}16}$ in the Pacific Northwest and across most regions east of the Mississippi. For instance, where β values are below 0.1 for ${\text{ET}}_{\text{EB}}^{\text{MOD}16}$ and ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$ for several basins in the New England and Mid-Atlantic regions (suggesting no hydrologic consistency), they range between 0.1 and 0.4 for ${\text{ET}}_{\text{EB}}^{\text{NOAH}}$. This suggests that in these regions, inter-annual errors in NLDAS-based basin P likely play a role in the variability of non-closure errors. Still, the β (R²) values for the NOAH model are consistently below 0.5 (0.25) for many eastern regions of the CONUS, indicating that there are other drivers of non-closure error besides errors in P.

Figure 4:

a: Geographically weighted β estimates and b: local R² for centered and scaled data (Eqn. 3.1), where each dot represents a basin. c: Geographically weighted β estimates and d: local R² for unscaled data (Eqn. 3.2). Outlines represent USGS HUC02 Hydrologic regions across CONUS.

We also explore how the variance differs between ET_EB and ET_WB. Pooling data from all gages across the CONUS, the inter-annual variance of ET_WB is (17167.8), which is much larger than that for MOD16 (1344.1), NOAH (1890.9), and to a lesser extent, ALEXI (2751.6). The catchment level standard deviations of all ET estimates, as well as the ratios of variances between ET_EB and ET_WB for each basin are shown in Supplemental Figure S5. This variance bias is also reflected in Figure 4c and d, which shows the β and R² values for the GWR on unscaled data (Eq 3.2). These β values are substantially lower than those for the scaled data (Figure 4a), highlighting the large variance biases between ET_WB and ET_EB. Figure 4 and Figure S5 show that, in regions where hydrologic consistency between ${\text{sET}}_{\text{WB}}^{\prime }$ and ${\text{sET}}_{\text{EB}}^{\prime }$ is highest (see Figure 4a), the variance of ET_EB is about a quarter of that for ET_WB, regardless of energy balance model. In regions where hydrologic consistency is moderate or low, the variance of ET_EB is almost two orders of magnitude less than that of ET_WB. This suggests that there is significant variance bias in either or both of the energy and water balance based estimates. We speculate that for the water balance model, this may be related to inflated variance in basin-averaged estimates of annual precipitation.

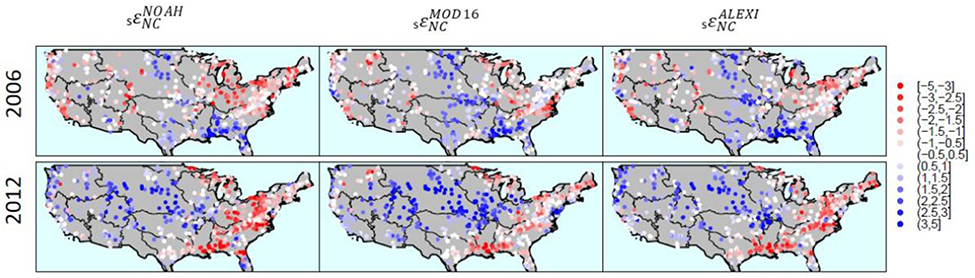
Figure 4 and the comparison of β and R² values between the energy balance models indicate that annual errors in basin P have a large role in non-closure errors, but other factors are also likely important. To explore this further, we first examine the distribution _sε_NC in individual years to determine if there are spatial patterns in the error term. Any clustering in _sε_NC in certain regions and years would suggest that characteristics of specific climate events contribute substantially to discrepancies between sET’_EB and sET’_WB. Figure 5 shows the values of _sε_NC for 2 years with large-magnitude errors (2006 and 2012), with all years shown in Figure S6. Clustering in _sε_NC is clearly apparent. For instance, in 2012, all three sET’_EB estimates were well above sET’_WB in the Northeast region, whereas in 2006 the opposite trend occurs. Further, in 2006, the errors are of much higher magnitude for MOD16 than the other products. Clustering of higher magnitude annual _sε_NC appears to be strongest in regions where hydrologic consistency between ET_EB and ET_WB is lowest (Figure 4).

Figure 5:

2006 and 2012 spatial patterns in ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{NOAH}}$ (left), ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\text{MOD}16}$(middle), and ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{ALEXI}}$ (right).

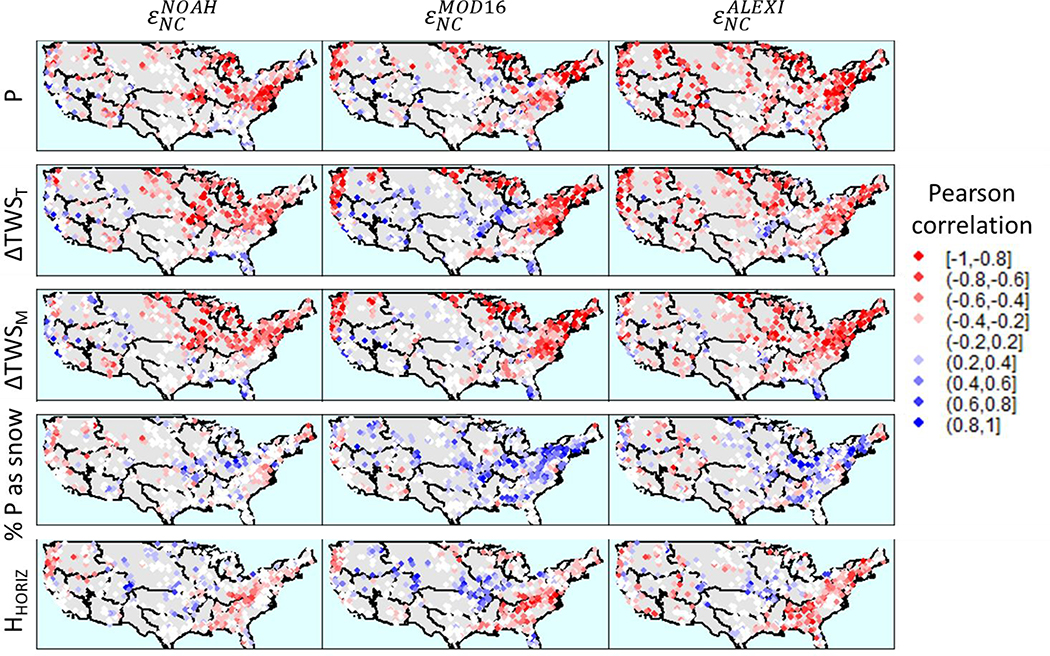
To further diagnose this clustering and the cause of inconsistencies (i.e., low β and R² values and low variance ratios) revealed in the regressions above, scaled, non-closure errors (_sε_NC) are related to a series of atmospheric and meteorological proxies that could represent the cause of errors in ET_WB or ET_EB estimates. The first row of Figure 6 shows the correlation between _sε_NC and basin P. ${}_{\mathrm{s}}{\epsilon }_{NC}^{ALEXI}$ shows broad negative correlations with basin P estimates across CONUS, particularly in the Northeast, suggesting that scaled anomalies of ${\text{ET}}_{\text{EB}}^{\text{ALEXI}}$ are low relative to scaled anomalies in ET_WB when P is above average. For ${}_{\mathrm{s}}{\epsilon }_{NC}^{MOD16}$ and ${}_{\mathrm{s}}{\epsilon }_{NC}^{NOAH}$, the pattern of correlation coefficients for P is similar to that for ALEXI but somewhat muted, particularly along the Rocky Mountains. These results could be interpreted to suggest that when estimates of P are either too high or too low, the error propagates into ET_WB and contributes to non-closure errors (i.e., we have high variance bias in P). Alternatively, it might suggest that errors in ET_EB could be anti-correlated with P.

Figure 6:

Basin specific correlations between ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{NOAH}}$ (left), ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\text{MOD}16}$(center), and ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{ALEXI}}$ (right), and annual P (top row), annual ΔTWS_T (second row), annual ΔTWS_M (third row), % P as snow (fourth row) and JJA vertically integrated sensible heat flux (H_HORIZ, bottom row).

However, the similarity of the relationship between P and both ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\text{MOD}16}$ and ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{NOAH}}$ is somewhat surprising, given similar formulations of the NOAH and MOD16 products and that the NOAH product is the only ET_EB model based on the same P data as the ET_WB model. This may be partially explained by correlations between the precipitation products used by NOAH (NLDAS-2) and MOD16 (GMAO). This may also be partially explained when examining the correlations between ΔTWS and _sε_NC. Like Han et al. (2015), we examine how _sε_NC relates to ΔTWS, but examine this relationship for both the Tellus and Mascon GRACE products (Figure 6, rows 2 and 3) to evaluate whether recent advances in processing of GRACE data has improved ΔTWS estimates. The _sε_NC values for all three models show high negative correlation with both GRACE products in the Souris Red Rainy, Great Lakes, New England, and Mid-Atlantic regions. ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{NOAH}}$ and ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{ALEXI}}$ also show strong, negative correlations with ΔTWS_M and ΔTWS_T in the Upper Mississippi basin, while ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\text{MOD}16}$ and ${}_{\mathrm{s}}{\mathrm{\epsilon }}_{\mathrm{NC}}^{\mathrm{ALEXI}}$ show strong negative correlations with both GRACE products in the Pacific Northwest. The results are very similar across both GRACE products, although some differences can be seen (e.g.,for MOD16 in the Ohio River basin), and the relationships are slightly stronger with the newer Mascon data compared to the Tellus data (see Figure S7), which exhibits slightly more inter-annual variability than Tellus (Figures 2 and S7). We note these results were seen in spite of the fact that many basins used in this study were well below the minimum spatial resolution of the GRACE products. We also note that if ΔTWS is included directly in the ET_WB estimates, the sign of _sε_NC generally does not change, and there are only modest impacts to the magnitude of non-closure errors (Figures S8 and S9). These modest impacts may be caused by a variance bias in either P or ΔTWS, motivating the use of the correlation analysis in Figure 6 to control for these potential biases and maximize the potential signal between non-closure errors and ΔTWS (Supplemental Text 3).

Overall, the correlations between _sε_NC and ΔTWS are strongest in many of the same basins with strong correlations between P and _sε_NC. These results indicate that the correlations between P and _sε_NC may be the result of errors in ET_WB linked to ΔTWS that are strongest when conditions are wet. This makes it difficult to assess whether errors in P or the omission of ΔTWS is driving the non-closure error. Furthermore, both NOAH and MOD16 scale ET by moisture availability, and so in theory, errors in this scaling process could lead to the correlations between _sε_NC, P, and ΔTWS seen in Figure 6. However, ALEXI does not scale ET based on moisture and still has similar correlations between _sε_NC, P, and ΔTWS. Therefore, the strong relationships between _sε_NC and both P and ΔTWS suggest that some combination of uncertainties linked to ET_WB play a large role in non-closure errors.

We are also interested in whether violations of assumptions in the energy balance models drive non-closure errors, particularly as they relate to regional climate phenomena that could translate to regional clustering of _sε_NC. We consider two such phenomena: % P from snow (Figure 6, row 4) and large-scale horizontal heat advection (Figure 6, row 5). _sε_NC shows positive correlations to % P as snow in the Ohio River and northern Mid-Atlantic regions for all models, suggesting that in these areas, overestimation of _sET′_EB relative to _sET′_WB was higher in years when more P came as snowfall. This relationship is strongest for MOD16, suggesting that wintertime ET (associated with sublimation) may be overestimated in this routine. It should be noted, however, that P undercatch is accentuated during snowy conditions, which could further bias ET_WB downwards (Yang et al. 2005, Pan et al. 2003).

An interesting pattern also emerges when _sε_NC is compared to H_HORIZ. Years when H_HORIZ is high seem to be associated with underestimation of all three sET′_EB relative to sET′_WB in the Mid-Atlantic, southern Ohio, Tennessee, and South Atlantic Gulf regions. In contrast, large values of H_HORIZ appear to be associated with an overestimation of ${\text{sET}}_{\text{EB}}^{\text{MOD}16}$ relative to sET_WB at the corner of the Missouri, Upper Mississippi, Arkansas White-Red, and Lower Mississippi regions. Interestingly, in these same regions, MOD16 appears to differ most strongly from other ET products in general, though more research is needed to identify the reasons for this discrepancy. Overall, errors in P and ΔTWS appear more related to non-closure errors than % P as snow and H_HORIZ for most products and regions, although all variables appear important in at least some regions.

4. DISCUSSION AND CONCLUSION

In this study, long-term average and inter-annual ET from three gridded energy balance products were evaluated against ET calculated from a simple terrestrial water budget in 671 basins across CONUS for water years 2003–2015. For long-term biases, $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ showed evidence of some overestimation of annual ET relative to $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$, although this bias was mostly limited to basins with complex terrain. $\overline{{\text{ET}}_{\text{EB}}^{\text{NOAH}}}$ showed evidence of some systemic underestimation of annual ET across the entire CONUS region, while the mean of $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ was very close to the mean of $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$. All three $\overline{{\text{ET}}_{\text{EB}}}$ products seem capable of tracking ET climatology in the central part of the country, albeit with some underestimation from MOD16, while the three $\overline{{\text{ET}}_{\text{EB}}}$ products differed from $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$ and each other in the eastern third of CONUS and along the west coast, a result consistent with previous analysis (Anderson et al. 2013). Our examination of rank correlations between $\overline{{\mathrm{\epsilon }}_{\text{NC}}}$ and watershed characteristics (Figure 3) suggested that 1) $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$ is overestimated in basins with high mean annual precipitation and complex terrain, 2) $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ is also overestimated in basins with higher mean precipitation and complex terrain, but also underestimates ET in basins with more cloud cover (% NA retrievals from ALEXI as a proxy), and overestimates ET in basins with more summertime vertically integrated heat flux $(\overline{{\text{H}}_{\text{HORIZ}}})$.

Importantly, the high correlation coefficients seen between mean annual precipitation and $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{ALEXI}}}$ and $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{MOD}16}}$ where absent for $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{NOAH}}}$. Since NOAH has NLDAS-2 P as forcing, and is of similar model formulation to MOD16, the differences between these two products may highlight regions where long-term errors in P play an important role in depressing the bias term $\overline{{\mathrm{\epsilon }}_{\text{NC}}^{\text{NOAH}}}$. Accordingly, the regions with most prominent contrasts in bias terms between $\overline{{\text{ET}}_{\text{EB}}^{\text{NOAH}}}$ and $\overline{{\text{ET}}_{\text{EB}}^{\text{MOD}16}}$ (as well as $\overline{{\text{ET}}_{\text{EB}}^{\text{ALEXI}}}$) are in mountainous regions of the Eastern US and Pacific Northwest, where gage placement is expected to have an outsized role in long-term bias in gridded P estimates. However, information content of the remotely sensed inputs to MOD16 and ALEXI may be degraded in regions of complex terrain, so it is difficult to distinguish if long-term non-closure error in complex terrain is related to degradation of remotely sense data inputs or error in precipitation

This analysis also confirms that at very long time scales (10+ years, Figure 2), $\overline{\mathrm{\Delta }\text{TWS}}$ is a negligible part of the terrestrial water budget in most of the basins considered, reducing a potential error term in $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$. Taken together, the results above suggest that, at least on a long-term basis, the accuracy of at least some of the $\overline{{\text{ET}}_{\text{EB}}}$ estimates are degraded, particularly in humid regions. This is consistent with previous analyses of long-term bias (Sheffield et al. 2009, Gao et al. 2009). Further, we argue that the analysis presented here points most strongly to some degradation for the NOAH product, given that it shares the same precipitation forcing as and is biased downward against $\overline{{\mathrm{ET}}_{\mathrm{WB}}}$--a bias which cannot be explained by known, systematic sources of precipitation error (e.g., undercatch).

Many studies have indicated that ET_EB cannot be used to close annual terrestrial water budgets (Zhang et al. 2012, Zeng et al. 2014, Velpurri et al. 2013, Han et al. 2015, Liu et al. 2016). Our analysis indicates that in regions with water-limited ET and low inter-annual ET_WB variability—specifically in the central US ranging from Texas up through the High Plains—all three ET_EB products demonstrated hydrologic consistency with ET_WB. Even in these areas, however, the ET_EB products were still only able to capture less than half the magnitude of scaled inter-annual variance estimated by ET_WB Also, in many regions of the country like the Eastern US and the Pacific Northwest, no or weak consistency is seen between ${\text{sET}}_{\text{EB}}^{\prime }$ and ${\text{sET}}_{\text{WB}}^{\prime }$. In addition, the variance of unscaled ET_WB is twice to more than ten times the variance of unscaled ET_EB estimates throughout the CONUS, although this variance bias is smallest with the ALEXI product.

Clustering was seen in basin-level _sε_NC in certain regions and years, a phenomenon that suggests some of these errors are linked to specific climate events that contribute substantially to discrepancies between ET_EB and ET_WB. To explore whether errors in ET_WB or ET_EB were the cause of clustering in non-closure errors, we correlated _sε_NC with four key variables that might drive these errors in either ET_WB (P, ΔTWS), or ET_EB (% P as snow, and H_HORIZ). Results showed interesting patterns of correlation between _sε_NC and all of these variables, although correlations were largest and most widespread with P and ΔTWS. This was despite the mismatch in resolution between the GRACE-based ΔTWS estimates and basin sizes. These results generally support the conclusions of Han et al., 2015 that uncertainties in water budget ET estimates play a large role in inter-annual non-closure errors, although these conclusions should likely be modulated somewhat given the long-term biases in energy budget based methods and potential sources of inter-annual errors linked to sublimation and large-scale heat advection.

Further research is needed to identify whether large-scale climatic drivers of terrestrial ET, including phenomena that contribute to atmospheric coupling and the thresholds for energy limited ET, are adequately parameterized in continental-scale energy balance models. A significant question that remains is whether the variance bias contributing to ε_NC across CONUS is due to overestimation of inter-annual variability in ET_WB or underestimation of inter-annual variability in ET_EB. While some of this bias is due to inter-annual fluctuation in basin ΔTWS and inflated variance bias in estimates of basin P, it is unclear if this is the sole source. As ET is commonly assumed to have relatively low variability on an inter-annual basis, resolution to this question could serve to validate or challenge a critical assumption of terrestrial hydrologic models.

The modestly improved relationships seen between non-closure errors and the higher resolution GRACE Mascon data over the Tellus data suggest that further improvements in the resolution of ΔTWS estimates may be needed to help resolve these questions. We feel the mismatch in resolution between the ΔTWS data and basin sizes used in this study was a major limitation of the approach, despite the significant signals that were uncovered. Therefore, as new and higher resolution GRACE products continue to be developed, we argue for the importance of revisiting ET_WB and ET_EB comparisons in future work using this data.