Robust Empirical Bayesian Reconstruction of Distributed Sources for Electromagnetic Brain Imaging

Abstract

Electromagnetic brain imaging is the reconstruction of brain activity from non-invasive recordings of magnetic fields and electric potentials. An enduring challenge in this imaging modality is estimating the number, location, and time course of sources, especially for the reconstruction of distributed brain sources with complex spatial extent. Here, we introduce a novel robust empirical Bayesian algorithm that enables better reconstruction of distributed brain source activity with two key ideas: kernel smoothing and hyperparameter tiling. Since the proposed algorithm builds upon many of the performance features of the sparse source reconstruction algorithm - Champagne and we refer to this algorithm as Smooth Champagne. Smooth Champagne is robust to the effects of high levels of noise, interference and highly correlated brain source activity. Simulations demonstrate excellent performance of Smooth Champagne when compared to benchmark algorithms in accurately determining the spatial extent of distributed source activity. Smooth Champagne also accurately reconstructs real MEG and EEG data.

I. Introduction

Noninvasive functional brain imaging has made a tremendous impact in improving our understanding of the human brain. Functional magnetic resonance imaging (fMRI) has been the predominant modality for imaging the functioning brain during the past 2 decades. However, fMRI lacks the temporal resolution required to image the dynamic and oscillatory spatiotemporal patterns associated with activities in the brain. Direct non-invasive measurements of these neuronal oscillatory activity in the millisecond time scale can be achieved with magnetoencephalography (MEG) and electroencephalography (EEG), this temporal resolution is essential for epileptic form activity localization and for imaging dynamic of brain networks subserving perception, action and cognition.

MEG/EEG sensor data only provides qualitative information about underlying brain activities. Analysis is typically performed based on the qualitative analyses of experienced users regarding the sensitivity profile of the sensors. To extract more precise information from the sensor data, it is essential to reconstruct actual brain activity (source space reconstruction) from the recorded sensor data. This process involves two steps: the forward and inverse models. The forward model uses source, volume conductor, and magnetic field measurement models to calculate the lead field or gain matrix that describes a linear relationship between sources and the measurements. Inverse algorithms are then employed to estimate the parameters of neural sources from MEG and EEG sensor data. The illposed inverse problem for source localization with MEG/EEG data involves estimating brain activity from noise sensor data where the number of brain voxels (typically 3000 to 10000) is much larger than the number of sensors (typically ~ 300 sensors for MEG and ~ 128 electrodes for EEG).

A wide variety of source localization algorithms exist for estimating source activity to overcome the difficult inverse problem. These algorithms may be roughly organized into three classes: dipole fitting, spatial scanning, and tomography. Dipole fitting can produce very sparse results but with two major caveats. First, the process of nonlinear optimization can result in poor performance when multiple sources are present due to local minima in the solution space. Second, for adequate performance, the number of active neuronal sources must be known a priori. Scanning algorithms, also known as spatial filters, are based on reconstructing activity at a specific voxel of a discretized cortex. Spatial filter methods do not need a priori knowledge of the number of the brain sources. However, traditional spatial filter methods such as beamformers perform poorly when different regional brain activities are correlated in time. In contrast, tomographic methods are estimating activity at all voxels simultaneously. Some tomographic methods are able to promote sparseness in the solution [1], [2], [3], where the majority of the candidate locations do not have significant activity. Empirical evidence shows that a sparse source model can improve the accuracy of localization in a noisy environment.

Most source reconstruction algorithms from the three categories can be framed in a Bayesian schema [4]. This perspective is useful because it demonstrates that various source localization methods are interrelated and, in fact, can be thought of as implicity or explicity imposed prior distributions within a Bayesian framework. Algorithms such as MNE [5], [6], dSPM [7], sLORETA [8], MVAB (and other beamformers) [9], [10], [11], [12], [13] assume a known, fixed prior. Alternatively, the parameters of the prior distribution (hyperparameters) can be learned from the data for robust performance, commonly referred to as empirical Bayesian algorithms [4]. One such recent empirical Bayesian source reconstruction algorithm that we have developed is referred to as Champagne [1]. Champagne outperforms several benchmark algorithms in a variety of simulated source configurations, especially for sparse brain source activity [14]. Since the development of the original Champagne algorithm, we have proposed several extensions of this framework. We have proposed hierarchical spatiotemporal extensions of Champagne to deal with sparse spatial and smooth temporal sources [15]. Recently, we proposed a hierarchical version of the Champagne algorithm, called tree_Champagne, for reconstruction of sources with mixed spatial extents at a voxel and at a regional-level as specified by anatomical or functional atlases [16].

Here, we develop a novel algorithm designed for accurate reconstruction of source activity with distributed spatial extents. Since the algorithm builds upon the Champagne framework, we refer to it as Smooth Champagne. We propose two key ideas to better handle distributed source activity: kernel smoothing and hyperparameter tiling. First, we introduce a kernel filter that converts a spatially smooth generative model for brain sources into a sparse subspace. Second, we assume that this sparse subspace is clustered into regions or tiles, and we estimated variance hyperparameters for this model at a resolution of regions [1]. Model learning of Smooth Champagne deploys robust empirical Bayesian Inference and uses a principled cost function which maximizes a convex lower bound on the marginal likelihood of the data. Resulting update rules are fast and convergent. In Section II, we derive this new algorithm and in Sections III and IV we demonstrate its performance in simulated and real MEG and EEG data in comparison to benchmarks, followed by a brief discussion in Section V.

II. Theory

A. The probabilistic generative model

The generative model for the sensor data with distributed brain activity is defined as

$$\text{y}(t)=\sum _{i=1}^N{\text{L}}_i{\text{s}}_i(t)+\epsilon =\text{LS}(t)+\epsilon ,$$ (1)

where, y(t) = [y₁(t), …, y_M(t)]^T is the output of the sensors at time t, M is the number of channels, N is the number of voxels under consideration and ${\text{L}}_i\in {\Re }^{M\times q}$ is the lead-field matrix for i-th voxel, q is the number of directions for each voxel. The k-th column of L_i represents the signal vector that would be observed at the scalp given a unit current source/dipole at the i-th vertex with a fixed orientation in the k-th direction. It is common to assume q = 2 (for MEG) or q = 3 (for EEG), which allows flexible source orientations to be estimated in 2D or 3D space. Multiple methods based on the physical properties of the brain and Maxwell’s equations are available for the computation of each L_i [17]. ${\text{s}}_i(t)\in {\Re }^{q\times 1}$ is the brain activity for i-th voxel at time t with q directions. The term ε is the noise-plus-interference whose statistics are estimated from the baseline period. We assume that the columns are drawn independently from $\mathcal{N}\left(0,{\Sigma }_{\epsilon }\right)$, where Σ_ε is the noise covariance which could be estimated using a variational Bayesian factor analysis (VBFA) model [18]. Temporal correlations can easily be incorporated if desired using a simple transformation outlined in [19]. And L = [L₁, …, L_N] and S(t) = [s₁(t)^T, …, s_N(t)^T]^T. For simplicity, we define matrix Y = [y(1), …, y(T)] and S = [S(1), …, S(T)] as the entire sensor and source time series. T is the number of time points.

In order to reconstruct the distributed brain activity robustly, we assume that distributed brain source activity arises from a sparse set of clustered sources that (1) are spatially contiguous and (2) share a common time courses. We define the sparse brain activity with clustered sources at time t as Z(t) = [z₁(t)^T, z₂(t)^T, …, z_N(t)^T]^T, where ${\mathit{\text{z}}}_i(t)\in {\Re }^{q\times 1}$. We also define a local spatial smoothing kernel matrix as H = [h₁, h₂, …, h_N]^T and h_i = [h_i1, h_i2, …, h_iN]^T is the local spatial smoothing kernel for i-th voxel. S(t) = HZ(t) ensures spatial contiguity. The model of Eq. (1) can then be expressed as

$$\text{y}(t)=\text{LH}{\text{H}}^{-1}\text{S}(t)+\epsilon =\text{GZ}(t)+\epsilon ,$$ (2)

where G = LH is the new modified leadfield matrix, G = [G₁, …, G_N] and G_i = L_ih_i.

There are many ways to define the local spatial smoothing kernel matrix h_i. For mathematical convenience here, we define h_i, a smoothing kernel that includes flexible parameterization for different kernel properties such as width, pass-band and transition-band characteristic, as follows:

$$h_{ij}=\{\begin{array}{cc}1& j=i,\\ \mathit{\text{exp}}\left(-{\left(\frac{d_{ij}}{m\sqrt{\mathfrak{D}}}\right)}^p\right)& j\ne i,\end{array}$$ (3)

where, we denote the minimum distance between i-th and j-th (j ≠ i) voxel as $\mathcal{D}$ and the distance between i-th voxel and j-th voxel is denoted as d_ij. In the above formulation, the parameter m determines the width of the smoothing kernel, uniformity in the pass-band, and the parameter p determines the slope of the transition region of the kernel. For the rest of this manuscript, unless otherwise specified, the default values for p is 4 and for m is 2.

Additionally, we divide the whole brain voxels into R regions (or tiles) specified either anatomically or functionally and the r-th region contains N_r voxels. By default the number of regions is assumed to be around one tenth of the total number of voxels, regions are assumed to be non-overlapping in this paper. We assume that voxels within the same brain region share a common variance hyperparameter. The prior distribution for sources can be written as

$$p(\text{Z}|\Omega )=\prod _{t=1}^T\prod _{r=1}^R\prod _{n\in {\zeta }_r}\mathcal{N}\left({\mathit{\text{z}}}_n(t)|\mathit{0},{\Omega }_r\text{I}\right),$$ (4)

where Z = [Z(1), …, Z(T)] is the entire sparse time series, ζ_r is the set of voxels in r-th region and n ∈ ζ_r indicates that the n-th voxel is in r-th region. Ω_r is the prior variance hyperparameter of r-th region, I is a q×q identity matrix. If we use the distribution of noise and interference as $\epsilon ~N\left(0,{\Sigma }_{\epsilon }\right)$, the conditional probability p(Y|Z) can be expressed as

$$p(\text{Y}|\text{Z})=\prod _{t=1}^{T}p(\text{y}(t)|\text{Z}(t))=\prod _{t=1}^T\mathcal{N}\left(\text{y}(t)|\text{GZ}(t),{\Sigma }_{\epsilon }\right).$$ (5)

Eqs. (2), (4) and (5) form the sparse model appropriate for distributed sources, next, we will use Bayesian inference to derive the update rules of model parameters and hyperparameters. In the limit of when the kernel width or the tile/region size is equal to the number of voxels in the lead-field, the generative model will result in the algorithm commonly known as Bayesian minimum-norm algorithm. In such a limit, the algorithm will fail to capture distributed source clusters that are on the spatial scale of 5–35 contiguous voxels. Conversely, at the other limit of when the kernel width and the tile/region size is equal to that of a single voxel, the generative model will become similar to that for the Champagne algorithm, i.e. the algorithm will become more suited to reconstruct sparse source activity.

B. Bayesian inference

To estimate the sparse source activity Z, we use Bayesian inference and derive the posterior distribution p(Z|Y), which is given by

$$p(\text{Z}|\text{Y})=\prod _{t=1}^{T}p(\text{Z}(t)|\text{y}(t))=\prod _{t=1}^T\mathcal{N}\left(\text{Z}(t)|\overline{\text{Z}}(t),{\mathit{\Gamma }}^{-1}\right),$$ (6)

where the mean and the variance [1], [16], [20] are

$$\overline{\text{Z}}(t)={\Gamma }^{-1}{\text{G}}^T{\Sigma }_{\epsilon }^{-1}\text{y}(t),$$ (7)

$${\Gamma }^{-1}={\rm Y}+{\text{G}}^T{\Sigma }_{\epsilon }\text{G}.$$ (8)

ϒ is a qN × qN diagonal matrix expressed as

$${\rm Y}=\left[\begin{array}{cccc}{{\rm Y}}_1& 0& \cdots & 0\\ 0& {{\rm Y}}_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {{\rm Y}}_N\end{array}\right],$$ (9)

ϒ_i = Ω_rI if i-th voxel belongs to r-th region.

In order to compute $\overline{\mathit{\text{Z}}}\left(t\right)$ in Eq. (7), we need to know the hyperparameter Ω_r. The hyperparameter Ω_r is obtained by maximizing the cost function $\mathcal{F}(\Omega ,\Phi )$, with an auxiliary variable Φ, and is expressed as

$$\begin{gathered} \mathcal{F}=-\frac{1}{T}\sum _{t=1}^T{(\text{y}(t)-\text{G}\overline{\mathit{\text{Z}}}(t))}^T{\Sigma }_{\epsilon }^{-1}(\text{y}(t)-\text{G}\overline{\text{Z}}(t)) \\ -\frac{1}{T}\sum _{r=1,n\in {\zeta }_r}^R\sum _{t=1}^T{\overline{\mathit{\text{z}}}}_n{\left(t\right)}^T{\left({\Omega }_{r}I\right)}^{-1}{\overline{\mathit{\text{z}}}}_n(t) \\ -\sum _{r=1}^{R}tr\left({\Phi }_r{\Omega }_{r}I\right)+{\Phi }_0. \end{gathered}$$ (10)

Eq. (10) is a convex lower bound of the logarithm of marginal likelihood of the data p(Y|Ω) (details of the derivation of this function can be found in Appendix A).

We then set the derivative of the cost function $\mathcal{F}(\Omega ,\Phi )$ with respect to Ω to zero, the regional resolution level hyperparameter Ω_r for r-th region is given by [20]:

$${\Omega }_r=\frac{1}{q}\sqrt{\frac{\frac{1}{T{N}_r}\sum _{t=1,n\in {\zeta }_r}^T\mathit{\text{tr}}\left({\overline{\mathit{\text{z}}}}_n(t){\overline{\mathit{\text{z}}}}_n{(t)}^T\right)}{{\Phi }_r}}.$$ (11)

The optimization problem of Φ_r is equivalent to finding the hyperplane that forms a closest upper bound of log|Σ_y|. Such a hyperplane is found as the plane that is tangential to log|Σ_y|. Therefore, we set the derivative of log|Σ_y| with respect to ϒ to zero, the update rule for Φ_r is obtained as

$${\Phi }_r=\frac{1}{q}\sum _{n\in {\zeta }_r}\mathit{\text{tr}}\left(G_n^T{\Sigma }_y^{-1}{G}_n\right).$$ (12)

The update rule for ${\overline{z}}_n\left(t\right)$ can also be derived by setting the derivative of the new cost function $\mathcal{F}(\Omega ,\Phi )$ with respect to ${\overline{z}}_n\left(t\right)$ to zero. The source time course for the n-th voxel at r-th region is expressed as

$${\overline{\mathit{\text{z}}}}_n(t)={\Omega }_{r}I{\mathit{\text{G}}}_n^T{\mathbf{\Sigma }}_y^{-1}\mathit{\text{y}}(t).$$ (13)

The proposed algorithm then repeats the update steps Eqs. (11), (12) and (13) until the cost function Eq. (10) converges.

Finally, the estimated sparse brain activity for n-th voxel is Eq. (13) and the distributed brain activity is

$${\text{s}}_n(t)=h_n{\overline{\mathit{\text{z}}}}_n(t)=h_n{\Omega }_{r}I{G}_n^T{\Sigma }_y^{-1}\text{y}(t).$$ (14)

A summary of the proposed algorithm is shown in Table 1.

Table 1.

The Smooth Champagne Algorithm

1: Input sensor data y(t), leadfield matrix L.

2: Create the local smoothing kernel matrix H using Eq (3), calculate the new modified leadfield matrix using G = LH.

3: Set appropriate initial values to Ωr (r = 1,…, R), and ∑ε.

4: Compute Φr, and ${\overline{z}}_n\left(t\right)$, (n = 1,…, T) using Eq. (12) and Eq. (13).

repeat

5: Update Ωr using Eq. (11).

6: Update Φr, and ${\overline{\mathit{\text{z}}}}_n\left(t\right)$ using Eq. (12) and Eq. (13).

until The cost function Eq. (10) converges.

7: Derive the time course using Eq. (14), output s(t).

III. Performance evaluation on simulation and real data

This section describes algorithm performance evaluations for different simulated complex source configurations and real datasets. We also compared performance with benchmark source localization algorithms.

A. Benchmark algorithms for comparison

We chose the following representative source localization algorithms to compare with the performance of Smooth Champagne: (1) an adaptive spatial filtering method, linearly constrained minimum variance beamformer (referred to as Beamformer) [9], [10], [11], [12], two non-adaptive weighted minimum-norm method, (2) standardized low-resolution tomographic analysis (referred to as sLORETA) [7], [8], (3) a variant of mixed-norm algorithm (MxNE) specially tailored to handle multiple time-points and unconstrained source orientations [2], [3], and two Bayesian based algorithms: (4) Champagne [1] and (5) MSP [19]. Champagne, Beamformer, and sLORETA, were implemented using NUTMEG libraries (nuts_Champagne.m, nuts_LCMV_Vector_Beamformer.m and nuts_sLORETA.m) [21]. Standard implementation of MSP from SPM12 was used (spm_eeg_invert.m).

B. Initialization

The initialization of the parameters for Smooth Champagne are as follows. We learn the Σ_ε from the baseline period using Variational Bayesian Factor Analysis [18] and then assume it is fixed when estimating other model parameters from actual data. The local spatial smoothing kernel is set by Eq. (3) and after that, the value of h_ij less than 0.1 is set as 0 to eliminate the influence of voxels that are too far away. Initialization for Ω is set by first running Bayesian Minimum-Norm (BMN) [20] to determine a whole-brain level variance parameter, then the variance of region level is set by the average variance of voxels from the same region.

C. Choice of tuning parameters

In Smooth Champagne there are two free parameters namely the width of the smoothing kernel and the tile/region size. All other parameters are estimated from data. In principle, these two parameters can be estimated from data by computing the model evidence as a function of kernel width and the tile/region size. For other algorithms like MxNE, sLORETA and Beamformer the main free parameter is the regularization constant. In our implementation of MxNE, we set the regularization parameter based on the sensor noise levels from baseline data. For sLORETA, we use the default setting in NUTMEG software where the regularization parameter is equal to the maximum eigenvalue of the sensor data covariance [21]. For Beamformer, we set the regularization parameter to be 1e-3 times the maximum eigenvalue of the sensor data covariance.

D. Quantifying performance

To evaluate the performance of Smooth Champagne in simulations, we use free-response receiver operator characteristics (FROC) which shows the probability for detection of a true source in an image vs. the expected value of the number of false positive detections per image [22], [16], [14], [23]. Based on the FROC, we compute an A′ metric [24] which is an estimate of the area under the FROC curve for each simulation. If the area under the FROC curve is large, then the hit rate is higher compared to the false positive rate. The A′ metric is computed as follows:

$$A^{\prime }=\frac{H_R-F_R}{2}+\frac{1}{2}$$ (15)

We make modifications to this performance metric to be applicable for reconstruction of distributed and clustered sources that are balanced metrics across a variety of sparse and non-sparse reconstruction algorithms. We use the following definitions of hit rate and false rate for the performance evaluation. First, the voxels localized by each algorithm that are included in the calculation of hit-rates are defined as voxels that are i) at least 0.1% of the maximum activation of the localization result; and ii) within the largest 10% of all of the voxels in the brain.

Within these subset of voxels, we test whether each voxel is within the three nearest voxels to a true source cluster. If a particular voxel’s estimated activity lies within a true cluster, that voxel gets labeled as a ‘sub-hit’. If the number of ‘sub-hits’ within a particular true cluster is more than 50% of the number of voxels in that cluster, that cluster gets labeled as a ‘hit’. H_R is then calculated by dividing the number of hit clusters by the true number of clusters. For F_R, the false positive voxels localized by each algorithm are defined as voxels that lie within the largest 10% of the whole voxels. F_R is defined by dividing the number of potential false positive voxels by the total number of inactive voxels for each simulation. Lastly, we use Eq (15) to calculate the extent scores A′ metric which ranges from 0 to 1, with higher numbers reflecting better performance.

E. MEG simulations

In this paper, we generate data by simulating dipole sources with fixed orientation. Damped sinusoidal time courses are created as voxel source time activity and then projected to the sensors using the leadfield matrix generated by the forward model, assuming 271 sensors and a single-shell spherical model [17] as implemented in SPM12 (http://www.fil.ion.ucl.ac.uk/spm) at the default spatial resolution of 8196 voxels at approximately 5 mm spacing and unless otherwise indicated, we set the number of voxels in a region to be around eight resulting in about one thousand regions, and the average kernel width is set to around ten voxels. The time course is then partitioned into pre- and post-stimulus periods. In the pre-stimulus period (480 samples) there is only noise and baseline brain activity, while in the post-stimulus period (480 samples) there is also source activities of interest on top of statistically similarity distributed noise plus interfering brain activity. The noise activity, which is added to achieve a desired signal to noise ratio, consists of actual resting-state sensor recordings collected from a human subject presumed to have only spontaneous brain activity and sensor noise.

Signal-to-noise ratio (SNR), correlations between voxel time courses in the same cluster (intra-cluster α_intra), and correlations between voxel time courses from different clusters (inter-clusters α_inter) were varied to examine algorithm performance. SNR and time course correlation are defined in a standard fashion [16], [14]. The following configurations were tested:

1. Cluster number: 3, 5, 7, 11, 13, and 15 clusters were seeded with 20 sources each, corresponding to 60, 100, 140, 220, 260, and 300 active voxels. Each cluster consists of the center, chosen randomly, and 19 nearest neighbors.

2. Cluster size: 5 clusters were seeded with 5, 10, 15, 20, 25, 30, 35 and 40 active dipoles each.

3. SNR: Simulations were performed with 5 randomly seeded clusters at SNRs of 0 dB, 3 dB, 6 dB, 9 dB, 12 dB, and 15 dB.

4. Inter-cluster correlation: 5 clusters were seeded with 20 sources each. Correlation between clusters was varied from 0.1, 0.3, 0.5, 0.7, and 0.9. Intra-cluster correlation was set to 0.8.

5. Influence of width of local smoothing kernel and size of tiles: We evaluate the algorithm performance as a function of local smoothing kernel width. We examine performance for reconstruction of 5 clusters of different sizes (from 5–35 voxels per cluster). We increase the width of the local smoothing kernel from 3 voxels to 121 voxels while the tile size is maintained at 6 voxels. We also examine performance as a function of average tile size ranging from 4–132 voxels per tile and fix the average kernel width (15 voxels).

If not indicated above, each of the simulations was conducted with the following parameters: SNR of 10 dB, intra-cluster correlation coefficient of α_intra = 0.8, and inter-cluster correlation coefficient of α_inter = 0.25. Correlations within clusters were modeled higher than between clusters to simulate real cortical activity. Results for A′ and localization were obtained by averaging over 50 simulations for each of the configurations above.

F. EEG simulations

The algorithm was also tested on simulated EEG data with a scalar lead field computed for a three-shell spherical model in SPM12 (http://www.fil.ion.ucl.ac.uk/spm) with more than 5000 voxels at approximately 8 mm spacing and 120 sensors. EEG sensor recordings were simulated through the forward model in the same way as the MEG data. Since the algorithm has similar performance with EEG data as with MEG, only one specific example is shown in the paper. Three clusters are seeded with SNR of 20 dB, intra-cluster correlation of 0.9, and inter-cluster correlation of 0.9.

G. Real datasets

Real MEG data was acquired in the Biomagnetic Imaging Laboratory at University of California, San Francisco (UCSF) with a CTF Omega 2000 whole-head MEG system from VSM MedTech (Coquitlam, BC, Canada) with 1200 Hz sampling rate. The lead field for each subject was calculated in NUTMEG [21] using a single-sphere head model (two spherical orientation lead fields) and an 8 mm voxel grid. Each column was normalized to have a norm of unity. The data were digitally filtered from 1 to 160 Hz to remove artifacts and DC offset.

Six algorithms were run on three real MEG data sets: 1. Somatosensory Evoked Fields (SEF); 2. Auditory Evoked Fields (AEF); 3. Audio-Visual Evoked fields. The data sets have been reported in our prior publications using the Champagne algorithm, and details about these datasets can be found in [1], [14].

The EEG data (128-channel ActiveTwo system) was downloaded from the SPM website (http://www.fil.ion.ucl.ac.uk/spm/data/mmfaces) and the lead field was calculated in SPM8 using a three-shell spherical model at the coarse resolution of 5124 voxels at approximately 8 mm spacing. The EEG data paradigm involves randomized presentation of at least 86 faces and 86 scrambled faces. The averaged scrambled-faces data was subtracted from the averaged faces data to study differential response [25]. The EEG data has been reported in our prior publication using the Champagne algorithm, and details about our analyses of this dataset can be found in [16], [14].

IV. Results

A. Simulation Results

1). MEG simulations:

Figure 1 shows a representative example of localization results for an MEG simulation with 3 clusters. In this configuration, the SNR, correlation of dipole activities within the cluster and between clusters are 10 dB, 0.9 and 0.9, respectively. Compared with the ground truth, Beamformer and sLORETA can localize all three clusters but produce blurred and spurious activity, while MxNE can localize two of the three clusters but produces focal sources and misses one cluster. In contrast, MSP can localize all three clusters, but reconstructions are smoother than ground truth and produces additional sources that are not present in the simulations. Champagne can accurately localize all three clusters but estimates activity that is more focal than the true spatial extent of the sources. Smooth Champagne is able to localize three clusters which are the closest spatially distributed to the ground truth.

Fig. 1:

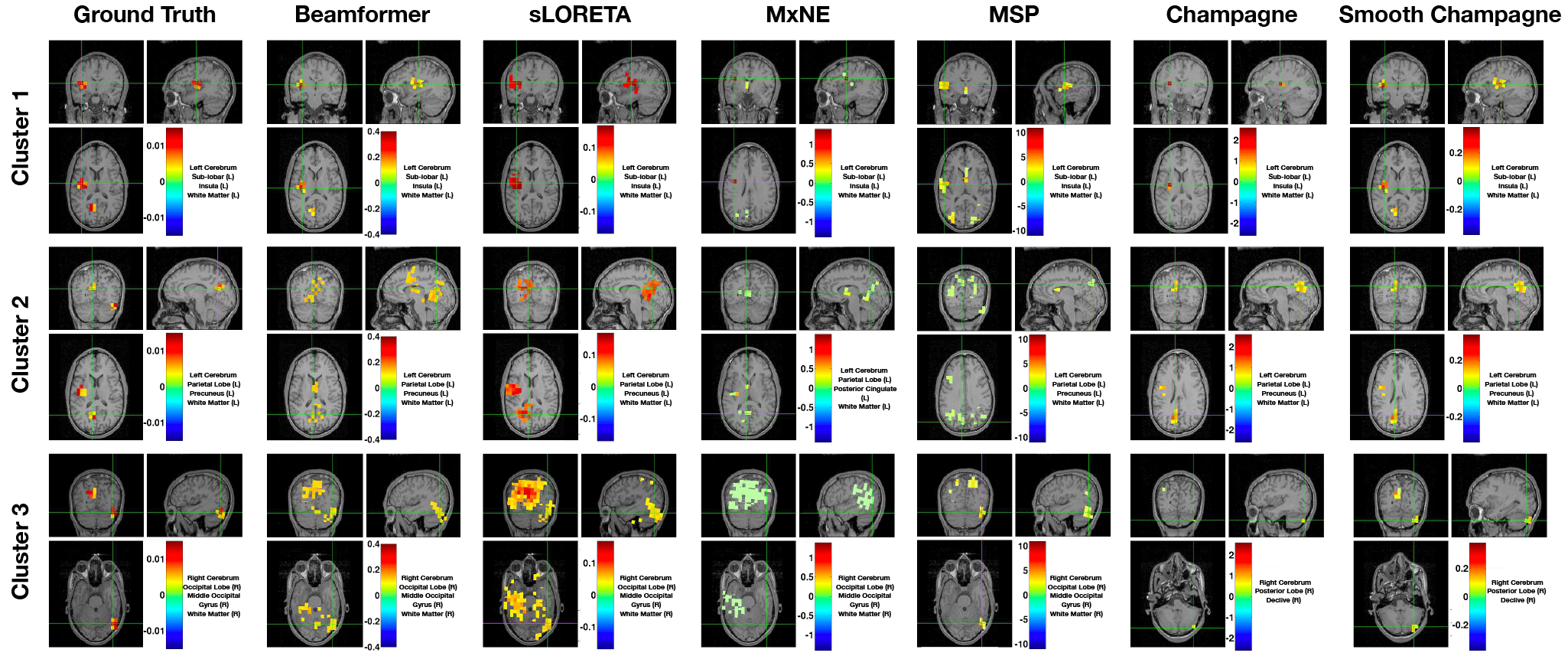
A single MEG simulation example of the localization results with three clusters for six algorithms: Beamformer, sLORETA, MxNE, MSP, Champagne and Smooth Champagne. The ground truth location of clusters are shown for comparison. Only Smooth Champagne captures the true spatial extent of all the sources. In this configuration, the SNR, correlation of dipole activities within the cluster and between clusters are 10 dB, 0.9 and 0.9, respectively.

1. Influence of the number of clusters - In Figure 2 (A), we plot the number of clusters versus A′ metrics at SNR levels of 10 dB and correlations within and between clusters as 0.8 and 0.25. All algorithms have the same trend, with decreasing performance as number of clusters increases. However, Smooth Champagne outperforms all benchmark algorithms. MxNE shows higher A′ scores than MSP, Beamformer and sLORETA.

2. Effect of increasing cluster size - Results of all algorithms in response to increasing cluster size are presented in Figure 2 (B). From the performance scores, Smooth Champagne outperforms all benchmarks except for when the size of clusters is less than 10 voxels. In this sparse source activity scenario, as to be expected, Champagne performs better than Smooth Champagne. Champagne performs better than other benchmark algorithms when cluster size is less than 35, when cluster size increases to 40, MSP outperforms Champagne. In contrast, MSP, MxNE, sLORETA and Beamformer show no change with increasing cluster size, MxNE outperforms MSP, sLORETA and Beamformer.

3. Effects of increasing SNR - In the subplot (C) of Figure 2, SNR versus performance score is plotted. All algorithms demonstrate improved performance with increasing SNR. Again, Smooth Champagne outperforms all benchmark algorithms. MxNE shows higher A′ scores than MSP, sLORETA and Beamformer.

4. Influence of the correlation between clusters - The subplot (D) of Figure 2 shows the influence of increasing the correlation between clusters on algorithm performance. Increasing the correlation between clusters has little influence on the performance of all algorithms. Based on the plots, it is clear that smooth Champagne outperforms all benchmarks. Champagne again outperforms MxNE, which outperforms MSP, sLORETA and Beamformer.

5. Influence of width of local smoothing kernel and size of tiles - Figure 3 (A) shows the performance of the novel algorithm as a function of local smoothing kernel width. We examine performance for reconstruction of 5 clusters of different sizes (from 5–35 voxels per cluster). We increase the width of the local smoothing kernel from 3 voxels to 121 voxels while the averaged tile size was maintained around 6 voxels. For small cluster sizes (of 5 voxels) performance deteriorates when smoothing kernel size is increased. However, for moderate to large clusters, performance is invariant to kernel size up to 42. Only for very large kernel size of 121 voxels does performance start to deteriorate. Figure 3 (B) shows the performance of the novel algorithm as a function of the tile size. We again examine performance for reconstruction of 5 clusters of different sizes (from 5–35 voxels per cluster). We examine performance as a function of average tile size ranging from 4–132 voxels per tile while the averaged smoothing kernel size was maintained around 7 voxels. Here, we observe that across all cluster sizes, performance deteriorates when the tile size increases. For optimal performance the size of the smoothing kernel and the tile/region size should be smaller than the true size of the clusters. If the kernel width exceeds the true cluster size, then some deterioration in performance is observed. If the tile/region size exceeds the true cluster size, performance also deteriorates. However, in real data and absence of ground truth, the true cluster size is unknown. Our analysis suggests that for cluster sizes between 15–35 voxels, which are thought to the size of blobs typically reported in fMRI studies and may represent realistic clustered brain activity, performance is fairly uniform for a range of kernel sizes from 3–40 and for tile sizes between 4–25. This indicates some robustness in algorithm performance. However, examining Figure 3 (A) and (B) indicates that robustness is conferred more by kernel size than by tile/region size, especially for smaller clusters. In this context, if there is a mismatch between the kernel width and the tile/region size, indeed performance will deteriorate due to the leadfield columns which are divergent such that the regional lead-field cannot fit the scalp topography.

Fig. 2:

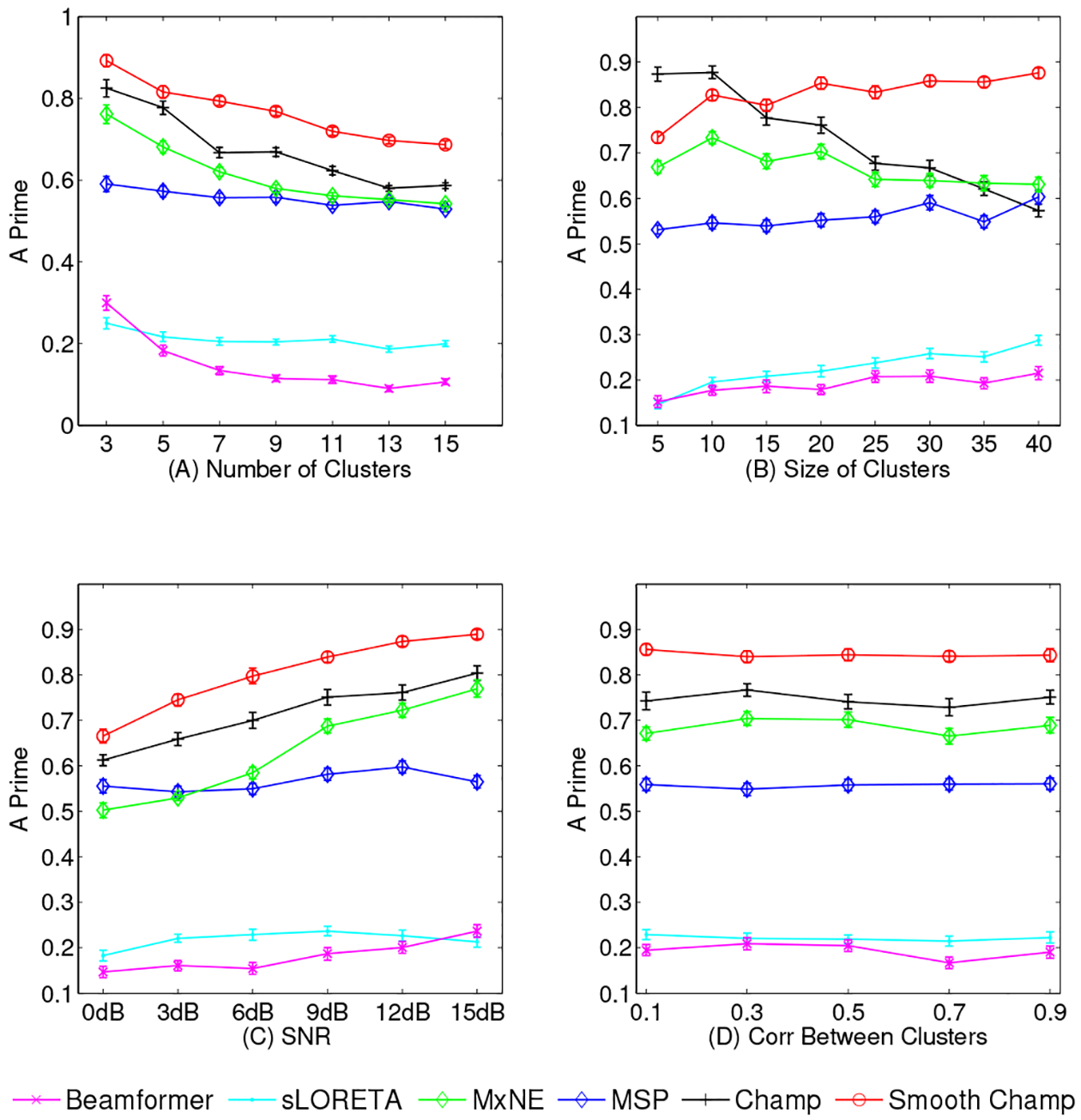
Simulation results of A′ metric with four different configurations. (A) Increasing cluster number; (B) Increasing cluster size; (C) Increasing SNR; (D) Increasing intra-cluster correlation. The results are averaged over 50 simulations at each data point and the error bars show the standard error.

Fig. 3:

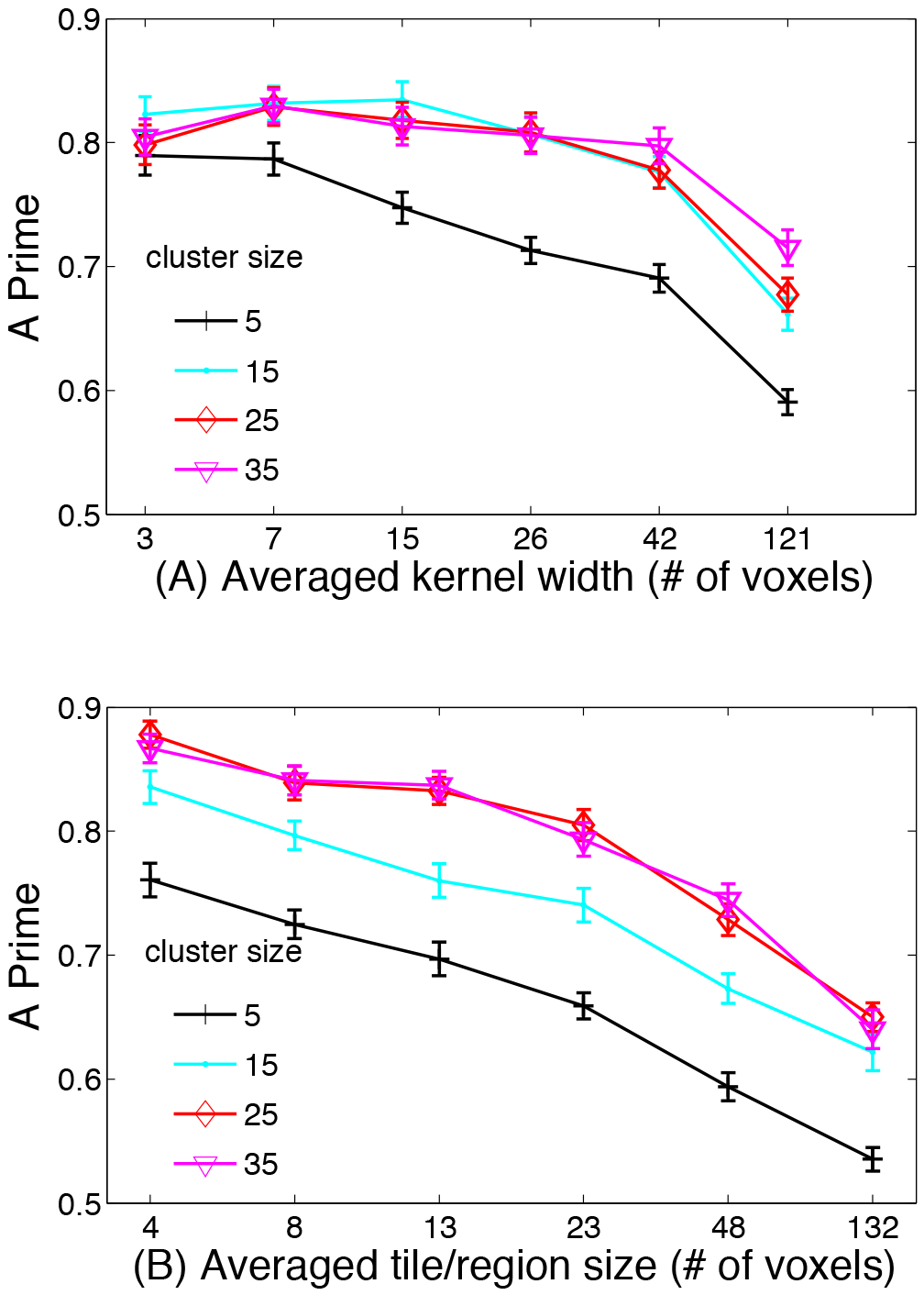
Simulation results of the performance of the novel algorithm as a function of local smoothing kernel width and the tile size. We examine performance for reconstruction of 5 clusters of different sizes (from 5–35 voxels per cluster). (A) Results of the performance as a function of increasing the width of the local smoothing kernel from 3 voxels to 121 voxels while the averaged tile size was maintained at 6 voxels. (B) Results of the performance as a function of average tile size ranging from 4–132 voxels per tile while the averaged smoothing kernel size was maintained around 7 voxels. The results are averaged over 50 simulations at each data point and the error bars show the standard error.

2). EEG simulations:

Figure 4 shows a representative example of localization results for an EEG simulation. In this configuration, the SNR, correlation of dipole activities within the cluster and between clusters are 20 dB, 0.9 and 0.9, respectively. As is shown, the performance of all algorithms for EEG simulation is almost the same as the performance for MEG simulations. Compared with the ground truth, Beamformer and sLORETA localize all three cluster activities but produce blurred and spurious solutions, while MxNE localizes all three clusters with several focal point sources. In contrast, MSP lcalizes all three clusters, but reconstructions are smoother than ground truth and additional sources that are not present in the simulations are produced. Champagne can localize all three clusters but it estimates activity that is more focal than the true spatial extent of the sources. Smooth Champagne outperforms the benchmarks as it most accurately localizes three clusters when compared to the ground truth.

Fig. 4:

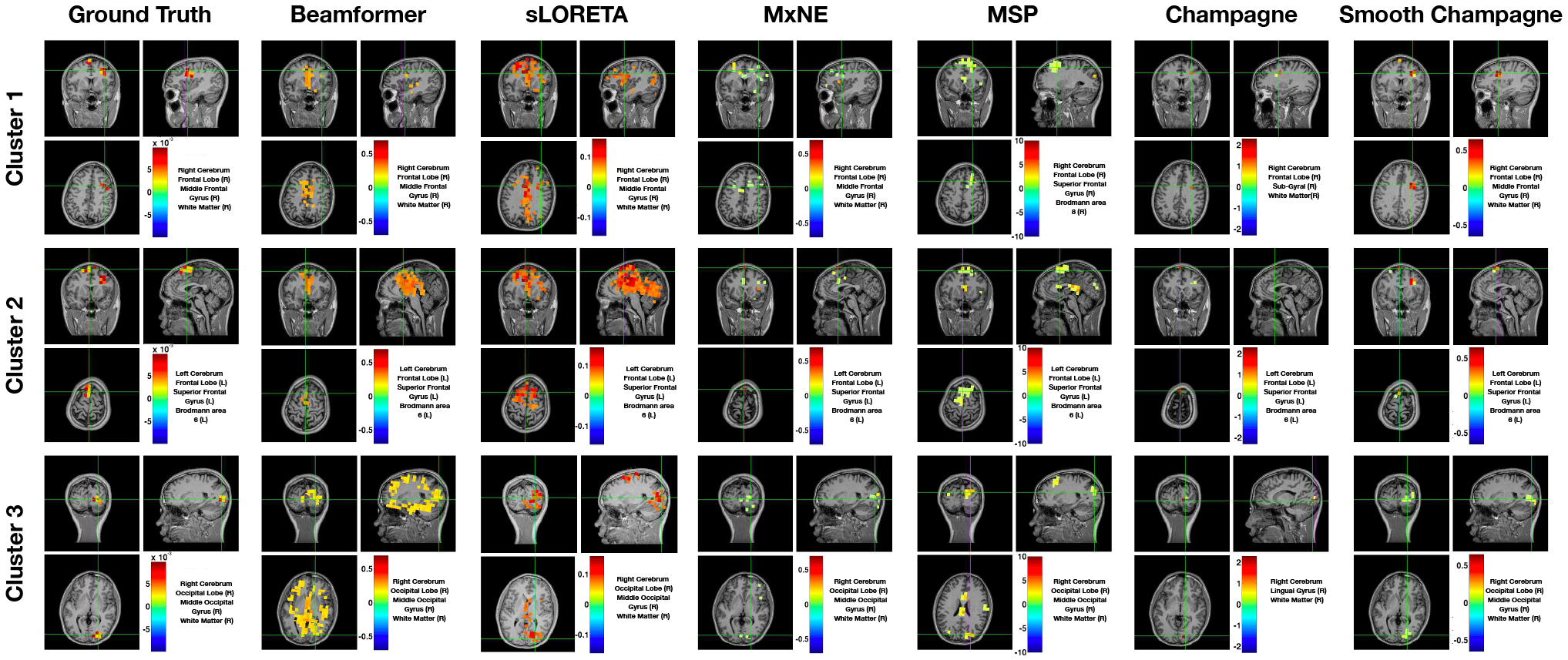
A single EEG simulation example of the localization results with three clusters for six algorithms: Beamformer, sLORETA, MxNE, MSP, Champagne and Smooth Champagne. The ground truth location of clusters are shown for comparison. In this configuration, the SNR, correlation of dipole activities within the cluster and between clusters are 20 dB, 0.9 and 0.9, respectively.

3). Summary for simulations:

As can be seen from the simulation results and analyses above, Smooth Champagne outperforms all the benchmark source reconstruction algorithms with various complex distributed source configurations. Next, we extend the evaluation of the performance using real MEG and EEG data.

B. . Results of real datasets

1). MEG - Somatosensory Evoked Field Paradigm:

Figure 5 shows the results of the somatosensory evoked field response due to somatosensory stimuli presented to a subject’s right index finger, average derived from a total of 240 trials. A peak is typically seen ~50 ms after stimulation in the contralateral (in this case, the left) somatosensory cortical area for the hand, i.e., dorsal region of the postcentral gyrus. All algorithms can localize this activation to the correct area of somatosensory cortex with focal reconstructions. MxNE and Champagne are the most focal while sLORETA produces the most diffuse reconstruction.

Fig. 5:

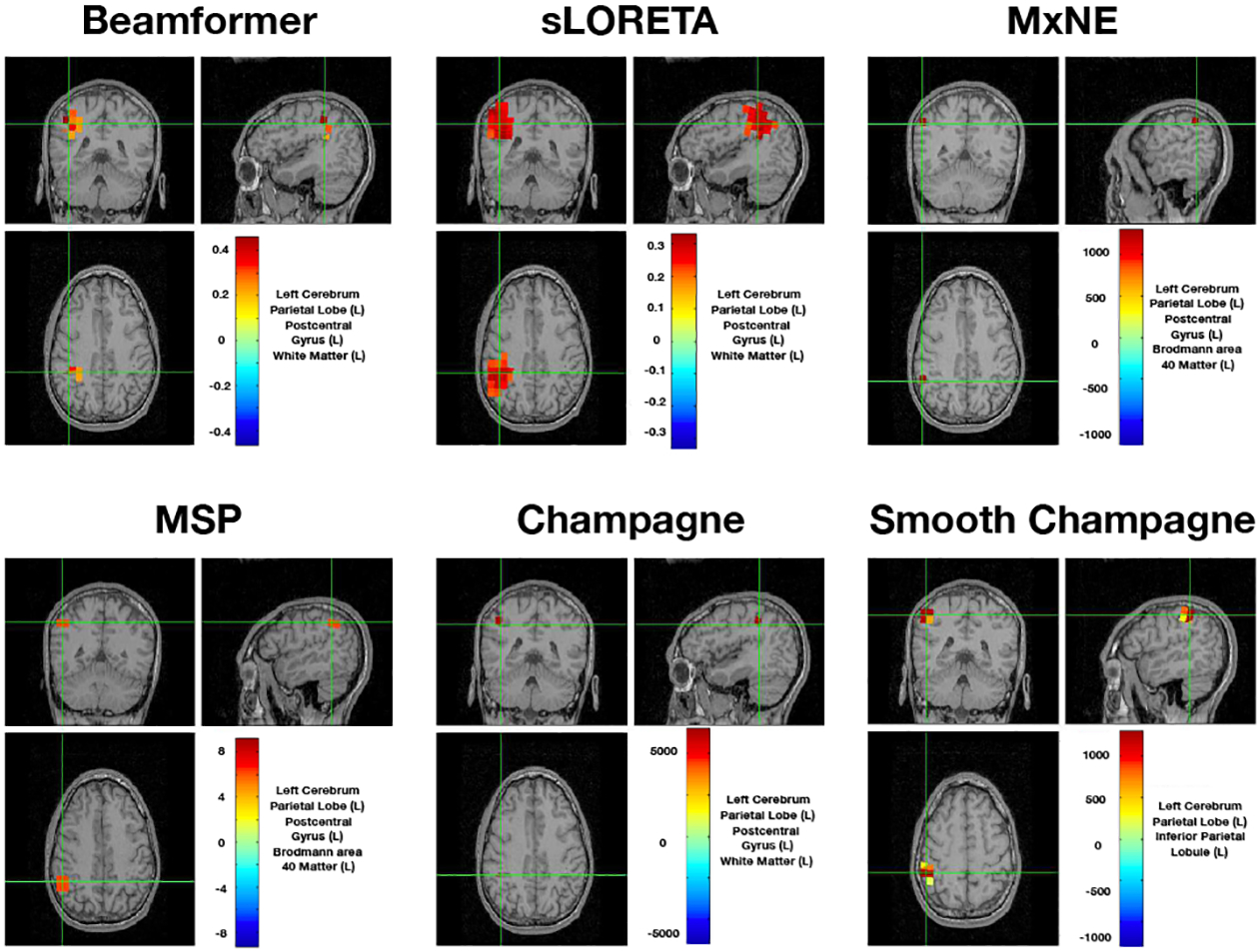
Sensory Evoked Field localization results. All six algorithms localize to somatosensory cortical areas. Here we set the threshold as half of the maximum value.

2). MEG - Auditory Evoked Fields

The localization results for AEF data from four subjects are shown in Figure 6. The power of at each voxel in a 50–75 ms window around M100 peak is plotted for every algorithm. MxNE, Champagne and Smooth Champagne are able to consistently localize bilateral auditory activity for all subjects (shown in the last two columns in Figure 6). The activity is in Heschl’s gyrus, which is the location of primary auditory cortex. The localization results of Smooth Champagne are more spatially distributed than MxNE and Champagne. Beamformer and sLORETA can find the two auditory cortices only in one subject, whereas for the rest of the subjects the activations are mostly biased towards the center of the head; suggesting that the correlation of bilateral auditory cortical activity greatly and negatively impacts the performance of Beamformer and sLORETA. MSP can localize bilateral auditory activity but with some location bias and diffuse activation.

Fig. 6:

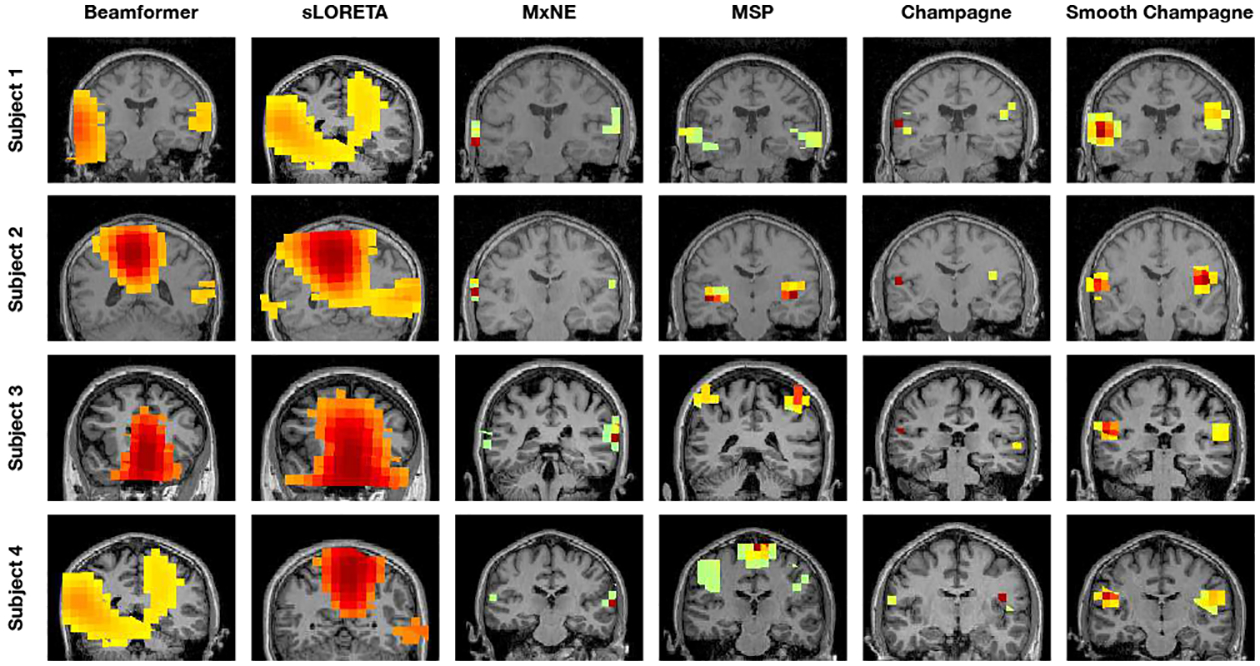
Auditory evoked field (AEF) results with four subjects for six algorithms: Beamformer, sLORETA, MxNE, MSP, Champagne and Smooth Champagne. The results from both Champagne and Smooth Champagne are shown in the last two columns, which outperform the other benchmark algorithms shown in the first to fourth columns.

3). MEG - Audio-Visual Evoked Fields:

Figure 7 shows results of the audio-visual evoked fields for Smooth Champagne. In subplot (A) and (B) we show the brain activations associated with the auditory stimulus. Smooth Champagne is able to localize bilateral auditory activity in Heschl’s gyrus in the window around the M100 peak, shown in the first row of Figure 7. The two auditory sources have the maximum power in the window around the M100 peak. We show the early visual response in the second row of Figure 7. Smooth Champagne is able to localize a source in the medial, occipital gyrus with a peak around 150 ms. We plot the power in the window around this peak and the time course of the source marked with the cross hairs. Our algorithm can localize a later visual response with a time course that has power extending past 150 ms. Compared to the results obtained with Champagne [14], Smooth Champagne shows more diffuse activation and smoother time courses.

Fig. 7:

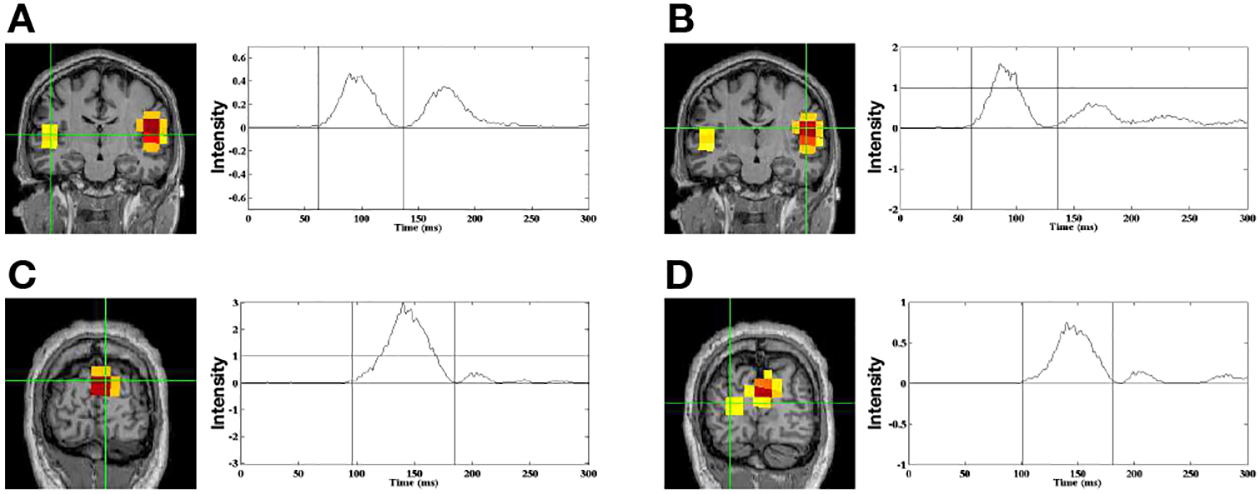
Audio-Visual data localization results from Smooth Champagne. Smooth Champagne is able to localize a bilateral auditory response at 100 ms after the simultaneous presentation of tones and a visual stimulus. For bilateral auditory activity, the results of locations and time courses are shown in (A), (B). Smooth Champagne can localize an early visual response at 150 ms after the simultaneous presentation of tones and visual stimulus shown in (C) and (D).

4). EEG - Face-Processing task:

In Figure. 8, we present the results from using five algorithms on the face-processing task EEG data set. Figure 8 shows the average power, M100 peak power, and M170 peak power at different rows separately. MxNE is unable to localize brain activity and localizes one focal activity for all conditions. Champagne is able to localize brain activity with sparse peaks at visual areas and fusiform gyrus [25], [26]. Smooth Champagne demonstrates spatially distributed activity in the appropriate corresponding locations. Performance of benchmarks algorithms on this dataset can be found in [14].

Fig. 8:

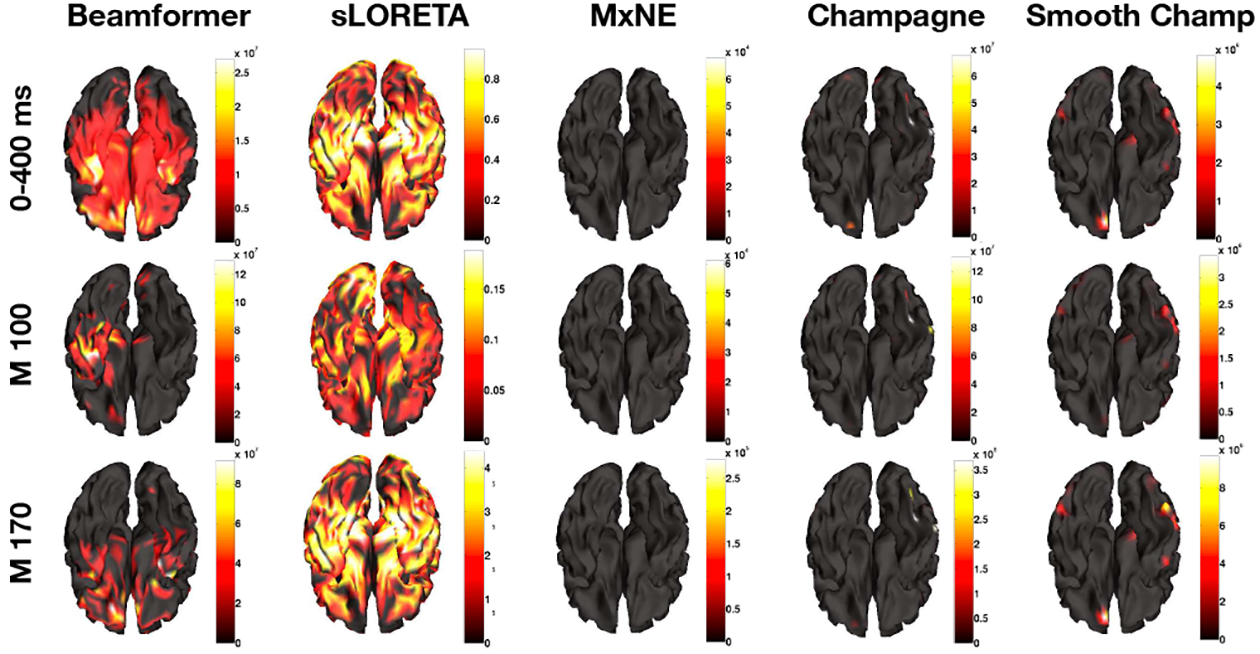
Face processing (EEG) localization results for five algorithms: Beamformer, sLORETA, MxNE, Champagne, and Smooth Champagne. The first row is the average power mapping from 0 ms to 400 ms, the second and third rows are for peak power activity at 100 ms and 170 ms separately.

V. Discussion

This paper derives a novel and robust Empirical Bayesian algorithm for accurate reconstruction of distributed source activity from MEG and EEG data. The algorithm, which we refer to as Smooth Champagne, readily handles a variety of configurations of distributed brain sources under high noise and interference conditions, especially correlated distributed sources with complex spatial extent - a situation that commonly arises even with simple imaging tasks. Smooth Champagne is based on a principled cost function which maximizes a convex lower bound on the marginal likelihood of the data and resulting update rules are fast and convergent. The algorithm displays significant theoretical and empirical advantages over many existing benchmark algorithms for electromagnetic brain imaging. We compared Smooth Champagne’s performance with benchmark algorithms such as Beamformer, sLORETA, MxNE, Champagne and MSP on both simulated and real data and demonstrated its superiority. Simulations of MEG and EEG data explored algorithm’s performance for complex source configurations with highly correlated time-courses and high levels of noise and interference. Smooth Champagne outperforms all benchmarks, including Champagne, for distributed source clusters as it demonstrates more accurate spatial extent reconstructions regardless of SNR or source correlations. In general it is difficult to evaluate localization algorithm performance with real data since the ground truth is unknown. For this reason, we chose real data sets that have well-established patterns of brain activity. Performance on these real MEG and EEG data sets demonstrates the superior ability of Smooth Champagne to localize real brain distributed brain activity across a variety of tasks (SEF, AEF, AV, and face-Processing) when compared to benchmarks.

Smooth Champagne builds upon our prior framework of Champagne for sparse brain source reconstructions with two key ideas: local spatial kernel smoothing and hyperparameter tiling both of which contribute to algorithm performance. Kernel size and tile/region size appear to independent affect performance. Our analysis suggests that for optimal performance the size of the smoothing kernel and the tile/region size should match the true size of the clusters. If the kernel width exceeds the true cluster size, then some deterioration in performance is observed. If the tile/region size exceeds the true cluster size, performance also deteriorates. However, in real data the true cluster sizes are unknown. Across simulations, we find that with a setting for the kernel and tile size around 10 voxels, i.e. the number of regions is 10% of the number of voxels in the lead field, we are able to accurately reconstruct distributed sources that are even larger in size. In principle, the kernel width parameter of the smoothing kernel and the tile/region size of the hyperparameter tiling can be estimated from data by computing the model evidence as a function of kernel width and the tile/region size, we relegate this effort to future work.

Related approaches for estimating distributed sources have used Type-1 penalized likelihood methods. Many publications have examined mixed-norm (MxNE) optimization for MEG, typically L1 priors to impose sparsity in space and L2 priors are used to impose smoothness in time [2], [3], [27], [28], [29], [30], [31]. For example, Haufe et al. [27] proposed Focal Vector Field Reconstruction (FVR) by defining the regulating penalty function, which renders the solutions unique, as a global l1-norm of local l2-norms. In contrast, Zhu et al. [28] proposed variation and wavelet based sparse source imaging (VW-SSI) to better estimate cortical source locations and extents, which utilizes the L1-norm regularization method with the enforcement of transform sparseness in both variation and wavelet domains. Extensions have also been proposed for time-frequency sparsity decompositions [3]. The latent parameters of both of these approaches are often estimated by a Second-Order Cone Program (SOCP). More recently, iterative reweighting strategies (IRES) have been used to penalize locations that are less likely to contain any source and can provide reasonable information regarding the location and extent of the underlying sources [3], [32]. In contrast to these Type-I likelihood estimation methods, in this paper we use a Type-II likelihood estimation method. We have previously shown that Type-I likelihood methods which make use of non-factorial, lead-field and noise-dependent priors can be shown to have a dual with Type-II likelihood methods with comparable performance [33]. However, in general, as we have shown here, performance of Type-II likelihood estimation methods yields superior results.

In the future, the Smooth Champagne framework can be incorporated into related hierarchical algorithms that we have proposed recently, such as tree_Champagne [16], that combines voxel and region level inferences for mixed source configurations which may include both distributed and sparse brain sources. The region-based variance model in Smooth Champagne is different from other approaches in several ways [34], [35]. First, in contrast to Bayesian model averaging (BMA), which implements multiple variance models and then averages the individual primary current density (PCD) for each model using gradient descent methods, Smooth Champagne uses a single generative model for all sources and uses empirical Bayesian inference to learn the regions distribution using closed-form update rules and built-in model selection features [4]. Second, unlike greedy algorithms like those proposed in Babadi et al. and Friston et al. [34], [36], which are approximation to Bayesian inference and are highly sensitive to initialization and have the possibility of sub-optimal solutions, our closed form solutions with principled cost functions that have convergence guarantees for Bayesian inference with no subspace selection or pruning. Finally, Smooth Champagne also has faster update rules based on convex-bounds on true marginal likelihood of the data [4].

Future directions of our work are motivated by several further extensions of the current algorithm. First, all priors in Smooth Champagne are assumed to be Gaussian. However, the algorithm could easily be modified to incorporate additional sparse priors both across space, and especially across time. Even within a Gaussian scale mixture modeling framework it is possible to incorporate many sparse priors implicitly [37], [38] and we plan to explore algorithm performance for such non-Gaussian extensions. Further more the current algorithm makes no assumptions about temporal smoothness for source reconstructions. It is possible to include various forms of priors about temporal information within our framework of covariance component estimation. One such idea is to use temporal basis functions [39], and another is to use autoregressive models for source distributions over time. Such autoregressive models can also include spatiotemporal correlations both in source time-courses and in the time-course of the background noise and interference in the data [40], [41], [42]. Another idea that we plan to pursue is to incorporate forward modeling errors by probabilistic modeling of the lead-field kernel within our framework, an approach similar to related to the following recent work [13], [43], [44].

Appendix A

Derivation of the cost function

Here, we derive the expression for the cost function $\mathcal{F}(\Omega ,\Phi )$ shown in Eq. (10). Taking the logarithm of the marginal likelihood of the data p(Y|Ω), then we make the use of the form [20] (pp.244)

$$\begin{gathered} \text{log}p(\mathit{\text{Y}}|\mathbf{\Omega })=E_{p(\text{Z}|\mathbf{\text{Y}})}\left[\text{log}\frac{p(\text{Y},\text{Z}|\Omega )}{p(\text{Z}|\text{Y})}\right] \\ =E_{p(\text{Z}|\text{Y})}[\text{log}p(\text{Y}|\text{Z})]+E_{p(\text{Z}|\text{Y})}[\text{log}p(\text{Z}|\Omega )] \\ -E_{p(\text{Z}|\text{Y})}[\text{log}p(\text{Z}|\mathit{\text{Y}})]. \end{gathered}$$ (A.1)

Substitution of Eqs. (4), (5) and (6) into Eq. (A.1) results in

$$\begin{gathered} \text{log}p(\mathit{\text{Y}}|\mathbf{\Omega })=-\frac{1}{T}\sum _{t=1}^T{(\mathit{\text{y}}(t)-\mathit{\text{G}}\overline{\mathit{\text{Z}}}(t))}^T{\mathit{\Sigma }}_{\epsilon }^{-1}(\mathit{\text{y}}(t)-\mathit{\text{G}}\overline{\mathit{\text{Z}}}(t)) \\ -\frac{1}{T}\sum _{r=1,n\in {\zeta }_r}^R\sum _{t=1}^T{\overline{\mathit{\text{z}}}}_n{\left(t\right)}^T{\left({\Omega }_{r}I\right)}^{-1}\overline{\mathit{\text{z}}}{\left(t\right)}_n \\ -\text{log}\left|{\Sigma }_{\text{y}}\right|, \end{gathered}$$ (A.2)

where Σ_y is the model data covariance matrix expressed as

$${\Sigma }_y=G{\rm Y}{G}^T+{\Sigma }_{\epsilon }.$$ (A.3)

Since log|Σ_y| is a concave function with respect to ϒ [4], we can find an auxiliary parameter, Φ_r(r = 1, …, R), that satisfies the relationship

$$-\sum _{r=1}^R\mathit{\text{tr}}\left({\Phi }_{r}I{{\rm Y}}_r\right)+{\Phi }_0\le -\text{log}\left|{\Sigma }_y\right|,$$ (A.4)

where, Φ₀ is a scalar term [45] [46]. Then we define a cost function $\mathcal{F}(\Omega ,\Phi )$, such that

$$\begin{gathered} \mathcal{F}(\Omega ,\Phi )=-\frac{1}{T}\sum _{t=1}^T{(y(t)-G\overline{\mathit{\text{Z}}}(t))}^T{\Sigma }_{\epsilon }^{-1}(y(t)-G\overline{\mathit{\text{Z}}}(t)) \\ -\frac{1}{T}\sum _{r=1,n\in {\zeta }_r}^R\sum _{t=1}^T{\overline{\mathit{\text{z}}}}_n{\left(t\right)}^T{\left({\Omega }_{r}I\right)}^{-1}{\overline{\mathit{\text{z}}}}_n(t) \\ -\sum _{r=1}^R\mathit{\text{tr}}\left({\Phi }_r{\Omega }_{r}I\right)+{\Phi }_0. \end{gathered}$$ (A.5)

Eq. (A.4) guarantees that the relationship

$$\mathcal{F}(\Omega ,\Phi )\le \text{log}p(\text{Y}|\Omega )),$$ (A.6)

always holds. That is, the cost function $\mathcal{F}(\Omega ,\Phi )$ forms a convex lower bound on the logarithm of the marginal likelihood p(Y|Ω)). When we maximize $\mathcal{F}(\Omega ,\Phi )$ with respect to Ω and Φ, such Ω also maximizes the marginal likelihood.