The frequency of snowline-region planets from four-years of OGLE-MOA-Wise second-generation microlensing

Abstract

We present a statistical analysis of the first four seasons from a “second-generation” microlensing survey for extrasolar planets, consisting of near-continuous time coverage of 8 deg² of the Galactic bulge by the OGLE, MOA, and Wise microlensing surveys. During this period, 224 microlensing events were observed by all three groups. Over 12% of the events showed a deviation from single-lens microlensing, and for ~1/3 of those the anomaly is likely caused by a planetary companion. For each of the 224 events we have performed numerical ray-tracing simulations to calculate the detection efficiency of possible companions as a function of companion-to-host mass ratio and separation. Accounting for the detection efficiency, we find that ${55}_{-22}^{+34}\%$ of microlensed stars host a snowline planet. Moreover, we find that Neptunes-mass planets are ~ 10 times more common than Jupiter-mass planets. The companion-to-host mass ratio distribution shows a deficit at q ~ 10⁻², separating the distribution into two companion populations, analogous to the stellar-companion and planet populations, seen in radial-velocity surveys around solar-like stars. Our survey, however, which probes mainly lower-mass stars, suggests a minimum in the distribution in the super-Jupiter mass range, and a relatively high occurrence of brown-dwarf companions.

1. INTRODUCTION

Over the last 20 years, our knowledge about planetary systems has increased dramatically, from one example with eight planets (our own Solar system) to over 1100 planetary systems hosting more than 1800 planets¹. The various planet-detection techniques are sensitive to different regions of the planetary parameter space, but the overall emerging picture from combining their results is that planetary systems are very common. The occurrence rate found by radial velocity and transits surveys, which have detected the majority of the known exoplanets, and are most sensitive to close-in planets, shows that, on average, about half of Sun-like stars host small planets (Earth to Neptune) within 1 AU, 10% have giant planets within a few AU, and about 10% among those giants are within a few hundredths of an AU (Winn & Fabrycky 2015). Moreover, systems with multiple close-in planets are not rare. The existence of close-in massive planets (“hot Jupiters”) requires a migration mechanism for those planets from beyond the ”snowline“, where they likely form according to planet formation scenarios (Ida & Lin 2005).

Complementing these discovery methods, gravitational microlensing, while having detected only tens of planets, offers a number of unique advantages. Microlensing is sensitive to planets at projected host separations of 1 to 10 AU, orbiting stars throughout a large volume of the Galaxy, among both the bulge and the disk populations (Gaudi 2012). Initial statistical analyses of microlensing surveys have suggested that, on average, every star in the Galaxy hosts at least one snowline planet (Cassan et al. 2012), and that the majority of them might be multiple-planet systems (Han et al. 2013). Microlensing surveys are also the only technique sensitive, in principle, to unbound planets. Sumi et al. (2011) argue that such free-floating planets are at least as common as main-sequence stars. However, due to the current small total number of microlensing-detected planets and the difficulties in turning these numbers into a statistical occurrence rate, the abundance of Solar-like planetary systems is still poorly known.

The traditional “first generation” strategy for exoplanet searches by the microlensing community has been to focus on specific microlensing events discovered by the OGLE (Udalski 2009) and the MOA (Sumi et al. 2003) microlensing surveys. These events have generally been bright and of high-magnification. Following alerts announced by the surveys, events that promised to be of high magnification (A ≳ 100) were monitored quasi-continuously by global follow-up networks, in order to search for planetary anomalies. The light curve of a bright and highly magnified event has a high signal-to-noise ratio (SNR), permitting observations with small (and even amateur) telescopes, which are a significant part of the follow up networks. The motivation for this strategy was that high-magnification events have the highest sensitivity to planets, since the source star image is distorted into a nearly full Einstein ring, and hence a planet anywhere in the Einstein ring vicinity will perturb the light curve and will be detected (Gould & Loeb 1992; Griest & Safizadeh 1998). Although this strategy was important for discovering the first microlensing planets, it also led to the main limitations of the first generation: (a) high-magnification events are rare (~1%) and hence overall a small number of microlensing planets have been discovered with this approach; (b) the alert and follow up process involves a complex social decision and communication process, sometimes after an event has already hinted at the possibility of an anomaly. This process is difficult to account for in a statistical analysis.

Exploiting the full planet discovery potential of microlensing requires a “second generation” (hereafter - genII) microlensing survey (Gaudi et al. 2009), in which a large fraction of all ongoing microlensing events toward the Galactic bulge - of both low and high magnification - are monitored continuously with a cadence that is high enough to detect planetary perturbations in the light curves. Apart from the larger number of expected planet discoveries, the “controlled experiment” nature of a genII survey allows for safer statistical inferences on the planet population. The requirements are straightforward - a network of 1m-class telescopes situated so as to allow 24-hour coverage of the bulge, equipped with degree-scale imagers.

There have been three main works to constrain snowline planet properties and frequencies based on first-generation surveys. Sumi et al. (2010) used the first ten microlensing-discovered planets to constrain the mass-ratio distribution of snowline region exoplanets and their hosts, and concluded that Neptune-mass planets are at least three times as common as Jupiters in this region. Gould et al. (2010) analyzed six planets discovered in high-magnification microlensing events that were intensively followed-up by the μFUN network (Gould 2008), and found that ~ 1/3 of microlensed stars host a snowline planet in the planet-to-star mass-ratio interval −4.5 < log q < −2, corresponding to the range of ice to gas giants. Moreover, since one of the systems had two planets with the same mass and distance ratios as Jupiter and Saturn to the Sun, they argued that the frequency of Solar-like systems around lens stars is about 1/6. Gould et al. (2010) argued that the chaotic nature of the “alert and follow-up” process results, in the end, in a randomization that minimizes selection effects and although it cannot be claimed to be a controlled experiment, it gives a high level of completeness. Finally, Cassan et al. (2012) combined the previous results and three additional planets that were discovered by the PLANET follow-up network (Albrow et al. 1998), and deduced a frequency of more than unity for snowline-region planets.

In June-July 2010, we carried out a 6-week pilot of a genII experiment. In 2011, we initiated the first full genII microlensing experiment, involving OGLE, MOA and the Wise Observatory microlensing group (Shvartzvald & Maoz 2012). During four observing seasons, we have monitored all events in a specific, 8 deg², field toward the Galactic bulge. In this paper we present a statistical analysis of these first four observing seasons (2011–2014) of our genII survey. The sample includes 224 microlensing events, monitored by all three groups. Over 12% of the events show clear anomalies in their light curves indicating a companion to the lens star. To assess the nature of the companions we perform a coarse grid-based search of the microlensing model parameter space for each event. Comparing the actual number of light curves having planetary anomalies to the total number of events, after accounting for the detection efficiency of each event, allows to estimate, for the first time, the frequency of planetary systems from a controlled microlensing experiment.

The paper is arranged as follows. In Section 2, we describe the observations and reductions of our sample of lensing events. In Section 3, we model each light curve in our sample with a single-lens model, describe our anomaly detection filter, and present the anomalous events among our sample. In Section 4 we derive the frequency and the mass-ratio distribution of snowline planets implied by our survey, and discuss the results in the context of current knowledge in Section 5.

2. OBSERVATIONS

2.1. Observational data and reduction

Our genII survey network is a collaboration between three groups: OGLE, MOA, and Wise. The OGLE and MOA groups regularly monitor a large region of the Galactic bulge, and routinely identify and monitor microlensing events. The Wise group monitors a field of 8 deg², within the observational footprints of both OGLE and MOA, having the highest event rates based on previous years’ observations (see Shvartzvald & Maoz 2012).

The OGLE group operates the 1.3m Warsaw University telescope at Las Campanas Observatory in Chile, with the 1.4 deg² field of view OGLE-IV camera. The genII survey’s 8 deg² footprint includes three extremely high-cadence OGLE-IV fields observed every ~15 minutes and five high-cadence OGLE-IV fields observed once per ~45 minutes. Standard OGLE observations are through an I filter. OGLE photometry used here was extracted by their standard difference image analysis (DIA) procedure (Udalski 2003). These OGLE data are the preliminary measurements posted on the Early Warning System website², which are not suitable for detailed modeling of the events, but sufficient for the anomaly-detection search and rough modeling that we perform here.

The MOA group operates the 1.8m MOA-II telescope in New Zealand with the MOA-cam3 camera, with a 2.2 deg² field of view (Sako et al. 2008). MOA-II monitors six extremely high-cadence fields (every ~15 minutes) which cover most of the genII 8 deg² field, and an additional six high-cadence fields (every ~45 minutes) which complement the network’s footprint. MOA uses a wide R/I filter (“MOA-Red”). The MOA data were reduced using their routine DIA procedure (Bond et al. 2001).

The Wise group’s main setup is the 1m telescope at Wise Observatory in Israel equipped with the LAIWO camera, with a 1 deg² field of view. The cadence for each of the eight Wise pointings (which define the survey footprint) is ~30 minutes. Observations are in the I band. In the first half of the 2012 season, the LAIWO camera had readout electronics problems and the Wise group used, as an alternative, the Wise C18 0.46m telescope with an I filter, with a 1 deg² field of view. The cadence for the eight C18 fields (which overlap with, but differ from the eight LAIWO fields) was ~1 hour. All Wise data were reduced using the pySis DIA software (Albrow et al. 2009).

2.2. Sample of lensing events

The sample of microlensing events analysed here consists of 224 events from the 2011–2014 bulge seasons, observed by all three groups, and with each group having data near the peak of the event. Without the last criterion, events with a long timescale that peak before the beginning of a season might enter the sample, while such events with a short timescale would not. Being the northernmost node of the network, with the shortest bulge observing season, Wise sets the time limits for the genII survey, from mid-April to mid-September of each season.

With the above criteria, and considering the limiting magnitudes of the various groups (see definition in Section 3.1), the initial sample has a relatively small number of events (230). After identifying anomalous events in our sample (see Section 3.3), we noted six events that passed the limiting magnitude criteria only because of the anomaly itself (due to a caustic crossing), and otherwise would not meet the criteria. Including these events would introduce a bias toward anomalous events, and therefore we exclude them from the sample. Table 2 lists the final sample of 224 events. For completeness, the excluded six events are listed separately at the end of the Table.

3. COMPANION DETECTIONS

3.1. Single-lens modeling of all events

As a first stage in our analysis, we model each of the 224 events with a single point-lens model, including the possibility of parallax and finite source effects. Such a model is necessary in order to subsequently detect those events that have lensing anomalies (Section 3.3), as well as to gauge the planet detection efficiency of each event (Section 3.2.2). Both of these elements of the analysis then enter our planet frequency calculation (Section 4).

The characteristic angular scale of a lensing phenomenon is the angular Einstein radius,

$${\theta }_E^2=\kappa M{\pi }_{rel},\kappa =\frac{4G}{c^{2}AU}\simeq 8.14\frac{mas}{M_{\odot }},$$ (1)

where M is the mass of the lens star, and the relative parallax is ${\pi }_{rel}=\mathrm{\text{AU}}\left(D_L^{-1}-D_L^{-1}\right)$, where D_S and D_L are the distances to the source and lens stars, respectively. A standard point-source, point-lens, microlensing model requires three “Paczyński parameters”: t_E—the event time scale, over which the source crosses one angular Einstein radius; u₀—the impact parameter, the minimal separation between the source star and lens star in angular Einstein radius units; and t₀—the time of minimal separation between the source star and the lens star. There are two higher-order effects, which can change the light curve even in the absence of a companion to the lens. First, the finite source size needs to be taken into account when the scale in the source plane over which the magnification varies is of the order of the source size. This effect is parametrized by the ratio between the angular size of the source, θ_*, and the angular Einstein radius, ρ = θ_*/θ_E. Second, the orbital microlens parallax, π_E, changes the relative proper motion between the source star and the lens during an event, due to the Earth’s orbit. The effect is parametrized by the size of the angular Einstein radius, projected onto the observer plane in astronomical units (AU), and can be represented by: π_E = (π_rel/θ_E)(μ/μ), where μ is the relative proper motion between the source and the lens. The microlens parallax is divided into a north and east component with respect to the Galactic coordinate system, π_E,N and π_E,E. The orbital parallax involves a well known u₀ ↔ −u₀ ecliptic degeneracy for sources near the ecliptic (Jiang et al. 2004; Poindexter et al. 2005), and we explore both options in our modeling.

During a microlensing event, an additional constant flux from stars along the line of sight to the source, that do not get magnified due to the lens (in particular, the lens star itself), contributes to the light curve. Thus the total flux, f(t), is the sum of the source flux, f_s, times the magnification, A(t), and the background flux, f_b. Due to the different filters and seeing conditions of each survey group, this is calculated separately for each dataset, i,

$$f_i\left(t\right)=f_{s,i}\cdot A\left(t\right)+f_{b,i\cdot }$$ (2)

When exploring the lens-model parameter space, we limit the ranges of some of the parameters, to avoid biases and unphysical solutions. First, we include only events with |u₀| < 1, i.e. with peak magnifications A > 1.34. In addition, we limit the crossing time scale to values t_E < 500 days. Finally, we limit each component of π_E to be less than 1.5. Events that exceed these limits on t_E and π_E can, in principle, occur for extreme configurations. However, their probability is negligible given the number of events in our sample.

The MOA and Wise fluxes were aligned to the OGLE I-band magnitude scale, and inter-calibrated to the single-lens microlensing model. In order to obtain the different photometric precision for each group, we construct an observed distribution of the residuals from the model for the entire dataset (from all events), and calculate its root mean square (RMS) as a function of OGLE I-band magnitude. This accounts for differences in telescope aperture, the different seeing conditions at each site, and overall systematics in the reduction pipelines. Figure 1 shows the RMS of the residuals for each group.

Figure 1.

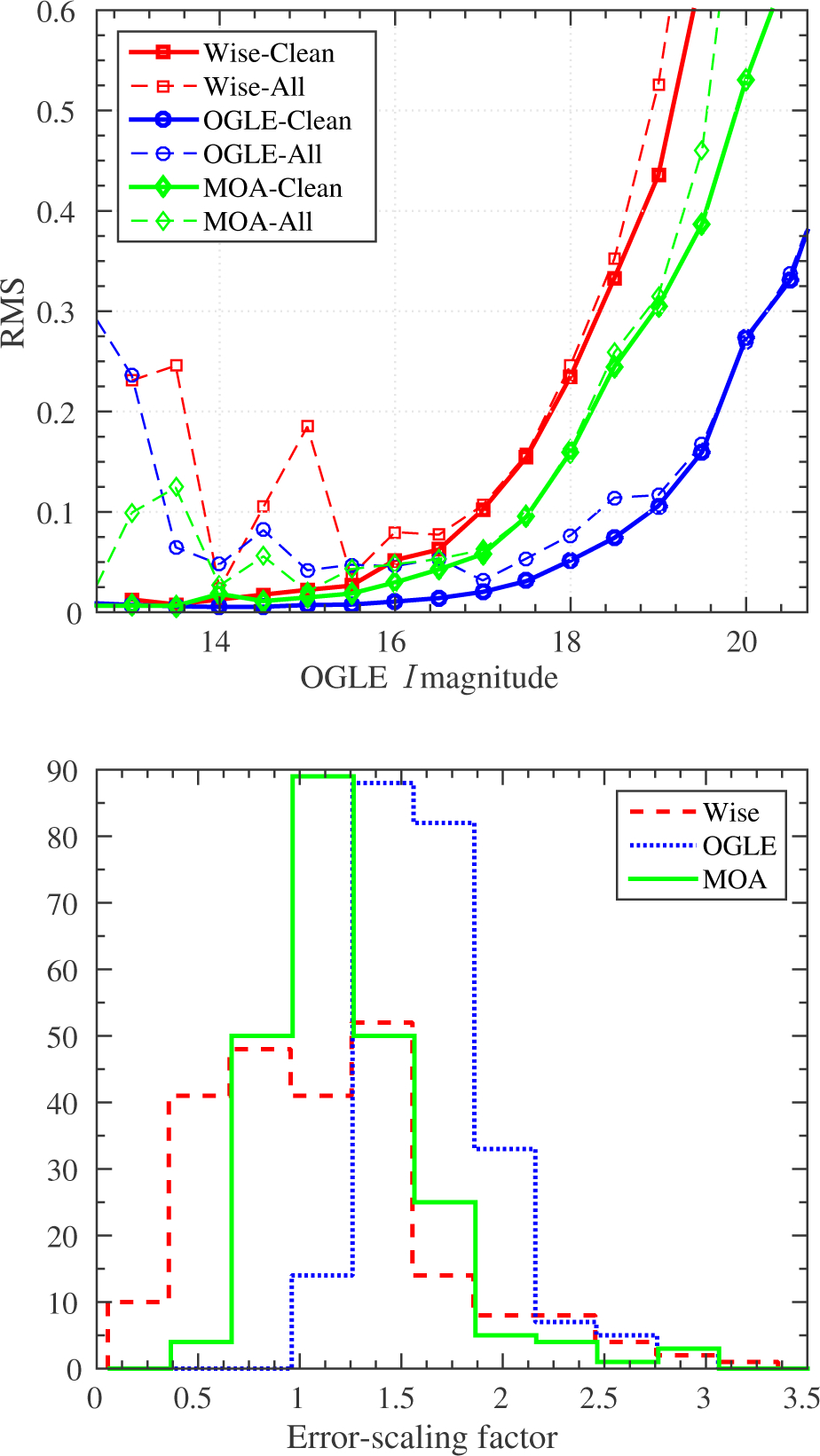
Top: root mean square (RMS) of residuals of best fits of single-lens microlensing models to all observed light curves, including all data (dashed line) and after excluding outliers and anomalies (solid line), for each group as a function of OGLE I-band magnitude at a given point in the light curve (OGLE - blue circles, MOA - green diamonds, Wise - red squares). The differences between groups reflect both the instrumental and site quality (collecting area, seeing conditions, CCD sensitivity) and the DIA pipeline for extracting the photometry. Bottom: error-scaling factor distributions for the 224 events, and for each group. Most of the pipeline-reported errors underestimate the real uncertainties. The tails shown by each distribution at large factors reflect events with long-duration anomalies.

Yee et al. (2012) have studied the effect of faint sources on microlens parameters for the lensing event MOA-2011-BLG-293, and found that when the measured flux errors are comparable to, or larger than the source flux, particularly near baseline, this leads to biases in the measured Einstein timescale. Based on their conclusions and by analyzing the precision at each site, found above, we exclude from each light curve in our sample data points for which the observed residual distribution corresponding to the underlying event’s I-magnitude (as suggested by the single lens model) has a root-mean square (RMS) greater than 0.33 mag (SNR~3, below that the microlensing signal cannot be reliably detected). This corresponds to events with Wise points with baseline magnitudes fainter than 18.5 mag, and MOA baseline points fainter than 19.5 mag. For OGLE we include all points.

Each microlensing event in our sample is modeled with the three Paczyński parameters, the two flux intercalibration parameters for each dataset, the finite source effects, and the orbital parallax (testing for both u₀ > 0 and u₀ < 0). We explore this parameter space and find the best model parameters, and their uncertainties, using a Markov-Chain Monte Carlo (MCMC) algorithm. Outlier data points and real microlensing anomalies will obviously draw our solution away from the true one. We therefore use an iterative algorithm for the exclusion of outliers (which naturally also applies to intervals in the light curve that include anomalies). The photometric errors reported by DIA programs are usually underestimates. Therefore, for each dataset we scale these errors to set χ² per degree of freedom (DOF) equal unity, without the outliers and anomalies which will bias the distributions, allowing to estimate the real precision of each dataset. Figure 1 shows the distribution of error scaling factors for each group. The median factors for OGLE, MOA and Wise are 1.74, 1.32 and 1.21, respectively. Finally, we initiate the entire modeling process again without the excluded outliers and with the rescaled errors. Figure 2 shows an example of the results of our outlier detection and exclusion algorithm, for an event with a strong parallax signal, where the single-lens model fits well the light curve after outlier points are excluded.

Figure 2.

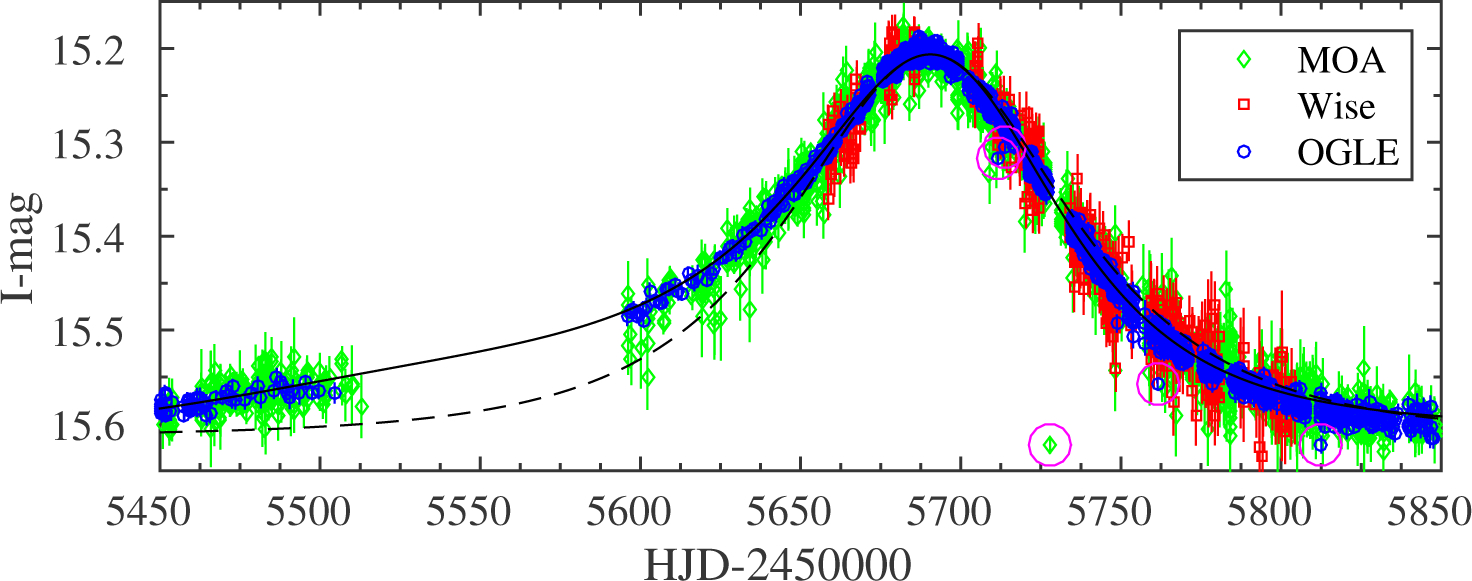
Example of detection and exclusion of outlier points from the single-lens model in event OGLE-11–0022/MOA-11–025, which has a strong microlens parallax signal (but no detected anomaly from a companion). The detected outlier points are circled. The solid line is the best-fit microlensing model including parallax, and the dash-dot line is one without parallax. The light curve is clearly asymmetric, and thus without including parallax it would have been flagged as anomalous.

Table 2 in Appendix A lists the best single-lens model parameters for each event in our sample, and their uncertainties, which were extracted from the MCMC estimation of the covariance matrix. Microlens parallax is significantly detected (Δχ² > 100 with respect to a model without parallax) in 10% of the non-anomalous events, while finite source effects are found in 3% of the non-anomalous events. The values for the microlens parallax and finite source parameters for those events are marked in boldface in the table. We do not mark the values for anomalous events, since the anomaly might affect those parameters, and they can be reliably detected only with a full binary-lens model.

Figure 3 shows, for the entire sample of events, the distributions of the best-fit values of the event timescale, t_E, and the impact parameter, u₀. The t_E distribution is shown fitted with a log-normal function, $N\propto \mathrm{\text{exp}}\left(-\frac{{\left(\mathrm{\text{log}}\left(t_{\text{E}}\right)-\mu \right)}^2}{2{\sigma }^2}\right)$, with median timescale of 19.5 days. u₀ should, in principle, follow a uniform probability. However, faint sources that undergo high magnification will be detected, while similar sources undergoing a lower magnification event will be missed, due to the limiting magnitudes of the surveys, introducing a bias towards high magnification (low u₀) events. The t_E and u₀ distributions of our sample are almost identical to the distributions of those parameters from previous years’ OGLE and MOA microlensing seasons (see Shvartzvald & Maoz 2012). This shows that our sample has no obvious biases, and thus represents a typical population of lenses and sources.

Figure 3.

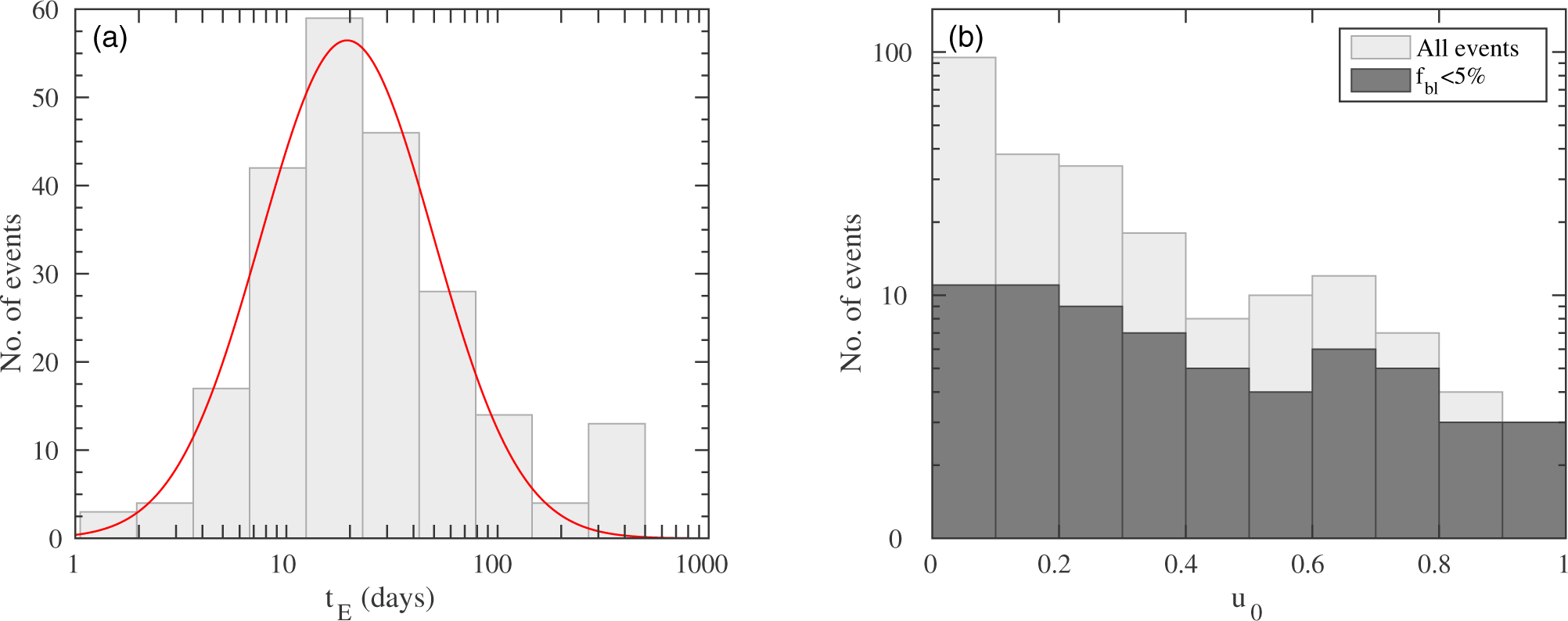
Best-fit single-lens parameters for the sample of 224 lensing events: (a) Distribution of event timescale, t_E. The solid curve is a lognormal fit,), $N\propto \mathrm{\text{exp}}\left(-\frac{{\left(\mathrm{\text{log}}\left(t_{\text{E}}\right)-\mu \right)}^2}{2{\sigma }^2}\right)$, with μ = 1.29 (corresponding to 19.5 days) and σ = 0.54; (b) Distribution of impact parameter, u₀ (light-gray). Due to selection favoring the detection of highly magnified faint events over weakly magnified faint events, there are more events at smaller impact parameters. The dark-gray histogram shows the distribution only for unblended (i.e. relatively bright) events, which are distributed more uniformly, as expected.

3.2. Anomaly detection filter

A companion (or multiple companions) to the lens star can break the symmetry of the microlensing light curve, introducing an anomaly with respect to the single-lens model. In order to identify microlensing anomalies in the light curves in our sample, we follow Shvartzvald & Maoz (2012) and define an anomaly detection filter using a ”running” χ² estimator,

$${\chi }_{\mathrm{\text{local}}}^2=\sum _{i=1}^N\frac{{\left(f_i-f_{\text{Pl}}\right)}^2}{{\sigma }_i^2},$$ (3)

where f_i and σ_i are the observed flux and the re-scaled error of each epoch, respectively, and f_pl is the point-lens model flux at that time. The local χ² is repeatedly calculated by advancing the center of the filter one observed epoch at a time. Since the relative duration of an anomaly is roughly proportional to the square root of the lens-companion mass ratio, we would like the time interval of each summation to be as short as possible, in order to be sensitive to low-mass planets. However, in order to avoid false-positive detections in short timescale events, N cannot be too small, and we study the sensitivity of our filter to N below (see Section 3.2.1 for more details). An anomaly is considered detected if:

1. ${\chi }_{\mathrm{\text{local}}}^2$ divided by the number of summed points, N, is larger than some threshold value, P_thresh.

2. at least three consecutive data points have at least a 3σ deviation from the point-lens model.

This latter criterion deals with the possibility that photometric outlier points will affect the local χ² test and can lead to false detections.

3.2.1. False-positive optimization

In order to optimize the number of false-positive detections (i.e. to reduce their numbers without overly sacrificing true detections), we have studied the sensitivity of our anomaly detection filter to its two parameters (N, P_thresh). For each of the 224 events in our sample, we use the fitted point-lens parameters to construct a magnification curve. We then sample the light curve at the exact epochs on which the event was observed by each group. With this we account for all gaps due to weather or technical failures, and for the different sampling cadence by each group and for each field. The theoretical magnification curve is then randomly noised, using the observed residual distribution that we have found for each group (see Section 2.1), and assigned the scaled-errors from the real data, to create 500 simulated point-lens light curves for each event. We then search for a false-positive anomaly in the simulated light curve (which has no real anomalies), varying the filter parameters.

We find that the fraction of simulated light curves that trigger the photometric outlier filter (i.e. three consecutive points with > 3σ) is 0.65%. Examining those triggers, we find that 92% of them have ${\chi }_{\mathrm{\text{local}}}^2/N<P_{\mathrm{\text{thresh}}}$, where P_thresh is in the range 7.5 to 8. The optimal P_thresh varies from event to event, and depends linearly on the maximum amplification (D_mag), which is the difference between the observed baseline magnitude of the event and its peak magnitude, with also a weak dependence on N. The optimal value of N is N = 40. For much smaller N, the ${\chi }_{\mathrm{\text{local}}}^2$ can be dominated by a single outlier point, while for much larger values, the anomalous region can be smoothed out and not detected. Using this N and the D_mag-dependent value of P_thresh, 8% of the 0.65% of the outlier-triggered events trigger an anomaly detection, and thus the resultant false-positive rate is at a low level of 0.05%. These high-threshold criteria help to reduce false-positive detections in the real data, but do not completely avoid them, due to the presence of red noise (i.e. correlated deviant points), a noise that is not included in these randomly noised simulations.

3.2.2. Detection efficiency

In order to estimate the sensitivity of our microlensing survey to planets and stellar binaries, we have constructed a large sample of simulated microlensing light curves for point-mass lenses with point-mass companions, which were calculated with an adaptive-mesh inverse ray-shooting microlensing light curve generator (see Shvartzvald & Maoz 2012 for details). Specifically, for each of the 224 events in the real sample, we created a model with the same best-fit point-lens parameters, as described above, plus a companion to the lens star. The companion introduces three additional parameters: q—the mass ratio between the companion and the lens star; and the two-dimensional projected position of the companion in the lens plane, relative to the host star position, given by means of a projected angular separation, s, in units of the angular Einstein radius, and an angle, α, measured counter-clockwise from the source trajectory in the lens plane. We explore a mass-ratio distribution, uniform in log q, in the range −6 < log q < 0, a uniform distribution in the scaled projected separation of 0.3 < s < 3 (which encompasses the region microlensing is sensitive to), and all possible angles α. Our working assumption is that the probability for a companion is independent of an event’s single-lens parameter probabilities, which incorporate the host-star properties of mass, proper motion, and distance. For every real event, 3000 simulated light curves, with a variety of companions, were generated.

The simulated magnification curves of each event are then sampled exactly like the real event and randomly noised, as described for the point-lens models used for the false-positive optimization procedure. We then search for anomalies in the simulated light curves with the same procedure and detection criteria that were used for the real data. Explicitly, each light curve is modeled with a point-lens and higher order effects (including error-scaling for each observatory), and we search for an anomaly with our detection filter, using the parameters we found for minimizing the false-positive rate.

The “lensing zone” is the range of separations, s, in which microlensing is sensitive to anomalies caused by a given mass ratio. For stellar binaries (i.e. q ⩾ 10⁻²), the lensing zone can extend over a factor of a few in s. For small companions, q ⩽ 10⁻³ (likely planets), we find that the range 0.5 ⩽ s ⩽ 2 covers over 95% of the detections, and therefore we calculate our detection efficiency for that range. The companion detection efficiency for each event as a function of mass ratio q was found by marginalizing over s and α:

$$\eta \left(q\right)=\frac{\iint \Theta \left(q,s,\alpha \right)sdsd\alpha }{\iint sdsd\alpha },\Theta \left(q,s,\alpha \right)=\{\begin{array}{c}1,\mathrm{\text{anomalous}}\\ 0,\mathrm{\text{no}}\mathrm{\text{anomaly}}.\end{array}$$ (4)

Figure 4 shows the results of our detection efficiency simulation. The sensitivity varies by over an order of magnitude among different events, due to the brightness of the event, its magnification and its timescale, as shown by the 90^th and 10^th percentile efficiency curves (dashed) in Figure 4. We find that our experiment is ~ 6 times more sensitive to q = 10⁻³ (corresponding to a ~Jupiter/Sun mass ratio) than to q = 10⁻⁴ (“super-Neptunes”).

Figure 4.

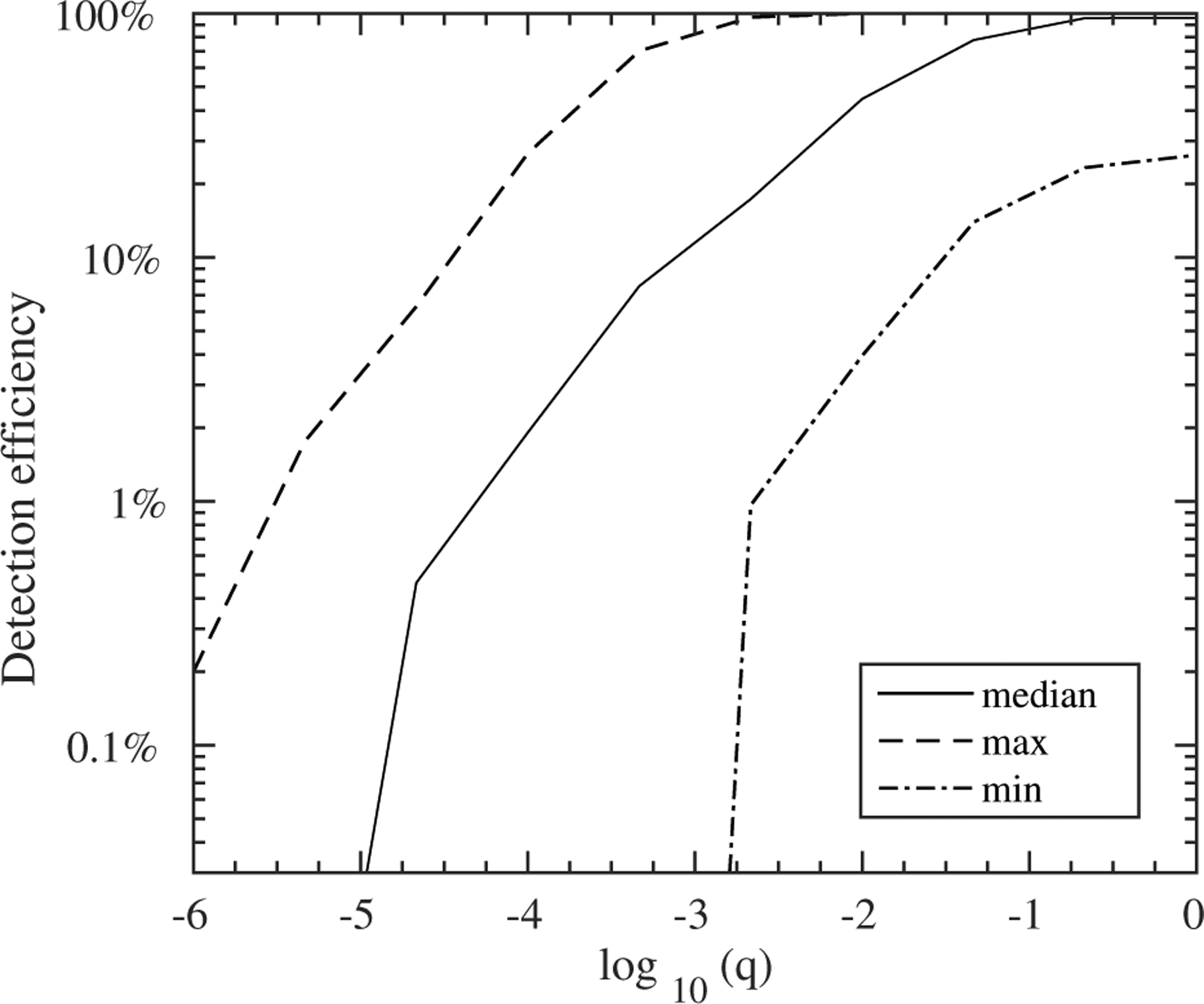
Detection efficiency for a single companion as a function of mass ratio, q. The event with median efficieny is shown as the solid line. The dashed curves represent events with 10^th and 90^th percentile sensitivities.

3.3. Anomalous events

3.3.1. Heuristic detections

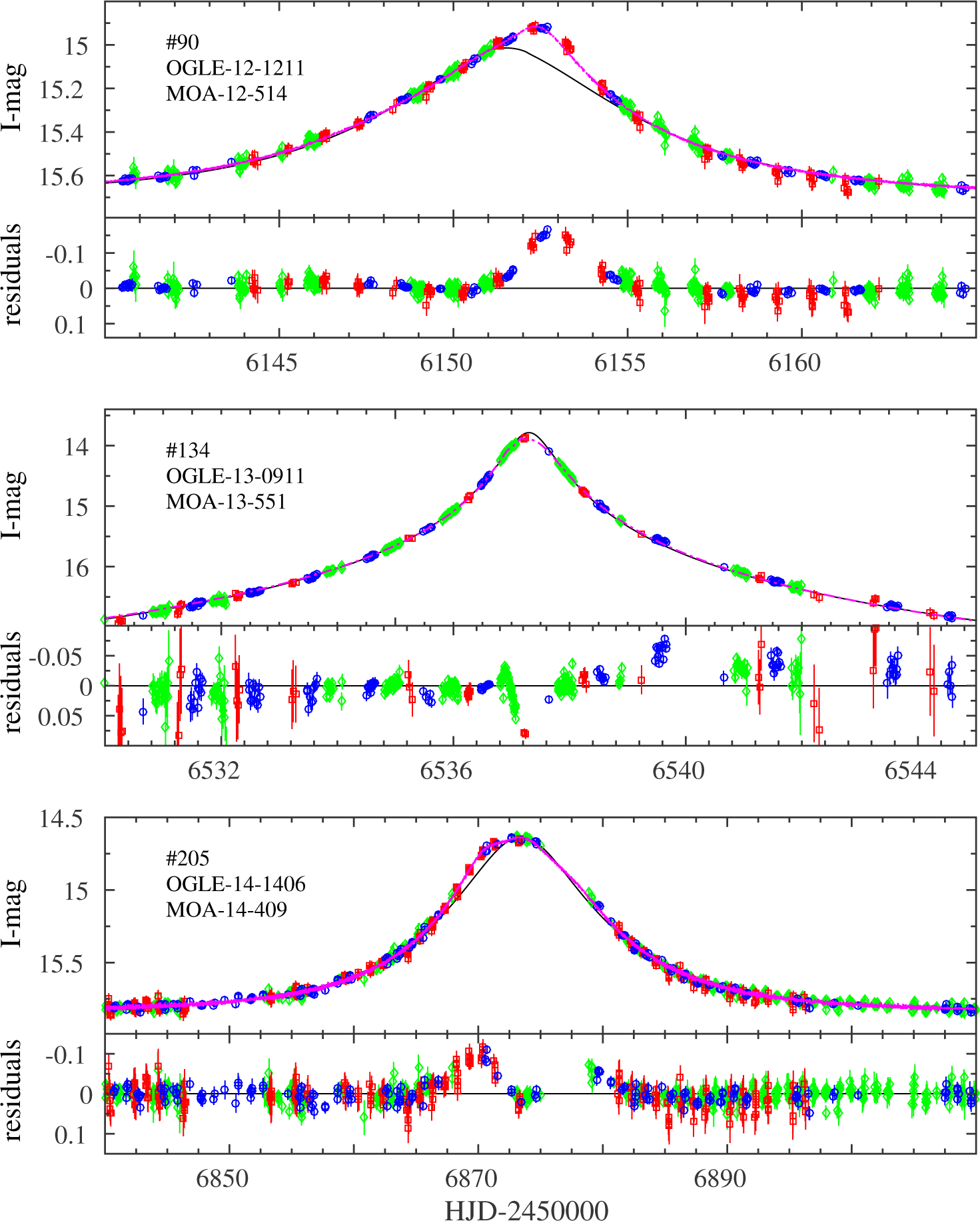
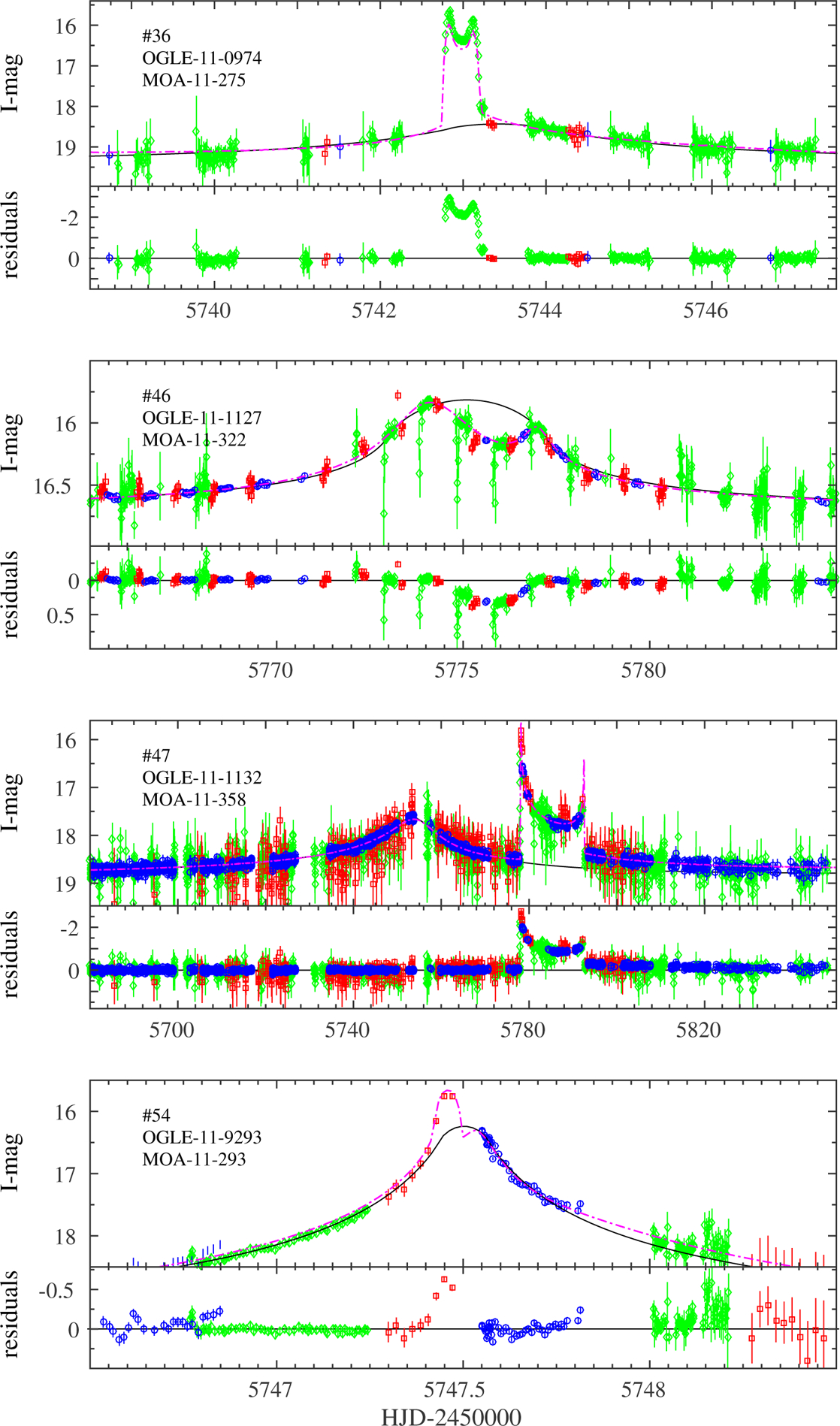
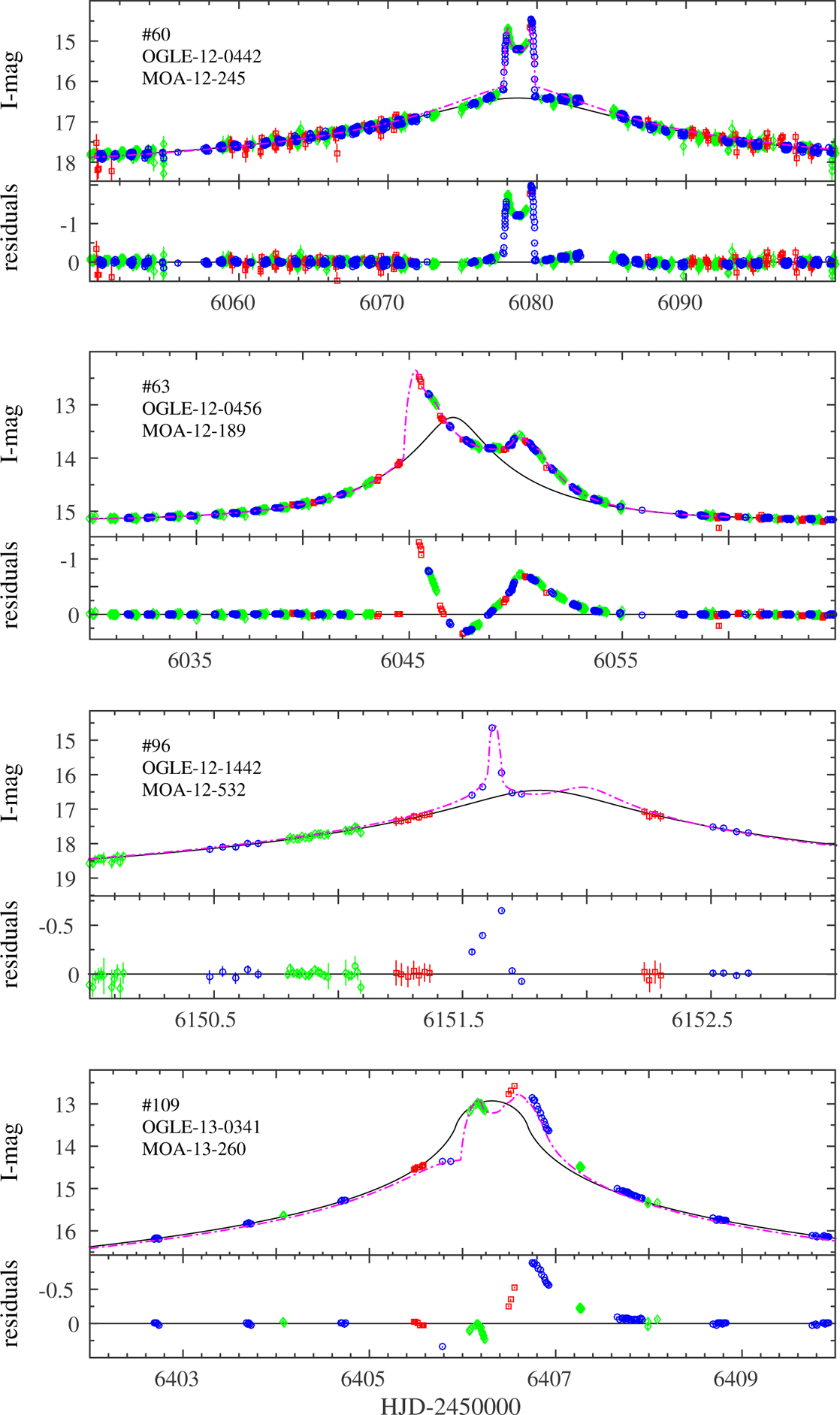
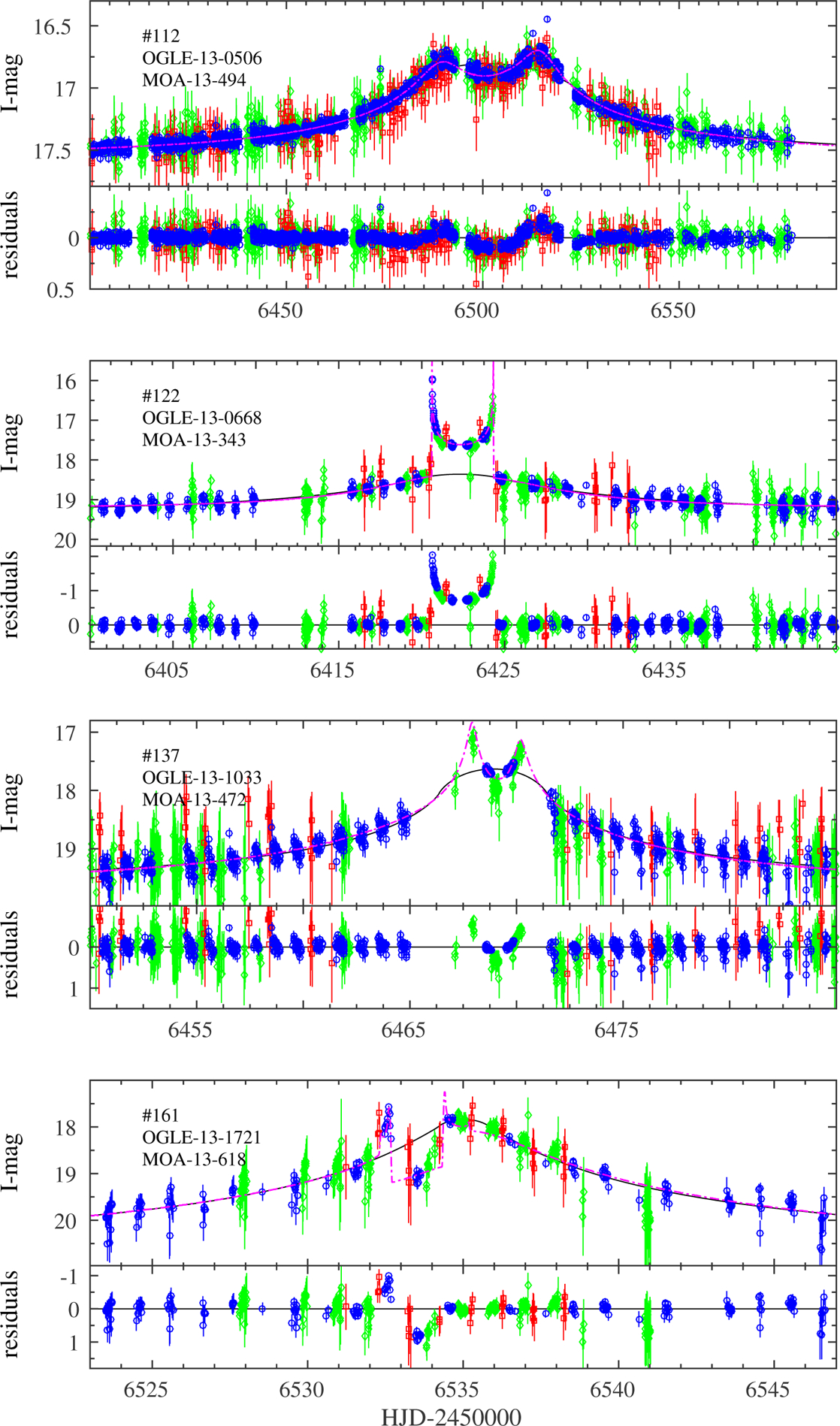
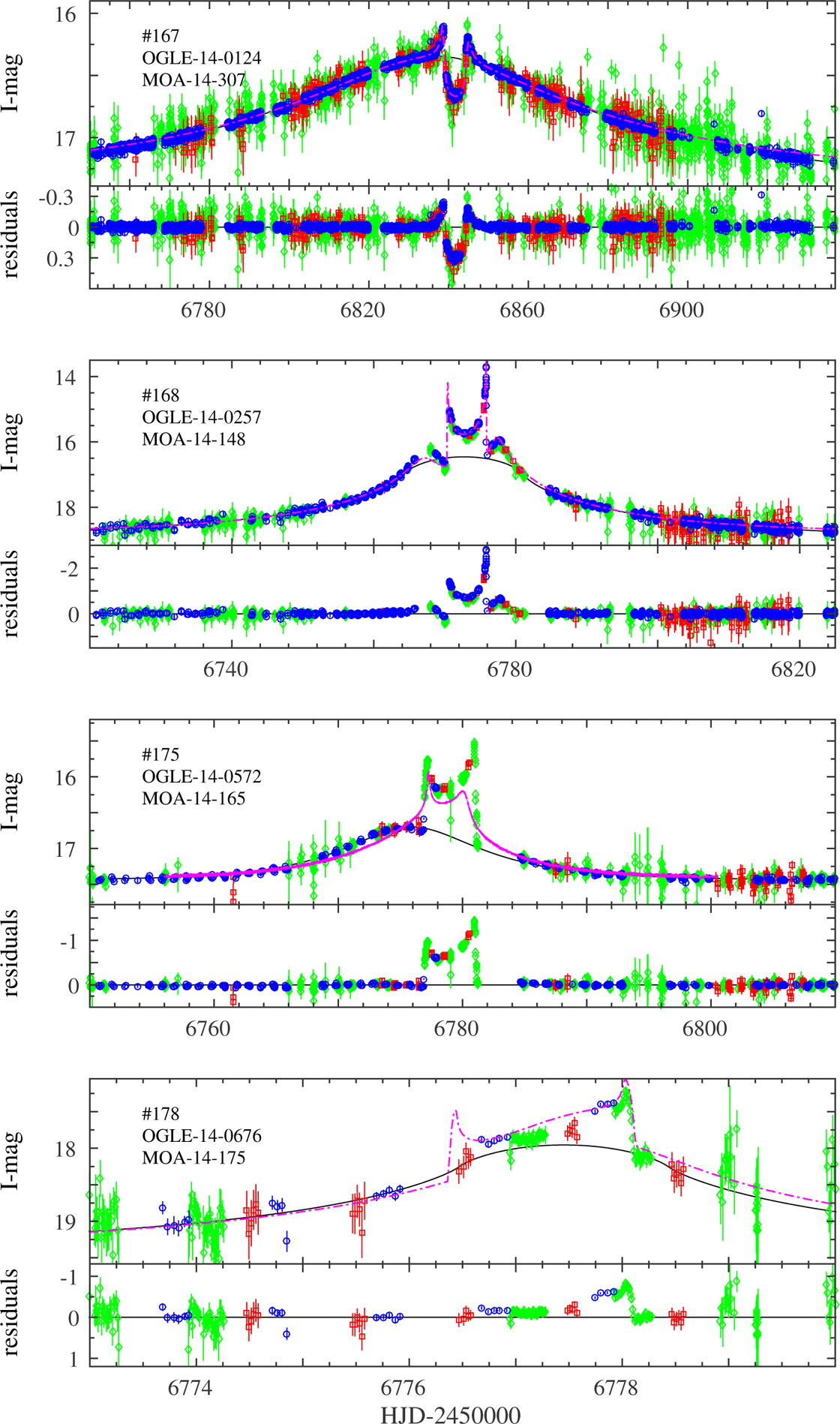
Before applying to the sample our objective automated anomaly detection filter, we have identified “by eye” 26 anomalous events among the sample in which deviations from the best-fit point-lens models are clear. Figures 5–11 show the inter-calibrated light curves of these 26 events and their best-fit single-lens models, obtained after excluding the anomalous regions from the fit (i.e., points detected by the anomaly detection filter). Eight of those anomalous events have already been modeled and published, as follows.

Figure 5.

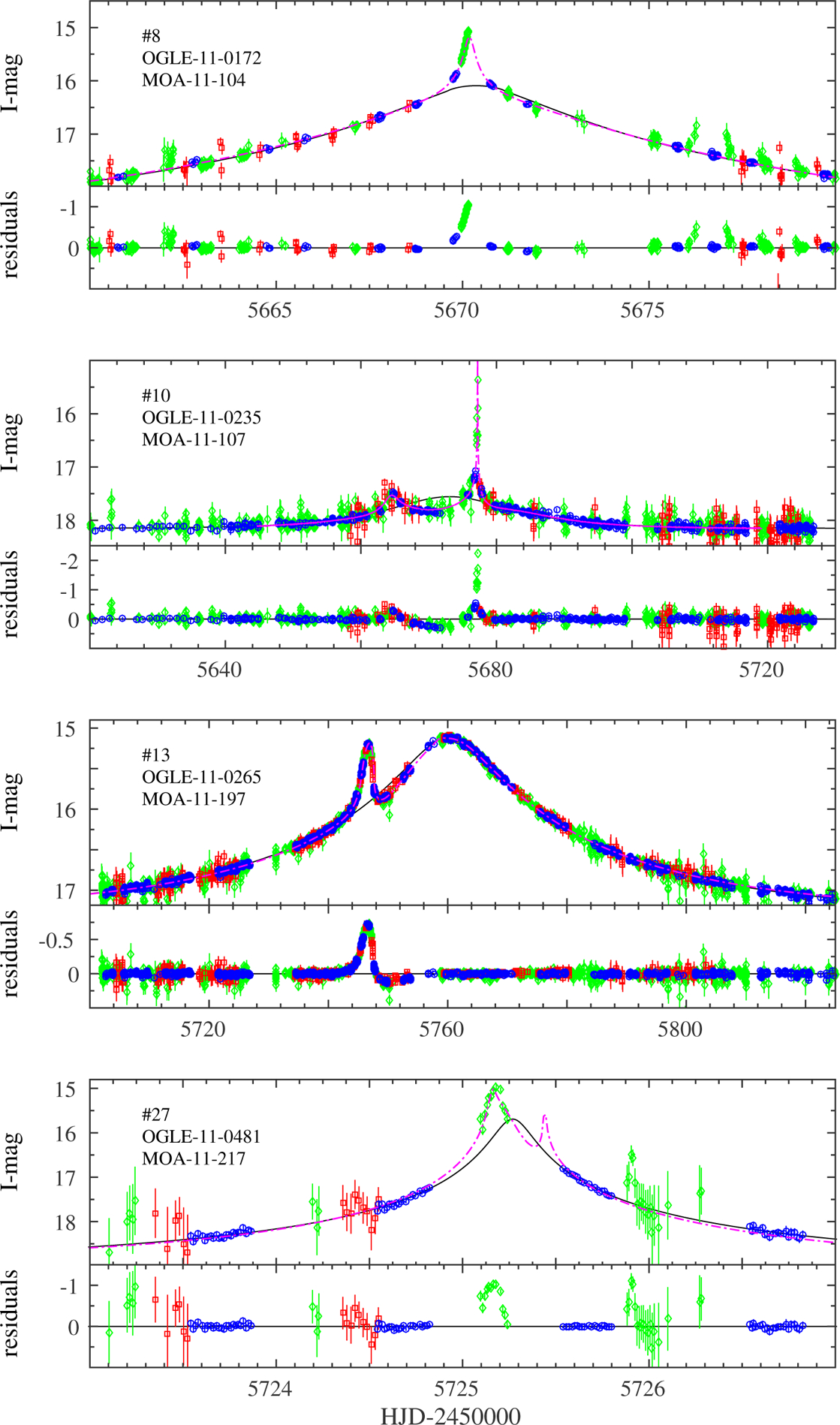
Inter-calibrated light curves of events with a clear anomaly that we identify by-eye: OGLE - blue circles, MOA - green diamonds, Wise - red squares. Magenta lines are the best-fit model, either published or from the grid search. The residuals from the point-lens model are shown in the lower panel of each event. The identifying number from Appendix A is marked in the upper-left corner.

Figure 11.

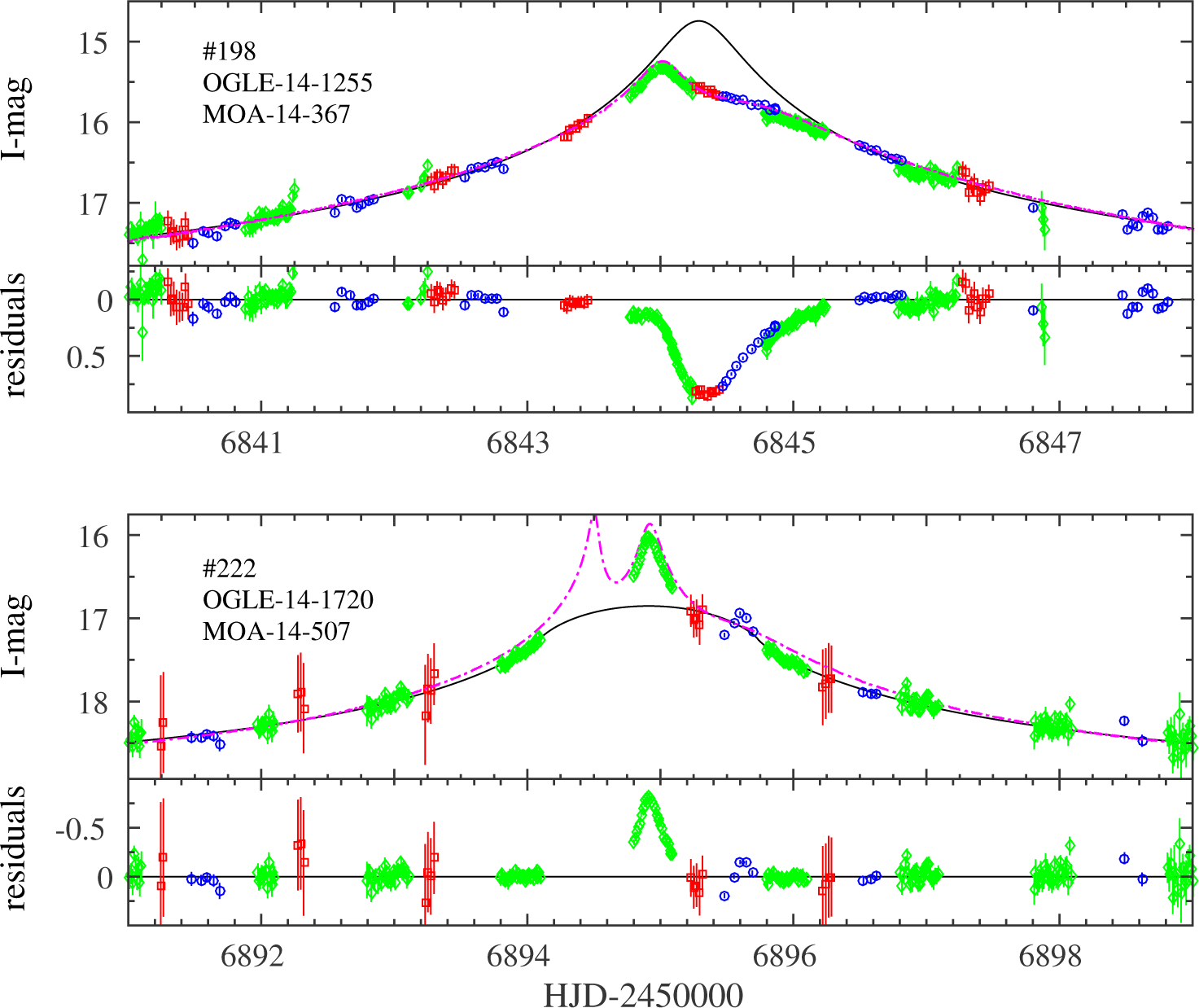
Inter-calibrated light curves of events with a clear anomaly that we identify by-eye: OGLE - blue circles, MOA - green diamonds, Wise - red squares. Magenta lines are the best-fit model, either published or from the grid search. The residuals from the point-lens model are shown in the lower panel of each event. The identifying number from Appendix A is marked in the upper-left corner.

1. MOA-2011-BLG-293 (Yee et al. 2012) was the first planet discovered by our genII survey. The event was highly magnified, and so was also followed up by several groups. However, Yee et al. (2012) showed that the survey data alone were sufficient to fully constrain the planetary model. Batista et al. (2014) used Keck adaptive optics observations to further constrain the system’s parameters by isolating the light from the lens star, and found that this ~ 5M_J planet is actually the first microlensing planet discovered in the habitable zone of its host star (a G-type main sequence star).

2. MOA-2011-BLG-322 (Shvartzvald et al. 2014), a moderate-magnification event that did not trigger alerts and follow up efforts, was the first planetary microlensing event that was detected and analyzed based solely on the genII survey data. Using a Bayesian analysis that incorporates a Galactic structure model, Shvartzvald et al. (2014) estimated that it is a ~ 12M_J planet orbiting an M-type dwarf.

3. OGLE-2011-BLG-0265 (Skowron et al. 2015) is a Jupiter-mass planet (with two degenerate solutions of ~ 1M_J and ~ 0.6M_J) orbiting an M dwarf. After the main anomaly was realized from the genII data, the event was alerted. Several follow-up groups monitored the event, allowing a better characterization of the secondary anomaly. This is an example of the problematic, in terms of an eventual statistical interpretation, process of the “first-generation” mode of surveys. The survey data alone were, again, sufficient to fully constrain the planetary model.

4. OGLE-2013-BLG-0341 (Gould et al. 2014) is a ~ 2M_⊕ planet in a ~1 AU orbit around one member of a ~15 AU separation binary M-dwarf system. The event was alerted and followed up since it was highly magnified, but the genII survey data cover all three anomaly regions. Moreover, the two lower-amplitude features, which are the ones that revealed the presence of a planet, were covered only by the genII survey data.

5. OGLE-2014-BLG-0124 (Udalski et al. 2015) is a ~ 0.5M_J planet orbiting a K-type dwarf. This was the first microlensing planet co-observed with the Spitzer space mission, and used to measure the microlens parallax from simultaneous observations from Earth and space. Udalski et al. (2015) use data only from OGLE and Spitzer, but the anomaly and the parallax signal are obvious also from the genII survey data alone.

6. The physical parameters of the companions in three additional published events have not been fully determined, but all of them are likely to be binary-star systems. MOA-2011-BLG-104 (Shin et al. 2012) is a binary with a candidate brown-dwarf companion (q ~ 0.09). OGLE-2012-BLG-0456 and MOA-2012-BLG-532 (Henderson et al. 2014) have mass ratios of q ~ 0.9 and q ~ 0.5, respectively.

We note that the anomalies seen in OGLE-2011-BLG-0481/MOA-2011-BLG-217, which appear only in MOA data, are possibly not real, and if not are an example of the type of false positives that can enter our sample after all. In line with our methodology, we include this event in our sample.

3.3.2. Objective detections

We next apply our automated detection filter to search for anomalies in each event in our sample, with the optimized false-positive filter parameters that we found. The 26 anomalous events, identified by eye in Section 3.3.1 are all easily re-detected by the automated filter. In addition, the automated filter detects three more anomalous events. The light curves of those events, and the residuals from their best-fit point-lens models, are shown in Figure 12.

Figure 12.

Inter-calibrated light curves of three anomalous events detected by our detection filter, in addition to those detected both by eye and by the filter, and shown in Figures 5–11. The residuals from the point-lens model are shown in the lower panel of each event, revealing the anomalous region.

Table 1 summarises all anomalous events and their estimated mass ratios. The mass ratios are either from the full binary-lens published models (eight events, see Section 3.3.1) or from a grid search of binary-lens models from a library we constructed, similar to the one used in Section 3.2.2 for the detection efficiency estimates, with 36,000 combination of s, q and α (20, 50 and 36 grid points respectively). We present the best-fit model, either published or from the grid search, as magenta lines in figures 5–12. From the χ² confidence interval of the grid-based fits, we estimate a precision of ~ 0.2 dex for the mass ratios. A full binary-lens model will obviously set stronger constraints on the mass ratio in each system. However, for the purpose of our present statistical analysis, the above precision is sufficient.

Table 1.

Anomalous events. The first 26 events display a clear anomaly and are detected both by eye and by the filter, while the last three, separated by double horizontal lines, are found only by our detection filter.

#	OGLE No.	MOA No.	q	mass from model	model reference
8	11–0172	11–104	0.121 ±0.005	0.02 ± 0.01Mʘ	Shin et al. (2012)
10	11–0235	11–107	~ 0.77
13	11–0265	11–197	(3.95 ± 0.06) × 10−3	0.6 ± 0.2MJ	Skowron et al. (2015)
27	11–0481	11–217	~ 0.014
36	11–0974	11–275	~ 0.24
46	11–1127	11–322	0.028 ± 0.001		Shvartzvald et al. (2014)
47	11–1132	11–358	~ 0.77
54	11–9293	11–293	(5.3 ± 0.2) × 10−3		Yee et al. (2012)
				4.8 ± 0.3MJ	Batista et al. (2014)
60	12–0442	12–245	~ 0.093
63	12–0456	12–189	0.944 ± 0.004		Henderson et al. (2014)
96	12–1442	12–532	0.47 ± 0.04		Henderson et al. (2014)
109	13–0341	13–260	(4.8 ± 0.3) × 10−5	2.3 ± 0.2M⊕	Gould et al. (2014)
			1.21 ±0.03	0.17 d= 0.01Mʘ
112	13–0506	13–494	~ 0.50
122	13–0668	13–343	~ 0.61
137	13–1033	13–472	~ 0.4
161	13–1721	13–618	~ 1.1 × 10−3
167	14–0124	14–307	(6.9 ± 0.4) × 10−4	0.5 ± 0.1MJ	Udalski et al. (2015)
168	14–0257	14–148	~ 0.24
175	14–0572	14–165	~ 0.15
178	14–0676	14–175	~ 1.4 × 10−3
182	14–0727	14–281	~ 0.77
188	14–0900	14–305	~ 0.77
191	14–0962	14–285	~ 0.98
195	14–1109	14–328	~ 0.83
198	14–1255	14–367	~ 0.19
222	14–1720	14–507	~ 0.093
90	12–1211	12–514	~ 0.19
134	13–0911	13–551	~ 2.6 × 10−4
205	14–1406	14–409	~ 0.19

4. PLANET OCCURRENCE FREQUENCY AND MASS-RATIO DISTRIBUTION

The overall abundance of planets near the snowline (0.5 < s < 2) can be estimated by integrating over the frequencies of companions up to a certain mass ratio, even without the need to fully constrain the absolute masses of the companions. The population of lenses in our monitored genII field is dominated by old bulge stars. The mass function of lenses toward the Galactic bulge, as modeled by Dominik (2006), is a narrow distribution, with the most probable lens mass of ~0.3M_⊙. If we define the planet mass limit at 13M_J (the limiting mass for thermonuclear fusion of deuterium, assuming Solar metallicity, e.g. Perryman 2011), then the corresponding planetary mass ratio limit is q = 4.1 × 10⁻². For the present analysis, we will therefore define planets as companions with log q < −1.4.

The underlying distribution of mass ratios between companions and primary stars in the population of stars that produce microlensing events can be inferred by correcting the observed distribution of our sample for the detection efficiencies that we derive from the simulations above. The frequency of companions for a given range of mass ratios is simply the number of detected companions within that range, N, divided by the sum of the detection efficiencies for that range, η, over all events in the sample,

$$f\left(q\right)=\frac{N\left(q\right)}{\sum \eta \left(q\right)}\cdot$$ (5)

Figure 13 shows the observed distribution of mass ratios for our sample in bins of 0.7 dex, and the recovered distribution after accounting for our detection efficiency. The right-hand vertical axis shows the frequencies as a function of mass ratio. We divide the planetary regime into two ranges of mass ratios, 10^−2.8 < q < 10^−1.4 and 10^−4.9 < q < 10^−2.8, which correspond to Jupiters and Neptunes, respectively. By choosing these ranges of 1.4 dex and 2.1 dex, we slightly reduce the Poisson uncertainties, though they still dominate over the detection efficiency uncertainties in each bin. The frequency of snowline Jupiters is

$$f\left({10}^{-2.8}<q<{10}^{-1.4}\right)={5.0}_{-2.4}^{+4.0}\%,$$ (6)

and the frequency of Neptunes is

$$f\left({10}^{-4.9}<q<{10}^{-2.8}\right)={50}_{-22}^{+34}\%\cdot$$ (7)

Thus, the total frequency of snowline planets of these masses is

$$f\left({10}^{-4.9}<q<{10}^{-1.4}\right)={55}_{-22}^{+34}\%\cdot$$ (8)

For the binary regime we find that the frequency of brown dwarf companions is

$$f\left({10}^{-1.4}<q<{10}^{-0.7}\right)={4.7}_{-1.8}^{+2.6}\%\cdot$$ (9)

and the frequency of stellar companions is

$$f\left({10}^{-0.7}<q<1\right)={7.8}_{-4.6}^{+4.9}\%\cdot$$ (10)

Figure 13.

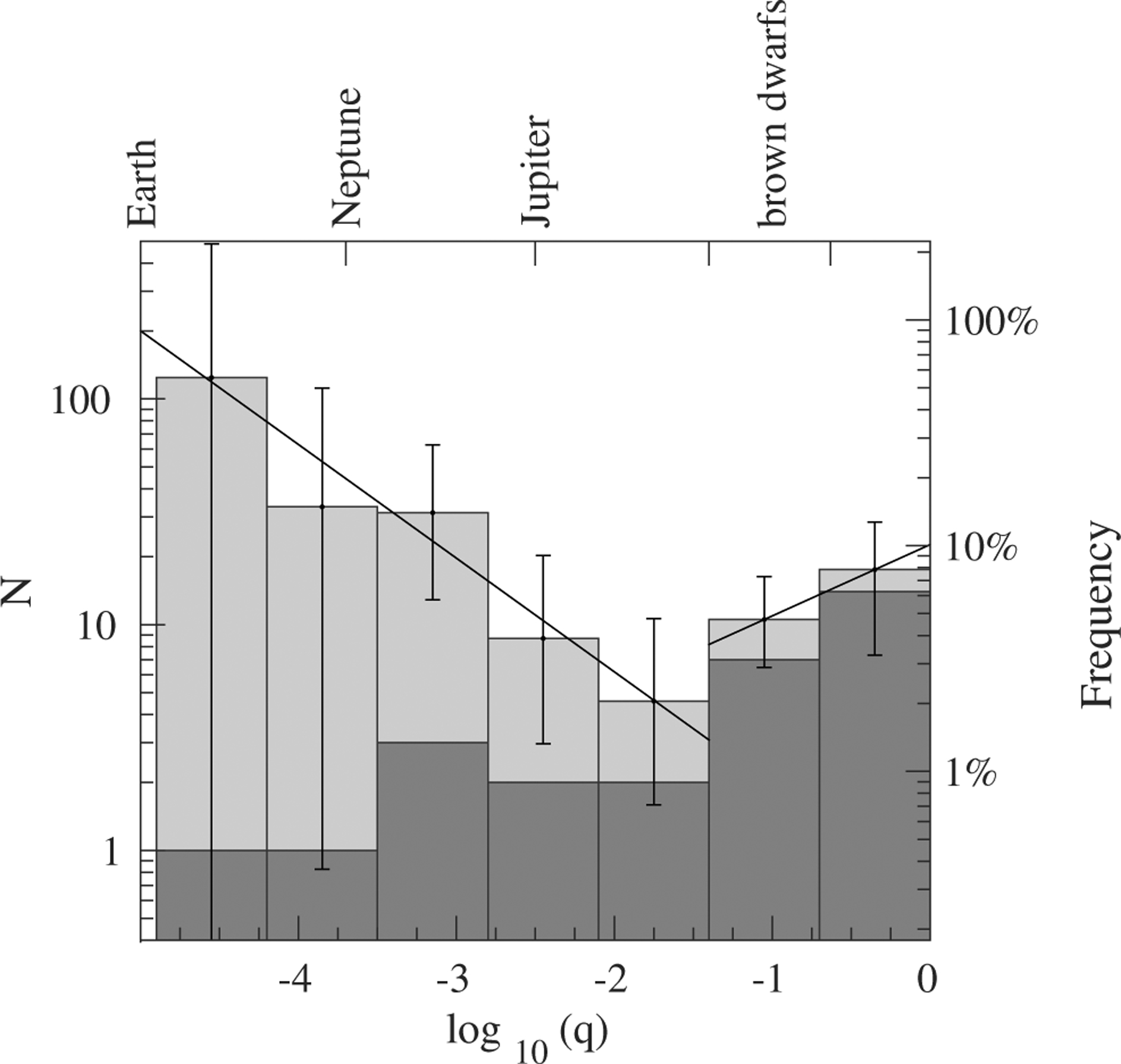
The distribution of estimated mass ratios of our sample, before (dark gray) and after (light gray) correcting for detection efficiency. The right-hand vertical axis shows the corresponding frequency. The top horizontal axis indicates the masses of Earth, Neptune, Jupiter and the brown dwarf range, for a typical host mass of 0.3M_⊙. The distribution hints at the existence of two populations, stellar binaries and planets, separated by a minimum that is analogous to the brown dwarf desert found by radial velocity surveys, although here the division appears to be in the super-Jupiter range. Solid lines are power laws d(log f)/d(log q) = −0.50 ± 0.17 (in the planetary regime) and d(log f)/d(log q) = 0.32 ± 0.38 (in the stellar binary regime).

For a flat intrinsic distribution in log q, we expect to find a monotonically rising number of detected companions as a function of log q, simply because of the larger cross section of the more massive planets, and the longer anomaly duration. The recovered mass ratio distribution in Figure 13 shows a deficit around q ⋍ 10⁻², and the corrected distribution can be fit with a broken—falling and rising—power law. This result echoes previous findings, by radial velocity surveys, that have shown two distinct populations of stellar companions at orbital periods shorter than a few years—planets and stellar binaries—likely produced via two different formation mechanisms (protoplanetary disks, and fragmentation in proto-stellar clouds, respectively). In those surveys, the two populations are separated by a gap at 13 – 80M_J, the “brown-dwarf desert” (e.g. Grether & Lineweaver 2006). (A recent analysis by Ranc et al. (2015) compiling current knowledge of brown-dwarf companions from various discovery techniques suggests a more complex brown-dwarf “landscape”, with a possible period dependence of brown-dwarf occurrence frequency). Our detection-efficiency-corrected mass-ratio distribution, assuming our typical primary has a mass of 0.3M_⊙, is suggestive of a similar picture, now possibly seen via microlensing. However, the gap between the two distributions appears to occur at a lower mass, ~ 3–13M_J, corresponding to “super Jupiters”. This difference, if real, could be the result of the fact that microlensing probes the companions of M stars (as opposed to FGK stars by other techniques), that microlensing probes larger separations than other techniques, or both. Due to the small number of total events in our survey, we cannot claim a significant detection of two populations. Furthermore, our mass bins are large, and thus we cannot resolve the region between the putative two populations. Finally, full modeling of the anomalous events, together with additional data (e.g. post-event detection of the lenses) that will help break possible degeneracies in those models, are required in order to give absolute masses rather than only mass ratios. For example, if the hosts of some of the companions in the brown-dwarf bin are in reality more massive than 0.3M_⊙, then their companions will be low-mass M stars. With all of these caveats in mind, the suggestion of a super-Jupiter gap in the M-star companion distribution is nevertheless intriguing. The overall slope we find for the planetary regime (10^−4.9 < q < 10^−1.4) is d(log f)/d(log q) = −0.50 ± 0.17, and for the binary regime (10^−1.4 < q < 1) we find d(log f)/d(log q) = 0.32 ± 0.38.

5. SUMMARY AND COMPARISON TO PREVIOUS WORK

We have presented a statistical analysis of the results, to date, of the first genII microlensing survey. This is the first controlled microlensing experiment for the abundance of snowline planets. Among the 224 events in our sample, 29 are anomalous, revealing the presence of a companion to the lens star. Our results show that about half of the stars have snowline planets with mass ratios in the range −4.9 < log(q) < −1.4, with Neptunes being ~ 10 times more common than Jupiters, consistent with previous microlensing findings (e.g. Sumi et al. 2010).

The absolute frequency we find is consistent with previous estimates from first generation microlensing surveys by Gould et al. (2010), who analyzed a sample of six detected planets from the follow-up of 13 high magnification events, and found that the frequency for the range −4.5 < log(q) < −2 is 36 ± 15%. The frequency we find is somewhat lower than, but consistent with, the estimates by Cassan et al. (2012), who used a control sample of 196 events from the PLANET collaboration with three detected planets (one Jupiter, one Neptune and one super-Earth), and derived a frequency of ${17}_{-9}^{+6}\%$ of Jupiters (in the range of 0.3 – 10M_J) and ${52}_{-29}^{+22}\%$ Neptunes (in the range of 10 – 30M_⊕). Our derived planet frequency is also consistent with results from other methods. Radial velocity surveys find that 10.5% of Sun-like stars host giant planets (in the range of 0.3 – 10M_J) with periods < 5.5 years (Cumming et al. 2008). Direct imaging surveys (Brandt et al. 2014), which are currently sensitive only to massive planets (> 5M_J), find that 1.0%–3.1% of stars host substellar companions.

For the binary regime, we have estimated from our survey that ~ 8% of lens stars have stellar companions with separations in the range 0.5 < s < 2. This is consistent with direct imaging estimates from the M-dwarfs in Multiples (MINMS) survey, of 8 ± 2% for companions to M stars with separations of 3–10 AU (Ward-Duong et al. 2015), and with radial-velocity surveys estimates of ~ 10% for companions to FGK stars with periods < 5 years (Grether & Lineweaver 2006; Raghavan et al. 2010). Although we cannot clearly identify the brown dwarf regime, we can estimate the frequency of brown-dwarf companions at ~ 5%. This is significantly higher than the estimates based on radial-velocity surveys of FGK stars, of < 1%, by Grether & Lineweaver (2006) for companions with periods < 5 years. Similarly, the frequency of brown-dwarf companions to white dwarfs found by Steele et al. (2011) is also low, f_WD+BD = 0.5% ± 0.3%. Typical white dwarfs, with masses of 0.6M_⊙, are descended from ~ 2M_⊙ stars. It is presently unclear whether brown-dwarf companions become more common with increasing separation. For example, Metchev & Hillenbrand (2009) estimate a frequency of ${3.2}_{-2.7}^{+3.1}\%$ of brown-dwarf companions in 28–1590 AU orbits around Sun-like stars. This fraction is consistent with all the various brown-dwarf companion estimates above.

The companion mass ratio distribution in our sample shows a decline from companions with similar masses (q ⋍ 1) towards companions with q ⋍ 10⁻². After accounting for the detection efficiency for different mass ratios, the distribution is suggestive of a rise in the planetary regime from massive planets towards less massive planets. As discussed above, the minimum in the distribution may be the microlensing manifestation of the bimodal companion distribution found by other techniques, but with the minimum shifted from the brown-dwarf mass range to the super-Jupiter range.

The slope we find for the planetary regime is consistent with what has been found for planetary companions to FGK stars from radial velocity surveys. For example, Cumming et al. (2008) find a a logarithmic slope of d(log f)/d(log M) = −0.31 ± 0.2 for companions in the mass range 0.3–10 M_J and with orbital periods of 2–2000 days. It is also consistent with direct-imaging exoplanet survey results, e.g., Brandt et al. (2014), who find a slope of d(log f)/d(log M) = −0.65±0.60 for the distribution of substellar companions with masses of 5–70M_J between 10 and 100 AU. For the binary regime our slope is shalower but, again, consistent with the d(log f)/d(log M) = 0.68 ± 0.21 found by radial velocity surveys (Grether & Lineweaver 2006) for companions with masses of 0.1 < (M/M_⊙) < 1, and with the d(log f)/d(log M) ~ 0.5 shown by Mazeh et al. (2003) for the companion distribution in that mass range.

Full binary-lens modeling of the anomalous events in our sample is required in order to confirm these estimates. For some of the events, the light curves show the signatures of high order effects, and thus the mass of the host star and its companion can be measured. For the rest of the sample, high resolution imaging in the coming years could refine estimates of the masses, by isolating the light from the lens. Together with increasing numbers of planetary detections from our ongoing genII survey, this will give a progressively clearer picture of the planetary mass distribution near the snowlines of low-mass stars in the Galaxy.

Figure 6.

Inter-calibrated light curves of events with a clear anomaly that we identify by-eye: OGLE - blue circles, MOA - green diamonds, Wise - red squares. Magenta lines are the best-fit model, either published or from the grid search. The residuals from the point-lens model are shown in the lower panel of each event. The identifying number from Appendix A is marked in the upper-left corner.

Figure 7.

Inter-calibrated light curves of events with a clear anomaly that we identify by-eye: OGLE - blue circles, MOA - green diamonds, Wise - red squares. Magenta lines are the best-fit model, either published or from the grid search. The residuals from the point-lens model are shown in the lower panel of each event. The identifying number from Appendix A is marked in the upper-left corner.

Figure 8.

Inter-calibrated light curves of events with a clear anomaly that we identify by-eye: OGLE - blue circles, MOA - green diamonds, Wise - red squares. Magenta lines are the best-fit model, either published or from the grid search. The residuals from the point-lens model are shown in the lower panel of each event. The identifying number from Appendix A is marked in the upper-left corner.

Figure 9.

Inter-calibrated light curves of events with a clear anomaly that we identify by-eye: OGLE - blue circles, MOA - green diamonds, Wise - red squares. Magenta lines are the best-fit model, either published or from the grid search. The residuals from the point-lens model are shown in the lower panel of each event. The identifying number from Appendix A is marked in the upper-left corner.

Figure 10.

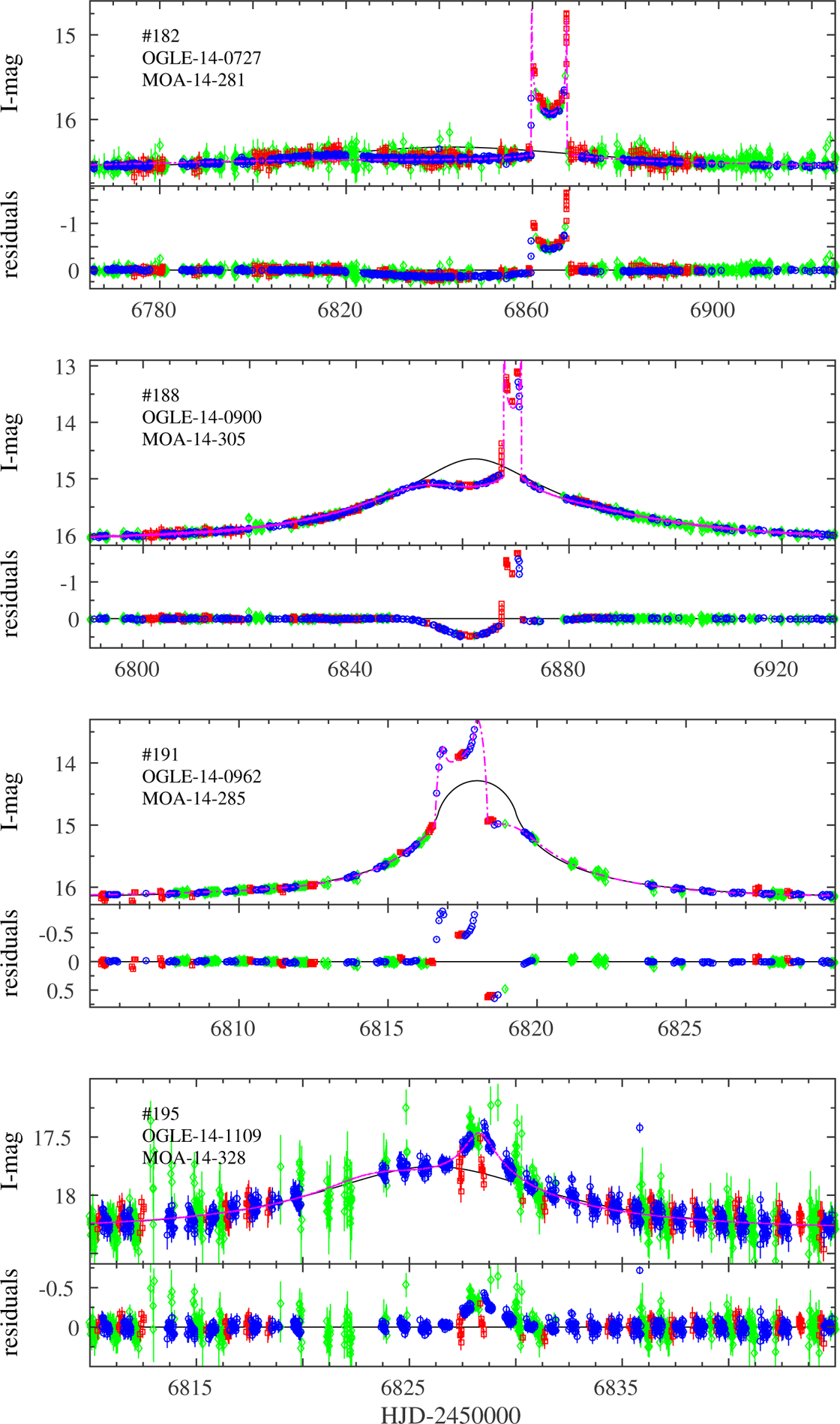
Inter-calibrated light curves of events with a clear anomaly that we identify by-eye: OGLE - blue circles, MOA - green diamonds, Wise - red squares. Magenta lines are the best-fit model, either published or from the grid search. The residuals from the point-lens model are shown in the lower panel of each event. The identifying number from Appendix A is marked in the upper-left corner.

APPENDIX A

Microlens event sample: best-fit point-lens model parameters. Significant detections of finite source effects and parallax are marked in bold.

At the end of the table, separated by double horizontal lines, we list the six anomalous events which passed the limiting magnitude criteria only because of the anomaly, and are therefore excluded from the sample (see Section 2.2 for details).

Table 2:

Event summary

#	OGLE no.	MOA no.	u0	t0 – 2450000 [HJD]	tE [Days]	ρ10−3	πE,E	πE,N	Ibl	fbl
1	11–0022	11–025	0.867	5690.508	56.584	0.000	−0.379	0.021	15.614	0.000
			(0.002)	(0.041)	(0.150)	(38.685)	(0.003)	(0.007)	(0.000)	(0.000)
2	11–0037	11–039	0.173	5807.481	128.572	2.284	0.263	−0.243	16.155	0.245
			(0.001)	(0.025)	(0.565)	(14.211)	(0.001)	(0.002)	(0.000)	(0.001)
3	11–0081	11–064	0.207	5658.523	106.779	223.877	0.437	0.457	16.460	0.952
			(0.003)	(0.128)	(1.568)	(3.383)	(0.014)	(0.011)	(0.000)	(0.000)
4	11–0082	11–103	0.295	5702.214	63.944	169.666	−0.205	−0.464	18.191	0.057
			(0.009)	(0.037)	(1.186)	(49.256)	(0.030)	(0.058)	(0.001)	(0.002)
5	11–0120	11–114	0.846	5670.592	26.837	0.000	0.015	1.496	16.964	0.003
			(0.031)	(0.109)	(0.698)	(71.112)	(0.040)	(0.044)	(0.001)	(0.004)
6	11–0138	11–082	0.042	5666.781	52.366	6.039	0.206	−0.203	19.672	0.251
			(0.001)	(0.008)	(0.920)	(5.511)	(0.027)	(0.143)	(0.002)	(0.002)
7	11–0168	11–091	0.351	5690.133	24.810	0.000	0.158	1.498	16.550	0.215
			(0.004)	(0.014)	(0.160)	(45.810)	(0.025)	(0.104)	(0.000)	(0.001)
8	11–0172	11–104	−0.050	5670.367	49.263	51.767	−0.046	−1.493	19.497	0.113
			(0.001)	(0.010)	(0.918)	(1.179)	(0.030)	(0.068)	(0.003)	(0.003)
9	11–0173	11–133	−0.696	5689.328	30.654	0.000	−0.160	−1.315	15.828	0.438
			(0.052)	(0.059)	(1.142)	(147.475)	(0.029)	(0.201)	(0.000)	(0.001)
10	11–0235	11–107	−0.669	5673.096	14.184	0.000	0.220	1.208	18.155	0.000
			(0.050)	(0.172)	(0.664)	(143.850)	(0.418)	(0.811)	(0.002)	(0.016)
11	11–0240	11–109	0.035	5659.760	9.381	44.823	1.424	−1.084	19.000	0.939
			(0.018)	(0.023)	(1.604)	(24.768)	(0.802)	(0.793)	(0.004)	(0.001)
12	11–0243	11–151	0.700	5714.091	26.304	0.000	0.461	1.499	16.707	0.000
			(0.011)	(0.057)	(0.243)	(98.704)	(0.068)	(0.068)	(0.000)	(0.000)
13	11–0265	11–197	−0.136	5760.259	51.582	0.000	0.061	0.628	17.287	0.000
			(0.000)	(0.009)	(0.152)	(10.814)	(0.017)	(0.110)	(0.000)	(0.000)
14	11–0266	11–115	0.664	5694.409	14.482	0.000	0.489	0.858	15.559	0.000
			(0.007)	(0.012)	(0.117)	(71.339)	(0.088)	(0.373)	(0.000)	(0.001)
15	11–0286	11–124	0.109	5680.101	12.338	76.999	1.494	−0.978	18.636	0.620
			(0.032)	(0.012)	(0.496)	(28.270)	(0.340)	(0.788)	(0.003)	(0.002)
16	11–0293	11–190	−0.476	5714.295	32.685	414.080	−0.037	1.483	18.501	0.033
			(0.026)	(0.052)	(1.163)	(119.996)	(0.151)	(0.941)	(0.002)	(0.004)
17	11–0297	11–166	0.015	5700.670	136.964	19.059	−0.605	−1.446	18.794	0.907
			(0.002)	(0.021)	(14.527)	(4.812)	(0.057)	(0.096)	(0.004)	(0.001)
18	11–0318	11–132	0.503	5682.097	1.055	356.525	1.312	−1.171	16.002	0.006
			(0.106)	(0.002)	(0.023)	(131.754)	(0.804)	(0.817)	(0.001)	(0.003)
19	11–0329	11–147	−0.005	5691.899	11.928	5.400	−0.663	−0.720	19.194	0.255
			(0.000)	(0.000)	(0.231)	(0.297)	(0.541)	(0.797)	(0.004)	(0.003)
20	11–0348	11–189	0.443	5713.657	19.410	85.249	0.674	1.484	18.349	0.073
			(0.038)	(0.041)	(0.423)	(111.233)	(0.446)	(0.828)	(0.001)	(0.004)
21	11–0364	11–154	0.019	5703.622	74.999	17.449	−0.798	−0.242	16.101	0.986
			(0.006)	(0.009)	(6.046)	(5.385)	(0.068)	(0.061)	(0.000)	(0.000)
22	11–0421	11–160	0.050	5705.967	7.771	0.583	−1.490	1.465	16.247	0.940
			(0.003)	(0.004)	(0.262)	(12.883)	(0.802)	(0.813)	(0.000)	(0.000)
23	11–0422	11–171	0.207	5709.443	17.937	218.483	1.490	−1.496	18.477	0.537
			(0.013)	(0.026)	(0.848)	(14.174)	(0.099)	(0.336)	(0.002)	(0.002)
24	11–0424	11–204	0.314	5732.063	16.901	193.531	−1.480	0.330	16.299	0.124
			(0.053)	(0.011)	(0.125)	(73.532)	(0.270)	(0.300)	(0.001)	(0.002)
25	11–0462	11–191	0.004	5763.322	179.829	2.950	−0.068	0.098	16.406	0.935
			(0.000)	(0.000)	(0.618)	(0.143)	(0.004)	(0.012)	(0.000)	(0.000)
26	11–0465	11–211	0.562	5781.460	35.139	109.840	−0.127	0.582	14.944	0.000
			(0.005)	(0.016)	(0.158)	(68.034)	(0.016)	(0.054)	(0.000)	(0.001)
27	11–0481	11–217	−0.018	5725.269	5.607	2.650	0.873	0.515	19.111	0.601
			(0.016)	(0.003)	(0.389)	(17.413)	(0.808)	(0.792)	(0.003)	(0.002)
28	11–0507	11–287	0.252	5750.747	35.440	0.000	−0.974	1.482	17.153	0.867
			(0.021)	(0.055)	(2.027)	(57.304)	(0.362)	(0.670)	(0.001)	(0.001)
29	11–0510	11–247	0.664	5741.451	8.633	270.825	−1.433	−1.496	16.884	0.000
			(0.013)	(0.010)	(0.101)	(104.230)	(0.541)	(0.568)	(0.000)	(0.000)
30	11–0519	11–273	0.257	5741.040	10.927	0.000	1.479	1.499	15.615	0.943
			(0.027)	(0.019)	(0.560)	(76.924)	(0.718)	(0.799)	(0.000)	(0.000)
31	11–0521	11–270	1.025	5746.899	7.426	38.738	−1.498	−1.491	14.231	0.001
			(0.033)	(0.016)	(0.173)	(52.255)	(0.106)	(0.178)	(0.000)	(0.002)
32	11–0535	11–354	−0.083	5768.233	73.757	82.167	−0.038	0.084	18.321	0.914
			(0.008)	(0.040)	(5.729)	(23.369)	(0.045)	(0.250)	(0.001)	(0.000)
33	11–0545	11–290	0.238	5751.104	17.559	0.000	−0.205	−1.447	19.099	0.001
			(0.064)	(0.045)	(0.360)	(60.034)	(0.564)	(0.795)	(0.004)	(0.008)
34	11–0944	11–297	−0.046	5767.394	12.273	1.624	0.288	−1.499	16.983	0.000
			(0.000)	(0.001)	(0.013)	(5.479)	(0.144)	(0.654)	(0.000)	(0.000)
35	11–0966	11–302	0.077	5758.121	16.523	17.351	0.128	−1.427	19.114	0.137
			(0.020)	(0.016)	(0.347)	(21.583)	(0.419)	(0.836)	(0.002)	(0.004)
36	11–0974	11–275	0.004	5743.417	267.266	4.783	−0.981	−1.404	19.485	0.995
			(18.946)	(0.092)	(122.304)	(16117.873)	(0.802)	(0.795)	(0.455)	(0.006)
37	11–0990	11–300	−0.012	5758.680	6.788	16.325	−0.975	−0.991	18.480	0.044
			(0.003)	(0.004)	(0.108)	(4.291)	(0.736)	(0.797)	(0.002)	(0.005)
38	11–0991	11–312	0.810	5801.829	25.457	192.278	0.320	−1.500	16.018	0.174
			(0.033)	(0.049)	(0.595)	(116.572)	(0.026)	(0.083)	(0.000)	(0.001)
39	11–0999	11–306	0.109	5760.856	5.487	44.185	1.419	1.178	19.616	0.197
			(0.021)	(0.006)	(0.255)	(33.615)	(0.802)	(0.800)	(0.003)	(0.005)
40	11–1003	11–298	0.071	5757.933	5.957	161.260	−1.142	−0.224	17.404	0.759
			(0.039)	(0.075)	(0.384)	(47.824)	(0.811)	(0.818)	(0.001)	(0.005)
41	11–1007	11–370	−0.273	5789.990	34.525	121.625	−0.045	−1.435	18.798	0.003
			(0.008)	(0.053)	(0.836)	(56.154)	(0.053)	(0.269)	(0.002)	(0.005)
42	11–1009	11–335	0.022	5774.069	180.284	6.455	0.029	−0.025	16.259	0.994
			(0.006)	(0.058)	(35.620)	(6.526)	(0.103)	(0.641)	(0.002)	(0.000)
43	11–1035	11–337	−0.052	5776.564	32.138	34.412	−0.343	0.032	19.026	0.796
			(0.005)	(0.010)	(1.419)	(17.005)	(0.159)	(0.521)	(0.002)	(0.001)
44	11–1036	11–372	−0.198	5791.009	34.887	2.241	0.027	0.025	18.932	0.230
			(0.018)	(0.048)	(1.452)	(69.196)	(0.066)	(0.671)	(0.003)	(0.005)
45	11–1072	11–346	0.006	5775.398	15.875	5.552	−1.496	−0.263	18.143	0.536
			(0.000)	(0.001)	(0.293)	(0.458)	(0.140)	(0.715)	(0.002)	(0.001)
46	11–1127	11–322	−0.005	5775.101	23.687	90.657	1.494	1.495	16.699	0.945
			(0.010)	(0.010)	(2.041)	(7.448)	(0.124)	(0.737)	(0.001)	(0.001)
47	11–1132	11–358	0.018	5753.381	298.017	17.452	0.721	−0.529	18.800	0.970
			(0.003)	(0.073)	(73.846)	(5.238)	(0.154)	(0.224)	(0.003)	(0.000)
48	11–1162	11–379	0.693	5799.155	10.703	1.114	−0.380	−1.497	17.437	0.089
			(0.035)	(0.037)	(0.349)	(128.940)	(0.286)	(0.808)	(0.001)	(0.004)
49	11–1195	11–389	−0.481	5804.265	23.892	459.210	0.055	1.376	18.218	0.150
			(0.092)	(0.110)	(2.200)	(132.287)	(0.141)	(0.832)	(0.009)	(0.015)
50	11–1200	11–381	−0.081	5799.188	13.837	83.545	−0.061	0.207	17.687	0.740
			(0.006)	(0.006)	(0.497)	(8.546)	(0.364)	(0.780)	(0.001)	(0.002)
51	11–1254	11–388	−0.006	5801.312	29.373	10.393	0.737	1.372	15.934	0.996
			(0.002)	(0.003)	(4.858)	(1.660)	(0.482)	(0.803)	(0.000)	(0.000)
52	11–9112	11–112	−0.310	5686.106	20.708	0.000	0.427	1.494	16.368	0.000
			(0.012)	(0.050)	(0.469)	(63.919)	(0.097)	(0.749)	(0.002)	(0.000)
53	11–9291	11–291	0.003	5747.950	58.011	1.766	−1.494	−1.490	17.420	0.988
			(0.001)	(0.001)	(2.370)	(0.749)	(0.100)	(0.250)	(0.001)	(0.000)
54	11–9293	11–293	0.001	5747.502	79.317	1.498	−1.457	−1.462	19.935	0.973
			(0.000)	(0.002)	(6.984)	(0.174)	(0.389)	(0.689)	(0.016)	(0.000)
55	11–9313	11–313	−0.189	5766.639	5.284	211.722	1.497	0.798	18.121	0.640
			(0.017)	(0.008)	(0.357)	(18.439)	(0.735)	(0.789)	(0.007)	(0.013)
56	11–9367	11–367	0.052	5787.101	9.833	3.286	1.452	1.316	18.770	0.314
			(0.003)	(0.002)	(0.202)	(16.151)	(0.399)	(0.804)	(0.002)	(0.002)
57	11–9393	11–393	0.001	5803.567	20.698	5.645	0.414	0.341	19.005	0.878
			(0.002)	(0.002)	(1.499)	(1.537)	(0.457)	(0.767)	(0.004)	(0.001)
58	12–0305	12–182	−0.685	6046.970	20.933	402.896	−0.356	0.217	16.333	0.207
			(0.025)	(0.046)	(0.611)	(123.591)	(0.057)	(0.575)	(0.001)	(0.002)
59	12–0325	12–166	0.972	6039.774	15.785	2.207	0.609	1.485	16.651	0.000
			(0.041)	(0.092)	(0.808)	(113.530)	(0.175)	(0.886)	(0.001)	(0.000)
60	12–0442	12–245	0.174	6078.680	31.894	105.718	−0.344	1.499	18.214	0.164
			(0.005)	(0.017)	(0.541)	(32.295)	(0.051)	(0.026)	(0.002)	(0.003)
61	12–0443	12–211	0.058	6046.093	24.627	41.639	−0.342	−0.109	19.515	0.215
			(0.002)	(0.011)	(0.705)	(14.238)	(0.164)	(0.667)	(0.005)	(0.005)
62	12–0449	12–216	−0.725	6058.735	35.066	706.358	−0.336	1.497	16.646	0.812
			(0.105)	(0.089)	(2.285)	(222.866)	(0.074)	(0.965)	(0.000)	(0.001)
63	12–0456	12–189	−0.169	6047.058	7.031	9.316	−1.494	1.422	15.179	0.000
			(0.008)	(0.013)	(0.019)	(35.654)	(0.070)	(0.573)	(0.000)	(0.000)
64	12–0462	12–271	0.055	6064.302	37.484	0.000	−0.014	1.499	19.046	0.000
			(0.000)	(0.006)	(0.186)	(6.292)	(0.049)	(0.083)	(0.001)	(0.000)
65	12–0591	12–430	0.175	6170.359	63.396	78.360	−0.013	−0.245	17.075	0.247
			(0.003)	(0.012)	(0.491)	(24.395)	(0.006)	(0.080)	(0.001)	(0.001)
66	12–0615	12–277	0.507	6060.504	4.098	1.809	−1.492	1.438	14.411	0.753
			(0.021)	(0.007)	(0.090)	(77.143)	(0.412)	(0.772)	(0.000)	(0.001)
67	12–0694	12–308	0.042	6070.255	12.163	11.372	1.372	−0.673	19.593	0.744
			(0.014)	(0.007)	(1.535)	(11.920)	(0.761)	(0.773)	(0.006)	(0.003)
68	12–0722	12–397	−0.173	6122.064	58.003	9.264	−0.067	−1.303	18.345	0.501
			(0.011)	(0.066)	(2.921)	(46.579)	(0.115)	(0.997)	(0.005)	(0.005)
69	12–0724	12–323	0.009	6071.042	15.176	11.708	−1.385	1.047	19.821	0.880
			(0.001)	(0.002)	(2.544)	(1.885)	(0.756)	(0.749)	(0.005)	(0.001)
70	12–0726	12–351	−0.204	6072.873	11.110	1.535	1.489	−1.473	18.183	0.503
			(0.075)	(0.030)	(0.644)	(71.483)	(0.478)	(0.806)	(0.003)	(0.004)
71	12–0784	12–337	−0.029	6085.181	88.027	27.140	−0.061	−0.027	16.176	0.988
			(0.005)	(0.018)	(24.624)	(6.748)	(0.084)	(0.252)	(0.000)	(0.000)
72	12–0825	12–451	0.352	6171.507	45.769	8.244	0.073	0.314	17.399	0.002
			(0.010)	(0.036)	(2.222)	(48.109)	(0.021)	(0.204)	(0.001)	(0.002)
73	12–0867	12–352	0.202	6110.261	13.949	0.000	0.128	−1.358	14.260	0.045
			(0.001)	(0.002)	(0.035)	(18.564)	(0.242)	(0.420)	(0.000)	(0.001)
74	12–1414	12–205	−0.043	6040.895	36.153	0.000	−0.195	−0.186	20.257	0.280
			(0.003)	(0.011)	(1.728)	(11.665)	(0.127)	(0.667)	(0.007)	(0.006)
75	12–1430	12–278	−0.002	6062.104	18.807	4.130	0.525	0.941	20.217	0.001
			(0.001)	(0.001)	(0.268)	(1.150)	(0.345)	(0.835)	(0.006)	(0.006)
76	12–0941	12–446	0.245	6126.169	36.883	0.000	−0.537	1.499	19.133	0.113
			(0.011)	(0.031)	(1.256)	(50.847)	(0.238)	(0.726)	(0.003)	(0.004)
77	12–0974	12–424	−0.069	6110.120	86.425	91.769	−1.477	−0.031	18.802	0.939
			(0.019)	(0.079)	(11.899)	(9.884)	(0.143)	(0.209)	(0.005)	(0.001)
78	12–0998	12–447	−0.518	6136.857	24.356	0.000	0.125	−1.439	16.957	0.482
			(0.036)	(0.033)	(0.513)	(179.737)	(0.069)	(0.881)	(0.000)	(0.001)
79	12–1013	12–449	0.643	6126.889	21.525	630.572	−0.858	0.248	18.599	0.209
			(0.108)	(0.078)	(2.017)	(197.902)	(0.286)	(0.627)	(0.002)	(0.006)
80	12–1049	12–438	−0.338	6117.274	7.192	152.796	−1.486	−1.069	18.302	0.371
			(0.098)	(0.017)	(0.309)	(95.418)	(0.732)	(0.802)	(0.002)	(0.003)
81	12–1051	12–477	0.200	6132.237	21.209	0.000	0.025	−0.565	18.494	0.017
			(0.026)	(0.014)	(0.273)	(37.963)	(0.115)	(0.741)	(0.002)	(0.004)
82	12–1418	12–435	0.018	6119.272	55.686	0.000	0.280	−0.016	20.142	0.539
			(0.001)	(0.003)	(3.094)	(3.930)	(0.209)	(0.518)	(0.006)	(0.003)
83	12–1067	12–444	−0.011	6116.566	7.158	0.396	−1.486	−1.430	18.966	0.848
			(0.001)	(0.000)	(0.470)	(2.402)	(0.797)	(0.816)	(0.003)	(0.001)
84	12–1069	12–452	−0.220	6129.142	22.575	0.913	0.281	−1.495	19.044	0.000
			(0.006)	(0.020)	(0.199)	(51.679)	(0.173)	(0.765)	(0.002)	(0.000)
85	12–1066	12–476	−0.132	6148.598	17.562	80.624	−0.086	0.405	16.670	0.048
			(0.002)	(0.004)	(0.096)	(19.811)	(0.050)	(0.548)	(0.001)	(0.001)
86	12–1074	12–519	−0.259	6154.066	40.088	183.433	0.215	0.052	19.280	0.001
			(0.013)	(0.050)	(1.301)	(60.351)	(0.050)	(0.579)	(0.003)	(0.005)
87	12–1183	12–478	−0.107	6130.447	7.131	128.561	0.926	1.082	19.427	0.593
			(0.015)	(0.028)	(0.611)	(38.220)	(0.807)	(0.818)	(0.008)	(0.008)
88	12–1193	12–498	0.106	6136.399	14.384	118.142	1.295	1.381	18.296	0.801
			(0.008)	(0.026)	(0.884)	(9.552)	(0.527)	(0.780)	(0.002)	(0.002)
89	12–1210	12–511	−0.368	6143.702	1.881	1.844	1.499	1.498	16.507	0.000
			(0.010)	(0.006)	(0.015)	(82.426)	(0.796)	(0.812)	(0.000)	(0.000)
90	12–1211	12–514	−0.614	6151.519	6.542	621.011	1.489	1.070	15.699	0.332
			(0.010)	(0.011)	(0.086)	(10.763)	(0.081)	(0.799)	(0.000)	(0.003)
91	12–1213	12–512	0.290	6144.519	18.487	327.066	−1.476	−1.420	19.538	0.000
			(0.045)	(0.057)	(0.570)	(111.028)	(0.175)	(0.744)	(0.005)	(0.000)
92	12–1250	12–515	0.060	6145.218	6.409	96.900	1.285	0.452	18.184	0.862
			(0.013)	(0.022)	(0.897)	(29.045)	(0.792)	(0.793)	(0.002)	(0.004)
93	12–1242	12–552	−0.059	6160.797	25.921	1.650	−0.380	0.219	19.306	0.581
			(0.003)	(0.009)	(0.863)	(13.699)	(0.130)	(0.724)	(0.002)	(0.002)
94	12–1244	12–555	0.214	6154.529	38.326	231.692	0.227	−0.978	19.626	0.534
			(0.066)	(0.093)	(6.447)	(86.241)	(0.165)	(0.871)	(0.006)	(0.006)
95	12–1245	12–575	−0.229	6173.239	41.186	0.000	0.056	0.125	19.264	0.320
			(0.028)	(0.137)	(4.094)	(63.580)	(0.101)	(0.660)	(0.005)	(0.007)
96	12–1442	12–532	0.025	6151.813	11.310	6.815	−0.388	−0.053	20.194	0.242
			(0.035)	(0.017)	(1.859)	(27.043)	(0.770)	(0.800)	(0.018)	(0.018)
97	12–1268	12–574	0.204	6171.071	21.705	0.311	0.259	−1.498	18.668	0.000
			(0.004)	(0.021)	(0.294)	(43.168)	(0.086)	(0.805)	(0.002)	(0.003)
98	12–1269	12–560	0.217	6160.201	12.653	202.708	−1.066	0.733	18.311	0.733
			(0.021)	(0.026)	(0.757)	(48.311)	(0.468)	(0.816)	(0.002)	(0.002)
99	12–1292	12–570	0.214	6165.816	5.658	89.066	−0.262	0.688	16.986	0.082
			(0.054)	(0.003)	(0.067)	(44.433)	(0.500)	(0.795)	(0.000)	(0.002)
100	12–1581	12–577	−0.149	6169.822	35.435	118.073	−0.091	−1.424	20.100	0.027
			(0.007)	(0.043)	(1.747)	(36.750)	(0.087)	(0.986)	(0.005)	(0.007)
101	12–1311	12–594	0.588	6170.085	20.773	0.000	1.056	0.782	17.841	0.646
			(0.127)	(0.172)	(2.486)	(216.333)	(0.260)	(0.811)	(0.001)	(0.004)
102	12–1364	12–580	−0.015	6164.630	16.616	0.000	1.399	1.491	18.465	0.739
			(0.005)	(0.003)	(0.987)	(3.781)	(0.314)	(0.815)	(0.003)	(0.001)
103	12–9582	12–582	−0.015	6162.944	1.920	30.483	−0.189	−0.202	18.060	0.929
			(0.012)	(0.002)	(4.803)	(15.692)	(0.794)	(0.798)	(0.011)	(0.027)
104	12–9591	12–591	0.006	6166.857	18.228	6.773	0.702	−0.735	18.644	0.991
			(0.003)	(0.009)	(5.984)	(3.041)	(0.785)	(0.788)	(0.012)	(0.001)
105	12–1350	12–603	−0.134	6175.036	10.578	136.409	−1.241	0.313	18.846	0.084
			(0.011)	(0.018)	(0.474)	(37.325)	(0.534)	(0.820)	(0.006)	(0.009)
106	13–0036	13–399	0.617	6406.163	47.908	0.000	0.040	0.141	15.971	0.038
			(0.011)	(0.036)	(0.393)	(101.668)	(0.010)	(0.041)	(0.000)	(0.001)
107	13–0145	13–110	0.467	6405.939	29.063	0.065	−0.009	0.562	16.310	0.000
			(0.007)	(0.019)	(0.226)	(54.737)	(0.024)	(0.233)	(0.000)	(0.002)
108	13–0183	13–332	−0.652	6495.203	103.843	15.347	−0.076	0.035	16.888	0.403
			(0.023)	(0.135)	(2.225)	(91.360)	(0.006)	(0.009)	(0.000)	(0.001)
109	13–0341	13–260	0.000	6406.313	28.880	13.446	1.063	−0.909	18.368	0.066
			(0.005)	(0.005)	(0.335)	(5.332)	(0.063)	(0.493)	(0.002)	(0.002)
110	13–0486	13–294	−0.154	6420.492	28.978	0.456	−0.171	−0.062	18.247	0.480
			(0.004)	(0.015)	(0.389)	(33.668)	(0.055)	(0.367)	(0.001)	(0.001)
111	13–0488	13–355	−0.011	6439.171	93.899	0.720	−0.173	−0.448	19.738	0.517
			(0.004)	(0.005)	(4.458)	(2.988)	(0.121)	(0.372)	(0.007)	(0.004)
112	13–0506	13–494	−0.089	6501.345	154.414	177.820	−0.057	−0.011	17.570	0.898
			(0.036)	(0.246)	(13.158)	(39.844)	(0.015)	(0.099)	(0.001)	(0.001)
113	13–0513	13–272	0.136	6407.452	28.801	0.000	0.502	1.481	19.766	0.202
			(0.010)	(0.038)	(1.433)	(37.790)	(0.145)	(0.854)	(0.005)	(0.006)
114	13–0601	13–292	−0.060	6414.867	17.778	80.207	−1.158	0.987	18.756	0.810
			(0.015)	(0.016)	(1.414)	(22.563)	(0.390)	(0.828)	(0.003)	(0.002)
115	13–0607	13–376	−0.956	6455.457	22.750	0.000	−0.189	1.492	16.383	0.001
			(0.024)	(0.044)	(0.434)	(141.951)	(0.171)	(0.885)	(0.000)	(0.002)
116	13–0608	13–308	−0.438	6426.720	14.260	378.693	0.559	0.521	17.388	0.023
			(0.088)	(0.023)	(0.310)	(102.202)	(0.224)	(0.736)	(0.001)	(0.003)
117	13–0610	13–401	0.253	6455.122	22.810	0.000	1.084	1.499	16.059	0.071
			(0.002)	(0.004)	(0.077)	(28.019)	(0.087)	(0.106)	(0.000)	(0.001)
118	13–0615	13–389	−0.349	6448.248	46.213	0.484	0.248	1.500	18.110	0.484
			(0.036)	(0.117)	(2.467)	(113.663)	(0.129)	(0.828)	(0.002)	(0.004)
119	13–0616	13–331	−0.355	6424.294	10.334	0.000	−0.841	1.490	17.882	0.381
			(0.084)	(0.019)	(0.377)	(97.568)	(0.430)	(0.775)	(0.001)	(0.002)
120	13–0619	13–351	−0.055	6427.437	21.427	0.000	0.571	1.497	20.215	0.169
			(0.003)	(0.007)	(0.708)	(14.559)	(0.330)	(0.839)	(0.006)	(0.006)
121	13–0621	13–344	−0.101	6425.046	30.293	85.822	−0.290	1.496	19.606	0.610
			(0.010)	(0.019)	(1.718)	(32.894)	(0.188)	(0.848)	(0.003)	(0.002)
122	13–0668	13–343	0.246	6422.307	22.570	266.126	0.806	0.020	19.287	0.693
			(0.068)	(0.058)	(2.768)	(82.594)	(0.348)	(0.771)	(0.003)	(0.004)
123	13–0674	13–346	−0.002	6426.021	57.315	0.000	−0.194	−1.473	20.105	0.738
			(0.000)	(0.000)	(1.205)	(0.251)	(0.194)	(0.880)	(0.006)	(0.002)
124	13–0682	13–388	0.727	6453.990	21.275	78.987	1.159	1.488	16.880	0.002
			(0.013)	(0.045)	(0.231)	(103.167)	(0.281)	(0.256)	(0.001)	(0.003)
125	13–0689	13–379	0.237	6434.013	21.510	8.974	−0.162	1.494	17.949	0.814
			(0.031)	(0.099)	(1.625)	(76.931)	(0.477)	(0.841)	(0.002)	(0.002)
126	13–0703	13–349	−0.151	6429.186	25.032	81.227	0.129	−0.119	19.014	0.146
			(0.044)	(0.019)	(0.740)	(28.229)	(0.170)	(0.650)	(0.003)	(0.004)
127	13–0731	13–377	−0.292	6437.552	18.103	0.000	−0.247	0.149	17.346	0.804
			(0.073)	(0.058)	(1.011)	(90.446)	(0.463)	(0.774)	(0.001)	(0.001)
128	13–0770	13–462	0.238	6471.819	26.446	98.029	−1.499	−0.862	17.449	0.342
			(0.008)	(0.023)	(0.508)	(49.735)	(0.026)	(0.178)	(0.001)	(0.002)
129	13–0801	13–386	0.047	6436.617	11.463	56.062	−1.473	1.028	18.103	0.949
			(0.008)	(0.007)	(1.440)	(9.493)	(0.769)	(0.780)	(0.003)	(0.001)
130	13–0835	13–400	−0.056	6449.971	9.743	0.000	−1.489	−0.011	18.184	0.204
			(0.001)	(0.001)	(0.092)	(9.652)	(0.692)	(0.781)	(0.002)	(0.002)
131	13–0850	13–470	0.959	6479.565	22.525	0.486	0.078	−0.607	17.165	0.007
			(0.070)	(0.072)	(1.258)	(152.823)	(0.280)	(0.352)	(0.001)	(0.003)
132	13–0861	13–502	0.363	6516.004	65.655	0.000	0.037	−0.502	17.402	0.324
			(0.017)	(0.101)	(1.497)	(87.172)	(0.020)	(0.079)	(0.001)	(0.002)
133	13–0891	13–433	−0.609	6476.835	18.930	0.000	0.322	−0.737	15.512	0.000
			(0.003)	(0.011)	(0.092)	(54.934)	(0.105)	(0.473)	(0.000)	(0.000)
134	13–0911	13–551	−0.003	6537.299	126.734	0.533	−0.131	0.218	19.362	0.444
			(0.000)	(0.000)	(1.934)	(0.720)	(0.004)	(0.077)	(0.003)	(0.002)
135	13–0925	13–493	−0.358	6501.455	43.130	171.945	−0.194	1.494	18.051	0.169
			(0.015)	(0.055)	(0.977)	(81.057)	(0.027)	(0.081)	(0.001)	(0.003)
136	13–0968	13–452	−0.168	6460.311	7.046	21.913	−1.489	1.279	17.675	0.049
			(0.004)	(0.002)	(0.056)	(32.723)	(0.783)	(0.750)	(0.001)	(0.001)
137	13–1033	13–472	−0.139	6468.808	21.183	196.985	−0.371	1.377	19.571	0.550
			(0.098)	(0.050)	(3.002)	(82.722)	(0.777)	(0.760)	(0.005)	(0.007)
138	13–1037	13–483	0.048	6473.098	36.512	1.531	−1.500	−0.754	20.185	0.437
			(0.015)	(0.019)	(3.706)	(16.175)	(0.511)	(0.697)	(0.013)	(0.009)
139	13–1078	13–460	0.000	6462.061	27.261	0.990	−1.210	1.338	20.259	0.929
			(0.000)	(0.000)	(1.700)	(0.072)	(0.798)	(0.806)	(0.015)	(0.002)
140	13–1080	13–456	0.004	6462.038	22.224	0.697	1.380	−1.492	20.388	0.904
			(0.002)	(0.001)	(4.915)	(1.221)	(0.808)	(0.818)	(0.007)	(0.001)
141	13–9455	13–455	0.058	6456.795	7.492	110.370	0.588	−1.359	18.519	0.684
			(0.030)	(0.023)	(1.567)	(32.662)	(0.811)	(0.812)	(0.012)	(0.019)
142	13–1114	13–485	0.008	6474.942	68.566	0.000	−0.707	−0.383	20.374	0.292
			(0.001)	(0.003)	(5.160)	(2.113)	(0.147)	(0.300)	(0.018)	(0.012)
143	13–1124	13–500	0.269	6489.987	22.335	0.727	0.671	−1.478	18.292	0.593
			(0.047)	(0.045)	(1.035)	(96.262)	(0.263)	(0.806)	(0.001)	(0.002)
144	13–1145	13–523	−0.053	6503.507	36.562	8.814	−0.173	1.443	18.536	0.654
			(0.011)	(0.009)	(1.204)	(13.386)	(0.131)	(0.886)	(0.002)	(0.001)
145	13–1157	13–490	−0.287	6504.274	13.587	140.112	0.116	−1.493	15.260	0.005
			(0.003)	(0.004)	(0.049)	(39.911)	(0.065)	(0.581)	(0.000)	(0.001)
146	13–1227	13–545	−0.052	6515.517	93.445	13.861	−0.165	0.803	17.576	0.924
			(0.003)	(0.027)	(3.798)	(10.893)	(0.022)	(0.121)	(0.001)	(0.000)
147	13–1250	13–516	0.552	6491.580	2.588	582.467	−0.264	0.240	15.668	0.925
			(0.117)	(0.019)	(0.302)	(208.685)	(0.801)	(0.789)	(0.000)	(0.001)
148	13–1253	13–519	−0.110	6497.594	7.984	18.925	1.469	1.476	17.138	0.786
			(0.006)	(0.008)	(0.260)	(27.287)	(0.593)	(0.803)	(0.001)	(0.001)
149	13–1257	13–556	0.253	6514.259	23.877	128.485	0.994	−1.475	18.625	0.513
			(0.068)	(0.038)	(0.839)	(85.036)	(0.157)	(0.771)	(0.001)	(0.002)
150	13–1279	13–518	0.082	6499.373	3.808	139.541	0.000	0.000	15.799	0.000
			(0.001)	(0.001)	(0.010)	(0.859)	(0.000)	(0.000)	(0.000)	(0.000)
151	13–1287	13–537	0.576	6503.415	13.465	0.000	0.163	−1.446	17.502	0.314
			(0.051)	(0.046)	(0.710)	(155.043)	(0.314)	(0.839)	(0.001)	(0.003)
152	13–1492	13–548	−0.243	6504.597	13.462	254.502	−1.064	0.286	17.274	0.911
			(0.074)	(0.054)	(2.230)	(111.644)	(0.757)	(0.795)	(0.002)	(0.002)
153	13–1498	13–568	−0.232	6517.917	18.762	184.671	0.737	−1.410	18.842	0.000
			(0.010)	(0.031)	(0.403)	(59.591)	(0.178)	(0.873)	(0.002)	(0.000)
154	13–1506	13–541	−0.110	6512.931	12.343	105.627	−0.742	0.612	16.009	0.017
			(0.004)	(0.002)	(0.125)	(8.549)	(0.135)	(0.816)	(0.001)	(0.002)
155	13–1551	13–572	−0.155	6517.452	15.373	163.872	−0.963	−0.276	19.404	0.506
			(0.022)	(0.024)	(1.063)	(53.582)	(0.505)	(0.833)	(0.005)	(0.005)
156	13–1598	13–570	−0.754	6532.931	10.952	4.218	−1.500	−1.461	15.584	0.133
			(0.035)	(0.024)	(0.325)	(69.121)	(0.019)	(0.858)	(0.000)	(0.003)
157	13–1617	13–560	−0.200	6515.385	11.019	163.536	−0.865	−0.955	17.642	0.152
			(0.007)	(0.007)	(0.225)	(41.817)	(0.296)	(0.777)	(0.001)	(0.003)
158	13–1669	13–585	−0.007	6527.163	52.476	9.301	0.163	1.496	20.463	0.013
			(0.000)	(0.003)	(2.138)	(0.471)	(0.111)	(1.054)	(0.019)	(0.019)
159	13–1678	13–595	−0.204	6531.602	7.545	0.000	1.494	1.379	18.312	0.413
			(0.028)	(0.018)	(0.479)	(77.941)	(0.469)	(0.811)	(0.003)	(0.006)
160	13–1689	13–593	−0.081	6534.384	5.177	47.757	0.931	−0.432	17.420	0.086
			(0.003)	(0.001)	(0.062)	(20.507)	(0.646)	(0.794)	(0.001)	(0.003)
161	13–1721	13–618	−0.086	6535.020	22.085	92.966	−0.336	−1.119	20.502	0.254
			(0.009)	(0.042)	(2.239)	(26.987)	(0.447)	(0.825)	(0.010)	(0.011)
162	13–1730	13–602	−0.214	6538.838	17.116	3.528	−0.216	−0.140	18.848	0.330
			(0.021)	(0.041)	(0.940)	(64.806)	(0.414)	(0.803)	(0.004)	(0.007)
163	13–1738	13–628	0.286	6542.673	12.642	8.011	−1.265	0.079	18.951	0.328
			(0.075)	(0.042)	(0.809)	(87.152)	(0.427)	(0.776)	(0.002)	(0.005)
164	13–1775	13–614	−0.008	6538.850	46.183	7.671	−0.060	−0.392	20.126	0.750
			(0.001)	(0.004)	(7.734)	(1.873)	(0.300)	(0.750)	(0.012)	(0.003)
165	14–0099	14–109	−0.343	6876.998	123.255	263.093	0.194	0.291	16.683	0.338
			(0.005)	(0.087)	(1.073)	(71.902)	(0.004)	(0.020)	(0.000)	(0.001)
166	14–0115	14–273	−0.348	6859.582	97.229	307.209	0.110	0.039	17.117	0.010
			(0.009)	(0.040)	(0.858)	(21.747)	(0.005)	(0.030)	(0.001)	(0.001)
167	14–0124	14–307	−0.160	6836.531	167.579	89.568	0.129	−0.074	17.382	0.712
			(0.004)	(0.047)	(5.816)	(38.330)	(0.014)	(0.027)	(0.001)	(0.001)
168	14–0257	14–148	0.001	6772.704	61.720	139.227	−0.140	−0.078	19.027	0.333
			(0.006)	(0.028)	(1.309)	(2.858)	(0.015)	(0.153)	(0.003)	(0.003)
169	14–0337	14–194	−0.543	6822.955	45.276	207.333	0.146	1.416	16.768	0.000
			(0.006)	(0.023)	(0.187)	(78.241)	(0.042)	(0.075)	(0.000)	(0.000)
170	14–0383	14–147	0.013	6761.393	15.139	10.691	−0.041	−0.549	18.032	0.583
			(0.004)	(0.001)	(0.293)	(3.899)	(0.171)	(0.753)	(0.002)	(0.001)
171	14–0419	14–283	−0.248	6822.954	47.010	0.000	−0.551	−0.861	17.918	0.194
			(0.012)	(0.024)	(1.166)	(57.567)	(0.175)	(0.333)	(0.002)	(0.002)
172	14–0512	14–157	0.675	6782.126	11.354	0.000	0.914	1.492	15.679	0.000
			(0.003)	(0.010)	(0.038)	(40.879)	(0.078)	(0.259)	(0.000)	(0.000)
173	14–0530	14–220	−0.117	6791.737	20.530	51.944	−0.034	−0.372	17.684	0.093
			(0.002)	(0.005)	(0.162)	(18.433)	(0.103)	(0.650)	(0.001)	(0.001)
174	14–0531	14–229	0.186	6784.771	41.753	1.559	0.151	−1.499	18.045	0.802
			(0.029)	(0.071)	(3.073)	(56.852)	(0.173)	(0.792)	(0.001)	(0.001)
175	14–0572	14–165	−0.561	6775.903	9.009	3.733	1.498	−1.480	17.445	0.000
			(0.007)	(0.036)	(0.083)	(65.306)	(0.052)	(0.555)	(0.001)	(0.000)
176	14–0582	14–151	0.005	6766.182	2.074	84.547	−1.127	0.463	19.220	0.453
			(0.028)	(0.026)	(0.245)	(32.638)	(0.793)	(0.805)	(0.004)	(0.006)
177	14–0617	14–215	0.141	6771.464	1.565	236.811	0.469	−0.516	18.756	0.718
			(0.085)	(0.007)	(0.162)	(67.919)	(0.802)	(0.778)	(0.003)	(0.004)
178	14–0676	14–175	0.004	6778.228	8.015	110.012	−0.910	0.487	19.537	0.456
			(0.077)	(0.226)	(5.435)	(50.335)	(0.828)	(0.789)	(0.016)	(0.026)
179	14–0692	14–214	0.255	6778.824	7.763	274.031	1.199	−0.476	18.853	0.762
			(0.057)	(0.037)	(0.737)	(74.266)	(0.738)	(0.769)	(0.002)	(0.004)
180	14–0696	14–199	0.405	6788.774	6.832	3.167	−1.393	1.496	14.183	0.000
			(0.001)	(0.003)	(0.011)	(24.469)	(0.098)	(0.512)	(0.000)	(0.000)
181	14–0734	14–243	−0.753	6791.432	5.851	424.005	1.483	−0.740	17.725	0.019
			(0.046)	(0.027)	(0.240)	(176.220)	(0.707)	(0.813)	(0.001)	(0.005)
182	14–0727	14–281	1.043	6842.546	38.110	0.000	−0.819	−0.075	16.607	0.056
			(0.162)	(2.346)	(4.552)	(306.481)	(0.142)	(0.127)	(0.001)	(0.013)
183	14–0729	14–262	−0.663	6799.616	6.557	4.023	−1.226	1.430	16.463	0.000
			(0.008)	(0.017)	(0.045)	(85.907)	(0.486)	(0.778)	(0.000)	(0.000)
184	14–0783	14–253	−0.017	6791.411	21.003	19.919	0.072	1.187	20.117	0.532
			(0.001)	(0.002)	(1.410)	(1.993)	(0.488)	(0.794)	(0.005)	(0.003)
185	14–0874	14–302	−0.199	6845.679	24.877	130.938	−0.030	1.482	15.887	0.000
			(0.004)	(0.006)	(0.096)	(41.271)	(0.083)	(0.351)	(0.000)	(0.000)
186	14–0893	14–296	−0.024	6809.366	74.901	0.000	0.000	0.000	19.660	0.857
			(0.007)	(0.014)	(8.718)	(6.110)	(0.243)	(0.551)	(0.007)	(0.002)
187	14–0894	14–333	−0.458	6846.403	28.577	0.000	0.213	−1.499	17.530	0.031
			(0.010)	(0.026)	(0.491)	(71.085)	(0.074)	(0.870)	(0.001)	(0.003)
188	14–0900	14–305	0.280	6862.267	33.421	0.000	−0.202	−1.499	16.060	0.000
			(0.010)	(0.041)	(0.238)	(73.755)	(0.022)	(0.017)	(0.001)	(0.000)
189	14–0928	14–361	−0.387	6877.343	55.656	106.812	−0.076	−1.402	16.570	0.181
			(0.014)	(0.043)	(1.576)	(66.610)	(0.023)	(0.068)	(0.000)	(0.001)
190	14–9958	14–275	0.090	6817.268	79.072	34.569	0.120	0.884	19.074	0.000
			(0.001)	(0.031)	(0.290)	(13.950)	(0.022)	(0.049)	(0.002)	(0.000)
191	14–0962	14–285	−0.002	6817.988	6.540	199.230	−1.476	1.493	16.171	0.524
			(0.027)	(0.014)	(0.085)	(10.398)	(0.237)	(0.622)	(0.000)	(0.002)
192	14–0996	14–310	−0.064	6812.742	16.899	1.083	1.257	1.409	20.275	0.000
			(0.002)	(0.007)	(0.150)	(15.487)	(0.650)	(0.812)	(0.003)	(0.000)
193	14–1029	14–312	0.002	6811.241	125.789	0.950	−1.425	0.101	20.353	0.984
			(0.001)	(0.005)	(53.289)	(0.855)	(0.282)	(0.381)	(0.006)	(0.000)
194	14–1101	14–362	0.713	6855.431	20.393	358.065	−0.897	1.372	16.892	0.000
			(0.035)	(0.045)	(0.499)	(167.500)	(0.319)	(0.745)	(0.000)	(0.000)
195	14–1109	14–328	0.785	6826.141	7.855	608.533	−1.414	1.499	18.304	0.044
			(0.085)	(0.076)	(0.681)	(205.985)	(0.805)	(0.747)	(0.002)	(0.011)
196	14–1111	14–401	−0.181	6861.902	32.831	2.518	0.077	0.676	18.740	0.006
			(0.005)	(0.026)	(0.587)	(36.410)	(0.089)	(0.706)	(0.003)	(0.004)
197	14–1153	14–389	−0.366	6853.536	16.342	0.000	0.081	−1.485	17.928	0.001
			(0.008)	(0.018)	(0.174)	(68.999)	(0.216)	(0.837)	(0.001)	(0.002)
198	14–1255	14–367	0.011	6844.289	25.208	0.000	0.050	1.400	18.551	0.636
			(0.013)	(0.006)	(1.188)	(11.132)	(0.589)	(0.770)	(0.004)	(0.002)
199	14–1284	14–392	0.037	6852.991	40.898	0.000	0.551	−0.992	19.230	0.687
			(0.009)	(0.010)	(1.745)	(7.153)	(0.217)	(0.785)	(0.003)	(0.001)
200	14–1285	14–370	−0.567	6848.987	6.316	0.000	1.500	1.180	16.076	0.000
			(0.007)	(0.008)	(0.033)	(72.928)	(0.464)	(0.812)	(0.000)	(0.000)
201	14–1308	14–357	0.493	6846.555	10.199	0.000	−0.894	−1.372	17.794	0.061
			(0.103)	(0.040)	(0.233)	(142.274)	(0.707)	(0.792)	(0.003)	(0.014)
202	14–1317	14–364	−0.045	6840.933	40.873	0.000	−1.484	−0.200	20.254	0.651
			(0.007)	(0.032)	(4.059)	(16.625)	(0.708)	(0.744)	(0.014)	(0.006)
203	14–1340	14–372	−0.084	6845.154	6.697	0.085	1.491	1.497	19.393	0.000
			(0.003)	(0.004)	(0.173)	(18.720)	(0.811)	(0.819)	(0.004)	(0.000)
204	14–1392	14–398	0.097	6854.863	13.448	97.901	−0.434	−0.910	20.017	0.191
			(0.007)	(0.010)	(0.571)	(22.785)	(0.593)	(0.795)	(0.004)	(0.005)
205	14–1406	14–409	−0.344	6873.449	12.544	0.000	0.100	−1.497	15.840	0.000
			(0.003)	(0.026)	(0.065)	(49.425)	(0.195)	(0.827)	(0.001)	(0.000)
206	14–1409	14–393	−0.029	6853.793	11.255	14.686	−1.192	0.144	18.945	0.890
			(0.006)	(0.010)	(1.519)	(12.319)	(0.794)	(0.810)	(0.002)	(0.001)
207	14–1410	14–424	0.199	6868.477	21.526	195.626	−0.268	−1.486	18.435	0.434
			(0.023)	(0.027)	(0.883)	(71.835)	(0.230)	(0.844)	(0.002)	(0.004)
208	14–1437	14–407	−0.056	6858.442	7.216	0.000	1.463	1.132	18.466	0.426
			(0.020)	(0.006)	(0.354)	(15.973)	(0.819)	(0.793)	(0.005)	(0.004)
209	14–1472	14–433	0.147	6864.195	12.511	40.003	0.426	0.926	19.705	0.007
			(0.006)	(0.022)	(0.413)	(34.658)	(0.705)	(0.814)	(0.006)	(0.009)
210	14–1483	14–506	0.063	6895.944	54.295	57.645	−0.009	0.261	18.862	0.762
			(0.003)	(0.029)	(2.656)	(14.109)	(0.060)	(0.394)	(0.002)	(0.001)
211	14–1486	14–423	−0.107	6864.709	5.525	82.538	1.428	1.499	16.596	0.565
			(0.004)	(0.001)	(0.055)	(26.708)	(0.535)	(0.813)	(0.000)	(0.000)
212	14–1498	14–456	−0.150	6881.422	25.862	0.000	0.000	0.037	19.411	0.336
			(0.006)	(0.032)	(0.753)	(33.263)	(0.112)	(0.659)	(0.002)	(0.003)
213	14–1501	14–426	0.007	6859.360	43.698	0.000	0.004	0.093	20.328	0.099
			(0.001)	(0.002)	(2.755)	(2.010)	(0.215)	(0.701)	(0.012)	(0.011)
214	14–1570	14–451	−0.697	6887.094	12.102	451.023	0.236	0.752	16.121	0.169
			(0.025)	(0.017)	(0.303)	(130.543)	(0.110)	(0.737)	(0.000)	(0.001)
215	14–1812	14–444	0.017	6873.149	68.707	26.821	1.459	1.003	21.368	0.243
			(0.002)	(0.017)	(14.538)	(3.729)	(0.187)	(0.797)	(0.072)	(0.053)
216	14–1596	14–445	−0.206	6874.945	16.352	210.268	−1.476	−0.359	18.457	0.575
			(0.014)	(0.057)	(0.760)	(53.485)	(0.343)	(0.771)	(0.003)	(0.005)
217	14–1598	14–448	−0.096	6874.447	3.484	0.844	−1.488	−1.155	19.253	0.121
			(0.031)	(0.008)	(0.238)	(28.613)	(0.823)	(0.801)	(0.004)	(0.008)
218	14–1600	14–494	−0.285	6889.198	27.047	0.000	−0.198	1.486	19.070	0.277
			(0.039)	(0.058)	(1.592)	(113.552)	(0.115)	(0.812)	(0.003)	(0.005)
219	14–1647	14–489	0.164	6892.046	16.237	0.000	−0.086	−1.482	17.716	0.840
			(0.012)	(0.018)	(0.580)	(49.741)	(0.310)	(0.842)	(0.001)	(0.001)
220	14–1701	14–488	−0.124	6891.664	6.797	122.430	−1.459	−1.397	17.559	0.668
			(0.005)	(0.005)	(0.162)	(9.349)	(0.652)	(0.790)	(0.001)	(0.001)
221	14–1706	14–502	−0.807	6892.816	3.298	0.000	−1.500	−0.994	17.221	0.000
			(0.038)	(0.024)	(0.104)	(141.679)	(0.729)	(0.815)	(0.001)	(0.010)
222	14–1720	14–507	−0.045	6894.912	13.556	75.223	−1.370	−0.662	19.072	0.718
			(0.004)	(0.006)	(0.817)	(5.115)	(0.631)	(0.788)	(0.005)	(0.004)
223	14–1748	14–496	−0.001	6891.179	6.973	0.000	−1.349	−1.282	19.827	0.664
			(0.002)	(0.001)	(0.976)	(1.931)	(0.796)	(0.834)	(0.011)	(0.006)
224	14–1816	14–498	0.065	6893.400	13.480	18.307	−1.496	−1.411	19.947	0.000
			(0.003)	(0.008)	(0.293)	(15.881)	(0.140)	(0.765)	(0.005)	(0.000)
X1	11–0975	11–305	0.408	5760.427	14.646	1145.523	−0.473	0.120	19.344	0.009
			(0.252)	(0.238)	(2.751)	(162.081)	(0.738)	(0.795)	(0.007)	(0.043)
X2	12–0937	12–405	−0.063	6102.288	9.248	725.970	1.226	1.221	20.328	0.071
			(0.131)	(0.099)	(0.523)	(37.411)	(0.806)	(0.800)	(0.008)	(0.019)
X3	12–1502	12–567	0.064	6138.430	393.584	71.659	−0.810	0.053	20.365	0.933
			(0.041)	(2.725)	(79.223)	(80.405)	(0.310)	(0.229)	(0.012)	(0.002)
X4	13–0966	13–428	−0.352	6450.141	8.388	223.542	1.180	−0.863	20.108	0.404
			(0.236)	(0.143)	(11.326)	(221.974)	(0.796)	(0.788)	(0.013)	(0.026)
X5	14–0289	14–092	0.572	6852.483	230.254	837.450	−0.260	1.061	18.813	0.243
			(0.170)	(28.456)	(113.809)	(395.201)	(0.456)	(0.200)	(0.031)	(0.082)
X6	14–0921	14–270	−0.003	6803.854	374.898	3.852	0.490	0.229	19.724	0.996
			(0.234)	(0.145)	(90.046)	(151.397)	(0.788)	(0.819)	(0.021)	(0.000)