Picosecond Laser-Induced Photothermal Skin Damage Evaluation by Computational Clinical Trial

Abstract

Background and Objectives

Computational clinical trial (CCT) in the field of laser medicine promotes clinical application of novel laser devices, because this trial carried out based on numerical modeling of laser-tissue interactions and simulation of a series of treatment process. To confirm the feasibility of the computational clinical trial of skin treatment with a novel picosecond laser, this paper presents an evaluation method of the safety.

Study Design/Materials and Methods

In this method, the light propagation and thermal diffusion process after ultrashort light pulse irradiation to a numerical skin model is calculated and the safety based on the photothermal damage is evaluated by computational modeling and simulation. As an example, the safety of a novel picosecond laser device was examined by comparing with several laser devices approved for clinical use.

Results

The ratio of the maximum thermal damage induced by picosecond laser irradiation was 1.2 × 10⁻² % at the epidermis, while that caused by approved laser irradiation was 99 % at the capillary vessels. The numerical simulation demonstrated that less thermal damage was observed compared with the approved devices. The results show the safety simulated by photothermal damage calculation was consistent with the reported clinical trials.

Conclusions

This computational clinical trial shows the feasibility of applying computational clinical trials for the safety evaluation of novel medical laser devices. In contrast to preclinical and clinical tests, the proposed computational method offers regulatory science for appropriately and quickly predicting and evaluating the safety of a novel laser device.

Introduction

In dermatology and plastic surgery, the use of picosecond laser devices has shown promising results for skin surgery, including tattoo removal and treatment of benign pigmented lesions and acne scars. ^1–5) Irradiation of ultra-short picosecond pulses induces instantaneous heating of target chromophores in skin tissue and causes greater destruction because of the higher peak power density, with less damage to the surrounding tissue. Accordingly, picosecond laser skin treatment is less invasive and more effective. ⁶⁾ Novel picosecond laser devices will continue to be applied for clinical use.

For the clinical application of a novel laser device, preclinical and/or clinical trials are required to evaluate the safety and efficacy of the treatment. In laser skin treatments, a significant amount of light energy is injected from the outside to produce the treatment effect. However, there is a risk of injury to areas other than the surgical site. Because laser treatments should be performed under the condition that the risk is acceptably small, safety evaluation is the basis for preclinical and clinical trials. The risk evaluation of laser treatments can be evaluated by ex vivo and in vivo experiments. ^7–9) The trials based on these experiments, however, are difficult to evaluate the physical phenomena induced by ultrashort pulsed light irradiation during treatment due to the ultrafast phenomena. For this reason, the conventional trials have required statistical evaluations based on comparison of in vivo experiments and clinical studies between a novel device and approved devices. ¹⁰⁾ The evidences for the safety are provided by comparing the outcomes at treatment endpoint by observing side effects including scaring and burning of skin tissue. Furthermore, the processes for such trials require massive amounts of time and cost, because a sufficient number of subjects is needed to obtain reliable clinical data, and consequently can prevent smooth clinical application. For example, in Japan, some picosecond lasers for medical use have been used without regulatory approval; as a result, medical malpractices or accidents have occurred because of laser irradiation with inappropriate parameters. ¹¹⁾ Because this problem presents a barrier for the development and application of epoch-making laser devices, a not merely qualitative and reproducible but also quick and cost-effective evaluation method of the safety is urgently required.

As a third trial in addition to preclinical and clinical studies, computational clinical trials evaluate the safety, efficacy, quality, and performance of medical devices. ¹²⁾ In computational clinical trials, preclinical and clinical tests are carried out by numerical modeling and simulation of a series of treatment process. This trial can offer more accurate scientific evidences, because computer simulation can reproduce physical phenomena induced by laser irradiation to tissue. According to reports by the Food and Drug Administration in the USA, computational clinical trials are helpful to address and investigate how a treatment behaves in many clinically relevant cases, without temporal, financial, or ethical considerations. ¹³⁾ Although bench testing, animal studies, and clinical trials have traditionally been based on relative comparisons of the outcomes for approval of the application of medical devices, computational clinical trials enable quantitative and reproducible evaluation based on the analysis of light-tissue interactions. Computational clinical trials can exclude individual differences among test subjects, variations in medical technique by operators in clinical trial data, and uncertainty of scientific evidence for extrapolation of animal study data to humans. The use of this trial can investigate differences between several laser devices in treatment outcomes under the same conditions without the unclear conditions including individual differences. Once computational clinical trials are established, it can bring out huge potential to reduce barriers to the development of novel laser devices and facilitate their rapid clinical application in medical device field.

For the analysis of interactions between light and tissue, physical models have been constructed in silico. By modeling light propagation in skin tissue, diffuse reflectance spectra of tissue can be simulated for quantitative monitoring and localization of chromophores in biological tissues. The algorithm used in the simulation yields results that agree reasonably well with in vivo measurements when a skin model is supplied with reasonable physical and structural parameters for internal tissues. ¹⁴⁾ By modeling the thermal response of tissue, laser coagulation of tissue has been simulated. ^{15, 16)} The validity of the simulation was verified by comparison with MRIbased temperature data acquired from in vivo experiments in rabbits. The model simulated temperature distribution and predicted lesion dynamics corresponding closely with MRI-based data. ¹⁵⁾ By modeling light and heat transfer in tissue, photothermal effects, including tissue ablation and coagulation, can be simulated. ^{17, 18)} For example, in laser treatment of the prostate, computational simulations were performed for analysis of the dependency of tissue ablation and coagulation on irradiation parameters. The simulated results were confirmed to fit those of physical experiments such as in vivo experiments. ¹⁷⁾ As the numerical simulations of light propagation and thermal diffusion in tissue can reproduce the physical phenomena with high accuracy, these simulations have been widely applied to computer simulation for the quantitative analysis of laser treatments and light-tissue interactions.

For the in silico evaluation of interactions between a picosecond laser and skin tissue, the physical mechanism during picosecond laser irradiation is required to be modeled. The interaction between picosecond laser light and skin tissue consists of a combination of photoacoustic and photothermal effects ¹⁹⁾. In a computer simulation related to the interaction, analysis to determine the optimal parameters has been conducted to examine the efficacy by investigating the fragmentation mechanism accompanying picosecond laser irradiation. ¹⁹⁾ Conversely, the quantitative evaluation of photothermal damage induced by picosecond laser irradiation with a computational method is required to examine the safety.

In this paper, we present a computational clinical trial to evaluate the safety of treatment with a novel picosecond laser device by computational modeling and simulation. With the computational clinical trial, quantitative and reproducible evaluation is performed in a short amount of time and with low cost. As an example, supposing a 755-nm wavelength picosecond laser device is tested for approval in clinical use, the safety can be tested by comparison with an approved clinical picosecond laser. Optical penetration depth, temperature rise, and thermal damage rate caused by picosecond pulsed light are analyzed numerically as indexes to evaluate the safety. From the safety perspective, we confirm that the computational clinical trial can provide the same results achieved by clinical and in vivo trials.

Materials and methods

Computational Clinical Trial Model

The computational clinical trial was carried out under harsh conditions to evaluate the safety. This computer simulation assumed that all the absorbed light energy was converted to heat energy to calculate the maximum photothermal damage induced by picosecond pulsed light irradiation. The laser device to be evaluated was an alexandrite picosecond laser with a wavelength of 755 nm (Device A). The approved laser devices for comparison were an alexandrite nanosecond laser with a wavelength of 755 nm (Device B) and a Nd:YAG picosecond laser with wavelengths of 1064 and 532 nm (Device C). Table 1 shows the specifications of the picosecond and nanosecond laser devices used in this computational modeling and simulation.

Table 1: Specifications of Laser Devices Numerically Evaluated in This Computational Clinical Trial.

	Device A	Device B	Device C
Wavelength	755, 532 nm	755 nm	1064, 532 nm
Pulse width	550–750 ps	50–100 ns	750 ps, 2 ns
Spot shape	1.5, 2–6, 8, 10 mm (□)	2, 3, 4, 5, 6 mm (φ)	2, 3, 4, 5, 6, 7, 8 mm (φ)
Fluence	0.21–6.37 J/cm2	1.6–18 J/cm2	0.2–10, 0.2–2.5 J/cm2
Repetition rate	Single, 1, 2.5, 5, 10 Hz	Single, 1, 2, 5, 10 Hz	Single, 1, 2, 3.3, 5, 10 Hz

In this study, the optical penetration depth, temperature rise, and thermal damage rate caused by irradiation to normal skin tissue with Devices A, B, and C were compared. Figure 1 describes the steps of the computational modeling: a Monte Carlo (MC) simulation of light propagation, ²⁰⁾ a finite difference method for thermal diffusion calculation, ²¹⁾ and an Arrhenius model to quantify thermal damage. ²²⁾ Light propagation in skin tissue is calculated to obtain the deposited energy in skin tissue. The MC simulation used in this study assumes linear absorption process. ²⁰⁾ Nonlinear absorption process such as two-photon absorption can occur under irradiation by short light pulses (10⁻⁹ to 10⁻¹² s). ¹⁾ Nonlinear absorption process induced by picosecond laser irradiation leads to the formation of laser induced breakdown and the subsequent creation of plasma above the irradiance threshold power density of 10¹²–10¹³ W/cm². ²³⁾ The irradiance threshold value is more than two orders of magnitude higher than the largest power density of the outputs by Devices A, B, and C. Then, this paper assumed the nonlinear absorption process is negligible for evaluating the devices. In addition, tissue damages by photoacoustic effects are assumed to be negligible. The largest stress wave generation by Device A was estimated as 0.1 MPa by referring to Ref. 24, 25. The calculated value is the three orders of magnitude smaller than the damage threshold of 30 MPa. ²⁶⁾ Here, heat diffusion during one pulse irradiation by ultrashort pulsed lasers can be negligible because the thermal confinement condition is satisfied. Using this approximation, the thermal diffusion can be calculated by setting the initial value of a heat source as the absorbed energy distribution after the laser pulse irradiation. From the calculated spatial distribution of the temperature rise, the ratio of thermal damage can be calculated. The degree of thermal damage depends on the temperature of skin tissue and the exposure time at that temperature. ^{27, 28)}

Fig. 1:

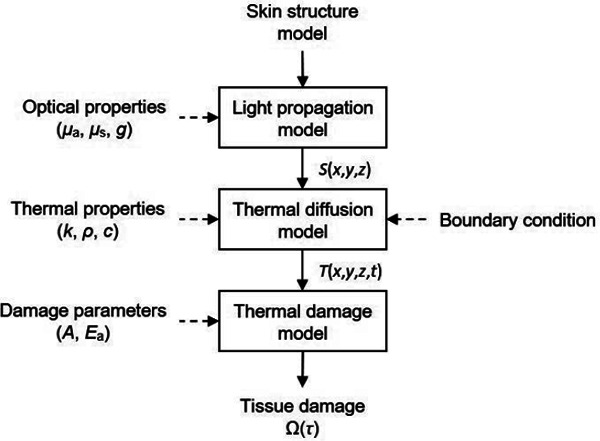
Schematic diagram of the computational modeling and simulation of light and heat transfer. After creating a numerical skin geometry model, light propagation in the skin model is calculated with optical properties to produce spatial distribution of energy deposition S(x,y,z). By using the absorbed energy distribution as the initial value of a heat source, thermal diffusion is analyzed to produce temperature distribution T(x,y,z,t). From the calculated spatiotemporal temperature change, a spatial distribution of thermal damage rate in the skin model is derived numerically.

Three-dimensional Numerical Skin Tissue Model

For execution of the computational clinical trial, a three-dimensional numerical skin tissue model was constructed, having a flat and multi-layered structure. The effect on normal skin tissue of picosecond laser irradiation was considered to evaluate the safety. As seen in Fig. 2, the skin model was composed of epidermis, dermis, and subcutaneous fat. The dermis layer included three different sizes of blood vessels; capillary vessels, upper dermis vessels, and deep dermis vessels. The skin tissue model was constructed with a cube voxel of 500 × 500 × 400 elements. The voxel size was 0.01 × 0.01 × 0.01 mm³. The depth direction of the skin model was along the z axis. The skin surface was set as z = 0 mm. The plane vertical to the z axis was defined as the xy plane. The xy plane center of the three-dimensional skin tissue model was (x, y) = (0 mm, 0 mm). For the comparative evaluation between Device A and Devices B and C, the layer thicknesses of epidermis, dermis, and subcutaneous fat were set as the mean values of 0.1, 1.1, and 2.8 mm, respectively. ²⁹⁾ Each voxel was assigned an absorption coefficient, scattering coefficient, and anisotropy factor for Caucasian people, corresponding to wavelength and tissue type as listed in Table 2. The absorption coefficients of dermis and subcutaneous fat were bloodless parameters. The parameters of blood vessels in the skin model were set as shown in Table 3. ⁴¹⁾ The capillary plexus was 150 µm in thickness. The upper dermis blood vessels and the deep dermis blood vessels lined at a depth of 290 and 1160 µm, respectively. The number of vessels was calculated based on the volume fractions of blood. The numbers of capillary vessels, upper dermis vessels, and deep dermis vessels were 382, 61, and 9, respectively.

Fig. 2:

(a) Three-dimensional structure of skin model and (b) its zx plane cut, consisting of epidermis, dermis, subcutaneous fat, and three kinds of blood vessels (capillary vessels, upper dermis vessels, and deep dermis vessels).

Table 2: Optical and Thermal Properties and Damage Parameters for Computational Modeling and Simulation of Laser Irradiation.

	Epidermis	Dermis	Subcutaneous fat	Blood
Optical properties
λ = 532 nm 30–33)
Absorption coefficient (µa) [cm−1]	14.3	0.527	0.91	100
Scattering coefficient (µs) [cm−1]	605	388	314	295
Anisotropy factor (g) [−]	0.9
λ = 755 nm 30, 31, 33, 34)
Absorption coefficient (µa) [cm−1]	4.55	0.254	0.09	3
Scattering coefficient (µs) [cm−1]	394	238	217	321
Anisotropy factor (g) [−]	0.9
λ = 1064 nm 30,31,33,35)
Absorption coefficient (µa) [cm−1]	1.61	0.244	0.5	2
Scattering coefficient (µs) [cm−1]	291	177	169	250
Anisotropy factor (g) [−]	0.9
Thermal properties 36–40)
Thermal conductivity (k) [×10−3 W/(cm·K)]	2.09	3.00	2.05	4.92
Specific heat (c) [J/(g·K)]	3.60	3.22	2.30	3.84
Density (ρ) [g/cm3]	1.19	1.12	0.97	1.00
Damage parameters 22)
Frequency factor (A) [1/s]	8.82×1094 (T ≤ 53·C), 1.297×1031 (T > 53°C)
Activation energy (Ea) [J/mol]	6.028×105 (T ≤ 53°C), 2.04×105 (T > 53°C)
Gas constant (R) [J/(mol·K)]	8.314

Table 3: Parameters for Blood Vessels.

	Depth [µm]	Volume fraction [%]	Diameter [µm]
Capillary vessel	175	4	10
Upper blood net plexus	290	30	50
Deep blood net plexus	1160	10	80

Light Propagation Calculation

To obtain the distribution of photons deposited in skin tissue, a Monte Carlo (MC) program named mcxyz developed by S. L. Jacques et al. at the Oregon Medical Laser Center was adopted for this study. ^{20, 42)} This model uses a statistical approach using random numbers to model light transfer in tissue, where photons experience absorption and scattering events. This model is able to calculate light propagation through skin tissue layer having complex structure including cylindrical structures of blood vessels. In this study, laser was irradiated from the top surface of skin tissue vertically as a uniform beam to simulate the actual irradiation conditions during a treatment session. The light wavelength was set to 532, 755, or 1064 nm, according to the specifications of the laser devices. The MC simulation was carried out for 12,000,000 photons to achieve a sufficient distribution of light absorbed by the skin tissue.

Thermal Diffusion Calculation

The temperature variation by absorption of the pulsed light is determined by the heat capacity and thermal conductivity of the skin tissue model, and the heat is diffused at a speed proportional to the temperature gradient. This diffusion promotes an increase in the temperature of normal tissues around the surgical site and can cause cell necrosis and protein coagulation. ⁴³⁾ In this study, combined with the internal heat generated from the light energy absorption calculated by the MC simulation, the time variation of temperature distribution in the skin tissue was obtained using the three-dimensional heat conduction equation: ²¹⁾

where ρ [g/cm³] is the density of each tissue type in the skin model, c [J/(g•K)] is the specific heat of each tissue type in the skin model, k [W/(cm•K)] is the thermal conductivity of each tissue type in the skin model, and S [W/cm³] is the internal heat source, as shown in Table 2. The heat source term was present only during laser pulse irradiation. This equation was solved with the finite difference technique.

Adiabatic boundary conditions were applied to boundaries at z = 4.0 mm and x, y = ± 2.5 mm. The convective surface boundary condition at the border of air and skin tissue was applied.

where h is the heat transfer coefficient between the skin surface and the air, equal to 0.001 [W/(cm²•K)], ⁴⁴⁾ T_air is the temperature at air [°C], and T_surface is the temperature at the surface of the skin model [°C]. The initial temperatures of the skin model and air were set to 32 and 24 °C, respectively. The temporal step size during and after laser irradiation were one hundredth of a pulse width and 10 nanoseconds, respectively.

Thermal Damage Calculation

Thermal damage depends on not only the temperature of the tissue, but also the duration of time at that temperature. ^{27, 28)} In this study, the Arrhenius model was used to quantify thermal damage to the skin model using experimentally derived parameters (frequency factor, A and activation energy, E_a). This model is based on a unimolecular formulation of the standard rate process model of tissue damage in chemical kinetics. This model can be used to predict the probability of irreversible thermal damage and to calculate a non-dimensional damage parameter Ω from

where C(t) is the remaining concentration of undamaged tissue at exposure time t [s], A [1/s] is the frequency factor, E_a [J/mol] is the activation energy for denaturation of molecules, and R [J/(mol•K)] is the gas constant, as shown in Table 2. The concentration ratio of the damaged tissue to the undamaged tissue at exposure time τ [s] was expressed using the damage parameter Ω with the following equation ²²⁾:

In this study, the thermal damage of 63.2 % (Ω ≥ 1) was applied as the threshold for irreversible thermal damage, including cell necrosis and protein coagulation.

Irradiation Conditions

The laser irradiation conditions for the three devices are summarized in Table 4. Severe conditions indicate the conditions providing the maximum fluence in the specification, as can be seen in Table 1. Clinical conditions indicate the typical conditions used in a clinical laser tattoo removal procedure. ^{10, 46)} The spot shape of Device A was square, while those of Devices B and C were circular. The repetition rates were set at 10 Hz. The thermal diffusion process by one light pulse irradiation was analyzed for 100 ms to compare Device A with Devices B and C. Because the repetition rates were the largest in their specifications, the temperature rise and the thermal damage were evaluated under severe conditions. Cooling during laser irradiation was not considered in this study.

Table 4: Simulation Conditions of Short Pulsed Laser Irradiation.

	Severe conditions				Clinical conditions
	Device A	Device B	Device C		Device A	Device B	Device C
Wavelength [nm]	755	755	1064	532	755	755	1064	532
Pulse width [ns]	0.5	50	0.75		0.5	50	0.75
Spot shape [mm]	2 (□)	2 (φ)	2 (φ)		3 (□)	3 (φ)	3 (φ)
Fluence [J/cm2]	6.37	18	10	2.5	2.83	10	4.6	1.65
Repetition rate [Hz]	10
Cooling	None

Results

Light Propagation in the Skin Model

Because the depth that light penetrates into tissue depends on the wavelength, the optical penetration depth was evaluated. The optical penetration depth was defined as the depth at which the distributed light fluence inside the skin model falls to 1/e (36.8 %) of its original fluence at the surface. Figure 3 (a) shows the spatial distribution of fluence. The light pulse delivered at the skin surface disperses radially into a distributed fluence. Figure 3 (b) shows the energy deposition in the skin model. Light energy was absorbed strongly in the epidermis layer and the blood vessels in the dermis layer. Figure 4 indicates the optical penetration depth after ultrashort pulsed laser irradiation. The optical penetration depth with Device A was 0.85 mm, while the depths with Device B, Device C with a wavelength of 1064 nm (Device C (λ = 1064 nm)), and Device C with a wavelength of 532 nm (the Device C (λ = 532 nm)) were 0.82, 0.86, and 0.51 mm. The optical penetration depth with Device A was positioned between the depths resulting from Device C (λ = 1064 nm) and Device C (λ = 532 nm). The optical penetration depth with Device A was revealed to be the same as that of Device C. Figure 5 shows the energy deposition on the z axis after ultrashort pulsed laser irradiation. Laser irradiation with Device B delivered more energy to the layer of subcutaneous fat than did Device A. Even though the optical penetration depth with Device A was larger than that with Device B, Device A was safer because more energy was deposited with Device B. Therefore, the optical penetration depth with Device A was confirmed to be equivalent to those of Devices B and C.

Fig. 3:

Spatial distributions of (a) light fluence and (b) energy deposition in the skin model on the zx plane after laser pulse irradiation with (i) Device A (755 nm, 2 mm □ 6.37 J/cm²), (ii) Device B (755 nm, 2 mm φ, 18 J/cm²), (iii) Device C (1064 nm, 2 mm φ, 10 J/cm²), and (iv) Device C (532 nm, 2 mm φ, 2.5 J/cm²) under severe conditions.

Fig. 4:

Optical penetration depth after laser pulse irradiation under severe conditions.

Fig. 5:

Energy deposition profiles in the skin model on the z axis with x and y equal to 0 mm after laser pulse irradiation under severe conditions.

Temperature Rise

The time variation of temperature profiles on the z axis for 100 ms after laser irradiation are shown in Fig. 6. Immediately after laser irradiation with Devices A, B, and C, temperature peaks were found at the epidermis, the capillary vessels, the upper dermis vessels, and the deep dermis vessels. The total light energy was incident, and the temperatures were maximum during the pulse irradiations. After 100 ms, the temperature peaks at the blood vessels nearly disappeared as a result of thermal diffusion. Although the temperature peak at the epidermis became smooth, the peak was still higher than that before laser irradiation. Figure 7 shows the maximum temperature of each tissue type in the skin model under ultrashort pulsed laser irradiation. Under severe conditions, the maximum temperature of each tissue type after laser irradiation with Device A was not the largest compared with Devices B and C. Moreover, except at the epidermis layer, the maximum temperature of each tissue type under severe conditions with Device A was lower than that determined under clinical conditions with Devices B and C. Therefore, the temperature rise with Device A was confirmed not to be inferior to those of Devices B and C.

Fig. 6:

Time variations of temperature profiles in the skin model for 100 ms after laser pulse irradiation with (a) Device A (755 nm, 2 mm □, 6.37 J/cm²), (b) Device B (755 nm, 2 mm φ, 18 J/cm²), (c) Device C (1064 nm, 2 mm φ, 10 J/cm²), and (d) Device C (532 nm, 2 mm φ, 2.5 J/cm²) under severe conditions.

Fig. 7:

Maximum temperature after laser pulse irradiation in (a) epidermis, (b) dermis, (c) capillary vessels, (d) upper dermis vessels, (e) deep dermis vessels, and (f) subcutaneous fat.

Concentration Ratio of Thermally Damaged Tissue

In the thermal damage calculations, heat diffusion data are converted into thermal damage using the Arrhenius model because the degree of photothermal damage is determined by the temperature and the exposure time at that temperature. In particular, the peak temperature achieved in each target tissue shown in Fig. 7 dominated the Arrhenius thermal damage calculation. After 100 ms, the peaks of the thermal damage rate were found at the epidermis, the capillary vessels, and the upper dermis vessels. The maximum ratio of thermal damage with Device A was 1.2×10⁻² % at most in the layer of epidermis, while those with Devices B and C (λ = 1064 nm) were 42 and 7.5 × 10⁻⁶ %, respectively in the layer of epidermis, and that with Device C (λ = 532 nm) was 99 % at capillary vessels. The thermal damage rates with Device A were much smaller than the damage threshold of 63.2 %. Therefore, thermal damage with Device A was confirmed to be equivalent to that with Devices B and C.

Discussion

Devices B and C used for comparison have been approved for clinical use and several clinical studies have already confirmed their safety in respect of thermal damage. ^{10, 45)} Although Device A has not yet been approved in Japan at the present moment, several clinical experimental studies have reported that skin treatments by Device A has less side effects caused by thermal damage than nanosecond laser skin treatments. ^46–48) This simulation results demonstrated that the safety of Device A was noninferior to that of Devices B and C in terms of thermal damage, which had consistency with the reported experimental results. In general, clinical trials and in vivo studies of novel laser devices require a time-consuming process and a sufficient number of cases, ranging from 5–25. ^{10, 46, 49–53)} In these cases, outcomes at the endpoint of treatment are provided as evidence supporting safety and efficacy. In this paper, however, a computational trial completed the evaluation using a computer in a shorter amount of time. These simulated results did not include variations in operation technique by physicians because the light pulse irradiation was performed under the same conditions. Computational modeling and simulation investigates interactions based on the physical mechanism during laser irradiation to tissue with high accuracy, which indicates that the phenomena during treatment are analyzed. This aspect enables computational clinical trials to offer quantitative and reproducible evaluation. The trial shows that it is feasible to apply computational clinical trials for the safety evaluation of novel medical laser devices.

In the numerical calculation, the MC simulation assumed the linear absorption of the picosecond laser pulse in skin tissue. Picosecond laser irradiation, however, can also induce nonlinear absorption due to the high power density, which affects calculation of light distribution and energy deposition of skin tissue. Light propagation model with nonlinear absorption will improve the accuracy of quantitative evaluation for the picosecond laser effects on skin tissue. ⁵⁴⁾ The safety of a novel picosecond laser was evaluated based on photothermal damage. The damage was acute and present immediately after the interaction between a laser device and skin tissue. Actually, as another laser-tissue interaction, ultrashort pulse irradiation of tissue produces a thermoelastic effect because of instantaneous thermal tissue expansion. However, in this simulation, it was assumed that all light energy was translated into heat to calculate the maximum photothermal damage. In this computational clinical trial, temperature is a required parameter for modeling after light absorption in a skin model because this trial considered acute damage. The calculation of temperature can be computationally reproduced using the three-dimensional heat conduction equation precisely. In addition, using numerical simulation is standard for evaluating thermal damage because a parameter needed for simulation, such as a threshold for irreversible thermal damage, has already been obtained. ⁵⁵⁾ Therefore, the safety was evaluated with high accuracy by calculating the temperature rise and thermal damage in the geometrical model representing normal skin tissue under both conditions of evaluated devices.

Comparing Fig. 6 (a) and (b), the shape of the temperature profiles is similar, while the degree is different. Under the simulated conditions, Devices A and B had the same wavelength, but the compared pulse width and fluence were different. The thermal diffusion coefficients α = k/ρc for epidermis, dermis, and subcutaneous fat in the skin model were 4.88×10⁻⁴, 8.32×10⁻⁴, and 9.19×10⁻⁴ cm²/s, respectively. The pulse width that satisfied the thermal confinement condition was represented by τ = d²/4α, where d indicates the thickness. τ values for each layer were 0.051, 3.6, and 21.3 s, respectively. Because the simulated pulse width was much shorter than τ, the condition was satisfied. Therefore, fluence had a more pronounced effect on temperature rise than did pulse width.

As can be seen in Fig. 6, the temperature after 100 ms was higher than the initial temperature of 32 °C for both conditions. Compared to Device B or C, Device A obtained smaller heat accumulation, which suggested that thermal damage induced by Device A are also estimated smaller in case of repeated irradiation at 10 Hz. Continuous pulse irradiation at the same place can cause excessive temperature rise because of heat accumulation. For this reason, it may be required to avoid continuous pulse irradiation at the same place, to provide a sufficient interval between pulsed light incidence, and to cool the skin tissue under operation.

In the numerical simulation, the thermal damages of Devices A, B, and C were compared using the same skin tissue model. Thicknesses of epidermis, dermis and subcutaneous fat, however, vary individually and site-dependently in actual. ²⁹⁾ Constructing a skin tissue models with these variances will improve the clinical applicability in future. This computational modeling and simulation overestimated the temperature rise and the thermal damage because of some following assumptions. First, the dynamics of the optical properties of skin tissue resulting from the temperature rise were not considered in the thermal diffusion calculation. Some references report that when tissue is thermally coagulated, optical penetration depth becomes smaller and more light energy is deposited around the surface. ^56–58) This suggest that thermal damage is moderated around the surface and becomes more severe with increased depth. Thereby, not considering the dynamic optical properties results in overestimation of the temperature rise and thermal damage. Moreover, the optical properties vary between races ³⁰⁾. Because of these racial differences, the degree of thermal damage can change. For example, when the absorption coefficient is doubled, the same amount of deposited energy theoretically can be obtained with half of the light fluence. Caucasian optical properties were applied in this simulation, and the safety evaluation of a laser device considering racial differences may be necessary. Second, because the cooling effect of blood perfusion was not included in the thermal diffusion calculation, the temperature rise was overestimated in the skin model. It is known that the cooling effect resulting from vasculature causes a change in temperature distribution and reduces the range of tissue where thermal damage is induced. ⁵⁹⁾ However, the knowledge of physical properties has not been accumulated sufficiently to reproduce the cooling effect by computer. Experimental analysis will require an appropriate design to model the cooling effect resulting from blood flow.

It is desirable to conduct the performance evaluation of laser devices with exhaustive combinations of parameters such as pulse width, spot shape, fluence, and repetition rate using an actual method. Compared with the traditional preclinical and clinical trials, computational modeling and simulation can complete tests rapidly and inexpensively by a simple operation of only setting parameters on a computer. Moreover, it can obtain data that is unmeasurable in traditional tests by simulating the performance of devices under arbitrary irradiation conditions, including clinically challenging conditions. Although the safety was only evaluated based on the photothermal effect when light pulses were irradiated on normal skin tissue, it is expected that a computational clinical trial can be applied to the efficacy evaluation of a novel laser device by designing modeling and simulation considering photoacoustic effects in skin models including tattoo particles and melanin.

Conclusions

The temperature rise and the thermal damage to skin tissue caused by picosecond laser irradiation were quantitatively evaluated by a computational clinical trial. The safety evaluation of a novel picosecond laser was carried out by comparison with picosecond and nanosecond laser devices already approved for medical use. In contrast to traditional preclinical and clinical studies, the proposed computational method leads to cost and time reduction for examination of novel laser devices. The accumulation of clinical data and physical parameters with high accuracy will improve the reliability of computational clinical trials and assist their development to serve as supporting evidence in medical device evaluation.

Disclosures

The authors have no financial interests and no other potential conflicts of interest to disclose in this article.