Foreword Realization, Maintenance and Dissemination of the Kilogram in the Revised SI

A substantial change to the International System of Units (SI) is currently under discussion and might become effective in 2019. The General Conference on Weights and Measures (CGPM) is scheduled to have its 26^th meeting in 2018 and will likely vote on a proposal put forward by the International Committee for Weights and Measures (CIPM) to revise the SI. According to this proposal, the structure of the SI will change fundamentally. The present SI is built upon seven base units: the metre, the second, the kilogram, the ampere, the kelvin, the mole, and the candela. Each of the seven base units has its own definition, which sometimes draws on other base units. The unit of mass, the kilogram, is defined via an artefact, the International Prototype of the Kilogram (IPK) that is kept at the International Bureau of Weights and Measures (BIPM).

The foundation of the revised SI is based on seven defining constants. In addition to the three existing defining constants of the hyperfine transition frequency Δv_Cs of caesium (Cs), the speed of light in vacuum c, and the luminous efficacy K_cd, four additional defining constants are introduced: the Planck constant h, the elementary charge e, the Boltzmann constant k, and the Avogadro constant N_A, see Figure 1. Unlike an artefact based definition that allows the realization of the unit only at the location of the artefact, a system based on defining constants allows the realization of the units everywhere. Hence, the revision of the SI will completely implement an idea conceived in the middle of the 18^th century by Charles-Marie de La Condamine [1] to establish a universal system of units “for all time, for all people” as a phrase of later coinage succinctly put it.

Figure 1.

Info-graphics of the new SI. The inner circle shows the seven defining constants (the hyperfine transition frequency of caesium, the speed of light in vacuum, the Planck constant, the elementary charge, the Boltzmann constant, the Avogadro constant, and the luminous efficacy), the outer circle shows the seven base units (second, metre, kilogram, ampere, kelvin, mole, candela) that can be realized from the defining constants. In order to realize the unit of mass, three defining constants (Δν, c, and h), for emphasis shown with lighter background, are necessary.

In 1900, Max Planck [2] suggested using fundamental constants of nature to establish a system of units for all civilizations; he even thought of extraterrestrial civilizations. Now, more than one century after Planck and more than two and a half centuries after La Condamine, these dreams are about to become reality.

Accepted methods to realize a unit at the highest level by using the fixed values of the seven defining constants are described in the mises en pratique (mep). For the realization of the mass unit, the kilogram, three defining constants are necessary: Δv_Cs, c, and h, see Figure 1.

A focus issue collates articles that may be published across several printed issues. This focus issue contains publications about the determination of the Planck constant and – for the time after the redefinition of the kilogram – of the realization, maintenance and dissemination of the mass unit.

Since 2013, the work leading up to the revision of the kilogram definition has been formalized by a roadmap, see Figure 2, jointly produced by the Consultative Committee for Mass and Related Quantities (CCM) and the Consultative Committee for Units (CCU). The work and considerations that led to the redefinition are summarized in the article “Foundation for the redefinition of the kilogram” [3] of this focus issue. The CCM has put forward four conditions for redefinition, named R1 through R4 and are shown as diamonds in Figure 2.

Figure 2.

Roadmap put forward by the Consultative Committee for Mass and Related Quantities (CCM) and the Consultative Committee for Units (CCU) [3]. The roadmap captures the major events and conditions starting in 2013 to the 26^th General Conference on Weights and Measures in the fall of 2018. This focus issue is labelled „Metrologia special edition“ above the pink arrow on the upper half of the plot starting at the beginning of 2016.

The first requirement R1 is to have three independent measurements of the Planck constant with two different measurement methods. All three measurements are required to have relative standard uncertainties below 5 parts in 10⁸. To date, two methods are available to measure the Planck constant with such small uncertainties: the X-ray crystal density method (XRCD) [4] and the watt balance method [5].

In the XRCD method, the number of atoms in a silicon sphere, with accurately measured volume, lattice parameter, isotopic composition, and mass, is determined. This method measures the Avogadro constant. Since the product of the Planck constant and the Avogadro constant is currently known to a relative standard uncertainty of 4.5 parts in 10¹⁰ from a physical connection via the Rydberg constant [6], the XRCD method also determines the Planck constant. The article “Realization of the kilogram by the XRCD method” [4] contains explanations of the required measurements and figures showing the scientific improvement of these measurements over the past decades.

The idea of the watt balance was conceived by Bryan Kibble and appeared in print in 1976 [7]. Unfortunately, Dr. Bryan Kibble passed away in 2016, two years before the planned revision of the SI. To honor Dr. Kibble’s contributions, the CCU has decided to refer to the watt balance as the Kibble balance in its forthcoming publications. In the Kibble balance experiment, a mechanical apparatus is used to precisely compare mechanical power to electrical power. Different implementations of the Kibble balance are described in the article “The watt or Kibble balance: a technique for implementing the new SI definition of the unit of mass” [5]. The short article “Bridging classical and quantum mechanics” [8] contains a description on how Kibble balances link the two energy equations E = mc² and E = hv together, allowing an experimental connection between h and the mass of a test mass.

The connection between the Avogadro constant and the Planck constant is described in the article “Precise determination of the ratio h/m_u: a way to link microscopic mass to the new kilogram” [9].

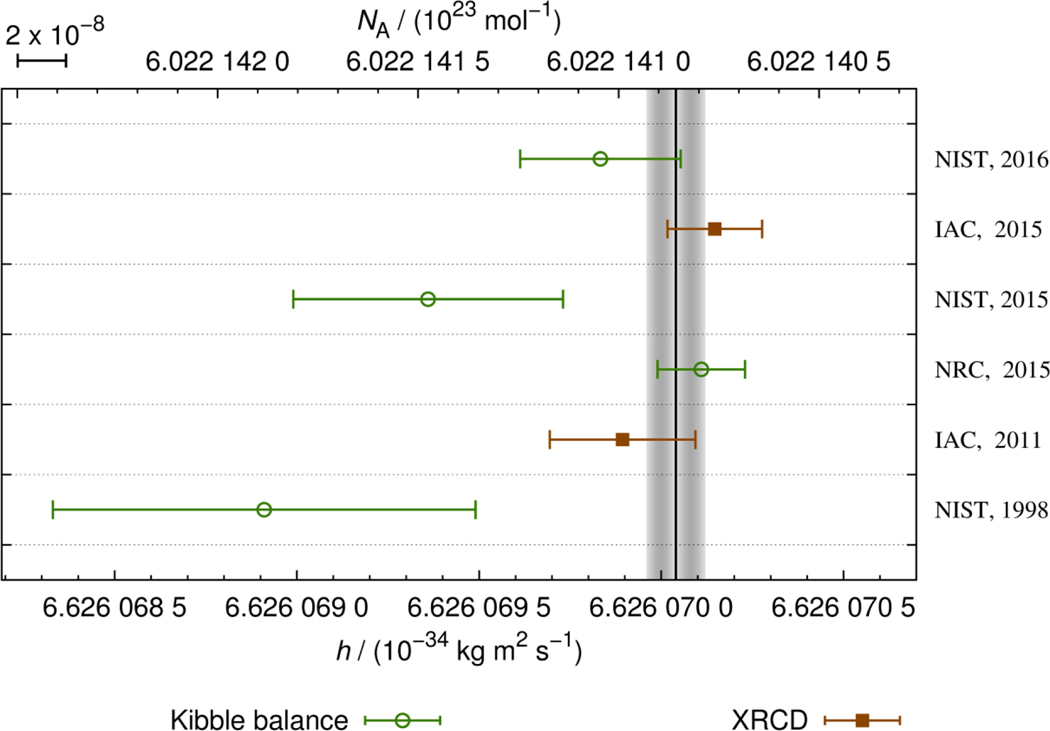
Published measurement results of the Planck constant and the Avogadro constant with the smallest uncertainties are shown in Figure 3. The data denoted with open circles were determined using a Kibble balance, the data denoted by solid squares were measured with the X-ray crystal density method. The vertical black line indicates the value currently recommended by the Task Group on Fundamental Constants of the Committee on Data for Science and Technology (CODATA) [6]. The agreement between the data is reasonable, the sum of the squared normalized residuals (chi squared) is 9.2. A sum this large or larger occurs statistically in 10 % of the cases with six measurements. The result with the smallest relative standard uncertainty, 18 parts in 10⁹, was measured with the Kibble balance at the National Research Council of Canada (NRC) [10,11]. For comparison, the most recent measurement of the International Avogadro Coordination (IAC) has a relative standard uncertainty of 20 parts in 10⁹ [12] and the value published by the National Institute of Standards and Technology (NIST) has a relative standard uncertainty of 34 parts in 10⁹ [13]. Thus, requirement R1 is met.

Figure 3.

Determinations of the Planck constant or the Avogadro constant with the smallest uncertainties. The data shown as open circles were obtained using Kibble balances. The data shown as solid squares were obtained using the X-ray crystal density (XRCD) method by the International Avogadro Coordination (IAC). The error bars denote the standard uncertainty reported by the experiment. The vertical black line denotes the recommended value based on the 2014 adjustment of fundamental constants carried out by the Task Group on Fundamental Constants by the Committee on Data for Science and Technology (CODATA). The gray band surrounding the black line gives the standard uncertainty associated with the recommended value. The results shown in the figure can be found in the references [11–13,18–20].

The second requirement for redefinition calls for one experiment to have a relative standard uncertainty of 2 parts in 10⁸. This requirement is met by the measurements carried out by NRC and IAC.

Requirement R3 pertains to the traceability of the data. To fulfill this requirement, extraordinary calibrations of the official copies and of several national prototypes against the IPK were performed in 2014. During the extraordinary calibrations it was found that the mass unit as maintained by the BIPM was different from the mass of the international prototype of the kilogram by as much as 35 μg/kg [14]. This discrepancy built up, because the IPK was not accessed between the third periodic verification of the national prototypes in 1990 and the extraordinary calibrations. Instead the mass unit was maintained by working standards used at the BIPM. The measurements of different working standards, discrepant values between them, and decisions that were made to deal with these discrepancies are summarized together with other interesting historical facts in the article “A brief history of the unit of mass: continuity of successive definitions of the kilogram” [15].

The last requirement R4 is the validation of the mise en pratique of the kilogram in the revised SI. This validation is presently underway in a pilot study, where the participants assume a fixed value of the Planck constant and use it to realize the kilogram. The unit of mass was then disseminated to travelling standards which were sent to the BIPM which functioned as the pilot lab for this study. The forthcoming report of the pilot study will be part of this focus issue and will be added to the collection of articles at a later time.

Realizing the unit of mass with either the XRCD method or the Kibble balance changes the environment where the realization of the unit takes place. In the artefact-based system, the mass unit is realized in air, since the IPK was used and stored in the ambient atmosphere. Both realization methods in the revised SI, however, will realize the unit of mass in vacuum. Since the dissemination of the mass unit will be performed in air, possible effects caused by transitioning the mass from vacuum to air must be well understood. These effects are described in detail in the article “Airvacuum transfer; establishing traceability to the new kilogram” [16].

Maintaining the mass unit is another theme in an article that will be added to this focus issue at a later date. This article will describe the ensemble of reference mass standards that has been established at the BIPM.

In the near future, an article will be included to this focus issue to describe the dissemination of the mass unit at the highest level after the redefinition of the kilogram. The revised SI opens other exciting possibilities; the unit of mass can be realized at nominal values different from 1 kg. The article with the title “Milligram mass metrology using an electrostatic force balance” [17] describes an electrostatic balance that can be used to realize milligram scale masses.

The breadth and depth of the articles in this focus issue are indicative of the fascinating world of mass metrology at the cusp of the revision of the International System of Units. Many groups worldwide are working tirelessly to gain better understanding of the issues involved. Several groups are working feverishly to complete better measurements of h or N_A before these two constants will be fixed in 2018. In order for a new value to be taken into account for this final least-squares adjustment of the four new defining constants, the publication describing the measurement must be accepted for publication by a scientific journal before July 1, 2017.

In closing, the redefinition of the unit of mass is a rare event which will likely occur in 2018/19. A large body of work has been accomplished by scientists around the world to make such a redefinition possible. This focus issue provides an overview of the state of the art immediately before a possible revision of the SI and will provide a comprehensive bibliography of the activities leading up to a unit of mass “for all time, for all people.”