Thermal response of a composite floor system to the standard fire exposure

Abstract

This paper discusses the development of a finite element (FE) model of a full-scale composite floor system and application of this model to predict the heating of steel members when exposed to a standard fire during fire resistance experiments. The model is verified by comparing the predicted heating profile of steel members at several locations during the tests with measured data. Such a verified model can be used to characterize the uncertainties in the prediction of the thermal history of structural elements exposed to a damaging fire. The output of this model can be used in a subsequent structural analysis model to determine the nonlinear behavior of structural members due to both thermal and mechanical loads. Additionally, the thermal effect of possible concrete spalling events and the resultant fireproofing dislodgement from steel members were numerically investigated and compared with measured data to determine the efficacy of the heat transfer model.

1. INTRODUCTION

Traditionally, the design for fire safety of structures has been based on prescriptive requirements and fire resistance ratings. These requirements and ratings have been established through standard fire resistance tests such as the ASTM E119 test (ASTM 2000) [1]. Such tests prescribe a standard fire exposure and limiting criteria that establish a fire resistance rating for a given component or sub-assembly. These ratings are given in terms of hours as established by the time to reach the first limiting criterion.

It is known, however, that the current prescriptive method provides only a relative comparison of how similar building components perform under a standard fire exposure and that it does not provide information about the actual performance of a component or sub-assembly in a real fire environment. Researchers are increasingly recognizing that current, component-based prescriptive method provides an understanding of a component behavior under standard fire exposure, not the real performance of the system as a whole under an actual fire exposure [2]. Also, the prescriptive approach does not describe fire-induced effect of thermal expansion on strength and stability of a structural assembly. A performance-based fire resistance approach could provide a more reasonable approach for determining fire resistance and may provide a more rational method for achieving the necessary fire resistance and describing the structural capacity when exposed to a real fire. In this context, obtaining an accurate temperature distribution is necessary for advanced structural calculations especially when thermal expansion is prevented due to restrained conditions, thereby resulting in an increase of internal forces [3]. As ref [2] points out, estimation of a building’s structural capacity and global stability during a fire exposure necessitates appropriate consideration of structural fire loads while developing a rational fire safety design.

An accurate modeling of structural behavior under fire would require a coupled fire modeling (with a computational fluid dynamics, i.e., CFD, code), heat transfer analysis, and structural analysis. However, as ref [4] and [5] point out, this is challenging as computational length scales and typical elements used in each analysis are different. Therefore, a sequential analysis (i.e., CFD for fire modeling followed by a heat transfer analysis and followed by a structural analysis) is often implemented where fire effects are used in a heat transfer model as proper boundary conditions, and temperature profile computed in the heat transfer model are included in the structural analysis along with mechanical loads. This approach inherently assumes that the fire modeling results affect heat transfer calculation, while reverse is not true. Similarly, it assumes that heat transfer analysis affects the structural calculation while structural calculation does not affect the heat transfer analysis. This can be construed as a weak coupling approach. But it is a very practical and a reasonable approach for large problems. The present paper deals with this sequential approach and is focused on conducting a heat transfer analysis on a composite floor assembly when exposed to a standard fire. It may be noted here that the two-way or full coupling issue has been addressed by Duthinh et. al. [4]. This may be applicable in prolonged and intense fires, where large structural deformation could cause damage to SFRM and possibly impact the thermal profile in a significant manner.

In a performance-based approach to the design for fire resistance, it is necessary to:

1. Estimate the hot gas temperatures produced by combustion of building components and furnishings,

2. Compute the heating of the structural elements by the hot gases from the exposing fire,

3. Determine the structural response of a building accounting for the reduced strength and stiffness of heated structural elements, and effects of restraint of thermal expansion.

No fire modeling is conducted in the present work. Instead, here a furnace heated with an ASTM E119 fire exchanges heat with the exposed surface of a composite floor assembly. Therefore, this study is focused on the ability to calculate the heating of structural elements, given a particular fire exposure. The ultimate goal is the determination of uncertainties associated with such calculations. There are uncertainties associated with the computed results in each of three steps of the sequential approach as stated above, which propagate from one step to the next [5, 6]. The predicted results need to provide time-dependent temperatures in structural members during a fire event, along with the associated uncertainties.

A comparison of numerical predictions of the temperature field against carefully controlled fire resistance experiments can provide insight into the uncertainties associated with prediction of the temperature histories of structural elements exposed to fire. But first the heat transfer model has to be verified against test data to determine the efficacy of the model. Such test data from such well controlled full-scale fire resistance tests are difficult to obtain from the literature. Since a rich set of data from the National Institute of Standards and Technology (NIST)’s fire resistance tests of composite floor systems is available, verification efforts have been focused on these tests. Toward this end, a simplified finite element (FE) heat transfer model of the composite floor truss section was constructed in ANSYS¹ [7] to model the heating profile of the structural members exposed to the standard fire. The focus of this study is to develop a numerical model that can predict the heating behavior of structural components during a full-scale fire test and also demonstrate through limited statistical analysis whether the model predictions are acceptable.

The fire resistance tests were conducted in both restrained and unrestrained conditions to study the performance of the floor systems under the standard fire exposure. Note that in a restrained test, thermal expansion at the supports of a load carrying element due to exposure to elevated temperatures in fire is resisted by forces external to the element. On the other hand, an element is free to expand and rotate at its supports in an unrestrained test.

Although the details of each fire resistance test are described in [8], a brief summary of the thermal behavior of steel members and characterization of the furnace environment are provided here. In this paper, the experimental set up and the fire resistance tests are described first. Then experimental data collected at several locations in the floor trusses and furnace are presented. Thereafter, numerical results from the heat transfer model are compared against experimental data. A quantitative estimate of the agreement between the experimental and simulation results is then provided along with a brief statistical analysis into the agreement. Future work will focus on estimating uncertainties in member temperatures. Finally, modeling of fireproofing dislodgement is demonstrated through a simple approach.

2. FIRE RESISTANCE TESTS

2.1. Composite Floor System

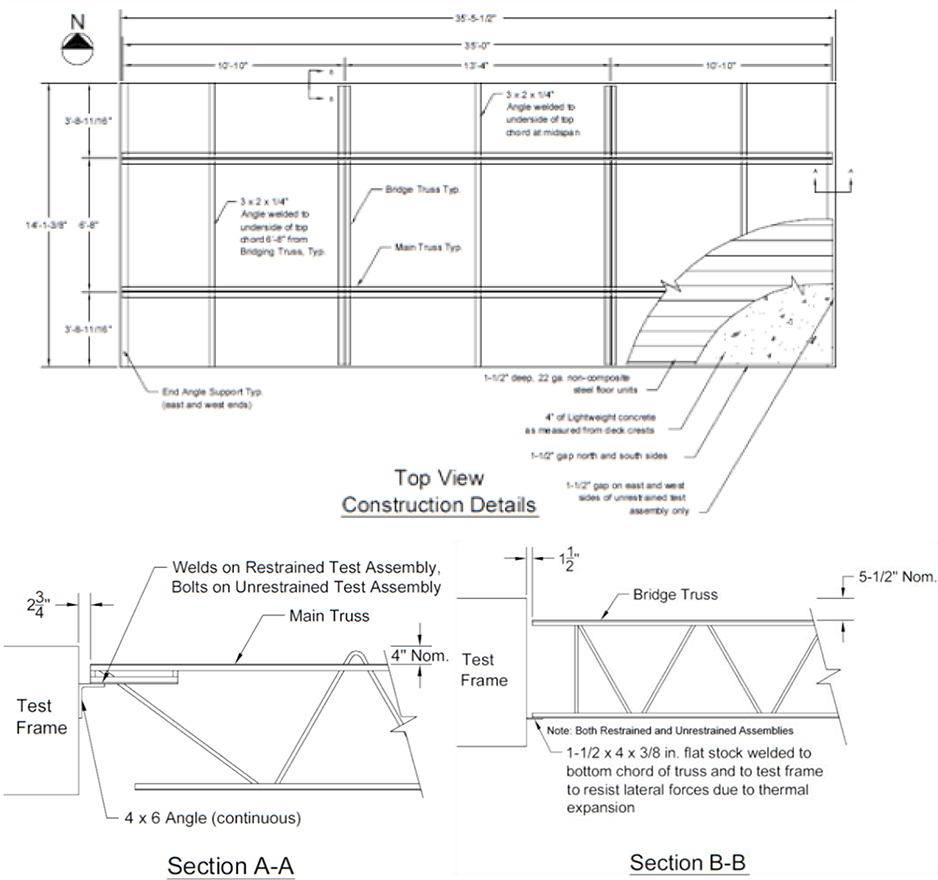
The floor system used in this experiment consisted of a lightweight concrete floor slab supported by steel trusses. The main composite trusses, which were used in pairs, had a nominal clear span of 35 ft (10.7 m). The steel trusses were fabricated using double-angles for the top and lower chords, and round bars for the webs. The web members protruded above the upper chord in the form of a “knuckle” which was embedded in the concrete slab to develop composite action. Figure 1 shows the construction details of the composite floor system. ASTM A572 Grade 50 steel test specimens were constructed to model the 35 ft. (10.7 m) span floor trusses. Passive fire protection was provided by spray applied fire resistive material (SFRM), commonly referred to as “fireproofing,” applied directly to the steel members of the trusses. The sprayed fire resistive material used on the test assemblies was BLAZE-SHIELD Type DC/F¹, which is manufactured by Isolatek International. The SFRM was applied to a thickness of ¾ in. (19 mm). with close tolerances of approximately 1/16 in. (1.6 mm). The deck consisted of 1½ in. (38.1 mm) deep 22-gauge galvanized sheet metal floor units. The test specimen comprised two main trusses, two bridging trusses, and a floor deck (Figures 1 and 4). The concrete design strength was specified to be 3,000 psi (20.7 MPa) and the lightweight density was specified to be 100 lb/ft³ (1601.85 kg/m³). The concrete for the floor slab consisted of lightweight haydite aggregate, sand, Type I Portland cement, and water. The mix design in Table 1 was used to produce a 3000 psi 28-day strength using lightweight aggregate [8].

Figure 1.

Construction details of Test 1 and 2 [8].

Figure 4.

Thermocouple locations in the main truss in the UL tests.

Table 1.

Concrete mix design per cubic yard of concrete [8].

Cement	Haydite "C"	Sand	Entrained Air	Water
(lb)	(lb)	(lb)	(%)	(lb)
522	940	1300	6	281

Two full-scale standard fire resistance tests were conducted at the fire testing facilities of Underwriters Laboratories (UL) in Canada:

1. Test 1: restrained test condition.

2. Test 2: unrestrained test condition.

For Test 1, the steel trusses were welded to steel support angles, which were attached to the test frame. Concrete was poured in contact with the frame. For Test 2, the steel trusses were bolted to steel support angles having 2.875 in. (73.02 mm) slot to allow for thermal expansion. Concrete was poured with a 1.5 in. (38.1 mm) gap between the concrete and test frame. With the exception of the restrain condition, the floor assemblies of both tests were constructed in the same manner. Ready-mixed concrete depth was 4 in. (101.6 mm) measured from the top plane of the 1.5 in. (38.1 mm) deep steel deck. A wooden trowel was used to generate a flat, smooth surface. Table 2 provides additional details of the concrete mix used and compressive strengths. Time elapsed from concrete casting to testing was 193 days for Test 1 and 189 days for Test 2. ASTM E119 test standard requires that the average relative humidity is maintained at 70% +/− 5%. In order to drive moisture out of concrete slab, test assemblies were kept at elevated temperature and in a low humidity environment following the initial 28-day curing in the ambient environment. The relative humidity of the slab was monitored in accordance with ASTM E 119–2000a, paragraph 12.1.3, Note 6 [1].

Table 2.

Details of concrete placement [8].

Test assembly	Wet Unit Weight*	Slump*	Air content*	Water added	Compressive strength at 28 days	Compressive strength at 56 days days
	(lb/ft3)	(in.)	(%)	(gal)	(psi)	(psi)
1	114.2/114.8	6/8	4.5/5.75	4	4177	4735
2	109.4	7.5	8.75	-	2937	3893

^*Results before and after water added

2.2. Standard Fire Tests

Two standard fire tests were conducted in a furnace with nominal dimensions of 35 ft (10.7 m) by 14 ft (4.3 m) thereby allowing full-scale tests of the 35 ft (10.7 m) span floor assemblies [8]. The furnace was heated following the ASTM E119 standard time-temperature curve (ASTM 2000) and furnace temperatures were monitored at 24 locations in the furnace. The average of these 24 thermocouple readings for both tests is shown in Figure 2 along with the prescribed ASTM E 119 time-temperature curve. Note that both plate and aspirated thermocouples were also used to measure gas temperatures. They were located at the level of the bottom chord of the main truss. Plate thermocouples are used to measure gas temperatures with a surface similar in terms of emissivity, size, and orientation to the specimen surface. Aspirated thermocouples help decrease the magnitude of error by reducing the radiative exchange between the thermocouple and its surroundings. In fact, temperatures measured by aspirated thermocouples are closer to the true gas temperatures [8]. Figures 3 shows temperatures measured by plate and aspirated thermocouples respectively. It is evident from these figures that the thermal environment in these two tests was similar.

Figure 2.

Average furnace temperatures of Test 1 and 2 along with ASTM E119 curve [8].

Figure 3.

Temperatures measured by (a) plate and (b) aspirated thermocouples in Test 1 and 2 [9].

Member test data (temperature vs. time) were recorded at several locations (e.g., A, B, E, F etc.) on the main truss (see Figure 4). At each location, there were eight thermocouples as shown; two on the upper chords, two at mid height of the web, and four on the lower chords. A total of 88 thermocouples were used to measure steel temperatures at various locations along the main trusses [8, 9]. Figure 4 shows thermocouple locations in the main trusses. Instrumentation was also added to measure temperature on the unexposed surface of the concrete slab at several locations [8, 9].

The average temperatures of the top (unexposed) surface of the floor assemblies is plotted in Figure 5. It is observed that the unexposed surface temperatures of both test assemblies were similar prior to the reported onset of significant concrete crushing and spalling that occurred at around 50 min in Test 1. Thereafter, the average unexposed surface temperature in Test 1 steadily increased in comparison to that in Test 2 as shown in Figure 5. Steel member heating trends for both the tests were generally similar [8]. A comparison of average temperatures recorded by the thermocouples at the upper chord (see Table 3 and [9]) of both the tests indicates that it is possible that dislodgement of SFRM took place at around (50 to 60) min in Test 1 near locations I, C, and E. This was estimated by a) checking the test log to see if any loud reports were recorded, b) looking at thermocouple data to see if there was any sudden abrupt jump in temperature around the same time, and c) careful post-test observations and inspection following the test. For Test 2, it appears that such possible dislodgement took place in the vicinity of location C at about 70 min into the test. Location E shows the most discrepancy in measured temperatures between Test 1 and 2 after about 60 min into the test [8, 9]. Most thermocouples at the upper chord recorded maximum temperatures of less than 400 °C after 2 hrs. of heating in both the tests. In general, final average upper chord temperatures in Test 2 was about 30 °C lower than that in Test 1.

Figure 5:

Average slab temperature on unexposed surface in Tests 1 and 2 [8].

Table 3.

Means and standard deviations of average temperatures at three locations on the main truss in tests 1 and 2 at 60 min and 120 min into the fire resistance tests.

	60 min				120 min
Location on main truss	Test 1		Test 2		Test 1		Test 2
	μ, °C	σ, °C	σ, °C	σ, °C	σ, °C	σ, °C	σ, °C	σ, °C
Lower Chord	445.7	81.8	446.4	54.3	773.3	69.8	772.0	37.9
Mid Web	600.4	35.0	576.5	36.6	860.3	70.3	872.2	42.9
Upper Chord	161.3	35.4	162.9	29.0	358.1	108.6	325.4	39.5

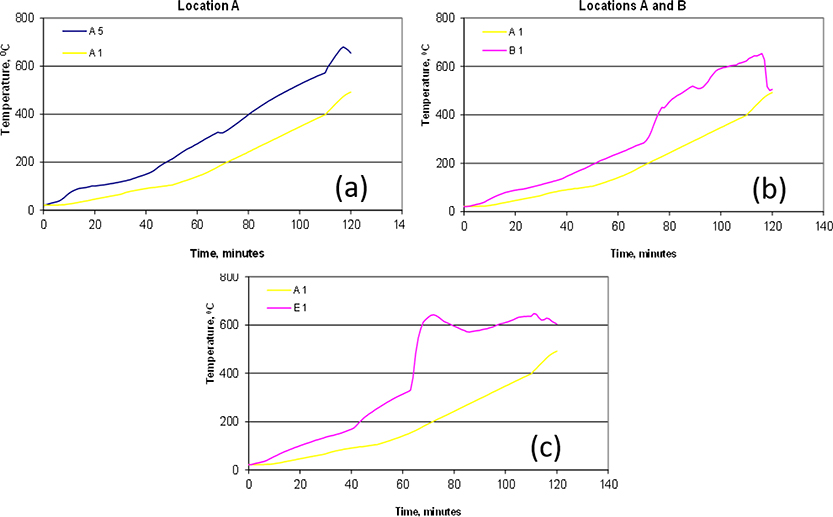
There are significant variations in recorded temperatures along the upper chord, (a) in the same position (e.g., A 1 and A 5 in Test 1), (b) in the same location at two main trusses (e.g., A 1 and B 1), and (c) at different locations along a truss length (e.g., A1 and E1) (see Figure 6). Such wide difference in recorded temperatures indicates the need to determine the variability in the time-dependent, non-uniform temperature distribution in steel members during a fire event. It is important to determine the factors that could possibly contribute to this variability. Some of these are: a) non-uniform heating as a result of varying gas temperatures based on locations, b) possible time-dependent change in “view factors” due to concrete spalling or SFRM buildup, c) change in net convective heat transfer due to changes in local gas temperatures near the vicinity of the thermocouples [2, 10–11]. The data shown in Figure 6 also indicate that the time-dependent variation of temperatures along the length of a member must be considered while conducting structural analysis during fire tests. These tests indicate that concrete spalling contributes significantly to the overall uncertainty in steel member temperatures. Variabilities in member thermophysical properties, fire/member heat exchange parameters, and gas temperatures must be considered to determine the overall uncertainties in member temperatures.

Figure 6:

Comparison of experimentally recorded temperatures in Test 1 for top chord locations.

3. FINITE ELEMENT (FE) MODELING

A FE model of the composite floor system described in section 2.1 was developed using the ANSYS finite element analysis (FEA) software [7]. The dimensions of the model were taken from Ref. [8]. The purpose of the heat transfer model is to simulate the transient heat diffusion in the standard fire-exposed composite floor system. The heat transfer model was used to compare average model predictions of temperatures with measured data at specific locations in the floor system where such measurements were available. Thermal data predicted by this verified heat transfer model can be subsequently used in a structural analysis model for predicting the time-dependent behavior of the floor system due to combined thermal and mechanical loads.

The FE model of the composite floor system included the following:

1. One steel main truss (without end supports) including the upper chord, web diagonals, and the lower chord.

2. Concrete slab (above the main truss) spanning the entire truss length and half the furnace width of 2.15 m (see Figure 7).

Figure 7:

(a) side, (b) isometric, and (c) end-view of the finite element (FE) model of the composite floor system.

Note that the bridging trusses and angles were not included. The spray applied fire resistive material (SFRM) was considered to be uniformly applied over the steel truss (no fireproofing was applied on the top surface of the upper chord). Additionally, the exposed surface of the slab was assumed to have an overspray of SFRM of about 19 mm based on experimental evidence to this effect. Note that the profiled steel metal deck was not specifically modeled since the metal deck is only 0.9 mm thick, while the slab is about 130 mm thick. Moreover, Lamont’s [12] results did not show a significant difference in the temperature prediction in the slab when a metal deck was specifically modeled in comparison with the case when the metal deck was not included. Therefore, as a first approximation, a uniform thickness of concrete slab was constructed over the steel trusses (see Figure 7 and 8 ). Also, the protrusion of the web members above the top chord was not included. The FE model numerically solves the conservation of the equation of energy in general form as shown below:

$$\rho C_p\left(\frac{\partial T}{\partial t}+\overrightarrow{v}\cdot \nabla T\right)+\nabla \cdot \overrightarrow{q}=\dot{Q}$$ (1)

where, ρ is the density, C_p is the specific heat capacity, T (x, y, z, t) is the temperature, t is the time, $\overrightarrow{v}$ is the velocity vector, $\overrightarrow{q}$ is the heat flux vector, and $\dot{Q}$ is the heat source term. The FE model of the composite floor assembly was developed using 3-D solid thermal elements (SOLID 70 element in ANSYS), which have eight nodes with a single degree of freedom (temperature) at each node. SOLID70 element has a 3-D thermal conduction capability. One major assumption when using this element is that temperature is considered to vary linearly in this element and so, the shape functions show linear variation in temperature. This element can be used for solving both steady state and transient heat transfer problems. Thermophysical property data (e.g., specific heat, enthalpy etc.) are evaluated at each integration point to allow for abrupt changes in behavior. The following are the assumptions associated with the use of this element: a) when convective heat transfer is described using this element, the film coefficient is evaluated at average of element and ambient temperature, b) element coordinate system is parallel to the global coordinate system, and c) mass transfer effects are not considered. The truss upper chords and lower chords were connected with the web members using conduction link elements (Link 33 element in ANSYS). These are uniaxial elements that can be used to model the transient heat transfer between the end nodes. The use of link elements allows the web diagonals to be meshed independently of the upper and lower chords and resulted in the minimum possible volumes in the model. Figures 7 and 8 show the FE model in detail. Note that adequate numbers of elements had to be used through the depth of each material to ensure that at least two free nodes existed at each section and that steep thermal gradients, if any, are handled correctly in the model.

Figure 8:

Discretization in the FE model of the composite floor system: (a) upper chord and slab; (b) lower chord.

During fire exposure, heat exchange occurs by both convection and radiation. At higher temperatures, radiation plays a more dominant role in thermal exchange. The convective heat exchange is addressed by the Newtonian heating/cooling mechanism. The radiative heat exchange is defined by the Stefan-Boltzmann law, which includes a parameter called “view factor”. The view factor is defined by the proportion of the radiation that leaves a surface (e.g., surface A) that strikes another surface (e.g., surface B). It can assume values from 0 to 1.

For modeling the furnace heating in the UL tests, the exposed surfaces of the composite floor system were subjected to convective and radiative heat exchanges. In order to accomplish this, surface effect elements (SURF 152) were generated in ANSYS and overlaid on the exposed surfaces of the solid elements. SURF152 is a 3-D thermal surface element. It may be used for various surface effect and load applications. Various loads and surface effects may be assigned simultaneously. An extra node (i.e., reference node, which is away from those of the base element) is used for convection or radiation effects. This node represents furnace heating. In other words, a Dirichlet-type boundary condition (prescribed temperature as a function of time) was assigned to this reference node. This element has been used for both convective and radiative heat transfer. The emissivity value of the surface (input as a material property card) is used for computing radiative heat transfer. Only one type of thermal surface load can be applied to a given element entity in ANSYS. For example, one cannot apply both a heat flux and a convection boundary condition directly to the faces of an element. Surface effect elements allow the use of multiple surface loads to a given element face. Two types of surface effect elements were created: one for the convective heat exchange and the other for the radiative heat exchange. For the convective surface elements, the fluid bulk temperature was designated as that of the reference node and appropriate convective heat transfer coefficients were used (see the next section). For the radiative heat exchange, surface effect elements were created with the reference node being subjected to the furnace heating following the ASTM E119 curve. A resultant emissivity value was specified while creating these surface effect elements. The resultant emissivity includes proper emissivity values of both the receiving and emitting surfaces. View factor effects in the radiation heat transfer were not considered, since the furnace was not explicitly modeled in this study and therefore, view factor values were set to 1 for all elements.

Thermophysical properties for materials used in the model (e.g., steel, concrete, and SFRM) are listed in tabular form in Appendix 1. The thermophysical properties that are needed for thermal analysis are: density, specific heat, emissivity, and thermal conductivity. Note that temperature-dependent thermophysical properties are needed to describe thermal behavior accurately. The values of these parameters often change significantly with the change in temperature. For example, thermal conductivity of fireproofing increases significantly with the increase in temperature (Appendix 1 and [13]). Proper boundary conditions are needed to model the heat transfer to/from the floor system both at the exposed and unexposed surfaces (e.g., top surfaces of the slab). For the convective surface effects elements at the exposed surface, a convective heat transfer coefficient is specified. A value of 25 W/m²/K has often been used [14]. Lamont et al. [12] used a base value of 23 W/m²/K, with minimum and maximum values of 5 W/m²/K and 30 W/m²/K in their sensitivity analysis. They suggested using a lower value of this heat transfer coefficient when the profiled metal deck is not explicitly modeled. This is because the profiled metal deck is known to separate from the rest of the concrete slab during progression of a fire event, thereby creating a gap that reduces the convective heat transport at the exposed surface of the slab. Therefore, in this analysis, a value of 15 W/m²/K was used for the convective heat transfer coefficient since the profiled metal deck was not modeled this study.

The effective emissivities for radiative heat exchange at the exposed surface depend on many factors such as flame emissivity, compartment walls, etc. For the surface emissivity of the steel member, a value of 0.7 is used. At the exposed surface of the slab, a value of 0.6 is used for effective emissivity as recommended by [12]. This value is slightly different from that of steel and was used as the metal deck was not explicitly modeled in this study. This is because of the air gap that forms at the interface between metal deck and concrete slab. Ref [12] found very good agreement between modeled and measured concrete slab temperatures when this value of emissivity was used. Although the focus of this study is not to determine the effect of uncertainties in values of parameters such as heat transfer coefficient, emissivities etc. on computed temperatures, previous work focused on demonstrating sensitivities of computed temperatures to variation in input parameters [15]. For example, it was shown that uncertainties in concrete emissivity and convective heat exchange parameters have most influence on concrete temperatures at exposed surface, and this influence gradually diminishes inside the slab.

Note that adiabatic boundary conditions were maintained at each end of the model in the longitudinal direction of the truss. Average time-temperature values for different segments on the unexposed surface of the concrete slab as determined from recorded thermocouple data during the two fire tests were used as Dirichlet boundary conditions (time varying) for nodes on the unexposed surface of the concrete slab. Note that this boundary condition is the only difference between Test 1 and Test 2 from the thermal modeling perspective. All nodes in the model were assigned an initial temperature of 25 °C. The input temperatures to the model are the ASTM E119 time-temperature curve assigned to the reference node as described in the previous section. This essentially assigns the furnace heating to this reference node. All exposed surfaces exchange convective and radiative heating with this node. Adiabatic conditions were maintained wherever any boundary conditions are not assigned. There are significant modeling challenges associated with this problem and some of these challenges and assumptions are listed below:

1. Uniform thickness of fireproofing assumption may not be valid. There is difficulty in capturing time-dependent build-up of fireproofing in the assembly as seen in the tests.

2. Uniform slab thickness was assumed. Therefore, variation of concrete slab thickness at locations of ribs versus locations where there were no ribs was not considered. Profiled metal floor deck was not constructed.

3. Modeling one half of the floor system and omission of the bridging truss from the model may not be the best possible representation of the tests.

4. Most of thermophysical properties of materials (e.g. steels, fireproofing, and concrete) were assumed to vary with temperature and such data were taken from past tests. However, the assumption of constant values of effective emissivities and convective heat transfer coefficients (in the absence of accurate temperature-dependent data in literature) as boundary conditions may not be strictly valid. Technically speaking, the values of these parameters vary as a function of temperature.

5. The model assumes a perfect contact between steel truss and concrete floor. In other words, no gap is assumed to occur at this interface. However, this perfect contact is impaired over time due to effects of nonuniform temperature distribution in different components. This is indirectly accounted for by using slightly lower values of emissivities and convective heat transfer coefficients.

6. No actual furnace was built. Instead, furnace heating was simulated by subjecting a node (away from the model) to the prescribed heating according the ASTM E119 fire. This assumption and the assumption of view factor of 1 on all exposed surfaces may not represent the reality of actual exchange of heating that took place during the tests.

7. Most fire exposure curves and parametric equations approximate temperatures in fully developed fires as uniform throughout the compartment. Similarly, nonuniformity of gas temperatures near the exposed surface is not considered also in this work.

3.1. Interpolation of Temperatures

The numerical model predictions are compared with measured time-temperature data at locations A, C, E, and I along the main truss (see Figure 4) at the upper chord, mid-web, and the lower chord for these four locations. Since there is often not a node at the exact location where a thermocouple was positioned, an interpolation approach was used to obtain an average temperature using a scheme as described below.

The model predictions of temperature at a given location (shown as point P at the bottom chord in figure) are obtained as shown schematically in Figure 9. For example, temperature at the position P is obtained by taking a weighted average of temperatures of all the FEM nodes available nearest to the point P on either side. In other words, first average temperatures at X and Y are obtained by finding the mean temperatures of all the nodes at X and Y (e.g., through the entire sections at X and Y). Then the temperature at the point of interest (P) is estimated by finding a weighted average of computed mean temperatures at X and Y using the proper distance of P from both locations X and Y. A script was written in ANSYS parametric design language (APDL) to output these temperatures as functions of time for the desired locations along the truss for upper chord, mid-web, and lower chord positions. These temperatures were then compared with measured temperatures available for these locations.

Figure 9:

Schematic illustration of the averaging approach used to interpolate temperatures.

4. EVALUATION OF THE FINITE ELEMENT (FE) MODEL

4.1. χ² Test of Goodness of Fit

After the thermal model was run, model predicted temperatures on the lower chord were compared to measured data to determine the χ² test of goodness of fit. The goal here is to provide a quantitative test of the discrepancies between the simulated temperatures (f_i) and the experimental values (F_i). If the agreement is poor, the computed χ² is large. The χ² test of goodness of fit is a nonspecific test as the test criterion is not directed against a particular deviation pattern. This test is applied to the data collected at two locations (A and E) for the lower chord in both the tests. Data points in the initial transient period were ignored for this comparison. This is because the experimentally recorded heating profile appears to lag the computed one in the initial transient, as there is a delay in gas temperatures reaching the temperatures specified in E119 curve in the vicinity of the trusses in reality. The agreement between the simulated and experimental data appears to be reasonable at both the 1 % and 0.5 % levels (see Table 4). Please note that the degrees of freedom in Table 4 refers to number of independent categories of observation. In other words, it refers to the number of data points where computed values are compared with test values. With the reasonable agreement established for the lower chord temperatures, the simulated results for the upper chord and the mid-web region can be compared with experimental values, where the variability is more pronounced.

Table 4.

χ² goodness of fit data for location A and E for the lower chord of the north truss in Test 1 and 2.

Test number	Locatio	Degree of freedom	χ2	χ20.005	χ20.01
1	A7	34	53.41	58.91	56.01
1	E3	44	61.44	71.86	68.67
2	A3	41	67.54	68.04	64.94
2	E7	43	63.21	70.59	67.43

4.2. Comparison between FE and measured temperatures in Test 1

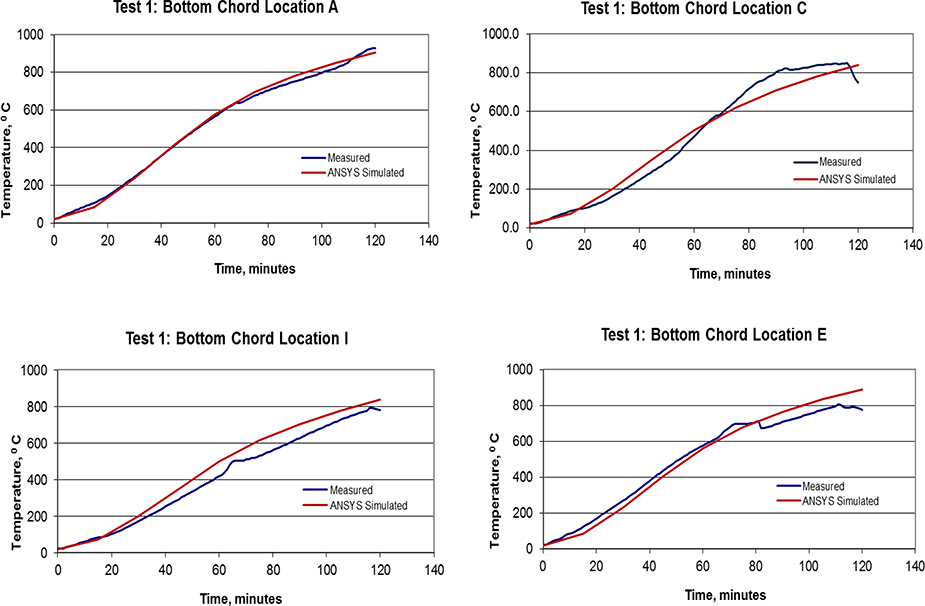
The numerical model predictions are compared with measured time-temperature data at locations A, C, E, and I along the north main truss (see Figure 4 and Table 5). These comparisons are performed at the lower chord, mid-web, and upper chord for these four locations (Figures 10, 11, and 12). However, often there is not a node in the FE model at the exact location where a thermocouple was positioned. Hence the interpolation approach described in section 3.1 was used. Whenever experimental data showed anomalous temperatures, readings from the south main truss for the identical location have been included in plots for comparison. Additionally, erroneous thermocouple data have not been included. Note that erroneous thermocouples are listed in the log of experimental data as reported in [8 and 9]. It is evident that the agreement is good for both lower chord and mid-web locations except for the location I at the lower chord (Figures 10 and 11), where the difference between the measured and computed temperatures was as high as 12 %. Such disagreement is also present in Test 2 [9].

Table 5:

A comparison of experimental and predicted temperatures at four times for Test 1.

Testl
Mid Web	Temperatures in C (% diff in absolute scale (K))
Time, min	Exp (A)	ANSYS (A)	% diff	Exp(C)	ANSYS (C)	% diff	Exp (1)	ANSYS (1)	% diff	Exp(E)	ANSYS (E)	% diff
30	331	285	−7.7	299	289	−1.7	320	285	−5.8	332	280	−8.6
60	647	626	−2.2	656	633	−2.4	618	625	0.7	621	617	−0.4
90	792	820	3.5	846	826	−1.8	770	817	4.5	775	811	3.4
120	−	929	−	−	934	−	899	927	2.4	933	923	−0.9
Bot Chord
Time, min	Exp (A)	ANSYS (A)	% diff	Exp(C)	ANSYS (C)	% diff	Exp(l)	ANSYS (1)	% diff	Exp(E)	ANSYS (E)	% diff
30	245	237	−1.7	180	200	4.5	172	198	5.8	195	229	7.4
60	565	578	1.5	477	502	3.4	417	498	11.7	461	561	13.6
90	752	782	2.9	747	709	−3.7	628	704	8.5	735	765	3.0
120	929	903	−2.1	−	841	−	781	838	5.3	768	889	11.6
Top Chord
Time, min	Exp (A)	ANSYS (A)	% diff	Exp(C)	ANSYS (C)	% diff	Exp (1)	ANSYS (1)	% diff	Exp(E)	ANSYS (E)	% diff
30	92	97	1.3	100	101	0.5	86	102	4.3	132	100	−7.9
60	209	1%	−2.7	−	203	−	169	203	7.5	−	151	−
90	382	278	−	−	284	−	254	284	5.8	−	282	−
120	574	348	−	−	353	−	336	353	2.8	−	351	−

Figure 10:

Time-temperature plots of the thermocouple data recorded for the lower chord at four locations on the north main truss in UL Test 1. Also shown are the average computed temperatures obtained from ANSYS.

Figure 11:

Time-temperature plots of the thermocouple data recorded for the mid-web position at four locations on the north main truss in UL Test 1. Also shown are the average computed temperatures obtained from ANSYS.

Figure 12:

Time-temperature plots of the thermocouple data recorded for the upper chord position at four locations on the north main truss in UL Test 1. Also shown are the average computed temperatures obtained from ANSYS.

A loud report was heard at 45 min when concrete spalling started occurring, resulting in dislodgement of fireproofing from the upper chord (see Appendix C in [8]). This resulted in an abrupt rise in steel temperatures as shown by experimental plots for the upper chord (Figure 12). These plots, however, show that the thermal model has been set up correctly since the initial rate of heating matches closely with the rate shown in the measured curves. Moreover, Table 5 shows that the agreement is within 10% for most mid-web and lower chord locations. Another observation can be made from Table 5: the discrepancies between measured and computed temperatures for mid-web and lower chord positions are somewhat large during the initial periods of the test. This discrepancy may be attributed to the fact that the model includes only one truss and transient effects due to non-uniform heating and heat exchanges between members such as bridging trusses, and the south main truss were not included here. This discrepancy diminishes at later times into the test as gas temperatures became more uniform in the furnace.

As seen in Test 1, the measured temperatures at location I in Test 2 are substantially lower than those predicted by the model (Table 5). The reason behind this is not quite clear. One possible explanation is that since the bridging truss intersects the main truss at location I (see Figures 1 and 4), it could act as heat sink. It may be noted that although the bridging truss was heated during the tests, it could still act as a heat sink because of its thermal mass. Since the bridging truss was not included in the model, this discrepancy could not be addressed. In the future, the computational model will include the entire floor system (e.g., both main trusses and bridging trusses).

4.3. Effect of SFRM Dislodgement

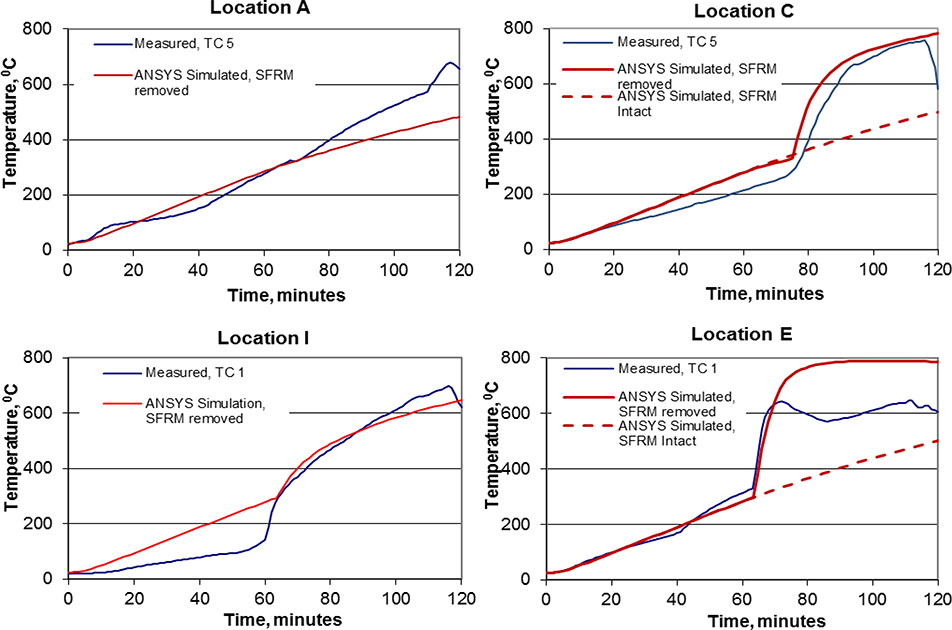
Figures 9(a) through 9(d) in [9] show that the time dependent average temperatures of upper chords at selected locations for the two tests are similar. However, the sudden increase in upper chord temperatures in Test 1 was noticed, which is also seen in Fig. 12 as shown above. It can be anticipated that the reduction in the thickness of SFRM on steel members as a result of dislodgement from concrete spalling possibly resulted in the sudden increase in the recorded temperatures for a few locations for Test 1. The aim in this section is to demonstrate an approach for estimating the effect of SFRM dislodgement at specific locations.

The analysis of Test 1 showed significant effects of concrete spalling on temperatures at the upper chord (Figure 12). ANSYS simulation was interrupted according to the timeline corresponding to the loud reports indicated in the log of observations [8 and 9] and 2 ft. (0.61 m) to 3 ft. (0.91 m) of SFRM in length were removed from the model at these locations. ANSYS simulation was then restarted and continued until the occurrence of the next loud report. A trial and error approach was followed to determine the range of possible amounts of SFRM dislodgement presumed to occur at each location. A schematic of SFRM dislodgement in model is shown in Figure 13.

Figure 13:

A schematic of the SFRM removal at locations A, C, I, and E in Test 1.

For Test 1, 0.5 in. (12.7 mm) of SFRM was removed at location A and 0.75 in. (19 mm) of SFRM was removed at locations I and E after 3800 s into the simulation. Simulation was then restarted and continued until 4500 s, when 0.75 in. (19 mm). of SFRM was removed at location C and then simulation was restarted. Figure 14 shows a comparison of computed and experimental data at the four locations along the upper chord in Test 1. For locations C and E, computed results are also shown for the hypothetical case of SFRM remaining intact. As expected, the temperature plots (for this case of SFRM remaining intact) continue along the “ANSYS simulated, SFRM intact” curves before abrupt heating took place during the onset of dislodgement of SFRM (see dashed plots for ANSYS simulation for locations C and E in Figure 14).

Figure 14:

Comparison of numerical results and experimental data for upper chord temperatures in Test 1 with SFRM removal.

5. CONCLUDING REMARKS

A heat transfer analysis was performed on one of the main trusses of the floor system used in NIST conducted standard fire resistance tests. The ASTM E119 time-temperature curve was used in an ANSYS model to describe the effect of the fire on the composite floor system. The experimental data were obtained from the test conducted by UL. The numerical results from the heat transfer model compared reasonably well with the experimental data obtained at several locations for the truss lower chord and mid-point of the web. However, there was wide variability in temperatures recorded for the upper chord. The current numerical model appears to over-predict the temperature for the upper chord. The source of this variability needs to be investigated. SFRM dislodgement due to concrete spalling contributed to sudden increase of temperatures for the upper chord and this theory was verified by conducting systematic FE modeling with restarts and changing the subsequent FE analysis with model that included effects of progressive SFRM dislodgement. This approach could be used as a possible investigative tool to determine whether fireproofing dislodgment from steel members and/or concrete spalling occurs during a fire event. Such a verified heat transfer model can also be used to characterize the uncertainties in the prediction of the temperature history of structural elements exposed to a damaging fire. Predicted and calibrated thermal fields from this model can be used to conduct structural analysis in the so-called performance-based approach for estimating fire resistance of structures. The surface temperature of an object exposed to a fire is often assumed equal to be equal to the gas temperature. Alternatively, adiabatic surface temperatures are used to provide an efficient way of transferring thermal results from a fire simulation to a thermal analysis [4]. This work demonstrates a new, simplified method that allows exposed nodes to exchange heat with the furnace using convective and radiative heat transfer. The furnace heating is simplified through assigning of time-dependent rise in temperature at a reference node in the vicinity of the assembly.

Appendix A: Thermophysical properties [9]

1. Steel

A. Density = 7856.2 kg/m³

Temperature	Specific heat
°C	J/kg/K
27	435.3
52	452.1
77	467.2
102	481.1
127	493.9
152	505.8
177	516.4
202	526.7
227	536.3
252	545.5
277	554.8
302	563.8
327	573.2
352	582.8
377	592.9
402	603.7
427	615.5
452	628.4
477	642.3
502	657.7
527	674.5
552	692.9
577	713.6
602	736.5
627	761.2
652	788.4
677	818.1
702	850.8
	Thermal
Temperature	Conductivity
°C	W/m/K
27	47.6
52	47.8
77	47.8
102	47.6
127	47.2
152	46.8
177	46.2
202	45.5
227	44.8
252	44.1
277	43.3
302	42.5
327	41.7
352	40.8
377	40.0
402	39.2
427	38.3
452	37.5
477	36.7
502	35.9
527	35.1
552	34.3
577	33.5
602	32.8
627	32.0
652	31.3
677	30.6
702	30.0

2. Concrete

Temperature	Density
°C	kg/m3
23	2101.7
600	1951.5
800	1701.3
1000	1701.3
Temperature	Specific heat
°C	J/kg/K
23	900.6
100	1000.6
800	1000.6
810	1501.0
1000	1501.0
	Thermal
Temperature	Conductivity
°C	W/m/K
23	1.5
800	1.0
1000	1.0

3. SFRM (fireproofing)

Temperature	Density
°C	kg/m3
25	237.0
50	236.3
100	230.3
200	224.8
300	222.3
400	220.5
500	219.2
600	218.4
800	361.4
1000	376.1
1200	432.4
Temperature	Specific heat
°C	J/kg/K
25	826.9
50	942.0
100	724.3
200	897.6
300	1020.7
400	1071.4
500	1098.2
600	1190.3
800	1259.4
1000	1326.0
1200	1392.5
	Thermal
Temperature	Conductivity
°C	W/m/K
25	0.0
50	0.1
100	0.1
200	0.1
300	0.1
400	0.1
500	0.2
600	0.2
800	0.3
1000	0.5
1200	0.5