Understanding and Tracking the Excess Proton in Ab Initio Simulations; Insights from IR Spectra

Abstract

Proton transport in aqueous media is ubiquitously important in chemical and biological processes. Although ab initio molecular dynamics (AIMD) simulations have made great progress in characterizing proton transport, there has been a long-standing challenge in defining and tracking the excess proton, or more properly the center of excess charge (CEC) created when a hydrogen nucleus distorts the electron distributions of water molecules in a delocalized and highly dynamic nature. Yet defining (and biasing) such a CEC is essential when combining AIMD with enhanced sampling methods to calculate the relevant macroscopic properties via free energy landscapes, which is standard practice for most processes of interest. Several CEC formulas have been proposed and used, but none have yet been systematically tested or rigorously derived. In this paper, we show that the CEC can be used as a computational tool to disentangle IR features of solvated excess proton from its surrounding solvent, and in turn, how correlating the features in the excess charge spectrum with the behavior of CEC in simulations enables a systematic evaluation of various CEC definitions. We present a new definition of CEC and show how it overcomes the limitations of those currently available both from a spectroscopic point of view and from a practical perspective of performance in enhanced sampling simulations.

Graphical Abstract

1. Introduction

Understanding proton transport (PT) is of central importance in many domains of biology and condensed-phase chemistry. The hydrated excess proton is often characterized by two limiting structures known as the Eigen (H₉O₄₊)^₁ and Zundel cations (H₅O₂₊)^₂, although it is more properly described as a dynamic, delocalized charge distribution that fluctuates around these limiting structures.^{_{3, 4}} Solvated protons diffuse significantly faster than other cations with similar charge and size in water due to their unique Grotthuss hopping mechanism, wherein the excess positive charge is transported through water molecules by rearranging covalent and hydrogen bonds.^{_{4, 5}}

When considering PT in complex systems such as weak acids or biomolecules, there are typically protonation and deprotonation rare events where intermediates are separated by barriers of 5 to 20 kcal/mol. In these cases, enhanced sampling is essential to capture the PT process in accessible simulation times. Popular enhanced sampling methods, including umbrella samplin,_{^{6, 7}} metadynamics,_^8–12 and adaptive bias force,_{^{13, 14}} involve the use of bias forces on one or more degrees of freedom of the system often called collective variables (CVs). A fundamental requirement for a CV is its differentiability in order for the bias forces to be decomposed onto individual atoms. Due to the delocalized nature of the positive excess charge and long time scale of many PT events, a CV that tracks the position of the excess proton is needed. The concept of a center of excess charge (CEC) was developed in the 90’s for this reason._^15,16 One might assume that integrating the net electron distribution (accounting for periodic boundaries) would yield the CEC. However, it is impossible to separate instantaneous charge fluctuations due to water-water interactions from the charge transfer induced by the excess proton. As pointed out by Konig et al.,_¹⁷ some early definitions did not accurately describe the location of the excess proton due to the contamination of irrelevant water molecules. Compared to these early definitions, Konig’s mCEC (modified CEC) has shown robustness in several test cases and was applied to model PT in several systems._^18–23 More recently, Pezeshki and Lin proposed another CEC definition called the proton indicator that was employed as collective variable in umbrella sampling of proton permeation through a hydrophobic carbon nanotube._²⁴ Although the mCEC and the proton indicator have been demonstrated in simulating explicit PT, they both involve ad hoc switching functions and parameters that lack clear physical meaning. Thus, a solid foundation and a rigorous definition of the CEC are still missing.

IR spectroscopy is a powerful technique to study the solvation structures and transport mechanism of the excess proton in acid solutions_^25–33. However, IR signals of condensed phase acid systems come from all of the proton-water complexes involved in the delocalized charge defect, and thus the experiments themselves are usually not sufficient to determine the molecular origin of the vibrational modes that are being excited and probed. Although the “bulk water part” of acid solution is typically subtracted off to get the difference spectrum, as shown in Figure 1A, the coupling and delocalization of vibrational modes as well as degeneracy of multiple motions in a certain frequency range makes the interpretation of IR spectra controversial._{^{34, 35}} Recent 2D-IR experiments by Elsaesser and co-workers suggested that a double minimum model best describes the proton transfer mode potential energy surface (PES),_³⁶ while similar experiments by Tokamokoff and coworkers claimed a PES with a single minimum._³⁷ They also have divided opinions on the lifetime of the proton complex: Tokamokoff claimed a lifetime over 480-fs,_³⁰ while Elsaesser observed a sub-100-fs population decay of the proton transfer mode first excited state._³⁶

Figure 1.

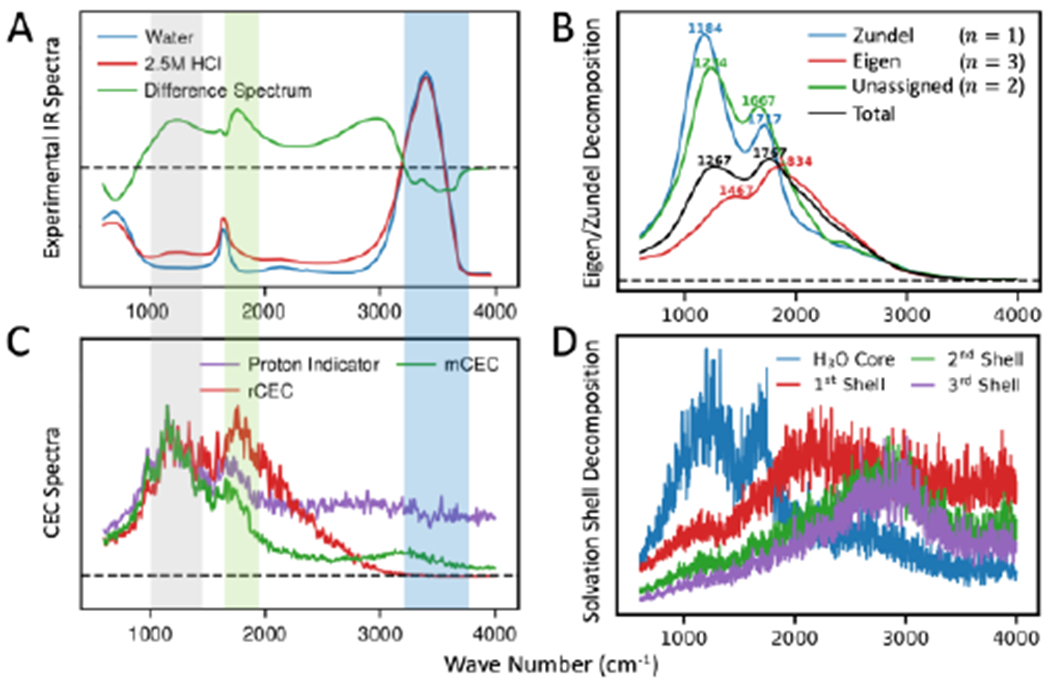
(A) Experimental IR spectrum of pure water (blue), 2.5M HCl solution (red) and their difference (green). The gray shadow highlights the PTM signal, the green shows the flanking water bending mode and the blue shows pure water stretching. (B) Decomposition of rCEC spectrum by number of unique special pairs (n). The position of peaks are denoted as wave numbers. The Zundel is defined as having one special pair (n = 1) and the Eigen is defined as having three special pairs (n = 3). The remaining case (n = 2) was not assigned to Eigen or Zundel but left independent. (C) CEC spectra computed from AIMD simulations. The rCEC spectrum (red) shows good agreement in the PTM and flanking water bending and decays to zero at the same position as experimental difference spectrum. The mCEC spectrum (green) shows non-vanishing signal at pure water stretching band. The proton indicator (purple) absorbs in the full frequency range. (D) Decomposition of rCEC spectrum by solvation shells. The absorption spectrum is blue-shifted with the increasing solvation shell.

The CEC, as described above and detailed below, describes the motions of the solvated proton but is by design insensitive to bulk water motions. This inspired us to investigate whether or not the CEC can, in addition to serving as a collective variable in enhanced sampling, also be used as a computational tool to study the IR spectroscopic properties of the protonated water complex in the aqueous environment under finite temperature with no need of extracting clusters_{^{34, 35, 38–42}}, solute-solvent partitioning_⁴³, independent simulations of pure water_{^{39, 44, 45}} nor the harmonic approximation for normal mode analysis_{^{35, 39}}. And in turn, can the spectrum decode the resulting collective motions, such that the spectra of different CEC definitions can inform us about the dynamical behaviors and performance of that CEC in enhanced sampling simulations?

However, defining the CEC is not trivial, as the positive charge due to the presence of an excess proton is distributed across many water molecules, each with an altered electron distribution, and over multiple solvation shells. Moreover, this distribution is highly dynamic with the partially covalent hydrogen bonding network shifting on the femtosecond timescale. A successful PT reaction is considered to occur when the dominant central hydronium-like water molecule changes identities, and is thought to happen on the picosecond timescale. According to the Eigen-Zundel-Eigen (EZE) proton transport mechanism validated in simulations, the most probable proton acceptor around the hydronium (the “special pair partner”) oscillates between the three waters surrounding the central hydronium on the 25-100 femtosecond timescale during a relatively long-lived Eigen-like period called the “special pair dancc”_³. Intermittent with this, there are Zundel-like periods in which one “special pair partner” is favored and the excess positive charge bounces back in forth between two waters, albeit in a highly asymmetric manner. A successful PT then occurs when the special pair partner in Zundel-like dynamics takes over and becomes the new central hydronium-like molecule, which is thought to depend on coordinated hydrogen bonding in the second solvation shell._{^{46, 47}}

Throughout the process, asymmetry is favored and the distribution of excess charge at any given time predominantly involves 6 water molecules and most resembles an asymmetric Eigen-like/Zundel-like structure in which one special pair partner involves more charge transfer than the other two and including the two water molecules that special pair partner is hydrogen-bonded to in the second solvation shell._⁴⁶ Thus, the symmetric Eigen and Zundel cations are somewhat limiting in our ability to describe or conceptualize the process as a whole. What is perhaps a better descriptor of the state of the excess proton is captured in its dynamics. In simulations, there are clear periods of Eigen-like dynamics featuring the special pair dance, and periods of Zundel-like dynamics in which one special pair partner is singled out. To properly track this highly dynamic behavior requires a rigorous definition of the CEC that resolves the identity of proton acceptor on-the-fly and enables smooth transitions among the most probable acceptors.

These complexities also impose challenges on modeling PT processes in computer simulations. One solution is the ah initio molecular dynamics (AIMD)_⁴⁸ where electronic structure is treated explicitly and thus the changing bonding topology is captured. AIMD can, in principle, achieve a high order of accuracy in computing the potential energy surface (PES) and thus has been widely used to study aqueous PT and solvations_{^{5, 48–55}}. However, the most accurate AIMD simulation of acid solutions may require electronic structure methods to determine intemuclear forces that correctly describe the dispersion, charge transfer and many-body effects_^56–58 in hydrogen bond networks, as well as possibly an appropriate treatment of nuclear quantum effect (NQE)._^59–62 These methods are generally too expensive for condensed phase simulations. Thus, the commonly used methods are more affordable generalized gradient approximation (GGA) level of density functional theory (DFT), which is known to produce over-structured condensed phase water and to under-estimate the diffusion of water._⁶³ Even at these levels, AIMD simulations still have a high computational cost that limits the time and space scales attainable. The time scale problem, for all simulations, can be addressed by combination with advanced enhanced sampling methods, which again underlines the importance of a well-behaved CEC definition.

An alternative solution is multi-scale reactive molecular dynamics (MS-RMD), that evolved from the multi-state empirical valence bond (MS-EVB) method and has been long developed by the Voth group._^64–73 The MS-RMD methodology has been benchmarked and demonstrated to describe proton solvation and transport in various aqueous and biomolecular systems._{^{20, 21, 71, 73–78}} In the MS-RMD framework, the system’s ground state PES is defined as a linear combination of ‘valence bond’ states in which electrons are considered to be localized in valence bonding orbitals and thus representative of specific bonding topologies. A Hamiltonian matrix describes state potential energies on diagonal terms and coupling between states on off-diagonal terms, thereby capturing the delocalized nature of the charge defect. Redefinition and weighting of the state contributions at every time step captures the dynamics of the charge defect and changing bonding topologies. The CEC position in MS-RMD is naturally defined as a linear combination of the charges in each valence bond state._⁷⁹ However, the MS-RMD Hamiltonian is only directly available in MS-RMD simulations and thus the MS-RMD CEC cannot be used in AIMD or other reactive models.

In this work, we introduce a new definition of the CEC, namely rCEC, which is designed to reproduce the MS-RMD CEC charge transfer behavior while still being available in AIMD simulations. We demonstrate that the spectrum of the CEC produces almost all of the signature features of the acid solution revealing that the collective motions of the protonated water complex and the surrounding hydrogen bond networks are all encoded in the motion of the center of excess charge. The two most commonly used existing AIMD CECs (mCEC and the proton indicator) are analyzed in detail and compared with the new rCEC, both from a spectroscopic point of view and in simulations. We show limitations of mCEC and the proton indicator reflected by their spectra and further validated in simulations, and how these limitations are overcome by the new rCEC.

2. Methods

2.1. Theory of MS-RMD and MS-RMD CEC

In the MS-RMD framework, the ground state of the molecular system |ψ〉 is expanded on a basis set where each basis state |i〉 corresponds to a distinct bonding topology (Figure 2), i.e.

$$|\psi \rangle =\sum _{i=1}^N{c}_i|i\rangle$$ (1)

where the c_i’s are the expansion coefficients and N is the total number of basis diabatic states. The c_i’s are obtained on-the-fly over the course of simulation by solving the eigenvalue problem using the Hamiltonian H = ∑_ij h_ij|i〉〈j|, such that

$$\mathbf{H}\mathit{c}=E_0\mathit{c}$$ (2)

where E₀ is the ground state energy and c = {c_i} is the ground state coefficient vector. The diagonal terms h_ii are expressed in two contributions, a molecular mechanics forcefield term $h_{\mathit{ii}}^{\mathrm{MM}}$ and a diabatic correction, $h_{\mathit{ii}}^{\mathrm{CORR}}$ for shifting the arbitrary baseline energy common to classical force fields. The off-diagonal term h_ij, which provides the mechanism for the system to transition between basis states, is typically a geometric function with tunable parameters. The details are well-illustrated elsewhere.^{_{71, 73}}

Figure 2.

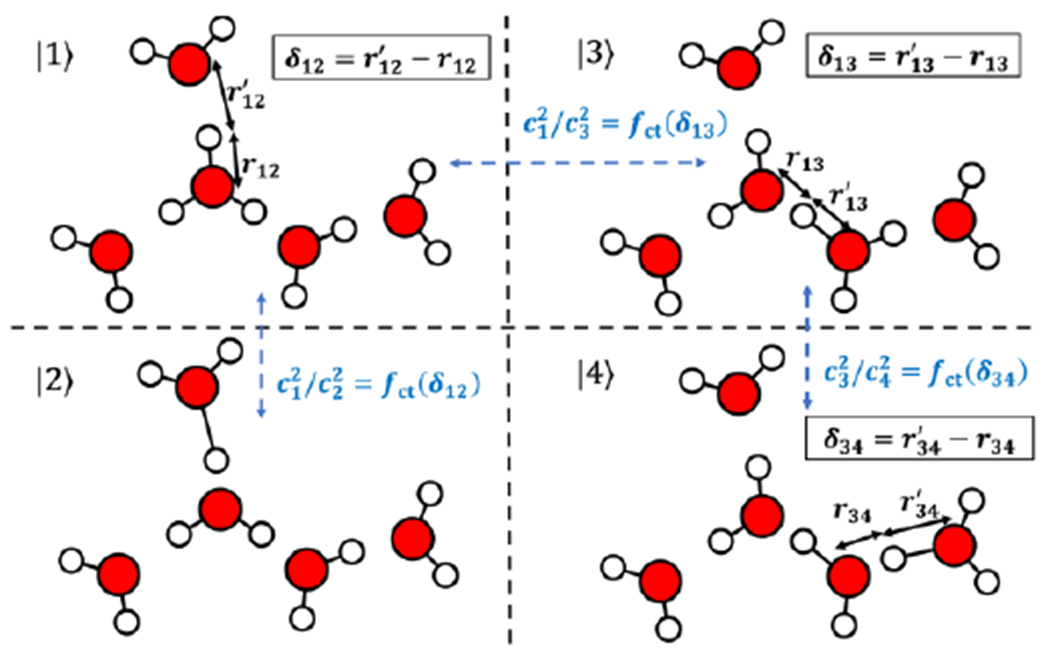
Illustration of the diabatic states and how the asymmetry coordinate δ and the combining coefficients $c_i^2$ are calculated for rCEC using H(H₂O)₅₊ as an example. The fifth diabatic state is not shown for clarity.

In each RMD diabatic state, the system is governed by classical mechanics where the bonding topology is well-defined and hydrogen bonds are purely described by non-bonded interactions. In such description, the excess proton is simply identified according to the bonding topology and thus the CEC is simply the center of charge (COC) of the moiety that owns the excess proton in entirety. The resulting definition of center of excess charge is then a linear combination of the center of charge (COC) in all MS-RMD states,

$${\mathit{r}}_{\mathrm{CEC}}=\sum _{i=1}^N{c}_i^2{\mathit{r}}_{\text{i}}^{\mathrm{coc}}.$$ (3)

Here, c_i is the ground state coefficient and the COC, ${\mathbf{r}}_i^{\mathrm{coc}}$, is essentially the “center of excess charge” in a given bonding topology of the i-th RMD state:

$${\mathit{r}}_i^{\mathrm{coc}}=\frac{\sum {}_{J\in Q_i}\left|q_J\right|{\mathit{r}}_J}{\sum {}_{J\in Q_i}\left|q_J\right|}$$ (4)

where subscript J goes over all atoms in the excess proton species (e.g., all the four atoms in a hydronium or the carboxylic hydroxyl for a protonated amino acid).

2.2. Definition of rCEC

Noting that the non-trivial parts in eq 3 are the c_i’s, one can easily compute CEC in AIMD as long as those coefficients are known. Thus, defining CEC in AIMD is essentially calculating c_i’s for each given atomic configuration. As c_i gives the magnitude of how much each COC contributes to the CEC, c_i’s is strongly correlated to some appropriate measure of the charge transfer (e.g., from the hydronium to its solvation waters). An energy decomposition analysis (EDA) study of the charge delocalization of an excess proton in water indicated that the following asymmetry coordinate (Figure 2) is a good measure of the charge-transfer energy:

$${\delta }_{IJK}=r_{JK}-r_{IK}$$ (5)

, where I, J are indices of the two proton-donor/acceptor oxygens while K is the index of hydrogen between them.

We found an exponential function of this delta value best fits how much charge is transferred from the central hydronium to its first solvation shell water (Figure 2):

$$\frac{c_j^2}{c_i^2}=f_{\mathrm{ct}}\left({\delta }_{IJK}\right)$$ (6)

Here, I indicates the HB donor atom in MS-RMD state |i〉, K is the proton to be transferred and J is the HB acceptor atom in MS-RMD state |j〉;

$$f_{\mathrm{ct}}\left(x\right)=\{\begin{array}{cc}{e}^{-kx}& x\le r_1\\ a_0+a_{1}x+a_2{x}^2+a_3{x}^3& r_1<x\le r_2\\ 0& x>r_2\end{array}$$ (7)

, where the damping term brings the exponential to exact zero. Interestingly, we note that eq 6 indicates the charge transfer factor $c_j^2/c_i^2$ is the Pauling bond order (BO) ratio of two waters and our fitted parameter agrees to some extent with what Pauling suggested for BO_⁸⁰ (Table 1).

Table 1.

Parameters of rCEC.

		Initial guess	Final result	Pauling’s Bond Order
Hydronium-Water	k (Å−1)	4.3937	4.9840	3.8462
Amino acid-Water	k (Å−1)		7.3433
	δ0 (Å)		0.29316

We further assume that this rule holds for charge transfer from the first solvation shell molecules to the second solvation shell and so on. With this assumption, the excess charge on the central hydronium follows the rule (eq 6) to propagate layer by layer along hydrogen bonding networks. The hydrogen bond donor/acceptor pairs are resolved on-the-fly by a state searching algorithm, which finds every possible bonding topology based on geometric criteria. In this work, the EVB3 state searching algorithm with three solvation shells was used as its good energy conserving behavior implies an exhaustive search is achieved._⁷³ First, every hydrogen is assigned to the closest oxygen. The oxygen with three assigned hydrogens (in the case of a single excess proton) is designated the central pivot oxygen (the most hydronium-like water). Then hydrogen bonds trace all potential bonding topologies within given number of solvation shells. The coefficient of the central hydronium is determined by exploiting the normalization condition, |c|² = 1:

$$c_1^2=\frac{1}{1+{\sum }_{i=2}^N{c}_i^2/c_1^2}$$ (8)

In the case of an amino acid solvated in water, the proton transfer reaction between the acid and a water is not symmetric as it is for water and water. Thus, it requires an extra parameter δ₀ to take this asymmetry into account. We use

$$f_{\mathrm{ct}}\left(x\right)=\{\begin{array}{cc}{e}^{-k\left(x-{\delta }_0\right)}& x\le r_1\\ a_0+a_{1}x+a_2{x}^2+a_3{x}^3& r_1<x\le r_2\\ 0& x>r_2\end{array}$$ (9)

to compute how much excess charge is transferred from the protonated amino acid to its first solvation shell while keeping the charge transfer behavior between water molecules the same. The coefficients in the polynomials in both f_ct’s are chosen to ensure f_ct’s C₁ smoothness:

$$\begin{gathered} f_{\mathrm{ct}}\left(r_1-\right)=f_{\mathrm{ct}}\left(r_1+\right) \\ {f}_{\mathrm{ct}}^{\prime }\left(r_1-\right)=f_{\mathrm{ct}}^{\prime }\left(r_1+\right) \\ {f}_{\mathrm{ct}}\left(r_2-\right)=0 \\ {f}_{\mathrm{ct}}^{\prime }\left(r_2-\right)=0 \end{gathered}$$ (10)

The four conditions determine the polynomial coefficients uniquely:

$$\begin{gathered} A\triangleq \exp {\left(-k\left(r_1-{\delta }_0\right)\right)/\left(r2-r1\right)}^3 \\ {a}_0=A\cdot r_2^2\left(3r_1+k{r}_1^2-r_2-k{r}_1{r}_2\right) \\ {a}_1=A\cdot r_2\left(6r_1+2k{r}_1^2-k{r}_1{r}_2-k{r}_2^2\right) \\ {a}_2=-A\cdot (3r_1+k{r}_1^2+3r_2+k{r}_1{r}_2 \\ -2k{r}_2^2) \\ {a}_3=A\cdot \left(2+k{r}_1-k{r}_2\right) \end{gathered}$$ (11)

2.3. Relation between CEC and IR spectrum

IR spectroscopy is a powerful tool of studying molecular events involving vibrational motions. It reflects how the system’s total dipole responds to an applied external electric field and thus it can be computed from the dipole-dipole time correlation function according to the fluctuation-dissipation theorem. In classical MD, the system dipole is expressed as the total dipole of nuclei point charges as the electronic DOFs are not explicitly treated:_⁸¹

$$\mathit{\mu }=\sum _I{q}_I{\mathit{r}}_I$$ (12)

For a proton in water, the total atomic charge can be decomposed into two contributions: the “intrinsic” charge, which is the partial charge on each atom in the absence of excess protons, and the excess charge, which is the additional atomic charge that arises from the delocalization and polarization of the protonic charge defect. Thus, the total dipole moment is expressed as:

$$\mathit{\mu }=\sum _I\left(q_I^{\mathrm{ex}}+q_I^{\mathrm{in}}\right){\mathit{r}}_I={\mathit{\mu }}^{\mathrm{ex}}+{\mathit{\mu }}^{\mathrm{in}}.$$ (13)

The IR absorption is thus decomposed into four terms:

$$\begin{gathered} I\left(\omega \right)\propto \int \langle \dot{\mathit{\mu }}\left(0\right)\dot{\mathit{\mu }}\left(t\right)\rangle e^{-i\omega t}\text{d}t \\ =\int \langle {\dot{\mathit{\mu }}}^{\mathrm{ex}}\left(0\right){\dot{\mathit{\mu }}}^{\mathrm{ex}}\left(t\right)\rangle e^{-i\omega t}\text{d}t \\ +\int \langle {\dot{\mathit{\mu }}}^{\mathrm{ex}}\left(0\right){\dot{\mathit{\mu }}}^{\mathrm{in}}\left(t\right)\rangle e^{-i\omega t}\text{d}t \\ +\int \langle {\dot{\mathit{\mu }}}^{\mathrm{in}}\left(0\right){\dot{\mathit{\mu }}}^{\mathrm{ex}}\left(t\right)\rangle e^{-i\omega t}\text{d}t \\ +\int \langle {\dot{\mathit{\mu }}}^{\mathrm{in}}\left(0\right)\dot{\mathit{\mu }}\left(t\right)\rangle e^{-i\omega t}\text{d}t \end{gathered}$$ (14)

Interestingly, the general form of the CEC for each of the CEC definitions studied herein is a summation of the product of atomic excess charge and position:

$${\mathit{r}}_{\text{CEC}}=\sum _I{q}_I^{\mathrm{ex}}{\mathit{r}}_I$$ (15)

, where ∑_I q_I = 1 holds for the reason that total excess charge induced by a proton is unitary. Thus, the CEC is actually the dipole of excess charges up to a factor of unit charge $\overline{e}$, i.e.

$${\mathit{\mu }}^{\mathrm{ex}}=\overline{\text{e}}{\mathit{r}}_{\text{CEC}}$$ (16)

This leads to the fact that the excess charge contribution to IR spectra is proportional to the Fourier transformation of CEC velocity-velocity correlation function

$$I^{\mathrm{ex}}\left(\omega \right)\propto \int \langle {\mathit{v}}_{\text{CEC}}\left(0\right){\mathit{v}}_{\text{CEC}}\left(t\right)\rangle e^{-i\omega t}\text{d}t$$ (17)

The formula coincides with the “vibrational density of states” (VDOS) of the center of excess charge. However, we should point out that the center of excess charge is not a real particle but instead a collective motion of hydrogen bonding networks, including many vibrations and charge fluctuations in the protonated water cluster and thus the VDOS of the CEC has a more profound physical meaning than the VDOS of real atoms. In contrast to the partial charges of atoms, the excess charges are expected to decay along increasing solvation shells of the excess proton and thus separate the protonated water complex IR absorption from the total absorption of the system.

2.4. rCEC spectrum decomposition

2.4.1. Solvation shell decomposition

Decomposing rCEC into solvation shell contributions is straightforward from eq 15:

$${\mathit{r}}_{\text{CEC}}={\mathit{r}}_D+\sum _{I\in \left\{{\text{H}}_3\text{O}\right\}}{q}_I^{\mathrm{ex}}{{\mathit{r}}^{\prime }}_I+\sum _{I\in \left\{1^{\mathrm{st}}\mathrm{Shell}\right\}}{q}_I^{\mathrm{ex}}{{\mathit{r}}^{\prime }}_I+\sum _{I\in \left\{2^{\mathrm{nd}}\mathrm{Shell}\right\}}{q}_I^{\mathrm{ex}}{{\mathit{r}}^{\prime }}_I+\sum _{I\in \left\{3^{\mathrm{rd}}\mathrm{Shell}\right\}}{q}_I^{\mathrm{ex}}{{\mathit{r}}^{\prime }}_I\triangleq {\mathit{r}}_D+{\mathit{r}}_{{\text{CEC},\text{H}}_3\text{O}}+{\mathit{r}}_{{\text{CEC},1}^{\text{st}}\text{Shell}}+{\mathit{r}}_{{\text{CEC},2}^{\text{st}}\text{Shell}}+{\mathit{r}}_{{\text{CEC},3}^{\text{rd}}\text{Shell}}$$ (18)

where r_D is the position of the donor atom (i.e. oxygen atom of the most probable hydronium) and r′_I = r_I − r_D is the relative positions of atoms with respective to the donor atom. The first solvation shell was defined as the direct hydrogen bond acceptors of the H₃O motif. The second shell was defined as the direct hydrogen bond acceptors of the first shell and so on. Similar to eq 17, the solvation shell dependent spectrum was computed by the Fourier transform of CEC velocity auto-correlation function of each solvation shell component.

2.4.2. Eigen/Zundel decomposition

At each timestep, the most probable hydronium oxygen (O₀) and the special pair oxygen (O_1x) were identified based on the two largest $c_i^2$. The whole trajectory was then partitioned into non-reactive segments separated by timesteps where O₀ is changed. In each segment, the number of unique O_1x identities (n) was counted. If n = 3, special pair dance happens in this segment and we assigned this segment as Eigen. If n = 1, only one special pair is favored and thus is assigned as Zundel. For segments with n = 2, it could be part of a concerted proton hopping or partial special pair dance, making any assignment controversial, so we keep this case independent instead of merging into Zundel or Eigen. The resulting population of each assignment is Zundel:Eigen:unassigned = ~1:5:1. Considering the n = 2 spectrum is closer to Zundel (Figure 1B), the Eigen/Zundel ratio is roughly 5:2, which corresponds to a roughly 0.55 kcal/mol free energy difference, agreeing well with Figure 2 in ref ₈₂.

According to the Wiener-Khinchin theorem, the excess charge spectrum (eq 17) can be rewritten as

$$I^{\mathrm{ex}}\left(\omega \right)\propto {\left|\int {\mathit{v}}_{\text{CEC}}\left(t\right)e^{-i\omega t}d\text{t}\right|}^2$$ (19)

This inspired us to use short time Fourier transform (STFT) to compute a time-resolved excess charge spectrum:

$$I^{\mathrm{ex}}(t,\omega )\propto |\int {\mathit{v}}_{\mathrm{CEC}}(\tau )W(\tau -t)e^{-i\omega t}\text{d}\tau {|}^2$$ (20)

, where w(t) is a Tukey window with a length of 175 fs. The choice of the length is a balance between time-resolution and Fourier transform accuracy. Other reasonable choices do not change the result qualitatively. Along with the Eigen/Zundel assignments at each time, the spectra computed by eq 20 were independently averaged according to the value of n.

2.5. Parametrization of rCEC

Reference charge transfer factors $c_j^2/c_i^2$ are obtained from diagonalizing the Hamiltonian matrix in MS-RMD simulations. We intend to find the optimal parameters k and δ₀ in f_ct functions to reproduce the reference MS-RMD charge transfer behaviors. Instead of minimizing the CEC position discrepancy, the following object function was used

$${\chi }^2(\{\theta \})=\langle |\Delta \mathit{c}{|}^2\rangle =\langle |{\mathit{c}}_{\mathrm{CEC}}-{\mathit{c}}_{\mathrm{MS}–\mathrm{RMD}}{|}^2\rangle$$ (21)

, where {θ} are the parameters to be fit, which is k in f_ct for hydronium-water or k and δ₀ for weak acids; brackets indicate the average in MS-RMD ensemble; c_CEC indicates the coefficients calculated by the algorithm described in Section 2.2 and c_MS–RMD is the reference coefficients from the MS-RMD model.

For proton and water, the MS-RMD ensemble was sampled for 500-ps of one excess proton and 256 waters (simulation details in Section 2.7.2). The rCEC parameters for the amino acid were fitted in the ensemble sampled from the 9 windows ranging from 1.25 Å to 2.50 Å of MS-RMD umbrella sampling. We used a two-step strategy to find the optimized parameters. In the first step, only the first solvation shell was considered, for which a deterministic least square fitting can be used. The obtained parameter value obtained was then fed as the initial guess for a second step Powell’s method that included the second and the third solvation shells and for which the first shell parameters depended_⁸³. The second step optimization was conducted with an in-house script which utilizes GNU parallel_⁸⁴ for acceleration. The final resulting parameter in step 2 is rather similar compared to those in step 1 (see Table 1), which validates our assumption in Section 2.2 that charge transfer along multiple shells follows the same exponential rule (eq 6).

2.6. Other CEC definitions

The mCEC uses a fermi function f_sw(x) = 1/[1 + exp((x − r_sw)/d_sw)] to switch between 0 and 1 (nonbonding to bonding) for each heavy atom-hydrogen atom pair, effectively counting the number of hydrogens each heavy atom is bonded to. The definition of mCEC reads^₁₇

$${\mathit{r}}_{\mathrm{mCEC}}=\sum _{I\in \{H\}}{\mathit{r}}_I-\sum _{J\in \{X\}}{w}_J{\mathit{r}}_{\mathrm{J}}-\sum _{I\in \{H\}}\sum _{J\in \{X\}}{f}_{sw}(r_{IJ})({\mathit{r}}_I-{\mathit{r}}_J)$$ (22)

where {H} is the collection of all hydrogen atoms and {X} is all heavy atoms that accept or donate protons. The weight w_J is defined as the number of protons boned to atom J in its reference state so that a heavy atom has close-to-zero contribution to the position of CEC if it is in its deprotonated state.

The definition of the proton indicator is as follows (details can be found elsewhere_⁸⁵)

$${\mathit{r}}_{\mathrm{Ind}}=\frac{1}{g_{\mathrm{Ind}}}\left({\mathit{r}}_D+\sum _{J\in S_X(r_{\mathrm{LIST}})}\sum _{I\in B_J}g({\rho }_{IJ}){\mathit{r}}_I\right)$$ (23a)

$$g_{\mathrm{Ind}}=1+\sum _{J\in S_X(r_{\mathrm{LIST}})}\sum _{I\in B_I}g({\rho }_{IJ})$$ (23b)

$${\rho }_{IJ}=\frac{{\mathit{r}}_{DI}·{\mathit{r}}_{DJ}}{|{\mathit{r}}_{DJ}{|}^2}$$ (23c)

where S_X(r_LIST) is the set of heavy atoms within r_LIST distance from the donor atom, D; B_J is the set of hydrogens bonded to heavy atom J; g is a function that switches from 0 when ρ_MJ is sufficiently small to 1 when ρ_MJ > 0.5.

2.7. Simulation Details

2.7.1. AIMD simulations

All AIMD simulations were conducted using the quickstep module in CP2K_⁸⁶ with the hybrid Gaussian and plane wave (GPW) scheme_⁸⁷ coupled with a modified version of PLUMED 2_⁸⁸. The protonated water system consists of 1 excess proton and 128 water molecules in a 15.66 Å × 15.66 Å × 15.66 Å box simulated in the NVE ensemble. The Gaussian and plane wave (GPW) method was employed and a plane wave cutoff of 400 Ry was used to expand the electron density. The Goedecker-Teter-Hutter pseudopotentials_⁸⁹ were used to describe core electrons. The orbital transformation method was used to optimize the wave function at each step with a convergence criteria of 10₋₇ a.u.. The electronic structure was described by BLYP/TZV2P level DFT. In addition, an empirical D3 correction_⁹⁰ and recently developed EDS correction_⁹¹ were employed. The choice of this level of AIMD is a reasonable balance between accuracy and computational cost and the EDS corrected version of BLYP is one of the best affordable ab initio methods for capturing water and hydrated proton solvation structure and dynamics._{^{82, 91, 92}} We also emphasize that our CEC definition does not rely on the underlying PES and thus can be applied to higher level of DFT simulations. A timestep of 0.5 fs was used to integrate the system. The total simulation time was ~225 ps.

The aspartic acid system consists of 1 neutral Asp solvated in 141 waters in a 16.175 Å × 16.175 Å × 16.175 Å box simulated at 300 K in the NVT ensemble with a timestep of 0.5 fs. The BLYP/TVZ2P with D3 correction was used. In order to describe the proton disassociation process, we define a collective variable ξ as the distance between CEC and its closest carboxyl oxygen:

$$\xi =-\frac{1}{\beta }\log (e^{-\beta (d_1-\overline{d})}+e^{-\beta (d_2-\overline{d})})+\overline{d}$$ (24)

, where d₁ = |r_CEC − r_O1| and d₂ = |r_CEC − r_O2| are the distances between the CEC and carboxyl oxygens and $\overline{d}=\frac{(d_1+d_2)}{2}$. A sufficient large β = 40 was chosen to ensure the expression gives precise min(d₁, d₂).

The initial structures for steered MD (SMD) were generated by extracting configurations and velocities every 25 fs in a 4.5 ps-long trajectory at 300 K after a ~3 ps long equilibration. The bias potential used in SMD was

$$U(t)=\frac{1}{2}\kappa ·{(\xi ({\mathit{r}}^{3N}(t))-{\xi }_0(t))}^2.$$ (25)

The force constant κ was 80 kcal/mol/Å₂. The restraint center was

$${\xi }_0(t)=\{\begin{array}{cc}{\xi (\mathit{r}}^{3N}(0))+\frac{1.5\AA }{25\text{fs}}t,& t<25\mathrm{fs}\\ {\xi (\mathit{r}}^{3N}(0))+1.5\AA ,& t\ge 25\mathrm{fs}\end{array}$$ (26)

A Gaussian hill height of 1 kcal/mol and addition pace of 25 fs used in metadynamics followed previous QM/MM metadynamics work93 while hill width of 0.2 Å was used and a bias factor γ = 16 was chosen based on an expected ~9 kcal/mol barrier for aspartate deprotonation_⁹⁴.

2.7.2. MS-RMD simulations

Taking the advantage of its efficiency, MS-RMD simulations were used for umbrella samplings, and unbiased simulations to generate ensembles for fitting. The simulations were conducted in LAMMPS with an in-house MS-RMD package, RAPTOR,_⁹⁵ coupled with PLUMED 2. The HCl solution system consists of 1 excess proton, 1 chloride and 256 water molecules in a 15.66 Å × 15.66 Å × 15.66 Å box. The MS-EVB 3.2 proton-water model was used._⁷² Four NVE trajectories were initiated from independent configurations generated from a NVT sampling at 300 K using Nose-Hover chain of length 3. A timestep of 0.5 fs was used and the total simulation time was ~2.7 ns.

The glutamic acid system consists of 1 neutral glutamic acid and 1001 waters, resulting in a 31.075 Å × 31.075 Å × 31.075 Å box. A timestep of 1.0 fs was used. The temperature was controlled at 310 K with a fixed box volume. The MS-RMD parameters were taken from references ₉₆ and ₉₄. The collective variable was defined as the distance between CEC and the center of mass of the carboxyl group. A 0.25 Å spacing of CV value was used for almost all the umbrella sampling windows while 0.1 Å was used for windows near the deprotonation transition state, resulting in 40 windows in total. All windows were run for over 1.5 ns.

3. Results and Discussion

3.1. rCEC spectrum decodes experimental IR spectrum for excess proton

By noting that CEC is actually the dipole moment of excess charges (eq 15), we compute the excess charge spectra (eq 17) of rCEC and the other two most commonly used CECs (mCEC and proton indicator) from AIMD to study the associated IR signals. All the CECs produce the acid continuum 1000 cm₋₁-3200 cm₋₁ (Figure 1C), which is the signature absorption of hydrated protons. The experimental IR spectrum^{_{30, 35}} features three broad peaks located at around 1200 cm₋₁, 1750 cm₋₁, and 2800 cm₋₁. As shown in Figures 1A and 1C, the rCEC spectrum not only outlines the overall shape of the experimental spectrum but also matches the 1200 and 1750 cm₋₁ frequency well, which are commonly assigned to the proton transfer mode (PTM) and the flanking water bending of the excess proton, respectively^{_{44, 97}}. This indicates that the CEC, originally designed for tracking the position of excess proton, is able to capture the motion of the excess proton as well as the associated stretching and bending motions of the protonated water complex.^{_{35, 43}} The rCEC spectrum decays to zero at around 3200 cm₋₁, which is the same position as the difference spectrum zero point, right before the bulk-like water O–H stretching band (~3200-3700 cm₋₁), validating the use of excess charge to compute IR spectrum of the protonated water complex without being contaminated by bulk water frequencies. The only deviation of the rCEC spectrum from experiment is that the intensity in the frequency range 2000 to 3200 cm₋₁ gradually decreases to zero as a function of frequency without showing a peak at 2800 cm₋₁. Noting that the excess charge also dissipates along solvation shells, this decaying intensity suggests that this frequency range is due to the hydrating water that is spectroscopically different from bulk-like water, but more remote from the central excess proton. This can be verified by decomposing the CEC spectrum into contributions from different solvation shells (Figure 1D), which clearly shows the spectral absorption of each shell is gradually blue-shifted when going from the 1_st to the 3_rd solvation shell. The H₃O₊ core exhibits clear frequencies commonly assigned as the PTM and flanking water bending, verifying that the central H₃O₊, is intimately involved in those vibrations. The first solvation shell shows a broad peak at around 2100 cm₋₁, possibly being the contributor to the continuum of 2000-2600 cm₋₁ in the difference spectrum. Interestingly, both the second and the third solvation shells absorb at around 2800 cm₋₁, the other signature signal of the experimental spectrum. However, the averaged excess charge for 2_nd and 3_rd shell atoms is 8 × 10⁻⁴ and 2 × 10⁻⁵ in unit charge respectively, which are both too small for this IR signal to be visible in the total CEC spectrum. This is further verified by plotting the vibrational density of states for the populations of the dominant valence bond states (Figures S3A & B), which show that the 2800 cm₋₁ is clearly captured by the 4_th valence bond state.

State-of-art 2D-IR experiments_{^{25, 30, 33, 36, 37, 98}} have advanced our thinking on the solvation and transport of the excess proton in aqueous solution, but it has been a long-standing challenge to clearly correlate the spectroscopic observations to molecular vibrations. One of the debates has been whether or not the dominant hydrated proton structure more resembles the Zundel or Eigen cation. As suggested by Swanson and Simons,_⁴⁶ the Zundel/Eigen species are perhaps better distinguished by their unique dynamical behaviors than by static geometric criteria. We thus decomposed the CEC spectrum according to Zundel/Eigen dynamics making use of the short-time Fourier transform (STFT) to get time-resolved CEC spectrum (eq 20). The AIMD trajectories were first partitioned into Zundel or Eigen segments according to the number of unique special pair identities (n) and the spectra for these segments are separately averaged. As shown in Figure 1B, both the Zundel (n = 1) and Eigen (n = 3) components exhibit very clear PTM and flanking water bending features. Noticeably, the Zundel has a stronger PTM that is slightly red-shifted while Eigen has a weaker and blue-shifted PTM. The same frequency shifting of Zundel/Eigen happens for the flanking water bending. The remaining unassigned spectrum component (n = 2) shows a mixture of Zundel and Eigen features with a PTM located between the Eigen/Zundel PTMs while a flanking water bending closer to Zundel, implying it is a mixture of controversial Zundel and Eigen. These components merge into the total spectrum PTM and flanking water bending forming single peaks at frequencies roughly in the middle of the corresponding Zundel and Eigen frequencies. The Zundel and Eigen are more spectroscopically distinguishable at PTM with Zundel ~280 cm₋₁ lower than Eigen, but less separable for the flanking water bending with Zundel ~170 cm₋₁ lower. The proximity of the Zundel/Eigen frequencies suggests lasers in IR experiments centered at the middle frequencies of the PTM and flanking water bending modes_{^{33, 37, 98}} likely excite both the Zundel and Eigen species.

3.2. CEC spectra reveal their behaviors in simulations

Proton transport in an aqueous environment involves the stretching and bending of the protonated water complex as well as concerted motions of hydrogen bonding network._{^{3, 47, 99}} Biasing the CEC in enhanced sampling is essentially enhancing the fluctuations in the direction of the collective motions related to PT. An optimal PT CV is expected to drive the system following the same path in phase space as PT naturally happens at equilibrium. As the collective motions of proton solvation and transport are captured in the IR spectrum, we expect the optimal CEC to match it (at least peak locations if not intensity). In this light, deviations from the difference spectrum can serve as a measure of the quality of a CEC definition. We thus investigated how the spectroscopic features of a CEC relate to that CEC’s performance in simulations.

As shown in Figure 1C, although the first two peaks are also produced by mCEC and the proton indicator, there are some distinct features compared to rCEC. The spectrum of proton indicator shows non-zero absorptions in the full frequency range computed (0 cm₋₁-30000 cm₋₁). This spectral feature can be understood by noting the proton indicator’s intrinsic discontinuity, as shown by its time series in Figures 3A and 3B. The x coordinate of the proton indicator, as an example of its xyz position, jumps over 1 Å multiple times within the 150-fs time segment, while smooth changes are observed for other CEC definitions (Figures 3A and 3C). In enhanced sampling, a continuous and differentiable collective variable is required to ensure a reliable resulting free energy profile; thus, the proton indicator should be revised to a differentiable form if it is going to be used in biased simulations.

Figure 3.

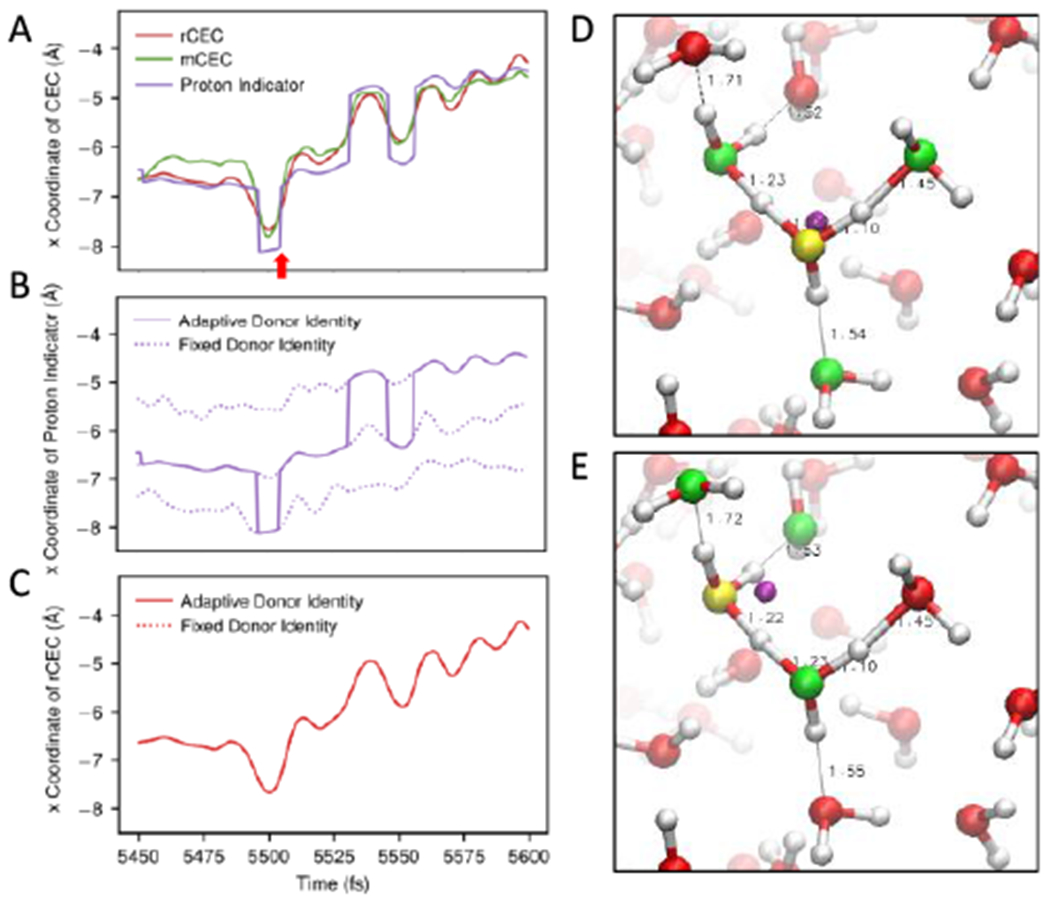
(A) A representative segment of time series of rCEC (red), mCEC (green) and proton indicator (purple). The red arrow highlights one of the discontinuous jumps of proton indicator and indicates the times of Figure 3D and 3E. (B) The time series of proton indicator in the same time period. The dotted curves show the time evolution of proton indicator with fixed proton donor identity (atom D in eq 23) while the solid line shows the one allowing updating the donor identity. (C) The time series of rCEC in the same time period. The dotted and solid curves have the same meaning as Figure 3B. Note that the curves are overlapping perfectly. (D) and (E) Snapshots of AIMD of protonated water from two adjacent timesteps as the red arrow denoted in Figure 3A. The donor oxygen of proton indicator is shown in yellow. The dominant acceptors are shown in green. The position of the proton indicator, shown by a purple ball, jumps over 1 Å in a single step introducing discontinuity.

In addition to a spectroscopic point of view, the proton indicator’s discontinuity can be directly understood by examining its definition. The definition of proton indicator (eq 23) depends on the proton donor oxygen identity, which undergoes discrete changes introducing discontinuity in the CEC. This is well illustrated by Figures 3D and 3E where we see a large displacement in proton indicator’s position within a 0.5 fs separation.

However, the proton indicator is continuous and differentiable for a fixed donor identity due to the smooth functions used in its definition, which can be checked by the smooth regions between jumps in Figure 3A or 3B. In other words, proton indicator hops between the smooth surfaces corresponding to different donor atom identities and the discrepancy in each surface results in its discontinuity (Figure 3B). It’s worth noting that the rCEC also requires a donor atom to initiate the state searching algorithm and thus its differentiability relies on the agreement between the surfaces, which is a property of rCEC that can be understood mathematically (see SI). It is also validated by Figure 3C where rCEC trajectories computed using different fixed pivot indices all overlay with the one computed with dynamically changing identity.

The most notable feature of mCEC is its non-vanishing absorption over 3200 cm₋₁ corresponding to the water stretching band (Figure 1C). This observation inspired us to examine if mCEC includes bulk water bond oscillations in addition to the motion of hydrated proton. In order to obtain meaningful statistics, we conducted an ensemble of steered MD simulations of deprotonating an aspartic acid solvated in water (Figure 4A). The distance between CEC and closest carboxylic oxygen (ξ) was employed as the CV (eq 24). The SMD protocol we used can be divided into two phases. The CEC was first pulled 1.5 A away from its initial position in 25 fs, which was implemented by applying a moving harmonic restraint on the collective variable ξ. Then the restraint was held at the final position of the first phase for another 75 fs. This mimics a standard procedure for using SMD to prepare initial configurations for umbrella sampling simulations. Figure 4B shows the magnitude of bias force acting on water atoms further than 6 Å from the carboxylic oxygens in each SMD run as a function of time.

Figure 4.

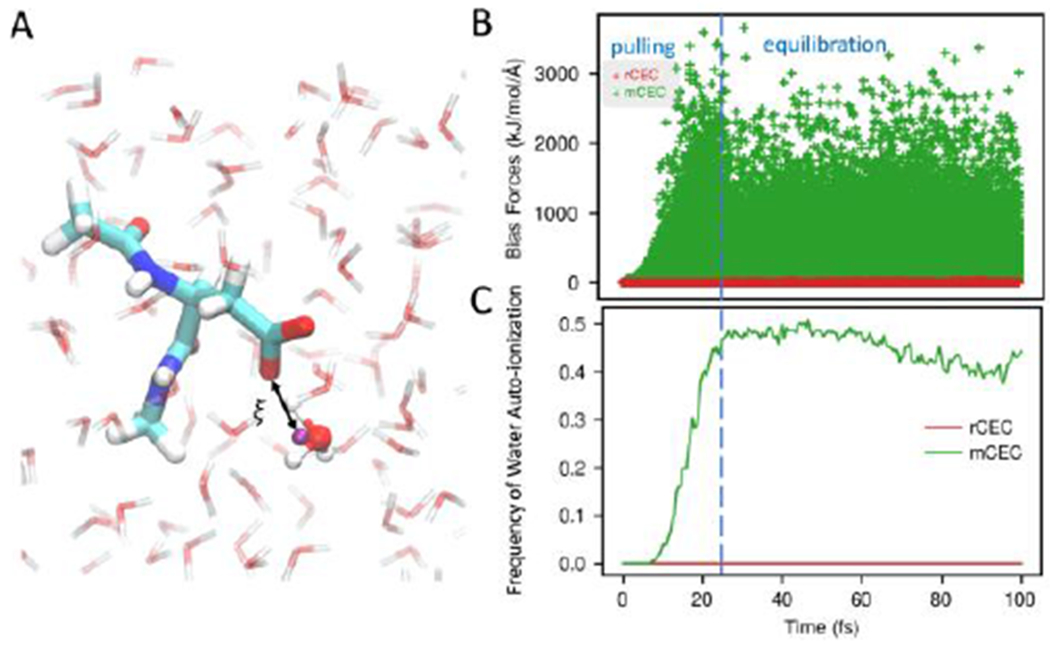
(A) System setup and collective variable definition of aspartic acid in water. The purple ball represents the CEC. (B) Bias forces acting on bulk water atoms which are beyond 6 Å in all SMD runs. Considerable bias forces exist when biasing mCEC (green) while negligible forces are found in the case of rCEC (red). (C) The ratio of SMD runs where broken water was observed as a function of simulation time. Biasing mCEC results in bulk water decomposition while rCEC is free of this issue.

In some SMD runs using mCEC, the bias forces are so large in the pulling phase that a water molecule will actually auto-ionize. To quantify how frequently this happens we construct water bonding topologies at each timestep by first assigning two closest hydrogens to each oxygen and then assigning the remaining excess proton to its closest oxygen. After we have the bonding topologies, we can monitor the O–H bond lengths of bulk waters that are 6 Å away from the carboxylic oxygens. If a water O–H bond is longer than 1.4 Å, we count it as a broken water. At each timestep, the number of simulations where broken waters are present was counted (Figure 4C). If the mCEC is used in SMD runs, the fraction of broken simulations rises to approximately 0. 5 in the pulling stage, and then remains at this level during equilibration. In comparison, biasing rCEC does not result in any water auto-ionization.

Metadynamics first developed by A. Laio and M. Parrinellos has become increasingly popular as an enhanced sampling method. In metadynamics the bias potential is gradually added in an adaptive fashion, which is significantly different from the case of a stiff moving restraint in SMD simulations. We applied both CECs in a metadynamics simulation of the same Asp system in order to check whether water auto-ionization is an artifact of large bias forces imposed by a short pulling stage in SMD runs. However, water decomposition was still observed when mCEC is biased (Figure S1). Similar water decomposition was observed in QM/MM simulations of human carbonic anhydrase when using mCEC where a water lost a proton to a nearby Histidine._{^{18, 100}} Based on our observations, the resulting “proton-hole” mechanism observed could possibly be an artifact of using mCEC in the reaction coordinate definition. In comparison, metadynamics biasing rCEC and using the same settings otherwise did not show water auto-ionization in the 30 ps run.

3.3. Benchmark of rCEC in umbrella sampling

We then calculated the potential of mean force for the deprotonation of a weak acid biasing our rCEC, and compared it to previous results biasing the exact MS-RMD CEC. Umbrella sampling biasing the MS-RMD CEC has been used extensively, and was shown to reproduce the experimental pKa when the parameters in the reactive potential are variationally mapped from electronic structure data._{^{94, 96}} Independent umbrella sampling runs biasing rCEC on the same system of water solvated glutamic acid were conducted. The resulting PMF shown in Figure 5A exhibits reasonable agreement with the reference PMF within statistical uncertainties, confirming the stability and usefulness of our new CEC in enhanced sampling.

Figure 5.

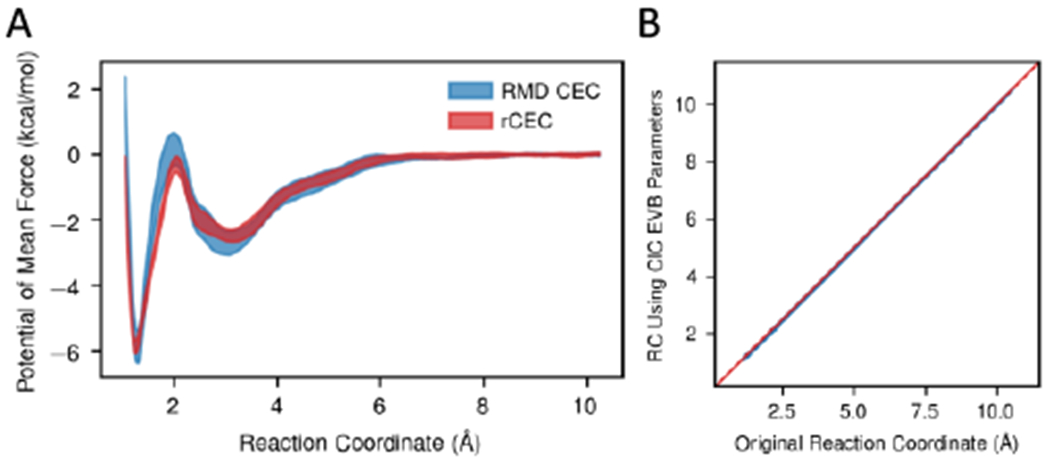
(A) Deprotonation potential of mean force computed from MS-RMD CEC and rCEC. The two PMFs match within statistical errors. (B) Scatter plot of the reaction coordinate recalculated using a different RMD model with respect to the original reaction coordinate. Data points are shown as blue dots and a red line is for indicating the position of diagonal. The CECs computed from different RMD model match perfectly well.

We further tested rCEC by examining how it performs in other environments. When going to a new system, one could reparametrize rCEC to ensure it reproduces the new charge transfer behavior. However, we show that the MS-RMD CEC position is not strongly dependent on the system itself and thus reparameterization is not necessary. We recalculated the MS-RMD CEC position on the configurations sampled every 2 ps in the original umbrella sampling runs, but using a different MS-RMD model for a glutamic acid developed for ClC-ec1,_¹⁰¹ a Cl₋/H₊ antiporter. As shown in the scatter plot Figure 5B, the resulting CV is nearly identical to the original CV with the largest deviation of only 0.05 Å.

4. Conclusions

In summary, we have discovered valuable spectroscopic properties of the center of excess charge of a hydrated proton, and presented a new CEC (rCEC) definition with improved properties. Since the excess charge vanishes on bulk-like waters, the rCEC spectrum provides a promising computational tool for studying IR properties of the solvated proton in an aqueous environment under room temperature perfectly disentangled from water bands. In turn, the spectral features of different CEC definitions provide insights into each CEC’s behavior, which was then validated by analyzing each CEC in various enhanced sampling simulations. In future work, we will apply our rCEC in AIMD simulations and QM/MM simulations of proton transport of more complicated systems. Further decomposing the excess charge according to motions has and will enable us to assign IR signals in more detail without the contamination of water absorption while directly working in condensed phase. Understanding the excess charge from a pure ab initio picture may derive from the constrained DFT (CDFT)_¹⁰² and multistate DFT (MS-DFT) framework_{^{103, 104}} while future efforts are required to accommodate biasing electronic degrees of freedom into Born-Oppenheimer MD if one wants to directly enhance the excess charge transfer via enhanced sampling. One possible solution is parametrizing our rCEC to reproduce the CDFT or MS-DFT charge transfer calculations so that the excess charge transfer can be indirectly biased through our CEC. Future work may also go beyond the center of excess charge, which is essentially the first moment of excess charge distribution. The second moment, which includes the spatial shape of excess charge distribution may also be useful to study recent polarization experiments on acidic solutions._{^{33, 98}}