Abstract
Multiphysics modeling of evolving topology in the electrosurgical dissection of soft hydrated tissues is a challenging problem, requiring heavy computational resources. In this paper, we propose a hybrid approach that leverages the regressive capabilities of deep convolutional neural networks (CNN) with the precision of conventional solvers to accelerate Multiphysics computations. The electro-thermal problem is solved using a finite element method (FEM) with a Krylov subspace-based iterative solver and a deflation-based block preconditioner. The mechanical deformation induced by evaporation of intra- and extracellular water is obtained using a CNN model. The CNN is trained using a supervised learning framework that maps the nonlinear relationship between the micropore pressure and deformation field for a given tissue topology. The simulation results show that the hybrid approach is significantly more computationally efficient than a FEM-based solution approach using a block-preconditioned Krylov subspace solver and a parametric solution approach using a proper generalized decomposition (PGD) based reduced order model. The accuracy of the hybrid approach is comparable to the ground truth obtained using a standard multiphysics solver. The hydrid approach overcomes the limitations of end-to-end learning including the need for massive datasets for training the network.
Keywords: Multi-physics modeling, Electrosurgery, Deep learning, Convolutional networks
1. Introduction
Electrosurgical procedures are widely used to simultaneously dissect and coagulate soft hydrated tissues [1]. Yet, the understanding of the underlying mechanisms of tissue damage in electrosurgery remains limited, causing a large number of accidental burns and tissue injuries each year [1]. Many models have been proposed to study the biophysical effects of radiofrequency (RF) current on the thermo-mechanical response of soft tissues [2–4]. However, efficient modeling of such procedures considering multiscale electro-thermo-mechanical interactions with high physical fidelity remains a challenging problem, for which state-of-the-art methods [3] require heavy computational resources, limiting their application to simplistic loading conditions. In this paper, we propose a hybrid approach that leverages the approximation capabilities of deep learning neural networks with the precision of conventional finite element solvers to accelerate multiphysics computations.
Multiphysics modeling of electrosurgical procedures requires the solution of the electro-thermo-mechanical problem in conjunction with a model to account for evaporative losses at the cellular level [3,5]. The multiphysics interactions may lead to tissue dissection, which must be captured in real-time for electrosurgical simulations. The solution of the linear momentum balance equation is known to be the most computationally expensive component, restricting real-time simulations to a few thousand degrees of freedom (DOF) using the finite element methods (FEM) [3,6]. The size of the high fidelity multiphysics problem to be solved in electrosurgical simulation grows with mesh refinement to possibly millions of DOFs. Efficient solution of these systems is critical for real-time applications in the field of virtual surgery for surgical training, pre-operative planning and intra-operative guidance [6–8]. Many solution techniques have been developed to tackle such large-scale problems including the use of graphics processing units (GPU) [9,10], efficient preconditioners for iterative solvers [5,11], and model order reduction techniques [12,13].
Model order reduction (MOR) techniques including proper orthogonal decomposition (POD) [14,15], proper generalized decomposition (PGD) [12,16], and reduced basis [17] are widely used to reduce the number of DOFs, thereby reducing the complexity of large-scale Multiphysics simulations. POD is a general technique for extracting the most significant features of a system’s behavior and representing them using a set of POD bases spanning the reduced-order subspace [13,14]. Another family of MOR techniques uses a reduced basis constructed by leveraging a greedy algorithm and a posteriori error indicators [17]. As for POD, the reduced basis method requires some amount of pre-computation and does not readily generalize. PGD-based MOR techniques are based on the use of separated representations of model parameters, also known as “extra-coordinates” [16]. This parameterized model assumption allows offline computation of the parametric solution that functions as a meta-model to be used online for real-time simulation. However, MOR techniques, including POD and reduced basis methods, are unable to deal with topological changes. Although PGD has been utilized to parametrize shape to obtain computational vademecum for real-time simulation using kernel PCA (kPCA) [12], we show in Section 3 that PGD-based techniques cannot deal with topological changes efficiently.
Deep learning is a recent progression in artificial neural networks (ANN). It has the advantage of approximating nonlinear mappings of a system based on data. Recent works have attempted to build neural models that can make predictions about constitutive equations of materials [18], optimized numerical quadrature [19], solutions of partial differential equations [20,21], and fluid flows [15,22,23]. Deep learning has also been used for MOR. In [24], the deep auto-encoder is used to reduce the dimensionality of distributed parameter systems. Wang et al. [15] proposed a data-driven technique that utilizes the predictive ability of the long short-term memory (LSTM) deep learning method to learn the evolving POD bases that represent the reduced fluid dynamics system.
Despite the advances in deep learning algorithms, a major limitation in their application to physical problems is that they require an end-to-end mapping dataset, often provided by solving high fidelity models. Hence, learning models are trained to predict the ground-truth output starting from an initial state produced by a high-fidelity solver with all the possible inputs and boundary conditions. This may yield errors that can accumulate quickly along the generated time sequence [28] and be infeasible for real-time simulation. Moreover, for multiphysics simulation of RF-activated soft tissue, end-to-end learning that predicts temperature evolution and topological changes at each time step directly based on the input current flux, may require an extremely large number of datasets for the problem to be well sampled for all possible combinations of thermodynamic states (e.g. pressure and temperature), rendering it infeasible for electrosurgical simulations. Further, the end-to-end learning approach may be slower to converge due to local optima [25].
To alleviate these issues, we propose a hybrid approach that leverages the regressive power of deep convolutional neural networks (CNN) for predicting the mechanical deformation induced by micromechanical pressure in RF-activated soft tissue. The electrical potential and temperature fields are obtained by solving the electro-thermal problem using the finite element methods in conjunction with an efficient block-preconditioned Krylov subspace solver (e.g. GMRES [26]). CNNs have been shown to be effective in the simulation of the Navier-Stokes equations [22,27]. The sparse local interaction and parameter sharing characteristics of CNNs enable them to have fewer weight parameters to be trained and properly capture the essential features with reduced memory and computational cost compared to fully connected neural networks [28]. A physical justification for the success of CNN-based simulation of the Navier-Stokes equations and a connection between CNN and the Mori-Zwanzig formalism for the dimensionality reduction of dynamical systems are provided in [29]. In this work, the CNN architecture [23] is employed to approximate the deformation field for the given micromechanical pressure and tissue topology. A non-trivial data augmentation is performed to generate input pressure. The corresponding deformation field and tissue topology are obtained by solving the high fidelity Multiphysics model [5]. In Section 3, we show that the proposed hybrid approach is stable and faster compared to efficient finite element method-based [5] and PGD-based parametric solution approaches.
The paper is organized as follows. Section 2 describes the basics of multiphysics simulation for RF activated soft tissues, our CNN-based hybrid approach, and a PGD-based parametric solution approach along with the implementation details. The accuracy and computational efficiency of the proposed hybrid approach are presented in Section 3, followed by conclusions and future work in Section 4.
2. Mathematical modeling
We begin with a description of the multiphysics model for radiofrequency (RF)-activated soft hydrated tissue in Section 2.1. A hybrid CNN-based model for predicting the mechanical deformation induced by micromechanical pressure is presented in Section 2.2. In Section 2.3, a PGD-based parametric solution approach is presented for comparison with the proposed hybrid CNN-based model for the electrosurgical cutting problem.
2.1. Multiphysics model
In this section, we briefly review the electro-thermo-mechanical model along with the micromechanical equation of state (EOS) and the level set model for interfacial evolution of soft tissue damage in electrosurgery. For a detailed derivation of the governing equations and the EOS, we refer to our previous publication on electrosurgical dissection of soft tissues [5].
Governing equations
The thermomechanical response of RF-activated soft tissues is treated within the framework of linear thermoelasticity. Let the soft tissue occupy an open region with an external boundary (Γ) over a time interval (0, τ), see Fig. 1. Ωd ⊂ Ω denotes the damaged region from which tissue is removed due to dissection, Ωh = Ω\Ωd denotes the healthy region, and Γi = ∂Ωh ⋂ ∂Ωd is the interface of Ωd and Ωh.
Fig. 1.
Computational domain with Dirichlet and Neumann boundaries for the electrical, thermal and mechanical problems. Boundaries are not necessarily overlapped for the three problems.
The governing equations for the electric potential (V), temperature (T), and displacement field (u) for all x ∈ Ω and t ∈ (0, τ) follow from the local electric charge conservation, energy balance, and linear momentum balance laws, respectively.
For the operating frequencies of the electrosurgical procedures, the characteristic wavelengths of the electromagnetic waves are much larger than the characteristic dimensions of the tissue. Hence, the electromagnetic effects can be treated by solving the Maxwell’s equations with a quasi-static approximation. The electric potential field can then be obtained by solving a boundary value problem for the charge conservation, i.e.
Find such that
| (1) |
subject to
with boundary Γ = Γj⋃Γv and Γj⋂Γv = ∅ and , where J is the current density, jn is the current density normal to the Neumann boundary Γj, n is the unit outward normal to Γj, and is the prescribed electric potential on the Dirichlet boundary Γv.
The capacitive losses are negligible for the frequencies used in electrosurgery; hence, heat generation is considered to be mainly resistive. The current density is then described by Ohm’s law as
| (2) |
where σ is the electrical conductivity and E is the electric field given by
| (3) |
The heat generated due to RF excitation is given as
| (4) |
Neglecting structural heating and dissipation due to tissue damage compared to Joule heating (Eq. (4)), the initial boundary value problem corresponding to the energy balance is given as
Find such that
| (5) |
subject to
with the boundary Γ = Γq⋃ΓT, Γq⋂ΓT = ∅, and , where q is the heat flux vector, q is the effective heat generation per unit volume, qn is the component of heat flux normal to the Neumann boundary Γq, n is the positive unit normal to Γq, is the prescribed temperature at the Dirichlet boundary ΓT, T0 is the initial temperature, and ρ and c are the effective density and effective specific heat capacity of the tissue, respectively. The heat flux is defined in terms of temperature gradient using generalized Fourier’s law as
| (6) |
where k is the effective thermal conductivity of the tissue.
The soft tissue deformation due to micropore pressure induced by evaporation of intra- and extracellular water under Joule heating is obtained by solving the linear momentum balance equation. However, the time scales over which temperature changes occur, during Joule heating of soft tissue, are orders of magnitude larger than the time scales of the elastic waves [30]. Hence, tissue deformation is obtained by solving the elastostatic boundary value problem:
Find such that
| (7) |
subject to
with boundary Γ = Γt⋃Γu, Γt⋂Γu = ∅, and , where σ is the Cauchy stress tensor, b is the body force, is the surface traction on the Neumann boundary Γt, is the prescribed displacement on the Dirichlet boundary Γu, n is the outward normal to Γt.
Assuming isotropic linear elastic constitutive response for the soft tissue, the Cauchy stress tensor can be split into a hydrostatic pressure (p) and the deviatoric stress (τ) as
| (8) |
The hydrostatic pressure (p) and effective parameters (ρ, c, and k) along with the effective heat generation (q) at a spatial point are obtained from the micromechanical model.
Micromechanical model
At the microscopic level, the conservation of mass along with thermodynamic and mechanical equilibrium is applied to obtain an EOS relating vapor mass fraction (x) to temperature (T) and pressure (p) as
| (9) |
where E and v, respectively, denote the Young’s modulus and Poisson’s ratio, p0 is the atmospheric pressure, r is the specific gas constant for water vapor, and ρw denotes the density of liquid water at the current thermodynamic state.
The vapor mass fraction is then obtained by solving a local microscopic energy balance equation along with the EOS (Eq. (9)). The effective density, specific heat capacity, and thermal conductivity of the tissue at x ∈ Ω are computed using vapor content x as
| (10) |
| (11) |
and
| (12) |
respectively, where m is the total water and vapor mass fraction, and subscripts v, w, and s represent properties corresponding to the vapor, water, and solid phase, respectively.
The effective heat generation at a spatial point x ∈ Ω is given by
| (13) |
Level set approach to tissue dissection
Topology change due to tissue dissection induced by thermal damage is tracked using a level set approach [31]. The damaged region (Fig. 1) is parameterized by means of the level set function
| (14) |
The level set function is evolved using the following equation [32]
| (15) |
where v is the interface velocity and ϕ0 is the initial signed distance from the traction-free surface. For the RF-induced tissue damage, the normal component of the interface velocity follows from the second law of thermodynamics. The normal interface speed is defined as the difference between the elastic strain energy and an experimentally-determined damage parameter [33].
Numerical solution approach
The weak form of the governing equations is solved using the finite element method. The computational domain is discretized using tri-linear tetrahedral finite elements with a single Gauss point per element. The time integration of the energy balance equation is performed using a midpoint rule. The resulting linear algebraic set of equations for the governing equations is solved using a GMRES [26] iterative solver with a recently developed efficient block preconditioning technique [34]. The level set evolution equation (Eq. (15)) is solved on triangulated domains using an explicit positive coefficient scheme proposed by Barth and Sethian [35]. The solution on the triangulation set is approximated using a standard piecewise linear finite element subspace. The detailed algorithmic description of the solution approach of multiphysics problem for electrosurgical cutting is provided elsewhere [5].
In [5], we have shown that the solution of the linear momentum balance equation in conjunction with the micromechanical model is the most computationally expensive component of the multiphysics modeling scheme. Therefore, it is imperative to approximate the solution of the mechanical problem using a powerful regressor such as a deep neural network to accelerate the electrosurgical cutting simulation.
2.2. The hybrid CNN-based solution approach
The CNN-based hybrid solution approach accelerates the solution of the elastostatic problem using a trained CNN, while the electric and thermal fields are solved using finite elements using a block-preconditioned GMRES solver (see Fig. 2). The CNN model is trained to learn a nonlinear relationship between the input micropore pressure distribution and tissue topology described by the level set signed distance (Eq. (14)), and output deformation field. We present the overall simulation algorithm below. The architecture of the CNN and its training are presented in Sections 2.2.1 and 2.2.2, respectively.
Fig. 2.
CNN-based hybrid approach for electro-thermo-mechanical simulations.
The simulation is initialized by assuming the tissue to be at atmospheric conditions and the level sets are initialized from the traction-free boundary. At any given time step of the simulation, the following steps are performed:
With current flux (jn) as the input to the electro-thermal finite element solver, compute the micropore pressure (p) based on the micromechanical EOS.
With the input micropore pressure and the current level set signed distance (Tg), compute the deformation field (u) using the trained CNN.
Using the deformation field (u), solve the level set evolution equation (Eq. (15)) to compute the evolved level set signed distance.
The level set signed distance is stored and used as the input to the CNN model for the next time step.
2.2.1. The CNN architecture
As explained earlier, we do not use CNN to learn an end-to-end mapping between the applied current flux and the final topological change at any time step, as this may require an extremely large number of datasets for the problem to be well-sampled. In the hybrid simulation approach, the CNN is used to learn the nonlinear relationship between the input micropore pressure (p) and current level set signed distance (Tg) and the output deformation field (u). For the three-dimensional (3D) problem, the inputs and outputs are spatially ordered sequence of p and Tg, and the deformation ui along spatial directions i ∈ {1,2,3}, respectively. These are represented by a 3D data structure of size n1 × n2 × n3, where ni, i ∈ {1,2,3} is the number of data points along the three spatial directions.
The CNN architecture is presented in Fig. 3. The internal structure of the network consists of 5 stages of volumetric convolution and rectifying linear activation layers [23]. The convolutional layer consists of k learnable filters (or kernels) with parameters wα, α ∈ {1,2, …, k} of size m × m × m, where m < ni. The input data is transformed using a convolution operation through filters wα into respective feature maps hα (Fig. 4), followed by leaky rectified linear unit (ReLU) activation. The leaky ReLU activation function is defined as
| (16) |
where is a component of the feature map hα. The ReLU function is known to avoid the vanishing gradient problem during training [39]. The component of the feature map at the location (j, k, l) is then computed as
| (17) |
where bα is the bias parameter corresponding to the filter wα. The filters are convolved across the span of 3D representation of the input data by a predetermined step size to compute the elements of 3D feature maps. The network learns the filters by optimizing the parameters wα and the bias bα to find the relationship between input and output training data.
Fig. 3.
The CNN architecture. Here, the 3D input data is of size 64 × 64 × 128; m ∈ {1,3} is the size of the convolutional filters (or kernels); and n = 2 is the filter size in the pooling layer.
Fig. 4.
Schematic of the convolution and average-pooling transformations of the inputs with filter size m = 2 and n = 2, respectively.
While single resolution feature maps are adequate to capture the local interactions, and hence, the relationship between the micropore pressure and tissue deformation, it would limit the network’s ability to learn the higher-level global topology changes. Hence, a multi-resolution feature map is added to learn the evolving overall topology by downsampling the first hidden layer twice (Fig. 4). The convolved features are divided into n × n × n contiguous regions with n ≥ 2 and an average of features is computed over these blocks. The aggregate of the averaged features constitutes the pooled convolved features of size (n1 × n2 × n3)/n. The convolution and average-pooling transformations are depicted in Fig. 4. Each resolution of the feature map is processed in parallel through the next hidden layer and then upsampled to the high-resolution feature maps before accumulating them. The accumulated feature maps are processed through the next two volumetric convolution and ReLU activation layers to produce the output deformation field u.
2.2.2. Training of the CNN
To train the network, we generate datasets that approximately sample the manifold of realistic micropore pressures and corresponding deformation fields for the given tissue topology. To this end, we use a pseudorandomized procedure outlined in Algorithm 1. We generate Nd = NsNt datasets comprising of Ns scenarios with Nt time-steps per scenario.
For each scenario, the pressure field is first initialized to be the atmospheric pressure and the level set is initialized with the signed distance from the traction-free surface. We randomly select a tetrahedron on the surface, as shown in Fig. 5a and assign a randomly generated pressure in the range of 101 kPa to 120 kPa to the integration point of this tetrahedron. This range of pressures mimics the micropore pressures due to evaporation of intra- and extracellular water in the RF-activated soft tissue [5,36]. The pseudorandom input pressure is generated using the Mersenne Twister algorithm [37]. We then compute the deformation field and topology, respectively, by solving the momentum balance equation (Eq. (7)) and level set evolution equation (Eq. (15)). The random pressure field along with the deformation field and topology (i.e., level set signed distance) constitute a single dataset.
Fig. 5.
Schematic of pseudorandomized procedure of data generation. (a) A randomly selected tetrahedron with single integration point, (b) random selection of a neighboring tetrahedron (blue) in the next time step, and (c) next immediate neighboring tetrahedron (green) randomly selected in the third time step.
In the next time step of the scenario, we select a tetrahedron neighboring to the previously selected tetrahedron randomly (Fig. 5b). We then assign a random pressure to the integration point, while also perturbing the pressure in the previously selected tetrahedron(s) by −5 to 5% ensuring that the pressure is within the 101–120 kPa range. As in the previous step, we compute the corresponding deformation field and topology to construct the next dataset. In successive time steps, we repeat the process by selecting a neighboring tetrahedron (Fig. 5c). After Nt time steps, a new scenario is initiated starting with a tetrahedron that has not been selected in previous scenarios.
Algorithm 1:
Pseudorandom procedural dataset generation per scenario
| 1: | Initialization: |
| 2: | Assign atmospheric pressure to the integration point of all the tetrahedra |
| 3: | Initialize level set with the signed distance from the traction-free surface |
| 4: | Choose a tetrahedron on the surface at random |
| 5: | SetRandomPressure(start tetrahedron); //Assign randomly generated pressure to the integration point |
| 6: | UpdateDeformation(); //Update the deformation field using mechanical solver |
| 7: | UpdateTopology(); //Update the topology using level set solver |
| 8: | MarkVisited(); //Mark the tetrahedron as visited |
| 9: | CollectData(); //Store the input pressure field, output deformation field and level set signed distance field for training |
| 10: | While t <τ do |
| //Get random neighbor of last visited tetrahedron; set random pressure and perturb pressure in previously visited tetrahedron(s) | |
| 11: | GetRandomNeighbor(last visited tetrahedron); |
| 12: | MarkVisited(); //Mark the new neighboring tetrahedron as visited |
| 13: | SetRandomPressure(all visited tetrahedra); |
| 14: | UpdateDeformation(); |
| 15: | UpdateTopology(); |
| 16: | CollectData(); |
| 17: | End while |
The data generation is a pre-processing step and can be automated. Once the datasets are generated, a standard backpropagation learning with the ADAM optimization algorithm [38] is used to compute the weights of the neural network by minimizing the difference between the ground truth deformation field () and the deformation field (u) predicted by the CNN as defined by the L2 error . A leave-one-out cross-validation (LOOCV) is performed for the independent assessment of the model. LOOCV is a type of cross-validation in which the learning algorithm is applied for each sample, using all other samples as the training set and using the selected sample as the single-item test set [39].
2.3. PGD-based parametric solution approach
We compare the efficiency of our hybrid CNN-based model with a PGD-based parametric solution approach. Much like the hybrid approach, the PGD method is used to approximate the deformation field, while the electro-thermal problem is solved using the FEM and a block-preconditioned GMRES iterative solver. PGD is an iterative method, generating an approximation to the solution composed of a finite sum of separable functions [16,40]. At iteration n of the PGD process, the approximate displacement is given as
| (18) |
where with i ϵ {1,2,3} refers to the ith component of the displacement vector, and functions , , , and represent the separated functions used to approximate the deformation field. The parameters x, s, p and Tg, respectively, represent the spatial coordinates, electrode position, pressure, and topological information parametrized by the application of kernel PCA techniques [12].
The algorithm proceeds by searching an improvement of this approximation in the next iteration. Therefore, the (n + 1)th term is given as
| (19) |
where Mi(x), Ni(s), Ri(p), and Si(Tg) are the sought functions which can be obtained using fixed-point iterations to improve the approximation [40].
This approach is based on an off-line/online procedure. During the offline phase, a general metamodel is computed, whereas, during the online phase, the solution is evaluated based on the metamodel as shown in Fig. 6. The solution accuracy can be improved by searching for an improvement of the previous approximation in the next iteration.
Fig. 6.
PGD-based multiphysics simulation architecture for electrosurgery.
This approach aims to generate a general solution for any type of topological change by parametrizing topological information using a minimal number of degrees of freedom dictated by the kernel PCA technique [12]. A total of Nd = NsNt topological datasets are compiled using Algorithm 1. However, if the solution is not in the manifold of generated topological states, solution accuracy will be compromised for real-time performance.
3. Numerical examples
A computational model of a rectangular tissue block of dimension 0.2×0.1×0.1 m3, as shown in Fig. 7, has been developed to investigate the efficacy of the hybrid approach. A ball-shaped active electrode with a radius of 1.17 mm is placed on the top surface of the tissue block. A current density of 0.0572 A/mm2 for 50 W power setting is applied to the active electrode. The bottom plane of the tissue block is placed on the dispersive electrode. All other surfaces are electrically insulated. A convective boundary condition is applied on all sides with a natural convection coefficient of 25 Wm−2K−1. A zero-displacement boundary condition is applied to the bottom surface of the tissue block. The model parameters are provided in Appendix I.
Fig. 7.
Schematic of the 3D model. The red dot indicates the position of the active electrode.
The computational domain of the tissue block is discretized into 63×63×127 cells. Each cell is further divided into 6 tri-linear tetrahedral finite elements with one Gauss point per element. The nodal values of the input micropore pressure (p) and level set signed distance (Tg) and the output deformation field (u) are stored in a 3D data structure of size 64×64×128. Here, the number of data points is equal to the number of nodes along the three spatial directions.
The CNN model is implemented in an open-source machine learning library PyTorch [41]. The implementation details of the high fidelity multiphysics model for the electrosurgical dissection are presented elsewhere [5]. The PGD-based parametric solution approach as described in Section 2.3 is implemented for comparison. The simulations are conducted on an Intel Core 4 Xeon(R) CPU and NVIDIA QUADRO K5000 graphics processor.
A comprehensive dataset of input pressures and output deformation fields corresponding to Nd = 200,000 topological configurations are generated using a pseudorandomized procedure described in Algorithm 1. A leave-one-out cross-validation (LOOCV) is performed for the independent assessment of the CNN model. In the LOOCV scheme, each data point is used as the validation set and the remaining Nd – 1 data points are used as the training sets. The test error is estimated by averaging the resulting L2 relative error in estimation of elastic strain energy errj as
| (20) |
The L2 relative error in elastic strain energy is defined as
| (21) |
where is the reference elastic strain energy obtained from the finite element analysis of the mechanical problem, is the predicted elastic energy density using the hybrid CNN-based approach or PGD-based parametric solution approach, and N is the number of the tetrahedra. The selection of the number of scenarios ‘Ns’ and time-steps within each scenario ‘Nt’ follows from a manual hyperparameter selection procedure based on the LOOCV error (Eq. (20)). The sufficiency of dataset is determined by Nd = NsNt and the variation of the dataset is guaranteed by both Ns and Nt. From Fig. 8, we see that the LOOCV error is the least for Ns = 500 and Nt = 400 with time-step size of 0.03s among all other combinations tested in this work. Hence, a total of Nd = NsNt = 200,000 dataset is generated using Algorithm 1.
Fig. 8.
The LOOCV errors for various combinations of Ns and Nt.
The L2 relative error in elastic strain energy with respect to each cross-validation is shown in Fig. 9. The CNN is shown to accurately predict the soft tissue deformation characteristics with LOOCV error of 10.3%, as defined in Eq. (20).
Fig. 9.
The relative error in elastic strain energy with respect to each cross-validation dataset.
Next, the CNN-based hybrid approach is used to simulate two specific test scenarios: (i) a fixed electrode scenario, where the active electrode is placed at a fixed location on the top surface of the tissue block, and (ii) a moving electrode scenario, in which the electrode is moved along an arbitrary path. For brevity, hereafter, the high fidelity multiphysics model, the hybrid CNN based approach, and the PGD-based parametric solution approach, are referred to as high-fidelity, hybrid-CNN, and hybrid-PGD models, respectively.
3.1. Fixed electrode
The proposed hybrid CNN model is compared with the high-fidelity and hybrid-PGD models for the fixed electrode scenario. A total of 15 modes (separate functions) are employed for the PGD approximation. We begin with studying the L2 relative error in the elastic strain energy as defined in Eq. (21) for the hybrid-CNN and hybrid-PGD models. The maximum errors for the hybrid-CNN and hybrid-PGD models are 6.9% and 13%, respectively. From Fig. 10, we see that for the hybrid-CNN model error does not accumulate with time, whereas, for the hybrid-PGD model it keeps increasing with time. The fluctuations in the error are due to insufficient regularization resulting in overfitting of the training data [42]. Further tuning, regularization and optimization of hyperparameters are left for future work.
Fig. 10.
L2 relative error in elastic strain energy density with increasing time. The solid lines indicate moving average error.
The accuracy of the PGD-based parametric solution approach can be improved by increasing the number of modes, as shown in Fig. 11. However, this compromises the computational efficiency of the algorithm as an online search is needed to compute the new basis functions.
Fig. 11.
The L2 relative error in elastic strain energy density with an increasing number of modes employed in the PGD expansion.
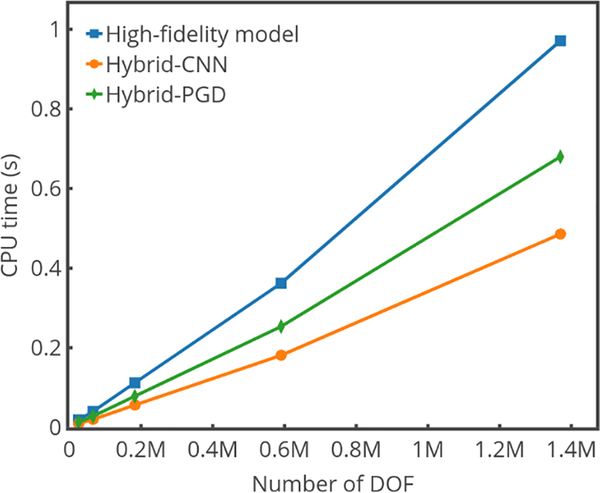
The average computational cost within a single time step of high fidelity, hybrid-CNN, and hybrid-PGD solution approaches are shown in Fig. 12. The hybrid-CNN approach outperforms the other two methods in terms of computational efficiency with satisfactory accuracy. The computational cost for the hybrid-CNN and hybrid-PGD models are predominated by the solution of electro-thermal problem.
Fig. 12.
Plots of CPU time (s) versus number of degrees of freedom (NDOF) when an h-refinement is performed on the tissue block.
The topological change for the three methods is compared in Fig. 13. It can be observed that both the hybrid-CNN and hybrid-PGD models predict the topological change similar to the high-fidelity model.
Fig. 13.
Comparison of topological changes between (a) high fidelity multiphysics model (b) hybrid-CNN model, and (c) hybrid-PGD model; corresponding cross-sections along the y-z plane are shown on the right side.
3.2. Moving electrode
In this example, the active electrode is moved along a curvilinear path at a speed of 12.35 mm/s [5]. The evolving topologies for the three methods are shown in Fig. 14. It can be seen from the figure that the hybrid-CNN approach predicts the topological change similar to the high-fidelity multiphysics model, with a maximum L2 relative error in the elastic strain energy density, as defined by Eq. (21), of 9.6% (Fig. 15). From Fig. 15, we also observe that the L2 relative error in the elastic strain energy density of the hybrid-CNN model does not accumulate with time; an issue that has been observed in end-to-end deep learning implementations [23, 48].
Fig. 14.
Topological change comparison between (a) high fidelity multiphysics model, (b) hybrid-CNN model, and (c) hybrid-PGD model; corresponding cross-sections along the dashed lines are shown on the right side.
Fig. 15.
The L2 relative error in elastic strain energy density for the hybrid-CNN and -PGD models with increasing time; solid lines indicate the moving average errors.
The hybrid-PGD model predicts well initially, however as the simulation proceeds to a state (e.g. cross-section along the dashed line in Fig. 14c) where the topological state may not be within the manifold of the pre-computed basis functions, the solution accuracy is significantly reduced with the maximum L2 relative error in elastic strain energy density close to 69%. The inaccurate prediction of strain energy density suppresses the evolution of level sets, and hence, the initiation of tissue dissection since the local strain energy density is much lower than that of the damage threshold. This leads to a non-physical representation of the tissue damage. Of course, the accuracy of the PGD-based parametric solution approach can be increased by adding modes employed in the PGD expansion. However, seeking an improvement of the approximated solution by computing separated functions online will significantly compromise the computational efficiency of the hybrid-PGD method.
Further, in Fig. 16, the average computational cost within a single time step of the CNN-based hybrid solution approach is compared with that of the high fidelity multiphysics model and the PGD-based parametric solution approach with increasing number of degrees of freedom (NDOF). The hybrid-CNN approach significantly outperforms the other two. To note that, the computational cost for the PGD-based parametric solution approach does not include the cost of seeking an improvement of the approximated solution online. The online computation of new PGD basis functions took ~3s on an average in our tests.
Fig. 16.
Plots of the CPU time (s) versus number of degrees of freedom (NDOF) when an h-refinement is performed on the soft tissue domain.
The CNN-based hybrid approach is observed to be more stable and efficient to deal with topological changes.
4. Conclusion
A hybrid approach for accelerating the solution of eletro-thermo-mechanical problem associated with electrosurgical dissection of hydrated soft tissues is proposed. In this approach, the electro-thermal problem is solved using a standard FEM with an efficient block preconditioned GMRES iterative solver. A deep CNN model is used to predict the deformation field induced by the micromechanical pressure due to evaporation of intra- and extracellular water. Our hybrid approach limits the learning task to the nonlinear regression between input micropore pressure and output deformation field for the given tissue topology. Further, the sparse interaction of the CNN enables it to have fewer weight parameters to be trained compared to a fully connected deep neural network. Hence, this approach circumvents the requirement of a larger dataset that would otherwise be needed for an end-to-end learning scenario where all possible thermodynamic states would have to be sampled. An interesting aspect of our hybrid model is that the dataset is compiled by seeding the mechanical and level set solvers with initial thermodynamic states generated by a random procedure, which effectively increases the dataset diversity. The hybrid approach is shown to avoid accumulated errors in a time-dependent simulation and is significantly faster compared to the standard FEM solver and the PGD-based parametric solution approach.
The convolutional network is used to accelerate the computation of the most computationally expensive component, i.e., the solution of the linear momentum balance equation, in the multiphysics simulation of electrosurgical dissection. It is worthwhile to test if an ensemble learning approach can be employed for predicting electrical, thermal, and mechanical responses in electrosurgical simulation with satisfactory accuracy, and without compromising the real-time interactive performance of the simulation. In addition, separable convolutions and other architectural enhancements can be used to reduce the runtime of the CNN. Techniques for creating generalized topological datasets need to be further investigated. The present implementation is limited to a regular tensor-product grid. The CNN based hybrid solution approach can further be extended to account for the general geometries and unstructured meshes using a graph-based CNN [43] or manifold-based CNN [44] approach.
Highlights.
A data-driven multiphysics model for the electrosurgical dissection of soft tissues
Accuracy of convolutional network-based hybrid model is comparable to standard solver
A pseudorandomized procedure adequately samples realistic manifold of the dataset
An efficient acceleration strategy for the solution of multiphysics problems
Acknowledgment
The authors gratefully acknowledge the support of this study by NIH/NIBIB (Grant No. 1R01EB014305-01A1, 2R01EB005807-05A1, 1R01EB010037-01, and 1R01EB009362-01A2).
Appendix I
Table I.1.
| Electrical conductivity (σ) | 0.33 S/m |
| Thermal conductivity (ks) | 0.512 W/(m·K) |
| Thermal conductivity (kv) | 0.03 W/(m·K) |
| Thermal conductivity (kw) | 0.6 W/(m·K) |
| Convection coefficient (h) | 25 W/(m2·K) |
| Young’s modulus (E) | 0.27 MPa |
| Poisson’s ratio (ν) | 0.4 |
| Damage parameter (κ) | 0.7 × 105 J/m3 |
| Average density (ρs) | 1.08 × 103 kg m−3 |
| Water content (w) | 70% |
| Vapor density (ρv) | 1.0 × 103 kg m−3 |
| Water density (ρw) | 0.994 × 103 kg m−3 |
| Specific heat capacity of solid part (cs) | 1.7 × 103 J kg−1 K−1 |
| Specific heat capacity of water part (cw) | 4.187 × 103 J kg−1 K−1 |
| Specific heat capacity of vapor part (cv) | 1.996 × 103 J kg−1 K−1 |
| Specific gas constant for water vapor (r) | 4.620 × 102 J kg−1 K−1 |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Feldman L, Fuchshuber P, and Jones D, The SAGES manual on the fundamental use of surgical energy (FUSE). New York, NY, USA: Springer, 2012. [Google Scholar]
- [2].Sankaranarayanan G, Resapu R, Jones D, Schwaitzberg S, and De S, “Common uses and cited complications of energy in surgery,” Surg. Endosc, vol. 27, no. 9, pp. 3056–3072, December 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Kuroda Y, Tanaka S, Imura M, and Oshiro O, “Electrical-thermal-structural coupling simulation for electrosurgery simulators,” in Engineering in Medicine and Biology Society,EMBC, 2011 Annual International Conference of the IEEE, 2011, pp. 322–325. [DOI] [PubMed] [Google Scholar]
- [4].Dodde RE, Miller SF, Geiger JD, and Shih AJ, “Thermal-electric finite element analysis and experimental validation of bipolar electrosurgical cautery,” J. Manuf. Sci. Eng. Asme, vol. 130, no. 2, pp. 1–8, April 2008. [Google Scholar]
- [5].Han Z, Rahul, and De S, “A multiphysics model for radiofrequency activation of soft hydrated tissues,” Comput. Methods Appl. Mech. Eng, vol. 337, pp. 527–548, August 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Lu Z, Arikatla VS, Han Z, Allen BF, and De S, “A physics-based algorithm for real-time simulation of electrosurgery procedures in minimally invasive surgery,” Int. J. Med. Robot. Comput. Assist. Surg, vol. 10, no. 4, pp. 495–504, December 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Maciel A and De S, “Physics-based real time laparoscopic electrosurgery simulation,” in Medicine Meets Virtual Reality 16, 2008, vol. 132, pp. 272–274. [PubMed] [Google Scholar]
- [8].Bifulco P et al. , “Investigating the role of capacitive coupling between the operating table and the return electrode of an electrosurgery unit in the modification of the current density distribution within the patients’ body,” Biomed. Eng. Online, vol. 12, no. 1, pp. 1–12, August 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Courtecuisse H, Jung H, Allard J, Duriez C, Lee DY, and Cotin S, “GPU-based real-time soft tissue deformation with cutting and haptic feedback,” Prog. Biophys. Mol. Biol, vol. 103, no. 2–3, pp. 159–168, December 2010. [DOI] [PubMed] [Google Scholar]
- [10].Han Z, Arikatla VS, and De S, “GPU-based parallel algorithms for simulation of electro-surgery procedures in real-time,” presented at 13th U.S. National Congress on Computational Mechanics (USNCCM13), San Diego, CA, 2015. [Google Scholar]
- [11].Han Z, López CA, and De S, “A fast Krylov subspace-based method for multi-physics modeling of electrosurgical cutting of soft tissue,” presented at VII International Conference on Coupled Problems in Science and Engineering, Rhodes Island, Greece, 2017. [Google Scholar]
- [12].González D, Aguado JV, Cueto E, Abisset-Chavanne E, and Chinesta F, “kPCA-based parametric solutions within the PGD framework,” Arch. Comput. Methods Eng, vol. 25, no. 1, pp. 69–86, January 2018. [Google Scholar]
- [13].Niroomandi S, Alfaro I, Cueto E, and Chinesta F, “Real-time deformable models of non-linear tissues by model reduction techniques,” Comput. Methods Programs Biomed, vol. 91, no. 3, pp. 223–231, September 2008. [DOI] [PubMed] [Google Scholar]
- [14].Liang YC, Lee HP, Lim SP, Lin WZ, Lee KH, and Wu CG, “Proper orthogonal decomposition and its applications - Part I: Theory,” J. Sound Vib, vol. 252, no. 3, pp. 527–544, May 2002. [Google Scholar]
- [15].Wang Z, Xiao D, Fang F, Govindan R, Pain CC, and Guo Y, “Model identification of reduced order fluid dynamics systems using deep learning,” Int. J. Numer. Methods Fluids, vol. 86, no. 4, pp. 255–268, February 2018. [Google Scholar]
- [16].Niroomandi S et al. , “Real-time simulation of biological soft tissues: a PGD approach,” Int. J. Numer. Method. Biomed. Eng, vol. 29, no. 5, pp. 586–600, May 2013. [DOI] [PubMed] [Google Scholar]
- [17].Hesthaven JS, Rozza G, and Stamm B, Certified reduced basis methods for parametrized partial differential equations. New York, NY, USA, Springer International Publishing, 2016. [Google Scholar]
- [18].Jung S and Ghaboussi J, “Characterizing rate-dependent material behaviors in self-learning simulation,” Comput. Methods Appl. Mech. Eng, vol. 196, no. 1–3, pp. 608–619, December 2006. [Google Scholar]
- [19].Oishi A and Yagawa G, “Computational mechanics enhanced by deep learning,” Comput. Methods Appl. Mech. Eng, vol. 327, pp. 327–351, December 2017. [Google Scholar]
- [20].Sirignano J and Spiliopoulos K, “DGM: a deep learning algorithm for solving partial differential equations,” arXivPrepr. arXiv1708.07469, December 2017. [Google Scholar]
- [21].Raissi M and Karniadakis GE, “Hidden physics models: machine learning of nonlinear partial differential equations,” J. Comput. phys, vol. 357, pp. 125–141, March 2018. [Google Scholar]
- [22].Yang C, Yang X, and Xiao X, “Data-driven projection method in fluid simulation,” Comput. Animat. Virtual Worlds, vol. 27, no. 3–4, pp. 415–424, May 2016. [Google Scholar]
- [23].Tompson J, Schlachter K, Sprechmann P, and Perlin K, “Accelerating eulerian fluid simulation with convolutional networks,” arXiv Prepr. arXiv1607.03597, July 2016. [Google Scholar]
- [24].Wang M, Li HX, Chen X, and Chen Y, “Deep learning-based model reduction for distributed parameter systems,” IEEE Trans. Syst. Man, Cybern. Syst, vol. 46, no. 12, pp. 1664–1674, September 2016. [Google Scholar]
- [25].Shalev-Shwartz S, Shamir O, and Shammah S, “Failures of gradient-based deep learning,” arXiv Prepr. arXiv1703.07950, March 2017. [Google Scholar]
- [26].Saad Y and Schultz M. h., “GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems,” SIAM J. Sci. Stat. Comput, vol. 7, no. 3, pp. 856–869, July 1986. [Google Scholar]
- [27].Chu M and Thuerey N, “Data-driven synthesis of smoke flows with CNN-based feature descriptors,” ACM Trans. Graph, vol. 36, no. 4, pp. 1–14, July 2017. [Google Scholar]
- [28].Ian Goodfellow AC, Bengio Yoshua, Deep learning. 2016.
- [29].Miyanawala TP and Jaiman RK, “An efficient deep learning technique for the Navier-Stokes equations: application to unsteady wake flow dynamics,” arXiv Prepr. arXiv: 1710.09099, August 2018. [Google Scholar]
- [30].Langtangen HP and Pedersen GK, “Scaling of differential equations,” 2016. [Online]. Available: https://link.springer.com/book/10.1007%2F978-3-319-32726-6. [Accessed: 19-Sep-2018].
- [31].Osher S and Sethian JA, “Fronts propagating with curvature-dependent speed - algorithms based on Hamilton-Jacobi formulations,” J. Comput. Phys, vol. 79, no. 1, pp. 12–49, 1988. [Google Scholar]
- [32].Osher S and Fedkiw R, Level set methods and dynamic implicit surfaces. New York, NY, USA: Springer-Verlag, 2003. [Google Scholar]
- [33].Han Z, “Real-Time Multi-physics modeling of radio-frequency electrosurgical proceduress,” Rensselaer Polytechnic Institute, 2018. [Google Scholar]
- [34].Rahul and De S, “An efficient block preconditioner for Jacobian-free global–local multiscale methods,” Int. J. Numer. Methods Eng, vol. 87, no. 7, pp. 639–663, February 2011. [Google Scholar]
- [35].Barth TJ and Sethian JA, “Numerical schemes for the Hamilton-Jacobi and level set equations on triangulated domains,” J. Comput. Phys, vol. 145, no. 1, pp. 1–40, September 1998. [Google Scholar]
- [36].Karaki W, Rahul, Lopez CA, Borca-Tasciuc DA, and De S, “A continuum thermomechanical model of in vivo electrosurgical heating of hydrated soft biological tissues,” Int. J. Heat Mass Transf, vol. 127, pp. 961–974, December 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Matsumoto M and Nishimura T, “Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator,” ACM Trans. Model. Comput. Simul, vol. 8, no. 1, pp. 3–30, January 1998. [Google Scholar]
- [38].Kingma DP and Ba J, “Adam: A method for stochastic optimization,” arXiv Prepr. arXiv1412, December 2014. [Google Scholar]
- [39].Sammut E, Claude, and Webb Geoffrey I., Encyclopedia of Machine Learning. 2011.
- [40].Niroomandi S, Alfaro I, González D, Cueto E, and Chinesta F, “Model order reduction in hyperelasticity: A proper generalized decomposition approach,” Int. J. Numer. Methods Eng, vol. 96, no. 3, pp. 129–149, 2013. [Google Scholar]
- [41].PyTorch Community, “Tensors and dynamic neural networks in python with strong GPU acceleration,” Github, 2016. [Online]. Available: https://github.com/pytorch/pytorch. [Google Scholar]
- [42].Sutskever I, Hinton G, Krizhevsky A, and Salakhutdinov RR, “Dropout: A simple way to prevent neural networks from overfitting,” J. Mach. Learn. Res, vol. 15, no. 1, pp. 1929–1958, 2014. [Google Scholar]
- [43].Defferrard M, Bresson X, and Vandergheynst P, “Convolutional neural networks on graphs with fast localized spectral filtering,” Advances in neural information processing systems, pp. 3844–3852, June 2016. [Google Scholar]
- [44].Monti F, Boscaini D, Masci J, Rodolá E, Svoboda J, and Bronstein MM, “Geometric deep learning on graphs and manifolds using mixture model CNNs,” in Proceedings - 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, 2017. [Google Scholar]
- [45].Gabriel C, “Compilation of the dielectric properties of body tissues at RF and microwave frequencies,” London, 1996. [Google Scholar]
- [46].Kemper AR, Santago AC, Stitzel JD, Sparks JL, and Duma SM, “Biomechanical response of human liver in tensile loading,” Ann. Adv. Automot. Med, vol. 54, pp. 15–26, January 2010. [PMC free article] [PubMed] [Google Scholar]
- [47].Hegemann J, “Efficient evolution algorithms for embedded interfaces: from inverse parameter estimation to a level set method for ductile fracture,” 2013.
- [48].Bengio S, Vinyals O, Jaitly N, Shazeer N, “Scheduled Sampling for Sequence Prediction with Recurrent Neural Networks,” arXivPrepr. arXiv 1506.03099, June 2015. [Google Scholar]