Genetic Endowments and Wealth Inequality

Abstract

We show that genetic endowments linked to educational attainment strongly and robustly predict wealth at retirement. The estimated relationship is not fully explained by flexibly controlling for education and labor income. We therefore investigate a host of additional mechanisms that could account for the gene-wealth gradient, including inheritances, mortality, risk preferences, portfolio decisions, beliefs about the probabilities of macroeconomic events, and planning horizons. We provide evidence that genetic endowments related to human capital accumulation are associated with wealth not only through educational attainment and labor income, but also through a facility with complex financial decision-making.

1. Introduction

Wealth inequality in the United States and many other countries is substantial and growing (Saez and Zucman, 2014; Jones, 2015). Income inequality explains only part of this phenomenon. After controlling for lifetime income, there remains significant heterogeneity in household wealth at retirement (Venti and Wise, 1998). Existing research attributes some of this variation to differences in fertility and other demographic choices (Scholz and Seshadri, 2007), differences in savings rates, and heterogeneity in the returns to wealth generated by different investment decisions (Benhabib, Bisin, and Zhu, 2011; Calvet, Campbell, and Sodini, 2007). Yet, the factors that produce differences in wealth accumulation are not fully understood. Learning more about these factors is important because policies are likely to have different effects depending on the origins of wealth inequality.

In this paper, we explore the relationship between genetic factors and household wealth. Our measure of genetic variation is a linear index of genetic markers, or polygenic score, associated with years of schooling. Polygenic scores have been constructed to predict a number of outcomes, and the score we use is specific to educational attainment. We demonstrate an economically large and statistically significant empirical relationship between the polygenic score and household wealth at retirement. We also document relationships between the score and a number of underlying factors relevant for wealth accumulation, including financial decisions and beliefs about the macroeconomy. Our results suggest that the genetic transmission of traits related to wealth may be one component of the intergenerational persistence of wealth (Charles and Hu first, 2003; De Nardi, 2004; Benhabib, Bisin, and Zhu, 2011; Black, Devereux, and Salvanes, 2005). They also suggest that an understanding of the intergenerational transmission of economic outcomes that does not account for the role of genetics is likely to be incomplete, possibly overstating the importance of other factors such as parental investments and financial transfers.

We begin by establishing a robust relationship between household wealth in retirement and the average polygenic score within the household. A one standard deviation increase in the score is associated with a 25 percent increase in household wealth (approximately $165,347 at the median wealth, in 2010 dollars). The relationship between the polygenic score and wealth is present across time and education groups. Measures of educational attainment, including years of education and completed degrees, explain over two thirds of this relationship. Using detailed income data from the Social Security Administration (SSA) as well as self-reported labor earnings from the HRS, we find that labor income can explain less than half of the gene-wealth relationship that remains. After conditioning on lifetime income and household education, we find that a one standard deviation increase in the score is associated with a 5 percent increase in household wealth (approximately $28,741 at the median).

Next, we explore additional mechanisms that may explain the gene-wealth gradient. Because individuals receive their genes from their parents, we first examine factors related to intergenerational transfers. We show that the polygenic score is positively related to parental education, which may proxy for transfers and advantageous family environments. We do not find a statistically significant relationship between higher scores and the probability of receiving an inheritance, nor with the size of the inheritance conditional on receiving one. The gene-wealth gradient remains economically large and statistically significant after controlling for both parental education and the size and incidence of inheritances.

We also consider savings behavior and portfolio choice as possible mechanisms through which genetic factors might operate. While the HRS is not well-suited for a direct analysis of savings rates, we examine whether previously documented determinants of savings are associated with the polygenic score. We find that higher individual polygenic scores predict lower objective probabilities of death as well as subjective beliefs about mortality, which may motivate higher savings rates in anticipation of longer lifespans.¹ We also document an association between an individual’s polygenic score and measures of risk tolerance constructed from responses to hypothetical income and wealth gambles, which may affect both the savings rate and how savings are invested. This is consistent with previous research suggesting a genetic basis for risk preferences (Cesarini et al., 2009). We find strong evidence that households with different scores differ in how they save. In particular, we find that higher polygenic-score households are more likely to invest in the stock market, and this appears to play a particularly important role in mediating the relationship between the score and wealth.

Motivated by the findings on stock market participation, we next analyze aspects of financial decision-making that might give rise to differences in investment behavior. We show that lower polygenic scores are associated with beliefs about the probabilities of macroeconomic events that are less accurate relative to objective benchmarks. Lower scores are also associated with a greater propensity to believe that these events will occur with probabilities of 0 percent or 100 percent (a phenomenon we refer to as “extreme beliefs”). Large deviations between subjective and objective probabilities may reflect difficulty with probabilistic thinking. We also find that higher polygenic score households report longer planning horizons for financial decisions. This may indicate that these households are more patient, or that they are more comfortable with complex and abstract decision problems and therefore adopt longer planning horizons.

While we do not observe returns directly, our results provide a possible genetic micro-foundation for the persistent differences in returns to wealth posited in a new wave of theoretical work. This line of research argues that cross-sectional heterogeneity in the returns to wealth is required to match the basic features of the wealth distribution (Benhabib, Bisin, and Zhu, 2011; Benhabib and Bisin, 2016). This argument is supported by a growing empirical literature that finds substantial heterogeneity in such returns (Fagereng et al., 2016; Benhabib, Bisin, and Luo, 2015; Bach, Thiemann, and Zucco, 2015). Much of this heterogeneity persists over time, with some individuals earning consistently higher returns to wealth (Fagereng et al., 2016). If the genetic gradient we study emerges from different returns to wealth brought on by differences in financial decision-making and beliefs about the macroeconomy, then relatively straightforward policy tools such as stronger public pension schemes may help to reduce wealth inequality stemming from genetic variation. This is especially relevant given the dramatic shift away from defined-benefit retirement plans towards options that give individuals greater financial autonomy (Poterba and Wise, 1998).

To explore this issue, our final set of results examines how the polygenic score interacts with a policy relevant variable: pensions. Because defined-benefit pensions offer recipients a guaranteed stream of income without requiring them to make choices about contribution rates or asset composition, such plans should reduce differences in wealth that arise from skill in financial decision-making. We find that the gene-wealth gradient is over four times as large for the subset of households who do not participate in defined-benefit pension plans. This exercise is useful for two reasons. First, it offers compelling support for the hypothesis that financial decisions may be a source of the gene-wealth gradient. Second, it also highlights a potentially important policy consideration. While more flexible plans like 401(k) accounts grant individuals greater freedom in planning for retirement, they may also reduce the welfare of those who find it more difficult to navigate complex financial choices.

This study relates to the literature on endowments, economic traits, and household wealth. One strand of this work examines how various measures of “ability,” such as IQ or cognitive test scores, predict household wealth and similar outcomes (Grinblatt, Keloharju, and Linnainmaa, 2011; Grinblatt et al., 2015; Lillard and Willis, 2001).² However, parental investments and other environmental factors can directly affect test performance, making it difficult to use test scores to separate the effects of endowed traits from endogenous human capital investments. In contrast, genetic measures are predetermined if not exogenous. That is, while polygenic scores are correlated with environmental factors, they are not directly manipulated by environments and investments in the same way as test scores.

A second strand of this literature focuses on genetic endowments, and seeks to estimate their collective importance using twin studies. Twin studies have shown that genes play a non-trivial role in explaining financial behavior such as savings and portfolio choices (Cronqvist and Siegel, 2014, 2015; Cesarini et al., 2010).³ However, while twin studies can decompose the variance of an outcome into genetic and non-genetic contributions, they do not identify which particular markers influence economic outcomes.⁴ This makes it more difficult to study the mechanisms through which genetic factors operate, or how they interact with environments. Moreover, it is typically impossible to apply twin methods to large and nationally representative longitudinal studies, such as the HRS, which offer some of the richest data on household wealth and related behavioral traits.

The remainder of this paper is organized as follows. Section 2 provides details on the genetic index used in this paper. Section 3 describes the data and provides details on key variables. Section 4 presents our main results on the relationship between the average household polygenic score and household wealth. Section 5 explores a host of possible mechanisms that can explain the gene-wealth gradient, including standard factors established in the literature along with measures of financial decision-making. Section 6 concludes.

2. Molecular Genetic Data and Economic Analysis

Following recent developments in behavioral genetics, we investigate the relationship between genetic factors related to educational attainment and household wealth by using a linear index known as a polygenic score. In this section, we first provide details on the construction of the polygenic score, and then discuss what this approach can add to economic analysis. Our description of genetic data and related empirical techniques are intentionally informal; throughout this section, we provide citations for more rigorous and detailed treatments of this material. Moreover, we note that much of the background information presented here on the human genome follows Beauchamp et al. (2011) and Benjamin et al. (2012).

2.1. The Human Genome

DNA (deoxyribonucleic acid) molecules contain instructions that allow organisms to develop, grow, and function. The human genome consists of 23 pairs of DNA molecules called chromosomes, with an individual inheriting one copy of a chromosome from each parent. A DNA molecule is shaped like a double-helix ladder, where each “rung” is formed by one of two possible nucleotide pairs: adenine-thymine (AT), or a guanine-cytosine (GC). The genetic index that we study in this paper is constructed to measure variation in these nucleotide pairs. Since each location in the genome can feature one of two possible molecules, it is sometimes said that “the code of life is written in binary.”

Across the entire human genome, there are approximately 3 billion locations featuring nucleotide base pair molecules. However, differences across people in these base pairs is observed at less than 1% of these locations.⁵ Variation in the base pair molecules at a particular location is referred to as a single-nucleotide polymorphism (SNP, pronounced “snip”). Because individuals inherit two sets of chromosomes — one from each parent — at each SNP an individual can have either two AT’s, two GC’s, or one AT and one GC. Genetic data thus most commonly take the form of a series of count variables indicating the number of copies of the reference molecule (AT’s or GC’s, depending on the location and conventions), possessed by an individual at each SNP: 0, 1, or 2. A central task in behavioral genetics involves determining which, if any, of these SNP variables are associated with behavioral outcomes.

2.2. GWAS and Polygenic Scores

Twins studies account for much of the existing literature on genetics and economic behaviors. A standard twins methodology estimates the fraction of the variance of a particular outcome attributable to genetic factors by comparing the outcomes of identical (monozygotic) twins and fraternal (dizygotic) twins. While identical twins share nearly all genetic markers in common, fraternal twins will share only about 50 percent of these markers. Twins studies often assume the following data generating process for an outcome of interest, Y_if, for individual i in family f:

$$Y_{if}=A_i+C_f+E_i.$$ (1)

Here A_i represents an additive genetic component, C_f represents common environmental factors affecting all individuals in family f, and E_i represents unique environmental factors affecting individual i. Differences in the covariance of Y_if between identical and fraternal twins allow one to identify the heritability of this outcome, which is the fraction of the variance of Y_if accounted for by genetic differences: $\frac{Var(A_i)}{Var(Y_{if})}$. Existing twins studies deliver heritability estimates of around 40% for education (Branigan, McCallum, and Freese, 2013).⁶

While twins studies provide an estimate of how much genetic factors collectively matter for explaining variation in a given trait, they do not reveal which specific SNPs are relevant. By contrast, Genome Wide Association Studies (GWAS) estimate associations between individual SNPs and outcomes of interest. A GWAS typically proceeds by gathering data on J observable SNPs, ${\left\{SN{P}_{ij}\right\}}_{j=1}^J$ and estimating J separate regressions similar to the following:

$$Y_i=\mu X_i^{\prime }+{\beta }_{j}SN{P}_{ij}+{ϵ}_{ij},$$ (2)

where SNP_ij ∈ {0, 1, 2} measures the number AT’s or GC’s (again depending on convention) possessed by individual i for SNP j, and X_i is a vector of control variables. Separate regressions for each SNP are estimated because in practice, one typically has many more genotyped SNPs than observations in a discovery sample.

The J individual regressions in a GWAS produce a set of coefficients ${\left\{{\widehat{\beta }}_j\right\}}_{j=1}^J$ — one for each SNP — with associated standard errors and p-values. Researchers interested in studying individual genetic markers typically focus on those SNPs exhibiting the strongest GWAS associations. Since traits like education are likely influenced by a large number of genetic markers, each with possibly small influences, the β_j estimated from (2) are often used to construct polygenic scores — indices formed by a linear combination of the GWAS coefficients. A polygenic score for a trait or outcome of interest is given by:

$$PG{S}_i=\sum _{j=1}^J{\tilde{\beta }}_{j}SN{P}_i.$$ (3)

where the ${\tilde{\beta }}_j$ in Equation (3) are versions of the ${\widehat{\beta }}_j$ coefficients estimated from Equation (2) that are adjusted to account for correlations between SNPs. There are many ways to perform this correction, and a detailed discussion of various methods is outside the scope of this paper. The polygenic score we use follows the Bayesian LDpred procedure of Vilhjalmsson (2015), which has been shown to perform better out of sample than other methods (Okbay et al., 2016), and we refer the reader to that study for details.

As shown in Equation (3), a polygenic score is simply a linear combination of SNPs and their effect sizes. While relatively few SNPs are likely to achieve genome wide significance⁷ — a stringent threshold for the statistical significance of a single β_j that accounts for multiple hypothesis testing and other factors — many polygenic scores include all SNPs included in the GWAS. In the case of educational attainment, previous studies have shown that a score using all SNPs produces better out-of-sample prediction than polygenic scores that use only genome wide significant SNPs (Okbay et al., 2016). In the context of Equation (1), the polygenic score can be thought of as the best SNP-based linear predictor of the common genetic component A_i.

2.3. The EA Score

GWAS have traditionally focused on medical or health-related outcomes, such as smoking (Bierut, 2010; Thorgeirsson et al., 2010) and obesity (Locke et al., 2015). However, the increasing availability of genetic data has made it possible to perform well-powered GWAS for behavioral traits with more distant relationships to underlying biological mechanisms. In particular, a series of landmark studies have delivered the first GWAS associations between individual SNPs and educational attainment, specifically years of schooling (Rietveld et al., 2013; Okbay et al., 2016; Lee et al., 2018). Existing work shows that polygenic scores for educational attainment based on these GWAS predict labor market outcomes, including earnings (Papageorge and Thom, 2018), and other measures of adult success (Belsky et al., 2016), even after controlling for completed education.

In this paper, we study a polygenic score based on the educational attainment GWAS results from Lee et al. (2018), which featured a discovery sample of over 1.1 million people.⁸ Importantly, HRS data are not used to estimate the GWAS associations ${\left\{{\widehat{\beta }}_j\right\}}_{j=1}^J$ for this score, so every analysis in this study is an out-of-sample exercise.⁹

Prediction results from Lee et al. (2018) suggest that this score explains approximately 10.6 percent of the variation of years of schooling in the Health and Retirement Study. In what follows, we refer to this score as the Educational Attainment, or EA score.¹⁰ It is reasonable to suspect that genetic endowments related to educational attainment may affect biological processes related to cognition that facilitate learning. Indeed, pathway analyses suggest that several of the SNPs most heavily tied to educational attainment are linked to biological processes known to be involved in brain development and cognitive processes (Lee et al., 2018; Okbay et al., 2016). Further, there is evidence of a high correlation between SNPs related to educational attainment and those associated with cognition (Okbay et al., 2016).¹¹ Results from Belsky et al. (2016) suggest that an earlier polygenic score for educational attainment predicts cognitive test scores for children in elementary school. However, it is important to note that the GWAS associations can reflect a range of traits — both cognitive and non-cognitive — that affect educational attainment through diverse mechanisms. We refrain from using the term “ability” when we refer to the EA score as it is likely too simplistic and may lead to the mischaracterization of the EA score as solely capturing cognitive function.

2.4. Interpretational Issues

Several caveats apply to the interpretation of variation in polygenic scores, and correlations between polygenic scores and outcomes. First, it is difficult to assign a causal interpretation to the estimated relationship between the score and outcomes. In particular, variation in the polygenic score may reflect differences in environments or parental investments rather than differences in genetic factors across individuals. Parents not only provide their children with genetic material, but also with the environments in which they are raised. It is therefore possible that higher polygenic scores could be associated with higher education and wealth largely through parental choices. We explore this point in greater detail when discussing our main findings.

Second, estimation error in the ${\widehat{\beta }}_j$ GWAS coefficients will generate measurement error in the polygenic score relative to a theoretical true genetic component A_i. In general, we expect this measurement error to attenuate the relationship between a polygenic score and an outcome.¹² As larger GWAS are conducted, the explanatory power of EA scores should in principle approach the theoretical upper bound, which is the heritability of educational attainment.

A third interpretational issue is related to functional form assumptions in the construction of polygenic scores. Polygenic scores like those in Equation 3 assume additively separable, linear relationships between SNPs and an outcome of interest. Of course, there may be nonlinearities and interactions between SNPs that would not be captured by this relationship. The presence of such departures from linearity may be one reason why polygenic scores tend to under-estimate the contribution of genetic factors relative to twins studies (Zuk et al., 2012).

Another concern is that associations between particular SNPs and an outcome of interest could reflect population stratification — that is, differences associated with characteristics of historical ancestry groups rather than biology at the individual level. For example, if a particular variant is more common in a specific ancestry group (e.g. Southern Europeans), then an observed association between this SNP and the outcome might reflect a combination of the biological function of the SNP and the common environment or social norms shared by this ancestry group. A common approach to control for such confounding effects is to include the first K principal components of the full matrix of SNP data in the GWAS control set X_i. In samples with ancestry differences, principal components have been shown to capture geographic variation, and therefore serve as controls for ancestral commonality (Price et al., 2006). Stated differently, the principal components help to control for ethnic background factors that would be absorbed by family fixed effects in research designs that exploit within-family variation. Unless otherwise noted, the first 10 principal components are always included in our empirical analyses.

A related concern is that GWAS results tend to best replicate in samples with a similar ancestral composition as the GWAS discovery sample. For this reason, we only consider individuals of genetic European ancestry as categorized by the HRS.¹³ The score that we study was constructed using results from a sample of individuals of European ancestry, and previous work has shown that polygenic scores based on GWAS of genetic Europeans lack predictive power, and in some cases can generate bizarre predictions, when applied to non-European sub-samples. For example, applying a polygenic score for height discovered on a sample of individuals of European descent predicts very low average height relative to the observed distribution if applied to individuals of African descent (Martin et al., 2017).¹⁴ It would thus be inappropriate to use this polygenic score for education to make predictions about individuals who are not of European descent.

3. The HRS Sample and Key Economic Variables

This section describes the definition of our analytic sample and the construction of key variables used in our analyses. We also address possible issues that arise from sample selection. Alternative samples and variables are discussed alongside the presentation of our main results in Section 4, although we note here that our main results are robust to a host of reasonable alternatives.

3.1. Sample Construction

The Health and Retirement Study (HRS) is a longitudinal study that follows Americans over age 50 and their partners. Surveys began in 1992 and occur every two years. The HRS collected genetic samples from just under 20,000 individuals over the course of four waves (2006, 2008, 2010, 2012). Our sample includes only those genotyped in the 2006 and 2008 waves, since the polygenic score we use has not yet been constructed for the 2010 and 2012 waves.

Our main analysis sample includes all households with at least one individual classified as a genetic European by the Health and Retirement Study. We drop households in which any member self-identifies as non-white. We further restrict our sample to include only retired households in years 1996, 1998, and 2002–2010.¹⁵ We also include only those households with one or two members, and exclude households where both members are of the same sex because such households may have faced unique circumstances during their primary wealth-accumulation years. Finally, to minimize selection bias related to mortality, we include only household-year observations in which both members are between 65 and 75 years old. Our restriction aims to balance concerns about measurement error in wealth with concerns about selection biases that arise if too many observations are excluded from the analysis. The resulting analytic sample includes 2,590 households and 5,701 household-year observations, with responses supplied for an average of 2.2 waves.

3.2. Education and Income

Table 1 provides summary statistics for key variables used in the main analyses. On average, the men in the sample were born two years before the women. While the mean years of education is similar for both men and women, the standard deviation is larger for men. Relatedly, men are more likely to have both high degree outcomes (College, MA, and Professional Degrees), and low degree outcomes (No Degree, GED).

Table 1:

Summary Statistics

Variable	Mean	SD	N
Year of Birth
Female	1935.10	5.59	2369
Male	1933.04	5.76	2015
Years of Education
Female	12.67	2.30	2369
Male	12.74	2.96	2015
Highest Degree
Female
No Degree	0.16	0.37	2369
GED	0.04	0.19	2369
High School Degree	0.60	0.49	2369
Some College	0.04	0.19	2369
College Degree	0.10	0.30	2369
MA	0.05	0.22	2369
Professional Degree	0.01	0.09	2369
Male
No Degree	0.19	0.39	2015
GED	0.06	0.24	2015
High School Degree	0.47	0.50	2015
Some College	0.03	0.18	2015
College Degree	0.13	0.34	2015
MA	0.08	0.27	2015
Professional Degree	0.04	0.18	2015
Household Income (× $1,000)
Mean	2,315.95	.	2377
Std. Dev.	1,405.43	.	2377
Avg. Years Top-Coded	12.67	.	2377
25th Percentile	1,287.80	.	2377
50th Percentile	2,255.30	.	2377
75th Percentile	3,082.30	.	2377
Household Wealth (× $1,000)
Mean	900.17	.	5621
Std. Dev.	1,411.22	.	5621
10th Percentile	168.74	.	5621
25th Percentile	303.82	.	5621
50th Percentile	593.64	.	5621
75th Percentile	1,031.48	.	5621
90th Percentile	1,706.83	.	5621
Median, No Housing	450.49	.	5621
Median, No Pensions	235.98	.	5621
Median, Neither	92.00	.	5621

Notes: Summary statistics for birth year, schooling, and highest degree completed are calculated separately for males and females. Income and wealth are computed at the household level. Additional statistics are found in Tables S1–S6 in the Appendix.

Labor income is computed at the household level. Our primary source of earned income data comes from the Respondent Cross-Year Summary Earnings data set in the HRS. These data link individuals in the HRS to income data available through the Master Earnings File (MEF) maintained by the Social Security Administration (SSA). The MEF is constructed using data from employers’ reports as well as Internal Revenue Service records including W-2 forms and other annual tax figures. The data include regular wages and salaries, tips, self-employment income, and deferred compensation (Olsen and Hudson, 2009).¹⁶ The Respondent Cross-Year Summary Earnings provides annual MEF income totals for individuals over the period 1951–2013.

Our baseline income measure is the sum of all earned income in the MEF associated with a household for all available years through 2010, converted to 2010 dollars. This may include earnings from deceased spouses that are not directly observed in the HRS.¹⁷ Table 1 summarizes the distribution of lifetime household income. The median household earned a total of $2.26 million. Lifetime income has a mean of just over $2.3 million with a standard deviation of just over $1.4 million.

One shortcoming of the SSA income data is that it is top-coded at the maximum taxable amount for Social Security payroll taxes. Table 1 shows that, on average, a household has over 12 years in which labor income is top-coded for at least one household member. As a partial solution, in cases where earnings are top-coded, we use Current Population Survey (CPS) data to impute the mean income for people earning at least the top-coded level in that year for the period 1961–2010 (Ruggles et al., 2018). In Section 4, along with our main results, we discuss the robustness of our results to alternative income measures, including self-reported HRS income variables that are not top-coded, but only record contemporaneous income.

3.3. Household Wealth

The HRS contains rich and detailed information on household wealth. Unfortunately, data related to household retirement wealth and stock market participation pose various challenges. Values of defined contribution plans from previous jobs are not asked in every wave; stock allocations in defined contribution plans are only asked in certain waves and only for plans associated with the current employer; and expected defined-benefit pension income is asked only of plans at the current employer. In some cases, such issues may be relatively unimportant. However, because this paper studies heterogeneity in wealth for elderly households, having a complete picture of retirement assets is of fundamental importance. While some data issues have no hope of being resolved, our sample comprises households for whom wealth data are most likely to be both accurate and comprehensive.

Our measure of total wealth is designed to encompass all components of household wealth. Our data include the present value of all pension, annuity, and social security income, which come from the RAND HRS income les, as well as the net value of housing (including primary and secondary residences as well as investment property), the net value of private businesses and vehicles, all financial assets including cash, checking accounts, savings accounts, CDs, stocks and stock mutual funds, bonds and bond mutual funds, trusts, and other financial assets, less the net value of non-housing debt. Each of these are taken from the RAND HRS wealth les.¹⁸ Further, we include the account value of all defined contribution retirement plans.¹⁹ We exclude the value of insurance policies from our wealth measure.²⁰ All monetary values are measured in 2010 dollars. Unless otherwise noted we winsorize the log of real total household wealth at the 1^st and 99^th percentiles.

We note that our measure of wealth includes both marketable securities, such as stocks which can be easily sold at publicly available prices, and non-marketable assets such as social security income. Our measure of wealth is therefore intended to capture the overall financial security of households rather than the market value of household assets. Our results are qualitatively unchanged if we limit household wealth to exclude retirement income and housing, which can be interpreted as the market value of households’ pure financial assets.

Table 1 also contains summary statistics that describe the distribution of household wealth across all household-year observations in our sample. Although the median value of wealth is roughly $593,640, the mean of $900,170 ($838,046 after winsorizing) indicates substantial skewness. Indeed, the 10^th percentile of wealth is $168,740, whereas wealth at the 90^th percentile is $1.7 million. The last three rows of Table 1 provide the median values of wealth after excluding housing and retirement accounts (defined contribution accounts as well as the present value of defined-benefit pensions and Social Security), separately, as well as their sum. The median value of wealth after excluding housing and pensions is approximately 15 percent of the baseline median. Additional details about the construction of the wealth and income measures, as well as summary statistics for the distribution of income, wealth, and other relevant variables are provided in Appendix A.

3.4. The EA Score in the HRS Sample

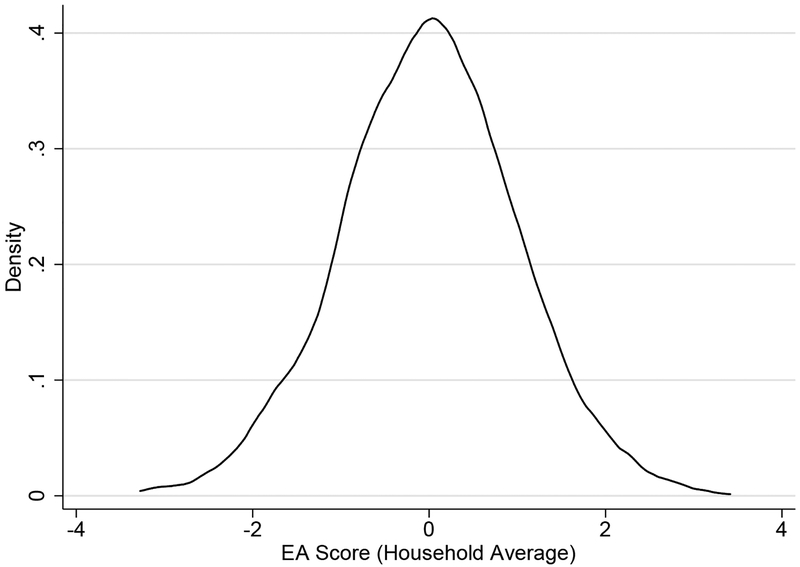
Since our unit of analysis is the household, we use the average EA score within households as our measure of genetic endowments. Hereafter, we use the term EA score to refer to the household average unless otherwise noted. Figure 1 plots the smoothed distribution of the EA score for our analytic sample. The score is normalized to have mean zero and variance of one, and is approximately normally distributed. Table 2 presents evidence of the raw relationships between the EA score and several key human capital measures and outcomes. Panel A of Table 2 presents the mean of education (years of schooling) and parental education, separately for men and women, by quartiles of the EA score distribution. Column [5] reports the difference between values in the first and fourth quartiles, while Column [6] reports the associated p-value. All three education measures are strongly and monotonically increasing in the EA score; women in the fourth quartile have nearly two more years of schooling than those in the first quartile, whereas men in the fourth quartile have nearly 2.4 more years than those in the first quartile. We again note that HRS data were not used in the construction of the score, so the relationship between the EA score and education documented in Table 2 constitutes an out-of-sample exercise. Similar patterns exist for parental education; individuals from households with higher EA scores tend to have parents with more education.

Figure 1:

Distribution of Household Average EA Score

Table 2:

Household EA Score Related to Key Economic Variables

	[1]	[2]	[3]	[4]	[5]	[6]
	Q1	Q2	Q3	Q4	Q4–Q1	Q4–Q1 p-value
Panel A
Avg. Household EA Score and Individual Variables
Female:
Education	11.73	12.19	13.02	13.71	1.99	< 0.01
Father’s Education	8.66	8.99	9.82	10.63	1.97	< 0.01
Mother’s Education	9.34	9.48	10.37	10.62	1.28	< 0.01
Male:
Education	11.58	12.23	13.17	13.96	2.38	< 0.01
Father’s Education	8.59	9.01	9.65	10.47	1.89	< 0.01
Mother’s Education	9.10	9.66	10.27	10.62	1.53	< 0.01
Panel B
Avg. Household EA Score and Household Variables
Avg. HH Income (in $1000)	2,132.02	2,260.31	2,361.22	2,513.39	381.37	< 0.01
Avg. HH Wealth (in $1000)	603.87	771.27	909.93	1,082.24	478.36	< 0.01

Notes: This table relates the EA score to key economic variables. Columns [1]-[4] separate individuals into quartiles of the individual EA score distribution and report average values of own and parents’ education, separately for males and females, for the genotyped individuals belonging to a household in the sample. Column [5] reports the difference in average values between the fourth and first quartiles, while Column [6] displays the p-value associated this difference. Panel B conducts a similar exercise for household wealth and income.

3.5. Sample Selection

We highlight two possible sources of selection bias in our sample: a) selection into genotyping, and b) selection based on retirement behavior and mortality outcomes. Appendix A provides summary statistics on differences between genotyped and non-genotyped HRS respondents. On average, genotyped individuals belong to older birth cohorts. Moreover, women and individuals with more education are more likely to agree to the collection of genetic data. Genotyped men, and individuals with lower levels of educational attainment may also be positively selected on unobserved factors that increase the likelihood of agreeing to the collection of biological data. If higher levels of education are associated with greater rates of participation, individuals with low EA scores who are genotyped may have higher than average values of other human capital traits. This form of selection bias could attenuate positive associations between the EA score and education or other related outcomes in our sample.

A second source of selection bias is linked to the criteria for inclusion in our sample. We limit our sample to retired households because defined benefit pension flows are important components of wealth for many households in the HRS, and they can only be measured for households that are retired and drawing these benefits. Including younger (non-retired) households would increase the size of our sample, but would introduce more measurement error in household wealth. However, restricting the sample to retired households may introduce selection bias if the EA score is associated with the timing of retirement.

In Table 3, we assess selection in our analytical sample by examining the relationship between the EA score and demographic characteristics that should be uncorrelated with the score in the absence of sample selection. Specifically, we divide individuals into quartiles based on their individual EA scores and report the fraction of males, average birth year, and average age for each quartile. Sex and birth year are measured cross-sectionally, while we include all person-year observations when calculating statistics for age. In Panel A we examine these patterns in our analytical sample, which includes all retired households with members aged 65–75. We indeed find selection on all three demographic variables. High EA individuals (fourth quartile) are 4.5% more likely to be male than low EA score individuals (first quartile). Because the SNPs used to construct the EA score are not found on sex chromosomes, the slightly higher representation of men in the fourth quartile of the EA score must result from selection. We also note that higher EA score individuals are more likely to belong to older birth cohorts, and are more likely to be observed at old ages. These age and cohort differences are likely to arise if individuals with higher EA scores live longer on average (which we explore in Section 5), and are therefore more likely to survive to be genotyped and less likely to die and exit the panel. While these differences are statistically significant, they appear to be modest in size. The average difference in birth year between the fourth and first quartiles is 1.2 years, while the average differences in age is 0.33 years.

Table 3:

EA Score and Selection

	[1]	[2]	[3]	[4]	[5]	[6]
Individual EA Score and Individual Variables	Q1	Q2	Q3	Q4	Q4–Q1	Q4–Q1 p-value
Panel A: Retired Households, Ages 65–75 (Main Sample)
Male	0.38	0.41	0.41	0.43	0.045	0.057
Birth Year	1935.19	1934.65	1934.28	1934.00	−1.19	< 0.01
Age	69.96	70.05	70.09	70.29	0.33	< 0.01
Panel B: Retired Households, Ages 55–85
Male	0.38	0.39	0.41	0.42	0.04	0.049
Birth Year	1934.89	1934.65	1933.30	1932.90	−1.98	< 0.01
Age	70.89	71.13	71.85	72.31	1.42	< 0.01
Panel C: All Households, Ages 50–75
Male	0.42	0.43	0.42	0.44	.026	0.13
Birth Year	1939.98	1939.64	1939.17	1939.31	−0.68	0.02
Age	63.64	63.40	63.62	63.43	−0.22	0.05
Panel D: All Households, Ages ≤ 85
Male	0.40	0.41	0.41	0.43	0.02	0.12
Birth Year	1938.56	1938.22	1937.28	1937.39	−1.17	< 0.01
Age	65.65	65.83	66.35	66.36	0.72	< 0.01

Notes: This table assesses the relationship between the EA score and gender, birth year and age in alternate samples. Columns [1]-[4] separate individuals into quartiles of the individual EA score distribution and report average values of demographic variables for each quartile. Column [5] reports the difference in average values of each variable between the fourth and first EA quartiles, while Column [6] reports the p-values associated with these differences. In Panel A, we consider our baseline sample of retired households with members aged 65–75. In Panel B, we report statistics for a larger sample that includes retired households with members aged 55–85. In Panel C, we consider a sample that includes all households (retired and non-retired households) with members aged 50–75. Panel D includes all households with members aged no more than 85.

The remaining panels of Table 3 display selection patterns for alternate samples. Panel B considers a sample of retired households with a wider range of ages (55–85). In this larger retired sample, there are substantially greater birth year and age differences between high and low EA score individuals compared to our analytical sample in Panel A. Panels C and D examine patterns among samples that include all households regardless of retirement status, for different age ranges (50–75 and ≤ 85, respectively). As one would expect, the samples that include all households feature smaller differences in these characteristics across EA score quartiles. However, the magnitudes of these differences are similar and relatively modest across alternate samples. Restricting our sample to retired households balances concerns about sample selection and measurement error.

4. The EA Score and Wealth

4.1. Main Association

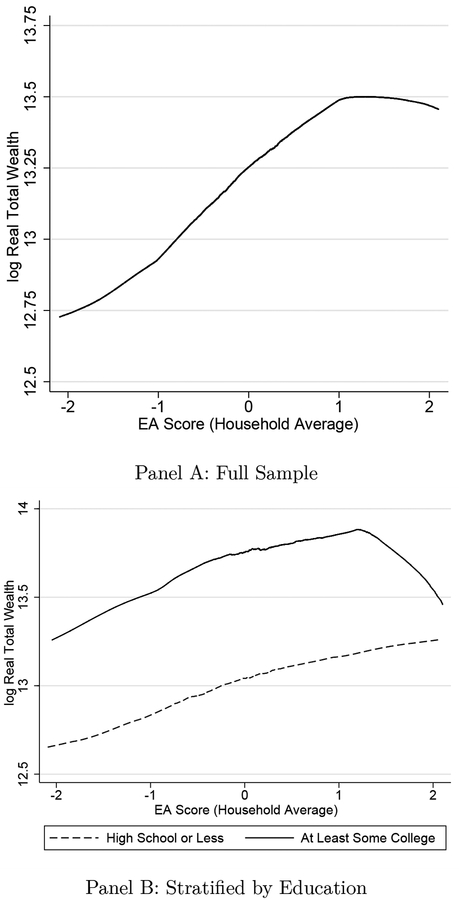
Figure 2 provides visual evidence of the association between the EA score and wealth. The top panel of Figure 2 plots the unconditional, nonparametric (Lowess) relationship between the log of total household wealth and the average household EA score in our sample. The relationship between the EA score and wealth is increasing for normalized values of the EA score between −2 and 1 (over 80% of the sample), although it flattens and even declines somewhat after an EA score of 1. The size of the wealth differences are economically large; moving from an EA score of −1 to 1 implies a change in log wealth of approximately 0.48, or the equivalent of over $200,000.

Figure 2:

Notes: Panel A plots average household EA score versus log household wealth using data for all household-year observations in the analytic sample. Panel B plots the same relationship for two subsamples of households, the first with a maximum education level of a high school degree or less and the second with at least one member having at least a college degree.

The second panel of Figure 2 examines whether the relationship between the EA score and wealth holds within education groups. We plot the relationship separately for households in which at least one member has at least some college, and those in which all members have at most a high school degree. In both education subsamples, the relationship between the EA score and wealth is positive and substantial for EA scores between −2 and 1. For values of the EA score greater than 1 the relationship becomes at (or even negative) for more educated households.

Panel B of Table 2 presents the (unconditional) mean of both total household income and household wealth for each EA score quartile. While total labor income is a cross-sectional measure with at most one observation per household, households may contribute multiple household-year observations for wealth. Panel B establishes our first main result: household wealth is strongly increasing in the EA score. A household in the fourth quartile of the household-average EA score has over $475,000 more wealth in retirement than those in the first quartile. The EA score also exhibits a large and statistically significant relationship with household income; households in the first quartile earned $2.13 million over their working lives compared to $2.51 million for those in the fourth quartile.

Figure 2 and Table 2 offer compelling evidence that the EA score and wealth are positively associated. We examine this relationship more formally in Table 4, which reports results from regressing log household wealth on the EA score for specifications with various sets of controls. Standard errors are clustered at the family level.²¹ Column [1] shows the unconditional relationship between the EA score and the log of household wealth with no additional covariates. A one standard deviation increase in the EA score is associated with 24.6% greater wealth, and this result is highly statistically significant. In Column [2], we add basic controls for age (separately for males and females in each household), birth year (separately for males and females), sex of the financial respondent, calendar time, and family structure.²² Throughout the paper, these constitute our standard controls. The inclusion of standard controls has only a modest effect on the coefficient on the EA score, which remains large and highly significant. In Column [3], we include the first 10 principal components of the genetic data and allow coefficients to vary for male and female household members.²³ These variables are intended to approximate family fixed-effects as explained in Section 2 (Benjamin et al., 2012). The principal components reduce the EA score coefficient from 0.221 to 0.218, and it remains statistically significant.

Table 4:

Average Household EA Score and Household Wealth

Dep. Var: Log Wealth	[1]	[2]	[3]	[4]	[5]	[6]	[7]
EA Score	0.246*** (0.022)	0.221*** (0.020)	0.218*** (0.020)	0.085*** (0.021)	0.070*** (0.023)	0.179*** (0.020)	0.047** (0.022)
Male Educ				0.061*** (0.009)
Female Educ				0.122*** (0.010)
Log Income						0.316*** (0.039)	0.263*** (0.038)
Obs.	5621	5621	5621	5621	5621	5308	5308
R2	0.054	0.251	0.279	0.368	0.435	0.349	0.479
Standard Controls		X	X	X	X	X	X
Principal Comp.			X	X	X	X	X
Years of Educ.				X
Full Educ. Controls					X		X

Notes: This table presents estimates from regressions of log household wealth on average household EA score and varying sets of controls. Column [1] includes no controls. Column [2] includes controls for age, birth cohort, sex of respondent, and calendar year, as described in Section 4.2. Column [3] adds controls for principal components of the genetic data for genotyped household members. Column [4] adds years of education separately for both female and male household members. Column [5] replaces the two schooling variables with our full set of education controls (dummies for years of education, degree dummies and interactions as described in Section 4.2). Column [6] includes the log of total household income, but excludes any controls for education. Column [7] includes our full set of controls including the detailed education variables and the log of total household income. Significance stars ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.10 levels, respectively. Standard errors are clustered at the family level.

In Column [4] of Table 4 we add controls for years of schooling for each member of the household. Including years of schooling significantly reduces the size of the gene-wealth gradient, decreasing the coefficient to 0.085. This is unsurprising; the EA score was developed based on years of schooling, and education undoubtedly affects income and wealth accumulation over the life cycle. It is important to note, however, that the coefficient remains statistically and economically significant even after controlling for years of schooling. A coefficient of 0.085 suggests a one standard deviation increase in the genetic score is associated with approximately 8.5% greater wealth during retirement. In Column [5], we include more flexible measures of education. Instead of the simple count of years of schooling for each member, we include the following: a complete set of dummy variables for each year of schooling for the male household member, dummies for every highest completed degree for the male household member, interactions between all male education dummies and an indicator for male-only households, an identical set of dummies for the female household member, and a full set of interactions between the male and female years of schooling dummies and degree dummies. We refer to this set as “full education controls”. Including the full set of education controls reduces the EA score coefficient to 0.070. Even in this specification the coefficient remains highly statistically significant.

In Column [6], we include the standard controls and principle components and add controls for labor income. In particular, we include the total of lifetime earnings for the household from the SSA data described in Section 3. Controlling for income reduces the coefficient on the EA score from 0.218 to 0.179, which remains statistically significant. In Column [7], we add the full set of education variables along with income and other controls. The results are consistent with Columns [5] and [6]. The coefficient on the EA score is 0.047, (p-value = 0.03), suggesting that a one standard deviation increase in the EA score is associated with 4.7% greater wealth.

Table 4 indicates that the EA score is associated with wealth even after controlling flexibly for completed schooling and degree type. One interpretation of this result is that the score measures genetic traits that promote wealth independently of any effects on the acquisition of human capital. However, it could also be that the education variables in the HRS are measured with error, or do not fully reflect the educational investments associated with genetic factors. If so, then the remaining genetic gradient in Column [7] may simply result from the effects of unobserved human capital investments rather than genetic factors. In particular, our control set does not include measures of school quality, which has been studied as a potentially important dimension of educational investment (Behrman and Birdsall, 1983).²⁴

Given results linking higher quality teachers to higher adult earnings (Chetty, Friedman, and Rockoff, 2014), observed lifetime earnings may contain information about the quality of schools that an individual attended. Since controlling for lifetime earnings attenuates the relationship between the EA score and wealth, higher values of the polygenic score may be associated with access to better quality schooling. However, controlling for lifetime income causes the coefficient on the polygenic score to shrink by at most one third, leaving a substantial unexplained gradient. Nonetheless, measurement error in income is still a concern. It may be that complete measures of income that do not suffer from top-coding or reporting biases fully account for the gene-wealth gradient once education (even improperly measured) is included. While we assess the robustness of our results to various income specifications below, the reader should interpret our results with these potential measurement issues in mind.

4.2. Robustness

Figure 2 and Table 4 show a strong, economically large relationship between the average household EA score and household wealth. In Table 5, we provide results from alternative specifications that address three potentially important choices in the formation of our main sample: the use of the average household EA score, the restriction to retired households, and the use of income data from the SSA. For each, we repeat the specifications in Columns [5] and [7] from Table 4.

Table 5:

Average Household EA Score and Household Wealth: Robustness

Dep. Var: Log Wealth	[1]	[2]	[3]	[4]	[5]	[6]
FR EA Score	0.083*** (0.025)	0.070*** (0.025)
Non FR EA Score	0.023 (0.023)	0.019 (0.022)
Avg. EA Score			0.079*** (0.018)	0.057*** (0.018)	0.071*** (0.025)	0.044* (0.023)
Log Income (SSA)		0.211*** (0.056)		0.284*** (0.029)		0.197*** (0.038)
Log Income (HRS)						0.221*** (0.030)
Obs.	1927	1870	18925	17563	3993	3833
R2	0.476	0.507	0.358	0.387	0.454	0.512
Include Non-Retired HH			X	X
Standard Controls	X	X	X	X	X	X
Principal Comp.	X	X	X	X	X	X
Full Educ. Controls	X	X	X	X	X	X

Notes: This table provides estimates from three different robustness checks. In each case, log household wealth is the dependent variable and we only show results analogous to estimates in Columns [5] (with the full set of education controls) and [7] (full set of education controls and log income) of Table 4. Columns [1] and [2] provide estimates from models where we condition on two EA scores per household, that of the financial respondent (FR) and of the non financial respondent (NFR). Columns [3] and [4] provide estimates from models where we have increased the sample to include non-retired households. Columns [5] and [6] provide estimates of models that include two measures of income, the SSA lifetime income measure used in our main analyses, along with the HRS measure of contemporaneous household income. Significance stars ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.10 levels, respectively. Standard errors are clustered at the family level.

Our measure of genetic endowments is the household average EA score. Averages can mask important differences across households depending on the degree of assortative mating and the structure of intra-household decision-making. In Appendix B, we find modest evidence of assortative mating; couples’ EA scores are correlated with a coefficient of ρ = 0.137, although we cannot reject random matching once we condition on education.

If EA scores are not highly correlated across individuals within a household, this raises the question of whose score matters. The intra-household division of tasks and financial decision-making may have a meaningful effect on our results. A reasonable hypothesis is that an individual’s EA score should matter more if they assume more financial responsibility within the household. In Columns [1] and [2] of Table 5, we replace the average household EA score with separate individual scores for the financial respondent (FR), who answers financial questions on behalf of the household, and non-financial respondent (NFR). The average individual EA score for the FR is 0.09, while it is −0.04 for the NFR, suggesting modest differences between the EA scores of the FR and NFR. If, for example, the FR has sole responsibility for the financial decisions of the household, the FR’s EA score may have a larger association with wealth than the household average score. Alternatively, complementarities would imply that conditional on the FR’s EA score, a higher EA score of the NFR could also associate with greater wealth.²⁵ Columns [1] and [2] show that the FR score is more predictive than the NFR’s score. While the coefficient on the NFR score remains positive even conditioning on the FR score (0.023 and 0.019 for the two specifications, respectively), it is statistically indistinguishable from zero at conventional levels. In other words, once we condition on household income and both spouses’ education along with the FR score, the NFR score no longer predicts household wealth.

In Columns [3] and [4] of Table 5, we relax the retirement requirement and include both retired and non-retired households. For non-retired households with defined-benefit pensions, economic resources are understated since we do not include expectations of future defined-benefit income. Compared to individuals in our main analytic sample, this sample includes individuals that are younger, more highly educated (by at least a third of a year of schooling for both men and women) and exhibit higher lifetime income ($2.4 million versus $2.3 million for our baseline sample). The coefficients on the EA score in columns [3] and [4] are 0.079 and 0.057, similar to our main results in Table 4, and remain highly statistically significant. This suggests our restriction to retired households is not an important factor driving the relationship between the EA score and wealth. Nonetheless, we maintain the retirement restriction for our main sample to ensure completeness of the wealth data and to facilitate our analysis of the gene-wealth gradient within defined-benefit pension participation in Section 5.

Finally, in Columns [5] and [6], we consider the log of the household’s average self-reported labor income in the HRS as an additional control.²⁶ For this specification, we necessarily restrict the sample to households that are ever observed in the HRS with at least one working member, since this is required to obtain an in-sample measure of total income. The self-reported income data in the HRS are not subject to top-coding like the SSA data. However, because the HRS is a sample of elderly Americans, this necessarily means that HRS labor income is observed toward the end of the life-cycle or not at all. These differences are meaningful. Average annual household income in our sample based on HRS data is $57,769 and the correlation coefficient between the log of this HRS average and the log of total income using SSA data is 0.32. Column [5] presents the coefficient on the EA score once we restrict the sample to households with non-missing HRS income. The results in Column [6] indicate that both the SSA and HRS income variables independently predict wealth. Nevertheless, the estimated coefficient on the EA score is 0.044 (p-val = 0.058) when both income measures are included — similar to the baseline estimates in Column [7] of Table 4.

In Appendix C we provide numerous robustness tests for the main association between the EA score and wealth documented in Table 4. Additional summary statistics, including those relevant for this section and later analyses, are included in Appendix A.2. In separate analyses, we test the importance of sample selection by using HRS sampling weights, using only one household-year per sample, and by restricting analyses to only coupled households — i.e., those where two members are observed for at least one household-year observation. We also examine robustness to alternate sample definitions with different age restrictions, as well as those that include non-retirees. Additional specifications control for more complicated functions of household income, including the number of years with top-coded income, and use alternate definitions of household wealth that exclude retirement and housing wealth. We also examine robustness to the use of different versions of the EA score, and to the inclusion of more extensive controls including cognitive ability, number of children, the death of a household member, and years since retirement. Generally, results in Table 4 are robust to these exercises.

4.3. Transfers and Parental Education

A likely candidate to explain the remaining portion of the gene-wealth gradient is parental transfers that are not captured by completed education or earned income. Individuals inherit their genetic material from their parents, and those parents shape childhood environments. Thus, differences in the EA score could reflect not only differences in genetic factors that promote educational attainment but also environmental factors that affect education and other outcomes regardless of one’s genes. As evidence of this possibility, Lee et al. (2018) find that associations between SNPs and educational attainment tend to be smaller using only within-family variation as opposed to within and across family variation. Moreover, Kong et al. (2018) show that even those SNPs carried by parents that are not passed on to children are correlated with children’s outcomes, presumably through parental environments. Indeed, one of the largest challenges in interpreting variation in the EA score comes from gene-environment correlations. An important limitation of our analyses is that we are not able to cleanly separate the association between the EA score and wealth into genetic and environmental components.

In Table 6, we examine the extent to which the transfer of resources from parents to children — either indirectly through more advantageous environments as proxied by parental education, or directly through monetary bequests — can explain the gene-wealth gradient.²⁷ Roughly 40% of households report receiving an inheritance and among those who do, the average amount is approximately $160,617. Average fathers’ and mothers’ education for the household are 9.47 years and 9.95, respectively.

Table 6:

Inheritances and Parental Education

Dep. Var: Log Wealth	[1]	[2]	[3]	[4]
EA Score	0.070*** (0.023)	0.064*** (0.022)	0.062*** (0.023)	0.058** (0.023)
Any Inheritance		−1.042*** (0.172)		−0.990*** (0.171)
Log Total Inheritance		0.121*** (0.016)		0.116*** (0.016)
Father Education (Male)			0.009 (0.007)	0.007 (0.007)
Father Education (Female)			0.021*** (0.007)	0.019*** (0.007)
Mother Education (Male)			0.014* (0.007)	0.010 (0.007)
Mother Education (Female)			−0.009 (0.007)	−0.012 (0.007)
Obs.	5621	5621	5621	5621
R2	0.435	0.456	0.442	0.461
Standard Controls	X	X	X	X
Principal Comp.	X	X	X	X
Years of Educ.	X	X	X	X
Full Educ. Controls	X	X	X	X

Notes: This table presents estimates from regressions of log household wealth on average household EA score and varying sets of controls. Column [1] includes the full set of controls from Column [5] of Table 4. Column [2] includes an indicator for ever receiving an inheritance in the HRS, as well as the log of received inheritances (set to 0 for those without an inheritance). Column [3] includes controls for parents’ years of education, along with separate dummy variables indicating missing values for each of the four parental education variables. Column [4] includes both the inheritance variables and the parental education variables. Significance stars ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.10 levels, respectively. Standard errors are clustered at the family level.

In Column [1] of Table 6, we provide a baseline specification that repeats Column [5] of Table 4 and includes the standard controls, principal components, and full education controls. In Column [2], we include an indicator for ever receiving an inheritance in the HRS data, and the log of total inheritances received by all members of the household while in the HRS. The log inheritance variable is set to zero for households that do not receive an inheritance. As expected, inheritances are highly correlated with household wealth. However, the inclusion of inheritances changes the coefficient on the EA score only marginally, from 0.070 to 0.064. Next, we include years of schooling for each parent of each member of the household, along with a set of dummy variables indicating missing values for these variables. The education of the father of the female member of the household appears to be related to wealth, but the inclusion of parental education as a control once again reduces the coefficient on the EA score only slightly. In Column [4], we include both parental education controls and the log of the sum of lifetime inheritances. The inclusion of the full set of proxies for parental investments reduces the coefficient on the EA score to 0.058, implying a one-standard deviation increase in the EA score increases total wealth by 5.8%, and remains statistically significant at the 5% level.

The results in Table 6 show that the remaining portion of the gene-wealth gradient does not fall substantially when we include additional parental background variables intended to capture direct and indirect transfers. It may be the case that parental investments are largely captured by respondents’ completed education and labor income. These results suggest that the EA-score wealth correlation may in part be driven by additional mechanisms not examined in this section. We address potential alternative mechanisms in the following section.

5. Additional Mechanisms

This section considers possible channels beyond income, education and parental transfers through which the EA score may relate to wealth. Specifically, we investigate risk aversion, mortality (which could affect savings), and investment decisions such as stock market participation, home ownership, and business ownership. We also consider how the EA score relates to different dimensions of financial decision-making, including beliefs about macroeconomic events and reported planning horizons. Finally, we show differences in the gene-wealth gradient depending on whether individuals receive income from defined-benefit pensions. A complete set of summary statistics for each potential mechanism are provided in Appendix A, but we provide means when analyzing each potential mechanism below. We also provide means for outcome variables in each corresponding table.

5.1. Mortality

One way in which wealth may be related to genetic endowments is through longevity, which has been shown to be correlated with genetic variants linked to education (Marioni et al., 2016). If individuals with higher individual EA scores expect to live longer, they may endogenously save more to finance these additional years of consumption. Furthermore, longer expected lives may lead to longer investment horizons, which may affect the mix of assets in household portfolios. We therefore examine whether the score is associated with realized and expected longevity in our sample. We forgo a direct analysis of savings rates because the HRS consumption and expenditure data are only available for a small sub-sample of households, which may leave tests to detect differences in savings rates underpowered. Further, given the age of the sample, the data do not include the prime working (and saving) years of the household, which are likely the most informative for such an analysis.²⁸

The one-year mortality rate in our sample (excluding years before genotyping) is 0.04. The average subjective probability of living to 75 years old, for individuals in our analytic sample is approximately 67 percent. We begin our analyses by directly estimating the empirical relationship between the individual’s EA score and mortality. Since here we are studying individual mortality outcomes, we use the individual’s own personal EA score as opposed to the household average score. We construct an indicator variable equal to one if the individual dies in the next year, and estimate a linear probability model of the likelihood of dying in a particular year as a function of the individual’s EA score, the principal components, and dummy variables for age, birth year, years of schooling, and degree. We restrict this regression to person-years in which an individual was between the ages of 50 and 90, and we drop years before an individual was genotyped. Table 7 provides the results of this regression. In Column [1] we include both females and males in the sample, and find that a one standard deviation increase in the individual’s EA score is associated with a 0.3 percentage point decline in the one-year mortality rate. Columns [2] and [3] consider females and males separately. The estimated association for females implies a 0.5 percentage point decline in the mortality rate for every one-standard deviation increase in the EA score. We find no relationship for males.

Table 7:

Mortality

Dep. Var:	Observed Mortality			Exp. Mortality Pr(Live to 75)
	All Ind.	Females	Males	All Ind.	Females	Males
	[1]	[2]	[3]	[4]	[5]	[6]
EA Score	−0.003* (0.001)	−0.005*** (0.002)	0.000 (0.002)	0.418 (0.286)	0.659* (0.370)	−0.316 (0.482)
Obs.	26733	14780	7419	29119	17433	11686
R2	0.035	0.032	0.029	0.118	0.130	0.150

Notes: This table investigates the relationship between the EA score, mortality, and mortality expectations. Column [1] presents estimates of a linear probability model for death in the next period for all individuals in our sample, while Columns [2] and [3] perform this separately for females and males, respectively. The specifications in Columns [1]-[3] include the following controls: individual principal components and dummy variables for each possible age, birth year, number of years of schooling, and degree. In Columns [4]-[6], the outcome variable is the reported probability an individual expects to live to age 75, again shown for the full sample and then separately for females and then males. The control set for these specifications is the same as our standard full control set in Column [5] of Table 4. Significance stars ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.10 levels, respectively. Standard errors are clustered at the family level.

We also consider beliefs about mortality. In principle, objective mortality should only affect behavior if individuals expect to live longer. In this sense, beliefs about mortality are perhaps the more relevant mechanism linking genetic endowments to wealth. The HRS repeatedly asks individuals to provide their subjective beliefs for the probability that they will live to the age of 75. In Column [4], we regress this subjective belief on the individual EA score, our standard controls, and the full set of education controls in a sample of individuals aged 50–65. We do not find a significant association between the EA score and the level of this subjective probability. We also estimate this regression for females and males separately in Columns [5] and [6], and find that for females a one standard deviation rise in the individual’s EA score predicts a 0.66 percentage point rise in reported beliefs about living to age 75. For males, the relationship is negative and statistically insignificant. In total, we find a non-trivial relationship between the EA score and mortality rates, but no association with expected mortality. This may offer some evidence that part of the gene-wealth gradient arises from the prospect of greater longevity.

5.2. Risk Aversion

We next examine if the EA score is associated with differences in how households save. A well-established source of heterogeneity in household wealth is returns to risky endeavors, such as participation in risky asset markets or business ownership. One mechanism that may therefore relate the EA score to wealth is aversion to risk. To examine the relationship between risk aversion and the EA score, we use questions in the HRS designed to elicit measures of risk tolerance based on hypothetical income and wealth gambles. Generally, these questions pose hypothetical scenarios in which the respondent faces a choice between a guaranteed endowment of wealth or stream of income, or a 50–50 gamble that will result in a permanent increase or decrease in that endowment or income. Specifically, respondents are asked to choose between two jobs: “The first would guarantee your current total family income for life. The second is possibly better paying, but the income is also less certain. There is a 50–50 chance the second job would double your total lifetime income and a 50–50 chance that it would cut it by X.” The series replaces X with a set of possible income losses: ten percent, twenty percent, one-third, one-half, or seventy five percent. Additionally, respondents are asked one of two hypothetical wealth gambles with a similar structure. One is based on an inherited business worth one million dollars today, or that may be sold in one month with a 50–50 chance of being worth two million dollars or X. The other is based on an immediate inheritance worth one million dollars, with the potential to participate in a risky business venture that has a 50–50 chance of doubling in value or falling in value by X. In each case, X varies by the same proportions as the hypothetical income gamble.

Based on the responses to these hypothetical gambles, each respondent can be grouped by the smallest downside for which they still reject the gamble. We create a dummy variable for each gamble that takes a value of one if an individual always responds with a preference for the guaranteed wealth or income. A value equal to one for this variable indicates the highest degree of risk aversion permitted with this set of questions. 39% of respondents comprise the most risk averse households, who would not take a 50–50 gamble that would double their income or cut it by 10%. Alternatively, only 5% of respondents would take a 50–50 gamble where the downside is a 75% reduction in income.

In Column [1] of Table 8, the dependent variable is our binary indicator for the highest degree of risk aversion based on the labor income gamble. We find a negative association between the average household EA score and risk aversion — a one standard deviation increase in the score is associated with a reduction in the probability of the most risk averse response by 2.2 percentage points. In Columns [2] and [3], we use indicators for greatest risk-aversion based on the inheritance and business risk questions as the dependent variables. We find no statistically significant relationship between the EA score and risk aversion for the inheritance question, but do find that the probability of a respondent giving the most risk averse response for the business risk question is 2.7 percentage points lower for a one standard deviation increase in the EA score, which is significant at the 0.05 level.

Table 8:

Risk Aversion

Dep. Var:	Risk Aversion: Indicator			Risk Aversion categories
	Income	Inheritance	Business	Income	Inheritance	Business
	[1]	[2]	[3]	[4]	[5]	[6]
EA Score	−0.022*** (0.007)	−0.004 (0.012)	−0.027** (0.011)	−0.045*** (0.015)	0.017 (0.029)	−0.057** (0.027)
Obs.	10512	2951	2912	10512	2951	2912
R2	0.105	0.210	0.246
Mean outcome	0.39	0.51	0.47
Standard Controls	X	X	X	X	X	X
Principal Comp.	X	X	X	X	X	X
Full Educ. Controls	X	X	X	X	X	X

Notes: This table presents estimates from regressions of measures of individual risk tolerance on the EA score and various controls. Risk tolerance is elicited from questions based on risky gambles over labor income, inheritance wealth, and business wealth. In Columns [1]-[3], the dependent variable is an indicator that takes a value of 1 for individuals that never choose the risky option over a guaranteed outcome. In Columns [4]-[6] we report estimates from ordered probit models where the outcome is a categorical variable that takes one of six values depending on the riskiest gamble that an individual accepts, with higher values indicating greater risk aversion. Significance stars ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.10 levels, respectively. Standard errors are clustered at the family level.

In Columns [4]-[6], we allow the outcome variable to be an ordered categorical variable indicating the riskiest gamble that a respondent accepts. This variables can take one of six values, with higher values corresponding to higher degrees of risk aversion. We estimate an ordered probit model in these specifications, and report coefficients for the latent index. Column [4] shows that the EA score is associated with a significant decrease in the latent index for risk aversion for income. Columns [5] and [6] repeat the ordered probit estimation for the inheritance and business wealth gambles, respectively. Again, we find no statistically significant relationship between the EA score and risk aversion based on the hypothetical inheritance wealth gambles, but do find a significant relationship with risk aversion for the business wealth gamble.

5.3. Stocks, Housing, and Business Ownership

Motivated by the relationship between the EA score and elicited measures of risk aversion, we examine whether the EA score is related to stock market participation, business ownership, and owning a home. Each of these asset classes is the subject of a well-established literature highlighting their importance as a source of heterogeneity in wealth accumulation over the life-cycle. Eighty-four percent of households own a house, while 8% own a business and 46% own stocks.

Panel A of Table 9 regresses indicator variables for stock market participation, business ownership, and home ownership on the average household EA score and our full set of standard controls, including education variables. Columns [1]-[3] also include the log of total lifetime household income from the SSA data as an additional control. In Column [1] we find no statistically significant relationship between home ownership and the EA score, but we do find a significant relationship between home ownership and lifetime earnings. In Column [2] of Panel A, we find no relationship between business ownership and the EA score, nor between business ownership and lifetime labor income. Column [3], however, shows a strong positive association between the EA score and stock market participation. A one standard deviation increase in the EA score is associated with a 5.2 percentage point increase in the probability of owning stocks, and this coefficient is statistically significant at the 1% level. Compared to an average rate of stock ownership of 46%, the coefficient suggests this predicted increase in participation is also economically meaningful.

Table 9:

Average Household EA Score and Portfolio Decisions

Panel A Dep. Var:	Owns House	Owns Business	Owns Stocks	Owns House	Owns Business	Owns Stocks
	[1]	[2]	[3]	[4]	[5]	[6]
EA Score	0.003 (0.008)	0.005 (0.006)	0.052*** (0.011)	−0.008 (0.008)	−0.001 (0.006)	0.040*** (0.011)
Log Income	0.033*** (0.008)	−0.004 (0.006)	0.062*** (0.011)	0.002 (0.008)	−0.021** (0.008)	0.021 (0.013)
Lagged Log Wealth				0.122*** (0.009)	0.047*** (0.007)	0.151*** (0.016)
Obs.	6460	6460	5450	4649	4649	4196
R2	0.304	0.160	0.348	0.399	0.217	0.435
Mean outcome	0.84	0.08	0.46	0.83	0.08	0.47
Standard Controls	X	X	X	X	X	X
Principal Comp.	X	X	X	X	X	X
Full Educ. Controls	X	X	X	X	X	X
Panel B Dep. Var: Log Wealth	[1]	[2]	[3]	[4]	[5]
EA Score	0.049** (0.023)	0.046** (0.021)	0.046** (0.022)	0.016 (0.021)	0.018 (0.019)
Owns Stocks				0.624*** (0.034)	0.507*** (0.029)
Has Business			0.594*** (0.049)		0.530*** (0.044)
Owns Home		0.887*** (0.054)			0.741*** (0.052)
Obs.	4912	4912	4912	4912	4912
R2	0.487	0.551	0.504	0.540	0.599
Standard Controls	X	X	X	X	X
Principal Comp.	X	X	X	X	X
Full Educ. Controls	X	X	X	X	X
Log Income	X	X	X	X	X

Notes: Panel A of this table presents estimates from regressions of indicators for ownership of different asset types on the EA score and various controls. Panel B presents estimates from regressions of log household wealth on the EA score, indicators for ownership of different asset types, and various controls. Significance stars ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.10 levels, respectively. Standard errors are clustered at the family level.

Of course, stock market participation is likely affected by accumulated wealth, which has already been shown to strongly correlate with the EA score. This suggests that the relationships between the EA score and stock market participation may operate purely through wealth. This possibility is addressed in Columns [4]-[6], which repeat the specifications in Columns [1]-[3] but also include the log of financial wealth from the previous wave. Consistent with the existing literature, we find that the coefficient on lagged wealth is large and statistically significant for all three asset types. We continue to find no evidence of a relationship between the EA score and home or business ownership after controlling for lagged wealth. However, the relationship between the EA score and stock ownership remains significant and economically meaningful after controlling for lagged wealth. A one standard deviation increase in the EA score is associated with a 4 percentage point higher likelihood of owning stocks, with statistical significance at the 1% level. Because stocks have traditionally offered substantially higher returns than other liquid securities such as money-market funds or bonds, this may be an important factor for explaining the gene-wealth gradient, and may also suggest that these genetic endowments provide a microfoundation for the persistent differences in returns to wealth.

To examine the extent to which the important components of household saving — home, business, and stock ownership — can be possible explanations for the association between the EA score and wealth, we include each in regressions of wealth on the EA score and our standard controls. Column [1] of Panel B in Table 9 establishes the baseline coefficient by repeating the final specification in Table 4, but restricting the sample to those households with non-missing values for the asset ownership variables. In Columns [2] and [3], we include indicator variables for whether the household owns their home or has ever owned a business during the sample. In both cases, the coefficient on the EA score declines to 0.046, but remains statistically significant at the 5-percent level.

In Column [4] of Table 9, we include an indicator for stock ownership. This reduces the coefficient on the EA score substantially, from 0.049 to 0.016, a reduction of roughly 67%. Further, the coefficient becomes statistically insignificant. This suggests that stock market participation may be an important explanatory factor for the gene-wealth gradient. However, we caution against over-interpreting this result; in other samples with less severe age and retirement restrictions, the coefficient on the EA score is larger and remains statistically significant when stock market participation is controlled for, suggesting that stock market participation is likely to be only one of potentially many relevant factors explaining the relationship between the EA score and wealth.

Finally, in Column [5], we include all three investment controls simultaneously. Together, they reduce the coefficient on the EA score to 0.018, which is not statistically significant. This offers preliminary evidence that investment decisions over the life-cycle, broadly defined, may be an important mediator of the gene-wealth gradient. We again emphasize that these results should be interpreted with care. For example, the empirical specifications in Panel B of Table 9 may be biased by measurement error in the right-hand-side variables. However, these results may be suggestive of possible relevant mechanisms relating the EA score to wealth. Motivated by these findings, we next evaluate the extent to which the EA score is related to financial decision-making.

5.4. Extreme Beliefs and Planning Horizons

An important element of financial decision-making is an assessment of the risks and uncertainties associated with the macroeconomy and the payoffs to alternative financial choices. Yet, inferring the likelihood of uncertain events can be difficult. Despite the typical assumption of rational expectations, it has long been recognized that individuals may have trouble forming accurate beliefs about probabilistic outcomes (Savage, 1954; Kahneman and Tversky, 1972). Further, a well-documented challenge for prudent savings and investment decisions is the complexity associated with intertemporal choices. Thinking about the distant future is difficult; as the planning horizon increases so too does the uncertainty around financial needs, investment and employment opportunities, family composition, and a host of other important considerations. In this section, we evaluate whether the EA score is associated with an aptitude for abstract and complicated financial decisions.

Recent literature examines the role of subjective expectations in economic decisions such as human capital investments (Wiswall and Zafar, 2015) and stock market participation (Arrondel, Calvo Pardo, and Tas, 2014). Another set of papers demonstrates links between subjective beliefs and investment behaviors that impact household wealth (Lillard and Willis, 2001; Dominitz and Manski, 2007; Hudomiet, Kézdi, and Willis, 2011).²⁹ Lumsdaine and Potter van Loon (2017) study differences in how individuals report beliefs about stock market returns, arguing that their findings reflect heterogeneity in individuals’ understanding of the laws of probability. In related work Lusardi, Michaud, and Mitchell (2017) demonstrate that heterogeneity in returns to savings, which are plausibly determined by financial knowledge, can explain a substantial proportion of wealth inequality.

We begin by investigating whether the average household EA score is associated with differences in beliefs about macroeconomic events that are relevant for financial choices. The HRS data are uniquely well-suited for this analysis, as most respondents are repeatedly asked to provide subjective probabilities of a range of events. Individuals are asked to provide a probability on a scale of 0 to 100 for the following three macroeconomic events:

• Stock Market Goes Up: “By next year at this time, what is the percent chance that mutual fund shares invested in blue chip stocks like those in the Dow Jones Industrial Average will be worth more than they are today?”

• Economic Depression: “What do you think are the chances that the U.S. economy will experience a major depression sometime during the next 10 years or so?”

• Double Digit Inflation: “And how about the chances that the U.S. economy will experience double-digit inflation sometime during the next 10 years or so?”

First, we construct one (of possibly many) measures of “objectively correct” responses to these questions. Our objective benchmark probability for the stock market going up in a single year is 71 percent, which is the probability the S&P 500 increases in value in a given year for the period 1992–2015. There is no common definition of an economic depression, but clearly this refers to an unusually severe period of economic contraction. We use data from the Federal Reserve Bank of Saint Louis on annual real GDP growth over the period 1948–2016, and define an unusually severe contraction as a year with growth less than or equal to −0.73 percent, which is the 25th percentile of the distribution of growth rates for negative-growth years. Based on this metric, the unconditional probability of a severe contraction is 4.4 percent per year, which implies a 36 percent probability for such an event over a 10 year period. Finally, the Bureau of Labor Statistics reports two years with double digit inflation (1980, 1981) over the period 1958–2015. This implies an approximate probability of 3.4 percent for double digit inflation in any year, or about a 29 percent chance for double digit inflation over a 10 year period.³⁰

Panel A of Table 10 provides estimates of the association between the average household EA score and individual beliefs about the probabilities of these macroeconomic events. We use the average household score rather than the individual EA score so as to be consistent with our analysis in Section 5.3, and to avoid decisions about intra-household information transfers. Our first measure is the absolute value of the deviation between the respondent’s subjective probability and the objective probability. We regress this deviation on our standard controls and the EA score in Column [1]. For all three events, higher values of the polygenic score are associated with a statistically significant reduction in the deviation between the respondent’s subjective probability and the objective probability. For example, in Column [1] of Panel A, the coefficient estimate of −0.567 suggests that a one standard deviation increase in the EA score is associated with a reduction in the deviation from the objective stock market increase probability of over one half of one percentage point. Coefficients of −0.550 and −1.054 are estimated for the depression and double-digit inflation questions, respectively.

Table 10:

Extreme Beliefs and Planning Horizons

Panel A Dep. Var:	The EA Score and Beliefs
	Deviation	Prob=0	Prob=0.5	Prob=1
	[1]	[2]	[3]	[4]
Stock Market Goes Up
EA Score	−0.567*** (0.162)	−0.006*** (0.002)	−0.003 (0.003)	−0.002 (0.001)
Obs.	35842	35842	35842	35842
R2	0.097	0.062	0.030	0.048
Mean outcome	28.31	0.05	0.30	0.04
Depression
EA Score	−0.550*** (0.138)	−0.005** (0.002)	−0.003 (0.003)	−0.008*** (0.002)
Obs.	35912	35912	35912	35912
R2	0.088	0.047	0.037	0.072
Mean outcome	24.94	0.07	0.26	0.06
Double Digit Inflation
EA Score	−1.054*** (0.193)	−0.004** (0.002)	−0.005 (0.004)	−0.011*** (0.002)
Obs.	22604	22604	22604	22604
R2	0.080	0.057	0.044	0.072
Mean outcome	26.10	0.06	0.34	0.07
Panel B Dep. Var:	The EA Score and Planning Horizons
	PH≥ 1 Yr.	PH≥ Few Yrs.	PH≥ 5–10 Yrs.	PH> 10
	[1]	[2]	[3]	[4]
EA Score	0.008*** (0.003)	0.011*** (0.004)	0.013*** (0.004)	0.004 (0.003)
Obs.	27752	27752	27752	27752
R2	0.072	0.081	0.077	0.045
Mean outcome	0.87	0.75	0.45	0.11
Standard Controls	X	X	X	X
Principal Comp.	X	X	X	X
Full Educ. Controls	X	X	X	X

Notes: Panel A of this table presents estimates from regressions of beliefs about probabilities of three macroeconomic events on the EA score and various controls. Separate estimates are given for three distinct macroeconomic events: an increase in the stock market over the next year, a major depression in the next 10 years, and double-digit inflation in the next 10 years. In Column [1] the dependent variable is the absolute value of the deviation of the respondent’s belief from an “objective” probability (as described in Section 5.5). The outcome variables in Columns [2], [3] and [4] are indicators for providing subjective probabilities of 0, 0.5 and 1, respectively. Panel B presents estimates from regressions of indicator variables for the length of a respondent’s financial planning horizon on the EA score and various controls. In Column [1] the dependent variable is an indicator for reporting a planning horizon greater than or equal to one year. In Columns [2], [3] and [4], the dependent variables are indicators for horizons of “greater than or equal to a few years;” “greater than or equal to 5–10 years;” and “greater than 10 years,” respectively. Significance stars ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.10 levels, respectively. Standard errors are clustered at the family level.

Columns [2]-[4] of Panel A in Table 10 examine binary outcomes indicating whether respondents answered with specific focal probabilities (0, 50, and 100, respectively). Using linear probability models, we relate these binary outcomes to the EA score. For all three events, we observe the same pattern of association: the EA score is negatively associated with providing a subjective probability indicating complete certainty (0 or 100), and is largely uncorrelated with providing a focal probability of 50 percent. The magnitudes of these associations are substantial. For example, findings on beliefs about a depression suggest that a one standard deviation increase in the EA score is associated with a 0.5 percentage point reduction in the probability of reporting a 0% probability that the economy will suffer a major depression in the next 10 years. For comparison, 7% of individuals report a 0% probability for this event. While we find no statistically significant association between the EA score and reporting a 100% probability that the stock market will increase, we do find a relationship between 100% beliefs about economic recessions and double-digit inflation.

These results suggest that individuals from households with lower polygenic scores are more likely to report beliefs that are at odds with objective probabilities. Moreover, lower scores are also associated with a greater tendency to report extreme beliefs. We next investigate whether the EA score is associated with the length of the financial planning horizon. The complexity of economic decisions increases with their scope, and households may be heterogeneous in the costliness of thinking about increasingly distant future periods. Those for whom such considerations are relatively low-cost will endogenously consider longer horizons. The HRS asks respondents about their planning horizons for spending and saving: “In deciding how much of their (family) income to spend or save, people are likely to think about different financial planning periods. In planning your (family’s) saving and spending, which of the following time periods is most important to you (and your husband/wife/partner): the next few months, the next year, the next few years, the next 5–10 years, or longer than 10 years?” 13% of respondents report planning horizons of less than 1 year. 12% have a planning horizon of at least a year, but less than a few years. 30% have a planning horizon of a few years, 34% indicate horizons in the range of 5–10 years, and 11% have planning horizons of more than 10 years.

In Panel B of Table 10, we test whether the EA score predicts planning horizon responses. The dependent variable in Column [1] is a dummy variable equal to one if the planning horizon is greater than a few months. The estimated coefficient is statistically significant, and suggests that a one standard deviation in the EA score is associated with a 0.8 percentage point increase in the probability of reporting a planning horizon longer than a few months. Columns [2]-[4] repeat this exercise, but with dummies equal to one for increasingly longer horizons. The dummy dependent variable in Column [2] is equal to one if the reported horizon is “a few years”, in [3] if “5–10 years”, and in [4] if “longer than 10 years”. In all but Column [4], the coefficient on the EA score is positive and significant at the 1% level. This suggests that the EA score is predictive of longer planning horizons for all but the longest horizon.

The results linking the length of the planning horizon to the EA score are consistent with an interpretation that higher EA score households are better able to think about complex and abstract decision problems. Alternatively, these results could be interpreted as an association between the EA score and patience. However, in results available from the authors and using the HRS questions designed to elicit patience parameters, we find little variation between households that report the shortest and longest planning horizons. This suggests it is unlikely that the planning horizon results are due to patience. Gabaix and Laibson (2017) provide a theoretical foundation for our interpretation. They demonstrate that infinitely patient, Bayesian households that receive noisy, unbiased signals about future events will behave as if they are impatient. A consequence of their model is that households that receive more precise signals will appear to behave as if they are more patient than others, even though all households are equally (infinitely) patient.

In Appendix C, we provide several additional analyses. First, we use the cognitive test score administered to HRS respondents to evaluate whether the gene-wealth gradient works through cognition. In particular, we include the test score as an additional control and find that it does little to mediate the gene-wealth gradient. This is not surprising given why and how the test is constructed: to capture cognitive decline through memory tasks and simple factual questions. Second, it is possible that reported macroeconomic beliefs are not related to individual behavior in a meaningful way, making these results interesting but not particularly useful for understanding the potential underlying mechanisms linking the EA score to financial decisions. This would be the case if either the HRS expectations questions do a poor job of eliciting true beliefs about these economic events, or if the events themselves were not relevant for the household’s choice problem. In Appendix B, we show that these elicited beliefs do indeed predict relevant behaviors such as stock market participation, and are associated with wealth. Further, excessive optimism about the stock market is actually associated with greater wealth, likely due to an increase in participation. This suggests that the direction of incorrect beliefs is important for their overall impact on wealth.

5.5. Pensions

One consequence of the apparent relationship between genetic endowments and financial decisions is that individuals with low EA scores may benefit from outsourcing certain economic choices, such as saving and investment decisions. Defined benefit pensions, which may be provided by one’s employer, offer one form of outsourcing by providing an employee a guaranteed stream of income in retirement without requiring the individual to choose the contribution rate or underlying investment allocations. Defined benefit plans effectively reduce the impact of the household’s financial decisions on accumulated wealth by ensuring a minimal level of resources at retirement. We investigate whether the reduced autonomy associated with defined-benefit pensions alters the relationship between genetic ability and wealth.³¹

Over half of households (57%) have a defined-benefit pension with an average present discounted value of $234,021. One primary concern is that pension participation is not randomly assigned. As a first step, we regress an indicator for defined-benefit pension participation on the average household EA score. Column [1] of Table 11 shows that after including our standard set of controls, there is no economically or statistically significant relationship between the EA score and defined-benefit pension participation. Column [2] shows that, conditional on participation in a defined-benefit pension plan, defined-benefit pension wealth (the present value of pension income) is also unrelated to the EA score. In general, selection into careers based on defined-benefit pension benefits appears to be uncorrelated with the EA score after controlling for education.

Table 11:

Pensions and Household Wealth

Dep. Var:	Has Pension	Pension Wealth	Log Wealth	Log Wealth
	[1]	[2]	[3]	[4]
EA Score	0.003 (0.011)	0.030 (0.035)	0.069*** (0.022)	0.125*** (0.035)
DB Pension			0.385*** (0.035)	0.181*** (0.051)
EA Score × DB Pension				−0.096*** (0.036)
Obs.	5621	3226	5621	5621
R2	0.215	0.400	0.460	0.474
Mean outcome	0.57	$234,021
Standard Controls	X	X	X	X
Principal Comp.	X	X	X	X
Full Educ. Controls	X	X	X	X

Notes: Columns [1]-[2] of this table present estimates from regressions of defined benefit (DB) pension participation and log pension wealth (conditional on participation) on the EA score and various controls. Columns [3]-[4] present estimates from regressions of log household wealth on the EA score, DB pension participation, an interaction between the EA score and pension participation, and various controls. Significance stars ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.10 levels, respectively. Standard errors are clustered at the family level.

Columns [3] and [4] of Table 11 investigate whether participation in a defined-benefit plan mitigates the role of the EA score in wealth accumulation. Column [3] shows that the coefficient on the EA score remains large and statistically significant when an indicator for defined-benefit pension wealth is included.³² In Column [4], we also include an interaction between the EA score and the pension-participation dummy. We also include interactions between the pension-participation dummy and all principal components variables to account for possible population stratification in obtaining defined-benefit pensions. The results are striking. The coefficient on the interaction is negative and statistically significant, and is economically large. For households that participate in a defined-benefit plan, the coefficient on the EA score is 0.029, compared to 0.125 for households that do not participate in a defined-benefit plan. Put differently, the relationship between the EA score and wealth is over four times as large for households that have more autonomy over their savings and investment choices. This offers strong evidence in support of the hypothesis that the gene-wealth association documented in this paper is in part determined by a household’s difficulty in making wise financial choices.

6. Conclusions

We study the genetic endowments linked to educational attainment, summarized as a linear index called a polygenic score (EA score). Using data from the HRS, we demonstrate that the average EA score in a household strongly and robustly predicts wealth at retirement. The estimated gene-wealth gradient is not fully explained by flexibly controlling for education and income, nor by parental transfers (bequests) and parents’ education, which may proxy for parental investments. We find the EA score is related to risk preferences and mortality, and strongly predicts stock ownership. Stock market participation appears to substantially mediate the gene-wealth association. Lower EA scores are associated with less accurate beliefs about macroeconomic probabilities, as well as shorter planning horizons. Finally, the EA score is much more strongly related to wealth within a subsample of individuals who do not receive defined-benefit pension benefits, and who presumably have greater autonomy over their financial decisions.

The associations we report not only help us to explain the gene-wealth gradient, but may also suggest why these particular genetic markers are associated with education. In particular, the finding that the EA score is related to probabilistic thinking, planning horizons, and decision-making under uncertainty may be useful for understanding the sources of heterogeneity in human capital accumulation. However, we offer important caveats for such an interpretation of these findings. First, measurement error in income, education, and parental transfers may lead us to incorrectly ascribe part of the gene-wealth gradient to other factors that would be unrelated if such variables were correctly measured. Second, genetic measures are likely endogenous to family environment, so one must be careful before assigning a causal interpretation to the gene-outcome gradients that we observe. Third, the polygenic score does not fully explain the amount of education that twin studies have suggested is heritable. Future GWAS will likely estimate more precise genetic associations which could lead to stronger empirical relationships between a polygenic score and completed schooling, and which could alter the empirical relationships documented here.

Economic research using information on genetic endowments is useful for understanding what has heretofore been a form of unobserved heterogeneity that persists across generations. Studies that ignore this type of heterogeneity when studying the intergenerational persistence of economic outcomes, such as income or wealth, could place too much weight on other mechanisms such as attained education or direct monetary transfers between parents and children. The use of observed genetic information can therefore help economists to develop a more accurate and complete understanding of inequality across generations.

Studying how genetic endowments implicated in one outcome, in this case education, relate to other outcomes, such as wealth, leads to a more complete picture of how these endowments function, including how they interact with policy-relevant environmental factors. Our results on pensions and the gene-wealth gradient are an illustration of how environmental factors can modify the relationship between genetic endowments and key economic outcomes. This is one example of what is often referred to as a gene by environment interaction.

Importantly, demonstrating a genetic basis for behavioral outcomes in no way precludes the possibility of effective public policies. A better understanding of why individuals with higher polygenic scores achieve better results may allow for a better design of policies and educational environments that help to improve outcomes. For example, it may be that children with lower polygenic scores begin to face challenges at particular ages or struggle to meet specific educational milestones. In that case, we could better target educational policies to help alleviate these roadblocks. In this manner, the future of genetic research is likely to be just as concerned with nurture as it is with nature. In short, studying how genes are connected to choices and behavior is important because it provides guidance for creating the kinds of environments where everyone, regardless of genetic endowments, has the opportunity to thrive.