Abstract
Background
On 11th March 2020, the World Health Organization declared COVID-19 as Pandemic. The estimation of transmission dynamics in the initial days of the outbreak of any infectious disease is crucial to control its spread in a new area. The serial interval is one of the significant epidemiological measures that determine the spread of infectious disease. It is the time interval between the onset of symptoms in the primary and secondary case.
Objective
The present study aimed at the qualitative and quantitative synthesis of the currently available evidence for the serial interval of COVID-19.
Methodology
Data on serial intervals were extracted from 11 studies following a systematic review. A meta-analysis was performed to estimate the pooled estimate of the serial interval. The heterogeneity and bias in the included studies were tested by various statistical measures and tests, including I2 statistic, Cochran's Q test, Egger's test, and Beggs's test.
Result
The pooled estimate for the serial interval was 5.40 (5.19, 5.61) and 5.19 (4.37, 6.02) days by the fixed and random effects model, respectively. The heterogeneity between the studies was found to be 89.9% by I2 statistic. There is no potential bias introduced in the meta-analysis due to small study effects.
Conclusion
The present review provides sufficient evidence for the estimate of serial interval of COVID-19, which can help in understanding the epidemiology and transmission of the disease. The information on serial interval can be useful in developing various policies regarding contact tracing and monitoring community transmission of COVID-19.
Keywords: COVID-19, Serial interval, Systematic review, Meta-analysis, Epidemiology
1. Introduction
On 31st December 2019, the outbreak of pneumonia cases of unknown etiology occurred in Wuhan and Hubei Province of China.1 As per the WHO's report, the outbreak was found to be associated with the seafood and the wet market in Wuhan.2 China reported the outbreak to the World Health Organization on 7th January 2020 stating that a new type of virus was identified as a coronavirus (2019-nCoV).3 The estimates from various reports of early stages show that the reproduction number of COVID-19 was found to greater than 1 (ranges between 2.24 and 3.58).4 It is a zoonotic coronavirus which is similar to SARS and MERS coronavirus.5 With the alarming levels of spread and severity, WHO declared the outbreak of COVID-19 as Pandemic on 11th March 2020.6
According to the World Health Organization, on 8th May 2020, there are 215 countries with approximately 3.7 million cases of COVID-19, with the death toll of around 0.26 million deaths.7 The transmissibility of COVID-19 from human to human is sufficient to support sustained transmission unless specific control measures are implemented.8 Hence, the estimation of transmission dynamics in the initial days of the outbreak of the disease becomes a thing of utmost importance.9
The serial interval is one of the significant epidemiological measures that determine the spread of infectious disease. It is defined as the time for which the infector and infectee show the symptoms, i.e., the time interval between the onset of symptoms in the primary (infector) and secondary case (infectee). It is required to understand the turnover of case generation and transmissibility of the disease.10 It is often not easy to find links between the cases and hence, it becomes difficult to calculate the serial interval. The serial interval can also be a time dependent quantity, as its value can contract if the prevalence of disease increases during the course of pandemic.11 The serial interval consists of an incubation period (from infection to symptoms) and an infectious period (from exposure to infection).12 The serial interval is also referred as generation time, which is defined as the average time taken for the secondary cases to be infected by a primary case.13 It is used in various epidemiological models such as SEIR, SIR, etc. which are used for the prediction of new cases and outbreaks in the community. The estimation of reproductive number can be sensitive to the choice of serial interval.14 The precision in the estimation of serial interval lead towards the accurate estimation of reproductive number, which is helpful in understanding the growth of any infectious disease.15 The serial interval can be used in disease surveillance. It is also useful in studies of predictive epidemiology and outbreak studies as it helps to identify the epidemiological link between the infector and infectee.16 The utility of this indicator can also be seen in studying the impact of various interventions and to inform authorities on how to control and mitigate outbreaks of any infectious disease. The present study focuses on the currently available evidence of the serial interval for COVID-19 and aims at qualitative and quantitative synthesis of the results obtained from the studies related to serial interval of COVID-19 pandemic.
2. Methodology
2.1. Search databases and strategies
The literature on the serial interval for COVID-19 was searched through popular research databases, including Google Scholar, Scopus, PubMed, and Science Direct, and google search. The search was accomplished by using the combination of keywords as “COVID 19 and serial interval”, “2019-nCoV and serial interval”, “Coronavirus and serial interval”. We also performed a manual search by checking the reference list of the articles found in the search to avoid the omission of any eligible and important study. There was no restriction in the time period while searching the literature to possibly attain all the literature on the serial interval of COVID-19 to till date.
2.2. Inclusion and exclusion criteria
Inclusion criteria were as follows:
-
a)
The study should be published in the English language.
-
b)
The serial interval must be a primary outcome of the study.
-
c)
The serial interval must be calculated based on the transmission chain of infections or symptoms of infector – infected pairs.
Exclusion criteria were as follows:
-
a)
Duplicate studies.
-
b)
The serial interval is taken as an input in the model from a different study.
2.3. Data extraction from the studies
All the articles were selected based on the inclusion and exclusion criteria. After selecting the final list of articles, the information regarding the name of the first author, study region, time period for data collection, adopted methodology in the study to estimate serial interval, estimates of the serial interval, and its 95% confidence interval were extracted from the study. The 95% confidence interval was calculated for the studies reporting mean serial interval with its standard deviation by using the following formula
where μ = mean serial interval, s = standard deviation, and n = sample size of the study. A study has reported mean serial interval with its range, the standard deviation of that study was approximated to ‘Range/4’ by assuming the normal distribution of the serial intervals.17 , 18
2.4. Statistical analyses
All the meta-analyses were performed using Stata 14.1 software. The pooled effect size was calculated using fixed and random effects model. The heterogeneity between the studies was examined by Cochran's Q statistic and was quantified by Higgin's & Thompson's I2 statistic and Tau-squared (τ2). The bias introduced in the meta-analysis by small study effects was tested by Egger's and Begg's test for small-study effects. The Forest plot for the meta-analysis was plotted by using the random-effect model. A funnel plot at 95% confidence interval was also plotted to testify the publication bias in the meta-analysis.
3. Results
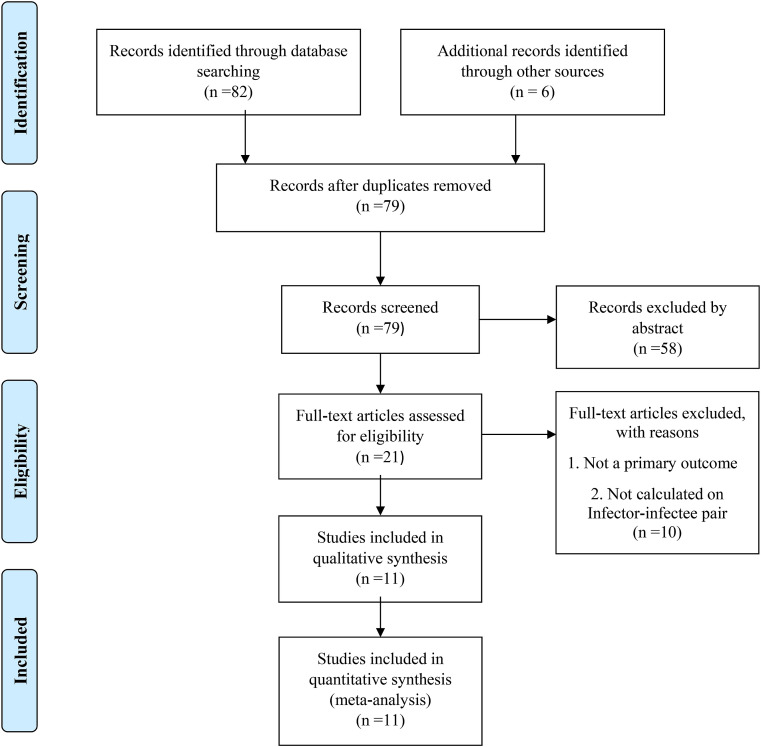
Altogether 88 studies were identified through initial retrieval from search databases. After implementing the inclusion and exclusion criteria, a total of 11 studies with 12 estimates of the serial interval were included in the meta-analysis of serial interval of COVID-19. Fig. 1 describes the complete flowchart for selection of the studies in the qualitative and quantitative synthesis of the serial interval for COVID-19 (Fig. 1). Since the dynamics of COVID-19 is still under exploration and researchers are exploring it worldwide, we included both published literature in peer-reviewed journals and available preprints. The available literature in the form of preprint cannot be ignored in view of current pandemic situation. However, we have not included any incomplete study or working paper in the qualitative or quantitative synthesis.
Fig. 1.
Flow Chart for the selection of studies in systematic review and meta-analysis.
3.1. Review of the included studies in the meta-analysis
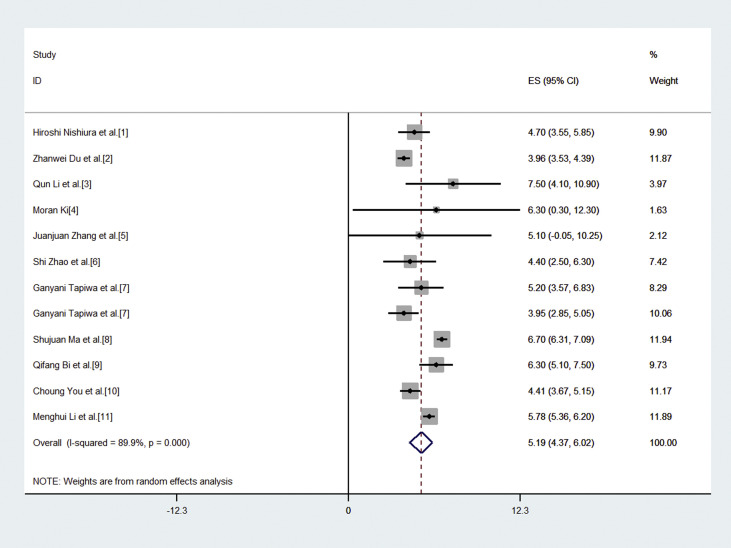
Table 1 describes the characteristics of the included studies in the meta-analysis of the serial interval of COVID-19. The mean serial interval varies from 3.95 (2.80, 5.10) to 7.50 (4.10, 10.9) days in the included studies. Since the evidence of coronavirus was first found in China, we have included seven studies from China. Other than these, single study from each country Singapore, Hong Kong, Korea, and one with global data are also used in the review. The majority of the studies have used parametric distribution to compute the mean and standard deviation of the serial interval, including gamma and normal distribution. Four studies used the Bayesian approach to compute the serial interval from the transmission chain of infections. The period of data collection for computing serial interval was from the end of January 2020 till the start of March 2020 in the studies. The sample size of infector – infected pairs varies considerably from 6 to 689 in the included studies for meta-analysis [Table 1].
Table 1.
Characteristics of the included studies in the meta-analysis of serial interval (SI) of COVID-19.
| Authors | Study Area | Time Period | Methodology | Sample Size | SI | 95% CI | |
|---|---|---|---|---|---|---|---|
| Hiroshi Nishiura et al.19 | World | Up to 12th February 2020 | Bayesian Approach with double interval censoring | 28 | 4.7 | 3.7 | 6.0 |
| Zhanwei Du et al.20 | China | 21st January – 8th February 2020 | Fitting a normal distribution | 468 | 3.96 | 3.53 | 4.39 |
| Qun Li et al.21 | Wuhan | Up to 22nd January 2020 | Fitting a gamma distribution for laboratory-confirmed cases | 6 | 7.5 | 4.1 | 10.9 |
| Moran Ki17 | Korea | Up to 20th January 2020 | Calculating the mean of differences in time of symptoms | 7 | 6.3 | 4.1 | 8.5 |
| Juanjuan Zhang et al.22 | China | 19th January – 17th February 2020 | Fitting a gamma distribution | 35 | 5.1 | 1.3 | 11.6 |
| Shi Zhao et al.23 | Hong Kong | 16th January – 15th February 2020 | Fitting a gamma distribution | 21 | 4.4 | 2.9 | 6.7 |
| Ganyani Tapiwa et al.24 | Singapore | 21st January – 26th February 2020 | Bayesian Framework | 27 | 5.2 | 3.6 | 6.8 |
| Ganyani Tapiwa et al.24 | Tianjin (China) | 14th January – 27th February 2020 | Bayesian Framework | 57 | 3.9 | 2.8 | 5.1 |
| Shujuan Ma et al.25 | Seven Countries | 29th February – 2nd March 2020 | Fitting a normal distribution | 689 | 6.7 | 6.3 | 7.1 |
| Qifang Bi et al.26 | China | 14th January – 12th February 2020 | Fitting a gamma distribution | 48 | 6.3 | 5.2 | 7.6 |
| Choung You et al.27 | China | Up to 2nd February 2020 | Calculating the mean of differences in time of symptoms | 71 | 4.4 | 3.7 | 5.1 |
| Menghui Li et al.28 | China | 21st January – 29th February 2020 | Bayesian Approach with the doubly interval-censored likelihood | 337 | 5.8 | 5.4 | 6.2 |
3.2. Summary statistics for meta-analysis
Table 2 describes the summary statistics after performing the meta-analysis for the included studies. The pooled estimate for the serial interval was 5.40 (5.19, 5.61) and 5.19 (4.37, 6.02) days by the fixed and random effects model, respectively. The heterogeneity between the studies was found to be 89.9% by I2 statistic. The Cochran's Q test was statistically significant at 5% level of significance, suggesting the evidence for the heterogeneity between the included studies. The value for Tau squared (τ2) was found to be 1.4834. The Egger's test and Begg's test also suggested that there is no potential bias introduced in the meta-analysis due to small study effects [Table 2].
Table 2.
Summary statistics for meta-analysis.
| Overall Effect Size | |
| Fixed Effect Model | 5.40 (5.19,5.61) |
| Random Effect Model |
5.19 (4.37,6.02) |
| Test for Heterogeneity | |
| I2 Statistic | 89.9% |
| Tau squared (τ2) | 1.4384 |
| Cochran's Q |
109.17* |
| Small Study Effects | |
| Egger's testa | p = 0.679 |
| Begg's testa | p = 0.631 |
∗p < 0.05.
H0: There are no small study effects.
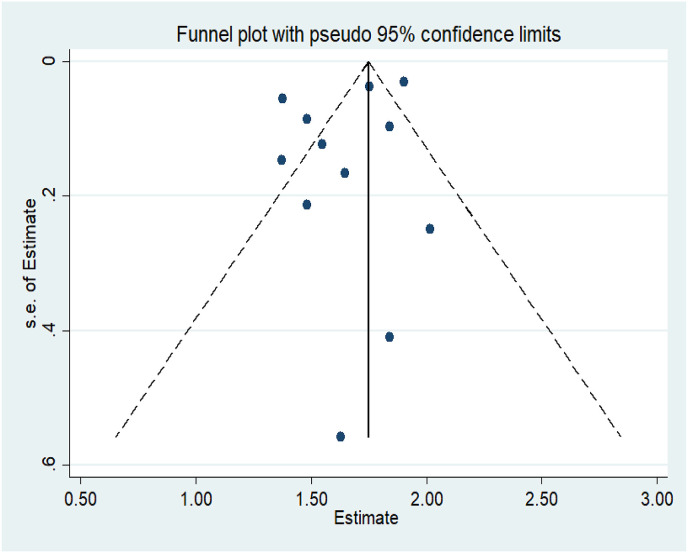
The forest plot (Fig. 2 ) provides the effect size of the individual studies with their weightage in the pooled estimate and a pooled estimate of the serial interval by random effect model, i.e., 5.19 (4.37, 6.02). The funnel plot (Fig. 3 ) with pseudo 95% confidence interval was plotted for the included studies in the meta-analysis, which suggests that there is no noticeable bias in the meta-analysis of studies. The little asymmetry in the funnel plot may be attributed to reporting bias and inadequate methodology adopted in the study.29
Fig. 2.
Forest plot for the meta-analysis of serial interval for COVID-19.
Fig. 3.
Funnel Plot with a 95% confidence interval for included studies in the meta-analysis.
4. Discussion
The systematic review, in addition to meta-analysis, provides an opportunity to examine the existing literature and critically evaluate it with a statistical combination of results of comparable studies.30 The present meta-analysis provides sufficient evidence for the serial interval of COVID-19 through various studies, which can help in understanding the epidemiology and transmission of the disease. This review included 11 studies with 12 estimates of serial interval consisting data from total 1794 infector – infectee pairs of transmission, which used different methods to estimate the serial interval. The time period for the included studies varied from 14th January 2020 to 2nd March 2020. Initial studies provided a higher estimate of serial interval of around 6 to 7, which significantly reduced to 4 to 5 in the later studies. The pooled estimate from random effect model is more appropriate due to the presence of considerable heterogeneity in the included studies for the meta- analysis.31 The pooled estimate was also consistent with some studies.19 , 22 , 24 The statistical tests also suggested the absence of any potential bias in the included studies for meta-analysis. Hence, the present meta-analysis provides a valid and reliable estimate of serial interval for COVID-19.
The pooled estimate of serial interval for COVID-19 from this meta – analysis i.e. 5.19 (4.37, 6.02) days was lower than the serial interval of other similar infectious diseases such as, MERS [7.6 (2.5, 23.1) days] and SARS [ 8.4 (SD = 3.8) days].32 , 33 The serial interval of human influenza is [3.6 (2.9, 4.3) days] which is lower than serial interval of COVID-19.34 The other infectious diseases such as smallpox (SI = 17.7 days), measles (SI = 11.7 days), rubella (SI = 18.3 days) and mumps (SI = 18 days) have higher serial interval.16 The estimation of serial interval is also important from policy perspectives, particularly for formulating the control strategies for reducing the growth of infection in the new area. The information on serial interval is useful for the contact tracing of infected cases and monitoring the community transmission of any infectious disease. The shorter serial interval of COVID-19 suggests that rapid contract tracing and case isolation is necessary to curtail the growth of infection in the next generation cases. The estimate of serial interval is also relevant for surveillance of infectious disease as it provides interval for reporting new cases infected by primary or index case. The information on serial interval along with the incubation period can be used as an aid to check the asymptomatic transmission of COVID-19.35
The differences in serial intervals may be attributable to several factors, including the nature of contacts and incidence of infection, which can vary among studies conducted at different times in different places.12 , 36 The precision of estimates of the serial interval can be improved further when detailed data on transmission, i.e., who-infected-whom becomes available in the near future.16 However, the epidemiological investigation of COVID-19 is still in under investigation globally. In that case, this review can provide insights into the early estimation of the serial interval, which is an important characteristic of any infectious disease. The studies included in this analysis were mostly from China and its provinces; however, it would be better to include studies with a broad geographical scope to get a more comprehensive understanding of serial interval for COVID-19.
Funding
There was no funding for the study.
Declaration of competing interest
All the authors declare no conflict of interests.
References
- 1.Lu H., Stratton C.W., Tang Y. Outbreak of pneumonia of unknown etiology in wuhan China: the mystery and the miracle. J Med Virol. 2020:25678. doi: 10.1002/jmv.25678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.World Health Organization 2020. https://www.who.int/csr/don/12-january-2020-novel-coronavirus-china/en/ Available at:
- 3.Corman V.M., Landt O., Kaiser M., et al. Detection of 2019 novel coronavirus (2019-nCoV) by real-time RT-PCR. Euro Surveill. 2020;25(3) doi: 10.2807/1560-7917.ES.2020.25.3.2000045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhao S., Lin Q., Ran J., et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. Int J Infect Dis:IJID: Off Publ Int Soc Infect Dis. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu Y., Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J Trav Med. March 2020;27(2):taaa021. doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.World Health Organization 2020. https://www.who.int/docs/default-source/coronaviruse/transcripts/who-audio-emergencies-coronavirus-press-conference-full-and-final11mar2020.pdf?sfvrsn=cb432bb3_2 Available at:
- 7.World Health Organization Coronavirus disease 2019 (COVID-19) situation report. 2020:107. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200506covid-19-sitrep-107.pdf?sfvrsn=159c3dc_2 Available at: [Google Scholar]
- 8.Natsuko Imai, Cori Anne, Dorigatti Ilaria, et al. Imperial College London; 2020. Report 3: Transmissibility of 2019-nCoV. COVID-19 Response Team.https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-transmissibility-25-01-2020.pdf Available at: [Google Scholar]
- 9.Viboud C., Sun K., Gaffey R., et al. The RAPIDD ebola forecasting challenge: synthesis and lessons learnt. Epidemics. 2018;22:13–21. doi: 10.1016/j.epidem.2017.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fine P.E.M. The interval between successive cases of an infectious disease. Am J Epidemiol. 2003;158(11):1039–1047. doi: 10.1093/aje/kwg251. [DOI] [PubMed] [Google Scholar]
- 11.Kenah E., Lipsitch M., Robins J.M. Generation interval contraction and epidemic data analysis. Math Biosci. 2008;213(1):71–79. doi: 10.1016/j.mbs.2008.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Svensson Å. A note on generation times in epidemic models. Math Biosci. 2007;208(1):300–311. doi: 10.1016/j.mbs.2006.10.010. [DOI] [PubMed] [Google Scholar]
- 13.Anderson R.M., Fraser C., Ghani A.C., et al. Epidemiology, transmission dynamics and control of SARS: the 2002–2003 epidemic. Phil Trans Roy Soc Lond B Biol Sci. 2004;359(1447):1091–1105. doi: 10.1098/rstb.2004.1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wallinga J., Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc Biol Sci. 2007;274(1609):599–604. doi: 10.1098/rspb.2006.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.White L.F., Wallinga J., Finelli L., et al. Estimation of the reproductive number and the serial interval in early phase of the 2009 influenza A/H1N1 pandemic in the USA. Influenza Other Respir Viruses. 2009;3(6):267–276. doi: 10.1111/j.1750-2659.2009.00106.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vink M.A., Bootsma M.C.J., Wallinga J. Serial intervals of respiratory infectious diseases: a systematic review and analysis. Am J Epidemiol. 2014;180(9):865–875. doi: 10.1093/aje/kwu209. [DOI] [PubMed] [Google Scholar]
- 17.Ki M. Epidemiologic characteristics of early cases with 2019 novel coronavirus (2019-nCoV) disease in Korea. Epidemiol Health. 2020;42 doi: 10.4178/epih.e2020007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hozo S.P., Djulbegovic B., Hozo I. Estimating the mean and variance from the median, range, and the size of a sample. BMC Med Res Methodol. 2005;5(1) doi: 10.1186/1471-2288-5-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nishiura H., Linton N.M., Akhmetzhanov A.R. Serial interval of novel coronavirus (COVID-19) infections. Int J Infect Dis. April 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Du Z., Xu X., Wu Y., Wang L., Cowling B.J., Meyers L.A. Serial interval of COVID-19 among publicly reported confirmed cases. Emerg Infect Dis. 2020;26(6):1341. doi: 10.3201/eid2606.200357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N Engl J Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhang J., Litvinova M., Wang W., et al. Evolving epidemiology and transmission dynamics of coronavirus disease 2019 outside Hubei province, China: a descriptive and modelling study. Lancet Infect Dis. July 2020;20(7):793–802. doi: 10.1016/S1473-3099(20)30230-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhao S., Gao D., Zhuang Z., Chong M., Cai Y., Ran J., et al. Estimating the serial interval of the novel coronavirus disease (COVID-19): a statistical analysis using the public data in Hong Kong from 16th January to 15th February, 2020. medRxiv. 2020 doi: 10.1101/2020.02.21.20026559. [DOI] [Google Scholar]
- 24.Ganyani T., Kremer C., Chen D., et al. Estimating the generation interval for coronavirus disease (COVID-19) based on symptom onset data, March 2020. Euro Surveill. 2020;25(17):2000257. doi: 10.2807/1560-7917.ES.2020.25.17.2000257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ma S., Zhang J., Zeng M., Yun Q., Guo W., Zheng Y., et al. Epidemiological parameters of coronavirus disease 2019: a pooled analysis of publicly reported individual data of 1155 cases from seven countries. medRxiv. 2020 doi: 10.1101/2020.03.21.20040329. [DOI] [Google Scholar]
- 26.Bi Q., Wu Y., Mei S., Ye C., Zou X., Zhang Z., et al. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. Lancet Infect Dis. August 2020;20(8):911–919. doi: 10.1016/S1473-3099(20)30287-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.You C., Deng Y., Hu W., Sun J., Lin Q., Zhou F., et al. Estimation of the time-varying reproduction number of COVID-19 outbreak in China. Int J Hyg Environ Health. 2020:113555. doi: 10.1016/j.ijheh.2020.113555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li M., Liu K., Song Y., Wang M., Wu J. Serial interval and generation interval for respectively the imported and local infectors estimated using reported contact-tracing data of COVID-19 in China. medRxiv. 2020 doi: 10.1101/2020.04.15.20065946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sterne J.A., Sutton A.J., Ioannidis J.P., Terrin N., Jones D.R., Lau J., et al. Recommendations for examining and interpreting funnel plot asymmetry in meta-analyses of randomised controlled trials. Br Med J. 2011;343:d4002. doi: 10.1136/bmj.d4002. [DOI] [PubMed] [Google Scholar]
- 30.Fagard R.H., Staessen J.A., Thijs L. Advantages and disadvantages of the meta-analysis approach. J Hypertens. 1996;14(2):S9–S12. doi: 10.1097/00004872-199609002-00004. Suppl: Official journal of the International Society of Hypertension. [DOI] [PubMed] [Google Scholar]
- 31.Borenstein M., Hedges L., Rothstein H. Meta-analysis: fixed effect vs. random effects. Metaanalysis. com. 2007. https://www.metaanalysis.com/downloads/Metaanalysis%20fixed%20effect%20vs%20random%20effects%20072607.pdf Retrieved from. Accessed on Jun 5, 2020.
- 32.Assiri A., McGeer A., Perl T.M., et al. Hospital outbreak of Middle East respiratory syndrome coronavirus. N Engl J Med. 2013;369(5):407–416. doi: 10.1056/NEJMoa1306742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lipsitch M., Cohen T., Cooper B., Robins J.M., Ma S., James L., et al. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300(5627):1966–1970. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cowling B.J., Fang V.J., Riley S., Peiris J.M., Leung G.M. Estimation of the serial interval of influenza. Epidemiology (Cambridge, Mass.) 2009;20(3):344. doi: 10.1097/EDE.0b013e31819d1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fraser C., Riley S., Anderson R.M., Ferguson N.M. Factors that make an infectious disease outbreak controllable. Proc Natl Acad Sci Unit States Am. 2004;101(16):6146–6151. doi: 10.1073/pnas.0307506101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.te Beest D.E., Wallinga J., Donker T., van Boven M. Estimating the generation interval of influenza A (H1N1) in a range of social settings. Epidemiology. 2013:244–250. doi: 10.1097/EDE.0b013e31827f50e8. [DOI] [PubMed] [Google Scholar]