Highlights
-
•
Proposed automatic COVID screening (ACoS) system for detection of infected patients.
-
•
Random image augmentation is applied to incorporate the variability in the images.
-
•
Applied hierarchical (two phase) classification to segregate three classes.
-
•
Majority vote based classifier ensemble is used to combine model’s prediction.
-
•
Proposed method show promising potential to detect nCOVID-19 infected patients.
Keywords: Coronavirus, Chest X-Ray, nCOVID-19, Pneumonia, SARS-COV-2, Contagious, Pandemic
Abstract
Novel coronavirus disease (nCOVID-19) is the most challenging problem for the world. The disease is caused by severe acute respiratory syndrome coronavirus-2 (SARS-COV-2), leading to high morbidity and mortality worldwide. The study reveals that infected patients exhibit distinct radiographic visual characteristics along with fever, dry cough, fatigue, dyspnea, etc. Chest X-Ray (CXR) is one of the important, non-invasive clinical adjuncts that play an essential role in the detection of such visual responses associated with SARS-COV-2 infection. However, the limited availability of expert radiologists to interpret the CXR images and subtle appearance of disease radiographic responses remains the biggest bottlenecks in manual diagnosis. In this study, we present an automatic COVID screening (ACoS) system that uses radiomic texture descriptors extracted from CXR images to identify the normal, suspected, and nCOVID-19 infected patients. The proposed system uses two-phase classification approach (normal vs. abnormal and nCOVID-19 vs. pneumonia) using majority vote based classifier ensemble of five benchmark supervised classification algorithms. The training-testing and validation of the ACoS system are performed using 2088 (696 normal, 696 pneumonia and 696 nCOVID-19) and 258 (86 images of each category) CXR images, respectively. The obtained validation results for phase-I (accuracy (ACC) = 98.062%, area under curve (AUC) = 0.956) and phase-II (ACC = 91.329% and AUC = 0.831) show the promising performance of the proposed system. Further, the Friedman post-hoc multiple comparisons and z-test statistics reveals that the results of ACoS system are statistically significant. Finally, the obtained performance is compared with the existing state-of-the-art methods.
1. Introduction
The recent outbreak of the novel coronavirus disease (nCOVID-19) has infected millions of people and killed several individuals across the world (“Coronavirus Disease 2019, 2020”; “Johns Hopkins University, Corona Resource Center, 2020”). The World Health Organization (WHO) has declared this epidemic a global health emergency. nCOVID-19 is caused by a highly contagious virus named severe acute respiratory syndrome coronavirus-2 (SARS-COV-2) in which transmission of infection can even occur from the asymptotic patients during the incubation period (Huang et al., 2020, Kooraki et al., 2020). As per the expert's opinion, the virus mainly infects the human respiratory tract leading to severe bronchopneumonia with symptoms of fever, dyspnea, dry cough, fatigue, and respiratory failure, etc. (N.Chen et al., 2020, Cheng et al., 2020). There is no specific vaccine or medication available to cure the disease and prevent further spread. Also, the standard confirmatory clinical test – reverse transcription-polymerase chain reaction (RT-PCR) test for detecting nCOVID-19 is manual, complex, and time-consuming (Chowdhury, Rahman, Khandakar, Mazhar, Kadir, Mahbub, & Reaz, 2020). The limited availability of test-kits and domain experts in the hospitals and rapid increase in the number of infected patients necessitates an automatic screening system, which can act as a second opinion for expert physicians to quickly identify the infected patients, who require immediate isolation and further clinical confirmation.
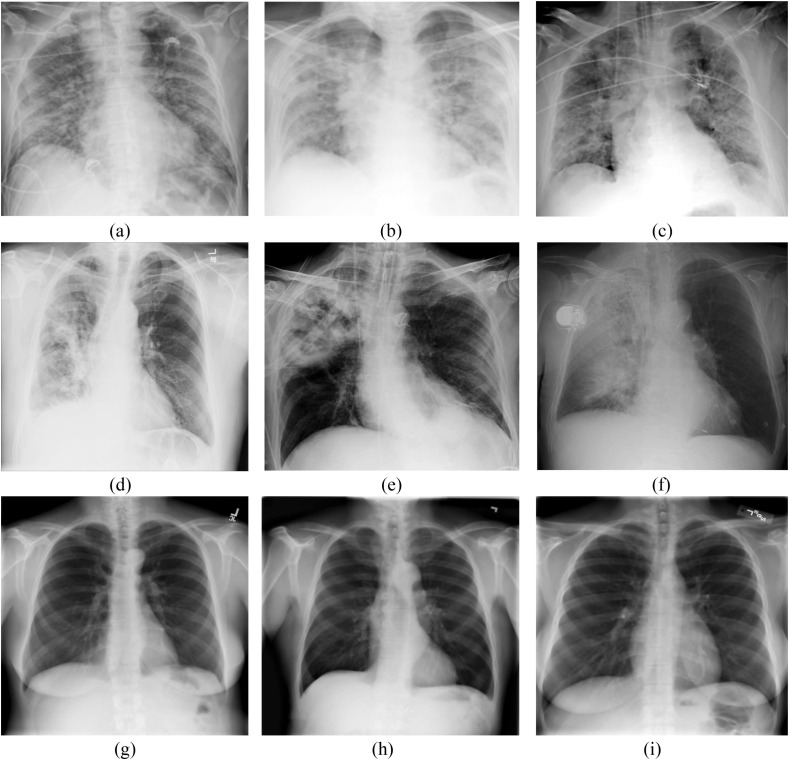
Chest X-Ray (CXR) is one of the important, non-invasive clinical adjuncts that play an essential role in the preliminary investigation of different pulmonary abnormalities (Chandra & Verma, 2020, Chandra and Verma, 2020a, Chandra et al., 2020, Ke et al., 2019). It can act as an alternative screening modality for the detection of nCOVID-19 or to validate the related diagnosis, where the CXR images are interpreted by expert radiologists to look for infectious lesions associated with nCOVID-19. The earlier studies reveal that the infected patients exhibit distinct visual characteristics in CXR images, as shown in Fig. 1 (Cheng et al., 2020, Chowdhury et al., 2020, Chung et al., 2020, Zhang et al., 2020). These characteristics typically include multi‐focal, bilateral ground‐glass opacities and patchy reticular (or reticulonodular) opacities in non-ICU patients, while dense pulmonary consolidations in ICU patients (Hosseiny, Kooraki, Gholamrezanezhad, Reddy, & Myers, 2020). However, the manual interpretation of these subtle visual characteristics on CXR images is challenging and require domain expert (Kanne, Little, Chung, Elicker, & Ketai, 2020; L. Wang & Wong, 2020). Moreover, the exponential increase in the number of infected patients makes it difficult for the radiologist to complete the diagnosis in time, leading to high morbidity and mortality (AsnaouiEl Chawki & Idri, 2020).
Fig. 1.
(a–c) nCOVID-19 infected chest X-Ray images (d–f) Pneumonia infected chest X-Ray (h-i) Normal chest X-Ray images.
To fight against nCOVID-19 epidemic, the recent machine learning (ML) techniques can be embedded to develop an automatic computer-aided diagnosis (CAD) system. In this direction, many clinical and radiological studies have been reported, describing various radio-imaging findings and epidemiology of nCOVID-19 (N. Chen et al., 2020, Huang et al., 2020, Kooraki et al., 2020, Yoon et al., 2020). Further, many deep-learning models like deep convolutional network, recursive network, transfer learning models, etc. have been implemented to automatically analyze the radiological disease characteristics (Chouhan et al., 2020, Jaiswal et al., 2019). Xue et al. (2018) used a convolutional neural network (CNN) to assign a class label to different superpixels extracted from the lungs parenchyma and localize tuberculosis-infected regions in CXR images with average dice index of 0.67. Another work by Pesce et al. (2019), used two novel models, the first model is based on backpropagation neural network that uses weakly labeled CXR images and generates visual attention feedback for accurate localization of pulmonary lesions; the second model used reinforcement learning-based recurrent attention model, which learns the sequence of images to find the nodules. Recently, Purkayastha, Buddi, Nuthakki, Yadav, and Gichoya (2020) introduced CheXNet—deep learning (DL) based model integrated with LibreHealth Radiology Information System, which analyzes uploaded CXR images and assigns one of 14 diagnostic labels.
Motivated by the promising performance of DL models reported in the literature and urgent need of an alternate screening tool for early detection of nCOVID-19 infected patients, the research community has applied different DL techniques on chest radiograph images (Abbas, Abdelsamea, & Gaber, 2020; S. Wang et al., 2020, Xu et al., 2020). The detailed description of different state-of-arts methods, including the imaging modality, dataset size, algorithms, and obtained performance, are recapitulated in Table 1 . Initially, the authors have used a mixture of CXR images collected from different hospitals, publications, and older repositories (Abbas, Abdelsamea, & Gaber, 2020, Hemdan, Shouman, & Karar, 2020, Narin et al., 2020). However, the limited availability of annotated CXR images for nCOVID-19 cases to train the data-hungry DL models turned out to be the biggest bottleneck (X. Wang et al., 2017). Latter, to avoid the overfitting of the models, the studies used data augmentation techniques, which generates different variants of the source image by applying random photometric transformations like blurring, sharpening, contrast adjustment, etc. (Chowdhury et al., 2020; S. Wang et al., 2020, Xu et al., 2020). Further, the CT images have also been used to perform in-depth volumetric analysis of subtle disease responses (similar to viral pneumonia or other inflammatory lung diseases) (Maghdid, Asaad, Ghafoor, Sadiq, & Khan, 2020; S. Wang et al., 2020, Xu et al., 2020).
Table 1.
Existing literature for detection of nCOVID-19 using DL approaches. (Abbreviations: CXR: Chest X-Ray, CT: Computed Tomography, nCOVID: Novel Coronavirus Disease, AUC: Area Under Curve, CNN: Convolutional Neural Network, DT: Decision Tree, SVM: Support Vector Machine, KNN: k-Nearest Neighbor, VGG: Visual Geometry Group).
| Articles | Imaging Modality | Dataset Size |
Class | Algorithms/Techniques | Performance |
||||
|---|---|---|---|---|---|---|---|---|---|
| nCOVID-19 | Pneumonia | Normal | Augmented | ACC (%) | AUC | ||||
| Ozturk et al. (2020) | CXR | 127 | 500 | 500 | – | 3 | DarkNet | 87.02 | |
| Xu et al. (2020) | CT | 219 | 224 | 175 | 2634 patches nCOVID, 2661 patches Pneumonia,6576 patches Normal |
3 | ResNet-18 | 86.70 | – |
| Panwar et al. (2020) | CXR | 142 | – | 142 | – | 2 | nCOVnet | 88.10 | 0.88 |
| S. Wang et al. (2020) | CT | 79 | 180 | – | 1065 (740 Negative, 325 nCOVID) | 2 | Deep Learning | 89.50 | – |
| Hemdan, Shouman, and Karar (2020) | CXR | 25 | – | 25 | – | 2 | VGG19, DenseNet201, ResNetV2, InceptionV3, InceptionResNetV2, Xception, MobileNetV2 | 90.00 | – |
| Pathak, Shukla, Tiwari, Stalin, and Singh (2020) | CT | 413 | 439 | – | 2 | ResNet-50 | 93.02 | 0.93 | |
| L. Wang et al. (2020) | CXR | 385 | 5538 | 8066 | – | 3 | COVID-Net | 93.30 | – |
| Maghdid, Asaad, Ghafoor, Sadiq, and Khan (2020) | CXR CT |
85 CXR 203 CT |
– | 85 CXR 158 CT |
– | 2 | AlexNet, Modified CNN | 94.00 CXR 82.0 CT |
– |
| Abbas, Abdelsamea, and Gaber (2020) | CXR | 105 | 11 | 80 | – | 3 | DeTraC | 95.12 | – |
| AsnaouiEl Chawki and Idri (2020) | CXR | – | 4273 | 1583 | – | 2 | CNN, VGG16 VGG19, Inception_V3, Xception, DensNet201, MobileNet_V2, Inception_ Resnet_V2, Resnet50 | 96.61 | – |
| Chowdhury et al. (2020) | CXR | 423 | 1485 | 1579 | 6540 | 3 | AlexNet, ResNet18, DenseNet201, SqueezeNet | 97.94 | – |
| Narin et al. (2020) | CXR | 50 | – | 50 | – | 2 | ResNet50, ResNetV2, InceptionV3 | 98.00 | – |
| Ucar and Korkmaz (2020) | CXR | 66 | 3895 | 1349 | 4608 | 3 | Deep Bayes-SqueezeNe | 98.26 | – |
| Nour, Cömert, and Polat (2020) | CXR | 219 | 1345 | 1341 | 765 | 3 | CNN, SVM, DT, KNN | 98.97 | – |
| Ardakani, Kanafi, Acharya, Khadem, and Mohammadi (2020) | CT | 510 | 510 | – | – | VGG-16, ResNet-18, ResNet-101, AlexNet, VGG-19, Xception, SqueezeNet, GoogleNet, MobileNet-V2, ResNet-50 | 99.51 | 0.99 | |
| Toğaçar et al. (2020) | CXR | 295 | 98 | 65 | – | 3 | MobileNetV2, SqueezeNet, SVM | 99.27 | 1.00 |
After the retrospective analysis of the above literatures, we found that the existing studies had been performed using a limited number of input CXR or CT images, which may lead to under-fitting of the data-hungry DL models (X. Wang et al., 2017). Moreover, the DL approach requires huge computational resources along with a large number of accurately annotated CXR images to train the model, which restrain its clinical acceptability (Altaf et al., 2019, Ho and Gwak, 2019). Conventional ML techniques can be better integrated with CAD systems to overcome these shortcomings. Despite several studies, no one has used conventional ML approaches with ensemble learning using majority voting for the classification of normal and nCOVID-19 infected CXR images.
In this study, we tailored an automatic COVID screening (ACoS) system that employs hierarchical classification using conventional ML algorithms and radiomic texture descriptors to segregate normal, pneumonia, and nCOVID-19 infected patients. The major advantage of the proposed system is that it can be easily modeled using the limited number of annotated images and can be deployed even in a resource-constrained environment.
1.1. Contribution and Organization of paper
The contributions of this study are recapitulated as follows:
-
–
Proposed an ACoS system for detection of nCOVID-19 infected patients using hierarchical classification and augmented images. The proposed model can be used as a retrospective tool or to validate the related diagnosis.
-
–
Applied majority vote based classifier ensemble to aggregate the prediction results of five supervised classification algorithms.
-
–
Review and compare the performance of the proposed ACOS system with the state of the art methods.
The remaining sections of the paper is organized as follows. Section 2 describes the materials and methods used in this study. The obtained results and its detailed analysis are discussed in Section 3. The paper is concluded in Section 4.
2. Materials and methods
2.1. Data acquisition, preprocessing, and augmentation
In this study, we have used dataset from three public repositories – COVID‐Chestxray set (Cohen, Morrison, & Dao, 2020), Montgomery set (Candemir et al., 2014, Jaeger et al., 2014), and NIH ChestX-ray14 set (X. Wang et al., 2017). The detailed statistics of the number of posterior-anterior (PA) view CXR images used from each repository are shown in Table 2 . Initially, all input images are preprocessed, which includes image resizing (512 × 512 pixels), format conversion (Portable Network Graphics), and color space conversion (Gray Scale). Subsequently, the texture preserving guided filter is applied to reduce the inherent quantum noise (Sprawls, 2018). The choice of the de-noising filter is based on our previous study (Chandra & Verma, 2020a).
Table 2.
Statistics of the number of CXR images used from different repositories for performance evaluation in training, testing, and validation set.
| Dataset property | COVID‐Chestxray Set | Montgomery Set | NIH ChestX-ray14 Set | Augmented images | Training -Testing set (80%) | Validation set (20%) |
|---|---|---|---|---|---|---|
| Number of nCOVID-19 CXR images | 434 | – | – | 348 | 696 | 86 |
| Number of Pneumonia X-ray images | 89 | – | 345 | 348 | 696 | 86 |
| Number of normal X-ray images | 19 | 80 | 335 | 348 | 696 | 86 |
| Total Number of X-ray images | 542 | 80 | 680 | 1044 | 2088 | 258 |
The preprocessed images are divided into two sub-sets: training-testing set (80%) and validation set (20%). Further, the image augmentation technique is applied to the images of the training-testing set to build a generalized model by incorporating the possible variability in the images, which might occur due to diverse imaging conditions. We applied different random photometric transformations with random parameters between the specified ranges, as described in Table 3 .
Table 3.
Image augmentation using various photometric transformations.
| Transformations | Range | |
|---|---|---|
| Sharpening | Automatic | Highlight the fine details by adjusting the contrast between bright and dark pixels. |
| Gaussian Blur | Random smoothing of texture information between the specified range of sigma. | |
| Brightness | Randomly increase or decrease the pixel’s intensity between the given range. | |
| Contrast adjustment | Automatic | Adjust the contrast of the image. |
2.2. Feature extraction and feature selection
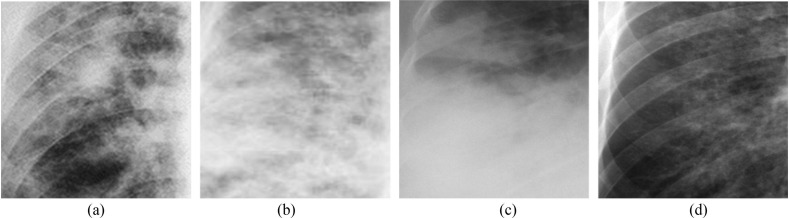
The nCOVID-19 infected patients exhibit different radiographic texture patterns such as patchy ground-glass opacities (Fig. 2 a), pulmonary consolidations (Fig. 2c), reticulonodular opacities (Fig. 2b), etc. on CXR images (Hosseiny et al., 2020). These subtle visual characteristics can be efficiently represented with the help of radiomic texture descriptors. The study uses eight first order statistical features (FOSF) (Srinivasan & Shobha, 2008), 88 grey level co-occurrence matrix (GLCM) (Gómez et al., 2012, Haralick et al., 1973) features (in four different orientations) and 8100 histogram of oriented gradients (HOG) (Dalal & Triggs, 2005, Santosh and Antani, 2018) features. The FOSF describes the complete image at a glance by using the mean, variance, roughness, smoothness, kurtosis, energy, and entropy, etc. It can easily quantify the global texture patterns; however, it does not contemplate the local neighborhood information. To overcome this shortcoming, the GLCM and HOG feature descriptor are used to perform the in-depth texture analysis. The GLCM feature describes the spatial correlation among the pixel intensities in radiographic texture patterns along four distinct directions (i.e.,) whereas the HOG feature encodes the local shape/texture information. The selection of these statistical texture features is motivated by the fact that it can efficiently encode the natural texture patterns and is widely used in medical image analysis (Chandra and Verma, 2020a, Chandra et al., 2020, Santosh and Antani, 2018, Vajda et al., 2018).
Fig. 2.
nCOVID-19 infected Chest X-ray images showing: (a) Ground‐glass opacities, (b) Reticular opacities, (c) Pulmonary consolidation, (d) Mild opacities.
In this study, a total of 8196 features (8 FOSF, 88 GLCM, 8100 HOG) are extracted from each CXR image (described in Appendix-A). However, not all the extracted features are relevant for accurate characterization of visual indicators associated with nCOVID-19. Thus, to select the most informative features, we used a recently developed meta-heuristic approach called—binary grey wolf optimization (BGWO) (Mirjalili et al., 2014, Too et al., 2018). The method imitates the leadership, encircling, and hunting strategy of grey wolfs. Unlike the other evolutionary algorithms, the method does not get trapped in local minima, which motivated us to use it in our study (Emary, Zawbaa, & Hassanien, 2016).
Mathematically, the grey wolfs are divided into four categories denoted by alpha (), beta (), delta (), and omega (). The -wolf is the decision-maker and administers the hunting process with the help of beta. The -wolfs are the fittest candidate to replace the alpha when the alpha is very old or dead. The -wolfs are the next in the hierarchy, which obey the orders from and -wolfs but command omega wolfs. The -wolfs are the lowest in the hierarchy and report to these leader wolfs. The encircling strategy of the wolfs is described in Eq. (1).
| (1) |
| (2) |
where, denotes the position of the pray and grey wolf in ‘’ iteration, respectively. The A and C are the coefficient vectors computed using equations Eqs. (3) and (4), respectively.
| (3) |
| (4) |
where, denotes the two random numbers between 0 and 1, and ‘’ denotes the linearly decreasing encircling coefficient (from 2 to 0) used to balance the tradeoff between searching and exploitation.
Further, the optimal position of the wolfs () at iteration ‘t’ are updated using Eqs. (5), (6), (7), (8); are computed using Eq. (3); and are calculated using Eq. (2).
| (5) |
| (6) |
| (7) |
| (8) |
2.3. Proposed methodology
To develop a robust ACoS system, we hypothesized the following:
Hypothesis 1
The image augmentation technique could improve the robustness of the ACoS system by incorporating variability in input CXR images, which might occur due to diverse imaging modality, exposure time, radiation dose, and varying patient’s posture.
Hypothesis 2
The solid mathematical foundation and better generalization capability of support vector machine (SVM) could uncover the subtle radiological characteristics associated with nCOVID-19.
Hypothesis 3
The majority voting based classifier ensemble could act as a multi-expert recommendation and reduce the probable chance of false diagnosis.
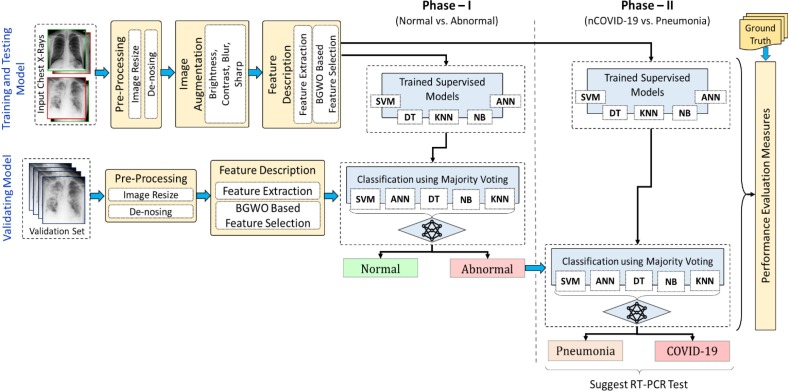
To evaluate the hypothetical assumptions, we proposed a prototype (ACoS system) model, as shown in Fig. 3 . The proposed system consists of five major steps: pre-processing, image augmentation, feature extraction, classification, and performance evaluation. Initially, to examine Hypothesis 1, the input CXR images are preprocessed (resize, de-noise), and the image augmentation technique is applied (described in Section 2.1). Subsequently, the radiomic textures descriptors are extracted from the complete CXR image and binary gray wolf optimization (BGWO) (Emary et al., 2016, Mirjalili et al., 2014) based feature selection technique is applied to pick the most relevant features. Further to examine Hypothesis 2, the selected features are used to train the model using five supervised classification algorithms, namely – decision tree (DT) (Shalev-Shwartz & Ben-David, 2014), support vector machine (SVM) (Vapnik, 1998), k-nearest neighbor (KNN) (Han, Kamber, & Pei, 2012), naïve Bayes (NB) (Rish et al., 2001) and artificial neural network (ANN) (Artificial Neural Network, 2013). The proposed methodology uses two-phase classification approach. In phase-I, the normal and abnormal (containing nCOVID-19 and Pneumonia) images are segregated. Subsequently, the abnormal images are further classified in phase-II to segregate the nCOVID-19 and pneumonia. Moreover, the fully trained model is validated using a separate validation set. The final prediction of the validation set is the majority vote of seven benchmark classifiers (ANN, KNN, NB, DT, SVM (linear kernel), SVM (radial basis function (RBF) kernel), and SVM (polynomial kernel)), which reduce the probable chance of misclassification (Hypothesis 3). Finally, the performance measures are evaluated for testing and validation sets. All the experiments in this study are implemented using MATLAB R2018a.1
Fig. 3.
The prototype of the proposed automatic COVID screening (ACoS) system. (Abbreviations: BGWO: Binary Gray Wolf Optimization, SVM: Support Vector Machine, DT: Decision Tree, KNN: k-Nearest Neighbor, NB: Naïve Bayes, ANN: Artificial Neural Network).
2.4. Classification
To compute the discriminative performance of the aforementioned features we have used the popular supervised classification algorithms: SVM (linear, radial bias function, polynomial) (Chandra and Verma, 2020a, Vapnik, 1998), ANN (Artificial Neural Network, 2013), KNN (Han, Kamber, & Pei, 2012), NB (Khatami et al., 2017, Venegas-Barrera and Manjarrez, 2011), and DT (Han, Kamber, & Pei, 2012, Pantazi, Moshou, & Bochtis, 2020). These algorithms are very fast and are widely used in the literature for the classification of pulmonary diseases using CXR images (Chandra and Verma, 2020a, Santosh and Antani, 2018). The selection of these classifiers is motivated by the fact that these algorithms can be efficiently trained using smaller datasets without compromising with the performance. In this study, a discrete set of models were created for phase-I and phase-II, respectively. In phase-I, the models were trained using normal and abnormal images (containing nCOVID-19 and pneumonia) from training –testing set. However, in phase-II, only abnormal images (containing nCOVID-19 and pneumonia) were used to train the models. In both the phases, the performance of the classifiers was evaluated using a 10 fold cross-validation setup. In each fold, all the optimizable learning hyper-parameters were tuned using the Bayesian automatic optimization method (Snoek, Larochelle, & Adams, 2012).
In general, the learning hyper-parameters can be optimized in two ways, called manual and automatic searching. The manual parameter tuning requires expertise. However, when dealing with numerous models and larger datasets, even expertise may not be sufficient (Ucar & Korkmaz, 2020). To overcome this shortcoming, an automatic parameter tuning is used as an alternative. In this study, grid search algorithm is used to select the best hyper-parameters by minimizing the cross-validation loss automatically.2
Moreover, to examine the Hypothesis 3, majority vote based classifier ensemble technique (described in Appendix B, Algorithm 1) is applied (shown in Fig. 3) using a separate validation set (258 CXR images). In order to select the optimal combination of evaluated classifiers for majority vote, we implemented an exhaustive search using recursive elimination method (Chatterjee, Dey, & Munshi, 2019; Q. Chen, Meng, & Su, 2020). Initially, the method starts with all evaluated classifiers, according to the selection criteria, it iteratively eliminates the classifiers until all possible combinations exhausted.
2.5. Performance evaluation metrics
The performance of the proposed ACoS system is assessed using seven performance measures, as shown in Eqs. (9), (10), (11), (12), (13), (14), (15) (Han, Kamber, & Pei, 2012), where, the number of infected and normal CXR images correctly predicted by the proposed system is denoted by true positive (TP) and true negative (TN), respectively; the false positive (FP) and false-negative (FN) denotes the misclassification of normal and infected images, respectively; P = TP + FN and N = TN + FP.
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
Finally, the obtained results is statistically validated using z-test and Friedman average ranking and Holm (Holm, 1979) and Shaffer (Shaffer, 1986) post-hoc multiple comparison methods.
3. Experimental results and discussion
This section presents a detailed discussion of the obtained experimental results of the proposed ACoS system. To evaluate the hypothetical assumptions (Hypothesis 1, Hypothesis 2, Hypothesis 3), the following experiments were formulated:
Experiment 1—Different photometric transformations were randomly applied to input CXR images, and classification performance was evaluated (Hypothesis 1).
Experiment 2—The classification performance of SVM was assessed and compared with the other benchmark classifiers (Hypothesis 2).
Experiment 3—The classification performance of the majority voting technique and individual benchmark classifiers are evaluated using a separate validation set (Hypothesis 3).
In this study, we used two-phase classification technique to discriminate the normal, nCOVID-19 and pneumonia X-ray images. Initially, two sets of classification models were created for phase-I and phase-II, respectively using original CXR images from the training-testing set. Subsequently, the image augmentation was performed using different photometric transformations as discussed in Section 2.1. The augmented images along with the original CXR images were used to re-train the models and classification performance was evaluated. From the obtained results shown in Tables 4 and 5 , it was observed that the supervised models trained using augmented images performed significantly better compared to the models trained using original CXR images for both the phases (phase-I and phase-II), which confirms the validity of Hypothesis 1. The obtained promising performance using augmented images can be justified by the fact that the augmented images provide sufficient instances to train the model for possible variations in input CXR images, which might occur due to diverse imaging parameters and platforms in different hospitals.
Table 4.
Phase-I (Normal vs. Abnormal) classification performance of different supervised models using Training-Testing in 10-fold cross-validation setup. (Abbreviations: SVM: Support Vector Machine, DT: Decision Tree, KNN: k-Nearest Neighbor, NB: Naïve Bayes, ANN: Artificial Neural Network, STD: Standard Deviation, AUC: Area Under Curve, MCC: Matthews Correlation Coefficient, Note: best performance is highlighted with bold letters).
| Classification algorithms | Accuracy (±STD) | Specificity (±STD) | Precision (±STD) | Recall (±STD) | F1-Measure (±STD) | AUC (±STD) | MCC (±STD) |
|---|---|---|---|---|---|---|---|
| Without using Augmented Images | |||||||
| SVM (RBF Kernel) | 66.70 ± 0.83 | 3.40 ± 2.22 | 66.96 ± 0.79 | 98.56 ± 0.95 | 79.74 ± 0.57 | 0.51 ± 0.01 | 0.06 ± 0.09 |
| DT | 90.73 ± 5.03 | 85.95 ± 6.04 | 92.95 ± 3.11 | 93.12 ± 4.97 | 93.02 ± 3.89 | 0.90 ± 0.05 | 0.79 ± 0.11 |
| NB | 97.22 ± 1.15 | 97.71 ± 3.24 | 98.85 ± 1.13 | 96.98 ± 0.82 | 97.90 ± 0.86 | 0.97 ± 0.02 | 0.94 ± 0.03 |
| KNN | 97.41 ± 2.08 | 98.28 ± 1.20 | 98.14 ± 1.00 | 96.99 ± 3.26 | 98.02 ± 0.64 | 0.98 ± 0.02 | 0.94 ± 0.04 |
| SVM (Poly Kernel) | 98.47 ± 0.81 | 97.97 ± 2.39 | 99.00 ± 0.86 | 98.71 ± 0.81 | 98.85 ± 0.61 | 0.98 ± 0.01 | 0.97 ± 0.02 |
| ANN | 98.47 ± 1.12 | 98.29 ± 1.48 | 99.13 ± 0.75 | 98.56 ± 1.18 | 98.84 ± 0.85 | 0.98 ± 0.01 | 0.97 ± 0.02 |
| SVM (Linear Kernel) | 98.85 ± 1.09 | 98.57 ± 1.51 | 99.21 ± 0.76 | 98.99 ± 0.98 | 99.13 ± 0.73 | 0.99 ± 0.01 | 0.97 ± 0.02 |
| Using Augmented Images | |||||||
| SVM (RBF Kernel) | 82.90 ± 1.71 | 48.71 ± 5.09 | 79.62 ± 1.63 | 98.17 ± 0.35 | 88.64 ± 1.01 | 0.74 ± 0.03 | 0.62 ± 0.04 |
| DT | 95.88 ± 1.04 | 93.38 ± 3.6 | 96.75 ± 1.73 | 97.13 ± 1.17 | 96.92 ± 0.76 | 0.95 ± 0.02 | 0.91 ± 0.02 |
| NB | 96.70 ± 1.55 | 97.28 ± 1.84 | 98.60 ± 0.95 | 96.41 ± 1.76 | 97.49 ± 1.19 | 0.97 ± 0.02 | 0.93 ± 0.03 |
| ANN | 99.33 ± 0.25 | 98.13 ± 1.55 | 99.18 ± 0.56 | 99.43 ± 0.34 | 99.50 ± 0.16 | 0.99 ± 0.01 | 0.98 ± 0.02 |
| SVM (Poly Kernel) | 99.38 ± 0.55 | 99.57 ± 0.17 | 99.78 ± 0.15 | 99.19 ± 0.17 | 99.13 ± 0.52 | 0.99 ± 0.01 | 0.99 ± 0.01 |
| KNN | 99.41 ± 0.51 | 99.71 ± 0.90 | 99.86 ± 0.13 | 99.31 ± 0.40 | 99.71 ± 0.28 | 1.00 ± 0.01 | 0.99 ± 0.01 |
| SVM (Linear Kernel) | 99.67 ± 0.31 | 99.57 ± 0.27 | 99.79 ± 0.67 | 99.86 ± 0.14 | 99.82 ± 0.17 | 1.00 ± 0.00 | 0.99 ± 0.00 |
Table 5.
Phase-II (nCOVID vs. Pneumonia) classification performance of different supervised models using Training-Testing set in 10-fold cross-validation setup.
| Classification algorithms | Accuracy (±STD) | Specificity (±STD) | Precision (±STD) | Recall (±STD) | F1-Measure (±STD) | AUC (±STD) | MCC (±STD) |
|---|---|---|---|---|---|---|---|
| Without using Augmented Images | |||||||
| DT | 72.98 ± 3.54 | 70.93 ± 12.06 | 73.06 ± 6.20 | 74.96 ± 8.82 | 73.41 ± 3.22 | 0.73 ± 0.04 | 0.47 ± 0.07 |
| ANN | 74.29 ± 5.28 | 74.29 ± 32.99 | 74.29 ± 8.57 | 74.29 ± 30.07 | 74.29 ± 17.5 | 0.74 ± 0.05 | 0.49 ± 0.13 |
| SVM (RBF Kernel) | 80.03 ± 4.40 | 80.18 ± 10.61 | 81.05 ± 8.12 | 79.91 ± 7.44 | 80.01 ± 4.30 | 0.80 ± 0.04 | 0.61 ± 0.09 |
| KNN | 80.17 ± 4.62 | 83.30 ± 7.82 | 82.68 ± 6.42 | 77.03 ± 7.23 | 79.47 ± 4.92 | 0.80 ± 0.05 | 0.61 ± 0.09 |
| NB | 80.46 ± 6.03 | 79.57 ± 6.26 | 80.00 ± 5.71 | 81.36 ± 7.70 | 80.58 ± 6.18 | 0.80 ± 0.06 | 0.61 ± 0.12 |
| SVM (Poly Kernel) | 83.34 ± 3.46 | 85.89 ± 5.63 | 85.42 ± 4.37 | 80.77 ± 5.81 | 82.87 ± 3.63 | 0.83 ± 0.03 | 0.67 ± 0.07 |
| SVM (Linear Kernel) | 85.07 ± 6.94 | 87.09 ± 9.64 | 87.11 ± 8.73 | 83.08 ± 7.39 | 84.83 ± 6.74 | 0.85 ± 0.07 | 0.71 ± 0.14 |
| Using Augmented Images | |||||||
| NB | 84.63 ± 6.75 | 85.94 ± 6.26 | 85.51 ± 6.43 | 83.31 ± 8.46 | 84.32 ± 7.12 | 0.85 ± 0.07 | 0.69 ± 0.13 |
| DT | 84.84 ± 5.27 | 84.19 ± 4.82 | 84.36 ± 4.85 | 85.49 ± 6 | 84.91 ± 5.34 | 0.85 ± 0.05 | 0.7 ± 0.11 |
| ANN | 94.93 ± 2.54 | 94.2 ± 3.52 | 94.29 ± 3.1 | 95.65 ± 3.5 | 94.96 ± 2.55 | 0.95 ± 0.03 | 0.9 ± 0.05 |
| KNN | 97.27 ± 1.86 | 95.83 ± 2.5 | 95.98 ± 2.35 | 98.7 ± 1.25 | 97.31 ± 1.81 | 0.97 ± 0.02 | 0.95 ± 0.04 |
| SVM (RBF Kernel) | 97.7 ± 1.85 | 97.41 ± 2.17 | 97.49 ± 2.27 | 97.99 ± 1.91 | 97.71 ± 1.82 | 0.98 ± 0.02 | 0.95 ± 0.04 |
| SVM (Poly Kernel) | 97.98 ± 1.99 | 97.7 ± 2.26 | 97.75 ± 2.18 | 98.19 ± 1.58 | 97.89 ± 2.05 | 0.98 ± 0.02 | 0.95 ± 0.04 |
| SVM (Linear Kernel) | 98.78 ± 0.96 | 98.14 ± 1.69 | 98.19 ± 1.68 | 99.23 ± 0.72 | 98.79 ± 0.95 | 0.99 ± 0.01 | 0.98 ± 0.02 |
Moreover, the results obtained using different supervised algorithms for phase-I (shown in Table 4) and phase-II (shown in Table 5) demonstrates that the SVM (linear kernel) outperformed the others using a selected feature set (1546 features for phase-I and 2018 features for phase-II). The significant better performance of SVM is due to its generalization capability and ability to learn and infer the intricate natural patterns by efficiently adapting the hyperplane and the soft margins using support vectors. Further, the obtained higher accuracy (ACC) of 99.67 ± 0.31%, area under the curve (AUC) of 1 ± 0.00, and Matthews Correlation Coefficient (MCC) of 0.99 ± 0.00 for phase-I and ACC of 98.78 ± 0.96, AUC of 0.99 ± 0.01, and MCC of 0.98 ± 0.02 for phase-II demonstrates its promising performance and thus justifying the validity of Hypothesis 2.
The nCOVID-19 is highly contagious, and even a single false negative may lead to community spread of the infection. Therefore, to reduce the probable chance of misclassification, we used the majority voting based classifier ensemble of seven benchmark supervised models, as shown in Fig. 3. Further, the classification performance of the majority voting technique and individual benchmark classifiers are evaluated using a separate validation set (which was not used during training of the models). The set consists of 258 CXR images (86 normal, 86 nCOVID-19 and 86 pneumonia). Initially, the radiomic texture features (described in Section 2.2) were extracted from the input CXR images and classified using different supervised models in phase-I. The output of each model acts as an expert suggestion to segregate the input CXR images into normal or abnormal (nCOVID-19 or pneumonia). The classification performance of each model using validation set in phase-I is shown in Table 6 . From the obtained results, it can be observed that the performance of majority voting algorithm in phase-I (ACC of 98.062%, AUC of 0.977, and MCC of 0.956) is significantly better compared to the others. Further, all the images which were classified to abnormal category in phase-I were passed to phase-II for differential diagnosis between nCOVID-19 and pneumonia.
Table 6.
Phase-I (Normal vs. Abnormal) classification performance of different supervised models and majority voting algorithm using the validation set. (Abbreviations: SVM: Support Vector Machine, DT: Decision Tree, KNN: k-Nearest Neighbor, NB: Naïve Bayes, ANN: Artificial Neural Network, STD: Standard Deviation, AUC: Area Under Curve, MCC: Matthews Correlation Coefficient). (Note: best performance is highlighted with bold letters).
| Classification algorithms | Accuracy (%) | Specificity (%) | Precision (%) | Recall (%) | F1-Measure (%) | AUC | MCC |
|---|---|---|---|---|---|---|---|
| NB | 88.372 | 73.256 | 87.766 | 95.930 | 91.667 | 0.846 | 0.734 |
| DT | 90.698 | 80.233 | 90.659 | 95.930 | 93.220 | 0.881 | 0.788 |
| SVM (RBF Kernel) | 95.349 | 89.535 | 94.944 | 98.256 | 96.571 | 0.939 | 0.895 |
| KNN | 95.736 | 94.186 | 97.076 | 96.512 | 96.793 | 0.953 | 0.904 |
| SVM (Linear Kernel) | 96.124 | 90.698 | 95.506 | 98.837 | 97.143 | 0.948 | 0.913 |
| SVM (Poly Kernel) | 96.124 | 91.860 | 96.023 | 98.256 | 97.126 | 0.951 | 0.912 |
| ANN | 96.512 | 93.023 | 96.571 | 98.256 | 97.406 | 0.956 | 0.921 |
| Majority voting | 98.062 | 96.512 | 98.266 | 98.837 | 98.551 | 0.977 | 0.956 |
In phase-II, the abnormal input images were classified using each supervised model, and prediction results were aggregated using majority voting based classifier ensemble. From the obtained results shown in Table 7 , it was observed that majority voting based classifier ensemble achieved significantly higher performance (ACC of 91.279%, AUC of 0.913, and MCC of 0.830) compared to the individual models, which confirms the robustness of the proposed ACoS system (justifying the validity of Hypothesis 3).
Table 7.
Phase-II (nCOVID vs. Pneumonia) classification performance of different supervised models and majority voting algorithm using the validation set. (Note: best performance is highlighted with bold letters).
| Classification algorithms | Accuracy (%) | Specificity (%) | Precision (%) | Recall (%) | F1-Measure (%) | AUC | MCC |
|---|---|---|---|---|---|---|---|
| KNN | 72.093 | 76.744 | 74.359 | 67.442 | 70.732 | 0.721 | 0.444 |
| ANN | 73.256 | 53.488 | 66.667 | 93.023 | 77.670 | 0.733 | 0.506 |
| DT | 79.070 | 82.558 | 81.250 | 75.581 | 78.313 | 0.791 | 0.583 |
| NB | 80.814 | 72.093 | 76.238 | 89.535 | 82.353 | 0.808 | 0.626 |
| SVM (Linear Kernel) | 81.977 | 83.721 | 83.133 | 80.233 | 81.657 | 0.820 | 0.640 |
| SVM (Poly Kernel) | 86.047 | 79.070 | 81.633 | 93.023 | 86.957 | 0.860 | 0.728 |
| SVM (RBF Kernel) | 86.628 | 83.721 | 84.615 | 89.535 | 87.006 | 0.866 | 0.734 |
| Majority voting | 91.329 | 86.207 | 87.368 | 96.512 | 91.713 | 0.914 | 0.831 |
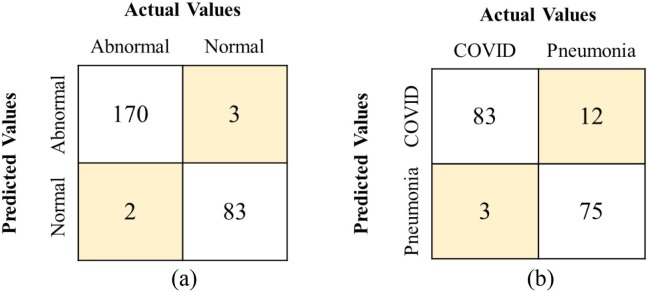
To breakoff, the community spread of the nCOVID-19, one of the desired properties in any ACoS system is that it should have the least number of Type-II (false negative) errors without compromising with the number of Type-I (false positive) errors. Fig. 4 (a) and (b) show the confusion matrix (CM) for majority voting algorithm for phase-I and phase-II, respectively using validation set. From the CM, it was observed that the majority voting approach outperformed the others achieving fewer Type-I and Type-II errors.
Fig. 4.
Confusion matrix using validation set for (a) Majority voting (Phase-I), (b) Majority voting (Phase-II).
3.1. Statistical analysis
In this section describes the statistical significance of the obtained results from the various experiments performed in this study. Initially, the statistical significance of obtained performance (ACC and F1-measure) of different supervised models using augmented images and without using augmented images for phase-I and phase-II were validated using z-test statistics. The test consider the null hypothesis as the performance of supervised models before and after applying image augmentation is equal. Alternatively, the models trained using augmented images exhibit higher performance. The test statistics for phase-I and phase-II at 95% confidence interval (or ) are shown in Table 8 . From the statistical results of phase-I, it was observed that the classification performance of ANN, SVM (linear and RBF kernel), DT, and KNN models are significantly higher using augmented images (accepting the alternate hypothesis) compared to the models trained using original CXR images. Similarly, in phase-II, all the models strongly accept the alternate hypothesis (i.e., models trained using augmented images exhibit higher performance or ).
Table 8.
Computed z-score for comparing the performance (accuracy and F-measure) of different supervised models using augmented images vs. without using augmented images for Training-Testing set in 10-fold cross-validation setup (at 95% significance level or alpha = 0.05). (Abbreviations: SVM: Support Vector Machine, DT: Decision Tree, KNN: k-Nearest Neighbor, NB: Naïve Bayes, ANN: Artificial Neural Network, STD: Standard Deviation, AUC: Area Under Curve, MCC: Matthews Correlation Coefficient, Note: Bold value denotes the rejection of alternate hypothesis).
| Classifiers | Phase-I |
Phase-II |
||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy |
F1-Measure |
Accuracy |
F1-Measure |
|||||
| Z-Score | P-Value | Z-Score | P-Value | Z-Score | P-Value | Z-Score | P-Value | |
| ANN | −2.78686 | 0.00821 | −2.84720 | 0.00693 | −16.78630 | 0.00000 | −16.83080 | 0.00000 |
| SVM (Linear Kernel) | −2.32891 | 0.02649 | −2.04164 | 0.04963 | −13.50650 | 0.00000 | −13.70514 | 0.00000 |
| SVM (RBF Kernel) | −10.23706 | 0.00000 | −6.70490 | 0.00000 | −18.81539 | 0.00000 | −18.84667 | 0.00000 |
| SVM (Poly Kernel) | −2.51459 | 0.01690 | −0.77056 | 0.29647 | −15.24470 | 0.00000 | −15.41234 | 0.00000 |
| DT | −5.79733 | 0.00000 | −5.03525 | 0.00000 | −7.96144 | 0.00000 | −7.74892 | 0.00000 |
| NB | 0.79659 | 0.29048 | 0.71026 | 0.31000 | −2.94058 | 0.00529 | −2.62549 | 0.01271 |
| KNN | −4.74345 | 0.00001 | −4.86842 | 0.00000 | −16.23091 | 0.00000 | −16.75614 | 0.00000 |
The statistical significance of the proposed ACoS system was evaluated using Friedman average ranking method and Holm and Shaffer pairwise comparison method for validation set (Chandra and Verma, 2020a, Chandra et al., 2020). The Friedman test statistics compare the mean ranks of different classifiers assuming that the performance of all classifiers are equal (null hypothesis). From the average ranks shown in Table 9 , we found that the test strongly accepts the alternate hypothesis while rejecting the null, which confirms the substantial difference in the performance of different classification algorithms (at ) for both the phases. The result can also be verified from the Friedman test (at 7 degrees of freedom) with for phase-I and for phase-II. Further, the validity of Hypothesis 3 can be verified from the fact that the majority voting algorithm achieved minimum rank (first rank) in both the phases.
Table 9.
Average ranking of classifiers based on different classification performance metrics using the Friedman test with 7 degrees of freedom. (Note: the minimum value represents the better rank and is highlighted in bold).
| Classification algorithms | Average ranking of classification algorithms |
|
|---|---|---|
| Phase - I | Phase - II | |
| NB | 7.929 | 5.214 |
| DT | 7.071 | 5.714 |
| SVM (RBF Kernel) | 5.714 | 2.429 |
| KNN | 4.000 | 7.571 |
| SVM (Linear Kernel) | 3.714 | 4.071 |
| SVM (Poly Kernel) | 3.929 | 3.357 |
| ANN | 2.571 | 6.643 |
| Majority Voting | 1.071 | 1.000 |
Further, the Friedman average rankings shown in Table 9 demonstrate that the mean ranks of different classification algorithms are significantly different (), therefore it is meaning full to perform the pairwise post-hoc comparisons. In this study, Holm (Holm, 1979) and Shaffer (Shaffer, 1986) post-hoc procedures were used to perform multiple pairwise comparisons. The method considers the null hypothesis as all algorithms performed equally.
In this study, 28 pairs of classification algorithms (denoted by ‘’) were compared at level of significance. The Holm and Shaffer method reject those hypotheses that have an unadjusted and, respectively for both phase-I and phase-II. The test statistics for phase-I and phase-II are shown in Tables 10 and 11 , respectively. From the statistical results, it was observed that the performance of the proposed majority vote based classifier ensemble method is significantly better compared to the other classification algorithms for both the phases confirming the validity of Hypothesis 3.
Table 10.
p-value and adjusted p-value for pairwise multiple comparisons of different supervised classification algorithms (Phase-I: Normal vs. Abnormal) using the validation set at (Abbreviations: SVM: Support Vector Machine, DT: Decision Tree, KNN: k-Nearest Neighbor, NB: Naïve Bayes, ANN: Artificial Neural Network, STD: Standard Deviation, AUC: Area Under Curve, MCC: Matthews Correlation Coefficient).
| i | Algorithms | Holm | Shaffer | Adjusted p-Value |
|||
|---|---|---|---|---|---|---|---|
| 28 | NB vs. Majority Voting | 5.2372 | 0.0000 | 0.0018 | 0.0018 | 0.0036 | 0.0036 |
| 27 | DT vs. Majority Voting | 4.5826 | 0.0000 | 0.0019 | 0.0024 | 0.0037 | 0.0048 |
| 26 | NB vs. ANN | 4.0916 | 0.0000 | 0.0019 | 0.0024 | 0.0038 | 0.0048 |
| 25 | SVM (RBF Kernel) vs. Majority Voting | 3.5460 | 0.0004 | 0.0020 | 0.0024 | 0.0040 | 0.0048 |
| 24 | DT vs. ANN | 3.4369 | 0.0006 | 0.0021 | 0.0024 | 0.0042 | 0.0048 |
| 23 | NB vs. SVM (Linear Kernel) | 3.2187 | 0.0013 | 0.0022 | 0.0024 | 0.0043 | 0.0048 |
| 22 | NB vs. SVM (Poly Kernel) | 3.0551 | 0.0023 | 0.0023 | 0.0024 | 0.0045 | 0.0048 |
| 21 | NB vs. KNN | 3.0005 | 0.0027 | 0.0024 | 0.0024 | 0.0048 | 0.0048 |
| 20 | DT vs. SVM (Linear Kernel) | 2.5641 | 0.0103 | 0.0025 | 0.0025 | 0.0050 | 0.0063 |
| 19 | DT vs. SVM (Poly Kernel) | 2.4004 | 0.0164 | 0.0026 | 0.0026 | 0.0053 | 0.0063 |
| 18 | SVM (RBF Kernel) vs. ANN | 2.4004 | 0.0164 | 0.0028 | 0.0028 | 0.0056 | 0.0063 |
| 17 | DT vs. KNN | 2.3458 | 0.0190 | 0.0029 | 0.0029 | 0.0059 | 0.0063 |
| 16 | KNN vs. Majority Voting | 2.2367 | 0.0253 | 0.0031 | 0.0031 | 0.0063 | 0.0063 |
| 15 | SVM (Poly Kernel) vs. Majority Voting | 2.1822 | 0.0291 | 0.0033 | 0.0033 | 0.0067 | 0.0067 |
| 14 | SVM (Linear Kernel) vs. Majority Voting | 2.0185 | 0.0435 | 0.0036 | 0.0036 | 0.0071 | 0.0071 |
| 13 | NB vs. SVM (RBF Kernel) | 1.6912 | 0.0908 | 0.0038 | 0.0038 | 0.0077 | 0.0077 |
| 12 | SVM (RBF Kernel) vs. SVM | 1.5275 | 0.1266 | 0.0042 | 0.0042 | 0.0083 | 0.0083 |
| 11 | SVM (RBF Kernel) vs. SVM | 1.3639 | 0.1726 | 0.0045 | 0.0045 | 0.0091 | 0.0091 |
| 10 | SVM (RBF Kernel) vs. KNN | 1.3093 | 0.1904 | 0.0050 | 0.0050 | 0.0100 | 0.0100 |
| 9 | ANN vs. Majority Voting | 1.1456 | 0.2519 | 0.0056 | 0.0056 | 0.0111 | 0.0111 |
| 8 | KNN vs. ANN | 1.0911 | 0.2752 | 0.0063 | 0.0063 | 0.0125 | 0.0125 |
| 7 | DT vs. SVM (RBF Kernel) | 1.0365 | 0.3000 | 0.0071 | 0.0071 | 0.0143 | 0.0143 |
| 6 | SVM (Poly Kernel) vs. ANN | 1.0365 | 0.3000 | 0.0083 | 0.0083 | 0.0167 | 0.0167 |
| 5 | SVM (Linear Kernel) vs. ANN | 0.8729 | 0.3827 | 0.0100 | 0.0100 | 0.0200 | 0.0200 |
| 4 | NB vs. DT | 0.6547 | 0.5127 | 0.0125 | 0.0125 | 0.0250 | 0.0250 |
| 3 | KNN vs. SVM (Linear Kernel) | 0.2182 | 0.8273 | 0.0167 | 0.0167 | 0.0333 | 0.0333 |
| 2 | SVM (Linear Kernel) vs. SVM | 0.1637 | 0.8700 | 0.0250 | 0.0250 | 0.0500 | 0.0500 |
| 1 | KNN vs. SVM (Poly Kernel) | 0.0546 | 0.9565 | 0.0500 | 0.0500 | 0.1000 | 0.1000 |
Table 11.
p-value and adjusted p-value for pairwise multiple comparisons of different supervised classification algorithms (Phase-II: nCOVID-19 vs. Pneumonia) using the validation set at.
| i | Algorithms | Holm | Shaffer | Adjusted p-Value |
|||
|---|---|---|---|---|---|---|---|
| 28 | KNN vs. Majority Voting | 5.0190 | 0.0000 | 0.0018 | 0.0018 | 0.0000 | 0.0000 |
| 27 | ANN vs. Majority Voting | 4.3098 | 0.0000 | 0.0019 | 0.0024 | 0.0004 | 0.0003 |
| 26 | KNN vs. SVM (RBF) | 3.9279 | 0.0001 | 0.0019 | 0.0024 | 0.0022 | 0.0018 |
| 25 | DT vs. Majority Voting | 3.6006 | 0.0003 | 0.0020 | 0.0024 | 0.0079 | 0.0067 |
| 24 | NB vs. Majority Voting | 3.2187 | 0.0013 | 0.0021 | 0.0024 | 0.0309 | 0.0270 |
| 23 | KNN vs. SVM (Poly) | 3.2187 | 0.0013 | 0.0022 | 0.0024 | 0.0309 | 0.0270 |
| 22 | ANN vs. SVM (RBF) | 3.2187 | 0.0013 | 0.0023 | 0.0024 | 0.0309 | 0.0270 |
| 21 | KNN vs. SVM (Linear) | 2.6732 | 0.0075 | 0.0024 | 0.0024 | 0.1578 | 0.1578 |
| 20 | ANN vs. SVM (Poly) | 2.5095 | 0.0121 | 0.0025 | 0.0025 | 0.2418 | 0.1934 |
| 19 | DT vs. SVM (RBF) | 2.5095 | 0.0121 | 0.0026 | 0.0026 | 0.2418 | 0.1934 |
| 18 | SVM (Linear) vs. Majority Voting | 2.3458 | 0.0190 | 0.0028 | 0.0028 | 0.3417 | 0.3037 |
| 17 | NB vs. SVM (RBF) | 2.1276 | 0.0334 | 0.0029 | 0.0029 | 0.5673 | 0.5339 |
| 16 | ANN vs. SVM (Linear) | 1.9640 | 0.0495 | 0.0031 | 0.0031 | 0.7926 | 0.7926 |
| 15 | DT vs. SVM (Poly) | 1.8003 | 0.0718 | 0.0033 | 0.0033 | 1.0772 | 1.0772 |
| 14 | SVM (Poly) vs. Majority Voting | 1.8003 | 0.0718 | 0.0036 | 0.0036 | 1.0772 | 1.0772 |
| 13 | KNN vs. NB | 1.8003 | 0.0718 | 0.0038 | 0.0038 | 1.0772 | 1.0772 |
| 12 | NB vs. SVM (Poly) | 1.4184 | 0.1561 | 0.0042 | 0.0042 | 1.8728 | 1.8728 |
| 11 | KNN vs. DT | 1.4184 | 0.1561 | 0.0045 | 0.0045 | 1.8728 | 1.8728 |
| 10 | SVM (Linear) vs. SVM (RBF) | 1.2548 | 0.2096 | 0.0050 | 0.0050 | 2.0957 | 2.0957 |
| 9 | DT vs. SVM (Linear) | 1.2548 | 0.2096 | 0.0056 | 0.0056 | 2.0957 | 2.0957 |
| 8 | SVM (RBF) vs. Majority Voting | 1.0911 | 0.2752 | 0.0063 | 0.0063 | 2.2019 | 2.2019 |
| 7 | ANN vs. NB | 1.0911 | 0.2752 | 0.0071 | 0.0071 | 2.2019 | 2.2019 |
| 6 | NB vs. SVM (Linear) | 0.8729 | 0.3827 | 0.0083 | 0.0083 | 2.2964 | 2.2964 |
| 5 | ANN vs. DT | 0.7092 | 0.4782 | 0.0100 | 0.0100 | 2.3910 | 2.3910 |
| 4 | SVM (Poly) vs. SVM (RBF) | 0.7092 | 0.4782 | 0.0125 | 0.0125 | 2.3910 | 2.3910 |
| 3 | KNN vs. ANN | 0.7092 | 0.4782 | 0.0167 | 0.0167 | 2.3910 | 2.3910 |
| 2 | SVM (Linear) vs. SVM (Poly) | 0.5455 | 0.5854 | 0.0250 | 0.0250 | 2.3910 | 2.3910 |
| 1 | DT vs. NB | 0.3819 | 0.7025 | 0.0500 | 0.0500 | 2.3910 | 2.3910 |
Finally, the performance of the proposed system is compared with the existing state of the art methods (summarized in Table 1). Initially, the proposed method is compared for two-class (normal vs. abnormal/nCOVID-19) as shown in Table 12 . From the table, it was observed that the proposed method performed significantly better compared to Panwar et al., 2020, Hemdan, Shouman, & Karar, 2020, Maghdid, Asaad, Ghafoor, Sadiq, & Khan, 2020. Further, it achieved comparably equal performance to Narin et al., 2020, Ozturk et al., 2020. However, one should note that Narin et al., 2020, Ozturk et al., 2020 used comparably less number of CXR images to train the DL model.
Table 12.
Two class (normal vs. abnormal) performance comparison of the proposed method with the state of art methods.
| Articles | Class | Algorithms/techniques | ACC (%) |
|---|---|---|---|
| Panwar et al. (2020) | 2 | nCOVnet | 88.10 |
| Hemdan, Shouman, and Karar (2020) | 2 | VGG19, DenseNet201, ResNetV2, InceptionV3, InceptionResNetV2, Xception, MobileNetV2 | 90.00 |
| Maghdid, Asaad, Ghafoor, Sadiq, and Khan (2020) | 2 | AlexNet, Modified CNN | 94.00 |
| Narin et al. (2020) | 2 | ResNet50, ResNetV2, InceptionV3 | 98.00 |
| Ozturk et al. (2020) | 2 | DarkNet | 98.08 |
| Proposed Method (Phase-I) | 2 | Majority vote based classifier ensemble | 98.06 |
Further, the overall accuracy (for three class: normal vs. nCOVID-19 vs. pneumonia) of the proposed model is evaluated and compared with the existing state of art methods, as shown in Table 13 . The table reveals that the proposed method performed significantly better in terms of overall accuracy (ACC = 93.411%) compared to Ozturk et al. (2020) andWang and Wong (2020). However, it achieved comparably lower performance than Abbas, Abdelsamea, & Gaber, 2020, Chowdhury et al., 2020, Ucar and Korkmaz (2020) and Toğaçar, Ergen, and Cömert (2020), which is due to the fact that the author Toğaçar et al., 2020, Abbas, Abdelsamea, & Gaber, 2020 used very less number of CXR image to train the DL models. Further, radiological responses of pneumonia and nCOVID-19 are subtle, which confuses the classifier. Overcoming such limitation is still an open-ended research area.
Table 13.
Three class (normal, nCOVID-19 and pneumonia) performance comparison of the proposed method with the state of art methods.
| Articles | Class | Algorithms/techniques | Total number of images | ACC (%) |
|---|---|---|---|---|
| Ozturk et al. (2020) | 3 | DarkNet | 87.02 | |
| L. Wang et al. (2020) | 3 | COVID-Net | 93.30 | |
| Abbas et al. (2020) | 3 | DeTraC | 196 | 95.12 |
| Chowdhury et al. (2020) | 3 | AlexNet, ResNet18, DenseNet201, SqueezeNet | 3487 | 97.94 |
| Ucar and Korkmaz (2020) | 3 | Deep Bayes-SqueezeNe | 5957 | 98.26 |
| Nour et al. (2020) | 3 | CNN, SVM, DT, KNN | 3670 | 98.97 |
| Toğaçar et al. (2020) | 3 | MobileNetV2, SqueezeNet, SVM | 458 | 99.27 |
| Proposed Method (Overall) | 3 | Majority vote based classifier ensemble | 2346 | 93.41 |
3.2. Discussion
The morbidity and mortality rate due to nCOVID-19 is rapidly increasing, with thousands of reported death worldwide. The WHO has already declared this pandemic as a global health emergency (Coronavirus Disease 2019, 2020). In this study, we presented an ACoS system to detect nCOVID-19 infected patients using CXR image data. We performed two-phase classification to segregate normal, nCOVID-19 and pneumonia infected images. The major challenges we experienced in this study are:
-
•
The publicly available nCOVID-19 infected CXR images are limited and lacking standardization.
-
•
The radiological characteristics of nCOVID-19 and pneumonia infections are ambiguous.
Moreover, several studies using DL approaches have been reported in the literature for detection of nCOVID-19 infection in CXR and CT images (as shown in Table 1). Although the DL methods reported promising performance, it suffers from the following shortcomings:
-
•
Resize the input CXR images to lower resolution (like 64 × 64 or 224 × 224, etc.) before processing, which may result in loss of crucial discriminative texture information.
-
•
Demands massive training data to sufficiently train the model.
-
•
Requires expertise to define suitable network architecture and set the many hyper-parameters (like input resolution, number of layers, filters, and filter shape, etc.).
-
•
Requires high computational resources, extensive memory and a significant amount of time to train the network.
-
•
Unlike conventional machine learning, DL approaches are unexplainable in nature.
To overcome the aforementioned limitations, we have used a combination of radiomic texture features with conventional ML algorithms. The following facts can justify the promising performance of the proposed ACoS system:
-
•
The radiomic texture descriptors (FOSF, GLCM, and HOG features) are highly efficient in encoding natural textures and thus can easily quantize the correlation attributes of radiological visual characteristics associated with nCOVID-19 infection.
-
•
The image augmentation technique provides sufficient instances to train the model for possible variable inputs, making the model robust.
-
•
The conventional ML algorithms can be efficiently trained using smaller datasets, fewer resources and minimal hyper-parameter tuning without compromising with the performance.
-
•
The majority vote based classifier ensemble method used in the proposed ACoS system acts as a multi-expert recommendation system and reduces the probable chance of misclassification.
The disadvantages of the proposed system are as follows:
-
•
The subtle radiographic responses of different abnormalities like TB, pneumonia, influenza, etc. confuses the classifier, limiting the diagnostic performance of the system.
In the proposed ACoS system, majority vote based classifier ensemble technique has been exploited to reduce the probable chance of misclassification of nCOVID-19 infected patients. Such method can be easily integrated into mobile radiology van and can work for the welfare of the society.
4. Conclusion
In this study, we have presented an ACoS system for preliminary diagnosis of nCOVID-19 infected patients, so that proper precautionary measures (like isolation and RT-PCR test) can be taken to prevent the further outbreak of the infection. The key findings of the study are summarized as follows:
-
•
The proposed ACoS system demonstrated the promising potential to segregate the normal, pneumonia, and nCOVID-19 infected patients, which can be verified from the significant performance of phase-I (ACC = 98.062%, AUC = 0.977, and MCC = 0.956) and phase-II (ACC = 91.329%, AUC = 0.914 and MCC = 0.831) using the validation set.
-
•
There are significant variations in the input CXR images due to diverse imaging conditions in different hospitals. The proposed system used augmented images, which generate sufficient variability to train the model and improve its robustness.
-
•
The radiomic texture descriptors like FOSF, GLCM, and HOG features are highly efficient in quantizing the correlation attributes of radiological visual characteristics associated with nCOVID-19 infection.
-
•
Unlike the data-hungry DL approaches, the proposed ACoS system used conventional ML algorithms to train the model with limited annotated images and less computational resources. This type of system may have greater clinical acceptability and can be deployed even in a resource-constrained environment.
-
•
The Friedman post-hoc multiple comparison and z-score statistics confirm the statistical significance of the proposed system.
The future work of this study should focus on improving the reliability and clinical acceptability of the system. The integration of the patient’s symptomatology and radiologist’s feedback with the CAD system could be helpful in making a robust screening system. Further, an in-depth analytical comparison of performances between conventional algorithms and deep learning methods could help in establishing its clinical acceptability.
CRediT authorship contribution statement
Tej Bahadur Chandra: Conceptualization, Methodology, Software, Validation, Investigation, Writing - original draft. Kesari Verma: Conceptualization, Formal analysis, Supervision, Writing - review & editing. Bikesh Kumar Singh: Formal analysis, Supervision, Writing - review & editing. Deepak Jain: Visualization, Validation. Satyabhuwan Singh Netam: Visualization, Validation.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
The authors would like to acknowledge J.P. Cohen and group for collecting images from various sources and making it publicly available (COVID‐Chestxray Database) for the research community.
Footnotes
Appendix A. Radiomic texture feature
The ambiguous texture patterns in CXR images due to different infectious diseases is challenging for the radiologist to diagnose and correlate the patterns to a specific disease accurately. nCOVID-19 exhibits various radiological characteristics, as described in Section 2.2. These visual indicators can be efficiently quantized using statistical texture descriptors (FOSF, GLCM, HOG feature). The FOSF encodes the texture according to the statistical distribution of pixel intensities over the entire image deriving a set of histogram statistics (like mean, variance, smoothness, kurtosis, energy and entropy etc.) by waiving the correlation among the pixels (Srinivasan & Shobha, 2008). Further, to encode the spatial correlation of grey-level distributions of disease texture patterns in the local neighborhood, the GLCM texture feature (Gómez et al., 2012, Haralick et al., 1973) is used. It considers the relative position of pixel intensities in a given neighborhood of size of an input image , encoding natural textures (Gómez et al., 2012). It represents the relative frequency of two grey levels ‘i’ and ‘j’ as statistical probability value or that occurs at pair of points separated by distance vector ‘’ along angle . The statistical probability value is described in Eq. (16). The summary of these features are recapitulated in Table 14 .
| (16) |
Table 14.
Radiomic texture features (FOSF, GLCM features) extracted from CXR images.
| Category of features | Number of features | Name of features |
|---|---|---|
| First Order Statistical Feature (FOSF) (Srinivasan & Shobha, 2008) | 8 | Mean (), Variance (), Standard deviation (), Skewness (), Kurtosis (), Smoothness (), Uniformity (), Entropy () |
| Gray Level Co-occurrence Matrix (GLCM) Texture Feature (Gómez et al., 2012, Haralick et al., 1973) | 88 (22 × 4) | Sum average, Sum variance, Difference variance, Energy, Autocorrelation, Entropy, Sum entropy, Difference entropy, Contrast, Homogeneity I, Homogeneity II, Correlation I, Correlation II, Cluster Prominence, Cluster Shade, Sum of squares, Maximum probability, Dissimilarity, Information measure of correlation I, Information measure of correlation II, Inverse difference normalized, Inverse difference moment normalized |
| Histogram of Oriented Gradients (HOG) (Dalal & Triggs, 2005, Santosh and Antani, 2018) | 8100 | f1, f2, f3, f4,…………………………………………., f8100 |
The HOG features (Dalal & Triggs, 2005, Santosh and Antani, 2018) extract the gradient magnitude and direction of local neighborhood, encoding the local shape and texture information. Initially, the input image is converted into smaller blocks for which gradient magnitude and orientation are computed, as shown in Eqs. (17) and (18), respectively. Further, the histogram bin is created and normalized to create a feature descriptor.
| (17) |
| (18) |
where, represents the gradient in and direction, respectively. represents the gradient direction.
Appendix B. Majority Voting of classifier ensemble
Initially, in step 1 and 2, each image from dataset D is retrieved, and class variables are initialized. The extracted images are tested via all the classification algorithms (i.e., SVM, ANN, KNN, NB, and DT), as shown in step 4. If the classifier classified the sample to a healthy class, the ‘Healthy’ class label would be incremented by 1 as shown in step 6. Similarly, for the samples classified to unhealthy class, the ‘Unhealthy’ class label will be incremented (shown step 8). Finally, based on the majority vote, a class label is assigned to each input image, as shown in step 11. Here, the majority vote acts as a multi-expert recommendation and reduce the probable chance of false diagnosis.
| Algorithm 1. Majority voting algorithm using ensemble of benchmark classifiers. |
|---|
| Input/Initialize |
| Validation dataset . // =number of images in the dataset |
| Classification model // = number of classification models |
| Healthy = 0; Unhealthy = 0; |
| Output |
| Prediction results of each image as healthy or infected. |
| Algorithm |
|
References
- Abbas, A., Abdelsamea, M. M., & Gaber, M. M. (2020). Classification of COVID-19 in chest X-ray images using DeTraC deep convolutional neural network. Retrieved from http://arxiv.org/abs/2003.13815. [DOI] [PMC free article] [PubMed]
- Altaf F., Islam S.M.S., Akhtar N., Janjua N.K. Going deep in medical image analysis: Concepts, methods, challenges and future directions. IEEE Access. 2019;7:99540–99572. http://arxiv.org/abs/1902.05655 Retrieved from. [Google Scholar]
- Ardakani A.A., Kanafi A.R., Acharya U.R., Khadem N., Mohammadi A. Application of deep learning technique to manage COVID-19 in routine clinical practice using CT images: Results of 10 convolutional neural networks. Computers in Biology and Medicine. 2020;121 doi: 10.1016/j.compbiomed.2020.103795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asnaoui, K. El Chawki, Y., & Idri, A. (2020). Automated methods for detection and classification pneumonia based on X-Ray images using deep learning. ArXiv Preprint ArXiv:2003.14363. Retrieved from http://arxiv.org/abs/2003.14363.
- Artificial Neural Networks. (2013). Retrieved August 8, 2018, from https://scholastic.teachable.com/courses/pattern-classification/lectures/1462278.
- Candemir S., Jaeger S., Palaniappan K., Musco J.P., Singh R.K., Xue Z.…McDonald C.J. Lung segmentation in chest radiographs using anatomical atlases with nonrigid registration. IEEE Transactions on Medical Imaging. 2014;33(2):577–590. doi: 10.1109/TMI.2013.2290491. [DOI] [PubMed] [Google Scholar]
- Chandra T.B., Verma K. Pneumonia Detection on Chest X-Ray Using Machine Learning Paradigm. In: Chaudhuri B.B., Nakagawa M., Khanna P., Kumar S., editors. Proceedings of third international conference on computer vision & image processing. Springer; Singapore: 2020. pp. 21–33. [DOI] [Google Scholar]
- Chandra T.B., Verma K. Analysis of quantum noise-reducing filters on chest X-ray images: A review. Measurement. 2020;153 doi: 10.1016/j.measurement.2019.107426. [DOI] [Google Scholar]
- Chandra T.B., Verma K., Jain D., Netam S.S. 2020 First international conference on power, control and computing technologies (ICPC2T) IEEE; 2020. Localization of the suspected abnormal region in chest radiograph images; pp. 204–209. [DOI] [Google Scholar]
- Chandra T.B., Verma K., Singh B.K., Jain D., Netam S.S. Automatic detection of tuberculosis related abnormalities in Chest X-ray images using hierarchical feature extraction scheme. Expert Systems with Applications. 2020;158 doi: 10.1016/j.eswa.2020.113514. [DOI] [Google Scholar]
- Chatterjee S., Dey D., Munshi S. Integration of morphological preprocessing and fractal based feature extraction with recursive feature elimination for skin lesion types classification. Computer Methods and Programs in Biomedicine. 2019;178:201–218. doi: 10.1016/j.cmpb.2019.06.018. [DOI] [PubMed] [Google Scholar]
- Chen Q., Meng Z., Su R. WERFE: A gene selection algorithm based on recursive feature elimination and ensemble strategy. Frontiers in Bioengineering and Biotechnology. 2020;8:496. doi: 10.3389/fbioe.2020.00496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen N., Zhou M., Dong X., Qu J., Gong F., Han Y.…Zhang L. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study. The Lancet. 2020;395(10223):507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng S.-C., Chang Y.-C., Fan Chiang Y.-L., Chien Y.-C., Cheng M., Yang C.-H.…Hsu Y.-N. First case of Coronavirus Disease 2019 (COVID-19) pneumonia in Taiwan. Journal of the Formosan Medical Association. 2020;119(3):747–751. doi: 10.1016/j.jfma.2020.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chouhan V., Singh S.K., Khamparia A., Gupta D., Tiwari P., Moreira C.…de Albuquerque V.H.C. A novel transfer learning based approach for pneumonia detection in chest X-ray images. Applied Sciences (Switzerland) 2020;10(2) doi: 10.3390/app10020559. [DOI] [Google Scholar]
- Chowdhury, M. E. H., Rahman, T., Khandakar, A., Mazhar, R., Kadir, M. A., Mahbub, Z. Bin, … Reaz, M. B. I. (2020). Can AI help in screening Viral and COVID-19 pneumonia? (March). Retrieved from http://arxiv.org/abs/2003.13145.
- Chung M., Bernheim A., Mei X., Zhang N., Huang M., Zeng X.…Shan H. CT imaging features of 2019 Novel Coronavirus (2019-nCoV) Radiology. 2020;295(1):202–207. doi: 10.1148/radiol.2020200230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen, J. P., Morrison, P., & Dao, L. (2020). COVID‐Chestxray Database. Retrieved June 20, 2020, from https://github.com/ieee8023/covid-chestxray-dataset.
- Coronavirus Disease 2019. (2020). Retrieved April 8, 2020, from World Health Organization website: https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
- Dalal N., Triggs B. In 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR’05) Vol. 1. 2005. Histograms of oriented gradients for human detection; pp. 886–893. [DOI] [Google Scholar]
- Emary E., Zawbaa H.M., Hassanien A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing. 2016;172:371–381. doi: 10.1016/j.neucom.2015.06.083. [DOI] [Google Scholar]
- Gómez W., Pereira W.C.A., Infantosi A.F.C. Analysis of co-occurrence texture statistics as a function of gray-level quantization for classifying breast ultrasound. IEEE Transactions on Medical Imaging. 2012;31(10):1889–1899. doi: 10.1109/TMI.2012.2206398. [DOI] [PubMed] [Google Scholar]
- Han J., Kamber M., Pei J. Data mining: Concepts and techniques. Morgan Kaufmann; San Francisco, CA, itd: 2012. [DOI] [Google Scholar]
- Haralick R.M., Shanmugam K., Dinstein I. Textural features for image classification. IEEE Transactions on Systems, Man, and Cybernetics. 1973;SMC-3(6):610–621. doi: 10.1109/TSMC.1973.4309314. [DOI] [Google Scholar]
- Ho T.K., Gwak J. Multiple feature integration for classification of thoracic disease in chest radiography. Applied Sciences. 2019;9(19):4130. doi: 10.3390/app9194130. [DOI] [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979;6:65–70. [Google Scholar]
- Hosseiny M., Kooraki S., Gholamrezanezhad A., Reddy S., Myers L. Radiology perspective of coronavirus disease 2019 (COVID-19): Lessons from severe acute respiratory syndrome and middle east respiratory syndrome. American Journal of Roentgenology. 2020;(October):1–5. doi: 10.2214/AJR.20.22969. [DOI] [PubMed] [Google Scholar]
- Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y.…Cao B. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. The Lancet. 2020;395(10223):497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeger S., Karargyris A., Candemir S., Folio L., Siegelman J., Callaghan F.…McDonald C.J. Automatic tuberculosis screening using chest radiographs. IEEE Transactions on Medical Imaging. 2014;33(2):233–245. doi: 10.1109/TMI.2013.2284099. [DOI] [PubMed] [Google Scholar]
- Jaiswal A.K., Tiwari P., Kumar S., Gupta D., Khanna A., Rodrigues J.J.P.C. Identifying pneumonia in chest X-rays: A deep learning approach. Measurement: Journal of the International Measurement Confederation. 2019;145:511–518. doi: 10.1016/j.measurement.2019.05.076. [DOI] [Google Scholar]
- Hemdan, E. E.-D., Shouman, M. A., & Karar, M. E. (2020). COVIDX-Net: A framework of deep learning classifiers to diagnose COVID-19 in X-Ray images. Retrieved from http://arxiv.org/abs/2003.11055.
- Johns Hopkins University, Corona Resource Center. (2020). Retrieved April 8, 2020, from https://coronavirus.jhu.edu/map.html.
- Kanne J.P., Little B.P., Chung J.H., Elicker B.M., Ketai L.H. Essentials for radiologists on COVID-19: An update-radiology scientific expert panel. Radiology. 2020;200527 doi: 10.1148/radiol.2020200527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ke Q., Zhang J., Wei W., Połap D., Woźniak M., Kośmider L., Damaševĭcius R. A neuro-heuristic approach for recognition of lung diseases from X-ray images. Expert Systems with Applications. 2019;126:218–232. doi: 10.1016/j.eswa.2019.01.060. [DOI] [Google Scholar]
- Khatami A., Khosravi A., Nguyen T., Lim C.P., Nahavandi S. Medical image analysis using wavelet transform and deep belief networks. Expert Systems with Applications. 2017;86:190–198. doi: 10.1016/j.eswa.2017.05.073. [DOI] [Google Scholar]
- Kooraki S., Hosseiny M., Myers L., Gholamrezanezhad A. Coronavirus (COVID-19) outbreak: What the department of radiology should know. Journal of the American College of Radiology. 2020;17(4):447–451. doi: 10.1016/j.jacr.2020.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirjalili S., Mirjalili S.M., Lewis A. Grey Wolf optimizer. Advances in Engineering Software. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
- Maghdid, H. S., Asaad, A. T., Ghafoor, K. Z., Sadiq, A. S., & Khan, M. K. (2020). Diagnosing COVID-19 pneumonia from X-Ray and CT images using deep learning and transfer learning algorithms. Arxiv.Org. Retrieved from https://arxiv.org/abs/2004.00038.
- Narin, A., Kaya, C., & Pamuk, Z. (2020). Automatic detection of coronavirus disease (COVID-19) using X-ray images and deep convolutional neural networks. ArXiv Preprint ArXiv:2003.10849. [DOI] [PMC free article] [PubMed]
- Nour M., Cömert Z., Polat K. A novel medical diagnosis model for COVID-19 infection detection based on deep features and Bayesian optimization. Applied Soft Computing. 2020;106580 doi: 10.1016/j.asoc.2020.106580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozturk T., Talo M., Yildirim E.A., Baloglu U.B., Yildirim O., Rajendra Acharya U. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Computers in Biology and Medicine. 2020;121 doi: 10.1016/j.compbiomed.2020.103792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantazi X.E., Moshou D., Bochtis D. Intelligent Data Mining and Fusion Systems in Agriculture. Elsevier; 2020. Artificial intelligence in agriculture; pp. 17–101. [DOI] [Google Scholar]
- Panwar H., Gupta P.K., Siddiqui M.K., Morales-Menendez R., Singh V. Application of deep learning for fast detection of COVID-19 in X-Rays using nCOVnet. Chaos, Solitons and Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pathak Y., Shukla P.K., Tiwari A., Stalin S., Singh S. Deep transfer learning based classification model for COVID-19 disease. IRBM. 2020 doi: 10.1016/j.irbm.2020.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesce E., Joseph Withey S., Ypsilantis P.P., Bakewell R., Goh V., Montana G. Learning to detect chest radiographs containing pulmonary lesions using visual attention networks. Medical Image Analysis. 2019;53:26–38. doi: 10.1016/j.media.2018.12.007. [DOI] [PubMed] [Google Scholar]
- Purkayastha S., Buddi S.B., Nuthakki S., Yadav B., Gichoya J.W. Evaluating the implementation of deep learning in LibreHealth Radiology on Chest X-Rays. Advances in Intelligent Systems and Computing. 2020;943:648–657. doi: 10.1007/978-3-030-17795-9_47. [DOI] [Google Scholar]
- Rish, I., et al. (2001). An empirical study of the naive Bayes classifier. IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence, 3(22), 41–46.
- Santosh K.C., Antani S. Automated chest x-ray screening: Can lung region symmetry help detect pulmonary abnormalities? IEEE Transactions on Medical Imaging. 2018;37(5):1168–1177. doi: 10.1109/TMI.2017.2775636. [DOI] [PubMed] [Google Scholar]
- Shaffer J.P. Modified sequentially rejective multiple test procedures. Journal of the American Statistical Association. 1986;81(395):826–831. [Google Scholar]
- Shalev-Shwartz S., Ben-David S. Cambridge University Press; 2014. Understanding machine learning: From theory to algorithms. [Google Scholar]
- Snoek J., Larochelle H., Adams R.P. Practical Bayesian optimization of machine learning algorithms. Advances in Neural Information Processing Systems. 2012;25:2951–2959. http://papers.nips.cc/paper/4522-practical-bayesian-optimization-of-machine-learning-algorithms.pdf Retrieved from. [Google Scholar]
- Sprawls, P. (2018). The physical principles of medical imaging, 2nd ed. Retrieved July 25, 2018, from http://www.sprawls.org/ppmi2/NOISE/.
- Srinivasan G., Shobha G. Statistical texture analysis. Proceedings of World Academy of Science, Engineering and Technology. 2008;36(December):1264–1269. http://staff.fh-hagenberg.at/wbackfri/Teaching/FBA/Uebungen/UE07charRecog/StatTextAnalysisSrinivasan08.pdf Retrieved from. [Google Scholar]
- Toğaçar M., Ergen B., Cömert Z. COVID-19 detection using deep learning models to exploit Social Mimic Optimization and structured chest X-ray images using fuzzy color and stacking approaches. Computers in Biology and Medicine. 2020;121 doi: 10.1016/j.compbiomed.2020.103805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Too J., Abdullah A., Mohd Saad N., Mohd Ali N., Tee W. A new competitive binary Grey Wolf optimizer to solve the feature selection problem in EMG signals classification. Computers. 2018;7(4):58. doi: 10.3390/computers7040058. [DOI] [Google Scholar]
- Ucar F., Korkmaz D. COVIDiagnosis-Net: Deep Bayes-SqueezeNet based diagnosis of the coronavirus disease 2019 (COVID-19) from X-ray images. Medical Hypotheses. 2020;140 doi: 10.1016/j.mehy.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vajda S., Karargyris A., Jaeger S., Santosh K.C.C., Candemir S., Xue Z.…Antani S. Feature selection for automatic tuberculosis screening in frontal chest radiographs. Journal of Medical Systems. 2018;42(8):146. doi: 10.1007/s10916-018-0991-9. [DOI] [PubMed] [Google Scholar]
- Vapnik, V. (1998). Statistical learning theory (Vol. 3). Wiley, New York.
- Venegas-Barrera C.S., Manjarrez J. Visual categorization with bags of keypoints. Revista Mexicana de Biodiversidad. 2011;82(1):179–191. doi: 10.1234/12345678. [DOI] [Google Scholar]
- Wang, L., & Wong, A. (2020). COVID-Net: A tailored deep convolutional neural network design for detection of COVID-19 cases from chest radiography images. ArXiv Preprint ArXiv:2003.09871. Retrieved from http://arxiv.org/abs/2003.09871. [DOI] [PMC free article] [PubMed]
- Wang, X., Peng, Y., Lu, L., Lu, Z., Bagheri, M., & Summers, R. M. (2017). Chestx-ray8: Hospital-scale chest x-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 2097-2106). doi:10.1109/CVPR.2017.369.
- Wang S., Kang B., Ma J., Zeng X., Xiao M., Guo J.…Xu B. A deep learning algorithm using CT images to screen for corona virus disease (COVID-19) MedRxiv. 2020 doi: 10.1101/2020.02.14.20023028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, X., Jiang, X., Ma, C., Du, P., Li, X., Lv, S., … Wu, W. (2020). Deep learning system to screen coronavirus disease 2019 pneumonia. Arxiv.Org. Retrieved from https://arxiv.org/abs/2002.09334. [DOI] [PMC free article] [PubMed]
- Xue Z., Jaeger S., Antani S., Long R., Karagyris A., Siegelman J.…Thoma G.R. Localizing tuberculosis in chest radiographs with deep learning. In: Zhang J., Chen P.-H., editors. Medical imaging 2018: Imaging informatics for healthcare, research, and applications. Vol. 3. 2018. p. 28. [DOI] [Google Scholar]
- Yoon S.H., Lee K.H., Kim J.Y., Lee Y.K., Ko H., Kim K.H.…Kim Y.-H. Chest radiographic and CT findings of the 2019 Novel Coronavirus Disease (COVID-19): Analysis of nine patients treated in Korea. Korean Journal of Radiology. 2020;21(4):494. doi: 10.3348/kjr.2020.0132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang N., Wang L., Deng X., Liang R., Su M., He C.…Jiang S. Recent advances in the detection of respiratory virus infection in humans. Journal of Medical Virology. 2020;92:408–417. doi: 10.1002/jmv.25674. [DOI] [PMC free article] [PubMed] [Google Scholar]