Human-robot mutual adaptation in collaborative tasks: Models and experiments

Abstract

Adaptation is critical for effective team collaboration. This paper introduces a computational formalism for mutual adaptation between a robot and a human in collaborative tasks. We propose the Bounded-Memory Adaptation Model, which is a probabilistic finite-state controller that captures human adaptive behaviors under a bounded-memory assumption. We integrate the Bounded-Memory Adaptation Model into a probabilistic decision process, enabling the robot to guide adaptable participants towards a better way of completing the task. Human subject experiments suggest that the proposed formalism improves the effectiveness of human-robot teams in collaborative tasks, when compared with one-way adaptations of the robot to the human, while maintaining the human’s trust in the robot.

1. Introduction

Robots are entering our homes and workplaces, complementing human abilities and skills in many application domains, including manufacturing, health-care, etc. They co-exist in the same physical space with humans and aim to become trustworthy partners in a team. Research on human teams shows that mutual adaptation, which requires all team-members involved to adapt their behaviors to fulfill common team goals, significantly improves team performance (Mathieu et al., 2000). We believe that the same holds for human-robot teams. Our main goal in this work is to develop a computational framework for human-robot mutual adaptation.

Consider, for example, the table-carrying task in Figure 1. A human and HERB (Srinivasa et al., 2010), an autonomous mobile manipulator, work together to carry a table out of a room. There are two strategies: the robot facing the door (Goal A) or the robot facing away from the door (Goal B). Assume that the robot prefers Goal A, as the robot’s forward-facing sensor has a clear view of the door, leading to better task performance. Not aware of this, an inexperienced human partner may prefer Goal B. Intuitively, if the human is adaptable and willing to accommodate the robot, the robot guides the human towards Goal A, which provides a better task performance overall. If the human is not adaptable and insists on his own preference, the robot then complies in order to complete the task, though sub-optimally. If the robot insists on its own preference, Goal A, it may lose the human’s trust, leading to a deteriorating team performance or even disuse of the robot (Hancock et al., 2011; Lee etal., 2013; Salem etal., 2015). The challenge is that when encountering a new human partner, the robot may not know his or her adaptability and must learn it on the fly through interaction.

Fig. 1.

A human and a robot collaborate to carry a table through a door. (a) The robot prefers facing the door (Goal A), as it has a full view of the door. (b) The robot faces away from the door (Goal B).

In this work, we propose a computational model for human-robot mutual adaptation in collaborative tasks. We build a model of human adaptive behaviors and integrate the model into a probabilistic decision process. One key idea here is the Bounded-Memory Adaptation Model (BAM), which is a probabilistic finite-state controller that captures human adaptive behaviors. The BAM assumes that the human operates in one of several collaboration “modes” and adapts the behavior by switching among the modes. To choose a new mode, the human maintains a finite history of past interactions and switches to the new mode probabilistically according to the adaptability level. The human’s adaptability level is a BAM model parameter unknown to the robot a priori. To work with such an adaptable human effectively, the robot must consider two sometimes conflicting objectives:

• gather information on the unknown parameter through interaction, in order to decide between complying with the human’s preference and guiding the human towards a better cooperation mode for task completion;

• choose actions towards the goal, e.g. moving the table out of the room.

We treat the unknown model parameter as a latent variable and embed the BAM in a probabilistic decision process, called the Mixed Observability Markov Decision Process (MOMDP) (Ong et al., 2010), for choosing robot actions. The computed MOMDP policy optimally balances the tradeoff between gathering information on human adaptability and moving towards the goal. Since the MOMDP model has the BAM embedded within, the chosen actions enable the robot to adapt to an adaptive human, thus achieving mutual adaptation as a result.

Our work contrasts with earlier approaches that rely on one-way adaptation of the robot to the human, such as crosstraining (Nikolaidis and Shah, 2013), a state-of-the-art method for human-robot team training. One-way adaptation focuses on computing a robot policy aligned with human preference. It ignores that the human preference may result in suboptimal task performance, as our example shows. Further, we cannot resolve this issue by having the robot insist on executing an optimal policy against the human’s preference. This may erode the human’s trust in the robot and lead to deteriorating team performance over time (Hancock et al., 2011; Lee et al., 2013; Salem et al., 2015).

Figure 2 shows examples of human and robot behaviors for three simulated humans in the table-carrying task (Figure 1). The robot estimates the unknown human adaptability through interaction. User 1 is fully non-adaptable with α= 0. The robot infers this after two steps of interaction and switches its action to comply with the human preference. User 3 is fully adaptable with α = 1 and switches to accommodate the robot preference after one step of interaction. User 2 is adaptable with α = 0.75. After several steps, the robot gets a good estimate on the human adaptability level and guides the human to the preferred strategy. We want to emphasize here that the robot executes a single policy that adapts to different human behaviors. If the human is non-adaptable, the robot complies to the human’s preferred strategy. Otherwise, the robot guides the human towards a better strategy.

Fig. 2.

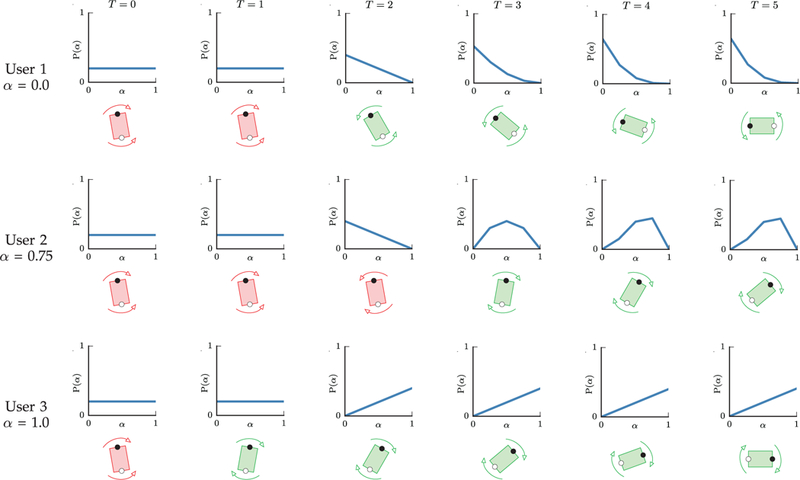
Sample runs on the human-robot table-carrying task, with three simulated humans of adaptability level α = 0, 0.75, and 1. A fully adaptable human has α = 1, while a fully non-adaptable human has α = 0. In each case, the upper row shows the probabilistic estimate on α over time. The lower row shows the robot and human actions over time. Red color indicates human (white dot) and robot (black dot) disagreement in their actions, in which case the table does not move. The columns indicate successive time steps. User 1 is non-adaptable, and the robot complies with his preference. Users 2 and 3 are adaptable to different extent. The robot successfully guides them towards a better strategy.

We are interested in studying whether a robot, under our proposed approach, is able to guide human partners towards a better collaboration strategy, sometimes against their initial preference, while still retaining their trust. We conducted a human subject experiment online via video playback (n = 69) on the simulated table carrying task (Figure 1). In the experiment, participants were significantly more likely to adapt, when working with the robot utilizing our mutually adaptive approach, when compared with the robot that cross-trained with the participants. Additionally, the participants found that the mutually adaptive robot has performance not worse than the cross-trained robot. Finally, the participants found that the mutually adaptive robot was more trustworthy than the robot in executing a fixed strategy optimal in task performance, but ignoring the human preference.

We are also interested in how adaptability and trust change over time. We hypothesized that trust in the mutually adaptive robot increases over time for non-adaptable participants, as previous work suggests that robot adaptation significantly improves perceived robot trustworthiness (Shah et al., 2011), and that the increase in trust results in a subsequent increased likelihood of human adaptation to the robot. A human subject experiment on repeated table-carrying tasks (n = 43) did not support this hypothesis.

To study the generality of our model, we hypothesized that non-adaptable participants in the table-carrying task would be less likely to adapt in a different collaborative task. A follow-up human subject experiment with a hallway-crossing task (n = 58) confirmed the hypothesis.

In the following, Section 2 reviews related work. Section 3 formally describes the problem setting. Section 4 and 5 presents BAM, the proposed model of human adaptation, and the integration of BAM in the robot decision making process using an MOMDP formulation. Section 6 and 7 describes our human subject experiments and presents the main findings that suggest significant improvement in human-robot team effectiveness, while human subject ratings on the robot performance and trust are comparable to those achieved by cross-training, a state-of-the-art human-robot team training practice. Finally, we discuss the effects of repeated trials on participants’ adaptability over time in Section 8 and the transfer of adaptability across tasks in Section 9.

2. Relevant work

There has been extensive work on one-way robot adaptation to humans. Approaches involve a human expert providing demonstrations to teach the robot a skill or a specific task (Argall et al., 2009; Atkeson and Schaal, 1997; Abbeel and Ng, 2004; Akgun et al., 2012; Chernova and Veloso, 2008; Nicolescu and Mataric, 2003). Robots have also been able to infer the human preference online through interaction. In particular, partially observable Markov decision process (POMDP) models have allowed reasoning over the uncertainty on the human intention (Broz et al., 2011; Doshi and Roy, 2007; Lemon and Pietquin, 2012). The MOMDP formulation (Ong et al., 2010) has been shown to achieve significant computational efficiency and has been used in motion planning applications (Bandyopadhyay et al., 2013). Recent work has also inferred human intention through decomposition of a game task into subtasks for game AI applications. One such study (Nguyen et al., 2011) focused on inferring the intentions of a human player, allowing a non-player character (NPC) to assist the human. Alternatively, Macindoe et al. (2012) proposed the partially observable Monte-Carlo cooperative planning system, in which human intention is inferred for a turn-based game. Niko-laidis et al. (2015) proposed a formalism to learn human types from joint-action demonstrations, infer online the type of a new user and compute a robot policy aligned to their preferences. Simultaneous intent inference and robot adaptation has also been achieved through propagation of state and temporal constraints (Karpas et al., 2015). Another approach has been the human-robot cross-training algorithm, where the human demonstrates their preference by switching roles with the robot, shaping the robot reward function (Nikolaidis and Shah, 2013). Although it is possible that the human changes strategies during the training, the algorithm does not use a model of human adaptation that can enable the robot to actively influence the actions of its human partner.

There have also been studies in human adaptation to the robot. Previous work has focused on operator training for military, space, and search-and-rescue applications, with the goal of reducing the operator workload and operational risk (Goodrich and Schultz, 2007). Additionally, researchers have studied the effects of repeated interactions with a humanoid robot on the interaction skills of children with autism (Robins et al., 2004), on language skills of elementary school students (Kanda et al., 2004), as well as on users’ spatial behavior (Green and Hütten-rauch, 2006). Human adaptation has also been observed in an assistive walking task, where the robot uses human feedback to improve its behavior, which in turn influences the physical support provided by the human (Ikemoto et al., 2012). While the changes in the human behavior are an essential part of the learning process, the system does not explicitly reason over the human adaptation throughout the interaction. On the other hand, Dragan and Srinivasa (2013) proposed a probabilistic model of the inference made by a human observer over the robot goals, and introduced a motion generating algorithm to maximize this inference towards a predefined goal.

The proposed formalism of human-robot mutual adaptation is an attempt to close the loop between the two lines of research. The robot leverages a human adaptation model parameterized by human adaptability. It reasons probabilistically over the different ways that the human may change the strategy and adapts its own actions to guide the human towards a more effective strategy when possible.

Mutual adaptation between agents has been studied extensively in game theory (Fudenberg and Tirole, 1991). Game theory often relies on strong assumptions on the rationality of agents and the knowledge of payoff functions. These assumptions may not be suitable when agents are unable or unwilling to reason about optimal strategies for themselves or others (Fudenberg and Levine, 1998). This is particularly true in the human-robot team setting, when the human is unsure about how the robot will act and has little time to respond. We propose a model of human adaptive behaviors based on a bounded memory assumption (Powers and Shoham, 2005; Monte, 2014; Aumann and Sorin, 1989) and integrate it into robot decision making.

This paper is an extension of our earlier work (Nikolaidis et al., 2016), with a new collaborative task where a human and a robot cross a corridor and with additional human subject experiments on human adaptability.

3. Problem setting

A human-robot team can be treated as a multi-agent system, with world state x^world ∈ X^world, robot action a^R ∈ A^R, and human action a^H ∈ A^H. The system evolves according to a stochastic state transition function T: X^world × A^R × A^H → $\Pi$ (X^world). At each time step, the human-robot team receives a real-valued reward R(x^world, a^R, a^H). Its goal is to maximize the expected total reward over time:${\sum }_{t=0}^{\infty }{\gamma }^{t}R(t),$, where the discount factor $\gamma \in [0,1)$ gives higher weight to immediate rewards than to future ones.

The robot and the human choose their actions independently. To compute the robot actions that maximize the total reward, we first model the human behavior. We assume that the human acts according to an adaptive stochastic policy ${\pi }^{\text{H}}:X^{\text{world}}\times H_t\to \Pi \left(A^{\text{H}}\right),$ which chooses the next action stochastically based on the current world state x^world and the history of interactions h_t = (x^world( 0), a^R( 0), a^H( 0),..., x^world( t – 1), a^R( t – 1), a^H( t – 1)). Specifically, BAM, our proposed model of human adaptation, defines a set M of modal policies or modes and assumes that the human switches among the modes stochastically A mode $\mu :X^{\text{ world }}\times H_t\times A^{\text{R}}\times A^{\text{H}}\to \{0,1\}$ is a deterministic policy that maps the current world state and history to joint human-robot actions. At each time step, the human follows a mode ${\mu }^{\text{H}}\in M$ and observes that the robot follows a mode ${\mu }^{\text{R}}\in M.$ To collaborate with the robot, the human may switch to μ^R at the next time step, with probability α. If α = 1, the human switches to μ^R almost surely. If α = 0, the human insists on the original mode μ^H and does not adapt at all. Intuitively, α captures the human’s inclination to adapt.

If the human is not adaptable, the robot must switch to μ^H eventually in order to complete the task. If the human is adaptable and μ^R provides higher total reward than μ^H, the robot then stays with μ^R, expecting the human to follow. The robot may interact with different humans, and the adaptability level α of a new human teammate is unknown in advance. What shall the robot do? To compute a policy for the robot, we treat α as a latent variable and embed the BAM for the human in an MOMDP (Figure 3), which is a structured version of the more common Partially Observable Markov Decision Process (POMDP) (Kaelbling et al., 1998). The solution to the MOMDP is a robot policy π^R that estimates the value of α through the history of interactions, and uses the estimate to predict future human actions and choose the best robot actions towards task completion. The policy is optimal in the sense that it achieves the maximum expected total reward among all policies for the humanrobot team, under the assumed human adaptive behavior model.

Fig. 3.

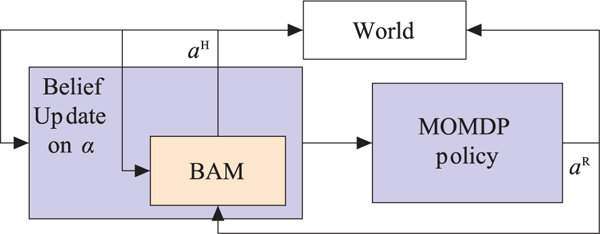
Integration of BAM (Bounded-Memory Adaptation Model) into MOMDP (Mixed Observability Markov Decision Process) formulation.

More details are given in the next two sections.

4. The bounded memory adaptation model

We model the human policy π^H as a probabilistic finite-state automaton (PFA), with a set of states $Q:X^{\text{ world }}\times H_t.$ A joint human-robot action a^H, a^R triggers an emission of a human and robot modal policy $f:Q\times M\times M\to \{0,1\},$ as well as a transition to a new state $P:Q\to \Pi (Q).$

4.1. Bounded memory assumption

Herbert Simon proposed that people often do not have the time and cognitive capabilities to make perfectly rational decisions, in what he described as “bounded rationality” (Simon, 1979). This idea has been supported by studies in psychology and economics (Kahneman, 2003). In game theory, bounded rationality has been modeled by assuming that players have a “bounded memory” or “bounded recall” and base their decisions on recent observations (Powers and Shoham, 2005; Monte, 2014; Aumann and Sorin, 1989). In this work, we introduce the bounded memory assumption in a human-robot collaboration setting. Under this assumption, humans will choose their action based on a history of k-steps in the past, so that $Q:X^{\text{ world }}\times H_k.$

4.2. Feature selection

The size of the state-space in the PFA can be quite large $\left({\left|X^{\text{ world }}\right|}^{k+1}{\left|A^{\text{R}}\right|}^k{\left|A^{\text{H}}\right|}^k|\right).$ Therefore, we approximate it using a set of features, so that $\varphi (q)=\left\{{\varphi }_1(q),{\varphi }_2(q),\dots ,{\varphi }_N(q)\right\}.$ We can choose as features the frequency counts ${\varphi }_{\mu }^{\text{H}},{\varphi }_{\mu }^{\text{R}}$ of the modal policies followed in the interaction history, so that

$${\varphi }_{\mu }^{\text{H}}=\sum _{i=1}^k\left[{\mu }_i^{\text{H}}=\mu \right]{\varphi }_{\mu }^{\text{R}}=\sum _{i=1}^k\left[{\mu }_i^{\text{R}}=\mu \right]\forall \mu \in M$$ (1)

${\mu }_i^{\text{H}}$and ${\mu }_i^{\text{R}}$ is the modal policy of the human and the robot i time-steps in the past. We note that k defines the history length, with k = 1 implying that the human will act based only on the previous interaction. Drawing upon insights from previous work which assumes maximum likelihood observations for policy computation in belief-space (Platt et al., 2010), we used as features the modal policies with the maximum frequency count

$${\mu }^{\text{H}}=\underset{\mu }{\arg \max }{\varphi }_{\mu }^{\text{H}}{\mu }^{\text{R}}=\underset{\mu }{\arg \max }{\varphi }_{\mu }^{\text{R}}$$ (2)

The proposed model does not require a specific feature representation. For instance, we could construct features by combining modal policies ${\mu }_i^{\text{H}},$ ${\mu }_i^{\text{R}}$ using an arbitration function (Dragan and Srinivasa, 2012).

For the case of fully observable modes, it is sufficient to retain only the k-length mode history, rather than H_k, simplifying the problem. In the general case of partially observable modes, though, the human would need to maintain a probability distribution over robot modes, and H_k may be required to model the human inference. We leave this case for future work.

4.3. Human adaptability

We define the adaptability as the probability of the human switching from their mode to the robot mode. It would be unrealistic to assume that all users are equally likely to adapt to the robot. Instead, we account for individual differences by parameterizing the transition function P by the adaptability α of an individual. Then, at state q the human will transition to a new state by choosing an action specified by μ^R with probability α, or an action specified by μ^H with probability 1 – α (Figure 4).

Fig. 4.

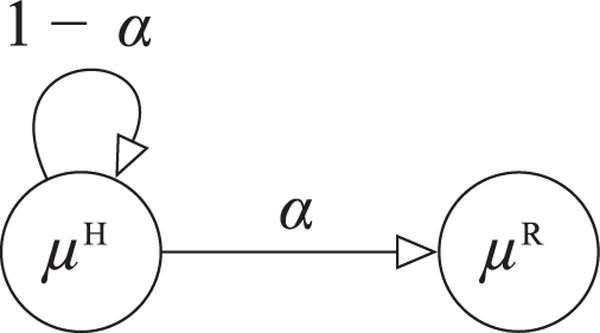
The BAM human adaptation model.

In order to account for unexpected human behavior, we assign uniformly a small, non-zero probability ϵ for the human taking a random action of some mode other than ${\mu }^{\text{R}},{\mu }^{\text{H}}.$ The parameter ϵ plays the role of probability smoothing. In the time-step that this occurs, the robot’s belief on α will not change. In the next time-step, the robot will include the previous human action in its inference of the human mode μ^H.

We note that the Finite State Machine in Figure 4 shows the human mode transition in one time-step only. For instance, if the human switches from μ^H to μ^R and k = 1, in the next time-step the new human mode μ^H will be what was previously μ^R. In that case, oscillation between μ^R and μ^H can occur. We discuss this in Section 7.3.

4.4. Characterizing modal policies

At each time-step, the human and robot modes are not directly observed, but must be inferred from the human and robot actions. This can be achieved by characterizing a set of modal policies through one of the following ways:

Manual specification.

In some cases the modal policies can be easily specified. For instance, if two agents are crossing a corridor (Section 9), there are two deterministic policies leading to task completion, one for each side. Therefore, we can infer a mode directly from the action taken.

Learning from demonstration.

In previous work, joint-action demonstrations on a human-robot collaborative task were clustered into groups and a reward function was learned for each cluster (Nikolaidis et al., 2015), which we can then associate with a mode.

Planning-based prediction.

Previous work assumes that people move efficiently to reach destinations by optimizing a cost-function, similarly to a goal-based planner (Ziebart et al., 2009). Given a set of goal-states and a partial trajectory, we can associate modes with predictive models of future actions towards the most likely goal.

Computation of nash equilibria.

Following a game-theoretic approach, we can view the interaction as a stochastic game and restrict the set of modal policies to the equilibrium strategies. For instance, we can formulate the example of human and robot crossing a corridor as a coordination game, where strategies of both agents moving on opposite sides strictly dominate strategies where they collide.

5. Robot planning

In this section we describe the integration of BAM in the robot decision making process using an MOMDP formulation. An MOMDP uses proper factorization of the observable and unobservable state variables S : X × Y with transition functions $T_x$ and$T_y$reducing the computational load (Ong et al., 2010). The set of observable state variables is $X:X^{\text{ world }}\times M^k\times M^k,$ where X^world is the finite set of tasksteps that signify the progress towards task completion and M is the set of modal policies followed by the human and the robot in a history length k. The partially observable variable y is identical to the human adaptability α. We assume finite sets of human and robot actions A^H and A^R, and we denote as π^H the stochastic human policy. The latter gives the probability of a human action a^H at state s, based on the BAM human adaptation model.

Given $a^{\text{R}}\in A^{\text{R}}$ and $a^{\text{H}}\in A^{\text{H}},$ the belief update becomes

$$\begin{gathered} b^{\prime }\left(y^{\prime }\right)=\eta O\left(s^{\prime },a^{\text{R}},o\right)\sum _{y\in Y}{\mathcal{T}}_x\left(s,a^{\text{R}},a^{\text{H}},x^{\prime }\right) \\ {\mathcal{T}}_y\left(s,a^{\text{R}},a^{\text{H}},s^{\prime }\right){\pi }^{\text{H}}\left(s,a^{\text{H}}\right)b(y) \end{gathered}$$ (3)

We use a point-based approximation algorithm to solve the MOMDP for a robot policy π^R that takes into account the robot belief on the human adaptability, while maximizing the agent’s expected total reward.

The policy execution is performed online in real time and consists of two steps (Figure 3). First, the robot uses the current belief to select the action a^R specified by the policy. Second, it uses the human action a^H to update the belief on α (equation (3)). Figure 5 presents the paths on the MOMDP policy tree that correspond to the simulated user behaviors presented in Figure 2. Figure 6 shows instances of actual user behaviors in the human subject experiment described in Section 6.

Fig. 5.

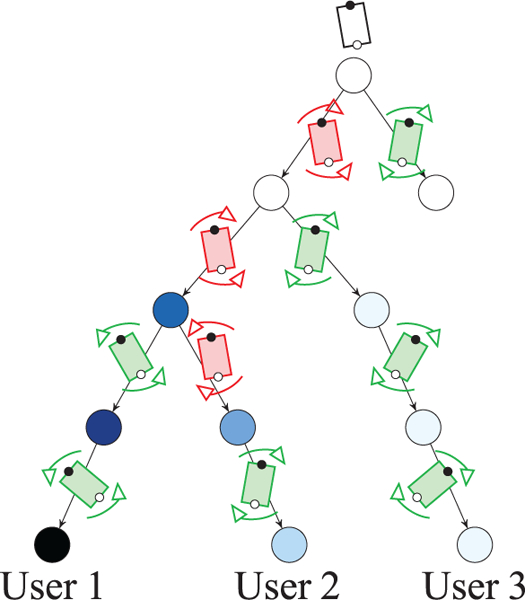
Different paths on MOMDP policy tree for human-robot (white/black dot) table-carrying task. The circle color represents the belief on α, with darker shades indicating higher probability for smaller values (less adaptability). The white circles denote a uniform distribution over α. User 1 is inferred as non-adaptable, whereas Users 2 and 3 are adaptable.

Fig. 6.

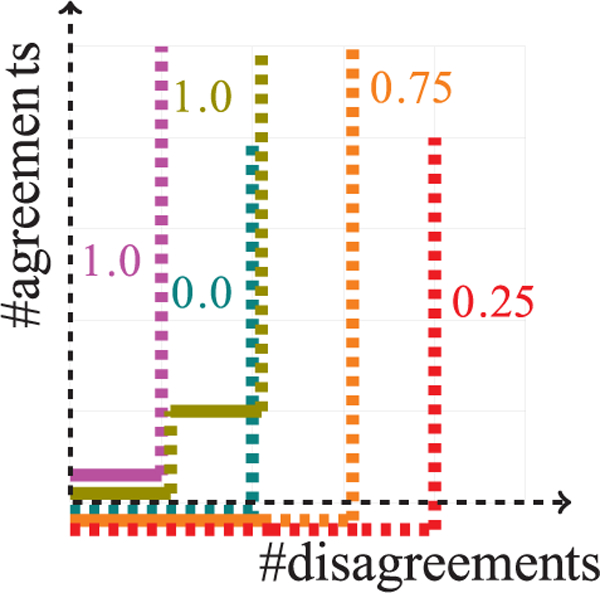
Instances of different user behaviors in the first trial of the Mutual-adaptation session of the human-subject experiment described in Section 6. A horizontal/vertical line segment indicates human and robot disagreement/agreement on their actions. A solid/dashed line indicates a human rotation towards the sub-optimal/optimal goal. The numbers denote the most likely estimated value of α.

6. Human subject experiment

We conducted a human subject experiment on a simulated table-carrying task (Figure 1) to evaluate the proposed formalism. We were interested in showing that integrating BAM into the robot decision making can lead to more efficient policies than the state-of-the-art human-robot team training practices, while maintaining human satisfaction and trust.

On one extreme, we can “fix” the robot policy so that the robot always moves towards the optimal —with respect to some objective performance metric —goal, ignoring human adaptability. This will force all users to adapt, since this is the only way to complete the task. However, we hypothesize that this will significantly impact human satisfaction and trust in the robot. On the other extreme, we can efficiently learn the human preference (Nikolaidis and Shah, 2013). This can lead to the human-robot team following a sub-optimal policy, if the human has an inaccurate model of the robot capabilities. We have, therefore, two control conditions: one where participants interact with the robot executing a fixed policy, always acting towards the optimal goal, and one where the robot learns the human preference. We show that the proposed formalism achieves a tradeoff between the two: When the human is non-adaptable, the robot follows the human strategy. Otherwise, the robot insists on the optimal way of completing the task, leading to significantly better policies compared to learning the human preference.

6.1. Independent variables

We had three experimental conditions, which we refer to as “Fixed,” “Mutual-adaptation”, and “Cross-training.”

Fixed session.

The robot executes a fixed policy, always acting towards the optimal goal. In the table-carrying scenario, the robot keeps rotating the table in the clockwise direction towards Goal A, which we assume to be optimal (Figure 1). The only way to finish the task is for the human to rotate the table in the same direction as the robot, until it is brought to the horizontal configuration of Figure 1a.

Mutual-adaptation session.

The robot executes the MOMDP policy computed using the proposed formalism. The robot starts by rotating the table towards the optimal goal (Goal A). Therefore, adapting to the robot strategy corresponds to rotating the table to the optimal configuration.

Cross-training session.

Human and robot train together using the human-robot cross-training algorithm (Nikolaidis and Shah, 2013). The algorithm consists of a forward phase and a rotation phase. In the forward phase, the robot executes an initial policy, which we choose to be the one that leads to the optimal goal. Therefore, in the table-carrying scenario, the robot rotates the table in the clockwise direction towards Goal A. In the rotation phase, human and robot switch roles, and the human inputs are used to update the robot reward function. After the two phases, the robot policy is recomputed.

6.2. Hypotheses

H1

Participants will agree more strongly that HERB is trustworthy, and will be more satisfied with the team performance in the Mutual-adaptation condition, when compared to working with the robot in the Fixed condition. We expected users to trust more the robot with the learned MOMDP policy, when compared with the robot that executes a fixed strategy ignoring the user’s willingness to adapt. In prior work, a task-level executive that adapted to the human partner significantly improved perceived robot trustworthiness (Shah et al., 2011). Additionally, working with a human-aware robot that adapted its motions had a significant impact on human satisfaction (Lasota and Shah, 2015).

H2

Participants are more likely to adapt to the robot strategy towards the optimal goal in the Mutual-adaptation condition, when compared to working with the robot in the Cross-training condition. The computed MOMDP policy enables the robot to infer online the adaptability of the human and guides adaptable users towards more effective strategies. Therefore, we posited that more subjects would change their strategy when working with the robot in the Mutual-adaptation condition, compared with cross-training with the robot. We note that in the Fixed condition all participants ended up changing to the robot strategy, as this was the only way to complete the task.

H3

The robot’s performance as a teammate, as perceived by the participants in the Mutual-adaptation condition, will not be worse than in the Cross-training condition. The learned MOMDP policy enables the robot to follow the preference of participants that are less adaptable, while guiding towards the optimal goal participants that are willing to change their strategy. Therefore, we posited that this behavior would result in a perceived robot performance not inferior to that achieved in the Cross-training condition.

6.3. Experiment setting: A table-carrying task

We first instructed participants in the task and asked them to choose one of the two goal configurations (Figure 1), as their preferred way of accomplishing the task. To prompt users to prefer the sub-optimal goal, we informed them about the starting state of the task, where the table was slightly rotated in the counter-clockwise direction, making the sub-optimal Goal B appear closer. Once the task started, the user chose the rotation actions by clicking on buttons on a user interface (Figure 7). If the robot executed the same action, a video played showing the table rotation. Otherwise, the table did not move and a message appeared on the screen notifying the user that they tried to rotate the table in a different direction than the robot. In the Mutualadaptation and Fixed conditions participants executed the task twice. Each trial ended when the team reached one of the two goal configurations. In the Cross-training condition, participants executed the forward phase of the algorithm in the first trial and the rotation phase, where human and robot switched roles, in the second trial. We found that in this task one rotation phase was enough for users to successfully demonstrate their preference to the robot. Following Nikolaidis and Shah (2013), the robot executed the updated policy with the participant in a task-execution phase that succeeded the rotation phase.

Fig. 7.

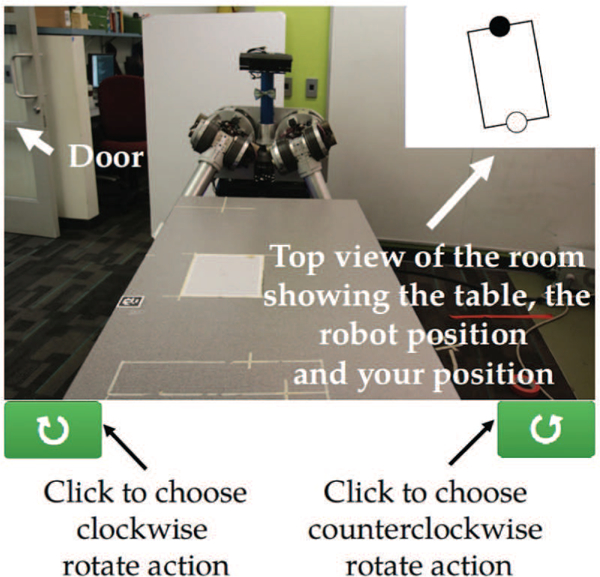
UI with instructions. UI: User Interface.

We asked all participants to answer a post-experimental questionnaire that used a five-point Likert scale to assess their responses to working with the robot (Table 2). We used the composite measures proposed by Hoffman (2013). Questions 1 and 3 are from Hoffman’s measure of “Robot Teammate Traits”, while questions 4–6 are from Hoffman’s adaptation of the “Working Alliance Index” for human-robot teams. Items 7–8 were proposed by Gombolay et al. (2014) as additional metrics of team-fluency. We added questions 9–10 were based on our intuition. Participants also responded to open-ended questions about their experience.

Table 2.

Post-experimental questionnaire.

Q1: “HERB is trustworthy.”

Q2: “I trusted HERB to do the right thing at the right time.”

Q3: “HERB is intelligent.”

Q4: “HERB perceived accurately what my goals are.”

Q5: “HERB did not understand how I wanted to do the task.”

Q6: “HERB and I worked towards mutually agreed upon goals.”

Q7: “I was satisfied with HERB and my performance.”

Q8: “HERB and I collaborated well together.”

Q9: “HERB made me change my mind during the task.”

Q10: “HERB’s actions were reasonable.”

6.4. Subject allocation

We chose a between-subjects design in order to not bias the users with policies from previous conditions. We recruited participants through Amazon’s Mechanical Turk service, all from the United States, aged 18–65 and with approval rates higher than 95%. Each participant was compensated $0.50. Since we are interested in exploring human-robot mutual adaptation, we disregarded participants that had as initial preference the robot goal. To ensure reliability of the results, we asked all participants a control question that tested their attention to the task and eliminated data associated with wrong answers to this question, as well as incomplete data. To test their attention to the Likert questionnaire, we included a negative statement with the opposite meaning to its positive counterpart and eliminated data associated with positive or negative ratings to both statements, resulting in a total of 69 samples.

6.5. MOMDP model

The observable state variables x of the MOMDP formulation were the discretized table orientation and the human and robot modes for each of the three previous time-steps. We specified two modal policies, each deterministically selecting rotation actions towards each goal. The size of the observable state-space X was 734 states. We set a history length k = 3 in BAM. We additionally assumed a discrete set of values of the adaptability : {0.0,0.25,0.5,0.75,1.0}. Although a higher resolution in the discretization of α is possible, we empirically verified that five values were enough to capture the different adaptive behaviors observed in this task. The total size of the MOMDP state-space was 5 × 734 = 3670 states. The human and robot actions a^H, a^R were deterministic discrete table rotations. We set the reward function R to be positive at the two goal configurations based on their relative cost, and 0 elsewhere. We computed the robot policy using the SARSOP solver (Kurniawati et al., 2008), a point-based approximation algorithm which, combined with the MOMDP formulation, can scale up to hundreds of thousands of states (Bandyopadhyay et al., 2013).

7. Results and discussion

7.1. Subjective measures

We consider hypothesis H1, that participants will agree more strongly that HERB is trustworthy, and will be more satisfied with the team performance in the Mutualadaptation condition, compared to working with the robot in the Fixed condition. A two-tailed Mann–Whitney–Wilcoxon test showed that participants indeed agreed more strongly that the robot utilizing the proposed formalism is trustworthy (U = 180,p = 0.048). No statistically significant differences were found for responses to statements eliciting human satisfaction: “I was satisfied with the robot and my performance” and “HERB and I collaborated well together”. One possible explanation is that participants interacted with the robot through a user interface for a short period of time, therefore the impact of the interaction on user satisfaction was limited.

We were also interested in observing how the ratings in the first two conditions varied, depending on the participants’ willingness to change their strategy. Therefore, we conducted a post-hoc experimental analysis of the data, grouping the participants based on their adaptability. Since the true adaptability of each participant is unknown, we estimated it by the mode of the belief formed by the robot at the end of the task on the adaptability α

$$\widehat{\alpha }=\underset{\alpha }{\arg \max }b(\alpha )$$ (4)

We considered only users whose mode was larger than a confidence threshold and grouped them as very adaptable if $\widehat{\alpha }>$ 0.75, moderately adaptable if 0.5 < $\widehat{\alpha }$ < 0.75, and non-adaptable if $\widehat{\alpha }$ < 0.5. Figure 10b shows the participants’ rating of their agreement on the robot trustworthiness, as a function of the participants’ group for the two conditions. In the Fixed condition there was a trend towards positive correlation between the annotated robot trustworthiness and participants’ inferred adaptability (Pearson’s r = 0.452, p = 0.091), whereas there was no correlation between the two for participants in the Mutual-adaptation condition (r = –0.066). We attribute this to the MOMDP formulation allowing the robot to reason over its estimate on the adaptability of its teammate and change its own strategy when interacting with non-adaptable participants, therefore maintaining human trust.

Fig. 10.

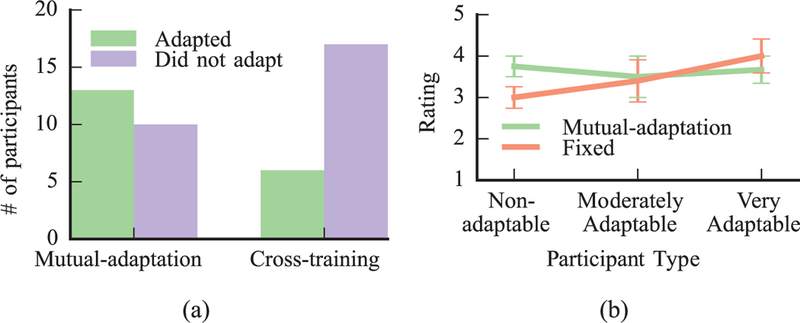
(a) Number of participants that adapted to the robot for the Mutual-adaptation and Cross-training conditions. (b) Rating of agreement to statement “HERB is trustworthy”. Note that the figure does not include participants, whose mode of the belief on their adaptability was below a confidence threshold and therefore were not clustered into any of the three groups.

In this work, we elicited trust at the end of the task using participants’ rating of their agreement to the statement “HERB is trustworthy”, which has been used in previous work in human-robot collaboration (Shah et al., 2011; Hoffman, 2013). We refer the reader to Desai (2012), Kaniarasu et al. (2013), Xu and Dudek (2015) and Yanco et al. (2016) for approaches on measuring trust in real-time.

We additionally coded the participants’ open-ended comments about their experience with working with HERB, and grouped them based on the content and the sentiment (positive, negative, or neutral). Table 3 shows the different comments and associated sentiments, and Figure 9 illustrates the participants’ ratio for each comment. We note that 20% of participants in the Fixed condition had a negative opinion about the robot behavior, noting that “[HERB] was poorly designed”, and that probably “robot development had not been mastered by engineers” (C8 in Table 3). On the other hand, 26% of users in the Mutual-adaptation condition noted that the robot “attempted to anticipate my moves” and “understood which way I wanted to go” (C2). Several adaptable participants in both conditions commented that “[HERB] was programmed to move this way” (C5), while some of them attempted to justify HERB’s actions, stating that it “was probably unable to move backwards” (C4).

Table 3.

Participants’ comments and associated sentiments.

	Description	Sentiment
Cl	“The robot followed my instructions.”	Positive
C2	“The robot adapted to my actions.”	Positive
C3	“The robot wanted to be efficient.”	Positive
C4	“The robot was unable to move.”	Neutral
C5	“The robot was programmed this way.”	Neutral
C6	“The robot wanted to face the door.”	Neutral
C7	“The robot was stubborn.”	Negative
C8	“The robot was poorly programmed.”	Negative

Fig. 9.

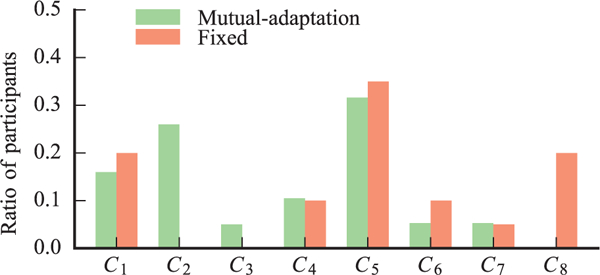
Ratio of participants per comment for the Mutualadaptation and Fixed conditions.

Recall hypothesis H3: that the robot’s performance as a teammate in the Mutual-adaptation condition, as perceived by the participants, would not be worse than in the Cross-training condition. We define “not worse than” similarly to Dragan et al. (2013) using the concept of “non-inferiority” (Lesaffre, 2008). A one-tailed unpaired t-test for a non-inferiority margin Δ = 0.5 and a level of statistical significance α = 0.025 showed that participants in the Mutualadaptation condition rated their satisfaction on robot performance (p = 0.006), robot intelligence (p = 0.024), robot trustworthiness (p < 0.001), quality of robot actions (p < 0.001), and quality of collaboration (p = 0.002) not worse than participants in the Cross-training condition. With Bonferroni corrections for multiple comparisons, robot trustworthiness, quality of robot actions, and quality of collaboration remain significant. This supports hypothesis H3 of Section 6.2.

7.2. Quantitative measures

To test hypothesis H2, we consider the ratio of participants that changed their strategy to the robot strategy towards the optimal goal in the Mutual-adaptation and Cross-training conditions. A change was detected when the participant started as a preferred strategy a table rotation towards Goal B (Figure 1b), but completed the task in the configuration of Goal A (Figure 1a) in the final trial of the Mutual-adaptation session, or in the task-execution phase of the Cross-training session. As Figure 10a shows, 57% of participants adapted to the robot in the Mutual-adaptation condition, whereas 26% adapted to the robot in the Cross-training condition. A Pearson’s chi-square test showed that the difference is statistically significant (${\chi }^2(1,N=46)=4.39,p=0.036$). Therefore, participants that interacted with the robot of the proposed formalism were more likely to switch to the robot strategy towards the optimal goal, than participants that cross-trained with the robot, which supports our hypothesis.

In Section 7.3, we discuss the robot’s behavior for different values of history length k in BAM.

7.3. Selection of history length

The value of k in BAM indicates the number of time-steps in the past that we assume humans consider in their decision making on a particular task, ignoring all other history. Increasing k results in an exponential increase of the state space size, with large values reducing the robot’s responsiveness to changes in the human behavior. On the other hand, very small values result in unrealistic assumptions on the human decision making process.

To illustrate this, we set k = 1 and ran a pilot study of 30 participants through Amazon-Turk. Whereas most users rated highly their agreement to questions assessing their satisfaction and trust in the robot, some participants expressed their strong dissatisfaction with the robot behavior. This occurred when human and robot oscillated back and forth between modes, similarly to when two pedestrians on a narrow street face each other and switch sides simultaneously until they reach an agreement. In this case, which occurred in 23% of the samples, when the human switched back to their initial mode, which was also the robot mode of the previous time-step, the robot incorrectly inferred them as adaptable. However, the user in fact resumed their initial mode followed before two time-steps, implying a tendency for non-adaptation. This is a case where the 1-step bounded memory assumption did not hold.

In the human subject experiment of Section 6, we used k = 3, since we found this to describe accurately the human behavior in this task. Figure 8 shows the belief update and robot behavior for k = 1 and k = 3, in the case of mode oscillation.

Fig. 8.

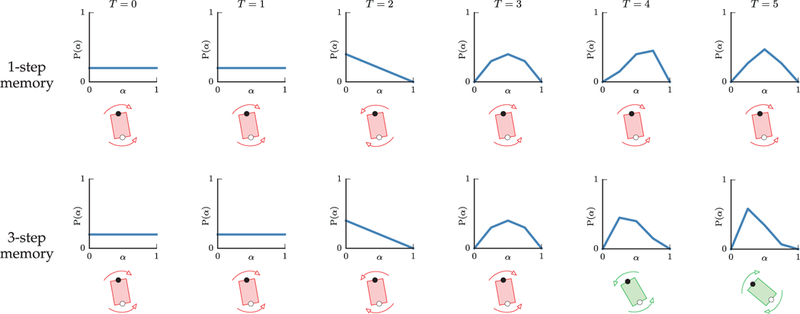
Belief update and table configurations for the 1-step (top) and 3-step (bottom) bounded memory models at successive time-steps. (T = 1) After the first disagreement and in the absence of any previous history, the belief remains uniform over α. The human (white dot) follows their modal policy from the previous time-step, therefore at T = 2 the belief becomes higher for smaller values of α in both models (lower adaptability). (T = 2) The robot (black dot) adapts to the human and executes the human modal policy. At the same time, the human switches to the robot mode, therefore at T = 3 the probability mass moves to the right. (T = 3) The human switches back to their initial mode. In the 3-step model the resulting distribution at T = 4 has a positive skewness: the robot estimates the human to be non-adaptable. In the 1-step model the robot incorrectly infers that the human adapted to the robot mode of the previous time-step, and the probability distribution has a negative skewness. (T = 4,5) The robot in the 3-step trial switches to the human modal policy, whereas in the 1-step trial it does not adapt to the human, who insists on their mode.

7.4. Discussion

This online study in the table-carrying task seems to suggest that the proposed formalism enables a human-robot team to achieve more effective policies, compared to state-of-the-art human-robot team training practices, while achieving subjective ratings on robot performance and trust that are comparable to those achieved by these practices. It is important to note that the comparison with the human-robot cross-training algorithm is done in the context of human adaptation. Previous work (Nikolaidis and Shah, 2013) has shown that switching roles can result in significant benefits in team fluency metrics, such as human idle time and concurrent motion (Hoffman and Breazeal, 2007), when a human executes the task with an actual robot. Additionally, the proposed formalism assumes as input a set of modal policies, as well as a quality measure associated with each policy On the other hand, cross-training requires only an initialization of a reward function of the state space, which is then updated in the rotation phase through interaction. It would be very interesting to explore a hybrid approach between learning the reward function and guiding the human towards an optimal policy, but we leave this for future work.

7.5. Information-seeking behavior

We observe that in the experiments, the robot always starts moving towards the optimal goal, until it is confident that the human is non-adaptable, in which case it adapts to the human. The MOMDP chooses whether the robot should adapt or not, based on the estimate of the human adaptability, the rewards of the optimal and suboptimal goal and the discount factor.

In the general case, information-seeking actions can occur at any point during the task. For instance, in a multi-staged task, where information gathering costs differently in different stages (i.e. moving a table out of the room / through a narrow corridor), the robot might choose to disagree with the human in a stage where information-seeking actions are cheap, even if the human follows an optimal path in that stage.

7.6. Generalization to complex tasks

The presented table-carrying task can be generalized without significant modifications in the proposed mathematical model, with the cost of increasing the size of the state-space and action-space. In particular, we made the assumptions: (1) discrete time-steps, where human and robot apply torques causing a fixed table-rotation, (2) binary human-robot actions, (3) fully observable modal policies. We discuss how we can relax these assumptions;

1. We can approximate a continuous-time setting by increasing the resolution of the time discretization. Assuming a constant displacement per unit time v and a time-step dt, the size of the state-space increases linearly with ( 1 /dt): $(1/dt):O\left(\left|X^{\text{ world }}\right||M{|}^{2k}\right)=O(({\theta }_{\max }-{\theta }_{\min })*(1/v)*(1/dt)*|M{|}^{2k}),$where θ is the rotation angle of the table.

2. The proposed formalism is not limited to binary actions. For instance, we can allow torque inputs of different magnitudes. The action-space of theMOMDP increases linearly with the number of possible inputs.

3. While we assumed that the modal policies are fully observable, an assumption that enables the human and the robot to infer a mode by observing an action, in the general case different modal policies may share the same action selection in some states, which would make them undeterminable. In this case, the proposed formalism can be generalized to include the human modal policy as additional latent variable in the MOMDP Similarly, we can model the human as inferring a probability distribution over modes from the recent history, instead of inferring the robot mode with the maximum frequency count (equation (2) in Section 4.2). We leave this for future work.

Finally, we note that the presented formalism assumes that the world-state, representing the current task-step, is fully observable, and that human and robot have a known set of actions. This assumption holds for tasks with clearly defined objectives and distinct task-steps. In Section 9, we apply our formalism in the case where a human and a robot cross a hallway and coordinate to avoid collision, and the robot guides the human towards one side of the corridor. Applicable scenarios include also a wide range of manufacturing tasks (e.g. assembly of airplane spars), where the goal and important concepts, such as tolerances and completion times, are defined in advance, but the sequencing of subtasks is flexible and can vary based on the individualized style of the mechanic (Nikolaidis et al., 2015). In these scenarios, the robot could lead the human to strategies that require less time or resources.

8. Adaptability in repeated trials

Previous work by Shah et al. (2011) has shown that robot adaptation significantly improves perceived robot trustworthiness. Therefore, we hypothesized that trust in the mutually adaptation condition would increase over time for non-adaptable participants, and that this increase in trust would result in a subsequent increased likelihood of human adaptation to the robot. We conducted four repeated trials of the table-carrying task. Results did not confirm our hypothesis: even though trust increased for non-adaptable participants, a large majority of them remained non-adaptable in the second task as well.

8.1. Experiment setting

The task has two parts, each consisting of two trials of task execution. At the end of the first part, we reset the robot belief on participants’ adaptability to a uniform distribution over α. Therefore, in the beginning of the second part, the robot attempted again to guide participants towards the optimal goal, identically to the first part of the task. We recruited participants through Amazon’s Mechanical Turk service, using the same inclusion criteria as in Section 6.4. Each participant was compensated $ 1. Following the data collection process described in Section 6.4, we disregarded participants that had as initial preference the robot goal, resulting in a total of 43 samples. All participants interacted with the robot following the MOMDP policy computed using the proposed formalism. After instructing participants in the task, as well as after each trial, we asked them to rate on a five-point Likert scale their agreement to the following statements:

• “HERB is trustworthy”;

• “I am confident in my ability to complete the task”.

We used the ratings as direct measurements of participants’ self-confidence and trust in the robot.

8.2. Hypotheses

H4

The perceived initial robot trustworthiness and the participants’ starting self-confidence on their ability to complete the task will have a significant effect on their likelihood to adapt to the robot in the first part of the experiment. We hypothesized that the more the participants trust the robot in the beginning of the task, and the less confident they are on their ability, the more likely they would be to adapt to the robot. In previous work, Lee and Moray found that control allocation in a supervisory control system is dependent on the difference between the operator’s trust of the system and their own self-confidence to control the system under manual control (Lee and Moray, 1991).

H5

The robot’s trustworthiness, as perceived by non-adaptable participants, will increase during the first part of the experiment. We hypothesized that working with a robot that reasons over its estimate on participants’ adaptability and changes its own strategy accordingly would increase the non-adaptable participants’ trust in the robot. We base this hypothesis by observing in Figure 10b that non-adaptable participants in the Mutual-adaptation condition agreed strongly to the statement “HERB is trustworthy” at the end of the task. We focus on non-adaptable participants, since they observe the robot changing its policy to their preference, and previous work has shown that robot adaptation can significantly improve perceived robot trustworthiness (Shah et al., 2011).

H6

Participants are more likely to follow the robot optimal policy in the second part of the experiment, compared to the first part. We hypothesized that if, according to hypotheses H4 and H5, trust is associated with increased likelihood of adapting to the robot in the first part of the experiment, and non-adaptable participants trust the robot more after the first part, a significant ratio of these participants would be willing to change their strategy in the second part. Additionally, we expected participants that switched to the robot optimal policy in the first part to continue following that policy in the second part, resulting in an overall increase in the number of subjects that follow the optimal goal.

8.3. Results and discussion

We consider Hypothesis H4, that the perceived robot trustworthiness and the participants’ self-confidence on their ability to complete the task, as measured in the beginning of the experiment, will have a significant effect on their likelihood to adapt to the robot in the first part of the experiment. We performed a logistic regression to ascertain the effects of the participants’ ratings on these two factors on the likelihood that they adapt to the robot. The logistic regression model was statistically significant ${\chi }^2(2)=13.58,p=\text{0}.001.$ The model explained 36.2% (Nagelkerke R²) of the variance in the participant’s adaptability and correctly classified 74.4% of the cases. Participants that trusted the robot more in the beginning of the task (β = 1.528,p = 0.010) and were less-confident (β = –1.610,p = 0.008) were more likely to adapt to the robot in part 1 of the experiment (Figure 11). This supports hypothesis H4 of Section 8.2.

Fig. 11.

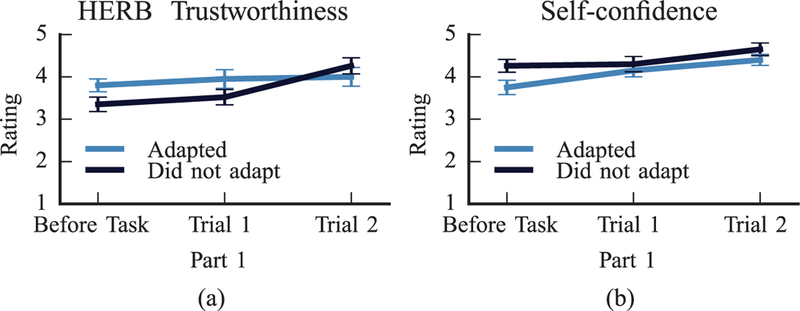
(a) Rating of agreement to the statement “HERB is trustworthy”. for the first part of the experiment described in Section 8. The two groups indicate participants that adapted / did not adapt to the robot during the first part. (b) Rating of agreement to the statement “I am confident in my ability to complete the task”.

Recall Hypothesis H5, that the robot trustworthiness, as perceived by non-adaptable participants, will increase during the first part of the experiment. We included in the non-adaptable group all participants that did not change their strategy when working with the robot in the first part of the experiment. The mean estimated adaptability for these participants at the end of the first part was $\widehat{\alpha }$ = 0.16 [SD = 0.14]. A Wilcoxon signed-rank test indeed showed that non-adaptable participants agreed more strongly that HERB is trustworthy after the first part of the experiment, when compared to the beginning of the task (Z = –3.666, p < 0.001), as shown in Figure 11a). In the same figure we see that adaptable participants rated highly their agreement on the robot trustworthiness in the beginning of the task, and their ratings remained relatively similar through the first part of the task. The results above confirm our hypothesis that working with the robot following the MOMDP policy had a significant effect on the non-adaptable participants’ trust in the robot.

To test Hypothesis H6, we consider the ratio of participants that followed the robot optimal policy in the first part of the experiment, compared to the second part of the experiment. In the second part, 53% of the participants followed the robot goal, compared to 47% in the first part. A Pearson’s chi-square test did not find the difference between the two ratios to be statistically significant (${\chi }^2$(1,N = 43) = 0.42,p = 0.518). We observed that all participants that adapted to the robot in the first part, continued following the optimal goal in the second part, as expected. However, only 13% of non-adaptable participants switched strategy in the second part. We observe that even though trust increased for non-adaptable participants, a large majority of them remained non-adaptable in the second task as well. We attribute this to the fact that users, who successfully completed the task in the first part with the robot adapting to their preference, were confident that the same action sequence would result in successful completion in the second part, as well. In fact, a Wilcoxon signed-rank test showed that non-adaptable participants rated their self-confidence on their ability to complete the task significantly higher after the first part, compared to the beginning of the task (Z = –2.132,p = 0.033, Figure 11b). It would be interesting to assess the adaptability of participants after inducing drops in their self-confidence, for instance by providing limited explanation about the task or introducing task “failures”, and we leave this for future work.

This experiment showed that non-adaptable participants remained unwilling to adapt to the robot in repeated trials of the same task. Can this result generalize across multiple tasks? This is an important question, since in real-world applications such as home environments, domestic robots are expected to perform a variety of household chores. We conducted a follow-up experiment, where we explored whether the adaptability of participants in one task is informative of their willingness to adapt to the robot at a different task.

9. Transfer of adaptability across tasks

The previous experiment showed that non-adaptable participants remained unwilling to adapt to the robot in repeated trials of the same task. To test whether this result can generalize across multiple tasks, we conducted an experiment with two different collaborative tasks: a table-carrying task followed by a hallway-crossing task. Results showed that non-adaptable participants in the table-carrying task would be less likely to adapt in the hallway-crossing task.

9.1. Hallway-crossing task

We introduced a new hallway-crossing task, where a human and a robot cross a hallway (Figure 12). As in the table-carrying task, we instructed participants of the task and asked them for their preferred side of the hallway. We then set the same side as the optimal goal for the robot, in order to ensure that the robot’s optimal policy would conflict with the human preference. The user chose moving actions by clicking on buttons on a user interface (left / right). If the human and robot ended up in the same side, a message appeared on the screen notifying the user that they moved in the same direction as the robot. The participant could then choose to remain on that side, or switch sides. The task ended when human and robot ended up in opposite sides of the corridor.

Fig. 12.

(a) Hallway-crossing task. The robot’s optimal goal is to move to the right side (top), compared to moving to the left side (bottom). (b) The user faces the robot. They can choose to stay on the same side or switch sides.

9.2. MOMDP model of hallway-crossing task

The observable state variables x of the MOMDP formulation were the discretized position of the human and the robot, as well as the human and robot modes for each of the three previous time-steps. We specified two modal policies, each deterministically selecting moving actions towards each side of the corridor. The size of the observable state-space X was 340 states. As in the table-carrying task, we set a history length k = 3 and assumed a discrete set of values of the adaptability : {0.0,0.25,0.5,0.75,1.0}. Therefore, the total size of the MOMDP state-space was 5 × 340 = 1700 states. The human and robot actions a^H, a^R were deterministic discrete motions towards each side of the corridor. We set the reward function R to be positive at the two goal states based on their relative cost, and 0 elsewhere. We computed the robot policy using the SARSOP solver (Kurniawati et al., 2008).

9.3. Experiment setting

We first validated the efficacy of the proposed formalism by doing a user study (n = 65) that included only the hallway-crossing task. We recruited participants through Amazon’s Mechanical Turk service, using the same inclusion criteria as in Section 6.4. Each participant was compensated $0.50. 48% of participants adapted to the robot by switching sides, a ratio comparable to that of the table-carrying task experiment (Section 7.2). The mean estimated adaptability for participants that adapted to the robot, which we call “adaptable”, was $\widehat{\alpha }$ = 0.85 [SD = 0.25], and for participants that did not adapt (“non-adaptable”) was $\widehat{\alpha }$ = 0.07 [SD = 0.13].

We then conducted a new human subject experiment, having users do two trials of the table-carrying task described in 6.3 (part 1), followed by the hallway-crossing task (part 2). Similarly to the repeated table-carrying task experiment (Section 8), we reset the robot belief on the human adaptability at the end of the first part. We recruited participants through Amazon’s Mechanical Turk service, using the same inclusion criteria as in Section 6.4, and following the same data collection process, resulting in a total of n = 58 samples. Each participant was compensated $1.30. We make the following hypothesis:

H7

Participants that did not adapt to the robot in the table-carrying task are less likely to adapt to the robot in the hallway task, compared to participants that changed their strategy in the first task.

9.4. Results and discussion

In line with our hypothesis, a logistic regression model was statistically significant ${\chi }^2$ ( 1) = 5.30,p = 0.021), with participants’ adaptability in the first task being a significant predictor of their adaptability in the second task (β = 1.335,p = 0.028). The model explained 11.9% (Nagelkerke R²) of the variance and correctly classified 62.5% of the cases. The small value of R² indicates a weak effect size. Interestingly, whereas 79% of the users that did not adapt to the robot in the first task remained non-adaptable in the second task, only 50% of the users that adapted to the robot in the table-carrying task, adapted to the robot in the hallway task (Figure 13).

Fig. 13.

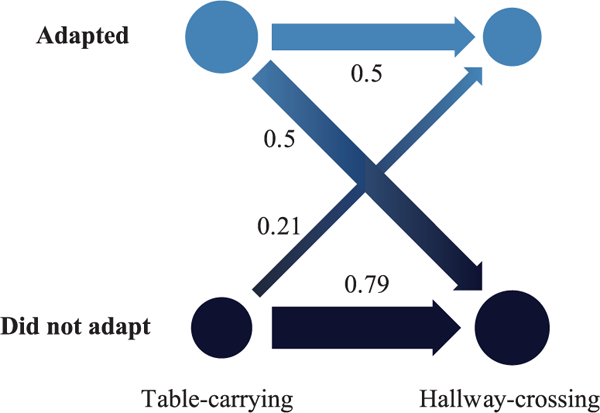
Adaptation rate of participants for two consecutive tasks. The lines illustrate transitions, with the numbers indicating transition rates. The thickness of the lines is proportional to the transition rate, whereas the area of the circles is proportional to the number of participants. Whereas 79% of the users that insisted in their strategy in the first task remained non-adaptable in the second task, only 50% of the users that adapted to the robot in the table-carrying task, adapted to the robot in the hallway-crossing task.

We interpret this result by observing that all participants that were non-adaptable in the first task saw the robot changing its behavior to their preferred strategy. A large majority expected the robot to behave in the same way in the second task, as well: disagree in the beginning but eventually adapt to their preference, and this encouraged them to insist on their preference also in the second task. In fact, in their answers to the open-ended question “Did you complete the hallway task following your initial preference?”, they mentioned that “The robot switched in the last [table-carrying] task, and I thought it would this time too”, and that “I knew from the table-turning task that HERB would eventually figure it out and move in the opposite direction, so I stood my ground” (J1 in Table 1, Figure 14). On the other hand, adaptable participants did not have enough information on the robot ability to adapt, since they aligned their own strategy with the robot policy, and they were evenly divided between adaptable and non-adaptable in the second task. 47% of participants that remained adaptable in both tasks attributed the change in their strategy to the robot’s behavior (J4). Interestingly, 29% of participants that adapted to the robot in the table-carrying task but insisted on their strategy in the hallway task stated that they did so, “because I was on the correct side (you should walk on the right hand side) and I knew eventually he would move” (J3). We see that task-specific factors, such as social norms, affected the expectation of some participants on the robot adaptability for the hallway task. We hypothesize that there is an inverse relationship between participants’ adaptability, as it evolves over time, and their belief on the robot’s own adaptability, and we leave the testing of this hypothesis for future work.

Table 1.

Participants’ response to question “Did you complete the hallway task following your initial preference? Justify your answer”.

	Justification	Example quote
J1	Expectation on robot behavior	“I knew that the robot would change if I stood my ground.”
J2	Simplicity	“I thought it would be easier that I switched.”
J3	Task-specific factors	“I was on the correct side (you should walk on the right hand side).”
J4	Robot behavior	“HERB decided to go the same way as I did.”
J5	Task completion	“To finish the task in the other end of the hall.”
J6	Other	“I tend to stick with my initial choices.”

Fig. 14.

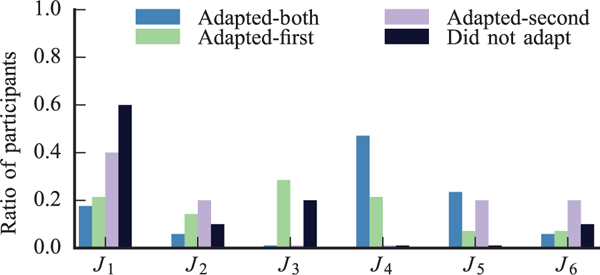
Ratio of participants per justification to the total number of participants in each condition. We group the participants based on whether they adapted in both tasks (Adapted-both), in the first [table-carrying] task only (Adapted-first), in the second [hallway-crossing] task only (Adapted-second) and in none of the tasks (Did not adapt).

10. Conclusion

We presented a formalism for human-robot mutual adaptation, which enables guiding the human teammate towards more efficient strategies, while maintaining human trust in the robot. First, we proposed BAM, a model of human adaptation based on a bounded memory assumption. The model is parameterized by the adaptability of the human teammate, which takes into account individual differences in people’s willingness to adapt to the robot. We then integrated BAM into an MOMDP formulation, wherein the adaptability was a partially observable variable. In a human subject experiment (n = 69), participants were significantly more likely to adapt to the robot strategy towards the optimal goal when working with a robot utilizing our formalism (p = 0.036), compared to cross-training with the robot. Additionally, participants found the performance as a teammate of the robot executing the learned MOMDP policy to be not worse than the performance of the robot that cross-trained with the participants. Finally, the robot was found to be more trustworthy with the learned policy, when compared with executing an optimal strategy while ignoring human adaptability (p = 0.048). These results indicate that the proposed formalism can significantly improve the effectiveness of human-robot teams, while achieving subjective ratings on robot performance and trust comparable to those of state-of-the-art human-robot team training strategies.

We have shown that BAM can adequately capture human behavior in two collaborative tasks with well-defined task steps on a relatively fast-paced domain. However, in domains where people typically reflect on a long history of interactions, or on the beliefs of the other agents, such as in a poker game (Von Neumann and Morgenstern, 2007), people are likely to demonstrate much more complex adaptive behavior. Developing sophisticated predictive models for such domains and integrating them into robot decision making in a principled way, while maintaining computational tractability, is an exciting area for future work.