Radial Expansion Facilitates the Maintenance of Double Antibiotic Resistances

Most microbes live in spatially confined subpopulations. Under spatial structure conditions, the efficacy of natural selection is often reduced (relative to homogeneous conditions) due to the increased importance of genetic drift and local competition. Additionally, under spatial structure conditions, the fittest genotype may not always be the one with better access to the heterogeneous distribution of nutrients. The effect of radial expansion may be particularly relevant for the elimination of antibiotic resistance mutations, as their dynamics within bacterial populations are strongly dependent on their growth rate.

ABSTRACT

Most microbes live in spatially confined subpopulations. Under spatial structure conditions, the efficacy of natural selection is often reduced (relative to homogeneous conditions) due to the increased importance of genetic drift and local competition. Additionally, under spatial structure conditions, the fittest genotype may not always be the one with better access to the heterogeneous distribution of nutrients. The effect of radial expansion may be particularly relevant for the elimination of antibiotic resistance mutations, as their dynamics within bacterial populations are strongly dependent on their growth rate. Here, we use Escherichia coli to systematically compare the allele frequency of streptomycin, rifampin, and fluoroquinolone single and double resistance mutants after 24 h of coexistence with a susceptible strain under radial expansion (local competition) and homogeneous (global competition) conditions. We show that there is a significant effect of structure on the maintenance of double resistances which is not observed for single resistances. Radial expansion also facilitates the persistence of double resistances when competing against their single counterparts. Importantly, we found that spatial structure reduces the rate of compensation of the double mutant RpsL^K43T RpoB^H526Y and that a strongly compensatory mutation in homogeneous conditions becomes deleterious under spatial structure conditions. Overall, our results unravel the importance of spatial structure for facilitating the maintenance and accumulation of multiple resistances over time and for determining the identity of compensatory mutations.

INTRODUCTION

Natural populations are generally subdivided, with various degrees of migration connecting them. This structure is especially important for many bacterial species that colonize and transmit between hosts. Theory predicts that spatial structure can affect the fate of deleterious and beneficial mutations, mainly by buffering the effects of mutations and intensifying genetic drift (1–8).

Another level of spatial structure occurs in surfaces and within hosts, where microbial populations radially expand. Radial expansion differs from well-mixed settings in several major ways. First, cells in radially expanding populations face mostly local competition, in contrast to what happens in well-mixed settings, where global competition dominates (7, 9, 10). Moreover, clones in the outer layer of the radial expansion will have better access to nutrients than the ones in the inner layers, leading to better survival and reproduction rates, independent of their fitness (11). Thus, during radial expansions, both local competition and genetic drift will compete with natural selection in determining the genetic composition of the population (12). Second, cells in radial expansion will switch from exponential to linear growth when space is limiting (instead of mostly exponentially as expected for homogeneous populations), which means that over the same absolute time, there will be a different number of generations (13).

Chromosomal mutations in bacteria can lead to antibiotic resistance (AR) but are often associated with a deleterious effect on the organism’s fitness in the absence of antibiotic, the so-called fitness costs of resistance (14, 15). This is not surprising, since mutations which cause antibiotic resistance often target key cellular functions, such as transcription and protein synthesis, cell wall synthesis, or nucleic acid synthesis (14–16). The existence of a fitness cost caused by AR leads to the prediction that fitter susceptible strains should outcompete resistant strains over time (15, 17). Indeed, a decrease in antimicrobial resistance has been observed in clinical settings when the use of certain antimicrobials is halted (18–21). However, this does not always occur, and it is difficult to predict, simply from the cost of antibiotic resistance, which resistances will decline in frequency upon stopping the antibiotic treatment. The fitness costs of AR mutations are typically measured in a homogeneous growth medium (e.g., liquid rich medium) without spatial structure, where there is global competition between all cells. While it has been clearly established that the fitness cost of AR mutations strongly depends on the choice of medium (22), much less is known about the direct influence of spatial structure on the fitness effect of AR mutations.

Here, we test how the competitive ability of AR mutants is affected by spatial structure. We set up competitive assays between a susceptible Escherichia coli strain and streptomycin, rifampin, and fluoroquinolone single and double resistance mutants in both homogeneous (LB liquid in shaking conditions) and structured media (LB agar plates in static conditions, where bacterial growth occurs through radial expansion). We show that radial expansion has the potential to facilitate the maintenance of double antibiotic resistance mutations and that adaptation to compensate for the cost of double resistance occurred at a lower rate. Overall, our results suggest that spatial structure strongly affects the evolutionary process by increasing the ability to maintain genetic diversity and shifting the genetic targets of future adaptive evolution.

RESULTS AND DISCUSSION

Spatial structure facilitates the maintenance of double antibiotic resistance.

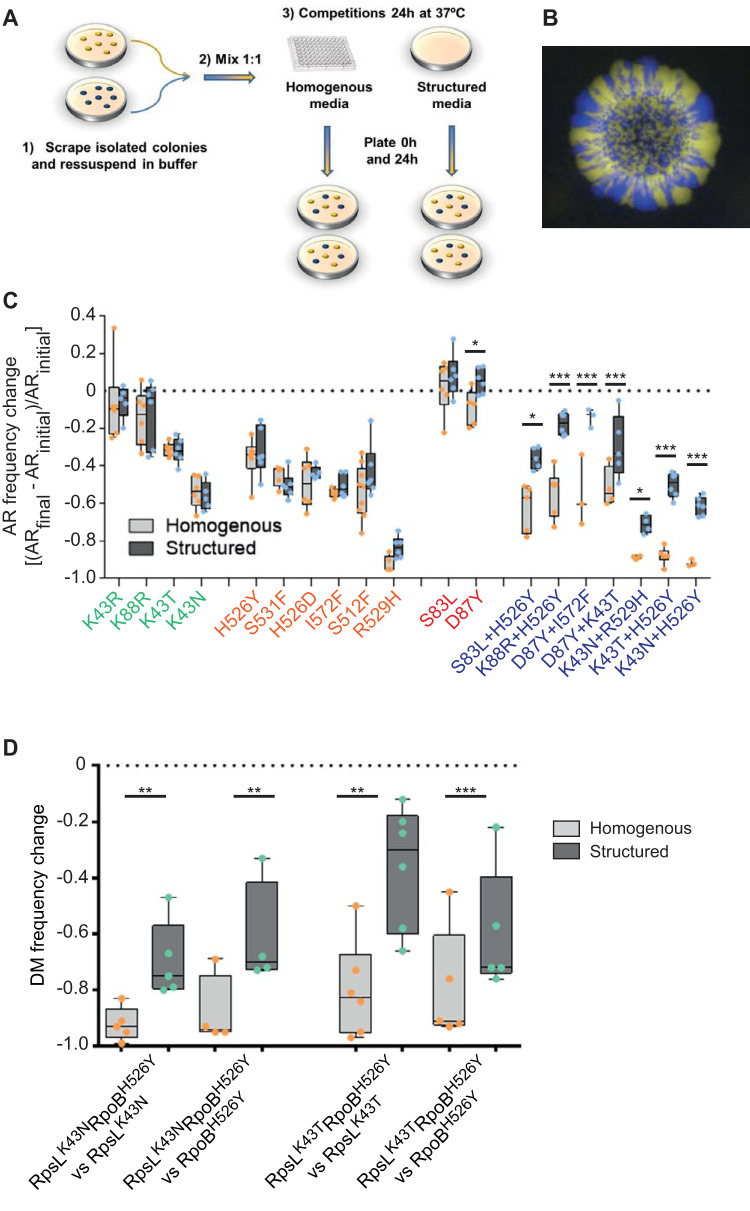
To understand the effects of spatial structure on the persistence of mutations, we measured the frequency change of antibiotic-resistant mutants when in competition with a susceptible strain in a homogeneous environment, where all cells compete against each other, and in a structured environment, where competition is more local and cell growth leads to radial expansions with sectored colonies (Fig. 1A and B) (4, 23–26). The antibiotic resistance mutations studied spontaneously arise and are easily selected under streptomycin, nalidixic acid, and/or rifamycin (27). While competitions under homogeneous conditions were performed in liquid LB with shaking, the competitions under spatial structure were carried out on static LB agar plates (radial expansion) and designed to mimic a more natural environment since enterobacteria, such as E. coli, usually live either in dense communities in the gut or in biofilms and (micro)colonies in the environment. (28). We measured the frequency change of 12 single and 7 double mutants of E. coli carrying mutations in rpoB, rpsL, or gyrA (see Table S1 in the supplemental material), which confer resistance to the antibiotics rifampin, streptomycin, and fluoroquinolones, respectively. This was done by competing the fluorescently labeled antibiotic-resistant (AR) strains against a susceptible strain carrying a different fluorescence for 24 h (Fig. S1).

FIG 1.

Structured populations facilitate the maintenance of double antibiotic resistances. (A) Scheme of the experimental setup used to measure the frequency allele of the antibiotic resistance (AR) mutations in either liquid or 1.5% agar LB medium without antibiotics, using the susceptible strain as reference. (1) Frozen stocks were streaked to isolate single colonies from each mutant, which after overnight growth (2) were used to mix in a 1:1 ratio with the susceptible strain. (3) The same mix was used to start the competitions in homogeneous and structured populations. The initial mix (t = 0 h) and the final mix (t = 24 h) were plated with the proper dilution to count CFU/ml. For more details see Materials and Methods. (B) Example of segregation of E. coli genotypes (susceptible strain-YFP versus a susceptible strain-CFP) due to radial expansion observed in LB agar plates after 24-h competitions. (C) Frequency change of AR mutants in homogeneous populations (light gray bars) and in structured populations (dark gray bars). All the mutants competed with the susceptible background in pairwise competitions in both homogeneous and structured populations. Frequency change was calculated using the formula ([AR_initial − AR_final]/AR_initial), where AR_initial and AR_final stand for the frequency of the resistance mutation at time 0 h (initial mix) and after 24 h of competition, respectively. The colors in the x axis represent resistance to different antibiotics, i.e., mutations in rpsL conferring resistance to streptomycin are in green. (D) Frequency change of the double resistant mutants when competing against their single resistant counterparts in homogeneous and structured populations. The double mutant is found in a significantly higher percentage when the populations are structured.

When analyzing the effect of medium and mutation on the frequency change of AR mutants, we observed that there was a significant interaction between these two factors [F_(1,18) = 4.88, P < 0.0001; analysis of variance (ANOVA)]. Of the 19 mutants tested, only 8 showed a significant difference in frequency change across environments (Fig. 1C). These included all of the double mutants and only one single mutant, indicating that the observed effect is specific for the double resistances. The single AR mutant whose frequency was increased under radially expanding populations was GyrA^D87Y (t = −2.2; P = 0.029). This mutant generally decreased in frequency under homogeneous conditions but increased slightly in frequency under structured conditions. The double mutants always decreased in frequency, but the frequency change in structured conditions was buffered by 0.08 to 0.21 (Gyr^S83L RpoB^H526Y: t = −2.3, P = 0.02; Gyr^D87Y RpoB^I572F: t = −4.7, P < 0.0001; Gyr^D87Y RpoB^K43T: t = −3.6, P = 0.0004; RpsL^K43N RpoB^R529H: t = −2.0, P = 0.047; RpsL^K43N RpoB^H526Y: t = −4.7, P < 0.0001; RpsL^K43T RpoB^H526Y: t = −6.3, P < 0.0001; and RpsL^K88R RpoB^H526Y: t = −5.8, P < 0.0001; post hoc contrasts). Even though double resistances typically have higher fitness costs (measured in homogeneous conditions; Fig. S2), the differences between the two regimes does not seem to correlate with the fitness costs of AR. Interestingly, it was previously described that mutations conferring resistance to streptomycin, rifampin and nalidixic acid strongly interact (16, 27). Thus, the observed effect may be particular to these mutations which are known to be epistatic in between them. Future studies may help disentangle if this effect is more general or specific to the chosen mutations.

Our results are in agreement with the previous finding that the frequency of mutants resistant to rifampin or kanamycin (also an inhibitor of protein synthesis like streptomycin) in biofilm populations of E. coli was able to remain very high even 45 days after an antibiotic treatment regimen (29). Conversely, the frequency of resistant cells dramatically decreased in a competition against sensitive clones in liquid medium (29). Similarly, biofilms of Staphylococcus aureus also accumulate cells resistant to rifampin, and further competition assays demonstrated that the isolated rifampin mutants have a growth advantage in biofilms but not in planktonic culture (30). Other interesting studies have demonstrated that in aging (starved) colonies of E. coli, there is an increase in the frequency of rifampin- and nalidixic acid-resistant mutants (28, 31). This is thought to be partially due to an increase of the growth advantage (31, 32), suggesting that some AR mutations may become less deleterious or even beneficial during radial expansion.

The strong persistence of double resistance leads to the prediction that structured populations should promote the accumulation of resistances. Thus, we measured the allele frequency of the double resistant mutants RpoB^H526Y RpsL^K43T and RpoB^H526Y RpsL^K43N when competing against their single-resistance counterparts (RpoB^H526Y, RpsL^K43T, and RpsL^K43N) (Fig. 1D). According to the expectations, the two double mutants tested were maintained at significantly higher percentages when competing against the single resistances in structured settings (P < 0.05, double-sided paired t test). This suggests that spatial structure also reduces the speed of elimination of multiple resistances and increases the time for compensation of the costs to occur.

It is important to notice that the observed maintenance effect of double AR resistance in structured conditions is probably dependent both on the population size of the original inoculum and on the area that it covers (4, 11, 13, 33). For instance, a bigger area covered by the biomass will likely increase genetic drift, leading to longer persistence of double AR mutations. Conversely, a larger population size will increase competition, therefore decreasing the persistence effect. Calculating with precision the number of generations occurring during a radial expansion is not an easy task since it depends on an estimation of when the growth will change from exponential to linear. Finally, the mechanical aspects of colony growth and how it impacts evolution also need to be considered (11, 12, 34, 35). For instance, it has been found that deleterious mutations are selected less strongly than expected because of mechanical pushing forces which distribute the cost of slower growth across a large fraction of the growing colony front (12, 35).

Spatial structure slows down compensatory evolution of RpsL^K43N RpoB^H526Y.

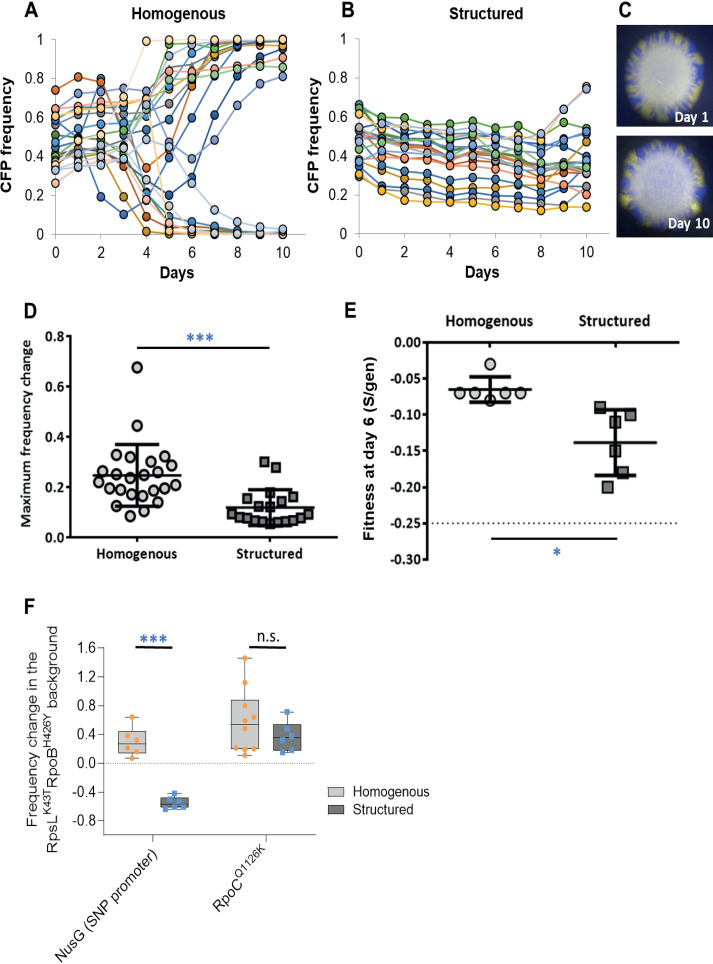
To study the dynamics and pace of compensatory evolution (i.e., to recover from the AR cost) in homogeneous and structured populations, we performed experimental evolution, in antibiotic-free medium, of double resistant RpsL^K43N RpoB^H526Y clones, carrying either a cyan fluorescent protein (CFP) or a yellow fluorescent protein (YFP) neutral marker, mixed in an ∼1:1 proportion. This double mutant was chosen because its frequency after 24 h is much lower in homogeneous versus structured populations (−92% ± 2 [2 standard errors (SE)] and −62% ± 4 [2SE], respectively) (Table S1). We carried a 10-day propagation with a daily bottleneck (at a high population size) and followed the changes in marker frequencies in several independently evolving populations (n = 24 for homogeneous populations and n = 19 for structured populations) (Fig. 2A and B). The neutral marker dynamics allowed us to readily identify the emergence of strong compensatory mutations, as the frequency of a neutral marker is expected to rapidly deviate from its starting value when adaptive mutations are acquired by either the CFP or YFP clones. The large population size and the mild bottlenecks during the propagations (see Materials and Methods) ensured that adaptation will mostly be driven by positive selection (36–38). As predicted, the fluorescent markers deviated from their initial frequency earlier and with steeper slopes in homogeneous than in structured conditions, and we observed frequent changes in the dominant fluorescent marker, which indicates strong clonal interference. Moreover, the slower compensation in structured settings allows for the coexistence of the YFP and CFP markers until the end of the propagation in all populations (Fig. 2C), an observation that is much less frequent in homogeneous settings where ≈83% of the populations fixed one of the markers (>0.90; 12 fixed CFP; 8 fixed YFP). In only 5 days of evolution (∼41 generations), 23 out of 24 double-resistant populations in homogeneous conditions showed a signature of strong adaptation, indicated by the maximum changes in marker frequency of each population, which either reach frequencies close to fixation (>0.90) or show strong fluctuations. In contrast, in structured populations, the fluorescent markers never got close to fixation (>0.90 [Fig. 2D]; unpaired t test with Welch’s correction; P < 0.001), even after 10 days, and only 2 out of 19 populations showed strong fluctuations from day 8 onward.

FIG 2.

The compensation rate of RpsL^K43N Rpo B^H526Y is reduced in spatial populations. (A and B) Dynamics of a fluorescent neutral marker during compensation in rich medium without antibiotics of ∼1:1 mixtures of yellow fluorescent protein (YFP)/cyan fluorescent protein (CFP) cells in (A) 24 independent E. coli populations resistant to both streptomycin and rifampin (RpsL^K43N RpoB^H526Y) in homogeneous conditions and in (B) 19 populations of the same double mutant in solid and static settings. The double mutant was chosen due to the significant difference of frequency allele in the competitions in homogeneous and structured populations (AR frequency allele of −49.8 ± 1.4% and −31.9 ± 1.4%, respectively; P = 1.0 × 10⁻⁶). The dynamics of the fluorescence markers indicate a much slower compensatory process in structured populations. (C) Stereoscope imaging of a representative lineage throughout the compensation experiment in structured settings which clearly shows that there are no sweeps during the propagation under these conditions. (D) Analysis of the maximum frequency change per day of each replica population in the homogeneous and structured populations as a proxy for the occurrence of strong compensatory mutations (where each symbol represents a lineage from that background that was propagated). Lines represent the mean and the standard deviation. (E) Competitive fitness of RpsL^K43N RpoB^H526Y YFP and CFP evolved populations (after 6 days) against a nonfluorescent susceptible reference strain. Competitions were performed in homogeneous settings for both propagations, where the initial cost of the double resistant mutant was S_/g = −0.25 (shown by the dashed line). Lines represent the mean and the standard deviation. ANOVA with Tukey’s multiple-comparison test was performed to calculate significance as follows: *, P < 0.05; **, P < 0.01; ***, P < 0.001. (F) The effect of mutations compensating for the cost of resistance in homogeneous settings (16) is not necessarily the same in structured populations. For instance, the NusG mutation did not increase the frequency of the double mutant background in structured populations, in contrast to what was observed in homogeneous populations.

To understand whether the fluorescent marker dynamics reflected differences in the rate of fitness increase, we also performed competitions between six evolved populations (isolated at day 6) and a nonfluorescent susceptible reference strain (as a control, we also competed the ancestral RpsL^K43N RpoB^H526Y against the same reference). As expected from the marker dynamics, we found that while fitness significantly increased in both types of populations, this increase was significantly lower for populations evolving in structured settings (Fig. 2E; P < 0.05 ANOVA).

Our current and previous results (16) show that antibiotic-resistant mutants can fully compensate high fitness costs in just a few generations in unstructured populations. We partially attribute the slower rate of RpsL^K43N RpoB^H526Y when expanding radially to the effect of structure on the fitness cost given that the rate of fitness increase generally shows a positive correlation with starting fitness (16, 39–41). However, an additional contributing factor to the slower compensation dynamics might be that the effective population size in structured populations might be lower than in homogeneous populations (since only cells within some margin of the edge of the inoculum droplet have a chance to expand radially into the medium and contribute to the next generation). This should also increase the effect of drift and reduce the efficacy of purifying selection.

The lower rate of compensation in structured populations may also be related to the selection of a different set of mutations than the ones observed in homogeneous populations, and/or be because the same compensatory mutations have weaker fitness effects. It has been previously shown that strong compensatory mutations emerge during propagation in homogeneous conditions of the double mutant RpsL^K43T RpoB^H526Y (16). These mutations include a regulatory mutation in the promoter region of the secE-NusG bicistronic transcript (NusG here) and an amino acid replacement, RpoC^Q1126K (16). To test if these two mutations are still compensatory in structured populations, we measured the fitness effect of NusG and RpoC^Q1126K during radial expansions (Fig. 2F). Interestingly, the NusG promoter mutation changes from beneficial (30% ± 16%) in homogeneous conditions to clearly deleterious (–55% ± 7%) in structured populations (P = 2 × 10⁻⁶, paired t tests). The different effect of NusG in the two conditions suggests that some of the genetic targets of compensation are different in structured versus homogeneous populations.

Conclusion.

Our experimental design enabled us to show that spatial structure—under radial expansion growth—can facilitate the maintenance of double antibiotic resistance relative to unstructured media. This is in agreement with theoretical work predicting that the time to extinction of deleterious mutations increases under radial expansion (7, 12). Studying the allele frequency and compensation in structured environments is likely to be particularly important if we want to predict the dynamics of AR mutants in natural environments, such as the mammalian gut, or within biofilms (29), where local competition is likely to be more common than global competition. Even though there is little information about population structures within the host, we reason that multiple antibiotic resistance frequencies may also be more easily maintained in the human gut microbiota due to spatial structure. In fact, it is thought that population structure in the gut varies both longitudinally (small to large intestine) and transversally (mucosa to lumen) (42–45). Nevertheless, the clinical relevance of our results is currently unknown since most frequent clinical isolates of several pathogens tend to already have low fitness costs in homogeneous populations (15, 46), meaning that the mitigation provided by population structure may not be the main determinant for the survival of some costly multiantibiotic resistances in clinical settings.

MATERIALS AND METHODS

Strains.

All the strains used in this study are derivatives of a lac-negative E. coli K-12 MG1655 which constitutively express either YFP or CFP, which is inserted in the galK locus (ΔlacIZYA galK::cat::PLlacO-1-YFP/CFP) (47, 48). Throughout the text, this pair of strains is referred as the susceptible strains. The antibiotic-resistant mutants harbor, additionally, single or pairs of chromosomal mutations in the rpoB, rpsL, and gyrA genes, conferring resistance to rifampin, streptomycin, or fluoroquinolones, respectively (Table S1). All antibiotic-resistant mutants were constructed in both the YFP and CFP backgrounds. All strains are isogenic apart from the resistance mutation and the fluorescence marker (47, 48).

Competition assays.

LB medium without antibiotics—either liquid or with 1.5% agar—was used in all the experiments. The allele frequency change (and in some cases, the fitness effects) of the resistance mutations were measured with competitive assays, using the YFP or CFP susceptible strain as reference, unless stated otherwise. Briefly, after an overnight growth culture, each resistant mutant carrying one fluorescence (i.e., YFP) was mixed with the susceptible strain carrying the other fluorescence (i.e., CFP) in a 1:1 ratio. From the initial mixes, 2-μl drops, representing a mix of 1 · 10³ cells of resistant mutant and 1 · 10³ cells of susceptible strain, were either plated in an LB agar plate (spatially structured populations) or diluted in 198 μl of LB in a 96-well plate (homogeneous populations). Competitions were performed at 37°C for 24 h. The LB agar plate was incubated under static conditions, whereas the 96-well plate was incubated under constant shaking (700 rpm). For the competition assays in structured populations, the entire colony was scraped after 24 h of growth since the initial drop represents ≈0.0002% compared to the new growth of cells. The absolute abundance of each strain, in the initial and final ratios, was estimated by plating appropriate dilutions of the mixture in LB agar plates and counting YFP and CFP colonies. The allele frequency change of the resistance was estimated by subtracting the initial frequency of the resistance from the final one and correcting this value by the initial frequency ([AR_initial – AR_final]/AR_initial). This analysis allows the direct determination of a proportion of decrease (or increase) of resistance frequency over time. At least three independent assays were done for each resistant clone, and assays were done using both YFP and CFP backgrounds. As a control, we also measured the frequency allele for completely isogenic susceptible strains carrying different fluorescence markers. This showed that the fluorescence marker had a negligible effect in both structured and homogeneous environments (Fig. S1). Competitions of compensatory mutations were performed as previously described for homogeneous settings.

Experimental evolution for compensation.

We propagated strains RpsL^K43N RpoB^H526Y YFP and CFP in both homogeneous and structured populations using the same bottleneck of 10⁵ cells. For the homogeneous compensation experiment, we first acclimatized bacteria to the environment by growing strains separately from frozen stocks in LB medium (150 μl per well) in 96-well plates at 37°C with shaking (12 replicates per strain were inoculated in a checkered format to avoid cross-contamination). After 24 h, 10 μl of bacterial culture diluted by a factor of 10⁻¹ was transferred into 140 μl fresh LB medium and allowed to grow for an additional 24 h. Isogenic strains differing only in the marker were diluted again by a factor of ≈10⁻² and then mixed based on their cell numbers given by the flow cytometer (LSR Fortessa) in order to obtain an initial ratio of 1:1. CFP was excited with a 442-nm laser and measured with a 470/20-nm pass filter. YFP was excited using a 488-nm laser and measured using a 530/30 nm pass filter. A total of 24 competitions were initiated by inoculating 140 μl of LB medium with 10 μl of each mixed population, which were allowed to grow for 24 h, reaching a concentration of approximately 10⁹ CFU/ml. The separate growths were done to minimize the occurrence of common compensatory mutations during acclimatization, a phenomenon that is difficult to avoid. After every 24 h of growth, and for 22 days, these cultures were propagated by serial passage with a constant dilution factor of 10⁻² (10 μl of 10⁻² diluted culture was transferred into 140 μl of fresh medium), leading to a bottleneck of ≈10⁵ cells. In parallel, cell numbers were counted using the flow cytometer in order to measure the frequency of each strain in the mixed population during the experiment by collecting a sample (10 μl) from the spent culture each day. In order to prepare the biological replicas for the compensatory experiment in structured populations, we grew the strains overnight separately on LB plates at 37°C. Afterward, we scraped individual colonies and resuspended the bacteria with 250 μl phosphate-buffered saline (PBS) and read the absorbance at 600 nm. Based on the absorbance, we calculated the appropriate volume of distilled water to be added to the individual replica in order to obtain a concentration of 10⁸ CFU/ml. We mixed both strains in a 1:1 ratio, and drops of 2 μl were plated (bottleneck of 10⁵ cells) and grown at 37°C for 24 h. The drops were propagated by scrapping and diluting them. Flow cytometry was used as described above to count the frequency of CFP and YFP bacteria of each individual mix during the propagation. Propagation was performed for 10 days either in liquid LB with shaking or on solid LB medium (1.5% agar) without antibiotics. Samples were frozen at days 1, 3, 6, 8, and 10.

Note that the number of generations per day is ∼8.2 and 7.4 for homogeneous and structured environments, respectively, assuming a logarithmic growth in both cases.

Colony imaging.

Images were acquired on a Zeiss Stereo LUMAR stereoscope equipped with a Hamamatsu Orca-ER charge-coupled device (CCD) camera and GFP fluorescence filter set, controlled with the MicroManager v1.14 software. The magnification used was 12.6×, and CFP was excited using a 436-nm laser and measured using a 480/40 filter set. YFP was excited using a 500-nm laser and measured using a 535/30 filter set. The CFP or YFP pictures were merged with ImageJ, making colored composites.

Statistical analysis.

All statistical analyses were performed in R (v3.5.1) (49) or GraphPad Prism 8. ANOVA was used to test whether the frequency change was affected by the medium (structured versus homogeneous), the resistance mutation, the fluorescence background, or their interaction. Fluorescence background had no significant effect (P > 0.05) either as a main term or as part of the interaction terms. The emmeans function from the emmeans R package v1.2.3 (50) was used to carry post hoc contrasts to identify mutants showing a significant effect of structure on their mean frequency changes. Paired t tests were performed to analyze the competitions of the single versus the double mutants using GraphPad Prism 8.