Bayesian cure-rate survival model with spatially structured censoring

Abstract

We propose a Bayesian spatial model for time-to-event data in which we allow the censoring mechanism to depend on covariates and have a spatial structure. The survival model incorporates a cure rate fraction and assumes that the time-to-event follows a Weibull distribution, with covariates such as race, stage, grade, marital status and age at diagnosis being linked to its scale parameter. With right censoring being a primary concern, we consider a joint logistic regression model for the death versus censoring indicator, allowing dependence on covariates and including a spatial structure via the use of random effects. We apply the models to examine prostate cancer data from the Surveillance, Epidemiology, and End Results (SEER) registry, which displays marked spatial variation.

1. Introduction

Recent decades have witnessed many applications of survival analysis in various disciplines, including medicine, public health and epidemiology [1, 2, 3]. In this paper we introduce a Bayesian hierarchical cure rate survival model that incorporates spatial heterogeneity in the censoring mechanism using spatial random effects. The fact that cancer death rates may approach normal rates after a certain period of time, led to the development of mixture cure rate models [4], which assume that a fraction of the cancerous population is considered cured from cancer, while the rest are considered noncured and subject to higher rates. There is a growing literature on the development of survival models using cure rates [5, 6, 7, 8, 9, 10]. There are two general classes of cure models, mixture and nonmixture models. In the mixture model, it is assumed that the studied population is a mixture of susceptible individuals who experience the event of interest and non-susceptible individuals that supposedly will never experience it. In the non mixture model, an asymptote is defined for the cumulative hazard and hence for the cure fraction. The advantage of the mixture model, which we used for this work, is the ease of interpretation, the proportion of cured and non-cured individuals being given directly in the survival function expression. Further complications of the analysis of spatial data is the presence of censoring for outcomes, which is very frequent in epidemiological studies. It is important to distinguish between cure and censoring, cure referring to subjects who do not experience the outcome in a reasonable amount of time, while censoring refers to subjects who do not fail within the monitor time window of the study or are lost to follow up. Although a cure is never observed due to finite monitoring time, estimating this probability of cure in the population is useful to analyze time trends in patient survival, since it gives valuable information about the population under study. Only a few studies have considered the case of dependent censoring. Liu et al. [11] used a semiparametric additive hazards model for current status data incorporating the association between failure time and covariates and extended the model to allow the dependence of censoring time on covariates. Dependent censoring was accounted for solely through covariates shared by these two models. Zhang et al. [12] extended the model proposed by Liu et al. by incorporating random effects in the censoring and event time models. While these models are reasonable, they do not incorporate the geographical variation in the censoring model. Due to availability of geographical information about the subjects, modeling spatial variation in survival data has recently emerged as an area of active research since it often reveals underlying factors that can assist in identifying regions requiring attention. Several studies have been conducted to model survival data accounting for spatial variation. Data and analyses of prostate cancer (PrCa) are available at international [13, 14], national [15] and smaller scale [16, 17, 18, 19], the disease showing a large spatial variability. The incidence of prostate cancer is highest in Scandinavian countries and lowest in China [20]. The reasons for these geographic variations are unknown but this spatial pattern and clustering can play an important role in identifying the impact of risk factors and can contribute towards the identification of etiology of prostate cancer. Location accounts for dissimilarities in the composition of populations and differentiates risks that are the product of physical and social environments. The Surveillance, Epidemiology and End Results (SEER) database [21] of the National Cancer Institute has been used extensively for modeling prostate cancer survival, accounting for the county level spatial variation [16, 17, 18, 19]. The SEER Program registries routinely collect data on patient demographics, primary tumor site, tumor morphology and stage at diagnosis, first course of treatment, and follow-up for vital status. The SEER Program is the only comprehensive source of population-based information in the United States that includes stage of cancer at the time of diagnosis and patient survival data. Initially, the SEER Program’s central cancer registry receives cancer-related data from local sources, including hospital registries, pathology laboratories, and physician offices. SEER performs active follow-up of patients for vital status through these sources. Additional information and follow-up data are received passively by linking with other organizations, such as the Social Security Administration, state vital records departments, the National Death Index, and the Centers for Medicare and Medicaid Services [23].

In this article we extend the survival cure rate modeling framework by also including a joint logistic model for the death versus censoring indicator variable, and allowing it to have a spatial structure via the use of random effects. We apply this model using the prostate cancer SEER data for Louisiana during the years 2007 through 2010, accounting for parish level variability. The plan of the next sections of the paper is as follows. Section 2 describes the model formulation. Section 3 describes the prior distributions used in the Bayesian framework. Section 4 refers to the computational approach. Section 5 includes an application of the model using the SEER dataset for prostate cancer subjects. Section 6 describes the results of the simulations used to assess the performance of our model. Finally, section 7 provides a discussion and concluding remarks.

2. Statistical model

Our model assumes that the population consists of two groups of individuals: a group of cured individuals that will never experience the endpoint and a group of non cured susceptible individuals. We denote by π the probability of being cured. The survival function in the non cured group is S₀(t) = P(T > t), where T is the lifetime of the individual in the non cured group. The population survival function is defined as a mixture S(t) = π + (1-π)S₀(t).

The format of the data consists of a time to event variable for each individual (t), the parish of residence, and individual level covariates. Let n = number of subjects, t_i = survival times, i = 1,...,n, independent with density function f(t), ${\mathbf{m}}_{\mathbf{i}}={\left(m_i^1,\dots ,m_i^p\right)}^{\prime }$, i = 1,...,n a vector of covariates for subject i, p = number of covariates, c_i = censoring time, i = 1,...,n, y_i is the minimum between survival and censoring time:

$$y_i=min\left(c_i,t_i\right).$$

The death indicator is defined as follows:

$${\nu }_i=\{\begin{array}{l}1\text{if}{t}_i\le c_i\hfill \\ 0\text{if}{t}_i>c_i.\hfill \end{array}$$

Let y = (y₁,y₂,…,y_n)′ and ν = (ν₁,ν₂,...,ν_n)′. The contribution of (y_i,ν_i) to the likelihood function is given by:

$L_i={\left[f\left(y_i\right)\right]}^{{\nu }_i}{\left[S\left(y_i\right)\right]}^{1-{\nu }_i}$, where f(t) is the probability density function and S(t) is the survival function.

Denoting f₀(t) the probability density function for the non cured individuals, f(t) is computed as f(t) = (1 − π)f₀(t) and therefore the likelihoodi i contribution of (y_i,ν_i) is defined as: $L_i={\left[(1-\pi )f_0\left(y_i\right)\right]}^{{\nu }_i}{\left[\pi +(1-\pi )S_0\left(y_i\right)\right]}^{1-{\nu }_i}$.

The log-likelihood is given by:

$$lnL={\displaystyle \sum _{i=1}^n\left({\nu }_i\right)}ln(1-\pi )+{\displaystyle \sum _{i=1}^n\left({\nu }_i\right)}ln\left(f_0\left(t_i\right)\right)+{\displaystyle \sum _{i=1}^n\left(1-{\nu }_i\right)}ln\left(\pi +(1-\pi )S_0\left(t_i\right)\right).$$

We assumed that the temporal probability distribution for the susceptible individuals is Weibull(μ,λ_i), μ and λ_i representing the shape and scale parameters respectively. The Weibull distribution is commonly used for time to event data since it can model a decreasing, constant or increasing failure rate over time, if its shape parameter μ is less, equal or greater than 1 respectively. One of the reasons for the popularity of the Weibull distribution is that it includes other useful distributions as special cases or close approximations. For example, when μ=1, the Weibull distribution becomes the exponential distribution and the hazard rate remains constant as time increases. In addition, the Weibull distribution allows the inclusion of covariates, usually linked to its scale parameter. The scale parameter λ_i of the Weibull distribution is known as the characteristic life and can be modeled in terms of covariates. Therefore, using the Weibull distribution, the probability density function is

$$f_0\left(y_i\right)=\mu {\lambda }_i{\left(y_i\right)}^{\mu -1}{e}^{-{\left(y_i\right)}^{\mu }{\lambda }_i}.$$

To accommodate the modeling of the death indicator, two models were fitted jointly, a survival model and a logistic model for the death indicator. Since the covariates could impact both the binary death indicator and survival, we considered and compared models with and without covariates. Therefore, we assumed that death occurs with a probability depending on the covariates and random effects. Since we did not have prior knowledge about the covariates that may influence censoring, we used the same set of covariates in both survival and logistic models, specifically race, marital status, stage, grade and age of diagnosis, which were available in the data set. In the survival model, the covariates and random effects were linked to the log(λ) parameter.

There are various approaches to the incorporation of spatial heterogeneity in survival models, the most common is the Besag, York and Mollie (BYM) [24] convolution model, including both uncorrelated (UH) and correlated (CH) random effects. The role of the random effects is to allow for confounding beyond the fixed values of the covariates employed in the analysis by accounting for the spatial correlation at the parish level. Covariates are added additively to the random effects components. In our approach to investigating spatial correlation we considered models including correlated and uncorrelated random effects as follows:

log(λ_i) = β₀ + β′m_i + ξ_j,i∈j + v_j,i∈j, where i = 1,...,n indicates the individual , i ∈ j indicates that subject i belongs to county j, β₀ is the intercept and β = (β₁,...,β_p)′ is a vector of regression parameters, ξ_j are the uncorrelated random effects and υ_j are spatially correlated parish level random effects.

A joint logistic regression was considered for modeling the death indicator, ν_i, which was assumed to have a Bernoulli distribution with parameter p_i.

The probability p_i is modeled as follows:

$ln(\frac{p[i]}{1-p[i]})={\alpha }_0+{\mathit{\alpha }}^{\prime }{\mathbf{m}}_{\mathbf{i}}+{\xi }_{j,i\in j}^c+v_{j,i\in j}^c,$ where α₀ is the intercept, α = (α₁,...,α_p)′ is a vector of regression parameters, ${\xi }_j^c$ are uncorrelated parish level random effects and $v_j^c$ are spatially correlated random effects.

3. Prior distributions

Under a full Bayesian approach, prior distributions are assumed for all parameters. For each of the coefficients in the main model, β₀,...,β_p, and in the censoring model, α₀,...,α_p, Normal prior distributions $N(0,{({\sigma }_0^{\beta })}^2),\dots ,N(0,{({\sigma }_p^{\beta })}^2)$ and $N(0,{({\sigma }_0^{\alpha })}^2),\dots ,N(0,{({\sigma }_p^{\alpha })}^2)$ were used respectively, where the hyperparameters ${\sigma }_0^{\beta },\dots {\sigma }_p^{\beta }$ and ${\sigma }_0^{\alpha },\dots {\sigma }_p^{\alpha }$ each were assumed to have a Uniform (0,10) distribution. For the log of the shape parameter log(μ) of the Weibull distribution, a Normal distribution with zero mean and variance 0.1² was assigned. Since μ is a power term, a small variance was used for the prior distribution of the log(μ) parameter. The unstructured spatial random effects ξ_j in the main model were assumed to have a normal distribution with mean zero and variance ${\sigma }_{\xi }^2$, with the hyperparameter σ_ξ having a Uniform(0,10) distribution. Similarly, the unstructured random effect ${\xi }_j^c$ in the censoring model was assumed to have a $N(0,{\sigma }_{({\xi }^c)}^2)$ distribution, with ${\sigma }_{{\xi }^c}~$ Uniform(0,10). The spatially correlated random effects υ_j and $v_j^c$ in the survival and logistic regressions models were assumed to have conditionally autoregressive (CAR) prior. A Beta(1,1) distribution was assumed for π, the probability of cure. Sensitivity analyses have been performed by changing the fixed parameters of the prior distributions. Similar posterior estimates have been obtained, suggesting that the posterior estimates are not influenced by the choice of the prior distributions. In summary:

$$\begin{gathered} {\beta }_l~N(0,{({\sigma }_l^{\beta })}^2),{\sigma }_l~Uniform(0,10),l=0,\dots ,p, \\ {\alpha }_l~N(0,{({\sigma }_l^{\alpha })}^2),{\sigma }_l~Uniform(0,10),l=0,\dots ,p, \\ log(\mu )~N(0,{0.1}^2), \\ {\xi }_j~N(0,{\sigma }_{\xi }^2),{\sigma }_{\xi }~\mathit{Uniform}(0,10) \\ {\xi }_j^c~N(0,{\sigma }_{({\xi }^c)}^2),{\sigma }_{{\xi }^c}~Uniform(0,10) \end{gathered}$$

$v_j|v_{-j}~Normal({\displaystyle \sum _{k\in {\rho }_j}\frac{v_k}{n_{{\rho }_j}}},\frac{{\psi }^2}{n_{{\rho }_j}})$, where ψ is a hyperparameter assumed to have a Uniform(0,10) distribution, ρ_j is the set of neighbors corresponding to parish j, and υ₋j is the n−1 dimensional vector without the j^th coordinate of υ, $v_j^c|v_{-j}^c~Normal({\displaystyle \sum _{k\in {\rho }_j}\frac{v_k^c}{n_{{\rho }_j}}},\frac{{({\psi }^c)}^2}{n_{{\rho }_j}})$, where ψ^c is a hyperparameter assumed to have a Uniform(0,10) distribution, ρ_j is the set of neighbors corresponding to j, and $v_{-j}^c$ is the n − 1 dimensional vector without the j^th coordinate of υ^c.

4. Computational approach and software

Advances in computing power and software have made Markov chain Monte Carlo (MCMC) [25, 26] one of the most important computational tools in Bayesian biostatistics. For our approach we used MCMC via a MetropolisHastings algorithm [27] for sampling from the posterior distribution of the parameters, using the “zeros trick” for arbitrary likelihoods, implemented in WinBUGS [28]. Models were run for 20000 iterations, the first 10000 being discarded as burn-in. Preliminary data analysis was performed using R [29] and SAS [30] software.

4.1. Goodness of fit and convergence diagnostics

The selection of best model is important in any statistical inference. In the Bayesian field, there are several types of model selection procedures with selection tools like Bayes factor [31] and approximations such as Bayesian Information Criterion (BIC) [32] and Deviance Information Criterion (DIC) [25, 33]. The most recently developed measure of model fit, the WatanabeAkaike information criterion (WAIC) [34], relies on pointwise calculations by partitioning the data into n pieces, which is not computationally easy to implement in some spatially structured-data settings [35]. Therefore, we have compared the models based on the DIC, which is widely used in Bayesian analysis and is the only measure of goodness of fit implemented in Bayesian software such as WinBUGS [25]. DIC is a measure of predictive accuracy based on the deviance and takes into consideration the model complexity. Let θ be the vector of parameters of interest. The deviance, denoted by D, is defined as −2 times the log likelihood, D(θ) = –2logL(θ/Y). The posterior mean of the deviance is $\overline{D(\theta )}=E(D(\theta )|\mathbf{y})$ and the deviance calculated at the posterior means for θ is $D(\overline{\theta })=D(E(\theta |\mathbf{y}))$. The difference between these two measures, $p_D=\overline{D(\theta )}-D(\overline{\theta })$, is an estimate of the effective number of parameters in the model. The DIC adds p_D to the posterior mean difference, giving a measure of fit that is penalized for model complexity: $DIC=\overline{D(\theta )}+p_D$.

In order to compute the overall DIC for our models, we have used the “zeros trick” in WinBUGS [53]. If we have an arbitrary likelihood l_i = log(y_i/θ) we can rewrite this likelihood as $f(\mathbf{y}|\theta )={\displaystyle \prod _{i=1}^n{e}^{l_i}}={\displaystyle \prod _{i=1}^n\frac{e^{-(-l_i)}{(-l_i)}^0}{0!}},$ which is a Poisson distribution. In order to ensure that –l_i is positive, a constant C can be added, such that $f(\mathbf{y}|\theta )={\displaystyle \prod _{i=1}^n\frac{e^{-(-l_i)+C}{(-l_i+C)}^0}{0!}}.$

The DIC that WinBUGS calculates when the “zeros trick” is used, denoted DIC_zero, is on a different scale than the DIC which would be reported from a direct model for the data. Since we used the “zeros trick” in WinBUGS, we have adjusted the DIC as follows, suggested by Lunn et al. [36]: DIC = DIC_zero − 2nC, where C is the constant applied and n is the numbers of observations. Lower values of DIC indicate a better fit of the model, also taking into account the model complexity, which is estimated by the parameters degrees of freedom (pD). Higher pD values indicate a more complex model with a larger number of parameters. For computational reasons, a single chain was run for each model. Convergence was assessed first informally using visual examination of the trace plots. Furthermore, we constructed two chains from the remaining iterations after discarding the burn-in and used Gelman and Rubin’s convergence diagnosis [37].

5. Application

5.1. Prostate cancer

Prostate cancer is the most common nonskin cancer and the second leading cause of cancer-related death in men in the United States [38]. About 1 man in 7 will be diagnosed with prostate cancer during his lifetime and about 1 man in 38 will die of prostate cancer [39]. It is estimated that 164,690 new cases of prostate cancer will be diagnosed and 29,430 will die of prostate cancer in 2018 [39]. It occurs mainly in older men, with the mean age of diagnosis being 66 [39]. Risk factors include but are not limited to age, race, family history, genetics and geographical location. Spatial referencing is important in understanding the variation in PrCa outcomes [40, 41, 42]. As such, geographic analysis of prostate cancer incidence rates, in combination with known risk factors, may be a source of hypotheses about carciogenesis. Newer treatments are being developed, and improvements are being made among many standard prostate cancer treatment methods [43]. Surgical techniques used to treat prostate cancer are constantly improving, with the goal of removing all of the cancer while lowering the risk of complications and side effects from the surgery [43]. Advances in the technology of radiation therapy are making it possible to aim radiation more precisely than in the past. Current methods such as conformal radiation therapy (CRT), intensity modulated radiation therapy (IMRT), and proton beam radiation help doctors avoid giving radiation to normal tissues as much as possible. In addition, men who choose not to have treatment for their localized prostate cancer may be able to slow its growth with intensive diet and lifestyle changes [44]. Death rates for prostate cancer have been decreasing in many developed countries [45]. Therefore cure rate models can be a useful tool to analyze and describe prostate cancer survival data.

5.2. Data

We examined cancer registry data from the SEER Louisiana registry for the years 2007 through 2010. SEER registry data has been used previously in the development of spatial survival methods [46, 47, 48, 49]. The data included only malignant cancer cases. For stage definition we used SEER historic stage, which was available for our selected years and was defined as having the following categories: localized, regional and distant. Localized refers to a cancer confined to the prostate with no penetration of the capsule. Regional indicates a cancer that involves the regional lymph nodes and/or penetration of the prostatic capsule with or without direct extension beyond the limits of the prostatic capsule into the surrounding organs or tissues. Distant means that the cancer has spread to parts of the body remote from the primary tumor. For PrCa, the SEER staging system combines localized and regional cases into one stage group. We selected only observations with complete dates available and excluded subjects with survival time zero since these subjects were not in the risk set for any length of time. For our time to event outcome we used the time to death from any causes as the prostate only cancer deaths were too infrequent. The model was adjusted for variables that were available and thought a-priori to be associated with the vital outcome. The individual-level patient data that were used in this study include: race (African-American versus Whites/Other), marital status at diagnosis (married (including both married with certificate or domestic partner of same sex or opposite sex or unregistered) versus single/separated/divorced/widowed), stage (distant versus localized/regional), grade (grades 1 and 2 versus grades 3 and 4) and age (age at diagnosis in years). Values labeled “unknown” were considered missing and excluded from the analysis.

The data selection process is summarized as follows: 1) we downloaded the male genital cancers with 336795 observations; 2) we selected only the Louisiana registry, the resulting data contained 37555 observations; 3) we selected only years 2007–2010, the resulting data had 15135 observations; 4) we selected only PrCA, the resulting data contained 14622 observations; 5) we excluded one subject with in situ historic stage, the resulting data had 14621 observations; we excluded the observations with survival time zero, the resulting data has 14184 observations; 6) we selected only the observations with complete dates available, including days (for more information see SEER description on the calculation of the survival times [22]), the resulting data had 13835 observations; 7) we excluded observations with missing values for the covariates of interest, the final resulting data had 11943 observations.

5.3. Results

The demographic characteristics of the subjects have been described in Onicescu et al. [18, 19]. The range of age of diagnosis was 34 to 98 years, with the mean being 66 (sd=9.41). Mean time to death or censoring was 22.60 months (sd=13.58), ranging from 1 to 47. The majority of the subjects were white (67%) versus 32.52% black and only 0.48% other races. The majority of the cancer stages were localized/ regional (95.94%) with only 4.06% distant. Of all subjects, 92.82% were alive by the end of the study period, while 7.83% died of any cause. Most cancers were grade 2 (44.65%) and 3 (54.18%) with only 0.87% Grade 1 and 0.30% Grade 4. Due to the small number in grade categories 1 and 4, for estimation we grouped the grade variable and compared grades 3 and 4 versus grades 1 and 2. In our data 73.08% of the subjects were married, 12.77% were single and 14.15% were separated, divorced or widowed.

5.3.1. Model selection and goodness of fit assessment

DIC and p_D values are given for the models in Table 2. Adding the covariates in the main and censoring model significantly decreased the DIC, suggesting a better fit of the model when the covariates are included. The smaller DICs have been estimated for model 5 (UH, all covariates in both main and logistic model) and model 6 (UH, all covariates in main model and all covariates in censoring model). It is to be noted that the parameters degrees of freedom are considered in the calculation of the DIC, increasing the DIC for increased pD. The average deviance for model 5 is lower than the average deviance for model 6, suggesting that, if we do not take into account the model complexity, model 5 provides a better fit. Although it is more complex, model 5 is more informative, providing information regarding the spatial structure of the censoring mechanism. Therefore, we present the results from Model 5, which includes uncorrelated random effects in both the survival model and the logistic model for the death indicator and is adjusted for all covariates.

Table 2:

Model fit diagnosis.

	Main model	Censoring model	DIC	pD
Model 1	UH+CH, no covariates	UH+CH, no covariates	15470	20.01
Model 2	UH+CH, all covariates	UH+CH, all covariates	13960	32.44
Model 3	UH+CH, all covariates	UH+CH, no covariates	14700	20.14
Model 4	UH+CH, no covariates	UH+CH, all covariates	14730	26.01
Model 5	UH, all covariates	UH, all covariates	13950	27.28
Model 6	UH, all covariates	all covariates	13950	14.035
Model 7	UH, all covariates	UH, all covariates, spatially varying fraction rate	13970	56.56

5.3.2. Estimation

Table 3 displays the posterior means and 95% credible intervals (CI) of the coefficients in the main model, higher coefficients in the main model indicating lower survival times. The coefficients in the main model represent the change in the log(λ) parameter of the Weibull distribution for a category level of a variable versus the reference or for a unit increase in a continuous variable. The coefficients in the censoring model are coefficients in a logistic regression modeling the probability of death and therefore represent changes in the log odds of death for a category level of a variable versus the reference or for a unit increase in a continuous variable. We estimated that black race (versus white and others), distant stage (versus localized/regional), higher grade (grades 3 and 4 versus 1 and 2) and higher age at diagnosis are associated with lower survival, while being married is associated with higher survival. In the logistic regression model, the log odds of observed death versus censoring was higher for black race (versus white and others), distant stage (versus localized/regional) and higher age at diagnosis and lower for married (versus not married). The probability of cure was estimated to be 0.11 (95% CI: (0.011, 0.24)). Although the prior for the probability of cure was non informative, the posterior was well estimated, suggested by the short length of the credible interval. Figure 1 displays maps of uncorrelated(UH) parish level random effects in the main and censoring models. The uncorrelated random effects do not display spatial clustering in the spatial or logistic models.

Table 3:

Parameter estimates and 95% credible intervals (CI)

	Survival model Estimate (95 % CI)	Logistic model Estimate (95 % CI)
Intercept	−7.085 (−7.42, −6.73)*	−3.16 (−3.37, −2.95)*
Race
White and Other races	Ref.	Ref.
Blacks	0.44 (0.25,0.62)*	0.44 (0.27,0.62)*
Marital status
Not Married	Ref.	Ref.
Married	−0.41 (−0.58, −0.23)*	−0.37 (−0.54, −0.20)*
Stage
Localized/ Regional	Ref.	Ref.
Distant	2.074 (1.84,2.30)*	2.15 (1.89,2.40)*
Grade
1 and 2	Ref.	Ref.
3 and 4	0.22 (0.054,0.39)*	0.14 (−0.022, 0.32)
Age at diagnosis (standardized)	0.76 (0.68,0.84)*	0.79 (0.70,0.87)*
	Estimate (95 % CI)
π (probability of being cured)	0.11 (0.011, 0.24)

^*indicates that the credible interval does not include zero.

Figure 1.

Map of random effects: A) map of uncorrelated random effects in the main model; B) map of uncorrelated random effects in the censoring model.

6. Simulation

To evaluate the spatial method proposed, we carried out a simulation study where we generated data where we know the values of the parameters of interest and see how well we recover these values from our proposed model, assuming that we use the posterior mean of the parameters as the estimates. For this purpose, we generated 100 datasets to see how well our estimator performs in terms of mean squared error (MSE), computed as the mean of squared differences between the estimator from the proposed model and the truth value, over all the simulations. We considered various simulation scenarios, including unstructured and spatially structured random effects and considering different values for the coefficients.

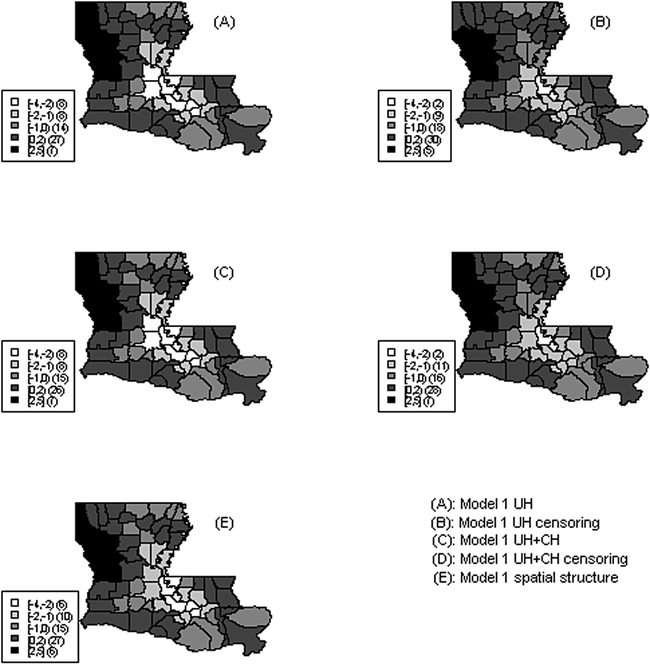
The process of simulating survival data requires certain specific characteristics, including simulation of survival times and the censoring mechanism. The temporal survival distribution was generated to depend on a set of covariates and to have a spatial structure. The spatial structure was included by adding a spatially structured variable, simulated using a stationary isotropic covariance model, the corresponding covariance function depending only on the distance between the two points. This was implemented in R [29] using the RMGauss function in the RandomFields package. The censoring model had as dependent variable a spatially dependent death indicator, constructed using a logistic regression, modelling the probability of death versus censoring. The model included both non spatial covariates and a spatial structure via a spatially correlated covariate. The death indicator variable for each subject is was estimated as a Bernoulli with probability estimated from the logistic regression model. A map of the spatial structure induced by the spatial covariate is included in Figure 2,(E).

Figure 2.

Map of random effects: A) map of uncorrelated random effects, simulated data model 1 UH; B)map of uncorrelated random effects in the censoring model, simulated data model 1, UH; C) map of sum of uncorrelated and correlated random effects, simulated data model 1 UH+CH; D) map of sum of uncorrelated and correlated random effects in the censoring model, simulated data model 1 UH+CH; E) map of spatially correlated covariate.

Table 4 displays the simulation results from two models with varying truth values of the coefficients. The table includes the mean and standard deviations of the estimated coefficients over the 100 iterations and the mean square error (MSE) for each coefficient, calculated as the mean of the square difference between the estimated coefficient at each iteration and the truth value. The coefficients of each covariate in both models were close to the true values. While the MSE values of most coefficients were low, we noticed a slightly higher MSE for the estimated intercept in the main model, which, as in many survival models should be interpreted with caution, especially for censored data. This is consistent with prior research suggesting that the intercept cannot be estimated consistently in some survival models due to the existence of censoring [50, 51].

Table 4:

Simulation scenario

Model	Coeff.	Truth	Est.	sd.	MSE.	DIC	pD
Model 1 UH	β0	1	0.63	0.19	0.14	637717.7	123.71
	β1	1	1.20	0.043	0.04
	β2	1	1.21	0.026	0.044
	α0	2	1.97	0.20	0.012
	α1	2	2.00	0.15	0.024
	α2	2	2.0032	0.096	0.0069
Model 1 UH+CH	β0	1	0.68	0.041	0.10	637702.7	115.17
	β1	1	1.20	0.044	0.041
	β2	1	1.21	0.026	0.044
	α0	2	2.00	0.11	0.012
	α1	2	2.019	0.15	0.024
	α2	2	2.016	0.096	0.0072
Model 2 UH	β0	0	-0.47	0.22	0.22	643702.9	126.82
	β1	1	1.19	0.046	0.039
	β2	1	1.20	0.027	0.041
	α0	1	0.95	0.19	0.0080
	α1	1	1.0016	0.099	0.0095
	α2	1	1.0057	0.057	0.0029
Model 2 UH+CH	β0	0	−0.49	0.045	0.24	643690.4	119.64
	β1	1	1.20	0.047	0.040
	β2	1	1.20	0.027	0.041
	α0	1	0.98	0.079	0.0061
	α1	1	1.010	0.099	0.0095
	α2	1	1.0095	0.057	0.0030

Figure 2 displays maps of estimated random effects obtained from the simulated data in Model 1 using uncorrelated heterogeneity (UH) and both uncorrelated and correlated heterogeneity (UH+CH) for the main and censoring models respectively, as well as a map of the simulated spatially correlated covariate that generates the spatial structure. We notice that the estimated spatial structure in both main and censoring models is similar to the true spatial structure generated by the spatial covariate, displayed in Figure 2, (E), with parishes of high risk in the North-West of the state and some parishes with low risk in South-Central part of the state. The censoring component models the probability of observing a death versus censoring and therefore a higher random effect indicates a higher percentage of observed deaths.

7. Discussion

This paper presented a methodology for modelling spatial variability in the censoring mechanism in the context of cure rates survival data for the state of Louisiana obtained from the SEER database. Although most of the covariates had similar effect on both survival and censoring mechanism, higher grade (grade 3 and 4 versus grades 1 and 2) was associated only with lower survival and did not show an association in the modeling of the death indicator, suggesting that inclusion or exclusion of covariates should be considered separately for each model since they may have different effects.

The cure fraction model with spatial censoring can be used for a wider range of diseases, especially for cancer, where current therapies are believed to induce a cure among a subset of patients. An extension of our analysis would be the inclusion of multiple outcomes, such as different cancers with cause specific cure fractions. Although the spatially referenced cure fraction model was not chosen as the best model for our data, it had the best deviance and therefore the best fit not considering the model complexity. Therefore, it could be a very useful model in other contexts or datasets, where it is important to model the probability of cure for specific parishes. The basic modeling framework can further be extended in several ways. In this work, we assumed that the time to event had a Weibull distribution but the method could be used under other assumptions such as accelerated failure time (AFT) with various distributions of survival times. To extend our work, a spatially referenced cure fraction probability can be used, allowing for different probability of cures in different parishes. However, for our particular data, based on the DIC, this model did not perform better that other models so we did pursue this approach here. Although based on the DIC the spatially referenced censoring model (Model 5) had a similar fit with other models who did not include random effects in the censoring mechanism, it is to be noted that this model had a larger complexity in terms of the number of estimated parameters. As the model complexity is considered in the calculation of the DIC, the model can be considered to have a better fit if we ignore model complexity and also provides additional information on the spatial structure of the censoring.

We also ran an additional model similar to model 5 and not including the joint censoring model, this being equivalent with the usual survival cure rate model in which the censoring times are independent, identically distributed. It is to note that we cannot directly compare the total DIC (13950) with the DIC for the survival only model (9220) since they use essentially different data. In the survival only model, the death indicator variable is considered fixed, being part of the data. In the proposed joint model, in addition to the survival model, a joint logistic regression was considered for modeling the death indicator, therefore in the joint model the death indicator is no longer a fixed variable and part of the data. Therefore, the DIC for the survival only model is not directly comparable with the DIC for the joint model. However, the DIC for this model was similar to the DIC obtained for the survival component of the joint model.

The model can also be extended by differentiating between the two types of censoring, specifically censoring due to follow-up and censoring due to study termination.

In our study we included prostate cancer patients and we used death from any cause as our endpoint of interest. Prostate cancer tends to affect older men and has a very slow progress. The prevalence of comorbidity increases with advanced age and therefore other causes of death are an important contributor to the death rates in prostate cancer patients [54]. In a study comparing the causes of deaths in a prostate cancer population with a similar cohort [54], it was found that causes of death among prostate cancer patients not dying of prostate cancer were similar to those among the nonprostate cancer cohort decedents. Prostate cancer was the underlying cause for 39% of the subjects. The initial treatment influenced the underlying cause of death reported, the percentage of prostate cancer reported death being higher for the patients aggressively treated [54].

It it to be noted that interpretation of prostate cancer survival information needs to be interpreted with caution due to the possibility of early detection of the cancer due to screening such as PSA testing. The survival time is calculated as the difference between the date of diagnosis and the date of death, and therefore can be increased by early detection of the cancer, as well as by effective treatments [14]. The data used for our study was collected before 2012, when the U.S. Preventive Services Task Force recommended against PSA-based screening for prostate cancer [52]. However, the recommendations for PSA screening during the time window used in our study was the same for all the regions within the Unites States and therefore it is unlikely to have a major contribution to the geographical variation of the disease.

Our study highlights the need for geographic-specific interventions to better control disease within at-risk parishes and for further research analysis related to social and contextual factors that contribute to observed risk differences.

Table 1:

Demographic characteristics

	Mean+/−SD	Range
Age at diagnosis	66.12+/−9.41	34–98
N. missing	2
Survival time(months)	22.60 +/−13.58	1–47
	N	(%)
Marital status
Single	1590	(12.77%)
Married	9097	(73.08%)
Separated/Divorced/Widowed	1761	(14.15%)
N. missing	1387
Race
White	9258	(67.00%)
Black	4494	(32.52%)
Other	66	(0.48%)
N. missing	17
Grade
I	116	(0.87%)
II	5957	(44.65%)
III	7229	(54.18%)
IV	40	(0.30%)
Stage
Distant	554	(4.06%)
Localized/ Regional	13101	(95.94%)
N. Missing	180
All causes death indicator
Alive	12842	(92.82%)
Died	993	(7.83%)