Measurement error correction in the least absolute shrinkage and selection operator model when validation data are available

Abstract

Measurement of serum biomarkers by multiplex assays may be more variable as compared to single biomarker assays. Measurement error in these data may bias parameter estimates in regression analysis, which could mask true associations of serum biomarkers with an outcome. The Least Absolute Shrinkage and Selection Operator (LASSO) can be used for variable selection in these high-dimensional data. Furthermore, when the distribution of measurement error is assumed to be known or estimated with replication data, a simple measurement error correction method can be applied to the LASSO method. However, in practice the distribution of the measurement error is unknown and is expensive to estimate through replication both in monetary cost and need for greater amount of sample which is often limited in quantity. We adapt an existing bias correction approach by estimating the measurement error using validation data in which a subset of serum biomarkers are re-measured on a random subset of the study sample. We evaluate this method using simulated data and data from the Tucson Epidemiological Study of Airway Obstructive Disease (TESAOD). We show that the bias in parameter estimation is reduced and variable selection is improved.

1. Introduction

Technology to measure concentrations of circulating biomarkers has evolved from single biomarker to multiplex assays, the latter of which are now available on multiple platforms. Multiplex technologies have many critical advantages over single biomarker assays in that they have the ability to measure multiple serum biomarkers at a given time, require less sample volume, and are efficient in time and cost. However, precision and validation of measurements from multiplex assays need to be assessed.^1,2 Measurements of serum biomarkers from multiplex assays may have high intra- and inter-assay variability³ and the corresponding coefficient of variation (CV) may be greater as compared to single biomarker assays.⁴ Although this variability may be biomarker and platform dependent^5,6 and, in some cases CV measured for specific serum biomarkers by single biomarker assays may yield greater variability as compared to a multiplex platform,5 single biomarker assays continue to be the best validated approach for serum biomarker measurement. Accordingly, it is recommended to confirm results obtained by multiplex assays with a single biomarker assay.^1,7,8 Yet, this strategy can be expensive both in monetary cost and sample volume. The development and implementation of statistical methods that account for this added variability in multiplex assay measurements has also been recommended,^2,3 since variability or measurement error in these data may bias parameter estimates in regression models, which could distort true associations of biomarkers with an outcome⁹ and can have unpredictable consequences in the variable selection process.

The Least Absolute Shrinkage and Selection Operator (LASSO) is a popular penalized regression method that may be used for variable selection of these high dimensional data.¹⁰ The LASSO method minimizes the residual sum of squares and places a bound on the sum of the absolute value of the coefficients.¹⁰ This bound is controlled by a shrinkage parameter that might cause some coefficients to be shrunk towards zero or set to be zero. The shrinking process might produce biased estimates, but it may improve both variable selection and interpretation.¹⁰ Nevertheless, when the covariates are subject to measurement error, variable selection by the LASSO method has been shown to be unstable.¹¹

A simple measurement error correction method for penalized methods has previously been proposed. For the linear regression model with covariates measured with error, Xu and You studied a simple correction method that subtracts a bias correction term from the least squares function which has been penalized by the smoothly clipped absolute deviation (SCAD) penalty.¹² This method was shown to perform well at eliminating false positives.¹² Similarly, Liang and Li proposed a correction method for the partially linear model with measurement error using the SCAD penalty.¹³ They demonstrated an improvement in both estimation accuracy and variable selection.¹³ Furthermore, Sorensen, Frigessi, and Thoresen showed that the bias correction term applied with the LASSO penalty improved estimation accuracy and reduced the number of false positives.¹⁴

For the previously proposed error correction method, the subtraction of the bias correction term is simple to implement, can reduce bias, and improve variable selection. However, it is usually assumed that the distribution of the measurement error for the bias correction term is completely known or has been estimated with replication data. In the Tucson Epidemiological Study of Airway Obstructive Disease (TESAOD; details to be introduced in Section 4), a potentially important serum biomarker was re-measured using a single biomarker assay to examine whether results of a multiplex assay were comparable. In this study, we adapt the existing approach to correct for the measurement error in the LASSO model using validation data, in which a subset of serum biomarkers are re-measured on a random subset of the study sample. Utilization of such an approach would have limited impact on the budget and sample utilization, while possibly improving variable selection and parameter estimation.

The remainder of this article is organized as follows. In section 2, we review the LASSO method and the existing corrected least squares method (corrected LASSO). We then present details on the error correction method based on validation data. In section 3, we evaluate the corrected LASSO method based on validation data through a simulation study with the validation data consisting of one to five biomarkers for 10% and 20% of the full study sample. In section 4 we illustrate the proposed procedure on data from TESAOD, in which a large panel of biomarkers were measured by multiplex assays and one of them was also re-measured using a “gold standard” single biomarker assay.

2. Corrected LASSO procedure

2.1. Measurement error model with serum biomarkers

We consider the linear regression model. For the ith subject,

$${\mathit{Y}}_i={\beta }_0+{\mathbf{X}}_i^{\mathrm{T}}\beta +{\epsilon }_i,\text{for}i=1,\dots ,n$$

where Y_i represents a continuous response, X_i = (x_i1, x_i2, … , x_ip)^T represents the unobserved error-free vector of p biomarkers, β = (β₁, β₂, … , β_p)^T is a p-vector of regression parameters, and ε_i is the model error with E(ε_i∣X_i) = 0. Instead of X_i we observe W_i, an error-prone version of X_i that were actually measured by the multiplex assay. We assume the classical error model, W_i = X_i + U_i, where the p-vector U_i represents the non-differential measurement errors with mean 0 and covariance matrix Σ_uu. Furthermore, we assume U_i and X_i, are independent.

Ignoring measurement error in these data could lead to biased estimates and loss of power.⁹ First, consider the simple linear regression model where only one error-prone explanatory variable W_i is observed instead of X_i, where X_i has variance ${\sigma }_{\mathrm{X}}^2$, and U_i = W_i – X_i has variance ${\sigma }_{\mathrm{u}}^2$. Further consider that the error about the regression line has variance ${\sigma }_{\epsilon }^2$. For simple linear regression where a single covariate W_i is observed instead of X_i, rather than estimating β_x, an attenuated slope λβ_x is estimated where $\lambda =\frac{{\sigma }_X^2}{{\sigma }_X^2+{\sigma }_u^2}<1$. This attenuating factor produces estimates that are biased toward zero.⁹ Furthermore, the residual variance of the observed data is ${\sigma }_{\epsilon }^2+\lambda {\beta }_X^2{\sigma }_u^2$. This introduces additional noise and increased error about the line, thus power is decreased.⁹ Extending beyond simple linear regression, linear regression with multiple covariates measured with error presents increased challenges. In addition to attenuation, effects of these measurement errors may introduce bias away from zero, may change the sign of the estimate, and can lead to invalid hypothesis testing procedures.⁹

2.2. Review of the corrected LASSO procedure

The motivation for the corrected LASSO procedure is that the least squares loss function that includes the error prone covariates W_i, instead of X_i is biased. That is,

$$\begin{gathered} E[({\mathit{Y}}_i-{\beta }_0-{\beta }^{\mathrm{T}}{\mathbf{W}}_i{)}^2\mid {\mathbf{X}}_i]=E[({\mathit{Y}}_i-{\beta }_0-{\beta }^{\mathrm{T}}({\mathbf{X}}_i+{\mathbf{U}}_i){)}^2\mid {\mathbf{X}}_i] \\ =E[({\mathit{Y}}_i-{\beta }_0-{\beta }^{\mathrm{T}}{\mathbf{X}}_i-{\beta }^{\mathrm{T}}{\mathbf{U}}_i{)}^2\mid {\mathbf{X}}_i] \\ =E[({\mathit{Y}}_i-{\beta }_0-{\beta }^{\mathrm{T}}{\mathbf{X}}_i{)}^2-2{\beta }^{\mathrm{T}}{\mathbf{U}}_i(Y_i-{\beta }_0-{\beta }^{\mathrm{T}}{\mathbf{X}}_i)+{\beta }^{\mathrm{T}}\mathbf{U}{\mathbf{U}}^{\mathrm{T}}\beta \mid {\mathbf{X}}_i] \\ =E[(Y_i-{\beta }_0-{\beta }^{\mathrm{T}}{\mathbf{X}}_i{)}^2\mid {\mathbf{X}}_i]+{\beta }^{\mathrm{T}}{\Sigma }_{\text{uu}}\beta . \end{gathered}$$

When the covariance matrix Σ_uu is known, the penalized least squares correction method^12-14 simply subtracts the bias correction term from the penalized least squares function and minimizes the corrected function:

$$\frac{1}{2}\cdot \sum _{i=1}^n(Y_i-{\beta }_0-{\mathbf{W}}_i^{\mathrm{T}}\beta {)}^2-\frac{n}{2}\cdot {\beta }^{\mathrm{T}}{\Sigma }_{\text{uu}}\beta +n\cdot \lambda \cdot \sum _{j=1}^p\mid {\beta }_j\mid$$

where the second term is the bias correction and the third term is the LASSO penalty.

2.3. Corrected LASSO procedure with validation data

We adapt the correction approach reviewed above to the analysis of multiplex serum biomarker data. The corrected LASSO procedure assumes that the error-prone serum biomarkers are measured on all study subjects and that Σ_uu is known or is estimated from replicate data. For this study, we assume that all biomarkers are measured by the multiplex assay for the full study sample, and that a subset of biomarkers are measured using a more precise method (the gold standard) for a randomly selected subset of the study sample (the internal validation set), and consider that these biomarkers are selected based on prior knowledge and budget of the investigation. We then calculate the error corrected penalized least squares function based on data from the validation set.

In deriving the corrected penalized least squares function, we use the accurate X if it is available (for subjects in the validation set) and use the error-prone W if X is not available (for subjects not in the validation set). For the ith subject (i = 1,…, n), we define an indicator for the internal validation set: ξ_i = 1 if the ith subject is in the validation set and ξ_i = 0 otherwise. Let ${\overline{\xi }}_i=1-{\xi }_i$. Then we consider a modification to the corrected LASSO

$$\frac{1}{2}\cdot \sum _{i=1}^n[Y_i-{\beta }_0-({\xi }_i{\mathbf{X}}_i^{\mathrm{T}}{\beta }_{\mathrm{X}}+{\overline{\xi }}_i{\mathbf{W}}_i^{\mathrm{T}}{\beta }_{\mathrm{W}}){]}^2-{\overline{\xi }}_i\left(\frac{n}{2}\cdot {\beta }_{\mathrm{X}}^{\mathrm{T}}{\widehat{\Sigma }}_{\text{uu}}{\beta }_{\mathrm{X}}\right)+n\cdot \lambda \cdot \sum _{j=1}^p\mid {\beta }_j\mid$$

where the covariance matrix ${\widehat{\Sigma }}_{\text{uu}}$ is an estimate of the unknown covariance matrix Σ_uu and is estimated by the internal validation set. The subtraction of the bias correction term is only implemented for subjects not in the validation set.

Coordinate descent is an efficient algorithm that has been used to obtain the LASSO estimates and has previously been described.¹⁵ Briefly, this iterative method minimizes a function over one parameter at a time, keeping all other parameters fixed. We derive a modified coordinate descent algorithm that accounts for the bias correction term and have included details in the Online Appendix.

3. Simulation study

A simulation study was performed to compare the corrected LASSO with validation data to the uncorrected LASSO with validation data. The former approach includes the bias correction term that is estimated from the validation data. For both methods, W_i is replaced by X_i measured in the validation set. We generate 1000 datasets, each with a sample size of n = 1000 and with p = 100 serum biomarkers measured with error. The error-free biomarker vector X_i is generated from a multivariate normal distribution with 0 as the mean and the identity matrix as the variance-covariance matrix, so all biomarkers are uncorrelated. We consider both moderate and large measurement error for each biomarker, where the error is generated from a normal distribution with mean 0 and standard deviation 0.5 for moderate measurement error and 1.0 for large measurement error. W_i is obtained by adding the measurement error vector to X_i.

Table 1 shows eight different scenarios for the simulation study. Scenarios 1–4 involve sparse models with a small number of true signals, i.e. only a small number of biomarkers have non-zero coefficients, and Scenarios 5–8 involve non-sparse models with a moderate number of true signals. For sparse models, we consider five true signals (β₁ = β₂ = β₃ = β₄ = β₅ = 1) and 95 noise covariates (β₆ = β₇ = … = β₁₀₀ = 0). For the non-sparse models, we consider 40 true signals (β₁ = β₂ = β₃ = β₄ = β₅ = 1, β₆ = β = 7 = … = β₄₀ ~ Uniform Distribution (0.1, 1)) and 60 noise covariates (β₆₀ = β₆₁ = … = β₁₀₀ = 0).

Table 1.

Simulation scenarios (n = 1000 with 1000 simulated data sets).

	Data generation		Measurement error correction
Scenario	Number of true signals	Non-zero coefficients in multiple linear regression models	SD of error	Number of corrected covariates	Validation data
1	5	β1 = β2 = β3 = β4 = β5 = 1	0.50	1,2,3,4,5	10%
2	5	β1 = β2 = β3 = β4 = β5 = 1	0.50	1,2,3,4,5	20%
3	5	β1 = β2 = β3 = β4 = β5 = 1	1.00	1,2,3,4,5	10%
4	5	β1 = β2 = β3 = β4 = β5 = 1	1.00	1,2,3,4,5	20%
5	40	β1 = β2 = β3 = β4 = β5 = 1, β6 = β7 =…= β40 ~ ∪ (0.1, 1)	0.50	1,2,3,4,5	10%
6	40	β1 = β2 = β3 = β4 = β5 = 1, β6 = β7 = … = β40 ~ ∪ (0.1, 1)	0.50	1,2,3,4,5	20%
7	40	β1 = β2 = β3 = β4 = β5 = 1, β6 = β7 = … = β40 ~ ∪ (0.1, 1)	1.00	1,2,3,4,5	10%
8	40	β1 = β2 = β3 = β4 = β5 = 1, β6 = β7 = …= β40 ~ U (0.1, 1)	1.00	1,2,3,4,5	20%

We compare the corrected LASSO with validation data to the uncorrected LASSO with validation data. The LASSO shrinkage parameters were estimated using 10-fold cross validation in order to minimize model mean squared error. The optimal shrinkage parameter λ found by cross validation was used to penalize all coefficients equally.

We consider estimation accuracy as the median of squared error (MSE) over the 1000 simulations. The error is the difference between the estimated coefficient from the error-prone models and that from the true values. We present the MSE for each of the first five non-zero coefficients and the MSE across all 100 predictors. We also consider variable selection performance measures as the mean number of true positives (TP) and false positives (FP) selected by each model.

Table 2 shows results for Scenarios 1 and 2, which represent sparse models and moderate measurement error. For the uncorrected model without validation data, the overall MSE for all predictors is 0.299 with mean number of five TP and 14 FP. As expected, the MSE decreases with increased number of corrected variables and with increased validation data. For Scenario 1 with 10% validation data, after correcting for one variable the overall MSE is 0.258, which decreases to 0.147 after correcting for five variables. Results for Scenario 2 with 20% validation show similar results, albeit with less bias. Using 10% validation data, correction for one variable reduces the mean number of FP to six and correction for five variables reduces the mean number of FP to almost zero. The mean number of TP remains at five for all models.

Table 2.

Sparse solution, moderate measurement error.

Scenarios	Method	Median of squared error						Variable selection
		W1b	W2b	W3b	W4b	W5b	All Predictorsc	True Positive (mean)	False Positive (mean)
No validation dataa	Uncorrected	0.058	0.059	0.058	0.059	0.057	0.299	5	13.995
Scenario 1:	Uncorrected	0.050	0.059	0.058	0.059	0.057	0.291	5	14.063
1 corrected, 10%	Corrected	0.003	0.062	0.061	0.063	0.061	0.258	5	5.543
Scenario 1:	Uncorrected	0.050	0.051	0.058	0.058	0.057	0.283	5	14.150
2 corrected, 10%	Corrected	0.007	0.007	0.072	0.073	0.072	0.237	5	1.139
Scenario 1:	Uncorrected	0.050	0.051	0.050	0.059	0.057	0.274	5	14.142
3 corrected, 10%	Corrected	0.013	0.013	0.013	0.086	0.085	0.217	5	0.126
Scenario 1:	Uncorrected	0.050	0.051	0.050	0.051	0.057	0.267	5	14.13
4 corrected, 10%	Corrected	0.020	0.020	0.020	0.020	0.099	0.187	5	0.014
Scenario 1:	Uncorrected	0.049	0.051	0.050	0.051	0.050	0.258	5	13.912
5 corrected, 10%	Corrected	0.027	0.026	0.027	0.028	0.028	0.147	5	0.002
Scenario 2:	Uncorrected	0.043	0.058	0.058	0.059	0.057	0.283	5	14.18
1 corrected, 20%	Corrected	0.003	0.062	0.061	0.062	0.060	0.253	5	6.265
Scenario 2:	Uncorrected	0.043	0.044	0.057	0.058	0.057	0.267	5	14.063
2 corrected, 20%	Corrected	0.006	0.006	0.068	0.069	0.068	0.221	5	1.685
Scenario 2:	Uncorrected	0.043	0.044	0.044	0.058	0.057	0.252	5	13.867
3 corrected, 20%	Corrected	0.010	0.011	0.010	0.080	0.080	0.197	5	0.215
Scenario 2:	Uncorrected	0.042	0.043	0.042	0.043	0.057	0.235	5	14.075
4 corrected, 20%	Corrected	0.016	0.016	0.016	0.016	0.092	0.161	5	0.018
Scenario 2:	Uncorrected	0.042	0.043	0.042	0.042	0.042	0.218	5	14.186
5 corrected, 20%	Corrected	0.022	0.022	0.022	0.021	0.022	0.116	5	0.001

^aThe first row shows results for the error-prone model without validation data. This would represent the model with only multiplex data.

^bThe covariates W₁–W₅ include validation data and represent the five of 100 covariates that may be corrected. These columns show the bias (MSE) for each of the individual estimates.

^cThis column represents the MSE for all 100 predictors.

Table 3 shows the results for Scenarios 3 and 4, which represent sparse models and large measurement error. Similar results are seen as compared to the models with moderate measurement error, though with greater bias. For the uncorrected model without validation data, the MSE for all predictors is 1.537 with a mean number of five TP and 14 FP. For Scenario 3 with 10% validation data, after correcting for one variable the overall MSE is 1.525, which decreases to 0.694 after correcting for five variables. Scenario 4 with 20% validation data shows similar results, again with less bias. For variable selection, correction for one variable using 10% validation data reduces the mean number of FP to less than one and correction for five variables reduces the mean number of FP to almost zero. The mean number of TP again remains at five for all models.

Table 3.

Sparse solution, large measurement error.

Scenarios	Method	Median of squared error						Variable selection
		W1b	W2b	W3b	W4b	W5b	All Predictorsc	True Positive (mean)	False Positive (mean)
No validation dataa	Uncorrected	0.303	0.306	0.303	0.307	0.304	1.537	5	13.897
Scenario 3:	Uncorrected	0.277	0.306	0.303	0.307	0.303	1.507	5	14.159
1 corrected, 10%	Corrected	0.042	0.370	0.365	0.371	0.365	1.525	5	0.76
Scenario 3:	Uncorrected	0.277	0.279	0.302	0.306	0.302	1.479	5	14.397
2 corrected, 10%	Corrected	0.086	0.090	0.426	0.429	0.424	1.474	5	0.034
Scenario 3:	Uncorrected	0.277	0.280	0.277	0.307	0.303	1.452	5	14.085
3 corrected, 10%	Corrected	0.107	0.110	0.114	0.450	0.450	1.272	5	0.002
Scenario 3:	Uncorrected	0.276	0.279	0.276	0.280	0.303	1.423	5	14.302
4 corrected, 10%	Corrected	0.113	0.115	0.116	0.116	0.457	0.999	5	0
Scenario 3:	Uncorrected	0.275	0.278	0.276	0.279	0.276	1.398	5	14.337
5 corrected, 10%	Corrected	0.114	0.113	0.116	0.116	0.116	0.694	4.999	0
Scenario 4:	Uncorrected	0.250	0.305	0.304	0.305	0.303	1.478	5	14.05
1 corrected, 20%	Corrected	0.035	0.356	0.354	0.355	0.353	1.464	5	0.877
Scenario 4:	Uncorrected	0.249	0.252	0.301	0.304	0.303	1.422	5	14.179
2 corrected, 20%	Corrected	0.077	0.078	0.410	0.415	0.414	1.407	5	0.015
Scenario 4:	Uncorrected	0.247	0.251	0.250	0.304	0.302	1.360	5	14.359
3 corrected, 20%	Corrected	0.150	0.108	0.104	0.445	0.445	1.222	5	0
Scenario 4:	Uncorrected	0.247	0.251	0.247	0.250	0.301	1.304	5	14.679
4 corrected, 20%	Corrected	0.113	0.117	0.118	0.113	0.456	0.965	5	0
Scenario 4:	Uncorrected	0.246	0.250	0.246	0.249	0.247	1.245	5	14.877
5 corrected, 20%	Corrected	0.118	0.122	0.120	0.114	0.115	0.636	5	0

^aThe first row shows results for the error-prone model without validation data. This would represent the model with only multiplex data.

^bThe covariates W₁–W₅ include validation data and represent the five of 100 covariates that may be corrected. These columns show the bias (MSE) for each of the individual estimates.

^cThis column represents the MSE for all 100 covariates.

Table 4 shows results for Scenarios 5 and 6, which represent non-sparse models and moderate measurement error. For the uncorrected model without validation data, the MSE for all predictors is 1.225 with a mean number of 40 TP and 34 FP. While there was a reduction in MSE for the individually corrected predictors, the MSE for all predictors remain relatively similar. For Scenario 5 with 10% validation data, the overall MSE with one corrected variable is 1.228 as compared to 1.212 for the uncorrected model with validation data. For five corrected variables, the overall MSE is 1.147 as compared to 1.181 for the uncorrected model with validation data. A similar trend is seen for Scenario 6 with 20% validation data. For variable selection, correction for one variable using 10% validation data reduces the mean number of FP to 26.5 and correction for five variables reduces the mean number of FP to18.5. The mean number of TP remains at 39 to 40 for all models.

Table 4.

Non-sparse solution, moderate measurement error.

Scenarios	Method	Median of squared error						Variable selection
		W1b	W2b	W3b	W4b	W5b	All Predictorsc	True Positive (mean)	False Positive (mean)
No validation dataa	Uncorrected	0.053	0.053	0.055	0.054	0.053	1.225	39.887	33.700
Scenario 5:	Uncorrected	0.046	0.053	0.055	0.054	0.053	1.212	39.884	33.718
1 corrected, 10%	Corrected	0.003	0.054	0.057	0.056	0.055	1.228	39.163	26.495
Scenario 5:	Uncorrected	0.047	0.045	0.055	0.054	0.053	1.202	39.897	33.762
2 corrected, 10%	Corrected	0.004	0.004	0.058	0.057	0.056	1.206	39.086	24.439
Scenario 5:	Uncorrected	0.046	0.045	0.048	0.053	0.053	1.202	39.887	33.715
3 corrected, 10%	Corrected	0.004	0.004	0.004	0.059	0.058	1.178	38.998	22.365
Scenario 5:	Uncorrected	0.046	0.046	0.048	0.047	0.053	1.189	39.895	33.538
4 corrected, 10%	Corrected	0.004	0.005	0.005	0.005	0.059	1.161	38.925	20.472
Scenario 5:	Uncorrected	0.046	0.045	0.048	0.047	0.046	1.181	39.897	33.569
5 corrected, 10%	Corrected	0.005	0.005	0.005	0.005	0.004	1.147	38.835	18.546
Scenario 6:	Uncorrected	0.039	0.053	0.055	0.054	0.053	1.202	39.880	33.635
1 corrected, 20%	Corrected	0.003	0.054	0.057	0.055	0.055	1.220	39.170	26.733
Scenario 6:	Uncorrected	0.040	0.040	0.056	0.054	0.053	1.189	39.892	33.652
2 corrected, 20%	Corrected	0.003	0.003	0.058	0.057	0.056	1.191	39.119	24.897
Scenario 6:	Uncorrected	0.040	0.040	0.041	0.053	0.053	1.169	39.887	33.587
3 corrected, 20%	Corrected	0.003	0.003	0.003	0.058	0.058	1.158	39.055	23.358
Scenario 6:	Uncorrected	0.040	0.040	0.041	0.040	0.053	1.155	39.897	33.67
4 corrected, 20%	Corrected	0.003	0.004	0.004	0.003	0.059	1.124	38.998	21.639
Scenario 6:	Uncorrected	0.039	0.040	0.041	0.039	0.040	1.136	39.902	33.819
5 corrected, 20%	Corrected	0.004	0.004	0.004	0.003	0.004	1.092	38.925	20.140

^aThe first row shows results for the error-prone model without validation data. This would represent the model with only multiplex data.

^bThe covariates W₁–W₅ include validation data and represent the five of 100 covariates that may be corrected. These columns show the bias (MSE) for each of the individual estimates.

^cThis column represents the MSE for all 100 covariates.

Table 5 shows results for Scenarios 7 and 8, which represent non-sparse models and large measurement error. For the uncorrected model without validation data, the MSE for all predictors was 6.093 with a mean number of 38 TP and 31 FP. For both scenarios, again while the individual corrected predictors showed less bias, the overall MSE was greater for the corrected models. For variable selection, correction for one variable using 10% validation data reduces the mean number of FP to18 and correction for five variables reduces the mean number of FP to four. The mean number of TP is reduced for the corrected models at 31.5 when correcting for five variables using 10% validation data.

Table 5.

Non-sparse solution, large measurement error.

Scenarios	Method	Median of squared error						Variable selection
		W1b	W2b	W3b	W4b	W5b	All Predictorsc	True Positive (mean)	False Positive (mean)
No validation dataa	Uncorrected	0.297	0.298	0.299	0.297	0.299	6.093	38.274	31.384
Scenario 7:	Uncorrected	0.273	0.298	0.299	0.299	0.299	6.076	38.289	31.292
1 corrected, 10%	Corrected	0.020	0.318	0.315	0.316	0.319	6.229	36.205	18.174
Scenario 7:	Uncorrected	0.271	0.271	0.300	0.299	0.297	6.037	38.307	31.482
2 corrected, 10%	Corrected	0.027	0.027	0.336	0.336	0.336	6.359	35.036	12.74
Scenario 7:	Uncorrected	0.271	0.271	0.272	0.298	0.297	6.012	38.312	31.458
3 corrected, 10%	Corrected	0.033	0.036	0.037	0.359	0.356	6.545	33.881	8.931
Scenario 7:	Uncorrected	0.270	0.272	0.273	0.273	0.298	5.985	38.300	31.31
4 corrected, 10%	Corrected	0.044	0.045	0.040	0.045	0.379	6.754	32.589	6.065
Scenario 7:	Uncorrected	0.270	0.270	0.272	0.272	0.273	5.942	38.322	31.609
5 corrected, 10%	Corrected	0.055	0.056	0.055	0.057	0.052	6.990	31.481	4.195
Scenario 8:	Uncorrected	0.244	0.297	0.298	0.297	0.298	6.032	38.305	31.468
1 corrected, 20%	Corrected	0.015	0.312	0.314	0.312	0.314	6.132	36.476	19.591
Scenario 8:	Uncorrected	0.244	0.245	0.297	0.297	0.299	5.973	38.310	31.530
2 corrected, 20%	Corrected	0.018	0.018	0.327	0.325	0.329	6.166	35.629	14.697
Scenario 8:	Uncorrected	0.244	0.245	0.244	0.296	0.297	5.914	38.319	31.551
3 corrected, 20%	Corrected	0.021	0.025	0.023	0.342	0.341	6.209	34.877	11.075
Scenario 8:	Uncorrected	0.243	0.245	0.243	0.244	0.299	5.855	38.374	31.639
4 corrected, 20%	Corrected	0.026	0.031	0.029	0.030	0.357	6.257	33.991	8.135
Scenario 8:	Uncorrected	0.242	0.243	0.243	0.243	0.246	5.800	38.371	31.670
5 corrected, 20%	Corrected	0.034	0.038	0.034	0.036	0.036	6.277	32.997	5.902

^aThe first row shows results for the error-prone model without validation data. This would represent the model with only multiplex data.

^bThe covariates W₁–W₅ include validation data and represent the five of 100 covariates that may be corrected. These columns show the bias (MSE) for each of the individual estimates.

^cThis column represents the MSE for all 100 covariates.

4. Application study

TESAOD is a population-based prospective cohort study initiated in 1972 in Tucson, Arizona. Details of the study have been previously reported.¹⁶ For the current study, serum biomarkers were measured by a multiplex assay on 879 non-Hispanic white participants who were between the ages of 21 and 70 at study enrollment. Cryopreserved serum samples were analyzed at the Myriad-Rules Based Medicine (RBM) facilities (Austin, TX, USA) using the Human Multi-Analyte Profile panel version 1.6, a bead-based suspension multiplex assay based on Luminex immunoassay technology. One biomarker measured by this multiplex panel, C-Reactive Protein (CRP) was additionally measured by a single biomarker assay, namely an enzymatic solid-phase chemiluminescent immunometric assay (Immulite 2000, Siemens Diagnostics, Tarrytown, NY, USA). These additional CRP measurements were obtained for all study subjects who had samples measured by the multiplex assay. The mean coefficient of variation computed from these samples was 8.7% and 2.7% for CRP levels obtained by multiplex and single-biomarker assays, respectively. There was strong correlation between CRP levels measured by the two assays (Pearson’s correlation coefficient: 0.80, p < 0.0001).

CRP has a known association with body mass index (BMI). The goal of the current study was to investigate the estimation of the association between CRP and BMI when a subset of single-biomarker measurements of CRP is available to use for correction of multiplex-derived CRP measurements. The University of Arizona Institutional Review Board (IRB) approved the TESAOD study (IRB approval 08-0741-01). Written informed consent was obtained from all study participants.

Using these data, we consider the penalized linear regression model using the LASSO penalty. There are a total of 82 serum biomarkers measured by the multiplex assay on 851 subjects with available BMI information. Although CRP measurements were available for all 851 subjects by both methods, to evaluate the corrected LASSO method using internal validation data, we first randomly select 10% of the study sample and apply the proposed method. We then repeat this random selection 1000 times and consider the median of squared difference (MSD) for these 1000 random samplings, where MSD describes the difference between the estimated coefficients from the model with CRP measured by a single biomarker assay. This procedure is repeated for a 20% validation set. Standardized values were used for all measurements.

Table 6 shows the MSD and the number of non-zero coefficients for the application study. The uncorrected model without validation data had MSD of 0.137 for CRP. This decreased to 0.108 for the uncorrected model with 10% validation data for CRP and 0.085 with 20% validation data for CRP. The corrected models had MSD of 0.034 with 10% validation data for CRP and 0.019 with 20% validation data for CRP. Of note, MSD was lower for the corrected model with 10% validation data for CRP (0.034) as compared to the uncorrected model with 20% validation data for CRP (0.085). This suggests that incorporation of the correction method with as little as 10% validation data, may lead to more precise estimates than simply obtaining additional measurements from the single biomarker assay.

Table 6.

Application.

Scenarios	Method	Median of squared differenceb	Variable selection
		CRP	CRP correctly identified (proportion)	Number of non-zero coefficients (mean)
CRP measured by single biomarker  assay, Measurements from all subjects	Single biomarker	-	1/1	17c
CRP measured by multiplex assay,  Validation data not used	Multiplex assay, Uncorrected	0.137	1/1	18c
CRP corrected, 10% validation dataa	Uncorrected	0.108	1000/1000	19.84
	Corrected	0.034	1000/1000	22.07
CRP corrected, 20% validation dataa	Uncorrected	0.085	1000/1000	19.42
	Corrected	0.019	1000/1000	23.30

^aCalculated as the median of 1000 random samplings.

^bCalculated as the difference between estimates from the model with CRP measured by a single biomarker assay.

^cObserved value.

5. Discussion

We considered two adaptations to the penalized corrected least squares method for the linear regression model with validation data. First, we considered obtaining more precise measurements on a small number of serum biomarkers that were likely associated with the outcome and then applying bias correction to this subset of important markers. Second, we estimated the measurement error distribution based on a random subset of the study sample (either 10% or 20% of the samples). Using this internal validation data to estimate the measurement error distribution, we adapted the existing methods to get a simple statistical measurement correction. Utilizing such an approach greatly reduces the costs associated with serum biomarker measurement. In addition to the financial and time saving aspects, it would also decrease the minimum size of the samples obtained or eliminate the necessity to obtain additional serum samples on study subjects.

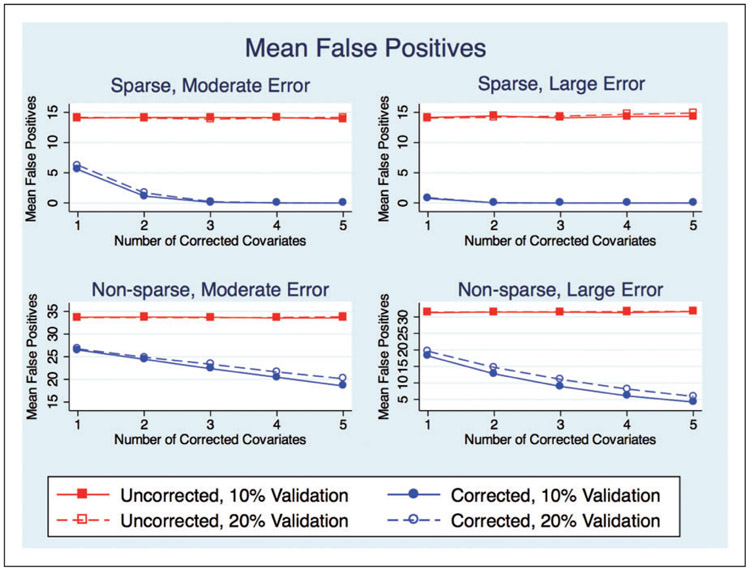
Most notably, what this study shows is that improvement in variable selection (Figure 1) can be achieved even when we correct for only one biomarker using as few as 10% validation data. For the models with large measurement error, these scenarios reduced the mean number of FP from 14 to less than one for the sparse models and from 31 to 18 for the non-sparse models. Furthermore, the mean number of TP remains relatively unchanged, with the exception of models with non-sparse solution and large measurement error. This is analogous to results shown by Sorensen et al.¹⁴ They show that in the presence of measurement error, the LASSO selects a large number of FP and that after bias correction the number of FP is greatly reduced.¹⁴ Similar to our results for non-sparse models (Tables 4 and 5), they show the uncorrected LASSO to have slightly higher TP as compared to the corrected LASSO.¹⁴

Figure 1.

Mean number of false positives.

As shown previously by others,^12-14 we also show a decrease in bias in most situations (Figure 2) with the exception of the non-sparse model with large measurement error, albeit still with reduction in FP. Results indicate that while bias is reduced for each of the corrected estimates, bias for the remaining uncorrected estimates are slightly larger for the corrected LASSO as compared to the uncorrected LASSO (W₁–W₅ in Table 5). Given that the corrected LASSO with validation data only corrects for a subset of covariates, this may in part explain the increase in overall MSE.

Figure 2.

Median of squared error for all predictors.

Following the recommendation to utilize multiplex assays as a screening tool to identify promising biomarker candidates, then to measure individual candidates using single biomarker assays,⁸ it may be reasonable to consider applying the corrected LASSO procedure using validation data. When a small group of biomarkers of interest are identified (or known a priori), they could be re-measured by a more precise method in a small randomly selected subset of patients and then used in the error correction method to fit the LASSO model. In addition to decreased bias and improved variable selection, utilization of the adapted penalized least squares method may improve efficiency and reduce costs of laboratory measurements.