Deconstructing Odorant Identity via Primacy in Dual Networks

Abstract

In the olfactory system, odor percepts retain their identity despite substantial variations in concentration, timing, and background. We study a novel strategy for encoding intensity-invariant stimulus identity that is based on representing relative rather than absolute values of stimulus features. For example, in what is known as the primacy coding model, odorant identities are represented by the conditions that some odorant receptors are activated stronger than others. Because, in this scheme, the odorant identity depends only on the relative amplitudes of olfactory receptor responses, identity is invariant to both changes in intensity and monotonic non-linear transformations of its neuronal responses. Here we show that sparse vectors representing odorant mixtures can be recovered in a compressed sensing framework via elastic net loss minimization. In primacy model, this minimization is to be performed under the constraint that some receptors respond to a given odorant stronger than others. Using duality transformation, we show that such a constrained optimization problem can be solved by a neural network whose Lyapunov function represents the dual Lagrangian and whose neural responses represent the Lagrange coefficients of primacy and other constraints. The structure of connectivity in such a dual network resembles known features of connectivity in the olfactory circuits. We thus propose that networks in the piriform cortex implement dual computations to compute odorant identity with the sparse activities of individual neurons representing Lagrange coefficients. More generally, we propose that sparse neuronal firing rates may represent Lagrange multipliers, which we call the dual brain hypothesis. We show such a formulation is well-suited to solve problems with multiple interacting relative constraints.

1. INTRODUCTION

Sensory systems face the problem of identifying stimulus features that are invariant to various transformations. The olfactory system, for example, has to identify stimuli despite substantial variations in odorant concentration. Computing concentration invariant odor identity is necessary to enable a stable perception in chemical gradients and turbulent odorant plumes. How can the olfactory system robustly represent odorant identity despite variable stimulus intensity? The first step of olfactory processing involves odorants binding to and activating a set of molecular sensors known as olfactory receptors (ORs). ORs are proteins expressed by olfactory sensory neurons (OSNs) located in the nose. Most mammalian olfactory systems contain ~1000 types ORs, while humans rely on the responses of only 350 (Firestein, 2001; Koulakov et al., 2007; Zhang and Firestein, 2002). Importantly, every OSN expresses only a single type of OR chosen randomly out of the large ensemble. Odorant identity is then interpreted from the patterns of activation of OR and, by extension, OSNs. Here we examine the hypothesis that stimulus identity is inferred by the relative amplitudes of OSN responses. In particular, we propose that odorant identity can be determined using only the information that a subset of receptors individually respond more strongly than all other receptors. We call this type of representation the primacy model. The primacy model is inspired by a recent experimental observation that odorant identity is recognized on the basis of inputs present within the first 100 milliseconds of the animal’s sniff cycle (Wilson et al., 2017). We will show that the coding scheme based on the primacy model yields odorant representations that are independent of absolute odorant concentration. We will formulate this identity decoding scheme using a dual Lagrange-Karush-Kuhn-Tucker problem and argue that this dual problem can be solved by a neural network that we call a dual network. Dual networks that implement the primacy model share many features with real olfactory networks. Our goal is therefore to derive the structure of olfactory circuits from first principles, based on the primacy model.

2. RESULTS

2.1. Representing odorants by sparse vectors.

Ethologically important odorant stimuli are mixtures of monomolecular components. Such stimuli can be represented by a vector of concentrations $\overrightarrow{x}$. Each component of this vector x_j is equal to the concentration of an individual monomolecular component numbered by index j. The number of potential monomolecular components, which is equal to the dimensionality of vector $\overrightarrow{x}$, will be denoted here by M. This number can be estimated to be around several million, M ~ 10⁶, based on the count of potentially volatile molecules with molecular weight less than 300 Dalton in the popular database PubChem (Kim et al., 2016). However, ethological odorant mixtures do not contain all of these molecules at the same time, and are therefore represented by sparse vectors $\overrightarrow{x}$. For the purposes of olfactory system, sparseness of the concentration vector is further increased by inability of the system to detect or recognize individual components. Indeed, psychophysical studies suggest that the number of monomolecular components of the vector $\overrightarrow{x}$ detectable by a human observer K is close to 12 (Jinks and Laing, 1999). Overall, we suggest that ethologically relevant odorants can be defined by highly dimensional (M ~ 10⁶), sparse concentration vectors $\overrightarrow{x}$ with very few non-zero elements (K ~ 10).

Odorant mixtures then enter the olfactory system through the responses of ORs $\overrightarrow{r}$. These responses, to the first approximation, can be represented by a linear nonlinear function of the concentration vector $\overrightarrow{x}$. In the simplest model, using receptors with only one binding site and no cooperativity, the law of mass action yields:

$$r_i=F(y_i)$$ (2.1)

$$y_i=\sum _j{A}_{ij}{x}_j$$ (2.2)

Here index i = 1…N enumerates OR types. The total number of functional OR types, N, varies between 350 in humans and 1100 in rodents. Matrix element A_ij can be interpreted as the affinity of molecule type j to receptors of type i. F(y) = y/(1+y) is the nonlinear function describing activation of a receptor (Appendix A).

The problem solved by the olfactory system can then be formulated as follows: find the identity of the odorant stimulus x_j given the set of responses of olfactory sensory neurons r_i.

2.2. Sparse olfactory stimulus recovery.

In many concentration regimes, it is reasonable to approximate the receptor response r_i using only its linear input y_i. In this case, the problem solved by olfactory system (how to find $\overrightarrow{x}$ given $\overrightarrow{y}$) can be reduced to solving the system of linear equations (2.2). This problem is not entirely trivial, because the number of unknowns (components of $\overrightarrow{x}$, M ~ 10⁶) is substantially larger than the number of equations (components of $\overrightarrow{y}$, N ~ 10³). Some help comes from the fact that the vector of unknowns is sparse. The problem of recovering a sparse vector from a system of linear equations has been addressed in compressed sensing (Baraniuk, 2007; Donoho and Tanner, 2005, 2006). In this framework, vector $\overrightarrow{x}$ can be found exactly, despite the fact that it contains more components than equations. This is because the vector $\overrightarrow{x}$ is sparse and the number of non-zero components is small. To be able to find $\overrightarrow{x}$ exactly, a certain condition has to be met relating parameters M, N, and K. This condition can be understood by comparing the amounts of information contained in the input and output space. One can accurately determine the unknowns, if the information capacity of $\overrightarrow{y}$ exceeds that of $\overrightarrow{x}$. These two amounts can be estimated by using the statistical physics definition of the amount of information:

$$H=\text{log}\Gamma$$ (2.3)

Here H and Γ are the amount of information and the number of states a variable can take, respectively. For example, a string of N binary numbers contains H = N bits of information, which follows from equation (2.3) if the number of possible values of the binary string is Γ = 2^N. The number of values taken by the receptor response vector $\overrightarrow{y}$ can then be estimated as Γ_y ~ 2^N (for the purposes of our order-of-magnitude estimate, we assume here that the elements of $\overrightarrow{y}$ are binary). The number of possible combinations contained in the concentration vector $\overrightarrow{x}$ can be estimated as the number of ways to place K non-zero elements into M bins, i.e. ${\Gamma }_x~C_M^K~M^K$. Similar to the estimate for receptor responses, we assume here that concentrations are binary. This assumption is reasonable if the number of distinguishable concentrations for an element of $\overrightarrow{x}$ is much less than the total number of elements in $\overrightarrow{x}$, M. Thus, equation (2.2) can be solved exactly if the number of combinations contained in vector $\overrightarrow{y}$ is larger than the number of possible states of the concentration vector $\overrightarrow{x}$, i.e. Γ_y > Γ_x, which, given our estimates, yields the following condition:

$$N>K\text{log}M$$ (2.4)

This condition can be recognized as the necessary condition for sparse signal recovery using l₁ norm minimization obtained by Donoho and Tanner (Donoho and Tanner, 2005, 2006). For K ~ 10 and M ~ 10⁶ we obtain the following constraint for the number of OR types necessary for the recovery of the sparse stimulus: N > 200, which is satisfied for both humans (N ≈ 350) and mice (N ≈ 1100). Thus, equation (2.2) can in principle be solved with the existing machinery in the olfactory system. This means that, with linear responses, the olfactory system can reconstruct K ~ 10 monomolecular components given the responses of N ≈ 1100 ORs.

To determine $\overrightarrow{x}$ given $\overrightarrow{y}$ within compressed sensing, one can use sparse signal recovery via minimization of the l₁ norm (Baraniuk, 2007; Donoho and Tanner, 2005, 2006):

$$\overrightarrow{x}=\underset{\begin{array}{l}\overrightarrow{y}=A\overrightarrow{x}\\ x_j\ge 0\end{array}}{\text{arg}\text{min}}\sum _j{x}_j$$ (2.5)

Here, because molecular concentrations $\overrightarrow{x}$ are constrained to be non-negative, minimization of l₁ norm is equivalent to minimization of the sum of the components of $\overrightarrow{x}$. Because the system is overcomplete, there are many vectors $\overrightarrow{x}$ for which $y_i=\sum _j{A}_{ij}{x}_j$ is satisfied exactly. Minimization of l₁ norm ensures that the solution is sparse.

Solving the decoding problem using equation (2.5) is somewhat unrealistic because receptor responses are non-linear. Furthermore, the solution of equation (2.5) is not concentration invariant. That is, doubling the mixture concentration results in doubling of each component of the concentration vector $\overrightarrow{x}$, and, as a result, the doubling of the vector of receptor responses $\overrightarrow{y}=A\overrightarrow{x}$. Solving equation (2.5) under the constraint of doubled vector $\overrightarrow{y}$ results in a doubled reconstructed vector of concentrations $\overrightarrow{x}$. Our goal, however, is to build a representation that is concentration invariant, and not to be limited to regimes where receptor response is linear. More specifically, we want a representation of an odor which is invariant to multiplication of the concentration vector of that odor by a scalar. This means that we would like to obtain a framework in which doubling receptor responses $\overrightarrow{y}$ or the presence of non-linearities, such as given by equation (2.1), does not impact the reconstructed stimulus. Such a model would yield a concentration invariant odorant identity. Next, we show how a primacy-based decoding model can implement such a computation.

2.3. Concentration invariant decoding algorithm via primacy.

To achieve an odorant representation which is invariant to both concentration fluctuations and monotonic nonlinearities of receptor responses, we reformulate the sparse recovery problem to use only relative constraints. Conceptually, the relative constraints we introduce isolate a set of receptor types, each of which respond more strongly than all other receptor types. We call this strongly-responding set of receptors the primacy set P, while all other receptors are denoted by $\overline{P}$. The primacy set is expected to include p ≪ 1000 receptor types. For these two sets we can state:

$$r_P\ge r_{\overline{P}}$$ (2.6)

Here, r_P is the set of components of vector $\overrightarrow{r}$ that belong to the primacy group P of the given odorant. The expanded version of equation (2.6) is therefore r_i ≥ r_j for any i ∈ P and $j\in \overline{P}$. Because the non-linearity relating r_i and y_i is monotonic, equation (2.6) results in the same constraint on components of vector $\overrightarrow{y}$:

$$y_P\ge y_{\overline{P}}$$ (2.7)

Importantly, the inequality (2.7) is invariant to changes in concentration, because concentration changes ($\overrightarrow{x}\to \alpha \overrightarrow{x}$) multiply both sides of equation (2.7) by the same factor. Also, the identities of the ORs forming the primacy set, P, are unaffected by the non-linearity relating r to y, so long as this non-linearity is monotonically increasing. Thus, reconstructions of $\overrightarrow{x}$ using these inequalities inherently have the desired invariances. We therefore reformulate the sparse recovery problem (2.5) as follows:

$$\overrightarrow{x}=\underset{\begin{array}{l}{y}_P\ge y_{\overline{P}}\\ x_j\ge 0\end{array}}{\text{arg}\text{min}}\sum _j{x}_j$$ (2.8)

We implement this minimization and show that it converges to reconstruct the stimulus vector $\overrightarrow{x}$ in Figure 1. For this simulation and all subsequent simulations in this paper, we use N=400 receptors and M=1000 molecules. We generate affinities A_ij from a zero-mean Gaussian distribution truncated at zero such that all affinities are non-negative. In Supplemental Figure 2 we show that this assumption on the distribution of A_ij is unnecessary and that our algorithm works for uniform or lognormally distributed A_ij matrices for a wide range of the number of receptors N and molecules M.

Figure 1.

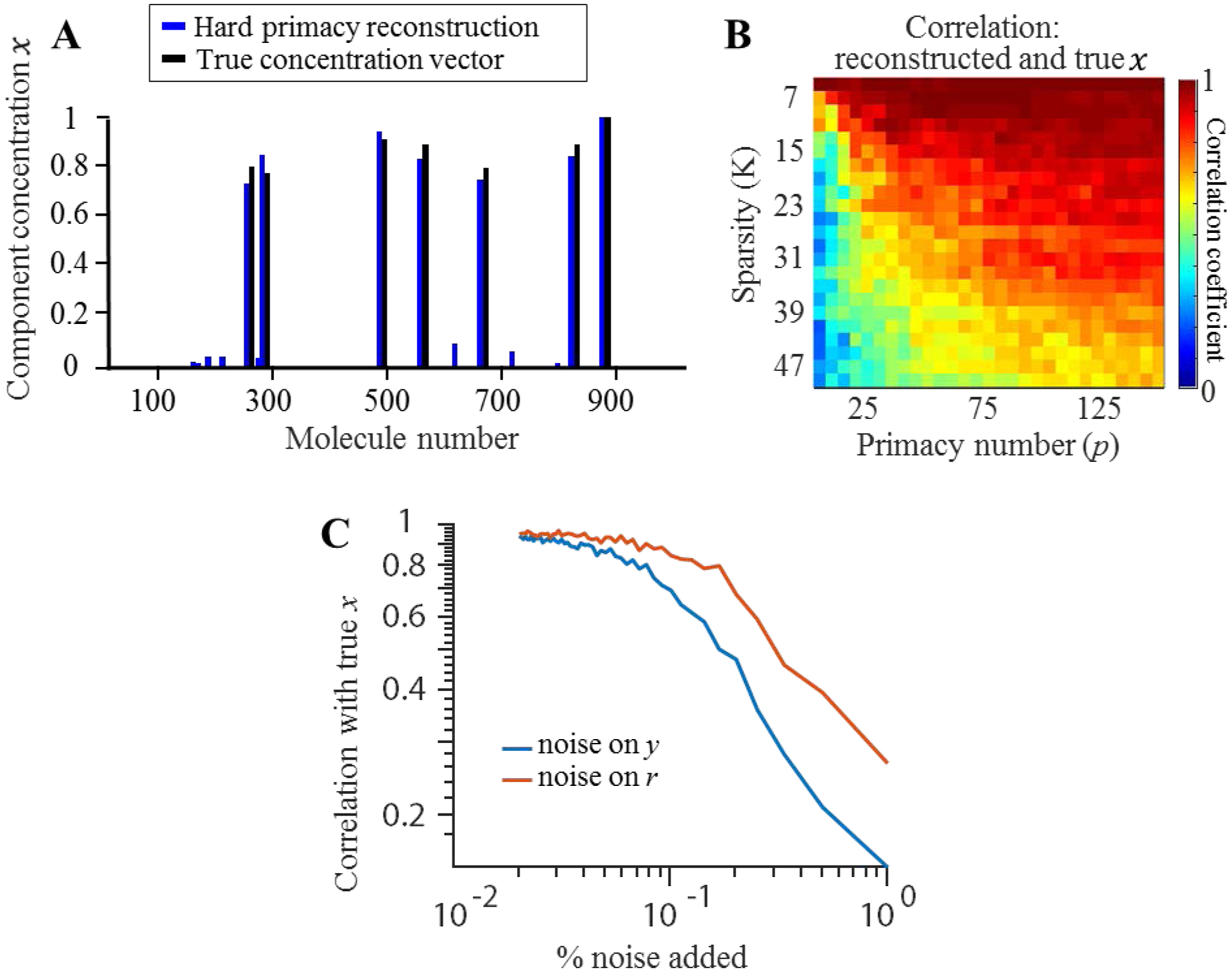
Using relative values of receptor responses can solve the problem of recovering sparse concentration vector $\overrightarrow{x}$. (A) An example concentration vector x alongside its reconstruction (blue) using only relative information that a group of receptors P respond more strongly than the rest. (B) Correlation between the reconstructed and true concentration vectors for different sparsity (K) values and number of primary receptors (p). (C) Correlation between reconstruction and stimulus with various levels of noise injected on input signal$\overrightarrow{y}$(blue) and input neuron response$\overrightarrow{r}$(red).

The nonlinearity on each receptor (2.1) is likely to be similar but not identical. The primacy model would not yield invariant odorant representations when nonlinearities are highly variant for each component of $\overrightarrow{y}$. In this case, large changes in concentration for certain odorants would illicit a different perception as sometimes seen in human perception (Arctander, 1969).

Overall, using the relative rather than the absolute values of sensor responses to recover odorant identity results in invariance with respect stimulus intensity. Using relative responses of sensors has a long history in neuroscience, and includes color constancy (Foster, 2011), responses of differentiating (ON/OFF-center) cells in retina, edge detection in the visual cortex (Rodieck, 1998), and relying on the relative responses of OSNs in the olfactory bulb implemented by normalization (Cleland et al., 2011; Cleland et al., 2007). Although we demonstrated this idea for the particular example of primacy coding, we propose that this neural relativity rule is used to produce perceptual invariance and invariant signal recovery with respect to other stimulus transformations.

In addition to invariance to changes in concentration and monotonic transformations of receptor signals, primacy codes are inherently robust to noise. Not only are the strongest responding receptors the most reliable, but many neighboring concentration vectors share the same primacy set. Furthermore, neighboring primacy sets can produce similar reconstructions. The result is a code unaltered by even high levels of noise, as shown in Figure 1.

Instead of minimizing the pure l₁ norm to find sparse solutions, one can minimize the elastic net functional:

$$\overrightarrow{x}=\underset{\begin{array}{l}{y}_P\ge y_{\overline{P}}\\ x_j\ge 0\end{array}}{\text{arg}\text{min}}\sum _j\left(x_j+\epsilon \frac{x_j^2}{2}\right)$$ (2.9)

The equation (2.9) is the same as the l₁ norm minimization (2.8) when the parameter ε → 0. For small parameter ε, equation (2.9) yields sparse solutions similar to equation (2.8). Problem (2.9), however allows for an easier dual space formulation. We will therefore use the elastic net minimization [equation (2.9)] to recover olfactory stimuli in the rest of the paper with a sufficiently small parameter ε such that the elastic net and l₁ solutions are close.

2.4. Number of receptors needed to implement primacy coding.

Since we are using relative response information to decode the sensory input, we have to amend our estimate (2.4) of the number of receptors necessary to fully recover a sparse stimulus. In the primacy model, the amount of information in $\overrightarrow{y}$ is reduced as we are only concerned with the p strongest responding receptors. Therefore, the number of combinations in $\overrightarrow{y}$ is given by the binomial coefficient ${\Gamma }_y~C_N^p~N^p$. By keeping the estimate for the number of combinations in $\overrightarrow{x}$ the same, i.e. Γ_x ~ M^K, and assuming that, for reconstructing $\overrightarrow{x}$, the number of combinations of $\overrightarrow{y}$ has to exceed the number of combinations in $\overrightarrow{x}$, we easily arrive at the following condition:

$$p>K\frac{\text{log}M}{\text{log}N}$$ (2.10)

For a typical mammal, such as mouse, in which the number of ORs is approximately N ≈ 1000, we obtain p > 2K. For humans, in which the number of functional ORs is N ≈ 350, the primacy number (the size of the primacy receptor set) required is somewhat higher, p > 2.4K. In both of these estimates we assumed that the number of molecule types available in the environment is close to M ~ 10⁶. If one assumes that the number of discernable molecular components in each mixture is K ~ 12, as follows from human psychophysics (Jinks and Laing, 1999), we obtain the primacy number p > 30 which is substantially less than the total number of receptors in humans N ≈ 350.

2.5. Hard primacy conditions.

Problem (2.9) includes various inequality constraints, including the primacy constraints (2.6) $y_P\ge y_{\overline{P}}$. These conditions can be reformulated in a more convenient form. Indeed, conditions (2.6) have no scale in them. Therefore, minimization of the l₁ norm or elastic net functional of $\overrightarrow{x}$ connected to $\overrightarrow{y}$ via a set of positive coefficients A ($\overrightarrow{y}=A\overrightarrow{x}$) results in the trivial solution $\overrightarrow{x}=0$. To obtain a non-zero solution, one has to introduce a finite scale into the conditions (2.6). A set of conditions with the constrained magnitude is

$$y_P\ge \gamma ,\gamma \ge y_{\overline{P}}$$ (2.11)

where γ ≥ 0 is the scale parameter. The value of this parameter is arbitrary and so we use γ = 1 in all simulations. In addition to providing a nonzero solution, introduction of a scale parameter also reduces the number of constraints in equation (2.6) from p(N − p) to N. By introducing a sign variable u_i = +1 for i ∈ P and u_i = −1 for $i\in \overline{P}$, equation (2.11) can be rewritten as a single set of conditions

$$u_i(y_i-\gamma )\ge 0$$ (2.12)

Here $y_i=\sum _j{A}_{ij}{x}_j$ where the affinity of receptor i to odorants j are given by a set of non-negative numbers A_ij. Problem (2.9) combined with constraints (2.12) represents our primal optimization problem. Constraints defined by equation (2.12) will be called the ‘hard primacy conditions’.

2.6. Soft primacy conditions.

As an alternative to (2.12), we propose a simpler set of conditions:

$$y_i-u_i\gamma \ge 0$$ (2.13)

These conditions operate differently for primary versus non-primary receptors. For the primary set, i ∈ P, they are equivalent to conditions (2.12), i.e. y_i ≥ γ. Therefore, these inequalities ensure that the responses of primary receptors are larger than parameter γ. For non-primary receptors, these inequalities become y_i ≥ −γ. Since $y_i=\sum _j{A}_{ij}{x}_j$, and both A and x are non-negative, this inequality is always satisfied. Therefore, conditions (2.13) define the lower limit for the primary set of receptors, but not for the non-primary receptors. We therefore call inequalities (2.13) the ‘soft primacy conditions’.

Interestingly, however, the soft primacy conditions implicitly constrain the non-primary receptors as well. Although conditions (2.13) for non-primary receptors become trivial, i.e. y_i ≥ −γ, minimization of vector $\overrightarrow{x}$ minimizes the unconstrained elements of vector $\overrightarrow{y}$, or non-primary elements. In practice, we find that, after minimizing the ${\mathcal{l}}_1$ norm of $\overrightarrow{x}$, non-primary receptors obey $y_{\overline{P}}<\gamma$, as required by the hard primacy conditions. Thus, for practical purposes, the soft primacy conditions are equivalent to the hard ones. As we showed before (Kepple, 2016), the hard primacy conditions result in dual networks with an interaction matrix dependent on odor stimuli, i.e. vector u_i, which is difficult to implement biologically. Below, we show that the soft primacy conditions can be implemented by a network with weights independent on the odorants presented. Thus, the network implementation based on the soft primacy conditions is more biologically plausible. We will therefore adopt the soft primacy conditions for the remainder of this paper. The approximate equivalence between soft and hard primacy conditions is illustrated in Figure 2. We therefore formulate the following primal problem that can potentially be solved by the olfactory system:

$$\overrightarrow{x}=\underset{\begin{array}{l}{y}_i-u_i\gamma \ge 0\\ x_j\ge 0\end{array}}{\text{arg}\text{min}}\sum _j\left(x_j+\epsilon \frac{x_j^2}{2}\right)$$ (2.14)

Figure 2.

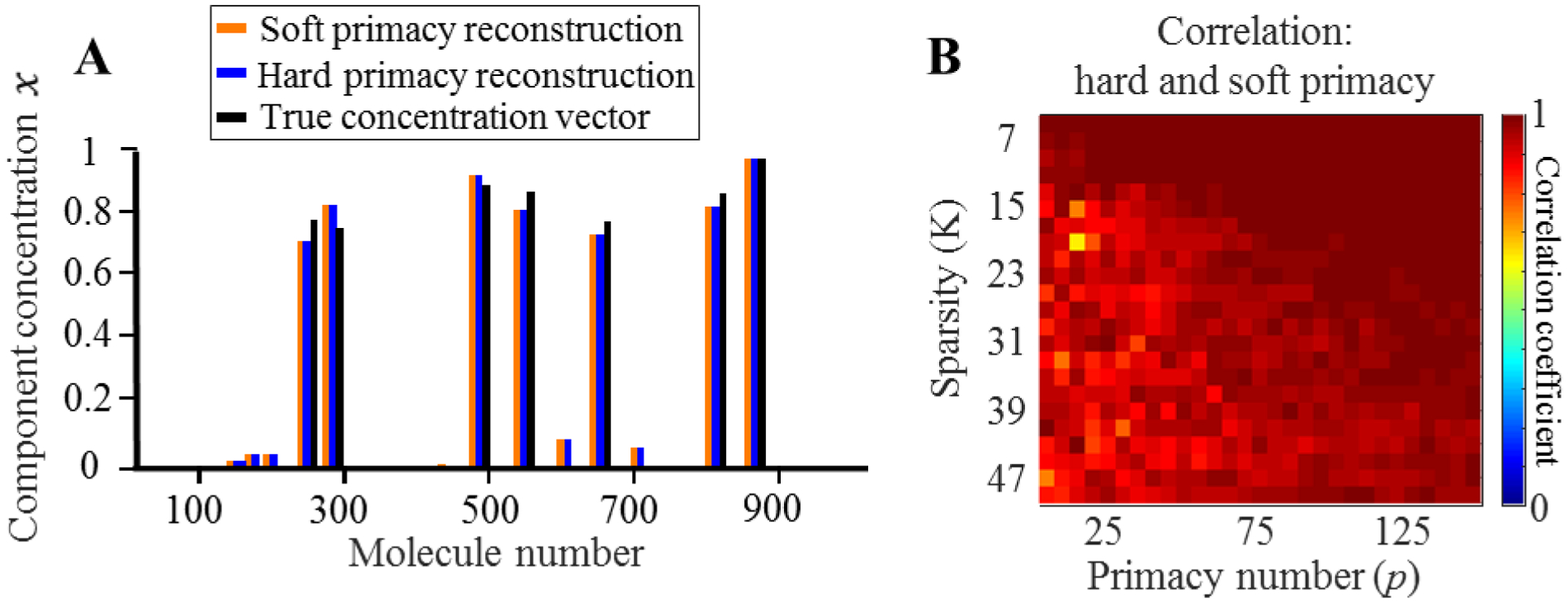
The solutions provided by soft and hard primacy conditions are similar. (A) An example concentration vector $\overrightarrow{x}$ alongside its hard primacy reconstruction (blue) and the soft primacy reconstruction (orange). (B) The correlation between the hard and soft primacy solutions for various sparsity K and primacy number p.

2.7. Formulation of the dual problem.

The primal problem (2.14) cannot be easily solved by a neural network. To implement a neural network solution, we use its dual formulation. To transform the primal minimization problem (2.14) into its dual problem, we introduce a cost function (Lagrangian) with two sets of Lagrange multipliers, α_i and β_j. Each multiplier α_i, with i = 1..N, enforces an individual soft primacy constraint (2.13), y_i − u_iγ ≥ 0. Each β_j enforces a constraint x_j ≥ 0 for j = 1..M. The full Lagrangian for the elastic net minimization problem (2.14) is as follows

$$L(\overrightarrow{x},\overrightarrow{\alpha },\overrightarrow{\beta })=\sum _j(x_j+\epsilon x_j^2/2)-\sum _i{\alpha }_i(\sum _j{A}_{ij}{x}_j-u_i\gamma )-\sum _j{\beta }_j{x}_j$$ (2.15)

In this equation, the Lagrange multipliers α_i and β_j represent the importance of different constraints. Because the cost function (2.15) will be minimized with respect to $\overrightarrow{x}$, Lagrange multipliers are constrained to have non-negative values, i.e. α_i,β_j ≥ 0 (Boyd and Vandenberghe, 2004). This ensures that at the minimum of the cost function, the target conditions, y_i − u_iγ ≥ 0 and x_j ≥ 0, are satisfied. If, for example, one of the coefficients β_j were negative in equation (2.15), decreasing the corresponding x_j below zero may be found to be advantageous from the point of view of minimizing the cost function.

To derive the dual formulation of the primal optimization problem (2.14), we minimize Lagrangian (2.15) with respect to $\overrightarrow{x}$ as if no constraints were present. We therefore find the optimal value of $\overrightarrow{x}$ denoted here as ${\overrightarrow{x}}^{*}$. We then rewrite the Lagrangian with this optimal value of $\overrightarrow{x}$ which depends only on $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$. The resulting function is called the dual Lagrangian $\theta (\overrightarrow{\alpha },\overrightarrow{\beta })$:

$$\frac{\partial L(\overrightarrow{x},\overrightarrow{\alpha },\overrightarrow{\beta })}{\partial \overrightarrow{x}}=0\to x_j^{*}=\frac{1}{\epsilon }\left(\sum _i{\alpha }_i{A}_{ij}+{\beta }_j-1\right)$$ (2.16)

$$\begin{gathered} \theta (\overrightarrow{\alpha },\overrightarrow{\beta })\equiv L({\overrightarrow{x}}^{*},\overrightarrow{\alpha },\overrightarrow{\beta })=-\frac{1}{2\epsilon }\sum _{ik}{\alpha }_i{G}_{ik}{\alpha }_k-\frac{1}{\epsilon }\sum _{ij}{\alpha }_i{A}_{ij}{\beta }_j- \\ -\frac{1}{2\epsilon }\sum _j({\beta }_j^2-2{\beta }_j)+\gamma \sum _i{\alpha }_i{u}_i+\frac{1}{\epsilon }\sum _i{\alpha }_i\sum _j{A}_{ij} \end{gathered}$$ (2.17)

Here $G_{ik}=\sum _j{A}_{ij}{A}_{kj}$ is the Gramm matrix (the matrix of pairwise scalar products) for rows of affinity matrix $\widehat{A}$.

According to optimization theory (Boyd and Vandenberghe, 2004; Dantzig, 1963) the dual Lagrangian $\theta (\overrightarrow{\alpha },\overrightarrow{\beta })$ is to be maximized to find the optimal values of $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$. These values can then be used to find the solution of the primal problem using equation (2.16). One can think of dual Lagrangian, a function of the constraint multipliers $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$, as a lower bound for the primal problem. Thus we maximize the dual Lagrangian because we want to find the greatest lower bound for our minimization problem. The dual problem can therefore be formulated as follows

$$({\overrightarrow{\alpha }}^{*},{\overrightarrow{\beta }}^{*})=\underset{\begin{array}{l}{\alpha }_i\ge 0\\ {\beta }_j\ge 0\end{array}}{\text{arg}\text{max}}\theta (\overrightarrow{\alpha },\overrightarrow{\beta })$$ (2.18)

The dual problem is formulated in terms of Lagrange multipliers $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$. This makes it different from the primal optimization problem (2.14), which is formulated in terms of $\overrightarrow{x}$. The solution to the dual problem, however, is also the solution to the primal problem, since they are connected via equation (2.16).

The reason why the dual problem (2.18) is sometimes preferred to the primal problem (2.14) is in the simplicity of its constraints. In many cases, the constraints α_i,β_j ≥ 0 are easier to implement than the primal problems inequalities. The important observation that we make here is that neural systems are well suited for implementing dual optimizations. For example, it is especially easy to impose non-negativity constraints, because neural responses are described by firing rates that cannot fall below zero. Motivated by this observation, we argue that the Lagrange multipliers $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$ could be represented by responses of different types of olfactory neurons that solve the dual rather than the primal representation problem.

Another motivation for linking neural activity with Lagrange multipliers can be derived from the Karush-Kuhn-Tucker theorem (KKTT) (Boyd and Vandenberghe, 2004; Kuhn and Tucker, 1951). According to KKTT, at the maximum of a dual Lagrangian, such as (2.17), the Lagrangian contributions in equation (2.15) vanish, i.e.

$${\alpha }_i(\sum _j{A}_{ij}{x}_j-u_i\gamma )=0$$ (2.19)

$${\beta }_j{x}_j=0$$ (2.20)

These equations are valid for all values of i and j. The former equation implies that either α_i = 0, in which case $\sum _j{A}_{ij}{x}_j-u_i\gamma$ can assume any non-negative value (inactive constraint), or $\sum _j{A}_{ij}{x}_j-u_i\gamma =0$, which allows α_i to be non-zero (active constraint). The Lagrange coefficients α_i = 0 describe constraints that have no impact on the solution of the optimization problem, explaining why they are called inactive. This observation implies that many α_i are expected to be zero, making the vector of responses $\overrightarrow{\alpha }$ sparse. This observation could provide rationale to the observed sparsity of neural activities in the olfactory system (Kay and Laurent, 1999; Koulakov and Rinberg, 2011; Rinberg et al., 2006; Stettler and Axel, 2009) and beyond (DeWeese and Zador, 2006; Hromadka et al., 2008; Lehky et al., 2005; Vinje and Gallant, 2000). A mapping between the dual problem and neural responses could thus explain sparsity of neural responses as a corollary of KKTT.

2.8. Dual networks.

We will now describe neural networks that can solve the dual problem (2.18). We associate vectors $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$ with the firing rates of two groups of neurons (cell types). The conditions α_i ≥ 0 and β_j ≥ 0 are then satisfied automatically as the firing rates of neurons cannot be negative. We assume that the neurons are connected into a network and the Lyapunov function of that network $H(\overrightarrow{\alpha },\overrightarrow{\beta })$ is proportional to the negative of the dual Lagrangian. We use the negative dual Lagrangian in order to follow the convention of constructing networks which minimize a Lyapunov function (whereas the dual Lagrangian is to be maximized). For simplicity, we will assume that the Lyapunov function of the network is $H(\overrightarrow{\alpha },\overrightarrow{\beta })=-\epsilon \theta (\overrightarrow{\alpha },\overrightarrow{\beta })$. For the Lyapunov function, from equation (2.17), we obtain

$$\begin{gathered} H(\overrightarrow{\alpha },\overrightarrow{\beta })=\frac{1}{2}\sum _{ik}{\alpha }_i{G}_{ik}{\alpha }_k+\sum _{ij}{\alpha }_i{A}_{ij}{\beta }_j+ \\ +\sum _j({\beta }_j^2/2-{\beta }_j)-\epsilon \gamma \sum _i{\alpha }_i{u}_i-\sum _i{\alpha }_i\sum _j{A}_{ij} \end{gathered}$$ (2.21)

To be able to interpret equation (2.21) as a Lyapunov function, we have to propose a network whose dynamics minimizes it. To generate network equations for each neuron in the network, we define internal variables that can be viewed as the total synaptic input current for each neuron. For α_i and β_j neurons, these currents will be denoted a_i and b_j respectively. Consider the following equations for a_i and b_j

$${\dot{a}}_i+a_i=-\sum _k{W}_{ik}{\alpha }_k-\sum _j{A}_{ij}{\beta }_j+\epsilon \gamma u_i+\sum _j{A}_{ij}$$ (2.22)

$${\dot{b}}_j+b_j=-\sum _i{\alpha }_i{A}_{ij}+1$$ (2.23)

$$W_{ik}=G_{ik}-{\delta }_{ik}$$ (2.24)

$${\alpha }_i={[a_i]}_{+},{\beta }_j={[b_j]}_{+}$$ (2.25)

Here and throughout this paper we use $\dot{x}\equiv dx/dt$. The first equation describes inputs into neurons with firing rates α_i connected to each other by weights −W_ik. Connectivity between α-neurons is symmetric. These cells are also connected to β_j neurons with synaptic weights −A_ij, i.e. the affinity matrix. α-neurons receive an external excitatory drive equal to $\epsilon \gamma u_i+\sum _j{A}_{ij}$. Equation (2.23) describes β_j neurons that are connected symmetrically to α-neurons. For both cell types, their firing rates (α_i and β_j) are related to their inputs (a_i and b_j) by rectifying threshold-linear relationships (ReLU) (2.25) ([x]₊ = x for x ≥ 0 and [x]₊ = 0 for x < 0). The circuit diagram for the network described here is presented in Figure 3.

Figure 3.

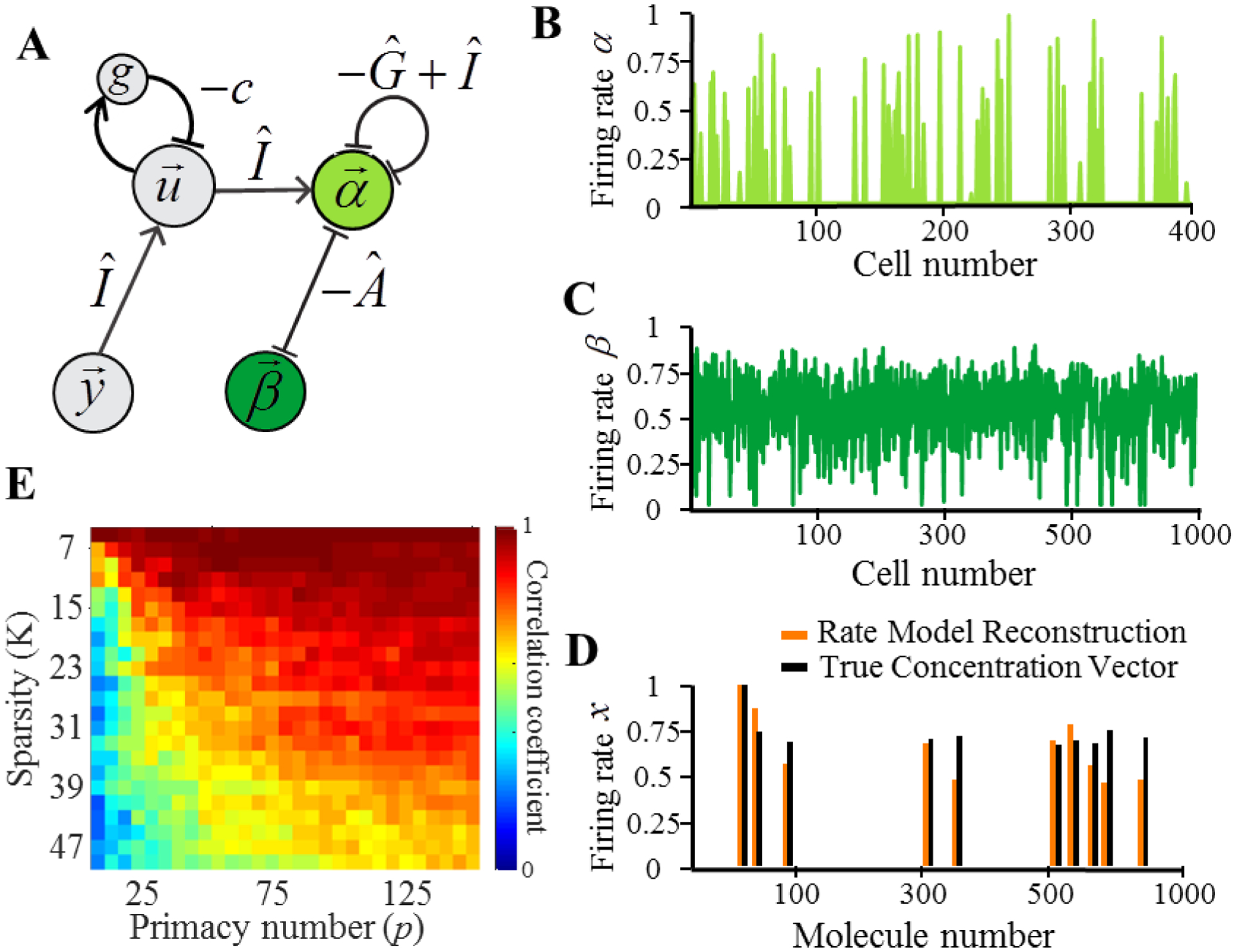
The dual network model described by equations (2.22) through (2.25). (A) The structure of the network. α cells (light green) implement the dual representation of the concentration vector. β cells (dark green) implement the non-negativity constraints on the concentration vector. (B) Example firing rates of alpha cells. (C) Example firing rates of beta cells. (D) Example of the firing rate model’s reconstruction (orange) of the concentration vector compared with the original concentration vector (black). (E) Correlation between the firing rate reconstruction of the concentration vector and the true concentration vector for a range of stimulus and network parameters, K and p.

It is straightforward to verify that these equations can be rewritten as a gradient descent.

$${\dot{a}}_i=-\frac{\partial H(\overrightarrow{\alpha },\overrightarrow{\beta })}{\partial {\alpha }_i}$$ (2.26)

$${\dot{b}}_j=-\frac{\partial H(\overrightarrow{\alpha },\overrightarrow{\beta })}{\partial {\beta }_j}$$ (2.27)

Here $H(\overrightarrow{\alpha },\overrightarrow{\beta })$ is the Lyapunov function given by equation (2.21). To show that $H(\overrightarrow{\alpha },\overrightarrow{\beta })$ is indeed a Lyapunov function, i.e. a function that is not increasing and bounded, we follow conventional methods. To prove monotonicity of time evolution, we observe that

$$\begin{gathered} \frac{dH(\overrightarrow{\alpha },\overrightarrow{\beta })}{dt}=\sum _i\frac{\partial H(\overrightarrow{\alpha },\overrightarrow{\beta })}{\partial {\alpha }_i}{\dot{\alpha }}_i+\sum _j\frac{\partial H(\overrightarrow{\alpha },\overrightarrow{\beta })}{\partial {\beta }_j}{\dot{\beta }}_j= \\ =-\sum _i{\dot{a}}_i{\dot{\alpha }}_i-\sum _j{\dot{b}}_j{\dot{\beta }}_j=-\sum _{i}f\text{'}(a_i){\dot{a}}_i^2-\sum _{j}f\text{'}(b_j){\dot{b}}_j^2\le 0 \end{gathered}$$ (2.28)

Here f(x) = [x]₊, f′(x) ≥ 0. Because, according to equation (2.28), $dH(\overrightarrow{\alpha },\overrightarrow{\beta })/dt\le 0$, and because equation (2.21) is bounded from below, our network will minimize the Lyapunov function (2.21). Due to the physically imposed non-negativity of firing rates, the variables in (2.25) will stay non-negative throughout course of this optimization-- automatically satisfying the inequalities needed to solve the dual problem. We conclude therefore that our two cell type network can solve the dual optimization problem (2.17) and thereby compute accurately molecular composition of a mixture in dual space.

2.9. Implementing the primacy variables u_i.

The purpose of the variables u_i is to identify the set of primary variables y_i, i.e. the set of p components of vector $\overrightarrow{y}$ that are larger than all others. For primary/non-primary y_i, variables u_i are expected to be equal to +1/−1 respectively. To compute these variables, we introduce a p-winners-take-it-all network that identifies p strongest inputs and suppresses the representations of the remainder of inputs. This network contains a population of inhibitory neurons, g, which are activated by the firing of p of the primacy neurons u. The equations specifying the dynamics of such a network are:

$$g=h\left(\sum _{k}h(u_k)-p\right)$$ (2.29)

$$u_i=s\left(r_i-T-cg\right).$$ (2.30)

Here h(x) is the Heaviside function, while s(x) is a hysteretic sign function. The latter function is activated (changes activity from −1 to +1) when x > 0 and is deactivated at very low levels of input. Other parameters include c, the strength of inhibition from neurons of type g, and T, a detection threshold of the u neurons. Odorants that do not activate receptors above T will not be perceived. Because the activities of each u_i is controlled by its input from receptor r_i, u- cells with the strongest inputs (primary) win over the cells with weaker inputs (non-primary). This dynamic will select a certain number of cells that have the strongest receptor input (Supplementary Figure 1).

We found that this network finds robust solutions if s(x) function, the activation function for the u- cells in equation (2.30), is hysteretic, similarly to previous studies (Sanders et al., 2013; Sanders et al., 2014; Wilson, 2017). This is because activities of receptors are often transient, and therefore the sustained activity of hysteretic neurons following an initial activation makes representations stable until the end of the sniff cycle. Such behavior ensures that primary cells identified early in a sniff cycle remain primary even though receptor responses undergo adaptation or are affected by other network dynamics. This behavior is consistent with presence of non-linear voltage-dependent synaptic currents in the piriform cortex (Poo and Isaacson, 2011).

2.10. Networks implementing primacy.

Figure 3 displays the network implementing the dual problem (2.17). It contains five cell types, each designated by a letter. Receptor neurons (y- cells) are connected to u- cells via feedforward excitatory connections. u- cells then connect to g cells and α neurons. g cells enforce the primacy conditions and α neurons compute the dual representations of the stimulus. α- neurons interact with each other by structured inhibitory connections as indicated. They also form inhibitory connections to β- neurons described by the affinity matrix $\widehat{A}$. In turn, β- neurons inhibit α- cells with the same strength. α- cells enforce the soft primacy constraints (2.13). β- cells represent Lagrange-KKT coefficients that enforce non-negativity of concentrations of individual monomolecular components of the stimulus vector $\overrightarrow{x}$.

Overall, we propose a network that can solve dual constrained optimization problems with time-dependent firing rates. These networks capitalize on the ease with which neural firing rates can implement the dual problem’s non-negativity conditions compared to much more complex conditions in the primal problem. We therefore call these circuits dual networks.

2.11. Simplicial dual networks.

In the previous network architecture (Figure 3), the dual variables u_i receive inputs from the receptor neurons y_i via an identity weight matrix. This implies that the number of dual variables u_i = ±1 is equal to the number of ORs. This assumption is not biologically justified and is unnecessary. Instead, we could amend our soft primacy conditions (2.13) to include weighted combinations of activities of ORs, i.e. $y_i\to \sum _j{S}_{ij}{y}_j$. In this case, the soft primacy conditions read:

$$\sum _j{S}_{ij}{y}_j-u_i\gamma \ge 0$$ (2.31)

The number of soft primacy conditions, indexed by i, is then arbitrary and is not limited by the number of receptors. Matrix S_ij determines the weights with which each receptor contributes to a given condition. For example, if $\widehat{S}=\widehat{I}$, the identity matrix, the previous primacy conditions (2.13) are recovered. If $\widehat{S}$ is a sparse matrix of zeros and ones, each primacy condition will constrain the sum of various receptor responses as opposed to individual receptor responses.

In the simplest case, each row of the matrix $\widehat{S}$ contains exactly s non-zero values that are all equal to one. Condition (2.31) then enforces, for each u_i = +1, that a sum of s receptor responses is larger than γ. Thus, matrix $\widehat{S}$ generalizes primacy from relating the responses of individual receptors to relating the responses of groups of receptors. We will now explore the consequences of such a generalization on the architecture of our dual network. Because the subsets of s receptors form simplexes in the $\overrightarrow{y}$ -space, we call this network simplicial.

Since we changed the structure of our soft primacy conditions (2.31), we must also update the information-theoretic argument for mixture recovery (2.10). Assume that matrix $\widehat{S}$ contains q rows, i.e. the total number of simplexes is q. In this case, the primacy conditions imply that p sums of receptor responses are larger than the q −p remaining sums. The number of distinct configurations of receptor activities can therefore be described by Γ_y ∝ q^p. Since Γ_x ∝ M^K, as before, we conclude that stimulus recovery in the simplicial model is possible if

$$p\ge K\frac{\text{log}M}{\text{log}q}$$ (2.32)

This condition is less restrictive than in the case of individual receptor-based primacy [equation (2.10)]. This is because the number of primacy conditions q can substantially exceed the number of receptors N.

Including the generalized soft primacy conditions (2.31) into our approach is straightforward. Before, $y_i=\sum _k{A}_{ik}{x}_k$ and equation (2.13) lead to $\sum _k{A}_{ik}{x}_k\ge \gamma u_i$. Equation (2.31) states instead that $\sum _{jk}{S}_{ij}{A}_{jk}{x}_k\ge \gamma u_i$. To include the generalized condition into our approach, one should replace the affinity matrix A_ik with the new matrix $V_{ik}\equiv \sum _j{S}_{ij}{A}_{jk}$ throughout. We thus obtain, instead of equation (2.21) the following equation for the dual Lyapunov function of the network:

$$\begin{gathered} H(\overrightarrow{\alpha },\overrightarrow{\beta })=\frac{1}{2}\sum _{ik}{\alpha }_i{\Gamma }_{ik}{\alpha }_k+\sum _{ij}{\alpha }_i{V}_{ij}{\beta }_j+ \\ +\sum _j({\beta }_j^2/2-{\beta }_j)-\epsilon \gamma \sum _i{\alpha }_i{u}_i-\sum _i{\alpha }_i\sum _j{V}_{ij} \end{gathered}$$ (2.33)

Here ${\Gamma }_{ik}=\sum _j{V}_{ij}{V}_{kj}$ is the interaction matrix between the coefficients α, which is also a Gramm matrix for the rows of matrix $\widehat{V}$. The network that minimizes function (2.33) can also be derived as before [equation (2.22)–(2.25)]. For completeness, we will list these equations here.

$${\dot{a}}_i+a_i=-\sum _k{W}_{ik}{\alpha }_k-\sum _j{V}_{ij}{\beta }_j+\epsilon \gamma u_i+\sum _j{V}_{ij}$$ (2.34)

$${\dot{b}}_j+b_j=-\sum _i{\alpha }_i{V}_{ij}+1$$ (2.35)

$$W_{ik}={\Gamma }_{ik}-{\delta }_{ik}$$ (2.36)

$${\alpha }_i={[a_i]}_{+},{\beta }_j={[b_j]}_{+}.$$ (2.37)

These equations can be obtained from equations (2.22)–(2.25) by replacing $\widehat{G}\to \widehat{\Gamma }$ and $\widehat{A}\to \widehat{V}$.

Equations for the primacy variables u_i can be obtained from equation (2.30) by replacing r_i with $\sum _i{S}_{ij}{r}_i$.

2.12. Sparse incomplete representations (SIR) in simplicial dual networks.

The Lyapunov function [equation (2.33)] is a relatively simple function on the activities of β -cells. This function could be explicitly optimized with respect to β cell activity, resulting in a substantial simplification of the network’s dynamics. Indeed, the optimal value of β_j in equation (2.33) is

$${\beta }_j^{*}={[1-\sum _i{\alpha }_i{V}_{ij}]}_{+}$$ (2.38)

Instead of integrating the time-dependent equations (2.35), we can evaluate the instantaneous optimal β-cell membrane voltage $b_j=1-\sum _i{\alpha }_i{V}_{ij}$ and equation (2.38) to obtain β-cell firing rates. Variables given by equation (2.38) are not sparse. Indeed, when the values of α-cell responses are small, i.e. during the early stages of network dynamics, β-cell firing rates would be close to 1. It would only be after some time that values of ${\beta }_j^{*}$ approach zero. The dense β-cell representation comes as a consequence of the KKT theorem. Because the concentration vector $\overrightarrow{x}$ is sparse, $\overrightarrow{\beta }$, which enforces non-negativity on the zero components of $\overrightarrow{x}$, is dense. To obtain a more biologically plausible network, we introduce a variable ${\overline{\beta }}_j\equiv {\beta }_j-1+\sum _i{\alpha }_i{V}_{ij}$ which provides a sparse representation of the non-negativity constraints. The optimal values of this variable are

$${\overline{\beta }}_j^{*}={\beta }_j^{*}-1+\sum _i{\alpha }_i{V}_{ij}={[\sum _i{\alpha }_i{V}_{ij}-1]}_{+}$$ (2.39)

By comparing this equation with equation (2.16), we observe that each ${\overline{\beta }}_j^{*}$ represents a component of the reconstructed concentration vector $\overrightarrow{x}$:

$${\overline{\beta }}_j^{*}=\epsilon x_j$$ (2.40)

As such, ${\overline{\beta }}_j^{*}$ are expected to inherit the sparsity of the concentration vector. In previous work, we suggested by independent logic that granule cells could function directly as the components of the concentration vector (Kepple et al., 2018; Koulakov and Rinberg, 2011). There, we proposed that granule cells in the olfactory bulb form a sparse representation of components in odor mixtures. In that work, we assumed that representations were either temporarily or spatially incomplete. Therefore, we called it the sparse incomplete representation (SIR) model. Here, we associate the variables ${\overline{\beta }}_j^{*}$ which represent the concentration vector $\overrightarrow{x}$ with responses of the olfactory bulb’s granule cells which are also found to be sparse (Cazakoff et al., 2014). The dual network relying on responses ${\overline{\beta }}_j^{*}$ can therefore implement the previously proposed SIR model (Kepple et al., 2018; Koulakov and Rinberg, 2011).

That ${\overline{\beta }}_j^{*}$ represent components of the reconstructed concentration vector also has implications for later olfactory processing. In particular, as seen in equations (2.39) and (2.40), the stimulus can be reconstructed by a relatively simple operation on α cells. That is, α cells alone form a full dual representation of the stimulus, no information about the responses of β cells is required. α cell representation contains a unique identifier for each odorant which is concentration invariant and can be used by other brain regions.

Network equations describing the dual SIR network are obtained by expressing the values of β_j from equation (2.39) and plugging these values in equations (2.34) through (2.37)

$${\dot{a}}_i+a_i=\epsilon \gamma u_i-\sum _j{V}_{ij}{\overline{\beta }}_j^{*}$$ (2.41)

$${\alpha }_i={[a_i]}_{+}$$ (2.42)

$${\overline{\beta }}_j^{*}={[\sum _i{\alpha }_i{V}_{ij}-1]}_{+}.$$ (2.43)

These equations describe a much simpler network than previously [(2.34)-(2.37)]. Indeed, as follows from equation (2.41), this new network lacks structured recurrent connectivity between α-cells (Figure 5). Interestingly, connectivity between α and ${\overline{\beta }}^{*}$-cells is antisymmetric: the connectivity is described by the same matrix $\widehat{V}=\widehat{S}\widehat{A}$ in both directions, but has an opposite sign.

Figure 5.

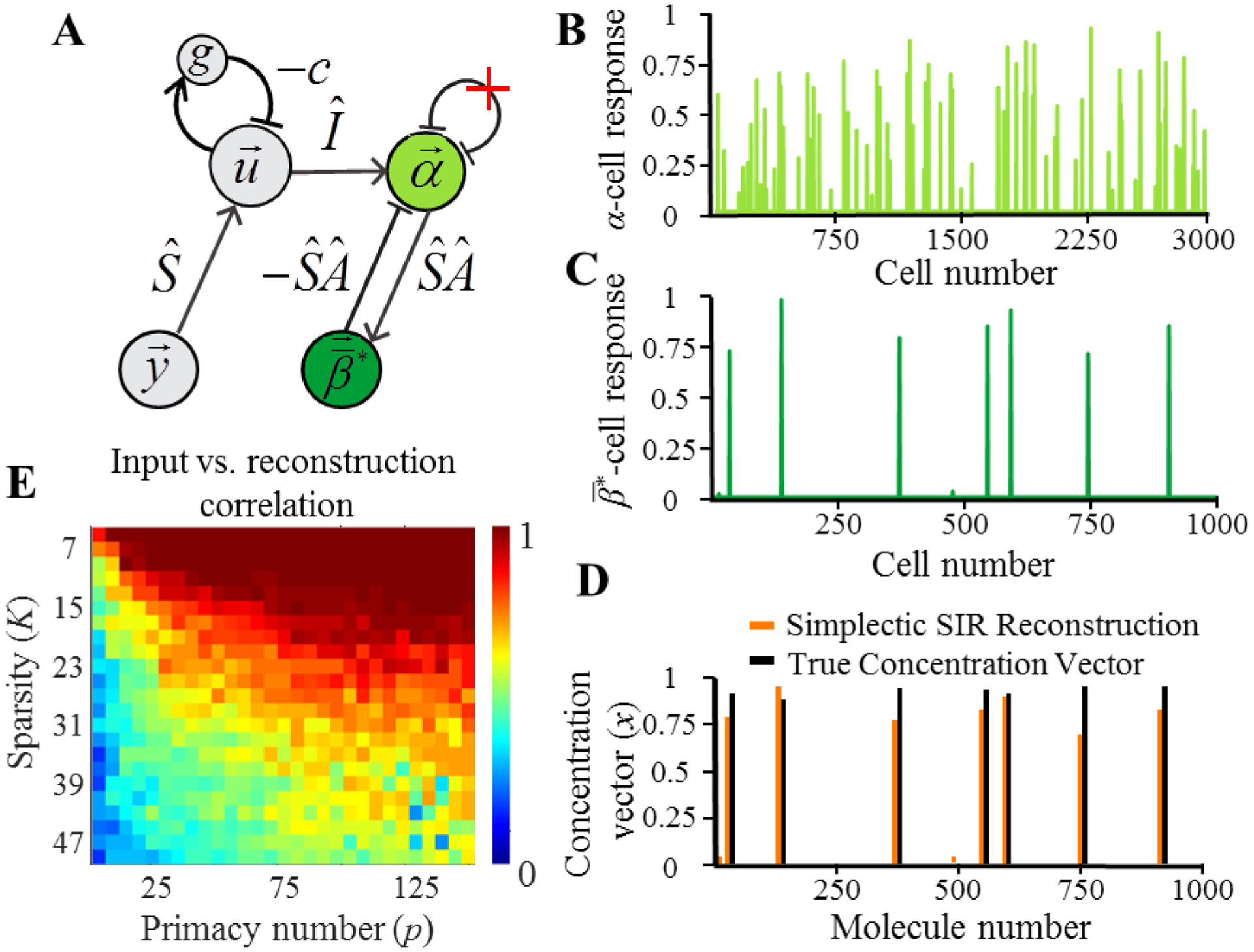
(A) The structure of the dual network implementing SIR model. α cells (light green) implement the dual representation of the concentration vector. ${\overline{\beta }}^{*}$ cells (dark green) represent the reconstruction of the concentration vector. (B) Example firing rates of α cells. (C) Example of the sparse firing rates of ${\overline{\beta }}^{*}$ cells. (D) Comparison of the simplicial SIR model’s reconstruction (orange) and the concentration vector. (E) Correlation between simplicial SIR model’s reconstruction of the concentration vector and the true concentration vector for a range of stimulus and network parameters, K and p.

Equation (2.40) suggests that ${\overline{\beta }}^{*}$-cells build representations of olfactory mixtures, with activities of individual neurons encoding the concentrations of individual mixture components. As we mentioned, a similar suggestion was made for the activities of granule cell neurons of the olfactory bulb, within the SIR model. We thus can identify ${\overline{\beta }}^{*}$-cells in our present model with granule cells of the olfactory bulb. In agreement with this suggestion, the number of granule cells (a few million) matches our estimate of the number of monomolecular chemical compounds.

3. DISCUSSION

Herein we propose a novel model for intensity-invariant encoding of olfactory stimuli. According to the primacy model, an odor can be identified from the identities of the p strongest responding ORs. Importantly, this does not mean that our model uses only p receptors to identify the stimulus. Instead, weakly responding receptors are still informative of which odors are not present. Because the primacy model relies only on the relative rather than absolute strengths of receptor responses, the recovered stimulus is independent of the absolute molecular concentrations of the stimulus. Although we demonstrated this idea for the particular example of primacy coding in olfaction, we suggest that this principle could be used to produce intensity invariant signal recovery for more complex conditions and in other modalities.

We formulated a solution of the olfactory decoding problem from first principles, using optimization theory with inspiration from compressed sensing. Since, within the primacy model, the constraints for inferring a stimulus use relative relationships between the responses of sensors (ORs), we attempted to formulate the problem using a Lagrangian approach to optimize under inequality constraints. Our solution thus involves minimizing a Lagrangian cost function containing two sets of Lagrange coefficients, $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$. Lagrange coefficients represent weights on different constraints in the optimization problem. They describe the importance of individual constraints, i.e. which constraints were actually used in a particular inference problem. The first set of Lagrange coefficients, $\overrightarrow{\alpha }$, described the importance of individual primacy conditions, while the second set, $\overrightarrow{\beta }$, described non-negativity constraints imposed on individual molecular concentrations. Solving the sparse optimization problem under inequality constraints is often performed in the dual representation, via optimizing the dual Lagrangian. Dual optimization is performed in the dual space, i.e. using only the Lagrange coefficients and not the primal variables, i.e. values of molecular concentrations.

The driving observation that we make in this study is that neural systems are well suited for implementing dual optimizations. The nonnegativity of Lagrange coefficients is especially easy to enforce in neural responses described by firing rates that cannot physically fall below zero. Furthermore, a well-known theorem in optimization theory states that the Lagrange coefficient acting on an unused constraints is zero. For a dual neural network, we showed that this can result in sparse neural activity. These observations led us to propose the dual brain theory – that firing rates of individual neurons represent the Lagrange coefficients for a set of conditions of varying complexity.

It has been known for a while that recurrent neural nets can minimize cost functions of firing rates, known as Lyapunov functions (Hertz et al., 1991). Mapping a dual Lagrangian onto a Lyapunov function of a recurrent neural network shows that this network solves the dual problem. Using this approach, we found the structure of the neural network whose Lyapunov function matches the dual Lagrangian for the problem of olfactory stimulus recovery.

Although we presented a conceptual model in which our initial approach was to implement a mathematical concept rather than to describe the biology of the olfactory system, we found that some features of our network bear resemblance to the real olfactory networks. In the dual network, the sets of Lagrange multipliers $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$ are represented by the firing rates of two cell types, α and β cells. The firing rates of β cells represent individual molecular components of the olfactory stimulus mixture. In our previous work, we proposed that granule cells form a representation of odorant components (Kepple et al., 2018; Koulakov and Rinberg, 2011). Since, in our present study, β cells perform a similar function, we argued that the β cells of our network [more precisely, ${\overline{\beta }}^{*}$ neurons, equation (2.39)] are analogous to the granule cells in the real olfactory bulb. The number of β cells in our network is equal to the number of potential molecular components in the environment. Encouragingly, the number of granule cells (several million) (Shepherd, 1972) is also similar to the number of potential volatile monomolecular compounds present in PubChem (Kim et al., 2016).

Because of the downstream position of α neurons from receptor input $\overrightarrow{y}$ and their excitatory effect on putative granule cells β, we suggest that α cells could reside in the piriform cortex which is known to feedback to the olfactory bulb. The inhibition from putative granule cells β to putative cortical cells α is then possible through an indirect pathway, via inhibition of mitral cells projecting to the piriform cortex. For this reason, we suggest that receptor input instead travels through the distinct tufted cell channel. As a result, we place u cells in the anterior olfactory nucleus (AON) which receives most projections from tufted cells (Haberly and Price, 1977). Due to the ab initio nature of our approach, the mapping of our dual network onto the real biological network needs further refinement. Overall, we suggest that, within the dual network approach, each neuronal cell type can be associated with a set of Lagrange coefficients implementing individual constraints.

In our study, we presented networks that are capable of inferring concentration-invariant odorant representations by performing a sparse norm minimization (l₁ norm or elastic net). We proposed therefore that ORs implement compression of the odorant concentration vector and relied on elements of compressed sensing in olfactory decoding. Several recent studies have argued that decoding algorithm in the olfactory system may use compressed sensing (Grabska-Barwinska et al., 2017; Krishnamurthy et al., 2017; Tootoonian and Lengyel, 2014; Zhang and Sharpee, 2016). These studies usually assume a linear encoding scheme similar to equation (2.2) and a decoding mechanism based on a sparse norm minimization. Some of these studies place the representation of individual component concentrations into the piriform cortex or, equivalently, insect mushroom body (Tootoonian and Lengyel, 2014; Zhang and Sharpee, 2016). Similarly, a study of (Grabska-Barwinska et al., 2017) suggests a Bayesian inference-based approach that relies on representing odors in the activity of cortical cells.

A significant distinction of our study from the previous approaches is that we assume that the activity of cortical neurons (α cells) is representative of, but distinct from, the vector of molecular concentrations. Thus, the vector of molecular concentrations can be decoded uniquely from the activities of α cells but activities of individual neurons cannot be interpreted as molecular concentrations. In this regard our model is similar to the recent study by (Krishnamurthy et al., 2017). We place the vector of molecular concentrations into the olfactory bulb (β cells, Figure 6). In doing so, we propose that the information of molecular composition of the odorant mixture is retained within olfactory bulb, while cortical neurons contain a dual representation of the mixture that is synthetic, i.e. constructed rather than reconstructed. Thus, in our model, the activity of cortical cells displays similar statistics in case of both mixtures and monomolecular stimuli. The reconstruction of the stimulus into monomolecular components performed by the granule cells in the olfactory bulb (β cells) that receive inputs from the cortex (α cells, Figure 6). The purpose of this reconstruction is to check whether the synthetic cortical representation is consistent with any possible mixture of monomolecular compounds. In a separate work, we suggest that this reconstruction could be useful during olfactory learning (Kepple et al., 2018).

Figure 6.

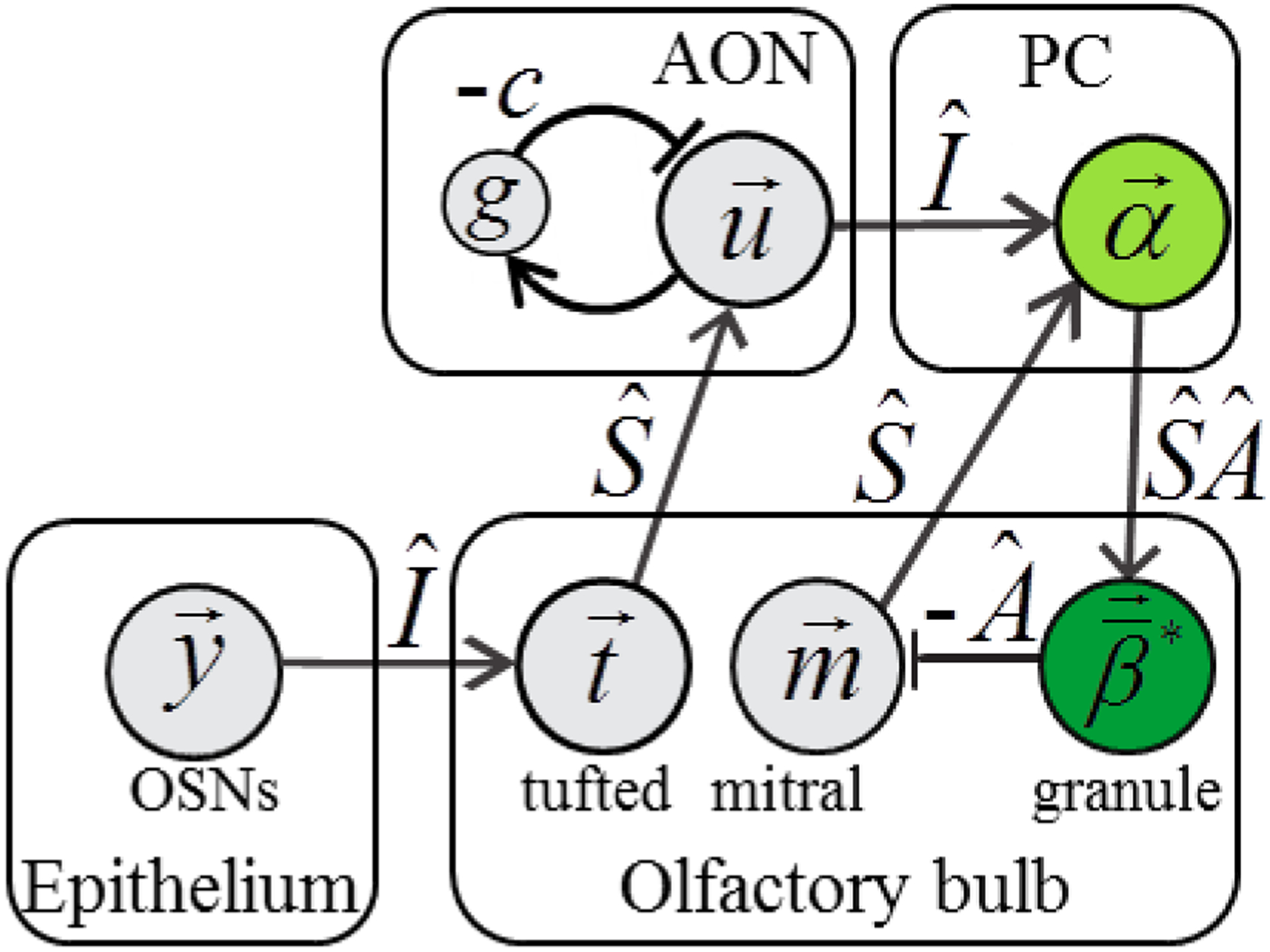
Possible mapping of our simplicial dual network implementing the primacy model to the known olfactory circuitry. The neurons of our network are depicted with circles and the corresponding brain region we suggest for those neurons are shown in the surrounding box. The suggested analogy with specific cell types are given outside each circle. AON, PC, and OSNs stand for anterior olfactory nucleus, piriform cortex, and olfactory sensory neurons respectively.

In formally linking the neurons of our dual network to biological neuronal cell types, we are able to make specific predictions about connectivity in the olfactory system. In particular, our theory suggests that feedback and feedforward connections between the bulb and cortex are dependent. Thus, the feedback connection matrix from cortex ($\widehat{S}\widehat{A}$, Figure 6) is a product of feedforward connectivity ($\widehat{S}$) and granule-to-mitral cell connectivity ($\widehat{A}$). We also suggest that granule cells represent the olfactory system’s reconstruction of the stimulus, consequently predicting that more complex stimuli (mixtures) should evoke more complex activity in granule cells than monomolecular odorants. More generally, using our dual brain theory to connect the activity of a specific cell types to a class of Lagrange coefficients enables one to determine connectivity on both mesoscopic and single-neuron scales.

Biologically it is known that OSN responses to an odor are roughly exponential distributed. This fact has been used to motivate maximum entropy models of olfactory coding (Stevens, 2016). For these models, the exponential distribution of OSN firing rates is important as it provides a maximal entropy code under certain assumptions. For our primacy-based model, however, there is very little constraint on the distribution of firing rates. Indeed, we show that we can construct the affinity matrix A with elements that have Gaussian, lognormal, or even uniform distributions [Supplementary Figure 2]. This finding results from the primacy model’s invariance to any uniform, monotonic nonlinearity relating r to y.

Our model uses relative rather than absolute responses of ORs to solve the decoding problem. This allowed us to encode the stimulus in a concertation invariant manner, even if the responses of receptors are non-linear. One mechanism for concentration invariance that has been proposed previously is based on normalization of bulbar output (Banerjee et al., 2015; Cleland et al., 2011; Cleland et al., 2007; Kato et al., 2013; Miyamichi et al., 2013; Olsen et al., 2010). This mechanism uses global inhibition to change the gain of receptor responses. The primacy model proposed here is distinct from the normalization model, although they share similar circuit features, such as broadly projecting inhibitory elements. Although we also implement inhibition to achieve concentration invariance, we place the inhibitory circuits in cortex with the goal of identifying the strongest responding receptors. Our mechanism may therefore account for fast odor guided decisions that are dependent on receptors with high-affinity to odorants. We thus propose that normalization and primacy models may operate in series on different levels of olfactory processing.

Tootoonian and Lengyel (Tootoonian and Lengyel, 2014) have proposed that the maximum a posteriori (MAP) solution to the inference problem of recovering a sparse N-dimensional odor vector $\overrightarrow{x}$ can be achieved in a low-dimensional measurement space, reflecting the known biology of olfactory processing (Tootoonian and Lengyel, 2014). In their study, the compressed sensing problem was formulated as an l₁ norm minimization of the odor concentration vector $\overrightarrow{x}$ subject to the linear equality encoding constraint $\overrightarrow{y}=\widehat{A}\overrightarrow{x}$ and solved by considering the problem in dual space. The resulting generalized energy function for their network reflects the equality constraints and, as such, their proposed network implementation differs significantly from our solution. Our networks rely on Karush-Kuhn-Tucker-type inequality conditions that implement primacy. Our formulation of the decoding problem is therefore distinct from the work of Tootoonian et al. In particular, our formulation allows to decode an odorant composition even if the encoding problem is non-linear [equation (2.6) and the following discussion]. In addition, due to our inclusion of inequality constraints and the Karush-Kuhn-Tucker theorem, the responses of neurons in our dual network are expected to be sparse.

Two features of dual networks are worth mentioning. First, according to the Karush-Kuhn-Tucker theorem (KKTT), dual Lagrangians are optimized under the constraint of the non-negativity of Lagrange coefficients. Neuronal responses can naturally enforce these constraints, because they are described by firing rates that cannot fall below zero. Thus, dual neural networks could be viewed as analog computers that convert complex conditions, such as those imposed by primacy theory, into non-negativity constraints. The latter constraints can be relatively easily implemented by neuronal firing rates. Second, due to KKTT (Boyd and Vandenberghe, 2004), a large number of the Lagrange coefficients are likely to be zero. This observation is consistent with the observed sparsity of neuronal responses, both in olfaction (Kay and Laurent, 1999; Koulakov and Rinberg, 2011; Rinberg et al., 2006; Stettler and Axel, 2009) and beyond (DeWeese and Zador, 2006; Hromadka et al., 2008; Lehky et al., 2005; Vinje and Gallant, 2000), further strengthening the possible association between neuronal responses and Lagrange coefficients. We therefore propose that neural networks may implement optimization of dual Lagrangians with the responses of individual neurons representing Lagrange multipliers corresponding to a set of individual constraints.

Figure 4.

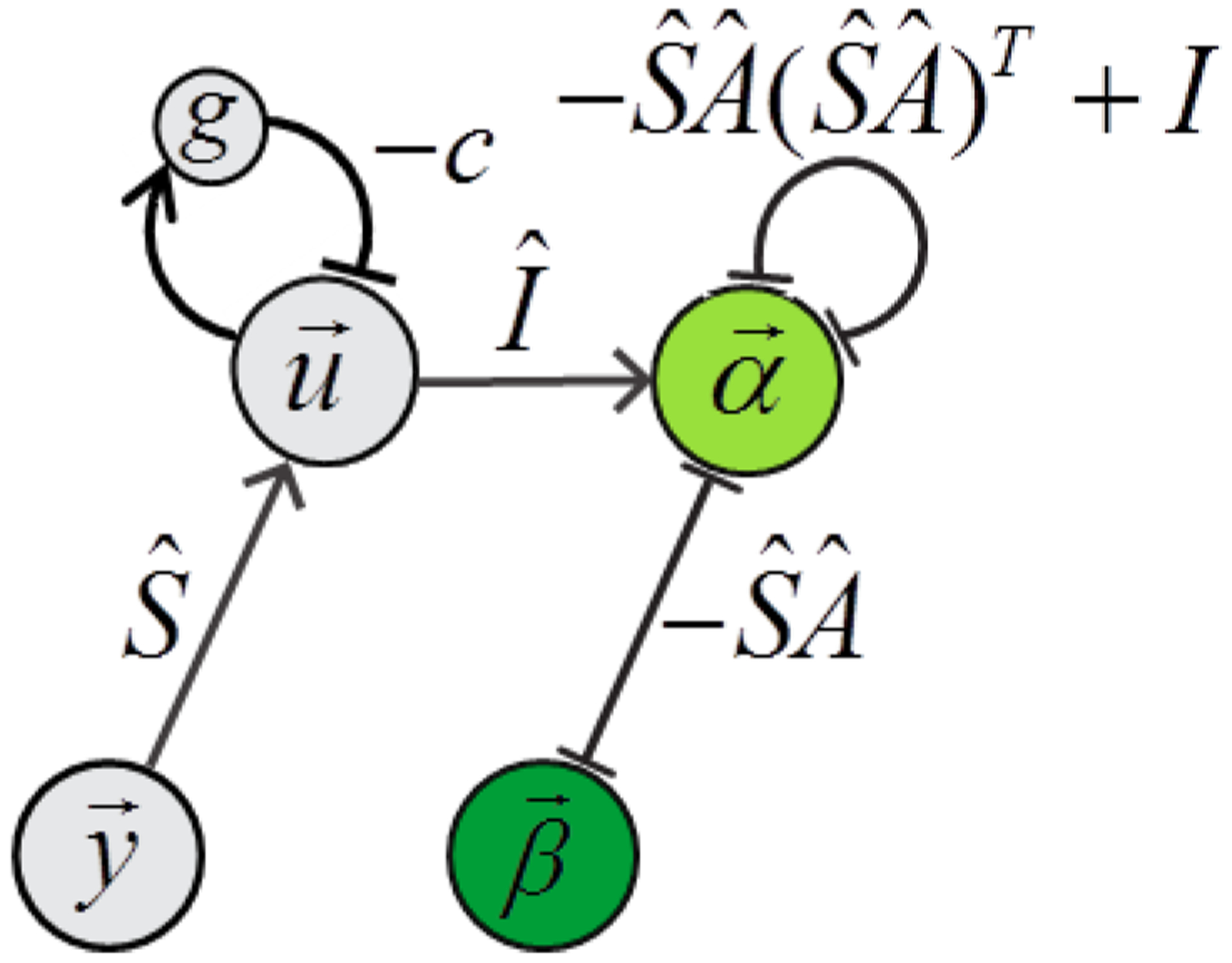
Network diagram of the simplicial dual network.

APPENDIX A

Derivation of equation (2.1) and (2.2):

Consider the mass-action law for an OR number i binding odorant number j. For the number of receptor molecules bound by the odorant, R_ij, we have

$$d{R}_{ij}/dt=-{\gamma }_{ij}{R}_{ij}+{\alpha }_{ij}{x}_j{R}_i^{*}$$ (A.1)

Here α_ij and γ_ij are binding and unbinding rates, and the number of available (unbound) available receptors, $R_i^{*}$, is given by

$$R_i^{*}=R_{i0}-\sum _j{R}_{ij}$$ (A.2)

Here R_i0 is the total number of OR molecules of type i exposed to odorant binding. Because in the equilibrium dR_ij/dt = 0 and $R_{ij}={\alpha }_{ij}{x}_j{R}_i^{*}/{\gamma }_{ij}\equiv A_{ij}{x}_j{R}_i^{*}$, the total number of unbound receptors can be found from equation

$$R_i^{*}=R_{i0}-R_i^{*}\sum _j{A}_{ij}{x}_j$$

We thus obtain $R_i^{*}=R_{i0}/(1+\sum _j{A}_{ij}{x}_j)$ and the number of active receptors

$$R_i=\sum _j{R}_{ij}=R_{i0}\sum _j{A}_{ij}{x}_j/(1+\sum _j{A}_{ij}{x}_j)$$

Assuming that activity of the cell reflects its relative OR activation we obtain

$$r_i\equiv R_i/R_{i0}=y_i/(1+y_i)$$ (A.3)

With $y_i=\sum _j{A}_{ij}{x}_j$.