Identifying policy challenges of COVID-19 in hardly reliable data and judging the success of lockdown measures

Abstract

Identifying structural breaks in the dynamics of COVID-19 contagion is crucial to promptly assess policies and evaluate the effectiveness of lockdown measures. However, official data record infections after a critical and unpredictable delay. Moreover, people react to the health risks of the virus and also anticipate lockdowns. All of this makes it complex to quickly and accurately detect changing patterns in the virus’s infection dynamic. We propose a machine learning procedure to identify structural breaks in the time series of COVID-19 cases. We consider the case of Italy, an early-affected country that was unprepared for the situation, and detect the dates of structural breaks induced by three national lockdowns so as to evaluate their effects and identify some related policy issues. The strong but significantly delayed effect of the first lockdown suggests a relevant announcement effect. In contrast, the last lockdown had significantly less impact. The proposed methodology is robust as a real-time procedure for early detection of the structural breaks: the impact of the first two lockdowns could have been correctly identified just the day after they actually occurred.

To know is to know that you know nothing.

Socrates

Introduction

The fight against the novel coronavirus outbreak requires a mix of different social distancing measures. Decisions on implementing, stopping, or renewing restrictive measures require quick and reliable information about infection trends and the impact of already implemented measures. At the same time, however, time is needed before the effects of particular measures can be observed, and there is a delay from contagion until the moment when it appears as a confirmed case in official statistics, i.e., the detection delay. In addition, people may react to the virus and anticipate social distance restrictions (using, e.g., media reports, the internet, and their own observations). All of these factors complicate the accurate identification of changes in the pattern of contagion.

We propose a machine learning procedure to identify structural breaks in pandemic dynamics induced by lockdowns using regional data. With an iterative procedure based on the Akaike information criterion (AIC), we select the best model that gives us the relative impact of each lockdown measure and the date when the corresponding structural breaks are recorded in the data.

We move in the same direction as Casella (2020) and Dehning et al. (2020), who calibrate a detection delay in epidemic models. Our model is not epidemic but involves a theoretical, data-driven approach that allows avoiding any prior assumptions about the number and time distribution of the structural breaks. Thus, we neither assume, ex ante, that all lockdowns are effective nor do we exclude further structural breaks. The lack of restrictions also allows coping with possible announcement effects that may reduce the final detection delay1. Moreover, we do not need to assume that each measure has the same delay. This is important since, as shown in our analysis, delays vary consistently from one lockdown to another.

We consider the case of Italy, the first non-Asian country where COVID-19 resulted in a large number of deaths. Three national lockdowns were implemented: the closure of schools (including universities), the main lockdown, and the shutdown of non-essential economic activities. According to our results, the first lockdown started to effectively slow the daily growth of COVID-19 cases 17 days after its introduction, and the detection delay in the structural break determined by the second lockdown was even larger (19 days). In addition, we highlight that the school closure had a greater impact despite the relatively weaker prescriptions. This may confirm that, in particular in the case of an unprepared country, this first measure also has an announcement effect, making people adopt less risky behaviors beyond the official prescriptions. In contrast, the last lockdown was hardly effective.

After discussing these results, we use the interaction terms analysis to inspect some side effects of the specific lockdowns across the Italian territory. Finally, we show that the proposed machine learning procedure can also be used in a real-time methodology to promptly detect any changes in the outbreak pattern. In this case, the structural breaks predicted with shorter series are the same, and they can be correctly identified from the first day after they occurred, with the exception of the third and least effective lockdown. This evidence reveals that important policy implications can emerge from procedures like the one we developed, since the first lockdown’s effects on the spread of COVID-19 could have been detected at the beginning of the political debate on the possible implementation of the business lockdown.

The structure of the paper is as follows. Section 2 contains a review of the recent literature related to our analysis, while Section 3 briefly describes the Italian case (features and timing of the lockdowns) and provides some descriptive evidence. Section 4 presents the econometric strategy. The following four sections present the results. Section 5 shows the results of the machine learning procedure that allows determining the detection delays. Section 6 analyzes the coefficients of the best model selected, while in Section 7 we include some interactions with space-variant variables in the structural break model to assess for lockdown-specific features. Section 8 provides an ex post validation of model sensitivity. The last section offers some concluding remarks. Robustness checks are reported in the Appendix together with a description of the data.

Related literature

The academic effort of analyzing and forecasting the pandemic dynamics of COVID-19 is huge. However, the quality of many studies does not always correspond to a comparable quality of the available data. The time series of confirmed cases are the most relevant example. This is not only because of the dependency of the data on the number of swabs and thus on the different testing policies and capacities. A further problem comes from the delay between contagion and its recording in official statistics.

Different delays combine to determine the overall one. The first and more commonly assessed delay is the incubation time, which ends when the first symptoms emerge, a timespan that the literature suggests is about 5.2 days and may last up to 14 days, as reported by Backer et al. (2020), WHO (2020), and Lauer et al. (2020), among others,2 and that may be related to the features of the infected individual. In the analyses of spatial data, this might involve a bias related to the corresponding features of the population in different territorial units. In addition, unless a person is tested for other reasons, once symptoms appear, a medical consultation may occur only after some days, with individuals waiting for some time in the hope of seeing an improvement in their condition, and in particular when the population has little knowledge and is not accustomed to the virus. Time may also be necessary for individuals to be allowed to take the test, in particular when extensive testing policies are not set up and swabs are limited to cases with severe symptoms. Furthermore, available technologies and health system quality also impact the time needed to analyze the swabs. A final delay occurs for the confirmed case to be included in official “daily” statistics. All of these delays can be very different both in space and time.

The literature usually determines the overall delay by considering only the average incubation time. The extent of this delay varies from 10 days, as in Pedersen and Meneghini (2020), to 2 weeks, as in Qiu et al. (2020). Some others consider a higher, though exogenously fixed, delay to take into account the other components of the detection delay. For instance, Fanelli and Piazza (2020) consider 20 days, while Remuzzi and Remuzzi (2020) use 15–20 days.

The only exceptions are Casella (2020) and Dehning et al. (2020). The first calibrates the additional components of the detection delay by using data from China and Italy’s Lazio region to argue against the option of this data to assess feedback control strategies. The second, focusing on Germany, considers lockdown delays on restricted and early ranges. Indeed, more than a methodological challenge, this is a relevant issue for the assessment of proper policies since many countries are going to relax social distancing measures using daily data as signals of inherently exponential growth paths restarting. Furthermore, in the same countries such delays might vary in time because of changing test policies and swab analysis capacities. This might be particularly relevant outside East Asia, for countries having found themselves not prepared to manage the virus in its early stages and having learned how to cope with it through the mistakes made over time. Variation in this delay may also be related to the level of contagion, in the case of saturated health facilities and testing infrastructure. Moreover, testing technology has been changing throughout the pandemic, reducing the time required to perform the test and analyze the swabs (Sheridan 2020; Edwards 2020). Finally, lockdown measures may change the various delays both directly by changing the features of the infected population and indirectly through the different channels mentioned above.

Although the research aims differ from ours, another study analyzing the COVID-19 outbreak is worthy of mentioning as it also adopts a machine learning methodology. Liu et al. (2020) indeed combine disease estimates from an agent-based mechanistic model and Internet searches on Baidu, via cluster-level machine learning procedures, to forecast COVID-19 contagion in Chinese provinces in real time. Their methodology allows for the production of stable and accurate forecasts 2 days ahead of current time in most of Chinese provinces.

The case of Italy

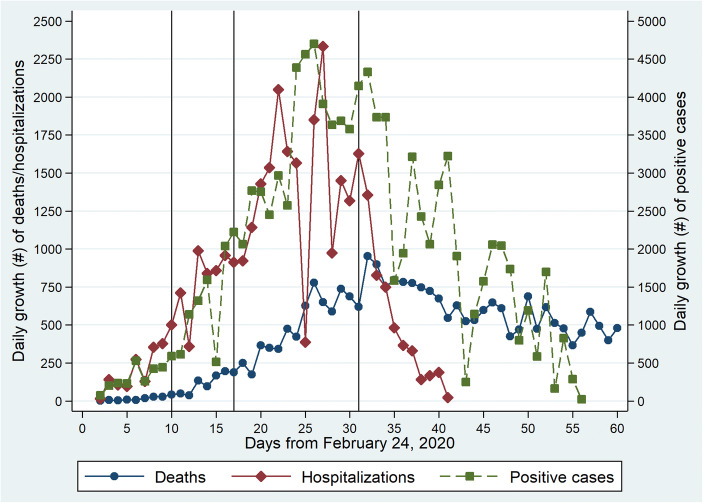
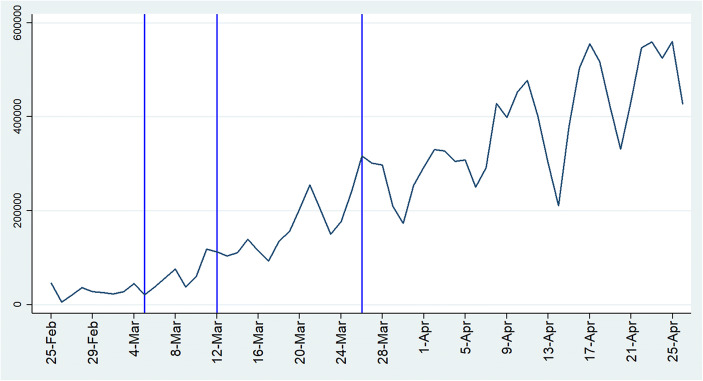
Italy was the first non-Asian country to experience the rapid and extensive spread of COVID-19. Based on data provided by the Italian Civil Protection Department (2020),3 Fig. 1 shows the dynamics of positive cases, hospitalizations, and deaths from the 24th of February onwards.

Fig. 1.

Daily growth of COVID-19 deaths, hospitalizations, and positive cases at the national. Source: Civil Protection Department (2020). “Positive cases” refers to the overall number of COVID-19 cases, excluding those who died or recovered. The three vertical lines represent the days on which the school lockdown, main lockdown, and business lockdown were introduced, respectively

The dynamics of positive cases and hospitalized people became significant by the end of February, with an exponential trend reaching a peak in the second half of March; afterwards, the respective variations took a declining path. Deaths followed a similar path, with approximately a 10-day delay, although levels were still significant at the end of April.

A first measure taken by the national government to prevent the outbreak was implemented on the 30th of January, before the virus was officially detected in the country. This involved blocking all flights to and from China and declaring a state of emergency, thus allowing for higher discretional policies. On the 21st of February, when a cluster of cases was detected in the Lombardy region, the government decided to declare “red areas” and tried to isolate some small municipalities. Nevertheless, the virus spread throughout the northeast of the country, and on the 23rd of February, Italy became the European country with the highest number of infected people recorded.

From the beginning of March, the Italian government reacted to the emergency through a series of increasingly stringent rules for social distancing. Italy has been the first European country to implement significant restrictions to citizens’ mobility and personal freedom. The first measure at the national level was announced and signed by the Prime Minister, Giuseppe Conte, on March 4 and became effective the day after. The main restriction concerned the suspension of school activities for all grades.4

On March 8, the Italian government signed another extraordinary restriction act for Lombardy and another 14 northern provinces (i.e., Modena, Parma, Piacenza, Reggio Emilia, Rimini, Pesaro–Urbino, Alessandria, Asti, Novara, Verbano–Cusio–Ossola, Vercelli, Padova, Treviso, and Venezia). This measure became effective the day after, although the national press spread the news the day before the act was signed. On March 12, the day after the World Health Organization declared a “pandemic” and with the virus already spreading to other regions and provinces, the Italian government extended the same measures to the whole country.5 The measures involved the shutdown of all commercial and retail business activities, except for those considered basic necessities. Even food services such as bars and restaurants were closed, with the exception of take-away services. Furthermore, mobility was restricted to going to work, shopping for food, and emergencies.

The vertical lines in Fig. 1 correspond to the starting dates of the national lockdown measures. The third vertical line on the graph, on March 26,6 corresponds to the last containment measure adopted: the closure of all “non-essential” economic activities. The enforcement of this lockdown had a fuzzy evolution: a first version of the decree was announced on March 21, published on March 22, and then modified after a meeting with workers’ unions and entrepreneur representatives.7 After this measure, only 53% of firms were allowed to remain open (Centra et al. 2020).

Many studies have tried to forecast the contagion dynamics in Italy (Remuzzi and Remuzzi 2020; Grasselli et al. 2020; Fanelli and Piazza 2020), or in Italy and other countries (see among others, Zhang et al. 2020). Some studies have also focused on the lockdown’s effect, trying to evaluate the impact in terms of saved lives and contagion reduction (Lavezzo et al. 2020; Hsiang et al. 2020). Casella (2020) compares two types of restrictive measures: the tight lockdown adopted in China and the significant but less severe measures adopted in the Lazio region (the closure of schools and the main lockdown). He develops a control-oriented model capturing the control-relevant dynamics to homogenize territories. He concludes that suppression strategies can be effective if enacted very early, while mitigation strategies are prone to failure.

Pedersen and Meneghini (2020) implement a SIQR (Susceptible, Infectious, Quarantined, Recovered) model through which they evaluate the effect of lockdown measures in the north of Italy using data until March 19. They conclude that restriction measures slowed down the exponential growth rate but did not incisively reduce the spread of COVID-19. Giordano et al. (2020) propose a SIDARTHE (Susceptible, Infected, Diagnosed, Ailing, Recognized, Threatened, Healed, Extinct) model able to predict the epidemic’s trend. Considering the period from February 20 to April 5, they analyze how the progressive restrictions have affected the spread of the epidemic. They found that lockdown measures had a moderate effect, probably due to their incremental nature. The main conclusion of the paper is that lockdown measures have to be combined with widespread testing and contact tracing to defeat the virus. The document redacted by Direzione Centrale Studi e Ricerche INPS (DCSR – INPS 2020) tries to quantify the effect of the third lockdown measure by exploiting spatial variation in the degree of closure of economic activities. This report claims that the reduction in COVID-19 cases started from the day the decree was introduced, without any delay. In any case, all of these studies, except Casella (2020), suffer from the same set of limitations in terms of the specification of the detection delay that was stressed above. Furthermore, except for the DCSR-INPS study, they are more focused on the forecasting of possible future scenarios and none performed a retrospective analysis of the features of the different kinds of restrictive measures.

Finally, what the literature has understated is that measures have both direct impacts due to the specific measures adopted and the particular dates on which they are enforced, and indirect effects for which things can be different and the distinction between lockdowns fuzzy. A prominent example is the announcement effect. Indeed, COVID-19’s reproduction number also depends on individual behaviors such as avoiding skin contact between people or hand washing, which can be modified by the perception and knowledge of the virus. Both the announcement and implementation of restrictive measures can have a relevant impact on these, in particular in a country that has been one of the most affected by the novel coronavirus.

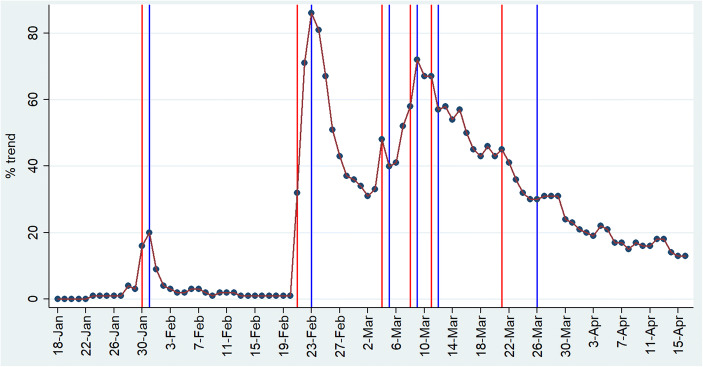
Figure 2 reports the Google Trends in Italy for “Coronavirus Italia” from mid-January to mid-April 2020.8 The red line corresponds to the announcement date of the corresponding restrictive measures, whose actual introduction corresponds to the blue line. The first peak in Google searches corresponds to the date of air traffic closure between China and the state of emergency announcement. The second peak is recorded at the announcement and implementation of “red-zones” in some northern municipalities. The next peak occurs on the 4th of March, when the first national lockdown was announced. From this day onwards, the Google searches increased up to the implementation of the subsequent lockdown in the northern regions and started to decline on March 12, when the second lockdown was implemented at the national level. The upsurge of interest in the phenomenon related to the announcement of the previous restrictive measures might have affected the epidemic’s path independently from the direct impact of the specific measures.

Fig. 2.

Google Trends for “Coronavirus Italia” in Italy. Source: Authors’ elaborations from https://trends.google.it

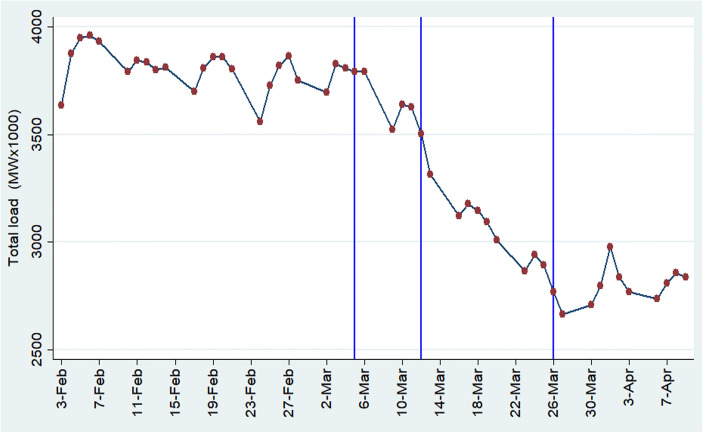
The same increased awareness might have other indirect effects through a massive shift of white-collar workers towards smart working (see Bonacini et al. 2020) and the decision of many firms to reduce their overall activities because of the incoming fall in final demand. Figure 3 displays the trends in electricity consumption in Italy from February 3 to April 9, 2020. Blue lines correspond to the dates when the three national lockdowns were implemented. The reduction in electricity consumption begins with the first lockdown, but it decreases sharply after the second (main) lockdown. Thus, standard economic activities seem to have decreased their electricity consumption already after the first lockdowns, although the shutdown was imposed only on a minority of economic activities—mainly schools, food facilities, and some retail, leisure, and cultural activities. The last lockdown, which imposed the closure of all (remaining) non-essential activities, seems to have had a lesser impact on energy consumption, which even showed a slight increase some days later.

Fig. 3.

Daily energy consumption in Italy, weekends excluded. Source: Authors’ elaboration from https://www.terna.it

All these descriptive indicators reinforce the need for a non-epidemic econometric strategy to deepen the detection delay issue and to assess the effects of the different lockdowns by also inspecting possible indirect and side effects. This is what we try to do in the next section.

Econometric strategy

Our underlying hypothesis is that the lockdown involves a structural change in the dynamics of the contagion. This structural change occurs after a time span, the detection delay. This might vary from one lockdown to another according to the specificity of the lockdown, the changing policies on testing, the progressive technological improvement in the analysis of test results, and the change in the administrative procedures for counting COVID-19 cases. Moreover, we assume no priors about the features of the dates when these structural breaks should occur, nor about their number, thus avoiding assuming ex ante that all or some of the three lockdowns are effective or that some other factors have caused additional structural breaks.

The econometric strategy is composed of two sequential parts. In the first, we analyze the overall effect of the lockdown on the dynamics of COVID-19 cases by using a machine learning algorithm of model selection to select the best structural change dates. Since there actually turn out to be three, we can thus obtain the delay for each of the three lockdowns and obtain the best model to assess their effectiveness. However, the result is not the delay of the lockdowns but the date when they become effective, since, as we discussed in Section 3, a portion of lockdown effects could be related to their announcement in previous days. In the second stage, we exploit the spatial variability of some variables by studying their interaction with the structural break dynamics.

For the first part, we consider the following baseline panel data model specification:

$$∆y_{\mathit{it}}=\alpha +\mathit{\beta }{\mathit{X}}_{\mathit{it}}+\gamma y_{i\left(t-1\right)}+{\gamma }_1{I}_t^{t1}{y}_{i\left(t-1\right)}+{\gamma }_2{I}_t^{t2}{y}_{i\left(t-1\right)}+\dots +{\gamma }_k{I}_t^{\mathit{tk}}{y}_{i\left(t-1\right)}+{\theta }_t+{\eta }_i+{\epsilon }_{\mathit{it}}$$

where y_it is the number of COVID-19 cases in province i at time t, and X_it is a vector of two time varying province-level control variables: the number of recovered and the number of deaths at the regional level weighted by the share of province-level COVID-19 cases over the regional level ones.9 A more detailed description of both the dependent variable and control variables can be found in Appendix (Table 4). The variables $I_t^{\mathit{tj}}$ are time-variant dummies taking a value of 1 when t ≥ t_j and 0 elsewhere and k is the number of lockdowns considered. The dummy variable $I_{\mathit{ti}}^{t2}$ also has the province index since, for the 26 provinces that experienced the second lockdown 3 days before (i.e., on March 9 rather than March 12), we correspondently give it a value of 1 also for t_j − 3 ≤ t < t_j. θ_t and η_i are respectively time and province dummy variables and ε_it is the error term.

Table 4.

Data and variable descriptions

Variable	Source (Year of reference)	Definition	Mean	Std. dev.
Daily growth in COVID-19 cases	Civil Protection Department (2020)	Dependent variable Difference between the overall COVID-19 cases at time t and the overall COVID-19 cases at time t-1 at the provincial level	30.07	61.97
Number of deaths	Civil Protection Department (2020)	Number of people deceased with COVID-19 infection at the provincial level. As this information is available at the regional level only, the variable is calculated for each province weighting regional COVID-19 deaths by its share of regional COVID-19 cases.	93.63	271.78
Number of recovered	Civil Protection Department (2020)	Number of people recovered from COVID-19 infection at the provincial level. As this information is available at the regional level only, the variable is calculated for each province weighting regional COVID-19 recoveries by its share of regional COVID-19 cases.	156.44	452.55
Population density	ISTAT (2019)	Ratio between total provincial population and total surface area (km2)	270.13	380.48
Proximity to a hospital	Ministry of Economic Development (2014)	Share of provincial population living in a municipality with at least one 1st level DEA hospital (i.e., a hospital providing first aid, resuscitation, and general surgery services)	0.333	0.171
Proximity to a railway station	Ministry of Economic Development (2014)	Share of provincial population living in a municipality with at least one silver railway station (i.e., a station with morethan 2500 daily visitors on average)	0.456	0.180
Hospital dismissals by the elderly	ISTAT (2018)	Share of hospital dismissals of people aged 65 or above (average for 2016–2018) at the provincial level	0.460	0.049
Mortality for infectious diseases	ISTAT (2017)	Mortality rate for infectious diseases at the provincial level (× 10,000 inhabitants)	2.488	0.957
High school students	ISTAT (2018)	Share of students attending upper secondary schools at the provincial level out of the total population aged 64 or below	0.058	0.007
University students	ISTAT (2017)	Number of students attending universities at the provincial level out of the total population aged 64 or below	0.025	0.026
Nursing homes	ISTAT (2011)	Number of nursing homes at the provincial level (× 10,000 inhabitants)	1.129	0.638
Unemployment rate	ISTAT (2019)	Unemployment rate among people aged 15–74 at the provincial level	0.104	0.057
Poverty rate	INPS (2018)	Share of households declaring an ISEEa lower than 6000 euros out of the total provincial population of households	0.072	0.039

^aThe ISEE is an indicator combining household income and wealth and it is generally declared when applying for social benefits. It consists of the sum of household income and 20% of household wealth (in terms of both financial assets and property) divided by an ad hoc equivalence scale. The ISEE equivalence scale is equal to the number of household members raised to the power of 0.65

For a given k and t₁ … t_k, the model is a panel model with time and space fixed effects and k structural breaks for the effect of the lagged variable y on its variation at time t, where t_j corresponds to the time at which the structural break occurs. To select the best k and t_j, we use a machine learning algorithm by estimating the model for k varying from 0 to 5 for all the possible combinations of the t_k parameters, from the 5th of March to the 24th of April.

The same procedure is repeated for different specifications of the model that exclude, alternately, the control variables and the time dummies. Specifically, we define (1) Model 1 as the model specification with neither time dummies nor control variables; (2) Model 2 as the specification with time dummies but no control variables; (3) Model 3 as the specification with both time dummies and control variables; and (4) Model 4 as the specification with control variables but no time dummies.

The best specification of the model is assessed by applying the Akaike information criterion on all three model estimations and all possible combinations of k t₁ … t_k. For further robustness, we perform the same test also including a quadratic specification of the y_{i(t − 1)} variable or substituting absolute values with values relative to province-level population. Finally, the Bayesian information criterion (BIC) of model selection is also applied alternatively to the AIC, and results are confirmed. On the final model selected, we conduct the standard Chow test for each structural break.

The machine learning methodology selects k = 3 and the optimal t₁, t₂, and t₃, for each model specification. Thus, we can analyze the coefficients of the best model selected to assess the relative impact of each of the three lockdowns. For this model, we also perform some further robustness checks that are reported in the Appendix.

For the last part, we add to the best model selected the interaction with some variables of interests:

$$∆y_{\mathit{it}}=\alpha +\mathit{\beta }{\mathit{X}}_{\mathit{it}}+\gamma y_{i\left(t-1\right)}+{\delta }_0{z}_i{y}_{i\left(t-1\right)}+{\gamma }_1{I}_t^{t1}{y}_{i\left(t-1\right)}+{\delta }_1{z}_i{I}_{\mathit{ti}}^{t1}{y}_{i\left(t-1\right)}+{\gamma }_2{I}_t^{t2}{y}_{i\left(t-1\right)}+{\delta }_2{z}_i{I}_t^{t2}{y}_{i\left(t-1\right)}+{\gamma }_3{I}_t^{t3}{y}_{i\left(t-1\right)}\gamma y_{i\left(t-1\right)}+{\delta }_3{z}_i{I}_t^{t3}{y}_{i\left(t-1\right)}+{\theta }_t+{\eta }_i+{\epsilon }_{\mathit{it}}$$

where z_i is a province-variant time-fixed variable that will be different for specifications we perform among a set of variables of interest. We consider each variable separately as it allows us to test, together with the changing impact of the variable over the four time span set up by the three lockdown thresholds t₁, t₂, and t₃, also the impact of adding the variable on the coefficients of the baseline model. The variable z_i without interaction is omitted since we already consider province fixed effects.

Identification of structural breaks

The methodology presented in Section 4 allows for the identification of the dates of structural breaks in the path of COVID-19 cases. The procedure automatically selects the number and dates of structural breaks and the best model specification using the Akaike information criterion (AIC). The model with three structural breaks is always selected as the best one, indicating that the three lockdowns have all had significant impacts. We thus define the corresponding date of the structural break as the effectiveness date of each lockdown.

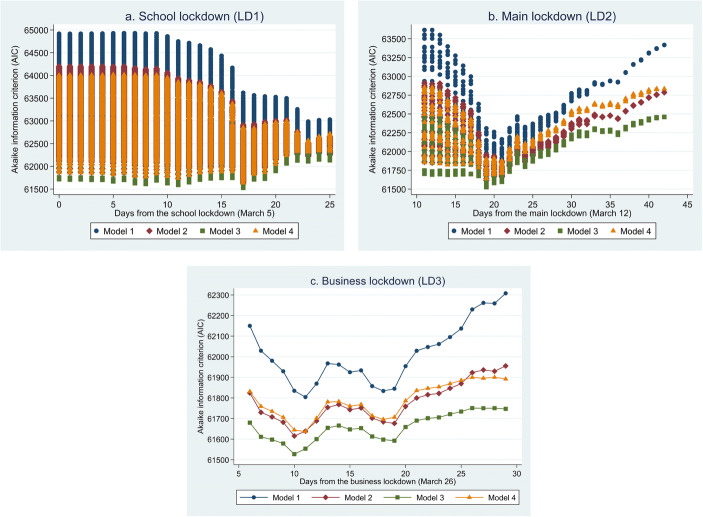
For the sake of simplicity, to comment on the results of the machine learning algorithm, we present here the best model selection through a clearer step-by-step procedure. In this case, to find the best model, we first select the effectiveness day for the first lockdown (LD1), making the dates of the two other lockdowns vary; then, we select the effectiveness day for the second lockdown (LD2), fixing LD1 according to the first step. Finally, we select the effectiveness day for the last lockdown (LD3), setting LD1 and LD2 according to steps two and three. This nested iterative procedure gives the same results as the non-nested (unrestricted) one presented in Section 4. Figure 4 a shows the AICs of all of the corresponding regressions, for each combination of parameters and model specification presented in Section 4, using the days from the introduction of the lockdown as reference. We recall that the best model, and thus the combination of days/parameters representing the detection delay of the lockdowns, corresponds to the model with the lowest AIC value.

Fig. 4.

Akaike information criterion values by model specification and values of the t_j parameters. a School lockdown (LD1). b Main lockdown (LD2). c Business lockdown (LD3). The LD1 effectiveness day in models illustrated in panel b is set to 17 days after the introduction of LD1. The LD1 and LD2 effectiveness days in models illustrated in panel c are set to, respectively, 17 and 19 days after their introductions

Results in Fig. 4 highlight that models that perform better in explaining the trend of COVID-19 cases are those where the algorithm sets the LD1 effectiveness day 17 days after its introduction (i.e., March 22). Interestingly, the school lockdown therefore appears to become effective after a number of days greater than the standard incubation period of the novel coronavirus (2–14 days after exposure to the virus, as reported by Backer et al. (2020), WHO (2020), and Lauer et al. (2020), among others), confirming the relevance of the further components of the detection delay. The same effectiveness day for LD1 is further confirmed by the other model specifications we developed. From the estimations illustrated in Fig. 4, we can also argue that Model 3 (i.e., the model specification including time dummies and the number of deaths and recovered at the provincial level) is the best one to explain the trend in COVID-19 cases, as its AIC values are always smaller than those reported by the other models.

Once the effectiveness day for LD1 is identified, we select the day from which LD2 became effective by looking at models with the lowest AIC values among those presenting this constraint. As a simplification of the algorithm results, panel B of Fig. 4 therefore shows the AIC values of models where effectiveness days for LD2 and LD3 vary and the one for LD1 is fixed and is equal to 17. Estimates in Fig. 4b highlight that the combinations of parameters that better perform in explaining the trend in COVID-19 cases are those where the algorithm sets LD2’s effectiveness at 19 days after its introduction. This means that the main lockdown starts to be effective on March 28 for Lombardy and the other 14 provinces listed in the Prime Ministerial Decree of the 8th of March 2020, and on March 31 for the rest of Italy. In this case as well, the detection delay of LD2 seems to be greater than the presumed incubation period for COVID-19, but the same evidence is confirmed by the other model specifications we developed. The long detection delay of LD2, which is even greater than of the LD1 one, may be explained by the fact that the highest daily growth values of people hospitalized because of the novel coronavirus at the national level were registered just a few days after the introduction of the main lockdown (see Fig. 1 for details). The massive burden of patients suffered by the local health systems in that period, as well as the critical growth of COVID-19 cases, probably slowed down the conducting and analysis of swab tests, thus further delaying the day from which the daily count of COVID-19 cases at the provincial level reports the start of LD2’s effectiveness.

Finally, keeping constant the effectiveness day for LD1 (i.e., 17 days after its introduction) and for LD2 (i.e., 19 days after its introduction), this simplification of the machine learning algorithm results displays the day from which LD3 became effective (panel C of Fig. 4). In contrast to what is seen in panels a and b of Fig. 4, the estimates presented here do not show a perfect concurrence between the model specifications analyzed in terms of the LD3 effectiveness day. In particular, the business lockdown became effective 10 days after its introduction (i.e., April 5) according to Models 2 and 3, while the LD3 effectiveness day occurred 1 day later (i.e., April 6) in Models 1 and 4. This slight difference in results is likely related to the exclusion of time dummies in the last two model specifications, which does not allow controlling for possible time-variant (but space-invariant) factors. LD3 has thus been the lockdown with the shortest detection delay (i.e., 10/11 days versus 17 days for LD1 and 19 days for LD2). There are different potential reasons for this evidence. First, the greater knowledge regarding the novel coronavirus among the Italian population probably led to a reduction in symptom signaling. Second, the improvement of pandemic management abilities by local authorities, together with the mitigation of the health crisis in most affected areas, probably resulted in a decrease in the average time to swab potentially infected people and to communicate test results. Third, the technology regarding COVID-19 tests improved, leading to swabs that provide test results in a shorter period of time (Sheridan 2020; Edwards 2020). Finally, the marked increase in the number of swabs performed daily (see Figure 6) might have also played an effective role in reducing the detection delay.

Fig 6.

Daily swabs performed at the national level. Source: Civil Protection Department (2020)

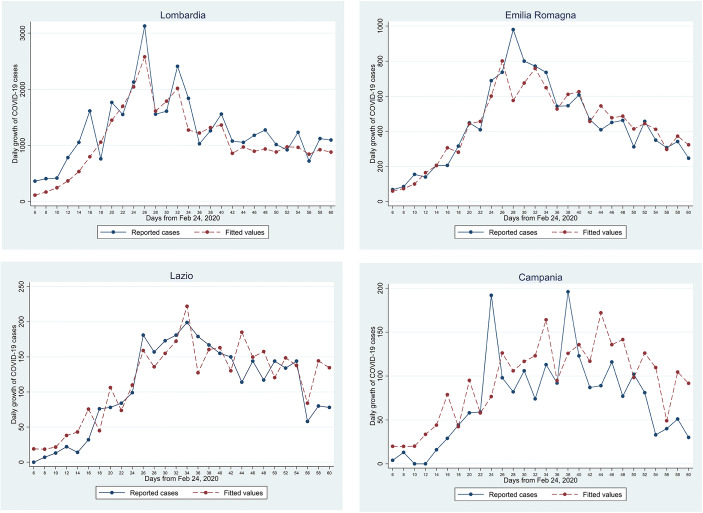
The AIC value of the best specification is 61,527.2. The Chow test accepts the structural break hypothesis for each of the structural breaks in each model specification. The same optimal specification is chosen using the alternative Bayesian information criterion (BIC). In the Appendix (Table 5), we report some further robustness checks on the model specification we use to identify the detection delays of the three lockdowns. In particular, we test the results of our machine learning algorithm (i) including, without and with time dummies, a quadratic (instead of linear) term for the lagged COVID-19 cases and its interactions with lockdown variables (i.e., Models 5–6); (ii) replacing control variables at the provincial level with those at the regional level (i.e., Model 7); and (iii) adding as a control variable the number of swab tests conducted at the provincial level (i.e., Model 8).10 Robustness check results in Table 5 overall confirm, for each lockdown, the same effectiveness days we detect in our best model specification (i.e., Model 3). The only specification reporting different delays (especially for LD3) is Model 5. This discrepancy, however, may be explained by the fact that, not including time dummies, Model 5 is not able to catch time-variant province-invariant factors, such as the improvements in swab test technology that occurred at the end of March. Figure 7 in the Appendix shows how the model fits actual data provided by the Civil Protection Department for the two regions most affected by the novel coronavirus (i.e., Lombardy and Emilia-Romagna) and the most populated region for each of the two other macro-regions of Italy (i.e., Lazio for the center and Campania for the south).

Table 5.

Detection delay by lockdown and model specification

Lockdown	Effectiveness delay (number of days from introduction)
	Model 3	Model 5	Model 6	Model 7	Model 8
School lockdown (LD1)	17	17	17	17	17
Main lockdown (LD2)	19	21	19	19	19
Business lockdown (LD3)	10	18	10	10	10

Unlike Model 3, Model 5 includes a quadratic polynomial of COVID-19 cases at time t-1 and its interactions with lockdowns variables, but there are no time dummies. Model 6 adds time dummies to Model 5. In contrast to Model 3, Model 7 includes the number of COVID-19 deaths and recovered at the regional level instead of the provincial one. Model 8 adds to Model 3 the number of swab tests undertaken at the provincial level. As this information is available at the regional level only, the variable is calculated for each province weighting regional COVID-19 swab tests by its share of regional COVID-19 cases

Fig 7.

Fitted values of the daily growth in COVID-19 cases at the regional level. Fitted values are based on our best model specification (Model 3)

Lockdown effects on the trend of COVID-19 cases

The optimal identification of structural breaks allows us to estimate the relative effects on the dynamics of COVID-19 cases limiting as much as possible any arbitrary assumptions.

As explained in Section 4, we estimate lockdown effects on the spread of COVID-19 in Italy through a fixed-effects panel model based on four different specifications and using as dependent variable the daily growth in COVID-19 cases at the provincial level. Lockdowns are included in all model specifications as interactions between their specific time dummy and the variable reporting the overall number of COVID-19 cases at the provincial level at time t-1. Specifically, the dummy LD1 is equal to 1 from March 22 onwards (i.e., the 27th day after February 24); the dummy LD2 is equal to 1 from March 28 onwards for both Lombard provinces and the other 14 provinces listed in the Prime Ministerial decree dated March 8, 2020, while it is equal to 1 from March 31 onwards (i.e., the 36th day after February 24) for the remaining Italian provinces; the dummy LD3 is equal to 1 from April 5 onwards (i.e., the 41st day after February 24) in Models 2 and 3, while it is equal to 1 from April 6 onwards in Models 1 and 4 (see Section 5 for details).

Estimation results of Model 1 indicate that all three lockdowns resulted in a significant alleviation in the spread of COVID-19 once they became effective (Table 1). Looking at magnitudes, the school lockdown appears to be the most important one in reducing the growth of cases in Italy (the difference in interaction coefficients between LD1 and LD2 is statistically significant at the 1% level). The predominant effect produced by the school lockdown is likely to be related to its ability to reduce mobility and keep a large portion of the population (composed of children, upper secondary school and university students, teachers and professors, and parents with child-care tasks) at home.

Table 1.

Effects of the three lockdowns on the daily growth of COVID-19 cases (fixed-effects panel model)

Variables	Model 1	Model 2	Model 3	Model 4
COVID-19 casest-1	0.120***	0.117***	0.125***	0.129***
LD1 * COVID-19 casest-1	− 0.059***	− 0.060***	− 0.058***	− 0.057***
LD2 * COVID-19 casest-1	− 0.031***	− 0.028***	− 0.027***	− 0.029***
LD3 * COVID-19 casest-1	− 0.015***	− 0.015***	− 0.012***	− 0.012***
Number of deaths			0.011	0.021
Number of recovered			− 0.052**	− 0.067***
Constant	8.165**	0.200	0.178	6.511**
Time dummies	No	Yes	Yes	No
Observations	6313	6313	6313	6313
R-squared	0.428	0.455	0.463	0.444
Number of provinces	107	107	107	107

Standard errors are clustered by Italian province. ***p < 0.01, **p < 0.05, *p < 0.1

In contrast, Table 1 highlights that the business lockdown was the one with the smallest alleviation effect on the growth of cases in Italian provinces (the difference in interaction coefficients between LD3 and LD2 is statistically significant at the 1% level). Similarly to LD1, the reason for the smaller effect of LD3 is probably linked to the lower number of people involved in the business lockdown (i.e., workers in “non-essential” economic sectors of activity). The smaller magnitude of the LD3 interaction variable may also be related to two other important aspects. First, economic activity was seriously indirectly affected already, as a result of the main lockdowns (see the discussion of Fig. 2 in Section 3). Second, the sectors of activity defined as “essential” by the Italian government were not necessarily less exposed to COVID-19. Third, many companies belonging to “non-essential” economic sectors requested and obtained exemptions from the lockdown from local authorities.11

Table 1 shows that estimated effects of the three lockdowns on the growth of COVID-19 cases, as well as the main conclusions of our analysis, remain overall the same when including time dummies in the model specification (Model 2) and/or the controls for the number of deaths and recovered at the provincial level (Models 3 and 4).

As a sensitivity analysis, in the Appendix (Table 6), we replicate the analysis presented in Table 1 for our best model specification (Model 3) in some subsamples. First, given that daily counts of new COVID-19 cases may be affected by different (unobservable) strategies by local authorities (e.g., the number of swabs conducted or analyzed), we run Model 3 estimates in a subsample considering even (or odd) days only. Second, as Lombardy has been the most COVID-19-affected region and its provinces may represent outliers, we replicate Model 3 estimates in a subsample excluding 12 Lombard provinces. Third, we exclude 26 provinces listed in the Prime Ministerial Decree of the 8th of March 2020, in order to explore the potential heterogeneity in the LD2 alleviation effect since the main lockdown was introduced 3 days in advance in these provinces. Finally, we replicate our analysis referring to COVID-19 case variables defined in relative terms with respect to the provincial population. Specifically, both the dependent variable and the lagged COVID-19 case variables were divided by the number of inhabitants at the provincial level and then multiplied by 10,000. Results of these sensitivity analyses in Table 6 overall confirm the robustness of our evidence on lockdown effects on the daily growth of the cases of the novel coronavirus at the provincial level. Interestingly, when excluding provinces listed in the Prime Ministerial Decree of the 8th of March 2020, no significant differences are observed in the LD2 effect, whereas LD3 had a similar impact to LD2 in this case. However, the latter evidence is likely to depend on the fact that the 26 provinces that started the main lockdown on March 9 (rather than March 12) are all in the north of Italy (except for Pesaro–Urbino), the area of the country where both most of the “essential” economic sectors are located and where many more exemptions from the business lockdown have been requested.

Table 6.

Lockdown effects on the daily growth in COVID-19 cases by subsample and definition of dependent variable (fixed-effects panel model)

Variables	Model 3	Only even days	Only odd days	No Lombard provinces	No provinces listed in the Prime Ministerial Decree of March 8, 2020	COVID-19 cases per every 10,000 inhabitants	No Lombard provinces and COVID-19 cases per every 10,000 inhabitants	No provinces listed in the Decree of March 8, 2020, and COVID-19 cases per every 10,000 inhabitants
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
COVID-19 casest-1	0.125***	0.129***	0.121***	0.115***	0.126***	0.069***	0.081***	0.113***
LD1 * COVID-19 casest-1	− 0.058***	− 0.060***	− 0.056***	− 0.055***	− 0.068***	− 0.038***	− 0.052***	− 0.080***
LD2 * COVID-19 casest-1	− 0.027***	− 0.024***	− 0.029***	− 0.024***	− 0.021***	− 0.019***	− 0.022***	− 0.023***
LD3 * COVID-19 casest-1	− 0.012***	− 0.012***	− 0.013***	− 0.018***	− 0.025***	− 0.007**	− 0.015***	− 0.021***
Number of deaths	0.011	− 0.029	0.054	0.149**	0.246***	0.05	0.206**	0.295**
Number of recovered	− 0.052**	− 0.047*	− 0.059***	− 0.056***	− 0.056***	− 0.019	− 0.018	− 0.019
Constant	0.178	0.172	1.979	0.367	0.105	0.008	0.01	0.004
Time dummies	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Observations	6313	3210	3103	5605	4779	6313	5605	4779
R-squared	0.463	0.461	0.475	0.391	0.410	0.250	0.241	0.210
Number of provinces	107	107	107	95	81	107	95	81

Standard errors are clustered by Italian province. ***p < 0.01, **p < 0.05, *p < 0.1. Column 6 replicates estimates in Model 3 but all COVID-19 cases are considered in relative terms with respect to the provincial population. Specifically, both the dependent variable and the “COVID-19 cases at time t-1” variable are divided by the number of inhabitants at the provincial level and then multiplied by 10,000. Column 7 is the same as Column 6 but replicates the analysis in a subsample excluding 12 Lombard provinces. Column 8 is the same as Column 6 but replicates the analysis in a subsample excluding 26 provinces listed in the Prime Ministerial Decree of the 8th of March 2020.

Interactions with province-level characteristics

Because of the strong heterogeneity across Italian provinces in terms of demographic and economic characteristics (see, among others, Bratti et al. 2007; Gallo and Pagliacci 2020), in this section, we explore to what extent some of them interacted with the three COVID-19 lockdowns. To do this, as explained in Section 4, we add interaction terms with the variable of interest in Model 3 (i.e., our best model specification; see Section 5).

The flourishing literature studying differential rates of compliance to social distancing highlights that both individual social and political characteristics and contextual variables are strong determinants. Chiou and Tucker (2020) and Wright et al. (2020) study the correlation between income and the propensity to comply with social distancing orders. The first finds that both income and internet access are positively correlated with the ability to stay at home. The second suggests that the poorest communities are the least likely to comply with social distancing orders. Allcott et al. (2020), Barrios and Hochberg (2020), and Painter and Qiu (2020) document for the USA that Republicans are less likely to respect social distancing orders. Egorov et al. (2020) reach a coherent conclusion showing that the reduction in mobility is stronger in more multi-ethnic cities and those with higher levels of xenophobia. Simonov et al. (2020) point out a negative correlation between Fox News viewership in US regions and the propensity to stay at home during the pandemic. Doganoglu and Ozdenoren (2020) explain that generalized trust is associated with less social distancing. Borgonovi and Andrieu (2020) note that a larger drop in social mobility is correlated with higher social capital. Finally, Beland et al. (2020), using a difference-in-differences approach on US data, find that stay-at-home orders unequally increased unemployment rates since younger, less-educated, and immigrant workers were more affected by the lockdown experience.

We focus here on four categories of demographic and economic characteristics. First, we look at provincial territory and infrastructure (i.e., population density, proximity to a hospital, proximity to a railway station) to observe whether restrictive measures were more effective on commonly crowded places. Second, we explore heterogeneous effects at provincial level by some characteristics of the local health system and disease vulnerability (i.e., share of hospital dismissals of people aged 65 or above, past mortality rates for infectious diseases). The first variable wants to detect whether the (likely) greater presence of the elderly (i.e., vulnerable people reported highest COVID-19 mortality rates) in the hospitals played a role on the outbreak, while the second variable should shed light on some kind of “historical” local vulnerability to infectious diseases. Third, we analyze the territorial dimensions regarding students and nursing homes (i.e., share of high school and university students in the total population of persons aged 64 or less, number of nursing homes), because they were subject of an important and deep public debate for, respectively, the controversial effects of closing schools and the incorrect management of restrictive measures in the first stage of pandemic. Fourth, in line with the literature on the compliance to social distancing measures, we consider two variables describing the local labor market and income levels (i.e., unemployment rate among people aged 15–74, share of poor households in the total population based on administrative data) to indicate whether the lockdown measures were less effective in the poorer areas. More details on these variables are presented in the Appendix (Table 4).12

Estimates in Table 2 show that the spread of COVID-19 has been more severe in Italian provinces with higher population density or where a greater number of provincial inhabitants live in municipalities with at least one hospital or railway station (i.e., our proxies of proximity to a hospital/railway station). This evidence is largely expected because hospitals and crowded places like railway stations or metropolitan areas have probably been important sources of contagion (Lau et al. 2004; Koganti et al. 2016). Nonetheless, as reported by the structural break coefficients of population density, more densely populated provinces are those in which the three lockdowns have been more effective, thus the ones where the daily growth of COVID-19 cases decreased the most in the last part of our reference period. These results are consistent with those of Qiu et al. (2020). Instead, the proximity to a hospital or a railway station increased the LD3 alleviation effect only.

Table 2.

Interactions of province-level characteristics (infrastructures, local health system, and diseases vulnerability) with lockdowns (fixed-effects panel model)

Variables	Variable of interest (VoI)
	Population density	Proximity to a hospital	Proximity to a railway station	Hospital discharge of the elderly	Mortality for infectious diseases
COVID-19 casest-1	0.097***	0.078***	0.071***	0.411***	0.129***
LD1 * COVID-19 casest-1	− 0.039***	− 0.036***	− 0.035**	− 0.196***	− 0.060***
LD2 * COVID-19 casest-1	− 0.023***	− 0.027***	− 0.030***	− 0.088***	− 0.038***
LD3 * COVID-19 casest-1	− 0.006***	− 0.007***	− 0.005**	− 0.072***	− 0.014***
VoI * COVID-19 casest-1	0.014***	0.045**	0.054*	− 0.305***	− 0.006
VoI * LD1 * COVID-19 casest-1	− 0.008***	− 0.024	− 0.029	0.146**	0.002
VoI * LD2 * COVID-19 casest-1	− 0.001***	− 0.001	0.003	0.065***	0.012***
VoI * LD3 * COVID-19 casest-1	− 0.002***	− 0.007***	− 0.010***	0.066***	0.001
Number of deaths	-0.016	0.028	0.051*	0.015	0.025
Number of recovered	− 0.063***	− 0.044**	− 0.046**	− 0.063***	− 0.055***
Constant	0.211	0.201	0.189	0.248	0.185
Time dummies	Yes	Yes	Yes	Yes	Yes
Observations	6313	6313	6313	6313	6313
R-squared	0.493	0.492	0.493	0.482	0.469
Number of provinces	107	107	107	107	107

Standard errors are clustered by province. All variables of interest are normalized to mean 1 before being interacted with lockdown variables. ***p < 0.01, **p < 0.05, *p < 0.1

Looking at the characteristics of the local health system and disease vulnerability, the last two columns of Table 2 indicate that the spread of COVID-19 was lower in provinces with more hospital dismissals of the elderly in the previous year and where the mortality rate for infectious diseases was higher in the past.13 In the latter case, the interaction term with the number of COVID-19 cases at time t-1 is insignificant. After the introduction of lockdowns, however, the coronavirus infection is relatively greater in these areas. This evidence suggests that lockdown measures may be less effective in less healthy provinces. The same evidence is also confirmed by the third column of Table 3, i.e., the one regarding nursing homes.

Table 3.

Interactions of province-level characteristics (incidence of students, nursing homes, local labor market, and income levels) with lockdowns effects (fixed-effects panel model)

Variables	Variable of interest (VoI)
	High school students	University students	Nursing homes	Unemployment rate	Poverty rate
COVID-19 casest-1	0.482***	0.083***	0.175***	0.110***	0.095***
LD1 * COVID-19 casest-1	− 0.254**	− 0.039***	− 0.090***	− 0.058***	− 0.045**
LD2 * COVID-19 casest-1	− 0.075***	− 0.025***	− 0.037***	− 0.038***	− 0.037***
LD3 * COVID-19 casest-1	− 0.056**	− 0.007***	− 0.018***	− 0.003	0.001
VoI * COVID-19 casest-1	− 0.390**	0.032***	− 0.067***	0.016	0.042
VoI * LD1 * COVID-19 casest-1	0.215**	− 0.018***	0.043***	0.002	− 0.020
VoI * LD2 * COVID-19 casest-1	0.053*	− 0.002	0.013***	0.022***	0.016***
VoI * LD3 * COVID-19 casest-1	0.049*	− 0.005***	0.009*	− 0.021***	− 0.022***
Number of deaths	− 0.005	0.022	0.019	0.028	0.016
Number of recovered	− 0.062***	− 0.047***	− 0.061***	− 0.039**	− 0.042**
Constant	0.193	0.225	0.239	0.191	0.188
Time dummies	Yes	Yes	Yes	Yes	Yes
Observations	6313	6313	6313	6313	6313
R-squared	0.479	0.497	0.476	0.477	0.471
Number of provinces	107	107	107	107	107

Standard errors are clustered by province. All variables of interest are normalized to mean 1 before being interacted with lockdown variables. ***p < 0.01, **p < 0.05, *p < 0.1

The share of high school and university students in the provincial population aged 64 or less, as well as the presence of nursing homes, also had a significant role in explaining the trend of COVID-19 cases (Table 3). The daily growth of COVID-19 cases appears higher in the first stage of the pandemic in provinces with a greater share of university students, and the school lockdown alleviates this effect, as does the business lockdown, probably because of the working students.14 Instead, our estimation results suggest that the opposite occurred in provinces with larger relative numbers of high school students. The public debate on LD1 had indeed pointed to the possible controversial effects of closing schools without further social distancing measures because the alternative use of time by teenagers could expose them more to infections.

Finally, last two columns of Table 3 highlight that lockdown effects differ when accounting for the spread of unemployment and poverty at the provincial level. As for the poverty definition, we used administrative data on declarations of ISEE (namely, Indicatore della Situazione Economica Equivalente, i.e., an indicator combining equivalized household income and wealth and that is generally declared when applying for social benefits in Italy). For each province, we consider as poor households those declaring an ISEE value lower than 6000 euros.15 These two economic dimensions seem not to have influenced LD1’s effect on the growth of COVID-19 cases, but they significantly reduced the effect of LD2. This evidence may be related to the fact that, in Italian provinces with high unemployment and poverty rates, a larger portion of the population was probably already at home (or, at least, it moved less frequently) before the main lockdown. Moreover, the lower effect of the main lockdown in provinces with more poor households may also be explained by the fact that the poor often live in larger households or in lower health conditions (Lanjouw and Ravallion 2020; Sarti et al. 2017). By keeping the poor at home more, LD2 might have exposed them to a greater risk of infection.

Since the spread of the novel coronavirus increases the future economic and non-economic damages, this territorial analysis raises great concerns about the effects of the main lockdown on income inequalities. At same time, the opposite signs on inequalities are related to the third and less effective lockdown. This is not an expected outcome as the target of the business lockdown was to reduce the number of people leaving home for work-related reasons, producing a greater effect in provinces with more active labor markets. This peculiar outcome raises further doubts on the selection process of “essential activities” since it seems to be biased towards more developed and richer regions,16 the ones most affected by the virus.

Ex post validation of the model’s early detection performance

In this section, we try to assess the strength of our methodology to detect early the incurring structural break along the infection path. We re-simulate the performance of our model along our reference period (February 24–April 24) through a real-time procedure. We start by applying our methodology to a restricted sample that consists of the first 15 days of the pandemic only (i.e., until March 10) and then progressively increasing the length of the time series up to the whole set of data considered in the main analysis.

Since we start from a very short set of data, the estimated coefficients tend to be less significant and the dates recognized as changing points may vary slightly. To strengthen the methodology adopted here, we therefore add two constraints to our model selection procedure. All in all, we only require that the best model selection for reduced samples has the same robustness properties as the full sample case. First, we require the estimated coefficients for both lagged cases (i.e., COVID-19 cases at time t-1) and structural breaks to all be statistically significant (at least) at the 10% level. Second, once the best model is selected for a k number of breaks (i.e., we identify the set of dates for breaks reporting the lowest AIC value), we impose that the best selection of dates does not change for the first k breaks when a k + 1 number of breaks is considered. Note that these conditions are always satisfied in the case of the full time series because both coefficients are indeed significant and the dates of the structural breaks are nested by the number of breaks considered.

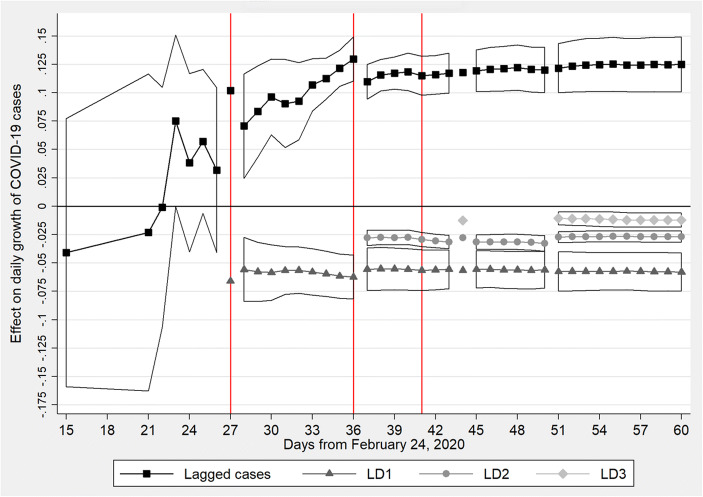
Figure 5 shows estimated effects—referring to the best model selected—for lagged cases and the three lockdown interactions on the daily growth of cases by the length of the analyzed time series. The coefficient of lagged cases is always insignificant when our best model specification (i.e., Model 3; see Section 5) for zero and one break is estimated on samples of 15 to 26 days after February 24 (i.e., to March 10 or March 21, respectively).17 In estimates on samples at least 21 days long, a first structural break is actually identified by our model selection procedure on day 21 (i.e., March 16), 6 days before the definitive effectiveness day we highlighted in Section 5 (if, as we believe, this break coincides with LD1). However, the statistical insignificance of lagged cases leads us to not consider it as a “best model.” The statistical significance criterion starts to be satisfied when the analyzed time series has a length of 27 days, but the first break date becomes stable at day 27 (i.e., March 22) when the sample counts at least 28 days. Therefore, the identification of the day from which LD1 became effective could have been spotted through our model selection procedure already from 28 days after February 24 (i.e., March 23).

Fig. 5.

Effects of lockdowns on the daily growth of COVID-19 cases by time series length. Outlined areas represent confidence intervals at the 5% level. “Lagged cases” refers to the COVID-19 cases at time t-1, while “LD1,” “LD2,” and “LD3” stand for the three lockdown interaction terms in Table 1. The three vertical lines represent, respectively, the effectiveness days of the school lockdown, main lockdown, and business lockdown, as shown in Section 5

Moving to the identification of the second structural break, our second condition (i.e., structural breaks nested by number of breaks considered) starts to be satisfied in estimates based on 37-day-long time series, where the second break date is on day 36.18 Thus, both LD1 and LD2 could have been clearly identified the day after their effectiveness day. Conversely, this is not the case for LD3. Although it became effective on the daily growth of COVID-19 cases on day 41 (see Section 5), LD3 is clearly identified from our model selection procedure only when samples with at least 51 days are considered (and only temporarily in estimates on time series counting 44 days from the beginning of the pandemic). The longer period needed to identify LD3 may be related to its lower alleviation effect on the daily growth of cases. Estimates based on reduced samples, however, point out that the LD3 effectiveness day is on day 41 (i.e., April 5), thus confirming all dates identified in our main analysis.

In conclusion, this ex post validation analysis highlights two important aspects. First, from the day the three lockdowns are identified through our model selection procedure, social distancing measures have an alleviation effect on the daily spread of the novel coronavirus that is quite stable and similar to the one estimated in the full time series. Second, the effectiveness of the school lockdown could have been spotted already on March 23 (and even earlier, although less clearly). This means that the business lockdown introduced on March 26 could perhaps have been avoided as its announcement and consequent discussion started on March 21. It should be noted that the period during which the introduction of LD3 was under debate was characterized by the highest growth rates of COVID-19 cases and deaths (Fig. 1), and a common perception was that something more had to be done to stop the pandemic’s rampage. Nonetheless, the slight alleviation effects reported by the business lockdown and its economic effects confirm the importance of verifying in advance the need for additional restrictive measures.

Conclusions

In this paper, we have proposed a machine learning procedure to identify structural breaks in the dynamics of the COVID-19 outbreak to assess the impact of social distancing measures. By considering the case of Italy, three structural breaks are identified, and they can be associated respectively with each one of the three main restrictive measures enforced at the national level.

Analyzing the coefficients of the best model selected, we show that the first lockdown was the most effective one. Descriptive evidence suggests that, together with the direct effect of school closure, this lockdown has also had a strong indirect announcement effect, making people more aware of the phenomenon at hand. The impact of the last measure, the shutdown of “non-essential” activities, appears to have been hardly relevant. This may be due to the fact that both the business lockdown and the transition to working from home were underway well before the closure was imposed, as the electricity data seems to suggest, but rather to a loose definition of essentiality.

The results also show that the time elapsing between the implementation of restrictive measures and their impact on the infection outbreak data varies significantly. Indeed, the detection delay was 17 days for the first measure, 19 days for the main lockdown restricting freedom of mobility and imposing the shutdown of leisure and retail activities, and 10 days for the third lockdown. The increase from the first to the second detection delay can be attributed to the saturation of health facilities since the same days following the second lockdown correspond to the peak of contagion, but also to possible mistakes in communication procedures that increased geographic mobility in the timespan between the announcement of the measure and its enforcement. The remarkable decrease in the third detection delay, while being partially rooted in the lower severity of hospitalization and infection conditions, can also be related to an improvement in testing procedures and technology, as well as to the greater ability of individuals to recognize the symptoms.

The variability of the detection delay, the saturation, and the communication effects can be a useful evidence to increase the effectiveness of feedback control strategies and they also suggest that widespread testing campaigns could also decrease the overall detection delay, avoiding the risk of such strategies to fail. Furthermore, they confirm the adequacy of the data-driven methodology, which avoids any prior assumption about the effectiveness and the time distribution of the structural changes.

By exploiting the huge spatial variation in the social, health, and economic features of Italian provinces, we have confirmed the interpretation of the results above and deepen the peculiarities of each restrictive measure.

The same methodology can also be used to detect early the structural breaks on daily updated data. If applied backward to our case study, the first two structural breaks could have been correctly identified just the day after they occurred, while the detection of the third one would have needed 2 days more. It is relevant to be noticed that the effectiveness of the school lockdown could have been spotted at the beginning of the political debate on the possible implementation of the business lockdown. This evidence reveals that important policy implications can emerge from methodologies being able to verify in advance the need for additional restrictive measures, because the slight alleviation effects reported by the business lockdown and its potential (massive) negative effects on the national GDP could perhaps be avoided. Results like this seem crucial, in particular, in relation to whether a second wave of COVID-19 cases will really occur in the near future.

Compliance with ethical standards

Disclaimer

The views expressed in this paper are those of the authors and do not necessarily reflect those of INAPP.