Examining metastatic behavior within 3D bioprinted vasculature for the validation of a 3D computational flow model

3D printed vasculature paired with a 3D in silico model interrogates biophysical forces of circulating tumor cells.

Abstract

Understanding the dynamics of circulating tumor cell (CTC) behavior within the vasculature has remained an elusive goal in cancer biology. To elucidate the contribution of hydrodynamics in determining sites of CTC vascular colonization, the physical forces affecting these cells must be evaluated in a highly controlled manner. To this end, we have bioprinted endothelialized vascular beds and perfused these constructs with metastatic mammary gland cells under physiological flow rates. By pairing these in vitro devices with an advanced computational flow model, we found that the bioprinted analog was readily capable of evaluating the accuracy and integrated complexity of a computational flow model, while also highlighting the discrete contribution of hydrodynamics in vascular colonization. This intersection of these two technologies, bioprinting and computational simulation, is a key demonstration in the establishment of an experimentation pipeline for the understanding of complex biophysical events.

INTRODUCTION

The ultimate killers in cancer are the metastases—particularly those to the brain and other vital organs. It has been known for more than 150 years that cancers can exhibit organ tropism for secondary site invasion and tumor formation (1, 2), but within an organ system, predicting the specific, intraorganal locations of metastasis development and metastatic potential of a given tumor remains impossible. Our inability to find and treat early metastases poses a major obstacle for successful cancer treatment, as brain metastases are almost uniformly fatal (3, 4). Some regions of the brain are more susceptible to breast cancer metastasis (5–7), but the mechanisms of local susceptibility remain poorly understood and impossible to ssprevent.

Many aspects of the physical and biological interplay between circulating cells and the vasculature remain difficult to study and impossible to control within in vivo systems, specifically with regard to vascular geometry and discrete circulating tumor cell (CTC) attachment events and due to the presence of a variety of confounding factors such as red blood cells, dynamic blood pressure, and immune responses. Even evaluating the effects of possible influential mechanical forces, such as dynamic fluid flow, requires substantial simplification of the in vivo scenario. In silico models designed to model vascular fluid dynamics offer one of the only mechanisms to investigate physiological blood flow through complex vascular geometries to better understand its influence over preferential tissue targeting during metastasis (8). Developing and validating these models are essential for testing open hypotheses on the role of flow patterns, vascular geometry, cell compliance, and tissue compliance in endovascular seeding.

While much of the current work in this area has focused on the development of computational models, validation methods are currently limited to primarily microfluidic devices (9). Conventional microfluidic chips, which mimic vascular geometries using molded channels, do not have most of the important characteristics found in vivo, such as tubular channels and vessel compliance, severely limiting their ability to reproduce the vascular dilation and contraction in response to flow pressure changes that are found in biological systems. Traditional microfluidic channels are fabricated using polydimethylsiloxane (PDMS) and glass, which typically require coatings of adhesion-promoting proteins to ensure endothelial cell attachment (10) and lack the flexibility to adapt to changes in the surrounding environment. These types of devices lack the full range of attachment sites available to CTCs in vivo, with patent vessels bound fully within extracellular matrix (ECM), which constrains their potential as vascular proxies for CTC attachment studies. This limitation has led to the use of specialized compartments that expose small subsections of the flow channel to hydrogel surfaces upon which cells can attach to examine CTC behaviors such as extravasation. More recently, advanced microfluidic devices have also been used to generate self-assembled microvasculature by encapsulating endothelial cells in hydrogels, followed by cultivation under perfusion. While these advanced chip systems can reproducibly generate perfused microvasculature fully encapsulated by ECM-like hydrogel, the geometries of the vasculature formed in these devices are difficult to control and nonreproducible between devices (11, 12) . While devices having self-assembled microvasculature are valuable tools for investigating mechanistic tumor cell and endothelial interactions in vitro (12–17), the lack of control over the resulting geometries limits their potential as tools for specifically validating predictive three-dimensional (3D) computational models. Recent work using a photolithographic technique to engineer microvessel-scale channels has demonstrated the potential for reproducible and controlled design for investigating flow dynamics in capillary size channels with high geometric fidelity to in vivo through a synthetic hydrogel material for the purpose of validating a computational flow model (18). While this approach is an important method for examining physiological flow behaviors at this scale, it must trade off the unique ability to fabricate these channels with the inability to line these vessel proxies with a living endothelium, which may limit its potential for specifically examining CTC-endothelium interactions in future studies.

As a result of certain in vitro approach limitations, basic questions in tumor cell attachment and extravasation remain unanswered. Significant evidence from genomic and transgenic lineage tracing experiments shows that metastases tend to be polyclonal (19, 20). Some studies have shown evidence that CTCs tend to embolize within small capillaries with diameters similar to the CTCs themselves, allowing them to attach and begin the extravasation process (19), while other studies have demonstrated the CTCs’ ability to compress and pass through these small capillaries (14, 21). This poses the possibility that immobilization within the capillaries may not be the only method of CTC attachment to the endothelium in vivo, which then poses the further question of what specifically drives CTC attachment within larger diameter vessels.

Here, we demonstrate a hydrogel-based vascular flow device with the capability of both informing and testing the predictive capabilities of an experimental computational dynamic flow model. This device has luminal channels, formed within a hydrogel via 3D printing of sacrificial ink material, which can be seeded with human brain microvascular endothelial cells and subsequently perfused to promote cell growth and formation of blood vessel–like tissue. A range of complex vascular geometries can be fabricated to test and measure the flow dynamics within the vessels, resulting in data that can be directly inputted into computational flow models. Here, simplified straight and branching geometries are examined to demonstrate the feasibility of this approach and its future potential for interrogating the contributions of physical forces and events such as vascular shear stresses and the physical impingement of CTCs upon the endothelium. By generating vessels in the size of small arteries, with two hierarchal 45° branching points with daughter vessels having increasingly smaller diameters, we have the opportunity to evaluate how slight changes to geometry may affect CTC attachment in larger vessels while simplifying the inherent complexity of in vivo vasculature for initial in silico modeling comparisons. In addition, this device offers the opportunity to determine whether circulating cells within a vessel lumen display different flow characteristics as compared to idealized particles of a similar diameter when suspended in a flowing fluid. Furthermore, using this approach, the effects of flow in an endothelialized channel running through an ECM-like matrix can be compared to idealized rigid walled channels without cell lining. While these factors can currently only be estimated, they highlight critical considerations when developing predictive computational models for simulating CTC behaviors. Using advanced simulation in conjunction with complex experimentation, we provide new insight, from a detailed hydrodynamic perspective, to the mechanisms underlying CTC flow dynamics and attachment behaviors.

RESULTS

Bioprinting endothelialized vessels for in vitro CTC evaluation

Analyzing the flow dynamics that affect CTCs requires a device, which has fully endothelialized channels with compliant, controllable geometries to recapitulate critical aspects of the in vivo CTC environment. To this end, we have modified and adapted the process flow from Kolesky et al. (22) to form complex artificial vasculature, which can be easily imaged using microscopy and directly amenable to flow velocity measurements. Briefly, a sacrificial ink, Pluronic F-127, was patterned using a custom-built extrusion-based bioprinter and then embedded in a gelatin-fibrin hydrogel (Fig. 1A). After gelation of the hydrogel, channels were evacuated and, in some cases, seeded with immortalized human cerebral microvascular endothelial cells (hCMECs) that attached and lined the patterned channel, forming a vascular mimic. These bioreactor systems were connected to a pneumatic fluidic feeding system with a controller maintaining flow at 10 μl/min (fig. S1).

Fig. 1. Bioprinting endothelialized vascular beds with complex geometry.

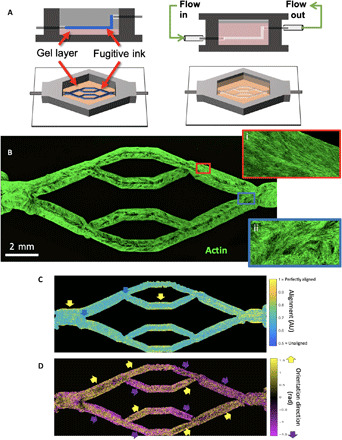
(A) Schematic representation of vascular bed printing using the sacrificial ink method. (B) Cytoskeletal morphology of microvascular endothelial cells shows high alignment in straight regions of the vascular bed (inset i, red border), with chaotic cytoskeletal alignment in the fork regions (inset ii, blue border). (C) Alignment of cytoskeleton (scale of 0.5 for randomly aligned to 1 for perfectly aligned) in perfused engineered beds shows high actin alignment in the wall of straight vascular regions (yellow arrows), whereas fork regions exhibit weak alignment (blue arrows). AU, arbitrary units. (D) Direction of preferential alignment follows flow direction. Colored arrows indicate principle flow direction (up, yellow; down, purple), which tends to agree with orientation direction of endothelial cell alignment.

After 7 days in vitro, the endothelial cells had completely covered all exposed channel surfaces, forming a confluent layer of endothelial lining (Fig. 1B). Cytoskeletal staining revealed that the endothelial cells aligned with the direction of flow, angled diagonally from the channel edge toward the bottom of the channel (Fig. 1B, insets). Using quantitative image processing, endothelial cells were shown to highly align in the straightaways (Fig. 1C), whereas less directionality was observed at the branching points, with essentially no cytoskeletal alignment in these areas (Fig. 1C and fig. S2). Furthermore, endothelial cytoskeletal alignment was observed to correlate closely with the direction of medium flow (Fig. 1D), suggesting that hCMEC reorganization was directly responding to flow rates as low as 10 μl/min. This corresponded to wall shear stresses (WSSs) as low as 0.004, 0.0082, and 0.012 dyne/cm² at the vessel walls for large (D = 1.6 mm), medium (D = 1 mm), and small (D = 0.7 mm) channels, respectively, with a measured medium viscosity of 0.9949 centipoise, assuming that cylindrical channels and flow are divided equally at each branch point. Flow-induced alignment of these hCMECs is in agreement with previous work that demonstrated significant morphological differences in alignment under flow conditions compared to static controls (23).

The influence of endothelial cells on the compliance of printed vascular channels

Bare and endothelialized channels were subjected to a range of flows and simultaneously imaged with confocal microscopy (Fig. 2, A to D) to evaluate how the vascular device responds to variable flow rates. The acellular device expanded to 166.22% of its original volume when the vessel was exposed to flow (1 ml/min; Fig. 2, A to C). In contrast, the endothelialized vessel exhibited a volume change of only 8.92% at the same flow rate (Fig. 2, A to C), demonstrating a substantial decrease in compliance relative to the acellular vessel. To assess the gelatin-fibrin hydrogel’s mechanical fidelity to human brain tissue and its contribution to the printed vessel compliance, we performed rheology to measure the final modulus of the material after complete cross-linking. Rheological results demonstrated that the final storage modulus of the gel material is 1.1 ± 0.1 kPa, which is comparable to the reported mechanical properties of brain tissue (fig. S4) (24) and is sufficiently pliant to result in the high levels of compliance observed when exposed to fluid flow.

Fig. 2. Endothelial cells can remodel bioprinted vascular beds.

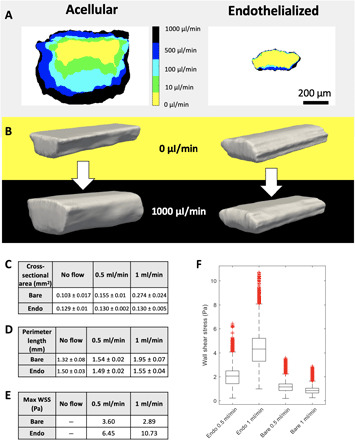
(A) Cross-sectional area collected at increasing flow rates for both acellular and endothelialized printed vessels. (B) Rendered 3D reconstructions of confocal image stacks of both acellular and endothelialized devices under static conditions and exposed to flow (1 ml/min). (C) Vessel volume measurements collected from rendered 3D vessel reconstructions with SDs of 400 measurements at different positions along the vessel length. (D) Vessel perimeter length measurements collected from rendered 3D vessel reconstructions with SDs of 400 measurements along the vessel length. (E) Maximum WSS values calculated with HARVEY from rendered vessels at different flow rates show that the deformable acellular vessel experiences lower WSS with higher flow, whereas the relatively stiff endothelialized vessel experiences fivefold greater peak WSS with 2× increase in flow. (F) WSS distribution in endothelialized geometry increases with increased flow, whereas lower WSS is observed in the acellular geometry.

These results demonstrate a marked mechanical change to vessel distensibility when endothelial cells are present. To determine the origin of this change, we performed staining for the basement membrane protein laminin after 7 days of perfused culture and found a robust basement membrane–like layer containing laminin, which lined the printed vessel (fig. S5). Despite being unlikely that laminin is the sole driver of this compliance shift, this demonstrates that the endothelium actively remodels its surrounding ECM and suggests that it is likely that other structural proteins, such as collagens, are present within this secreted membrane layer.

Given the marked changes in vascular compliance (Fig. 2, C and D), the WSS was calculated for the top, bottom, left, and right walls of the vessel (Fig. 2, E and F) to determine how the expansion of the vessel walls affects the fluid forces within. Mean WSS was observed to decrease with increasing flow rate for the bare channel, while mean WSS increased by fivefold for the endothelialized channel (Fig. 2E and fig. S3]. The higher compliance of the acellular vessel logically results in a drop in WSS as it expands, despite the increase in flow rate, while the endothelialized channel’s minor change in volume causes WSS to rise markedly under high flow rates.

The flow characterization of a vessel having an endothelium as compared to bare gel channels

In addition to influencing vessel wall compliance, the presence of endothelial cells may have additional effects on the characteristics of fluid flow through the vessel. For example, some groups have hypothesized that the surface morphology or glycocalyx of the endothelium would invalidate the no-slip condition commonly assumed in computational fluid dynamics (25, 26). Thus, to assess whether fluid flow behavior differed between acellular and endothelialized branching vessels, we performed particle image velocimetry (PIV) analysis and compared it to computational simulation results, followed by assessment of flow pattern error (Fig. 3). Simulations were performed using HARVEY, a massively parallel computational fluid dynamics solver (27, 28), which used 3D rendered versions of the in vitro device, to compare computational calculations to experimental velocity measurements obtained by PIV. Good qualitative agreement was observed between predicted and experimentally determined flow patterns for both endothelialized and acellular vessels (Fig. 3, A to D), with only minor variations in flow dynamics of these devices when compared to simulation data.

Fig. 3. PIV compared to modeled flows in compliant vascular beds.

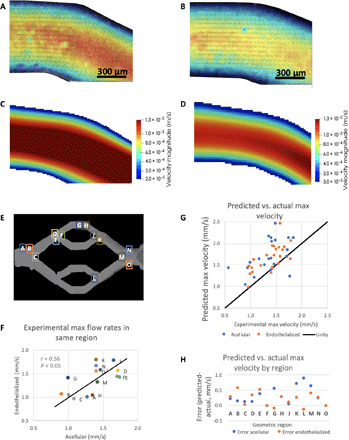
(A and B) Example images collected from experimental PIV measurements in acellular (A) and endothelialized (B) printed vascular beds. (C and D) HARVEY simulations of velocity magnitude field (meters per second) in corresponding regions for acellular (C) and endothelialized (D) vessel. (E) Comparing maximum flow rates in PIV (experimental) and HARVEY (predicted) demonstrates an average of 30% error for both endothelialized and acellular geometries. (F) Bland-Altman plot for error across flow rates shows no bias for error with mean flow rate, suggesting that error is relatively consistent. (G) Geometric regions where PIV and simulations were compared for both acellular and endothelialized vessels. (H) Comparison of error for acellular and endothelialized vessels by geometric location appears to show more error in outflow regions compared to inflow regions. Colored bars indicate mean error for this subset of regions.

When comparing PIV of 15 geometrical regions (Fig. 3E), it was found that the maximum flow rate in these two devices had a correlation coefficient of 0.56 (P < 0.05; Fig. 3F), demonstrating good accordance in flow between acellular and endothelialized devices. Error in the maximum velocity measurements analyzed between experimental PIV measurements and the simulation results revealed that predicted maximum velocities were higher than experimentally measured maximum flow rates for both geometries (38 ± 36% for acellular and 27 ± 24% for endothelialized; Fig. 3G). We noted that error in the plane used for flow characterization could explain some of this error (fig. S6). It should also be noted that an additional source of error may arise from the use of an epifluorescence microscope–based PIV system, which may capture the movement of particles above and below the intended plane of focus and, therefore, closer to the vessel boundary, due to the depth of field of the objective. Comparing flow rate error by region (Fig. 3H), we noted that outflow regions appeared to be more error prone (K, L, M, and N). To rule out flow rate bias, we performed Bland-Altman plotting (fig. S6).

This analysis demonstrates that, while biologically important, our measurements failed to detect an effect of the endothelial cell layer specifically upon the flow dynamics acting upon particles entrained in the engineered vessels within the device. Furthermore, predictions of flow patterns were equally accurate for endothelialized and nonendothelialized vessels. Therefore, the presence of an endothelial layer could be ignored in the subsequent computational modeling efforts described here, which focused upon particle or cell movement through vasculature using this system under the described conditions.

Flow characterization of CTCs as compared to idealized spheres

When modeling CTCs or other objects transported by fluid flow, many groups treat the entrained particles as rigid spheres for computational tractability (29–31). However, unlike rigid spheres, cells are capable of deformation under external forces, which may lead to complications when using simplifying assumptions to model their behavior when entrained in a flowing liquid. To test whether there were measurable differences between the flow behaviors of CTCs in solution relative to idealized rigid, spherical particles, we repeatedly performed PIV on the same channel so that any differences in flow behavior could be attributed to the particles and not the flow patterns. Visually, flow partitioning of CTCs into the center of the fluidic channel was observed (Fig. 4A), whereas the distribution of rigid microbeads was relatively homogeneous (Fig. 4B). To better understand these differences, we identified and plotted cell or microbead positions as a function of lateral distribution within the channel (Fig. 4C), and then we analyzed the spatial distribution of each by comparing variance and kurtosis of particle positions (Fig. 4, D and E). It should be noted that this analytic technique quantifies all cells or beads in each PIV frame leading to the oversampling of slow moving cells, specifically those at the channel walls, as they are present within multiple frames and resulting in minor peaks due to artificially higher counts at those positions. However, despite this artifact, this analysis demonstrates that 10-μm beads had a significantly lower kurtosis than cells, indicating that the beads had a more homogeneous spatial distribution across the channel width, while cells portioned toward the vessel center.

Fig. 4. Flow partitioning of metastatic mammary gland carcinoma cells compared to rigid particles.

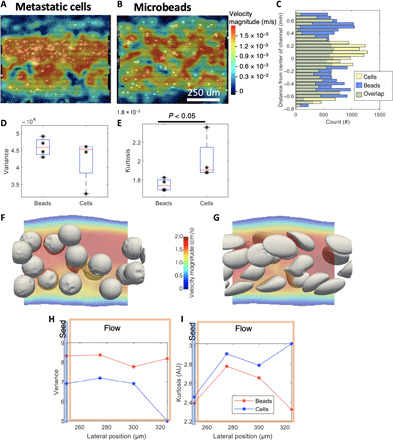
(A) PIV of carcinoma cells flowing through an acellular channel demonstrating partitioning of cells toward the center of the vessel. (B) Rigid microbeads of similar size (D = 10 μm) exhibiting relatively homogeneous distribution across the channel (note that the same channel and position were used for these two experiments). (C) Histogram of lateral position for carcinoma cells (yellow) and microbeads (blue) across 100 frames shows that cells tend to cluster in the center of the vessel, whereas beads are more homogeneously spread. (D) The variance of lateral position is not statistically different between beads and cells (Kruskal-Wallis test, P = 0.5, with n = 4 replicates; 110 frames analyzed per replicate). (E) The kurtosis, or “tailedness” of the bead positions, indicates that cells tend to be more centrally located compared to beads (Kruskal-Wallis test, P < 0.05, with n = 4 replicates; 110 frames analyzed per replicate). (F) HARVEY example simulation snapshots of relatively stiff beads with a shear elastic modulus, G_s, of 10⁻³ N/m, as compared to (G) example snapshots of deformable cells G_s = 10⁻⁵ N/m. (H) Variance from HARVEY data in distance from centroid to center of channel tracking from the particle’s initial seed position (blue line) to its location further down the flow stream (orange rectangle). (I) Kurtosis along the simulated channel for both simulated sets of particles from HARVEY data.

To simulate this flow partitioning phenomenon in rigid versus deformable cells, we scaled down the original 3D reconstructed model of the channel by a factor of 20 to decrease the computational time required to arrive at a result. To ensure that the flow dynamics were similar, we also reduced the flow rate by a factor of 20, resulting in the same Reynolds number as in the original channel. Computational modeling revealed that deformable particles tended to partition to the center of the vessel, whereas rigid particles appeared to stay more well dispersed (Fig. 4, F and G, and movies 1 and 2). We identified the centroid for each cell, analyzed the position of centroids along the channel (Fig. 4, H and I), and observed lower variance in distance from centroid to center of channel and higher kurtosis along the channel under the deformable cell condition. This observation is in accordance with previous works on the effect of cell deformability on the cell-free layer (32). The simulation result was readily reflected in the experimental results, validating the simulation prediction and highlighting the contribution of the soft, deformable nature of CTCs when exposed to hydrodynamic forces.

The effects of in vitro vessel geometry on CTC attachment

Having investigated the flow dynamics within the printed in vitro vascular channels, we then evaluated how the geometry of the artificial vasculature affected the probability of CTC attachment to either acellular or endothelialized vessel walls. Fluorescently labeled metastatic mammary gland carcinoma cells were filtered through a 40-μm nylon cell strainer and then perfused through bioprinted devices at an average flow rate of 1690 μl/min in culture medium for 1 hour. Devices were then fixed, stained, and imaged to determine where CTCs attached in the vessel geometry.

Visually, CTCs exhibited a preference for the vessel branching points relative to the straight portions of the vessels (Fig. 5, A and B), and CTC attachment was much greater on the arterial, or “in flow,” side of the device (Fig. 5, A and B, insets i and iii) as compared to the venous, or “out flow,” of the device. Further, very few CTCs were observed to attach within the exiting converging branch points or straight vessels after passing the middle point of the geometry (Fig. 5, A and B, insets ii and iv). Notably, more CTCs attached to the acellular channel versus the endothelialized channel, suggesting that the presence of the endothelium presents an antifouling, poor adhesion surface to CTCs, relative to the proteinaceous surface presented by the acellular channel walls. In addition, the high compliance of the acellular channel, as noted in earlier experiments, may have led to an increase in acellular channel diameter, which would correspondingly have resulted in lower WSSs occurring with these channels, relative to the lower compliance endothelial devices.

Fig. 5. Attachment sites of CTCs shows differences between acellular and endothelialized channels with differences at fork points.

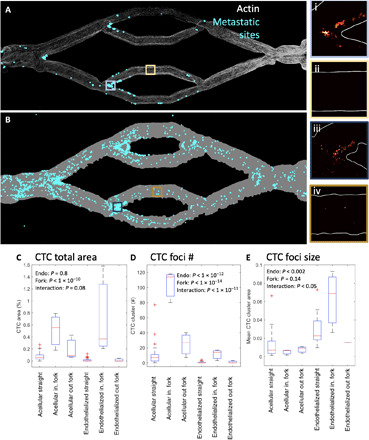
(A) Full endothelialized vascular bed with identified CTC sites (cyan). In inset i, high attachment is seen in an incoming (in.) fork, whereas in inset ii, a straight channel shows no attachment. (B) Full acellular vascular bed exhibits greater CTC burden compared to endothelialized (4% of vessel area versus 2%). In inset iii, an incoming fork shows high CTC burden, but cells tend to be isolated, and no large clusters are observed; in inset iv, a straight region shows some CTC attachment. (C) CTC area is higher in incoming fork regions, with a significant interaction between endothelialization and geometric feature. out, outcoming. (D) Many more CTC foci are observed in the acellular geometry and in incoming forks with a significant interaction. (E) CTC foci size is highest in endothelialized geometries, with an interaction demonstrating larger average CTC cluster size in endothelialized incoming forks.

To analyze these attachment differences, we filtered and thresholded maximum intensity projection images of CTCs and endothelial cells or suspended microbeads within the channels. Results revealed that CTCs covered 4.03% of the acellular vessel geometry area and 2.65% of the endothelialized vessel geometry. Morphological operations were used to define foci of CTC cells or contiguous CTC clusters; this analysis demonstrated difference in the spatial distribution of CTCs between acellular and endothelialized vessels: 691 CTC foci were identified in the acellular channel, of which 39 were multicellular, versus 54 total foci in the endothelialized channel, of which 22 were multicellular. Correspondingly, the CTC foci in the acellular channel had a mean projected area of 81 μm². In contrast, in the endothelialized channel, the mean CTC area was 660 μm². Similarly, multicellular CTC foci represented 5.6% (39 of 691) of CTC foci in the acellular channel versus 41% (22 of 54) of CTC foci in the endothelialized channels, with 14% of identified CTC sites being larger than 1000 μm². Despite filtering CTCs to ensure single-cell introduction into the vascular channels, most CTC attachment sites in the endothelialized channel anchored a large number of cells; this suggests that this clustering is the result of a biological interaction with the endothelium, rather than due to the hydrodynamics of the channels.

To compare CTC attachment to geometric features, we used points where the vessel geometry curvature changed to generate a Delaunay tessellation of the channel areas. Once complete, it was then possible to directly compare the CTC coverage area (Fig. 5C and fig. S8] and focus numbers (Fig. 5, D and E, and fig. S8] to the total area of each vessel region. Statistical analysis revealed that incoming fork points (regions 3, 8, and 9) contained a higher CTC area (P < 1 × 10⁻¹²) and more CTC foci (P < 1 × 10⁻⁷). The acellular geometry contained statistically more CTC foci (P < 1 × 10⁻⁵), but no difference in CTC area was detected (P = 0.15). A statistically significant interaction term between fork regions and endothelialization (P < 1 × 10⁻⁸) indicated that endothelialized vessels showed a higher preference for CTC foci at the incoming forks versus acellular vessels. This suggests that CTCs are less likely to attach to endothelialized vessels overall, but when cells do attach, large clusters aress particularly likely to form at the branch points.

If fluid forces alone dictate where CTCs will anchor to the vessel wall, then areas with lower shear stress should see the greatest probability of attachment as this frictional force would directly interfere with cell immobilization during flow. It was observed that the incoming forks were most vulnerable to CTC attachment, despite similar WSS values in both incoming and outgoing forks (Fig. 6). This suggests that it is potentially a feature of the endothelial cells present in these portions of the device, possibly in response to the greater WSS in these regions, which enhance the anchorage and subsequent attachment of the cancer cells, despite being subjected to greater median shear stresses relative to the larger, straight channels. When comparing the attachment preference in the straight portions of the differently sized vessels, CTCs preferred to attach within channels of the smallest diameter (D = 700 μm), despite the slightly higher median vessel WSSs present in this portion of the device (fig. S8). The finding that CTCs attach in greater numbers in areas of the endothelialized channels where wall stress is the greatest would also fail to fully explain the twofold greater attachment of CTCs within the acellular channels, if WSS is the only driver of CTC attachment. It was also noted from the simulation data that the Reynold’s number of the topmost branch of the device was found to be approximately 100 within the endothelialized vessels under the same conditions used for the CTC perfusion experiments. This area was suspected to be among the most susceptible to turbulent flow due to being highly constricted, relative to the larger vessels, but was found to be far below the common threshold of approximately 2400 required for the transition from laminar to turbulent flow in straight tubes. These results suggest that the flow within these devices was highly laminar for all experiments described and that turbulence did not play a significant role in either CTC attachment or endothelial phenotype.

Fig. 6. WSS and laminar flow during CTC perfusion.

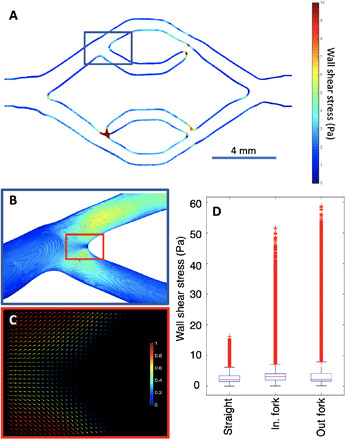
(A) WSS profile from the vessel sidewalls at center Z slice, gathered from simulation data generated with parameters matching those used for CTC perfusion experiments. Note that appearance of seemingly disconnected channel branches occurs because of Z height variation within the print, not true channel breaks. (B) Zoom in of the topmost vessel in-flow branching point, having the same heatmap as in (A), presenting the WSS present at both the sidewalls and vessel floor. (C) 2D quiver plot of topmost branching point velocity field simulates from the CTC perfusion experiment using scaled magnitudes, with 1 being the maximum flow velocity, demonstrating laminar, nonturbulent flow at the branching point at flow (1690 μl/min). (D) Whisker plot showing the WSS comparison between the straight vessels, in-flow branches, and out-flow branches, within the endothelialized device showing similar median values, with high-peak outliers present in the branching regions gathered from 13 × 10⁶ total data points originating from HARVEY simulation.

DISCUSSION

One of the simplest fundamental questions in computational modeling is how complex a model must be to replicate in vivo biological processes in silico. Answering this question, however, remains the most difficult challenge in the field. As it stands, there are few test beds that retain the complexity inherent in a convoluted biological process similar to metastatic endovascular colonization while permitting the detailed biophysical and quantitative analyses necessary to characterize model performance. In this work, we answer this challenge by bioprinting living models of the human vasculature and directly comparing the behavior of these controlled, interrogatable, living analogs to computational fluid dynamics simulations of increasing complexity. As a result, our in silico models are as complex as they need to be and permit accurate, computationally efficient study. This intersectional study using tumor biology, bioengineering, and computation represents a new approach to informing computational models of biological processes and gives new access to the fundamental biology and biophysics of endothelial colonization of CTCs during metastasis. Using this approach, effects resulting from physical phenomena such as vascular shear stress, flow turbulence, and CTC impingement upon the endothelium can begin to be decoupled; however, this will require further experimentation to reveal their impacts beyond this demonstration. This work provides a unique and important experimental pipeline for examining these factors in a more straightforward manner than is currently possible in vivo while maintaining a higher degree of physiological relevance than conventional in vitro microfluidic channels by combining the ability to generate predesigned vasculature with fully endothelialized channels.

We used these informed computational models and bioprinted analogs to decouple biological and physical aspects of CTC attachment to the vascular endothelium, which represents the first step in metastatic colonization of distant organs. Researchers have suggested that metastasis occurs because of trophic effects between the primary tumor cells and the specific organ microenvironment that facilitate their growth, also known as the “soil and seed” theory (33). In addition, circulation-mediated metastasis caused by changes in flow within a capillary has been empirically implicated as an explanation for organ-specific metastatic spread (34). The extravasation process into the brain particularly takes longer than into any other organ, taking up to 14 days in some types of cancer, during which time the CTCs are surviving in the vasculature (35). While the microenvironment may need to be attractive to home the cells, given the lengthy amount of time the cells spend in the circulation before extravasation, the anatomical or mechanical features of the brain vasculature must also play a key role in metastatic dissemination.

A key aspect of blood flow through in vivo vasculature is the compliance of the vessel itself. The compliance of vessels in the body permit the vasculature to adapt dynamically to a range of physiological pressures to regulate fluid conductance and deliver blood across the body without interruption or rupture. CTCs are also subjected to these changes in pressure and flow rate, which affects not only their flow characteristics but also the physical geometry of the vessels in which they are circulating. One benefit in generating perfusable channels within an artificial ECM is the ability to recapitulate much higher compliances than possible within conventional, endothelialized PDMS channel–based microfluidic devices or within common medical or fluidic tubing, all of which have very low relative compliances. To accurately model the pathing of CTCs in silico, understanding how the geometry of the harboring vessels in vivo will change in response to pressure changes is critical. In addition, building better computational models for predicting CTC attachment and extravasation will require incorporation of this important aspect into their simulations, depending on the choice of simulated flow rates, to ensure their accuracy. Validation of these predictive systems requires both in vivo measurements and advanced in vitro models having variable compliance to begin unraveling the nuanced effects of blood vessel distention on hydrodynamics and its biological consequences for CTC endothelial attachment and subsequent metastatic events. Our acellular printed channels show substantial compliance, expanding to over twice their volume at the highest tested flow rate, unlike conventional microfluidic models that use stiff substrates for channel generation. The distension of these acellular vessels also demonstrates that these vessel beds show considerable flow resistance at flow rates greater than 500 μl/min. The starkly lower compliance of endothelialized vessels better corresponds to microfluidic analogs; however, unlike these models, we observe exquisite reproduction of endothelial cell health as assessed by basement membrane secretion and flow alignment.

Note that the accuracy of the computational results is significantly affected by the vessels’ reconstruction process. The successful reconstruction of the vessels depends on the clarity of the images obtained by flow imaging or PIV, further highlighting the importance of characterizing device compliance under physiological flow rates. In addition, computational modeling accuracy is contingent on the subjective decision of the exact vessel wall’s location. Because of the relation of the spatial and temporal resolutions inherent in the lattice Boltzmann method (LBM), fine spatial resolutions often translate to millions of LBM iterations. However, the scalability of HARVEY allows for the simulation of fluid flows in realistic vessels with a micron spatial resolution.

Although cultured under low flow conditions, the results in terms of cytoskeletal alignment are in good agreement with previous work that cultured these brain endothelial cells at more physiological flow conditions (23). Cerebral vasculature WSS can range from 0 to 30 dynes/cm² and 5 to 23 dynes/cm² in the small vessels (36–38). Throughout the experimentation, the in vitro vessel lining proved to be sturdy enough to a withstand flow of 1 ml/min [resulting in physiological average WSS (36–38) of 10 to 45 dynes/cm², or 1 to 4.5 Pa] or greater, without disruption or delamination from the surrounding hydrogel material, demonstrating the robust health and function of this endothelium and its versatility to accommodate a wide range of flow rates. We suspect that cell-secreted ECM and cell-cell junctions both provided reinforcement and resistance to distension under flow. This endothelial wall reinforcement, whatever its origin, massively simplified our computational modeling, as the distensibility of these walls can be largely ignored for flow rates up to 1 ml/min, although higher flow rates need further experimental validation. While this result appears to be true for these printed vessels having diameters of 0.5 mm at the flow rates delineated in Fig. 2, it should be noted that compliance may play a greater role in smaller vessels or at higher flow rates, necessitating reexamination of vessel compliance within the device when experimental parameters are shifted from these values.

To further determine which specific features of in vivo vasculature were implicitly required to establish meaningful and accurate computational simulation of CTC flow behaviors, we first tested the effects of an endothelial vessel lining on the resulting hydrodynamics within the in vitro lumen. When experimental flow velocity profiles in both endothelialized and acellular vessels were compared to the in silico predictions, differences in maximum velocities did not differ with endothelium and did not appear to correlate to any specific geometric features or conditions. Thus, the surface of the endothelium could therefore be disregarded in our subsequent modeling efforts. The resulting lack of endothelial influence over the physical vascular hydrodynamics simplifies ongoing computational efforts across the field and suggests that current 3D flow models that neglect this feature are likely accurate at these scales in this regard without requiring further modification.

The next in vivo effect studied was the treatment method of cell-scale particles entrained within the perfused vasculature. To this end, both rigid, spherical particles and CTCs were perfused through the same printed acellular channel and had their positions within the vessel recorded while under flow. After analysis, it was noted that while rigid spherical particles were dispersed uniformly across the channel width during perfusion, the CTCs were undergoing flow partitioning behavior and preferentially focused toward the center streamlines within the vessel. Computational modeling using HARVEY was performed to determine which feature of the CTCs was responsible for this flow partitioning phenomena. Simulations treating the entrained particles as either rigid or deformable spheres resulted in simulated particle distributions that matched closely with the experimental results of 10-μm beads and CTCs, respectively. This demonstrates that, to accurately model the pathing of CTCs within the vasculature, the cells themselves must be treated as deformable spheres as this deformability under flow results in unique flow-focusing patterns for CTCs that are not present when they are considered as simple rigid spheres.

One of the primary purposes of developing computational 3D vascular flow models is to investigate the effects of the vascular geometry upon the resulting flow dynamics within the vessel with good physiological fidelity. However, because of limitations of the sacrificial ink printing method, the vessels in this study range from 0.5 to 1.5 mm in diameter, which results in vessels that resemble small arteries in size. While there is substantial evidence that CTC endovascular attachment occurs frequently in capillaries and other microvessels during mouse tail-vein injections due to physical entrapment and embolization (39), CTCs circulate through vessels of all sizes, which leaves open the possibility of CTC attachment events occurring in larger vessels; as does the demonstrations that CTCs, even as large clusters, can pass through small capillaries (40–43). In addition, controlling the discrete geometries of endothelial capillary networks generated in vitro is currently not possible, making reproducible studies of microvessel dynamics with respect to CTC behavior challenging (18). Here, we have sacrificed the most physiologically relevant vessel size for CTC colonization for the advantage of being able to generate a wide range of larger vessels in a reproducible manner to suit the systematic study of geometric effects.

If the geometry of the vessel, and its direct effect on flow dynamics, plays a role in governing CTC attachment in larger vessels, then specific regions of the vessel geometry should exhibit variable attachment numbers. In addition, if CTC attachment is partially governed by interaction with endothelial cells, as opposed to strictly hydrodynamic forces, then differential CTC attachment trends should be observed when endothelial cells are absent. To test these phenomena, we perfused CTCs through both acellular and endothelialized devices having similar vascular geometries. While we did not previously detect significant differences between flow patterns in endothelialized and acellular vessel walls experimentally or computationally, the distribution of attached CTCs differed substantially in spatial distribution, likelihood of clustering, and total CTC burden between acellular and endothelialized vessels. In both devices, preferential attachment was observed in the bifurcated branch points, regardless of the presence of the endothelium; however, substantially greater total CTC attachment was observed within the acellular vessels, suggesting that the endothelium itself presents an antifouling surface within the remaining vasculature features, which prevents a majority of CTC attachment when compared to a bare, ECM wall. This demonstrates that CTC vascular attachment behavior is not solely governed by either geometric flow dynamics or endothelial cell interactions, but rather, it is a combination of these two features, which are responsible for in vivo vascular colonization events.

While there is substantial evidence that implicate endothelial interactions as drivers of CTC vascular colonization, comparatively, little attention has been given to the mechanical influences of flow dynamics and vessel biophysics upon metastatic events (44). For example, it remains unclear whether metastatic tumors are seeded by single cells or clusters. We found that filtered single cells were particularly likely to accumulate at branch points in both acellular and endothelialized vessels, with greater preferential accumulation and propensity for CTC clustering exhibited in the endothelialized vessels. It is also worth noting that the flow partitioning of CTCs previously observed in straight channels likely contributes to the probability of CTC impingement with the apex of the branching points, with a greater number of cells colliding with this portion of the vessel geometries, relative to other vessel regions. In addition, lowering the CTC concentration-to-volume ratio, the presence of CTC clusters, and the inclusion of red blood cells within the perfusion medium at physiological cell densities will likely affect CTC partitioning, impingement, and attachment to the endothelium, representing an important consideration for future study.

The significant difference in CTC attachment preference and cluster formation within the endothelialized branches when compared to the acellular branch points observed using this simplified perfusion medium is an interesting fact that suggests a strong biological basis for this behavior that cannot be explained simply by the action of hydrodynamic forces. Our initial hypothesis that areas of low WSS would lead to greater CTC attachment, while seemingly reinforced by the finding of greater CTC attachment numbers in the more compliant acellular channels, became confounded upon examination of the geometric attachment preferences observed in the endothelialized channels. These observations highlight the importance of not only fluid dynamics but also the contribution of the CTC-endothelial interaction, and further interrogation of this phenomena merits future work focused on understanding the interaction between the CTCs themselves and the possibly flow-activated endothelium.

Metastatic colonization of distant organs by CTCs is a complex process, which involves the interaction of biological and physical factors. An extensive, active body of research is focused on the biological and biochemical factors regulating metastasis (14, 45). Biological processes, such as priming, extravasation (46–48), and tumor dormancy and regrowth (49, 50), have been studied extensively in animal models and cell culture systems. Given the large body of work related to biological factors, we chose to focus on biophysical factors as these aspects are currently impossible to examine thoroughly within in vivo models, although our platform is also amenable to studying biological processes. In this work, we construct living vascularized channels that are responsive to mechanical cues, such as exhibiting flow-induced alignment, and are capable of secreting basement membrane proteins. As we work with engineered vascular systems, the size of vessels, endothelial cell state, and interstitial matrix can be tuned to achieve a truer in vivo scenario. To increase the biofidelity of our model for more biologically focused interrogations would require further characterization of the brain vasculature (e.g., tight junction proteins, permeability values, etc.) and more brain-specific ECM.

We chose the cell lines used in this work to ensure a high probability of metastatic attachment and, thus, selected a rapidly metastatic mammary gland carcinoma cell line, which has been extensively used in the literature (51, 52). After 1 hour of CTC circulation, we found a large burden of attached CTCs. That being said, we chose to use human endothelial cells and mouse CTCs, and we acknowledge that the species mismatch may have had unknown effects on attachment patterns. While further characterization is needed to enable more in-depth biological study, such as the expression of endothelial surface receptors and their critical role in CTC vascular attachment, in this work, we combine advanced simulations in conjunction with 3D printed hydrogel-based vascular flow devices. This experiment was specifically performed to interrogate the biophysical aspects of vasculature not currently accessible via other methods. Here, we demonstrate a powerful method of validating the outcomes of computational flow simulations using highly versatile in vitro models. As this approach is iterated upon and enhanced, insights into metastatic events and the opportunity to aid in the development of next-generation predictive computational models for accurately simulating metastatic behavior will become possible.

MATERIALS AND METHODS

Cell culture

Immortalized (hCMECs/D3, Cedarlane) were cultured in vented T-75 culture flasks (Corning) coated with rat tail collagen type 1 (150 μg/ml; Corning) containing EndoGRO-MV (EMD Millipore) endothelial cell growth medium supplemented with basic fibroblast growth factor (1 ng/ml; Sigma-Aldrich) and penicillin/streptomycin (100 U/ml; Gibco). Mouse mammary gland carcinoma cells [4 T1, American Type Culture Collection (ATCC)] were maintained in RPMI 1640 supplemented with 10% fetal bovine serum (ATCC) and penicillin/streptomycin (100 U/ml). For both cell types, culturing and subculturing methods followed the vendors’ protocol. All cells were incubated in a humidified incubator maintained at 37°C with 5% CO₂. For all experiments, endothelial cells were used between passages 30 and 31 and, for 4 T1, passages 19 to 21.

For experiments introducing CTCs into the bioreactors, 4 T1 cells were labeled with Vybrant Dil lipophilic dye (Invitrogen). Briefly, trypsinized cells were resuspended in RPMI 1640 at a density of approximately 1 × 10⁶ cells/ml and incubated with Dil lipophilic dye at a concentration of 0.01 mM for 30 min. To facilitate the homogenous staining of cells and maximizing viability, cells were gently agitated every 5 min and kept at 37°C. At the end of the 30-min incubation, cells were spun down to remove exogenous lipophilic dye and then resuspended in EndoGRO-MV medium. The cell suspension was gently strained to remove cell aggregates with a 40-μm nylon cell strainer (VWR) before further diluting to a final cell density of 100,000 cells/ml.

Bioreactor side wall fabrication

Bioreactor walls were fabricated using custom injection stainless steel molds designed to permit rapid casting of the PDMS, SYLGARD 184 (Dow Corning), walls prepared with a 10:1 elastomer-to-catalyst ratio. After casting and curing in an oven at 65°C for at least 8 hours, the resulting PDMS walls were bonded to glass slides using a printed layer of SE1700 (Dow Corning). The PDMS walls were aligned to the printed silicone and pressed firmly into contact with the slide. Assembled devices were cured at 65°C for at least 2 hours to irreversibly bond the walls to the glass surface.

Bioreactor fabrication

Stock solutions used for preparation of bioreactor gels consisted of gelatin (150 mg/ml; type A, 300 Bloom, Sigma-Aldrich), fibrinogen (50 mg/ml; type I-S, Sigma-Aldrich), transglutaminase (TG; 120 mg/ml; type TI, Modern Pantry), 250 mM CaCl₂ (Sigma-Aldrich), and thrombin (200 U/ml; Sigma-Aldrich). Phosphate-buffered saline (PBS) without ions (Gibco) was used as the solvent for all solutions unless otherwise noted. Gelatin solution was prepared by heating the mixture at 70°C for 16 hours with gentle stirring until completely dissolved. The resulting gelatin solution was then brought to pH 7.5, filter-sterilized, aliquoted, and stored at 4°C.

Before printing, a base layer gel was cast within the bioreactor sidewalls to form a thin, flat layer to support printing of the sacrificial ink. Sacrificial ink was prepared by creating a 35% (w/w) solution of Pluronic F-127 (Sigma-Aldrich) by weighing 35 g of dry pluronic powder before adding 65 g of sterile filtered deionized water (diH₂O). Solution was mixed using an ARV-310 planetary mixer (THINKY USA) and stored at 4°C until use to maintain its liquid phase. Before printing, a sterile thrombin solution at 4000 U/ml in diH₂O was incorporated into the sacrificial ink at a final concentration of 100 U/ml. Base layer protein solution [final composition of gelatin (75 mg/ml), fibrinogen (10 mg/ml), TG (2 mg/ml), and 2.5 mM CaCl₂) was incubated at 37°C for 20 min before mixing with thrombin [final concentration of thrombin (1 U/ml)]. The gel mixture was then quickly casted and allowed to cross-link and slightly dry for 25 min before printing. After drying, the vascular channel geometry was patterned using sacrificial ink. Perfusion pins (Scanivalve) were pushed into contact with the sacrificial ink to permit the channel to be later connected to fluidic tubing. A second gelatin-fibrin hydrogel was then prepared identically to the first and cast over the sacrificial ink. Last, a glass slide was then placed on top of the printed reactor sidewalls, and the entire device was then clamped within a custom-designed reactor housing. The reactor housing had viewing windows on the top and bottom, which permitted imaging through the device at any time without compromising the seal between the sidewalls and slides. The device was then incubated at 37°C for 1 hour to enable full cross-linking of the fibrin and then transferred to 4°C for 20 min to assist in liquifying the sacrificial ink within the gel. After the incubation periods, silicone tubing was connected to the perfusion pins, and the sacrificial ink was carefully evacuated using gentle suction. Chilled EndoGRO-MV medium was then slowly pushed through the device to remove residual sacrificial ink from the channel.

Perfusion fluidics setup

The device was connected to flow through fluidic tubing (IDEX) at the pins. Fluidic lines were connected at one end to an MFS3 flow rate sensor (Elveflow) leading back to a GL45 glass bottle reservoir (Corning) with a two-port, 1/4-28 threaded cap (Diba Omnifit), which is connected to an OB1 microfluidic flow controller (Elveflow) to enable pressure control over the medium within the reservoir (fig. S1). On the other end, tubing was connected to an exit reservoir. The air tubing connected to the exit reservoir had one polyethersulfone syringe filter in line to release the pressure within the reservoir as medium is passed through the device. Initially, 85 ml of medium equilibrated with 5% CO₂ was introduced into the entry reservoir and 15 ml into the exit reservoir. Bioreactors were maintained under flow with the same 100 ml of medium for the duration of their culture. Medium was perfused through cleared channels overnight at 10 μl/min.

Bioreactor culture

For endothelialized vascular channels, assembled reactors were taken offline after overnight flow perfusion and seeded with hCMECs via injection at a density of 1 × 10⁶ cells/ml. Cells were encouraged to attach to all faces of the channel walls by slow rotation of the device: Seeded devices were incubated for 15 min at 37°C face up, and at which point, the device was inverted and allowed to incubate for another 15 min for six total inversions. The device was then incubated for an additional 4 hours before connection to flow for further culture. Both cellular and acellular bioreactors were cultured for 7 days under flow conditions, where medium was exchanged from the exit reservoir back to the entry reservoir under sterile conditions on the fourth day.

Measuring compliance

For both acellular and cellular vascular channels, compliance measurements were measured in a single-channel device, one with endothelial cells and one with bare gel walls, after 7 days of flow. A solution of fluorescent (D = 1 μm) FluoSpheres (Thermo Fisher Scientific), introduced into the channels via a KDS210 syringe pump (KD Scientific), was used to visualize the internal volume of the vessels. Confocal microscopy using an LSM700 microscope (Carl Zeiss) was performed at various steady flow rates, ranging from 0 to 1 ml/min, directly at the longitudinal midpoint of each channel. After imaging, 3D vessel reconstructions were generated and analyzed to determine cross-sectional area and perimeter at each position (n = 400) along the channel length to measure the change in vessel volume in response to specific flow rates to determine the compliance of the channels within HARVEY.

CTC attachment evaluation

Cell solution, as prepared in the “Cell culture” section, was loaded into the fluidic line and connected to the device. The device was then placed in an incubator at 37°C, and flow was driven by a peristaltic pump (MRC Scientific Instruments) set to achieve a resulting average flow rate of 1690 μl/min, as measured by an MFS5 flow sensor (Elveflow), and allowed to run for 1 hour. The WSS generated within the flowing device was calculated using the equation

$$\mathrm{\tau }=\mathrm{\mu }\frac{\mathrm{\partial }u}{\mathrm{\partial }r}$$

This flow rate resulted in a shear stress of 0.63, 1.30, and 1.89 dyne/cm² at the vessel walls for large (D = 1.6 mm), medium (D = 1 mm), and small (D = 0.7 mm) channels, respectively, assuming flow divided equally at each branch point. After running for 1 hour, the device was disconnected, rinsed with 3 ml of warm EndoGRO-MV medium at approximately 3 ml/min to remove any unattached cells, fixed in 4% paraformaldehyde (Alfa Aesar) for 30 min, and rinsed thrice in PBS. The device was imaged using confocal microscopy to map all CTC attachments within the device. CTC location analysis was performed using MATLAB as detailed below in the “Image processing” section.

PIV measurements and geometric profiling

PIV was performed on day in vitro 7 in all experiments involving endothelialized channels. PIV was conducted using an IX83 (Olympus) inverted microscope equipped with Flowmaster 2-C components (LaVision), including an Imager M-lite 2-M complementary metal oxide semiconductor (CMOS) camera, a 1-W, 532-nm gateable diode-pumped solid-state (DPSS) laser, and a programmable timing unit (PTU)–X HS. For PIV measurements using beads as tracking particles, solutions were prepared containing either 3.57% (v/v) 1-μm 580/605 red fluorescent FluoSpheres or stock concentration of 10-μm 580/605 red fluorescent FluoSpheres (Thermo Fisher Scientific) suspended in Hank’s balanced salt solution (HBSS) with positive ions (Gibco). Particle solution (either FluoSpheres or cell suspension) was perfused through the artificial vasculature using a KDS210 syringe pump set to a volumetric flowrate of 10 μl/min for 10-μm FluoSpheres and the cell suspension in straight channels or 40 μl/min for 1-μm FluoSpheres in branching geometries. PIV imaging was performed at predetermined positions within the artificial vasculature, and the Z plane of imaging was selected by determining the focal point at the widest diameter of the vessel. PIV images were captured and processed using DaVis 10 software (LaVision) and exported as .dat files for comparison and incorporation into the fluid dynamics computational model. Cell- and bead-observed sizes were measured manually in Fiji.

After PIV imaging, printed vessel geometries were measured and reconstructed using tile-stitched Z stack images gathered via confocal microscopy and Zen 2012 SP1 software (Carl Zeiss). Mesh files from confocal images of 3D bioprinted vessels were created by segmenting the data files with commercial image processing software Materialise Mimics. For each axial image, a mask was created encompassing the region between the vessel walls. Once the above process was completed for all the provided axial images, a 3D reconstructed vessel model was exported as a mesh file in stereolithography (STL) file format for further mesh processing. The open source software MeshLab and Blender were used for mesh editing, such as cleaning, smoothing, and extruding, to convert the mesh file format from STL to object file format (OFF). The edited OFF mesh file was then read by HARVEY for performing simulations.

Computational flow modeling

HARVEY, our in-house massively parallelized computational fluid dynamics solver, based on the LBM and finite element method to resolve the flow field and cell dynamics, respectively, was used for all computational simulations. The fluid-structure interaction is resolved using the immersed boundary method.

In the LBM framework, the fluid, considered here to be incompressible and Newtonian, is assumed to be particle patches. Distribution functions $f_i(\overrightarrow{x},t)$ representing the density of particles at position $\overrightarrow{x}$ and time t with velocity $\overrightarrow{c_{\mathrm{i}}}$ along the ith lattice direction are tracked. The evolution of the distribution functions is governed by the lattice Boltzmann equation (LBE), where the Bhatnagar-Gross-Krook collision operator (53) and the forcing scheme $\overrightarrow{F_{\mathrm{i}}}$ of Guo et al. (54) are used

$$f_i(\overrightarrow{x}+\overrightarrow{c_i}\mathrm{\Delta }t,t+\mathrm{\Delta }t)=f_i(\overrightarrow{x},t)-\frac{\mathrm{\Delta }t}{\mathrm{\tau }}[f_i(\overrightarrow{x},t)-f_i^{\text{eq}}(\mathrm{\rho },\overrightarrow{u})]+\mathrm{\Delta }t{F}_i$$

The equilibrium distribution function is given by the Maxwell-Boltzmann distribution function. The relaxation time τ is related to the fluid kinematic viscosity ν by $\mathrm{\nu }=c_{\mathrm{s}}^2(\mathrm{\tau }-\frac{\mathrm{\Delta }t}{2})$, with $c_{\mathrm{s}}=\mathrm{\Delta }x/(\sqrt{3}\mathrm{\Delta }t)$ being the speed of sound, and Δx and Δt are the lattice spacing and time step, respectively. The fluid density ρ and velocity $\overrightarrow{u}$ can then be found as the zeroth and first moments of the distribution function

$$\begin{array}{c}\mathrm{\rho }(\overrightarrow{x},t)={\sum }_i{f}_i(\overrightarrow{x},t),\\ \overrightarrow{u}(\overrightarrow{x},t)=({\sum }_i{\overrightarrow{c}}_i{f}_i(\overrightarrow{x},t)+\frac{\mathrm{\Delta }t}{2}\overrightarrow{f}(\overrightarrow{x},t))/\mathrm{\rho }(\overrightarrow{x},t)\end{array}$$

where $\overrightarrow{f}$ accounts for the external and cell forces. The half-way bounce-back scheme (55) is used for imposing the no-slip boundary condition on the vessel walls, while the Zou-He scheme (56) is used for imposing the desired velocity and pressure at the vessel inlet and outlet, correspondingly.

The WSS vector components are computed by

$${\mathrm{\tau }}_{\mathrm{\alpha }}={\mathrm{\sigma }}_{\mathrm{\alpha }}{\overrightarrow{n}}_{\mathrm{\beta }}-({\overrightarrow{n}}_{\mathrm{\beta }}{\mathrm{\sigma }}_{\mathrm{\gamma }\mathrm{\beta }}{\overrightarrow{n}}_{\mathrm{\gamma }}){\overrightarrow{n}}_{\mathrm{\alpha }}$$

where n is the unit normal vector and σ_αβ denotes the viscous stress tensor components given by

$${\mathrm{\sigma }}_{\mathrm{\alpha }\mathrm{\beta }}=-\frac{\mathrm{\nu }}{c_{\mathrm{s}}^2 \mathrm{\tau }}{\sum }_i(f_i-f_i^{\text{eq}}){\overrightarrow{c}}_i{\overrightarrow{c}}_i$$

The WSS can then be calculated as the norm of τ.

The rigid beads and deformable CTCs are modeled here as initially spherical capsules, consisting of an outer membrane and the inner fluid. For simplicity, the capsule’s inner fluid is considered to have the same density and viscosity as the surrounding fluid. The membrane is composed of an isotropic and hyperelastic material obeying Skalak’s law (57) for its strain energy

$$W_{\mathrm{s}}=\frac{G_{\mathrm{s}}}{4}(I_1^2+2I_1-2I_2+C{I}_2^2)$$

The shear elastic modulus G_s is taken equal to 10⁻³ N/m in the case of rigid beads and 10⁻⁵ N/m for the deformable cells. The dimensionless parameter C represents the area incompressibility and is set here to 100; I₁and I₂ are the strain invariants of the Green-Lagrange strain tensor. The beads/cells membrane is discretized by considering successive refinements of an icosahedron, resulting in a triangular mesh of high homogeneity and isotropy (58).

To reproduce the effect of the cell membrane force $\overrightarrow{F_{\mathrm{m}}}=\frac{d{W}_{\mathrm{s}}}{d\overrightarrow{X_l}}$ on the fluid flow, denoted here by $\overrightarrow{f_{\text{IB}}}$, the following spreading operation is considered

$$\overrightarrow{f_{\text{IB}}}(\overrightarrow{x},t)=\sum _l\overrightarrow{F_{\mathrm{m}}}{\mathrm{\delta }}_{\mathrm{h}}(\overrightarrow{x}-\overrightarrow{X_l}) \mathrm{\Delta }s$$

The function δ_h denotes the discretized Dirac delta, $\overrightarrow{X_l}$ represents the position of the lth membrane vertex, and Δs is the initial distance between two neighboring vertices. The so-called two-point support (59) is considered here for δ_h. Once the force $\overrightarrow{f_{\text{IB}}}$ is known, we can obtain the macroscopic fluid variables at the next time step by solving the LBE. The velocity field $\overrightarrow{u}(\overrightarrow{x},t+\mathrm{\Delta }t)$ is then interpolated at the cell’s membrane as

$$\overrightarrow{U}(\overrightarrow{X_l},t+\mathrm{\Delta }t)=\sum _{\overrightarrow{x}}\overrightarrow{u}{\mathrm{\delta }}_{\mathrm{h}}(\overrightarrow{x}-\overrightarrow{X_l}) {(\mathrm{\Delta }x)}^d$$

with d = 3 being the domain dimensionality. The updated membrane position can then be found by Euler’s rule

$$\overrightarrow{X_l}(t+\mathrm{\Delta }t)=\overrightarrow{X_l}(t)+\overrightarrow{U}(\overrightarrow{X_l},t+\mathrm{\Delta }t) \mathrm{\Delta }t$$

Fluorescence staining and imaging

Bioreactor flow experiments were terminated after 7 days, and the printed tissue constructs were fixed in a 4% paraformaldehyde in PBS solution for 30 min. After fixation, tissues were rinsed thrice in PBS to remove residual fixative and stored at 4°C. Bulk stained gels (i.e., Fig. 1B) were permeabilized in 0.5% (v/v) Tween 20 (MilliporeSigma) in PBS for 15 to 30 min, and then gels were stained with 1:40 Alexa Fluor 488 phalloidin (A12379, Thermo Fisher Scientific) and Hoechst 33342 (62249, Thermo Fisher Scientific; at 10 μg/ml) in PBS for 1 hour at room temperature or overnight at 4°C. Gels were then washed in PBS + 0.1% (v/v) Tween 20.

For immunofluorescence-stained sections, fixed gels were first sucrose-protected in 30% (w/v) sucrose (VWR) in PBS. Samples were embedded in Tissue-Tek optimum cutting temperature (OCT) compound (Sakura Finetek) within Peel-A-Way embedding molds (Polysciences Inc.) and frozen in a 1:1 slurry mix of 70% ethanol (Decon Labs) and dry ice. Tissues were then stored at −80°C and cryosectioned using a Leica CM 1850 cyrostat microtome set to a thickness of 50 μm. Sections were carefully mounted on gelatin-subbed slides (Southern Biotech) and stored at −80°C for further staining. Before staining, sectioned tissues were thawed at room temperature, followed by fixation once more in formalin (VWR) for 15 min to ensure sample adhered to the slide. Samples were incubated at room temperature for 1 hour in blocking buffer composed of 0.5% (v/v) Triton X-100 (Sigma-Aldrich), 3% (w/v) bovine serum albumin (BSA; Sigma-Aldrich), and 10% normal goat serum (Vector Laboratories) in PBS. Sections were then incubated for 3 days at room temperature either with antilaminin primary antibody (L9393, MilliporeSigma) diluted at 1:100 in blocking solution or in blocking buffer without primary antibodies added. Primary solutions were then removed, and slides were washed thrice with 0.5% (v/v) Triton X-100 and 3% (w/v) BSA in PBS before incubating with secondary antibody (goat anti-rabbit Alexa Fluor 647; A-21245, Invitrogen) diluted at 1:500 in blocking solution for 1 hour at room temperature. Slides were then counterstained with Alexa Fluor 488 phalloidin (diluted 1:40) and Hoechst 33342 (at 10 μg/ml) in PBS for 1 hour at room temperature, followed by one wash with PBS, and then mounted in ProLong Gold antifade reagent (Invitrogen). Cover-slipped slides were allowed to cure overnight before imaging.

Samples were imaged with a confocal microscope using a plan-apochromat 10×/0.45–numerical aperture air immersion lens for both whole gels and sections. Slice spacing of Z stacks were set to match the optimal Z interval determined by the software (Zen Black, Zeiss) based on stack size, objective lens, and pinhole diameter. For whole-gel imaging, voxel size was set to 1.25 μm by 1.25 μm by 7.38 μm, and Z stacks were tiled to cover the entire geometry for a total image size of 18 mm by 7.6 mm by 1 mm. Z stacks with contrast adjusted manually are displayed as maximum intensity projections (created in Zen Blue, Zeiss or in MATLAB, MathWorks as described below).

Image processing

Confocal images were read into MATLAB (MathWorks) using BioFormats and processed using custom written scripts. For analysis of endothelial cell alignment, maximum intensity projections of the actin staining were divided into 21 × 21 pixel regions, and regions containing endothelial cells were analyzed using autocorrelation. For each patch, the image autocorrelation was calculated and fit to an arbitrary 2D Gaussian function, as described previously (60). The ratio of major and minor axis was used as a proxy for alignment and mapped back to the vessel geometry, and the angle of the major axis was mapped as a metric of alignment direction.

For vessel distensibility, XZ sections through the vessel geometry were thresholded and processed with morphological operations to generate filled regions corresponding to the cross-section of the vessel. Images were then stacked by centroid and false-colored to demonstrate distensibility.

For CTC flow partitioning, 100 frames from four independent flow experiments were read into MATLAB, and beads and cells were identified by size filtering with a Laplacian of Gaussian filter and thresholding. Lateral positions across the vessel for >10,000 particles per experiment were then processed to calculate mean position, variance (i.e., the second moment of position), and kurtosis (i.e., the fourth moment of position). Kurtosis and variance were compared between bead and cell experiments for four replicates each using the Kruskal-Wallis test due to the non-normal characteristic of these data.

For CTC attachment, vessel geometry was extracted from maximum intensity projections of either endothelial cells (endothelialized) or fluorescent microbeads (acellular). Focus points where the geometry changed direction were manually identified and used for Delaunay tessellation to divide the geometry into 34 regions, of which 12 were fork regions. Attached CTCs were also identified by thresholding, and contiguous regions were then filtered on the basis of integrated intensity to remove debris. Identified CTC regions were mapped to the Delaunay tessellation of the geometry to determine their region, and total CTC area normalized to region area and number of CTC foci were plotted. CTC clusters were determined heuristically to have an area of more than 300 μm². CTC area and number were compared across region type and vessel type using two-way analysis of variance (ANOVA).

Mechanical testing of hydrogel

Bulk rheological properties were measured using an MCR 102 rheometer (Anton Paar) with a humidity chamber. Gel samples were prepared as followed before transferring onto the rheometer: Bioreactor gel solution was cast into 25-mm-diameter silicone molds, allowed to set at 37°C for 1 hour in a humidity controlled incubator, and cooled at 4°C for 15 min before incubating submersed in EndoGRO-MV medium at 37°C for 24 hours in a humidity-controlled incubator. Oscillatory rheometry was performed using a stainless-steel parallel plate geometry (PP25/TG) set to a gap height of 1 mm at 37°C at a frequency range between 0.01 and 100 with 1% strain.

Viscometry of bead and cell solutions

Complex viscosity measurements for HBSS with ions, EndoGRO-MV medium, and 3.57% (v/v) 1-μm FluoSpheres tracer solutions were performed using an MCR 102 rheometer with a 25-mm stainless steel cone and plate geometry with an angle of 1° (CP25-1/TG). Using a humidity chamber and solvent trap to minimize drying effects, frequency sweeps were performed in triplicate at 25°C within a frequency range of 1 to 1000 rad/s at 1% strain.

The kinematic viscosity of EndoGRO-MV medium, HBSS with ions, and 3.57% (v/v) 1-μm bead tracer solutions were measured using a Cannon-Ubbelohde viscometer (Cannon Instrument Company). Solutions were allowed to reach 22°C, and the time for the fluid to freely efflux through the bulb was measured to the nearest 0.01 s. This was repeated four to six times and averaged, and then the dynamic viscosity in centipoise (cP) was calculated by multiplying average efflux time d by the viscometer constant (0.007239 cSt/s) by the density of the liquids as measured with an analytical balance (Toledo).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/35/eabb3308/DC1