Abstract
We demonstrate a successful deep learning strategy for cell identification and disease diagnosis using spatio-temporal cell information recorded by a digital holographic microscopy system. Shearing digital holographic microscopy is employed using a low-cost, compact, field-portable and 3D-printed microscopy system to record video-rate data of live biological cells with nanometer sensitivity in terms of axial membrane fluctuations, then features are extracted from the reconstructed phase profiles of segmented cells at each time instance for classification. The time-varying data of each extracted feature is input into a recurrent bi-directional long short-term memory (Bi-LSTM) network which learns to classify cells based on their time-varying behavior. Our approach is presented for cell identification between the morphologically similar cases of cow and horse red blood cells. Furthermore, the proposed deep learning strategy is demonstrated as having improved performance over conventional machine learning approaches on a clinically relevant dataset of human red blood cells from healthy individuals and those with sickle cell disease. The results are presented at both the cell and patient levels. To the best of our knowledge, this is the first report of deep learning for spatio-temporal-based cell identification and disease detection using a digital holographic microscopy system.
1. Introduction
Digital holographic microscopy is an optical imaging technology that is capable of both quantitative amplitude and phase imaging [1]. Many studies have shown digital holographic microscopy as a powerful imaging modality for biological cell imaging, inspection, and analysis [2–18]. Furthermore, digital holographic microscopy has been used successfully in cell and disease identification [16] for various diseases including malaria [2], diabetes [4], and sickle cell disease [6,19]. Digital holographic microscopy has additionally been used for discrimination between various inherited red blood anemias by considering Zernike coefficients [20]. Other forms of quantitative phase imaging, such as optical diffraction tomography can similarly be used for analysis of biological cells [21,22]. However, the single-shot capabilities of digital holographic microscopy, make it an ideal choice for analysis of spatio-temporal dynamics in live biological cells [6,14,23–25]. In particular, in [6] a compact and field-portable digital holographic system was presented for potential diagnostic application in sickle cell disease using spatio-temporal information. In this current work, we advance those capabilities by combining the use of dynamic cellular behavior with deep learning strategies to provide better cell identification capabilities and diagnostic performance in a low-cost and compact, digital holographic microscopy system. While the presented work uses a shearing-based compact digital holographic microscope, the proposed deep-learning method can be applied for cell identification tasks using any system that offers video-rate holographic imaging capabilities. This includes but is not limited to other forms of off-axis digital holography such as those using the Michelson arrangement [26,27], various forms of wavefront-division systems [28,29], and in-line holographic systems [30].
Deep learning refers to the multi-level representation learning methods where the complexity of the representation increases as the number of layers grow [31]. These methods have been found to be extremely useful for finding intricate structures from high level data and routinely outperform conventional machine learning algorithms, all without the need for carefully engineering feature extractors. For image processing tasks specifically, convolutional neural networks (CNNs) are paramount among deep learning strategies. CNNs notably make use of convolutional layers where each unit of a convolutional layer connects to local patches of the previous layer. This allows for combinations of local features to build upon each other in generation of more global features and makes CNNs well-suited for easily identifying local patterns at various positions across an image. Developments in hardware and software since the inception of CNNs have resulted in CNNs becoming the dominant approach for nearly all recognition and detection tasks today [31].
Following the expansion in use of convolutional neural networks [31] for many image processing tasks, deep learning has similarly grown increasingly popular for cell imaging tasks in recent years [32,33]. These tasks include, but are not limited to, cell classification, cell tracking [32], and segmentation of living cells [34]. Moreover, deep learning has been used in holographic imaging specifically for reconstruction, super-resolution imaging, and pseudo-colored phase staining to mimic conventional brightfield histology slides [35]. Additionally, the use of convolutional neural networks in quantitative phase imaging has been presented for screening of biological samples, such as for the detection of anthrax spores [36], classification of cancer cell stages [37], and classification between white T-cells and colon cancer cells [38]. While much of this research for deep learning in holographic cell imaging thus far has primarily dealt with stationary phase images, recurrent neural networks such as long-short term memory (LSTM) networks [39], also make deep learning an attractive option for dealing with time-varying biological data [40].
In this paper, we present a deep learning approach for cell identification and disease diagnosis using dynamic cellular information acquired in digital holographic microscopy. Handcrafted morphological features, and transfer learned [32,41] features from a pretrained CNN are extracted from every reconstructed frame of a recorded digital holographic video, then these features are input into a Bi-LSTM network which learns the temporal behavior of the data. The proposed method is demonstrated for cell identification between cow and horse red blood cells, as well as for classification between healthy and sickle cell diseased human red blood cells. The proposed deep learning approach provides a significant improvement in terms of classification accuracy in comparison to our previously presented approach utilizing conventional machine learning methods [6,19]. To the best of our knowledge, this is the first report of deep learning using spatio-temporal cell dynamics for cell identification and disease diagnosis in digital holographic microscopy video data.
The rest of the paper is organized as follows: the optical imaging system used for data collection is described in Section 2 followed by the details of the feature extraction and the long short-term memory network. Results for the two datasets are given in Section 3 followed by discussions in Section 4 and finally, the conclusions are presented in Section 5.
2. Materials and methods
2.1. Compact and field-portable digital holographic microscope
All data was collected using a previously described compact and field-portable 3D-printed shearing digital holographic microscope [6]. Shearing-based interferometers are off-axis common-path arrangements that provide a simple setup and highly stable arrangement for digital holographic microscopy [3,17]. The 3D-printed microscope consists of a laser diode (λ = 633 nm), a translation stage to axially position the sample, one 40X (0.65 NA) microscope objective, a glass plate, and a CMOS image sensor (Thorlabs DCC1545M).
The beam emitted from the laser diode passes through the cell sample, is magnified by the microscope objective lens, then falls upon the glass plate at an incidence angle of 45-degrees. The light incident on the glass plate is reflected from both the front and back surfaces of the plate to generate two laterally sheared copies of the beam. These beams will self-interfere and form an interference pattern that is recorded by the image sensor. The fringe frequency of the recorded pattern is determined by the radius, r, of curvature of the wavefront, as well as the vacuum wavelength of the source beam, λ, and the lateral shear induced by the glass plate, S, where . In this equation, tg is the glass plate thickness, β is the incidence angle upon the glass plate, and n is the refractive index of the glass plate [42,43]. Due to a shearing configuration, there will exist two copies of each cell, however, when the lateral shear is greater than the size of the magnified object, the cells will not overlap with their copies, and the normal processing of off-axis holograms is followed [3]. Furthermore, the capture of redundant sample information can be avoided by ensuring the lateral shear is greater than the sensor size [12]. This shearing digital holographic microscopy system provides a field-of-view of approximately 165 µm x 135 µm, and the theoretical resolution limit was calculated as 0.6 µm by the Rayleigh criterion [6,19]. Furthermore, the temporal stability of the system was reported as 0.76 nm [6], when measured in the hospital setting that served as the site of the human red blood cell data collection, making the system well suited to study red blood cell membrane fluctuations which are on the order of tens of nanometers [6,44]. A diagram of the optical system and depiction of the 3D-printed shearing digital holographic microscope are provided in Fig. 1.
Fig. 1.
(a) Optical schematic of lateral shearing digital holographic microscope. (b) 3D-printed microscope used for data collection.
Using the described system, thin blood smears are examined, and video holographic data is recorded. Following data acquisition, each individual frame of a segmented red blood cell is numerically reconstructed. Based on the thin blood smear preparation, the red blood cells are locally stationary, but continue to exhibit cell membrane fluctuations. Given the high sensitivity of the system to axial changes, the system can detect small changes in the cell membrane (i.e. cell membrane fluctuations). These slight changes in the overall cell morphology are studied over the duration of the videos to provide information related to the spatio-temporal cellular dynamics of the sample. Further details related to the suitability of DHM in studying red blood cell membrane fluctuations are provided in Refs. [6] and [14].
2.2. Human subjects, blood collection and preparation
This study was approved by the Institutional Review Boards of the University of Connecticut Health and University of Connecticut-Storrs. All subjects were at least 18 years old and were ineligible to participate if they had a blood transfusion within the previous three months. Blood was collected once from both healthy control subjects and subjects with sickle cell disease (SCD). 7 ccs of blood was collected via venipuncture into two 3.5 mL lavender top vacutainer tubes for complete blood count with leukocyte differential, hemoglobin electrophoresis, and blood smears. Demographic information including age, race, and ethnicity was recorded.
2.3. Digital holographic reconstruction
Following the recording of a holographic video by the CMOS sensor, the video frames are computationally processed to extract the phase profiles of the objects under inspection. Based on the off-axis nature of the shearing interferometer, we use the common Fourier spectrum analysis [3,45,46] in processing of the holograms. From the recovered complex amplitude of the sample, Ũ (ξ, η), the object phase calculated as Ф=tan-1[Im{Ũ}/Re{Ũ}], where Im{·} and Re{·} represent the real and imaginary functions, respectively. The extracted phase is then unwrapped by Goldstein’s branch-cut method [47]. System abberations are reduced by subtracting the phase of a cell-free region of the blood smear [3,48]. Given the unwrapped object phase (Фun), the optical path length (OPL) is computed as OPL= Фun[λ/(2π)]. When the refractive indices of both the object and background media are known, the OPL can be directly related to the height or thickness of the object through the expression h = OPL/Δn, where h is the height and Δn is the refractive index difference. Typical values for human red blood cells and plasma are 1.42 and 1.34, respectively [49], however, these values cannot be assumed for all samples in the follwing analysis, thus all analysis in this paper is performed using the OPL values.
2.4. Hand-crafted morphological feature extraction
To characterize the cells under inspection, morphological features related to the cell shape are calculated for each segmented cell. The use of morphological features is a long-standing method for qualitative and quantitative assessment of biological specimen [50]. The morphological features extracted here provide easily interpretable cell characteristics that are related to the three-dimensional cell shape and composition. In total, we use fourteen handcrafted morphological features. Eleven of these features relate to the instantaneous characteristics of the cell (i.e. static features) whereas three of these features are designed to capture the time-varying or motility-based features and encode the spatio-temporal behavior of the cells [6]. The static features are used in both the conventional machine learning algorithm and the proposed deep learning method. However, because the proposed deep learning method learns the spatio-temporal behavior from the static features at each time step, the three motility features mentioned in this section are used only in the conventional machine learning algorithm for comparison to the proposed method. Details regarding extraction of spatio-temporal features for use in conventional machine learning algorithms are provided in [6]. Table 1 provides a brief description for all hand-crafted features examined in this work [5,6,12,14].
Table 1. Handcrafted feature extraction.
| Extracted Feature Name | Description of Feature |
|---|---|
| Mean optical path length | Average measured optical thickness of the sample |
| Coefficient of variation | Variance of the optical thickness |
| Projected cell area | Total projected area of the cell |
| Optical volume | Total projected volume of the cell |
| Cell thickness skewness | Third central moment of the cell optical thickness |
| Cell thickness kurtosis | Fourth central moment of the cell optical thickness |
| Cell perimeter | Length along the outer boundary of the cell |
| Cell circularity | Measure of how circular the cell is |
| Cell elongation | Measure of how elongated the cell is |
| Cell eccentricity | Measure of irregularity in cell shape |
| Cell thickness entropy | Measure of randomness over the cell thickness |
| a Optical flow | Measure of cell lateral motility |
| a Standard deviation of the 2D mean OPL map | Measure of the differences in average OPL over the cell |
| a Standard deviation of the 2D STD OPL map | Measure of differences in cell fluctuations over the cell |
Spatio-temporal features are used only in the conventional machine learning approach for comparison. The proposed deep learning method extracts its own representation of spatio-temporal information.
2.5. Feature extraction through transfer learning
Alternatively, instead of carefully designing handcrafted features, convolutional neural networks can be used to find effective feature representations for a given dataset. Recently, thanks in part to openly available databases for training such as ImageNet [51], the use of pretrained networks in transfer-learned image classification tasks has grown significantly. Transfer learning enables the use of powerful deep learning models to be used on smaller, ‘target’ datasets by first pre-training the network on a larger ‘source’ dataset [32]. When using a pretrained network, a complex convolutional neural network is trained on an extremely large database to learn features that generalize well to new tasks. Then the pretrained network is adapted for a new dataset. This sometimes involves retraining several terminal layers of a network using the target dataset, however, the simplest form of transfer learning is to use a pretrained network as a feature extractor for new tasks. To apply these pretrained networks as a feature extractor, after training on a source dataset, the target training set is passed through the CNN up to the last fully connected layer, then the feature vector from this last layer is used to train a new classifier such as a support vector machine [39]. In doing so, transfer learning removes the need for long training process on new datasets, requires the data to only pass through the network once for feature extraction, and greatly reduces both the time and computational resources needed to leverage the benefits of deep learning models.
In this work, we use the DenseNet-201 convolutional neural network [52], pretrained on ImageNet, as a feature extractor for classification tasks. The DenseNet is a specific type of CNN architecture wherein the input to any given layer includes the feature maps from all preceding layers rather than only the most recent layer as in more traditional architectures. This arrangement was shown to be beneficial in reducing issues due to vanishing gradients, reducing the number of parameters, and strengthening feature propagation [52]. Following feature extraction using the pretrained network, 1000 features are output by the network. These features have no easily interpretable meaning but do offer robust features for most image classification tasks. As with the static handcrafted morphology-based features, the transfer learned features were extracted at each frame of the reconstructed video data providing a time-varying signal of the feature values for input to our deep learning model.
2.6. Long short-term memory (LSTM) network
To make classifications on sequential data, a special form of neural network is required. Recurrent neural networks (RNNs) are the specific type of artificial neural network designed to handle sequences of data and map the dynamic temporal behavior. RNNs use a looped architecture to allow some information to be maintained from the previous time step. They work by processing sequential data one element at a time and maintaining a ‘state vector’ for hidden units to incorporate the information from past input elements [31]. Theoretically, these networks should be able to handle arbitrarily long signals. In reality, however, RNNs are sensitive to exploding and vanishing gradients as the sequences get longer. To help alleviate the gradient-related issues, the long short-term memory network (LSTM) [39] was introduced and has since become one of the most used network architectures for sequential deep learning tasks. The LSTM architecture uses a cell state and cell gate arrangement to handle longer sequences of data and to mitigate the vanishing gradient problem [39]. Through several interacting gates that control the cell state as it is passed from the previous LSTM block to the following LSTM block, the LSTM network controls how memory is maintained through the system. A forget gate determines how much of the previous information regarding the cell state is to be discarded, an input gate determines how much information of the current cell state needs to be updated, and an output gate determines what information of the current cell is output to the following block.
To use an LSTM network, features are extracted at each time instance of a time-varying signal and input into the LSTM network as a matrix wherein each column is a feature vector corresponding to a different time step and each row is a different feature. During the training process, the LSTM network learns the mapping for the time-varying behavior of the data to accomplish the given task. A popular variant of the original LSTM architecture is the bi-directional LSTM (Bi-LSTM) architecture [53] which simultaneously learns in both the forward and reverse directions and is used in this work. An explanatory diagram for the Bi-LSTM network is provided by Fig. 2.
Fig. 2.
Explanatory diagram of the Bi-LSTM network architecture. (a) Shows the general overview of the network structure starting from the input feature vectors at each time step, xt, which are fed through the Bi-LSTM layer enclosed by the dashed box. The output of the Bi-LSTM layer feeds to a fully connected layer followed by a softmax then classification layer. (b) Shows a close-up look at an individual LSTM block of the network. Internal operation of the LSTM block is discussed in the paragraph below.
From Fig. 2, we see that feature vectors for each time-step are input to the network as xt. Each LSTM block, uses the input feature vector (xt), and the previous cell’s hidden state (ht-1) to update the cell state from Ct-1 to Ct, as well as outputting a new hidden state (ht) to be fed to the following LSTM block. The outputs from the Bi-LSTM layer are passed to a fully connected layer, followed by a softmax then classification layer. Inside, each LSTM block, as shown by Fig. 2(b) several operations take place which give the LSTM architecture its unique functionality in comparison to traditional RNNs.
For operation of the Bi-LSTM network, the cell state (Ct), is passed through the repeating blocks of the Bi-LSTM layer and updated by several interacting gates, where each gate is composed of a sigmoid function to determine how much information should be passed along and a multiplication operation. From left to right in the diagram shown in Fig. 2(b), the first of these sigmoidal functions is the activation function for the forget gate (ft) which uses the previous hidden state (ht-1) and the current input (xt) to determine how much of the previous cell state (Ct-1) is discarded. The second sigmoid function is the activation function of the input gate (it), which determines the values of the cell state to be updated. The input gate is multiplied with a vector of potential new values to be added to the previous cell state, (t), produced by a hyperbolic tangent function, then combined with the previous cell state to obtain the current cell state (Ct). The third sigmoid is the activation function for the output gate (Ot) to determine which part of the cell state to output as the updated hidden state. The current cell state (Ct) is passed through a hyperbolic tangent function then multiplied with the output gate (Ot) to produce the updated hidden state (ht). These defining interactions can be described mathematically as follows [39]:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Where i, f, and O are the input, forget and output gates, respectively, C is the cell state vector, and Wkk and bkk, , are the weights and biases of the network. σ and tanh represent the sigmoidal and hyperbolic tangent functions, respectively. Since a Bi-LSTM layer is used, the output of the Bi-LSTM layer to the fully connected layer is the concatenation of the final outputs from the both the forward and reverse directions.
For the Bi-LSTM network used in this work, both the handcrafted morphological features, and the transfer learned features which have been extracted for every time frame are used as inputs. Note that for the handcrafted features, we are unable to extract the three handcrafted motility features at each individual frame. Instead, we use the statistical means of the optical flow vector magnitudes and orientations as additional static features to incorporate the information obtained from the optical flow algorithm.
During processing, all videos were limited to the first two hundred frames to reduce the computational requirements. The Bi-LSTM network used a dropout rate of 0.4 following the Bi-LSTM layer and was optimized using the Adam optimizer. For the animal RBC task, the Bi-LSTM layer contained 400 hidden units and was trained for 60 epochs with a learn rate of 0.001 for the first 30 epochs and 0.0001 for the final 30 epochs. These hyperparameters were chosen based on the performance of a single randomly chosen video as the test set. For the human RBC task, the Bi-LSTM layer contained 650 hidden units and was trained for 40 epochs with an initial learn rate of 0.0001 that dropped to 0.00001 for the final 10 epochs. Similarly, these hyperparameters were chosen based on the performance for a single randomly chosen patient as the test set. All processing, classification, and analysis was performed using MATLAB software. During feature extraction, approximately 100 cells were processed per minute for video sequences of 200 frames. After feature extraction, including training time, classification of a single patient’s RBCs took less than 1 minute using a NVIDIA Quadro P4000 GPU.
2.7. Performance assessment
To demonstrate the performance of our proposed method, we study two distinct red blood cell (RBC) datasets. First, we consider classification between cow and horse RBCs. Second, we consider a previously studied dataset of healthy and sickle cell disease RBCs from human volunteers [6]. In each case, the datasets are classified using a conventional machine learning strategy as well as the proposed deep learning method for comparison. The conventional machine learning algorithm uses the handcrafted features of Section 2.4 in a random forest classifier [54], then these results are compared to our proposed method using an LSTM deep learning model. To further illustrate the benefit of using time-varying signals as inputs for classification, we also consider a support vector machine classifier using the same features as the proposed LSTM model but extracted from only the first time frame.
The classification performance is assessed based on classification accuracy, area under the receiver operating characteristic curve (AUC), and Mathew’s correlation coefficient (MCC). The area under the curve provides the probability for a classifier that a randomly chosen positive class data point is ranked higher than a randomly chosen negative class data point. For this metric, 1 represents perfect classification of all data points, 0 represents incorrect classification of all points and 0.5 represents a random guess. Mathew’s correlation coefficient is a machine learning performance metric that effectively returns the correlation coefficient between the observed and predicted classes in a binary classification task. Values of MCC range from -1 (total disagreement) to 1 (perfect classification) with 0 representing a random guess. The MCC is considered to be a balanced measure and provides a reliable metric of performance even when dealing with classes of varied sizes.
The full process for cell identification and disease diagnosis is overviewed by Fig. 3. Each red blood cell dataset is considered under two conditions: pooled data, and cross-validated data. For the pooled data, all cells are grouped together and randomly partitioned with an 80%/20% split for training and testing. Cross-validation, on the other hand, provides a more accurate representation of real-world applications by testing the cells in a manner similar to that which they were collected. For the human red blood cell dataset, cross-validation is performed at the patient level. That is, we test one patient at a time, ensuring no cells from the current test patient are present in the training data. The testing is repeated for each patient’s data while the remaining patients comprise the training set, and the results are averaged. For the animal red blood cell dataset, cross-validation is performed at the video level. By this we mean all cells extracted from a given video were grouped together, and only the cells from a single video were used as the current test set. This ensures that no data from the current testing video data is present in the training set. As with the human RBC dataset, the results are averaged over all individual videos acting as the test set.
Fig. 3.
Flow chart depicting an overview of the deep learning-based cell and disease identification system. Video holograms of biological samples are recorded using the system depicted in Fig. 1. Following data acquisition, each time frame is reconstructed, and individual cells are segmented. Features are extracted from the segmented cells and input into a Long Short-Term Memory network for classification. xt and ht denote the input and output through a portion of an LSTM network at time-step t.
3. Experimental results
3.1. Cell identification: classification of cow and horse red blood cells
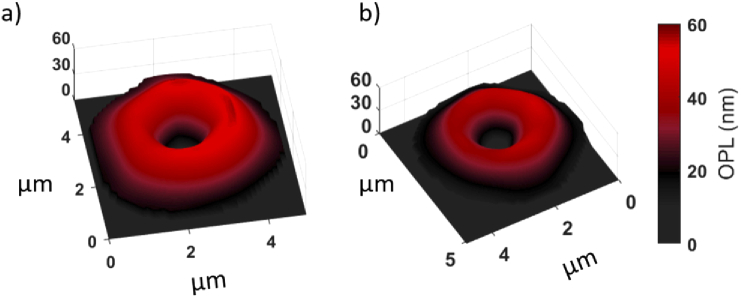
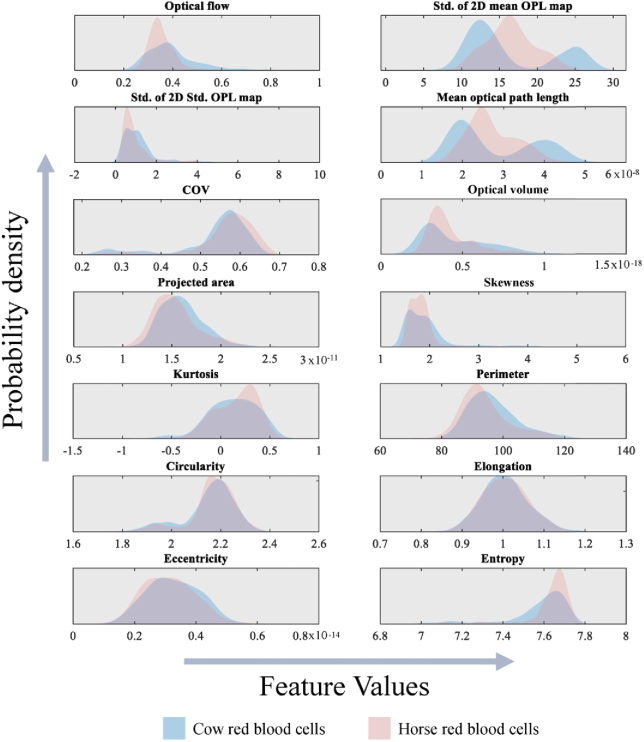
The dataset for cow and horse red blood cells consisted of 707 total segmented RBCs (376 Cow, 331 Horse). The two animal cell types were chosen based on morphological similarity as both animal RBC types are biconcave disk-shaped and between 5-6 µm in diameter [55]. The animal red blood cells were obtained as a 10% RBC suspension taken from multiple specimens and suspended in phosphate-buffered saline (as provided by the vendor). Thin blood smears of the blood samples were prepared on microscope slides and covered by a coverslip, then imaged using the digital holographic microscopy as shown in Fig. 1. No additional buffer medium was used, and all cells were imaged prior to the slide drying out due to exposure to air. Video holograms were recorded at 20 frames per second for 10 seconds. Following hologram acquisition, the cells were segmented, reconstructed, then features were extracted as described in the above paragraphs. Segmentation was performed using a semi-automated algorithm wherein potential cells were identified through simple thresholding and an input expected size. Once potential cells are identified, morphological operators included in the Matlab image processing toolbox were used to automatically isolate the segmented cell from its background medium at each time frame. Human supervision during the segmentation process allows for quality control to remove any data from the dataset when multiple cells overlap, or segmentation was not performed properly. Examples of segmented cow and horse RBCs are provided by Fig. 4. Notably both cell types have similar size and shape, presenting a non-trivial classification problem. Video reconstructions of the segmented cells are available online. Furthermore, we provide the probability density functions for each of the hand-crafted features in Fig. 5, which show significant overlap between the two classes, indicating their similarity.
Fig. 4.
Segmented digital holographic reconstructions of (a) cow, and (b) horse red blood cells, with noted similarity in both size and shape. Video reconstructions for each cell are available online.
Fig. 5.
Probability density functions of each hand-crafted feature for cow (blue curve) and horse (red curve) red blood cells. Mean optical path length is reported in meters, projected area in meters squared, optical volume in cubic meters, and all other features in arbitrary units.
The resulting confusion matrices for the cross-validated data are provided in Table 2, and the receiver operating characteristic curves comparing the random forest and LSTM models for the cross-validated data are shown in Fig. 6.
Table 2. Confusion matrices for cross-validation classification of cow and horse RBCs.
| Random Forest Model | Combined Features in an LSTM network | Combined Features from a single frame in SVM | ||||
|---|---|---|---|---|---|---|
| Predicted Cow | Predicted Horse | Predicted Cow | Predicted Horse | Predicted Cow | Predicted Horse | |
| Actual Cow | 299 | 77 | 293 | 83 | 212 | 164 |
| Actual Horse | 94 | 237 | 71 | 260 | 115 | 216 |
| Classification Accuracy | 75.81% | 78.22% | 60.54% | |||
Fig. 6.
Receiving operating characteristic (ROC) curves for classification between cow and horse red blood cells.
From Table 2, we note a slight increase in classification accuracy when using the proposed LSTM classification strategy over the previously reported random forest model for cell identification using spatio-temporal cell dynamics [6,19]. Furthermore, both the random forest and LSTM models outperform the SVM model which uses features extracted from only a single time frame, highlighting the benefits of considering the dynamic cellular behavior. Figure 6 shows the ROC curves for both the random forest and LSTM models on the cross-validated data using different extracted features for classification.
The random forest model was tested under three conditions: (1) using only static-based features, (2) using only the motility-based features and (3) when the combination of all features was used. The LSTM model was also tested for three conditions: (1) using only the handcrafted morphological features, (2) using only the transfer learned features, and (3) using the combination of all features. Amongst the random forest classifiers, the highest area under the curve (AUC = 0.8511) was achieved when the combination of both static and motility-based features was used. Overall, the LSTM model using combined features provided the best overall performance, having an AUC of 0.8615. A summary of the classification performance for all tested conditions, including both the pooled and cross-validated results are given in Table 3.
Table 3. Summary of classification results for cow and horse RBCs.
| Dataset | Method | Accuracy | AUC | MCC |
|---|---|---|---|---|
| Pooled Data | Random Forest – static features only | 77.46% | 0.8650 | 0.5432 |
| Random Forest – motility features only | 84.51% | 0.8981 | 0.6814 | |
| Random Forest – combined features | 83.80% | 0.9285 | 0.6674 | |
| LSTM – morphological features only | 79.58% | 0.8896 | 0.5965 | |
| LSTM – transfer learned features only | 83.10% | 0.8040 | 0.6600 | |
| LSTM – combined features | 84.51% | 0.8388 | 0.7067 | |
| Cross Validated Data | Random Forest – static features only | 73.41% | 0.7978 | 0.4652 |
| Random Forest –motility features only | 77.09% | 0.8405 | 0.5391 | |
| Random Forest – combined features | 75.81% | 0.8511 | 0.5134 | |
| LSTM – morphological features only | 77.65% | 0.8314 | 0.5580 | |
| LSTM – transfer learned features only | 68.46% | 0.7403 | 0.3696 | |
| LSTM – combined features | 78.22% | 0.8615 | 0.5639 | |
For the pooled data, the proposed LSTM model achieves the highest classification accuracy and MCC values, whereas for the cross-validated data, the proposed LSTM model achieves the highest values of classification accuracy, AUC, and MCC values.
3.2. Detection of sickle cell disease (SCD)
For validation on a clinically relevant dataset, we test our proposed method on a previously studied dataset of healthy and sickle cell disease human RBCs [6,19]. Sickle cell disease is recognized as a global health issue by both the World Health Organization (WHO) and the United Nations. The inherited blood disease is characterized by the presence of abnormal hemoglobin which cause mishappen red blood cells and affects oxygen transport throughout the body. The disease is particularly devasting in less developed regions of the world, such as some regions of Africa, where approximately 1,000 children with SCD are born every day and over half will die before their fifth birthday [56]. The only cure for SCD is a bone marrow transplant which carries significant risks and is rarely used for cases of SCD [57]. Most often, treatments include medications and blood transfusions [57]. Early and accurate detection of sickle cell disease is important for establishing a treatment plan and reducing preventable deaths. Cells with the abnormal sickle hemoglobin often form irregular rod-shaped and sickle shaped cells which give the disease its name. However, not all RBCs from a SCD patient will be sickle shaped. Despite some cells having normal appearance under visual inspection, all RBCs produced by a person with sickle cell disease will have abnormal intracellular hemoglobin which may contribute to abnormal cell behavior.
Standard procedures for identification of sickle cell disease use gel electrophoresis or high-performance liquid chromatography to analyze a blood sample and screen it for the presence of abnormal hemoglobin. The major downside of these strategies is that they require dedicated laboratory facilities, the processing takes several hours, and due to cost-saving measures, the patient may not receive the results for up to two weeks after the initial blood draw [6]. These drawbacks severely limit the testing abilities in areas of the world where the disease is most prevalent. To address these limitations, rapid point of care systems are currently being developed and tested [58,59]. Furthermore, optical methods such as multi-photon microscopy [60], and digital holographic microscopy [6,13,19], have also been used to study sickle cell disease and as potential diagnostic alternatives.
For generation of this dataset, 151 cells from six healthy (i.e. having no hemoglobinopathy traits) volunteers (4 female, 2 male) and 152 cells from eight patients with sickle cell disease (2 female, 6 male) were segmented from blood samples. After whole blood was drawn from the volunteers, a thin blood smear was prepared on a standard microscope slide with a coverslip for analysis in the digital holographic microscopy system (Fig. 1). All data was collected before the samples dried out from exposure to air. Video holograms were recorded for 20 seconds at 30 frames per second. Following data acquisition, the individual cells were segmented and numerically reconstructed to allow for feature extraction and classification. Due to the presence of abnormally shaped cells, all reconstructed RBCs in this dataset were manually segmented. Visualizations of both healthy and SCD RBCs are shown in Fig. 7. Furthermore, video reconstructions of these cells are available online. Again, we provide the probability density finctions for each of the hand-crafted features to illustrate the non-trivial classification problem in Fig. 8.
Fig. 7.
Segmented digital holographic reconstructions of (a) healthy red blood cell, and (b) sickle cell disease red blood cell. Note, sickle cell disease red blood cells can have various degrees of deformity and may present morphologically similar to healthy RBCs. Video reconstructions for each cell available online.
Fig. 8.
Probability density functions of each feature for healthy (blue curve) and sickle cell disease (red curve) red blood cells. Mean optical path length is reported in meters, projected area in meters squared, optical volume in cubic meters, and all other features in arbitrary units.
The resulting confusion matrices for the cross-validated data are provided in Table 4, and the receiver operating characteristic curves comparing the random forest and LSTM models for the cross-validated data are shown in Fig. 9. The confusion matrices in Table 4 show we achieved the best performance using the proposed LSTM model for cross-validated classification of the human RBC dataset (81.52% accuracy). The proposed method outperformed the previously presented random forest model (72.93% accuracy) and outperforms an SVM classifier using features extracted from only a single time frame (76.23% accuracy). Likewise, Fig. 9 shows the ROC curves for both the random forest and LSTM models on the cross-validated data using different extracted features for classification.
Table 4. Confusion matrices for patient-wise cross-validation classification of healthy RBCs and SCD-RBC.
| Random Forest Model | Combined Features in an LSTM network | Combined Features from a single frame in SVM | ||||
|---|---|---|---|---|---|---|
| Predicted Healthy | Predicted SCD | Predicted Healthy | Predicted SCD | Predicted Healthy | Predicted SCD | |
| Actual Healthy | 112 | 39 | 125 | 27 | 110 | 42 |
| Actual SCD | 43 | 109 | 29 | 122 | 30 | 121 |
| Classification Accuracy | 72.93% | 81.52% | 76.23% | |||
Fig. 9.
Receiving operating characteristic curves (ROC) for classification between healthy and SCD red blood cells.
From Fig. 9, the LSTM model using the combination of handcrafted morphological and transfer-learned features provided the highest AUC. A summary of the classification performance for all tested conditions, including both the pooled and cross-validated results are given in Table 5. In both the pooled data and the cross-validated data, the proposed LSTM model achieves the highest values of classification accuracy, AUC, and MCC values.
Table 5. Summary of classification results for healthy and sickle cell disease RBCs.
| Dataset | Method | Accuracy | AUC | MCC |
|---|---|---|---|---|
| Pooled Data | Random Forest – static features only | 93.44% | 1.0000 | 0.8743 |
| Random Forest – motility features only | 77.05% | 0.8333 | 0.5559 | |
| Random Forest – combined features | 98.36% | 0.9978 | 0.9674 | |
| LSTM – morphological features only | 75.41% | 0.8626 | 0.5435 | |
| LSTM – transfer learned features only | 95.08% | 0.9665 | 0.9468 | |
| LSTM – combined features | 98.36% | 1.0000 | 0.9674 | |
| Cross Validated Data | Random Forest – static features only | 70.96% | 0.7989 | 0.4192 |
| Random Forest – motility features only | 66.66% | 0.6816 | 0.3333 | |
| Random Forest – combined features | 72.94% | 0.8358 | 0.4589 | |
| LSTM – morphological features only | 65.35% | 0.6821 | 0.3091 | |
| LSTM – transfer learned features only | 65.68% | 0.7640 | 0.3186 | |
| LSTM – combined features | 81.52% | 0.8645 | 0.6304 | |
4. Discussions
The classification results show the proposed method provided the best overall performance for both identification of different animal red blood cell classes and detection of sickle cell disease in human RBCs. The improvement of classification performance on two distinct datasets provides strong evidence that the proposed approach may be beneficial to various biological classification tasks including potential for diagnosis of various disease states. The results further demonstrate that the inclusion of spatio-temporal cellular dynamics can be used to improve classification performance.
For the animal RBC data, the proposed method provides approximately a 3% increase in classification accuracy. The proposed method was especially beneficial for the human RBC data, wherein, we achieve a nearly 10% increase in classification accuracy using the proposed approach in comparison to the previously published random forest classifier on the cross-validated dataset. Several factors may be responsible for this difference in performance between the two RBC datasets. Firstly, from the video reconstructions, the sickle cell disease RBC shows very limited membrane fluctuations, potentially indicative of increased cell rigidity in comparison to the healthy human RBC (video reconstructions available online). The LSTM network’s ability to represent this spatio-temporal information may explain why a greater improvement in performance is achieved for the human RBC dataset. Another possible explanation is that the transfer learned features are particularly helpful for distinguishing the irregularly shaped diseased cells. This explanation finds support by the fact that the combination of handcrafted and transfer-learned features from a single frame using an SVM outperformed the previously used random forest model incorporating both static and spatio-temporal information (Table 4).
The results of the sickle cell disease dataset also highlight the importance of cross-validation when dealing with human disease detection (Table 5). When pooling all cells together and not considering the separation of individual patient data, the same dataset achieves nearly perfect classification with 98.36% classification accuracy and an AUC of 1 as opposed to the 81.52% classification accuracy and AUC of 0.8645 attained with patient-wise cross-validation. We believe that the drop off from pooled data to cross-validated data was more evident in the human RBC group because of the smaller size of the dataset and the inter-patient variability, leading to a less homogenous dataset than in the animal RBC data. Classification accuracy on human data should be expected to improve with larger datasets, even at the patient level as the training data will become a better representation of the overall population that the testing data is drawn from. Furthermore, as data driven methods, deep learning approaches tend to increase in accuracy along with growing data availability whereas conventional machine learning methods reach a plateau in performance. Therefore, we believe the inclusion of cell motility information, and the utilization of deep learning as demonstrated here will continue to have an important role in cell and disease identification tasks.
It is important to also discuss the advantages of the presented system and methodology with respect to traditional medical diagnostics as well as with respect to other machine-learning based approaches. Firstly, the presented offers several advantages in terms of cost, field-portability, and time to results over conventional medical tests. The proposed methodology can provide classification of a patients’ cells on the order of minutes, whereas a typical electrophoresis assay takes several hours, and oftentimes the assays are batched to reduce costs which can extend the time for results to up to a week or more. Furthermore, these traditional systems require dedicated lab facilities and highly trained personnel. The presented system is field-portable, provides near rapid results, and does not require extensive training. Lastly, since the system requires only a small sample of blood, it can easily be used in the field. In combination, these factors make the presented system an attractive option for potential use as diagnostic system, especially in areas of limited resources.
Whereas several machine learning and deep learning approaches have been presented for classification of biological samples in digital holographic imaging [6,14,23–25,36–38], to the best of our knowledge, this is the first report of a deep-learning approach based on spatio-temporal dynamics. Previously presented works considering time-dynamics of living cells focus on cell monitoring [14,23,24], tracking of cell states over time [25] or use hand-crafted motility-based features [6] to include temporal information in classification using conventional machine learning algorithms. On the other hand, previous deep-learning approaches for biological cell classification [36–38] using convolutional layers do not consider temporal behavior of the cells. The proposed methodology enables the use of time-varying behavior in a deep learning framework by utilizing a Bi-LSTM network architecture and shows improved performance over classification using handcrafted motility-based features in conventional machine learning approaches [6].
5. Conclusions
In conclusion, we have presented a deep learning approach for cell identification and disease detection based on spatio-temporal cell signals derived from digital holographic microscopy video recordings. Holographic videos were recorded using a compact, 3D-printed shearing digital holographic microscope, then individual cells were segmented and reconstructed. Hand-crafted morphological features and features extracted through transfer learning using a pretrained convolutional neural network were extracted at each time frame to generate time-varying feature vectors as inputs to the LSTM model. The proposed approach was demonstrated for cell identification between two morphologically similar animal red blood cell classes using a clinically relevant dataset consisting of healthy and sickle cell disease human red blood cells. In each instance, the cross-validated data had improved performance using the proposed approach over conventional machine learning methods with substantial improvement noted for sickle cell disease detection. The proposed approach also outperformed a classifier using data from only a single timeframe, indicating the benefit of studying time-evolving cellular dynamics. Future work entails continued study of time-varying biological signals, increased patient pools for clinically relevant studies, and testing on various disease states. Additional future work may also consider Zernike coefficients in combination with morphological or transfer learned features using the proposed spatio-temporal deep learning strategy as well as the use of the proposed methodology to distinguish between various disease states that may appear morphologically similar [20].
Acknowledgments
T. O’Connor acknowledges support via the GAANN fellowship through the Department of Education. B. Javidi acknowledges support by Office of Naval Research (N000141712405).
Funding
Office of Naval Research10.13039/100000006 (N000141712405).
Disclosures
The authors declare no conflicts of interest.
References
- 1.Schnars U., Jueptner W., Digital Holography: Digital Hologram Recording, Numerical Reconstruction, and Related Techniques (Springer, 2005). [Google Scholar]
- 2.Anand A., Chhaniwal V., Patel N., Javidi B., “Automatic Identification of Malaria-Infected RBC With Digital Holographic Microscopy Using Correlation Algorithms,” IEEE Photonics J. 4(5), 1456–1464 (2012). 10.1109/JPHOT.2012.2210199 [DOI] [Google Scholar]
- 3.Anand A., Chhaniwal V., Javidi B., “Tutorial: Common path self-referencing digital holographic microscopy,” APL Photonics 3(7), 071101 (2018). 10.1063/1.5027081 [DOI] [Google Scholar]
- 4.Doblas A., Roche E., Ampudia-Blasco F., Martinez-Corral M., Saavedra G., Garcia-Sucerquia J., “Diabetes screening by telecentric digital holographic microscopy,” J. Microsc. 261(3), 285–290 (2016). 10.1111/jmi.12331 [DOI] [PubMed] [Google Scholar]
- 5.Girshovitz P., Shaked N. T., “Generalized cell morphological parameters based on interferometric phase microscopy and their application to cell life cycle characterization,” Biomed. Opt. Express 3(8), 1757 (2012). 10.1364/BOE.3.001757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Javidi B., Markman A., Rawat S., O’Connor T., Anand A., Andemariam B., “Sickle cell disease diagnosis based on spatio-temporal cell dynamics analysis using 3D printed shearing digital holographic microscopy,” Opt. Express 26(10), 13614–13627 (2018). 10.1364/OE.26.013614 [DOI] [PubMed] [Google Scholar]
- 7.Javidi B., Moon I., Yeom S., “Three-dimensional identification of biological microorganism using integral imaging,” Opt. Express 14(25), 12096–12108 (2006). 10.1364/OE.14.012096 [DOI] [PubMed] [Google Scholar]
- 8.Matoba O., Quan X., Xia P. A. Y., Nomura T., “Multimodal imaging based on digital holography,” Proc. IEEE 105(5), 906–923 (2017). 10.1109/JPROC.2017.2656148 [DOI] [Google Scholar]
- 9.Moon I., Anand A., Cruz M., Javidi B., “Identification of Malaria Infected Red Blood Cells via Digital Shearing Interferometry and Statistical Inference,” IEEE Photonics J. 5(5), 6900207 (2013). 10.1109/JPHOT.2013.2278522 [DOI] [Google Scholar]
- 10.Moon I., Javidi B., “Shape tolerant three-dimensional recognition of biological microorganisms using digital holography,” Opt. Express 13(23), 9612–9622 (2005). 10.1364/OPEX.13.009612 [DOI] [PubMed] [Google Scholar]
- 11.Moon I., Javidi B., Yi F., Boss D., Marquet P., “Automated statistical quantification of three-dimensional morphology and mean corpuscular hemoglobin of multiple red blood cells,” Opt. Express 20(9), 10295–10309 (2012). 10.1364/OE.20.010295 [DOI] [PubMed] [Google Scholar]
- 12.Rawat S., Komatsu S., Markman A., Anand A., Javidi B., “Compact and field-portable 3D printed shearing digital holographic microscope for automated cell identification,” Appl. Opt. 56(9), D127–D133 (2017). 10.1364/AO.56.00D127 [DOI] [PubMed] [Google Scholar]
- 13.Shaked N., Satterwhite L., Patel N., Telen M., Truskey G., Wax A., “Quantitative microscopy and nanoscopy of sickle red blood cells performed by wide field digital interferometry,” J. Biomed. Opt. 16(3), 030506 (2011). 10.1117/1.3556717 [DOI] [PubMed] [Google Scholar]
- 14.Jaferzadeh K., Moon I., Bardyn M., Prudent M., Tissot J., Rappaz B., Javidi B., Turcatti G., Marquet P., “Quantification of stored red blood cell fluctuations by time-lapse holographic cell imaging,” Biomed. Opt. Express 9(10), 4714–4729 (2018). 10.1364/BOE.9.004714 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yi F., Moon I., Javidi B., “Cell Morphology-based classification of red blood cells using holographic imaging informatics,” Biomed. Opt. Express 7(6), 2385–2399 (2016). 10.1364/BOE.7.002385 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Anand A., Moon I., Javidi B., “Automated Disease Identification With 3-D Optical Imaging: A Medical Diagnostic Tool,” Proc. IEEE 105(5), 924–946 (2017). 10.1109/JPROC.2016.2636238 [DOI] [Google Scholar]
- 17.Singh A. S., Anand A., Leitgeb R. A., Javidi B., “Lateral shearing digital holographic imaging of small biological specimens,” Opt. Express 20(21), 23617–23622 (2012). 10.1364/OE.20.023617 [DOI] [PubMed] [Google Scholar]
- 18.Mico V., Ferreira C., Zalevsky Z., García J., “Spatially-multiplexed interferometric microscopy (SMIM): converting a standard microscope into a holographic one,” Opt. Express 22(12), 14929 (2014). 10.1364/OE.22.014929 [DOI] [PubMed] [Google Scholar]
- 19.O’Connor T., Anand A., Andemariam B., Javidi B., “Overview of cell motility-based sickle cell disease diagnostic system in shearing digital holographic microscopy,” JPhys Photonics 2(3), 031002 (2020). 10.1088/2515-7647/ab8a58 [DOI] [Google Scholar]
- 20.Mugnano M., Memmolo P., Miccio L., Merola F., Bianco V., Bramanti A., Gambale A., Russo R., Andolfo I., Iolascon A., Ferraro P., “Label-free optical marker for red-blood-cell phenotyping of inherited anemias,” Anal. Chem. 90(12), 7495–7501 (2018). 10.1021/acs.analchem.8b01076 [DOI] [PubMed] [Google Scholar]
- 21.Park Y., Diez-Silva M., Popescu G., Lykotrafitis G., Choi W., Feld M. S., Suresh S., “Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum,” Proc. Natl. Acad. Sci. U. S. A. 105(37), 13730–13735 (2008). 10.1073/pnas.0806100105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kim K., Yoon H., Diez-Silva M., Dao M., Dasari R., Park Y., “High-resolution three-dimensional imaging of red blood cells parasitized by Plasmodium falciparum and in situ hemozoin crystals using optical diffraction tomography,” J. Biomed. Opt. 19(1), 011005 (2013). 10.1117/1.JBO.19.1.011005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Midtvedt D., Olsen E., Hook F., “Label-free spatio-temporal monitoring of cytosolic mass, osmolarity, and volume in living cells,” Nat. Commun. 10(1), 340 (2019). 10.1038/s41467-018-08207-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dubois F., Yourassowsky C., Monnom O., Legros J., Debeir IV O., Van Ham P., Kiss R., Decaestecker C., “Digital holographic microscopy for the three-dimensional dynamic analysis of in vitro cancer cell migration,” J. Biomed. Opt. 11(5), 054032 (2006). 10.1117/1.2357174 [DOI] [PubMed] [Google Scholar]
- 25.Hejna M., Jorapur A., Song J. S., Judson R. L., “High accuracy label-free classification of single-cell kinetic states from holographic cytometry of human melanoma cells,” Sci. Rep. 7(1), 11943 (2017). 10.1038/s41598-017-12165-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kemper B., Vollmer A., Von Bally G., Rommel C. E., Schnekenburger J., “Simplified approach for quantitative digital holographic phase contrast imaging of living cells,” J. Biomed. Opt. 16(2), 026014 (2011). 10.1117/1.3540674 [DOI] [PubMed] [Google Scholar]
- 27.Roitshtain D., Turko N. A., Javidi B., Shaked N. T., “Flipping interferometry and its application for quantitative phase microscopy in a micro-channel,” Opt. Lett. 41(10), 2354–2357 (2016). 10.1364/OL.41.002354 [DOI] [PubMed] [Google Scholar]
- 28.Cacace T., Bianco V., Mandracchia B., Pagliarulo V., Oleandro E., Patruzo M., Ferraro P., “Compact off-axis holographic slide microscope: design guidelines,” Biomed. Opt. Express 11(5), 2511–2532 (2020). 10.1364/BOE.11.002511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yang Y., Huang H.-Y., Guo C.-S., “Polarization holographic microscope slide for birefringence imaging of anisotropic samples in microfluidics,” Opt. Express 28(10), 14762–14773 (2020). 10.1364/OE.389973 [DOI] [PubMed] [Google Scholar]
- 30.Seo S., Isikman S., Sencan I., Mudanyali O., Su T., Bishara W., Erlinger A., Ozcan A., “High-Throughput Lens-Free Blood Analysis on a Chip,” Anal. Chem. 82(11), 4621–4627 (2010). 10.1021/ac1007915 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.LeCun Y., Bengio Y., Hinton G., “Deep Learning,” Nature 521(7553), 436–444 (2015). 10.1038/nature14539 [DOI] [PubMed] [Google Scholar]
- 32.Sun J., Tarnok A., Su X., “Deep Learning-based single cell optical image studies,” Cytometry 97(3), 226–240 (2020). 10.1002/cyto.a.23973 [DOI] [PubMed] [Google Scholar]
- 33.Jo Y., Cho H., Lee S., Choi G., Kim G., Min H., Park Y., “Quantitative Phase Imaging and Artificial Intelligence: A Review,” IEEE J. Sel. Top. Quantum Electron. 25(1), 1–14 (2019). 10.1109/JSTQE.2018.2859234 [DOI] [Google Scholar]
- 34.Soltanian-Zadeh S., Sahingur K., Blau S., Gong Y., Farsiu S., “Fast and robust active neuron segmentation in two-photon calcium imaging using spatiotemporal deep learning,” Proc. Natl. Acad. Sci. U. S. A. 116(17), 8554–8563 (2019). 10.1073/pnas.1812995116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rivenson Y., Wu Y., Ozcan A., “Deep learning in holography and coherent imaging,” Light: Sci. Appl. 8(1), 85 (2019). 10.1038/s41377-019-0196-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jo Y., Park S., Jung J., Yoon J., Joo H., Kim M., Kang S., Choi M. C., Lee S. Y., Park Y., “Holographic deep learning for rapid optical screening of anthrax spores,” Sci. Adv. 3(8), e1700606 (2017). 10.1126/sciadv.1700606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rubin M., Stein O., Turko N. A., Nygate Y., Roitshtain D., Karako L., Barnea I., Giryes R., Shaked N. T., “TOP-GAN: Stain-free cancer cell classification using deep learning with a small training set,” Med. Image Anal. 57, 176–185 (2019). 10.1016/j.media.2019.06.014 [DOI] [PubMed] [Google Scholar]
- 38.Chen C., Mahjoubfar A., Tai L., Blaby I. K., Huang A., Niazi K. R., Jalali B., “Deep Learning in Label-free Cell Classification,” Sci. Rep. 6(1), 21471 (2016). 10.1038/srep21471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hochreiter S., Schmidhuber J., “Long short-term memory,” Neural Comput. 9(8), 1735–1780 (1997). 10.1162/neco.1997.9.8.1735 [DOI] [PubMed] [Google Scholar]
- 40.Vicar T., Raudenska M., Gumulec J., Balvan J., “The Quantitative-Phase Dynamics of Apoptosis and Lytic Cell Death,” Sci. Rep. 10(1), 1566 (2020). 10.1038/s41598-020-58474-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yichuan T., “Deep learning using linear support vector machines,” in Workshop on Representation Learning, ICML (2013).
- 42.Malacara D., “Testing of optical surfaces”, Ph.D. dissertation (University of Rochester, 1965).
- 43.Shukla R., Malacara D., “Some applications of the Murty interferometer: a review,” Opt. Lasers Eng. 26(1), 1–42 (1997). 10.1016/0143-8166(95)00069-0 [DOI] [Google Scholar]
- 44.Lee S., Park H., Kim K., Sohn Y., Jang S., Park Y., “Refractive index tomograms and dynamic membrane fluctuations of red blood cells from patients with diabetes mellitus,” Sci. Rep. 7(1), 1039 (2017). 10.1038/s41598-017-01036-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.De Nicola S., Finizio A., Pierattini G., Ferraro P., Alfieri D., “Angular spectrum method with correction of anamorphism for numerical reconstruction of digital holograms on tilted planes,” Opt. Express 13(24), 9935 (2005). 10.1364/OPEX.13.009935 [DOI] [PubMed] [Google Scholar]
- 46.Ferraro P., De Nicola S., Coppola G., Finizio A., Alfieri D., Pierattini G., “Controlling image size as a function of distance and wavelength in Fresnel-transform reconstruction of digital holograms,” Opt. Lett. 29(8), 854 (2004). 10.1364/OL.29.000854 [DOI] [PubMed] [Google Scholar]
- 47.Goldstein R., Zebker H., Werner C., “Satellite radar interferometry: two-dimensional phase unwrapping,” Radio Sci. 23(4), 713–720 (1988). 10.1029/RS023i004p00713 [DOI] [Google Scholar]
- 48.Ferraro P., De Nicola S., Finizio A., Coppola G., Grilli S., Magro C., Pierattini G., “Compensation of the inherent wave front curvature in digital holographic coherent microscopy for quantitative phase-contrast imaging,” Appl. Opt. 42(11), 1938 (2003). 10.1364/AO.42.001938 [DOI] [PubMed] [Google Scholar]
- 49.Hammer M., Schweitzer D., Michel B., Thamm E., Kolb A., “Single scattering by red blood cells,” Appl. Opt. 37(31), 7410 (1998). 10.1364/AO.37.007410 [DOI] [PubMed] [Google Scholar]
- 50.Thurston G., Jaggi B., Palcic B., “Measurement of Cell Motility and Morphology with an Automated Microscope system,” Cytometry 9(5), 411–417 (1988). 10.1002/cyto.990090502 [DOI] [PubMed] [Google Scholar]
- 51.Deng J., Dong W., Socher R., Li L., Li K., Fei-Fei L., “ImageNet: A large-scale hierarchical image database,” in 2009 IEEE Conference on Computer Vision and Pattern Recognition (2009). [Google Scholar]
- 52.Huang G., Liu Z., Van Der Maaten L., Weinberger K. Q., “Densely Connected Convolutional Networks,” 2017 IEEE Conf. Comput. Vis. Pattern Recogn. 1, 2261–2269 (2017). 10.1109/CVPR.2017.243 [DOI] [Google Scholar]
- 53.Schuster M., Paliwal K., “Bidirectional recurrent neural networks,” IEEE T. Signal Proces. 45(11), 2673–2681 (1997). 10.1109/78.650093 [DOI] [Google Scholar]
- 54.Breiman L., “Random Forests,” Mach. Learn. 45(1), 5–32 (2001). 10.1023/A:1010933404324 [DOI] [Google Scholar]
- 55.Adili N., Melizi M., Blebbas H., “Species determination using the red blood cells morphometry in domestic animals,” Vet. World 9(9), 960–963 (2016). 10.14202/vetworld.2016.960-963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Grosse S., Odame I., Atrash H., Amendah D., Piel F., Williams T., “Sickle cell disease in Africa: a neglected cause of early childhood mortality,” Am. J. Prev. Med. 41(6), S398–S405 (2011). 10.1016/j.amepre.2011.09.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Centers for Disease Control and Prevention , “Sickle Cell Disease (SCD),” https://www.cdc.gov/ncbddd/sicklecell/.
- 58.Steele C., Sinski A., Asibey J., Hardy-Dessources M., Elana G., Brennan C., Odame I., Hoppe C., Geisberh M., Serrao E., Quinn C., “Point-of-care screening for sickle cell disease in low-resource settings: A multi-center evaluation of HemoTypeSC, a novel rapid test,” Am. J. Hematol. 94(1), 39–45 (2019). 10.1002/ajh.25305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Alapan Y., Fraiwan A., Kucukal E., Hasan M. N., Ung R., Kim M., Odame I., Little J. A., Gurkan U. A., “Emerging point-of-care technologies for sickle cell disease screening and monitoring,” Expert Rev. Med. Devices 13(12), 1073–1093 (2016). 10.1080/17434440.2016.1254038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Vigil G. D., Howard S., “Photophysical characterization of sickle cell disease hemoglobin by multi-photon microscopy,” Biomed. Opt. Express 6(10), 4098 (2015). 10.1364/BOE.6.004098 [DOI] [PMC free article] [PubMed] [Google Scholar]