First experience with spatial frequency domain imaging and red-light excitation of protoporphyrin IX fluorescence during tumor resection

Abstract

Fluorescence-guided surgery (FGS) enhances intraoperative visualization of tumors to maximize safe resection, and quantitative fluorescence imaging (qFI) of protoporphyrin IX (PpIX) has provided additional information for guidance during intracranial tumor surgery. Previous developments in fluorescence quantification have demonstrated that the depth of fluorescence signals can be estimated given known optical properties in a lab setting, and now with the work described here that these optical properties can be determined in vivo in human brain tissue in the operating room (OR) during tumor resection procedures. More specifically, we report the first depth estimation of subsurface tumor intraoperatively, achieved with the combination of spatial frequency domain imaging (SFDI) for optical property measurement and red-light excitation of PpIX. We modified a commercial surgical microscope (Zeiss) with a digital light processing module (DLI Austin, TX) to modulate light from a xenon arc lamp to illuminate the field. White-light excitation and a liquid crystal tunable filter (LCTF Verispec) were used to measure diffuse reflectance at discrete wavelengths of 670 nm and 710 nm on a sCMOS camera. An illumination-side filter wheel allowed excitation of PpIX fluorescence at 405 nm and 635 nm, and the LCTF measured fluorescence emissions at 670 nm and 710 nm. Data acquisition and processing generated wide-field images of the depth of PpIX fluorescence within 1 minute in the OR. The ability of the clinical microscope to perform optical property mapping with SFDI and convert these wide-field estimates into images of the depth of fluorescence was tested in tissue simulating phantoms and in vivo during a craniotomy for brain tumor resection. Results indicate that wide-field optical property estimates with SFDI can be combined with depth sensing algorithms to produce maps of the depth of PpIX when exposed to red-light in the OR.

1. Introduction

Primary brain malignancies remain among the most challenging to treat and come with poor prognoses, accordingly. Primary tumors, even low-grade cancers, are infiltrative and often progress rapidly. Extent of resection influences patient survival and quality of life [1], though even small amounts of residual disease can negatively impact the efficacy of adjuvant therapies [2,3]; therefore, methods to increase completeness of resection are valuable. Fluorescence imaging techniques continue to improve surgical guidance [4–6], though limitations still exist. Aminolevulinic Acid (ALA) has recently been approved by the US Food and Drug Administration (FDA) for fluorescence guidance as it leads to endogenous synthesis of visibly fluorescent protoporphyrin IX (PpIX) [7]. The main absorption peak of PpIX is 405 nm; however, the correspondingly high absorption of blood results in only superficial fluorescence excitation of the agent. To guide resection effectively in practice, some depth detection over a wide field-of-view (FOV) is desirable. Red-light excitation of PpIX fluorescence at 635 nm produces signal from tumors below the surface [8]. Furthermore, techniques have been developed to estimate the depth at which the fluorescence emissions are measured [9,10]. These methods, however, rely on knowledge of tissue optical properties, namely absorption and transport scattering coefficients, and they have not been applied to tissue in vivo to date nor used during surgery in the operating room (OR), in part because of lack of viable methods for determining optical properties over the surgeon’s FOV.

Spatial frequency domain imaging (SFDI) is an approach that can be used to interrogate tissue at multiple effective source-detector separations by illuminating it with sinusoidal patterns having different spatial frequencies. By spatially resolving diffuse reflectance of turbid media illuminated with different spatial frequencies, SFDI recovers wide-field maps of tissue optical properties [11–16]. The technique is attractive because of its data acquisition and computational simplicity, but its viability in practice, for example during surgery, depends on the performance that can be attained under these more complex conditions. In this paper, we build on previous work [16] by demonstrating that SFDI can be combined with red-light excitation of PpIX to achieve quantitative sensing of fluorophore depth over the surgeon’s FOV.

Specifically, we incorporate optical properties estimated from SFDI with depth estimation methods we developed in the past [9,10] to generate spatially-resolved maps of the depth of fluorescent inclusions for the first time. Performance of the new technique, both in terms of the lateral resolution of the SFDI optical property estimates and the accuracy of the fluorophore depth determination, is reported for tissue simulating phantoms that mimic the range of optical properties expected in human brain tissue, with and without fluorescent inclusions. Feasibility of human brain imaging with this combination of methods for depth sensing is also demonstrated, and a wide-field fluorophore map of PpIX depth is shown in the OR for the first time. Results indicate that optical property estimation with SFDI can be used to generate wide-field maps of fluorophore depth under red-light excitation of PpIX in vivo.

2. Methods

2.1. Instrumentation

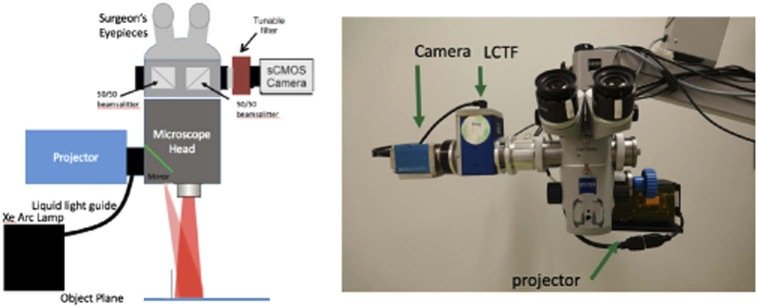
The schematic diagram of a surgical microscope (S1, Zeiss) that was modified for SFDI applications in the OR is presented in Fig. 1. Illumination was provided by a xenon arc lamp via a liquid light guide (Sutter Instruments) and focused onto a DMD module (DLI, TX) used to generate spatially-modulated patterns on an object plane at a working distance of approximately 20 cm. A detection module consisting of a liquid crystal tunable filter (LCTF, Perkin Elmer) and a 14-bit sCMOS camera (PCO Edge 4.2, PCO, Kelheim, Germany) was used for measuring diffuse reflectance and fluorescence signals. Imaging field-of-view (FOV) and magnifications were consistent with operating conditions.

Fig. 1.

(a) Schematic diagram of the clinical SFDI system and (b) photograph of the system. The Xe Arc lamp (not shown) is mounted to the base of the microscope stand.

2.2. Depth estimation method

Our method for depth estimation of fluorescence signal has been described previously and is summarized briefly here [9,10]. For a point-like fluorescent inclusion, the general form of the diffusion equation solution can be simplified to

$$\text{ln}(\Gamma )=m\times d+b$$ (1)

where Γ is the ratio (I_λ2/I_λ1) of fluorescence intensity measured at two distinct wavelengths, d is the depth of the signal, b is a normalization constant and

$$m=\frac{1}{{\delta }^{{\lambda }_2}}-\frac{1}{{\delta }^{{\lambda }_1}}$$ (2)

To determine the normalization constant, b, the intensity ratio (I_λ2/I_λ1) is measured at a depth, d = 0. In the clinical setting normalization can be achieved by measuring the intensity ratio on tumor tissue located in the field of view, directly on the surface of the surgical cavity. For our experiments, the wavelengths, λ₁=670 nm and λ₂=710 nm, were used which correspond to the greatest difference in metHb absorption that still provides significant fluorescence signal when PpIX is excited at 635 nm (Fig. 2)

Fig. 2.

Emission spectra of PpIX when excited at 635 nm and absorption of metHb. 670 nm and 710 nm were the wavelengths chosen to calculate fluorescence intensity ratio, (I_λ2/I_λ1).

To determine m, we find the effective depth penetration at our desired wavelengths which depends on optical properties at our wavelengths of interest such that

$$\delta =\sqrt{\frac{D}{{\mu }_a}}$$ (3)

where D is the diffusion coefficient which is a function of the absorption and reduced scattering coefficients,

$$D=\frac{1}{3({\mu }_a-{{\mu }_s}^{\mathrm{\prime }})}$$ (4)

By using the optical scattering parameters estimated with SFDI and determining the diffusion coefficient and effective depth penetration, we estimate m to solve for the depth, d, in Eq. (1). This technique has been shown to resolve multiple fluorescent inclusions in phantom studies at depths up to 8 mm [11].

2.3. Tissue simulating phantoms

Diffuse reflectance and fluorescence images were acquired with our clinical SFDI system on tissue-simulating phantoms. Two experiments were conducted to (1) evaluate the spatial resolution of PpIX concentration estimation, and establish a profilometry calibration, and (2) determine the accuracy of recovering the depth of a PpIX inclusion. Figure 3 shows the experimental setups for the two phantom configurations. Phase profilometry correction was achieved by projecting an intensity sine wave with three different phase shifts and recovering the fringe phase at each pixel with the phantom positioned in multiple orientations and at different heights. The linear relationship between the inverse of the sample height variation and the inverse of phase variation is then estimated [17–19]. The height of the system was varied over a 3-cm range using a z-translation stage, while tilt angle was varied from −20 deg to +20 deg by rotating the head of the clinical microscope to determine the height-dependent and angle-dependent intensity calibrations.

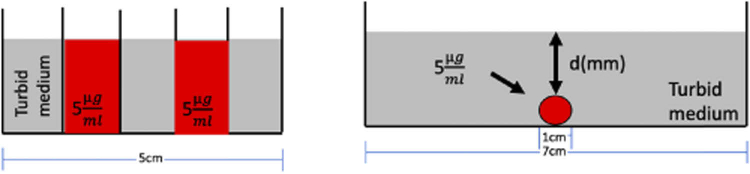
Fig. 3.

Diagram of phantom experiments evaluated (a) Experiment 1: lateral resolution of spectrally fitting PpIX with planar illumination vs. SFDI and (b) Experiment 2: recovering depth, d, after estimating the optical properties of the turbid medium.

2.3.1. Experiment 1: spatial resolution

For Experiment 1, solutions were placed in a container that had 5 sections, each being 3cm x 1cm x 2 cm deep and separated by 0.17 mm glass cover slips [Fig. 3(a)]. For these solutions, wells were alternated to contain no PpIX or concentrations of 5μg/mL. Bulk media for the phantom consisted of five solutions varying from low scattering (μ_s’ = 0.4mm⁻¹) and absorption (μ_a= 0.001mm⁻¹) to high scattering (μ_s’ = 2.4mm⁻¹) and absorption (μ_a= 0.3mm⁻¹). The phantom was imaged in various orientations of the microscope head, including 4 front and 4 side tilt angles spanning -20° to +20° (inclusive of a horizontal, 0°, setting) at each of 4 heights over a range of 3 cm for a total of 36 configurations. By imaging in multiple orientations, we were able to assess the system’s ability to estimate PpIX concentration under different sample-detector distances simulating more complex clinical conditions. Excitation light was filtered with a 10 nm bandpass centered at 405 nm and illuminated the phantom at seven spatial frequencies, including f = 0 (corresponding to planar illumination), 0.1, 0.3, 0.5, .0.6, 0.8, and 1 mm^-1. Fluorescence images were acquired over a range of 600 nm to 720 nm in 3 nm increments, and included 41 planar illumination images and 123 images associated with each spatial frequency leading to a total of 779 acquisitions. For fluorescence excited with spatially modulated light, the 123 images were demodulated, and data for each spatial frequency were fit spectrally using a method previously described [5,6] to determine concentrations of PpIX. Edge response functions were averaged over the different phantom orientations and compared between planar and modulated illumination patterns.

2.3.2. Experiment 2: depth estimation

For Experiment 2, a 7 cm diameter x 11 mm deep well was filled with liquid bulk media that represented different absorption and transport scattering coefficients and were produced by varying concentrations whole bovine blood (Lampire) and intralipid (Intralipid 20%, Patterson Veterinary Supply), respectively, to span the range of optical properties found in human brain tissue [20]. Six values of absorption coefficient (between 0.0001 and 0.3 mm^-1 in 3x intervals), and 9 values of scattering coefficient (between 0.4 and 2.0 mm^-1 in intervals of 0.2 mm^-1) were combined to generate a total of 54 pairs of optical properties at 670 nm. A fluorescence inclusion (1 mm inner diameter) was placed at the bottom of the well and filled with a solution of bulk matching optical properties and a PpIX concentration of 5 μg/mL. Depth of the fluorescent inclusion, d, was increased from 0 (corresponding to surface fluorescence) to 10 mm in 1 mm increments [Fig. 3(b)].

An acquisition sequence consisting of white light modulated at the two frequencies (f = 0, 1 mm^-1) was executed to measure diffuse reflectance at 670 nm and 710 nm for each frequency. Light was then processed with a 10 nm bandpass filter centered at 635 nm and modulated to a frequency of 0.05 mm^-1 to measure PpIX fluorescence intensities at 670 nm and 710 nm. The diffuse reflectance images illuminated with f = 0, 1 mm^-1 were compared to a 2-frequency lookup table (LUT) constructed by measuring diffuse reflectance of a reference set of phantoms of varying optical properties, at the chosen frequencies. Using this method developed by Cuccia et al [11], we were able to recover optical properties at the chosen wavelengths. These optical properties were combined with the intensity ratios from the fluorescence images at the two wavelengths based on the depth estimation algorithm described in Section 2.2.

2.4. In vivo measurements

To evaluate the clinical SFDI system in an operative setting, data were acquired under a protocol approved by the Institutional Review Board at Dartmouth Hitchcock Medical Center to estimate absorption and scattering parameters of the exposed cortex intraoperatively. Three images with spatial frequency of 0.10 mm⁻¹ were obtained for profilometry at each wavelength. For acquisition of diffuse reflectance values at f = 1 mm⁻¹ and f = 0 mm⁻¹, three phases of f=1 mm⁻¹, one uniform illumination (f=0 mm⁻¹), and one dark image were recorded at each wavelength. For acquisition of fluorescence intensity, three images with spatial frequency of f = 0.05 mm^-1 at 635 nm were obtained for the 670 nm and 710 nm measurement wavelengths (totaling 20 images, requiring ∼9 s total). The 0.05 mm^-1 spatial frequency was used for 635 nm illumination since it provided the deepest penetration of the modulated light [21] while maintaining a lateral resolution in the fluorescence signal better than 1 mm based on Experiment 1. Images were processed for height and optical property estimation with profilometry correction. Data acquisition and processing generated wide-field images of the depth of PpIX fluorescence within 1 minute in the OR.

3. Results

For diffuse reflectance images at 670 nm and 710 nm with planar illumination, incident light intensities were 0.58 mW/cm² and 0.47 mW/cm², respectively, while fluorescence was excited with planar illumination having an intensity of 0.61 mW/cm². Results from the two phantom experiments included measurements over all frequencies and are summarized below.

3.1. Phantom experiment 1: spatial resolution

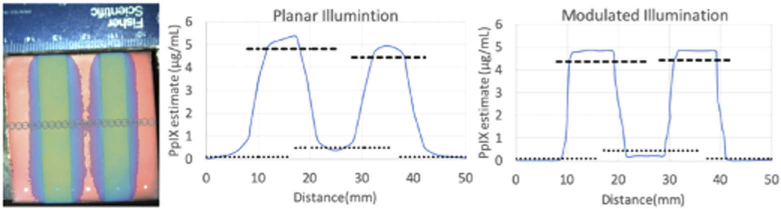
Spatial resolution was evaluated by measuring the edge response function across a phantom when the 5 wells were filled with alternating PpIX concentrations of 0 and 5 μg/mL. Optical properties of solutions were varied so that spatial resolution could be averaged over the range of values found in brain tissue. Edge response functions were measured and averaged for all orientations. Figure 4(a) shows a representative RGB photo of the phantom with a spectrally fit concentration map superimposed, along with the average edge response function when the phantom was excited with planar illumination (Fig. 4(b)), and the average edge response function when the phantom was illuminated with spatially modulated light [Fig. 4(c)]. To define spatial resolution, we used the distance in pixels to transition from a PpIX level of 10% [dotted line in Figs. 4(b), 4(c)] to 90% [dashed line Figs. 4(b), 4(c)] of the estimated values in wells containing PpIX, as described elsewhere [11]. When excited with planar illumination, across the four well transitions, the spatial resolution was determined to be 3.2 mm with a standard deviation of 0.8 mm. When excited with spatially modulated illumination, the spatial resolution was measured to be 0.93 mm with a standard deviation of 0.1 mm. For the planar illumination case, comparing the resolution across the wells of changing optical properties, we saw a range in the resolution measurements from 2.85 to 3.95 mm. For spatially modulated illumination, comparing the resolution across the wells, we saw a range in resolution measurements from 0.90 to 0.95.

Fig. 4.

(a) Photograph of the heterogeneous phantom overlaid with an example of spatially fit fluorescence quantification. Average edge response functions for fluorescence excited with (b) planar illumination and (c) spatially modulated illumination. Dashed lines correspond to 90% and dotted lines correspond to 10% of the estimated PpIX in the wells containing the fluorophore.

3.2. Phantom experiment 2: depth estimation

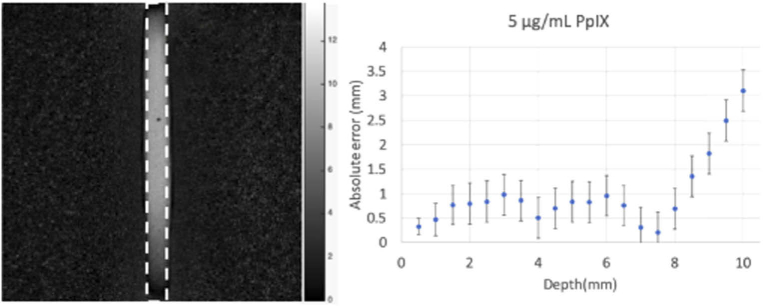
Depth estimation was evaluated by applying the Section 2.2 method which relies on a linear relationship between the fluorescence intensity ratio measured at two wavelengths in the emission range, given the optical properties of the intervening medium. In the Experiment 2 phantom, optical properties were found from the 2-frequency LUT derived from the diffuse reflectance images, and Γ, the fluorescence intensity ratio, was recovered from the fluorescence images, and substituted into Eq. (1) to generate a depth map for the fluorescence inclusion. A region of interest (ROI) corresponding to the true size of the fluorescent inclusion was selected in the depth map [dotted line, Fig. 5(a)]. It was determined by the size of the inclusion in the FOV, overlaid on the image, and used to calculate average error over the region. Error in depth estimation versus actual depth was then averaged over ROIs from experiments performed over the range of bulk optical properties, and determined to be 0.69 +/- 0.25 mm for depths up to 9 mm. Figure 5(b) shows error in depth estimation relative to true depth over the span of depths evaluated.

Fig. 5.

(a) Depth map where intensity corresponds to depth estimation for an inclusion placed 9 mm below the surface. Dotted line ROI corresponding to the actual position of the fluorescent inclusion and (b) error in predicted depth vs. true depth of the 5 μg/mL PpIX inclusion over the span of depths evaluated. Error bars represent relative standard deviation over the selected ROI at each depth.

3.3. In vivo imaging

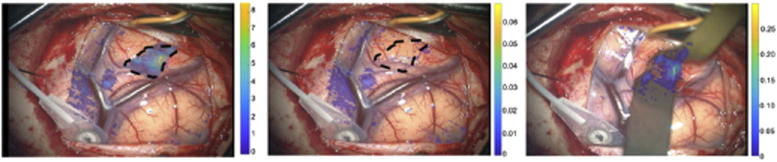
Processing of acquired images into profilometry corrected absorption and transport scattering values and calculating fluorescence intensity ratios to produce 2-D depth estimation maps required about 1 min of computation time. A depth estimation sequence (white-light SFDI followed by modulated illumination of 635 nm excitation of PpIX fluorescence) was acquired at the start of surgery with the SFDI-modified microscope, after the dura was opened. This research unit was then removed from the surgical field, and the standard-of-care operating microscope (Pentero, Zeiss) was brought in and used to continue the surgical procedure. An RGB image was acquired with this operating microscope, and the 2D depth estimation map acquired with the research microscope was registered to the Pentero’s field-of-view (its RGB image) using mutual information (Matlab function) and overlaid on the Pentero’s RGB image of the surgical field, as shown in Fig. 6(a). Figure 6(b) presents an overlay of a PpIX concentration map when fluorescence was excited with 405 nm light with the Pentero at the same point in time during the procedure. Comparing areas outlined by the dashed lines in Figs. 6(a) and 6(b), SFDI with red-excitation light estimates fluorescence exists up to 8 mm below the surface, whereas no significant fluorescence is observed from 405 nm excitation of the subsurface tumor as expected. As surgery progressed, another fluorescence concentration map was acquired with 405 nm excitation [Fig. 6(c)], in which a significant amount of PpIX was observed below the cortical surface, as expected based on results from the SFDI red-excitation data.

Fig. 6.

(a) Depth estimation of PpIX fluorescence using optical properties acquired with SFDI and 635 nm excitation with color bar in mm (b) PpIX concentration using 405 nm excitation with color bar corresponding to μg/mL; the contour of tumor at depth as determined in (a) has been superposed retrospectively on the image, (c) Same as (b) but later in surgery when subsurface fluorescence was exposed.

4. Discussion and conclusions

In this study, we demonstrated the value of combining SFDI with red-light excitation of PpIX in order to produce wide-field image estimates of the depth of the fluorophore, PpIX. Previously, wide-field mapping of PpIX concentration has been limited to the surgical surface, and has required acquisition of reflectance and fluorescence signals intraoperatively [5–7]. Further, fluorescence depth estimation techniques have relied on prior knowledge of tissue optical properties [9,10] and have not been applied in vivo, and especially not in the human OR, because of lack of methods for estimating the required tissue optical properties, efficiently and effectively, over the surgeon’s FOV. By combining SFDI reflectance to estimate tissue absorption and scattering properties over the surgical field, generation of tumor depth estimation maps is possible with red-light excitation of PpIX fluorescence.

The spatial frequency of 1 mm⁻¹ for light patterns projected onto the imaging plane to acquire diffuse reflectance data was chosen because it was the highest spatial variation available that was not degraded by the resolution of the projector. As previously reported [17–19], the effective penetration depth of light decreases with spatial frequency of the projected pattern, and a frequency of 1 mm⁻¹ probes only the superficial layers in tissue. Use of a single spatial frequency assumes tissue is optically homogeneous. Clinically, optical homogeneity is not likely the case; hence, some error is expected in the depth estimate of any subsurface tumor. To address this limitation, future clinical work will apply multiple spatial frequencies, and take advantage of differences in penetration depth at each frequency to approximate optical sectioning techniques for estimating optical properties at multiple depths within the surgical field.

In its current configuration, red-light excitation of PpIX for depth estimation is limited by the need to normalize to the superficial fluorescence signal, but incorporating SFDI and red-light excitation modules into standard clinical microscopes would allow a surgeon to switch between modes rapidly to update concentration and depth estimation maps throughout the course of resection. Another limitation is loss of light from the complicated optical paths required for modulated light illumination. This light loss, when coupled with inefficiencies in the filtering of emitted light with the LCTF, results in decreased throughput at our wavelengths of interest, thereby, increasing errors in depth estimates. In future studies, we will incorporate a detection system that separates and acquires image data more efficiently, and at multiple wavelengths simultaneously, within a single module. With these advances, we expect to improve the utility of SFDI with red-light excitation of PpIX even further.

Given the current SFDI processing time of 1min, acceleration of the method is needed to provide quantitative fluorescence information in real time. In this report, we focused on the instrumentation and methods required for image acquisition, intraoperatively, and ignored optimization of the processing algorithm (it also executed on the available CPU). With an upgrade to the graphics card of our clinical computer, the code is currently being optimized to execute on GPUs to handle the optical property LUT much more efficiently.

Fluorescence guided resection is a powerful tool for surgical removal of brain tumors. However, fluorescence signals from below the surgical bed are challenging to interpret without knowledge of tissue absorption and scattering parameters. By modifying a surgery-ready microscope to spatially modulate illumination light, we have demonstrated that depth estimation maps of brain-tissue-like phantoms can be estimated rapidly and accurately with errors < 2 mm at spatial resolutions better than 1 mm over fields of view of > 7 cm. Further, the first in vivo results obtained during a brain tumor resection indicate the feasibility and potential of the approach, even if processing times in the current implementation are in need of improvement. As described in Section 2.2 and implemented here, red light excitation of PpIX for depth estimation does require normalization to the superficial fluorescence signal which is a potential limitation. However, incorporating SFDI and red-light excitation modules into single, fully-enabled operating microscope would allow a surgeon to switch between modes rapidly in order to update concentration and depth estimation maps throughout the course of resection. Overall, these results suggest that SFDI is likely to enhance fluorescence-guided resection of brain tumors even further.

Funding

National Institutes of Health10.13039/100000002 (R01NS052274-01A2).

Disclosures

Drs. Roberts, Wilson, and Paulsen have equity in InSight Surgical Technologies LLC.