Global sensitivity analysis of biological multi-scale models

Abstract

Mathematical models of biological systems need to both reflect and manage the inherent complexities of biological phenomena. Through their versatility and ability to capture behavior at multiple scales, multi-scale models offer a valuable approach. Due to the typically nonlinear and stochastic nature of multi-scale models as well as unknown parameter values, various types of uncertainty are present; thus, effective assessment and quantification of such uncertainty through sensitivity analysis is important. In this review, we discuss global sensitivity analysis in the context of multi-scale and multi-compartment models and highlight its value in model development and analysis. We present an overview of sensitivity analysis methods, approaches for extending such methods to a multi-scale setting, and examples of how sensitivity analysis can inform model reduction. Through schematics and references to past work, we aim to emphasize the advantages and usefulness of such techniques.

1. Introduction

Multi-scale models (MSMs) are becoming increasingly popular for use as a tool in systems biology due to the vast range of spatial and temporal scales involved in capturing biological processes. For example, a model may explicitly span biological dynamics representing genome, molecular, cellular, tissue, whole body, or population scales. Examples of MSMs and their analysis, validation, and applications in systems biology have been previously reviewed [39, 7]. MSMs tend to be highly complex models and have a large number of parameters, many of which have unknown or uncertain values, leading to epistemic uncertainty in the system. There may also be aleatory uncertainty present that arises from stochasticity in the model. Quantifying these uncertainties is essential for interpreting model outputs and for increasing understanding of the system under study.

Uncertainty in models can be assessed using sensitivity analysis. Sensitivity analysis is an area of study that involves the development of tools that assess sources of uncertainty in computational models of biological systems, and that help elucidate the relationships between parameters/mechanisms and model outcomes. This type of analysis has been used in many different systems biology settings, such as models for cancer [11, 18, 27, 6], immune response [1, 40, 8], ecology [4, 21], drug resistance and antibiotic treatment [26], and vaccine efficacy [30, 14]. There are also many other uses for sensitivity analysis, such as assisting in model fitting/calibration, evaluating differences between different modeling approaches, and determining where models can be simplified to reduce computational cost or to increase understanding of, and confidence in, simulated results. Sensitivity analysis can be local, whereby parameters are varied around a single set of parameter values, or global, where the effects of parameters are evaluated by varying the parameters simultaneously over a large range of values using methods such as Latin Hypercube Sampling (LHS) or Extended Fourier Amplitude Sensitivity Testing (eFAST) [25, 28].

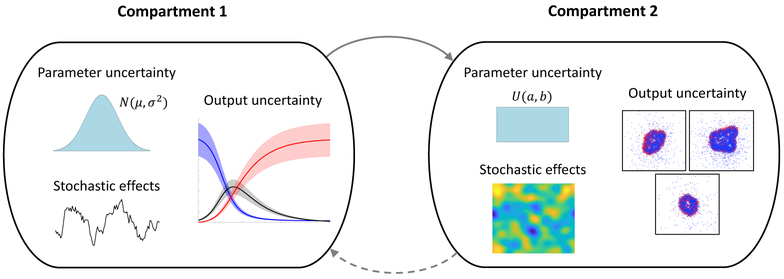
Methods for global sensitivity analysis in the context of systems biology models have been reviewed in the last decade [23, 43]. Here we focus on the special considerations of multi-scale modeling such as the increased computational cost associated with bridging model scales and the possibility of exploiting nested or multi-compartmental structures of models. In this review, we discuss approaches for global sensitivity analysis for multi-scale and multi-compartment models. Figure 1 illustrates a hypothetical example of such a model that combines different model scales, modeling techniques (i.e., hybrid), wide parameter distributions, and different dimensionalities.

Figure 1:

An example of a two-scale (or two-compartment) model. Within each scale, there is epistemic uncertainty in the parameter values and aleatory uncertainty arising from stochastic effects; both lead to uncertainty in model output. Examples of submodel outputs are shown for a stochastic differential equation model (left) and an agent-based model with spatial heterogeneity due to stochastic effects (right). Communication between scales, i.e., passing of information such as the values of dynamic quantities or calculated parameters, may be one-way or two-way.

We begin with a brief overview of commonly used methods for parameter sensitivity analysis. We then discuss approaches for extending these methods to a multi-scale setting, keeping in mind the growing complexity and computational cost. Finally, we will discuss examples where sensitivity analysis has been used to analyze outcomes from simplifying (i.e., reducing) models to determine in what scenarios a simplified model is sufficient.

2. Sensitivity methods for a single model scale

2.1. Sampling techniques

Most methods for sensitivity analysis require a comprehensive sampling of the biologically relevant parameter space. Commonly, parameter values are sampled uniformly within specified ranges, though other distributions such as normal distributions may also be used if more information about parameter values or distributions are known. Since ranges of values for different model parameters may differ by several orders of magnitude, parameters are often scaled or log-transformed. The most straightforward technique for sampling a parameter space is simple random sampling, in which each sample is independently generated from a probability distribution using a random number generator. However, it is possible that by chance, a simple random sample may not evenly cover the parameter space. For accuracy, it is necessary to cover the entirety of the parameter space; however, the potential exists for either inefficient sampling in which multiple values are chosen close together or for large sections of the parameter space to be missed entirely. Several sampling methods have been proposed to remedy this issue, such as Latin hypercube sampling (LHS) [25]. LHS is a popular choice for uncertainty analysis in systems biology due to its accuracy and flexibility [23]. LHS ensures that the entire parameter space is represented, i.e., that the range of each parameter is fully stratified [33]. In contrast to random sampling which, although straightforward to implement requires “sufficiently large” samples, LHS offers a viable alternative when “large” samples are not computationally feasible [33].

If the system being studied is a stochastic model then there will be variability in model output, even from the same input parameter set, due to stochastic random effects (i.e. aleatory uncertainty). To capture this variability, multiple replications should be performed for each parameter set in the sample. Multiple techniques have been developed to determine the optimal number of replications to perform for each parameter set [32]. Law et al. advocate a rule of thumb approach where they recommend that at least three to five replications are performed [17]. This approach does not account for characteristics of model output, however; in reality, many more replications need to be performed in order to reduce variability of highly stochastic data.

Another approach for determining the number of runs to use is the graphical method described in [32]. This method requires plotting the cumulative mean of results increasing the number of runs until the mean becomes relatively stable. The final method discussed in [32] is the confidence interval method. Using this method, a confidence interval is developed to show how accurately the mean result is being estimated. A narrower interval means more accurate results, a wider interval less so. [28] used the Vagha-Delaney A test to estimate sample size, but this test is highly conservative, often resulting in large numbers of required runs [28, 3].

2.2. Measures of sensitivity

The most common approach to performing sensitivity analysis is correlation-based sensitivity. When using this approach, one must first decide on the type of correlation to use; for example, Pearson correlation measures the strength and direction of a linear relationship, while rank (Spearman) correlation measures the strength and direction of any monotone relationship. Rank correlation is thus more widely applicable since nonlinear relationships often arise in biological models. In addition, the use of partial correlation allows a measure of sensitivity of the model output to a given parameter while controlling for the effects of other model parameters. Thus, a popular choice for correlation-based sensitivity is the partial rank correlation coefficient (PRCC). This method is described in detail in [23]. Statistical tests (namely z-tests) can be performed to determine whether a parameter’s PRCC is significantly different from zero or from the PRCC of another parameter as a way to compare sensitivities.

In some model systems, relationships between parameters and model outputs are not monotonic. In this case, correlation-based sensitivity analysis should not be used as the results may be misleading. Instead, one may choose to use a sensitivity method based on decomposition of variance. Such methods include the extended Fourier Amplitude Sensitivity Test (eFAST) and analysis of variance (ANOVA) based sensitivities such as the Sobol sensitivity index [23, 42, 15]. These variance-based sensitivity methods measure the fraction of output variance that can be explained by variance in the input parameters. For these methods, statistical inference may be performed via the use of a dummy parameter to determine what value of the sensitivity index is significantly different from zero [23].

For continuous models, such as differential equations models, one may also use derivative-based sensitivity, where partial derivatives with respect to model parameters are calculated or estimated [35]. Partial derivatives can be computed analytically for some model systems, but most commonly these derivatives are approximated via finite difference. This is called one-at-a-time (OAT) sensitivity since it involves varying one parameter at a time while keeping others fixed. Though the derivative is a local property, it can be evaluated throughout the parameter space in order to derive global information. While this is more expensive than performing correlation-based sensitivity analysis since the finite difference approximation requires more model evaluations, it also provides more information. For example, one may consider both the expected value of the partial derivatives as well as their variance in order to better understand how parameter sensitivities change across the parameter space [15]. For models whose partial derivatives can be computed analytically, there is no substantial increase in computational cost.

The above methods, and the scenarios in which they are typically applied, are summarized in Table 1.

Table 1:

Summary of single-scale sensitivity methods and when to use them.

Method type	When to use	Model type
Correlation-based e.g., PRCC	Monotonic relationships	Continuous/stochastic
Variance-based e.g., eFAST, Sobol	Non-monotonic relationships	Continuous/stochastic
Derivative-based e.g., OAT	Inexpensive/simple model	Continuous

2.3. Using surrogate models to assist in evaluating sensitivity

Performing sensitivity analysis on a large MSM can be highly computationally expensive. To understand epistemic uncertainty, stochastic uncertainty must be quantified and controlled for, requiring large numbers of repetitions of each parameter generated under LHS. A surrogate tool, or emulator, converts a set of parameter values into a prediction of the simulation response that is representative of a high number of replicates. A well-trained emulator that is capable of accurately predicting a simulated response at a population level is a highly efficient method of mediating the high computational cost associated with eliminating stochastic uncertainty. Alden et al. [2] discuss several methods for the development of such emulators for sensitivity analysis. Examples are given for a model of Payers Patch formation in the gut, and they include neural networks, random forests, generalized linear models, support vector machinery, and Gaussian processes. The authors also describe the development of an ensemble that combines the output from several machine learning techniques to improve accuracy of results. Using this methodology, the maximum processing time of simulating an LHS analysis using the emulator was just 12 minutes, with the quickest model, the Generalized Linear Model, taking just 0.2 seconds. It is clear that there is a huge advantage to using this technique over a traditional sensitivity analysis that, in the case of Alden et al., required running 500 simulations for each parameter set, with an average running time of 98 seconds per simulation. Using an emulator, the authors were able to replicate previously published sensitivity analysis results [2]. This technique was also used by Cicchese et al. who used surrogate-assisted optimization with a MSM to design new antibiotic treatment regimens for tuberculosis [5].

Surrogate models have also been used for deterministic but computationally expensive models, for example partial differential equations (PDE) models describing diffusion. One such example is the recent use of generalized polynomial chaos expansions to perform sensitivity analysis and parameter uncertainty quantification on a PDE model of yeast cell polarization [31]. The use of polynomial surrogates allows for capturing nonlinear relationships between parameters and model outputs, as any continuous function can be approximated by a polynomial. It also allows for fast derivative-based sensitivity analysis since the derivative of a polynomial can be easily computed analytically. In [31], the use of polynomial surrogate models afforded a 180-fold reduction in computational cost for evaluating parameter uncertainty from experimental data.

Of course, there are caveats as with all techniques. Models that are highly stochastic or have a discontinuous relationship with a given parameter may not be suitable for certain surrogate models. Further, a large number of simulated results are required to train the surrogate models, and if the underlying model changes in some way then the results of the surrogate may no longer apply and the surrogate model would have to be regenerated, adding further computational expense.

3. Sensitivity analysis across scales

3.1. All-in-one sensitivity

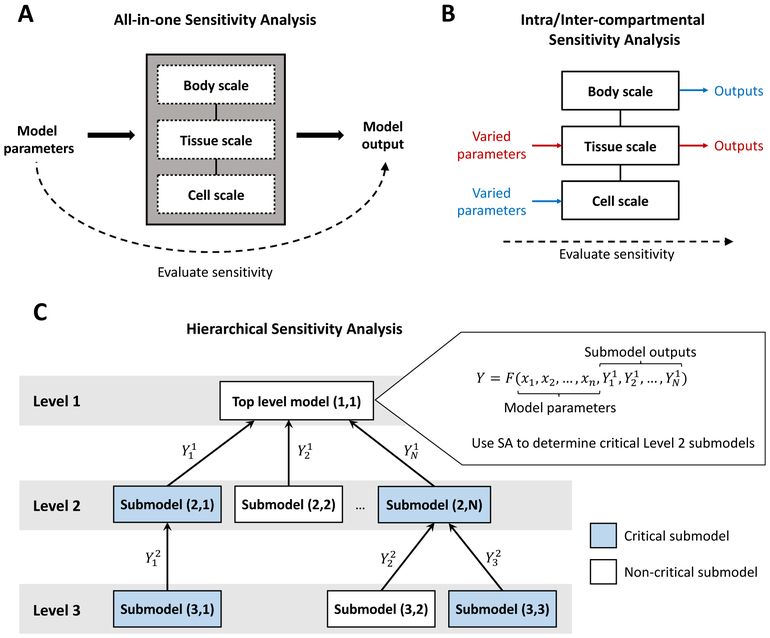
Conceptually, the simplest way to approach sensitivity analysis in a MSM is to simply treat the entire model as a black box (Figure 2A). In this approach, each sample requires a full MSM evaluation, and all (or a subset from each sub-scale) model parameters may be included in the sensitivity analysis. For relatively small and inexpensive models, this is both simple and practical. However, if a model is sufficiently complex, there may be issues with parameter interactions that complicate the sensitivity analysis. Further, if a model is computationally expensive then the large numbers of simulations required for effective sampling in the sensitivity analysis may be infeasible. One way to reduce the number of parameters varied in an all-in-one sensitivity analysis, and thus reduce the number of samples required, is to perform sensitivity analysis for the smaller-scale submodels first. Then, only the most sensitive parameters identified for each submodel need to be varied in the full model analysis. There is a danger, however, that parameters that are important when combined with other scales may not be deemed important to the individual-scale model itself. In addition, even this parameter space reduction may be insufficient in reducing computational costs if the full MSM is expensive to evaluate.

Figure 2:

(A) All-in-one sensitivity analysis: the full model is treated as a black box with all or a subset of model parameters being varied. (B) Intra/inter-compartmental sensitivity analysis: parameters for a given scale are varied and compared to outputs from the same (intra; red) or a different (inter; blue) scale. In this example, intra-compartmental analysis is performed on the tissue scale and inter-compartmental analysis is performed by varying the cell scale parameters and comparing to the whole-body scale outputs. (C) Hierarchical sensitivity analysis: analysis is first performed on the top level model, replacing the outputs of Level 2 submodels as constant parameters, to determine which Level 2 submodels are critical. This is then repeated for the critical Level 2 submodels to determine if any Level 3 submodels are critical. Each submodel has an output $Y_i^j$ that is used as input for the next highest level of the hierarchy.

3.2. Intra- and inter-compartmental sensitivity analyses

When building MSMs, using an approach where each of the scale (or compartment) models are well analyzed independently and understood prior to linking to the middle scale model is an important goal. However, sensitivity analyses of individual submodels in isolation may not fully explain the behavior of the submodel when linked within the context of the full MSM, nor will it shed light on the interactions between different compartments or scales. Instead, one may perform sensitivity analysis while varying only the parameters from a certain submodel but still evaluating multiple compartments/scales or even the full MSM. The input parameters for the model can then be compared with outputs from the same compartment to perform intra-compartmental sensitivity analysis (Figure 2B, red), or with outputs from any other submodel to perform inter-compartmental sensitivity analysis (Figure 2B, blue). This approach differs from all-in-one sensitivity (Figure 2A) in that the model is not considered a black box; its compartments/scales are considered to be separate but interacting components. Inputs and outputs may be compared for several combinations of scales, allowing for a comprehensive understanding of the model behavior across scales.

3.3. Hierarchical sensitivity

If a MSM has a clear hierarchical structure, i.e. each level receives input only from the linked smaller/lower level model, then one option is to perform sensitivity analysis for each scale in a top-down manner. At each level of the hierarchy, parameter sensitivity analysis is performed for each submodel independently. Sensitivity analysis at larger scales can be performed without needing to evaluate smaller scale submodels by replacing the submodels with parameters that represent the submodel outputs. These parameters can also be included in the sensitivity analysis to represent a range of outcomes from the submodel and allows determination of which smaller-scale submodels are important in capturing the larger scale dynamics.

In a top-down approach, one begins with sensitivity analysis at the top level of the hierarchy (typically the largest scale). A submodel is deemed critical if its output is a sensitive parameter in the larger scale model. Further sensitivity analyses can then be done independently for only the critical submodels; submodels that are not deemed critical can be coarse-grained or even eliminated from the model. This process can be repeated for successively lower levels in the hierarchy until there are no more critical submodels or until the lowest level of the hierarchy has been reached. Sensitivity results for each level of the hierarchy can then by aggregated into a global sensitivity index [41]. This methodology has been explored in various engineering contexts [20, 41] and is demonstrated in Figure 2. The top-down approach relies on the ability to replace smaller-scale submodels by their scalar outputs or mean field approximations, which is not always practical in biological models, particularly spatial and/or agent-based models. If biological MSMs are to be useful for predictions, then model reduction may not preserve important biological features of the model, and alternative approaches for reducing models are needed that not only reduce the model complexity but preserve biological representation. A systematic way to do this is a current need in the field and one overview approach along these lines is tuneable resolution [16], discussed next.

In a multi-scale agent-based model, each agent may contain its own smaller-scale submodel with its own unique parameter set. In addition, the behavior and types of interactions among agents within the MSM may not translate to a clear input/output hierarchy. In this case, hierarchical sensitivity is not a reasonable choice and one should utilize other sensitivity methods along with techniques to reduce computational cost.

4. Using sensitivity analysis to guide coarse- and fine-graining of models

The development and analysis of MSMs at a whole-systems level often requires abstractions of lower-level behaviors, both for cost considerations and for ease of model understanding and implementation. For example, a model of autoimmune encephalomyelitis developed by [29] uses constant cytokine secretion rates as a cellular level abstraction to represent complex molecular level dynamics. The GranSim model of granuloma formation in TB also demonstrates several levels of abstraction in describing the dynamics of the cytokine TNF, including non-mechanistic (indirect) [34], cellular level [36], and a complex molecular scale representation [9]. All of these models are useful in answering specific questions, but as the complexity of the model increases, so does the computational burden.

Tuneable resolution is a technique that enables the development of models whose different resolution levels can be chosen among depending on the type and complexity of the question under study. By coarse-graining smaller scales of a model, i.e., by replacing submodels with less detailed and cheaper alternatives, MSMs can be constructed with multiple levels of resolution (and thus computational cost) that users can toggle among [16]. Depending on the model and the questions being addressed, a coarse-grained version may or may not be desirable. In order to make an informed choice on the required granularity for a specific model system when toggling between fine- and coarse-grained resolutions, users should be aware of the consequences of this choice on the dynamics of interest. Sensitivity analysis can be used to determine the differences in behavior between coarse- and fine-grained submodels, and to determine the impacts that these differences have at larger scales. We may also wish to simplify a model by coarse-graining portions that do not contribute significantly to the dynamics of interest, thereby reducing the uncertainty and complexity in the model and allowing both the model and our understanding to focus on the most important processes.

Sensitivity analysis techniques play important roles in developing models of various resolutions. One utility of sensitivity analyses in this context is to guide fine-graining and sub-model development by highlighting key mechanisms in a model. In practice this would mean developing a fine-grained model that adds detail to processes suggested by sensitivity analysis as significant. Alternatively, sensitivity analyses can indicate which pathways in a fine-grained model do not have a significant impact on model behaviors and are therefore suitable candidates for coarse-graining. Another utility of sensitivity analyses in applying tuneable resolution is to ensure that sensitive relationships are maintained across levels of resolution [16].

There is also a temporal aspect to tuneable resolution. Certain mechanisms can be highly important at certain timepoints in a model but not at others. [44, 12] demonstrate an example of tuneable resolution where fine-grained and coarse-grained models are used interchangeably at different timepoints in the simulation depending on local conditions, which can even be done in an automated fashion [12]. Sensitivity-informed tuneable resolution is an extremely effective technique allowing for the development of complex models while maintaining computational tractability.

5. Comparing model behaviors: 2D vs. 3D simulation

In developing computational models of biological systems, modelers need to balance the need to reflect biological reality with the need for computational efficiency. Whereas 3D models generate simulated data that are often more directly comparable with experimental data, the higher computational cost and runtime required can prove limiting. Although 2D models can accommodate the simulation of more complex and detailed biological processes, their comparison with 3D biological phenomena is less straightforward, and justification of “scalability” to 3D is non-trivial.

Sensitivity analyses offer a useful way to assess the role of dimensionality in model outcomes, and thereby to determine under what conditions a 2D versus 3D model representation can be used. In [24], Marino et al. present a hybrid, agent-based multi-scale computational model of granuloma formation and highlight the value of sensitivity analysis in determining when to use a 2D versus 3D version of the model. Through performing an uncertainty pilot study as well as sensitivity analysis (PRCC) on 2D and 3D in silico granulomas, [24] found that crowding phenomena and mechanisms in which cells must locate each other in space and time are particularly sensitive to the choice of 2D versus 3D models, and often will require the 3D model. Through the lens of an agent-based model of the lymph node, Gong et al. present similar conclusions regarding the role of sensitivity analysis in identifying parameters/conditions that contribute to different model outcomes in 2D and 3D [13, 12]. The findings of Gadhamsetty et al. further support the notion that model dimensionality may influence interpretation of spatially-sensitive biological processes; through the use of cellular Potts model simulations, they show that cytotoxic T cell mediated killing rate is sensitive to cell density, which is impacted by 2D versus 3D tissue simulation frameworks [10]. The comparison of sensitivity analysis of a 2D model with that of a 3D model can thus highlight the potential limitations of a 2D model (e.g., crowding), and identify what types of questions (e.g., spatial) are best addressed by which model. Parameter significance in both 2D and 3D can reinforce the importance of a given parameter to the overall system behavior, while significance in only one dimension informs the level of resolution necessary to address particular questions.

6. Discussion

The methodologies discussed in [23] have been widely used in diverse systems biology models. Here, we have presented an updated overview of commonly used methods in sensitivity analysis, extensions of these methodologies to multi-scale and multi-compartment models, and applications of sensitivity analysis to evaluating the validity of model coarse-graining.

A major consideration in uncertainty quantification and sensitivity analysis is defining an appropriate response function or quantity of interest (i.e., defining the “model output”). This may be straightforward if there is a clear desired outcome or existing experimental data that the model is being compared against; however, in more exploratory and theoretical applications where the desired outcome of the system is unknown, this can be a significant challenge. Modelers may want to consider several different response functions and model outputs to get a comprehensive idea of important model behaviors.

While we have focused on sensitivity methods in the context of constant scalar outputs, these methods can also be performed over time for time-dependent models. This can be done by evaluating sensitivity measures at specified discrete time points; this has previously been applied by Marino et al. to a model of macrophage polarization in tuberculosis granulomas [22]. Through looking at sensitivity temporally and observing the time intervals over which parameters are significant (e.g., whether parameters remain significant over the entire simulation time or only in certain time windows), one can develop testable hypotheses about the time course of a biological system. For example, Marino et al. predicted which therapeutic targets would be most beneficial early in infection.

Currently, the techniques discussed herein can be used to adequately analyze models for which the model output is a scalar function of time. What is lacking, however, is a standard methodology for analyzing uncertainty and sensitivity over a spatial domain. Some progress has been made in this area for environmental GIS-based models [19], though there may be issues in applying these methods when properties of the spatial domain are not fixed inputs. One way to incorporate spatial features while maintaining a scalar response function is to consider topological measures. This could be especially valuable in models where organizational structure is more important than physical distance or location. Topological data analysis has recently been applied to biological agent-based models [37, 38]; while these techniques have not yet been combined with conventional methods for sensitivity analysis in systems biology, this could provide valuable insight for models that demonstrate spatial organization.