Cells in New Light: Ion Concentration, Voltage, and Pressure Gradients across a Hydrogel Membrane

Abstract

The ionic compositions of the intra- and extracellular environments are distinct from one another, with K⁺ being the main cation in the cytosol and Na⁺ being the most abundant cation outside of the cell. Specific ions can permeate into and out of the cell at different rates, bringing about uneven distribution of charges and development of negative electric potential inside the cell. Each healthy cell must maintain a specific ion concentration gradient and voltage. To account for these functions, various ionic pumps and channels located within the cell membrane have been invoked. In this work, we use a porous alginate hydrogel as a model gelatinous network representing the plant cell wall or cytoskeleton of the animal cell. We show that the gel barrier is able to maintain a stable separation of ionic solutions of different ionic strengths and chemical compositions without any pumping activity. For the Na⁺/K⁺ concentration gradient sustained across the barrier, a negative electric potential develops within the K⁺-rich side. The situation is reminiscent of that in the cell. Furthermore, also the advective flow of water molecules across the gel barrier is restricted, despite the gel’s large pores and the osmotic or hydrostatic pressure gradients across it. This feature has important implications for osmoregulation. We propose a mechanism in which charge separation and electric fields developing across the permselective (gel) membrane prevent ion and bulk fluid flows ordinarily driven by chemical and pressure gradients.

Introduction

Two general features characterize a healthy cell: its ability to maintain an ion concentration gradient across the cell membrane and its ability to generate an electric potential difference between the cytosol and the extracellular fluid.¹ Inside a cell, the concentration of potassium ions (K⁺) is much higher than that of sodium ions (Na⁺), while the situation is reversed outside of the cell. It is recognized that the difference in ion concentrations is maintained by adenosine 5′-triphosphate (ATP)-driven (i.e., energy-consuming) pumps located in the cell’s membrane. An associated theory is that of membrane channels, which allow ions to move through the membrane down their concentration gradients, but at different rates. Because K⁺ ions move out of the cell at a faster rate than Na⁺ ions that penetrate inward, a difference in voltage across the cell membrane is created. This results in a negative voltage inside of a cell with respect to the outside. Both membrane pumps and channels are highly specific biological entities permeable to only particular types of ions.

Some concern has been expressed that the cell’s own metabolic energy may not suffice for supporting the functioning of all ionic pumps.^2,3 Experiments in which ion concentration gradients could be sustained even without the intact cell membrane⁴ have implied that other mechanisms might contribute to this phenomenon. In accordance with those earlier results, a recent study has in fact shown that the bare cytoskeleton of membrane-permeabilized neurons can generate voltage oscillations underlying action potentials.⁵ This feature is commonly thought to result solely from the performance of membrane pumps and channels. Yet, this electrical activity was shown to be due to microtubule bundles acting as ion-selective barriers, thanks to the negative charges and porosity of their cytoskeleton-building network.⁵

The cytoskeleton, able to induce intracellular electric fields,^5,6 was also demonstrated to transmit information between cell’s organelles via electric signals.⁶ Therefore, some electrical properties manifested in a cell could result from features of the cytoskeleton, even without the pumping and channeling activity of membranous components. Other works have shown that some synthetic hydrogels (porous, negatively charged networks) can be a good experimental approximation of the cell’s cytoskeleton in terms of its mechanical and electrical properties.⁷⁻¹⁰ Furthermore, the cytoplasm of mammalian cells has been shown to resemble a hydrogel.¹¹

In this work, we use an alginate gel to examine the role of gelatinous components of a cell in sustaining its main electrochemical properties. Alginate is a naturally occurring polysaccharide derived from brown algae, where it constitutes the main structural component of the algal cell wall.¹² Due to its many carboxyl functional groups, just as those present within a cytoskeleton, the alginate hydrogel forms a negatively charged porous network within a cell. We explore the ability of the alginate hydrogel to support a Na⁺/K⁺ ion concentration gradient across the gel membrane, generate an electric potential difference, and respond to osmotic or hydrostatic pressure gradients.

Results and Discussion

The calcium–alginate hydrogel, as used in our study, consists of a highly porous three-dimensional network with reported pore sizes ranging from few nanometers to micrometers (depending on the technique used to determine pore diameter).¹³ Such pores are large enough to allow for diffusion of ions and water molecules throughout the network, unless specific interactions are present. Indeed, it is recognized that ions and larger solutes diffuse through the gel at rates sufficient to support the metabolism of gel-encapsulated cells (alginate is commonly used for cell immobilization). Motions of those solutes are restricted to different degrees, mainly due to steric obstructions created by the gel framework.^14,15 Nonetheless, the supply of solutes, from the bathing solution, through the gel, to the embedded cell, is assured. Yet, in the particular arrangement of our experimental system, neither ions nor water molecules could be exchanged across the alginate gel between the two aqueous reservoirs, as implied by conductivity measurements and observations on the effect of pressure gradients (see the Results and Discussion section). Thus, in our case, alginate creates a virtually impermeable barrier, so that interconnected solutions do not mix. Below, we present details of the experimental results, as well as specific conditions that need to be fulfilled to prevent ion and water penetrations across the gel. The underlying phenomena of charge separation at the gel/water interface, manifested in the measured electric potential difference across the gel, are also discussed.

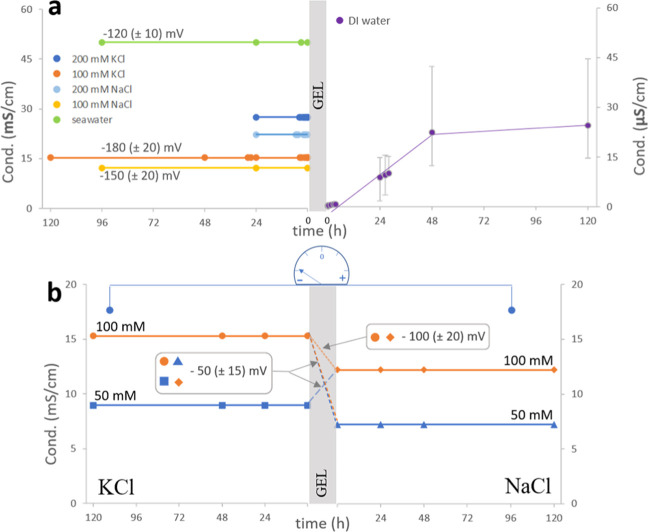
Conductivity changes are directly correlated to ion concentrations (for ionic solutions of low concentration). In the two ionic solutions used in our experiments, these changes allow us to monitor the extent of solution mixing through the interconnecting bridge. We found that the conductivity of the salt solutions of different ionic strengths, separated by the gel, did not change over a time scale of a few days (Figure 1). This implies that there is no net migration of ions across the barrier between the solutions.

Figure 1.

Conductivity measured over time in the interconnected-by-alginate-bridge solutions of (a) the left panel, from top to bottom: seawater, 200 mM KCl, 200 mM NaCl, 100 mM KCl, 100 mM NaCl, and DI water (right panel); (b) KCl (left, from top to bottom: 100 and 50 mM) and NaCl (right, from top to bottom: 100 and 50 mM). Note the 3-orders-of-magnitude difference in scale values for salt and DI water containers. The average values of the electric potential difference (mV) registered for (a) ionic solutions with respect to DI water and (b) KCl with respect to NaCl solution are depicted and yield (a) −180, −150, and −120 mV for 100 mM (KCl, NaCl, and seawater, respectively) and (b) −50 mV for interconnected solutions of KCl and NaCl of different ionic strengths, and −100 mV for equimolar solutions.

Although ions are expected to move down their concentration gradients to reach a uniform concentration in the two communicating vessels, such mixing does not occur. On the contrary, a stable ion concentration gradient is maintained across the gel barrier, as confirmed by conductivity measurements. In fact, a very slight increase in the conductivity of the DI water reservoir can be observed with time. Yet, that conductivity remains 3 orders of magnitude lower than in the interconnected salt solution. Therefore, although a very limited number of ions may possibly penetrate the gel barrier, no substantial mixing occurs between the two reservoirs that would lead to concentration equilibration.

Moreover, the imposed difference between the liquid column heights of the salt solutions and DI water across the gel barrier is also stably maintained. This indicates no variation of the hydrostatic pressure gradient over time (see Figure 2). The gradient is sustained, despite the porosity of the bridge interconnecting the two reservoirs. The pores, as already stated, should be large enough to allow for diffusion of water molecules. Indeed, if the gel separates two columns of different heights containing only water, these columns do eventually equilibrate to attain the same level, according to the principle of communicating vessels. Yet, if the interconnected solutions have different ionic strengths (DI water as the salt solution), no net water flow tending to equilibrate the pressure difference could be registered. Even when the osmotic force and hydrostatic pressure act in the same direction, the liquid levels in the reservoirs remain unchanged. That situation is illustrated in the case when a KCl solution is adjoined to a column of DI water of greater height (right-hand side, Figure 2). Thus, in these cases, the presence of a gel barrier cancels the effect of hydrostatic and osmotic forces.

Figure 2.

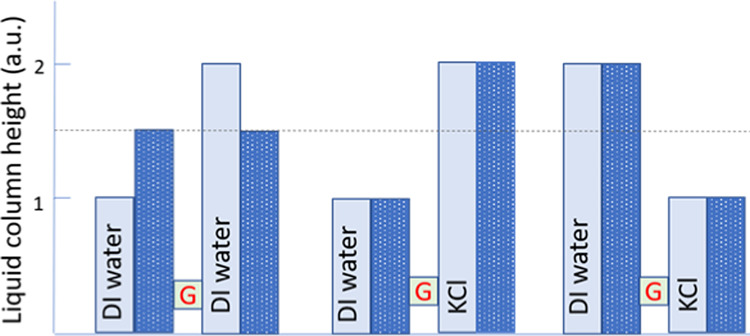
Changes in solution levels (liquid column heights) in the two vessels interconnected by the alginate gel bridge (G) and containing DI water and 100 mM KCl solution. The light blue columns represent the liquid level at the beginning of the experiment, while the dark blue dotted columns show a steady liquid level at the end of the experiment.

The reason for the latter effects originates from the intrinsic properties of the uniformly charged porous alginate hydrogel, further in the study termed also “gel membrane” due to its function to separate the solutions.

Alginate Hydrogel as a Permselective Membrane

The alginate hydrogel is a negatively charged porous matrix that allows only cations (but not their counterions) to penetrate through.¹⁸ Mobile ions from the bathing solution may migrate into the gel interior, driven by an attraction exerted by the fixed gel matrix charges.¹⁸ Many anionic polyelectrolyte gels are known to exhibit permselectivity similar to that of alginate, being largely impermeable to anionic species.¹⁶ Such behavior of the alginate gel is supported also by our spectroscopic measurements. In these experiments, water imbibition by the gel (swelling) results in an increased anion absorption band (thus concentration) in the bathing solution (Figure 3). This means that only water and/or cations can infiltrate the gel, while the anion concentration in the solution effectively increases due to reduced solvent volume, now partially accommodated within the gel matrix.

Figure 3.

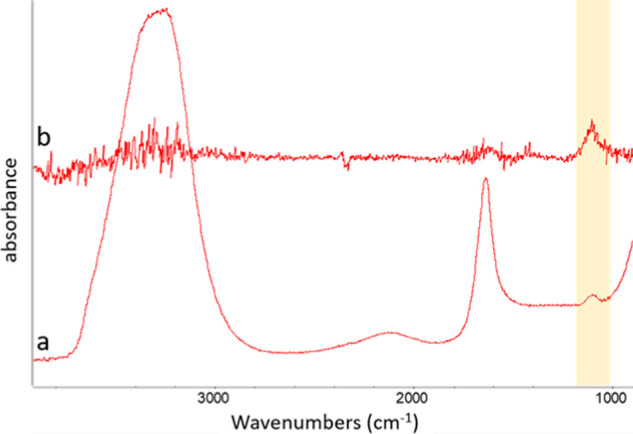
(a) FTIR-attenuated total reflection (ATR) spectra of a 0.05 M K₂SO₄ solution and (b) a difference spectrum of the K₂SO₄ solution before and after a piece of alginate gel was soaked and swelled in it. Note an increase in an absorption band of SO₄^2– (highlighted in yellow), expressed as the positive peak in difference spectra, after the solution contacts with a gel.

When only cations selectively penetrate into the alginate gel, their parent solution is left with excess negative charges. Separated charges—positive ions migrating into the gel and negative ions repelled from the gel—create an electric potential difference. In our experiments, a negative voltage is always registered at the ionic side for the following solution combinations: KCl/water, NaCl/water, or seawater/water (Figure 1a). This result is in agreement with the inferred mechanism, where only cations permeate within and/or across the gel barrier, making their parent solution negatively charged with respect to the DI water reservoir. The magnitude of the registered negative voltage can be understood by considering differences in ion affinity toward alginate. K⁺ ions, which form the weakest ion pairs with carboxylate groups of alginate, can penetrate the gel network to a greater extent than Na⁺ ions with their stronger affinity toward COO^–.¹⁷⁻¹⁹ The ease of penetration translates into a greater separation of charges, provided by cations infiltrating the gel and leaving their counterions behind in solution. This consideration is in agreement with the measured voltage, being the highest (most negative) across the gel in contact with the KCl solution and the lowest (least negative) in the case of the gel exposed to seawater. In the latter scenario, minor components of seawater, like Ca²⁺ or Mg²⁺, form strong complexes with alginate. Therefore, these ions are trapped in the gel’s pores and effectively screen fixed negative charges of alginate that are responsible for the gel’s selective permeability and voltage-generating capacity. For the KCl/NaCl system, a negative potential develops always on the KCl side (Figure 1b). Such an outcome can be explained by the fact that K⁺ ions penetrate the gel more readily than do Na⁺ ions;¹⁷⁻¹⁹ hence, the K⁺ ions migrate away from their solution at a faster rate than do the Na⁺ ions. Therefore, the KCl side becomes negatively charged with respect to the interconnected NaCl solution.

The question, then, is why the cross-migration of ions stops altogether, so that there is no net mixing between the solutions, but the concentration gradient, as well as the electric potential difference, is stably maintained across the barrier (Figure 1). This can be understood by considering how the gel’s permselectivity affects ion distribution in the gel vicinity.

Ion Exclusion Zone

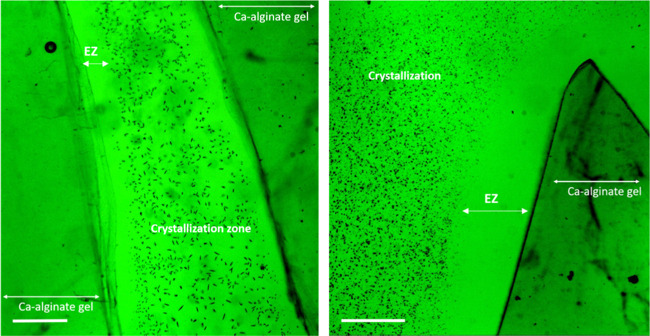
After some of the cations penetrate the alginate gel, the excess anions left in the solution are now electrostatically repelled from the negatively charged gel surface and cannot approach it closely without their counterions. As a consequence, a zone depleted in ions (cations and anions) is formed next to the gel interface. This phenomenon has been already widely exploited in designing water desalination and separation/preconcentration devices.²⁰⁻²⁸ Water that is free of ions and other charged species could be collected in the immediate vicinity of the permselective membrane. At the same time, the solutes tended to preconcentrate at the ion-free/bulk solution boundary. The existence of such solute-free water layers has been observed next to many hydrophilic surfaces and, thanks to its properties, was given a generic name of exclusion zone (EZ).²⁹⁻³³ We were able to confirm the presence of an ion-depleted EZ water layer adjacent to the alginate hydrogel in experiments in which crystal precipitation was induced in situ in a solution containing the alginate gel. Crystals formed from dissolved ions do not appear close to the gel surface (Figure 4). This implies that the region in the immediate vicinity of the gel is free of any ions that could serve to build crystals.

Figure 4.

Optical microscope images of the ion-depleted exclusion zone (EZ) water, expressed as a zone devoid of the crystals (black dots in the image) formed in the solution next to the alginate gel surface. The ion-depleted EZ could be observed under the microscope only for gels prone to swelling (after shorter dialysis time). The scale bar is 200 μm.

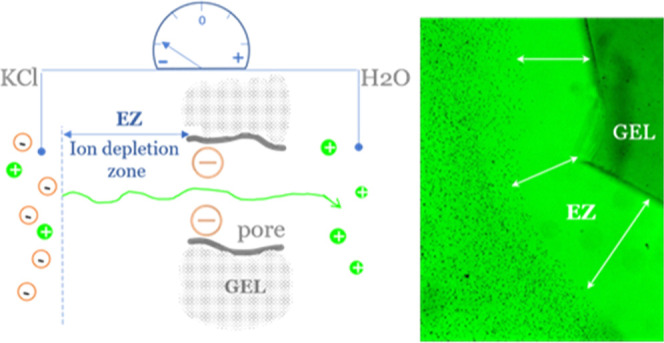
Due to the charge separation across the EZ layer (positive ions within the gel and their negative counterions at the EZ/bulk solution boundary), an electric force is created that opposes the chemical force driven by the concentration gradient. Thus, cations migrating away from the solution and within the gel are attracted back to their negatively charged counterions. After the equilibrium between these forces has been established, a stable concentration gradient and voltage are maintained (Figure 5), as seen in our experiments.

Figure 5.

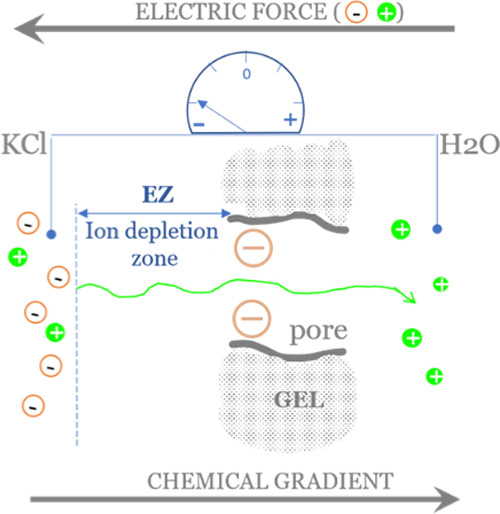
Schematic illustration showing the mechanism of formation of the ion-depleted EZ layer next to the negatively charged gel. Salt ions migrate according to the concentration gradient from the KCl solution to water. Due to the negative charge of the gel matrix, only cations can pass, and the KCl solution is left with excess negative charges. These negative charges are now repelled from the negatively charged gel body, thus creating an ion-depleted exclusion zone of water. The initially ion-free water reservoir (right side) gains some extra positive charges. The resulting electric force (cations attracted back by their counterions) opposes the chemical force due to the concentration gradient of ions between the two solutions.

Very notably, this is the situation analogous to that existing in a cell, where different ionic compositions between inside and outside, with the electric potential difference, are expressed across the cell membrane. The intrinsic properties of a permselective hydrogel are thus sufficient prerequisites to express these features, without the energy expenditure required in the case of membrane pumps.

In fact, the ion-depleted EZ, sustaining charge separation (by balanced chemical and electric forces), should develop on both sides of a gel membrane, but more extensively on the side exposed to K⁺-containing solution—the larger EZ being due to K⁺ migrating toward/within the gel faster than does Na⁺. Therefore, the electric potential difference between solutions separated by the gel membrane is determined by the relative partitioning of mobile ions from solution within the gel matrix (Figure 6).

Figure 6.

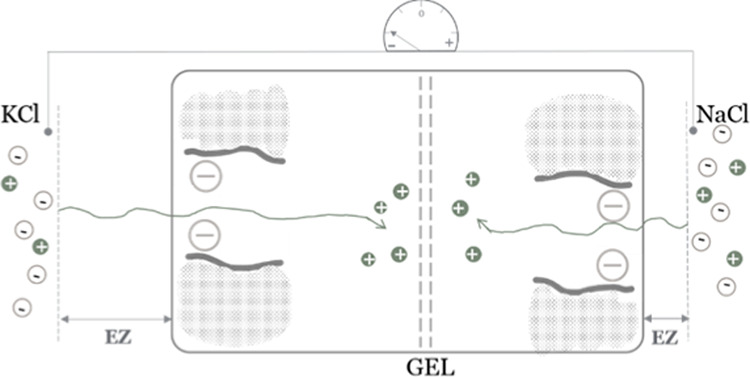
Schematic illustration of the mechanism of development of electric potential difference between two ionic solutions separated by a permselective gel. K⁺ migrates within the gel at higher rates than does Na⁺. As their Cl^– counterions are left behind (cannot penetrate negatively charged pores), those anions are repelled by a charged gel creating an ion-depleted EZ at both sides of the gel membrane. Due to the faster migration of K⁺, the KCl solution is left with more excess negative charges than the NaCl solution. This relative difference is expressed in the measured negative electric potential of the KCl solution.

Yet, it is interesting to note that if the potential difference was measured between the gel and its adjacent solution on either side, the gel matrix should exhibit a negative voltage relative to the solution due to gel excess fixed negative charges. This is a known property of anionic polyelectrolyte gels. In principle, the presented mechanism of voltage generation across the gelatinous barrier is consistent with the ideas put forward in Ling’s association-induction theory.^2−4,34,35 Ling suggested that the electric potential of a cell results from the selective association of particular ions with components of the cytoplasm. If, rather than cross-migration of ions, we assume preferential accommodation of K⁺ ions within the alginate gel, then our experimental results could be interpreted in the view of Ling’s theory. K⁺ ions infiltrating the gel membrane, even without crossing it, to a greater extent than Na⁺ ions, leave behind a larger number of unbalanced anions in their parent solution. Therefore, the solution in the K⁺-rich side of the barrier becomes more negative in relation to the Na⁺-rich side.

The reason behind the apparent impermeability of the gel barrier toward ions can now be understood by considering the development of an ion-depleted EZ supporting sustained charge separation.

Interfacial Water Ordering and Pressure Gradients

Apart from the migration of ions, there are still forces, both osmotic and hydrostatic, that should drive the flow of water molecules between the interconnected solutions. Nevertheless, as shown in our experiments with different solution levels (Figure 2), there is no net water flow across the gel.

Generally, the liquid in communicating vessels tends to equilibrate the pressure felt at any point within the liquid’s entire volume by adjusting the liquid level in each compartment to the same height. This is because the pressure at any point in the homogeneous liquid depends only on the depth of the point in the liquid. In our case, however, the solution levels remain unequal regardless of the hydrostatic and osmotic pressure gradients.

The law of communicating vessels applies only to liquids, where intermolecular forces cannot counteract any pressure-driven displacements. In our system, it seems that forces acting between water molecules within the gel are strong enough to counteract any such pressure-induced translational motions. It is important to remember that this resistance to hydrostatic (as well as osmotic) pressure could be observed only in the presence of ions. Any physical pore clogging by the ions should not be possible. In fact, the alginate gel swells in the presence of a low concentration of monovalent salts, so pore volume increases.^16,17 Then, both Na⁺ and K⁺ ions form fully soluble complexes with alginate.¹⁷ The observed resistance to a pressure-gradient-driven advective flow of water, as illustrated in experiments with different liquid columns’ heights, can be explained by considering the invoked charge separation and electric potential development, as described in the next paragraph.

In our experiments, voltage emerges across the porous gel network separating the two solutions. It has been previously shown that an electric field applied to a nanochannel can enhance the alignment of water molecules inside the channel, forming a liquid-crystalline phase.³⁶ Weak electric fields, of the strength comparable to that acting across the cell membrane, have been demonstrated to restrict water flow within a nanochannel due to this increased water structuring.³⁶ Water structure, resembling the liquid-crystalline state, has been previously suggested to exist next to many hydrophilic surfaces, termed the EZ water layer.²⁹⁻³¹ The voltage that develops in our experimental system (comparable in magnitude to that of the cell resting potential)³⁷ can therefore be expected to make water molecules in the porous network of the gel more ordered. Such water may resist the transfer of pressure information between the two communicating vessels in our study. Osmotic flow is also driven by pressure gradients, just as is hydrostatic flow.³⁸ Therefore, water molecules confined within alginate gel pores and/or adjacent to the gel–water interface could create an effective barrier, attenuating the impact of both osmotic and hydrostatic forces and effectively restricting flow.

Cell-Like Features of Gels

The alginate hydrogel is generally considered mainly as the structural component of the algal cell wall.¹² Our study shows it to be able to sustain a Na⁺/K⁺ concentration gradient, support the development of an electric potential difference, and attenuate osmotic pressure. These features in fact closely resemble the characteristics of each healthy cell: the ability to maintain a specific chemical identity of the intracellular environment, generate voltage, and maintain constant volume.

We have observed that the size of the gel-induced EZ increases on gel swelling. This can be understood by the advective water influx carrying ions to the gel matrix and has been confirmed by our microscopy observations (Figure 4) and indirectly by Fourier transform infrared (FTIR) measurements (Figure 3). The increase of ion exclusion on gel swelling is also in agreement with previous findings.²² The size of the ion-depleted EZ is indicative of the extent of charge separation, and the greater the separation, the higher should be the resulting voltage. We did not perform systematic experiments on the latter relationship, but our individual observations on the effect of gel swelling on the registered voltage support such a notion. Then, the voltage affects water structuring in small pores, manifested as resistance to (osmotic) pressure. For marine algae living in tidal areas and experiencing periodic desiccation, an increase of EZ on rehydration (Figure 7) may support these organisms in maintaining critical cellular homeostasis in salty environments. Especially, large EZ developing next to the swelling algae can help to prevent osmotically driven water outflux from the cells. This is because cells are not in contact with salty water anymore, but are separated from it by the surrounding ion-depleted EZ. The negative electric potential of a gel, mimicking the cytoskeletal components—a porous, negatively charged network—also becomes more negative after gel swelling.⁷ This observation is in agreement with our considerations on the correlation between swelling, EZ size, and voltage, and because swelling can be induced by preceding mechanical contraction, it has been suggested that the intrinsic properties of the gel-like cytoskeleton could be mainly responsible for the mechanoelectric response of cells.⁷

Figure 7.

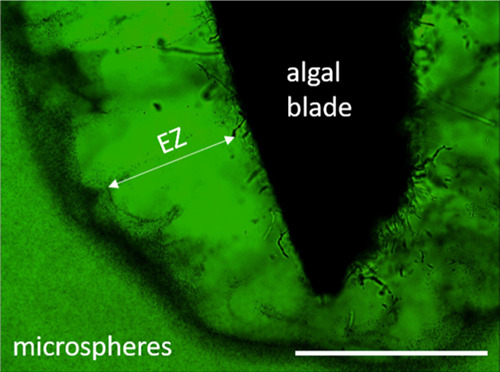
Optical microscopy image showing the EZ water layer, expressed as a zone devoid of microspheres, developing next to a rehydrating algal blade. Note the solute enrichment (dark region) at the boundary between the EZ and bulk solutions, a feature consistent with the formation of an ion-depletion zone.²⁰⁻²⁷ The scale bar is 4 mm.

Notably, it is recognized that in the immediate vicinity of almost every cell there is a layer of unstirred water, within which flow is highly restricted.^39,40 This layer is also known as a layer of stagnant solutes. The largest of the known unstirred layers develops next to the intestinal membranes within their highly mucous (gelatinous) environments.⁴¹ Our results imply that electric fields acting next to permselective membranes may well contribute to the establishment of unstirred water layers (UWLs). This is because he advective flow of water and solutes (ions) is restricted across/next to the gel, just as it is within UWL.

Conclusions

Our results show that a permselective, porous, and uniformly charged gel such as alginate can effectively constitute a membrane across which an ion concentration gradient and an electric potential difference can be stably sustained. The latter features are the fundamental characteristics of healthy cells and are now commonly ascribed exclusively to the activity of channels and energy-consuming pumps embedded within the cell membrane. Our results thus imply that the plant cell wall and/or the animal cytoskeleton, being charged gelatinous networks, can potentially contribute to maintaining those essential physicochemical properties of living cells.

We propose a mechanism allowing the gel barrier to restrict the net flux of ions or water molecules despite concentration or pressure gradients imposed across the gel. The underlying cause for this apparent impermeability may be the presence of an ion-depleted EZ water layer developing next to a permselective barrier. Charge separation across the EZ layer generates a potential difference. The electric force acting in the direction opposite to the chemical drive creates a steady state, in which no net ion flow is observed. Furthermore, the potential difference acts on water molecules, making them more ordered within the gel pores so that a pressure gradient cannot be easily transmitted across the gel. Therefore, any pressure-driven water advection is highly attenuated. It seems plausible that homeostasis of a cell in terms of its ionic composition, electric potential, and volume (resistance to osmotic stress) can be supported by the cell’s gelatinous components without the need for energy expenditure.

Experimental Section

Stock solutions of NaCl, KCl, CaCl₂, BaCl₂, Na₂SO₄, K₂SO₄, and sodium alginate (all chemicals from Sigma-Aldrich) were prepared with deionized (DI) water from a Barnstead D3750 Nanopure Diamond purification system and diluted to the desired experimental concentration. Artificial seawater was prepared according to the recipe by Cold Spring Harbor Protocols.⁴²

Alginate Gel Preparation

To make an alginate gel bridge, a glass capillary (internal diameter 1.12 mm, World Precision Instruments, Inc.), cut to a length of 2 cm, was filled with 2% solution of sodium alginate and immersed in a bath of 0.2 M CaCl₂ solution for a minimum of 24 h for complete gelation to occur. Ca²⁺ ions, as well as other divalent cations, act as cross-linking agents and transform soluble sodium alginate into a hydrogel.^43,44 Gel-filled capillaries were then dialyzed against deionized water for a minimum of 48 h to remove any nonspecifically bound ions. The capillaries were then stored in DI water until the time of the experiment.

The preparatory method for alginate gels used for microscopic observations and spectroscopic measurements varied slightly from that used for the gel bridge, above. Instead of a capillary, a small Petri dish (35 mm × 10 mm, Falcon) was filled with sodium alginate solution so as to just cover the dish bottom. The CaCl₂ solution was then gently poured over it. Before experiments, the formed gel was cut with a stainless steel blade to pieces of the desired size, usually about (5 mm × 5 mm).

For those experiments examining gel swelling, the gel substrate was dried in air and then fully rehydrated in water before use. During dehydration, some unspecific linkages are formed between those gel compartments that are not cross-linked.^45,46 On immersion in a solution of monovalent salts of low ionic strength, water-rehydrated gels swell additionally due to substitution of nonspecifically bound divalent cations by monovalent ones.⁴⁵ Shorter dialysis times, resulting in noncomplete removal of free Ca²⁺ entrapped within the gel network, were also used in our work to permit increased swelling when the gel was in contact with monovalent salts.

Experimental Setup

The alginate gel bridge was used to interconnect two reservoirs containing either NaCl or KCl at different concentrations relevant to the cell environment. Solutions included artificial seawater or DI water in different combinations: salt/salt, salt/DI water, and seawater/DI water (see Table 1). We used 2 mL Eppendorf microcentrifuge tubes as reservoirs. Holes were drilled at the 1 mL level mark of each tube, and the ends of the capillary were inserted through the holes. The reservoirs were filled to the top with the respective solutions. Solutions fully covered the capillary entries.

Table 1. Composition of Solutions Interconnected by the Gel Bridge.

compound	conc. (mM)		conc. (mM)	compound (mM)
KCl	200	gel		DI water
NaCl
KCl	100
NaCl
seawater	600 (NaCl)a
	100		100
KCl			50	NaCl
	50		100

^aMolarity of the main component of seawater.

Conductivity

To quantify ion permeability through the gel, we followed conductivity changes of the reservoir solutions. Conductivity results from the presence of mobile ions in solution, so changes of conductivity therefore directly relate to the permeability of the gel. Conductivity was measured with the use of a conductivity meter (OAKTON, CON 100 Series).

Electric Potential Difference

To check for permeability of the barrier to specific ions, we measured the development of a potential difference between the two reservoirs. For voltage measurement, a digital multimeter (TENMA 72-7750) was used with either steel or gold probes. The electric potential difference (voltage) between the two containers can develop in a situation when one solution becomes positively/negatively charged with respect to the other. Solutions of salts have no net charge, as each cation is counterbalanced by an anion. When only one type of ion, either positively or negatively charged, can selectively pass through the barrier, charges on both sides of the bridge may no longer remain balanced. Conductivity and voltage changes were followed for the course of at least 48 h and up to 120 h.

Pressure Gradient

To check for the effect of hydrostatic and/or osmotic pressure differences, the solution levels in the two reservoirs were made uneven (1 mL vs 2 mL) for salt/water and water/water interconnected systems: 1 mL 100 mM KCl/2 mL DI water; 2 mL 100 mM KCl/1 mL DI water; and 1 mL DI water/2 mL DI water. For these experiments, the alginate bridge was inserted closer to the bottom of the reservoirs to assure full coverage of capillary entries by the solutions. Changes in the solution levels were tracked over the course of the experiment (120 h). In communicating vessels, pressure is expected to equilibrate by adjusting the liquid level to the same height in each compartment. This is due to the fact that pressure (P) exerted at any point in the static fluid depends only upon the depth of the fluid (h), the density of the fluid (), and the acceleration of gravity (g), P = hg. Because g is constant and density () of the DI water and of 100 mM KCl is identical up to the third decimal place, the pressure felt at any point in the liquid in our communicating vessels should depend only on the liquid column height.

Crystallization Experiments

For microscopic evaluation of ion-depletion-zone development next to the alginate gel, crystallization experiments were employed. The gel specimen (approx. 5 mm× 5 mm × 2 mm) was immersed in 0.01 M Na₂SO₄ or 0.01 M K₂SO₄, covered with a glass slide, and left to equilibrate for 15 min. A cover slide was supported on gel pieces, so that a solution-filled clearance of about 2 mm persisted between the cover and the bottom of the setup. Then, with the use of an automatic pipette, a solution of 0.01 M BaCl₂ was added to the equimolar bathing solution of either Na₂SO₄ or K₂SO. The Ba²⁺ and SO₄^2– combine to form a very insoluble BaSO₄ precipitate that is observed immediately after mixing of the solutions.

We inspected our samples in situ for the presence of crystallization-free zones next to the alginate surface. The layer void of crystals means that there are no ions from which crystals could form. Both fully swollen and prone to swelling (rehydrated or with shorter dialysis time) gels were used in these experiments.

Behavior of Natural Algae

To visualize the solute-free zone forming next to the alginate-containing natural seaweed, we used a dried Wakame (Undaria pinnatifida) blade and immersed it in a suspension of 1 μm polystyrene microspheres with carboxyl functional groups (Polysciences Inc., 08226). The ratio of the aqueous microsphere suspension to DI water was 45 μL (1 drop) to 15 mL. The formation of a zone void of microsphere solutes was observed on blade rehydration and swelling.

Spectroscopic Experiments

We performed Fourier transform infrared (FTIR) spectroscopy measurements using an attenuated total reflectance (ATR) sampling technique to analyze the ion-selective permeability of the alginate gel by following the procedure described further in this section. A Thermo Scientific Nicolet Nexus 670 Spectrophotometer was employed. Spectra were recorded using 256 infrared-beam scans and a wavenumber resolution of 4 cm^–1. OMNIC software was used to perform the analysis. We used the K₂SO₄ solution as a gauge for gel permeability due to a characteristic infrared absorption feature of aqueous SO₄^2– at 1104 cm^–1.

After collecting the spectra of 0.05 M K₂SO₄, a piece of alginate hydrogel (of a volume comprising about 1/3 of a K₂SO₄ solution volume) was immersed in the solution. As the gel swelled, changes in the height of the SO₄^2– absorption band were monitored in the solution. To assure swelling (solution infiltration), previously dehydrated gels (as described in the Alginate Gel Preparation section) were used in the experiments. Due to the negative charges of gel pores provided by fixed carboxyl groups, the alginate gel is expected to be selectively permeable to cations but impermeable to anions.⁴⁷ Therefore, an increased concentration of SO₄^2– anions in solution (expressed as the height of the absorption band) can be expected when only water molecules (and cations), but not anions, penetrate into the gel.

Author Contributions

The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

The Software AG Foundation (SAGST) and Anonymous.

The authors declare no competing financial interest.