Abstract
The mechanical properties of semicrystalline PLLA containing exclusively α′- or α-crystals have been investigated. The connection between experimental elastic moduli and phase composition has been analyzed as a function of the polymorphic crystalline form. For a complete interpretation of the mechanical properties, the contribution of the crystalline regions and the constrained amorphous interphase or rigid amorphous fraction (RAF) has been quantified by a three-phase mechanical model. The mathematical approach allowed the simultaneous quantification of the elastic moduli of (i) the α′- and α-phases (11.2 and 14.8 GPa, respectively, in excellent agreement with experimental and theoretical data reported in the literature) and (ii) the rigid amorphous fractions linked to the α′- and α-forms (5.4 and 6.1 GPa, respectively). In parallel, the densities of the RAF connected with α′- and α-crystals have been measured (1.17 and 1.11 g/cm3, respectively). The slightly higher value of the elastic modulus of the RAF connected to the α-crystals and its lower density have been associated to a stronger chain coupling at the amorphous/crystal interface. Thus, the elastic moduli at Troom of the crystalline (EC), mobile amorphous (EMAF), and rigid amorphous (ERAF) fractions of PLLA turned out to be quantitatively in the order of EMAF < ERAF < EC, with the experimental EMAF value equal to 3.6 GPa. These findings can allow a better tailoring of the properties of PLLA materials in relation to specific applications.
1. Introduction
The growing request of “green” chemicals and processes has progressively increased the interest toward the application of more environmentally friendly polymeric materials. Bio-based and biodegradable polymers have become the topic of many investigations by both academia and industry. Poly(lactic acid) (PLA) is one of the bio-based and biodegradable polymers most studied because it is widely present on the market, especially for biomedical and packaging purposes. In addition to its biodegradability and renewability, PLA exhibits stiffness and strength comparable to those of traditional petroleum-based polymers, with an elastic modulus of about 3–4 GPa and a tensile strength in the range of 40–60 MPa.1 On the other hand, drawbacks for its utilization are a high cost with respect to traditional petroleum-derived polymers and a low toughness, which makes it a brittle polymer. A maximum elongation at break of around 4% strongly limits its applications when fracture toughness and high ductility are required. Nevertheless, the mechanical properties of PLA remain very attractive1 and can be modulated as a function of (i) l- and d-lactic acid unit content and, consequently, (ii) the morphology and crystal structure. It is well known that the term PLA designates a variety of polymers containing different sequences and ratios of l- and d-units, whereas PLLA or PDLA refer to the homopolymers or copolymers containing a very small amount of d-units or l-units, respectively. The effects of the enantiomeric l- and d-units on the thermal properties of PLA have been extensively studied.2 With respect to PLLA, an increase in the percentage of d-lactic acid units produces a decrease in the crystallization rate, crystallinity degree, and melting temperature due to the exclusion of d-units from the PLLA crystals. PLA copolymers containing more than 10–15% of randomly distributed d-units are totally amorphous and noncrystallizable.3 As the majority of the bacteria utilized for fermentation produce l-lactic acid, PLLA is a product that is commercially very important. For this reason, PLLA is the polymer investigated in the present study.
PLLA exhibits polymorphism as a function of the crystallization conditions under normal industrial processing conditions (i.e., injection molding and extrusion).4 The α-form, the most stable polymorph characterized by two left-handed antiparallel 103 helical conformations packed in an orthorhombic cell, grows during melt and cold crystallizations at temperatures higher than 110 °C. At temperatures lower than about 100 °C, the growth of a slightly distorted and disordered form, the α′-form, is observed. This modification is characterized by a chain conformation more disordered with respect to the α-form, loose 103 helical packing, and slightly larger unit cell dimensions with respect to the α-form.5,6 In the intermediate Tc range between 100 and 110 °C, both α′- and α-forms grow under normal processing conditions, with the percentage of α-form increasing with Tc.6−9 The conformationally disordered α′-modification is metastable below 150 °C, and it converts irreversibly into the α-form around 160 °C upon heating at rates that are typically applied in conventional DSC.10,11 Additional crystal polymorphic forms, as the trigonal β-form, which develops upon stretching the α-phase at elevated temperature, and the orthorhombic γ-form, which grows on hexamethylbenzene substrates, are not interesting from an industrial point of view.4
Semicrystalline PLLA exhibits also different amorphous fractions, which, due to their various distances from the crystalline regions, are characterized by dissimilar mobility.12 Besides a mobile amorphous fraction (MAF), which vitrifies/devitrifies in the glass transition (Tg) region, in PLLA, there exists also a constrained or rigid amorphous fraction (RAF) located at the crystal/amorphous interface. This interphase, found in almost all semicrystalline polymers,13 presents nanometric dimensions and reduced mobility due to the coupling with the close crystalline regions. This implicates that its vitrification/devitrification temperature is higher than Tg. The percentage of RAF in semicrystalline polymers depends not only on the crystallization conditions but also on the complete thermal history of the material.14 For PLLA, the rigid amorphous fraction was found to develop in parallel to the crystalline phase at low crystallization temperatures, whereas at higher temperatures, RAF formation was not observed or detected only during the final stages of the crystallization process.14,15
A detailed description of the semicrystalline polymers, as composed of three different fractions, crystalline, mobile amorphous, and rigid amorphous fractions, is crucial for a full comprehension of the structure and properties of these materials because many macroscopic properties, as for example, mechanical and gas permeability properties, depend on their micro- and nanostructures. Thus, the physical properties of semicrystalline polymers can be interpreted correctly by taking into account not only the crystal phase and mobile amorphous fraction but also the RAF contribution.
Mechanical properties of semicrystalline polymers strongly depend on the polymorphic crystalline structure.16,17 For PLLA, the different regularity of chain conformation and packing along with different lattice dimensions influences the mechanical properties of the α- and α′-crystals.18 Experimental and theoretical evaluation of the ultimate elastic modulus of the α- and α′-forms of PLLA led to values slightly higher for the α-form (13.8 and 14.7 GPa, respectively) with respect to the α′-modification (12.6 and 12.9 GPa, respectively).18 This difference was found to reflect also on the elastic moduli of semicrystalline PLLA bulk samples.18
On the other hand, as regard to the rigid amorphous fraction, several investigations on different semicrystalline polymers have reported experimental evidence that the elastic modulus of the RAF could be close to that of the crystal phase.19−23 For polyethylene, theoretical estimations of the mechanical properties of the RAF, performed by Monte Carlo simulation24 and micromechanical modeling,25,26 showed that the modulus of the rigid noncrystalline interlamellar phase is intermediate between those of the crystalline and amorphous bulk phases, thus attesting that the interphase plays an important role on the stress transfer between the crystalline and mobile amorphous phases. For poly(ethylene terephthalate), micromechanical modeling demonstrated that the interphase stiffness is approximately 1.6 times the modulus of the amorphous phase.27
All the mechanical models used to predict the properties of fiber-reinforced composites (for example, Kerner, Hashin–Shtrikman, Hirsch, Coran, Paul, Cox, etc., treatments),28 can in principle be adapted to semicrystalline polymers because semicrystalline polymers can be considered mechanically similar to composites if the crystalline regions are assumed as a dispersed phase within the amorphous matrix.29
The simplest mechanical models to estimate the elastic modulus (E) of a semicrystalline polymer, considered as a two-phase material, are given by the “parallel” and “series” models, which suppose parallel and series arrangements of the crystalline and amorphous phases. For the parallel arrangement, a uniform strain is assumed, whereas a uniform stress is presumed for the series arrangement.28 For the parallel model, E = VC·EC + VA·EA, whereas for the series model, 1/E = VC/EC + VA/EA, where EC and EA are the elastic moduli of crystalline and amorphous phases, and VC and VA are the corresponding volume fractions. These two simple models represent the upper and lower bounds of the tensile modulus predictions.
A more complex approach was provided by the two-phase Takayanagi model.30,31 This model relates a semicrystalline material to a combination of series and parallel elements (parallel model and series model) to take into account the different deformation that the crystalline and amorphous phases undergo under stress. The classical Takayanagi model has been widely applied to the prediction of the elastic modulus of semicrystalline polymers32−35 but also, as it is a two-phase approach, of polymeric blends,36,37 copolymers,38 and composites39,40 due to its relatively simple analytical form.
Despite its extensive utilization, the original two-phase Takayanagi model is not able to describe in detail the mechanical behavior of semicrystalline polymers because it does not take into account the amorphous/crystal interphase, which exhibits organization and mobility markedly different from the bulk amorphous phase and moreover can be present in a high percentage.14,15 The same drawback has been reported, for example, if the model is applied to nanocomposites.41,42 In the case of filler percolation or in the presence of strong interactions between the nanofillers and the polymeric matrix, the introduction in the model of a third component became necessary. Examples of extension of the classical Takayanagi model to a three-phase system, to take into account the agglomerated fillers or the interfacial region in polymer nanocomposites, can be found in the literature.41,42
Recently, a modified three-phase Takayanagi mechanical model has been utilized to quantify the elastic moduli at Troom of the crystalline (EC), mobile amorphous (EMAF), and rigid amorphous (ERAF) fractions of poly(3-hydroxybutyrate-co-3-hydroxyvalerate) copolymers.43 The mathematical resolution of the model allowed the direct determination of the moduli of the three fractions, which turned out to be quantitatively in the order of EMAF < ERAF < EC, in perfect agreement with experimental and theoretical expectations.
Also in the present study, for the first time, the elastic modulus of the rigid amorphous fraction of PLLA is theoretically estimated by means of a three-phase Takayanagi model. To characterize separately the rigid amorphous fraction linked to α′- and α-crystals, PLLA was isothermally crystallized at two different temperatures, 95 and 110 °C, respectively, to prepare semicrystalline PLLA containing exclusively either α′- or α-crystals. As the application of the model allows the simultaneous quantification of the elastic moduli of the rigid amorphous fraction and crystalline fraction, the comparison of the calculated EC’s with the corresponding experimental and theoretical values, reported in the literature for the α′- and α-crystals, can constitute a proof of the validity and reliability of the derived ERAF data.
2. Results and Discussion
2.1. XRD Analysis of PLLA after Different Crystallization Times at Tmold = 95 and 110 °C
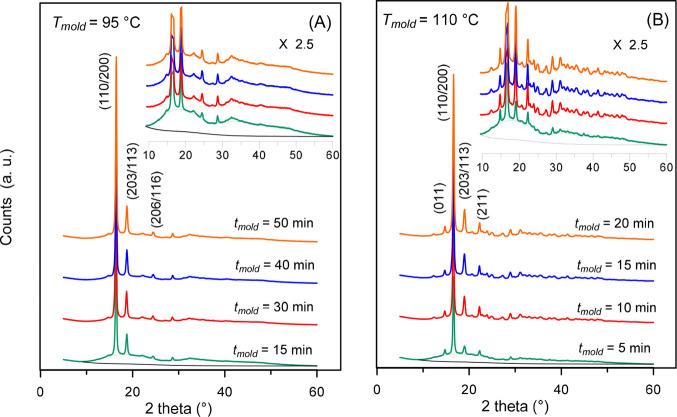
Figure 1 shows the XRD patterns of PLLA at Troom after crystallization at the molding temperatures (Tmold’s) of 95 and 110 °C for different molding times (tmold). All the patterns display features of semicrystalline specimens, with several peaks overlapped to a broad bell-shaped background. The crystalline phase of the samples prepared at Tmold = 110 °C belongs uniquely to the α-phase. It can be easily identified by the position of the most intense (110/200) and (203/113) peaks at the 2θ scattering angles of 16.6° and 19.0° and by the (011) and (211) peaks at 14.7° and 22.3°, respectively, as well as for several other less intense reflections at higher angles.5,7 Samples prepared at Tmold = 95 °C show uniquely the pattern of the α′-phase: the positions of the most intense (110/200) and (203/113) peaks are shifted at 16.5° and 18.8°, respectively, and in addition, the presence of a peculiar (206/116) peak at 24.5° is well evident; no peaks ascribable to the α-phase are present. It can be concluded that, exclusively, α′- and α-phases grow during crystallization at Tmold = 95 and 110 °C, respectively.
Figure 1.
XRD patterns of PLLA after crystallization at Tmold = (A) 95 °C and (B) 110 °C for the indicated molding times (tmold). For the conditions Tmold = 95 °C, tmold = 15 min, and Tmold = 110 °C, and tmold = 5 min, the scattering of the amorphous fraction (black dashed lines) and the background (black solid line) are also shown. The insets are enlargements of the patterns.
From the position of the most intense peaks, the mean crystallographic parameters were derived for the α′- and α-phases, as reported in Table 1. These values are very close to literature data.5,7 From the unit cell parameters, the density values of 1.245 and 1.265 g/cm3 were calculated for the totally crystalline α′- and α-phases of PLLA, respectively, in excellent agreement with literature data.18 The crystal fraction (XC) values, calculated for all the specimens from the entire XRD profiles, are listed in Table 2 and discussed in the following section.
Table 1. Unit Cell Parameters of PLLA α′- and α-Crystals.
| crystal | a (Å) | b (Å) | c (Å) | V (Å)3 |
|---|---|---|---|---|
| PLLA α′-phase | 10.74 ± 0.04 | 6.15 ± 0.03 | 29.10 ± 0.07 | 1922 ± 21 |
| PLLA α-phase | 10.70 ± 0.03 | 6.14 ± 0.02 | 28.82 ± 0.06 | 1893 ± 15 |
Table 2. Glass Transition Temperatures (Tg), Crystal Fraction (XC), Mobile Amorphous Weight Fraction (XMAF), Rigid Amorphous Weight Fraction (XRAF), Experimental Elastic Modulus (E), Tensile Strength at Break (TS), and Elongation at Break Measured at Troom for PLLA after Crystallization at Tmold = 95 and 110 °C for Different Molding Times.
| condition | Tg (°C)a | XCb | XMAFb | XRAFc | E (GPa) | TS (MPa) | elongation at break (%) |
|---|---|---|---|---|---|---|---|
| amorphous | 57.0 | 0.00 | 1.00 | 0.00 | 3.60 ± 0.19 | 60.3 ± 2.2 | 3.60 ± 0.50 |
| Tmold = 95 °C, tmold = 15 min | 59.0 | 0.29 | 0.48 | 0.23 | 3.86 ± 0.18 | 58.6 ± 1.2 | 1.68 ± 0.10 |
| Tmold = 95 °C, tmold = 30 min | 63.5 | 0.38 | 0.39 | 0.23 | 3.83 ± 0.14 | 57.8 ± 1.1 | 1.68 ± 0.10 |
| Tmold = 95 °C, tmold = 40 min | 64.5 | 0.39 | 0.38 | 0.23 | 3.82 ± 0.20 | 57.9 ± 2.7 | 1.67 ± 0.10 |
| Tmold = 95 °C, tmold = 50 min | 65.0 | 0.40 | 0.36 | 0.24 | 3.92 ± 0.17 | 54.6 ± 1.7 | 1.60 ± 0.10 |
| Tmold = 110 °C, tmold = 5 min | 58.0 | 0.18 | 0.75 | 0.07 | 3.95 ± 0.22 | 50.8 ± 3.0 | 1.37 ± 0.10 |
| Tmold = 110 °C, tmold = 10 min | 60.0 | 0.38 | 0.47 | 0.15 | 4.08 ± 0.22 | 50.8 ± 3.2 | 1.36 ± 0.17 |
| Tmold = 110 °C, tmold = 15 min | 61.0 | 0.40 | 0.42 | 0.18 | 4.19 ± 0.19 | 50.6 ± 2.5 | 1.31 ± 0.15 |
| Tmold = 110 °C, tmold = 20 min | 62.0 | 0.42 | 0.38 | 0.20 | 4.42 ± 0.10 | 49.7 ± 3.0 | 1.24 ± 0.24 |
Estimated error from repeated measurements: ±0.5 K.
Estimated error from repeated measurements: ±0.02.
Estimated errors from repeated measurements: ±0.04.
2.2. Thermal Characterization of Amorphous PLLA and after Different Crystallization Times at Tmold = 95 and 110 °C
Figure 2 shows the cp,app and cp,rev curves of the amorphous PLLA. The glass transition temperature (Tg), which is overlapped by a small enthalpy recovery peak connected to the structural relaxation occurred during the storage of 3 days at Troom after preparation, is centered around 56 °C, in agreement with literature data.44 The specific heat capacity increment at Tg confirms that the specimen is completely amorphous.
Figure 2.
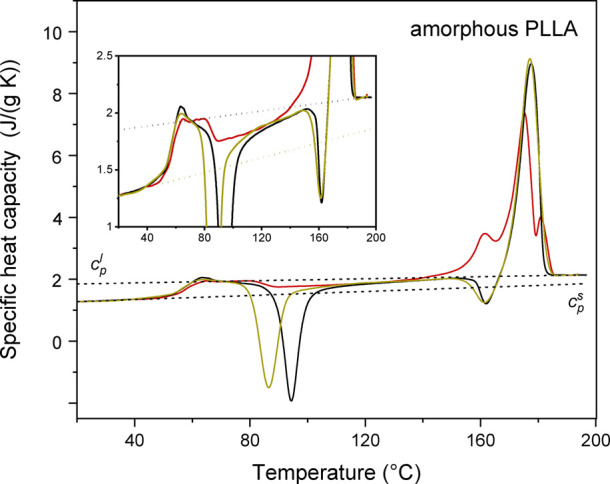
Apparent specific heat capacity (cp,app) at the heating rate of 10 K/min (black line) and at the average heating rate of 2 K/min (yellow line), and reversing specific heat capacity (cp,rev, red line) at the average heating rate of 2 K/min (p = 120 s) for amorphous PLLA. The inset is an enlargement of the cp,app and cp,rev curves. The black dotted lines are the thermodynamic solid and liquid specific heat capacities (cps and cpl) of PLLA, adapted with permission from ref (44). Copyright (2005) American Chemical Society.
It is worth noting that the glass transition in the cp,rev curve is observed at temperatures slightly higher with respect to the cp,app curves. This behavior can be explained considering that the apparent specific heat capacity represents the devitrification process that takes place at Tg upon linear heating rate, whereas the reversing heat capacity defines the “dynamic” glass transition, which is observed when the experimental timescale is close to the relaxation time of the amorphous segments.45 For this reason, the dynamic glass transition is a function of the modulation period, shifting to higher temperatures with increasing modulation frequency.45 In a TMDSC experiment, devitrification is a process characterized by a longer timescale with respect to the dynamic glass transition because many modulations occur during the glass transition.46 Thus, an experiment performed with conventional linear heating rate could correspond to a TMDSC scan with low modulation frequency, with the result that the glass transition observed in the cp,app curves occurs at lower temperatures with respect to typical cp,rev curves.47,48
Between approximately 75 and 110 °C, the cp,app curves exhibit an intense cold crystallization process, which as expected, is centered at increasing temperature with increasing heating rate. In correspondence with the cold crystallization peak, the cp,rev curves display a sharp decrease due to the irreversible nature of the cold crystallization process and the increase in the crystalline fraction.49 In the temperature range of the cold crystallization, mainly the α′-crystals grow,6−9 as also proven by the typical exothermic peak in the cp,app curves at about 160 °C, which is connected with the reorganization of the disordered α′-crystals into the more ordered α-form.10,11 At higher temperatures, the main melting observed in the cp,app curve is due to the fusion of the newly formed α-crystals. As the reversing heat capacity in the melting region originates from melting/crystallization processes that can be reversed by the temperature modulation, which generally do not involve the entire crystal fraction, the shape of the cp,rev peak is usually different from that of the cp,app curve.13
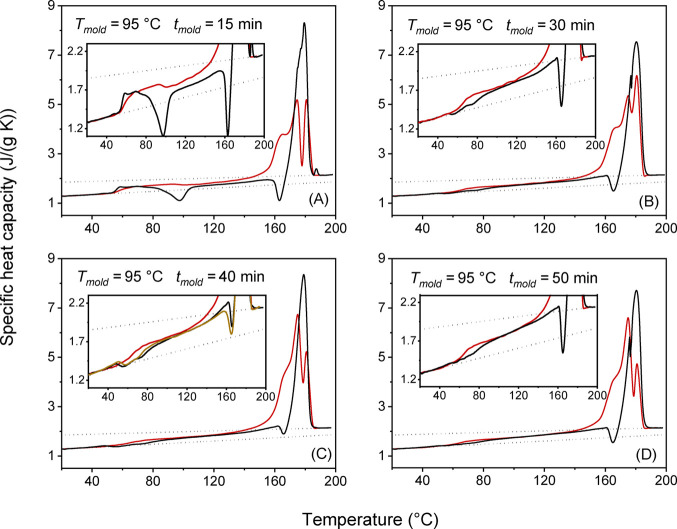
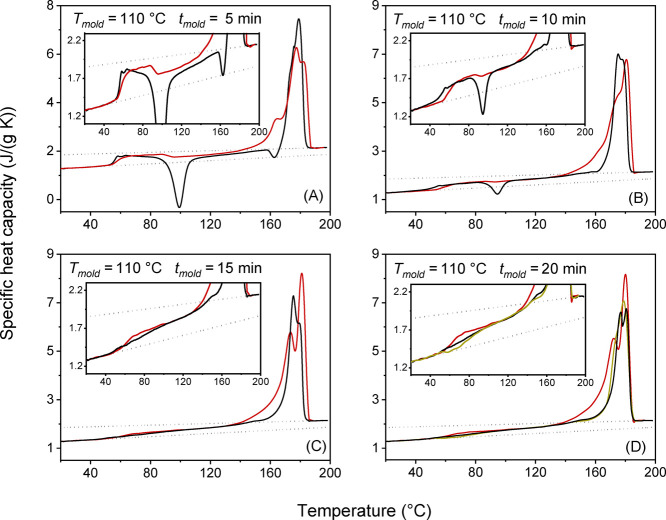
Figures 3 and 4 show the cp,app and cp,rev curves of the semicrystalline PLLA specimens after crystallization for different times at Tmold = 95 and 110 °C. Above the glass transition, in the range between 80 and 110 °C, a cold crystallization exotherm is observed in the cp,app curves after low molding times. The exotherm disappears for tmold ≥ 30 min at Tmold = 95 °C and tmold ≥ 15 min at Tmold = 110 °C, which means that after these molding times, crystallization is almost complete or complete.
Figure 3.
(A−D) Apparent specific heat capacity (cp,app, black lines) at the heating rate of 10 K/min, and reversing specific heat capacity (cp,rev, red lines) at the average heating rate of 2 K/min (p = 120 s) for PLLA after molding at Tmold = 95 °C for the indicated molding times (tmold). The apparent specific heat capacity (cp,app) at the average heating rate of 2 K/min (yellow line) is also shown for tmold =40 min. The insets are enlargements of the cp,app and cp,rev curves. The black dotted lines are the thermodynamic solid and liquid specific heat capacities (cps and cpl) of PLLA, adapted with permission from ref (44). Copyright (2005) American Chemical Society.
Figure 4.
(A−D) Apparent specific heat capacity (cp,app, black lines) at the heating rate of 10 K/min, and reversing specific heat capacity (cp,rev, red lines) at the average heating rate of 2 K/min (p = 120 s) for PLLA after molding at Tmold = 110 °C for the indicated molding times (tmold). The apparent specific heat capacity (cp,app) at the average heating rate of 2 K/min (yellow line) is also shown for tmold = 20 min. The insets are enlargements of the cp,app and cp,rev curves. The black dotted lines are the thermodynamic solid and liquid specific heat capacities (cps and cpl) of PLLA, adapted with permission from ref (44). Copyright (2005) American Chemical Society.
The comparison between the cp,app and cp,rev curves in the glass transition region shows that the Tg value from the cp,rev curves is higher than that from the cp,app curves after low molding times, i.e., in a condition of incomplete crystallization, according to the trend usually observed, as discussed above. The opposite behavior is observed after higher molding times when crystallization is almost complete or complete. (It is worth noting that similar cp,app curves are observed also at 2 K/min, as proven in Figures 3 and 4 for Tmold = 95 °C/tmold = 40 min and Tmold = 110 °C/tmold = 20 min.)
According to TMDSC fundamentals, cp,rev originates from the amplitude of the endothermic and exothermic events that follow the temperature modulation, occurring separately in the two semiperiods, whereas the latent heats released or absorbed sum algebraically in the apparent specific heat capacity.50 If irreversible endothermic or exothermic events occurs simultaneously with the devitrification process, then the glass transition can be partially or completely masked in the cp,app curve and exhibit a shape completely different from the typical heat capacity step. On the other hand, the cp,rev curve is able to separate and resolve the glass transition, also in the presence of nonreversing events, because the glass transition is a reversing process that can follow the temperature modulation.45 Thus, the cp,rev curve in the Tg region represents the baseline heat capacity,45 which means that the difference between cp,app and cp,rev has to be associated to nonreversing processes that irreversibly absorb or release enthalpy.
The different shape of the cp,app and cp,rev curves in the Tg region, observed in Figures 3 and 4 after high molding times, can originate from the concomitant occurring of the glass transition and exothermic events, for example, a cold crystallization and/or an enthalpy release due to pressure and strain effects caused by the molding process.51 The presence of an exothermic event in the glass transition region has been reported for drawn PLLA with a draw ratio higher than 2 and explained as due to a strain-induced crystallization in the presence of oriented amorphous chains.52,53 Also in the PLLA specimens investigated in the present study, a certain unknown chain alignment can be produced during the processing by injection molding.54,55 However, the oriented amorphous chains are expected to relax, at least partially, at the quite high molding temperatures,56 and certainly, the relaxation rate decreases as the crystallization proceeds due to constraints imposed by the newly formed crystals on the close amorphous segments.57 However, most likely, the exothermic event in proximity of the glass transition has to be ascribed to enthalpy relaxation because it is detected only after high molding times. It is known that exothermic peaks can be caused by release of mechanically induced excess enthalpy.51 This event occurs when a pressure-densified glass relaxes to a less dense glass with lower enthalpy. The PLLA specimens molded for different times at Tmold = 95 and 110 °C, after quick cooling to Troom, undergo volume and enthalpy adjustments as a consequence of both temperature and pressure decreases. These adaptations can be more favored at Troom in the unconstrained amorphous regions that characterize a semicrystalline material at the beginning of the crystallization process but can become hindered in an amorphous phase that experiences physical constraints imposed by the surrounding crystalline regions.14,57 This could explain why the enthalpy release is observed above Troom, in the Tg region, only for the specimens almost completely or completely crystallized.
Figures 3 and 4 display that the melting behavior of PLLA is largely affected by the crystallization conditions. The exothermic peak at about 160 °C, connected with the reorganization of the disordered α′-crystals into the more stable α-form,10,11 is present in the cp,app curves of (i) PLLA crystallized at Tmold = 95 °C, because at this temperature, only α′-crystals grow, and (ii) PLLA crystallized at Tmold = 110 °C for tmold = 5 min due to α′-crystals that develop during the cold crystallization process in the temperature range between 70 and 100 °C. It is worth noting that the melting peak is single if the crystallization process produces only original α′-crystals, which upon heating, transform into the more ordered α-phase so that the final melting peak is associated to the fusion of the newly crystallized α-crystals. Conversely, a double melting is observed in the presence of only α-crystals: the peak at lower temperatures is due to the fusion of original α-crystals, whereas the peak at higher temperature is due to the fusion of α-crystals recrystallized upon heating58,59 as, commonly, reorganization and recrystallization overlap the entire fusion process in semicrystalline polymers at a relatively low heating rate.60
The Tg values for all the PLLA specimens, determined at half of the heat capacity increment of the cp,rev curves, are reported in Table 2. As expected, the Tg values of the semicrystalline PLLA appear higher than those of the amorphous PLLA, progressively increasing with tmold. The slightly higher Tg values after crystallization at Tmold = 95 °C are in agreement with literature data14 and are ascribable to the devitrification of a mobile amorphous phase slightly more constrained with respect to the one that develops during crystallization at higher temperatures. This slightly constrained MAF has not to be confused with the rigid amorphous fraction, which mobilizes above the Tg region, being subjected to greater constraints.
The mobile amorphous weight fractions (XMAF) were calculated at Tg as XMAF = Δcp/Δcpa, where Δcp is the specific capacity increment from the cp,rev curves, and Δcpa is the specific heat capacity increment of the completely amorphous PLLA (Δcpa = 0.52 J/g K). Due to the presence of cold crystallization exotherms, with additional growth of both α′- and α-crystals with unknown percentages upon heating, a correct determination of the crystallinity degree is not attainable from all the cp,app curves, by taking into account the different enthalpy of melting values of 100% crystalline α′- and α-forms.61 Thus, the crystalline weight fractions were assumed equal to the crystal fractions obtained by XRD analysis, and the rigid amorphous weight fractions (XRAF) were deduced by difference (XRAF = 1 – XC – XMAF). All these data, listed in Table 2, show that for the two PLLA series crystallized at Tmold = 95 and 110 °C, the crystal fraction increases with the molding time, whereas in parallel, the mobile amorphous fraction decreases. The rigid amorphous fraction appears approximately independent of tmold after crystallization at Tmold = 95 °C, whereas it increases with XC for Tmold = 110 °C. It has to be pointed out that the XRAF values collected in Table 2 are calculated at Tg, and therefore, they include the rigid amorphous fraction that develops (i) during the crystallization at Tmold and (ii) during the successive cooling to Troom. For PLLA, it has been proven that the RAF amount that develops during isothermal crystallization decreases with increasing crystallization temperature;14,15 therefore, it can be supposed that after crystallization at Tmold = 110 °C, the rigid amorphous fraction mainly develops upon the successive cooling to Troom. A high rigid amorphous fraction approximately independent of the crystallization time and crystallinity degree has been reported in the literature after crystallization at low temperatures,62,63 in perfect agreement with the present trend for Tmold = 95 °C. Likely at low temperature, at the beginning of the crystallization process, the low mobility of the chains leads to the growth of very imperfect crystals, with a high RAF amount at the amorphous/crystal interfaces. As crystallization proceeds, the organization of the crystal phase slightly improves, which can lead to a decrease in the XRAF/XC ratio in bulk PLLA, as also reported for poly(3-hydroxybutyrate).64 It is worth noting that a different XRAF/XC evolution has been observed for nanoconfined PLLA,65 which proves that the crystal/amorphous coupling strongly depends on the geometrical dimensions of the sample under investigation. The present results demonstrate that formation of rigid amorphous fraction is favored at lower crystallization temperatures.
2.3. Tensile Characterization of Amorphous PLLA and after Different Crystallization Times at Tmold = 95 and 110 °C
The values of the experimental elastic modulus (E), tensile strength at break (TS), and elongation at break of PLLA, after crystallization at Tmold = 95 and 110 °C for different molding times, measured at Troom, are listed in Table 2. It can be noted that, with increasing molding time and, therefore, crystallinity, the elastic modulus slightly increases, whereas in parallel, the tensile strength and elongation at break decrease. For similar XC values, the elastic modulus of the semicrystalline PLLA containing α′-crystals is lower than that of the samples containing α-crystals, whereas the tensile strength and elongation at break data are higher. The fracture behavior of all the PLLA semicrystalline specimens appears fragile, as typically reported for PLLA:1,66 the crystalline regions act as stress concentrators, which leads to premature failure of the materials. The value of the elastic modulus of PLLA in the glassy state at Troom is in perfect agreement with literature data.1,66
To correlate the mechanical properties with the structure of semicrystalline PLLA, the crystalline, mobile amorphous, and rigid amorphous weight fractions listed in Table 2 were transformed into the corresponding volumetric fractions, VC, VMAF, and VRAF, after determination of the respective density values.
The measurement of the density at Troom = 21 °C of (i) the amorphous PLLA (ρMAF = 1.240 ± 0.005 g/cm3) and (ii) the semicrystalline PLLA crystallized at Tmold = 95 °C for tmold = 50 min and at Tmold = 110 °C for tmold = 20 min (ρ = 1.225 ± 0.005 and 1.222 ± 0.005 g/cm3, respectively) allowed the determination of the density of the rigid amorphous fraction (ρRAF) according to the following relationship
| 1 |
with the density of the crystalline α′- and α-phases (ρC) assumed equal to 1.245 and 1.265 g/cm3, respectively, as reported above. The density of the RAF connected with the α′-crystals turned out to be 1.17 g/cm3, approximately 3% lower than ρMAF, whereas the density of the RAF connected with the α-crystals came out to be 1.11 g/cm3, about 10% lower than ρMAF.. To the best of our knowledge, this is the first determination of the RAF density for PLLA. The finding that ρRAF is lower than ρMAF is in perfect agreement with (i) theoretical expectations, because the higher vitrification temperature of the RAF induces a higher free volume in its glassy state with respect to the MAF,67 and (ii) experimental evidence of de-densification occurring during crystallization.68 Indeed, some studies have proven that in semicrystalline polymers, the rigid amorphous fraction has a significant and detrimental impact on the barrier properties because it counterbalances the positive influence of the crystalline regions.69,70 An important result of the present investigation is that the density of the RAF linked to the more ordered α-crystals is lower with respect to that of the RAF connected to the conformationally disordered α′-modification. It is likely that the tight chain arrangement of the α-form produces a higher stress and stronger coupling at the amorphous/crystal interface, which hinders significantly the relaxation of the amorphous segments, so that a higher free volume remains trapped in proximity of the crystals.
By assuming the density data above reported, the calculated VC, VMAF, and VRAF values turned out to be substantially equal to the XC, XMAF, and XRAF data listed in Table 2 (see Tables 3–6).
Table 3. Crystalline (VC) and Rigid Amorphous (VRAF) Volume Fractions, Texture Parameters (λ and φ), Elastic Modulus of the Semicrystalline PLLA (E), and Elastic Modulus of the α′-Crystals (EC) Predicted by eqs 2 and 3.
| tmold at Tmold = 95 °C (min) | VC | VRAF | λ (eq 2) | λ (eq 3) | φ (eq 2) | φ (eq 3) | E (GPa) (eq 2) | E (GPa) (eq 3) | EC (α′) (GPa) (eq 2) | EC (α′) (GPa) (eq 3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 15 | 0.29 | 0.24 | 0.10 | 0.17 | 0.10 | 0.20 | 3.90 | 3.82 | 3.9 | 13.1 |
| 30 | 0.37 | 0.24 | 0.10 | 0.18 | 0.10 | 0.21 | 3.90 | 3.84 | ||
| 40 | 0.38 | 0.24 | 0.10 | 0.18 | 0.10 | 0.21 | 3.90 | 3.84 | ||
| 50 | 0.39 | 0.25 | 0.10 | 0.20 | 0.10 | 0.24 | 3.90 | 3.90 |
Table 6. Crystalline (VC) and Rigid Amorphous (VRAF) Volume Fractions, Texture Parameters (β and γ), Elastic Modulus of the Semicrystalline PLLA (E), Elastic Modulus of the α-Crystals (EC), and Elastic Modulus of the RAF (ERAF) Connected to α-Crystals Predicted by eq 4.
2.4. Modeling of the Elastic Modulus of the Rigid Amorphous Fraction and α′- and α-Phases of PLLA
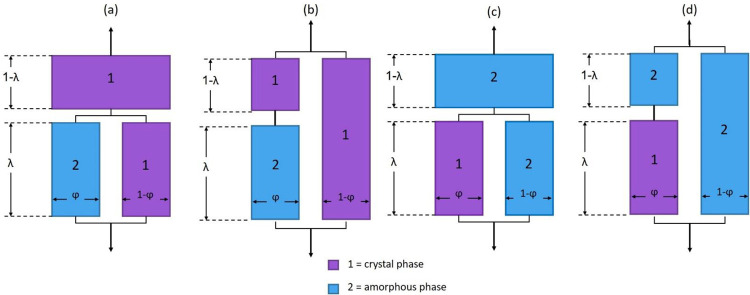
A simple schematization of the original two-phase Takayanagi model is reported in Figure 5. Different arrangements can be assumed. In the series–parallel models (Figure 5a,c), which represent a situation of good stress transfer normal to the applied tensile stress, the strain of phase 2 is equal to that of the element close to it, whereas in the parallel–series models (Figure 5b,d), the strain of phase 2 is different from that of the other elements due to poor stress transfer. The combinations shown in Figure 5c,d represent situations with the crystalline domains dispersed in the continuous amorphous phase, which holds especially for semicrystalline polymers with a low or intermediate crystallinity degree, whereas the models depicted in Figure 5a,b describe the opposite condition with high crystal content. It was proven that the models shown in Figure 5a,c are more suitable for the calculation of the equivalent elastic modulus of semicrystalline polymers because they better interpret the strain distribution under stress in these materials.30−35 Thus, only these latter arrangements are considered here.
Figure 5.
(a–d) Schematic representation of the two-phase Takayanagi mechanical models of semicrystalline polymers.
The equations that allow the calculation of the elastic modulus, according to the model described in Figure 5a,c, are respectively
| 2 |
| 3 |
where E, EC, and EA are the elastic moduli of the semicrystalline polymer, crystal phase, and amorphous phase, respectively, whereas λ and φ, which range between 0 and 1, are texture parameters connected with the phase composition and related to the degree of parallel and series coupling of the two phases, respectively. In the original Takayanagi treatment, a spherical shape was assumed for the dispersed phase. According to this supposition, the product φ·λ equals the volume fraction of the dispersed phase, i.e., the amorphous phase or crystal phase according to the models depicted in Figure 5a,c, respectively. To avoid the recourse to this approximation, a preliminary estimation of the texture parameters for the two-phase models shown in Figure 5a,c was performed by means of an iterative numerical method (using Excel Data Solver Function). Experimental evidence reported in the literature has suggested that the elastic modulus of the RAF is higher than that of the MAF and probably closer to that of the crystal phase;19−27 thus, as a first approximation, a single block containing these two fractions was assumed due to the tight connection between the crystal phase and RAF. Consequently, the φ texture parameter becomes connected to the mechanical response of the amorphous fraction or the coupled crystalline and rigid amorphous fractions. A minimization of the mean square error between the experimental and theoretical elastic moduli predicted by eqs 2 and 3 was carried out for the semicrystalline PLLA containing α′- and α-crystals to calculate the parameters λ, φ, and EC by keeping the experimental elastic modulus of the amorphous phase fixed (EA = 3.6 GPa). The final results of the mathematical iterations for the two semicrystalline PLLA series are reported in Tables 3 and 4, respectively.
Table 4. Crystalline (VC) and Rigid Amorphous (VRAF) Volume Fractions, Texture Parameters (λ and φ), Elastic Modulus of the Semicrystalline PLLA (E), and Elastic Modulus of the α-Crystals (EC) Predicted by eqs 2 and 3.
| tmold at Tmold = 110 °C (min) | VC | VRAF | λ (eq 2) | λ (eq 3) | φ (eq 2) | φ (eq 3) | E (GPa) (eq 2) | E (GPa) (eq 3) | EC (α) (GPa) (eq 2) | EC (α) (GPa) (eq 3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 0.18 | 0.08 | 0.20 | 0.21 | 0.20 | 0.22 | 4.18 | 4.00 | 4.2 | 16.5 |
| 10 | 0.37 | 0.17 | 0.20 | 0.25 | 0.20 | 0.26 | 4.18 | 4.10 | ||
| 15 | 0.39 | 0.20 | 0.20 | 0.27 | 0.20 | 0.28 | 4.18 | 4.16 | ||
| 20 | 0.41 | 0.22 | 0.20 | 0.34 | 0.20 | 0.28 | 4.18 | 4.34 |
Tables 3 and 4 show that the λ, φ, and EC values obtained by applying eq 2, which is related to the mechanical configuration of Figure 5a, are not realistic because the calculated EC data are close to EA and much lower than the experimental and theoretical EC values reported in the literature,18 although a combined lower contribution of the RAF is expected. Furthermore, the values of the texture parameters (λ and φ), as well as the predicted E values, are not coherent as they do not vary with tmold and, consequently, with the phase composition. Actually, λ and φ must necessarily vary with the phase composition due to change in the crystalline and amorphous phase block extension. These results demonstrate that the model depicted in Figure 5a, theorized for polymers having a dominant crystalline phase, is not suitable to describe the present PLLA semicrystalline systems. Conversely, the model shown in Figure 5c provides more coherent data not only of the crystalline elastic moduli, which are very close to experimental and theoretical data found in the literature, but also of the texture parameters and the predicted E values, which increase with the crystal content.
This two-phase representation is however still imprecise because the separate and different contribution of the RAF is not taken into consideration. Thus, the Takayanagi model was modified by inserting the RAF block between the MAF and the crystal blocks. The configuration adopted for the three-phase model, already applied successfully to poly(3-hydroxybutyrate-co-3-hydroxyvalerate) copolymers, is shown in Figure 6. Two texture parameters, β and γ, correlated to the RAF and crystal phase, respectively, were introduced. The equation that describes the equivalent elastic modulus of the semicrystalline polymer according to the configuration of Figure 6 is
| 4 |
Figure 6.
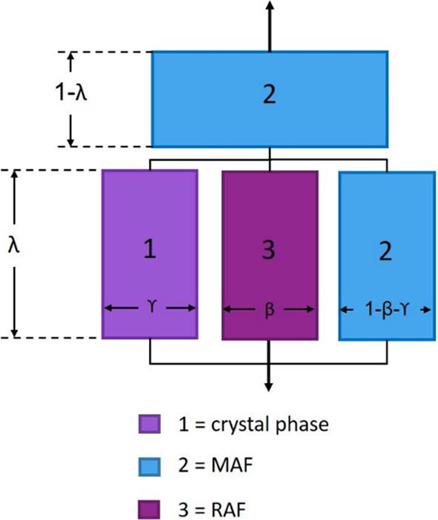
Schematic representation of the three-phase Takayanagi mechanical models of semicrystalline polymers.
An iterative process was again carried out by minimizing the mean square error between the experimental and theoretical elastic moduli predicted by eq 4, with the aim of calculating the parameters β, γ, EC, and ERAF, having the experimental elastic modulus of the amorphous phase (EMAF = 3.6 GPa) fixed, as well as the parameter λ, calculated via eq 3 and listed in Tables 3 and 4. The results of the minimization procedure are reported in Tables 5 and 6 for the α′- and α-phases, respectively.
Table 5. Crystalline (VC) and Rigid Amorphous (VRAF) Volume Fractions, Texture Parameters (β and γ), Elastic Modulus of the Semicrystalline PLLA (E), Elastic Modulus of the α′-Crystals (EC), and Elastic Modulus of the RAF (ERAF) Connected to α′-Crystals Predicted by eq 4.
The results obtained are in excellent agreement with intuitive expectation because the modulus of rigid amorphous fraction is found to be lower than that of the crystal phase for both the α′- and α-crystals. This trend can be rationalized by considering that, with respect to the crystal phase, higher free volume and weaker intermolecular bonding can favor chain rearrangement under stress in the RAF regions. It is worth noting that at Troom, at which the experimental elastic moduli were measured, all the three fractions of PLLA (crystalline, mobile amorphous, and rigid amorphous) are solid. With respect to the RAF, the mobile amorphous fraction in the glassy state is characterized by a lower free volume but also by fewer physical constraints. This latter property can explain the slightly higher ERAF value with respect to the experimental elastic modulus of the MAF.
Very impressive are the values of the elastic moduli of the two crystalline forms of PLLA. The calculated EC data are in perfect agreement with the experimental and theoretical evaluation of the ultimate elastic modulus of the α′- and α-forms of PLLA (12.6 and 12.9 GPa for the α′-form and 13.8 and 14.7 GPa for the α-form).18 Polymer crystals generally exhibit mechanical anisotropy, with the highest modulus in the chain axis direction and lower moduli in the other directions.71 For PLLA, the elastic modulus of the α-phase was found approximately constant in all the directions, whereas a stronger anisotropy was detected for the α′-modification.18 This can explain the slightly lower EC value here derived for the α′-phase with respect to the theoretical and experimental data by taking into account the different orientations of the real crystals with respect to the load direction.
The very good correspondence between the EC values determined from the three-phase Takayanagi mechanical model and the experimental and theoretical values reported in the literature for the α′- or α-crystals constitutes a proof of the validity and reliability of the derived ERAF data. Interestingly, the values of the elastic modulus of the RAF linked to the α-form turned out to be slightly higher with respect to RAF connected to the disorder α′-phase, likely due to the stronger constraints imposed by the more ordered crystalline form.
Finally, Tables 5 and 6 show also that the texture parameters β and γ, determined with no empirical assumptions, increase with the crystalline and RAF amounts, confirming that these parameters are correctly connected with the extensions of the different blocks, i.e., with the composition of the semicrystalline polymer and the fractions of the different phases.
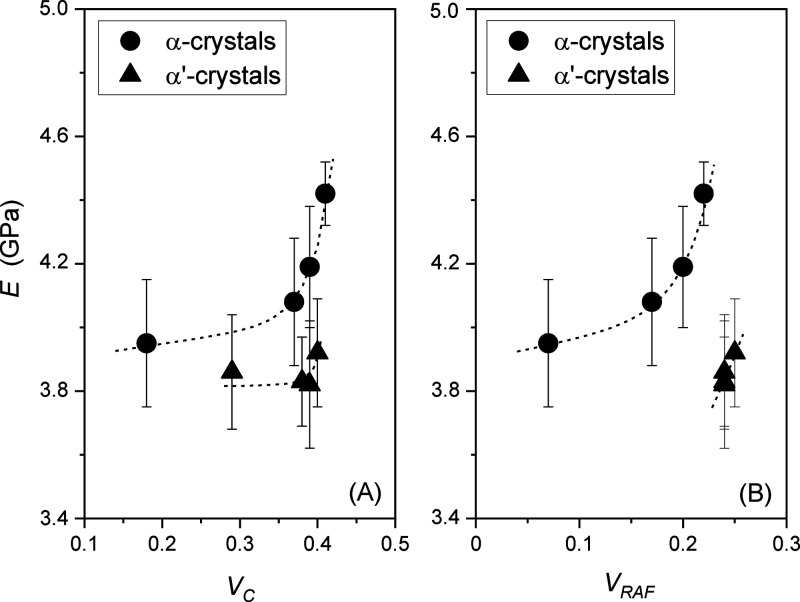
The comparison between the experimental moduli of the semicrystalline PLLA specimens containing α′- and α-crystals and the values predicted by the three-phase Takayanagi model (eq 4) is shown in Figure 7. As all the fractions (crystalline, mobile amorphous, and rigid amorphous) together influence the elastic modulus and the relationship between E and EC and ERAF is complex, the calculated E values are reported separately as functions of the crystalline and rigid amorphous volume fractions. The graphical comparison proves that the three-phase Takayanagi model describes satisfactorily the experimental E data of semicrystalline PLLA samples.
Figure 7.
Comparison between the experimental elastic moduli of semicrystalline PLLA containing α′- and α-crystals and the values predicted by the three-phase modified Takayanagi model (dotted lines) as a function of (A) the crystalline volume fraction (VC) and (B) the rigid amorphous volume fraction (VRAF). The bars are the experimental errors.
3. Conclusions
In the present study, the evolution of the mechanical properties of semicrystalline PLLA after different crystallization times at Tmold = 95 and 110 °C has been investigated. The two different crystallization temperatures allowed us to obtain samples containing exclusively α′- and α-crystals, as proven by XRD analysis.
In particular, the connection between the measured elastic modulus and phase composition of the semicrystalline samples has been analyzed in detail. The crystalline, mobile amorphous, and rigid amorphous fractions for all the samples have been quantified by combined XRD, DSC, and TMDSC measurements. With increasing molding time and, therefore, the crystallinity, the elastic modulus was found to slightly increase, whereas in parallel, the tensile strength and elongation at break decreased. For a similar crystallinity degree, the elastic modulus of the semicrystalline PLLA containing α′-crystals turned out to be lower than that of the samples containing α-crystals, in agreement with experimental and theoretical evaluation of the ultimate elastic modulus of the α- and α′-forms of PLLA.18 It is known that the possible presence of polymorphism can influence the physical and mechanical properties of semicrystalline polymers because different polymorphic forms of the same polymer may show completely different physical and mechanical properties.16,17 This means that the crystallization conditions can markedly control and tailor the final performance of these materials. Actually, a complete interpretation of the physical properties of semicrystalline polymers must take into account not only the crystal phase and mobile amorphous fraction but also the constrained amorphous interphase or rigid amorphous fraction contribution.
The novelty proposed by the present study is the estimation of the elastic modulus at Troom of the rigid amorphous fraction connected to PLLA α′- and α-crystals, respectively. The calculations have been performed on the basis of a mechanical model widely applied to semicrystalline polymers, which has been here transformed into a three-phase approach. The procedure, which allows the simultaneous quantification of the elastic moduli of the RAF and the crystalline fraction, led to EC values for the α′- and α-phases (11.2 and 14.8 GPa, respectively), in excellent agreement with the corresponding experimental and theoretical values reported in the literature, with the difference between the two forms interpreted as due to dissimilar chain conformation regularity and lattice dimensions. Also, the elastic moduli of the RAF linked to the disordered α′-form were found to be slightly lower with respect to RAF connected to the α-phase (5.4 and 6.1 GPa, respectively), likely due to the stronger constraints imposed by the more ordered α-crystalline form. Thus, the elastic moduli at Troom of the crystalline, mobile amorphous, and rigid amorphous fractions of PLLA turned out to be quantitatively in the order of EMAF < ERAF < EC, with the experimental EMAF value equal to 3.6 GPa. The trend appears to be totally in agreement with experimental results and theoretical expectations: the fewer physical constraints that characterize the mobile amorphous fraction, which is in the glassy state at Troom, with respect to the rigid amorphous fraction can explain the lower EMAF value with respect to the derived elastic modulus of the RAF. On the other hand, the much weaker intermolecular bonding and higher free volume of the constrained RAF regions with respect to the crystal phase can better favor chain rearrangement under stress and leads to ERAF values considerably lower than the EC data.
4. Materials and Methods
4.1. Materials
Commercial PLA granules derived from natural resources, purchased from NatureWorks LLC, were used. PLA Ingeo 3100HP, containing 0.3% of d-lactic acid units [melt flow index (MFR): 24 g/10 min (210 °C, 2.16 kg); nominal average molar mass: 120,000 g/mol; density: 1.24 g/cm3] is a PLA grade designed to crystallize during processing in most conventional injection molding equipment. As the commercial PLA used in the present study is a l-isomer-rich copolymer, the abbreviation PLLA is used.
The granules were dried in a Piovan DP 604-615 dryer at 60 °C before the injection molding, which was carried out using a Megatech H10/18 injection molding machine, to obtain Haake Type 3 dog-bone specimens (width: 5 mm; length: 25 mm; thickness: 1.5 mm). Amorphous and semicrystalline PLLA specimens were prepared by varying the molding temperature (Tmold) and molding time (tmold). The molding temperatures were chosen to prepare specimens containing exclusively either α′- or α-crystals with tmold values as small as possible. The operative parameters of the injection molding process are reported in Table 7. After processing, the PLLA specimens were quickly cooled to Troom in less than 1 min by means of cold air.
Table 7. Operating Conditions Used for the Injection Molding Process of the PLLA Specimens.
| condition | amorphous PLLA | semicrystalline PLLA α′-crystals | semicrystalline PLLA α-crystals |
|---|---|---|---|
| temperature of the feeder/injection zone (°C) | 190/195 | 190/195 | 190/195 |
| injection holding time (s) | 15 | 15 | 15 |
| injection pressure (bar) | 80 | 80 | 80 |
| molding temperature (Tmold) (°C) | 50 | 95 | 110 |
| molding time (tmold) (min) | <1 | 15–30–40–50 | 5–10–15–20 |
After preparation, all the Haake Type 3 dog-bone specimens were stored in a climatic chamber at room temperature, in conditions of relative humidity of 50%, and analyzed after 3 days by differential scanning calorimetry (DSC), temperature-modulated differential scanning calorimetry (TMDSC), X-ray diffraction analysis (XRD), and mechanical testing.
4.2. X-ray Diffraction (XRD) Analysis
XRD patterns were collected at Troom using a PANalytical X’PertPro diffractometer in reflection mode, equipped with copper radiation (λ = 0.15418 nm) and a fast solid-state X’Celerator detector. The X-ray crystal fraction (XC) was calculated as the ratio of the areas of the crystalline peaks and the total area of the background-corrected diffraction profile. To take into account the air and incoherent scattering, a scan without a sample was performed and properly scaled for each scan. The lattice constants were calculated from the positions of the most intense reflections by least-squares refinements.
4.3. Thermal Characterization by Differential Scanning Calorimetry (DSC) and Temperature-Modulated Differential Scanning Calorimetry (TMDSC)
DSC and TMDSC measurements were performed with a PerkinElmer Calorimeter DSC 8500 equipped with an IntraCooler III as refrigerating system. The instrument was calibrated in temperature with high-purity standard materials (indium, naphthalene, and cyclohexane) at zero heating rate according to the procedure for conventional DSC.72 Enthalpy calibration was performed with indium. To gain precise apparent specific heat capacity data (cp,app) from the heat flow rate signal, each scan was accompanied by an empty pan run (blank run). The mass of the blank and sample aluminum pans matched within 0.02 mg. To minimize the instrumental thermal lag, the sample mass was lower than 10 mg. Dry nitrogen was used as purge gas at a rate of 30 mL/min. The temperature of the samples during heating was corrected for the thermal lag, determined as the average by using different standard materials. This lag was 0.05 min, which for the heating rates of 2 and 10 K/min, corresponds to a temperature correction of −0.1, and −0.5 K, respectively.
The PLLA specimens prepared by injection molding were analyzed (i) by conventional DSC from 20 to 200 °C at the heating rate of 10 K/min to obtain apparent specific heat capacity (cp,app) curves and (ii) by TMDSC, with a saw-tooth modulation temperature program, at the average heating rate of 2 K/min, with a temperature amplitude (AT) of 0.5 K and a modulation period (p) of 120 s, to obtain apparent specific heat capacity (cp,app) curves and reversing specific heat capacity (cp,rev) curves. According to the mathematical treatment of TMDSC data, the modulated temperature and heat flow rate curves can be approximated to discrete Fourier series and separated into underlying and periodic components.73,74 The underlying components are equivalent to the conventional linear program of the temperature and corresponding conventional heat flow rate signal, from which the cp,app curve can be derived. Conversely, from the periodic component, the cp,rev curve is calculated according to the following equation
| 5 |
where AHF and AT are the amplitudes of the first harmonic of the modulated heat flow and temperature, respectively, ω is the fundamental frequency of temperature modulation (ω = 2π/p), m is the mass of the sample, and K(ω) is the frequency-dependent calibration factor. The average K(ω) values, determined by calibration with sapphire, was 1.00 ± 0.02 for p = 120 s.
4.4. Tensile Characterization
Tensile tests on the PLLA specimens were carried out at Troom, with a crosshead speed of 10 mm/min, by means of an Instron universal testing machine 5500R equipped with a 10 kN load cell and interfaced with a computer running MERLIN software (INSTRON version 4.42 S/N–014733H). At least 10 specimens were tested for each sampling and the average values were reported.
4.5. Density Measurements
Density measurements were performed by means of an analytic balance Sartorius RC 210 D (0.01 mg resolution), equipped with the density determination kit YDK 01-0D, in accordance with ASTM D792 (Standard Test Methods for Density and Specific Gravity of Plastics by Displacement). The density values, determined at Troom = 21 °C, were obtained as the average of at least 20 measurements.
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
References
- Anderson K. S.; Schreck K. M.; Hillmyer M. A. Toughening Polylactide. Polym. Rev. 2008, 48, 85–108. 10.1080/15583720701834216. [DOI] [Google Scholar]
- Saeidloua S.; Huneaulta M. A.; Li H.; Park C. B. Poly(lactic acid) Crystallization. Progr. Polym. Sci. 2012, 37, 1657–1677. 10.1016/j.progpolymsci.2012.07.005. [DOI] [Google Scholar]
- Urayama H.; Kanamori T.; Kimura Y. Microstructure and Thermomechanical Properties of Glassy Polylactides with Different Optical Purity of the Lactate Units. Macromol. Mater. Eng. 2001, 286, 705–713. . [DOI] [Google Scholar]
- Pan P.; Inoue Y. Polymorphism and Isomorphism in Biodegradable Polyesters. Progr. Polym. Sci. 2009, 34, 605–640. 10.1016/j.progpolymsci.2009.01.003. [DOI] [Google Scholar]
- Wasanakuk K.; Tashiro K. Crystal Structure and Disorder in Poly(l-lactic acid) δ form (α′ form) and the Phase Transition Mechanism to the Ordered α form. Polymer 2011, 52, 6097–6109. 10.1016/j.polymer.2011.10.046. [DOI] [Google Scholar]
- Kawai T.; Rahman N.; Matsuba G.; Nishida K.; Kanaya T.; Nakano M.; Okamoto H.; Kawada J.; Usuki A.; Honma N.; Nakajima K.; Matsuda M. Crystallization and Melting Behavior of Poly(l-lactic acid). Macromolecules 2007, 40, 9463–9469. 10.1021/ma070082c. [DOI] [Google Scholar]
- Pan P.; Zhu B.; Kai W.; Dong T.; Inoue Y. Polymorphic Transition in Disordered poly(l-lactide) Crystals Induced by Annealing at Elevated Temperatures. Macromolecules 2008, 41, 4296–4304. 10.1021/ma800343g. [DOI] [Google Scholar]
- Pan P.; Zhu B.; Kai W.; Dong T.; Inoue Y. Effect of Crystallization Temperature on Crystal Modifications and Crystallization Kinetics of Poly(l-lactide). J. Appl. Polym. Sci. 2008, 107, 54–62. 10.1002/app.27102. [DOI] [Google Scholar]
- Zhang J.; Tashiro K.; Tsuji H.; Domb A. J. Disorder-to-Order Phase Transition and Multiple Melting Behavior of Poly(l-lactide) Investigated by Simultaneous Measurements of WAXS and DSC. Macromolecules 2008, 41, 1352–1357. 10.1021/ma0706071. [DOI] [Google Scholar]
- Androsch R.; Schick C.; Di Lorenzo M. L. Melting of Conformationally Disordered Crystals α′-phase of poly(l-lactic acid). Macromol. Chem. Phys. 2014, 215, 1134–1139. 10.1002/macp.201400126. [DOI] [Google Scholar]
- Hu J.; Wang J.; Bhoje Gowd E.; Yuan Y.; Zhang T.; Duan Y.; Hu W.; Zhang J. Small- and Wide-Angle X-ray Scattering Study on α′-to-α Transition of Poly(l-lactide acid) Crystals. Polymer 2019, 167, 122–129. 10.1016/j.polymer.2019.01.088. [DOI] [Google Scholar]
- Righetti M. C. Amorphous Fractions of Poly(lactic acid). Adv. Polym. Sci. 2018, 279, 195–234. 10.1007/12_2016_14. [DOI] [Google Scholar]
- Wunderlich B. Reversible Crystallization and the Rigid Amorphous Phase in Semicrystalline Macromolecules. Prog. Polym. Sci. 2003, 28, 383–450. 10.1016/S0079-6700(02)00085-0. [DOI] [Google Scholar]
- Righetti M. C.; Prevosto D.; Tombari E. Time and Temperature Evolution of the Rigid Amorphous Fraction and Differently Constrained Amorphous Fractions in PLLA. Macromol. Chem. Phys. 2016, 217, 2013–2026. 10.1002/macp.201600210. [DOI] [Google Scholar]
- Righetti M. C.; Tombari E. Crystalline, Mobile Amorphous and Rigid Amorphous Fractions in Poly(l-lactic acid) by TMDSC. Thermochim. Acta 2011, 522, 118–127. 10.1016/j.tca.2010.12.024. [DOI] [Google Scholar]
- Tashiro K. Molecular Theory of Mechanical Properties of Crystalline Polymers. Progr. Polym. Sci. 1993, 18, 377–435. 10.1016/0079-6700(93)90013-3. [DOI] [Google Scholar]
- De Rosa C.; Scoti M.; Di Girolamo R.; Ruiz de Ballesteros O.; Auriemma F.; Malafronte A. Polymorphism in Polymers: A Tool to Tailor Material’s Properties. Polym. Cryst. 2020, 3, e10101 10.1002/pcr2.10101. [DOI] [Google Scholar]
- Wasanasuk K.; Tashiro K. Theoretical and Experimental Evaluation of Crystallite Moduli of Various Crystalline Forms of Poly(l-lactic acid). Macromolecules 2012, 45, 7019–7026. 10.1021/ma3010982. [DOI] [Google Scholar]
- Rastogi R.; Vellinga W. P.; Rastogi S.; Schick C.; Meijer H. E. H. The Three-Phase Structure and Mechanical Properties of Poly(ethylene terephthalate). J. Polym. Sci., Part B: Polym. Phys. 2004, 42, 2092–2106. 10.1002/polb.20096. [DOI] [Google Scholar]
- Di Lorenzo M. L.; Righetti M. C. The Three-Phase Structure of Isotactic Poly(1-butene). Polymer 2008, 49, 1323–1331. 10.1016/j.polymer.2008.01.026. [DOI] [Google Scholar]
- Kolesov I.; Androsch R. The Rigid Amorphous Fraction of Cold-Crystallized Polyamide 6. Polymer 2012, 53, 4770–4777. 10.1016/j.polymer.2012.08.017. [DOI] [Google Scholar]
- Martin S.; Exposito M. T.; Vega J. F.; Martinez-Salazar J. Microstructure and Properties of Branched Polyethylene: Application of a Three-Phase Structural Model. J. Appl. Polym. Sci. 2013, 128, 1871–1878. 10.1002/app.38290. [DOI] [Google Scholar]
- Nguyen T. L.; Bédoui F.; Mazeran P.-E.; Guigon M. Mechanical Investigation of Confined Amorphous Phase in Semicrystalline Polymers: Case of PET and PLA. Polym. Eng. Sci. 2015, 55, 397–405. 10.1002/pen.23896. [DOI] [Google Scholar]
- in ’t Veld P. J.; Hütter M.; Rutledge G. C. Temperature-Dependent Thermal and Elastic Properties of the Interlamellar Phase of Semicrystalline Polyethylene by Molecular Simulation. Macromolecules 2006, 39, 439–447. 10.1021/ma0518961. [DOI] [Google Scholar]
- Sedighiamiri A.; Van Erp T. B.; Peters G. W. M.; Govaert L. E.; Van Dommelen J. A. W. Micromechanical Modeling of the Elastic Properties of Semicrystalline Polymers: A Three-Phase Approach. J. Polym. Sci., Part B: Polym. Phys. 2010, 48, 2173–2184. 10.1002/polb.22099. [DOI] [Google Scholar]
- Ghazavizadeh A.; Rutledge G. C.; Atai A. A.; Ahzi S.; Rémond Y.; Soltani N. Micromechanical Characterization of the Interphase Layer in Semi-crystalline Polyethylene. J. Polym. Sci. Polym. Phys. 2013, 51, 1228–1243. 10.1002/polb.23319. [DOI] [Google Scholar]
- Gueguen O.; Ahzi S.; Makradi A.; Belouettar S. A New Three-Phase Model to Estimate the Effective Elastic Properties of Semi-Crystalline Polymers: Application to PET. Mech. Mater. 2010, 42, 1–10. 10.1016/j.mechmat.2009.04.012. [DOI] [Google Scholar]
- Ahmed S.; Jones F. R. A Review of Particulate Reinforcement Theories for Polymer Composites. J. Mater. Sci. 1990, 25, 4933–4942. 10.1007/BF00580110. [DOI] [Google Scholar]
- Halpin J. C.; Kardos J. L. Moduli of Crystalline Polymers Employing Composite Theory. J. Appl. Phys. 1972, 43, 2235–2241. 10.1063/1.1661482. [DOI] [Google Scholar]
- Takayanagi M.; Uemura S.; Minami S. Application of Equivalent Model Method to Dynamic Rheo-Optical Properties of Crystalline Polymer. J. Polym. Sci., Part C: Polym. Symp. 1964, 5, 113–122. 10.1002/polc.5070050111. [DOI] [Google Scholar]
- Takayanagi M.; Imada K.; Kajiyama T. Mechanical Properties and Fine Structure of Drawn Polymers. J. Polym. Sci., Part C: Polym. Symp. 1966, 15, 263–281. 10.1002/polc.5070150118. [DOI] [Google Scholar]
- Bouquerel F.; Bourgin P.; Perez J. Viscoelastic Behavior of Thin Bioriented Poly(ethylene terephthalate) Films Under Low and Medium Stresses. Polymer 1992, 33, 516–525. 10.1016/0032-3861(92)90728-F. [DOI] [Google Scholar]
- de Oca H. M.; Ward I. M. Structure and Mechanical Properties of PGA Crystals and Fibres. Polymer 2006, 47, 7070–7077. 10.1016/j.polymer.2006.07.045. [DOI] [Google Scholar]
- Lai C.; Ayyer R.; Hiltner A.; Baer E. Effect of Confinement on the Relaxation of Poly(ethylene oxide). Polymer 2010, 51, 1820–1829. 10.1016/j.polymer.2010.02.016. [DOI] [Google Scholar]
- Aliotta L.; Cinelli P.; Coltelli M. B.; Righetti M. C.; Gazzano M.; Lazzeri A. Effect of Nucleating Agents on Crystallinity and Properties of Poly(lactic acid) (PLA). Eur. Polym. J. 2017, 93, 822–832. 10.1016/j.eurpolymj.2017.04.041. [DOI] [Google Scholar]
- Woo E. M.; Su C. C.; Kuo J.-F.; Seferis J. C. Model with Experimental Evidences for the Morphology of Binary Blends of a Thermosetting Polycyanate with Thermoplastics. Macromolecules 1994, 27, 5291–5296. 10.1021/ma00097a008. [DOI] [Google Scholar]
- Parulekar Y.; Mohanty A. K. Biodegradable Toughened Polymers from Renewable Resources: Blends of Polyhydroxybutyrate with Epoxidized Natural Rubber and Maleated Polybutadiene. Green Chem. 2006, 8, 206–213. 10.1039/B508213G. [DOI] [Google Scholar]
- Stanford J. L.; Young R. J.; Day R. J. Formation and Properties of Urethane Diacetylene Segmented Block Copolymers. Polymer 1991, 32, 1713–1725. 10.1016/0032-3861(91)90410-K. [DOI] [Google Scholar]
- Hearle J. W. S.; Prakash R.; Wilding M. A. Prediction of Mechanical Properties of Nylon and Polyester Fibers as Composites. Polymer 1987, 28, 441–448. 10.1016/0032-3861(87)90197-2. [DOI] [Google Scholar]
- Lia F.; Gao Y.; Jiang W. Design of High Impact Thermal Plastic Polymer Composites with Balanced Toughness and Rigidity: Toughening with One Phase Modifier. Polymer 2019, 170, 101–106. 10.1016/j.polymer.2019.03.004. [DOI] [Google Scholar]
- Loos M. R.; Manas-Zloczower I. Reinforcement Efficiency of Carbon Nanotubes – Myth and Reality. Macromol. Theory Simul. 2012, 21, 130–137. 10.1002/mats.201100099. [DOI] [Google Scholar]
- Zare Y.; Rhee K. Y. Accounting the Reinforcing Efficiency and Percolating Role of Interphase Regions in Tensile Modulus of Polymer/CNT Nanocomposites. Eur. Polym. J. 2017, 87, 389–397. 10.1016/j.eurpolymj.2017.01.007. [DOI] [Google Scholar]
- Righetti M. C.; Aliotta L.; Mallegni N.; Gazzano M.; Passaglia E.; Cinelli P.; Lazzeri A. Constrained Amorphous Interphase and Mechanical Properties of Poly(3-Hydroxybutyrate-co-3-Hydroxyvalerate). Front. Chem. 2019, 7, 790. 10.3389/fchem.2019.00790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pyda M.; Wunderlich B. Reversing and Non-Reversing Heat Capacity of Poly(lactic acid) in the Glass Transition Region by TMDSC. Macromolecules 2005, 38, 10472–10479. 10.1021/ma051611k. [DOI] [Google Scholar]
- Schick C.Temperature Modulated Differential Scanning Calorimetry (TMDSC)—Basics and applications to polymers. In Handbook of Thermal Analysis and Calorimetry; Cheng S. Z. D., Ed.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2002; Volume 3, p 713. [Google Scholar]
- Lacey A. A.; Price D. M.; Reading M.. Theory and Practice of Modulated Temperature Differential Scanning Calorimetry. In Modulated Temperature Differential Scanning Calorimetry; Reading M. D. J., Hourston D. J., Eds.; Springer: Dordrecht, The Netherlands, 2006; p 1. [Google Scholar]
- Donth E.; Korus J.; Hempel E.; Beiner M. Comparison of DSC Heating Rate and HCS Frequency at the Glass Transition. Thermochim. Acta 1997, 304-305, 239–249. 10.1016/S0040-6031(97)00027-0. [DOI] [Google Scholar]
- Hensel A.; Schick C. Relation Between Freezing-in Due to Linear Cooling and the Dynamic Glass Transition Temperature by Temperature-Modulated DSC. J. Non-Cryst. Solids 1998, 235-237, 510–510. 10.1016/S0022-3093(98)00607-3. [DOI] [Google Scholar]
- Righetti M. C. Crystallization of Polymers Investigated by Temperature-Modulated DSC. Materials 2017, 10, 442. 10.3390/ma10040442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Righetti M. C.; Di Lorenzo M. L.; Tombari E.; Angiuli M. The Low-Temperature Endotherm in Poly(ethylene terephthalate): Partial Melting and Rigid Amorphous Fraction Mobilization. J. Phys. Chem. B 2008, 112, 4233–4241. 10.1021/jp076399w. [DOI] [PubMed] [Google Scholar]
- Wunderlich B. Thermal Analysis of Polymeric Materials; Springer-Verlag: Berlin, 2005; p 689. [Google Scholar]
- Delpouve N.; Stoclet G.; Saiter A.; Dargent E.; Marais S. Water Barrier Properties in Biaxially Drawn Poly(lactic acid) Films. J. Phys. Chem. B 2012, 116, 4615–4625. 10.1021/jp211670g. [DOI] [PubMed] [Google Scholar]
- Billimoria K.; Heeleyb E. L.; Parsonsa N.; Figiela Ł. An Investigation into the Crystalline Morphology Transitions in Poly-l-lactic acid (PLLA) Under Uniaxial Deformation in the Quasi-Solid-State Regime. Eur. Polym. J. 2018, 101, 127–139. 10.1016/j.eurpolymj.2018.01.031. [DOI] [Google Scholar]
- Tadmor Z. Molecular Orientation in Injection Molding. J. Appl. Polym. Sci. 1974, 18, 1753–1772. 10.1002/app.1974.070180614. [DOI] [Google Scholar]
- Kantz M. R.; Newman H. D. Jr.; Stigale F. H. The Skin-Core Morphology and Structure–Property Relationships in Injection-Molded Polypropylene. J. Appl. Polym. Sci. 1972, 16, 1249–1260. 10.1002/app.1972.070160516. [DOI] [Google Scholar]
- Lu X. F.; Hay J. N. Crystallization Orientation and Relaxation in Uniaxially Drawn Poly(ethylene terephthalate). Polymer 2001, 42, 8055–8067. 10.1016/S0032-3861(01)00295-6. [DOI] [Google Scholar]
- Delpouve N.; Saiter A.; Mano J. F.; Dargent E. Cooperative Rearranging Region Size in Semi-crystalline Poly(l-lactic acid). Polymer 2008, 49, 3130–3135. 10.1016/j.polymer.2008.04.045. [DOI] [Google Scholar]
- Yasuniwa M.; Sakamo K.; Ono Y.; Kawahara W. Melting Behavior of Poly(l-lactic acid): X-ray and DSC Analyses of the Melting Process. Polymer 2008, 49, 1943–1951. 10.1016/j.polymer.2008.02.034. [DOI] [Google Scholar]
- Tábi T.; Hajba S.; Kovács J. C. Effect of Crystalline Forms (α′ and α) of Poly(lactic acid) on its Mechanical, Thermo-Mechanical, Heat Deflection and Creep Properties. Eur. Polym. J. 2016, 82, 232–243. 10.1016/j.eurpolymj.2016.07.024. [DOI] [Google Scholar]
- Minakov A. A.; Mordvintsen D. A.; Schick C. Melting and reorganization of poly(ethylene terephthalate) on fast heating (1000 K/s). Polymer 2004, 45, 3755–3763. 10.1016/j.polymer.2004.03.072. [DOI] [Google Scholar]
- Righetti M. C.; Gazzano M.; Di Lorenzo M. L.; Androsch R. Enthalpy of melting of α′- and α-crystals of poly(l-lactic acid). Eur. Polym. J. 2015, 70, 215–220. 10.1016/j.eurpolymj.2015.07.024. [DOI] [Google Scholar]
- Guinault A.; Sollogoub C.; Ducruet V.; Domenek S. Impact of Crystallinity of Poly(lactide) on Helium and Oxygen Barrier Properties. Eur. Polym. J. 2012, 48, 779–788. 10.1016/j.eurpolymj.2012.01.014. [DOI] [Google Scholar]
- Varol N.; Delpouve N.; Araujo S.; Domenek S.; Guinault A.; Golovchak R.; Ingram A.; Delbreilh L.; Dargent E. Amorphous Rigidification and Cooperativity Drop in Semi Crystalline Plasticized Polylactide. Polymer 2020, 194, 122373. 10.1016/j.polymer.2020.122373. [DOI] [Google Scholar]
- Di Lorenzo M. L.; Righetti M. C. Effect of Thermal History on the Evolution of Crystal and Amorphous Fractions of Poly[(R)-3-hydroxybutyrate] upon Storage at Ambient Temperature. Eur. Polym. J. 2013, 49, 510–517. 10.1016/j.eurpolymj.2012.11.004. [DOI] [Google Scholar]
- Nasser S. F.; Domenek S.; Guinault A.; Stoclet G.; Delpouve N.; Sollogoub C. Stuctural and Dynamic Heterogeneity in the Amorphous Phase of Poly(l,l-lactide) Confined at the Nanoscale by the Coextrusion Process. Macromolecules 2018, 51, 128–136. 10.1021/acs.macromol.7b02188. [DOI] [Google Scholar]
- Liu H.; Zhang J. Research Progress in Toughening Modification of Poly(lactic acid). J. Polym. Sci., Part B: Polym. Phys. 2011, 49, 1051–1083. 10.1002/polb.22283. [DOI] [Google Scholar]
- Lin J.; Shenogin S.; Nazarenko S. Oxygen Solubility and Specific Volume of Rigid Amorphous Fraction in Semicrystallline Poly(ethylene terephthalate). Polymer 2002, 43, 4733–4743. 10.1016/S0032-3861(02)00278-1. [DOI] [Google Scholar]
- del Rio J.; Etxeberria A.; Löpez-Rodríguez N.; Lizundia E.; Sarasua J. R. A PALS Contribution to the Supramolecular Structure of Poly(l-lactide). Macromolecules 2010, 43, 4698–4707. 10.1021/ma902247y. [DOI] [Google Scholar]
- Drieskens M.; Peeters R.; Mullen J.; Franco D.; Lemstra P. J.; Hristova-Bogaerds D. G. Structure versus Properties Relationship of Poly(lactic acid). I. Effect of Crystallinity on Barrier Properties. J. Polym. Sci., Part B: Polym. Phys. 2009, 47, 2247–2258. 10.1002/polb.21822. [DOI] [Google Scholar]
- Fernandes Nassar S.; Guinault A.; Delpouve N.; Divry V.; Ducruet V.; Sollogoub C.; Domenek S. Multi-scale Analysis of the Impact of Polylactide Morphology on Gas Garrier Properties. Polymer 2017, 108, 163–172. 10.1016/j.polymer.2016.11.047. [DOI] [Google Scholar]
- Tashiro K.; Kobayashi M. Molecular Theoretical Study of the Intimate Relationship Between Structure and Mechanical Properties of Polymer Crystals. Polymer 1996, 37, 1775–1786. 10.1016/0032-3861(96)87293-4. [DOI] [Google Scholar]
- Sarge S. M.; Hemminger W.; Gmelin E.; Höhne G.; Cammenga H.; Eysel W. Metrologically Based Procedures for the Temperature, Heat and Heat Flow Rate Calibration of DSC. J. Therm. Anal. 1997, 49, 1125–1134. 10.1007/BF01996802. [DOI] [Google Scholar]
- Wurm A.; Merzlyakov M.; Schick C. Reversible Melting Probed by Temperature Modulated Dynamic Mechanical and Calorimetric Measurements. Colloid Polym. Sci. 1998, 276, 289–296. 10.1007/s003960050242. [DOI] [Google Scholar]
- Androsch R.; Moon I.; Kreitmeier S.; Wunderlich B. Determination of Heat Capacity with a Sawtooth–Type, Power Compensated Temperature Modulated DSC. Thermochim. Acta 2000, 357-358, 267–278. 10.1016/S0040-6031(00)00397-X. [DOI] [Google Scholar]