Locally private frequency estimation of physical symptoms for infectious disease analysis in Internet of Medical Things

Abstract

Frequency estimation of physical symptoms for peoples is the most direct way to analyze and predict infectious diseases. In Internet of medical Things (IoMT), it is efficient and convenient for users to report their physical symptoms to hospitals or disease prevention departments by various mobile devices. Unfortunately, it usually brings leakage risk of these symptoms since data receivers may be untrusted. As a strong metric for health privacy, local differential privacy (LDP) requires that users should perturb their symptoms to prevent the risk. However, the widely-used data structure called sketch for frequency estimation does not satisfy the specified requirement. In this paper, we firstly define the problem of frequency estimation of physical symptoms under LDP. Then, we propose four different protocols, i.e., CMS-LDP, FCS-LDP, CS-LDP and FAS-LDP to solve the above problem. Next, we demonstrate that the designed protocols satisfy LDP and unbiased estimation. We also present two approaches to implement the key component (i.e., universal hash functions) of protocols. Finally, we conduct experiments to evaluate four protocols on two real-world datasets, representing two different distributions of physical symptoms. The results show that CMS-LDP and CS-LDP have relatively optimal utility for frequency estimation of physical symptoms in IoMT.

1. Introduction

With the explosive development of Internet of Medical Things (IoMT), there have been various medical applications and services in a large number of mobile devices (e.g., smart phones and wearable devices) [1], [2], [3]. It is efficient and convenient for hospitals or disease prevention departments (i.e., the third party) to estimate the frequency of physical symptoms for mobile users by their devices so as to monitor and predict infectious diseases. For example, if disease prevention departments want to know potential spread range and speed of coronavirus disease 2019 (COVID-19) [4], it is secure for them to remotely estimate the frequency of typical symptoms of peoples by smart phones, including fever, cough and shortness of breath. The novel estimation model reduces the labor costs and improves the detection efficiency. Although human beings benefit from the estimation model in IoMT, users inevitably face leakage risks of disease information, especially when the third party are untrusted [5], [6]. Once disease information is leaked, it may cause a heavier psychological burden for the society and individuals.

In fact, health privacy has been one of the biggest concerns of not only individuals but also the whole society (e.g., European GDPR law) [7], [8], [9], [10], [11], [12]. Therefore, it is necessary to protect individuals’ health privacy when collecting and analyzing their symptoms. Differential privacy (DP) [13], [14] is a strong privacy metric in a central setting. It assumes that there is a trusted third party to collect and perturb symptoms from users and then share them with others. However, DP ignores that it is possible for the third party to threaten users’ health privacy, especially in IoMT. To this end, local differential privacy (LDP) [15] is proposed in the local setting. It requires that each mobile user should locally perturb his/her symptoms before sending to the third party and make them indistinguishable.

In recent years, there have been a series of works to design various protocols for frequency estimation of physical symptoms under LDP in both academia and industry [16], [17], [18], [19]. In the existing privacy protocols, physical symptom is defined as categorical data. For categorical data, it consists of three important components, i.e., encoding, perturbation and aggregation [20], [21], [22], [23], [24]. The first two components are operated by the user while the last one is executed by the third party. Most of perturbation mechanisms to guarantee privacy are based on the Randomized Response (RR) technique, in which reporting a real answer for a Boolean query is derived from a certain probability [25]. Wang et al. [24] surveyed the previous protocols and classified encoding methods into four types, including direct [26], histogram [22], unary [23], [27] and local hashing [20], [21], [24] encoding (i.e., DE, HE, UE and LHE). Protocols based on UE need higher communication cost, while those based on DE and HE have relatively lower accuracy. As a result, protocols based on LHE are a promising solution to balance computation complexity and data utility.

However, the previous protocols do not make full use of the widely applied data structures for frequency estimation of physical symptoms. Sketch is one of the most fundamental and most efficient data structures to estimate frequency for physical symptoms. In general, it uses a small vector to index the position of a symptom by a certain number of hash functions, which saves space but faces possible conflict. There are some basic and classic sketches, such as Count Sketch (CS) [28], Count-Min Sketch (CMS) [29], Fast-AGMS Sketch (FAS) [30] and Fast-Count Sketch (FCS) [31]. The focus of the paper is on how to design the sketch-based protocols for frequency estimation of physical symptoms satisfying local differential privacy. If so, it is convenient for others to directly apply the proposed protocols to estimate the frequency of physical symptoms.

There are two main challenges to solve the above problem. The first one is that the existing private protocols cannot be directly used to perturb query result by sketches. The reasons are that (i) perturbation and aggregation of symptoms are executed by the user and the third party, respectively. It implies that only the RR technique can be leveraged; and (ii) hash functions used in the sketches need to stay the same implying that the existing encoding methods (e.g., DE, HE and UE) are not applicable. The second one is that the designed private sketches should satisfy two important properties, including unbiased estimation and local differential privacy. In other words, it needs to balance privacy guarantee and utility of perturbed data.

To address the above challenges, we make full use of LHE and RR. In brief, we leverage the sketch vector to implement encoding of physical symptoms and then perturb it by RR to achieve privacy guarantee. At first, we propose two CMS- and FCS-based protocols, namely CMS-LDP and FCS-LDP to guarantee privacy. Then, we propose two CS- and FAS-based protocols, namely CS-LDP and FAS-LDP to ensure privacy. In particular, the formers utilize perturbation mechanism of optimal local hashing (OLH) in [24], while the latter directly use RR to perturb each entry of the sketch vector. Finally, we do other operations to make sure that the protocols satisfy unbiased estimation. It is noted that our protocols only increase computation cost rather than space overhead. This is consistent with the initial purpose, i.e., space save. To the best of our knowledge, there are few works to utilize the sketch under LDP to estimate the frequency of symptoms. The contributions of this paper can be summarized as follows:

• •We formulate the problem of designing sketches under LDP by mathematical definitions and strong privacy metric to estimate the frequency of physical symptoms in IoMT.
• •We propose four different protocols for frequency estimation of symptoms with privacy protection, including CMS-LDP, FCS-LDP, CS-LDP and FAS-LDP. We also demonstrate that all of the protocols satisfy two important properties, including unbiased estimation and LDP. We also analyze the variance of frequency estimation in four protocols.
• •We present two approaches to implement universal hash functions. We also evaluate and compare the proposed protocols on two real-world datasets, representing two different distributions of physical symptoms.

The rest of this paper is organized as follows. Section 2 surveys related work about privacy protection in IoMT. Section 3 introduces the preliminaries and gives problem definitions. Section 4 proposes four different protocols for sketches under LDP to estimate the frequency of symptoms. Section 5 analyzes unbiased estimation, privacy guarantee and variance. Section 6 presents two methods to implement universal hash functions. Section 7 evaluates proposed protocols on real datasets. Finally, Section 8 concludes this paper.

2. Related work

2.1. Health privacy protection in IoMT

In IoMT, there are vast amounts of users’ healthy information generated by various mobile devices every day. However, the information is left from mobile users and may be faced with leakage risk from untrusted data collectors or data adversaries [6]. In order to guarantee privacy, there have been a number of protection techniques, including identification, anonymity and differential privacy [5], [7], [14]. In detail, identification technique utilizes authentication mechanism for each mobile user, who must login the system by his/her identity. On the other hand, data collectors use perturbation techniques (e.g., $k$-anonymity [32], $l$-diversity [33] and DP [13]) to perturb raw data from mobile users. These techniques provide a certain degree of privacy protection in some specified scenes.

However, these techniques are not fully suited to applications in IoMT due to their respective shortcomings. Identification and anonymity cannot offer enough privacy protection, while DP usually assumes that the third party is trusted. That is, the third party does not illegally leak users’ health information. Unfortunately, it does not hold in some real environments of IoMT. The reason is that users cannot know the receivers of their healthy information in the local setting so that they do not trust them. In order to overcome the disadvantages, local differential privacy [15] has been proposed to protect private information of each user against the threat from the untrusted third party. Both academical researchers and industrial engineers focus on how to achieve local differential privacy from theory and application.

2.2. Local differential privacy

Different from DP, LDP has higher privacy requirement in a local setting, which requires probability limit between any two values, instead of any two datasets in DP [15]. To this end, the existing mechanisms of DP cannot be fully applied to LDP, including the Laplace mechanism [34] and the exponential mechanism [35]. In order to implement LDP, there have been a number of works to design proper mechanisms [16], [17], [18], [19]. Most of them leveraged the Randomized Response (RR) mechanism [25] or its refinements. RR reports a random answer derived from a certain amount of probability for a Boolean question. For categorical data, Kairouz et al. [36], [37] proposed an extremal privatization mechanism ($k$-RR), which is universally optimal in the low and high privacy regimes. For ordinal data, the value is firstly encoded to a binary one and then perturb it by RR [17], [38], [39]. In general, the proposed algorithms need to satisfy both unbiased estimation and LDP. In addition, these perturbation privacy mechanisms are widely applied to various scenes, including heavy hitter identification, itemset mining, marginal release, data mining, medical analysis and infectious disease prediction [40].

In the industry, there have been a lot of applications to satisfy local differential privacy. RAPPOR is the first product from Google to collect users’ data and ensure privacy [27]. The user firstly encodes his/her data by a special data structure called Bloom filter and then perturbs the encoded output by the randomized response mechanism. The third party collects and decodes perturbed data from the users to get statistical information. In 2017, Apple [41] published a white paper to propose efficient and scalable algorithms satisfying local differential privacy. Microsoft [38] also presented new algorithms with local differential privacy to estimate mean and histogram for telemetry data.

2.3. Frequency estimation under LDP for physical symptoms

Frequency estimation under LDP for physical symptoms is an efficient and convenient way for infectious disease prediction. There have been a few of works to design effective mechanisms for different types of health information, including categorical (e.g., sex and symptoms), ordinal (e.g., age) [36], [37], [40], [42]. The main objective of the existing mechanisms is to maximize the utility and reduce communication cost and computation complexity.

Bassily et al. [21] proposed efficient mechanisms by utilizing Random Matrix Projection. Running time of the third party and the user is $O\left(n^{5∕2}\right)$ and $O\left(n^{3∕2}\right)$, respectively. Meanwhile, the estimation error is $O\left(\sqrt{log\left(m\right)∕\left({ϵ}^{2}n\right)}\right)$ with high probability where $n$ is the number of users and $m$ is the size of domain. They also proposed improved algorithms, in which server time is $O\left(n\right)$ and user time is $O\left(1\right)$ [20]. Bun et al. [22] presented an algorithm called PrivateExpanderSketch, which achieved optimal worst-case error as a function of all possible parameters. Wang et al. [24] introduced a framework to analyze all the previous mechanisms for frequency estimation under LDP. They also proposed an Optimal Local Hashing (OLH) to estimate the frequency with better utility. Different from the previous environment with only an attribute, Qin et al. [23] estimated frequency over set-valued data under LDP. However, to the best of our knowledge, there are few works to combine sketch under LDP to estimate the frequency of physical symptoms in IoMT. Therefore, the focus of this paper is to solve the problem.

3. Preliminaries and problem definition

As aforementioned, the focus of the paper is on frequency estimation of physical symptoms in IoMT. There are two key roles, i.e., an untrusted third party and a large number of mobile users. The third party collects perturbed health information from the users. In the following section, we formulate the frequency estimation problem in the context of local differential privacy.

3.1. Preliminaries

Suppose that there are a set of $n$ users denoted by $\mathcal{U}=\{u_1,u_2,\dots ,u_n\}$. Each user $u_i$ has a symptom $d_i$. Then, $\mathcal{I}=\{d_1,d_2,\dots ,d_n\}$ is defined as a set of symptoms from users. The domain of elements in $\mathcal{I}$ is $\mathcal{D}$ with size $m$. An untrusted third party plans to collect statistical information of users’ symptoms. Assume that the untrusted third party has known the domain $\mathcal{D}$. Each element in $\mathcal{D}$ is generalized to an integer $j\in \left[m\right]=\{1,2,\dots ,m\}$. For example in Fig. 1, the domain $\mathcal{D}$ consists of $m$ types of symptoms of COVID-19, such as fever, cough and shortness of breath. Each symptom is labeled as an integer (e.g., fever is labeled by $1$). Therefore, in the following section, we have $d_i\in \mathcal{D}=\left[m\right]$.

Fig. 1.

Symptoms of COVID-19.

Here, we focus on the frequency estimation of physical symptoms as follows:

Definition 1 Frequency Estimation of Symptoms [39] —

A query $f:\mathcal{D}\to \mathbf{Z}$ for frequency estimation of some symptom is to compute the frequency of users whose symptom is the same with $d\in \mathcal{D}$. Formally, for any $d\in \mathcal{D}$,

$$f\left(d\right)=|\left\{d_i|\exists d_i=d\right\}|.$$ (1)

Obviously, the range of $f\left(d\right)$ is $[0,n]$.

However, in infectious disease prediction, it is not necessary and impossible to count accurate frequency estimation for physical symptoms. For example, if some disease prevention department wants to estimate the speed or range of COVID-19 by the number of patients with specified symptoms (e.g., fever, cough or shortness of breath), there is no need for the department to get the accurate count for each symptom. What is more, it is not realistic to spend a large amount of labor cost in dealing with it. Thus, an approximate frequency estimation is proposed as follows:

Definition 2 ($\xi ,\delta$)-Approximate Frequency Estimation of Symptoms [39] —

A query $\hat{f}:\mathcal{D}\to \mathbf{Z}$ is to solve the problem of ($\xi ,\delta$)-approximate frequency estimation of symptoms if and only if for any symptom $d\in \mathcal{D}$, $\hat{f}\left(d\right)$ satisfies the following requirement:

$$Pr\left[|f\left(d\right)-\hat{f}\left(d\right)|\le n\xi \right]\ge 1-\delta ,$$ (2)

where $\xi \in [0,1]$ represents the expected error and $\delta \in [0,1]$ is the confidence probability.

Unfortunately, the third party may be untrusted because that he/she possibly utilizes health information of users to get illegal profit. Therefore, the users have to perturb their information so as to avoid privacy leakage. Differential privacy [13], [14] is the most common and strong privacy protection metric, which is usually suited for the central setting. Different from DP, local differential privacy is proposed in the local setting, in which it assumes that the third party is untrusted. This means that before the users send their symptoms, perturbation of symptoms should satisfy the following privacy measurement:

Definition 3 Local Differential Privacy [15] —

A sanitized algorithm $\mathcal{M}$ satisfies $ϵ$-local differential privacy if and only if for any pair of input values $d_i,d_j\in \mathcal{D}$ and for any output $y\in Range\left(\mathcal{M}\right)$, we have

$$Pr[\mathcal{M}\left(d_i\right)=y]\le exp\left(ϵ\right)\cdot Pr[\mathcal{M}\left(d_j\right)=y],$$ (3)

where $Range\left(\mathcal{M}\right)$ denotes the set of all possible outputs of the algorithm $\mathcal{M}$ and $ϵ$ is privacy budget.

$ϵ$ represents the strength of privacy protection. The lower value of $ϵ$ corresponds to the stronger privacy protection. With the same as DP, LDP has also the composition properties as follows.

Lemma 1 Sequential Composition [43] —

Assume that each privacy algorithm ${\mathcal{M}}_i$ satisfies ${ϵ}_i$ -local differential privacy. A group of ${\mathcal{M}}_i\left(\cdot \right)$ applied to the same dataset satisfy $\left({\sum }_i{ϵ}_i\right)$ -local differential privacy.

Lemma 2 Parallel Composition [43] —

Assume that each privacy algorithm ${\mathcal{M}}_i$ satisfies ${ϵ}_i$ -local differential privacy. A group of ${\mathcal{M}}_i\left(\cdot \right)$ applied to a set of disjoint datasets satisfy $max\left\{{ϵ}_i\right\}$ -local differential privacy.

In the algorithms designed by the paper, we will make full use of the composition properties of local differential privacy.

3.2. Private framework

In order to solve the frequency estimation problem under LDP for symptoms, the proposed mechanism should satisfy the privacy measurement as follows:

Definition 4 Frequency Estimation of Symptoms under LDP —

A sanitized protocol $\mathcal{M}:{\mathcal{D}}^n\to \mathbf{Z}$ for frequency estimation of symptoms satisfies $ϵ$-local differential privacy if and only if $\mathcal{M}=\mathcal{A}({\mathcal{M}}_1\left(\cdot \right),{\mathcal{M}}_2\left(\cdot \right),\dots ,{\mathcal{M}}_n\left(\cdot \right))$, in which each ${\mathcal{M}}_i:\mathcal{D}\to \mathbf{Y}$ is a local random processor that satisfies $ϵ$-local differential privacy, and $\mathcal{A}:{\mathbf{Y}}^n\to \mathbf{Z}$ is some post-processing function.

Based on the above definition, the key functions are the local random processor ${\mathcal{M}}_i\left(\cdot \right)$ and the post-processing function $\mathcal{A}\left(\cdot \right)$. Each user executes the local random processor, while the third party executes the post-processing function. Furthermore, Wang et al. [24] surveyed the previous work and concluded that a protocol for frequency estimation under LDP generally consists of the following steps:

• • Encoding. This operation $\mathsf{Encode}\left(\cdot \right)$ is executed by the user. In detail, input $d$ of the user is generally encoded as a histogram, a vector [27], a single bit [21], or an integer [24] by encoding and decoding algorithms or hash functions.
• • Perturbing. The mechanism $\mathsf{Perturb(\cdot )}$ is also executed by the user. Meanwhile, the perturbed mechanism should satisfy $ϵ$-local differential privacy. The input of $\mathsf{Perturb}\left(\cdot \right)$ is the output of $\mathsf{Encode}\left(\cdot \right)$. Therefore, ${\mathcal{M}}_i\left(\cdot \right)$ in Definition 4 is $\mathsf{Perturb}\left(\mathsf{Encode}\left(\cdot \right)\right)$.
• • Aggregating. The operation $\mathsf{Aggregate}\left(\cdot \right)$ is executed by the third party. At first, the third party receives data from users, which is perturbed with the combination of $\mathsf{Encode}\left(\cdot \right)$ and $\mathsf{Perturb}\left(\cdot \right)$. Then, he/she aggregates the data and extracts approximate frequency estimation.

Fig. 2 shows the concrete operations and interactions between mobile users and the third party. It is obvious to see that users need to encode and perturb their symptoms locally, while the third party aggregates perturbed data. As a result, these operations increase extra overhead for users, including computation, communication and storage. To this end, it is necessary to make full use of the existing data structure named sketch to decrease the overhead.

Fig. 2.

The framework for frequency estimation of symptoms under LDP.

3.3. Problem formulation

In order to solve the approximate frequency estimation of categorical data (e.g., physical symptoms), Charikar et al. [28] firstly proposed an algorithm by using a special data structure, i.e., Count Sketch, which achieved good space bounds. After that, the refined versions were proposed, such as Fast-AGMS Sketch [30], Count-Min Sketch [29] and Fast-Count Sketch [31]. However, to the best of our knowledge, there are few works to design the new data structure Sketch under LDP to solve the approximate frequency estimation of physical symptoms. In the following sections, we propose improved protocols based on Count Sketch, Fast-AGMS Sketch, Count-Min Sketch and Fast-Count Sketch, which satisfy unbiased estimation, i.e., $\forall d\in \mathcal{D},E\left[\hat{f}\left(d\right)\right]=f\left(d\right)$ and local differential privacy. In addition, we also compare the proposed protocols by experiments.

4. Protocols for frequency estimation of symptoms under LDP

In this section, we propose four novel protocols to solve the approximate frequency estimation of physical symptoms under LDP. These protocols are based on CS, FAS, CMS and FCS. We will analyze unbiased estimation and privacy protection of proposed protocols in the next section.

Under no privacy preservation, the third party receives physical symptoms and uses a small vector to count the frequency of each element in $\mathcal{D}$, while users do nothing. However, in order to protect privacy, the user should send perturbed symptoms rather than raw values. Therefore, the user needs to generate a small vector locally and then send it to the third party. Finally, the third party aggregates these vectors and derives the full sketch.

4.1. Protocol CMS-LDP

CMS is a simple and effective data structure, which was proposed by Cormode et al. [29]. For a frequency estimation query $\hat{f}\left(d\right)$, its values by CMS is $\left[f\left(d\right),f\left(d\right)+\xi {\Vert f_{-d}\Vert }_1\right]$ with a probability $1-\delta$, in which $f_{-d}$ is the real frequency except $d$. Here, we propose corresponding protocols based on optimal local hashing in [24] to implement CMS under local differential privacy.

Algorithm 1 shows a protocol CMS-LDP for privacy estimation of symptoms under LDP. The protocol consists of four key components. The first one is an initial process, in which $b$ and $t$ are computed by the input parameters $\xi$ and $\delta$ (line $1\sim 3$). $b$ represents the domain of universal hash functions, while $t$ is the number of hash functions. Then, each user calls ${\mathcal{M}}_{\text{client-CMS-LDP}}$ to report the perturbed record to the server-side (line $4\sim 6$). Next, Line $7$ implements the key component, namely Sketch-CMS-LDP. The last one implements the query of server-side (line $8\sim 10$). By the above four parts, the algorithm solves the approximate frequency estimation problem of physical symptoms.

Each user executes Algorithm 2 to implement the function of Perturb(Encode ($\cdot$)) in Section 3.2. Algorithm 2 utilizes an existing technique, namely $b$-Randomized Response ($b$-RR), to ensure $ϵ$-local differential privacy, which was designed by Kairouz et al. [37]. In detail, Algorithm 2 firstly implements $\mathsf{Encode}\left(\cdot \right)$ by universal hash function $h_i$ to map the input $d$ into a $b$-length bit array in line $4$. Then, a $b$-RR technique is used to perturb the output of $\mathsf{Encode}\left(\cdot \right)$ in line $5$. Finally, the user returns the result to the server-side.

After the third party receives perturbed symptoms from users, he/she computes a data structure, namely Sketch-CMS-LDP by Algorithm 3. Compared to CMS, our proposed mechanism ${\mathcal{M}}_{\text{Sketch-CMS-LDP}}$ has extra operations, i.e., Line $7\sim 9$. Sketch-CMS-LDP firstly generates an initial sketch, which is a multidimensional array in line $1$. Then, all arrays from $n$ users are added to the sketch in line $2\sim 6$, which is the same with CMS. Finally, Line $7\sim 9$ is to ensure unbiased estimation of CMS-LDP, which will be proved in Section 5.1.

Algorithm 4 gets the approximate estimation for each frequency query $\hat{f}$, which is executed by the third party. The combination of Algorithms 3 and 4 implement the function of $\mathsf{Aggregate(\cdot )}$ in Section 3.2. For each query $\hat{f}\left(d\right)$, the algorithm chooses the minimum of $t$ values, each of which is from an array $\mathcal{V}\left[i\right],i\in \left[t\right]$. The position of each value in the array is decided by hash function $h_i$ and $d$. By Algorithm 1$\sim$4, we solve the problem of frequency estimation under local differential privacy.

For each user in the client-side, the time complexity is $O\left({log}_2(1∕\delta )\right)$ and the space complexity in $\mathsf{Perturb}\left(\mathsf{Encode}\left(\cdot \right)\right)$ is $O\left(\frac{1}{\xi }{log}_2(1∕\delta )\right)$. For ${\mathcal{M}}_{\text{server-CMS-LDP}}$ in the server-side, the time complexity is $O\left(\frac{1}{\xi }{log}_2(1∕\delta )\right)$ and the space complexity is $O\left(\frac{1}{\xi }{log}_2(1∕\delta )\right)$. Besides, the communication overhead between each user and the server is $O\left(\frac{1}{\xi }{log}_2(1∕\delta )\right)$. Thus, for the third party, our proposed protocol does not increase the space overhead. Section 5.1 will analyze the proposed algorithms in terms of the error bound, unbiased estimation and local differential privacy.

4.2. Protocol FCS-LDP

Thorup et al. [31] proposed a refined version of Count-Min Sketch, namely Fast-Count Sketch (FCS). Compared with CMS, FCS uses a family of $4$-universal hash functions, instead of $2$-universal hash function.

The protocol to implement Fast-Count Sketch under local differential privacy, namely Algorithm $\text{FCS-LDP}$, is similar with Algorithm 1. $\text{FCS-LDP}$ also consists of three important components, i.e., ${\mathcal{M}}_{\text{client-FCS-LDP}}$, ${\mathcal{M}}_{\text{Sketch-FCS-LDP}}$ and ${\mathcal{M}}_{\text{server-FCS-LDP}}$. Different from $\text{CMS-LDP}$, $\text{FCS-LDP}$ replaces $2$-universal hash functions with $4$- universal hash functions in line $3$ in Algorithm 1. Besides, ${\mathcal{M}}_{\text{Sketch-FCS-LDP}}$, ${\mathcal{M}}_{\text{client-FCS-LDP}}$ and ${\mathcal{M}}_{\text{server-FCS-LDP}}$ have the same operations with Algorithm ${\mathcal{M}}_{\text{Sketch-CMS-LDP}}$, ${\mathcal{M}}_{\text{client-CMS-LDP}}$ and ${\mathcal{M}}_{\text{server-CMS-LDP}}$, respectively. Here, we do not repeat the same algorithms. Meanwhile, these algorithms have the same time and space complexity with Algorithm 1$\sim$4 for each user and the third party.

4.3. Protocol CS-LDP

Among all of various formats of the special data structure called sketch, Count Sketch was firstly proposed in 2002 [28]. The data structure is generally used to point query, range query, inner product query and so on. Compared with Count-Min Sketch, CS needs higher space cost, i.e., $O({log}_2\left(\delta \right)∕{\xi }^2)$. Meanwhile, CS also satisfies unbiased estimation and the value for a frequency estimation query $\hat{f}\left(d\right)$ about $d$ is $\left[f\left(d\right)-\xi {\Vert f_{-d}\Vert }_2,f\left(d\right)+\xi {\Vert f_{-d}\Vert }_2\right]$ with a confidence probability $1-\delta$. In the following, we will introduce algorithms to implement CS with LDP.

In Algorithm 5, we describe the overview of protocol CS-LDP to implement CS under LDP. It consists of four key parts, i.e., initialization, perturbation in client-side, construction of sketch and frequency estimation in server-side. In the initial process (line $1\sim 4$), it requires $t$ hash function pairs $〈h_i,g_i〉$. Hash function $h_i$ maps some symptom into $\lceil c∕{\xi }^2\rceil$-length bits in which c is some constant, while function $g_i$ maps some input value into $\{-1,+1\}$. Both two classes of hash functions are independent with each other. Compared with $\lceil 1∕\xi \rceil$-length bits of hash function $h_i$ in Algorithm 1, CS-LDP needs more space cost. Then, each user executes ${\mathcal{M}}_{\text{client-CS-LDP}}$ to perturb his/her data (line $5\sim 7$), which implements the function of $\mathsf{Perturb(Encode(\cdot ))}$. Next, the third party constructs a special data structure, namely Sketch-CS-LDP, to collect data from users by ${\mathcal{M}}_{\text{Sketch-CS-LDP}}$ (line $8$). Finally, for each frequency estimation $\hat{f}\left(d\right)$, the third party calls ${\mathcal{M}}_{\text{server-CS-LDP}}$ to compute the result (line $9\sim 11$).

Before each user sends his/her symptom to the third party, Algorithm 6 is executed. ${\mathcal{M}}_{\text{client-CS-LDP}}$ firstly initializes a multidimensional integer array $\mathcal{V}$, i.e., ${\{-1\}}^{t\times b}$ (line $1$). The array only consists of two elements, i.e., $-1$ and $+1$. Then, because of the property of sequential composition of local differential privacy, it computes smaller privacy parameter ${ϵ}^{\prime }$ for each hash function (line 2). Next, the specified position $h_i\left(d\right)$ of each row in $\mathcal{V}$ is set as $g_i\left(d\right)$ (line $3\sim 5$), which implements the function of $\mathsf{Encode}\left(\cdot \right)$. For each entry in array $\mathcal{V}$, it uses Randomized Response (RR) [25] to ensure ${ϵ}^{\prime }$-local differential privacy (line $6\sim 10$), which implements the function of $\mathsf{Perturb}\left(\cdot \right)$. At last, the result is returned to the third party.

After the third party receives perturbed symptoms from users, he/she uses Algorithm 7 to get the data structure Sketch-CS-LDP. Firstly, ${\mathcal{M}}_{\text{Sketch-CS-LDP}}$ initializes a $t\times b$-integer array, i.e., ${\left\{0\right\}}^{t\times b}$ (line $1$). Then, line 2 is to compute a parameter $c_{ϵ}$, which is used to ensure unbiased estimation due to randomized response. Since data from perturbed mechanism ${\mathcal{M}}_{\text{client-CS-LDP}}$ is biased, it needs to be calibrated. Therefore, Algorithm 7 adjusts the data from each user (line $3\sim 5$) to get the estimated frequency of each entry in each array ${\mathcal{V}}_i$. Finally, all adjusted arrays are added to sketch (line $6\sim 9$). In Section 5.2, we will prove unbiased estimation and local differential privacy of our proposed protocol CS-LDP.

Algorithm 8 is used to answer the frequency estimation $\hat{f}\left(d\right)$ for the third party. The combination of Algorithms 7 and 8 implements the function of $\mathsf{Aggregate}\left(\cdot \right)$. We use function $\mathsf{median}\left(\cdot \right)$ to choose a proper value from the candidates as the final estimation for $d$, rather than function $\mathsf{mean}\left(\cdot \right)$. Charikar et al. [28] has demonstrated that function $\mathsf{mean}\left(\cdot \right)$ is sensitive to outliers, while $\mathsf{median}\left(\cdot \right)$ is robust. By Algorithm 5$\sim$8, we solve the problem of frequency estimation with local differential privacy.

Compared with CMS-LDP, CS-LDP needs the higher time and space cost, and has the shaper bound for the frequency estimation. For each user in ${\mathcal{M}}_{\text{client-CS-LDP}}$, the time cost is $O\left(\frac{1}{{\xi }^2}{log}_2(1∕\delta )\right)$ due to sampling each entry of the matrix by Randomized Response, while the space cost is $\frac{1}{{\xi }^2}{log}_2(1∕\delta )$. For the third party, the cost of time and space is $O\left(\frac{1}{{\xi }^2}{log}_2(1∕\delta )\right)$ and $O\left(\frac{1}{{\xi }^2}{log}_2(1∕\delta )\right)$ in ${\mathcal{M}}_{\text{Sketch-CS-LDP}}$, respectively. The cost of time and space is $O\left({log}_2(1∕\delta )\right)$ and $O\left(\frac{1}{{\xi }^2}{log}_2(1∕\delta )\right)$ in ${\mathcal{M}}_{\text{server-CS-LDP}}$, respectively. Therefore, the total time cost for the third party is $O\left(\frac{1}{{\xi }^2}{log}_2(1∕\delta )\right)$, while the total space cost is $O\left(\frac{1}{{\xi }^2}{log}_2(1∕\delta )\right)$.

4.4. Protocol FAS-LDP

Fast-AGMS Sketch (FAS) is a refined version of Count Sketch [30], which guarantees logarithmic-time sketch update and tracking costs. The only difference between Count Sketch and Fast-AGMS Sketch is that the latter replaces $2$-universal hash functions $\mathcal{G}$ of the former with $4$-universal hash functions.

Protocol $\text{FAS-LDP}$ to achieve Fast-AGMS Sketch under local differential privacy is similar with CS-LDP. The only change is that a set of hash functions, namely $\mathcal{G}$, are chosen independently from a $4$-universal family of hashing functions mapping $\mathcal{D}$ to $\{-1,+1\}$. Besides, other mechanisms, i.e., ${\mathcal{M}}_{\text{client-FAS-LDP}}$, ${\mathcal{M}}_{\text{Sketch-FAS-LDP}}$ and ${\mathcal{M}}_{\text{server-FAS-LDP}}$ in client-side and server-side are the same with ${\mathcal{M}}_{\text{client-CS-LDP}}$, ${\mathcal{M}}_{\text{Sketch-CS-LDP}}$ and ${\mathcal{M}}_{\text{server-CS-LDP}}$, respectively. As a result, these algorithms have the same time and space cost with Algorithms 5$\sim$8 for each user and the third party.

5. Theory analysis of protocols

The protocols that implement the approximate frequency estimation of physical symptoms under LDP must satisfy two fundamental requirements, i.e., unbiased estimation and local differential privacy. In the section, we will demonstrate that our proposed protocols satisfy two requirements. Besides, we discuss the variance of protocols.

5.1. CMS-LDP and FCS-LDP

For the proposed protocols, the most important property is to satisfy local differential privacy. We prove that protocol CMS-LDP satisfies the requirement as follows:

Theorem 3

Protocol CMS-LDP satisfies $ϵ$ -local differential privacy.

Proof

Each user utilizes mechanism ${\mathcal{M}}_{\mathsf{client-CMS-LDP}}$ in CMS-LDP to encode and perturb his/her symptom $d$. According to Eq. (4), for two different value $d_i$ and $d_j$, it satisfies the follow equation:

$$\frac{Pr[\mathsf{Perturb}\left(\mathsf{Encode}\left(d_i\right)\right)=y]}{Pr[\mathsf{Perturb}\left(\mathsf{Encode}\left(d_j\right)\right)=y]}\le \frac{e^{{ϵ}^{\prime }}}{e^{{ϵ}^{\prime }}+b-1}∕\frac{1}{e^{{ϵ}^{\prime }}+b-1}=e^{{ϵ}^{\prime }}$$

Therefore, for each hash function, perturbation satisfies ${ϵ}^{\prime }$-local differential privacy. Because that there are $t$ hash functions for the same symptom $d$, the combination of $t$ hash functions satisfy $ϵ$-local differential privacy for each user according to Lemma 1. On the other hand, the third party receives perturbed symptoms from all users. Since records between different users are disjoint, it satisfies $ϵ$-differential privacy for all perturbed symptoms according to Lemma 2.  ■

Theorem 4

For each $2$ -universal hash function $h_i$ in protocol CMS-LDP, it satisfies unbiased estimation for frequency estimation of symptoms after $\mathsf{Encode}\left(\cdot \right)$ . Meanwhile, its variance is $\frac{(b-1-bp)}{bp-1}\cdot f+\frac{n(b-1)}{{(bp-1)}^2}$ , in which $p=\frac{e^{{ϵ}^{\prime }}}{e^{{ϵ}^{\prime }}+b-1}$ .

Proof

For each hash function $h_i$, the third party receives $n$ reported symptoms from all users. Let $y$ any possible output and $\mathcal{S}$ the set of symptoms that are hashed to $y$ by $\mathsf{Encode}\left(\cdot \right)$. Then, the probability that any symptom in $\mathcal{S}$ is perturbed to $y$ is $p$. That is, for any $s_i\in \mathcal{S}$, we have

$$p=Pr[\mathsf{Perturb}\left(\mathsf{Encode}\left(s_i\right)\right)=y]=\frac{e^{{ϵ}^{\prime }}}{e^{{ϵ}^{\prime }}+b-1},$$

and

$$q=Pr[\mathsf{Perturb}\left(\mathsf{Encode}\left(s_i\right)\right)\ne y]=\frac{1}{e^{{ϵ}^{\prime }}+b-1}.$$

For another input value $d_j⁄\in \mathcal{S}$, it is still possibly mapped to $y$. Let $q^{\prime }$ the probability that $d_j$ is mapped to $y$. In line $10$ of mechanism ${\mathcal{M}}_{\text{Sketch-LMS-LDP}}$, the third party makes the extra operations for the raw records. Thus, the probability $q^{\prime }$ is computed by as follows:

$$q^{\prime }=\frac{1}{b}\cdot p+\frac{b-1}{b}\cdot q=\frac{1}{b}\cdot \frac{e^{{ϵ}^{\prime }}}{e^{{ϵ}^{\prime }}+b-1}+\frac{b-1}{b}\cdot \frac{1}{e^{{ϵ}^{\prime }}+b-1}=\frac{1}{b}$$

In mechanism ${\mathcal{M}}_{\text{Sketch-LMS-LDP}}$, we get the final sketch by line $11$. The expectation that the number of elements in $\mathcal{D}$ which are mapped to $y$ is

$$\mathrm{E}\left[\hat{f}\right]=\mathrm{E}\left[\frac{f-n\cdot q^{\prime }}{p-q^{\prime }}\right]=\frac{E\left[f\right]-n\cdot q^{\prime }}{p-q^{\prime }}=\frac{p\cdot f+(n-f)\cdot q^{\prime }-n\cdot q^{\prime }}{p-q^{\prime }}=f$$

where $f$ is the number of elements in $\mathcal{S}$. Therefore, for each $2$-universal hash functions, protocol CMS-LDP satisfies unbiased estimation. The variance is

$$\mathrm{Var}\left[\hat{f}\right]=\mathrm{Var}\left[\frac{f-n\cdot q^{\prime }}{p-q^{\prime }}\right]=\frac{\mathrm{Var}\left[f\right]}{{(p-q^{\prime })}^2}=\frac{f\cdot p(1-p)+(n-f)\cdot q^{\prime }(1-q^{\prime })}{{(p-q^{\prime })}^2}=\frac{f{b}^{2}p(1-p)+(n-f)(b-1)}{{(bp-1)}^2}=\frac{(b-1-bp)}{bp-1}\cdot f+\frac{n(b-1)}{{(bp-1)}^2}■$$

By the above proof, CMS-LDP satisfies unbiased estimation and LDP. Since protocol FCS-LDP is similar with CMS-LDP except for hash functions, FCS-LDP also satisfies unbiased estimation and local differential privacy. Besides, it has the same variance. The corresponding proof is omitted.

5.2. CS-LDP and FAS-LDP

Here, we firstly prove that protocol CS-LDP satisfies local differential privacy as follows:

Theorem 5

Protocol CS-LDP satisfies $ϵ$ -local differential privacy.

Proof

Assume that there are two users $u_i$ and $u_j$. Both of them have different input values $d_i$ and $d_j$ and the same output $\mathcal{O}\in {\{-1,+1\}}^b$. For each pair $(h_i,g_i)$ of hash functions, the third party receives two perturbed arrays $\mathit{\upsilon }$ and $\mathit{\omega }$ from these two users. Because that all of hash functions $h_i$ and $g_i$ are independent with each other, we have

$$\frac{Pr[{\mathcal{M}}_{\text{Client-CS-LDP}}\left(d_i\right)=\mathcal{O}]}{Pr[{\mathcal{M}}_{\text{Client-CS-LDP}}\left(d_j\right)=\mathcal{O}]}=\frac{\prod _{\kappa =1}^{b}Pr[{\mathit{\upsilon }}_{\kappa }={\mathcal{O}}_{\kappa }]}{\prod _{\kappa =1}^{b}Pr[{\mathit{\omega }}_{\kappa }={\mathcal{O}}_{\kappa }]}=\prod _{\kappa =1}^b\frac{Pr[{\mathit{\upsilon }}_{\kappa }={\mathcal{O}}_{\kappa }]}{Pr[{\mathit{\omega }}_{\kappa }={\mathcal{O}}_{\kappa }]}▿=\frac{Pr[{\mathit{\upsilon }}_{h_i\left(d_i\right)}={\mathcal{O}}_{h_i\left(d_i\right)}]Pr[{\mathit{\upsilon }}_{h_i\left(d_j\right)}={\mathcal{O}}_{h_i\left(d_j\right)}]}{Pr[{\mathit{\omega }}_{h_i\left(d_j\right)}={\mathcal{O}}_{h_i\left(d_j\right)}]Pr[{\mathit{\omega }}_{h_i\left(d_i\right)}={\mathcal{O}}_{h_i\left(d_i\right)}]}▵$$

The reason for $▿⟹▵$ is presented as follows. In detail, $\mathit{\upsilon }=\{{\mathit{\upsilon }}_1,{\mathit{\upsilon }}_2,\dots ,{\mathit{\upsilon }}_b\}$ and $\mathit{\omega }=\{{\mathit{\omega }}_1,{\mathit{\omega }}_2,\dots ,{\mathit{\omega }}_b\}$. Each entry ${\mathit{\upsilon }}_{\kappa }$ in $\mathit{\upsilon }$ is derived from $\{-1\cdot y,+1\cdot y\}$, in which $y\in \{-1,+1\}$ is sampled from Eq. and only an entry is $+1$ with position decided by hash value $h_i\left(d_i\right)$. $\mathit{\omega }$ is similar with $\mathit{\upsilon }$. In Eq. $▿$, only two entries in ${\mathit{\upsilon }}_{h_i\left(d_i\right)}$ are different from two entries in ${\mathit{\omega }}_{h_i\left(d_j\right)}$, while the others have the same probability. Therefore, Eq. $▿$ is derived to Eq. $▵$.

For Eq. $▵$, there are two different cases, i.e., $h_i\left(d_i\right)=h_i\left(d_j\right)$ and $h_i\left(d_i\right)\ne h_i\left(d_j\right)$. For the first case in which $h_i\left(d_i\right)=h_i\left(d_j\right)$, we have

$$▵=\frac{Pr[{\mathit{\upsilon }}_{h_i\left(d_i\right)}={\mathcal{O}}_{h_i\left(d_i\right)}]}{Pr[{\mathit{\omega }}_{h_i\left(d_j\right)}={\mathcal{O}}_{h_i\left(d_j\right)}]}=\frac{Pr[{\mathit{\upsilon }}_{h_i\left(d_i\right)}={\mathcal{O}}_{h_i\left(d_i\right)}]}{Pr[{\mathit{\upsilon }}_{h_i\left(d_j\right)}={\mathcal{O}}_{h_i\left(d_j\right)}]}=1$$

For the second case in which $h_i\left(d_i\right)\ne h_i\left(d_j\right)$, we have

$$▵=\frac{Pr[{\mathit{\upsilon }}_{h_i\left(d_i\right)}={\mathcal{O}}_{h_i\left(d_i\right)}]}{Pr[{\mathit{\omega }}_{h_i\left(d_i\right)}={\mathcal{O}}_{h_i\left(d_i\right)}]}\cdot \frac{Pr[{\mathit{\upsilon }}_{h_i\left(d_j\right)}={\mathcal{O}}_{h_i\left(d_j\right)}]}{Pr[{\mathit{\omega }}_{h_i\left(d_j\right)}={\mathcal{O}}_{h_i\left(d_j\right)}]}.$$

Assume that $g_i\left(d_i\right)=+1$ and $g_i\left(d_j\right)=+1$. Then, ${\mathit{\upsilon }}_{h_i\left(d_i\right)}=+1\cdot y_1$, ${\mathit{\omega }}_{h_i\left(d_i\right)}=-1\cdot y_2$, ${\mathit{\upsilon }}_{h_i\left(d_j\right)}=-1\cdot y_3$ and ${\mathit{\omega }}_{h_i\left(d_j\right)}=+1\cdot y_4$. If ${\mathcal{O}}_{h_i\left(d_i\right)}=+1$, then $y_1=+1$, $y_2=-1$, $y_3=-1$ and $y_4=+1$. Therefore, according to Eq. , we have

$$e^{-2{ϵ}^{\prime }}\le \frac{Pr[{\mathit{\upsilon }}_{h_i\left(d_i\right)}={\mathcal{O}}_{h_i\left(d_i\right)}]}{Pr[{\mathit{\omega }}_{h_i\left(d_i\right)}={\mathcal{O}}_{h_i\left(d_i\right)}]}\cdot \frac{Pr[{\mathit{\upsilon }}_{h_i\left(d_j\right)}={\mathcal{O}}_{h_i\left(d_j\right)}]}{Pr[{\mathit{\omega }}_{h_i\left(d_j\right)}={\mathcal{O}}_{h_i\left(d_j\right)}]}\le e^{2{ϵ}^{\prime }},$$

in which ${ϵ}^{\prime }=ϵ∕2t$. Therefore, for each pair $(h_i,g_i)$ of hash functions in the above cases, it satisfies $ϵ∕t$-local differential privacy. Since there are $t$ hash functions to perturb the same symptom, ${\mathcal{M}}_{\text{Client-CS-LDP}}$ of each user satisfies $ϵ$-local differential privacy according to Lemma 1. Since records between different users are disjoint, it satisfies $ϵ$-differential privacy for all perturbed records according to Lemma 2.  ■

Theorem 6

Protocol CS-LDP satisfies unbiased estimation. For any value $j^{\ast }\in \left[m\right]$ , the variance of $\hat{f}\left(j^{\ast }\right)$ is $\left(\frac{b-1}{b}\cdot c_{ϵ}^2-1\right)f^2\left(j^{\ast }\right)+\frac{c_{ϵ}^2}{b}{\Vert f\Vert }_2^2$ .

Proof

Protocol CS-LDP satisfies unbiased estimation if and only if $\mathrm{E}\left[\hat{f}\left(d\right)\right]=f\left(d\right)$. Assume that there is a fixed constant $j^{\ast }\in \left[m\right]$. For any $j\in \left[m\right]$, $Y_j$ is denoted as follows:

$$Y_j=\left\{\begin{array}{cc}1\hfill & \text{if }h\left(j\right)=h\left(j^{\ast }\right)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right)$$

Meanwhile, assume that there is a perturbation function $p\left(\cdot \right)$, namely, Eq. . Then, $\hat{f}\left(j^{\ast }\right)$ is equal to

$$g\left(j^{\ast }\right)\cdot \mathcal{V}\left[h\left(j^{\ast }\right)\right]=g\left(j^{\ast }\right)\cdot \sum _{i=1}^{n}g\left(d_i\right)p{c}_{ϵ}{Y}_i=g\left(j^{\ast }\right)\cdot \sum _{j=1}^{m}f\left(j\right)g\left(j\right)p{c}_{ϵ}{Y}_j=g{\left(j^{\ast }\right)}^{2}f\left(j^{\ast }\right)p{c}_{ϵ}{Y}_{j^{\ast }}+\sum _{j\ne j^{\ast }}f\left(d_j\right)g\left(d_{j^{\ast }}\right)g\left(d_j\right)p{c}_{ϵ}{Y}_j=f\left(j^{\ast }\right)p{c}_{ϵ}+\sum _{j\ne j^{\ast }}f\left(j\right)g\left(j^{\ast }\right)g\left(j\right)p{c}_{ϵ}{Y}_j$$

For the expected value of $\hat{f}\left(j^{\ast }\right)$, we have

$$\mathrm{E}\left[\hat{f}\left(j^{\ast }\right)\right]=\mathrm{E}\left[f\left(j^{\ast }\right)p{c}_{ϵ}+\sum _{j\ne j^{\ast }}f\left(j\right)g\left(j^{\ast }\right)g\left(j\right)p{c}_{ϵ}{Y}_j\right]=\mathrm{E}\left[f\left(j^{\ast }\right)p{c}_{ϵ}\right]+\mathrm{E}\left[\sum _{j\ne j^{\ast }}f\left(j\right)g\left(j^{\ast }\right)g\left(j\right)p{c}_{ϵ}{Y}_j\right]=f\left(j^{\ast }\right)c_{ϵ}\mathrm{E}\left[p\right]+\sum _{j\ne j^{\ast }}f\left(j\right)c_{ϵ}\mathrm{E}\left[g\left(j^{\ast }\right)g\left(j\right)p{Y}_j\right].$$

For $\mathrm{E}\left[p\right]$, it is equal to $(+1)\cdot \frac{e^{{ϵ}^{\prime }}}{e^{{ϵ}^{\prime }}+1}+(-1)\cdot \frac{1}{e^{{ϵ}^{\prime }}+1}=\frac{e^{{ϵ}^{\prime }}-1}{e^{{ϵ}^{\prime }}+1}$. Since hash functions $g_i$ are independent with each other, we have $E\left[g\left(j^{\ast }\right)g\left(j\right)Y_j\right]=E\left[g\left(j^{\ast }\right)\right]E\left[g\left(j\right)Y_j\right]=0$ for $j\ne j^{\ast }$. Therefore, $\mathrm{E}\left[\hat{f}\left(j^{\ast }\right)\right]=f\left(j^{\ast }\right)$.

For the variance of $\hat{f}\left(j^{\ast }\right)$, $\mathrm{Var}\left[\hat{f}\left(j^{\ast }\right)\right]$ is derived as follows:

$$\mathrm{E}\left[{\left(\hat{f}\left(j^{\ast }\right)-\mathrm{E}\left[\hat{f}\left(j^{\ast }\right)\right]\right)}^2\right]=\mathrm{E}\left[{\left(\hat{f}\left(j^{\ast }\right)-f\left(j^{\ast }\right)\right)}^2\right]=\mathrm{E}\left[{\left(f\left(j^{\ast }\right)(1-p{c}_{ϵ})+\sum _{j\ne j^{\ast }}f\left(j\right)g\left(j^{\ast }\right)g\left(j\right)p{c}_{ϵ}{Y}_j\right)}^2\right]=\mathrm{E}\left[f^2\left(j^{\ast }\right){(1-p{c}_{ϵ})}^2+{\left(\sum _{j\ne j^{\ast }}f\left(j\right)g\left(j^{\ast }\right)g\left(j\right)p{c}_{ϵ}{Y}_j\right)}^2+2f\left(j^{\ast }\right)(1-p{c}_{ϵ})\sum _{j\ne j^{\ast }}f\left(j\right)g\left(j^{\ast }\right)g\left(j\right)p{c}_{ϵ}{Y}_j\right]=\mathrm{E}\left[f^2\left(j^{\ast }\right){(1-p{c}_{ϵ})}^2\right]+\mathrm{E}\left[{\left(\sum _{j\ne j^{\ast }}f\left(j\right)g\left(j^{\ast }\right)g\left(j\right)p{c}_{ϵ}{Y}_j\right)}^2\right]+\mathrm{E}\left[2f\left(j^{\ast }\right)(1-p{c}_{ϵ})\sum _{j\ne j^{\ast }}f\left(j\right)g\left(j^{\ast }\right)g\left(j\right)p{c}_{ϵ}{Y}_j\right]=\mathrm{E}\left[f^2\left(j^{\ast }\right)\right]\cdot \mathrm{E}\left[1-2p{c}_{ϵ}+p^2{c}_{ϵ}^2\right]+\mathrm{E}\left[\sum _{i\ne j^{\ast }}\sum _{j\ne j^{\ast }}f\left(i\right)f\left(j\right)g\left(i\right)g\left(j\right)p^2{c}_{ϵ}^2{Y}_i{Y}_j\right]=(c_{ϵ}^2-1)f^2\left(j^{\ast }\right)+\sum _{i\ne j^{\ast }}\sum _{j\ne j^{\ast }}f\left(i\right)f\left(j\right)\mathrm{E}\left[g\left(i\right)g\left(j\right)p^2{c}_{ϵ}^2{Y}_i{Y}_j\right]=(c_{ϵ}^2-1)f^2\left(j^{\ast }\right)+\sum _{j\ne j^{\ast }}{f}^2\left(j\right)\mathrm{E}\left[p^2{c}_{ϵ}^2{Y}_j^2\right]=(c_{ϵ}^2-1)f^2\left(j^{\ast }\right)+\sum _{j\ne j^{\ast }}{c}_{ϵ}^2{f}^2\left(j\right)\mathrm{E}\left[Y_j\right]=(c_{ϵ}^2-1)f^2\left(j^{\ast }\right)+\frac{c_{ϵ}^2}{b}\sum _{j\ne j^{\ast }}{f}^2\left(j\right)=\left(\frac{b-1}{b}\cdot c_{ϵ}^2-1\right)f^2\left(j^{\ast }\right)+\frac{c_{ϵ}^2}{b}{\Vert f\Vert }_2^2$$

Therefore, we complete the proof.  ■

Since protocol FAS-LDP is similar with CS-LDP except for hash functions, FAS-LDP also satisfies unbiased estimation and local differential privacy. Besides, it has the same variance. The corresponding proof is omitted.

6. Implementation of universal hash functions

In the section, we introduce the implementation of $k$-universal hash functions. In detail, we propose two different methods to implement universal hash functions. That is, CW-Trick hashing is used to the case in which $k=2$ while Tabulation based hashing is used to $k=4$.

6.1. Universal hash function

In the protocols proposed by Section 4, the most important component is $k$-universal hash functions, which are defined as follows:

Definition 5 $k$-universal Class of Hash Functions [44] —

A class $\mathcal{H}$ of hash functions from $\mathcal{D}$ into $\left[b\right]$ is a $k$-universal class of hash functions if for any distinct $d_0,d_1,\dots ,d_{k-1}\in \mathcal{D}$ and any possibly identical $v_1,v_2,\dots ,v_{k-1}\in \left[b\right]$,

$$\forall i\in \left[k\right]\underset{h\in \mathcal{H}}{Pr}[h\left(d_i\right)=v_i]=1∕b^k,$$ (6)

where $k$ is an positive integer.

According to Definition 5, a large number of values can be hashed to a relatively small set of keys. Meanwhile, there may be collisions, in which two different values are hashed to a key. Parameter $k$ is the factor that influences the collision. For example, as parameter $k$ increases from $2$ to $4$, the probability of collision decreases from $1∕b^2$ to $1∕b^4$. Here, we focus on how to design the proper hash functions that satisfy Definition 5. In the following section, we present two different implementations for $k$-universal hash functions, i.e., CW-Trick and Tabulation based hash functions.

6.2. CW-trick hashing

The first method for $k$-universal hash functions is implemented by the following equation:

$$h\left(x\right)=\sum _{i=0}^{k-1}{a}_i{x}^{i}modp,$$ (7)

where $p$ is a prime that is greater than value $x$ and $a_i$ is picked randomly from $\left[p\right]$. This equation was proposed by Wegman et al. [44]. It is obvious to see that this method is very simple and easy to implement. However, it has a disadvantage, especially when $p$ is very large. That is, if $p$ is an arbitrary prime, this method is fairly slow because the ‘mod $p$’ is relatively slow. In order to solve the problem, Thorup et al. [31] proposed a simple method, namely CW-trick, in which $p$ is a so-called Mersenne prime of the form $2^i-1$. In our experiments, we will use $p=2^{61}-1$. The CW-Trick hashing is used to $k=2$.

6.3. Tabulation based hashing

If CW-Trick hashing is used to $k=4$, the time is slow. Thorup et al. [31] proposed another method, namely Tabulation based hashing, to implement $k$-universal hash functions. They compared their method with CW-trick in terms of running time, which shows that the former is faster than the latter by at least a factor of $5$. However, the weakness of Tabulation based hashing is that it requires large pre-computed tables and thus needs the extra space to store.

We firstly introduce Theorem 2.3 in [31] to compute hash value of $x$ by $4$-universal hash functions.

Theorem 7 Theorem 2.3 in [31] —

There are any $q$ characters $\overrightarrow{x}=(x_0{x}_1\cdots x_{q-1}),x_i\in \left[2^c\right]$ . $G$ is a $q\times r$ generator matrix, which satisfies that any square sub-matrix has full rank over prime field ${\mathbf{Z}}_p$ , where $p\ge max\{2^c,q+r\}$ is an odd prime. $\overrightarrow{y}=\overrightarrow{x}G$ are $r$ additional characters $(y_0{y}_1\cdots y_r),r=q-1$ . Then, hash function of $\overrightarrow{x}$ is

$$h\left(\overrightarrow{x}\right)=h_0\left(x_0\right)\oplus \cdots \oplus h_{q-1}\left(x_{q-1}\right)\oplus {\overline{h}}_0\left(y_0\right)\oplus \cdots \oplus {\overline{h}}_{r-1}\left(y_{r-1}\right).$$ (8)

$h\left(\cdot \right)$ is a $4$ -universal hashing function if $h_i$ and ${\overline{h}}_j$ are independent $4$ -universal hash functions into $\left[2^l\right]$ .

In our experiments, assume that value $d_i$ of each user $u_i$ has 32 bits and each character has $16$ bits.1 Therefore, $q=2$ and $r=1$. In detail, value $d_i$ can be divided into two sub-values with 16-bits, i.e., $d_i^1$ and $d_i^2$ as the following equation:

$$d_i\left(32\mathrm{bits}\right)⟹\underset{d_i^1\left(16\mathrm{bits}\right)}{\underbrace{1010\cdots 1010}}\underset{d_i^2\left(16\mathrm{bits}\right)}{\underbrace{0101\cdots 0101}}$$

Besides, $4$-universal hash functions $h_i$ and ${\overline{h}}_j$ are implemented by tabulation based hashing. That is, we use precomputed tables to replace hash functions $h_i$ and ${\overline{h}}_j$. That is, Eq. (8) is changed as

$$h\left(\overrightarrow{x}\right)=T_0\left[x_0\right]\oplus \cdots T_{q-1}\left[x_{q-1}\right]\oplus T_q\left[y_0\right]\oplus \cdots \oplus T_{q+r-1}\left[y_{r-1}\right],$$ (9)

where $T_i$ is a fully random table of size $2^c$ with values from $\mathbf{R}$. Tabulation based hashing thus takes time $O(q+r)$ and space $O\left((q+r)2^c\right)$.

7. Experimental evaluation

In the section, our main goal is to study (1) the impact of different parameters on data utility; and (2) the application of protocols for frequency estimation of physical symptoms. The experiments are performed over two real datasets, representing two different distributions of symptoms.

7.1. Experimental setting

The evaluation is performed on a desktop computer, which has $4$G of RAM and Inter(R) Pentium(R) CPU P6200 running Windows $7$ operating system. All of protocols are implemented by Python. All of testing datasets are real.

Parameter settings. The number of hash function $〈h_i,g_i〉$ is $100$ and we will choose $t$ hash function pairs from them. The implementation of hash functions is based on CW-Trick and Tabulation-based hashing in Section 6. The values of $t$ and $b$ depend on error $\xi$ and confidence probability $\delta$. We mainly evaluate four protocols on different values of privacy budget $ϵ$, error $\xi$ and confidence probability $\delta$.

Datasets. We use two real datasets to evaluate our protocols, including WISDM and BMBD. We select an attribute to estimate its frequency in these two datasets, which represent two different distributions of physical symptoms. The datasets are presented as follows:

• • WISDM [45]. The dataset is collected from the accelerometer and gyroscope sensors of a smart-phone and smart-watch as $51$ subjects. It is about diverse activities of daily living and has $15,630,426$ records. We select attribute Activity from seven attributes to estimate its frequency. There are $18$ activities, including walking, jogging, Sitting and so on.
• • BMBD [46]. The dataset is collected from a public website Bixi,2 which offers bike rental service. It contains bike share information for Bixi Monetreal from $2016$ to $2019$, including start and end station ID of a trip. We select attribute Start_station_code from six attributes to estimate its frequency.

Table 1 shows the statistical information of attribute Activity in WISDM and Start_station_code in BMBD. The distributions of these two attributes are different. Activity is uniformly distributed, while Start_station_code is loose. Therefore, we use them to evaluate our protocols for different distributions of symptoms.

Table 1.

Statistical information of datasets.

	WISDM	BMBD
$\mathrm{Attribute}$	Activity	Start_station_code
$\mathrm{Num.}$	$18$	$621$
$\mathrm{Min.}\left(f\right)$	$833,208$	$28$
$\mathrm{Max.}\left(f\right)$	$901,381$	$188,306$
$\mathrm{Avg.}\left(f\right)$	$868,357$	$31,501$
$\mathrm{Med.}\left(f\right)$	$870,532$	$25,238$
$\mathrm{Total}$	$15,630,426$	$19,561,549$

Evaluation Metrics. We evaluate the top-$k$ frequent elements $\mathcal{C}=\{d_{i_1},d_{i_2},\dots ,d_{i_k}\}$ in $D$ by RE and MSE, which have the most frequencies [47], [48], [49]. The concrete metrics are presented as follows:

• •
  Relative Error (RE). The metric is usually used for SUM/ COUNT/AVG queries and measures how large the error is relatively to the true answer for each query $\hat{f}\left(d\right)$ by the following equation:

  $$\text{RE}=\frac{1}{k}\sum _{j=0}^{k-1}\frac{|f\left(i_j\right)-\hat{f}\left(i_j\right)|}{f\left(i_j\right)},i_j\in \left[m\right]$$ (10)

  Furthermore, for the top-$k$ elements, we evaluate them by the average and median value of relative errors, i.e., ARE and MRE.
• •
  Mean Square Error (MSE). It is used to measure the estimation accuracy by the average of the squared errors, namely,

  $$\text{MSE}=\frac{1}{k}\sum _{j=0}^{k-1}{\left[\hat{f}\left(i_j\right)-f\left(i_j\right)\right]}^2,i_j\in \left[m\right]$$ (11)

  where $f\left(i_j\right)$ is the true frequency of users taking value $i_j$.

7.2. Experimental results

In the following section, we show the impact of three key parameter $\xi$, $\delta$ and $ϵ$ in terms of RE and MSE for different datasets. Then, we show the effectiveness of protocols by estimating top-$k$ in different cases. In order to reduce the error, we repeat each experiment $10$ times. Since frequency of different records in BMBD is different, we will consider two cases, including top-$10$ and top-$30$. That is, we estimate $10$ and $30$ elements with the most frequency, respectively.

7.2.1. Impact of parameter $\xi$

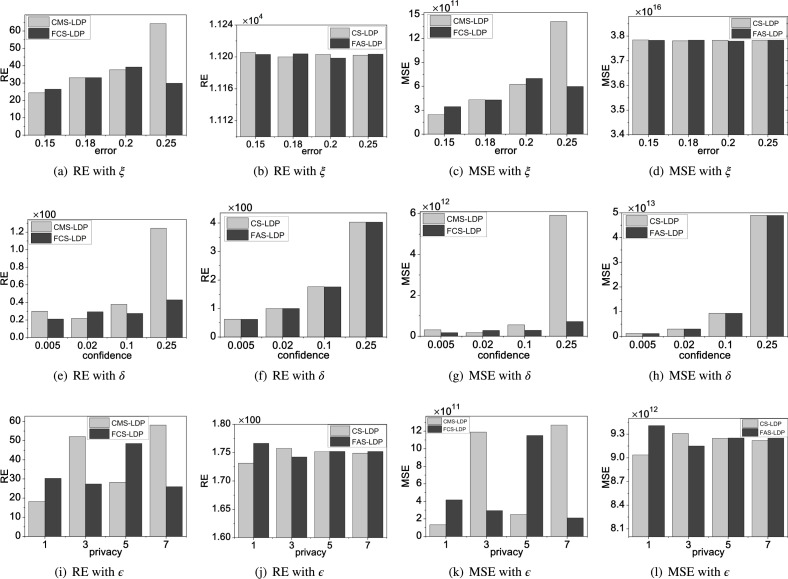
In order to analyze impact of parameter $\xi$, we firstly set the parameters. That is, confidence probability $\delta$ is 0.1 and privacy budget $ϵ$ is $3$. $\xi$ of WISDM is $[0.15,0.18,0.2,0.25]$ while that is $[0.004,0.0044,0.005,0.00571]$ for BMBD.

Figs. 3(a)–3(d) show RE and MSE of WISDM by different protocols, including CMS-LDP, FCS-LDP, CS-LDP and FAS-LDP. It is intuitive to see that RE and MSE in CMS-LDP and FCS-LDP increase as $\xi$ increases from 0.15 to 0.25 in Fig. 3, Fig. 3. This is consistent to CMS and FCS without LDP. This implies that addition of privacy preservation does not change influence of parameter $\xi$. However, Fig. 3, Fig. 3 show that $\xi$ has little impact on CS-LDP and FAS-LDP, since RE and MSE do not change as $\xi$ increases from 0.15 to 0.25.

Fig. 3.

Results for Top-$18$ of WISDM.

Figs. 4(a)–4(d) and 5(a)–5(d) show RE and MSE of BMBD in two different cases by four private protocols. Compared to WISDM, it has the opposite results for protocol CMS-LDP and FCS-LDP. That is, with $\xi$ increasing from 0.004 to 0.00571, RE and MSE decrease. The key factor for this opposition is size of $b$ mapped by hash function $\mathcal{H}$, in which the size in BMBD is far greater than that in WISDM. Thus, perturbation for privacy preservation is the dominant factor for BMBD, while conflict probability is relatively less. As size of $b$ decreases, it leads to less expected error. Fig. 4, Fig. 4 and Fig. 5, Fig. 5 show that RE and MSE of BMBD by CS-LDP and FAS-LDP have no much difference with $\xi$ increasing. That is, $\xi$ has little impact on CS-LDP and FAS-LDP.

Fig. 4.

Results for Top-$10$ of BMBD.

Fig. 5.

Results for Top-$30$ of BMBD.

Therefore, the impact of $\xi$ on CMS-LDP and FCS-LDP depends on the size of $b$. In contrast, it has little impact on CS-LDP and FAS-LDP.

7.2.2. Impact of parameter $\delta$

Here, we consider the impact of parameter $\delta$ for four LDP protocols. The expected error $\xi$ is 0.18 for WISDM, while that is 0.005 for BMBD. Privacy budget $ϵ$ is $3$. The range of $\delta$ is $[0.005,0.02,0.1,0.25]$.

For WISDM, Figs. 3(e)–3(h) show RE and MSE of four protocols. It is intuitive to find that RE and MSE increase with $\delta$ increasing. This implies that adding the number of hash functions can efficiently improve the accuracy for perturbed data. Meanwhile, it needs more time for the users and the third party. From Figs. 3(e)–3(h), RE and MSE are fast increasing once $\delta$ is greater than 0.25. Therefore, $\delta <0.25$ is a good choice.

For BMBD, Figs. 4(e)–4(h) and 5(e)–5(h) show RE and MSE of four protocols. Two cases have the similar results. It is easy to see that the impact of $\delta$ on CMS-LDP and FCS-LDP is counter to that on CS-LDP and FAS-LDP. In detail, RE and MSE of CMS-LDP and FCS-LDP decrease as $\delta$ increases while those of CS-LDP and FAS-LDP have the opposite results. This means that it should add the number of hash functions for FCS-LDP and FCS-LDP and decrease the number for CS-LDP and FAS-LDP.

Thus, the impact of $\delta$ on CS-LDP and FAS-LDP is consistent, while that on CMS-LDP and FCS-LDP is changing in different datasets.

7.2.3. Impact of parameter $ϵ$

In order to analyze the impact of $ϵ$, $\xi$ for WISDM is 0.18, while that is 0.005 for BMBD. Confidence probability $\delta$ is 0.1. The range of privacy budget $ϵ$ is $[1,3,5,7]$.

For WISDM, Figs. 3(i)–3(l) show RE and MSE of four protocols. Fig. 3, Fig. 3 show that RE and MSE of CMS-LDP and FCS-LDP do not decrease with $ϵ$ increasing. In contrast, they have big fluctuation. Compared to those for BMBD in Figs. 4(i), 4(k), Fig. 5, Fig. 5, the possible reason is the size of $b$. For CS-LDP and FAS-LDP, the accuracy increases as privacy budget increases. However, it does not change once privacy budget exceeds some threshold (e.g., $5$ in Fig. 3, Fig. 3).

For BMBD, Figs. 4(i)–4(l) and 5(i)–5(l) show RE and MSE of four protocols. We can find that top-$10$ and top-$30$ have the same results about RE and MSE. For four protocols, both of RE and MSE decrease as privacy budget $ϵ$ increases. In other words, the increase of RE and MSE in CMS-LDP and FCS-LDP is fast, while that in FCS-LDP and FAS-LDP is not obvious. Once privacy budget exceeds some threshold (e.g., $3$ in Fig. 4(j)), RE and MSE have little change for CS-LDP and FAS-LDP. The threshold is $5$ for CMS-LDP and FCS-LDP.

According to the above results, we can derive that privacy budget $ϵ$ has the important impact on four protocols. Meanwhile, once $ϵ$ exceeds some threshold, the impact can be ignored.

7.2.4. Protocol applications in IoMT

By our experiments, we analyze two different distributions of symptoms for some infectious disease in IoMT. That is, the symptoms are uniformly distributed in case (i), while those are loose in case (ii). Generally speaking, we have two important findings in Fig. 3, Fig. 4, Fig. 5. The first one is that the utility of CMS-LDP and FCS-LDP is greater than that of CS-LDP and FAS-LDP. Since the time of CMS-LDP and FCS-LDP is smaller than that of CMS-LDP and FAS-LDP, Therefore, CMS-LDP and FCS-LDP are relatively optimal in terms of utility and computation overhead. The second one is that protocol CMS-LDP is not absolutely better than FCS-LDP, and vice versa. Furthermore, different distributions of symptoms have an important influence for the choices of different parameters, including $\xi$, $\delta$ and $\sigma$. In case (i), FCS-LDP has better stability than CMS-LDP as different parameters change. In case (ii), CMS-LDP and FCS-LDP have the similar changes. Parameter $\xi$, $\delta$ and $\sigma$ should be as small as possible to maximize the utility.

8. Conclusions

The focus of the paper is on how to estimate the frequency of symptoms under local differential privacy for infectious disease analysis in IoMT. Based on basic sketches, this paper has proposed four protocols, including CMS-LDP, FCS-LDP, CS-LDP and FAS-LDP. We have proved that our proposed protocols satisfy two important properties, i.e., unbiased estimation and local differential privacy. Meanwhile, we have presented the variance of four protocols. Through empirical analysis, CMS-LDP and CS-LDP are relatively optimal protocols for frequency estimation of physical symptoms in IoMT. We plan to design better encoding methods to reduce the computation complexity and perturbation techniques to improve the accuracy of our protocols in the future.

CRediT authorship contribution statement

Xiaotong Wu: Conceptualization, Methodology, Formal analysis, Writing - original draft. Mohammad Reza Khosravi: Conceptualization, Methodology, Writing - original draft. Lianyong Qi: Software, Data curation, Validation. Genlin Ji: Writing - review & editing, Computation resources, Project administration. Wanchun Dou: Supervision, Writing - review & editing, Project administration. Xiaolong Xu: Conceptualization, Writing - review & editing, Investigation, Validation, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.