Abstract
Deformation of flexible vesicles suspended in a fluid medium due to an applied electric field can provide valuable insight into deformation dynamics at a very small scale. In an electric field, the response of the vesicle membrane is strongly influenced by the conductivity of surrounding fluid, vesicle size and shape, and the magnitude of applied field. We studied the electrodeformation of vesicles immersed in a fluid media under a DC electric field. An immersed interface method is used to solve the electric field over the domain with conductive or non-conductive vesicles while an immersed boundary method is employed to solve fluid flow, fluid-solid interaction, membrane mechanics and vesicle deformation. Initial force analysis on the membrane surface reveals almost linear influence of vesicle size, but the vesicle size does not affect the long-term deformation which is consistent with experimental evidence. Highly nonlinear effect of the applied field as well as the conductivity ratios inside and outside of the vesicle are observed. Results also point towards an early linear deformation regime followed by an equilibrium stage for the membranes. Modeling results suggest that electrodeforming vesicles can create unique external flows for different conductivity ratios. Moreover, significant influence of the initial aspect ratio of the vesicle on the force distribution is observed across a range of conductivity ratios.
Keywords: Vesicle electrodeformation, Giant vesicles, Immersed interface method, Immersed boundary method
1. Introduction
Biological cell manipulation, cellular nutrient transport, and drug delivery are some of the most intensive topics in biophysical research. In each of these emerging research areas, bio-vesicles are playing a fundamental role. Their functions are as varied as their size. For example, HIV-1 infected cells release nanoscale extracellular vesicles (exosomes) that mediate virus attachment and fusion to target cells [1]. At the same time, a host of biomimetic vesicles can be engineered as nanoscale drug carriers to target inflamed tissues [2,3]. Another important example is the endosomal vesicles which continuously perform innumerable intracellular tasks in cellular endocytosis and exocytosis. At the microscale, most eukaryotic cells themselves are yet another example of large biological vesicles (aka giant vesicle). Prediction of the adaptive response of each of these vesicles in a given environment requires the understanding of their behavior. More specifically, critical understanding of their dynamics is needed for proper manipulation in a specific targeted application like drug delivery. One promising approach is the study of lipid membrane or cell deformation through interaction with electric fields.
Application of an electric field on microparticles, such as vesicles, bubbles, and beads suspended in a liquid medium results in altered kinetics, electro-osmotic flow, and electrodeformation. Depending on the surface charge, geometry, and electrical properties, different vesicles produce varying levels of response. These responses include rotation, translation, assembly and orientation [4], deformation, electroporation and fusion [5]. Both alternating current (AC) and direct current (DC) fields are being actively employed in tissue ablation, cell deformation and characterization of the mechanical properties of lipid vesicles [6,7]. Application of DC fields facilitates the investigation of vesicle transport as well as electrodeformation [8], while AC fields allow for observation of a wide range of membrane mechanics using electric field magnitude and frequency as control parameters [9]. In biomedical and biotechnology applications, electrodeformation has been extensively used for studying mechanics of cell and label-free microfluidic characterization. For example, electrodeformation has been used to characterize TGF-β dependent epithelial to mesenchymal transition of cancer cells [10]. It has also been successfully employed to separate malaria-infected red blood cells from healthy ones in a microfluidic device [11]. Engineered giant lipid vesicles (generally a few tens of micrometers in diameter) is another major avenue under study with electric fields due to their close resemblance to biological cells [12]. The size of both naturally occurring and engineered vesicles can range from nanometers to tens of microns. Giant vesicles have been predominantly used for the measurement of rheological and mechanical properties of the membrane since they are easily observable under optical microscope and can be manipulated directly. They have also been studied to understand electric field induced deformation as well as fluid movement inside the vesicle [13].
Considering the varied functions and sizes of the bio-vesicles, continuous characterization of the membrane deformation under varying conditions is generally tedious and often very difficult to observe experimentally. Additionally, molecular interactions in smaller vesicles are affected by their membrane curvature which leads to uncertainties in experimental results [14]. Several analytical approaches have been presented to understand the fundamental physics of the membrane behavior [15–17]. However, due to the complex multiphysics nature of the problem, the analytical solutions often require restrictive assumptions. Sadik et al. presented a detailed theoretical analysis on the effects of using strong DC electric field on vesicles with different conductivities and compared their results with experimental observations [18]. However, the analytical model in their work, as well as the works of Hyuga et al [16] only valid for vesicles that are regular ellipsoids at the start and must maintain an ellipsoidal shape while they deform. Moreover, a number of hydrodynamic assumptions and simplifications are required for these analytical models in order to solve the governing equations. Numerical treatments of the problems have opened a wide window of opportunities in understanding these complex behaviors. Li et al. studied frequency dependence of membrane deformation in a non-uniform AC electric field [7]; MacQueen et al. investigated the change in elastic properties of cells due to electrodeformation using an effective dipole moment assumption [19]. However, most of these studies were either limited to the linear small deformation regime of the vesicles [18] or used the dipolar approximation that is not valid for deformed cells [20]. More recently, Hu et al. have presented detailed works on an algorithm development combining immersed interface and immersed boundary approaches for studying electrodeformation [21,22].
Despite the importance of these vesicles, a complete understanding of membrane behavior as well as fluid-structure interactions under electric fields are still lacking. In the present work, we investigate the electrodeformation dynamics of lipid vesicles under a wide range of applied DC electric fields. The vesicle membrane is represented as a massless immersed boundary. The bulk conductivity of the vesicle is adjusted accordingly to consider the heterogeneous electrical properties of the vesicle. The induced force of electric field is obtained using Maxwell stress tensor approach. Effects of applied voltage, conductivity ratio, vesicle size and initial aspect ratios on the electrodeformation dynamics are investigated in detail. The model is validated using several experimental results.
The rest of the paper is arranged as follows. In Section 2, we present the mathematical model for a scenario where a vesicle placed inside a microfluidic setup and subjected to a uniform applied electric potential difference. In Section 3, we first compare experimental data with numerical results. Afterward, effects of the magnitude of the applied field and the conductivity ratio on the deformation dynamics are observed. We also present the interaction of surrounding fluid media with deforming membrane and explore the electrodeformation phenomena for different initial vesicle aspect ratios.
2. Mathematical Model
We consider a physical scenario where a vesicle is submerged in an aqueous medium as shown in Fig. (1a). This is similar to a biological cell suspended in buffer solution inside a microfluidic channel. The vesicle is subjected to a DC electric field. Here it is assumed that the vesicle is neutrally charged before the application of any external electric fields. Moreover, owing to a negligibly small electric double layer, electro-osmotic contributions can also be excluded [23]. Also, we do not consider van der Walls force since compared to electrostatic forces, the van der Walls and Brownian forces are negligible in these kinds of systems [24].
Fig. 1.
Rectangular computational domain Ω used to model the vesicular microenvironment. (a) Boundary conditions for the electrostatic problems are shown. The vesicles in the domain have a finite size with membrane boundaries denoted by Γ. The undeformed circular vesicle has a radius of 10 μm while the domain dimensions are a = b = 150 μm. (b) Detail of the immersed boundary representation of the membrane. Vesicle membrane location in the regular Cartesian domain was calculated using spline interpolation [31].
It is also assumed that the submerged aqueous medium is Newtonian with viscosity μ and density ρ. The electrical conductivity of the fluid outside the membrane is σout and that of the content inside is σin. When an electric field is applied through voltage difference on the left and right electrodes, the ensuing scenario can be described as a coupled electrostatic and fluid dynamic problem. In a microfluidic system, the advection and diffusion currents are much smaller than the drift current. Thus, for a DC electric field, the charge conservation equation can be simplified as
| (2.1) |
The electric field () is related to the electrical potential (ϕ) through
| (2.2) |
Substituting Eqs. (2.2) into the charge conservation equation, we arrive at the relation for the electric potential in the domain
| (2.3) |
where ϕin and ϕout are the potentials inside and outside the membrane. Imposing the jump in electric potential across the vesicle membrane and the continuity of normal current, we get the interface conditions on the membrane as
| (2.4) |
| (2.5) |
where denotes the unit normal vector on the membrane, m(s) and n(s) are parametric representations of the jump conditions, and the parameter s tracks the material points of the interface. It must be noted that, every leaky dielectric, especially cell membranes will act like a capacitor and have a finite charging time in an electric field. From Maxwell’s equations, the characteristic time for electric phenomena is given by the ratio of dielectric permeability and conductivity of the membrane (εmemε0/σmem) [25], where εmem is the dielectric constant of the membrane, ε0 is the vacuum permittivity and σmem is the membrane conductance. Considering the membrane dielectric constant to be around 20 [26], and the conductivity on the order of 10−7 S/m [27], the characteristic time for electric phenomena is in the order of milliseconds. However, the capacitive charge build-up starts as soon as the lipid membranes are placed under an electric field leading to a voltage difference across it. Defining the transmembrane voltage Vmem as (ϕin-ϕout), the instantaneous membrane capacitive charging can be described by [22,28],
| (2.6) |
In Eq. 2.6, the membrane is modeled as a two-dimensional interface with effective capacitance Cmem = εmem/h and conductance Gmem = σmem/h where h is the membrane thickness.
Force density on the membrane due to this electrostatic interaction can be found from the Maxwell stress tensor as
| (2.7) |
where ε is the permittivity of the media where the force is being calculated and is a unit tensor. The rectangular domain has two insulating boundaries at the bottom and top surfaces as shown in Fig. 1(a). Electrodes are placed on the left and right boundaries, where a prescribed potential is maintained to create an electric field. For simplicity, the vesicle is always placed at the geometric center of the domain, while the electrodes carry potentials of equal magnitude but opposite sign. The boundary conditions for the electric potential are presented in Table 1.
Table 1:
Boundary conditions for the governing equation in the domain
| Inlet (x = 0) | Outlet (x = a) | Bottom Wall (y = 0) | Top Wall (y = b) | |
|---|---|---|---|---|
| Electrostatic Description | ||||
| Fluid Dynamic Description | Periodic | Periodic | a | a |
and are the unit normal and unit tangent vectors to the walls
The electric field driven viscous flow field can be described using the incompressible Navier-Stokes equations and continuity equation [29] as
| (2.8) |
| (2.9) |
Here, is the local velocity and is the body force density acting on the fluid. This body force is a combination of the elastic forces in the membrane as well as the tensile or compressive forces arising from the applied electric field. In the fluid description, the domain is considered periodic in the horizontal direction which implies,
| (2.10) |
The top and bottom channel walls are assumed solid with no slip and no penetration boundary conditions as listed in Table 1. All required geometric, mechanical, electrical parameters as well as fluid properties are reported in Table 2.
Table 2:
Geometric, mechanical and electrical parameters used for the calculation of vesicle deformation
| Parameter | Value |
|---|---|
| Conductivity of the membrane, σmem | 10−7 S/m [27] |
| Conductivity of the vesicle content, σenc | 0.5 S/m [27] |
| Vesicle membrane thickness, h | 5 nm |
| Vesicle radius, R | 5~15 μm |
| Permittivity of the membrane, εmem | 1.77×10−10 F/m [26] |
| Permittivity of the surrounding fluid medium, ε | 7×10−10 F/m [20] |
| Density of the surrounding fluid medium, ρ | 1000 kg/m3 |
| Viscosity of the surrounding fluid medium, μ | 0.001 kg/(m · s) |
As shown in Figs. 1(a) and 1(b), the rectangular (a × b) computational domain Ω is discretized with a uniform and fixed Eulerian grid. The immersed membrane boundary is outlined as Γ, where the interface is tracked in a Lagrangian manner with control points distributed on the membrane. Both immersed boundary and immersed interface descriptions represent the membrane in terms of localized force density formulations, where the interface is taken as one dimension smaller than the overall domain problem (e.g. 1D interface for a 2D domain) [30]. However, lipid vesicle membranes have a finite and often non-negligible thickness (~5–10 nm), and the properties of the membrane can be very different from the properties of the bulk fluid inside the vesicle. Therefore, the heterogeneous electrical characteristics of the vesicle, such as membrane electrical conductivity (σmem) and electrical conductivity of the fluid encapsulated by membrane (σenc) are replaced with an equivalent homogeneous conductivity, σin as [27,31]:
| (2.11) |
where R is the radius of the vesicle. It should be mentioned that, Eqs. (2.1) is valid only when h << R which is met by our description of the vesicle.
The elastic nature of membrane as well as the fluid media outside and inside the membrane allow it to deform under an applied force. The magnitude of the applied force depends on vesicle shape as well as the electrical properties of the media inside and outside of the vesicle. To study these forces and its effects on surrounding fluids, we formulated a hybrid immersed interface-immersed boundary method. The solution methodology for the coupled electric and hydrodynamic system and details of the membrane mechanical models for deformation due to electric field are given in the appendix.
3. Discussion of Results
Before analyzing electrodeformation in a microfluidic system, the parameters need to be chosen accordingly so that the investigation is meaningful, and the results can be translated to understand broader physical phenomena. In this study, we first adjusted the stiffness parameter of the membrane to represent a lipid vesicle undergoing electrodeformation. Following experimental conditions from [18], first, a sample case was chosen where a vesicle of 26 μm initial diameter is exposed to a uniform electric field of 0.9 kV/cm. The conductivity ratio λ = σin/σout was kept fixed at 53.0. Although the vesicle is initially circular, depending on the applied field, it generally takes an ellipsoidal shape after deformation. For the ease of discussion, we formally define the term aspect ratio, α, as the ratio of the ellipsoid axis along the horizontal (x-axis) to the axis along the vertical (y-axis). Thus, for a perfect sphere, α = 1.0; it is greater than 1.0 for an oblate spheroid and less than 1 for a prolate one. After 500 μs, the experimental results show a deformation of the spherical vesicle (α = 1.0) to an oblate spheroid (α = 1.31), which is shown in Fig. 2(a) and 2(b) with corresponding numerical results found after adjusting the stiffness parameter. Next, using the same stiffness parameter, we studied a different case with a nominal applied field strength of 1.5 kV/cm and λ = 46.9. The initial diameter of the vesicle was 28.8 μm and after 500 μs, it was deformed into an oblate spheroid with α = 3.43. Comparison with experimental data shows less than 4% difference as presented in Fig. 2(b) and 2(d). In this preliminary mechanical model of the artificial vesicle membrane, we decided to use the simplest model that adequately captures the experimental findings. Unlike biological cells, the lipid vesicles used in the experiments do not have any underlying cytoskeleton. For that reason, the simple Hookean springs connecting each immersed boundary points to all other points yields satisfactory results over a wide range of applied voltage and conductivity ratios. For all the cases considered in our study, the 150 μm square domain is discretized with a 512×512 uniform spatial grid and the step-size in time is 10 ns. Detailed convergence study of the numerical scheme, grid dependence and error analysis with the chosen domain parameters have been presented in [20].
Fig. 2.
Model result comparison with experimental data from Sadik et al [18]. Vesicles are initially circular before application of an electric field in (a) and (c). (b) The deformation dynamics was tuned using experimental data after 500 μs at 0.9 kV/cm nominal applied field with conductivity ratio, λ=53. (d) The tuned model captures vesicle deformation at higher applied voltage (1.5 kV/cm) and different conductivity ratio (λ=46.9) as seen in the experiments [18].
3.1. Effect of Electric Field Magnitude and Conductivity Ratio
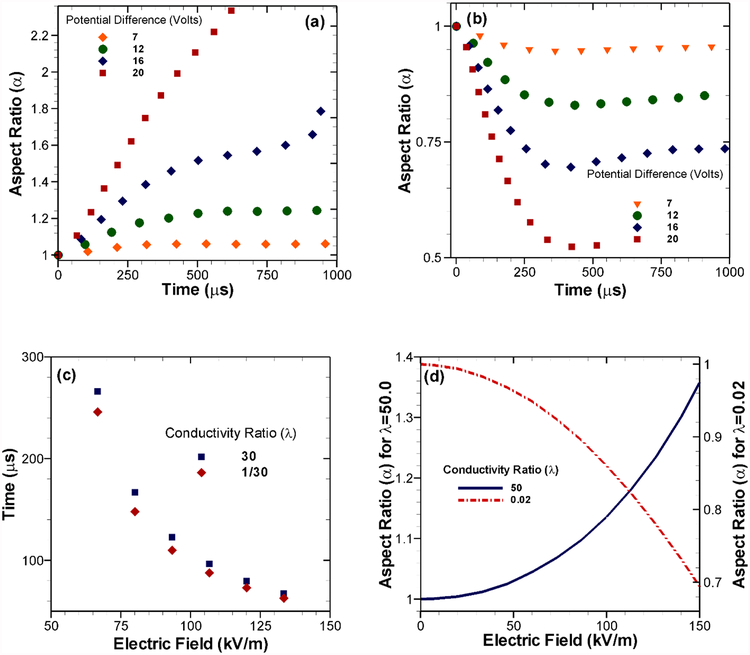
The extent of deformation of the flexible membrane with respect to the applied electric field is not a linear phenomenon. While comparing our model results, for validation with experimental data from [18] as presented in Fig. 3(a), we can observe a couple of distinct features. Firstly, the variation of aspect ratio (α) shows a rapid rise as the conductivity ratio (λ) is increased from 1. Later, it reaches a plateau for high λ values for a given applied electric field. Secondly, the effect of increasing electric field has a dramatic effect on the deformation dynamics, which we will discuss in the Fig. 4 in detail. Theoretically, under some restrictive assumptions it has been shown that in the initial phase of increasing λ, the normal component of the Maxwell stress scales quadratically [18]. For larger values of λ, it converges to a constant value which explains the features in Fig. 3(a) where the normal component of the Maxwell stress is resulting in a horizontal pulling force on the vesicle from both directions. Our model results capture the experimental trends for a wide range of λ and different levels of the applied electric field. It should be noted that, for higher levels of applied voltage, electroporation occurs very early in the experiments. In this study, we have not considered that regime. It should be mentioned that experimental evidences did not point to any conclusive effect of initial vesicle size on the deformation dynamics (Fig. 3 in [18]). However, their analytical model which did not consider any capacitive charging of the vesicle membrane showed clear dependence of the final aspect ratio on the vesicle size (Fig. 7 in [18]). In order to explore this scenario, we observed the deformations in our model under two different conditions. In the first case (Fig. 3(b)), the jump across the membrane is set to zero which corresponds to the analytical model in [18] while in the second case (Fig. 3(c)), we computed the voltage jump across the membrane. In the first case, our model predicts higher deformations for smaller vesicles. However, when membrane charging is considered, there was no clear relation between size and deformation. These results strongly indicate the induced charging behavior of the membrane under applied electric field.
Fig. 3.
Calculated aspect ratio (α), with respect to changing conductivity ratio (λ) for different applied potentials. Experimental results from [18] are included for comparison. The electric fields shown are nominal. (b) Change in aspect ratio after 500 μs for different conductivity ratios at 1.5 kV/cm nominal applied field corresponding to Sadik et al [18] with the voltage jump across the membrane set to zero and the same scenario at (c) with voltage jump originating from membrane charging.
Fig. 4.
Effect of the magnitude of applied potential difference with different conductivity ratios. Deformation of the vesicle in terms of the aspect ratio (α) with time for (a) conductivity ratio, λ = 30 and (b) λ = 1/30. (c) Starting from a perfect circle (α = 1), the time required to reach α = 1.11 for λ = 30 and α = 0.9 for λ = 1/30. (d) Starting from α = 1, the aspect ratios for both λ > 1 and λ < 1 at 125 μs with increasing applied potential.
Fig. 7.
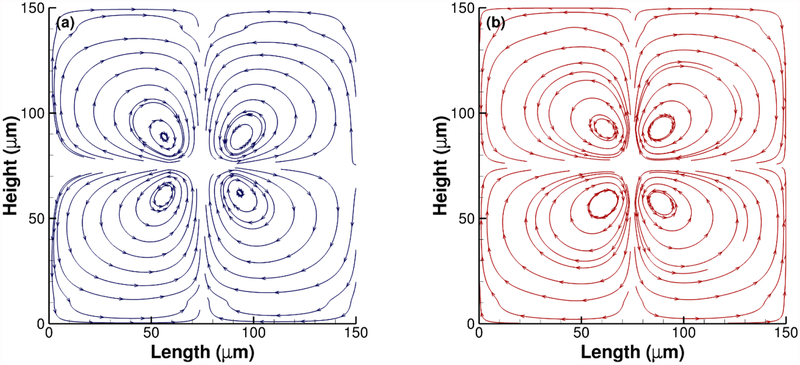
Response of the surrounding fluid media due to the deformation of vesicles for an applied potential difference of 7 volts. Streamlines for conductivity ratio (a) λ = 50 and (b) λ = 1/50. The four vortices switch directions in case (b) due to compressive force.
Most of the experimental studies involving bio-membranes are performed either in a buffer solution due to its chemical stability or in some other stable aqueous medium. In general, common buffer solutions have much higher (from 10 to 10,000 times higher) electrical conductivity compared to the bio-vesicles. However, in case of artificial biomimetic vesicles, it is possible to alter the vesicle conductivity by altering the internal fluid media. [18]. Therefore, it is possible to have a wide range of experimental scenarios depending on the magnitude of conductivities of the media inside and outside the membrane. In order to compare our numerical results to the experimental observations from [18], we chose the conductivity ratio within the range of 1–50. It should be noted that this range physically corresponds to different concentrations of NaCl in aqueous solution as membrane-enclosed media and glucose solution as the surrounding media. For cases where the bulk conductivity of the vesicle is greater than the surrounding fluid, the conductivity ratio λ is fixed at 30 while for the opposite scenario, it is set at 1/30 in our model. Later, we also explore scenarios where λ itself is varying and discuss its implications. Several aspects of increasing the applied voltage on the electrodeformation are presented in Fig. 4. From a theoretical point of view, the electrostatic force obtained from the Maxwell stress tensor has a quadratic relation to the applied electric field as shown in Eq. (2.7). Analytic expansion of Eq. (2.7) for specific geometry have also shown this quadratic dependence [16]. This quadratic scaling is evident in Fig. 4(a) where λ > 1 and 4(b) where λ < 1. In both cases, a range of voltages was applied on the vesicle and the deformation in terms of α is presented against time. For deformation from circular/spherical to oblate spheroids, α is greater than 1. For prolate spheroids, it is less than 1. The voltage range explored in our study is 7 to 20 volts which correspond to the nominal electric field strength of 46.667 kV/m to 133.33 kV/m. For cases with the weaker applied field, the vesicles show slow extension/compression and they reach an apparent steady state. However, for cases with stronger fields, the behavior switches to a rapid deformation. The quadratic scaling is more apparent in Fig. 4(c) where we calculated the time taken by the vesicle to reach an aspect ratio of α = 1.1 for λ > 1 or α = 0.9 for λ < 1. Vesicles with an applied voltage lower than 7 volts never get extended (or compressed) enough to reach this level. However, as the voltage is further increased, the time needed to reach the deformed shape decreases in a quadratic manner. Coupled with this observation, we studied the level of deformation after 125 μs under the whole range of applied field for λ = 50 and 1/50. The choice of time cut-off is influenced by the tendency of loss of integrity of the vesicle membrane under the applied nominal potential (20 volts). As shown in Fig. 4(d), the applied field is a major factor in determining the extent of electrodeformation.
3.2. Effect of Vesicle Size
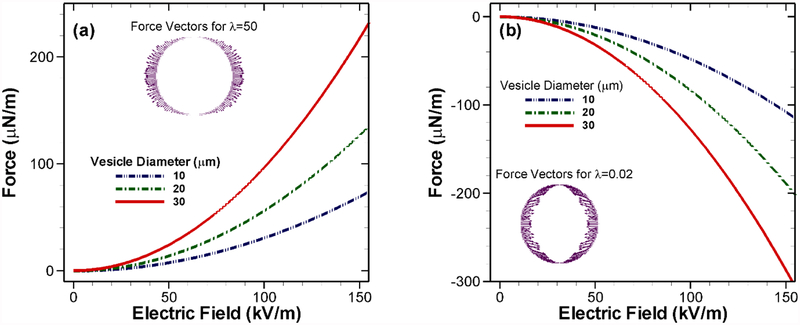
Theoretically, stress generated by the electric field, and hence the tensile or compressive forces acting on the boundary also shows dependence on the vesicle size. We varied the vesicle diameter from 10 to 30 μm and observed an almost linear increase in the initial force density with increasing size for a given applied voltage difference (Figs. 5(a) and 5(b)). It should be noted that we considered the tensile force generated when λ = 50 in Fig 5(a) to be positive. Consequently, for the case with λ = 1/50 shown in Fig. 5(b) the increasing compressive forces are more negative. The force vectors on the vesicles (shown as insets in Fig. 5(a) and 5(b)) also indicate this change in direction. However, the effect of vesicle size is not conclusive on the long-term deformation behavior of the vesicle as shown in Fig. 3(c) as well as in the experiments [18].
Fig. 5.
Calculated force density on vesicles with different initial diameters. (a) Increase in force with increasing applied potential for λ = 50 and (b) λ = 1/50.
The contrast in electric field distribution between cases with λ > 1 and λ < 1 are presented in Fig. 6. In both cases, we start with a perfect circular shape (α = 1). The vesicle deformations are shown in the electric field plots with field lines at α = 1.5 for λ = 30 and α = 1/1.5 for λ = 1/30. Also, in both cases, applied voltage at the left electrode is 10 volts while at the right electrode it is −10 volts. When the aqueous electrolyte media is subjected to a DC voltage gradient, ions in the fluid media start to migrate towards opposite electrodes. The ions inside the vesicles also gets localized following the same principle. Thus, there is a build-up of opposite ions inside the vesicle (negative ions on the left side since the left electrode is the anode, and vice versa). However, since the fluid media outside is less conductive (Fig. 6(a)), the electric current cannot drive enough positive ions just outside the membrane to counter the build-up inside. As a result, a net negative charge accumulates around the left half of the vesicle with an equal amount of positive charge accumulating around the right half at the interface [32]. One critical point here is the time scale of this charge relaxation effect, which can be estimated from the electrical properties of the electrolyte in question. For the dilute aqueous media, this timescale is expressed as the ratio of the Debye screening length squared to the diffusivity of the electrolyte . For aqueous solutions, the Debye screening length ℓDebye is between 1 to 100 nm while the diffusivity (D) is on the order of 10−9 m2/s [33]. This leads to rather fast bulk charge relaxation time which is on the order of nanoseconds. Consequently, the local changes in electric field is instantaneous which further justifies the use of the steady-state governing equation (Eqs. (2.1)) for electric potential.
Fig. 6.
Electric field distributions with field lines showing electrodeformation from spherical to prolate/oblate spheroids with an applied potential difference of 20 volts. (a-b) Deformation from circular (α = 1) to an oblate ellipse (α = 1.5) for λ = 30. (c-d) Deformation from circular to a prolate ellipse (α = 1/1.5) for λ = 1/30.
Our numerical results indicate that the vesicle with an overall 30 times higher conductivity compared to the surrounding media behaves like a conductor with electric field lines entering and exiting the vesicle boundary as perpendicular lines (Figs. 6(a–b)). As the ions at the inner side of the membrane dominate over the fluid medium ions on the interface, they experience a tensile pull towards the electrodes at the boundaries as shown in the force vector in Fig 5(a). The exact opposite scenario (Figs. 6(c–d)), with the fluid medium conductivity being 30 times higher than the vesicle results in the vesicle behaving like an insulator. In this case, there is an accumulation of net positive charge on the left half of the vesicle while an equal amount of net negative charge accumulates at the right half. For this reason, electric field lines are expelled from the surface. The corresponding electric field induced force is shown in Fig. 5(b). In this case, the force distribution is compressive in nature i.e. vesicle experiences inward forces. In both cases, owing to the nature of the induced forces, the vesicle deforms continuously becoming an oblate ellipsoid for λ > 1 and a prolate one for λ < 1.
3.3. Electric Field Induced Flow Field
In most works with bio-vesicles, the surrounding flow patterns were ignored. However, for deformable vesicles, the fluid-solid interaction can produce interesting flow patterns. Two of these secondary flow patterns are shown as streamlines in Fig. 7(a) and 7(b), which are produced early in the transient deformation stage. Here, four vortices are created around the vesicle following bilateral symmetry with the major and minor axes of the spheroid as axes of symmetry. However, depending on the conductivity ratio, the vortices switch direction. When the vesicle is getting extended in the horizontal direction, the surrounding fluid layer follows it and generates vortices that follow the general direction of the force on the boundary to satisfy fluid continuity. The opposite is seen (Fig. 7(b)) in case of compressive deformation where all four vortices switch direction. It should be noted that these flow patterns are resulting from a short but continuous deformation resulting from the DC electric field. When the electric field is removed, the vesicle would try to return to its resting undeformed state. That will reverse the flow directions in both cases. Similarly, in case of an oscillatory pulsed DC field application, this reversal of local vortices can be used for micro-scale mixing applications. The velocity field, in that case, is very similar to that of immersed bubbles in streaming motion. In future, we plan to see the fluid behavior for multiple vesicles with same or different conductivities.
3.4. Effects of Vesicle Shape
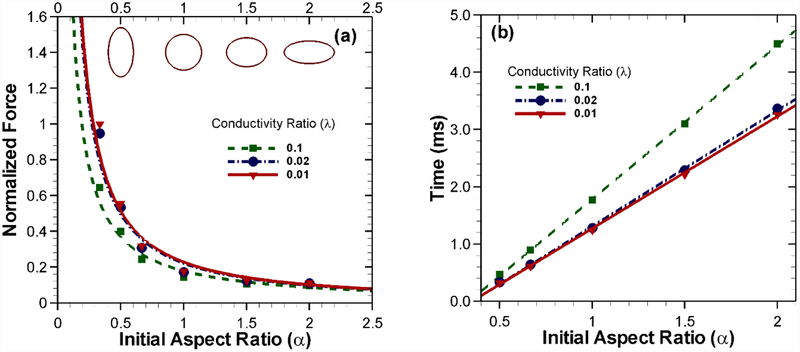
All our simulations thus far began with an initially circular/spherical vesicle. In general, the artificial vesicles or cells in experimental conditions have a wide range of initial aspect ratios. Here we compare the differences in the force dynamics for vesicles with several different initial aspect ratios. For this purpose, seven different initial aspect ratios were chosen (α = 1/3,1/2,1/1.5,1.0,1.5,2.0,3.0) with λ = 1/10,λ = 1/50 and λ = 1/100 while a nominal applied field of 133.33 kV/m is used (Fig. 8(a)). Since the vesicle is in equilibrium due to balancing forces on the left and right half, here we present the integration of force density on the left half with all the results normalized by the maximum force (778 μN/m) at α = 1/3 for λ = 1/100. As the aspect ratio decreases from 1, the effective area for the horizontal compressive force increases. This results in the increased compressive force. However, with increasing aspect ratio, this trend tends to become flattened. A logical reasoning could be drawn based on the magnitude of the available area for each case by comparing it with the perfectly circular case. With lower aspect ratios (α < 1), the compressive stress has a much higher normal surface to act upon. While in higher aspect ratios (α > 1) the available surface area normal to the horizontal compressive force drops off relatively slowly, which explains the force approaching an asymptote. The time required to deform such a vesicle to an aspect ratio of α = 1/3 consequently is smallest for the case with an initial aspect ratio α = 0.5 and largest for an initial aspect ratio α = 2.0, as shown in Fig. 8(b). The time required is influenced by both the magnitude of the force and initial aspect ratio which controls the available normal surface for the force to act upon.
Fig. 8.
(a) Effect of initial shape on the force experienced by the vesicle for different conductivity ratios with an applied potential difference of 20 volts. (b) Time required to deform to an aspect ratio of α = 1/3 for each case with the same applied voltage difference.
4. Conclusions
In the studies of bio-vesicles like cell, virus and artificial lipid vesicles, electric field application has become one of the most prominent manipulation techniques. Still, much remains unknown about the transient membrane deformation process due to electrostatic interactions arising from the differences in electrical properties of the media surrounding the membrane as well as membrane properties and cell configurations. Electrodeformation of flexible vesicles under a wide range of applied electric field has been studied in the present work. The electric field distribution was calculated using immersed interface method, while the fluid-membrane interactions were obtained by solving the flow-field using an immersed boundary approach. The membrane deformation dynamics under different electric fields and conductivity ratios were verified against experimental data. The numerical results show a number of transient deformation phenomena that are difficult to observe experimentally. Our study explores the transient deformation mechanisms which can help in the design of future experiments and assist in novel applications of electric field induced vesicle deformation.
Dependence on the electric field strength was clearly observed in our results. Numerical results demonstrated the scaling behavior of the applied force arising from the electric field which were substantiated with analytical results. Our study also pointed out the relative levels of force experienced by vesicles of different initial shapes. We plan to explore the implications of the initial membrane shape on a number of parameters such as stiffness and bending rigidity in a future work.
Interesting fluid behavior was observed around the deforming vesicle that also showed variation based on the change in conductivity ratio. Vortices created by these deforming vesicles can be used for mixing in microchannels. Also, an extension of the current model to a three-dimensional description of the vesicle will help to provide further insight into the discrepancies between current experimental and numerical studies.
6. Acknowledgment
This work was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R01GM122081. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Appendix
A. Numerical Model and Methods
The coupled hydrodynamic and electric system is solved using a hybrid immersed boundary and immersed interface technique. Both these methods employ a non-body-fitted Cartesian gridding approach in discretizing the physical domain (Fig. 1). This is computationally advantageous due to almost no cost for grid generation. However, for the grid points near the membrane interface, which are much smaller in number compared to regular grid points, special treatment is required. In the immersed boundary method, the localized variables (e.g. force and velocity) on the membrane are interpolated to nearby grid point using an approximate delta function. The immersed interface approach avoids the smearing by altering the discretized equations near the interface. Due to the inherent numerical accuracy and stability, immersed interface method is very well suited for the elliptic electromagnetic interface problem [34]. The immersed boundary method, on the contrary, is appropriate for the fluid-structure interaction problem encountered in the electrodeformation of the immersed biological membranes [35,36]. Previously, we have combined the immersed interface and the immersed boundary methods to study particle-particle dielectrophoretic and electrophoretic interactions [20,24]. Recently, similar numerical approach was taken by Hu et al. to further develop the algorithm for electrodeformation problems [21,22]. Although the underlying numerical methods are same for both their and our works, there are difference in the implementations of both immersed interface and immersed boundary methods. For example, treatment of jump conditions, the membrane dynamics, localization and spreading of membrane forces are approached differently in each study. The specific details of the numerical method pertinent to the electrodeformation problem are presented below.
The electrostatic problem (Eqs. (2.1)–(2.5)) at a given instant is independent of the fluid description and hence, is solved directly by the immersed interface technique by first transforming it to an equivalent elliptic problem with piecewise constant conductivity and modified interface conditions. Here the governing equations and the jump conditions are modified as,
| (A1) |
| (A2) |
| (A3) |
| (A4) |
where ϕr (x, y) is a solution set of the modified problem taken as a function of r(s). The instantaneous solution of the equation for capacitive charging (Eq. 2.6) at each immersed interface point yields the transmembrane potential which is used to calculate the voltage jump across the membrane in (Eq. A3). Now, if we consider ϕ*(x, y) as a solution to the original problem (Eqs. (2.1)–(2.5)) and define , then it can be shown that ϕ*(x, y) also satisfies the modified problem and jump conditions, thus r(s) ≡ r* [34]. Which implies ϕr* (x, y) and
| (A5) |
Thus, the original problem is solved by finding r(s) through r* and ϕr*(x, y) from the solution of the modified problem. The assumption of piecewise constant conductivity makes the modified description (Eq. A1–A4) a Poisson problem which can be solved by fast solvers. With h being the uniform mesh size in the Cartesian grid, and nx and ny as the number of grid points in the coordinate directions, the modified governing equation can be written in the discrete form for any arbitrary grid point inside the domain (p, q) as,
| (A6) |
Here the correction term Cpq on the right side is zero everywhere except at the grid points, where the interface cuts through the five-point stencil (points 2, 3 and 5 in Fig. 1(b)). In a compact matrix-vector form, Eq. (A6) can be written as
| (A7) |
where A and B are coefficient matrices for the solution Φ, R is the discrete form of the modified interface jump condition r* and Θ is a vector. The correction term Cpq is also mapped into BR in Eq. (A7). Since ϕ*(x,y) satisfies the discrete form of Eq. (2.5), and the solutions inside and outside the interface depend linearly on Φ and R [34], we get the final equation as,
| (A8) |
where K and E are coefficient matrices and Ξ is a vector. The linear systems of equations are combined by eliminating Φ using G = (E – KA−1B) and H = (Ξ – KA−l·Θ) which gives,
| (A9) |
Equation (A9) is solved for R using a GMRES routine with a weighted least squared interpolation scheme [37]. Finally, with the knowledge of R, the discretized system of equations is solved iteratively through successive calls to the PARDISO solver [38]. Further details on the formulation of the hybrid method, convergence, grid refinement, and accuracy can be found in [20,24].
Once the electric potential from the electrostatic equations are found, we can calculate the body force term () in Eq. (2.8), which is then supplied to the fluid flow equations. In order to solve Eqs. (2.8) and (2.9) using the immersed boundary approach, we assume the elastic immersed membrane to be neutrally buoyant. Based on this assumption, the membrane boundary Γ can be expressed as singular force density contributions in the body force term in Eq. (2.8) following the immersed boundary approach as [39],
| (A10) |
Here, is the Eulerian force density acting on the fluid, while is the Lagrangian boundary force density with respect to ds. In Eq. (A10), is a two-dimensional Dirac delta function which ensures the mathematical representation of the physical membrane as body force terms in the two-dimensional domain as required at a given time [20]. Although is singular on the immersed boundary, we note that in the numerical method we use a regularized Delta function such that the force density at the immersed boundary is well defined. This integral over the delta function provides the resulting force exerted by the section of the immersed boundary on the fluid in that control volume [40]. On the right side of Eq. (A10), the term represents the massless immersed boundary as a simple closed curve of length L with and 0 ≤ s ≤ L. The parameter s tracks the material points of the boundary which is carried along with the fluid by the local fluid velocity as
| (A11) |
The Eulerian forces due to the applied electric field () from Eq. (2.7) are interpolated on the Lagrangian immersed boundary points and added to the elastic force density () to compute the total body force on the membrane. Further details on the specific delta function and the numerical integration have been discussed in detail in [24].
The Lagrangian force density can be generated from the combination of elastic stretching, bending or stiff tethering of the immersed boundary. For our previous works on dielectrophoresis with rigid particles [20,24], we considered each immersed boundary point on the interface to be connected to all other points on that immersed boundary through elastic links which obey a generalized Hooke’s law following,
| (A12) |
Aforementioned equation describes the boundary force density at time t in terms of the boundary configuration at that time. The function satisfies the generalized Hooke’s law [24]. For example, considering two arbitrary immersed boundary points i and j, the force due to the elastic link between the two points can be obtained by,
| (A13) |
where κ is the stiffness parameter of the link and is the initial resting length of the link. As the membrane deforms due to the applied field, it’s initial resting position is altered resulting in the generation of elastic forces. Consequently, these body forces alter the flow field surrounding the membrane. Therefore, after solving the electric field, discretized forms of Eqs. (2.8–2.9) are solved using Fast-Fourier-Transform (FFT) [41]. The discrete forms are given as,
| (A14) |
| (A15) |
where D+, D−, and D0 are the forward, backward, and central spatial difference operators, and are the upwind and gradient difference operators respectively as defined in [40]. From the flow-field solution, local velocities of the immersed boundary points are updated using the discrete form of Eq. (A10). It should be mentioned that, owing to the very low Reynolds number in the microfluidic channel, solving only the Stokes equations might have been enough. However, numerical implementation of the solution procedure of time-dependent Stokes flow using immersed boundary method with periodic boundaries does not offer significant computational advantage over solving the full Navier-Stokes equations. Moreover, we are using fast-Fourier transform based Navier-Stokes solvers which have been shown to perform very well at low Reynolds numbers [42].
Contributor Information
Adnan Morshed, School of Mechanical and Materials Engineering Washington State University, Pullman, WA 99164.
Prashanta Dutta, School of Mechanical and Materials Engineering Washington State University, Pullman, WA 99164.
Mohammad Robiul Hossan, Department of Engineering and Physics University of Central Oklahoma, Edmond, OK 73034.
Robert Dillon, Department of Mathematics and Statistics Washington State University, Pullman, WA 99164.
References
- [1].Arakelyan A, Fitzgerald W, Zicari S, Vanpouille C, and Margolis L, Scientific Reports 7 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Molinaro R et al. , Nature Materials 15, 1037 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Yang B, Dong X, Lei Q, Zhuo RX, Feng J, and Zhang XZ, Acs Applied Materials & Interfaces 7, 22084 (2015). [DOI] [PubMed] [Google Scholar]
- [4].Rezanoor MW and Dutta P, Biomicrofluidics 10, 024101 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Dimova R et al. , Soft Matter 5, 3201 (2009). [Google Scholar]
- [6].Dimova R and Riske KA, Handbook of Electroporation, 235 (2017). [Google Scholar]
- [7].Li H, Ye T, and Lam KY, Journal of Applied Physics 110, 104701 (2011). [Google Scholar]
- [8].Kakorin S, Liese T, and Neumann E, Journal of Physical Chemistry B 107, 10243 (2003). [Google Scholar]
- [9].Jubery TZ, Srivastava SK, and Dutta P, Electrophoresis 35, 691 (2014). [DOI] [PubMed] [Google Scholar]
- [10].Teng Y, Pang MS, Huang JY, and Xiong CY, Sensors and Actuators B-Chemical 240, 158 (2017). [Google Scholar]
- [11].Du E, Dao M, and Suresh S, Extreme Mechanics Letters 1, 35 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Riske KA, Bezlyepkina N, Lipowsky R, and Dimova R, Biophysical Reviews and Letters 1, 387 (2006). [Google Scholar]
- [13].Vlahovska PM, Gracia RS, Aranda-Espinoza S, and Dimova R, Biophysical Journal 96, 4789 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Dimova R, Aranda S, Bezlyepkina N, Nikolov V, Riske KA, and Lipowsky R, Journal of Physics-Condensed Matter 18, S1151 (2006). [DOI] [PubMed] [Google Scholar]
- [15].Winterhalter M and Helfrich W, Journal of Colloid and Interface Science 122, 583 (1988). [Google Scholar]
- [16].Hyuga H, Kinosita K, and Wakabayashi N, Japanese Journal of Applied Physics Part 1-Regular Papers Short Notes & Review Papers 30, 1141 (1991). [Google Scholar]
- [17].Yamamoto T, Aranda-Espinoza S, Dimova R, and Lipowsky R, Langmuir 26, 12390 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Sadik MM, Li JB, Shan JW, Shreiber DI, and Lin H, Physical Review E 83, 066316 (2011). [DOI] [PubMed] [Google Scholar]
- [19].MacQueen LA, Buschmann MD, and Wertheimer MR, Journal of Micromechanics and Microengineering 20, 065007 (2010). [Google Scholar]
- [20].Hossan MR, Dillon R, and Dutta P, Journal of Computational Physics 270, 640 (2014). [Google Scholar]
- [21].Hu WF, Lai MC, and Young YN, Journal of Computational Physics 282, 47 (2015). [Google Scholar]
- [22].Hu WF, Lai MC, Seol Y, and Young YN, Journal of Computational Physics 317, 66 (2016). [Google Scholar]
- [23].Ai Y and Qian SZ, Journal of Colloid and Interface Science 346, 448 (2010). [DOI] [PubMed] [Google Scholar]
- [24].Hossan MR, Dillon R, Roy AK, and Dutta P, Journal of Colloid and Interface Science 394, 619 (2013). [DOI] [PubMed] [Google Scholar]
- [25].Saville DA, Annual Review of Fluid Mechanics 29, 27 (1997). [Google Scholar]
- [26].Tian P, Chemical Society Reviews 39, 2071 (2010). [DOI] [PubMed] [Google Scholar]
- [27].Pavlin M and Miklavcic D, Biophysical Journal 85, 719 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Seiwert J, Miksis MJ, and Vlahovska PM, Journal of Fluid Mechanics 706, 58 (2012). [Google Scholar]
- [29].Dutta P, Beskok A, and Warburton TC, Numerical Heat Transfer Part A-Applications 41, 131 (2002). [Google Scholar]
- [30].Li Z and Ito K, The Immersed Interface Method: Numerical Solutions of PDEs Involving Interfaces and Irregular Domains (Society for Industrial and Applied Mathematics, 2006). [Google Scholar]
- [31].Pauly v. H. and Schwan H, Zeitschrift für Naturforschung B 14, 125 (1959). [PubMed] [Google Scholar]
- [32].Hossan Mohammad R, Dutta D, Islam N, and Dutta P, Electrophoresis 39, 702 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Bazant MZ, Thornton K, and Ajdari A, Physical Review E 70, 021506 (2004). [DOI] [PubMed] [Google Scholar]
- [34].Li ZL, Siam Journal on Numerical Analysis 35, 230 (1998). [Google Scholar]
- [35].Peskin CS, Journal of Computational Physics 25, 220 (1977). [Google Scholar]
- [36].Bagchi P, Biophysical Journal 92, 1858 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Saad Y and Schultz MH, Siam Journal on Scientific and Statistical Computing 7, 856 (1986). [Google Scholar]
- [38].Schenk O and Gartner K, Electronic Transactions on Numerical Analysis 23, 158 (2006). [Google Scholar]
- [39].Peskin CS, Acta Numerica 11, 479 (2002). [Google Scholar]
- [40].Lai MC and Peskin CS, Journal of Computational Physics 160, 705 (2000). [Google Scholar]
- [41].Hsu CY and Dillon R, Bulletin of Mathematical Biology 71, 1228 (2009). [DOI] [PubMed] [Google Scholar]
- [42].Peskin CS and McQueen DM, in Case Studies in Mathematical Modeling — Ecology, Physiology, and Cell Biology, edited by Othmer HG et al. (Prentice-Hall, 1997), pp. 309. [Google Scholar]