SCARLET: Single-cell tumor phylogeny inference with copy-number constrained mutation losses

Abstract

A small number of somatic mutations drive the development of cancer, but all somatic mutations are markers of the evolutionary history of a tumor. Prominent methods to construct phylogenies from single-cell sequencing data use single-nucleotide variants (SNVs) as markers but fail to adequately account for copy-number aberrations (CNAs), which can overlap SNVs and result in SNV losses. Here, we introduce SCARLET, an algorithm that infers tumor phylogenies from single-cell DNA sequencing data while accounting for both CNA-driven loss of SNVs and sequencing errors. SCARLET outperforms existing methods on simulated data, with more accurate inference of the order in which mutations were acquired and the mutations present in individual cells. Using a single-cell dataset from a patient with colorectal cancer, SCARLET constructs a tumor phylogeny that is consistent with the observed CNAs and suggests an alternate origin for the patient’s metastases. SCARLET is available at: github.com/raphael-group/scarlet

Graphical Abstract

eTOC

Both single-nucleotide variants (SNVs) and copy-number aberrations (CNAs) accumulate during cancer evolution, and these mutations may overlap on the genome. We introduce SCARLET (Single-cell Algorithm for Reconstructing Loss-supported Evolution of Tumors), an algorithm to construct phylogenies from single-cell DNA sequencing data using both SNVs and CNAs.

Introduction

Cancer arises from an evolutionary process during which somatic mutations accumulate in a population of cells. Different cells within a tumor acquire distinct complements of somatic mutations, resulting in a heterogeneous tumor. Quantifying this intra-tumor heterogeneity and reconstructing the evolutionary history of a tumor is crucial for diagnosis and treatment of cancer (Burrell et al. 2013; Tabassum and Polyak 2015). The evolution of a tumor is typically described by a phylogenetic tree, or phylogeny, whose leaves represent the cells observed at the present time and whose internal nodes represent ancestral cells. Tumor phylogenies are challenging to reconstruct using DNA sequencing data from bulk tumor samples, since this data contains mixtures of mutations from thousands–millions of heterogeneous cells in the sample (Jiao et al. 2014; El-Kebir et al. 2015; Malikic et al. 2015; Popic et al. 2015; Deshwar et al. 2015; El-Kebir et al. 2016; Jiang et al. 2016; Alves, Prieto, and Posada 2017; Satas and Raphael 2017; Pradhan and El-Kebir 2018; Zaccaria et al. 2018; Miura et al. 2019; Myers, Satas, and Raphael 2019). Recently, single-cell DNA sequencing (scDNA-seq) of tumors has become more common, and new technologies such as those from 10X Genomics (10X Genomics, n.d.), Mission Bio (Mission Bio, n.d.), and others (Gawad, Koh, and Quake 2016; Zahn et al. 2017; Navin 2015) are improving the efficiency and lowering the costs of isolating, labeling, and sequencing individual cells. While scDNA-seq overcomes the difficulties of phylogeny reconstruction from bulk samples, it introduces a new challenge of higher rates of missing data and errors due to DNA amplification errors, undersampling, and sequencing errors (Gawad, Koh, and Quake 2016).

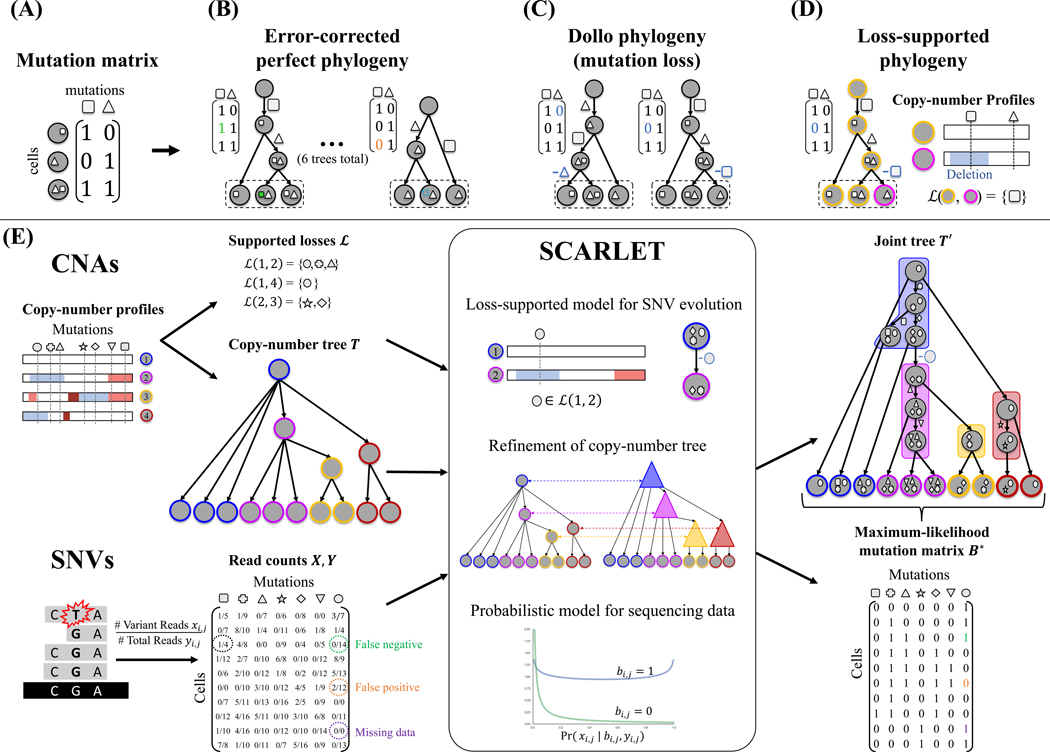
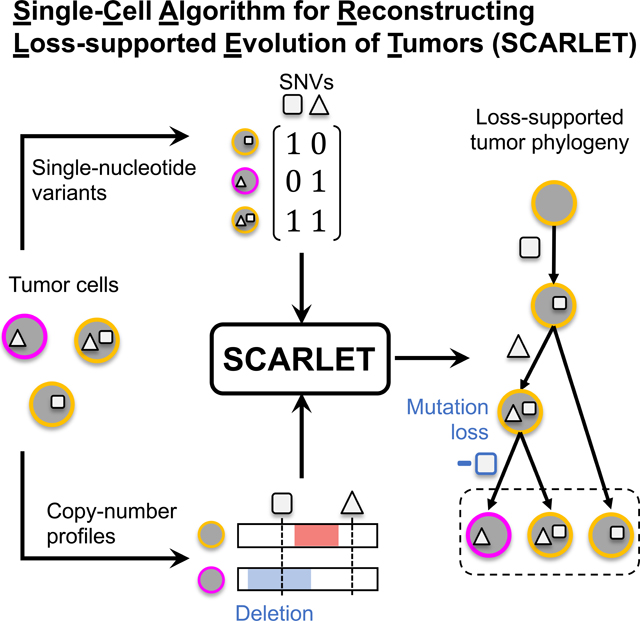
Early work in phylogeny inference from scDNA-seq data uses single-nucleotide variants (SNVs) as phylogenetic markers. A particular challenge for SNV-based analysis is high rates (up to 30% for high-depth scDNA-seq (Gawad, Koh, and Quake 2016)) of allele dropout errors, where only one of two alleles is observed at a heterozygous site. Methods address this challenge by using an evolutionary model to infer a phylogeny while simultaneously imputing missing data and correcting errors in the observed SNVs. Algorithms such as SCITE (Jahn, Kuipers, and Beerenwinkel 2016), OncoNEM (Ross and Markowetz 2016), SciΦ (Singer et al. 2018), and B-SCITE (Malikic, Jahn, et al. 2019) use the simplest phylogenetic model for SNVs, the infinite sites model. In this model, a locus in a cell has one of two states: an SNV (or mutation) iseither present at the locus (state 1) or absent (state 0). Transitions between states are constrained in the phylogeny such that each mutation is gained (0 → 1) at most once during evolution, and never subsequently lost (1 → 0). A phylogeny that respects the infinite sites model is known as a perfect phylogeny and the state of mutations in the leaves of the phylogeny is summarized by a mutation matrix whose binary entries indicate the presence (state 1) or absence (state 0) of every mutation in each observed cell (Fig. 1(A)). On error-free data, the perfect phylogeny is unique (Gusfield 1991). However, on typical scDNA-seq data, errors in the mutation matrix must be corrected to yield a perfect phylogeny model. Because many such corrections are possible, multiple phylogenies are typically equally consistent with the data (Fig. 1(B)). An additional challenge in inferring phylogenies from cancer sequencing data is that somatic mutations in tumors occur across all genomic scales from SNVs to copy-number aberrations (CNAs), which amplify or delete larger genomic regions. CNAs may overlap SNVs and affect the state of SNVs in cells; e.g., a deletion that overlaps an SNV may result in a mutation loss (1 → 0). The infinite sites model does not allow mutation losses and therefore may yield incorrect phylogenies when applied to SNVs in regions containing CNAs. One solution is to exclude regions containing CNAs and build phylogenies from SNVs in diploid, or copy-neutral, regions. However, ≈90% of solid tumors are highly aneuploid (Taylor et al. 2018), containing extensive CNAs, and ≈30% of solid tumors have whole-genome duplications (Bielski et al. 2018). Identifying collections of SNVs with no possibility of overlapping CNAs during evolution of such tumors may be challenging. Recently, several methods (El-Kebir 2018; Ciccolella et al. 2018; McPherson et al. 2016; Zafar et al. 2017; Zafar et al. 2019; Malikic, Mehrabadi, et al. 2019) have been introduced for single-cell phylogeny inference that allow loss of mutations. SPhyr (El-Kebir 2018), SASC (Ciccolella et al. 2018), and PyDollo (McPherson et al. 2016) use the Dollo model (Dollo 1893), which relaxes the infinite sites model. In the Dollo model, a mutation may be gained (0 → 1) at most once, but may be lost (1 → 0) multiple times. SiFit (Zafar et al. 2017), SiCloneFit (Zafar et al. 2019), and PhiSCS (Malikic, Mehrabadi, et al. 2019) use the finite sites model, a further relaxation that allows mutation to be gained more than once. A challenge in using these less stringent evolutionary models is that they increase the ambiguity in phylogenetic reconstruction (Fig. 1(C)). Even in simple cases with no error, multiple phylogenies are consistent with the data and the number of phylogenies further increases when there are errors and uncertainty in the mutation matrix. Both the errors in scDNA-seq data and the mutation losses in the phylogeny conspire to yield considerable challenges and ambiguity in the single-cell phylogeny inference problem. This ambiguity is further amplified because both sequencing errors and losses result in the same signal in the observed data: an observed ‘0’ in the mutation matrix instead of a ‘1’. Thus, it is particularly difficult to distinguish between errors in the data and potential mutation losses.

Figure 1: Loss-supported phylogeny model, and SCARLET algorithm for the Maximum Likelihood Loss-Supported Refinement Problem.

(A) A mutation matrix with two mutations in three cells does not admit a perfect phylogeny. This may be due to either errors or mutation losses. (B) Under the infinite sites model, existing methods correct errors in the observed matrix to yield a perfect phylogeny. (C) Under the Dollo model, existing methods identify mutation losses to explain violations of the infinite sites model. Both the infinite sites and Dollo models yield multiple equally-plausible phylogenies. (D) The loss-supported model overcomes this ambiguity by using copy-number data to constrain mutation losses. (E) SCARLET algorithm for the Maximum Likelihood Loss-Supported Refinement problem. SCARLET integrates single-nucleotide variants (SNVs) and copy-number aberrations (CNAs) for tumor phylogeny inference. For CNAs, observed copy-number profiles indicate amplified (red) or deleted (blue) genomic regions along the entire genome and are used to obtain two inputs for SCARLET. First, supported loss sets ℒ(c, c′) for pairs of copy-number profiles (empty sets are not shown) indicate mutations that are affected by deletions. Second, a copy-number tree T which describes the ancestral relationships between observed cells (leaves) as determined by copy-number profiles. For SNVs, variant X and total Y read counts are provided to SCARLET for every cell and every mutation. SCARLET computes a joint tree T′ on the observed cells and a maximum-likelihood mutation matrix B* by constraining mutation losses to the supported loss sets ℒ, computing a refinement T′ of T, and selecting the maximum-likelihood B* using a probabilistic model for the presence (b_i,j = 1) or absence (b_i,j = 0) of each SNV in each cell.

A major limitation in using the Dollo or finite sites models to allow mutation losses is that neither of these models consider evidence from CNAs that support or refute a mutation loss at a locus. While more general multi-state models of tumor evolution have been used to infer phylogenies from bulk tumor sequencing data (Deshwar et al. 2015; El-Kebir et al. 2016; Jiang et al. 2016), these approaches neither model the errors in scDNA-seq data nor scale to hundreds–thousands of observed cells. Since mutation losses are the major complication in SNV evolution and responsible for most of the violations of the infinite sites model in scDNA-seq data (Kuipers et al. 2017; McPherson et al. 2016), the full generality of a multi-state model may not be necessary to obtain accurate phylogenies from scDNA-seq data. Rather, we describe an approach that constrains mutation losses by using copy-number data from the same cells.

We introduce SCARLET (Single-Cell Algorithm for Reconstructing Loss-Supported Evolution of Tumors), an algorithm that infers phylogenies from scDNA-seq data by integrating SNVs and copy-number data. SCARLET is based on the loss-supported phylogeny model that constrains mutation losses to loci where the copy-number data has evidence of a deletion (Fig. 1(D)). The loss-supported phylogeny generalizes the infinite sites and Dollo models. SCARLET also relies on a probabilistic model of the read counts for each SNV to address errors and missing data that are common in scDNA-seq. On simulated data, we show that SCARLET infers more accurate phylogenies compared to existing methods. We then use SCARLET to analyze scDNA-seq data from a metastatic colorectal cancer patient from (Leung et al. 2017). We find that the published phylogeny – constructed from SNVs under the infinite sites model – has the implausible conclusion that genome-wide copy-number profiles evolved twice independently during the evolution of this tumor. In contrast, SCARLET infers a loss-supported phylogeny that has three mutation losses, with each loss supported by a copy-number change at the locus. Moreover, the SCARLET phylogeny supports the hypothesis of a single migration between the colon primary tumor and liver metastasis (monoclonal seeding). In contrast, previous published phylogenies (Leung et al. 2017; Zafar et al. 2019) reported a more complex origin of the metastasis with multiple migrations (polyclonal seeding). By integrating information from both SNVs and CNAs, SCARLET obtains more accurate reconstructions of tumor evolution at single-cell resolution.

Results

SCARLET algorithm for Loss-supported Phylogeny Model

We developed an algorithm, SCARLET (Single-Cell Algorithm for Reconstructing Loss-supported Evolution of Tumors) to infer phylogenetic trees from single-cell DNA sequencing (scDNA-seq) data by integrating data from both single-nucleotide variants (SNVs) and copy-number aberrations (CNAs). SCARLET has three important features (Fig. 1(E)): (1) the loss-supported phylogeny model, which constrains mutation losses to loci where there is a corresponding decrease in copy number; (2) an algorithm to compute a loss-supported phylogeny by refinement of a coarse phylogenetic tree derived from copy-number data alone; (3) maximum-likelihood inference of SNVs using a probabilistic model of observed read counts in scDNA-seq data. We describe each of these key features below.

The loss-supported model is a model of SNV evolution where mutation gains (0 → 1) occur at most once, but mutation losses (1 → 0) are constrained by sets ℒ of supported losses that are defined by CNAs in the same cells (Fig. 1(D)). Specifically, we assume that for each cell we measure both a mutation profile b of SNVs and a copy-number profile c. For each pair (c, c′) of copy-number profiles, we define the supported loss set ℒ(c, c′) as the set of SNVs at loci where there is a decrease in copy number (e.g., due to a deletion or loss-of-heterozygosity (LOH) event) between profiles c and c′. In the loss-supported phylogeny, a mutation loss at an SNV loci a is allowed between cells v and w only if a is in ℒ(c_v, c_w). The loss-supported model can thus be viewed as a generalization of other models for SNV evolution: the perfect phylogeny model is the special case where ℒ = ∅, while the Dollo model and finite sites model corresponds to ℒ being the complete set of all mutations. In contrast to these extremes, the loss-supported model allows for intermediate values of ℒ derived from copy-number data. The loss-supported model depends on the copy-number profiles of both the observed and ancestral cells. However, we do not directly measure the copy-number profiles of the ancestral cells. To overcome this limitation, SCARLET takes as input a copy-number tree T which is derived from the copy-number profiles of the observed cells using methods such as (Schwarz et al. 2014; Chowdhury et al. 2015; El-Kebir et al. 2017; Zaccaria et al. 2018) (Fig. 1(E)). SCARLET computes the supported loss sets ℒ from the copy-number profiles of the observed cells (leaves of T) and the copy-number profiles of the ancestral cells (internal vertices of T). Typically, scDNA-seq data of SNVs (e.g., from targeted sequencing) measures copy-number profiles with low resolution, and thus tumor cells share a limited number of distinct copy-number profiles. Consequently, the copy-number tree T has many multifurcations, or unresolved ancestral vertices with more than two children. SCARLET finds a joint tree T′ that is a loss-supported phylogeny and a refinement (Wang et al. 2014) of T by resolving multifurcations in T using the mutation profiles of the observed cells (Fig. 1(E)). Data from scDNA-seq typically has high error rates in identifying SNVs, and particularly high rates of false negatives and missing data due to amplification bias and allele dropout (Gawad, Koh, and Quake 2016). SCARLET models these errors using a beta-binominal distribution (Singer et al. 2018) of the observed read counts. As such, SCARLET computes the loss-supported refinement T′ that maximizes the likelihood of the observed sequencing data under this probabilistic model (Fig. 1(E)).

Simulated Data

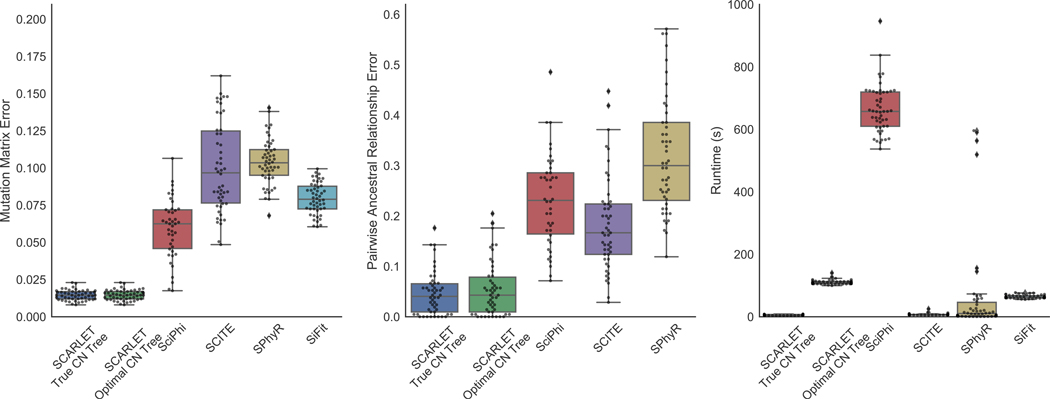
We compared SCARLET to four existing algorithms that build phylogenies from single-cell sequencing data, SCITE (Jahn, Kuipers, and Beerenwinkel 2016), Sci0 (Singer et al. 2018), SPhyR (El-Kebir 2018), and SiFit (Zafar et al. 2017), on simulated data. We simulated 50 trees, each with 20 mutations, 4 copy-number profiles, and 1–8 mutation losses per tree. From these trees, we simulated 100 observed cells with each cell having equal probability of being a child of any vertex in the simulated tree, and simulated sequencing data with an expected sequencing depth of 100× and allelic dropout rate of 0.15.Additional details of simulated data and parameters of each method are included in STAR Methods. We evaluated the phylogenies output by the methods by two measures that have been previously used in tumor evolution studies (Ciccolella et al. 2018; Myers, Satas, and Raphael 2019; Govek, Sikes, and Oesper 2018; Singer et al. 2018; El-Kebir 2018; Satas and Raphael 2017). First, the mutation matrix error $M(\mathbf{B},\widehat{\mathbf{B}})=\frac{1}{mn}{\sum }_{i=1}^m{\sum }_{j=1}^n|b_{i,j}-{\widehat{b}}_{i,j}|$ is the normalized Hamming distance between the inferred binary mutation matrix $\widehat{\mathbf{B}}$ and the true binary mutation matrix B and assesses the accuracy of the error-corrected mutation profiles for each observed cell. Second, the pairwise ancestral relationship error $E(T,\widehat{T})$ is the proportion of pairwise ancestral relationships between mutations in the inferred tree $\widehat{T}$ that differ from the ancestral relationships in the true tree T. Specifically, every pair a, a′ of mutations has one of four possible ancestral relationships in $\widehat{T}$ and in T: (1) a and a′ occur on the same branch; (2) a is ancestral to a′; (3) a′ is ancestral to a; (4) a and a′ are incomparable. Note that only mutation gains are considered in the calculation of this error, so that all methods are evaluated on the same set of mutations. We do not calculate the pairwise ancestral relationship error for SiFit because it uses a finite sites model which allows mutations to recur and consequently pairs of mutations may not have a unique relationship.

SCARLET outperforms all other methods on both mutation matrix error and ancestral relationship error (Fig. 2(A)–(B)). The high errors of SCITE and SciΦ were expected since these methods use an infinite sites model while the simulations include mutation losses which violates the model assumptions. However, the methods that do allow mutation losses, SPhyR (based on the k-Dollo model) and SiFit (based on the finite sites model), do not exhibit improvement over the other methods and perform worse than SCARLET. These results confirm that models that include unconstrained mutation losses have significant ambiguity as it is difficult to distinguish between true mutation losses and false positives/negatives in the data (Fig. 1). By using copy-number information to constrain mutation losses, SCARLET overcomes the ambiguity in phylogeny reconstruction and obtains lower error in the inferred mutation matrix and phylogeny.

Figure 2: SCARLET outperforms existing methods for phylogeny inference on simulated single-cell data.

(Left) Mutation matrix error, (Center) Pairwise ancestral relationship error, and (Right) Runtime for each method. SCARLET was run either knowing (‘True CN Tree’) or not knowing (‘Optimal CN Tree’) the true copy number tree.

We evaluated the effect of the input copy number tree on SCARLET’s accuracy by running SCARLET in two modes: when the true copy-number tree is either known (‘SCARLET True CN Tree’) or unknown (‘SCARLET Optimal CN Tree’). In this latter case, we enumerated all copy-number trees, ran SCARLET once for each copy-number tree, and output the solution with the highest likelihood. In both cases, we provided SCARLET with the true copy-number profiles of each cell and the true set ℒ of supported losses. SCARLET exhibited comparable performance when running with or without knowledge of the copy-number tree (Fig. 2(A)–(B)). Notably, in 46/50 simulated instances, the maximum likelihood solution obtained when running SCARLET with unknown copy-number tree was identical to the solution found when providing the true copy-number tree. Clearly, running SCARLET with all possible copy-number trees (16 copy-number trees in this simulation) increases the runtime (Fig. 2(C)), but the runtime remains reasonable when the number of copy-number profiles is small, which is the case for many real datasets (see below).

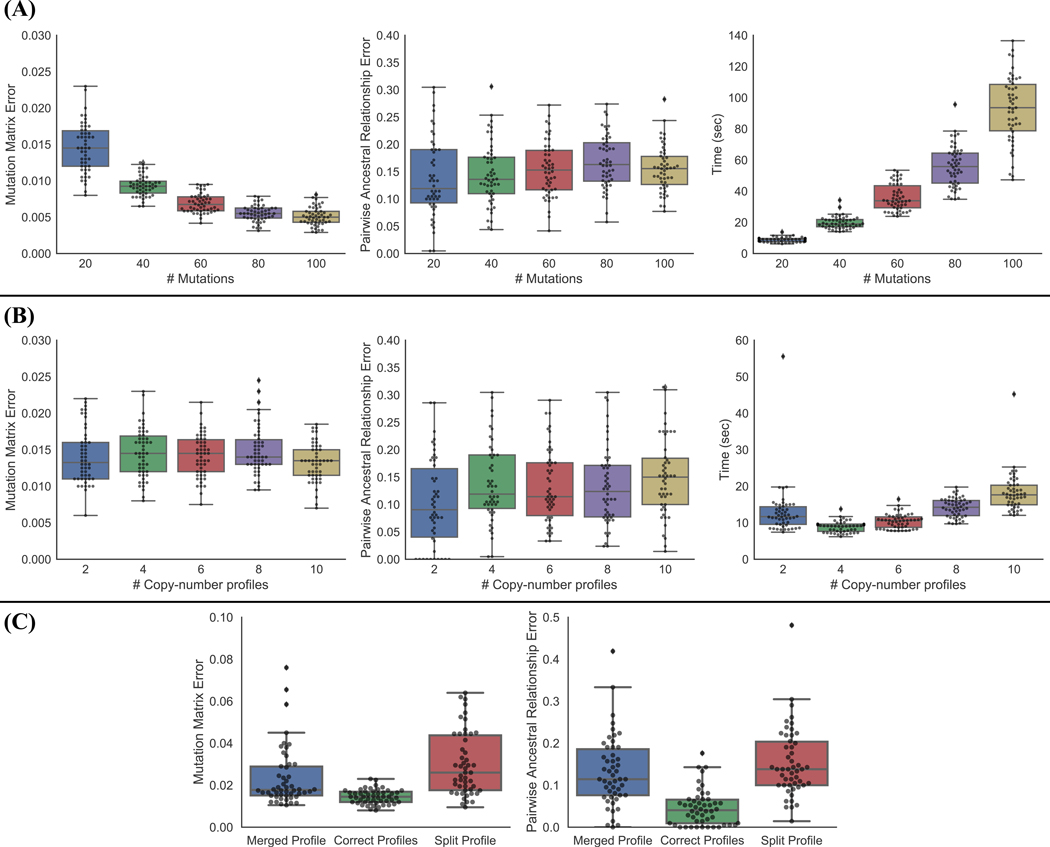
We further tested SCARLET to evaluate scalability to datasets for larger numbers of mutations (up to m = 100) and larger number of copy-number profiles (up to k = 10) (Fig. 3(A–B)). SCARLET has no loss of accuracy for larger datasets and in some cases has better accuracy on larger datasets. The runtime of SCARLET increases with m, and increases moderately with k, but remains reasonable (with all simulated instances taking < 3 minutes to run). In addition, we tested how errors in inferring the correct number of copy-number profiles affected the accuracy of SCARLET (Fig. 3(C)). In particular, we tested two types of errors. In ‘merge’ errors, two sets of cells with distinct copy-number profiles are merged together into one. In ‘split’ errors, one set of cells is split and inferred to have two distinct copy-number profiles. With either type of error, SCARLET outperforms other algorithms, with ‘split’ errors leading to a larger reduction in performance than ‘merge’ errors.

Figure 3: SCARLET scales to larger datasets and tolerates errors in copy-number profiles.

(A) SCARLET results on simulated data with varying number of mutations, n = 100 cells and k = 4 copy-number profiles. (Left) Mutation matrix error; (Center) pairwise ancestral relationship error; (Right) runtime. (B) SCARLET results on simulated data with varying number of copy-number profiles, n = 100 cells and m = 20 mutations. (Left) Mutation matrix error; (Center) pairwise ancestral relationship error; (Right) runtime. (C) SCARLET results on simulated data with incorrect number of copy-number profiles. We introduce errors in the number of copy-number profiles by either merging two distinct copy-number profiles together (“Merged Profile”), or splitting one copy-number profile into two (“Split Profile”) and compare performance against the correct number of copy-number profiles.

Single-cell phylogeny of metastatic colorectal cancer

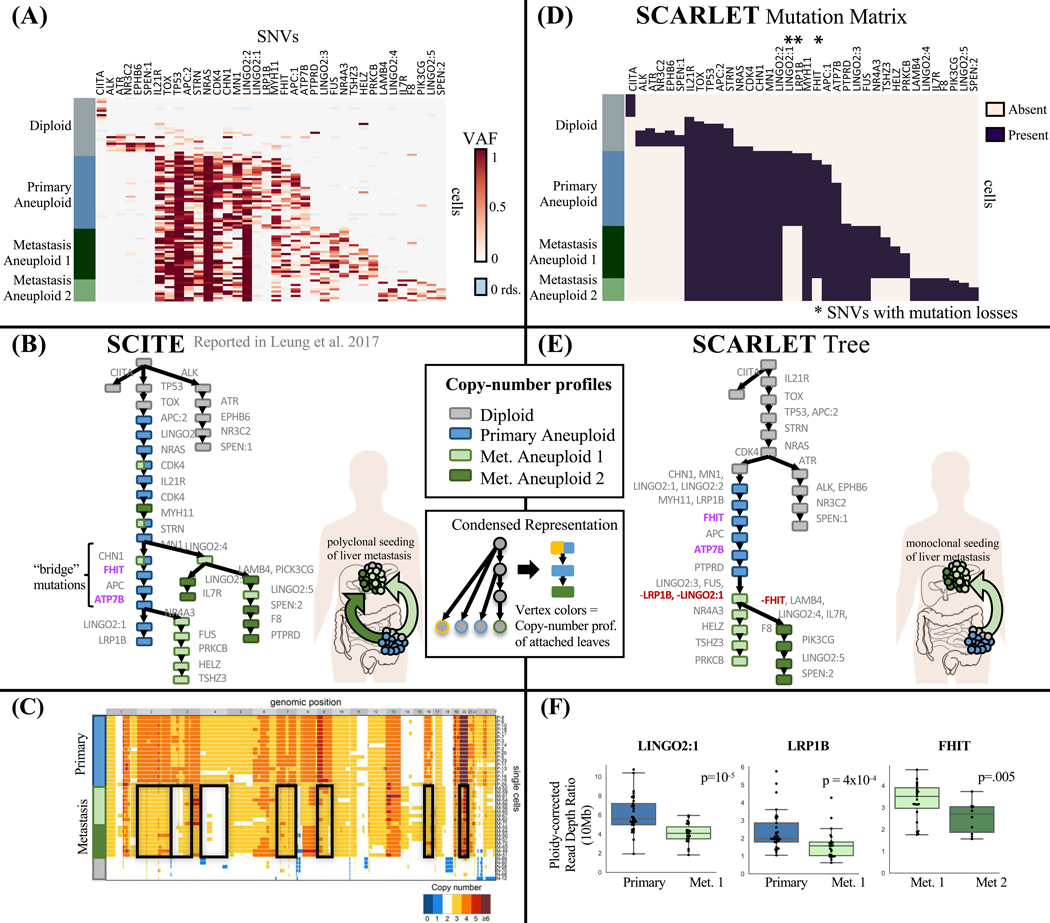
We used SCARLET to analyze single-cell DNA sequencing of a metastatic colorectal cancer patient CRC2 from (Leung et al. 2017). This data set included targeted sequencing of 1000 genes in 141 cells from a primary colon tumor and 45 cells from a matched liver metastasis (Fig. 3(A)). The authors identified 36 single-nucleotide variants (SNVs) and used SCITE (Jahn, Kuipers, and Beerenwinkel 2016) to derive a perfect phylogeny from these SNVs (Fig. 3(B)). This perfect phylogeny tree shows two distinct branches of metastatic cells, and (Leung et al. 2017) concluded that this was evidence of polyclonal seeding of the liver metastasis; i.e., two distinct cells (or groups of cells) with different complements of mutations migrated from the primary colon tumor to the liver metastasis. Examining the copy-number data, one finds a curious discrepancy between the SCITE tree and the single-cell copy-number profiles. Whole-genome sequencing of 42 single cells from the same patient reveals that all metastatic cells share losses of chromosomes 2, 3p, 4, 7, 9, 16, 22 relative to the cells in the primary tumor (Fig. 3(C)). According to the SCITE tree, all of these large copy-number aberrations (CNAs) would had to have occurred twice independently in the two distinct branches of metastatic cells. Although CNAs can exhibit homoplasy, this high rate of occurrence of the exact same events seems highly unlikely. Thus, we observe an inconsistency between the copy-number data and the SCITE tree constructed using only SNV data. Notably, this same dataset was recently analyzed by SiCloneFit (Zafar et al. 2019) using a finite sites model. The SiCloneFit tree also showed two branches of metastastic cells and concluded that there was polyclonal seeding of the metastases. Thus, the SiCloneFit phylogeny also has the same inconsistency between the SNV phylogeny and copy-number data.

We analyzed this dataset using SCARLET to see whether joint analysis of SNVs and CNAs data could help resolve the inconsistency between the tree derived from SNVs and the observed copy number profiles. We first derived four distinct copy-number profiles by hierarchical clustering of ploidy-corrected read-depth ratios from the targeted single-cell sequencing data. These copy-number profiles included an aneuploid profile for all primary cells (P), two different aneuploid profiles for metastatic cells (M1 and M2), and the profile of diploid cells (D); (Leung et al. 2017) similarly derived four copy-number profiles from whole-genome sequencing of a different set of 42 cells from the same patient. Since four copy-number profiles is a small number to infer a tree using a copy-number evolution model, we instead ran SCARLET in the ‘Optimal CN Tree’ setting selecting the copy-number tree that produced the highest likelihood. Specifically, we ran SCARLET on all nine possible rooted copy-number trees with the root having the diploid profile (D), and internal vertices labeled by one of the three aneuploid copy profiles (P, M1, M2). For each copy-number tree, we derived the set ℒ of supported losses as the mutation loci that exhibited significant decreases in read depth (i.e., number of aligned sequencing reads). Additional details are included in STAR Methods.

SCARLET constructed a tree (Fig. 3(D–E)) with a single clade containing all metastatic cells. This is consistent with the copy-number data, since the shared chromosomal losses could have have occurred once in a common ancestor of all metastatic cells. Moreover, this tree suggests that the liver metastasis was the product of monoclonal seeding; i.e., a single cell (or small group of cells) with the same somatic mutations migrated from the primary colon tumor to the metastasis and all metastatic cells descended from the founder cells present in this single migration. This result contradicts previous results (Leung et al. 2017; Zafar et al. 2019) of a more complicated polyclonal seeding of the metastasis. The SCARLET tree contains three mutation losses: in genes FHIT, LRP1B, and LINGO2. Each of these losses is supported by a significant decrease in read depth (Fig. 3(D)), providing evidence that the loci containing these mutations were likely affected by deletions. Notably FHIT and LRP1B are located in fragile sites in the genome (Smith et al. 2006), which are known regions of genomic instability. In addition, the loss of the mutation LINGO2:1 in LINGO2 is further supported by a shift in the variant allele frequency of another mutation, LINGO2:2, in the same gene. Specifically, the variant allele frequency of LINGO2:2 is ≈1 in the metastatic cells (Fig. 3(A)), suggesting that this mutant allele is homozygous, consistent with a deletion or loss of heterozygosity event where the LINGO2:1 mutation was lost.

We examined further the evidence for polyclonal seeding in the initial study of this patient. Leung et al.(Leung et al. 2017) included a statistical analysis of the variant read counts of the four “bridge mutations”, ATP7B, FHIT, APC and CHN1 that occurred between the first and second metastatic branches in the SCITE tree. This analysis showed that mutations in ATP7B and FHIT were present in a subset of primary tumor cells and in the second metastatic branch (detected in 10/13 and 13/13 cells respectively) while being absent in the second metastatic branch (detected in 1/15 and 1/15 cells respectively). Under the infinite sites model used by SCITE, mutation loss is not allowed and thus polyclonal seeding is necessary to explain the absence of these mutations. The same analysis found high uncertainty regarding the placement of mutations in APC and CHN1 and thus these were not cited as evidence for polyclonal seeding.

The loss-supported model used by SCARLET provides an alternate explanation for the absence of FHIT and ATP7B. SCARLET identifies a supported mutation loss to explain the presence of the mutation in FHIT only in a subset of metastatic cells (M1). This loss is supported by a shift in read depth (p = 0.005) in the 10Mb region containing the locus (Fig 3F). SCARLET does not identify a supported mutation loss to similarly explain ATP7B as we did not observe a significant decrease in read depth for the corresponding locus (p = 0.34). However, this lack of a significant decrease in read depth at the ATP7B locus does not necessarily imply that there was no mutation loss. In particular, because targeted sequencing was performed for only 1000 genes, the copy number data is fairly low resolution and we calculated read depth in 10Mb bins. Thus, we may lack the statistical power to identify a shorter deletion, especially a deletion present in only the 10 metastatic cells with copy number profile M2. In summary, we argue that the sequencing data provides stronger evidence for the phylogeny constructed by SCARLET, which is consistent with both SNV and copy-number data, and supports a more parsimonious explanation of monoclonal seeding of the liver metastasis.

Discussion

Somatic mutations in tumors range across all genomic scales, from single-nucleotide variants (SNVs) through large copy-number aberrations (CNAs). To date, most methods for constructing phylogenies from single-cell DNA sequencing (scDNA-seq) data (Jahn, Kuipers, and Beerenwinkel 2016; Singer et al. 2018; Ross and Markowetz 2016; Zafar et al. 2017; Zafar et al. 2019; El-Kebir 2018; Ciccolella et al. 2018; McPherson et al. 2016; Malikic, Jahn, et al. 2019; Malikic, Mehrabadi, et al. 2019) used only SNVs, ignoring CNAs and thus throwing out important information for phylogenetic inference. Here, we introduced SCARLET, which uses measurements of both SNVs and CNAs to reconstruct tumor phylogenies from scDNA-seq data. SCARLET is based on a loss-supported evolutionary model, which constrains mutation losses to loci containing evidence of a CNA. By using the information about CNAs that is readily available in scDNA-seq data, the loss-supported model has less ambiguity in the phylogeny inference than the Dollo and finite sites models which allow mutation losses to occur anywhere on the tree. In scDNA-seq data, where there is often considerable uncertainty in the mutations present in each cell, this reduction in ambiguity enables more accurate phylogeny inference. On simulated scDNA-seq data, we find that SCARLET outperforms existing methods that do not utilize copy-number data. On targeted scDNA-seq data from a metastatic colorectal cancer patient, we showed that SCARLET found a phylogeny containing three mutation losses. Notably, SCARLET’s tree was both more consistent with the copy-number data and provided a simpler explanation of monoclonal seeding of the liver metastasis, compared to the more complex phylogenies reported previously (Leung et al. 2017; Zafar et al. 2019). Thus, accurate modeling of mutations losses results in different conclusions regarding the migration patterns of metastasis.

There are a number of directions for future improvement. First, the current implementation of SCARLET either requires the copy-number tree in input or enumerates all possible copy-number trees and selects the maximum likelihood result. This approach is applicable when the number of distinct copy-number profiles is small; e.g., in the case of targeted scDNA-seq data (Mission Bio, n.d.; Xu et al. 2012; Leung et al. 2016) where copy-number data typically is lower resolution. However, with higher-quality copy-number data, extensions to larger numbers of copy-number profiles is needed. One approach is to use copy-number evolution models (Chowdhury et al. 2015; Schwarz et al. 2014; El-Kebir et al. 2017; Zaccaria et al. 2018) to identify a modest number of copy-number trees that summarize the uncertainty in the copy-number evolutionary history. Second, one could extend the loss-supported model into a unified evolutionary model for SNVs and CNAs. Indeed, the loss-supported model provides a natural framework to integrate SNVs directly with evolutionary models of CNAs. As single-cell sequencing technologies continue to improve, higher quality measurements of both SNVs and CNAs from the same sets of cells will become available. We anticipate that SCARLET and the loss-supported model will play a crucial role in the analysis of these data.

STAR Methods

Key Resources Table

Contact for Reagent and Resource Sharing

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Ben Raphael (braphael@princeton.edu). This study did not generate any reagents.

Method Details

Loss-supported phylogeny model

We model the evolutionary history of a tumor as a rooted, directed phylogenetic tree T = (V(T), E(T)), whose vertex set V(T) = L(T) ∪ I(T) consists of a set L(T) of n leaves corresponding to observed cells and a set I(T) of inner vertices corresponding to ancestral cells. A directed edge (v, w) ∈ E(T) indicates that cell v is an ancestor of cell w. We do not directly observe T but rather we measure a set of phylogenetic markers for every observed cell v ∈ L(T). In the case where the markers are somatic single-nucleotide variants (SNV), the measurements correspond to a binary mutation profile b_ν ∈ {0,1}^m for each observed cell ν, where b_ν,a = 1 indicates that cell ν has a somatic mutation at locus a and b_ν,a = 0 indicates that cell ν does not have a somatic mutation at locus a. We assume that the mutation profile b_r of the root r is ${\mathbf{b}}_r=\overrightarrow{0}$ since the root represents the normal cell that preceded the tumor. We define the mutation matrix B = [b_ν]_ν∈L(T) to be the matrix whose rows are the mutation profiles of leaves ν ∈ L(T).

The problem of phylogenetic tree inference is to find a tree T and an augmented mutation matrix B′ = [b′_ν]_ν∈V(T) whose rows correspond to binary mutation profiles of the vertices of T and where the submatrix [b′_ν]_ν∈L(T) is equal to B. Since there are many possible trees that relate the observed cells, methods for phylogeny inference find T and B′ that best fit a specific evolutionary model. The simplest evolutionary model for SNVs is the infinite sites, or perfect phylogeny model. In this model, each mutation is gained (0 → 1) at most once, and is never subsequently lost. A more general model the Dollo model allows mutations to be gained (0 → 1) at most once, but lost (1 → 0) multiple times. Formally, the Dollo model is defined as follows.

Definition 1

A phylogenetic tree T is a Dollo phylogeny with respect to augmented mutation matrix B′ provided that for every locus a, there is at most one edge (v, w) ∈ E(T) such that b′_ν,a = 0 and b>′_w,a = 1.

In contrast to the perfect phylogeny model, under the Dollo model there are often multiple phylogenies that are consistent with input data (Fig. 1).

DNA sequencing data often contains contains additional information about the genomic locations where mutation losses are possible. Specifically, we assume that for each cell v, we also observe a copy-number profile p_ν = [p_ν,1, …, p_ν,N] where p_ν,i indicates the number of copies of genomic segment i in cell ν. For simplicity, we label the unique copy-number profiles observed for all the cells by integers {1, …, k}, such that the vector c = [c_ν] represents the copy-number profile assignment c_ν ∈ {1, …, k} of every cell ν. The copy-number profiles of cells provide constraints on mutation losses. In particular, we allow mutation losses only at loci where an overlapping deletion or loss-of-heterozygosity (LOH) distinguishes the copy-number profiles. We record the information about the loci where losses are allowed in a collection ℒ of supported loss sets. For each pair c, c′ of distinct copy-number profiles we define the set ℒ(c, c′) ⊆ {1, …, m} of supported losses to be the set of all the mutation loci located in genomic regions with a decrease in copy number (indicating possible deletion or LOH) between c and c′. We define ℒ(c, c) = ∅ for all c. We denote the collection of supported losses as ℒ = {ℒ(c, c′): (c, c′) ∈ {1, …, k} × {1, …, k}}. We define a loss-supported phylogeny as a Dollo phylogeny where all mutation losses are supported.

Definition 2

Given copy number profiles c′ = [c_ν]_ν∈V(T) and supported losses ℒ, a phylogenetic tree T is a loss-supported phylogeny with respect to augmented mutation matrix B′ provided that: (1) T is a Dollo phylogeny; (2) If b′_ν,a = 1 and b′_w,a = 0 for edge (ν, w) then a ∈ ℒ(c′_ν, c′_w).

The loss-supported phylogeny inference problem is to infer a loss-supported phylogeny T given a mutation matrix B and copy-number profile vector c that label the leaves of T, as well as a set ℒ of supported losses. However, this general problem has a major complication: the copy-number profiles of the ancestral cells are unknown. Without knowledge of ancestral copy-number profiles, the loss sets ℒ cannot be used to constrain mutation losses. Ideally, one might infer copy-number profiles of ancestral cells (e.g., using a copy-number evolution model (Schwarz et al. 2014; Chowdhury et al. 2015; El-Kebir et al. 2017; Zaccaria et al. 2018)) while simultaneously inferring a loss-supported phylogeny on the SNVs. The derivation of a score/likelihood for such joint model is not straightforward, and is left for future work. Instead, in the next section, we describe an algorithm that infers a loss-supported phylogeny by refining a copy-number tree given in input.

Loss-supported Refinement Problem

In this section, we introduce the Loss-Supported Refinement (LSR) problem, a special case of the loss-supported phylogeny inference problem, where we have additional information about the evolutionary relationships between copy-number profiles. In particular, we assume that we are given a copy-number tree T = (V(T), E(T)) and a copy-number profile vector c = [c_ν]_ν∈V(T) for all vertices in T. A copy-number tree is a phylogenetic tree constructed using CNAs as evolutionary markers. Leaves of T correspond to observed cells, inner vertices of T to ancestral cells with distinct copy-number profiles, and edges to ancestral relationships. As single-cell DNA sequencing data of SNVs typically measures copy-number profiles with low-resolution, this copy-number tree typically has many multifurcations (i.e., unresolved ancestral vertices with more than two children). We use the mutation matrix B = [b_ν] for all ν ∈ L(T) to refine vertices in T, which results in a joint tree T′ that reflects the evolutionary history of both the SNVs and CNAs. This sequential approach is inspired by an asymmetry between SNVs and CNAs in the loss-supported model: CNAs affect the observed state transitions of SNVs as deletions result in SNV loss, but SNVs do not result in changes in copy-number state. The joint tree T′ is a refinement (Wu, Moulton, and Steel 2009) of T; i.e., L(T′) = L(T) and T may be obtained by contracting edges in T′.

A refinement is formalized as a mapping γ: V(T) → 2^V(T′), where for all ν ∈ V(T), γ(ν) is a rooted subtree T′[γ(ν)] in T′. Given T′ one can obtain T by contracting each subtree T′[γ(ν)] into a single vertex ν ∈ V(T). We refer to the set of subtrees defined by γ as the refinement subtrees.

We define the LSR problem as the problem of finding a refinement T′ of a copy-number tree T such that T′ is a loss-supported phylogeny.

Problem 1 Loss-Supported Refinement (LSR) problem

Given a copy-number tree T, a copy-number profile vector c = [c_ν]_ν∈V(T), a mutation matrix B = [b_ν]_ν∈L(T), and supported losses ℒ, find a refinement T′ of T, a copy-number profile vector c′ = [c_ν′]_{ν′∈V(T′)}, and an augmented mutation matrix B′ = [b′_ν′]_{ν′∈V(T′)} with b_ν′ = b′_ν′ for all ν′ ∈ L(T′), such that c′_ν′ = c_ν for all ν ∈ V(T) and ν′ ∈ γ(ν), and T′ is a loss-supported phylogeny with respect to B′, c′, and ℒ.

We provide four necessary and sufficient conditions for a solution T′, c′, B′ to the LSR problem. These conditions constrain the set of refinement subtrees defined by γ. The four conditions state that (1) each mutation occurs at most once, (2) mutations are not lost within refinement subtrees, (3) all mutation losses between refinement subtrees are supported, and (4) refinement subtree copy-number profiles are preserved. We formally define these four conditions as follows, using r(ν) to denote the root of subtree T′[γ(ν)] and p(r(ν)) to denote the parent of r(ν).

Theorem 1

Given copy-number tree T, copy-number profile vector c, mutation matrix B, and supported losses ℒ, a refinement T′ of T, copy-number profile vector c′, and augmented mutation matrix B′ are a solution to the LSR problem if and only if

• (1)For all loci a, there exists exactly one edge (ν′, w′) ∈ E(T′) with b′_ν′,a = 0 and b′_w′,a = 1; And for all ν ∈ V(T):
• (2)There does not exist any edge (ν′, w′) ∈ E(T′[γ(ν)]) with b′_ν′,a = 1 and b′_w′,a = 0;
• (3)If b′_p(r(ν)),a = 1 and b′_r(ν),a = 0, then a ∈ ℒ(c′_p(r(ν)), c′_r(ν));
• (4)c′_ν′ = c_ν for all ν′ ∈ γ(ν).

Note that, taken together, conditions (1) and (2) imply that each of these subtrees T′[γ(ν)] is a perfect phylogeny with respect to submatrix B′[γ(ν)]. We use this structure to solve the LSR problem in the next section.

Solving the Loss-Supported Refinement problem

In this section, we derive an efficient algorithm to solve the LSR problem. This algorithm decomposes the LSR problem into k = |I(T)| instances of the Incomplete Directed Perfect Phylogeny (IDP) problem (Pe’er et al. 2004) – one instance for each copy-number profile – using the characterization given in Theorem 1. Specifically, Theorem 1 characterizes LSR solutions by giving conditions on the set of refinement subtrees of T. We design an algorithm to find a set $\mathcal{T}=\{{T^{\prime }}_{\nu }:\nu \in V(T)\}$ of subtrees, an augmented mutation matrix B′, and copy-number profiles c′ that satisfy Theorem 1. Using $\mathcal{T}$ and B′, we then construct a refinement T′ such that T′[γ(ν)] = T′_ν and c′_ν′ = c_ν for all vertices ν′ ∈ V(T′_ν).

We present a recursive algorithm that refines T from the leaves to the root. The algorithm relies on three additional constraints on the solution T′, c′ and B′ that do not effect the existence of a solution, described in the following lemma.

Lemma 1

If there exists a solution to the LSR problem for a given T, c, B, ℒ, then there exists a solution T′, c′, B′ that satisfies the following conditions.

• (1)For all (ν, w) ∈ E(T), p(r(w)) is a leaf of subtree T′[γ(ν)].
• (2)For all ν ∈ V(T) \ {r}, if b′_ν′,a = 1 for all ν′ ∈ L(T′[γ(ν)]) then b′_r(ν),a = 1.
• (3)For all ν ∈ V(T) and all loci a, b′_p(r(ν)),a ≥ b′_r(ν),a.

Our recursive algorithm is composed of a base and recursive step.

Base step

The base step determines T′_ν and B′[V(T′_ν)] for leaf vertices ν ∈ L(T). For any leaf in a refinement T′, γ(ν) = {ν}. Thus the subtree ${T^{\prime }}_{\nu }\in \mathcal{T}$ is composed of a single vertex ν, with mutation profile b′_ν = b_ν and copy-number profile c′_ν = c_ν.

Recursive step

The recursive step aims to find T′_ν and B′[V(T′_ν)] for internal vertices ν ∈ I(T). We find T′_ν in two steps. First, we identify the set of constraints on the leaves L(T′_ν) of T′_ν given by Theorem 1. Second, given these constraints, we find mutation profiles B′[L(T′_ν)] for the leaves that respect a perfect phylogeny, as required by condition (1) and (2) of Theorem 1. These mutation profiles uniquely determine the structure of T′_ν as T′_ν is a perfect phylogeny (Gusfield 1991). We describe these steps in detail below.

By condition (i) of Lemma 1, T′_ν has a leaf for every (ν, w) ∈ E(T); thus L(T′_ν) = {p(r(w)): (ν, w) ∈ E(T)}. We first recursively solve for T′_w and B′[V(T′_w)] for every vertex w such that (ν, w) ∈ E(T). Thus, we know the mutation profile b′_r(w) of the root of each child subtree. We do not directly observe B′[L(T_ν)], but the mutation profile of a vertex is constrained by condition (3) of Theorem 1 and constraint (iii) of Lemma 1 given the mutation profile of a child. Specifically, the parent has the same mutation profile as the child, except if there is a mutation loss. The mutation profiles are further constrained by condition (1) of Theorem 1 as each mutation occurs at most once across all subtrees. We respect this condition by minimizing the number of mutation gains per locus, by only having a mutation gain at locus a in a subtree if a strict subset of the leaves have the mutation.

We summarize these leaf constraints on B′[L(T_ν)] as a ternary matrix ${{\overline{\mathbf{B}}}^{\prime }}_{\nu }={[{{\overline{\mathbf{b}}}^{\prime }}_{\nu }]}_{\nu \in L\left(T_{\nu }\right)}$ where ${\overline{\mathbf{b}}}_v=[{{\overline{b}}^{\prime }}_{v,a}]\in {\{0,1,?\}}^m.$ The first constraint fixes the values for some entries of B′[L(T_ν)], such that ${{\overline{b}}^{\prime }}_{p(r(w)),a}=1$ when ${b^{\prime }}_{r(w),a}=1,$ and ${{\overline{b}}^{\prime }}_{p(r(w)),a}=0$ when b′_r(w),a = 0 and a ∉ ℒ(c_ν, c_ν). The second constraint further sets some of the previously non-fixed entries in B′[L(T_ν)] to minimize the total number of mutation gains in T′_ν. If there exist leaves ν′, w′ ∈ L(T′_ν) where b_ν′,a = 0 and b_w′,a = 1), then mutation a must be gained in subtree T′_ν. To achieve the minimum number of mutation gains, we thus maximize the number of all-zero and all-one columns of ${{\overline{\mathbf{B}}}^{\prime }}_{\nu }:$ we set to 0 any previously undetermined entries ${\overline{b}}_{v^{\prime },a}$ for columns of ${\overline{\mathbf{B}}}^{\prime }$ that only have ‘0’ (‘1’, resp.) entries (setting of ${\overline{b}}_{v^{\prime },a}=0,{\overline{b}}_{v^{\prime },a}=1$ resp.). At last, we set any remaining undetermined entry of ${{\overline{\mathbf{B}}}^{\prime }}_v$ to be ‘?’.

Finally, we aim to find B′[L(T_ν)] by filling the ‘?’ entries of ${{\overline{\mathbf{B}}}^{\prime }}_v$. More specifically, given ${{\overline{\mathbf{B}}}^{\prime }}_v$, we seek B′[L(T_ν)] such that if ${\overline{b}}_{v^{\prime },a}\in \{0,1\}$ then ${b^{\prime }}_{v^{\prime },a}={{\overline{b}}^{\prime }}_{v^{\prime },a}$ for all mutations a and B′[L(T_ν)] is a perfect phylogeny matrix. This problem is known as the Incomplete Directed Perfect Phylogeny (IDP) problem and has been shown to be solvable in O(n2m) time (Pe’er et al. 2004). In our case n = |L(T_ν)| = d_ν where d_ν is the out-degree of vertex ν in T. Solving an instance of the IDP problem yields a perfect phylogeny mutation matrix B′[L(T_ν)], which in turn determines the perfect phylogeny tree T′_ν and mutation matrix B′[L(T′_ν)].

Maximum Likelihood Loss-supported Refinement Problem

The LSR problem assumes that the mutation matrix B is error-free. In practice, we do not observe this mutation matrix B, but instead we observe read counts from a sequencing experiment. Specifically, we measure a variant read count matrix X = [x_ν]_ν∈L(T) and a total read count matrix Y = [y_ν]_v∈L(T), where x_ν,a ∈ ℕ is the number of variant reads at locus a in cell ν and y_ν,a ∈ ℕ is the total number of reads. Whole-genome amplification (Gawad, Koh, and Quake 2016), which typically precedes single-cell DNA sequencing, introduces a considerable amount of error into these read count matrices. Specifically, single-cell sequencing SNV data has high rates of false negative errors (i.e., x_ν,a = 0 when b_ν,a = 1) and missing data (i.e., y_ν,a = 0). In addition, sequencing and whole-genome amplification introduce false positive errors (i.e., x_ν,a > 0 when b_ν,a = 0) as well. Most existing methods (Jahn, Kuipers, and Beerenwinkel 2016; Malikic, Jahn, et al. 2019; Malikic, Mehrabadi, et al. 2019; Zafar et al. 2017; Zafar et al. 2019; El-Kebir 2018; Ross and Markowetz 2016) for single-cell phylogeny inference discretize read counts into an observed mutation matrix $\tilde{B},$ using either two or three genotypes in addition to missing data $\text{(i.e},{\tilde{b}}_{v,a}\in \{0,1,?\}$ or ${\tilde{b}}_{v,a}\in \{00,01,11,?\}).$ However, discretizing the mutation data loses information about the likelihood of errors. For example, a locus with a single variant read is far more likely to be a false positive error than a locus with hundreds of variant reads, but a discretized mutation matrix does not distinguish between these cases.

We use a maximum-likelihood approach to model the observed variant and total read counts. Specifically, we aim to find the mutation matrix B* = argmax Pr(X | Y, B ) that admits a solution T′, B′, c′ to the LSR problem and maximizes the likelihood of the observed variant read counts X given the total read counts Y. Our approach to compute B* is not specific to a particular likelihood model for read counts but does assume that the likelihood has the form $\mathrm{Pr}(\mathbf{X}|\mathbf{Y},\mathbf{B})={\prod }_{v=1}^n{\prod }_{a=1}^m\mathrm{Pr}(x_{v,a}|y_{v,a},b_{v,a});$ i.e. the variant read counts X are independent of each other across cells and loci given Y and B. In this work, we used a beta-binomial model similar to the one previously used by SciΦ (Singer et al. 2018). If mutation a is absent in cell ν (i.e., b_ν,a = 0), then the probability of observing a variant read corresponds to the per-nucleotide rate of sequencing error $ϵ$. For Illumina sequencing reads, we use $ϵ=\mathrm{0.001.}$ If mutation a is present in cell ν (i.e., b_ν,a = 1), then we model the variant counts at a locus using a beta-binomial distribution. We estimate parameters α and β empirically from the distribution of heterozygous germline single-nucleotide polymorphisms (SNPs) in the data. We thus define the data likelihood for observing x_ν,a variant reads at locus a in cell ν as follows,

$$\mathrm{Pr}\left(x_{v,a}|y_{v,a},b_{v,a}\right)=\{\begin{array}{cccc}\text{Beta-Binomial}(x_{v,a}|n=y_{v,a},& \alpha ,& \beta )& \text{if}{b}_{v,a}=1,\\ \text{Binomial}(x_{v,a}|n=y_{v,a},& p=ϵ)& \text{if}{b}_{v,a}=0.\end{array}$$

Let ℬ_T,c,ℒ be the set of mutation matrices B such that there exists a solution T′, c′, B′ to the LSR problem given T, c, ℒ, and B. We formulate the problem as follows.

Problem 2 Maximum Likelihood Loss-Supported Refinement (ML-LSR) problem

Given variant read counts X = [x_ν]_ν∈L(T), total read counts Y = [y_ν]_ν∈L(T), copy-number tree T, copy-number profile vector c = [c_ν]_ν∈V(T), and supported losses ℒ, find ${\mathbf{B}}^{*}={\mathrm{argmax}}_{{ℬ}_{T,\mathbf{c}},ℒ}\mathrm{Pr}(\mathbf{X}|\mathbf{Y},\mathbf{B}).$

We show the ML-LSR is NP-hard by reduction from the Minimum Flip Problem (Chen et al. 2006) in “Proofs”. Since current datasets have mutation matrices with hundreds–thousands of cells, we derive an algorithm in the next section that finds an approximate solution to the ML-LSR problem by subdividing the ML-LSR problem into k instances of the maximum likelihood Incomplete Directed Perfect Phylogeny problem.

SCARLET Algorithm for Maximum-Likelihood Loss-Supported Refinement Problem

We introduce SCARLET (Single-Cell Algorithm for Reconstructing Loss-supported Evolution of Tumors), an algorithm to find a loss-supported phylogeny from single-cell DNA sequencing data. SCARLET aims to solve the ML-LSR problem, defined above in Problem 2, by finding the maximum likelihood mutation matrix B*. Since a solution B* of the ML-LSR is in ℬ_T,c,ℒ, there exists at least one tree T′, a copy-number profile vector c′, and an augmented mutation matrix B′ of B* such that (T′, B′, c′) is a solution to the LSR problem. Given solution (T′, B′, c′), B* is uniquely determined as B* = [b′_ν] _{ν ∈L(T)}. We thus proceed here by finding a solution (T′, B′, c′) to the LSR that yields a maximum-likelihood B*. To solve ML-LSR problem, we extend the algorithm we previously presented to solve the LSR problem. The LSR problem decomposes into a set of IDP instances if we know the mutation profiles R = [b′_r(ν)]_ν∈I(T) of the roots of subtrees $\mathcal{T}.$ In the LSR, we computed R recursively, starting with the leaves L(T) whose mutation profiles are given by B. In the ML-LSR, however, we are not given B, and thus do not know R. Therefore, SCARLET uses two-step procedure where we first compute the maximum-likelihood mutation profiles R* of the roots and then independently infer each maximum-likelihood refinement subtree given R*. Note that this two-step procedure is not guaranteed to find the overall maximum likelihood solution B*, as there may be cases where B* does not admit a solution with the maximum-likelihood roots R*. However, we show in Results that SCARLET is both accurate and fast in practice.

Finding maximum likelihood subtree roots

SCARLET aims to find the maximum-likelihood subtree roots R* = [r_ν]_ν∈V(T) such that there exists a loss-supported refinement T′, c′, B′ with subtree roots R*. The existence of a solution T′, c′, B′ constrains the possible mutation profiles of the roots. Specifically, by Definition [def:lsp] of a loss-supported phylogeny, a mutation at locus a is gained at most once in T′. Matrix R is a valid mutation state assignment for roots provided for each locus a, it is possible that a mutation at locus a occurred exactly once and was only lost when the loss was supported. Specifically, (1) there exists a subtree T_a of T such that for all ν ∈ V(T), r_ν,a = 1 if ν ∈ V(T_a) and ν is not the root of T_a and r_ν,a = 0 otherwise; and (2) for any edge (v, w) ∈ T such that ν ∈ T_a and w ∉ T_a, a ∈ ℒ(c_ν, c_w). Any valid R uniquely defines a subtree T_a for each locus a. Roots R admit a mutation profile b_a for locus a provided that b_a satisfies the following.

1. If ν ∉ T_a then mutation a is absent in all cells ν′ such that c_ν′ = c_ν.

2. If ν ∈ T_a and ν is not the root of T_a then mutation a is present in all cells ν′ such that c_ν′ = c_ν.

3. If ν ∈ T_a and ν is the root of T_a then mutation a is either present or absent, as mutation a occurred in $T_v^{\prime }$

The likelihood given roots R is computed by marginalizing over all admitted mutation profiles. Let β_R = {b_a: R admits b_a} be the set of mutation profiles for mutation a admitted by roots R. Then,

$$\mathrm{Pr}(\mathbf{X}|\mathbf{Y},\mathbf{R})=\prod _{a=1}^m\prod _{{\mathbf{b}}_a\in {\beta }_{\mathbf{R}}}\mathrm{Pr}\left({\mathbf{x}}_a|{\mathbf{y}}_a,{\mathbf{b}}_a\right)=\prod _{a=1}^m\prod _{v=1}^n\mathrm{Pr}\left(x_{v^{\prime },a}|y_{v^{\prime },a},\mathbf{R}\right)$$

such that

$$\mathit{Pr}\left(x_{v^{\prime },a}|y_{v^{\prime },a},\mathbf{R}\right)=\{\begin{array}{ll}\mathrm{Pr}\left(x_{v\prime ,a}|y_{v\prime ,a},b_{v^{\prime },a}=0\right)\hfill & \text{if}{c}_{v\prime }=c_v\text{and}v\notin S_a\hfill \\ \mathrm{Pr}\left(x_{v\prime ,a}|y_{v\prime ,a},b_{v\prime ,a}=1\right)\hfill & \text{if}{c}_{v\prime }=c_v,v\in S_a\text{and}v\text{is not root of}{S}_a\hfill \\ \frac{1}{2}\mathrm{Pr}\left(x_{v^{\prime },a}|y_{v^{\prime },a},b_{v^{\prime },a}=1\right)\hfill & \hfill \\ +\frac{1}{2}\mathrm{Pr}\left(x_{v^{\prime },a}|y_{v^{\prime },a},b_{v^{\prime },a}=0\right)\hfill & \text{otherwise}.\hfill \end{array}$$

We thus find R* by enumerating valid mutation state assignments for roots for each mutation locus a, then computing the maximum likelihood as above.

Finding refinement subtrees

As input for the ML-IDP, we define a ternary matrix ${{\overline{\mathbf{B}}}^{\prime }}_v={[{{\overline{\mathbf{b}}}^{\prime }}_w]}_{w\in L({T^{\prime }}_v)}$ for each vertex ν ∈ V(T) as before. For ν ∈ I(T), we define ${\overline{{\mathbf{b}}^{\prime }}}_{p(r(v))}$ as previously given the mutation profile b′_r(ν) of the root r(ν) of T′_ν. For ν ∈ L(T), we have that ${\overline{{\mathbf{b}}^{\prime }}}_{p(r(v))}={\mathbf{b}}_v$ but unlike in the LSR problem, we are not given the mutation profile b_ν in the ML-LSR problem. Instead, we compute the likelihood of b_ν as in Equation [eq:likelihood]. As such, finding B* is equivalent to find the maximum likelihood submatrices {B*[{ν: c_w = c_ν}]: ν ∈ I(T)} such that ${{\overline{\mathbf{B}}}^{\prime }}_v$ admits an incomplete directed perfect phylogeny.

We describe an integer-linear programming (ILP) formulation to compute these maximum likelihood submatrices. Given ternary matrix ${{\overline{\mathbf{B}}}^{\prime }}_v$ and read count matrices ${\mathbf{X}}_v={\left[{\mathbf{x}}_w\right]}_{w\in L\left(T_v\right)},{\mathbf{Y}}_v={\left[{\mathbf{y}}_w\right]}_{w\in L\left(T_v\right)},$ we aim to find matrix B′ where $\mathrm{Pr}({\mathbf{X}}_v|{\mathbf{Y}}_v,{{\mathbf{B}}^{\prime }}_v)$ is maximized subject to two constraints: (1) B′_ν is perfect phylogeny matrix, and (2) ${b^{\prime }}_{v,w,a}={{\overline{b}}^{\prime }}_{v,w,a}\text{if}{{\overline{b}}^{\prime }}_{v,w,a}\ne ?.\text{Let}{{\mathbf{B}}^{\prime }}_v\in {\mathcal{P}}_{{\overline{\mathbf{B}}}_v}$ indicate that constraints (1) and (2) are met. We thus aim to find ${\mathbf{B}}_v^{\prime *}={\mathrm{argmax}}_{{\mathbf{B}}_{\text{v}}^{\prime }\in {\mathcal{P}}_{{\overline{\mathbf{\text{B}}}}_v}}\mathrm{Pr}({\mathbf{X}}_v|{\mathbf{Y}}_v,{{\mathbf{B}}^{\prime }}_v)$ and we design an integer linear program (ILP) to find ${\mathbf{B}}_v^{\prime *}.$ For simplicity in the remainder of this section, we do not include subscripts for v − e.g., B′ = B′_ν, X = X_ν, Y = Y_ν. Below, we derive a linear objective for the ILP.

$$\begin{gathered} \mathrm{Pr}\left(\mathbf{X}|\mathbf{Y},{\mathbf{B}}^{\prime }\right)={\mathrm{argmax}}_{{{\mathbf{B}}^{\prime }}_v\in {\mathcal{P}}_{{\overline{\mathbf{B}}}_v}}\sum _w\sum _a\log \mathrm{Pr}\left(x_{w,a}|y_{w,a},{b^{\prime }}_{w,a}\right) \\ ={\mathrm{argmax}}_{{\mathbf{B}}_{\text{v}}^{\prime }\in {\mathcal{P}}_{{\overline{\mathbf{\text{B}}}}_v}}\sum _w\sum _a\left[\log \mathrm{Pr}\left(x_{w,a}|y_{w,a},{b^{\prime }}_{w,a}\right)-\log \mathrm{Pr}\left(x_{w,a}|y_{w,a},{b^{\prime }}_{w,a}=0\right)\right] \\ ={\mathrm{argmax}}_{{\mathbf{B}}_{\text{v}}^{\prime }\in {\mathcal{P}}_{{\overline{\mathbf{\text{B}}}}_v}}\sum _w\sum _a{b^{\prime }}_{w,a}\left[\log \mathrm{Pr}\left(x_{w,a}|y_{w,a},{b^{\prime }}_{w,a}=1\right)-\log \mathrm{Pr}\left(x_{w,a}|y_{w,a},{b^{\prime }}_{w,a}=0\right)\right] \\ ={\mathrm{argmax}}_{{\mathbf{B}}_{\text{v}}^{\prime }\in {\mathcal{P}}_{{\overline{\mathbf{\text{B}}}}_v}}\sum _w\sum _a{b^{\prime }}_{w,a}\cdot C_{w,a} \end{gathered}$$

where for observed cells w,

$$C_{w,a}=\log \mathrm{Pr}(x_{w,a}|y_{w,a},b_{w,a}=1)-\log \mathrm{Pr}(x_{w,a}|y_{w,a},b_{w,a}=0).$$

For unobserved cells, we constrain that ${b^{\prime }}_{w,a}={{\overline{b}}^{\prime }}_{w,a}\text{if}{{\overline{b}}^{\prime }}_{w,a}\ne ?$ by setting C_w,a as follows,

$$C_{w,a}=\{\begin{array}{ll}M\hfill & {{\overline{b}}^{\prime }}_{w,a}=1\hfill \\ -M\hfill & {{\overline{b}}^{\prime }}_{w,a}=0\hfill \\ 0\hfill & {{\overline{b}}^{\prime }}_{w,a}=?,\hfill \end{array}$$

where M is a large constant. We use an ILP to maximize ∑_w ∑_a b′_w,a ⋅ C_w,a subject to B′ being a perfect phylogeny matrix. We introduce a set of auxiliary variables F, G, H to enforce the three gametes condition, where F_a,b, G_a,b and H_a,b indicate that a pair of columns a, b show the (1,1), (0,1) and (1,0) gametes respectively, and F_w,a,b, G_w,a,b and H_w,a,b indicate that (b′_w,a, b′_w,b) show the (1,1), (0,1) and (1,0) gametes respectively. All auxiliary variables are constrained to be binary. This yields the following ILP.

$$\begin{array}{l}\text{maximize}\sum _{w,a}{b^{\prime }}_{w,a}\cdot C_{w,a}\\ \text{subject to}\\ F_{a,b}+G_{a,b}+H_{a,b}\le 2& \text{for all}a,b\\ {b^{\prime }}_{w,a}+{b^{\prime }}_{w,b}-1\le F_{w,a,b}\le \min \left({b^{\prime }}_{w,a},{b^{\prime }}_{w,b}\right)& \text{for all}a,b,w\\ \underset{w}{\max }{F}_{w,a,b}\le F_{a,b}\le \sum _w{F}_{w,a,b}& \text{for all}a,b\\ -{b^{\prime }}_{w,a}+{b^{\prime }}_{w,b}\le G_{w,a,b}\le \min \left(1-{b^{\prime }}_{w,a},{b^{\prime }}_{w,b}\right)& \text{for all}a,b,w\\ \max \underset{w}{G_{w,a,b}}\le G_{a,b}\le \sum _w{G}_{w,a,b}& \text{for all}a,b\\ {b^{\prime }}_{w,a}-{b^{\prime }}_{w,b}\le H_{w,a,b}\le \min \left({b^{\prime }}_{w,a},1-{b^{\prime }}_{w,b}\right)& \text{for all}a,b,w\\ \underset{w}{\max }{H}_{w,a,b}\le H_{a,b}\le \sum _w{H}_{w,a,b}& \text{for all}a,b\end{array}$$

Proofs

Proof of Theorem 1

Proof.

We first show that any solution that meets these constraints is a solution to the LSR problem. Constraint (1) of the LSR problem is explicitly enforced by condition (4) of Theorem 1. Constraint (2) is that T′ is a loss-supported phylogeny, i.e., every mutation occurs at most once (enforced by condition (1) of Theorem 1), and every mutation loss is supported. By condition (2), there are no mutation losses between cells that have the same copy-number state, and by (3) mutation losses that are not supported are not allowed between cells with different copy-number states. Thus, if (T′, B′, c′) meet the conditions of Theorem 1, then (T′, B′, c′) is a solution to the LSR.

We next show that any solution (T′, B′, c′) to the LSR meets the four conditions stated in Theorem 1. We will do this by showing that any (T′, B′, c′) that violates any one of these constraints cannot be a solution to the LSR.

1. This condition is directly required by the definition of a loss-supported phylogeny.

2. If this condition does not hold, there exists a mutation that is lost in subtree T′[γ(ν)]. As every vertex in T′[γ(ν)] has the same copy-number state (by condition (4), this mutation loss is not supported and thus T′ is not a solution to the LSR problem.

3. If this condition is violated, then there is a mutation loss that is not supported and thus T′ is not a solution to the LSR problem.

4. This condition is directly required by the LSR problem statement.

Proof of Lemma 1

Proof.

We will show by construction that for any solution (T′, B′, c′) that violates these constraints, there exists another solution (T″, c″, B″) that meets these constraints.

• (1)For all (ν, w) ∈ E(T), p(r(w)) is a leaf of subtree T′[γ(ν)].

  Consider an edge (p(r(w)), r(w)) ∈ E(T′) such that p(r(w)) is not a leaf of T′[γ(ν)]. That is, p(r(w)) has another child in T′[γ(ν)]. We construct T″ by splitting p(r(w)) into two vertices u and u′ such that there is an edge (u, u′) ∈ E(T″), b″_u = b″_u′ and c″_u = c″_u′, and the only outgoing edge from u′ is (u′, r(w)). Thus, u′ is now the parent of r(w) and u′ is a leaf. This split preserves the rest of the tree and does not introduce violations of any of the conditions in Theorem 1 or any of the other assumptions in this Lemma. Thus T″, B″, c″ is a solution to the LSR problem.

• (2)For all ν ∈ V(T) such that ν is not the root of T, b_r(ν) = 1 if b_ν′ = 1 for all ν′ ∈ L(T′[γ(ν)]).

  Assume that T′, c′, B′ meet condition 1. If this constraint is violated, this means that there is some mutation a that is gained in a subtree T′[γ(ν)] but there are no leaves of T′[γ(ν)] that do not contain a. Let T″ = T′, c″ = c′. Let b′_ν′,a = 1 if ν ∈ T′[γ(ν)]. This change does not violate any of the conditions in Theorem 1. Specifically, this change does not introduce new mutation gains, and as this only alters the mutation profiles of internal vertices of T′[γ(ν)] so this cannot introduce new mutation losses. As T″ and c″ are preserved, refinement and copy-number consistency conditions are automatically met. This change may introduce violations to Assumption 3 in this Lemma that can subsequently be corrected as below.

• (3)For all ν ∈ V(T) and all loci a, b_p(r(ν)),a ≥ b_r(ν),a.

  This constraint states that there are no mutation gains on edges between subtrees. We construct T″ by performing a similar split as we did for constraint (1). Suppose there’s an edge (p(r(ν)), r(ν)) ∈ E(T′) such that b_p(r(ν)),a = 0 and b_r(ν),a = 1. Split p(r(ν)) into vertices u, u′ such that b_u,a = 0 and b_u′,a = 1, and for all a′ ≠ a, b_u,a′ = b_u′,a′ and the only outgoing edge from u′ is (u′, r(w)). This split preserves the rest of the tree and does not introduce violations of any of the conditions in Theorem 1 or any of the other assumptions in this Lemma. Thus T″, B″, c″ is a solution to the LSR problem.

Hardness of ML-LSR

Lemma 2 The ML-LSR is NP-hard.

Proof.

We show this by reduction from the Flip problem (Chen et al. 2006) which is known to be NP-Complete.

Given a binary matrix B ∈ {0,1}^m×n and integer κ ∈ ℕ, decide whether there exists a directed perfect phylogeny matrix B′ ∈ {0,1}^m×n such that no more than κ entries in B′ differ from B.

Let (B, κ) be an instance of the Flip problem. For the corresponding instance of the ML-LSR problem, we let κ = 1 and define the inputs as follows:

1. T is the star phylogeny, where all leaves ν ∈ V(T) are attached to a single internal vertex;

2. $\mathbf{c}=\overrightarrow{1};$

3. No mutation losses are supported in ℒ;

4. X = B, and Y = [1]^m×n.

Define a likelihood function Pr(X | Y, B*) that is symmetric when x_ν,a ∈ {0,1} and y_ν,a = 1

$$\log \left(\mathrm{Pr}\left(x_{v,a}|y_{v,a},b_{v,a}\right)\right)=\{\begin{array}{ll}\alpha \hfill & \text{if}{x}_{v,a}=b_{v,a}\hfill \\ \beta \hfill & \text{if}{x}_{v,a}\ne b_{v,a}\hfill \end{array}$$

such that β < α. Thus the log-likelihood of a matrix B* is

$$\begin{gathered} \log \mathrm{Pr}\left(\mathbf{X}|\mathbf{Y},{\mathbf{B}}^{*}\right)=\sum _{v=1}^n\sum _{a=1}^m\log \left(\mathrm{Pr}\left(x_{v,a}|y_{v,a},b_{v,a}\right)\right) \\ =\lambda \cdot \beta +(mn-\lambda )\alpha \end{gathered}$$

We claim that there exists a perfect phylogeny matrix B′ with at most κ changes if and only if there exists a solution B* to the ML-LSR

$$\log \mathrm{Pr}\left(\mathbf{X}|\mathbf{Y},{\mathbf{B}}^{*}\right)\ge \kappa \cdot \beta +(mn-\kappa )\cdot \alpha$$

We first show the forward direction. If there exists a perfect phylogeny matrix B′ with at most κ changes from B′ = X, then the log-likelihood Pr(X | Y, B′) ≥ κ ⋅ β + (mn − n) ⋅ α. Thus for the maximum likelihood solution, B*, Pr(X | Y, B*) ≥ Pr(X | Y, B′).

We next show the reverse direction. If logPr(X | Y, B*) ≥ κ ⋅ β + (mn − n) then B* has at most κ changes from X = B. Thus, there exists a B′ = B*.

Quantification and Statistical Analysis

Simulation Details

We simulated 50 single-cell DNA sequencing datasets, each data set containing n=100 observed cells that were related by a phylogenetic tree containing m=20 mutations, and k=4 copy-number profiles. We simulated each data set in four steps. First, we simulated the topology of a tree. m + k + 1 = 25 vertices were randomly assigned to be in the trunk of the tree or in one of the k copy-number profiles. Vertices in the trunk were joined into a linear path, and vertices not in the trunk were assigned attachments uniformly at random, such that vertices in the same copy-number profile form connected subtrees. We assign the m mutations onto the 20 edges without copy-number profile changes. For each edge (ν, w) in the simulated tree with a change in the copy-number profiles c and c′, we also simulated the set ℒ(c, c′) of supported losses by selecting a random subset of the m loci such that |ℒ(c, c′)| ~ Poisson(0.2 * m). Third, we introduced with probability 0.5 a mutation loss in every genomic locus a ∈ ℒ(c, c′) if the mutation is contained in the parent p. To respect the k-Dollo model with k = 1, we enforce that the same mutation is lost at most once in the simulated tree. We thus obtained simulated trees with 1–8 mutation losses. Last, we add 100 leaves, corresponding to the observed cells, and we append those to a random vertex of the simulated tree.

We simulated read counts from all the cells of each simulated tree with errors specific of single-cell DNA sequencing data. Specifically, we generated a total read count y_ν,a and a variant read count x_ν,a for each locus a in cell v with an allelic dropout rate of d = 0.15, according to previous analyses (Gawad, Koh, and Quake 2016). First, we generated y_ν,a according to a Poisson distribution and assuming an expected sequencing coverage of 100 × such that y_ν,a ~ Poisson(100). Note that when both the alleles drop out, y_ν,a = 0. Second, we generated x_ν,a according to either the absence or presence of a mutation in locus a. If the variant is absent, $x_{v,a}~\text{Binomial}\left(t_{v,a},ϵ\right)\text{where}ϵ=0.001$ models the sequencing error rate. If the variant is present, we model the overdispersion in the variant read count x_ν,a resulting from whole-genome amplification using a Beta-Binomial model as in previous studies (Singer et al. 2018) such that x_ν,a ~ Binomial(t_ν,a, f_ν,a) and f_ν,a ~ max{Beta(α, α), ϵ} (with α = 0.25 in order to obtain an allele dropout rate of d ≈ 0.15).

Copy-number analysis of colorectal cancer patient

We describe the analysis of copy number aberrations in colorectal cancer patient CRC2 from Leung et al (Leung et al. 2017), which provides part of the input data for SCARLET. Leung et al (Leung et al. 2017) performed single-cell DNA sequencing of a 1000 cancer gene panel from 186 cells from a primary tumor and metastasis. We computed copy-number profiles c and supported losses ℒ from read-depth ratios as follows.

First, we computed read depth ratios in 10Mb genomic bins by calculating the read depth r_ν,i in every bin i of every cell ν, as the number of sequencing reads that align to the bin. To account for context-specific variation in read depth, we normalized r_ν,i using the corresponding read depth n_i in a matched normal sample. Moreover, to account for shifts in read depth due to differences in the ploidy of each cell, we further corrected r_ν,i by using the ploidy ϕ_ν of cells ν measured by DAPI staining (Leung et al. 2017) (ϕ_ν = 3.3 for primary aneuploid cells, ϕ_ν = 3.0 for metastatic aneuploid cells, ϕ_ν = 2.0 for diploid cells). Therefore, we obtain the resulting corrected read-depth ratio ${\widehat{r}}_{v,i}=\frac{r_{v,i}}{n_i}\frac{{\varphi }_v}{2}$ for every bin i in cell ν. We performed hierarchical clustering on read depth ratios ${\widehat{r}}_v$ for all cells ν to infer copy-number profiles c. In particular, we fixed the number of clusters to 4 according to the the number of copy-number clones previously identified (Leung et al. 2017).

We identified sets of supported losses in the same 186 cells by identifying significant shifts in the read depths of the bins that contain the 36 somatic single-nucleotide variants previously identified by Leung et al. (Leung et al. 2017). To test whether there was a loss of variant a in bin i between copy-number profiles j and k, we performed a signed Wilcoxon rank-sum test. The two groups of observations correspond to cells with copy-number profiles j and k, such that $G_j=\{{\widehat{r}}_{v,a};c_v=j\}\text{and}{G}_k=\{{\widehat{r}}_{v,a};c_v=k\}.$ The Wilcoxon Rank-sum Test tests whether observations in G_j and G_k are drawn from the same distribution. A mutation loss was supported if the test yielded a p-value p < .01.

Data and Software Availability

SCARLET software, simulated data, and processed CRC2 data are available at github.com/raphaelgroup/scarlet. Original CRC2 data was downloaded from NCBI Sequence Read Archive (SRA; https://www.ncbi.nlm.nih.gov/sra) under accession number SRP074289.

Figure 4: SCARLET infers a loss-supported phylogeny consistent with copy-number profiles from a metastatic colorectal cancer patient.

SCARLET was applied to targeted single-cell DNA sequencing of 141 single cells from the primary colon tumor (blue) and 45 single cells from the liver metastasis (green) of patient CRC2. (A) Variant allele frequencies of 36 somatic SNVs in 96 cells as inferred by SCITE. (B) Perfect phylogeny tree inferred by SCITE in (Leung et al. 2017) of patient CRC2. Two distinct branches of metastatic cells — suggesting polyclonal seeding of the liver metastasis – are separated by the four indicated “bridge mutations” occurring in cells of the primary tumor. (C) Published copy-number profiles from DOP-PCR whole-genome sequencing of 42 single cells from both the primary tumor and metastasis of CRC2 (figure adapted from (Leung et al. 2017)). All metastatic cells share deletions of six chromosomes (black boxes), but are separated into two groups (light and dark green) by a small number of additional CNAs. (D) Mutation matrix derived from the loss-supported phylogeny inferred by SCARLET on the same data. (E) The loss-supported phylogeny inferred by SCARLET has a single branch containing all metastatic cells – suggesting monoclonal seeding of the liver metastasis and consistent with the similar copy-number profiles of all metastatic cells. SCARLET identifies mutation losses (red) in LINGO2, LRP1B, and FHIT. (F) Significant decreases in read depths are observed at the loci of the three mutation losses identified by SCARLET.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit monoclonal anti-Snail	Cell Signaling Technology	Cat#3879S; RRID: AB_2255011
Mouse monoclonal anti-Tubulin (clone DM1A)	Sigma-Aldrich	Cat#T9026; RRID: AB_477593
Rabbit polyclonal anti-BMAL1	This paper	N/A
Bacterial and Virus Strains
pAAV-hSyn-DIO-hM3D(Gq)-mCherry	Krashes et al., 2011	Addgene AAV5; 44361-AAV5
AAV5-EF1a-DIO-hChR2(H134R)-EYFP	Hope Center Viral Vectors Core	N/A
Cowpox virus Brighton Red	BEI Resources	NR-88
Zika-SMGC-1, GENBANK: KX266255	Isolated from patient (Wang et al., 2016)	N/A
Staphylococcus aureus	ATCC	ATCC 29213
Streptococcus pyogenes: M1 serotype strain: strain SF370; M1 GAS	ATCC	ATCC 700294
Biological Samples
Healthy adult BA9 brain tissue	University of Maryland Brain & Tissue Bank; http://medschool.umaryland.edu/btbank/	Cat#UMB1455
Human hippocampal brain blocks	New York Brain Bank	http://nybb.hs.columbia.edu/
Patient-derived xenografts (PDX)	Children’s Oncology Group Cell Culture and Xenograft Repository	http://cogcell.org/
Chemicals, Peptides, and Recombinant Proteins
MK-2206 AKT inhibitor	Selleck Chemicals	S1078; CAS: 1032350-13-2
SB-505124	Sigma-Aldrich	S4696; CAS: 694433-59-5 (free base)
Picrotoxin	Sigma-Aldrich	P1675; CAS: 124-87-8
Human TGF-β	R&D	240-B; GenPept: P01137
Activated S6K1	Millipore	Cat#14-486
GST-BMAL1	Novus	Cat#H00000406-P01
Critical Commercial Assays
EasyTag EXPRESS 35S Protein Labeling Kit	Perkin-Elmer	NEG772014MC
CaspaseGlo 3/7	Promega	G8090
TruSeq ChIP Sample Prep Kit	Illumina	IP-202-1012
Deposited Data
Raw and analyzed data	This paper	GEO: GSE63473
B-RAF RBD (apo) structure	This paper	PDB: 5J17
Human reference genome NCBI build 37, GRCh37	Genome Reference Consortium	http://www.ncbi.nlm.nih.gov/projects/genome/assembly/grc/human/
Nanog STILT inference	This paper; Mendeley Data	http://dx.doi.org/10.17632/wx6s4mj7s8.2
Affinity-based mass spectrometry performed with 57 genes	This paper; and Mendeley Data	Table S8; http://dx.doi.org/10.17632/5hvpvspw82.1
Experimental Models: Cell Lines
Hamster: CHO cells	ATCC	CRL-11268
D. melanogaster: Cell line S2: S2-DRSC	Laboratory of Norbert Perrimon	FlyBase: FBtc0000181
Human: Passage 40 H9 ES cells	MSKCC stem cell core facility	N/A
Human: HUES 8 hESC line (NIH approval number NIHhESC-09-0021)	HSCI iPS Core	hES Cell Line: HUES-8
Experimental Models: Organisms/Strains
C. elegans: Strain BC4011: srl-1(s2500) II; dpy-18(e364) III; unc-46(e177)rol-3(s1040) V.	Caenorhabditis Genetics Center	WB Strain: BC4011; WormBase: WBVar00241916
D. melanogaster: RNAi of Sxl: y[1] sc[*] v[1]; P{TRiP.HMS00609}attP2	Bloomington Drosophila Stock Center	BDSC:34393; FlyBase: FBtp0064874
S. cerevisiae: Strain background: W303	ATCC	ATTC: 208353
Mouse: R6/2: B6CBA-Tg(HDexon1)62Gpb/3J	The Jackson Laboratory	JAX: 006494
Mouse: OXTRfl/fl: B6.129(SJL)-Oxtrtm1.1Wsy/J	The Jackson Laboratory	RRID: IMSR_JAX:008471
Zebrafish: Tg(Shha:GFP)t10: t10Tg	Neumann and Nuesslein-Volhard, 2000	ZFIN: ZDB-GENO-060207-1
Arabidopsis: 35S::PIF4-YFP, BZR1-CFP	Wang et al., 2012	N/A
Arabidopsis: JYB1021.2: pS24(AT5G58010)::cS24:GFP(-G):NOS #1	NASC	NASC ID: N70450
Oligonucleotides
siRNA targeting sequence: PIP5K I alpha #1: ACACAGUACUCAGUUGAUA	This paper	N/A
Primers for XX, see Table SX	This paper	N/A
Primer: GFP/YFP/CFP Forward: GCACGACTTCTTCAAGTCCGCCATGCC	This paper	N/A
Morpholino: MO-pax2a GGTCTGCTTTGCAGTGAATATCCAT	Gene Tools	ZFIN: ZDB-MRPHLNO-061106-5
ACTB (hs01060665_g1)	Life Technologies	Cat#4331182
RNA sequence: hnRNPA1_ligand: UAGGGACUUAGGGUUCUCUCUAGGGACUUAGGGUUCUCUCUAGGGA	This paper	N/A
Recombinant DNA
pLVX-Tight-Puro (TetOn)	Clonetech	Cat#632162
Plasmid: GFP-Nito	This paper	N/A
cDNA GH111110	Drosophila Genomics Resource Center	DGRC:5666; FlyBase:FBcl0130415
AAV2/1-hsyn-GCaMP6-WPRE	Chen et al., 2013	N/A
Mouse raptor: pLKO mouse shRNA 1 raptor	Thoreen et al., 2009	Addgene Plasmid #21339
Software and Algorithms
ImageJ	Schneider et al., 2012	https://imagej.nih.gov/ij/
Bowtie2	Langmead and Salzberg, 2012	http://bowtie-bio.sourceforge.net/bowtie2/index.shtml
Samtools	Li et al., 2009	http://samtools.sourceforge.net/
Weighted Maximal Information Component Analysis v0.9	Rau et al., 2013	https://github.com/ChristophRau/wMICA
ICS algorithm	This paper; Mendeley Data	http://dx.doi.org/10.17632/5hvpvspw82.1
Other
Sequence data, analyses, and resources related to the ultra-deep sequencing of the AML31 tumor, relapse, and matched normal.	This paper	http://aml31.genome.wustl.edu
Resource website for the AML31 publication	This paper	https://github.com/chrisamiller/aml31SuppSite

Box 1: Primer.

Cancer is an evolutionary process where cells in a tumor accumulate somatic mutations over time. While only a small number of these somatic mutations drive the development of cancer, all somatic mutations are a marker of the evolutionary history of a tumor. Recent single-cell DNA sequencing technologies enable the measurement of somatic mutations in individual cells from a tumor, providing data to construct a phylogenetic tree, or phylogeny, that represents the past evolution of the tumor.

Constructing a phylogenetic tree that describes the ancestral relationships between cells in a tumor relies on a choice of markers, or characters, that distinguish the individual cells, as well as an evolutionary model describing how these markers change over time. For single-cell DNA sequencing of tumors, a popular choice of markers is single-nucleotide differences between cancer cells, known as single-nucleotide variants (SNVs). However, current single-cell DNA sequencing technologies measure SNVs with high rates of missing data and errors due to technical limitations such as DNA amplification artifacts, undersampling, and sequencing errors. Standard phylogenetic methods do not handle such high rates of missing data and errors. Thus, specialized algorithms have been developed to construct phylogenetic trees from single-cell measurements of SNVs. Early works used the simplest evolutionary model for SNVs, the infinite sites model, where a position in the genome is mutated at most once.

However, SNVs are not the only type of somatic mutation that occur in cancer. In particular, most solid tumors have many copy-number aberrations (CNAs), mutations that duplicate or delete segments of the genome that range in scale from hundreds of nucleotides through whole chromosomes. CNAs often overlap SNVs; for example, a deletion may remove SNVs. The infinite sites model does not allow loss of SNVs, and thus methods that use this model do not accurately reconstruct the phylogenetic trees of tumors with many CNAs. More general evolutionary models that allow loss of SNVs, or mutation losses, have recently been used in single-cell phylogenetic analysis, such as the Dollo and finite sites models. However, these models do not examine the underlying DNA sequencing data for evidence of CNAs. Thus, such models are generally too permissive, admitting many different phylogenies even when these contradict the observed CNA data.

In this paper, we introduce a loss-supported evolutionary model that allows SNV losses only when accompanied by evidence in the DNA sequencing data of a deletion at the same locus. We use this loss-supported model as the basis for an algorithm, SCARLET (Single-Cell Algorithm for Reconstructing Loss-Supported Evolution of Tumors), that infer tumor phylogenies from single-cell DNA sequencing data, accounting for both mutation loss and sequencing errors. We show that SCARLET infers single-cell tumor phylogenies more accurately than existing methods.

Highlights.

• Single-nucleotide variants (SNVs) and CNAs are markers of cancer evolution.

• Copy number aberrations (CNAs) may overlap SNVs and result in SNV loss.

• Loss-supported model constrains SNV losses to loci with a decrease in copy number.

• SCARLET integrates SNVs and CNAs yielding more accurate single-cell phylogenies.