The dimensionality of neural representations for control

Abstract

Cognitive control allows us to think and behave flexibly based on our context and goals. At the heart of theories of cognitive control is a control representation that enables the same input to produce different outputs contingent on contextual factors. In this review, we focus on an important property of the control representation’s neural code: its representational dimensionality. Dimensionality of a neural representation balances a basic separability/generalizability trade-off in neural computation. We will discuss the implications of this trade-off for cognitive control. We will then briefly review current neuroscience findings regarding the dimensionality of control representations in the brain, particularly the prefrontal cortex. We conclude by highlighting open questions and crucial directions for future research.

Introduction

While pursuing their goals, humans can express an extraordinary range of behaviors in order to adapt to diverse and changing contexts. This capacity to adjust our behavior as circumstances dictate is often referred to as cognitive flexibility, and it is served by the neural mechanisms of cognitive control [2].

At the heart of most theories of cognitive control is a control representation that enables the integration of contexts and goals with pathways for action. Most theories of control assume that the control representation is maintained in working memory by networks that include the prefrontal cortex (PFC). While maintained, this representation can influence, organize, coordinate, or route ongoing processing.

Given the centrality of control representations for theories of control, it is important to understand the neural code these representations use, both in terms of content (i.e., what is encoded) and geometry (i.e., the structured relations among firing patterns across input conditions). This review focuses on one feature of the geometry of the neural population code termed representational dimensionality. In technical terms, representational dimensionality refers to the minimum number of axes needed to account for variance in neural population activity across input conditions. Theoretical neuroscience has demonstrated that the dimensionality of a neural population code balances a computational trade-off between separability and generalizability [3]. Understanding this tradeoff in the neural coding of control representations promises gains on some of the most fundamental problems in cognitive control, including the bases of cognitive flexibility, multitasking costs, and the controlled-to-automatic continuum of behavior.

This review considers the significance of the dimensionality of PFC representations for cognitive control. We first define what is meant by the control representation and its role in cognitive control theory. We then detail the computational tradeoff that is balanced by representational dimensionality with a focus on the implications of this tradeoff for the control representation in theories of cognitive control. We conclude with a brief review of the current state of empirical evidence for the dimensionality of control representations, highlighting current open questions and directions for future research.

The control representation and cognitive control

The control representation is central to most mechanistic theories of cognitive control function. For our purposes, a flexible control system can be defined as one where the same input state can lead to different outputs depending on internally maintained factors, like goals, rules, or contexts. In other words, there is flexible and contingent mapping between inputs and outputs. Control representations, then, are neither the inputs themselves nor are they the outputs. Rather, they are representations that enable flexible mapping between inputs and outputs conditional on a goal or context.

This normative conception of the control representation has subtly distinct instantiations across different theories of cognitive control. Several theories propose a control representation that provides a top-down influence on preexisting response pathways without being part of those pathways [4–6]. For example, the widely influential guided activation model of the Stroop task [1] relies on a representation of the current task demand, such as color naming, in its working memory. This control representation provides a top-down contextual signal that can bias the color-naming pathway in its competition against the inappropriate, but prepotent, word-reading pathway. This control representation is modulatory because it sits outside of the pathways between stimulus and response [5]. Without it, action would still unfold, but it does so contingent on the bottom-up influence of the stimulus. Hence, akin to automatic or habitual responding, without the control representation, behavior is stimulus driven and inflexible.

Other theories assume a transmissive role for the control representation. These theories posit an integrated control representation that incorporates all task-relevant information including goals, rules, stimuli, responses, rewards, and so forth in a flexibly addressable, context-dependent format [7–10]. Flexible readout from the diverse features in this integrated control representation drive subsequent stages of processing. These theories assume that efficient performance depends on assembling this integrated control representation. Thus, as it lies on the pathway from input to output, the properties of the control representation itself drive flexibility.

Whether modulatory or transmissive, theories of control consistently hypothesize that the fronto-parietal control system in general, and the dorsolateral prefrontal cortex (DLPFC) in particular, maintain control representations in working memory. Accordingly, there has been an emphasis on the content of DLPFC control representations, in terms of which features of a task they encode, such as stimuli, responses, rules, contexts, etc. In non-human animals, the content of neural representations has been conventionally investigated by measuring the change in activity of single neurons to stimulus inputs. These studies find that most, if not all, task relevant features are coded by PFC neurons [7, 11, 12]. In humans, the application of fMRI pattern analysis methods has found convergent evidence that multiple task-relevant features can be decoded from DLPFC [13, 14].

Importantly, however, far fewer studies have characterized the geometry or dimensionality of these PFC control representations. Dimensionality places fundamental constraints on network computation, and so has implications for both modulatory and transmissive theories of cognitive control. In the next sections, we consider the computational tradeoffs that produce these constraints and their implications for cognitive control.

The tradeoff between separability and generality

Theoretical neuroscience has demonstrated that representational dimensionality balances a computational tradeoff between generalizability and separability of neural representations [3, 15]. Broadly, neural computation proceeds in two conceptual stages [16, 17]. First, there are processes that yield a basis set of features encoded by a neural population, consisting of the patterns of neural activity that population exhibits in response to its inputs. A low dimensional representation will encode a diverse range of inputs into a small set of common, orthogonal activity patterns. A high dimensional representation will separate even similar inputs into orthogonal activity patterns, with neurons selective to the inputs and their non-linear interactions. Second, there are processes that permit readout from this basis set. Readout is enacted by downstream neurons and is generally modeled as a linear hyperplane, separating the feature bases of the population into classes. Those classes can reflect different task features, like colors or shapes or conjunctions like the word red printed in blue.

A highly expressive basis set is one that permits readout of lots of such classes from the same neural population. Expanding the representational dimensionality of a neural population leads to more linearly separable classes and so makes a population more expressive [3, 16, 18, 19]. To illustrate, consider the populations depicted in Figure 1. The lower dimensional representations (Figure 1a–c) will produce separable responses to different shape or color inputs, but not their conjunction. So, one can implement linear readout of shape or color using this population, but not their conjunction. A higher dimensional representation (Figure 1d–f) produces distinct responses for each combination of shape and color. Thus, by expanding dimensionality, one can read out shape, color, or any combination from this same population. The advantages of dimensional expansion for linear readout are well known and form the basis of the kernel trick in support vector machines [20] and the architecture of recurrent networks in reservoir computing [16].

Figure 1.

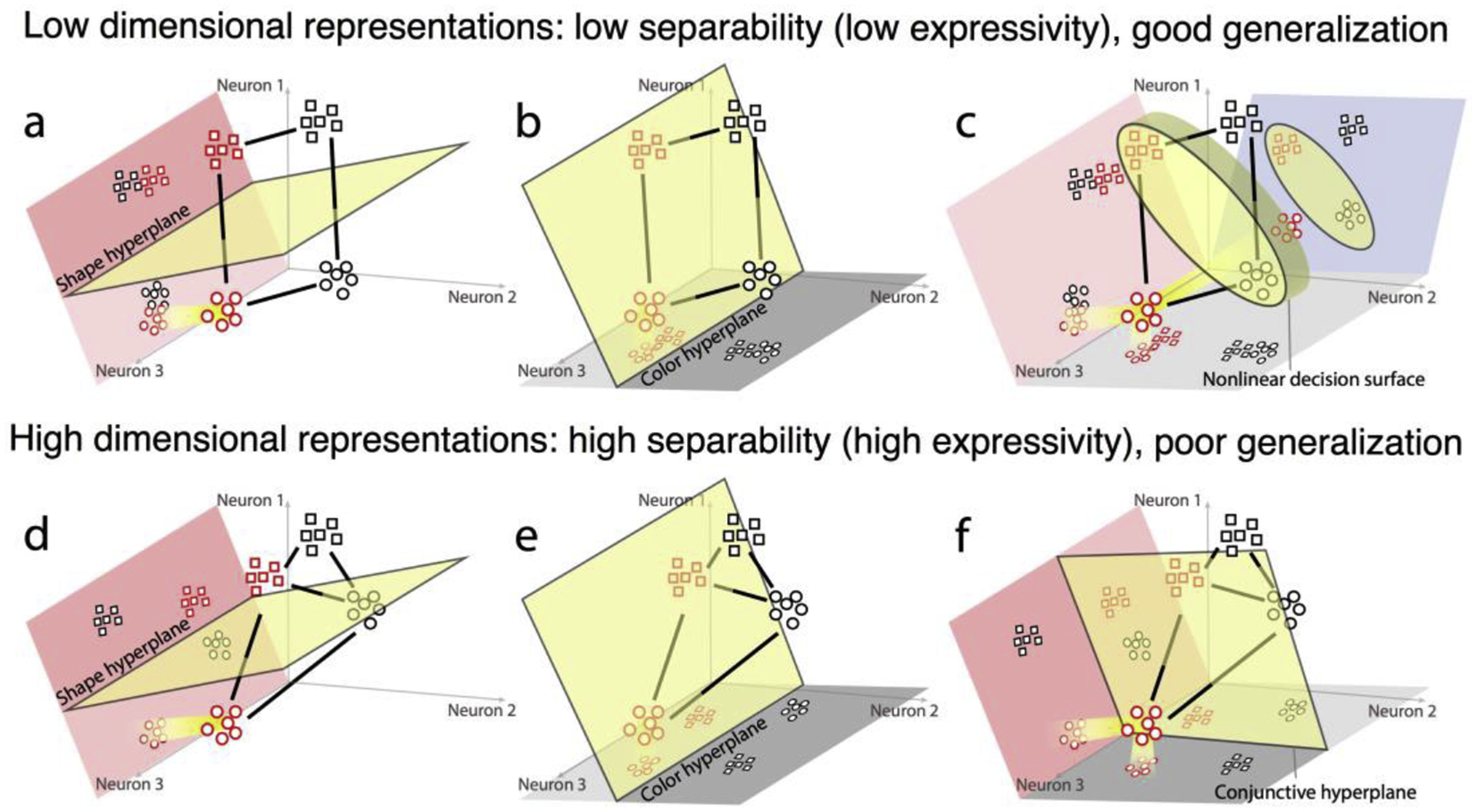
Schematic illustration of representational dimensionality and its computational properties. Each panel plots the response of a toy population of three neurons to stimuli that vary in shape (square or circle) and color (red or black). Axes represent the firing rates of single neurons and collectively define a multi-dimensional firing rate space for the population. Each point within this space represents the population response (i.e., activity pattern) for a given input (identified by colored shapes). Distance between points reflects how distinct responses are, and the jittered cloud of points reflect the trial-by-trial variability in responses to a given input. (a-c) show a low dimensional representation. Though the population is 3-dimensional (i.e., has three neurons), the representation defined by the population responses to the four stimuli defines a lower 2-dimensional plane (traced by solid black lines). A linear ‘readout’ of this representation is implemented by a ‘decision hyperplane’ (yellow) that divides the space into different classes, such as color and shape. The readout can be visualized by projecting (highlighted for red circles) the responses into a readout subspace. (a) In the shape subspace (peach), square and circle stimuli produce distinct, well-separated responses that generalize over different colors. (b) The color subspace (grey) separates red and black but generalizes over shape. (c) illustrates that it is impossible to linearly read out integrated classes (like red-square or black-circle vs black-square or red-circle) in this low-dimensional representation. A non-linear decision surface is required. This problem can be solved by a high-dimensional representation where the response patterns span 3 dimensions (d-f). As before, shape (d) and color (e) information can be linearly read out, though with poorer generalization along the irrelevant dimensions (reflected in the distance between clouds in the irrelevant dimension). Importantly, classes based on color-shape conjunctions (f) can also be linearly read out. Thus, high-dimensional representations are more expressive, making a wider variety of classes linearly separable. A population with a diversity of non-linear mixed selective neurons will have a higher representational dimensionality.

Neural populations may similarly take advantage of dimensional expansion [3, 16, 18, 19]. One means of expanding the dimensionality of a neural code is the inclusion of mixed selective neurons that show diverse, idiosyncratic preferences, including the non-linear interactions of multiple task features [3, 15]. Mixed-selective neurons are abundant in the brain, including in regions like DLPFC [21, 22] where they can make up 30–50% of task selective neurons [15].

Importantly, however, separability also comes with costs. The ability of high dimensional representations to separate similar input patterns into distinct output patterns makes them sensitive to noise [3]. As such, they can overweight small changes in the input and yield the wrong output firing pattern leading to misclassification during readout. Further, high dimensional representations will not benefit from partial similarity of new inputs to previously learned inputs when such similarity could be exploited, such as in highly structured environments. Low dimensional representations will re-use existing output patterns for similar input patterns, allowing generalization. Thus, the separability gained by a high dimensional code fundamentally trades off against the generalizability available from dimensionality reduction.

It should be noted that these characteristics of high and low dimensional representations define the extremes of a continuum. There are intermediate geometries wherein some separability is preserved while also enabling some degree of generalization [23–25]. Therefore, the dimensionality of a neural representation is a versatile computational property that can be leveraged to shape how its inputs are coded and read out.

Separability and generalizability in cognitive control function

The tradeoff between separability and generalizability when applied to control representations has important implications (Figure 2). The advantages of abstract, low dimensional representations for control have been discussed extensively elsewhere, and so we won’t detail them here. In brief, such representations may be particularly important for exerting control in novel settings, when preexisting control representations from similar settings can be generalized and re-used [26, 27]. They may also be important in complex environments where it is necessary to decompose a task into simpler constituents [28]. However, reliance on low dimensional representations may also come with costs, particularly in the flexibility of readout, and this is where the advantages of a high dimensional task representation become clearer.

Figure 2.

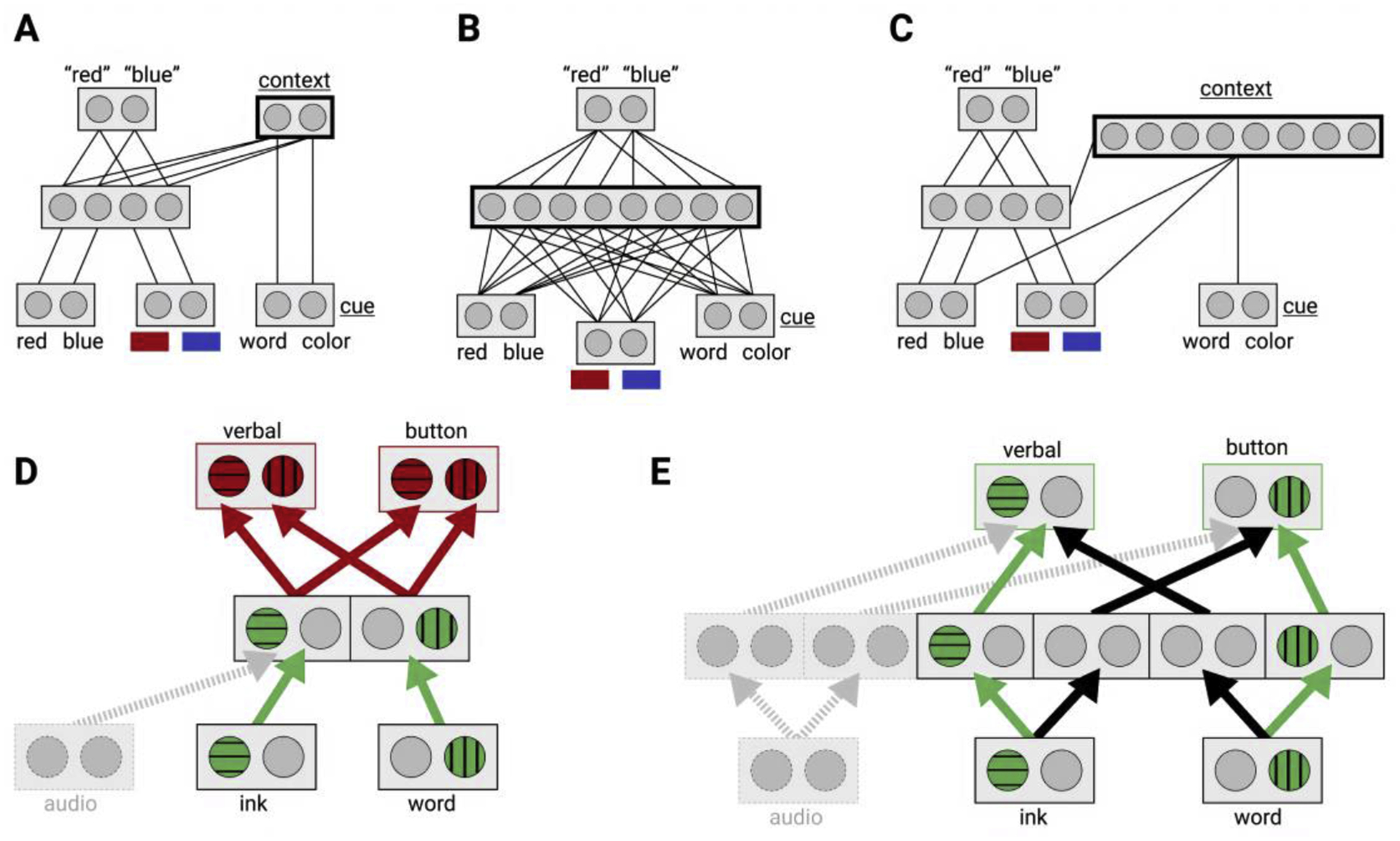
(a-c) Illustrations of control representations of different dimensionality across modulatory and transmissive architectures for cognitive flexibility. (a) A modulatory model of cognitive control based on the widely recognized Stroop model from Cohen et al. [1]. Localist units represent patterns of activity of a neural population. Input layers with the word and ink color feedforward to a hidden layer which feeds forward to a response layer at the top. A task cue input feeds forward to a low dimensional context layer. This is the control representation that biases the task-relevant response pathway to enable flexibility. (b) A transmissive architecture that achieves flexibility with a high dimensional hidden layer that mixes all inputs into separate pathways. Thus, the hidden layer is an expressive control representation that makes any combination of cue and stimuli available for direct readout by the response layer. (c) A modulatory model with a high dimensional context layer. This expressive control representation can use any combination of task cue and stimuli as a contextual input to bias the route from stimulus to response. (d)-(e) Illustrations of the tradeoffs of dimensionality for control. (d) A simplified representation of the architecture in 2a without the context layer and with an added output, following [32]. The combination of two input types and two ouput types makes four “tasks”. Arrows show pathways from input to output with active unites highlighted and distinguished by fill pattern. A low dimensional control representation can link an input to both verbal and button press responses. This is useful for fast learning; a new task involving auditory input can leverage this low dimensional representation to link to all available outputs. However, if two tasks are performed at once, there is cross-talk interference (red paths) (e) A higher dimensional control representation in the hidden layer, akin to 1b, separates the inputs across the tasks. This allows multitasking without interference, but a new task involving auditory input must learn entirely new pathways.

First, high dimensional representations mix multiple task features into separable patterns. As such, they can enable efficient, flexible adaptation to changing contexts to the degree that context is incorporated into its mixture. Such flexibility might be beneficial when responding to changing contingencies, such as during task switching. In task switching, the need for flexibility is high, but the task rules are known and generalization is not required. Recalling our definition of flexibility, input patterns in these settings will be highly correlated and may differ only in one critical contextual feature [15]. High dimensional representations can separate these similar input states into distinct outputs which aids their efficient readout.

Second, the expressive power of a higher dimensional control representation appears to match the similarly expressive range of human behavior, as in our ability to conduct just about any task that meets our goals. Of course, to harness the expressivity of the control representation, we still need mechanisms for learning selective readout of the relevant information as goals change. Such mechanisms may depend on cortico-striatal circuits and their modulation by midbrain dopaminergic signals [4, 29]. Certainly, after ample experience has provided the opportunity to learn the new classes, readout can avail itself of the many conjunctions available in a high dimensional representation.

Third, separability may have a mitigating effect on task interference. For example, recent work using neural network models has demonstrated a basic tradeoff between generalizability and interference in multitasking [30–32]. Specifically, lower dimensional representations are more generalizable and facilitate the learning of new tasks through the re-use of existing codes (Figure 2d). However, because multiple tasks learned this way would rely on the same basis set, they must compete for processing. Thus, networks that share low dimensional bases across tasks are susceptible to interference during multitasking. Increasing representational dimensionality and thus separability, reduces this interference, but it also slows learning because it cannot benefit from shared structure across tasks (Figure 2e).

Relatedly, dimensionality may affect where a task falls on the controlled-to-automatic continuum. As described above, the flexibility enabled by high dimensional representations might be critical during early performance of a new task or under conditions like task switching, when controlled behavior dominates. Another possibility, however, is that the formation of high dimensional codes matched to specific tasks may instead support the transition to automaticity. From this perspective, the cost paid in time to build such a control representation, or train its readout through experience, is rewarded by an efficient mapping from diverse input states to the desired output states. Task performance would be facilitated by a direct mapping from a mixture of inputs to an output. Multitasking would likewise be enhanced for the automated task, reducing its susceptibility to cross-task interference and the demands it places on attention.

In summary, then, the dimensionality of a representation controls a basic tradeoff between generalizability and separability, and this tradeoff is central to the core concerns of cognitive control. As such, characterizing the dimensionality of control representations should be a focus of the science of cognitive control. In this context, we next consider what neuroscience has revealed so far about the dimensionality of control representations.

The Dimensionality of PFC Control representations

As separability and generalizability are crucial for cognitive control function, experimental work testing the dimensionality of control representation in PFC networks is of high significance. Physiological recording in the macaque DLPFC has provided evidence of high dimensional representations [3, 15]. Rigotti et al. (2013) estimated that the representational dimensionality of neural population codes in DLPFC during a working memory task was near maximal, given the task variables. Further, this high dimensionality was behaviorally relevant, as trials on which the animal made an error were associated with reduced dimensionality. Subsequent studies have made similar estimates of near maximal dimensionality in DLPFC, again determined by the number of behaviorally relevant (i.e., reward driving) dimensions in the task [33].

Indeed, DLPFC will separate inputs even when the input could be described using a lower number of dimensions. For example, an early study recorded DLPFC responses to a continuum of vibro-tactile stimulation varying along a single dimension of frequency. Nonetheless, this single dimension of input was separated in DLPFC into a higher dimensional representation with distinct activity patterns for similar stimulus frequencies [34].

An important question is whether DLPFC obligatorily mixes task features into a high dimensional representation, regardless of whether such mixtures are needed by the task at hand. Obligatory mixing might be particularly helpful to the degree that such combinations could be useful parts of other future tasks, enhancing flexibility.

At present, this question remains open. No studies have directly manipulated the task relevance of mixed representations. However, lower-than-maximal dimensional estimates have been obtained for the DLPFC [23, 35]. For example, Brincat et al. [35] required animals to either categorize the color or motion feature of a stimulus on the basis of a preceding shape cue. In this study, low dimensional, abstracted representations of the behaviorally relevant categories were estimated in the DLPFC. This contrasted with higher dimensional estimates made in regions of visual and temporal cortex. Thus, one interpretation of this result is that the mixing of inputs and dimensionality of neural representations is shaped by task demands. Here, a low dimensional code that excluded irrelevant categories or specific exemplars was most useful. However, it is not yet clear what demands distinguished this task from other similar tasks that have observed non-abstract, high dimensional representations in DLPFC.

Finally, just as different tasks might afford different representational dimensionality, the dimensionality of a control representation may also change dynamically within epochs of a trial as a function of task demands. These temporal dynamics of representational dimensionality have received scant attention, at least directly, but initial results do point to a capacity for dimension expansion and reduction within a control episode.

Bernardi et al. [23] reported that in the interval prior to a trial of a reversal learning task, information about an on-going context, along with the action and outcome from the prior trial, were maintained together in the DLPFC using a low dimensional, abstract format. However, 100ms after stimulus presentation, the current trial stimulus and context were mixed into a non-linear, non-abstract representation, which expanded representational dimensionality. Further, dimensionality peaked to its maximum and then gradually declined, such that by the time of the response it had reached a low dimensional format close to that observed between trials. It was proposed that the abstract format between trials favored contextual learning based on preceding events, useful in this reversal task. However, the high dimensional coding within a trial may favor efficient responding. Thus, these dynamics in the feature basis sets might be a means of adaptively balancing separability and generalizability within a trial epoch.

These changes within a trial epoch do not mean that the population code is unstable. Time varying neural population codes could present a problem for readout, if a representation is not stable over time. Such a representation is of little use to downstream neurons, unless they can adapt with it. Crucially, then, it has been observed that while DLPFC can simultaneously encode mixtures of task-relevant features in distinct subspaces of its population code, these subspaces are themselves stable over time.

Parthasarathy et al. [36] observed that the presentation of distractors during a working memory task resulted in a dynamic change in the geometry of the task representation (i.e., morphing) coded by the population of mixed selective neurons, and this change was important for better behavioral performance. Within these flexible dynamics, there were temporally stable subspaces [37] that allowed readout of multiple task features [38]. Thus, mixed selective neurons not only afford high representational dimensionality and rapid morphing of population activity with respect to task features, but also stable readout over time, which is critical for downstream neurons making use of dynamic codes [39].

These dynamics of the dimensionality of control representations speaks to fundamental conceptions of how we prepare and select actions. A widely held view dating back to at least Broadbent [40] holds that control over task decisions proceeds serially and hierarchically through stages from stimulus to response. Each decision relies on a classification of low dimensional task elements, such as a decision about a stimulus, a rule, and a response. However, an important alternative class of model proposes that over the course of action planning, the system assembles an event (task) file which binds all task features at all levels – including the rule (i.e., context), stimulus, and response – into an integrated, conjunctive representation that is essential for an action to be executed [8].

Evidence of high dimensional codes in the lateral PFC and their rapid emergence following a stimulus is initially consistent with the event-file framework. However, these prior studies have not tied the evolution of high dimensional representations to action selection. In this context, Kikumoto et al. [10] analyzed spectral profiles of EEG data during response selection in humans and found evidence of a conjunctive representation that mixed relevant rules, stimuli, and responses. This conjunctive representation arose shortly following stimulus presentation and prevailed throughout the response selection period. Importantly, the trial-to-trial variability in strength of this conjunctive representation was the prime correlate of behavioral performance. Such an integrated code is not required by the simplest serial model, and yet in line with event-file theory, it appears important for action control. Thus, though not directly assessing dimensionality, these experiments imply that a representation which mixes task information plays a critical role in cognitive control in humans.

Conclusions and Future Directions

Understanding the relationship between the dimensionality of control representations and cognitive control function is an important frontier of research. The computational properties of high verses low dimensional representations bear on the central concerns of controlled behavior. Further, the role played by these representations and their placement along the pathway from stimulus to action may distinguish between modulatory and transmissive perspectives on the role of PFC networks in flexible behavior.

Nonetheless, before we can achieve this promise, significant gaps remain to be addressed. First, there has been little research on the dimensionality of control representations in the human brain. This is likely due, in part, to methodological limits of estimating dimensionality noninvasively (Box 1). To date, only two studies have applied methods to directly test dimensionality in humans. One did so during a reinforcement learning task. They found that individual differences in the dimensionality of brain activity, particularly in regions like hippocampus and temporal cortex, were positively related to learning the values of new classes [41]. However, this study did not directly address the dimensionality of the control representation or its relationship to flexible behavior within-subject. A second study, investigating concept learning, observed that representations in the ventromedial PFC incorporated only the dimensions necessary for a categorization, abstracting over irrelevant features in a task dependent way [42]. Though, this study left open how these concept representations operate during tasks demanding cognitive control or their relationship to control representations in more dorsal fronto-parietal networks conventionally associated with cognitive control function.

Box 1 -. Measuring representational dimensionality.

Consider an n-dimensional firing rate space with axes defined by the firing rates of n neurons in a population. The firing rate pattern elicited by c different input conditions will be a set of c points in this space. Dimensionality refers to the minimum number of axes required to define a sub-space that contains these c points. Formally, dimensionality is the rank of an activity matrix whose columns are the firing rate patterns across input conditions, which can have a maximum value of c. The more correlated the columns of this activity matrix, the lower the dimensionality. Therefore, if one can directly measure these firing rate patterns (for example, with single unit recordings in animals), one can employ linear dimensionality reduction methods like principal component analysis, singular value decomposition, or multi-dimensional scaling to identify linear, orthogonal components of the activity matrix and estimate its rank.

However, dimensionality estimation is greatly complicated by the presence of noise. Any random noise in the measurement of firing rate patterns reduces the correlation between columns of the activity matrix, and thus inflates the estimated dimensionality. Therefore, criteria must be established for identifying signal versus noise components. One approach has been to use a conservative (eigvenvalue) threshold for identifying the signal components. This threshold may be determined by estimating the ceiling for the number of noise components from the trial-by-trial variance in activity patterns [34, 43]. Another approach selects the number of components that maximize reconstruction accuracy for independent data [44, 45].

Rigotti et al. [15] introduced an alternate approach. Leveraging the relationship between dimensionality and expressivity, they counted the number of linear classifications (out of the 2^c possible) that could be successfully implemented, which grows exponentially with dimensionality. While computationally expensive, this approach considers the shape and direction of the noise relative to the coding dimension and is thus more accurate.

These dimensionality estimation methods have been extended to human fMRI data [41, 44, 45] with the assumption that the geometry of hemodynamic multi-voxel patterns in a multi-dimensional voxel space preserves the geometry of the underlying neural representation [46]. However, despite their importance, there has been minimal progress in estimating representational dimensionality of control representations in the human PFC using multi-voxel pattern analysis (MVPA).

In regions like the PFC, decoding information from multi-voxel patterns has proven difficult, with typical decoding accuracies barely above chance levels [47], a stark contrast from other areas of neocortex. In part, this may be due to the lower reliability of multi-voxel patterns in PFC. Another reason may be that MVPA relies on small biases in the distribution of selective neurons across voxels. The noted lack of mesoscale spatial clustering of neurons with similar selectivity in PFC may reduce differences between conditions at the voxel scale [34].

An alternate approach uses repetition suppression (RS) to query the representation’s geometry [48, 49]. RS is a decrease in a neuron’s firing rate when it is repeatedly driven over a short time scale and occurs at the single neuron level [50]. Thus, the aggregate suppression in a population of neurons when one task condition is followed by another estimates the overlap between two population neural representations, i.e., a distance in pattern space. These aggregate RS effects are accessible using fMRI [50]. Ongoing work in our lab is leveraging this approach to estimate representational dimensionality in the PFC, with promising results [48].

As a consequence of this gap in human neuroscience, little directly ties the valuable knowledge of PFC representational dimensionality gained from monkey physiology to cognitive control systems of the human brain. However, this link is important to establish. For example, monkeys are trained for thousands of trials under highly controlled conditions. So, there is considerable opportunity for neuroplastic change that may not be representative of the human participant who is verbally instructed on a task and performs it immediately. Likewise, humans may conceive of task structure differently than an animal whose performance is shaped through reinforcement. As such, it is important to study representational dimensionality of control representations in the human brain.

What about the hypothetical benefits of high versus low dimensionality for controlled behavior? The relationship of the separability vs. generalizability tradeoff to controlled behavior has yet to be tested. For example, we know of no evidence for enhanced flexibility or reduced interference in association with high dimensional representations. Indeed, though not testing dimensionality directly, the human EEG studies described above observed that strong conjunctive representations lead to worse switch costs on subsequent trials, particularly when features of the next trial are only partially different from the preceding one [10]. On face, this observation is at odds with the hypothetical advantage of a highly separated control representation on interference or flexibility. Likewise, little is presently known about how the dimensionality of control representations affects behavior when one first performs a task versus when one has had extensive experience. Thus, identifying the specific computational and behavioral benefits of high dimensionality for control is a crucial direction of future research.

As future experiments address these gaps and others (Box 2), we will gain a firmer understanding of how control representations organize task information in a way that yields computational benefits for controlled behavior. Those insights hold the promise of transforming not only our understanding of the role played by control representations, but of the nature of cognitive control itself.’

Box 2 – Control representation geometry: open problems and future directions.

1. How can the dimensionality of human PFC control representations be measured?

2. What is the dimensionality of human PFC control representations and what is their position on the separability vs. generality axis? How does this relate to human flexibility?

3. What task information enters a control representation and which factors influence this choice?

4. How are control representations assembled online during task performance? Is information entering a control representation obligatorily mixed in a high-dimensional code?

5. How does the dimensionality of PFC control representations relate to measures of control function and cognitive flexibility?

6. How are arbitrary control representations for novel tasks rapidly invoked with instruction and flexibly read out without prior training?

7. Does experience affect the dimensionality of control representations?

Highlights.

• A normative conception of control representations

• Representational dimensionality and the separability vs generalizability trade-off

• Implications of separability and generalizability for cognitive control

• Current findings on the dimensionality of control representations

• Directions for future research