Bayesian Phase I/II Biomarker-based Dose Finding for Precision Medicine with Molecularly Targeted Agents

Abstract

The optimal dose for treating patients with a molecularly targeted agent may differ according to the patient’s individual characteristics, such as biomarker status. In this article, we propose a Bayesian phase I/II dose-finding design to find the optimal dose that is personalized for each patient according to his/her biomarker status. To overcome the curse of dimensionality caused by the relatively large number of biomarkers and their interactions with the dose, we employ canonical partial least squares (CPLS) to extract a small number of components from the covariate matrix containing the dose, biomarkers, and dose-by-biomarker interactions. Using these components as the covariates, we model the ordinal toxicity and efficacy using the latent-variable approach. Our model accounts for important features of molecularly targeted agents. We quantify the desirability of the dose using a utility function and propose a two-stage dose-finding algorithm to find the personalized optimal dose according to each patient’s individual biomarker profile. Simulation studies show that our proposed design has good operating characteristics, with a high probability of identifying the personalized optimal dose.

1. Introduction

Precision or personalized medicine provides emerging approaches for disease treatment and prevention that take into account each person’s individual variability in genes, environment, and lifestyle. Precision medicine is revolutionizing the treatment of cancer and other diseases. Optimizing the treatment benefit under this paradigm requires the dose-finding method to account for the patient’s individual characteristics when searching for the optimal dose that is “personalized” for each patient.

To account for individual patient characteristics, the most natural approach is to include the patient’s individual characteristics as well as the interactions between those characteristics and the dose as covariates or the stratification variable in the dose-finding model. Piantadosi and Liu (1996) developed dose-finding methods that incorporate the patient’s pharmacokinetic data to improve the performance of the trial designs. Babb and Rogatko (2001) described a phase I clinical trial that utilizes patient covariate information. O’Quigley and Paoletti (2003), Yuan and Chappell (2004), and Ivanova and Wang (2006) proposed dose-finding methods for patient subgroups that are prespecified by certain prognostic factors. Thall, Nguyen and Estey (2008) proposed a patient-specific phase I/II dose-finding method based on bivariate (efficacy and toxicity) outcomes that account for patient characteristics and their interactions with the dose. A common limitation of these methods is that they can accommodate only a very small number (e.g., 1 or 2) of patient characteristics into the dose-finding process in order to avoid the curse of dimensionality when working with the small sample sizes that are typical of early-phase trials. For example, the method of Thall, Nguyen and Estey (2008) considered only two prognostic factors and their interactions with the dose. In practice, however, the number of patient characteristics that may affect the dose-response relationship can be easily more than two, and moreover these characteristics (e.g., some biomarkers) may be highly correlated. The direct inclusion of a large number of potentially highly correlated patient characteristics as covariates in regression models leads to extremely unreliable estimates or identification problems.

Our motivating example is a phase I/II trial for the purpose of finding the optimal doses of a novel molecularly targeted agent in patients with locally advanced or metastatic solid tumors that may harbor molecular alterations in five genes: the NTRK1 gene, NTRK2 gene, NTRK3 gene, ROS1 gene, and ALK gene. The types of molecular alterations include gene rearrangements, single-nucleotide polymorphisms, insertions, deletions, splice variants and gene amplifications. Molecular alterations in these target genes have been detected in various cancers, including non-small cell lung cancer, colorectal cancer, thyroid cancer, pancreatic cancer and neuroblastoma, and are expected to be predictive markers that may influence the treatment effect of the agent. In the study, the status of each of the five target genes is coded as positive (i.e., has alterations) or negative (i.e., no alterations), and is evaluated for each patient using next-generation sequencing. Patients receive the treatment agent orally, once daily in the morning for 28 consecutive days in repeated 4-week cycles. Toxicity is graded according to the National Cancer Institute Common Terminology Criteria for Adverse Events, Version 4.03, and coded as a three-level ordinal variable: grade 1 or 2, grade 3, or grade ≥4 adverse events. Efficacy is evaluated using the Response Evaluation Criteria In Solid Tumors, and coded as a three-level ordinal variable: progressive disease (PD), stable disease (SD), or partial or complete remission (PR/CR). Five doses (100, 300, 500, 700, 900mg/m²/day) are evaluated. The primary objective of the trial is to find the optimal dose that is safe and efficacious for each patient according to the patient’s specific pattern of molecular alterations of the five genes. For this trial, the straightforward approach that directly includes gene alterations and their interactions with the dose as covariates in the dose-toxicity and dose-efficacy models would not work because it results in an excessive number of covariates in the model (the dose, 5 gene alteration indicators, and 5 dose-gene alteration interactions). In addition, these covariates may be highly correlated.

We propose a Bayesian phase I/II personalized dose-finding method that can accommodate a more realistic number of patient characteristics or biomarkers. For brevity of description, we use “patient characteristic” and “biomarker” exchangeably hereafter. To circumvent the curse of dimensionality and potential high correlations among biomarkers, we employ the canonical partial least squares (CPLS) method to extract a small number of components from the covariate matrix consisting of dose, biomarker profile, and dose-by-biomarker interactions. These CPLS components capture most of the covariate information that is predictive of the response (Garthwaite, 1994). Conditional on the CPLS components, we take a latent-variable approach to model the ordinal toxicity and efficacy outcomes. We quantify the desirability of the doses using a utility function elicited from physicians that accounts for the risk-benefit tradeoff. A two-stage dose-finding algorithm is proposed to guide dose assignment and selection.

The remainder of this article is organized as follows. In Section 2, we present the joint probability model for the ordinal toxicity and efficacy outcomes. Section 3 describes a two-stage dose-finding algorithm. Section 4 examines the operating characteristics of the proposed design through simulation studies, and Section 5 provides concluding remarks.

2. Method

2.1. Canonical partial least squares

Partial least squares (PLS) is a dimension-reduction technique for modeling the relationship between response variable(s) and explanatory variables (Stone and Brook, 1990; Frank and Fridman, 1993; Garthwaite, 1994). It can be used for either univariate regression with one response variable or multivariate regression with multiple response variables. The basic idea is to construct a few PLS components, which are linear combinations of the explanatory variables, to capture most of the information contained in the explanatory variables for predicting the response variable(s). These PLS components can be used to replace the original high-dimensional explanatory variables in a subsequent regression analysis. Unlike the wellknown principal component analysis that extracts principal components solely based on the explanatory variables, PLS determines components using both the response variable(s) and the explanatory variables. Therefore, PLS is more relevant for regression and provides better prediction. PLS was originally developed for continuous response variables (Garthwaite, 1994). To handle categorical response variables, Indahl, Liland and Nas (2008) proposed the CPLS method, which integrates the PLS methodology with canonical correlation analysis. These authors show that CPLS is able to extract more information from the first few components than the ordinary PLS approach. This property is particularly attractive for early-phase clinical trials because of the small sample sizes. We favor the use of a parsimonious model with fewer CPLS components.

Suppose the response variable has J (≥ 2) categories and the sample size is n. Let X be the n × p covariate matrix, with each covariate centered at its mean, Y be the n × 1 categorical response vector, and A_Y be the n × J dummy coded group membership matrix for the response variable Y, with A_Y [i, j] = 1 if Y_i = j, and 0 otherwise. The CPLS algorithm is a sequential procedure that iteratively extracts components of X, each a linear combination of the original covariates, in such a way that the first component contains the most information for predicting Y, the second component contains less information than the first, and so on.

To begin, the CPLS algorithm first transforms the X matrix to R = XQ, where Q = X′A_Y . A CPLS component for predicting A_Y is found by maximizing the canonical correlation between R and A_Y . More specifically, the CPLS method finds vectors a, b ∈ ℝJ to maximize the correlation between Ra and A_Y b:

$$\text{cor}(\mathit{R}\text{a},{\mathit{A}}_Y\mathbf{\text{b}})=\frac{\mathbf{\text{a}}\prime \mathit{R}\prime {\mathit{A}}_Y\mathbf{\text{b}}}{\sqrt{\mathbf{\text{a}}\prime \mathit{R}\prime \mathit{R}\mathbf{\text{a}}}\sqrt{\mathbf{\text{b}}\prime {\mathit{A}}_Y\prime {\mathit{A}}_Y\mathbf{\text{b}}}}$$ (1)

This optimization problem is the canonical correlation analysis with respect to R and A_Y, so in this sense CPLS combines PLS and canonical correlation analysis. Maximization of (1) is equivalent to maximization of the function

$$f(\mathbf{\text{r}},\mathbf{\text{t}})={\mathbf{\text{r}}}^{\prime }{({\mathit{R}}^{\prime }\mathit{R})}^{-\frac{1}{2}}{\mathit{R}}^{\prime }{\mathit{A}}_Y{({\mathit{A}}_Y^{\prime }{\mathit{A}}_Y)}^{-\frac{1}{2}}\mathbf{\text{t}}$$ (2)

over unit vectors r and t (Indahl, Liland, and Nas, 2009). The solution of r and t is the dominant left and right singular vectors (with unit length) corresponding to the largest singular value in the singular value decomposition of the matrix ${({\mathit{R}}^{\prime }\mathit{R})}^{-\frac{1}{2}}{\mathit{R}}^{\prime }{\mathit{A}}_Y{({\mathit{A}}_Y^{{}^{\prime }}{\mathit{A}}_Y)}^{-\frac{1}{2}}$ The values of a and b that maximize the objective function (1) are given by $\mathbf{\text{a}}={({\mathit{R}}^{\prime }\mathit{R})}^{-\frac{1}{2}}\mathbf{\text{r}}$ and $\mathbf{\text{b}}={({\mathit{A}}_Y^{{}^{\prime }}{\mathit{A}}_Y)}^{-\frac{1}{2}}\mathbf{\text{t}}$, and the resulting CPLS component is c₁ = X w, a linear combination of the original covariates, where w = Qa /||Qa|| is the vector of the loading weights. This is the first CPLS component. Subsequent CPLS components (e.g., the second, third,…) are extracted in a similar way, in sequence, by replacing X and A_Y with their deflated matrices. For example, the second CPLS component c₂ is obtained by maximizing the objective function (1), with X and A_Y replaced by their deflated matrices $\tilde{\mathit{X}}=\mathit{X}-{({\mathit{c}}_1^{\prime }{\mathit{c}}_1)}^{-1}{\mathit{c}}_1{\mathit{c}}_1^{\prime }\mathit{X}$ and ${\tilde{\mathit{A}}}_Y={\mathit{A}}_Y-{({\mathit{c}}_1^{\prime }{\mathit{c}}_1)}^{-1}{\mathit{c}}_1{\mathit{c}}_1^{\prime }{\mathit{A}}_Y$. The deflation ensures that subsequent components contain information that is not explained by earlier components. The CPLS components can be extracted using the SIMPLS algorithm (de Jong, 1993) or the NIPALS algorithm (Burnham, Viveros, and MacGregor, 1996). When the response variable Y has only two categories, the CPLS reduces to the traditional PLS.

2.2. Probability models

Consider a phase I/II clinical trial with R prespecified doses (d₁, · · ·, d_R) of a molecularly targeted agent. Let Y_T and Y_E be the toxicity outcome and the efficacy outcome, respectively. We define Y_T = 1, 2, · · ·, J corresponding to increasing levels of severity of toxicity, and Y_E = 1, 2, · · ·, K corresponding to increasingly desirable efficacy. Unlike the method of Thall, Nguyen and Estey (2008), which dichotomizes Y_T and Y_E into binary variables, here we choose to model Y_T and Y_E as ordinal variables for several reasons. First, the ordinal variables reflect the actual scale used for measuring toxicity and efficacy in clinical studies. For example, in our motivating solid tumor trial, toxicity is scored as grades 1 to 5 and coded as a three-level ordinal variable (i.e., grades 1–2, grade 3, and grade ≥ 4), and efficacy is scored as PD, SD, or PR/CR. These refined scales contain more information than the dichotomized toxicity and efficacy outcomes for decision making (Yuan, Chappell, and Bailey, 2007; Houede et al., 2010). Second, and more importantly, although using binary toxicity and efficacy outcomes is generally appropriate for conventional cytotoxic agents, it is often problematic for the novel molecularly targeted agents on which we focus here. For example, the binary efficacy outcome typically defines CR/PR as a response, and PD/SD as a nonresponse. That is sensible for conventional cytotoxic agents that work by shrinking the tumor. However, many novel targeted agents are cytostatic agents, which function by stabilizing the tumor rather than shrinking it. For these agents, SD is often regarded as a favorable outcome, although not as desirable as CR/PR, and thus should be distinguished from PD.

Let n denote the number of patients enrolled in the trial at an interim decision time, $\mathit{X}={(X_1,···,X_p)}^{\prime }$ denote the vector of p binary biomarkers, each taking a value of “positive” or “negative”, and Z denote the dose with $Z\in (d_1,···,d_R)$. Define an n ×(1 + 2p) covariate matrix $\mathit{V}=(Z,X_1,···,X_p,Z{X}_1,···,Z{X}_p)$, where $Z{X}_1,···,Z{X}_p$ represent the interactions between dose Z and biomarkers X₁ to X_p. In our motivating trial, there are 5 genes (i.e., p = 5) and the dimension of the covariate matrix V is n × 11. Some covariates may be highly correlated. Since the sample size is typically small in a phase I/II clinical trial, directly regressing (Y_T, Y_E) on X suffers from the curse of dimensionality and the collinearity issue, resulting in highly unstable estimates. To overcome these issues, in our approach, we first use the CPLS to reduce the dimension of the covariate matrix, and then regress (Y_T, Y_E) on the reduced covariate matrix. Specifically, we extract the first q₁ CPLS components $W_T(Z,\mathit{X})=(W_{T,1}(Z,\mathit{X}),\cdot \cdot \cdot ,W_{T,q1}(Z,\mathit{X}))$ from V for predicting Y_T, and the first q₂ CPLS components $W_E(Z,\mathit{X})=(W_{E,1}(Z,\mathit{X}),\cdot \cdot \cdot ,W_{E,q2}(Z,\mathit{X}))$ for predicting Y_E, where q₁, q₂ < 1 + 2p. Each of these components is a linear combination of biomarkers X, dose Z and their interactions. We discuss how to choose q₁ and q₂ later. As biomarkers that are predictive of toxicity may differ from those that are predictive of efficacy, we extract the CPLS components independently for toxicity and efficacy. As a result, the jth component of W_T (Z, X) is not necessarily the same as that of W_E (Z, X). In practice, some biomarkers could affect the treatment efficacy but are less likely to affect the toxicity. The CPLS method will automatically detect such differences and assign different weights to different biomarkers for predicting efficacy and toxicity. When there is knowledge that some biomarkers are not expected to impact the toxicity or efficacy profile, we may use different sets of covariates to construct W _T (Z, X) and W_E (Z, X). For notational brevity, we suppress arguments Z and X in W_T (Z, X) and W_E (Z, X) when this does not cause confusion.

We take the latent variable approach to model the relationship between Y_k and W _k, where k = T or E. Let subscript i index patients. We assume that there are two latent normal variables $Y_{T,i}^{*}$ and $Y_{E,i}^{*}$ for patient i, which follow linear models

$$Y_{T,i}^{*}\left|{\mathit{W}}_{T,i},{\mathbf{\beta }}_T,{\theta }_i,{\tau }_{T,i}^2\right.\hspace{0.17em}\sim N({\theta }_i+{\mathit{W}}_{T,i}{\mathbf{\beta }}_T,{\tau }_{T,i}^2)$$

$$Y_{E,i}^{*}\left|{\mathit{W}}_{E,i},{\mathit{\beta }}_E,{\theta }_i,{\tau }_{E,i}^2\right.\hspace{0.17em}\sim N({\theta }_i+{\mathit{W}}_{E,i}{\mathit{\beta }}_E,{\tau }_{E,i}^2),$$

where β_T and β_E are vectors of the regression coefficients, and θ_i ∼ N (0, σ²) is a patient-specific random effect that is used to account for the correlation between $Y_{T,i}^{*}$ and $Y_{E,i}^{*}$. By integrating out θ_i, it is easy to see that the above random-effect model specification essentially assumes that marginally $Y_{T,i}^{*}$ and $Y_{E,i}^{*}$ follow a bivariate normal distribution

$$Y_{T,i}^{*},Y_{E,i}^{*}\left|{\mathit{W}}_{T,i},{\mathit{W}}_{E,i},{\mathit{\beta }}_T,{\mathit{\beta }}_E,{\tau }_{T,i}^2,{\tau }_{E,i}^2,{\sigma }^2\right.\sim N_2\left(\left(\begin{array}{c}{\mathit{W}}_{T,i}{\mathit{\beta }}_T\\ {\mathit{W}}_{E,i}{\mathit{\beta }}_E\end{array}\right),\left(\begin{array}{cc}{\tau }_{T,i}^2+{\sigma }^2& {\sigma }^2\\ {\sigma }^2& {\tau }_{E,i}^2+{\sigma }^2\end{array}\right)\right).$$

Although equivalent, presenting the model using the random effect facilitates the implementation of the Gibbs sampler as $Y_{T,i}^{*}$ and $Y_{E,i}^{*}$ are independent once conditional on random effect θ_i.

We assume that the observed toxicity and efficacy outcomes Y_T,i and Y_E,i for the ith patient are related to $Y_{T,i}^{*}$ and $Y_{E,i}^{*}$ of the form

$$Y_{T,i}=j\hspace{1em}\hspace{1em}\text{if}\hspace{1em}\hspace{1em}{\gamma }_{T,j-1}<Y_{T,i}^{*}\le {\gamma }_{T,j}$$

$$Y_{E,i}=k\hspace{1em}\hspace{1em}\text{if}\hspace{1em}\hspace{1em}{\gamma }_{E,k-1}<Y_{E,i}^{*}\le {\gamma }_{E,k},$$

where $-\infty \equiv {\gamma }_{T,0}<{\gamma }_{T,1}<···<{\gamma }_{T,J}\equiv \infty$ and $-\infty \equiv {\gamma }_{E,0}<{\gamma }_{E,1}<···<{\gamma }_{E,K}\equiv \infty$ are unknown cutoffs. Clearly, the above models are not identifiable. Using the toxicity model as an example, the scale parameter τ_T,i of the latent variable $Y_{T,i}^{*}$ is fully confounded with β_T and the cutoffs γ_T,j in the sense that we obtain the same likelihood when multiplying β_T, τ_T,i and γ_T,j by a constant. Similar confounding occurs in the efficacy model. To identify the toxicity model, we fix the scale of the latent variable $Y_{T,i}^{*}$ by setting $Y_{T,i}^2=1$ (Albert and Chib, 1993). This results in the familiar cumulative probit model for toxicity:

$${\mathrm{\Phi }}^{-1}\left[\text{Pr}(Y_{T,i}\le j\left|{\mathit{W}}_{T,i},{\theta }_i\right.,{\gamma }_{T,j},{\mathit{\beta }}_T)\right]={\gamma }_{T,j}-{\theta }_i-{\mathit{W}}_{T,i}{\mathit{\beta }}_T$$ (3)

for j = 1, · · ·, J − 1. Although we could directly model Y_T using the above model, taking the latent variable approach greatly simplifies the posterior sampling using the Gibbs sampler (Albert and Chib, 1993).

It is tempting to take the same approach to define a cumulative probit model for Y_E by setting ${\tau }_{E,i}^2=1$. However, the cumulative probit model such as (3) implies a stochastic ordering of the effects of the covariates on the outcome; that is, for any two doses d_r and $d_{r^{\prime }}$, either $\text{Pr}(Y_{T,i}\le j{\left|\mathit{W}\right.}_T(Z=d_r,\mathit{X}))\le \text{Pr}(Y_{T,i}\le j\left|{\mathit{W}}_T\right.(Z=d_{r^{\prime }},\mathit{X}))$ or $\text{Pr}(Y_{T,i}\le j\left|{\mathit{W}}_T(Z=d_r,\mathit{X})\right.)\ge \text{Pr}(Y_{T,i}\le j\left|{\mathit{W}}_T(Z=d_{r^{\prime }},\mathit{X})\right.)$ for all $j=1,\mathrm{\dots },J-1$. Such a monotonic assumption is typically reasonable for toxicity, but often problematic for efficacy because the efficacy behavior of molecularly targeted agents is more complex and the dose-efficacy relationship may not strictly monotonically increase. The dose-efficacy curve may plateau or sometimes be lower at higher doses (Postel-Vinay et al., 2009). To accommodate this feature of molecularly targeted agents, we set ${\tau }_{E,i}=\text{exp}(\tau Z_i)$, resulting in the following dispersed cumulative probit model (McCullagh, 1980; Cox, 1995; and Agresti, 2002),

$${\mathrm{\Phi }}^{-1}\left[\text{Pr}(Y_{E,i}\le k\left|{\mathit{W}}_{E,i},{\theta }_i,{\gamma }_{E,k},{\beta }_E\right.)\right]=\frac{{\gamma }_{E,k}-{\theta }_i-{\mathit{W}}_{E,i}{\mathit{\beta }}_E}{\text{exp}(\tau Z_i)},\hspace{1em}k=1,\cdot \cdot \cdot ,K-1.$$ (4)

By introducing the dispersion parameter, τ, $Y_E^{*}$will have different dispersions (or variances) across doses Z, and thus the model does not impose the stochastic ordering of the dose effect on efficacy (Agresti, 2002). When τ = 0, the model reduces to the standard cumulative probit model.

Based on the above formulation, the likelihood function for patient i is

$$\begin{gathered} p(y_{T,i},y_{E,i})=\text{Pr}(Y_{T,i}=y_{T,i},Y_{E,i}=y_{E,i})=\text{Pr}({\gamma }_T{{}_{,}}_{y_{T.i}-1}<Y_{T,i}^{*}\le {\gamma }_{T,y_{T,i}},{\gamma }_{E,y_{E,i}-1}<Y_{E,i}^{*}\le {\gamma }_{E,y_{E,i}}) \\ ={\int }_{{\gamma }_{T,}{}_{y_{T,i-1}}}^{{\gamma }_{T,}{}_{y_{T,i}}}{\int }_{{\gamma }_{E,y_{E,i-1}}}^{{\gamma }_{E,y_{E,i}}}{\varphi }_2(Y_{T,i}^{*},Y_{E,i}^{*}\left|{\mathit{\mu }}_Y,\sum Y\right.)d{Y}_T^{*}d{Y}_E^{*} \end{gathered}$$

where ${\varphi }_2(\cdot |\mathit{\mu },\sum )$ is the density of a bivariate normal distribution with mean vector µ and covariance matrix Σ,

$${\mu }_Y=\left(\begin{array}{c}{\mathit{W}}_{T,i}{\mathit{\beta }}_T\\ {\mathit{W}}_{E,i}{\mathit{\beta }}_E\end{array}\right),\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbf{\Sigma }}_Y=\left(\begin{array}{cc}{\tau }_{T,i}^2+{\sigma }^2& {\sigma }^2\\ {\sigma }^2& {\tau }_{E,i}^2+{\sigma }^2\end{array}\right).$$

Letting $\Theta =({\gamma }_{T,1},\mathrm{\dots },{\gamma }_{T,J},{\beta }_T,{\gamma }_{E,1},\mathrm{\dots },{\gamma }_{E,K},{\beta }_E,\tau ,{\sigma }^2)$ denote the parameters, and ${\mathcal{D}}_n=\{(Y_{T,i},Y_{E,i},Z_i,{\mathit{W}}_i),i=1,\mathrm{\dots },n\}$ denote the data from the n patients when an interim decision is to be made, the likelihood based on n patients is

$$\mathcal{L}({\mathcal{D}}_n|\Theta )\propto \prod _{i=1}^{n}p(y_{T,i},y_{E,i}).$$

Letting f (Θ) be the joint prior distribution for Θ, the joint posterior distribution of Θ is

$$f(\Theta |{\mathcal{D}}_n)\propto f(\Theta )\mathcal{L}({\mathcal{D}}_n|\Theta ).$$

We sample the posterior using the Gibbs sampler. The details are provided in the Supplementary Materials.

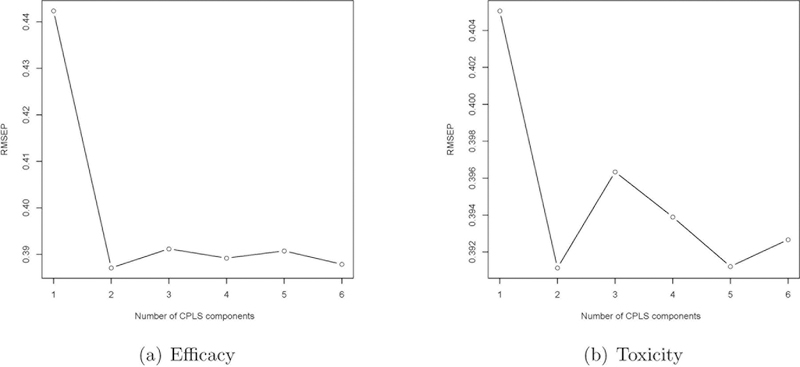
Next, we discuss how to choose the number of PLS components (i.e., q₁ and q₂) included in the toxicity and efficacy models. The choice of q₁ and q₂ requires balancing two, often conflicting, modeling considerations. On one hand, to avoid information loss and achieve estimation accuracy, it is desirable to include in the models all the PLS components that contain non-negligible information for predicting the outcomes; on the other hand, the small sample size and sequential accrual of patients in phase I/II trials prohibit us from including too many PLS components in the toxicity and efficacy models. A practical approach is to use the scree plot as a guidance to choose q₁ and q₂. The scree plot is widely used in principal component analysis and factor analysis to visually assess which components or factors explain most of the variability in the data and determine the number of important components or factors. In the principal component analysis, the scree plot displays the eigenvalues versus the number of components; whereas in our case, the scree plot displays the root mean squared error of prediction (RMSEP) for the response variable (Y_T or Y_E) versus the number of CPLS components. Given a specific number of CPLS components, the RMSEP can be obtained using a leave-one-out cross-validation or a k-fold cross-validation. The ideal pattern in a scree plot is a steep curve, followed by a bend and then a flat or horizontal line. We retain those CPLS components in the steep curve before the first point that starts the flat line trend. When the scree plot suggests a large number of CPLS components, we recommend restricting q₁, q₂ ≤ 4 because of the small sample size of phase I/II trials. In numerical studies described later, 2 CPLS components generally work well under a variety of scenarios. As an example, Figure 1 shows the scree plots for scenario 1, which indicates that 2 CPLS components are appropriate. Nguyen and Rocke (2002) showed that 3 to 5 PLS components are often adequate, even in applications with thousands of genes.

Figure 1:

Scree plots of the root mean squared error of prediction (RMSEP) versus the number of CPLS components for efficacy and toxicity.

2.3. Prior specification

Care should be taken when specifying the prior distribution f (Θ). Unlike typical inference problems with moderate or large sample sizes, for which conventional noninformative or flat priors are routinely used to make posterior estimation, noninformative priors are often not suitable for early-phase trial designs. This is because the sample size of an early-phase trial is typically small and only a few observations may be available at the beginning of the trial. In this case, using the standard flat priors often results in highly unreliable estimates and causes inappropriate dose escalation and de-escalation. On the other hand, because of the small sample size, we should avoid using priors that are substantially informative and thus would not allow the accumulating data to dominate the priors as the trial proceeds. For the purpose of early-phase trial designs, a desirable prior should be sufficiently regularized (or informative) so that the design and model estimates are reasonably stable throughout the trial, while also being vague enough so that the accumulating data can rapidly dominate the prior as the trial proceeds.

Our approach to specify priors follows a principle similar to that of Gelman et al. (2008), which states that the prior should be regularized to reflect that a typical change in a covariate is unlikely to lead to a dramatic change in the probability of the response variable. Under the probit model, a change of 2.5 on the probit scale moves a probability of Y_T or Y_E located in one category from 0.1 to 0.89. It is typically reasonable to assume that the effect of a covariate or biomarker is unlikely to be more dramatic than that. This is particularly true for dose-finding trials where the target toxicity and efficacy rates are rarely outside that range. Based on this consideration, to specify the priors of β_T and β_E, we first scale each covariate in W_T and W_E to have mean 0 and standard deviation 0.5, and then assign the independent normal prior distribution N (0, 1.25²) to each element of β_T and β_E. By doing so, a change in a covariate from one standard deviation below the mean to one standard deviation above the mean will result in a change mostly within the range of (0, 2.5) (i.e., a change of 2 standard deviations for the prior) on the probit scale. For the intercepts γ_T,j and γ_E,k, we use the same normal priors under the constraint that ${\gamma }_{T,1}<\mathrm{\dots }<{\gamma }_{T,J}$ and ${\gamma }_{E,1}<\mathrm{\dots }<{\gamma }_{E,K}$. The prior distributions for σ² and τ are chosen to be InvGamma(a, b) and Uniform(−c, c) distributions, respectively. The hyper-parameters are set to be a = 0.1 and b = 0.1 so that a priori the probability that the correlation between toxicity and efficacy is between 0.045 and 1 is 99%, and c = 4 to make the prior distribution of τ weakly informative so that the posterior distribution is dominated by the data.

2.4. Personalized optimal dose

Taking the setting of our motivating trial, both toxicity and efficacy outcomes are categorized as ordinal variables with 3 categories, with Y_T = 1, 2, 3 representing grade 1 or 2, grade 3, and grade ≥ 4 adverse events, respectively, and Y_E = 1, 2, 3 representing PD, SD, and PR/CR, respectively. To define the personalized optimal dose for each patient, we first define the range of acceptable doses to safeguard against using doses that are overly toxic or futile. Let π_T (3) ≡ Pr(Y_T = 3|Z, X), π_E(3) ≡ Pr(Y_E = 3|Z, X), and π_E(2, 3) ≡ Pr(Y_E = 2 or 3|Z, X). At an interim time with observed data D_n, for a patient with biomarker vector X, we define dose Z as having acceptable toxicity if

$$\text{Pr}({\pi }_T(3)\ge {\varphi }_T|W(Z,\mathit{X}),{\mathcal{D}}_n)\le {\delta }_T,$$ (5)

and acceptable efficacy if

$$\text{Pr}({\pi }_E(3)\le {\varphi }_{E,3}|W(Z,\mathit{X}),{\mathcal{D}}_n)\le {\delta }_{E,3}$$ (6)

or

$$\text{Pr}({\pi }_E(2,3)\le {\varphi }_{E,2}|W(Z,\mathit{X}),{\mathcal{D}}_n)\le {\delta }_{E,2},$$ (7)

where ϕ_T is the upper bound on the probabilities of toxicity, ϕ_E,3 and ϕ_E,2 are the lower bounds on the probabilities of efficacy, and δ_E,3, δ_E,2 and δ_T are non-negative cutoffs. The values of ϕ_T, ϕ_E,3 and ϕ_E,2 should be elicited from physicians, and δ_E,3, and δ_E,2 and δ_T should be calibrated to obtain good design operating characteristics. The definition of acceptable efficacy (6) and (7) accounts for the practical consideration that for a molecularly targeted agent, a dose is considered promising if it can achieve a certain rate of CR/PR or a certain rate of SD (if the rate of CR/PR is low). For targeted agents, SD is often regarded as a favorable outcome as many targeted agents prolong survival without much tumor shrinkage.

Given a dose that has acceptable toxicity and efficacy, we measure its desirability using a utility function that accounts for the risk-benefit tradeoff that underlies medical decisions in practice. The utility is elicited from physicians as follows: we fix the desirability of the most desirable outcome pair (i.e., y_T = 1, y_E = 3) as ζ(1, 3) = 100 and the desirability of the least desirable outcome pair (i.e., y_T = 3, y_E = 1) as ζ(3, 1)=0, and then ask physicians to use these two pairs as references to score the desirability of the other elementary outcome pairs {ζ(y_T, y_E), y_T = 1, 2, 3, y_E = 1, 2, 3} using the scale of (0, 100). For the solid tumor trial, we obtain the following utility table.

	yE=1	yE=2	yE=3
yT=1	10	50	100
yT=2	5	20	60
yT=3	0	10	20

Then, for patients with biomarker profile X, the personalized optimal dose is defined as the dose that maximizes the true mean utility

$$U_{true}(Z,\mathit{X})=\sum _{y_T=1}^3\sum _{y_E=1}^3\zeta (y_T,y_E)\text{Pr}(y_T,y_E|Z,\mathit{X},\mathrm{\Theta }),$$

while also having both acceptable toxicity and efficacy defined by (5)–(7). Note that U_true(Z, X) depends on biomarker profile X, and thus the target doses may be different for patients who have different biomarker profiles. In addition, since the true mean utility U_true(Z, X) depends on unknown parameters Θ, we need to estimate it based on the observed data. During the trial, given the interim data ${\mathcal{D}}_n$ collected from n patients, we evaluate the desirability of dose Z for a patient with biomarker profile X based on the posterior mean utility,

$$U_n(W_T(Z,\mathit{X}),W_E(Z,\mathit{X}))=\sum _{y_{T=1}}^3\sum _{y_{E=1}}^3\zeta (y_T,y_E)E_{\Theta }[\text{Pr}\{y_T,y_E|W_T(Z,\mathit{X}),W_E(Z,\mathit{X}),\Theta \}|{\mathcal{D}}_n].$$

3. Personalized Dose-finding Algorithm

In the beginning of an early-phase clinical trial, decision making is difficult because of the small amount of available data. This is especially true in personalized dose finding where we need to account for patient heterogeneity in the biomarkers. To alleviate this issue, we take the approach of a two-stage dose-finding scheme. In stage I, conventional dose escalation will be conducted with a maximum sample size of N₁ patients, based only on the toxicity outcome without considering the patients’ biomarker profiles. The objective is to evaluate the safety of the doses and collect some preliminary toxicity and efficacy data to facilitate the model fitting in stage II. To be consistent with the conventional approach, at this stage, we dichotomize toxicity into dose-limiting toxicity or not, and set ϕ_T as the target rate. We employ the Bayesian optimal interval design (BOIN; Liu and Yuan, 2015) to conduct dose escalation because of its ease of implementation and good operating characteristics. Under the BOIN design, the dose escalation and de-escalation rules can be prespecified, similar to the approach of the 3+3 design, but yields good operating characteristics comparable to those of more complicated model-based methods, such as the continuous reassessment method (CRM; O’Quigley, Pepe, and Fisher, 1990). We note that any other dose-finding design can also be used for dose escalation in this stage.

After stage I is completed, we move to stage II and perform personalized dose finding based on the proposed models, with a maximum sample size of N₂ patients. Since the optimal dose depends on the patient’s individual biomarker profile, in stage II, we treat patients one by one, rather than as a cohort, and continuously update the dose-toxicity and dose-efficacy curves to determine the personalized optimal dose for each patient. Specifically, assuming that n − 1 patients have been enrolled in the trial, we assign a dose to the nth patient who has biomarker profile X_n as follows.

1. Based on the observed data ${\mathcal{D}}_{n-1}$, we extract the CPLS components, fit the model and determine the acceptable dose set $\mathcal{A}({\mathit{X}}_n)$ for the nth patient, i.e., the set of doses that have acceptable toxicity and acceptable efficacy defined by (5) to (7). Note that as $\mathcal{A}({\mathit{X}}_n)$ depends on the patient’s individual biomarker profile, it varies from patient to patient.

2. If $\mathcal{A}({\mathit{X}}_n)$ is an empty set, it means that no dose is acceptable for that patient; thus, the patient is treated off protocol. If a certain number, say 10, contiguous patients are treated off protocol, then we terminate the trial and conclude that no dose is acceptable.

3. If $\mathcal{A}({\mathit{X}}_n)$ is not empty, we use adaptive randomization to choose a dose in $\mathcal{A}({\mathit{X}}_n)$. We randomize the patient to dose j with probability λ proportional to its posterior expected utility, i.e.,

   $$\lambda =\frac{U_{n-1}(W_T(Z=d_j,\mathit{X}),W_E(Z=d_j,\mathit{X}))}{{\sum }_{d_j\in \mathcal{A}(X_n)}{U}_{n-1}(W_T(Z=d_j,\mathit{X}),W_E(Z=d_j,\mathit{X}))}.$$

   Compared to the common “greedy” approach of always assigning the patient to the dose with the highest estimate of $U_{n-1}(W_T(Z=d_j,\mathit{X}),W_E(Z=d_j,\mathit{X}))$, the use of adaptive randomization here affords the dose-finding algorithm more freedom to move around and thus avoids trapping it at local optimal doses.

4. We repeat steps 1–3 until we reach the maximum sample size of N₂. We do not allow for dose skipping when a dose escalation occurs.

After stage II is completed, we determine the personalized optimal dose, for each possible biomarker profile X, as the dose in $\mathcal{A}(\mathit{X})$ with the largest posterior mean utility $U_N(W_T(Z,\mathit{X}),W_E(Z,\mathit{X}))$, where N = N₁ + N₂.

4. Simulation

4.1. Simulation setting

We conducted simulation studies to assess the operating characteristics of the proposed design. Taking the setting of our motivating trial, we considered 5 dose levels, (Z₁,…, Z₅) = (0.1, 0.3, 0.5, 0.7, 0.9), and 5 biomarkers, (X₁,…, X₅). Each of the biomarkers was scored as positive (“+”) or negative (“−”). We assumed a high correlation of 0.9 between X₁ and X₂ to accommodate the situation in which some biomarkers are highly correlated. Other biomarkers (i.e., X₃, X₄ and X₅) were assumed to be independent of each other and X₁ and X₂. The probabilities of the 5 biomarkers being positive (“+”) were 0.5, 0.55, 0.5, 0.7, and 0.3, which encompass moderate, high and low prevalence rates. The toxicity upper bound ϕ_T = 0.3, and the efficacy lower bounds ϕ_E,2 = 0.4 and ϕ_E,3 = 0.25. The maximum sample size was 60, with stage I sample size N₁ = 21 and stage II sample size N₂ = 39. The Bayesian optimal interval design was used to conduct the stage I dose escalation with a cohort size of 3 using the R package “BOIN”. In stage II, we used the R package “pls” (Mevik, 2013) to extract the first two CPLS components to fit the regression models for toxicity and efficacy.

We constructed 8 scenarios to evaluate the performance of the proposed design. For the first 7 scenarios, data were generated from the “full” model with 5 biomarkers and their interactions with the dose. Specifically, for the ith patient treated at dose Z_i, his/her toxicity and efficacy outcomes were generated from the following models:

$$\text{Pr}(Y_{T,i}\le j|Z_i,{\mathit{X}}_i,{\theta }_i)=\mathrm{\Phi }\{{\theta }_i+{\gamma }_{T,}{}_j+{\beta }_{T,1}{Z}_i+{\beta }_{T,2}{X}_1+\dots +{\beta }_{T,6}{X}_5+{\beta }_{T,7}{X}_1{Z}_i+\dots +{\beta }_{T,11}{X}_5{Z}_i\}$$

$$\begin{gathered} \text{Pr}(Y_{E,i}\le j|Z_i,X_i,{\theta }_i)= \\ \mathrm{\Phi }\left\{\frac{{\theta }_i{\gamma }_{E,j}+{\beta }_{E,1}{Z}_i+{\beta }_{E,2}{X}_1+\dots +{\beta }_{E,6}{X}_5+{\beta }_{E,7}{X}_1{Z}_i+\dots +{\beta }_{E,11}{X}_5{Z}_i}{\text{exp}(\tau Z_i)}\right\} \end{gathered}$$

where j = 1, 2 and ${\theta }_i\sim N(0,{\sigma }^2)$. The true model parameters for the seven scenarios are provided in the Supplementary Materials. Figures 2 and 3 provide graphical presentations of the main effects and interaction effects of the 5 biomarkers on efficacy and toxicity, respectively, for scenarios 1–7. As shown by Figures 2 and 3, the seven scenarios were chosen to cover different cases of biomarker effects. For example, in scenario 1, biomarkers 1 and 5 have main effects on toxicity, and biomarkers 1, 2, 4, and 5 interact with the dose to affect toxicity; biomarkers 1 and 3 have main effects on efficacy, and biomarkers 1 and 4 interact with the dose to affect efficacy. In scenario 2, none of the 5 biomarkers has a main effect on toxicity, only 1 biomarker (i.e., biomarker 3) interacts with the dose to affect the toxicity probability, and all 5 biomarkers are involved in the efficacy probability. Scenario 7 shows an interesting and common case with targeted agents: no treatment effect is observed except in the presence of some combination of biomarkers. The drug is effective only for the patients for whom the first 3 biomarkers are positive, regardless of the status of biomarkers 4 and 5. In other words, the treatment is effective only for four biomarker patterns: (+ + + + +), (+ + + − −), (+ + + − +), and (+ + + + −).

Figure 2:

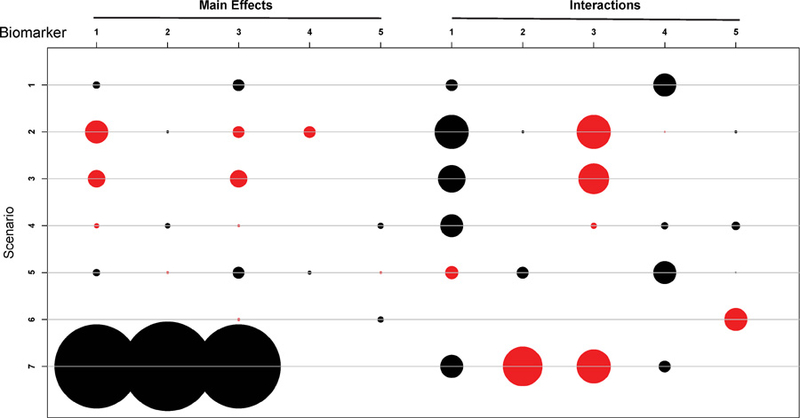
Main effects and interaction effects on efficacy probabilities for the eight scenarios. The radius of a circle is proportional to the absolute value of the coefficient. Red and black circles respectively represent positive and negative coefficients.

Figure 3:

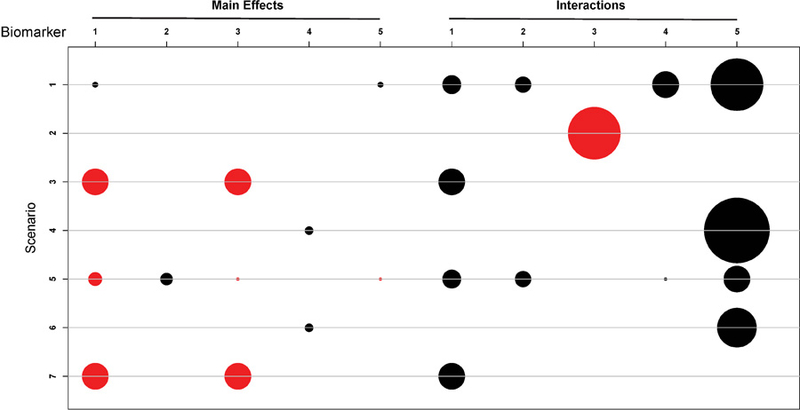
Main effects and interaction effects on toxicity probabilities for the eight scenarios. The radius of a circle is proportional to the absolute value of the coefficient. Red and black circles respectively represent positive and negative coefficients.

Scenario 8 is considered a special case in that as long as one of the first three biomarkers is positive, they cause the same effect on efficacy. Such a situation may occur when the three biomarkers represent molecular alterations in the same pathway, and any alteration in a pathway is sufficient to cause the same effect on efficacy. More precisely, the efficacy outcomes are generated from the following model:

$$\begin{gathered} \text{Pr}(Y_{E,i}\le j|Z_i,{\mathit{X}}_i{\theta }_i)= \\ \mathrm{\Phi }\left\{\frac{{\theta }_i+{\gamma }_{E,j}+{\beta }_{E,1}{Z}_i+{\beta }_{E,2}I(X_1+X_2+X_3>1)+{\beta }_{E,3}{X}_4+{\beta }_{E,4}{X}_5{X}_4{Z}_i+{\beta }_{E,6}{X}_5{Z}_i}{\text{exp}(\tau Z_i)}\right\} \end{gathered}$$

where $I(\mathcal{C})$ is an indicator function and equal to 1 if $\mathcal{C}$ is true.

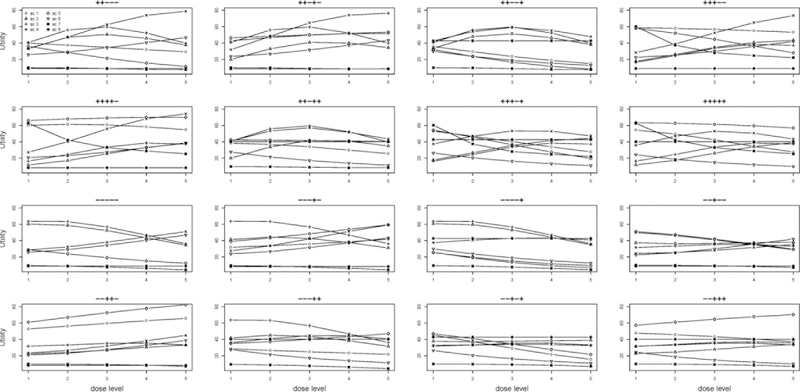
The eight chosen scenarios cover different shapes and magnitudes of utility, efficacy and toxicity probabilities. Because the efficacy and toxicity probabilities depend on the biomarkers, the shape of the dose-utility relationship varies across the biomarker patterns. Given 5 binary biomarkers, there were 2⁵ = 32 possible biomarker patterns. Figure 4 shows the shapes of the dose-utility curves under the 8 scenarios for 16 selected biomarker patterns. We can see that the dose-utility curves demonstrate various shapes: monotonically increasing, monotonically decreasing, increasing then decreasing, linear, and curved.

Figure 4:

Utility of the five doses for 16 biomarker patterns under the eight scenarios. Each graph shows the utility for one biomarker pattern. The symbols “+” and “−” above each graph indicate the status for the 5 biomarkers. The eight curves within each sub-group represent the utilities for the eight scenarios.

We compared our design to the “direct” approach, which directly includes dose, biomarkers, and the interactions between dose and biomarkers in the regression model. As it is not feasible to include all five biomarkers and their interactions with the dose (a total of 11 covariates) in the model, we included the dose, two biomarkers, X₁ and X₃, and their interactions with the dose in the model. To demonstrate the importance of accounting for the biomarker information in dose finding, we also compared our proposed design to a dose-only design that includes only the dose as the covariate in the toxicity and efficacy models. Under each scenario, we simulated 1000 trials.

4.2. Simulation results

Reporting the simulation results is not straightforward for personalized dose finding because under each scenario, there are 32 different biomarker patterns, and each pattern is associated with a unique set of dose-toxicity and dose-efficacy curves and optimal dose. Therefore, we report the results in two ways. Table 1 shows the mean and standard deviation of the percentage of correct selection (PCS) of the target doses across all 32 possible biomarker patterns under each of the 8 scenarios. This provides an overall average performance of the designs under each scenario. Here, the target doses are defined as the doses for which the utility values are at least 90% of that of the optimal dose. In the case in which there is no acceptable dose, due to either high toxicity or low efficacy at all dose levels, the PCS is defined as the percentage of inconclusive trials where no dose is selected as the optimal dose. In Table 2, we “zoom in” to report the selection percentage for each dose, given two representative biomarker patterns, in each scenario. This provides us with detailed information of how the designs perform for specific biomarker profiles. To cover more practical situations, we chose different representative biomarker patterns in different scenarios to obtain different dose-toxicity/efficacy/utility relationships, different numbers of target doses, and different locations of target doses. For example, in scenarios 1 and 2, the two biomarker patterns were selected to have different numbers and locations of target doses, and different shapes of the utility curves (monotonically increasing or decreasing with the dose); whereas in scenario 3, the dose-utility relationships are non-monotonic and the target doses are in the middle of the dose range for the second biomarker pattern. In Table 2, under each representative biomarker pattern in each scenario, the first three rows show the true marginal probabilities of Y_T = 3 and Y_E = 2 or 3, which determine the acceptability of the dose. The fourth row shows the utility of each dose, which determines the target doses.

Table 1:

The average and standard deviation (SD) of the percentage of correct selection (PCS) of target doses across 32 possible biomarker patterns under the proposed design, the direct approach, and the dose-only design.

Method	PCS	Scenario
		1	2	3	4	5	6	7	8
Proposed	Mean	0.697	0.710	0.708	0.775	0.729	0.697	0.683	0.820
	SD	0.18	0.21	0.14	0.30	0.24	0.11	0.27	0.17
Direct approach	Mean	0.589	0.829	0.815	0.637	0.601	0.489	0.650	0.480
	SD	0.16	0.14	0.06	0.42	0.23	0.32	0.30	0.27
Dose-only	Mean	0.461	0.510	0.501	0.500	0.455	0.195	0.285	0.257
	SD	0.26	0.23	0.16	0.22	0.30	0.02	0.0003	0.08

Table 2:

Selection percentage for each dose and the percentage of correct selection (PCS) for two representative biomarker patterns under each scenario. The numbers in boldface are target doses.

	Dose level					Percentage of correct selection
	1	2	3	4	5
	Scenario 1
	X = (+ + + + +)
P(YT = 3)	0.100	0.229	0.419	0.631	0.809
P(YE = 2)	0.197	0.117	0.052	0.017	0.004
P(YE = 3)	0.773	0.875	0.946	0.982	0.996
True utility	54.39	49.50	42.49	34.48	27.57
Sel % Proposed	0.720	0.139	0.069	0.031	0.037	0.859
Direct approach	0.524	0.144	0.124	0.076	0.132	0.668
Dose-only	0.198	0.196	0.196	0.228	0.182	0.394
	X = (− − − − +)
P(YT = 3)	0.051	0.071	0.096	0.126	0.164
P(YE = 2)	0.407	0.393	0.331	0.236	0.142
P(YE = 3)	0.183	0.099	0.043	0.015	0.004
True utility	25.75	18.72	13.20	9.38	6.93
Sel % Proposed	0.923	0.000	0.001	0.001	0.062	0.923
Direct approach	0.572	0.008	0.008	0.013	0.399	0.572
Dose-only	0.198	0.196	0.196	0.228	0.182	0.198
	Scenario 2
	X = (+ + + + +)
P(YT = 3)	0.003	0.005	0.009	0.015	0.023
P(YE = 2)	0.069	0.173	0.210	0.177	0.128
P(YE = 3)	0.002	0.032	0.131	0.257	0.357
True utility	11.78	17.48	26.16	34.11	38.98
Sel % Proposed	0.046	0.010	0.035	0.143	0.762	0.762
Direct approach	0.024	0.003	0.020	0.058	0.893	0.893
Dose-only	0.176	0.182	0.208	0.258	0.176	0.176
	X = (− − − − +)
P(YT = 3)	0.005	0.019	0.059	0.149	0.301
P(YE = 2)	0.467	0.333	0.238	0.170	0.120
P(YE = 3)	0.421	0.533	0.585	0.600	0.596
True utility	60.63	59.49	53.11	44.22	34.96
Sel % Proposed	0.421	0.139	0.125	0.106	0.208	0.560
Direct approach	0.424	0.224	0.222	0.089	0.041	0.648
Dose-only	0.176	0.182	0.208	0.258	0.176	0.358
	Scenario 3
	X = (+ + + + −)
P(YT = 3)	0.000	0.000	0.001	0.009	0.056
P(YE = 2)	0.148	0.243	0.239	0.184	0.129
P(YE = 3)	0.005	0.056	0.168	0.286	0.373
True utility	16.38	24.57	33.56	38.57	37.11
Sel % Proposed	0.083	0.032	0.164	0.332	0.387	0.719
Direct approach	0.078	0.005	0.091	0.453	0.371	0.824
Dose-only	0.224	0.226	0.160	0.196	0.194	0.390
	X = (+ + − + +)
P(YT = 3)	0.000	0.002	0.014	0.075	0.250
P(YE = 2)	0.517	0.401	0.259	0.170	0.116
P(YE = 3)	0.115	0.359	0.529	0.604	0.627
True utility	40.67	55.91	59.59	52.29	39.77
Sel % Proposed	0.303	0.319	0.275	0.087	0.016	0.594
Direct approach	0.204	0.378	0.370	0.046	0.002	0.748
Dose-only	0.224	0.226	0.160	0.196	0.194	0.386
	Scenario 4
	X = (+ + + + −)
P(YT = 3)	0.027	0.031	0.035	0.040	0.045
P(YE = 2)	0.416	0.507	0.391	0.187	0.056
P(YE = 3)	0.148	0.296	0.554	0.803	0.943
True utility	27.31	40.12	55.81	68.18	74.18
Sel % Proposed	0.001	0.003	0.009	0.107	0.880	0.987
Direct approach	0.000	0.002	0.012	0.122	0.864	0.986
Dose-only	0.118	0.186	0.216	0.242	0.238	0.480
X = (+ + − + +)
P(YT = 3)	0.040	0.091	0.177	0.300	0.458
P(YE = 2)	0.444	0.295	0.078	0.009	0.000
P(YE = 3)	0.350	0.672	0.920	0.991	1.000
True utility	40.89	53.29	57.07	51.68	43.60
Sel % Proposed	0.025	0.100	0.378	0.308	0.189	0.786
Direct approach	0.001	0.000	0.037	0.184	0.778	0.221
Dose-only	0.118	0.186	0.216	0.242	0.238	0.644
	Scenario 5
	X = (− − − − −)
P(YT = 3)	0.025	0.017	0.011	0.007	0.004
P(YE = 2)	0.407	0.393	0.331	0.236	0.142
P(YE = 3)	0.183	0.099	0.043	0.015	0.004
True utility	28.86	23.83	19.10	15.20	12.37
Sel % Proposed	0.824	0.003	0.000	0.000	0.159	0.824
Direct approach	0.324	0.004	0.008	0.009	0.655	0.324
Dose-only	0.200	0.210	0.208	0.166	0.216	0.200
	X = (− − − + −)
P(YT = 3)	0.026	0.018	0.012	0.008	0.006
P(YE = 2)	0.427	0.464	0.485	0.485	0.465
P(YE = 3)	0.319	0.341	0.374	0.417	0.471
True utility	39.00	43.36	48.36	53.77	59.36
Sel % Proposed	0.067	0.009	0.003	0.002	0.919	0.921
Direct approach	0.324	0.004	0.008	0.009	0.655	0.664
Dose-only	0.200	0.210	0.208	0.166	0.216	0.382
	Scenario 6
	X = (− − − − −)
P(YT = 3)	0.022	0.025	0.028	0.032	0.036
P(YE = 2)	0.394	0.484	0.534	0.535	0.492
P(YE = 3)	0.122	0.143	0.203	0.293	0.402
True utility	25.73	29.01	34.31	40.43	46.73
Sel % Proposed	0.156	0.002	0.003	0.003	0.836	0.836
Direct approach	0.152	0.003	0.006	0.015	0.824	0.824
Dose-only	0.176	0.184	0.218	0.209	0.213	0.213
	X = (− − − + −)
P(YT = 3)	0.035	0.040	0.045	0.050	0.057
P(YE = 2)	0.394	0.484	0.534	0.535	0.492
P(YE = 3)	0.122	0.143	0.203	0.293	0.402
True utility	23.74	26.64	31.52	37.28	43.26
Sel % Proposed	0.212	0.001	0.003	0.003	0.781	0.781
Direct approach	0.152	0.003	0.006	0.015	0.824	0.824
Dose-only	0.176	0.184	0.218	0.209	0.213	0.213
	X = (+ + + + +)
P(YT = 3)	0.000	0.000	0.001	0.009	0.054
P(YE = 2)	0.419	0.295	0.178	0.116	0.081
P(YE = 3)	0.399	0.229	0.187	0.195	0.226
True utility	62.59	42.16	32.89	28.78	25.36
Sel % Proposed	0.701	0.020	0.034	0.028	0.154	0.701
Direct approach	0.748	0.040	0.0586	0.0438	0.0913	0.748
Dose-only	0.286	0.104	0.058	0.091	0.176	0.286
	X = (+ − − + −)
P(YT = 3)	0.000	0.002	0.014	0.073	0.247
P(YE = 2)	0.000	0.000	0.000	0.001	0.008
P(YE = 3)	0.000	0.000	0.000	0.000	0.010
True utility	9.93	9.60	8.64	6.92	5.34
Sel % Proposed	0.010	0.000	0.000	0.008	0.038	0.944
Direct approach	0.283	0.020	0.023	0.043	0.114	0.519
Dose-only	0.286	0.104	0.058	0.091	0.176	0.285
	Scenario 8
	X = (+ + − − −)
P(YT = 3)	0.081	0.056	0.037	0.024	0.016
P(YE = 2)	0.287	0.333	0.368	0.386	0.385
P(YE = 3)	0.094	0.140	0.199	0.271	0.355
True utility	22.09	28.64	36.23	44.55	53.16
Sel % Proposed	0.066	0.008	0.008	0.002	0.830	0.830
Direct approach	0.065	0.000	0.000	0.005	0.733	0.733
Dose-only	0.153	0.063	0.075	0.175	0.353	0.353
	X = (+ + − + −)
P(YT = 3)	0.081	0.056	0.037	0.024	0.016
P(YE = 2)	0.002	0.004	0.009	0.016	0.027
P(YE = 3)	0.000	0.000	0.000	0.001	0.002
True utility	7.88	8.44	9.00	9.61	10.38
Sel % Proposed	0.012	0.004	0.000	0.002	0.076	0.906
Direct approach	0.065	0.000	0.000	0.005	0.733	0.198
Dose-only	0.153	0.063	0.075	0.175	0.353	0.181

Overall, as shown in Table 1, the proposed design outperformed the direct approach, with higher PCS and comparable or smaller standard deviations of PCS. The PCS of the proposed design was 10.8% to 34% higher than that of the direct approach for scenarios 1, 4, 5, 6, and 8, and slightly higher under scenario 7. The direct approach had higher PCS than the proposed design in scenarios 2 and 3 because in these two scenarios, the direct approach is correctly or approximately correctly specified. As shown in Figures 2 and 3, in scenario 3, only biomarkers X₁ and X₃ affect toxicity and efficacy, and in scenario 2, toxicity and efficacy are predominately determined by biomarkers X₁ and X₃. The dose-only design had substantially worse performance than the designs that account for the biomarker information. The PCS of the dose-only design was often lower than 50%, while that of the proposed design was often above 70%.

Similar results were observed for given biomarker profiles (see Table 2). Specifically, in scenario 1, for both representative biomarker patterns, utility decreases with the dose. The target doses are dose levels 1 and 2 for the first pattern, and dose level 1 for the second pattern. The target dose selection percentages were 20% and 35% higher under our proposed design than under the direct approach for the two patterns. The dose-only design yielded the worst performance. The PCS of the dose-only design was 46.5% and 72.5% lower than those of the proposed design. In scenario 2, the utility increases with the dose for the first representative pattern and decreases with the dose for the second representative pattern. The target dose is dose level 5 for the first pattern, and dose levels 1 and 2 for the second pattern. The direct approach yielded 10% higher PCS than the proposed design for the two representative patterns. This is because in this case, the direct approach correctly included all the biomarkers (i.e., X₁ and X₃) that affect toxicity and efficacy. For the same reason, the direct approach performed better in scenario 3. However, we bear in mind that scenarios 2 and 3 were intentionally constructed for the purpose of comparison. In practice, we would have little information to (correctly) pre-select the two biomarkers. If the selected biomarkers are not predictive or some other predictive biomarkers are not selected, the performance of the direct approach could be considerably worse. For example, in scenario 4, for biomarker pattern (+ + − + +), our proposed design yielded a 56% higher percentage of target dose selection than the direct approach; and in scenario 5, the PCS of the proposed design was 50% and 25% higher than that of the direct approach for the two representative patterns. In scenario 6, although the two designs had comparable performance for the two representative biomarker patterns, averaging across all possible biomarker patterns, the PCS of our design was 20.8% higher than that of the direct approach (see Table 1). In Scenario 7, the drug was effective only for patients for whom the first three biomarkers were positive. For biomarker pattern (+ + + + +), the target dose is dose level 1. The PCS of the proposed design was 70.1%, slightly lower than that of the direct method. For pattern (+ − − + −), the drug was not effective because biomarkers 2 and 3 were negative. In this case, no dose selection is the correct selection. The proposed design correctly concluded that the drug was not effective 94.4% of the time without selecting any dose. In contrast, the direct approach incorrectly selected futile doses 48.1% of the time. In scenario 8, the target dose for biomarker pattern (+ + − − −) was dose level 5. The PCS of the proposed design was 10% higher than that of the direct approach (83% versus 73.3%). For biomarker pattern (+ + − + −), all 5 dose levels had negligible efficacy, so no dose was acceptable. In this case, the PCS is defined as the percentage of trials in which no dose is selected. The PCS of the proposed design was 90.6%, i.e., the design correctly concluded that the drug is not effective for biomarker pattern (+ + − + −) 90.6% of the time. In contrast, because of using partial biomarker information (i.e., biomarkers 1 and 3), the PCS for the direct approach was only 19.8%. In other words, more than 80% of the time, the direct approach failed to recognize that the drug is not effective for patients with biomarker pattern (+ + − + −) and selected a futile dose as the optimal dose. This clearly demonstrates the importance of accounting for all biomarkers, and the advantage of the proposed method.

To further learn the behavior of the proposed design, we examined the accuracy of the posterior estimates of toxicity and efficacy probabilities. Figures S4 and S5 in the Supplementary Materials show the distributions of the empirical bias for the posterior estimates of toxicity and efficacy probabilities at the end of the trial under the 8 scenarios. We can see that the proposed method yielded reasonably accurate estimates and the empirical bias was generally close to 0 and mostly within the range of (−0.1, 0.1). We also examined the robustness of the estimated CPLS components, that is, did we obtain similar CPLS components across 1000 simulated trials? Figure S6 in the Supplementary Materials shows that the CPLS components extracted at the end of the trial were generally robust or similar across 1000 simulations.

4.3. Sensitivity analyses

We carried out a sensitivity analysis to examine the robustness of our proposed design to the number of CPLS components. Table 3 shows the average and standard deviation of the PCS of the target doses across 32 possible biomarker patterns with 2, 3, 4, and 5 CPLS components for the first three scenarios. We can see that the operating characteristics of the proposed design are generally robust to the number of CPLS components used in the dose-toxicity and dose-efficacy models.

Table 3:

Sensitivity analysis: the average and SD of the PCS of the target dose across 32 possible biomarker patterns with 2 to 5 CPLS components for the first three scenarios.

	2 components			3 components			4 components			5 components
	Scenario			Scenario			Scenario			Scenario
	1	2	3	1	2	3	1	2	3	1	2	3
Mean	0.70	0.71	0.71	0.74	0.75	0.75	0.74	0.75	0.72	0.74	0.74	0.72
SD	0.18	0.21	0.14	0.14	0.18	0.13	0.12	0.18	0.15	0.12	0.19	0.17

We evaluated the sensitivity of the proposed design to the specification of the utility function. We considered the following 2 alternative utility functions:

	Utility 1				Utility 2
	yE=1	yE=2	yE=3		yE=1	yE=2	yE=3
yT=1	0	50	100		0	65	100
yT=2	0	20	60		0	35	75
yT=3	0	10	20		0	25	35

The first new utility gives a desirability score of 0 to (y_T, y_E) as long as y_E = 1 (i.e., PD) regardless of the value of y_T. That is, if patients experience disease progression, toxicity does not affect the desirability of the drug. The second utility assigns higher desirability scores to (y_T, y_E) when y_E = 2 or 3 (i.e., SD or PR/CR). As shown in Table 4, the results under the two alternative utilities are generally similar to those reported in Table 1, suggesting that the proposed design is not sensitive to the elicited utility.

Table 4:

The average and standard deviation (SD) of the percentage of correct selection (PCS) of target doses of the proposed design under two alternative utility functions, or using the CRM in stage I.

PCS	Scenario
	1	2	3	4	5	6	7	8
Under utility 1
Mean	0.661	0.704	0.722	0.772	0.714	0.652	0.680	0.823
SD	0.20	0.24	0.16	0.30	0.23	0.19	0.27	0.17
Under utility 2
Mean	0.630	0.686	0.755	0.841	0.719	0.642	0.670	0.815
SD	0.23	0.25	0.18	0.26	0.26	0.19	0.28	0.17
Using CRM in stage I
Mean	0.717	0.711	0.696	0.772	0.719	0.721	0.685	0.824
SD	0.17	0.23	0.16	0.31	0.24	0.11	0.26	0.17

We also examined whether the proposed design is sensitive to the choice of the stage I dose escalation method by replacing the BOIN with the CRM. The results (see Table 4) are very similar to those reported in Table 1, suggesting that our design is robust to the choice of the stage I dose escalation method.

Lastly, we examined the impact of the number of biomarkers on the performance of the proposed method, compared to the direct approach. When there were 2 biomarkers, the direct approach performed slightly better because that method was correctly specified and no data reduction was involved (see Table S6 in the Supplementary Materials). However, when there were 3 biomarkers, the direct approach was problematic and suffered from numerical and convergence problems. In this case, the direct approach had a total of 20 parameters to estimate while the number of available observations was only 21 when the decision rules were first applied after the first stage of the trial. The proposed design (with dimension reduction) had 10 parameters and performed well with a reasonably high PCS. Therefore, we recommend the direct approach when the number of biomarkers is less than 3, and the proposed method when the number of biomarkers is 3 or more.

5. Discussion

We have proposed a Bayesian personalized dose-finding design for molecularly targeted agents with ordinal efficacy and toxicity outcomes. Our design uses the CPLS method to reduce the potentially large number of biomarkers and biomarker-dose interactions to a few CPLS components that capture most of the information from these variables for predicting toxicity and efficacy. By treating these CPLS components as covariates, we use a latent-variable approach to model toxicity and efficacy. We propose a two-stage dose-finding algorithm to assign patients to desirable doses based on their covariate vectors and select the personalized optimal doses for future patients. Simulation results show that our proposed design has good operating characteristics.

At the end of a trial that uses our design, we use the final data collected in the trial to recommend the optimal dose for each patient subgroup that has a specific set of biomarkers. Our method, however, does not have to stop there, and can be used to further update and refine the decision rule when the data for new patients outside of the trial become available. In principle, such a learn-as-we-go approach can be continued as long as we desire.

In our toxicity and efficacy models, random effects are used to capture the correlation between Y_T and Y_E. This approach assumes that Y_T and Y_E are positively correlated, which is generally reasonable since the tumor (responsible for efficacy) arises from the same normal tissue responsible for toxicity. The strength of the correlation between Y_T and Y_E has implications in the trial. When the correlation is very high, a higher level of efficacy often comes with a higher level of toxicity. As it is typically true that toxicity monotonically increases with the dose, this means that higher doses lead to both higher efficacy and higher toxicity. Therefore, if the utility function assigns a large reward to efficacy and a small penalty to toxicity, the optimal dose will be the maximum tolerated dose; if the utility function imposes a large penalty on toxicity, then the optimal dose may be a low or intermediate dose; and if the utility function rewards efficacy and penalizes toxicity in a comparable way, then all doses may have similar desirability and thus there may be no clear optimal dose.

Although the focus of our method is on dose selection, at the end of the trial, clinicians often want to know whether the optimal dose really varies between biomarker-defined subgroups of patients, and whether biomarker X is important. The first question can be answered by examining and comparing the posterior distributions of utility across the different subgroups. For example, given any two biomarker subgroups, we can obtain the posterior probability that they have the same optimal dose based on the posterior samples of the toxicity and efficacy models (3) and (4). The second question can be answered by examining the posterior distributions of the regression parameters β_T and β_E in the toxicity and efficacy models, combined with the loading weights of the CPLS components. Recall that biomarkers in profile X enter the efficacy and toxicity models in the form of a linear combination, with different loading weights (i.e., CPLS components). For a specific biomarker, the product of its loading weight and β_T (or β_E ) provides a natural measure of that biomarker’s effect on the clinical outcomes, which can be interpreted in the usual way as in the standard proportional cumulative probit model (Agresti, 2002). In this paper, efficacy is modeled as a three-level ordinal outcome. Although simple to use, it ignores some aspects of the data. For example, the ordinal efficacy outcome does not capture how long patients stay as SD. One possible remedy is to use a more informative endpoint like progression-free survival and model efficacy (and toxicity) as a time-to-event outcome (Yuan and Yin, 2009).

As in most existing phase I/II trial designs, the proposed design assumes that the outcomes are quickly ascertainable such that the decision rules can be applied to determine the dose assignment for the next new patient. In the motivating trial, the response is evaluated in the first cycle of 4 weeks. If the accrual rate is faster than 1 patient per month, it is likely that efficacy may not be observed soon enough to apply decision rules to choose treatments for new patients. One practical solution to this logistic difficulty is to take a group sequential approach, under which we update the model estimates and decision rules after every Γ patients. Between groups, we suspend accrual and wait for the outcomes of the previous group of patients to be scored, if needed, before enrolling the next group of patients. A more efficient approach that eliminates the requirement of accrual suspension is to apply the methodology proposed by Yuan and Yin (2011) and Jin et al. (2004), which accommodates the delayed efficacy outcome using Bayesian data augmentation or the expectation-maximization algorithm. Our design utilizes the CPLS to reduce the dimension of biomarkers. Other dimension reduction techniques can also be used. For example, we may use a model selection approach to select a few biomarkers based on the ongoing trial to overcome the dimensionality problem.