Anomalous Diffusion Characterization by Fourier Transform-FRAP with Patterned Illumination

Abstract

Fourier transform fluorescence recovery after photobleaching (FT-FRAP) with patterned illumination is theorized and demonstrated for quantitatively evaluating normal and anomalous diffusion. Diffusion characterization is routinely performed to assess mobility in cell biology, pharmacology, and food science. Conventional FRAP is noninvasive, has low sample volume requirements, and can rapidly measure diffusion over distances of a few micrometers. However, conventional point-bleach measurements are complicated by signal-to-noise limitations, the need for precise knowledge of the photobleach beam profile, potential for bias due to sample heterogeneity, and poor compatibility with multiphoton excitation because of local heating. In FT-FRAP with patterned illumination, the time-dependent fluorescence recovery signal is concentrated to puncta in the spatial Fourier domain, with substantial improvements in signal-to-noise, mathematical simplicity, representative sampling, and multiphoton compatibility. A custom nonlinear optical beam-scanning microscope enabled patterned illumination for photobleaching through two-photon excitation. Measurements in the spatial Fourier domain removed dependence on the photobleach profile, suppressing bias from imprecise knowledge of the point spread function. For normal diffusion, the fluorescence recovery produced a simple single-exponential decay in the spatial Fourier domain, in excellent agreement with theoretical predictions. Simultaneous measurement of diffusion at multiple length scales was enabled through analysis of multiple spatial harmonics of the photobleaching pattern. Anomalous diffusion was characterized by FT-FRAP through a nonlinear fit to multiple spatial harmonics of the fluorescence recovery. Constraining the fit to describe diffusion over multiple length scales resulted in higher confidence in the recovered fitting parameters. Additionally, phase analysis in FT-FRAP was shown to inform on flow/sample translation.

Significance

Fourier transform fluorescence recovery after photobleaching (FT-FRAP) with patterned illumination greatly improves the accuracy of diffusion assessments and simultaneously accesses information on both normal and anomalous diffusion in a single experiment.

Introduction

Fluorescence recovery after photobleaching (FRAP) is a well-established and widely accessible method for probing diffusion (1,2). In FRAP, a region of a fluorescently labeled sample is permanently photobleached using a short, high-intensity burst of light. After the photobleach, mobile fluorescent molecules diffuse into the region and mobile photobleached molecules diffuse out. This combined mobility results in a time-dependent recovery of fluorescence intensity in the photobleached region. Diffusion information can be obtained by fitting the fluorescence recovery to a mathematical model.

The first FRAP experiment was performed by Peters et al. in 1974 to measure the mobility of membrane proteins in red blood cell ghosts (3). More recently, FRAP has been used to probe epidermal growth factor receptor clustering in Chinese hamster ovary cell membranes (4), intercellular communication via septal junctions in multicellular cyanobacteria (5), and the dynamics of intermediate filament-like protein in the hyphae of Streptomyces venezuelae (6). FRAP has also been applied broadly in the pharmaceutical community to understand molecular transport in hydrogels (7, 8, 9, 10) and in extracellular matrices (11,12) in an effort to improve drug delivery outcomes. Recent efforts have also been made to utilize FRAP as a prescreening assay for in meso crystallization of membrane proteins in lipid cubic phase and mesophases (13, 14, 15, 16).

Despite the advantages of FRAP, quantitative diffusion analysis is typically complicated by the requirement for precise knowledge of the photobleaching profile (17,18). To support rapid diffusion measurements, FRAP is generally optimized for fast recovery by using a small photobleach spot. To compensate for low signal from a small photobleach spot, high photobleach depth is used to increase the signal-to-noise ratio (SNR). However, increasing the photobleach depth runs the risk of complicating reproducibility in the spatial photobleach profile by introducing nonlinearities from optical saturation and perturbations to diffusion from local heating (19). To address this issue, alternative photobleach patterns have been explored, most notably disk (20), line (21), and fringe pattern (22, 23, 24) illumination. Disk illumination has the advantage of increasing the overall number of molecules photobleached but largely negates the 1/f noise reductions from highly localized photobleaching and correspondingly fast recoveries. Line illumination is a reasonable compromise, supporting fast recovery in the direction orthogonal to the photobleach line and signal-to-noise averaging along the length of the line. With the possible exception of disk and fringe illumination, in which the contiguous photobleach spot is large relative to the optical point spread function (PSF), the point and line photobleach patterns with the greatest reduction in 1/f noise are most prone to artifacts from ambiguities in the photobleach PSF.

Spatial Fourier analysis (SFA) is one of the more successful strategies used to date for addressing ambiguities in the PSF for point excitation (20,25, 26, 27). In summary, normal diffusion in FRAP can be modeled as the convolution of the photobleach PSF with a time-varying Gaussian function. This convolution produces a function describing the real-space fluorescence recovery that is dependent on both time and the photobleach PSF. Moreover, this convolution generally produces a real-space recovery with no simple closed-form analytical solution, with a few notable exceptions for the photobleach PSF (e.g., Gaussian). However, in the Fourier transform (FT) domain, the convolution corresponds to simple multiplication, disentangling the time-dependent decay from the photobleach profile. The decay curves for each spatial frequency in SFA can be used individually or collectively for recovering the diffusion coefficient. In this manner, the detailed functional form for the initial PSF becomes less critical in the analysis because the fluorescence recovery is only dependent on time and not on the initial photobleach PSF for a single spatial frequency (28). For point excitation, SFA suffers by distributing the signal power from sharp features in the real-space image out over many low-amplitude frequencies in the SFA image, but the intrinsic SNR can be recovered through simultaneous, collective analysis at multiple spatial frequencies. When one or a small number of frequencies are used, this distribution of power can result in a reduction in SNR, the cost of which represents a tradeoff for the benefits in reducing ambiguities related to the PSF.

Furthermore, point-bleach FRAP lacks sensitivity for characterizing anomalous diffusion. Diffusion is categorized as anomalous when it deviates from normal Brownian diffusion. Whereas the mean-squared displacement (MSD) in normal diffusion evolves with a linear dependence on time, the MSD in anomalous diffusion exhibits a nonlinear dependence on time, resulting in a time-varying/distance-dependent diffusion coefficient (29,30). Anomalous diffusion has been observed in a variety of systems, such as the cell and polymeric networks (31, 32, 33, 34). Anomalous diffusion in point-bleach FRAP can be identified through a nonlinear fit of the fluorescence recovery to an anomalous diffusion model (35). However, the relatively subtle differences in the point-bleach recovery curves between normal and anomalous diffusion can complicate identification and quantification of deviations from normal diffusion. Further complications in accurately characterizing anomalous diffusion with point-bleach FRAP arise from the requirement for precise knowledge of the photobleaching PSF. In addition, significant covariance between fitting parameters can result in relatively large uncertainties in the recovered coefficients (e.g., the diffusion coefficient and an anomalous exponent).

Finally, point excitation poses particularly problematic practical challenges from local heating effects in multiphoton-excited FRAP measurements (36). Because of the general inefficiency of multiphoton excitation, a large flux of light is typically introduced, only a small fraction of which contributes to excitation and fluorescence. Weak-but-nonzero absorption of the incident light and Stokes Raman transitions leading to local heat deposition both compete with multiphoton excitation. When the excitation beam is fixed at a single location, local temperatures can quickly escalate until the rate of heat dissipation matches the rate of deposition. Depending on the steady-state temperature differential, this transient temperature gradient can potentially bias subsequent diffusion measurements based on isothermal assumptions.

In this work, comb patterns for illumination during photobleaching were demonstrated to support high SNR measurements of normal and anomalous diffusion in FT analysis of fluorescence recovery with multiphoton excitation. In brief, photobleach patterns were selected to concentrate signal to puncta in the spatial FT domain, rather than a point in the real-space image, as shown in Fig. 1. Patterned illumination using rapid line scanning distributed the power from the photobleach over much larger regions in the field of view, removing many of the potential nonlinearities and biases associated with highly localized excitation, while enabling multiphoton excitation with negligible artifacts from local heating. Probing diffusion at multiple length scales by interrogating multiple harmonics in the spatial frequency domain was shown to increase confidence in recovered fitting parameters in analysis of anomalous diffusion. The theoretical foundation for Fourier-transform fluorescence recovery after photobleaching (FT-FRAP) with patterned illumination is evaluated in proof-of-concept studies of model systems for characterizing normal and anomalous diffusion.

Figure 1.

Schematic depicting (A) conventional point-bleach FRAP illumination, (B) patterned illumination with comb excitation, and (C) spatial FT of the patterned illumination in (B). Conventional point-bleach FRAP produces a sharp point in real space. FT-FRAP with patterned illumination produces sharp puncta in the spatial Fourier domain.

Theoretical foundation

Fourier analysis of the diffusion equation

Before discussion of FT-FRAP with patterned illumination, it is useful to review conventional FRAP as a comparator within the FT framework. Fick’s Law of Diffusion is given by the following general expression:

$$\frac{\partial }{\partial t}C\left(\mathit{\rho },t\right)=\nabla \mathbf{D}\nabla C\left(\mathit{\rho },t\right),$$ (1)

in which C(ρ, t) is the concentration of the analyte of interest as a function of position ρ and time t and D is the three-dimensional diffusion tensor.

This differential equation is arguably simpler to evaluate by first performing the spatial FT to generate $\tilde{C}(\overline{\mathit{\nu }},0)$, in which $\tilde{C}$ is the spatial FT of C and $\overline{\mathit{\nu }}$ is the three-dimensional spatial wavevector. Upon FT of the diffusion equation given in Eq. 1, each derivative transforms as multiplication by the “diagonal” function $i2\pi \overline{\mathbf{\nu }}$,

$$\frac{\partial }{\partial t}\tilde{C}\left(\overline{\mathit{\nu }},t\right)=-4{\pi }^2{\overline{\mathit{\nu }}}^{\text{T}}\mathbf{D}\overline{\mathit{\nu }}\tilde{C}\left(\overline{\mathit{\nu }},t\right).$$ (2)

Evaluation of${\overline{\mathit{\nu }}}^{\text{T}}\mathbf{D}\overline{\mathit{\nu }}$considering diffusion just within the (x, y) plane yields the nonzero scalar products ${\overline{\nu }}_x^2{D}_{xx}+2{\overline{\nu }}_x{\overline{\nu }}_y{D}_{xy}+{\overline{\nu }}_y^2{D}_{yy}$. For a choice of (x, y) coordinates defined along the principal moments of the diffusion tensor D (including the case of constant diffusion in all (x, y) directions), D_xy = 0. In this case, the diffusion equation can be independently evaluated in each of the (x, y) directions. The expression for the x direction is given below, with an analogous expression present for the y direction:

$$\frac{\partial }{\partial t}\tilde{C}\left({\overline{\nu }}_x,t\right)=-4{\pi }^2{\overline{\nu }}_x^2{D}_{xx}\tilde{C}\left({\overline{\nu }}_x,t\right).$$ (3)

Because only $\tilde{\mathbf{C}}({\overline{\mathit{\nu }}}_x,t)$ in Eq. 3 depends on time, the expression in Eq. 3 is of the form f′(t) = kf(t), for which one general solution, subject to the constraint of a decay, is given by an exponential function of the form f(t) = f(0)e^kt_, with k < 0,

$$\tilde{C}\left({\overline{\nu }}_x,t\right)=\tilde{C}\left({\overline{\nu }}_x,0\right)e^{-4{\pi }^2{\overline{\nu }}_x^2{D}_{xx}t}.$$ (4)

This solution to the differential equation along the x direction is a Gaussian function in ${\overline{\nu }}_x$. Multiplication by a Gaussian in the spatial Fourier domain corresponds to convolution with a Gaussian in real space:

$$C\left(x,t\right)=C\left(x,0\right)\otimes \frac{1}{\sqrt{2\pi {\sigma }_t^2}}{e}^{-\frac{x^2}{2{\sigma }_t^2}};{\sigma }_t^2=2D_{xx}t.$$ (5)

The standard deviation (SD) of the spatial Gaussian distribution σ_t increases with the square root of time, corresponding to convolution with an ever-broadening Gaussian as diffusion proceeds.

Conventional FRAP

In the limit of a thin sample, diffusion in the z direction can be neglected, with diffusion expressed with respect to both x and y. Under these conditions in conventional FRAP (depicted in Fig. 1 A), the photobleach pattern for a symmetric Gaussian illumination pattern on the back of an objective is also Gaussian within the field of view:

$$C\left(x,y,0\right)=A{\left(2\pi {\sigma }_b^2\right)}^{-1}{e}^{-\frac{\left(x^2+y^2\right)}{2{\sigma }_b^2}}.$$ (6)

In isotropic media, diffusion is identical in both the x and y coordinates such that the diffusion tensor can be replaced by a single scalar diffusion coefficient D. In this limit, the convolution of two two-dimensional (2D) Gaussian functions (one from the initial photobleach and one from diffusion) has the convenient property of producing yet another Gaussian function, the width of which evolves in time:

$$C\left(x,y,t\right)=A{\left(2\pi {\sigma }_b^2\right)}^{-1}{e}^{-\frac{\left(x^2+y^2\right)}{2{\sigma }_b^2}}\otimes {\left(4\pi Dt\right)}^{-1}{e}^{-\frac{\left(x^2+y^2\right)}{4Dt}}.$$ (7)

Evaluation of the convolution results in the following expression for the time dependence:

$$C\left(x,y,t\right)=A{\left(2\pi {\sigma }_b^2+4\pi Dt\right)}^{-1}{e}^{-\frac{\left(x^2+y^2\right)}{2{\sigma }_b^2+4Dt}}.$$ (8)

If the system is anisotropic, selection of the principal spatial coordinates that diagonalize the diffusion matrix allows the diffusion equation to incorporate differences in diffusivity along different spatial dimensions as follows:

$$C\left(x,y,t\right)=A{\left(2\pi {\sigma }_b^2\right)}^{-1}{e}^{-\frac{\left(x^2+y^2\right)}{2{\sigma }_b^2}}\otimes \left[{\left(4\pi D_{xx}t\right)}^{-\frac{1}{2}}{e}^{-\frac{x^2}{4D_{xx}t}}{\left(4\pi D_{yy}t\right)}^{-\frac{1}{2}}{e}^{-\frac{y^2}{4D_{yy}t}}\right]$$ (9)

and

$$C\left(x,y,t\right)=A{\left[\left(2\pi {\sigma }_b^2+4\pi D_{xx}t\right)\left(2\pi {\sigma }_b^2+4\pi D_{yy}t\right)\right]}^{-\frac{1}{2}}{e}^{-\frac{x^2}{2{\sigma }_b^2+4D_{xx}t}}{e}^{-\frac{y^2}{2{\sigma }_b^2+4D_{yy}t}}.$$ (10)

In the more general case of a non-Gaussian function describing the photobleach pattern C(x, y, 0), the situation is significantly more complex. In general, no simple analytical forms are expected for the convolution of a Gaussian with non-Gaussian functions, requiring numerical methods for approximations. Unfortunately, non-Gaussian photobleach patterns are commonplace. Even when Gaussian patterns are intended, photobleaching can often approach saturating conditions when the peak photobleach depth approaches unity, resulting in “top-hat” initial photobleach peak shapes. In such cases, the shape of the recovered region can be complicated to integrate analytically into the diffusion analysis for recovery of the diffusion coefficient (19).

Comb photobleach FT-FRAP

In FT-FRAP, the initial photobleach pattern is selected to produce sharp puncta in the spatial frequency domain rather than in real space. One such pattern is a comb, or a periodic series of lines. For mathematical purposes, we will define the comb pattern to proceed along the x axis in the laboratory frame with constant illumination along the y axis, producing a series of photobleached stripes (depicted in Fig. 1 B). The initial photobleach pattern C(x, 0) is constant in the y axis and given below, in which ${\delta }_{x,\pm n/\left(2\pi {\overline{\nu }}_x^0\right)}$ is a delta function at the positions $\pm nx{\overline{\nu }}_x^0$ and n ∈ {0, 1, 2…}, C₀ is the initial concentration of the analyte of interest, and A is the photobleach depth

$$C\left(x,0\right)=C_0\left[1-A\sum _{n=0,1,\mathrm{2...}}\left({\delta }_{x,\pm n/\left(2\pi {\overline{\nu }}_x^0\right)}\otimes PSF\left(x\right)\right)\right].$$ (11)

By taking the spatial FT of this equation, the convolution of the photobleach PSF(x) with the comb pattern ${\delta }_{x,\pm n/\left(2\pi {\overline{\nu }}_x^0\right)}$ is replaced by a multiplication operation, simplifying the analysis. The initial (t = 0) spatial Fourier transform of C(x, 0) along the x direction is then given by the following expression, in which ${\Phi }_{PSF}\left({\overline{\nu }}_x\right)$ is the spatial FT of PSF(x) as follows:

$$\tilde{C}\left({\overline{\nu }}_x,0\right)=C_0\left[{\delta }_{{\overline{\nu }}_x,0}-A\sum _{n=0,1,\mathrm{2...}}{\delta }_{{\overline{\nu }}_x,\pm n{\overline{\nu }}_x^0}{\Phi }_{PSF}\left({\overline{\nu }}_x\right)\right]$$ (12)

and

$$\tilde{C}\left({\overline{\nu }}_x,0\right)=C_0{\delta }_{{\overline{\nu }}_x,0}-C_{0}A\sum _{n=1,\mathrm{2...}}{\delta }_{{\overline{\nu }}_x,\pm n{\overline{\nu }}_x^0}{\Phi }_{PSF,x}\left(\pm n{\overline{\nu }}_x^0\right).$$ (13)

In brief, the initial photobleach corresponds to a series of puncta in the spatial Fourier domain positioned at $\left({\overline{\nu }}_x,{\overline{\nu }}_y\right)=\left(\pm n{\overline{\nu }}_x^0,0\right)$, each of which is scaled in initial amplitude by the spatial FT of PSF(x), with additional amplitude at the origin $\left({\overline{\nu }}_x,{\overline{\nu }}_y\right)=\left(0,0\right)$ from the overall average fluorescence intensity.

The time-dependent behavior of each point in the FT can be evaluated by an approach analogous to that illustrated in Eq. 4 for the nth harmonic (n > 0):

$${\tilde{C}}_n\left({\overline{\nu }}_x,t\right)=\tilde{C}\left(\pm n{\overline{\nu }}_x^0,0\right)e^{-4{\pi }^2{\left(n{\overline{\nu }}_x^0\right)}^2{D}_{xx}t};{\tilde{C}}_n\left(\pm n{\overline{\nu }}_x^0,0\right)=-C_{0}A{\Phi }_{PSF,x}\left(\pm n{\overline{\nu }}_x^0\right).$$ (14)

For a given impulse in the FT image, a single-exponential decay is expected. Irrespective of the functional form for PSF(x), the time constant is given by $\tau ={\left[{\left(2\pi n{\overline{\nu }}_x^0\right)}^2{D}_{xx}\right]}^{-1}$. This single-exponential recovery is in stark contrast to conventional FRAP analysis, which is based on measurements performed in real space and for which the timescale for recovery depends sensitively on precise foreknowledge of PSF(x) for recovery of the diffusion coefficient. The time constant of the fluorescence recovery in FT-FRAP is independent of PSF(x), which allows for simplified mathematical recovery of D_xx, while circumventing error associated with imprecise estimates of PSF(x).

Through this analysis, comb photobleaching has the additional practical advantage of simultaneously enabling diffusion analysis over multiple length scales. For example, the fourth harmonic will probe diffusion over a length fourfold shorter than the first harmonic, and by nature of the quadratic dependence on spatial frequency, the fourth harmonic will recover 16-fold faster than the first harmonic for normal diffusion.

Anomalous diffusion

The capability of FT-FRAP to simultaneously measure diffusion over multiple length scales enables quantitative analysis of anomalous diffusion. Whereas normal diffusion is characterized by fluorescence recovery with a quadratic dependence on spatial frequency, anomalous diffusion will produce fluorescence recovery that deviates from a quadratic dependence. The ability to simultaneously interrogate diffusion over several discrete, well-defined distances by FT-FRAP with comb illumination provides a convenient route for quantifying anomalous diffusion if present.

Numerous mathematical models for anomalous diffusion can be found for trends anticipated under a diverse suite of conditions (30,37, 38, 39, 40, 41). A model based on continuous-time random walk and fractional diffusion is considered in this work because of its general applicability to systems with both time-varying and distance-dependent diffusion (29). In a continuous-time random walk model, diffusion is approximated as a series of random steps. Normal diffusion is characterized by a Gaussian pdf in step lengths (variance = 2σ²) and a Poisson pdf in wait times between steps (characteristic wait time = τ). Deviation from normal Brownian diffusion can arise from various sources, two of which we will consider in the anomalous diffusion model used in this work. First, anomalous diffusion can arise when the characteristic wait time τ diverges. When τ is finite, as in normal diffusion, the MSD exhibits a linear time dependence. When the distribution of wait times diverges because of binding or association, the time dependence of the MSD deviates from linear and scales with time to the power α as follows:

$$\langle x^2\rangle \sim t^{\alpha }.$$ (15)

Normal diffusion corresponds to α = 1, subdiffusion corresponds to 0 < α < 1, and superdiffusion corresponds to α > 1. The fluorescence recovery in this class of anomalous diffusion is modeled as a one-parameter Mittag-Leffler function E_α as follows:

$${\tilde{C}}_n\left({\overline{\nu }}_x,t\right)=\tilde{C}\left(\pm n{\overline{\nu }}_x^0,0\right)E_{\alpha }\left(-4{\pi }^2{\left(n{\overline{\nu }}_x^0\right)}^2{D}_{xx}{t}^{\alpha },\alpha \right).$$ (16)

The Mittag-Leffler function is a fractional generalization of an exponential function. The one-parameter Mittag-Leffler, E_α(z, α) converges to an exponential E₁(z, 1) = e^z for α = 1, and $E_0\left(z,0\right)=\left(1/1-z\right)$ for α = 0.

A second source of anomalous diffusion is a deviation in the step-length distribution. Normal diffusion exhibits a Gaussian step-length pdf with a variance of 2σ², leading to a quadratic dependence of the diffusion coefficient on spatial frequency. However, in cases in which the variance in the step-length distribution diverges, Lévy flight behavior is observed, and the anomalous diffusion coefficient will adopt a dependence on σ^μ instead of σ² for normal diffusion as follows:

$$D_{xx}\equiv {\sigma }^{\mu }/\tau .$$ (17)

Lévy flight diffusion produces an exponential decay in the spatial frequency domain, in which the spatial frequency is raised to the power μ rather than two for normal diffusion as follows:

$${\tilde{C}}_n({\overline{\nu }}_x,t)=\tilde{C}\left(\pm n{\overline{\nu }}_x^0,0\right)e^{-{\left(2\pi n{\overline{\nu }}_x^0\right)}^{\mu }{D}_{xx}t}.$$ (18)

A system can exhibit both subdiffusive and Lévy flight behavior when both τ and σ diverge. An equation describing such a system results from modification of the Mittag-Leffler function shown in Eq. 16 by replacing the quadratic dependence on the spatial frequency term with the exponent μ and by scaling the exponent of t by 2/μ:

$${\tilde{C}}_n\left({\overline{\nu }}_x,t\right)=\tilde{C}\left(\pm n{\overline{\nu }}_x^0,0\right)E_{\alpha }\left(-{\left(2\pi n{\overline{\nu }}_x^0\right)}^{\mu }{D}_{xx}{t}^{2\alpha /\mu },\alpha \right).$$ (19)

FT-FRAP is capable of sensitively characterizing anomalous diffusion because it can measure diffusion on multiple length scales. A fit to Eq. 19 involves parameters that are likely to have high covariance if the fit is performed with only one recovery curve. By performing a global fit with multiple recovery curves at multiple length scales, the fit can be constrained to recover more accurate values for the parameters describing anomalous diffusion.

Signal power

In comparison to analysis in real space, the Fourier domain analysis with patterned illumination provides a substantial advantage in terms of the available power of the detected signal. Power is conserved upon Fourier transformation, allowing direct comparisons across both representations. For a Gaussian photobleach spot with a width parameter σ and peak photobleach depth A_p, the power is generated by integration over the 2D Gaussian as follows:

$$P_{Gaussian}=\underset{0}{\overset{512}{\int }}\underset{0}{\overset{512}{\int }}{\left[C_0{A}_p{e}^{-\frac{\left[{\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2\right]}{2{\sigma }^2}}\right]}^{2}dxdy.$$ (20)

In a typical experiment, the Gaussian width is much smaller than the field of view to reduce measurement times by minimizing the diffusion length. In the limit that σ ≪ 512 pixels (assuming a field of view of 512 × 512 pixels), the discrete limits of integration can be safely evaluated as ± ∞. The integrals can be further simplified by substituting x′ = x − x₀ and noting that dx = dx′ (with analogous substitutions for y) as follows:

$$P_{Gaussian}\cong {\left(C_0{A}_P\right)}^2\underset{-\infty }{\overset{\infty }{\int }}{e}^{-\frac{x^{\text{'}2}}{{\sigma }^2}}d{x}^{\text{'}}\underset{-\infty }{\overset{\infty }{\int }}{e}^{-\frac{y^{\text{'}2}}{{\sigma }^2}}d{y}^{\text{'}}\cong \pi {\sigma }^2{\left(C_0{A}_p\right)}^2.$$ (21)

The power in the impulse in the FT image produced by comb illumination can be similarly calculated by evaluating the same power through integration of the real-space photobleach pattern. For a photobleach depth A_p, the power in a comb with N lines is given by the following expression:

$$P_{comb}=\underset{0}{\overset{512}{\int }}\underset{0}{\overset{512}{\int }}{\left[\sum _{n=1}^N\left(C_0{A}_p{\delta }_{x,\pm nx{\overline{\nu }}_x^0}\otimes PSF\left(x\right)\right)\right]}^{2}dxdy.\cong {\left(C_0{A}_p\right)}^2\left(512\right)\sum _{n=1}^N\underset{-\infty }{\overset{\infty }{\int }}{\left|PSF\left(x\right)\right|}^{2}dx\cong {\left(C_0{A}_p\right)}^2\left(512\right)N\sqrt{\pi {\sigma }^2}=P_{Gausian}\times \frac{512N}{\sqrt{\pi {\sigma }^2}}$$ (22)

The power advantage for comb excitation with a beam PSF with a characteristic width of two pixels relative to point excitation is ∼2300-fold greater than that in the Gaussian photobleach spot with an identical photobleach depth and 32 lines in the comb. This potential for signal-to-noise enhancement is particularly noteworthy because the peak photobleach amplitude A_p is bounded to be less than unity and is typically much less than 0.5 to reduce nonlinear effects from saturation and local heating. It is worth emphasizing that this signal increase represents the theoretical upper limit corresponding to a 2300-fold increase in the total power used for illuminating the sample. In practice, local heating and/or the availability of laser power may limit the practical advantages accessible experimentally. Fortunately, distribution of the power over the entire field of view should reduce perturbations associated with heating effects. Furthermore, advances in laser technology are increasing the availability of high-power lasers compatible with many photobleaching experiments.

In addition to the power advantage, FT-FRAP with a comb photobleach pattern provides an anticipated intrinsic signal-to-noise advantage through Fourier domain analysis. White noise is uniformly distributed in both space and spatial frequency. Localized detection in the Fourier domain that changes in amplitude, but not shape, maintains fixed noise contributions in spatial frequency. In contrast, the spread in the photobleach over time increases the noise contributions over which the signal is integrated. A more detailed comparison of the SNR for fixed bleach power is provided in the Supporting Materials and Methods.

Phasor analysis of flow in FT-FRAP

The preceding description is based on the assumption of even functions for the comb photobleach pattern relative to the origin of the image (typically, the center). Even assuming the initial photobleach pattern is symmetric around the origin, directional flow within the sample could result in displacements along the flow direction (assumed to be x for simplicity) over time. Displacements in real space correspond to shifts in phase in the Fourier domain such that phase analysis in the FT domain has the potential to inform on flow. Considering comb excitation, a shift of Δx in the initial photobleach pattern will produce shifts in the δ-functions associated with the comb as follows:

$$C\left(x,0\right)=C_0\left[1-A\sum _{n=0,1,\mathrm{2...}}\left(\delta \left(\Delta x\right)\otimes PSF\left(x\right)\right)\right],$$ (23)

in which $\delta \left(\Delta x\right)={\delta }_{x,\pm n\left(x+\Delta x\right){\overline{\nu }}_x^0}$. The influence of displacement is easily integrated into the FT analysis using the shift theorem (42), in which displacement by an offset from the origin of Δx is accounted for in the spatial FT through multiplication by $e^{i2\pi \overline{\nu }\Delta x}$ for a given value of n as follows:

$${\tilde{C}}_n\left({\overline{\nu }}_x,t\right)=\tilde{C}\left(\pm n{\overline{\nu }}_x^0,0\right)e^{-4{\pi }^2{\left(n{\overline{\nu }}_x^0\right)}^2{D}_{xx}t}{e}^{i2\pi \left(n{\overline{\nu }}_x^0\right)\Delta x}.$$ (24)

At t = 0, the initial phase angle of the nth reflection is related to the argument φ_n of ${\tilde{C}}_n\left({\overline{\nu }}_x,0\right)$, which is simply ${\phi }_n=2\pi n{\overline{\nu }}_x^0\Delta x$. In the absence of time-averaged flow in the x direction, the argument of the nth reflection will be preserved throughout the experiment. If flow is nonzero, then Δx is a function of time. Assuming a constant flow rate of q_x = Δx/t, then Δx can be replaced by q_xt + Δx₀ in Eq. 24, in which Δx₀ is the phase shift at t = 0. This substitution results in an argument for the nth peak given by the following equation:

$${\phi }_n=2\pi n{\overline{\nu }}_x^0\left(\Delta x_0+q_{x}t\right).$$ (25)

Notably, the rate of change in the phase shift from flow is proportional to n, such that the higher harmonics corresponding to higher spatial frequencies are likely to be more sensitive to flow than the lower harmonics. This trend mirrors analogous sensitivities to time in the fluorescence recovery from diffusion in Eq. 14, in which the higher harmonics report on fast diffusion times measured over short distances.

Materials and Methods

Two-photon excited fluorescence microscopy

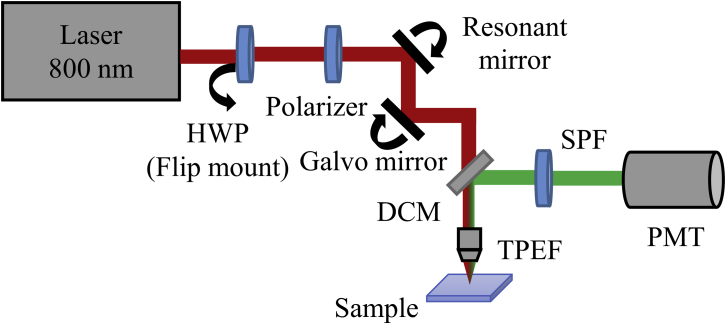
The experimental apparatus for two-photon excitation in FT-FRAP is depicted in Fig. 2. A tunable 80-MHz, Ti:sapphire, femtosecond laser (Mai Tai) purchased from Spectra-Physics (Santa Clara, CA) was used for the excitation source. The fundamental beam was raster-scanned across the sample using a 8.8-kHz resonant scanning mirror purchased from Electro-Optical Products (Ridgewood, NY) for the fast-scan axis and a galvanometer mirror purchased from Cambridge Technologies (Bedford, MA) for the slow-scan axis, both controlled by custom timing electronics built in-house (43). A 10×, 0.3 NA objective purchased from Nikon (Melville, NY) was used to focus the beam onto the sample, and the two-photon excited fluorescence (TPEF) signal was collected in the epi direction through the same objective used for delivery of the excitation beam. The laser was tuned to 800 nm with a power of ∼50 mW at the sample during imaging and ∼500 mW at the sample during photobleaching. A long-pass dichroic mirror (650DCXR) purchased from Chroma Technology (Bellows Falls, VT) and a bandpass filter (FGS900) purchased from Thorlabs (Newton, NJ) were used to isolate the TPEF signal before it was detected by a photomultiplier tube (PMT) (H7422P-40 MOD) purchased from Hamamatsu (Hamamatsu City, Japan). Responses of the PMT were digitized synchronously with the laser pulses by using a digital oscilloscope card (ATS9350) purchased from AlazarTech (Pointe-Claire, Québec, Canada) and mapped onto 512 × 512 images via custom software written in-house using MATLAB purchased from The MathWorks (Natick, MA) (43). The TPEF videos were recorded at approximately four frames per second.

Figure 2.

Instrument schematic of a nonlinear optical beam-scanning microscope used for multiphoton FT-FRAP. An HWP on a flip mount was used to modulate from low power (∼50 mW) to high power (∼500 mW) for the photobleach. Beam scanning was performed with galvanometer (slow axis) and resonant (fast axis) mirrors. DCM, dichroic mirror; HWP, half-wave plate; PMT, photomultiplier tube; SPF, short-pass filter; TPEF, two-photon excited fluorescence. To see this figure in color, go online.

Comb photobleach FT-FRAP

A simple change to the scan pattern of the galvanometer (slow axis) mirror was used to generate a comb photobleach pattern at the sample. After an initial low-power period for baseline TPEF microscopy of the full field of view, patterned photobleaching was performed simply by changing the number of steps in the ramp function driving the galvanometer mirror from 512 (used for normal imaging) to an integer fraction of 512 corresponding to the fundamental spatial frequency (e.g., 8, 16, or 32 pixels = 1/${\overline{\nu }}_0$). The dwell time per step was also increased proportionally such that the repetition rate of the slow axis mirror was independent of the number of lines in the comb photobleach pattern. A flip mount with a half-wave plate (depicted in Fig. 2) was synchronized to switch the excitation source from low power to high power concurrently with the reduction in ramp steps. This protocol resulted in a comb photobleach pattern, as seen in Fig. 3 A. After ∼2 s at high power, the flip mount was removed, reducing the laser power, and the number of steps for the slow axis mirror was changed back to 512 to facilitate normal imaging at low power to track the fluorescence recovery of the sample. A video of an FT-FRAP experiment on fluorescein isothiocyanate (FITC)-polydextran (2 MDa) in 22 mg/mL hyaluronic acid (HA) is shown in Video S1, in which the microscope images are shown on the left and the log of the spatial FT is shown on the right.

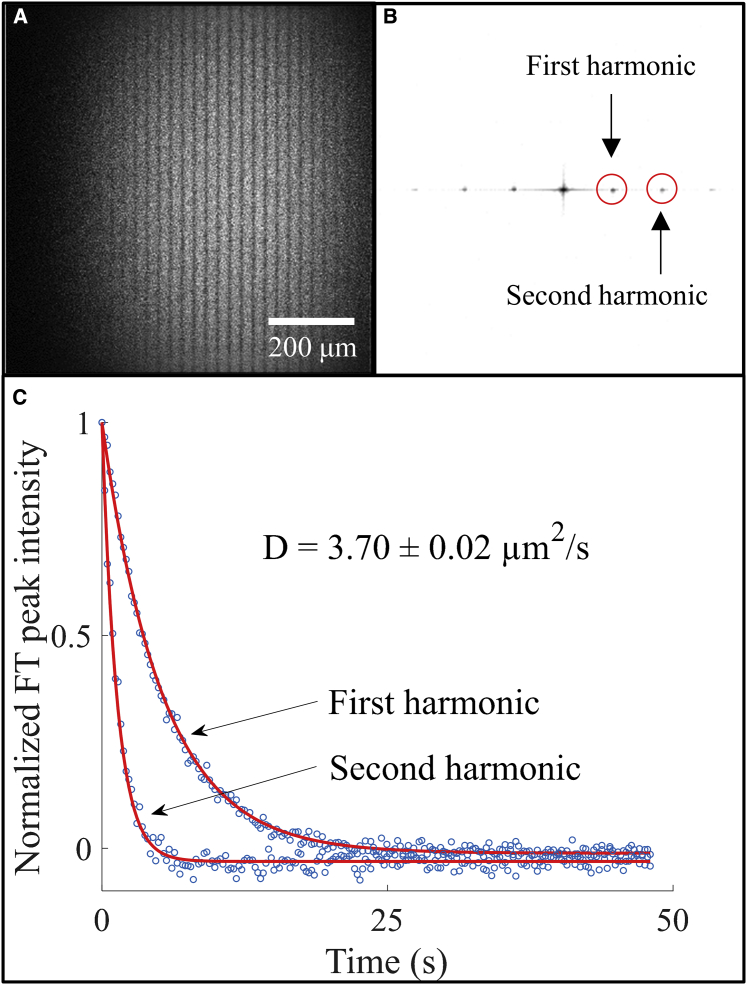
Figure 3.

Multiphoton excited FT-FRAP with comb photobleach of FITC-polydextran (2 MDa) dissolved in 50:50 glycerol/water. (A) Image of the solution immediately after a 32-line comb bleach. (B) 2D FT of (A) with the circled peaks corresponding to the first and second spatial frequency harmonics of the 32-line comb bleach. (C) Fluorescence recovery of the first and second harmonic peaks with best-fit curves recovering a diffusion coefficient (D = 3.70 ± 0.02 μm²/s). The reported uncertainty is the SD of the fit. To see this figure in color, go online.

Video S1. Video showing an FT-FRAP Experiment on FITC-Polydextran (2 MDa) in 22 mg/mL HA

The left side of the video shows the microscope images during the experiment. The right side of the video shows the log of the 2D spatial Fourier transform of the microscope images on the left. During the period of 0:00–0:06, the baseline fluorescence is recorded. During the period of 0:07–0:09, the sample is photobleached with patterned illumination. During the period of 0:10–1:15, the fluorescence recovery is recorded. Note the puncta that appear in the log of the 2D-FT from the patterned photobleach at 0:10 and fade thereafter.

Data analysis

Analysis of the FT-FRAP data was performed using custom software written in-house using MATLAB. A 2D FT was taken of each image. FT-FRAP curves were recovered by integrating over peaks in the FT magnitude. A fit was performed to recover the diffusion parameters using Eq. 14 for normal diffusion and Eq. 19 for anomalous diffusion. A MATLAB function, written by Roberto Garrappa, was used for evaluating the Mittag-Leffler function in Eq. 19 (44). Uncertainties in the fits were calculated based on the second derivative of χ²-space in the vicinity of the minimum. Phasor analysis of flow was performed by taking the argument of the complex-valued 2D-FT peaks and relating the phase back to flow velocity through Eq. 25.

Sample preparation

Solutions of 2 mg/mL FITC-polydextran (2 MDa) purchased from MilliporeSigma (Burlington, MA) were used to evaluate the FT-FRAP approach. These fluorescently labeled molecules were solubilized in either 50:50 glyercol/water or in an aqueous solution of 22 mg/mL HA (15 MDa) purchased from Lifecore Biomedical (Chaska, MN). Solutions were mixed thoroughly before FRAP analysis.

Results and Discussion

FT-FRAP characterization of normal diffusion

The capabilities of FT-FRAP were evaluated using polydextran, a model system for diffusion measurements. As shown in Fig. 3 A, a comb pattern was employed for photobleaching a solution of 2 mg/mL FITC-polydextran (2 MDa) in 50:50 glycerol/water. After photobleaching, spatial FT produced sharp puncta with symmetric amplitudes about the origin peak, as shown in Fig. 3 B. As diffusion progressed, the FT peak intensities exhibited simple exponential decays, as shown in Fig. 3 C. These observations are in excellent agreement with theoretical predictions in Eq. 4. Consistent with prior arguments on signal power, the FT-FRAP analysis clearly provides high signal-to-noise photobleaching curves by combining the analysis over the entire field of view.

Comb patterns for photobleaching enabled simultaneous analysis over multiple length scales through the nth spatial harmonics ${\overline{\nu }}_{x,n}$, as shown in Fig. 3. Theoretical predictions in Eq. 14 suggest an exponential decay of each impulse with a decay constant given by $\tau =1/\left[4{\pi }^2{\left(n{\overline{\nu }}_x^0\right)}^2{D}_{xx}\right]$. Higher harmonics are expected to exhibit faster decays with a quadratic dependence on n for normal diffusion. The decays of the first and second harmonic peaks were fitted to Eq. 14, recovering a diffusion coefficient of 3.70 ± 0.02 μm²/s. The reported uncertainty is the SD of the fit.

FT-FRAP characterization of flow

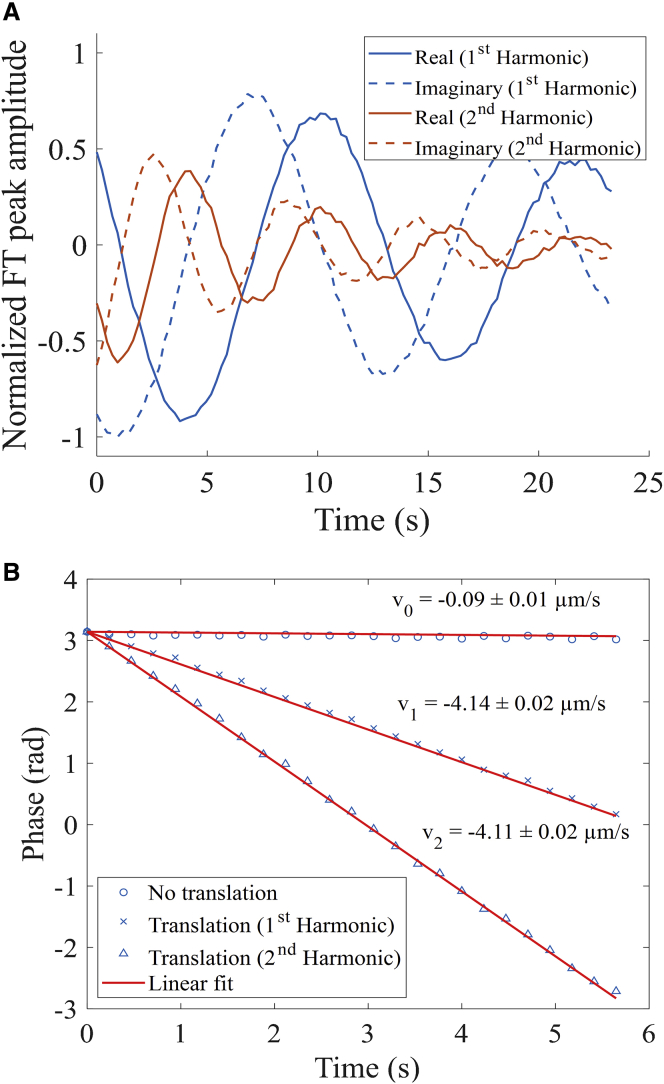
The impact of flow on the phase of the recovered FT peaks was evaluated in the results shown in Fig. 4, in which unidirectional fluid motion was simulated by sample translation with an automated stage during the fluorescence recovery. The sample under investigation was an aqueous solution of 2 mg/mL FITC-polydextran (2 MDa) in 50:50 glycerol/water. Recovery of the diffusion coefficient in FT-FRAP only requires analysis of the magnitude of the Fourier peaks. However, the real and imaginary components of the Fourier peaks contain information about the spatial phase of the photobleach pattern. Fig. 4 A shows an oscillatory decay of the real and imaginary components of the first and second harmonic peaks. The phase of the Fourier peak can be calculated using the argument of the complex number describing the peak at each time point. Fig. 4 B shows the phase shift of a sample that was not translated and the phase shift of the first and second harmonic peaks of a sample that was translated. Consistent with the expression in Eq. 25, the phase angle changed linearly with time for the system undergoing directional translation in the x direction of the photobleach comb, with a proportionality constant of $2\pi n{\overline{\nu }}_x^0{q}_x$. Consequently, the nth harmonic is predicted to exhibit an n-fold increase in the rate of phase angle change over time relative to the fundamental peak. From the results summarized in Fig. 4 B, precisely this trend was observed in the measurements, in excellent agreement with the theoretical predictions. The measured flow rate for the translated sample (4.14 ± 0.02 μm/s; uncertainty is the SD of the fit) matched the measured translation rate of the sample stage (4.0 ± 0.4 μm/s; uncertainty is the SD of three measurements).

Figure 4.

Bulk flow measured by FT-FRAP of FITC-polydextran (2 MDa) in 50:50 glycerol/water. (A) Real and imaginary amplitudes of the 2D FT fundamental and second harmonic peaks upon sample translation during diffusion. (B) Phase calculated from real and imaginary amplitudes of 2D FT peaks. The nontranslated sample has minimal bulk flow. The velocities calculated from the fundamental and second harmonic peaks of the translated sample are within one SD of each other and close to the translation rate of the sample stage (4.0 ± 0.4 μm/s) after correcting for bulk flow from convection. The reported uncertainties are the SD of the fit. To see this figure in color, go online.

Interestingly, a statistically significant flow of 0.09 ± 0.01 μm/s was observed even in the absence of sample translation. This subtle but nonzero flow is attributed to slow sample convection within the viscous 50:50 glycerol/water solvent. The sensitivity of phase analysis is noteworthy because this flow is >40 times slower than the sample translation and corresponds to a displacement of ∼1–2 pixels (2 μm) over the entire 25 s of data collection. It should be noted that flow (in the absence of mixing) only changes the phase of the FT peak and not the magnitude. Phase changes are independent of the magnitude and do not influence the fluorescence recovery curve.

Patterned versus point-bleach profiles

It is worthwhile to compare the FT-FRAP approach demonstrated herein with previous studies employing SFA of FRAP measurements. In those prior studies, Fourier analysis was performed to aid in interpretation of recoveries using conventional photobleach illumination of localized points. SFA provided similar computational benefits in the mathematical simplicity arising in the Fourier domain. However, FT-FRAP has a major signal-to-noise advantage over conventional point illumination. In the numerator, FT-FRAP supports major increases in the signal power (>2000-fold with comb illumination) by distributing the photobleach amplitude over the entire field of view, whereas conventional point illumination saturates (photobleach depth approaching unity) at a much lower integrated signal power. Furthermore, patterned illumination enables shifting of the signal to a quiet spatial frequency for noise suppression. By analogy with 1/f noise in electronics, analysis of natural images suggests a power spectrum obeying a $1/\overline{\nu }$ dependence (45). For optical detection in the shot-noise limit, the variance in signal is proportional to the mean. Because visible photons are often detectable with signal-to-noise approaching the shot-noise limit in instrumentation optimized for FRAP, it stands to reason that the noise in the Fourier domain will also scale with the signal power in an image with natural contrast. Consequently, the low-frequency noise power spectrum is also expected to scale with $1/\overline{\nu }$, in direct analogy with 1/f noise in electronics. As in electronics, shifting of the signal to a frequency regime with lower noise through modulation can provide a substantial noise reduction.

The illumination patterns investigated in this work were specifically designed for spatial FT analysis, and as such, differ significantly from a host of previous FRAP studies using patterned illumination. Previous work investigated the use of arbitrary photobleach patterns to select objects or regions of interest within the field of view (18,46,47). Alternatively, several investigators have explored measurements with line excitation (21,48). However, none of these previous patterned illumination studies incorporated intentional periodicity within the photobleach patterns that could subsequently integrate into FT-FRAP analysis. Control over the number of lines within the comb provides the advantage of matching the distances over which diffusion is measured and, correspondingly, the timeframe for recovery. Under high magnification, the field of view is reduced; this can be compensated for by reducing the number of lines within the patterned photobleach. Conversely, measurement time can be reduced to improve throughput by increasing the number of lines in the photobleach pattern to reduce the diffusion distances in the comb. The closest work to our study is, arguably, in studies by Lanni and Ware from the 1980s, in which sinusoidal modulation of a photobleach pattern was performed by passing the excitation beam through a grating (49). The apparatus was designed so that the image of the grating was at the focus of the sample, creating a photobleaching mask at high laser power. The subsequent fluorescence recovery was probed by translating the grating, producing a phase shift in the illumination pattern at the sample, which generated a periodic signal in the integrated fluorescence intensity over time as the grating was shifted. The integrated fluorescence signal was recorded on a single-channel detector, and the Fourier components were analyzed to recover the diffusion coefficient. The conceptual foundation for the studies by Lanni and Ware is aligned with the principles undergirding the work presented herein.

FT-FRAP characterization of anomalous diffusion

Additional results were obtained to characterize anomalous diffusion in a viscous matrix. Fig. 5 shows FT-FRAP measurements obtained with a comb photobleach pattern on FITC-polydextran (2 MDa) in 22 mg/mL HA. HA is a glycosaminoglycan polymer that is found throughout the connective tissues of the body. The physiological functions that involve HA include lubrication, wound repair, and cell migration. HA is known to increase viscosity when added to aqueous solutions. In this experiment, the fluorescence recovery of the first three spatial harmonics of the comb photobleach pattern was analyzed to characterize anomalous diffusion of FITC-polydextran in a solution with HA.

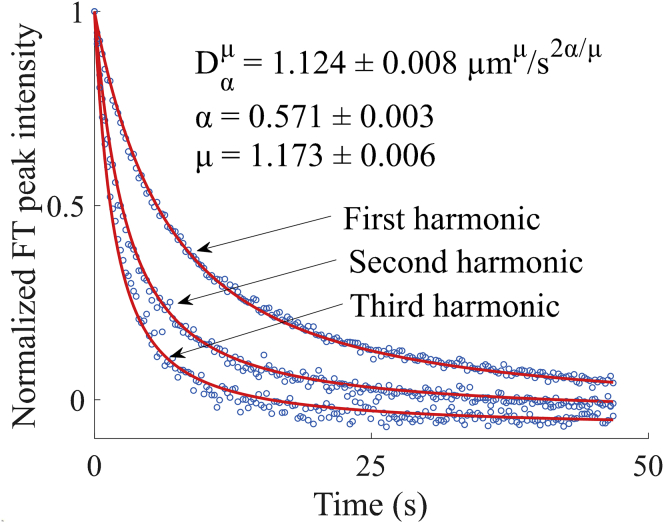
Figure 5.

Harmonic analysis of anomalous diffusion with FITC-polydextran (2 MDa) in 22 mg/mL HA. Fluorescence recovery of the first, second, and third harmonics are fitted to a modified Mittag-Leffler function to recover the anomalous diffusion coefficient (D = 1.124 ± 0.008 μm^μ/s^2α/μ), the subdiffusion parameter (α = 0.571 ± 0.003), and the Lévy flight parameter (μ = 1.173 ± 0.006). The recovered parameters reveal subdiffusive and Lévy flight behavior in the sample. The reported uncertainties are the SDs in the fit. To see this figure in color, go online.

Several models for anomalous diffusion were considered. First, the three harmonics were fitted to a model for systems with subdiffusive mobility described in Eq. 16. Subdiffusion was considered because of possible binding and unbinding or association and dissociation of the FITC-polydextran with the HA matrix. However, analysis with this model did not produce a satisfactory fit because the data did not exhibit a quadratic dependence on spatial frequency. Second, the data were fitted to a model for systems exhibiting Lévy flight described in Eq. 18. Lévy flight behavior was considered because of possible crowding or trapping by HA acting as an obstacle to constrict free diffusion of the FITC-polydextran. Whereas the Lévy flight model produced best-fit curves with a better match for the spatial frequency dependence, the shape of the best-fit curves was exponential and far from a good fit to the fluorescence recovery curves. Models incorporating just one of these two effects (subdiffusion or Lévy flight) were insufficient to describe the data.

Third, a global fit of the first three harmonics to a combined subdiffusion-Lévy flight model described in Eq. 19 was performed to recover the anomalous diffusion coefficient D = 1.124 ± 0.008 μm^μ/s^2α/μ, the subdiffusive parameter α = 0.571 ± 0.003, and the Lévy flight parameter μ = 1.173 ± 0.006. The reported uncertainties are the SD in the fit. The result of this fit is shown in Fig. 5. The combined model was able to account for both the spatial frequency dependence of the harmonics and the shape of the recovery curves, which deviate from exponential. The value of α < 1 indicates that the characteristic wait time diverges (subdiffusion). Furthermore, the value for μ < 2 indicates that the step-length variance diverges (Lévy flight).

The results of the analysis demonstrate that FT-FRAP can sensitively and precisely disentangle covariant parameters describing anomalous diffusion by simultaneously fitting to multiple harmonics acquired in parallel. The same analysis performed with only the first harmonic yielded lower confidence in the recovered parameters: D = 1.9 ± 0.1 μm^μ/s^2α/μ, α = 0.69 ± 0.01, and μ = 1.57 ± 0.05. The reduction in precision likely arose from the increase in covariance in the single-harmonic fit; the recovered parameters are highly correlated (D and α = 0.976, D and μ = 0.995, and α and μ = 0.993, where ±1 corresponds to perfectly correlated/anticorrelated parameters). By comparison, the correlation coefficients obtained in the three-harmonic fit are much less significant: D and α = −0.204, D and μ = 0.286, and α and μ = 0.850. Comparison with a one-harmonic fit demonstrates that measuring diffusion at multiple length scales with FT-FRAP can substantially increase statistical confidence in the parameters recovered from fitting to an anomalous diffusion model by constraining the model to describe diffusion globally.

Conclusion

In this work, FT-FRAP with patterned illumination has been described theoretically and demonstrated experimentally to characterize normal and anomalous diffusion. Relative to conventional point-bleach FRAP, FT-FRAP has the advantages of mathematical simplicity, higher SNR, representative sampling, and multiphoton compatibility. Proof-of-concept measurements with a model system (FITC-polydextran) showed good agreement with theory. Flow was quantified using the phase of the real and imaginary components of the FT peaks. Anomalous diffusion was characterized by FT-FRAP through a global fit to multiple harmonics of the photobleach pattern.

Future fundamental work includes experiments to test the ability of FT-FRAP with patterned illumination to characterize heterogeneous samples, in which diffusion varies across the field of view. In such cases, point illumination would only provide information about the localized diffusion recorded in the isolated region adjacent to the photobleach. In contrast, patterned illumination simultaneously interrogates diffusion within the entire field of view. In samples exhibiting heterogeneous diffusivity, the integrated heights of the FT peaks recover the average diffusion coefficient throughout the field of view. In principle, the shape of the FT peak can further inform on the spatial diversity in diffusion, which is currently under investigation for recovery of diffusivity maps. FT-FRAP can also be implemented in a variety of application spaces, including measurement of mobility in pharmaceutically relevant matrices, quantification of protein aggregation, and live-cell imaging.

Author Contributions

A.C.G. and G.J.S. developed the theory. A.C.G. and G.J.S. designed the microscope. A.C.G., C.J.S., and M.S.C. built the microscope. A.C.G., N.T., and D.M.H. collected data. A.C.G. analyzed data. A.C.G., N.T., C.J.S., M.S.C., D.M.H., and G.J.S. wrote and edited the manuscript.

Editor: Dimitrios Vavylonis.