Phase Separation of Toxic Dipeptide Repeat Proteins Related to C9orf72 ALS/FTD

Abstract

The expansion mutation in the C9orf72 gene is the most common known genetic cause for amyotrophic lateral sclerosis (ALS) and frontotemporal dementia (FTD). This mutation can produce five dipeptide repeat proteins (DPRs), of which three are known to be toxic: poly-PR, poly-GR, and poly-GA. The toxicity of poly-GA is attributed to its aggregation in the cytoplasm, whereas for poly-PR and poly-GR, several toxicity pathways have been proposed. The toxicity of the DPRs has been shown to depend on their length, but the underlying molecular mechanism of this length dependence is not well understood. To address the possible role of phase separation in DPR toxicity, a one-bead-per-amino-acid (1BPA) coarse-grained molecular dynamics model is used to study the single-molecule and phase-separation properties of the DPRs. We find a strong dependence of the phase-separation behavior on both DPR length and concentration, with longer DPRs having a higher propensity to phase separate and form condensed phases with higher concentrations. The critical lengths required for phase separation (25 for poly-PR and 50 for poly-GA) are comparable to the toxicity threshold limit of 30 repeats found for the expansion mutation in patient cells, suggesting that phase separation could play an important role in DPR toxicity.

Significance

C9orf72 ALS/FTD is caused by a repeat expansion mutation that typically has a length larger than 30 repeats. This expansion produces dipeptide repeat proteins (DPRs) that can induce length-dependent toxicity through several hypothesized pathways. However, no consensus has been reached on the prevailing toxicity pathway, and the underlying molecular mechanisms of the length dependence remain elusive. Here, we use a coarse-grained molecular dynamics model to explore the phase-separation behavior of the DPRs. We find the phase separation of the DPRs ensues only above a critical DPR length that is comparable to the toxicity threshold limit of 30 repeats found in patients, suggesting that phase separation of DPRs might play an important role in C9orf72 ALS/FTD.

Introduction

Hexanucleotide repeat expansion G₄C₂ in the C9orf72 gene is the most common genetic mutation in familial cases of amyotrophic lateral sclerosis (ALS) and frontotemporal dementia (FTD) (1,2). Healthy individuals typically have less than around 20 repeats of this expansion, whereas in most patient cells, the size of the expansions is estimated to be between several hundred and several thousand repeat units (1, 2, 3). There is no consensus on the critical expansion size for the onset of the disease, and different cutoffs between 30 and 80 repeats have been reported for the toxicity threshold (1,2,4,5).

The pathology initiated by the repeat expansion has been proposed to affect a wide range of cellular processes (6). The three main mechanisms of toxicity are loss of function of C9orf72 proteins (1,7) and toxic gain of function from the repeat expansion itself (8,9) or from dipeptide repeat proteins (DPRs) translated from sense and antisense transcripts of the repeat expansion (10, 11, 12). It has been shown that DPRs are capable of inducing toxicity without the repeat expansion in different cell types (12, 13, 14, 15, 16, 17).

Repeat-associated non-AUG (RAN) translation of the sense and antisense transcripts of the repeat expansion from all reading frames can produce five types of DPRs: poly-PR, poly-GR, poly-GA, poly-GP, and poly-PA (10,11). Poly-PR, poly-GR, and poly-GA can induce length-dependent and dosage-dependent toxicity (12,14,16,18, 19, 20, 21), of which especially the R-DPRs, i.e., poly-PR and poly-GR, are highly toxic. Poly-PR is known to be the most toxic DPR (12, 13, 14, 15,20,22). Several studies indicate no significant toxicity for poly-GP and poly-PA (12,20,23). In our study, we use the term toxic DPRs to refer to poly-PR, poly-GR, and poly-GA.

Poly-GA is the most abundant and the most aggregation-prone DPR (10,22). Poly-GA has only a few interactors in the cell (22). It has been suggested that poly-GA toxicity is due to the formation of cytoplasmic aggregates and direct sequestration of proteins (24, 25, 26, 27, 28). Poly-GA aggregates are shown to impair the nuclear import of TDP-43 (29) and enhance DNA damage (27). Poly-PR and poly-GR have many target proteins inside the cell (22,30) and are likely to be involved in several pathology pathways (reviewed in (6)). Significant attention has been drawn to nucleocytoplasmic transport defects, changes in the dynamics of membrane-less organelles through impaired liquid-liquid phase separation (LLPS), and nucleolar dysfunction (13,14,16,17,22,31,32). Recently, the toxicity of poly-PR has been related to changes in LLPS of heterochromatin protein 1α (HP1α) (17) and nucleophasmin (NPM1) (16) through their direct interaction with poly-PR inside the cell nucleus.

Depending on the type of DPR and the toxicity mechanism, the DPR pathology can start in the cytoplasm, nuclear pore complex (NPC), or nucleus. Despite the recent progress, a clear understanding is lacking on how the DPRs cause neurotoxicity in C9orf72 ALS/FTD. Because of the methodological difficulty of synthesizing repetitive sequences, it is highly challenging to study the length-dependent properties of DPRs that might provide insight into the DPRs’ length-dependent toxicity. As a result, almost all previous in vitro cell-free studies were limited to DPRs with less than 30 repeats (21,22,33,34) (only one recent study used 60 repeats of poly-PR (16)), which might not mimic the exact role of long DPRs in patients (35). Moreover, the concentration inside the condensed phases, which is important for further maturation of the phase-separated condensates (36), is not easily determined in experiments. These problems can be overcome by using experimentally calibrated coarse-grained molecular dynamics (MD) models that can capture the sequence specificity and are suitable for simulating high-density phases of proteins (37, 38, 39). In this study, we use our one-bead-per-amino-acid (1BPA) coarse-grained MD model (37,40,41) to investigate the single-molecule and phase-separation behavior of toxic DPRs in an attempt to identify possible mechanistic roles of DPR phase separation in causing toxicity.

Methods

Coarse-grained force field

We use our implicit-solvent coarse-grained 1BPA model (37,42), which 1) differentiates between the bonded potentials of glycine, proline, and other residues and 2) is fine-tuned to capture the properties of polyproline, polyglycine, and FG-Nup segments with the highest arginine content. More details are provided in the Supporting Materials and Methods.

Simulations

Langevin dynamics simulations are performed at 300 K and physiological salt concentration of 150 mM using GROMACS. Droplet simulations are performed in a cubic box of size 80 nm. Slab simulations are conducted based on the procedure described in (38). Phase-separation simulations are performed for ∼3 μs, which is sufficient to obtain converged density profiles. The density profiles are calculated using discrete cells of thickness 1 nm and time averaged for at least 1 μs at equilibrium. The critical repeat lengths required for phase separation are obtained with an error of less than five repeats. More details are provided in the Supporting Materials and Methods.

Results and Discussion

Single-molecule properties of toxic DPRs

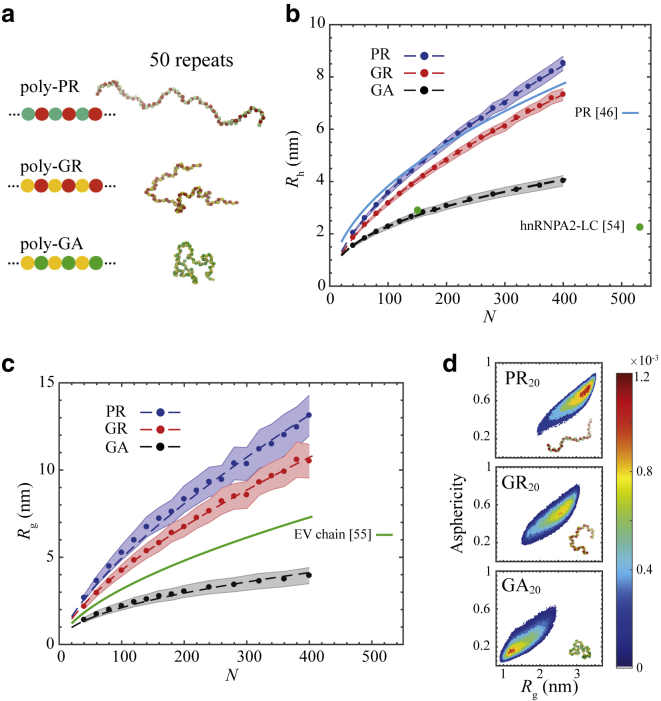
The dynamics of intrinsically disordered proteins (IDPs) is crucial for their function, including, for example, recognition and binding to target molecules (43, 44, 45). The dimension of IDPs can have a large effect on their functional properties. At a fixed temperature and solvent condition, the dimension of an IDP is determined by its amino acid sequence (43,46). The repetitive sequences of toxic DPRs contain only two types of amino acids (see Fig. 1 a and Video S2). Therefore, the overall properties of the DPRs strongly depend on the physiochemical properties of glycine, alanine, proline, and arginine and possibly the patterning of these residues. Alanine is hydrophobic, arginine is positively charged, and proline contributes to the rigidity and glycine to the flexibility of the protein backbone (47, 48, 49).

Figure 1.

Comparison between the single-molecule properties of poly-PR, poly-GR, and poly-GA. (a) A schematic representation of the DPRs (left) and simulation snapshots (right); see also Video S2. (b) Hydrodynamic radius R_h of the DPRs plotted against their chain length N (circles fitted with dashed lines). The solid light-blue line is a prediction for the R_h of poly-PR based on a closed-form expression (46). Experimental R_h-value for the LC domain of hnRNPA2 is shown by a green circle. (c) Radius of gyration R_g of the DPRs plotted against their chain length N (circles fitted with dashed lines). R_g of an EV chain is provided for comparison. In (b) and (c), the shaded regions indicate half of the standard deviation. (d) Two-dimensional probability distribution of the asphericity and R_g for PR₂₀, GR₂₀, and GA₂₀. To see this figure in color, go online.

We use our 1BPA MD model (details are provided in Methods) to study the dimensions of the three toxic DPRs. In Fig. 1, b and c, we show the hydrodynamic radius, R_h, and the radius of gyration, R_g, of poly-PR, poly-GR, and poly-GA. The results are shown for a range of chain lengths N between 40 and 400, with N being two times the number of repeats, n.

For the same chain length, the dimension of poly-PR is larger than poly-GR, which is larger than poly-GA. The electrostatic repulsion between the uniformly distributed arginine residues results in more expanded conformations for the R-DPRs compared with the hydrophobic poly-GA. This observation is consistent with previous studies on the effect of charged residues and their patterning on the dimension of IDPs (50, 51, 52). The observed difference between poly-PR and poly-GR, however, cannot be explained by the nonbonded interactions alone. Proline is more hydrophobic than glycine (37,53), and thus poly-PR is expected to have a more compact structure than poly-GR. Therefore, the larger R_h- and R_g-values for poly-PR can only be attributed to the different contribution of proline and glycine to the backbone stiffness. To prove this, we repeated the simulations for poly-GR and poly-PR by interchanging the hydrophobicity values of P and G while keeping the bonded potentials the same. The results in Fig. S2 convincingly show that the difference between poly-GR and poly-PR in Fig. 1, b and c is almost entirely due to the difference in backbone stiffness. Indeed, proline is much stiffer than glycine because of the cyclic structure of its side chain (47, 48, 49), which is incorporated in the 1BPA force field (42). Our results are consistent with the observed correlation between proline content and extended conformation of IDPs (46,48).

In Fig. 1 b, we compare our simulation results for R_h of poly-PR with the Marsh and Forman-Kay fit to the experimental R_h-values of 36 IDPs (46). The suggested expression takes into account the proline content and the absolute net charge of the chain. The difference between our simulation results and the prediction by Marsh and Forman-Kay expression is less than 16%. The observed difference for longer chains could be due to the fact that the patterning of amino acids has not been considered as an input variable in the suggested expression (46). To show the importance of sequence patterning, for instance, the R_h of three variants of proline-arginine chains with the same amino acid composition but different patterning of proline and arginine residues are depicted in Fig. S3. These results show that the chain favors a conformation with the highest R_h when the proline and arginine residues are well mixed, as in poly-PR. Poly-GA forms the most compact conformation because of the uniform distribution of hydrophobic alanine residues and the low stiffness of the glycine residues. We also compare the simulated R_h of poly-GA with the experimental R_h of the disordered low-complexity (LC) domain of hnRNPA2 (54); see Fig. 1 b. The hnRNPA2 LC domain contains hydrophobic residues (mainly phenylalanine and tyrosine) distributed along the sequence. It has been suggested that the high glycine content (47%) of hnRNPA2 LC domain contributes to its compactness (54). With the same chain length, the hydrodynamic size of poly-GA is very similar to that of the hnRNPA2 LC domain.

Relating the R_g of the DPRs to the chain length N via R_g ∝ N^ν (55) leads to scaling exponents of ν = 0.70 ± 0.02 for poly-PR, 0.67 ± 0.02 for poly-GR, and 0.48 ± 0.02 for poly-GA. Similar scaling exponents of around 0.70 have been obtained for extended variants of prothymosin α (ProTα) (with a mean net charge per residue of −0.46) in water (55). The scaling exponent of poly-GA is close to the value ν = 0.5 expected for a random coil, i.e., a polymer in a θ solvent, and lies in the range 0.46 ± 0.05 obtained for the unfolded state of proteins in experiment (55). The scaling exponent of poly-GA is also comparable to an average scaling exponent of 0.53 obtained for a set of IDPs and unfolded proteins using an improved generation of atomistic force fields (56). The R_g ∝ N^0.6 of an excluded volume (EV) chain is also plotted for comparison in Fig. 1 c (55). Poly-PR and poly-GR have an R_g that is larger than an EV chain because of the repulsion of like charges, whereas the flexible and more hydrophobic poly-GA has a lower R_g. In Fig. 1 d, we compare the asphericity, which measures the chain shape, versus R_g plots for DPRs with a repeat length n = 20. PR₂₀ samples conformations with a larger R_g and asphericity than GR₂₀ and GA₂₀, showing that poly-PR is more extended and assumes shapes closer to a rod-like conformation.

Phase separation of poly-GA

Poly-GA forms cytoplasmic aggregates (5,18,22,25) that are relatively stable in photobleaching experiments (22). Fourier transform infrared spectroscopy measurements show a random coil structure for GA₁₅ right after incubation (21). After a certain incubation time, the GA₁₅ molecules form aggregates as indicated by a change in the average particle size in the system (21). After a few hours, GA₁₅ starts to form fibrils containing cross-β-sheet structures with disordered molecules of poly-GA still in solution (21,57).

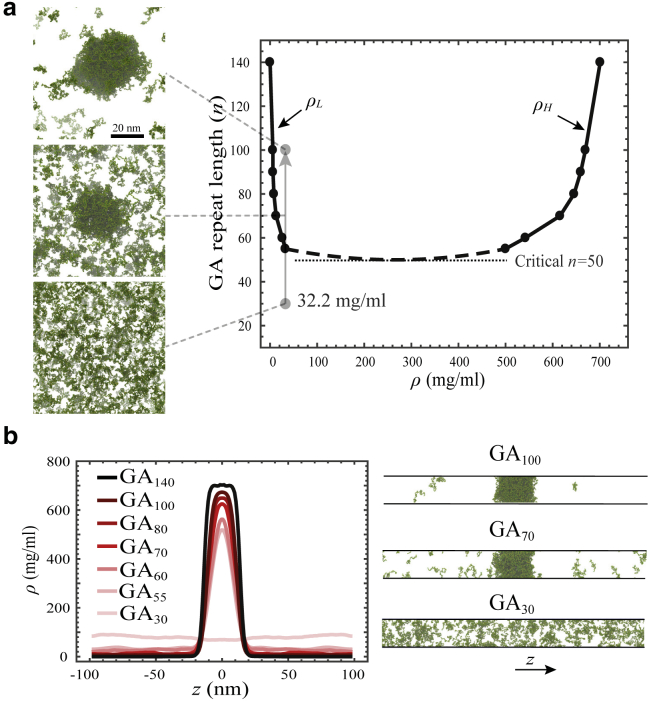
Our results show that poly-GA undergoes a length-dependent phase separation to form a condensed (high-density) phase and a dilute (low-density) phase (Fig. 2). The condensed phases of poly-GA are spherical and exchange molecules with the surroundings (see snapshots in Figs. 2 a and S4; Video S1). Because hydrogen bonding is not included in the modeling (see the description of our coarse-grained model in the Supporting Materials and Methods), we are not able to predict the final transition into relatively stable aggregates or higher-order β-type structures of poly-GA as observed in the experiments (21,22,25). However, our results do suggest that long-range hydrophobic interactions drive the formation of high-density phases of poly-GA, which brings the residues close enough for short-range hydrogen bonds to form (58). Further transition of liquid condensates to more solid-like structures have been experimentally observed for FUS and hnRNAPA1 (59, 60, 61). To find the critical repeat length required for phase separation, we constructed the coexistence phase diagram of poly-GA (Fig. 2 a) by determining the concentrations of the condensed phase (ρ_H) and dilute phase (ρ_L) using the slab method (Fig. 2 b; (38,62,63)). In the phase diagram in Fig. 2 a, the vertical axis is the repeat length n and the horizontal axis is the concentration ρ. Outside the coexistence curve (i.e., for concentrations lower than ρ_L and higher than ρ_H and lengths shorter than the critical repeat length), there is only a uniform phase, whereas inside it, the poly-GA molecules phase separate (see the snapshots at the left in Fig. 2 a). The black arrows in Fig. 2 a show the concentrations of the two phases. The critical repeat length for phase separation of poly-GA is found to be n = 50. Below this critical repeat length, no phase separation is observed at any concentration. This critical repeat length is in good agreement with the critical range of 46 < n < 61 found by Yamakawa et al. for the formation of aggregates of poly-GA in Neuro2a cells (5).

Figure 2.

Poly-GA length-dependent phase-separation and coexistence phase diagram. (a) Coexistence phase diagram of poly-GA obtained from slab simulations. Phase separation occurs above the critical repeat length n = 50 inside the coexistence region. ρ_H and ρ_L are the concentrations of the condensed phase and dilute phase, respectively. Simulation snapshots at the left show the results for GA₁₀₀, GA₇₀, and GA₃₀ for a total concentration of 32.2 mg/mL at equilibrium; see also Video S1. (b) Poly-GA slab density profiles (left panel) and sample slab simulation snapshots (right panel). To see this figure in color, go online.

The values of ρ_H and ρ_L depend on the repeat length, with longer poly-GA molecules forming condensed phases with higher concentrations and dilute phases with lower concentrations (see Fig. 2 a). The same trend has been observed in previous simulation studies for polymers and IDPs with different lengths (38,62). Also, in experiments using synthetic molecules, the saturation concentration, which is equal to ρ_L at equilibrium, was observed to decrease with chain length (64). For 60 ≤ n ≤ 100, we find the concentration range to be 6–33 mg/mL for the dilute phase and 500–670 mg/mL for the condensed phase. Using linear interpolation in Fig. 2 a, the molar concentration of the GA₇₆ condensed phases is found to be ∼34 mM, comparable to that of the 151-residue-long hnRNPA2 LC domain (30–40 mM) obtained in experiment (54). This is expected because the hnRNPA2 LC domain has a similar dimension as GA₇₆ (see Fig. 1 b). We also observed a lower exchange rate with the surroundings for the condensed phases formed by longer chains (see Table S2), suggesting that longer molecules form more stable condensed phases.

Cluster size distribution analysis of poly-GA at equilibrium shows a strong correlation between the poly-GA total concentration and its ability to phase separate at small concentrations at the left of the phase diagram (Figs. 2 a and S5). When phase separation occurs, a further increase of the total concentration has no effect on the ρ_H and ρ_L but only increases the size of the condensed phase (Fig. S6). The cluster size distribution results of Fig. S5 also reveal (see Fig. S7) that at a fixed concentration, the number of free molecules N_free is higher for shorter dipeptides and that, as expected, a drop in N_free can be taken as an indication of phase separation.

Phase separation of R-DPRs

R-DPRs have been observed to form liquid droplets in the presence of RNA (33,34), phosphate ions (33,57), and several RNA-binding proteins (16,22). Previous studies have pointed at the important role of electrostatic and cation-π interactions in the LLPS of R-DPRs with multivalent proteins and RNA molecules for these cases (16,22,33,34). The phase separation of PR₃₀ with different polyanions, known as complex coacervation, has recently been investigated using both in vitro experiments and coarse-grained dynamic Monte Carlo modeling (34).

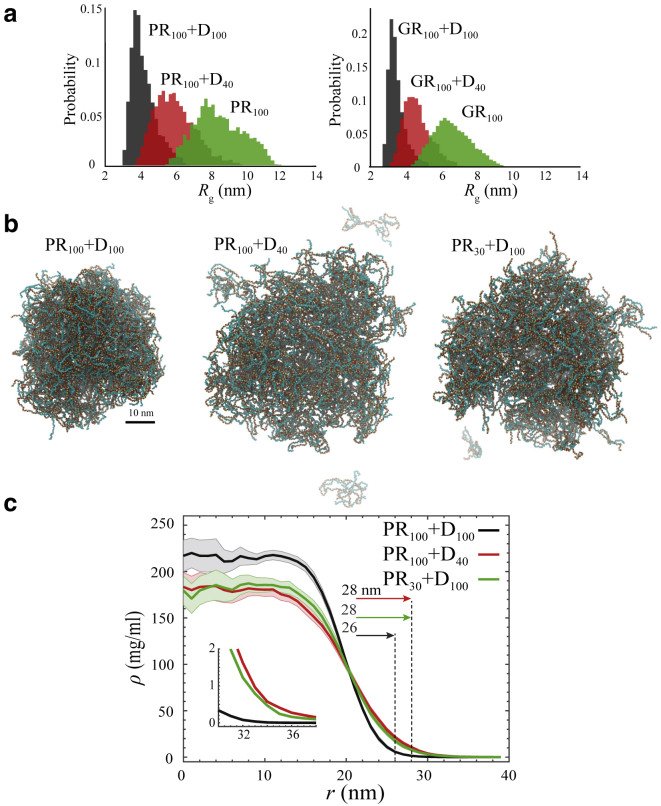
Our simulations show no phase separation of poly-PR and poly-GR as a consequence of the electrostatic repulsion between arginine residues; see Fig. S8 (top panels). The same result has been obtained in in vitro experiments with PR₂₀ in the presence of monovalent ions (33). The addition of anionic homopolymers (acidic molecules) of polyaspartate (poly-D) to the simulation box induces the phase separation of R-DPRs into liquid droplets (Fig. S8, top panels, and Video S3). R-DPRs bind to acidic molecules, and upon binding, they become more compact (see Fig. 3 a). In Fig. S9 a, we compare the potential of mean force associated with binding of the R-DPRs, with repeat lengths n = 30, to an acidic molecule of length N = 60. Despite the higher hydrophobicity of P compared to G, the binding of poly-GR to the acidic molecule is stronger than poly-PR, and poly-GR makes a greater number of contacts with the acidic molecule than poly-PR; see Fig. S9 and Video S4. This difference is attributed to the difference in the backbone stiffness, as reflected by the persistence lengths in isolation, which we calculate to be 2.06 bond lengths for poly-GR and 5.04 bond lengths for poly-PR. This is confirmed by additional simulations in which we interchanged the hydrophobic values of P and G (see Fig. S9 a), showing that the backbone stiffness plays a dominant role in accounting for the different binding strengths of poly-PR and poly-GR.

Figure 3.

Binding of R-DPRs to acidic molecules (poly-D) and length-dependent droplet formation of poly-PR. (a) Histograms for R_g of single PR₁₀₀ (left) and GR₁₀₀ (right) in the presence and absence of a D₄₀ and D₁₀₀ molecule. Binding to acidic molecules reduces the R_g of R-DPRs, with longer acidic molecules having a larger effect. (b) Simulation snapshots for length-dependent droplet formation of poly-PR with acidic molecules for a total concentration of 14.8 mg/mL and a poly-PR concentration ratio of r_PR = 0.57. (c) Radial density profiles measured from the center of mass of the droplets presented in (b). Light shades indicate half of the standard deviation as error bars. The vertical dashed lines indicate the droplet size (for details of the droplet radius calculation, see the Supporting Materials and Methods). The inset shows the zoomed density profiles for r > 30 nm. To see this figure in color, go online.

Long acidic tracts with length ranges of 12–41 amino acids can be found in the disordered regions of two nucleolar proteins: nucleolin (NCL_1–300) and NPM1_120–240; see the net charge per residue (NCPR) histograms in Fig. S10 (top panels). NCL mislocalization and disruption has been observed in ALS patient cells (65). NSR1, the yeast homolog of NCL, has also been observed to be a strong modifier of PR₅₀ toxicity. The toxicity was shown to be suppressed by deletion and enhanced by upregulation of NSR1 (14). A recent study also suggested that poly-PR-induced NPM1 mislocalization generates toxicity (16). Our simulations show binding of the R-DPRs to both NCL_1–300 and NPM1_120–240 through interaction with the acidic tracts (Fig. S10, bottom panels). These results are consistent with the experimentally observed binding of full-length NPM1 and NCL to the R-DPRs (16,22).

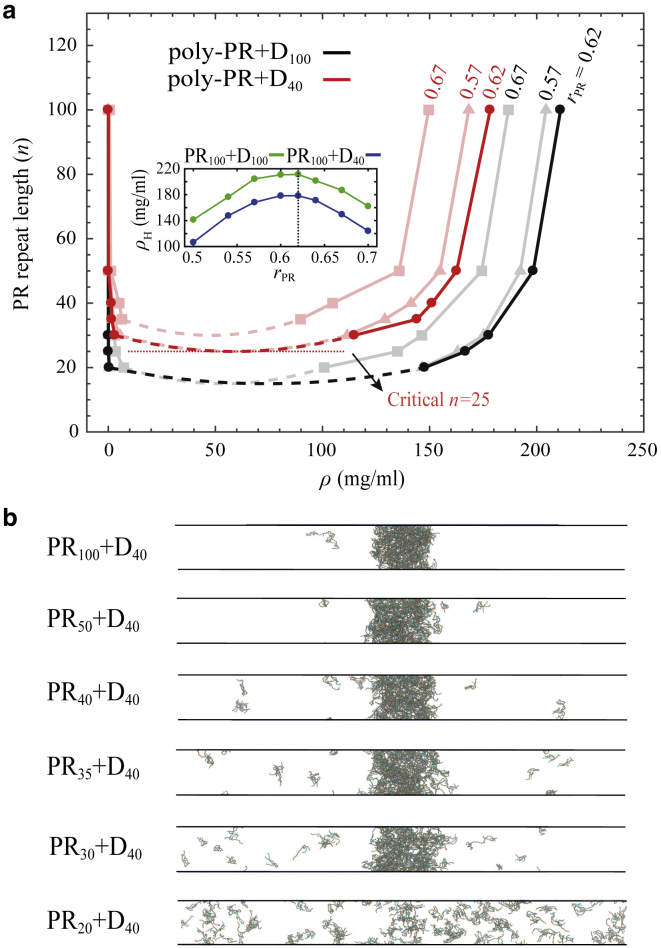
Figs. 3, b and c and 4 show that the phase separation of poly-PR not only depends on its length but also on the length of the acidic molecules. In these simulations, we use different mass concentration ratios of poly-PR, r_PR = (poly-PR mass concentration)/(total mass concentration). With this definition, the poly-PR:poly-D mass ratio can be calculated as 1:(1 − r_PR)/r_PR. At a fixed total mass concentration and r_PR, longer repeats of poly-PR and poly-D phase separate to smaller droplets with a higher concentration surrounded by a dilute phase with a lower concentration (see Fig. 3 c). Reduction of the length of acidic molecules (Fig. 3 b, middle panel) or poly-PR (Fig. 3 b, right panel) increases the size of the droplet and the concentration of the dilute phase (see Fig. 3 c).

Figure 4.

Length-dependent phase separation of poly-PR. (a) Phase diagrams for poly-PR phase separation with acidic molecules of lengths 40 and 100 for different poly-PR concentration ratios of r_PR = 0.57, 0.62, and 0.67; see the tilted numbers next to each phase diagram. Light shades are used for the phase diagrams constructed for r_PR = 0.57 and 0.67. The minimal critical repeat length for phase separation of poly-PR with D₄₀ is indicated with a horizontal dotted line. The inset shows the concentration of the high-density phases of PR₁₀₀ + D_40/100 for different poly-PR concentration ratios. (b) Slab simulation snapshots for length-dependent phase separation of poly-PR with D₄₀ for a poly-PR concentration ratio of r_PR = 0.62 are given. No phase separation can be observed below a critical poly-PR repeat length n = 25. To see this figure in color, go online.

To further study the phase separation of poly-PR, we use slab simulations to obtain the coexistence phase diagrams in Fig. 4 a. The phase diagrams are constructed for acidic poly-D molecules of lengths N = 40 and 100 and three different poly-PR concentration ratios r_PR = 0.57, 0.62, and 0.67. Similar to the trend observed in Fig. 3, b and c, we observe that longer repeats form condensed phases with higher concentrations and dilute phases with lower concentrations, in agreement with experimentally observed length-dependent complex coacervation of oppositely charged polyelectrolytes (66). We also observe that the condensed phases of longer PR molecules have a smaller exchange rate with the surroundings; see Table S2. The poly-PR condensed phase concentration ranges from 90 to 211 mg/mL, which is much lower than the concentration range 500–670 mg/mL obtained for poly-GA for n ≤ 100. As can be seen in the phase diagram, the critical poly-PR repeat length required for phase separation is lower for longer acidic molecules. The results in Fig. 4 a show an optimum concentration ratio of r_PR = 0.62 for phase separation of poly-PR with acidic molecules. At this concentration ratio, with fixed peptide lengths, poly-PR forms condensed phases with the highest concentration; see the inset of Fig. 4 a. In Fig. 4 a, we constructed the phase diagrams for two other concentration ratios of r_PR = 0.57 and 0.67 around the optimum value. For lower (<0.57) and higher (>0.67) r_PR-values, the concentration of the condensed phase is smaller, and the critical repeat length is larger. For r_PR > 0.8 and r_PR < 0.3, we observed no phase separation (data not shown). Our results are consistent with electrostatic-driven phase separation of R-DPRs with full-length NPM1, with phase separations that depend on concentration ratios of proteins and length of the R-DPRs (16,22). For D₄₀, which has almost the same length as the longest acidic tract in the nucleolar targets of R-DPRs (see Fig. S10), the critical repeat length of poly-PR required for phase separation is found to be n = 25 for the optimum concentration ratio r_PR = 0.62 (see the phase diagram in Fig. 4 a and the slab simulation snapshots in Fig. 4 b). Below this critical repeat length, poly-PR can bind to acidic molecules, but these small clusters are unable to phase separate (see Fig. 4 b). The slab density profiles used to obtain the phase diagram are presented in Fig. S11.

In Fig. S12, we compare the coexistence phase diagram of poly-PR and poly-GR with D₁₀₀ obtained for the same concentration ratios of r_PR = r_GR = 0.62. At a fixed repeat length n, poly-GR forms condensed phases with higher concentrations than poly-PR. This observation can be attributed to the sizes of the dipeptides and their free energy of binding to acidic molecules. With the same length, poly-GR is more compact than poly-PR irrespective of the presence of acidic molecules (see Figs. 1 and 3 a). This, together with the stronger binding of poly-GR to an acidic molecule (see Fig. S9 a), explains the differences in the phase diagrams. These findings provide insight into the experimentally observed differences between poly-PR and poly-GR in binding to their targets. For example, previous experimental measurements have indicated greater association of NCL with poly-GR than poly-PR (22). Consistent with this observation, photobleaching experiments for a single nucleolus labeled by GFP-NCL have shown that poly-GR is more effective than poly-PR in reducing the mobile fraction and fluorescence recovery rate of GFP-NCL (22). Our results suggest that the more stable physical interaction of poly-GR with the nucleolar components can be attributed to the stronger binding of poly-GR to the acidic tracts inside the nucleolus. In another study, poly-GR has been shown to have a higher tendency to accommodate different ligands compared with poly-PR (67). Our results suggest that the more flexible conformation of poly-GR might have contributed to this observation.

Conclusions

In this study, we used a coarse-grained, 1BPA model to study the properties of toxic DPRs with the aim of providing mechanistic insights into the possible role of LLPS of DPRs in C9orf72 toxicity. We showed that poly-PR favors the most extended conformations among all three toxic DPRs because of the patterning of charged arginine residues and the contribution of proline residues to the backbone rigidity. Our findings revealed a stronger binding of poly-GR to acidic molecules compared with poly-PR that is due to the different backbone stiffnesses of these DPRs. We observed that longer DPRs form condensed phases with higher concentrations and with lower exchange rates to the surroundings. This observation suggests that the more toxic nature of longer chains (12,16) can be due to the more stable structure of the condensates formed by longer DPRs. For poly-GA, we found that increasing the concentration increases the propensity for phase separation at small concentrations and increases the size of the condensed phase at larger concentrations, both consistent with the expected trend for liquid condensates (68). Increasing the length of DPRs increases the number of possible interactions and results in an increase in the multivalency of the system. Previous experiments and simulation studies have shown that a critical number of valences is required for the formation of biomolecular condensates (49,64,69, 70, 71) and that the propensity for phase separation increases with increasing multivalency of the system (38). These observations are in agreement with the phase diagrams presented in Figs. 2 a and 4 a. We observed an inverse correlation between the ρ_H and R_g of the DPRs. With the same chain lengths and the same concentration ratios of R-DPRs, the ρ_H of poly-PR is lower than poly-GR, which is lower than poly-GA, conceptually consistent with the observed correlation between the compactness of IDPs and their tendency to phase separate (72). A similar inverse correlation also exists between the ρ_H and the scaling exponent ν of DPRs for the same concentration ratios of R-DPRs and the same length of the acidic molecules.

Our results for poly-GA repeat lengths larger than 50 suggest that aggregate nucleation starts with liquid phase separation, as experimentally observed for several RNA-binding proteins (36,59). Care should be taken in comparing our poly-GA droplets with the insoluble aggregates observed in previous studies (21,22,25) because our 1BPA force field does not take into account secondary or higher-order structure formation of poly-GA. However, our coarse-grained MD model does capture the length-dependent phase separation of poly-GA (5). The critical repeat length of n = 50 for phase separation of poly-GA is in good agreement with the critical range of 46 < n < 61 found in Neuro2a cells for the formation of insoluble aggregates of poly-GA (5). Therefore, our findings suggest that the LLPS of poly-GA precedes the formation of insoluble aggregates (21,22,25) and could be the first step in the poly-GA toxicity pathway. The longest acidic tract found in the nucleolar targets of R-DPRs is 41 (see Fig. S10). We found the minimal critical repeat length for the phase separation of the most toxic DPR, i.e., poly-PR, with similar-sized acidic chains D₄₀ to be n = 25, which is between the expansion size in normal individuals (average around 20 repeats) and the lower bound of the toxicity threshold (30 repeats) found in patient cells (1,2,4). Therefore, our results indicate a substantial change in the poly-PR phase-separation behavior in the range 20–30 repeats, suggesting a likely connection between the phase separation of poly-PR and the toxicity threshold. Note that our results do not rule out a possible role of soluble DPRs in generating toxicity. Further investigation is needed regarding the interaction between DPRs (especially R-DPRs) of different lengths in the soluble phase and their targets such as RNA-binding proteins and transport components (22,67).

Author Contributions

H.J., E.v.d.G., and P.R.O. designed research. H.J. performed and analyzed research. H.J., E.v.d.G., and P.R.O. wrote the article.

Editor: Samrat Mukhopadhyay.

Supporting Citations

References (73, 74, 75, 76, 77, 78, 79, 80, 81, 82) appear in the Supporting Material.