Tautomeric Effect of Histidine on β-Sheet Formation of Amyloid Beta 1–40: 2D-IR Simulations

Abstract

Histidine state (protonated or δ or ε tautomer) has been considered the origin of abnormal misfolding and aggregation of β-amyloid (Aβ). Our previous studies reported that the δδδ isomer of Aβ (1–40) has a greater propensity for β-sheet conformation compared to other isomers. However, direct proof of the tautomeric effect has not been reported. In this context, we calculated histidine site-specific two-dimensional infrared spectroscopy of the δδδ, εεε, and πππ (all protonated histidine) systems within the framework of classical molecular dynamics simulations aiming at connecting our previous results with the current experimental observations. Our results showed that β-sheet formation is favored for the δδδ and πππ tautomers compared with the εεε tautomer, consistent with our previous studies. This result was further supported by contact map analyses and the strength of dipole coupling between the amide-I bonds of each residue. The two-dimensional infrared diagonal trace for each tautomer included three distinctive spectrally resolvable peaks near 1680, 1686, and 1693 cm⁻¹, as was also observed for histidine dipeptides. However, the peak positions at His6, His13, and His14 did not show a consensus trend with the histidine or protonation state but were instead affected by the presence of surrounding hydrogen bonds. Our study provides a deeper insight into the influence of tautomerism and protonation of histidine residues in Aβ (1–40) on amyloid misfolding and provides a connection between our previous simulations and experimental observations.

Significance

The amyloid hypothesis of Alzheimer’s disease is well recognized. However, there is no answer why amyloids aggregate. Recently, histidine tautomerism hypothesis has been proposed for the aggregation of amyloids by our group. Here, we tested 2DIR spectra to distinguish the histidine tautomers in amyloid beta peptide. The 2DIR diagonal peak of each tautomer shows three distinctive peaks; however, the peak positions at His6, His13, and His14 do not show a consensus trend with the histidine/protonation state, but rather, are affected by the presence of surrounding hydrogen bonding and donor-acceptor pairs. Our study provides a deeper insight into the effect of tautomerism/protonation of histidine residues in Aβ (1–40) on amyloid misfolding and provides a bridge between our previous simulations and experimental observations.

Introduction

Alzheimer’s disease (AD) is one of the most common forms of dementia, affecting more than 47 million people worldwide, and results in problems with language, disorientation, and mood swings. AD is generally thought to result from entanglement of τ proteins and/or aggregation and accumulation of senile β-amyloid peptide plaques (Aβ) (1,2). The Aβ hypothesis for the origin of AD is widely accepted, and Aβ is assumed to play an important role in AD. Even small perturbations of the physiological environment can influence the chemical and dynamic properties of peptides and destroy the balance of production and clearance of Aβ. Many studies have focused on the influence of external factors (3, 4, 5, 6) such as pH changes, amyloid precursor protein mutation, and the presence of metal ions on the aggregation of Aβ. In particular, slightly acidic conditions can promote formation of β-sheets and aggregation of Aβ, which may be one reason why the brains of AD patients are relatively acidic compared with the brains of normal people (7).

More recently, a tautomer hypothesis for the origin of AD has been suggested (8,9): the tautomeric state of the histidine side chain (Fig. 1) plays a crucial role in Aβ misfolding, which implies that Aβ aggregation may arise intrinsically rather than as a result of external factors. Histidine residues are critical to the stability of the fibril structure (10). As an example, the presence of three protonated histidine residues reduces the electrostatic repulsion between the two terminal regions of the Aβ protein, leading to greater probability of Aβ (1–42) misfolding and aggregation (11).

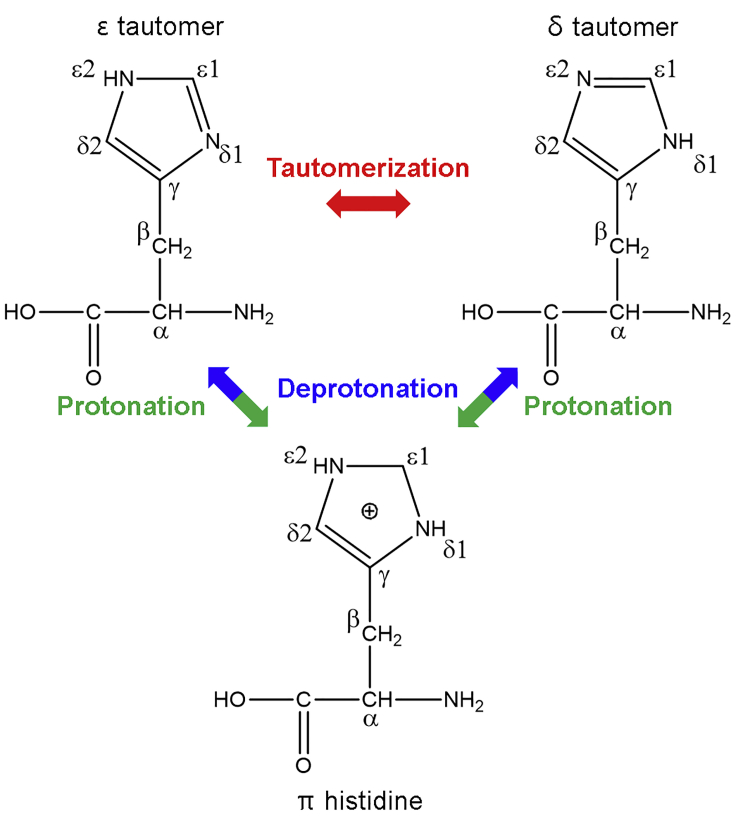
Figure 1.

Two tautomeric (δ and ε histidine) and protonated (π histidine) forms of histidine. To see this figure in color, go online.

Shi et al. (9) have used molecular dynamics (MD) simulations to demonstrate the tautomer effects of the Aβ (1–40) peptide, which, when containing the His6(δ)-His13(δ)-His14(δ) isomer (the so-called δδδ isomer), leads to the formation of greater amounts of antiparallel β-sheets between the central hydrophobic center (CHC) and C-terminus compared with the other seven isomers (δδε, δεδ, δεε, εεε, εεδ, εδε, εδδ). Our previous simulation studies regarding homodimers (12) and pentamers (13) confirmed such trends. However, the effect of tautomeric state of histidine within Aβ requires clarification. Some studies have focused on distinguishing the tautomeric forms of the histidine imidazole ring. Ghosh et al. (14) applied linear infrared (IR) spectroscopy to a histidine dipeptide system and reported that the δ form had a higher peak position compared to the ε form. In addition, Cheng et al. (15) and Vila et al. (16) postulated that the fraction of tautomeric forms within the imidazole ring in histidine dipeptides and tripeptides can be distinguished by applying NMR spectroscopy. However, the usefulness of NMR spectroscopy may be limited when tautomeric conversion is occurring faster than the NMR frequency. Furthermore, previous studies used a histidine dipeptide or tripeptide system, whereas native Aβ consists of 40 residues with histidine residues at the 6, 13, and 14 positions. In this respect, previous NMR experiments may not reflect the true properties of native Aβ, given that the properties of actual Aβ are highly influenced by the electrostatic potential created by many side chains (17). This phenomenon implies that the IR or NMR signals of amide-I mode or the imidazole ring can be affected by the presence of other amino acids, especially when the histidine residue forms a secondary structure. At a neutral pH, histidine can exist as either a major ε form or minor δ form in a 1:0.16 ratio, whereas in acidic environments, histidine may be present in a protonated state (Fig. 1), although slight changes in the surrounding environment can perturb the ratio of histidine residues present. In addition, tautomeric equilibrium is reached on a picosecond timescale (18). Therefore, the current experimental approaches are somewhat difficult for providing a clear understanding of the tautomeric behavior of the histidine residues in Aβ.

Femtosecond nonlinear two-dimensional infrared (2DIR) spectroscopy is a powerful tool for probing the dynamic properties of Aβ peptides in the amide-I frequency range. In particular, useful information regarding vibrational coupling between amide-I mode can be obtained by disentangling a congested one-dimensional spectrum into n dimensions to provide additional information on the secondary structures and their dynamics, such as inhomogeneous broadening and coupling between vibrational modes (19, 20, 21). Therefore, we performed histidine site-specific 2DIR calculations for amide-I bonds within the framework of classical MD simulation to investigate a possible connection between previous theoretical MD simulations and our experimental observations. We show that the δδδ and πππ (all protonated) tautomers exhibit a greater propensity for misfolding compared to the εεε tautomer, as reported in our previous studies. We also report that the amide-I vibrational mode shows three distinctive peaks due to the tautomeric or protonation state of histidine side chains.

Methods

Classical MD simulation

The initial tautomeric monomer structures were taken from our previous study (9), for which the crystal structure (PDB: 1BA4) was obtained from the Protein Data Bank. Herein, we refer to the protonated histidine residue as πππ, analogous to the notation for the δδδ and εεε residues, although it is not the universally used name. The two tautomeric isomers, δδδ and εεε, and the πππ protonated form (Fig. 1) were prepared by residual substitution with N^δ-H or N^ε-H at the 6, 13, and 14 histidine residues of Aβ (1–40). All MD simulations were performed with GROMACS 5.0 software (22) and the AMBER99SB force field (23). It was repeated with the CHARMM27 force field to validate our result. The monomer structures were solvated in TIP3P water with a minimal distance of 1.0 nm between structures and the edge of the box. Three Na⁺ ions were added to neutralize the system for the δδδ and εεε tautomers. Long-range electrostatic interactions were treated through the particle mesh Ewald (PME) method with 0.16 nm spacing. Temperature was controlled by the V-rescale method (24). The SETTLE algorithm (25) was used to constrain water molecules. MD simulations were carried out for at least 200 ns with time step of 2 fs with the output of trajectory at every 20 ps. The last 200 ps trajectory with a 1 fs time step was used for further frequency and 2DIR calculations. The trajectories were analyzed using visual molecular dynamics (VMD) software (26). To analyze the secondary structure of each δδδ, εεε, and πππ tautomer, we used the DSSP method of Kabsch and Sander (27), which assigns secondary structure types for residues based on backbone amide (N-H) and carbonyl (C=O) positions.

To compare our results with previous experimental results (14), we further carried out classical MD simulation for histidine dipeptide monomers. The histidine dipeptide tautomers were named as HIδ (δ form), HIε (ε form), and HIπ (protonated form) tautomers depending on their protonated state of imidazole rings. All dipeptides were acetylated at the N-terminus and methyl amidated at the C-terminus like the experimental study (14). The same computational strategy was applied to histidine dipeptide monomers, including AMBER99SB force field, TIP3P water, PME method, and SETTLE algorithm, etc. MD simulations were performed for 200 ns with a time step of 2 fs, and the last 200 ps trajectory with a 1 fs time step was used for 2DIR calculations.

Quantum calculation

Vibrational frequencies were calculated for HIδ, HIε, and HIπ using MP2 theory with a basis set of 6-31G^∗∗ and a Gaussian package (28). A total of three types of models—histidine residue, histidine residue with implicit water, and the histidine dipeptide (same as classical MD model)—were considered. To distinguish two amide-I bonds of histidine dipeptide models, the amide-I bond located at the C-terminus was isotope labeled with C¹³ and O¹⁸. The geometric structures were fully optimized, and anharmonic frequency calculations were carried out using the keyword freq=anharmonic, which uses numerical differentiation along modes, to determine the vibrational transitions of the amide-I bond.

Results and Discussion

Before analyzing the secondary structure of each tautomer, we calculated root mean-square deviations (RMSDs) to confirm equilibration of systems, using a backbone C_α atom with respect to the initial structure for each εεε, δδδ, and πππ tautomer during the MD simulation (Fig. S1). The obtained RMSDs were less than 0.3 nm for all systems, indicating that our simulations had converged well. For πππ, we found an abrupt RMSD change near 200 ns; hence, we performed additional 200 ns MD simulations and only used the last 200 ns trajectories for analysis and frequency calculation.

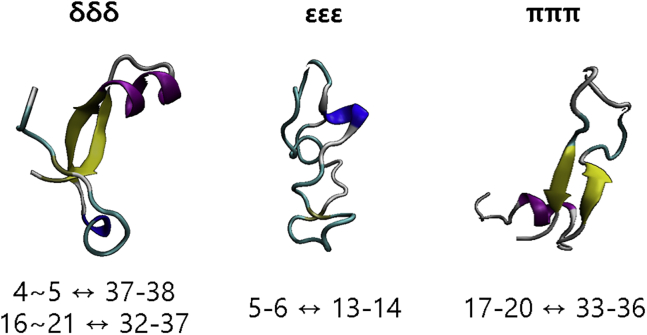
Next, evolution of the secondary structures over time was investigated with the DSSP algorithm, as described in Methods. Formation of β-sheets is generally regarded as an important precursor of amyloid aggregation of Aβ (29, 30, 31). The average β-sheet, α-helix, turn, and other characteristics were calculated as shown in Table 1. The δδδ, εεε, and πππ tautomers were composed of 17, 5, and 22% β-sheets, respectively. Specifically, the δδδ tautomer contained β-sheet structures between the C-terminus (residue 4∼5) and N-terminus (residue 37∼38), as well as between the CHC (residue 16∼21) and N-terminus (residue 32∼37); in contrast, the εεε tautomer contained a β-bridge between residues 5∼6 and 13∼14, and the πππ tautomer contained a β-sheet between the CHC (residue 17∼20) and N-terminus (residue 33∼36) (Fig. 2). This trend has been confirmed by our previous studies, which used ff02 (9), AMBER99SBILDN (13), and ff14SB force fields (32). To validate our results, we further carried out the same MD simulation with the CHARMM27 force field (33). The CHARMM27 force field has been known to provide a quite different conformational state for amyloid β proteins (34). Our RMSD result confirms the equilibration of the systems (Fig. S1). The DSSP analysis showed that δδδ, εεε, and πππ exhibited 13, 0, and 16% β-sheet components, which is consistent with the simulation performed with the ff99SB force field. We expect that the conformational state can be varied by the use of different force fields: the use of the AMBER12SB force field could reduce the contents of β-sheet, whereas the use of AMBER96, GROMOS45a3, GROMOS53a5, GROMOS53a6, GROMOS43a1, GROMOS43a2, and GROMOS54a7 force field could increase the composition of β-sheet in light of the previous report (35) about the relation between force field and protein conformational state.

Table 1.

Probability Distributions of Averaged Secondary Structures in the δδδ, εεε, and πππ Tautomers

	δδδ	εεε	πππ
Coil	33%	31%	30%
β-Sheet	17%	5%	22%
β-Bridge	1%	6%	5%
Bend	11%	45%	17%
Turn	11%	3%	7%
α-Helix	16%	0%	12%
3-Helix	11%	9%	7%

Figure 2.

Representative conformational states of the δδδ, εεε, and πππ tautomers. The green band/line with arrow represents the β-sheet/bridge structure, and the numbers below indicate the residue numbers at which the β-sheet/bridge was formed. To see this figure in color, go online.

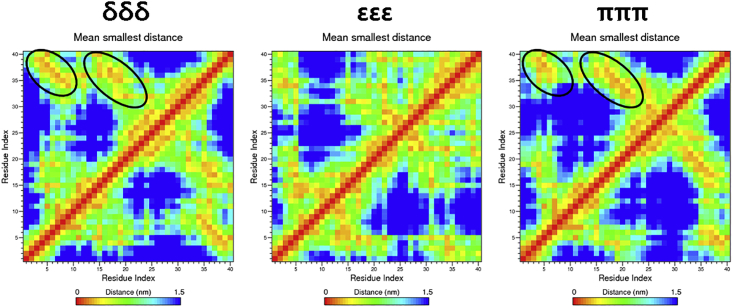
The contact map of each tautomer based on the C_α atom (Fig. 3) supported the secondary structure conformations. The contact map for the δδδ tautomer showed significant contacts between the 4∼5 and 33∼39 residues and between the 14∼21 and 33∼39 residues. The two regions in Fig. 3 marked with black circles show (anti)parallel conformations. In contrast, the εεε tautomer had some contacts between residues 4∼7 and 12∼15, indicating the presence of a β-bridge as illustrated in Fig. 2. This result is consistent with our previous theoretical calculations (9), indicating that δδδ shows a greater propensity for β-sheet formation compared with εεε. In addition, our results support previous experimental results indicating that β-sheets are easily produced between the CHC and C-terminus (36,37). Together, these findings indicate the influence of the tautomeric state of histidine on the structural properties and mechanism of Aβ aggregation (8,32,38). The πππ tautomer was found in similar locations to and had secondary structures more similar to those found in the δδδ tautomer than the εεε tautomer. Comparison of the πππ system with the tautomeric monomers (δδδ and εεε) has not been reported. On pathological examination, the brains of AD patients are relatively acidic compared with the brains of normal people. In an acidic environment, the histidine residue may be protonated with an N^δ-H bond. Comparing the pathological observations and the similarity of MD simulations for the πππ and δδδ tautomers, the presence of N^δ-H might lead to greater formation of β-sheet structures. Hence, it is important to distinguish the two tautomeric N^δ-H and N^ε-H forms using spectroscopic methods.

Figure 3.

Contact maps for the δδδ, εεε, and πππ tautomers. The x and y axes represent the residue numbers for each tautomer. Black circles represent the locations of the antiparallel β-sheets/bridges shown in Fig. 2. To see this figure in color, go online.

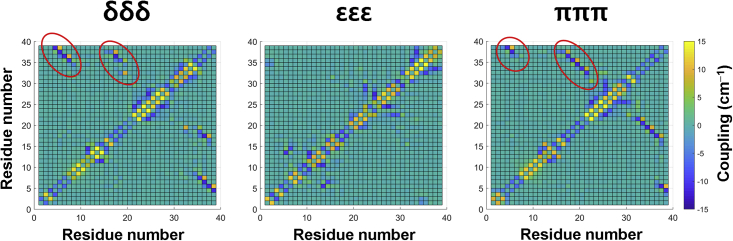
In addition to the contact maps, we calculated the strength of dipole coupling for the amide-I vibrational modes. We used an equivalent magnitude of transition dipole moment for all peptide bonds so that the coupling strength was attributed to the related secondary structure. The strength of the transition dipole was assumed to be 0.374 D, with the direction being indicated from the C=O bond toward the C-N bond at the same plane with a 20.0° angle (Fig. S3). This assumption was first suggested by Krimm et al. (39); since then, the strength of transition dipole and its angle against the C=O bond have been modified by many authors (40, 41, 42). It has been known that this approach provides qualitatively similar results compared with other method such as dipole approximation, transition charge coupling, local (normal) mode molecular orbital calculation, etc. (42, 43, 44, 45). The optimized location of the transition dipole was assumed to be r_C + 0.665n_CO + 0.258n_CN, where r_C represents the location of the carbon atom of the amide-I bond, n_CO = (r_O − r_C)/|r_O − r_C|, and n_CN = (r_N − r_C)/|r_N − r_C| (Fig. S3). The strength of dipole coupling (β_jk) between two amide-I modes was then calculated as

$${\beta }_{jk}=\frac{1}{4\pi {\epsilon }_0}\times \frac{\left(\partial {\mu }_j/\partial Q_j\right)\left(\partial {\mu }_k/\partial Q_k\right)-3\left[\left(\partial {\mu }_j/\partial Q_j\right)n_{jk}\right]\left[\left(\partial {\mu }_k/\partial Q_k\right)n_{jk}\right]}{R_{jk}^3},$$ (1)

where (∂μ_α/∂Q_α) (α = j, k) is the dipole derivative (transition dipole in D Å⁻¹ u^−1/2) of the amide-I vibration of the α^th peptide group, R_jk is the length (in Å) of the line connecting the j^th and k^th peptide groups, n_jk is the unit vector along this line, and ε₀ is the vacuum permittivity. The strength of dipole coupling was calculated for all pairs of amide groups at every trajectory and then averaged to obtain the coupling map as shown in Fig. 4. The coupling maps of the δδδ and πππ tautomers clearly showed strong dipole couplings between the N-terminus and C-terminus, as well as between the CHC and C-terminus, as marked with red circles in the figure. The dipole coupling at circled area showed −10 to −15 cm⁻¹, which corresponds to the general dipole coupling strength between antiparallel β-sheets, which ranges from −10 to −20 cm⁻¹ (46,47). In addition, the distances between transition dipoles ranged from 0.45 to 0.50 nm (Table S1), similar to the distance between antiparallel β-sheets of 0.47–0.48 nm (48). However, the coupling map of the εεε tautomer does not exhibit such strong coupling in that region. The (anti)parallel β-sheet yields a stronger oscillator coupling compared with other secondary structures because the β-strands are arranged adjacent to other strands and form an extensive hydrogen bond network with their neighbors. By comparing this result with Fig. 2, our transition dipole coupling map results provide a clue for the location of antiparallel β-sheet.

Figure 4.

Coupling maps showing the strength of oscillator couplings between amide-I bonds (unit: cm⁻¹). The x and y axes represent the residue numbers of each tautomer. Red circles represent the location of the antiparallel β-sheets/bridges shown in Fig. 2. To see this figure in color, go online.

The above findings, which support the tautomer hypothesis, have been supported by our previous studies (8,9,12,32,38) addressing homodimer and pentamer aggregation mechanisms using MD simulations. Experimentally, it has been reported that N^δ−H and N^ε-H of the histidine dipeptide and tripeptide can be distinguished using NMR techniques; linear IR and 2DIR (14) techniques have also been used to probe the tautomeric form of the histidine residues of the dipeptide. However, the previous results may not accurately reflect the actual Aβ system composed of 40–42 residues including three histidine residues. In addition, the Aβ structure is affected by surrounding water molecules on a femtosecond scale. Therefore, we calculated the frequencies and 2DIR spectra of the Aβ structure upon histidine tautomeric state to provide an experimentally comparable result in the following section.

Frequency calculations

Several parameterization schemes have been used to describe the calculation of the amide-I vibrational frequencies. Among them, we used CHO4 parametrization (49, 50, 51). The amide-I vibrational frequency $\left(\hslash {\omega }_n\right)$ of the n^th peptide bond located between residue r and r + 1 was calculated as

$$\hslash {\omega }_n=\hslash {\omega }_0+\sum _{s=C,O,N,H}{l}_s{\varphi }_{n,s}\left(t\right).$$ (2)

The sum is performed over the C, O, N, and H atoms of the amide bond n. The central band $\left(=\hslash {\omega }_0\right)$ frequency was set to 1600 cm⁻¹ with reference to the previous simulation study (17), which performed frequency calculation of the same Aβ (1–40) system. The values of the coefficient l_s are given as l_C = −0.00554e, l_O = 0.00160e, l_N = 0.00479e, and l_H = −0.00086e, where e is the electron charge. The electrostatic potential ϕ_n,s at the r_n,s(t) coordinate of atom s of the n^th amide bond was expressed as the sum of the contributions from water, backbone, and side chains, as follows:

$${\varphi }_{n,s}={\varphi }_{n,s}^{water}\left(t\right)+{\varphi }_{n,s}^{sidechains}\left(t\right)+{\varphi }_{n,s}^{backbone}\left(t\right),$$ (3)

$${\varphi }_{n,s}^P\left(t\right)=\frac{1}{4\pi {\epsilon }_0}\sum _{i\in P}\frac{q_i}{\left|r_i\left(t\right)-r_{n,s}\left(t\right)\right|},\left(P=\text{Water},\text{Side}\text{chains},\text{or}\text{backbone}\right),$$ (4)

where ${\varphi }_{n,s}^{water}\left(t\right)$, ${\varphi }_{n,s}^{sidechains}\left(t\right)$, and ${\varphi }_{n,s}^{backbone}\left(t\right)$ represent the electrostatic potential generated by the surrounding water molecules, side chains, and backbone atoms, respectively. The electrostatic potential contribution is calculated by sum of point charges, q_i, over distance |r_i(t) − r_n,s(t)| and the vacuum permittivity ε₀ for all atoms (i) in the water, side chain, or backbone atoms. The q_i of water molecules were calculated using TIP3P point charge, and that of the side chain was given by the ff99SB force field. Finally, the electrostatic potential generated by the amyloid backbone atoms, C, O, N, H, C_α, and H_α, was calculated based on Ham’s model (49,50), in which no effective charges are assigned to C_α or H_α atoms $\left(q_{C_{\alpha }}=0,q_{H_{\alpha }}=0\right)$, and q_C = 0.419, q_O = −0.871, q_N = 0.793, and q_H = −0.341.

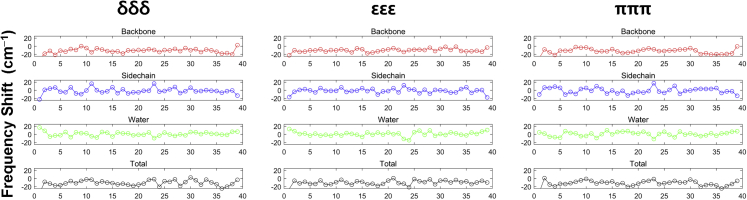
The average frequency shift, $\langle \hslash {\omega }_0-\hslash {\omega }_n\rangle$, of amide-I vibration induced by the electrostatic potential of the backbone, side chain, and water is shown in Fig. 5. We first noticed a large shift in both the N- and C-terminus, which corresponded to the head and tail of tautomers, respectively. Further, the frequency shift in the regions between residues Asp1–Arg5 was larger than for other regions, indicating the disordered structure of the N-terminus, as reported in previous studies (52,53). The ∼−20 cm⁻¹ frequency shift for the backbone was similar for all tautomers. This finding is consistent with the previous observation that most of the inhomogeneity of the frequency shift is dominated by the side chain contribution (17) and not by the backbone contribution, which further supports the importance of tautomeric form of histidine side chains for Aβ misfolding and aggregation. Next, we investigated the histidine site-specific 2DIR spectrum of each tautomer; however, for these analyses, we disregarded the water contribution to assess dried Aβ samples containing only one or two water molecules (54).

Figure 5.

Average frequency shifts of the δδδ, εεε, and πππ tautomers due to the backbone (red line), side chains (blue line), water solvent (green line), and entire system (black line). To see this figure in color, go online.

2DIR spectra

The 2DIR spectra were calculated using snapshots containing the coordinates of the εεε, δδδ, and πππ tautomers obtained at every 1 fs time step during the final 200 ps of their frequency trajectories. The amide-I vibrational anharmonicity was fixed at −16 cm⁻¹ as a typical value for peptides. The frequency fluctuation δω(t) = ω(t) − $\langle \omega \left(t\right)\rangle$ was obtained from the frequency trajectories ω(t) calculated in the previous section, where $\langle \omega \left(t\right)\rangle$ was the ensemble average. The frequency fluctuation correlation function (FFCF) $\langle \delta \omega \left(0\right)\delta \omega \left(t\right)\rangle$ was then calculated and used to obtain the lineshape function (21), g(t), as

$$\text{g}\left(\text{t}\right)=\underset{0}{\overset{t}{\int }}d{\tau }^{\prime }\underset{0}{\overset{{\tau }^{\prime }}{\int }}d{\tau }^{″}\langle \delta \omega \left(0\right)\delta \omega (t\rangle ,$$ (5)

from which the linear response function and the rephasing and non-rephasing third-order response functions were obtained using a cumulant approximation (21), as follows:

$$\begin{array}{c}{R}_{\mathrm{1,2,3}}\propto i{\mu }_{01}^4\left(e^{-i{\omega }_{01}\left(t_3-t_1\right)}-e^{-i\left(\left({\omega }_{01}-\Delta \right)t_3-{\omega }_{01}{t}_1\right)}\right)\times e^{-g\left(t_1\right)+g\left(t_2\right)-g\left(t_3\right)-g\left(t_1+t_2\right)-g\left(t_2+t_3\right)+g\left(t_1+t_2+t_3\right)},\\ R_{\mathrm{4,5,6}}\propto i{\mu }_{01}^4\left(e^{-i{\omega }_{01}\left(t_3+t_1\right)}-e^{-i\left(\left({\omega }_{01}-\Delta \right)t_3+{\omega }_{01}{t}_1\right)}\right)\times e^{-g\left(t_1\right)-g\left(t_2\right)-g\left(t_3\right)+g\left(t_1+t_2\right)+g\left(t_2+t_3\right)-g\left(t_1+t_2+t_3\right)},\end{array}$$ (6)

where Δ, μ₀₁, and ω₀₁ refer to vibrational anharmonicity (−16 cm⁻¹), the time-independent vibrational transition dipole moment, and the time-independent mean frequency, respectively. The FFCF can be integrated into the lineshape function either by numerically or analytically fitted to a parametrized form:

$$c\left(t\right)=\langle \delta \omega \left(0\right)\delta \omega \left(t\right)\rangle =a_1\cos \left(\gamma t\right)e^{-t/\tau 1}+a_2{e}^{-t/\tau 2}+a_3{e}^{-t/\tau 3},$$ (7)

where a₁, a₂, a₃, τ₁, τ₂, τ₃, and γ are parameters (21,55).

During the numerical integration, the direct relationship between the signal and FFCF is lost (56). For example, the first term of the correlation function is an attempt to catch the shorter time dynamics related to hydrogen bonded species, such as solvent fluctuations (57,58). The remaining two terms also provide a slower dynamic property of the system. Usually, an analytical integration cannot be obtained because the lineshape function shows a complicated set of integrals of exponential functions, but our FFCFs were well fitted to the parametrized correlation function; hence, the analytically integrated lineshape function was used to calculate response function as described above. Once the response functions R₁ to R₆ are known, the frequency-domain spectra are calculated via Fourier transformation of response function over t₁ and t₃.

$$S_{r/nr}\left({\omega }_1,t_2,{\omega }_3\right)=\underset{0}{\overset{\infty }{\int }}\underset{0}{\overset{\infty }{\int }}{R}_{r/nr}\left(t_1,t_2,t_3\right)e^{i{\omega }_1{t}_1}{e}^{i{\omega }_3{t}_3}d{t}_{1}d{t}_3,$$ (8)

where r/nr refers to rephasing and non-rephasing, respectively. After inverting the sign of ω₁ of the rephasing response function, the real part $\left(\mathbb{R}\right)$ of the sum of both rephasing and non-rephasing spectra is taken to calculate the purely absorptive 2DIR spectra,

$$S_{abs}\left({\omega }_1,t_2,{\omega }_3\right)=\mathbb{R}\left[S_r\left(-{\omega }_1,t_2,{\omega }_3\right)+S_{nr}\left({\omega }_1,t_2,{\omega }_3\right)\right].$$ (9)

The spectra were obtained for waiting time t₂ = 0 ps in this study.

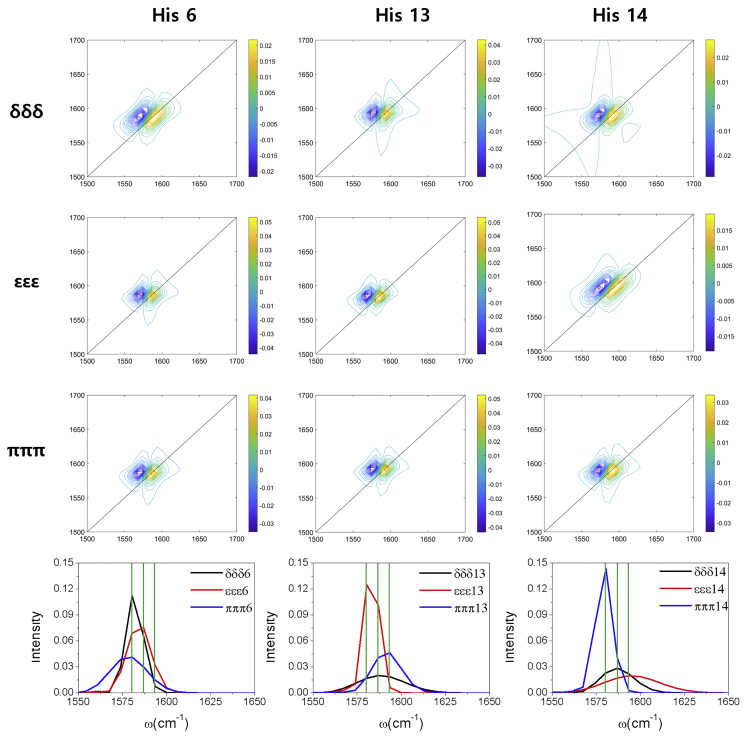
The site-specific 2DIR spectra at His6, His13, and His14 of each tautomer and their diagonal traces of 2DIR spectra at zero waiting time, t₂ = 0, are shown in Fig. 6. The diagonal traces for all the tautomers contain bands at ∼1580, ∼1586, and 1593 cm⁻¹, similar to previously reported experimental results (14) (1630, 1644, and 1656 cm⁻¹). The smaller peaks of our system compared with experimental data originated from isotope labeling of the amide-I bond, which reduces the vibrational band by 60 cm⁻¹. This isotope frequency shift of 60 cm⁻¹ was reported by previous studies (21,59) and provides the advantage of placing the isotope-labeled amide-I band between the unlabeled amide-I and II bands. The calculated bands can vary with the use of the different isotope frequency shift or the central band frequency, $\hslash {\omega }_0$; however, our results provide three resolvable amide-I spectra upon tautomerization or protonation, which validates our results. Specifically, at His6, the εεε tautomer exhibited a slightly higher peak (1586 cm⁻¹) than the δδδ and πππ tautomers (1580 cm⁻¹). In contrast, the εεε tautomer had a lower peak (1580 cm⁻¹) than the δδδ (1586 cm⁻¹) and πππ (1593 cm⁻¹) tautomers at His13. Again, 1593 cm⁻¹ and His14 peaks for the εεε tautomer were higher than those for the δδδ (1586 cm⁻¹) and πππ (1580 cm⁻¹) tautomers. These differences in diagonal peaks for the tautomeric/protonated state of the histidine residues of Aβ (1–40) have not previously been reported and are entirely new findings, to our knowledge.

Figure 6.

Histidine site-specific 2DIR spectra and their diagonal traces of the δδδ, εεε, and πππ tautomers for the 6th, 13th, and 14th amide-I bond of histidine residue. The black, red, and blue lines represent the diagonal traces of the δδδ, εεε, and πππ tautomers, respectively. The green lines represent the three peaks at 1580, 1586, and 1593 cm⁻¹. To see this figure in color, go online.

According to the previous experimental report (14) the HIδ dipeptide (histidine with N-H^δ bond) has a higher (∼1656 cm⁻¹) peak compared with that of the HIε dipeptide (N-H^ε bond). A density functional theory (DFT) study indicates the HIδ dipeptide exhibits an amide-I peak ∼5 cm⁻¹ higher than that of the HIε dipeptide. To verify our results, we also performed ab initio electronic structure and frequency calculations (see Methods) and summarized the results in Table S2. The HIδ and HIπ tautomers exhibited higher amide-I peaks compared to the HIε tautomer (∼10 and 12 cm⁻¹, respectively). However, when the solvent effect was included using an implicit water solvent model, the peak for the HIπ tautomer was similar to that for the HIε tautomer, whereas the HIδ tautomer peak remained ∼9 cm⁻¹ higher. In contrast, the dipeptide system, which included two amide bonds, showed the opposite trend: the two amide bonds in the dipeptide system were distinguishable by peak position because the vibrational frequency of the isotope-labeled amide-I bond (amidated C-terminus) was observed at the lower peak position compared with that of the nonlabeled bond (acetylated N-terminus). The relative magnitudes of the peak positions of the isotope-labeled amide-I bond were HIε > HIδ > HIπ, whereas the peaks for the nonlabeled amide-I bond were HIδ > HIε > HIπ.

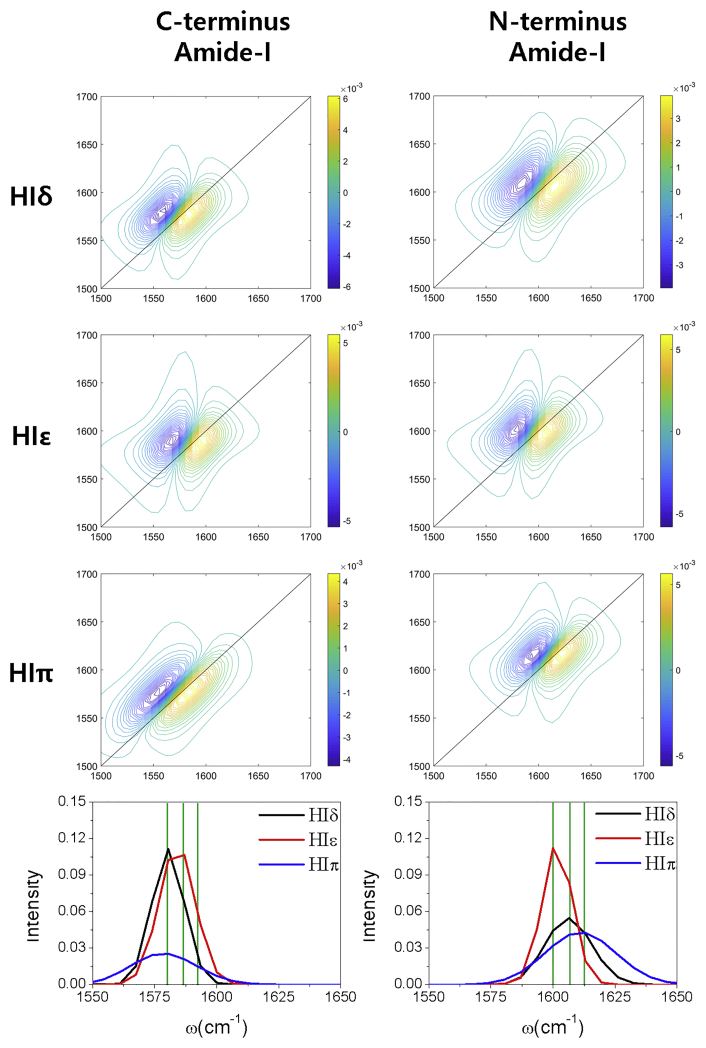
Next, we performed classical MD simulations for the HIδ, HIε, and HIπ tautomers using the same methodology applied to the δδδ, εεε, and πππ Aβ (1–40) systems (see Methods). The RMSDs obtained were less than 0.1 nm for all histidine dipeptides, indicating that our simulations had converged well (Fig. S2). Then, we calculated the 2DIR spectra and their diagonal traces of the HIδ, HIε, and HIπ histidine dipeptide systems as shown in Fig. 7. Herein, we name the two amide-I bonds as the N-terminus amide-I bond and the C-terminus amide-I bond. The bottom left figure shows the diagonal trace of the C-terminus amide-I bond, and the right figure shows the diagonal trace of the N-terminus amide-I bond. We found that the diagonal peak for histidine can be characterized by three peaks at ∼1580, ∼1586, and 1593 cm⁻¹. Specifically, the C-terminus amide-I bond for HIε has a peak at 1586 cm⁻¹, whereas HIδ and HIπ have peaks at 1580 cm⁻¹. In contrast, the 1600 cm⁻¹ peak for the N-terminus amide-I bond in HIε was lower than those for HIδ or HIπ (1607 or 1613 cm⁻¹, respectively).

Figure 7.

2DIR spectra and their diagonal traces of 2DIR spectra for amide-I vibration of HIδ, HIε, and HIπ dipeptides: C-terminus (left) and N-terminus (right) amide bonds. Black, red, and blue lines represent the diagonal traces of the HIδ, HIε, and HIπ dipeptides, respectively. Green lines represent the three peaks at 1580, 1586, and 1593 cm⁻¹ for isotope-labeled bonds and 1600, 1607, and 1613 cm⁻¹ for nonlabeled amide bonds. To see this figure in color, go online.

The above results indicated that the peak position for each tautomer may be highly dependent on the environment, such as the surrounding hydrogen bonds. The presence of a hydrogen bond lowers the peak position because they weaken the C=O bond strength. In this context, we calculated the average number of hydrogen bonds, for which the distance between donor (OH or NH groups) and acceptor (O, N atoms) is smaller than 0.35 nm, during the dynamics of each HIδ, HIε, and HIπ system (Table S3). The result shows that the average number of hydrogen bonds for the C-terminus amide bond is smaller for HIε (2.054) than for HIδ (2.967) or HIπ (2.533), whereas that for the N-terminus-amide bond is larger for HIε (3.450) than HIδ (3.413) or HIπ (3.109). This trend was consistent with the diagonal peak positions of the HIδ, HIε, and HIπ tautomer systems shown in Fig. 7. The protonation of the histidine imidazole ring results in charge redistribution in histidine amino acid. As a result, the HIπ tautomer has more positive C atoms and more negative O atoms compared with those of HIδ and HIε (Table S4). This indicates that for the C-terminus amide-I bond, the HIπ tautomer shows larger amide-I frequency because of a strong C=O bond than HIδ or HIε, which might lead to the higher propensity of hydrogen bond formation because of a strongly polarized O atom and its frequent oscillation. However, the larger number of hydrogen bonds for the HIπ former amide bond than HIε shifts the peak position lower than HIε, resulting in the higher peak position for HIε than HIδ and HIπ. In contrast, for the N-terminus amide-I bond, all three tautomers intrinsically have the same amide-I frequency, but the larger number of hydrogen bonds lowers the peak position of HIε more than HIδ and HIπ.

However, there are several reasons that we cannot directly compare our result with experimental observations. First, site-specific isotope labeling of histidine residue in polypeptides or proteins has not been reported yet. Ghosh’s work (14) is the only existing experimental study that compares IR and 2DIR spectra upon tautomerization or protonation. Hence, the comparison of our result is somewhat limited. Second, the 2DIR spectra of Ghosh’s work was obtained at different pH (e.g., pH 10, 6.5, and 2), whereas our system was neutralized. Third, the amide vibration of a histidine residue is an indirect probe of the side chain’s conformational state. Hence, Ghosh’s work (14) performed quantum calculation to calculate the amide-I vibrational frequency, but their DFT results were different from our results, which were performed based on wavefunction electronic structure method. Even the vibrational frequency within MP2 calculation was highly dependent on the solvation state. Finally, we used classical MD simulation to calculate 2DIR spectra of histidine dipeptide, which cannot elucidate the chemical exchanges. Hence, our 2DIR spectra at waiting time, t₂ = 3 ps, did not show crosspeaks as observed by experiments (Fig. S4). Nevertheless, we showed that our histidine dipeptide exhibits three spectrally resolvable features within the amide-I vibrational band of histidine.

We believe that the resolvable three peaks could be more accurately elucidated by using ab initio MD simulation or density functional tight-binding MD simulation, which can elucidate the bond-breaking phenomenon (intermolecular proton transfer process). The amide-I vibrational peak is highly influenced by the environment: our δδδ/εεε/πππ and HIδ/HIε/HIπ systems had different geometric structures, leading to different dynamics scenarios. However, the change of amide-I peak position, as well as the timescale of proton transfer, could be elucidated by investigating the 2DIR spectra of each system, which will be performed on a future study. We expect that this study could inspire further studies on the distinction of amide-I vibration by protonation or tautomerization of histidine side chains.

Conclusion

In summary, we calculated histidine site-specific 2DIR spectra within a classical MD simulation framework to investigate the effect of histidine tautomeric state on amyloid β-sheet misfolding and aggregation of Aβ (1–40). We found that the δδδ (17%) and πππ (22%) tautomers exhibited greater propensity for β-sheet formation between the C-terminus and N-terminus, as well as between the CHC and N-terminus, as compared with the εεε tautomer (5%). In particular, investigations of the dominant secondary structure for the πππ tautomer have not been previously reported. This trend was further confirmed by contact map analyses and dipole coupling mapping, which clearly showed the presence of (anti)parallel β-sheets for the δδδ and πππ tautomers. The histidine site-specific 2DIR diagonal peak of each tautomer showed three distinctive peaks near 1580, 1586, and 1593 cm⁻¹, as observed in the experiments for histidine dipeptides. However, the diagonal peaks did not show a similar trend for the histidine or protonation state and were instead affected by the presence of surrounding hydrogen bonds. In the future, obtaining a more detailed understanding of tautomerism for histidine residues may be possible as a result of performing ab initio MD simulations, which can elucidate proton exchange between histidine side chains and surrounding water molecules. Nevertheless, our study is the first, to our knowledge, to investigate the histidine site-specific 2DIR spectra for the amide-I vibrational mode of Aβ (1–40) in the histidine tautomeric state. We expect these results may validate 2DIR spectroscopy as a possible tool for studying the influence of aggregation of Aβ (1–40) arising from histidine tautomerism.

Author Contributions

Y.N. and J.Y.L. performed research, analyzed data, and wrote the manuscript. M.K. contributed to data analysis by analytic tools. S.S. and J.Y.L. designed research and wrote the manuscript.

Editor: Elsa Yan.