Abstract
Despite much effort, synthetic small diameter vascular grafts still face limited success due to vascular wall thickening known as intimal hyperplasia (IH). Compliance mismatch between graft and native vessels has been proposed to be one of a key mechanical factors of the synthetic vascular grafts that could contribute to the formation of IH. While many methods have been developed to determine compliance both in vivo and in vitro, the effects of compliance mismatch still remain uncertain. This review aims to explain the biomechanical factors that are responsible for the formation and development of IH and their relationship with compliance mismatch. Furthermore, this review will address the current methods used to measure compliance both in vitro and in vivo. Lastly, current limitations in understanding the connection between the compliance of the vascular grafts and the role it plays with the development and progression of IH will be discussed.
Graphical Abstract
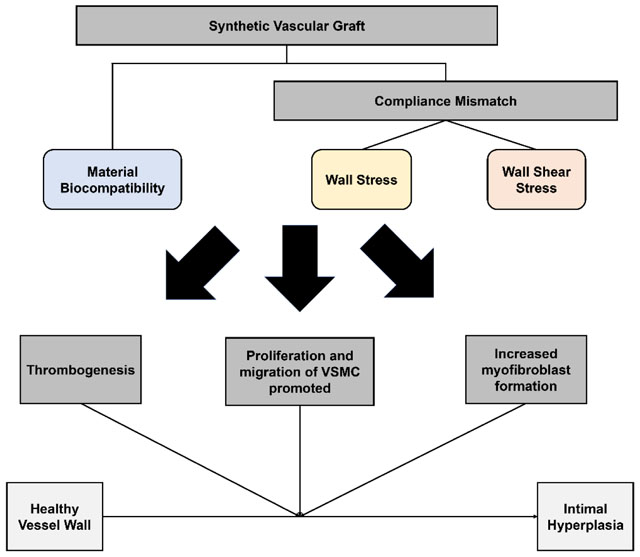
Review detailing the current methods utilized to study the effects of mechanical properties of synthetic vascular grafts on intimal hyperplasia.
Introduction
While synthetic vascular graft engineering has made striking advances, it still faces limited success as a solution for small diameter vascular graft due to intimal hyperplasia (IH). As a result of previous research, synthetic vascular grafts with an inner diameter larger than 6 mm have been approved by the Food and Drug Administration (FDA) and the standards for such grafts have been made.1 However, synthetic small diameter vascular grafts (sSDVGs), defined as vascular grafts with an inner diameter less than 6 mm, continue to show poor patency,2 most often caused by IH.3, 4 The lack of viable options for sSDVGs impacts more than 52 million people who suffer from peripheral arterial diseases (PAD) in the United States of America (USA) alone due to maintenance of the vascular graft implant.5, 6 Furthermore, the lack of synthetic options for arteriovenous grafts (AVGs), which are also sSDVGs, affects patients with end-stage renal disease.7 Due to poor patency, the annual cost for maintenance of AVGs for hemodialysis in the USA is $42 million.8
The leading cause of poor sSDVG patency is IH. IH is the thickening of the tunica intima of blood vessel walls, which is believed to be caused by either proliferation or migration of smooth muscle cells (SMCs), that results in either partial or complete occlusion of the blood vessel.9, 10 The factors associated with IH are mechanical or biological damage that leads to vascular endothelial injury.11–13 Since IH development is detrimental to the patency of implanted vascular grafts, both biological and mechanical causes of IH have been studied extensively. A common treatment for vascular occlusion, for example, is angioplasty. In angioplasty, the occurrence of IH mainly derives from the destruction of the endothelium from scraping and stretching of the vessel wall, followed by the molecular and cellular reaction. Biomechanical factors, such as wall stress (WS) and wall shear stress (WSS), also play a key role in the generation of IH for particularly synthetic vascular grafts. These biomechanical factors have been shown to be affected by the compliance mismatch between the vascular grafts and the native arteries. One of the mechanical properties that is being revisited is vascular compliance. Compliance in cardiovascular engineering is defined as the inverse of stiffness – it is the circumferential elasticity of the vascular graft with application of pressure.
The theory that compliance mismatch could affect the patency of vascular grafts has been around since the 1970s.14–16 Since then, many have tried to understand the effect of compliance mismatch using various methods—from flow analysis using simulations to in vivo graft implantation models. The significance of compliance mismatch remains controversial, as some studies found a significant drop in graft patency due to compliance mismatch,16–19 while others showed that the effect was negligible.20 This dispute could arise from comparing different types of grafts—biological vs. synthetic grafts. To avoid this potential confusion, this review will focus on the IH formation while using synthetic vascular grafts. This review aims to address the biological and mechanical factors that were found to affect IH and the significance of compliance mismatch in those mechanical factors. Lastly, this review will describe the current limitations in understanding the complete effect of compliance mismatch by assessing the methods that are used to analyze compliance mismatch.
The pathophysiology of intimal hyperplasia
Native blood vessel walls are made of three layers: tunica externa, tunica media, and tunica intima.21 Tunica externa is the acellular outermost layer composed of collagenous fibers and elastic fibers, and tunica media is the thick middle layer composed of SMCs.22 Tunica intima is the innermost layer composed of endothelial cells (ECs) and connective tissues.9 Intima is a single layer of ECs, endothelium, and an endothelial-specialized basement membrane of tunica intima. It contains laminin, collagen type IV, glycosaminoglycans, and proteoglycans such as heparan sulfate.23–25 Adventitia is the outermost layer of the native blood vessel that consists of loosely packed fibroblasts.
The endothelium serves as a non-thrombogenic barrier between blood and tissues and participates actively in maintaining homeostasis. ECs secrete various proteins and growth factors that prevents VSMC constriction and proliferation, such as nitric oxide (NO) and prostacyclin (PGI2),26 and synthesize heparin-like molecules that prevent platelet adherence, aggregation, and coagulation.27 VSMCs, elastin tissue, and collagen form the medial layer of native blood vessel walls. In a normal blood vessel, VSMCs are contractile, differentiated, and quiescent. However, upon vessel injury or vascular surgical interventional process, VSMCs change phenotype to a proliferative state and eventually migrate to the intima and form IH.
Formation of IH involves all the components in the blood vessel and occurs through the following process. The initiation is due to the damage or dysfunction of ECs, which exposes the underlying collagen and SMCs to blood components. Immediately, platelets start to adhere, aggregate, and activate to form thrombus and are followed by leukocyte chemotaxis. The activated platelets release growth factors, such as platelet-derived growth factor (PDGF).28–30 In response to all the changes, SMCs change phenotype from quiescent state to proliferative state, then start to proliferate and migrate from media to intima. Fibroblasts in adventitia also differentiate to myofibroblasts, proliferate, and then migrate to the lumen. Meanwhile, cells involved in the IH formation secrete and deposit extracellular matrix, further thickening the intima. Histological analysis of IH corroborates this process and shows abundant VSMCs, fibroblasts, myofibroblasts, and inflammatory cells (Fig. 1).31–35 Excessive damage to the adventitia can also lead to IH. During vascular surgeries, adventitia is frequently stripped by surgeons to enable a better grasp of vascular walls. However, studies have found that these injuries result in the remodelling of adventitia and increased proliferation of fibroblasts in adventitia within a few days.36, 37 The proliferating fibroblasts would further migrate from adventitia to intima and form myofibroblasts, contributing to the formation of IH.31, 32, 38
Figure 1.
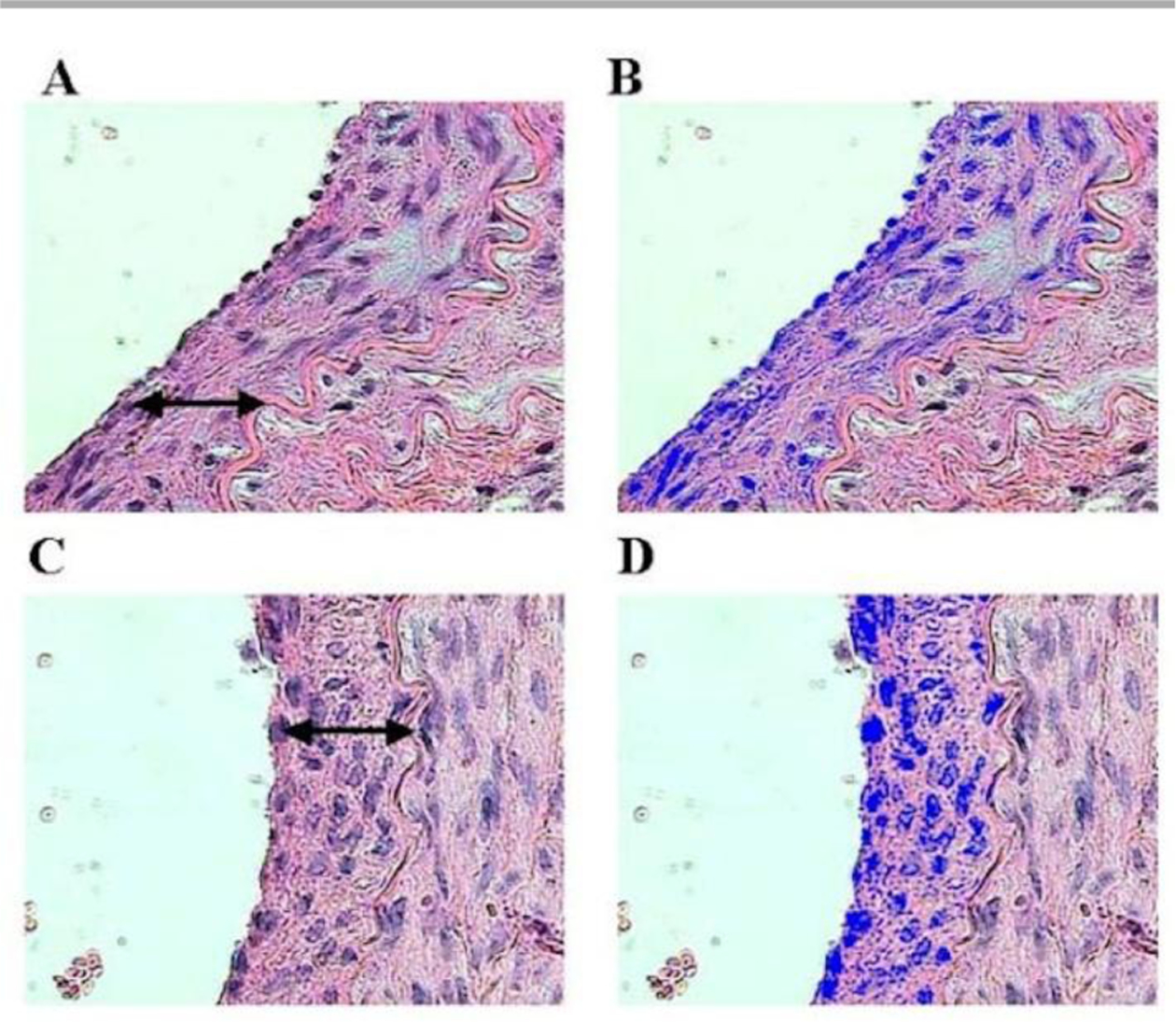
Photomicrographs by Costa et al. showing the nuclei of smooth muscle cells in intimal hyperplasia (↔), stained in blue. Irradiated group in A (21 days) and B image analysed by the computer system; control group in C (21 days) and D image analysed. (hematoxylin and eosin – 10x magnification).37
Triggers of intimal hyperplasia in vascular grafts
The IH formation in synthetic vascular grafts show a common pattern of spatial distribution: IH develops mainly at distal anastomosis in bypass grafts,39–42 and at graft-vein junctions of AVGs (Fig. 2).43–45 Surgical trauma, material bio-incompatibility, and biomechanical factors, have been found to contribute to IH formation in synthetic vascular grafts. Figure 3 summarizes the influence of these factors to the formation of IH. This section will discuss material bio-compatibility and biomechanical factors and their effects on IH formation.
Figure 2.
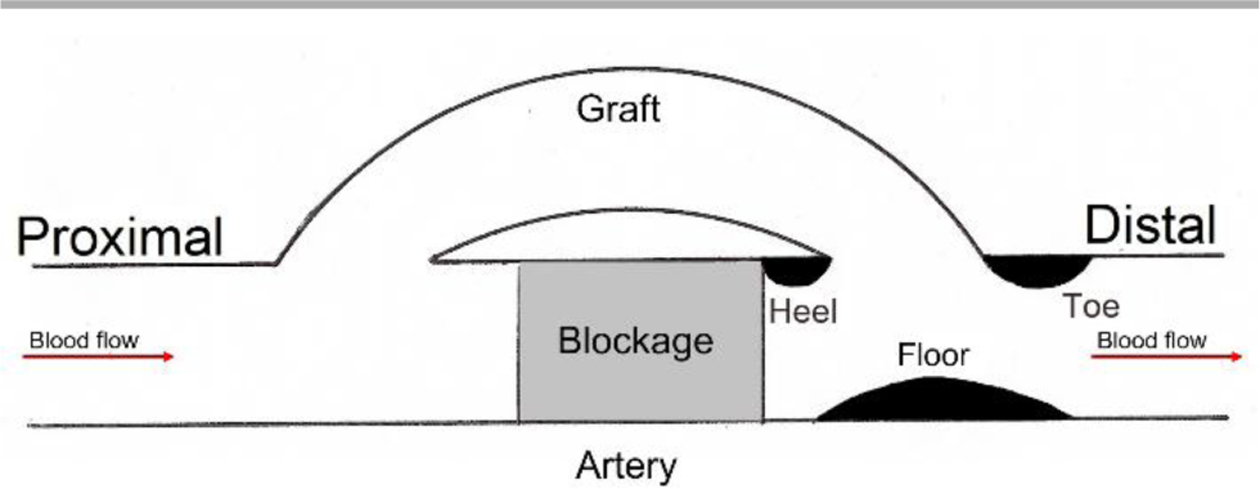
Locations of intimal hyperplasia formation in synthetic vascular grafts. IH in synthetic vascular grafts occur mainly at the floor of the native blood vessel and the toe, and heel and toe around the distal anastomoses.
Figure 3.
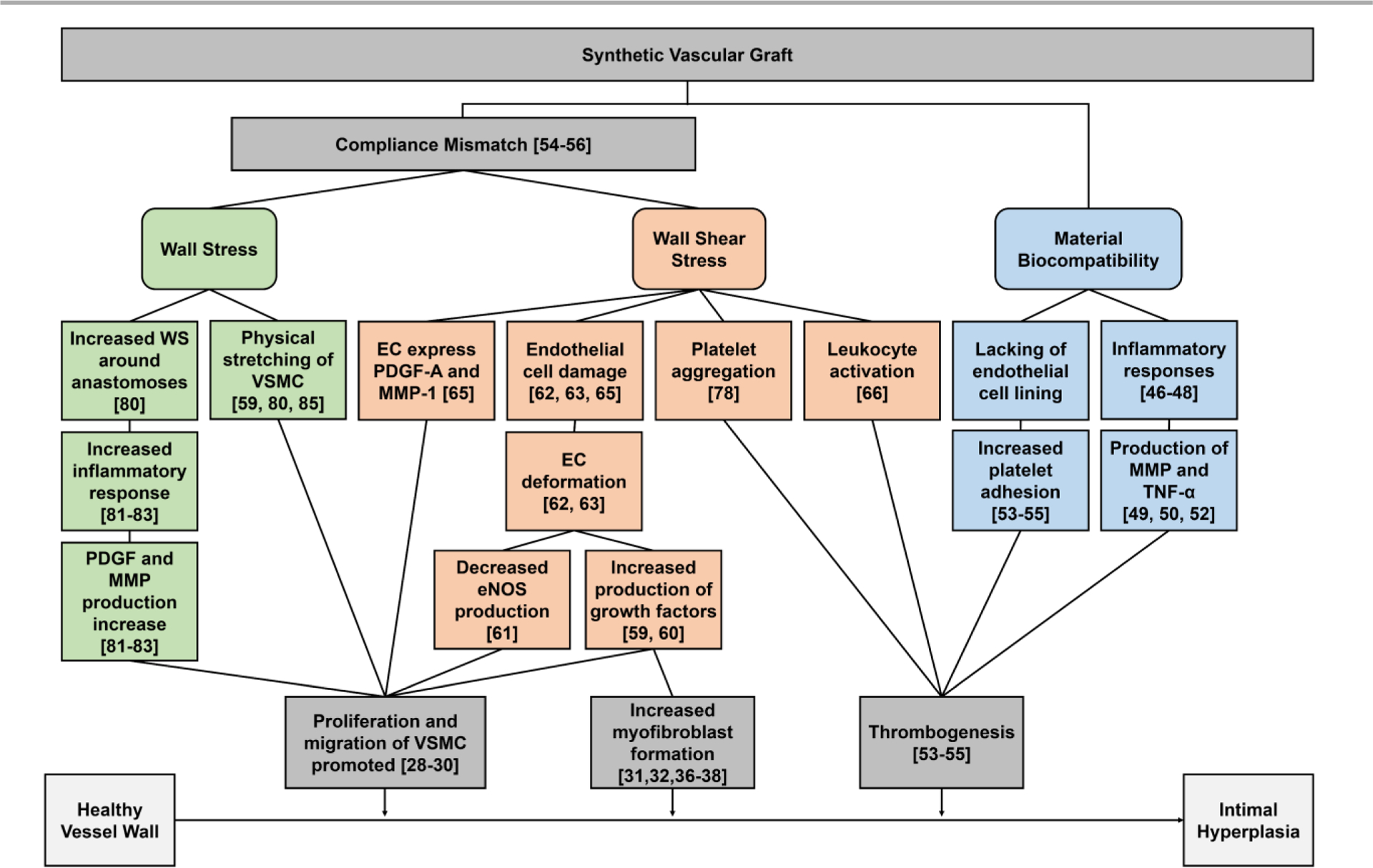
Factors that influence intimal hyperplasia formation. WS – wall stress, EC – endothelial cells, VSMC – vascular smooth muscle cells, PDGF – platelet-derived growth factors, MMP – metalloproteinase, TNF-α – tumor necrosis factor-α, and eNOS – endothelial nitric oxide synthase.
Material bio-incompatibility
Prosthetic, especially synthetic, vascular grafts are prone to triggering vascular inflammatory responses. Previous studies have shown an equal contribution of the inflammatory response and arterial injury to IH formation.46 For instance, macrophages were commonly observed in expanded polytetrafluoroethylene (ePTFE) graft stenosis.47 Furthermore, studies showed depleting macrophages could suppress IH, indicating the macrophages may regulate IH formation.48 Meanwhile, the inflammatory response stimulates the production of matrix metalloproteinases (MMPs) by VSMCs, which facilitate the migration and proliferation of VSMCs.49–51 T-lymphocytes have also been observed in the intima of injured vessels. They secrete tumor necrosis factor-α (TNF-α), which has been proven to induce migration of SMCs.52 In addition to inflammation, the lack of endothelial lining on the luminal surface of synthetic materials triggers platelet aggregation and thrombosis formation, resulting in narrowing of the lumen. Activated platelets and thrombin have also been demonstrated as mitogens of VSMCs and stimulate VSMC proliferation.53–55
Biomechanical factors
The mismatch of mechanical properties between grafts and native blood vessels has been proposed to be one of the important factors leading to IH in vascular grafts. The compliant arterial wall acts as an elastic reservoir, absorbing energy during systole and releasing in diastole. Introduction of a rigid segment, such as a stiff synthetic graft, interferes with the function. Compliance mismatch between a native artery and prosthetic graft was hypothesized to affect graft performance and result in a loss of patency by Abbott et al.56, 57 Later studies also confirmed the role of compliance mismatch in IH formation.58
Accompanied with compliance mismatch, the geometric discontinuity across the anastomoses between grafts and native blood vessels causes a blood flow disturbance around the anastomoses. Due to the configuration and mechanical mismatch between native vessel and graft, there is turbulence or flow separation around the anastomosis area. The flow separation causes endothelial injury and endothelial dysfunction by inducing different flow patterns at the heel and the toe, releasing growth factors causing SMC and myofibroblast proliferation.39, 59, 60 Also, the disturbed flow will trap platelets and cause platelets aggregation downstream, and will also promote fibrin thrombus formation.61
Wall shear stress (WSS) due to blood flow regulates the function and composition of blood vessels by affecting the phenotype and integrity of ECs.62, 63 Under physiological WSS, the phenotype of ECs changes from random orientation to aligned with flow direction during neovascularization. With high steady laminar shear force, ECs produced more NO, lowering the proliferation of SMCs and thus inhibiting the pathways leading to IH.64 However, with synthetic vascular grafts, ECs are exposed to abnormal shear stress and fail to express endothelial nitric oxide synthase (eNOS). Also, the distal anastomosis appears to induce a sharp shear stress change, with the directional change of shear force, which may lead to endothelial deformation.65 Low WSS is also not good as it will cause slow blood velocity inside the lumen and will decrease the proliferation of ECs and promote altered morphology. Monocyte adhesion was found to increase on the EC layer under low shear stress.66 In addition to WSS, DePaola et al. found gradient WSS near arterial branches could induce a change of endothelium and potentially contribute to IH formation.67 Later studies confirmed the hypothesis that the gradient shear stress induces platelet-derived growth factor-A (PDGF-A) and monocyte attractant protein-1 expression in ECs,68 and potentially regulates the direction of SMC migration.69 Ho et al. also found that immunoglobulin and proline-rich receptor-1 (IGPR-1) responded to shear stress and increased stiffness of the ECs.70 EC stiffness contributes to the alteration in WSS and induces transdifferentiation of VSMCs, exacerbating IH.70, 71 Meanwhile, endothelial NOTCH1 has been shown to affect cellular junctions and endothelial proliferation in response to shear stress.72
Other than in affecting ECs, the effect of WSS can be compounded with other factors that affect the blood vessel wall, such as SMCs, platelets, and leukocytes. In synthetic vascular grafts, vascular EC denudation at the anastomoses exposes underlying VSMCs to oscillatory WSS and regulates SMC proliferation, protein synthesis, and mitogenic activity.73 Extensive studies have shown that high, yet still within physiological range, steady laminar WSS inhibited proliferation of SMCs.74–76 However, when exposed to oscillatory shear stress, SMCs, had increased proliferation and cell survival.77 Furthermore, low shear stress due to reduced blood flow speed traps platelets and leukocytes.78 The attached platelets and leukocyte may become activated and trigger the formation of thrombus, further contributing to IH in a positive feedback loop (Fig. 4).
Figure 4.
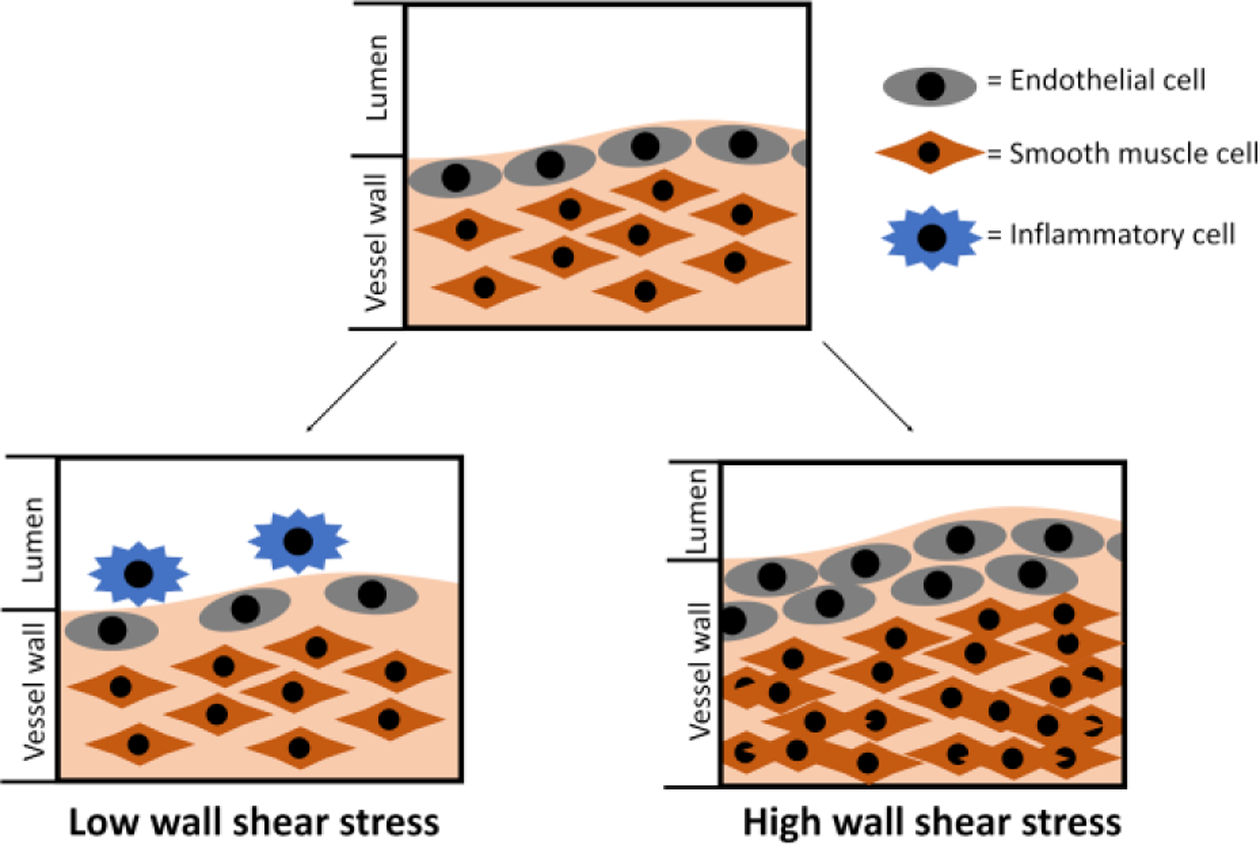
Vascular vessel wall remodelling due to alteration in wall shear stress.
In addition to WSS, vascular wall stress (WS) also plays an important role in IH formation, mainly for vein grafts or the venous side of AVGs.79 It has been found that compliance mismatch, and the resulting increase in WS, could also influence the formation and development of IH.59, 61, 80 Compliance mismatch has been shown to cause increased WS around the anastomoses.80 It was found that high WS may serve as an initiator of the inflammatory response, such as increased PDGF and MMP expression, that is important for SMC proliferation.81–83 Studies on PDGF responses to stress showed that upon increasing WS, PDGF secretion is promoted.84 Also, increased suture-line stress has been found at compliance mismatch anastomoses.80 As sutures are not elastic for the purpose of keeping the anastomoses closed, they result in contributing to the compliance mismatching at the anastomoses. The elevated suture-line stress may stretch SMCs and cause SMCs to proliferate, and contribute to IH formation.59, 85
Current limitations in understanding intimal hyperplasia
Despite many advancements in the field, the complete picture of the effect of mechanical stimuli in IH still remains elusive. To understand the complex relationship between biological and mechanical factors involved with IH, it is important to assess the current knowledge on the topic. In 2003, Paszkowiak and Dardik pointed out that the exact pathway that is associated with the EC sensing of the mechanical signals was unknown.86 IH still remains the primary problem with sSDVGs even with over decades of advancements.87–89
As addressed in the review paper by Pannier et al., there was no standardized measurement method available for identifying the compliance of native blood vessels.90 Furthermore, the difference in compliance of the vascular graft or native blood vessels are affected by the different measurement methods The lack of standardization is reflected on the equations used to calculate the compliance (Table 1). All of the equations can be applied to either in vitro or in vivo measurements. However, the sensitivity and accuracy of the measured value is dependent upon the measurement method used to make the measurements.
Table 1:
Equations used to calculate arterial stiffness.
| Equations | Unit | Ref. | |
|---|---|---|---|
| 1 |
PWV = pulse wave velocity, ρ = blood mass density, k = distensibility, D = vessel diameter, P = pressure |
104 | |
| 2 |
PWV = pulse wave velocity, D = distance, t = time |
105 | |
| 3 |
PWV = pulse wave velocity = arterial stiffness, E = vessel wall Young’s modulus, v = Poisson’s ratio, R = lumen radius, h = wall thickness, ρ = density of the wall |
102, 106 | |
| 4 |
Ci = volumetric compliance, Vi = volume, ρ = blood density, PWVi = pulse wave velocity |
107 | |
| 5 |
D = distensibility, V = volume, u = axial flow velocity, ρ = density of incompressible fluid, PWV = pulse wave velocity, η = ratio of the wall deflection to internal wall radii, C = compliance |
108 | |
| 6 |
AI = augmentation index, ΔP = pressure difference between peak blood pressure during systolic period and break point, PP = pulse pressure difference |
% | 101, 103, 109 |
| 7 |
RI = resistance index, Vmax = peak systolic velocity, Vmin = minimal diastolic velocity |
% | 91 |
| 8 |
kp = local vessel compliance, P = blood pressure, u = blood velocity, t = time, Ao = reverence vessel area, KR = fluid resistance |
110 | |
| 9 |
AC = aterial compliance, Ds = systolic diameter of the blood vessel, Dd = diastolic diameter of the blood vessel, Ps = systolic pressure, Pd = diastolic pressure |
109 | |
| 10 |
C = compliance, Pdist = pressure at the beginning of diastole, Pend dist = pressure at the end of the diastole, As = systolic area, Ad = diastolic area |
111 | |
| 11 |
Q = flow, C = compliance, P = pressure, t = time, R = total resistance |
112, 113 | |
| 12 |
Cder = compliance, A = lumen area, P = blood pressure |
114 | |
| 13 |
C = diametrical compliance, Ds = systolic diameter, Dd = diastolic diameter, Ps = systolic pressure, Pd = diastolic pressure |
115 | |
| 14 |
C = radial compliance, d120 = diameter of the graft at 120mmHg, d80 = diameter of the graft at 80mmHg |
% per 40mmHg | 116 |
| 15 |
C = compliance, Ds = systolic arterial diameter, Dd = diastolic arterial diameter, Ps = systolic pressure, Pd = diastolic pressure |
17 |
Measurement methods
One of the reasons why the influence of mechanical properties, specifically the compliance, is not well understood is that there is no set consensus on how to measure the compliance of native blood vessels. One of the fundamental disputes is of the parameters used to determine the compliance. Some use pulse wave velocity (PWV) by assessing fluid flow parameters along with augmented index (Aix) or resistance index.90, 91. Others use changes in the diameter of the blood vessel or vascular grafts using echo tracking systems to determine the compliance. Lastly, an ultrasound based method called arterial stiffness evaluation for non-invasive screening (ARTSENS), developed in 2015, can be used to measure the arterial stiffness.92–94 Different methods that can be used to measure the PWV and AIx (Table 1: Eq. 1–6), resistance index (RI; Table 1: Eq. 7), or compliance (Table 1: Eq. 8–15) are listed in Table 1. While all of the equations can be used in both in vitro, ex vivo, and in vivo, PWV ad Aix equations are most suitable for measuring compliance in vivo due to accuracy.
Common measurement methods use PWV and AIx to overcome the limitations of the Doppler ultrasound—low accuracy and sensitivity.90 In 2018, Joseph et al. developed magnetic plethysmography (MPG) to measure arterial compliance using PWV.95 Another method developed in 2016 is ARTSENS® Pen. The benefit of ARTSENS® Pen is that it is an automatic and image free method of measuring arterial stiffness with good accuracy.96, 97 This method is actively being tested for its accuracy, and recently showed repeatable and high sensitivity measurements through assessing 523 subjects in a clinical trial.98 Radial artery tonometry is also used to measure the arterial stiffness in diabetic children using PWV and Aix.99 AIx is a method using ascending aortic pressure waveform to measure the systemic arterial stiffness.99–101 It is often used in conjunction with PWV as an indirect method of measuring arterial stiffness102. In clinical practice, AIx is used as a method to measure arterial stiffness because it is independent of geometry and is determined by age and aortic PWV.103 The biggest benefit of AIx is the consensus in the equation used for calculation unlike others such as PWV and compliance.
The problem with these different types of devices lies with their potential for clinical applications. While many measurement options are commercially available, most clinicians still prefer to use Magnetic Resonance Imaging (MRI) or Doppler ultrasound due to ease of use for measuring arterial stiffness of the patients.90, 103, 117, 118 Unfortunately, this yields inaccurate results depending on the resolution of the imaging instrument used, the location of the blood vessel, and size of the blood vessel.91, 119 For example, some transcranial Doppler ultrasound cannot measure the arterial geometry, therefore requiring the flow velocity to be used for compliance measurement.119 As means to minimize the errors due to the measurement method, RI is used to assess the vascular stiffness instead of measuring vascular compliance of the native blood vessels directly.91, 120 Although these Aix and RI are closely associated with vascular compliance, they are not sufficient for the measurement of arterial compliance.121 Validation of using Doppler ultrasound has also been performed by comparing with other available methods. Mechanotransduers have verified the reliability and reproducibility of Doppler ultrasound techniques.103, 122, 123 However, these methods do not overcome the innate resolution problem Doppler ultrasound has; its accuracy and repeatability depends on the sonographer. The consensually most accurate method is using mechanotransducer.123 This is an invasive method as a probe has to be inserted to measure the blood flow and pressure, and thus it is not used in clinical settings.122, 123 Although many measurement methods are available, none of the currently available methods meet all of the requirements needed for accurate assessment of the mechanical properties affecting hemodynamics in both the clinics and in research.
Modelling methods
Recent advancement in computational fluid dynamics (CFD) and finite element modelling (FEM) made it possible to simulate the complex flow induced in vasculatures. CFD simulation allows researchers to model the effect of hemodynamics and the resulting WSS on the vessel walls without having to perform physical experiments. Similarly, FEM simulation allows estimation of WS applied on the vessel wall. For example, He et al. found that end-to-end anastomosis model showed the presence of significant disturbance in blood velocity, wall shear stress and pressure at the compliance mismatch region.124 Compliance mismatch can result in a change in the WSS exerted by the blood flow and, therefore, proper assessment of the flow regime gives insight to this phenomenon.18, 124 This conclusion is consistent with the earlier findings of Steinman et al., who showed that the magnitude of shear stress is directly related to the pressure exerted by the flowing fluid.125 As for WS, many tissue-engineered vascular grafts (TEVGs) use computational modelling to assess whether the TEVGs are suitable in physiological pressure.126 However, as the models often overlook biological factors, the models are not capable of accurately predicting the generation of IH.18, 19, 100 The computer models developed by Stewart and Lyman showed that protein transport patterns differ between compliance mismatched models and the compliance matched model, further giving weight to the importance of understanding compliance mismatch in vascular graft engineering.19, 125 While the development of CFD allowed for a better understanding of the mechanical properties of graft effects on hemodynamics, many simplifications are still used for the CFD to sufficiently and accurately describe the development of IH. In 2018, Szafron et al. showed that the biological factors that were often overlooked can be incorporated into one computational modelling when assessing WS.127 This is a great advancement for WS modelling, but it is yet to become the standard for WS computational modelling.
The improvement of computer simulations also shed light on the limitations of in vitro validation methods: the lack of high compliance materials and the lack of biomimetic available for in vitro setups. For synthetic vascular grafts, there is a basic requirement of good mechanical integrity for safety. Dacron and ePTFE, synthetic vascular grafts that are currently available in the market, has high mechanical integrity and high safety margin. However, these grafts lack compliance. As hydrogel can often be modified to have different mechanical properties, hydrogels have been used to fabricate various sSDVGs. For example, Wise et al. made an elastin/polycaprolactone hybrid vascular graft that can match the compliance of the native blood vessel with the same diameter.128 Similarly, polyvinyl alcohol grafts showed promise as a compliant synthetic vascular graft, and are being studied extensively.116, 129–131 However, the problem with synthetic vascular grafts is that they lack the high compliance variability of native blood vessels. For example, the native artery has the compliance of 8 ± 5.9 percent per 10−2 mmHg, whereas poly(carbonate) urethane-based synthetic compliant vascular graft has the compliance of 8.1 ± 0.4 percent per 10−2 mmHg.115 This is important as blood vessels must be able to compensate for different blood flow that naturally occurs due to physiological phenomena. Despite the developments of new and improved biomaterials, the materials that displays the qualities required to mimic the mechanical properties of small-diameter blood vessels is yet to be found.
The other drawback of using in vitro model is that the experimental setup used to measure the compliance is not an accurate representation of the in vivo condition. As depicted in Figure 5, various techniques can be used for in vitro testing of synthetic graft compliance.17, 102, 105, 106, 112, 116, 132–134 Due to the ease of setup, hydrostatic pressure-induced expansion has been used to measure the compliance of synthetic grafts.116 While this model can be used to make basic compliance measurements, it is not suitable for assessing the dynamic compliance of the grafts. As blood flow within the body has been well-characterized, many in vitro tests and cell culture use simulated physiological pulsatile flow.56, 133, 135, 136 For example, Gong et al. developed a culturing system that generated physiological pulsatile flow using a pump; they showed that dynamic culturing condition increased cellular attachment and improving compliance of the graft.133
Figure 5.
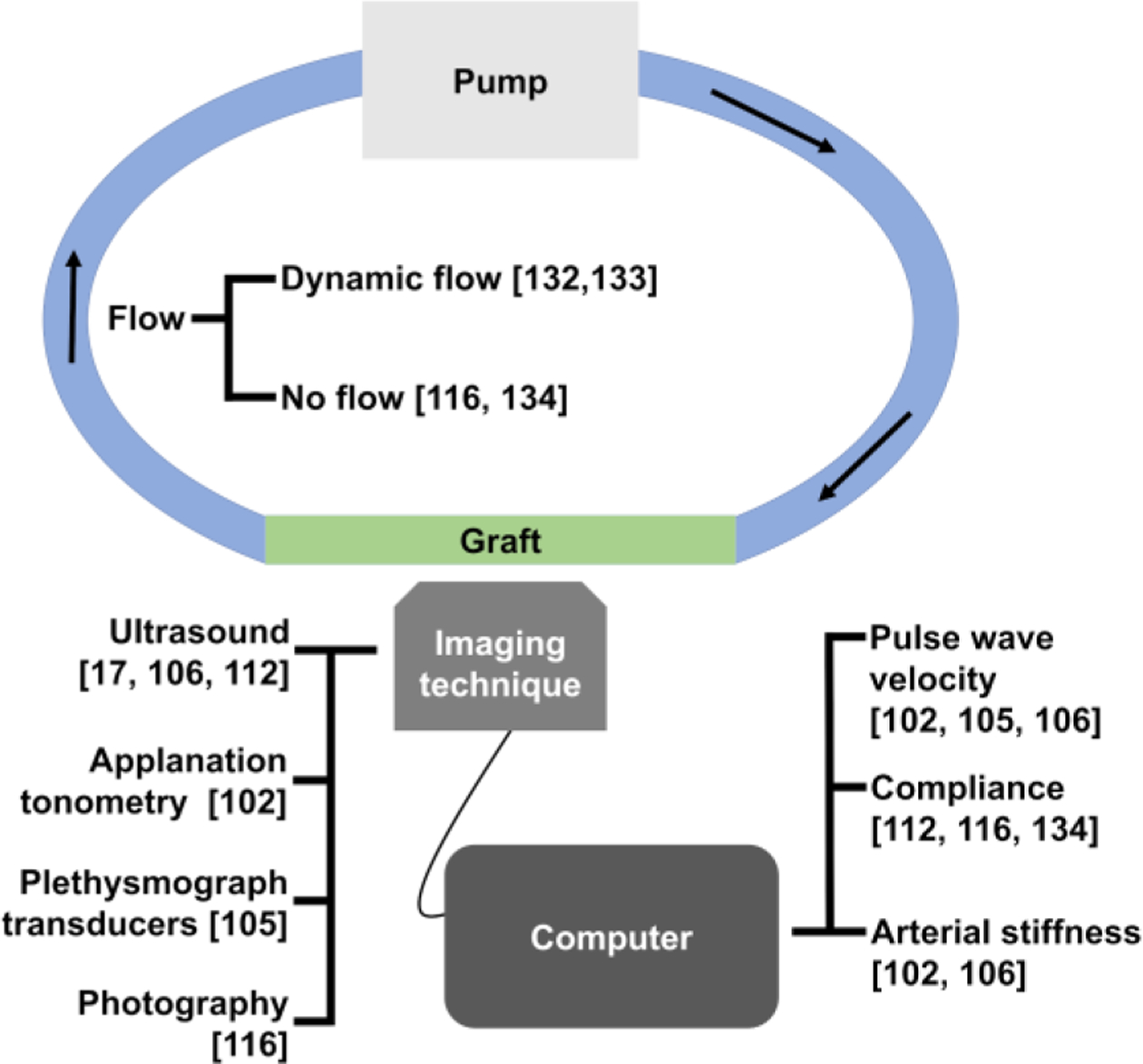
Summary of the techniques used for calculation of compliance of vascular grafts in vitro.
Even with the physiologically relevant culture conditions, it is impossible to get an accurate representation of the effect of mechanical properties on IH in vitro, as the biological factors involved, such as cells, platelets, and growth factors, in the formation and development of IH is either simplified or non- existent in the fluids used in in vitro cultures. The idea of blood-mimicking fluid (BMF) for the purpose of in vitro blood flow and vascular graft testing has been studied since late 1990’s.137 Despite the fact that BMFs are commercially available, these fluids mainly focus on the mimicking the biological acoustic noise for ultrasound imaging rather than the biological factors; they are mostly used for ultrasound imaging.138, 139 As shown in Figure 3, the biological factors such as inflammatory responses and thrombogenesis play an important role in development of IH. Without blood factors and cellular interactions to simulate these interactions, in vitro tests cannot accurately represent the in vivo environment. Furthermore, performing in vitro WSS and WS experiments relating to compliance and compliance mismatch are still difficult as experimental methods are still not well established.140 While particle tracing is the preferred method for measurement of WSS, this method is still yet to be used in conjunction with cell culture.141, 142 Unlike, the effects of WS on cellular behaviors have been studied in vitro.80 However, most of the recent publications focus on the FEM computer modelling rather than in vitro experiments.126, 143 In vitro methods without multiple biological components cannot be useful beyond being a tool to understand only the basic interaction between one cell type and synthetic vascular grafts rather than assessing the interaction of various biological factors with different compliance.
To overcome the drawbacks of in vitro models, ex vivo models are used to perform more physiologically relevant experiments while minimize the use of animals. Ex vivo models are more extensively used for biological or tissue-engineered vascular grafts as they provide a less invasive method to assess the graft’s hemocompatibility than in vivo experiments. There are two different types of ex vivo models that can be used to assess the effect of compliance mismatch: the ex vivo shunt model and ex vivo organ culture. The ex vivo shunt is a well-established procedure to test the hemocompatibility of synthetic vascular grafts.130, 144 Ex vivo shunts use externally reinforced vascular grafts surgically connected to a part of the animal. The limitation of this setup is that the shunt is supported by external structure, which masks any potential influence by the compliance. Recently, an ex vivo organ culture model for screening the synthetic vascular grafts have been developed.58 This system is different from ex vivo shunt since it uses ex vivo bioreactor rather than the animal itself.145 This system screens for the markers that are known to induce IH formation to screen for the synthetic vascular grafts their potential to form IH.58 The strength of this model is that it allows for screening of the biological effects of vascular grafts with difference compliance. Further development of ex vivo models would enhance the ability to easily test synthetic vascular grafts with different compliance while having higher accuracy than in vitro models.145 Ex vivo shunt or ex vivo bioreactor has the capacity to account for much higher variety of biological factors. Some have even developed ex vivo organ culture model for screening synthetic vascular grafts for compliance compatibility.58 However, the techniques are still young and require further validation before application.
The best and most physiologically relevant method of studying the relationship between the biological and mechanical factors and IH is using in vivo model. An example of a well-established vascular graft implantation model for SDVG is end-to-end rabbit common carotid arterial implantation.146–148 However, studies using in vivo model are extremely difficult due to many factors. First, non-invasive measurement methods are always preferred because of ethical concerns, easy procedures, clinical relevance, reduced trauma, and no unnecessary complications even though it is viewed as less accurate. In order to minimize usage of invasive procedures, but Doppler ultrasounds are not sensitive enough to isolate individual mechanical properties, and could not be used to accurately understand the extent to which the compliance and compliance mismatch influences IH.149 MRI techniques can also be used to measure compliance, but this method requires expensive instrument, long imaging time, and specialized facility set up and, therefore, is oftentimes not accessible for research labs.150, 151
Another limitation of in vivo models is inconsistency between protocols. When testing the biomaterials of vascular grafts in vitro, international standards and guideline such as International Standard Organization (ISO) has been established to which researchers can refer.152 However, there are still many different models to account for depending on the application, making it crucial to choose the most applicable models.147 For example, even though the end-to-side anastomosis is more common method of implanting SDVG clinically, small animal models predominantly use end-to-end anastomosis.153 On the other hand, end-to-side anastomosis in small animal model exists as well.131 Surgical parameters such as anastomosis type is important as these parameters can directly impact the patency of the implanted grafts.147 Finally, the type of animal used is very important. Different animals have different hemodynamic, different biological responses, different vascular sizes, and different compliances. All of these factors play a role in graft patency and IH formation. For example, having different diameters of vascular graft and the native blood vessel would decrease the blood flow around the anastomoses, which could cause thrombogenesis. Byrom et al. published a very comprehensive comparison between animal models and identified the potential animal models that are suitable for sSDVG application.147
In vitro, ex vivo models, and in vivo models are used to understand the effects of compliance mismatch on the pathophysiology of IH. While in vitro models provide a convenient method to test the compliance and basic cellular interaction with the synthetic vascular grafts, there lacks a connection between the compliance mismatch and the onset of IH. In vivo testing models are still the best models for testing the performance of vascular grafts even with all the difficulties it entails. However, these models are particularly difficult for assessing the influence of compliance mismatch on IH as an accurate and non-invasive compliance measurement method in vivo does not exist. In vivo models must be carefully chosen to have appropriate animals, correct procedures, appropriate anastomoses, and correct diameters between vascular graft and native blood vessel.
Conclusion
Despite the advances in technology, understanding the complex roles of the biological and mechanical factors in vascular graft engineering are yet to be completely understood. IH is a well-observed phenomenon in medicine, and the biological mechanism of its development has been studied extensively. The field is now trying to make connections between the mechanical factors and their influence on biological responses.
The knowledge of compliance mismatch has been shown to be important in vascular engineering. Compliance mismatch between the synthetic vascular graft and the native blood vessel influences the hemodynamics. The altered hemodynamics influence WSS through irregular flow patterns. The irregular mechanical signal then triggers irregular biological responses. These irregular biological behaviors then manifest as pathophysiological phenomena known as IH. While many strides have been made to understand the links between compliance mismatch and IH, there is still missing information that must be identified before the links can be understood completely (Fig. 618, 124, 141, 154–160).
Figure 6.
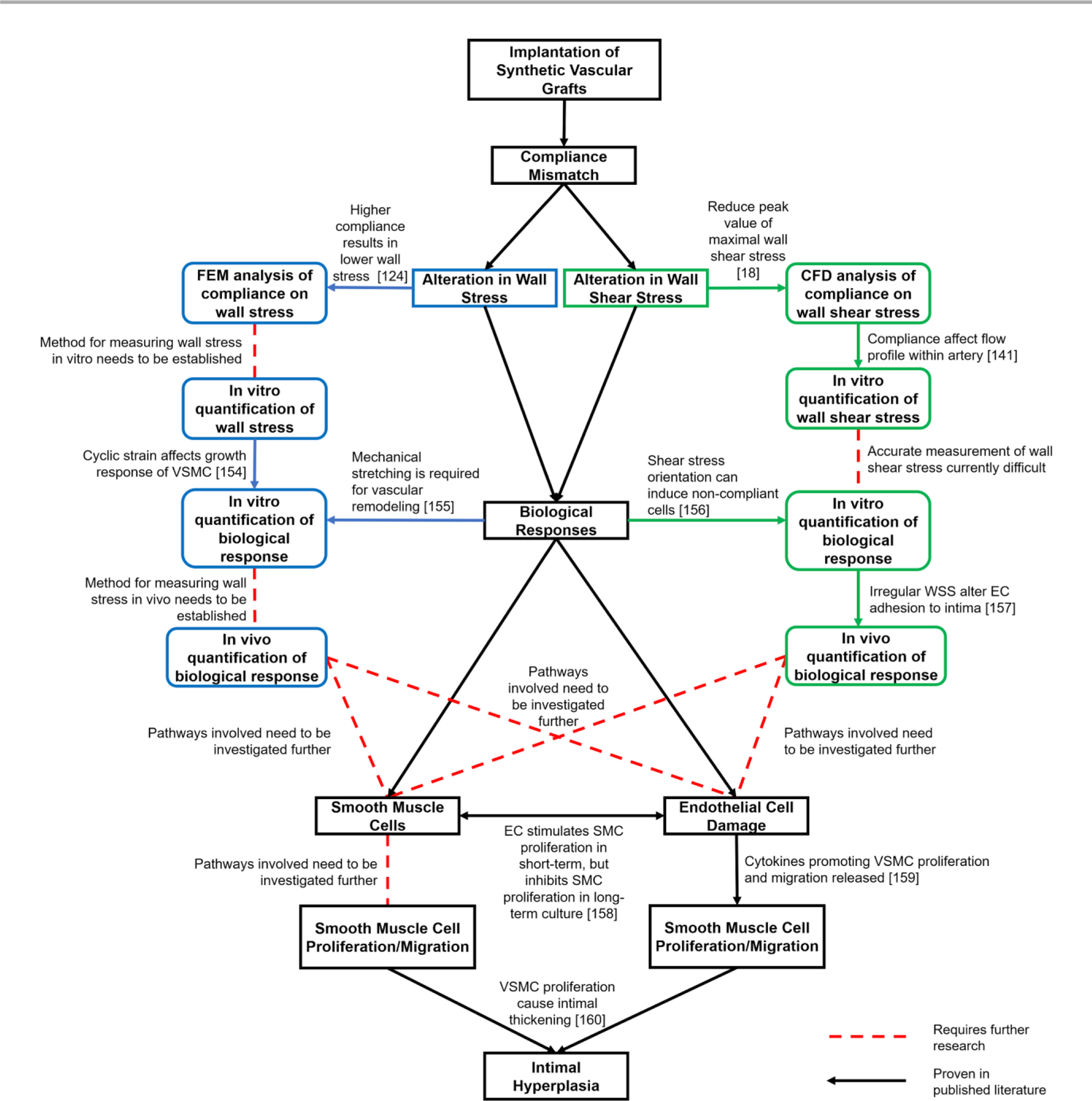
Summary of current progress in understanding intimal hyperplasia formation in synthetic vascular grafts.
Even though some of the molecular and biomechanical pathways have been shown to be associated with vascular remodelling, the relationship between compliance mismatch and those pathways are still unknown. Some takeaways from this review are:
Thorough studies detailing the mechanical properties of biomaterials should be performed for the biomaterials used to fabricate vascular grafts.
Longitudinal vs. circumferential compliance mismatch should be decoupled and studied individually.
In vitro models should become more sophisticated to account for various physiological reactions that occur in the body.
A consensus in in vitro compliance measurement should be reached so that compliance of different materials can be accurately compared.
Ex vivo organ culture is very promising as the development of convenient ex vivo organ culture would make testing mechanical mismatch using synthetic vascular grafts more facile and physiologically relevant.
Non-invasive in vivo compliance measurements methods need improvement to provide accurate and consistent results.
With the number of cardiovascular disease incidences increasing as time passes, the need to fabricate better vascular grafts is evident—especially so for sSDVGs.1, 2, 161 As IH is an important hurdle that must be overcome to achieve more successful AVGs and SDVGs, it is important to understand the biological factors associated with IH and the effect of mechanical properties, such as compliance mismatch, on hemodynamics that generate WSS. A platform that has the capacity to alter both the mechanical properties as well as the chemical properties is required so that the effects of the mechanical properties on the IH formation can be assessed without being influenced by the chemical and biochemical factors. Also, a way to ensure consistency in compliance measurements between in vivo experiments must be established so that the results from different vascular grafts can be compared to one another. This would not only enhance the reliability of the results, but also ensure the requirements of newly developed vascular grafts.
Acknowledgements
The authors would like to thank the National Institute of Health (NIH RO1 HL130274-01A1), NSERC-CREATE Training in Global Biomedical Technology Research and Innovation at the University of Waterloo (CREATE-509950-2018), NSERC Canada Discovery Grant (RGPIN-2016-04043) for financial support. The authors would also like to thank Clyde Overby for providing edits for this review article.
Footnotes
Conflict of interest
The authors declare no conflict of interest
References
- 1.F. a. D. Administration.
- 2.Pashneh-Tala S, MacNeil S and Claeyssens F, Tissue Engineering Part B: Reviews, 2016, 22, 68–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Al Shakarchi J, Houston G and Inston N, The Journal of Vascular Access, 2015, 16, 493–497. [DOI] [PubMed] [Google Scholar]
- 4.Albers FJ, Advances in renal replacement therapy, 1994, 1, 107–118. [DOI] [PubMed] [Google Scholar]
- 5.Dantzer R, O’Connor JC, Freund GG, Johnson RW and Kelley KW, Nature reviews neuroscience, 2008, 9, 46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Barker RA and Widner H, NeuroRx, 2004, 1, 472–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mousa AY, Patterson W, Abu-Halimah S, Hass SM, Alhalbouni S, Sadek BT, Nanjundappa A, Modak A, Stone PA, Emmett M and AbuRahma AF, Vascular and Endovascular Surgery, 2013, 47, 438–443. [DOI] [PubMed] [Google Scholar]
- 8.Gage FH, NATURE-LONDON-, 1998, 18–24. [PubMed] [Google Scholar]
- 9.Betts JG, Johnson E, Wise JA, Young KA and et al. , Journal, 2013. [Google Scholar]
- 10.Mills B, Robb T and Larson D, Perfusion, 2012, 27, 520–528. [DOI] [PubMed] [Google Scholar]
- 11.Chen D, Shrivastava S, Ma L, Tham E-L, Abrahams J, Coe JD, Scott D, Lechler RI, McVey JH and Dorling A, Arteriosclerosis, Thrombosis, and Vascular Biology, 2012, 32, 42–49. [DOI] [PubMed] [Google Scholar]
- 12.Allaire E and Clowes AW, The Annals of thoracic surgery, 1997, 63, 582–591. [DOI] [PubMed] [Google Scholar]
- 13.Sterpetti AV, Cucina A, Lepidi S, Randone B, Stipa F, Aromatario C, Travi D, D’Angelo LS, Cavallaro A and Stipa S, Journal of vascular surgery, 1996, 23, 568–575. [DOI] [PubMed] [Google Scholar]
- 14.Lyman DJ, Fazzio FJ, Voorhees H, Robinson G and Albo D, Journal of Biomedical Materials Research, 1978, 12, 337–345. [DOI] [PubMed] [Google Scholar]
- 15.Roberts G, McCormack H, Ketharanathan V, Macleish DG, Field PL and Milne PY, Journal of Biomedical Materials Research, 1989, 23, 443–450. [DOI] [PubMed] [Google Scholar]
- 16.Brossollet LJ, 1992.
- 17.Abbott WM, Megerman J, Hasson JE, L’Italien G and Warnock DF, Journal of vascular surgery, 1987, 5, 376–382. [PubMed] [Google Scholar]
- 18.Surovtsova I, Journal of Biomechanics, 2005, 38, 2078–2086. [DOI] [PubMed] [Google Scholar]
- 19.Stewart SFC and Lyman DJ, Annals of biomedical engineering, 2004, 32, 991–1006. [DOI] [PubMed] [Google Scholar]
- 20.Wu MH-D, Shi Q, Sauvage LR, Kaplan S, Hayashida N, Patel MD, Wechezak AR and Walker MW, Annals of Vascular Surgery, 1993, 7, 156–168. [DOI] [PubMed] [Google Scholar]
- 21.di Luca M, Hakimjavadi R, Burtenshaw D, Fitzpatrick E, Mathiue P, Lally C, Redmond EM and Cahill PA, in Muscle Cell and Tissue-Current Status of Research Field, IntechOpen, 2018. [Google Scholar]
- 22.Haudenschild CC, Journal of Vascular Surgery, 1989, 10, 591–592. [Google Scholar]
- 23.Tennant M and McGeachie JK, ANZ Journal of Surgery, 1990, 60, 747–753. [DOI] [PubMed] [Google Scholar]
- 24.Rohrbach DH and Timpl R, 1993, 448. [Google Scholar]
- 25.Iivanainen E, Kähäri V-M, Heino J and Elenius K, Microscopy Research and Technique, 2003, 60, 13–22. [DOI] [PubMed] [Google Scholar]
- 26.Radomski MW, Palmer RMJ and Moncada S, British Journal of Pharmacology, 1987, 92, 639–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Castellot J, Addonizio ML, Rosenberg R and Karnovsky MJ, The Journal of Cell Biology, 1981, 90, 372–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cirillo P, Golino P, Ragni M, Battaglia C, Pacifico F, Formisano S, Buono C, Condorelli M and Chiariello M, Cardiovascular research, 1999, 43, 210–218. [DOI] [PubMed] [Google Scholar]
- 29.Cirillo P, Golino P, Calabrò P, Ragni M, Forte L, Piro O, De Rosa S, Pacileo M and Chiariello M, Thrombosis Research, 2003, 112, 51–57. [DOI] [PubMed] [Google Scholar]
- 30.Weber A-A and Schror K, Platelets, 1999, 10, 77–96. [DOI] [PubMed] [Google Scholar]
- 31.Li G, Chen S-J, Oparil S, Chen Y-F and Thompson JA, Circulation, 2000, 101, 1362–1365. [DOI] [PubMed] [Google Scholar]
- 32.Siow RCM, Mallawaarachchi CM and Weissberg PL, Cardiovascular research, 2003, 59, 212–221. [DOI] [PubMed] [Google Scholar]
- 33.Spaet TH, Stemerman MB, Veith FJ and Lejnieks I, Circulation research, 1975, 36, 58–70. [DOI] [PubMed] [Google Scholar]
- 34.Li L, Terry CM, Shiu Y-TE and Cheung AK, Kidney International, 2008, 74, 1247–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Costa R. d. F. B. d., Fagundes DJ, Juliano Y, Novo NF and Vieira WTT, Acta Cirurgica Brasileira, 2003, 18, 86–96. [Google Scholar]
- 36.Scott NA, Cipolla GD, Ross CE, Dunn B, Martin FH, Simonet L and Wilcox JN, Circulation, 1996, 93, 2178–2187. [DOI] [PubMed] [Google Scholar]
- 37.Shi Y, O’Brien JE, Fard A, Mannion JD, Wang D and Zalewski A, Circulation, 1996, 94, 1655–1664. [DOI] [PubMed] [Google Scholar]
- 38.Oparil S, Chen S-J, Chen Y-F, Durand JN, Allen L and Thompson JA, Cardiovascular Research, 1999, 44, 608–614. [DOI] [PubMed] [Google Scholar]
- 39.Sottiurai V, International Journal of Angiology, 2011, 8, 1–10. [DOI] [PubMed] [Google Scholar]
- 40.Bassiouny HS, White S, Glagov S, Choi E, Giddens DP and Zarins CK, Journal of vascular surgery, 1992, 15, 708–716; discussion 716–707. [DOI] [PubMed] [Google Scholar]
- 41.Sottiurai, The International journal of angiology : official publication of the International College of Angiology, Inc, 1999, 8, 1–10. [DOI] [PubMed] [Google Scholar]
- 42.LoGerfo FW, Quist WC, Nowak MD, Crawshaw HM and Haudenschild CC, Annals of surgery, 1983, 197, 479–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tordoir JHM, Hofstra L, Leunissen KML and Kitslaar PJEHM, European Journal of Vascular and Endovascular Surgery, 1995, 9, 305–309. [DOI] [PubMed] [Google Scholar]
- 44.Fillinger MF, Reinitz ER, Schwartz RA, Resetarits DE, Paskanik AM, Bruch D and Bredenberg CE, Journal of vascular surgery, 1990, 11, 556–566. [PubMed] [Google Scholar]
- 45.Haruguchi H and Teraoka S, Journal of Artificial Organs, 2003, 6, 227–235. [DOI] [PubMed] [Google Scholar]
- 46.Kornowski R, Hong MK, Tio FO, Bramwell O, Wu H and Leon MB, Journal of the American College of Cardiology, 1998, 31, 224–230. [DOI] [PubMed] [Google Scholar]
- 47.Roy-Chaudhury P, Kelly BS, Miller MA, Reaves A, Armstrong J, Nanayakkara N and Heffelfinger SC, Kidney International, 2001, 59, 2325–2334. [DOI] [PubMed] [Google Scholar]
- 48.Hoch JR, Stark VK, van Rooijen N, Kim JL, Nutt MP and Warner TF, Surgery, 1999, 126, 428–437. [PubMed] [Google Scholar]
- 49.Ross R, New England Journal of Medicine, 1999, 340, 115–126. [DOI] [PubMed] [Google Scholar]
- 50.Newby AC and Zaltsman AB, The Journal of Pathology, 2000, 190, 300–309. [DOI] [PubMed] [Google Scholar]
- 51.Macarie RD, Vadana M, Ciortan L, Tucureanu MM, Ciobanu A, Vinereanu D, Manduteanu I, Simionescu M and Butoi E, Journal of cellular and molecular medicine, 2018, 22, 4366–4376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Goetze S, Xi X-P, Kawano Y, Kawano H, Fleck E, Hsueh WA and Law RE, Hypertension, 1999, 33, 183–189. [DOI] [PubMed] [Google Scholar]
- 53.Kanthou C, Benzakour O, Patel G, Deadman J, Kakkar VV and Lupu F, Thrombosis and haemostasis, 1995, 74, 1340–1347. [PubMed] [Google Scholar]
- 54.Nakajima T, Kitajima I, Shin H, Takasaki I, Shigeta K, Abeyama K, Yamashita Y, Tokioka T, Soejima Y and Maruyama I, Biochemical and Biophysical Research Communications, 1994, 204, 950–955. [DOI] [PubMed] [Google Scholar]
- 55.McNamara CA, Sarembock IJ, Gimple LW, Fenton JW, Coughlin SR and Owens GK, Journal of Clinical Investigation, 1993, 91, 94–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Baird RN and Abbott WM, Lancet (London, England), 1976, 2, 948–950. [DOI] [PubMed] [Google Scholar]
- 57.Baird RN, Kidson IG, L’Italien GJ and Abbott WM, American Journal of Physiology-Heart and Circulatory Physiology, 1977, 233, H568–H572. [DOI] [PubMed] [Google Scholar]
- 58.Post A, Diaz-Rodriguez P, Balouch B, Paulsen S, Wu S, Miller J, Hahn M and Cosgriff-Hernandez E, Acta biomaterialia, 2019, 89, 84–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sottiurai VS, Sue SL, Feinberg EL, Bringaze WL, Tran AT and Batson RC, European journal of vascular surgery, 1988, 2, 245–256. [DOI] [PubMed] [Google Scholar]
- 60.Chistiakov DA, Orekhov AN and Bobryshev YV, Acta physiologica, 2017, 219, 382–408. [DOI] [PubMed] [Google Scholar]
- 61.Reininger AJ, Heinzmann U, Reininger CB, Friedrich P and Wurzinger LJ, Thrombosis Research, 1994, 74, 629–641. [DOI] [PubMed] [Google Scholar]
- 62.Ballermann BJ, Dardik A, Eng E and Liu A, Kidney international. Supplement, 1998, 67, S100–108. [DOI] [PubMed] [Google Scholar]
- 63.Malek AM, Alper SL and Izumo S, JAMA, 1999, 282, 2035. [DOI] [PubMed] [Google Scholar]
- 64.Nadaud S, Philippe M, Arnal JF, Michel JB and Soubrier F, Circulation research, 1996, 79, 857–863. [DOI] [PubMed] [Google Scholar]
- 65.Ojha M, Circulation research, 1994, 74, 1227–1231. [DOI] [PubMed] [Google Scholar]
- 66.Walpola PL, Gotlieb AI and Langille BL, The American journal of pathology, 1993, 142, 1392–1400. [PMC free article] [PubMed] [Google Scholar]
- 67.DePaola N, Gimbrone MA, Davies PF and Dewey CF, Arteriosclerosis and thrombosis : a journal of vascular biology, 1992, 12, 1254–1257. [DOI] [PubMed] [Google Scholar]
- 68.Bao X, Lu C and Frangos JA, Arteriosclerosis, thrombosis, and vascular biology, 1999, 19, 996–1003. [DOI] [PubMed] [Google Scholar]
- 69.Liu SQ, Tieche C, Tang D and Alkema P, American Journal of Physiology-Heart and Circulatory Physiology, 2003, 285, H1081–H1090. [DOI] [PubMed] [Google Scholar]
- 70.Ho RX-Y, Tahboub R, Amraei R, Meyer RD, Varongchayakul N, Grinstaff MW and Rahimi N, The Journal of biological chemistry, 2019, DOI: 10.1074/jbc.RA119.008548,jbc.RA119.008548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Tone EIV, 2019.
- 72.Mack JJ, Mosqueiro TS, Archer BJ, Jones WM, Sunshine H, Faas GC, Briot A, Aragón RL, Su T, Romay MC, McDonald AI, Kuo C-H, Lizama CO, Lane TF, Zovein AC, Fang Y, Tarling EJ, de Aguiar Vallim TQ, Navab M, Fogelman AM, Bouchard LS and Iruela-Arispe ML, Nature Communications, 2017, 8, 1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Sterpetti AV, Cucina A, D’Angelo LS, Cardillo B and Cavallaro A, Surgery, 1993, 113, 691–699. [PubMed] [Google Scholar]
- 74.Kraiss LW, Kirkman TR, Kohler TR, Zierler B and Clowes AW, Arteriosclerosis and Thrombosis: A Journal of Vascular Biology, 1991, 11, 1844–1852. [DOI] [PubMed] [Google Scholar]
- 75.Sterpetti AV, Cucina A, Santoro L, Cardillo B and Cavallaro A, European Journal of Vascular Surgery, 1992, 6, 16–20. [DOI] [PubMed] [Google Scholar]
- 76.Meyerson SL, Skelly CL, Curi MA, Shakur UM, Vosicky JE, Glagov S, Christen T, Gabbiani G and Schwartz LB, Journal of Vascular Surgery, 2001, 34, 90–97. [DOI] [PubMed] [Google Scholar]
- 77.Haga M, Yamashita A, Paszkowiak J, Sumpio BE and Dardik A, Journal of Vascular Surgery, 2003, 37, 1277–1284. [DOI] [PubMed] [Google Scholar]
- 78.Rana A, Westein E, Niego B. e. and Hagemeyer CE, Frontiers in cardiovascular medicine, 2019, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Zwolak RM, Adams MC and Clowes AW, Journal of vascular surgery, 1987, 5, 126–136. [PubMed] [Google Scholar]
- 80.Ballyk PD, Walsh C, Butany J and Ojha M, Journal of biomechanics, 1998, 31, 229–237. [DOI] [PubMed] [Google Scholar]
- 81.Southgate KM, Mehta D, Izzat MB, Newby AC and Angelini GD, Arteriosclerosis, Thrombosis, and Vascular Biology, 1999, 19, 1640–1649. [DOI] [PubMed] [Google Scholar]
- 82.MAYR M, HU Y, HAINAUT P and XU Q, The FASEB Journal, 2002, 16, 1423–1425. [DOI] [PubMed] [Google Scholar]
- 83.Haga JH, Li Y-SJ and Chien S, Journal of Biomechanics, 2007, 40, 947–960. [DOI] [PubMed] [Google Scholar]
- 84.Wilson E, Vives F, Collins T and Ives HE, Hypertension, 1998, 31, 170–175. [DOI] [PubMed] [Google Scholar]
- 85.Predel HG, Yang Z, von Segesser L, Turina M, Bühler FR and Lüscher TF, Lancet (London, England), 1992, 340, 878–879. [DOI] [PubMed] [Google Scholar]
- 86.Paszkowiak JJ and Dardik A, Vascular and Endovascular Surgery, 2003, 37, 47–57. [DOI] [PubMed] [Google Scholar]
- 87.Viecelli AK, Mori TA, Roy-Chaudhury P, Polkinghorne KR, Hawley CM, Johnson DW, Pascoe EM and Irish AB, Seminars in Dialysis, 2018, 31, 244–257. [DOI] [PubMed] [Google Scholar]
- 88.Shiu Y-T, Rotmans JI, Geelhoed WJ, Pike DB and Lee T, American Journal of Physiology-Renal Physiology, 2019, 316, F794–F806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Purcell ST, Rao S and Bush RL, Journal, 2017, DOI: 10.1007/978-3-319-40061-7_28, 245–248. [DOI] [Google Scholar]
- 90.Pannier BM, Avolio AP, Hoeks A, Mancia G and Takazawa K, American journal of hypertension, 2002, 15, 743–753. [DOI] [PubMed] [Google Scholar]
- 91.Schwenger V, Keller T, Hofmann N, Hoffmann O, Sommerer C, Nahm AM, Morath C, Zeier M and Krumme B, American Journal of Transplantation, 2006, 6, 2721–2724. [DOI] [PubMed] [Google Scholar]
- 92.R. K. V., N. P.M, Joseph J and Sivaprakasam M, Journal, 2017, DOI: 10.1109/EMBC.2017.8036812, 262–265. [DOI] [PubMed] [Google Scholar]
- 93.Joseph J, Radhakrishnan R, Kusmakar S, Thrivikraman AS and Sivaprakasam M, IEEE journal of translational engineering in health and medicine, 2015, 3, 1900213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Joseph J, Thrivikraman AS, Radhakrishnan R and Sivaprakasam M, Journal, 2015, DOI: 10.1109/EMBC.2015.7319210, 3755–3758. [DOI] [PubMed] [Google Scholar]
- 95.Joseph J, P M N, Shah MI and Sivaprakasam M, PLOS ONE, 2018, 13, e0202480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Joseph J, Shah MI and Sivaprakasam M, Journal, 2016, DOI: 10.1109/MeMeA.2016.7533787, 1–6. [DOI] [Google Scholar]
- 97.Sahani AK, Joseph J and Sivaprakasam M, Physiological Measurement, 2014, 35, 1299–1317. [DOI] [PubMed] [Google Scholar]
- 98.Joseph J, Nabeel P, Shah MI, Bhaskar A, Ganesh C, Seshadri S and Sivaprakasam M, Biomedical Physics & Engineering Express, 2020, 6, 025013. [DOI] [PubMed] [Google Scholar]
- 99.Haller MJ, Samyn M, Nichols WW, Brusko T, Wasserfall C, Schwartz RF, Atkinson M, Shuster JJ, Pierce GL and Silverstein JH, Diabetes Care, 2004, 27, 2911–2917. [DOI] [PubMed] [Google Scholar]
- 100.London GM and Pannier B, Nephrology Dialysis Transplantation, 2010, 25, 3815–3823. [DOI] [PubMed] [Google Scholar]
- 101.Wilkinson IB, MacCallum H, Flint L, Cockcroft JR, Newby DE and Webb DJ, The Journal of physiology, 2000, 525, 263–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Močnik M, Nikolić S and Varda NM, The Indian Journal of Pediatrics, 2016, 83, 510–516. [DOI] [PubMed] [Google Scholar]
- 103.Laurent S, Cockcroft J, Van Bortel L, Boutouyrie P, Giannattasio C, Hayoz D, Pannier B, Vlachopoulos C, Wilkinson I, Struijker-Boudier H and E. N. f. N.-i. I. o. L. Arteries, European Heart Journal, 2006, 27, 2588–2605. [DOI] [PubMed] [Google Scholar]
- 104.Joseph J, Nabeel P, Shah MI and Sivaprakasam M, PloS one, 2018, 13, e0202480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Nabeel P, Joseph J and Sivaprakasam M, 2015.
- 106.Vappou J, Luo J and Konofagou EE, American journal of hypertension, 2010, 23, 393–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Vardoulis O, Papaioannou TG and Stergiopulos N, Annals of biomedical engineering, 2012, 40, 2619–2626. [DOI] [PubMed] [Google Scholar]
- 108.Liberson AS, Lillie JS, Day SW and Borkholder DA, Journal of biomechanics, 2016, 49, 3460–3466. [DOI] [PubMed] [Google Scholar]
- 109.Qiang Y, Ruijun G, Zhen C, Zhian L, Changyan L, Xiaohui Y, Shu L, Jie L, Yuanfeng M and Ruobing Z, Journal of Ultrasound in Medicine, 2014, 33, 1949–1956. [DOI] [PubMed] [Google Scholar]
- 110.McGarry M, Nauleau P, Apostolakis I and Konofagou E, Journal of biomechanics, 2017, 64, 136–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Vanden Eynden F, Bové T, Chirade M-L, Van Nooten G and Segers P, Pulmonary circulation, 2018, 8, 2045894018776882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Haluska BA, Jeffriess L, Downey M, Carlier SG and Marwick TH, Journal of the American Society of Echocardiography, 2008, 21, 123–128. [DOI] [PubMed] [Google Scholar]
- 113.Haluska BA, Jeffries L, Carlier S and Marwick TH, Atherosclerosis, 2010, 209, 474–480. [DOI] [PubMed] [Google Scholar]
- 114.Talts J, Raamat R and Jagomägi K, Computers in biology and medicine, 2009, 39, 707–712. [DOI] [PubMed] [Google Scholar]
- 115.Tai N, Salacinski H, Edwards A, Hamilton G and Seifalian A, British Journal of Surgery, 2000, 87, 1516–1524. [DOI] [PubMed] [Google Scholar]
- 116.Chaouat M, Le Visage C, Baille WE, Escoubet B, Chaubet F, Mateescu MA and Letourneur D, Advanced Functional Materials, 2008, 18, 2855–2861. [Google Scholar]
- 117.Knutsen RH, Beeman SC, Broekelmann TJ, Liu D, Tsang KM, Kovacs A, Ye L, Danback JR, Watson A and Wardlaw A, American Journal of Physiology-Heart and Circulatory Physiology, 2018, 315, H18–H32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Rivera-Rivera LA, Cody KA, Eisenmenger L, Cary P, Rowley HA, Carlsson CM, Johnson SC and Johnson KM, Journal of Cerebral Blood Flow & Metabolism, 2020, 0271678X20910302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Pattinson K, Wynne-Jones G and Imray CH, Continuing Education in Anaesthesia Critical Care & Pain, 2005, 5, 130–133. [Google Scholar]
- 120.Bude RO and Rubin JM, Radiology, 1999, 211, 411–417. [DOI] [PubMed] [Google Scholar]
- 121.Lee W-J, Jung K-H, Ryu YJ, Lee K-J, Kim J-M, Lee S-T, Chu K, Kim M, Lee SK and Roh J-K, Radiology, 2017, 284, 824–833. [DOI] [PubMed] [Google Scholar]
- 122.Calabia J, Torguet P, Garcia M, Garcia I, Martin N, Guasch B, Faur D and Vallés M, Cardiovascular Ultrasound, 2011, 9, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Weber T, Ammer M, Rammer M, Adji A, OʼRourke MF, Wassertheurer S, Rosenkranz S and Eber B, Journal of Hypertension, 2009, 27, 1624–1630. [DOI] [PubMed] [Google Scholar]
- 124.He F, Hua L and Gao L.-j., Applied Bionics and Biomechanics, 2015, 2015, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Steinman DA, Vorp DA and Ethier CR, Journal of Vascular Surgery, 2003, 37, 1118–1128. [DOI] [PubMed] [Google Scholar]
- 126.Szafron JM, Ramachandra AB, Breuer CK, Marsden AL and Humphrey JD, Tissue Engineering Part C: Methods, 2019, 25, 561–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Szafron J, Khosravi R, Reinhardt J, Best C, Bersi M, Yi T, Breuer C and Humphrey J, Annals of biomedical engineering, 2018, 46, 1938–1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Wise SG, Byrom MJ, Waterhouse A, Bannon PG, Ng MKC and Weiss AS, Acta Biomaterialia, 2011, 7, 295–303. [DOI] [PubMed] [Google Scholar]
- 129.Yao Y, Zaw AM, Anderson DE, Hinds MT and Yim EK, Biomaterials, 2020, 120011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Anderson DE, Truong KP, Hagen MW, Yim EK and Hinds MT, Acta biomaterialia, 2019, 86, 291–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Anderson DE, Pohan G, Raman J, Konecny F, Yim EK and Hinds MT, Tissue Engineering Part C: Methods, 2018, 24, 457–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Cheung DK, Chiu HC, Zhang L, Hu C, Shung KK and Alfred C, 2010.
- 133.Gong X, Liu H, Ding X, Liu M, Li X, Zheng L, Jia X, Zhou G, Zou Y, Li J, Huang X and Fan Y, Biomaterials, 2014, 35, 4782–4791. [DOI] [PubMed] [Google Scholar]
- 134.Kim Y, Chandran K, Bower T and Corson J, Annals of biomedical engineering, 1993, 21, 311–320. [DOI] [PubMed] [Google Scholar]
- 135.Banerjee MK, Ganguly R and Datta A, ISRN Biomathematics, 2012, 2012. [Google Scholar]
- 136.Gayathri K and Shailendhra K, Applied Mathematics and Mechanics, 2014, 35, 575–590. [Google Scholar]
- 137.Ramnarine KV, Nassiri DK, Hoskins PR and Lubbers J, Ultrasound in medicine & biology, 1998, 24, 451–459. [DOI] [PubMed] [Google Scholar]
- 138.Samavat H and Evans J, Journal of Medical Physics/Association of Medical Physicists of India, 2006, 31, 275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Ramnarine KV, Hoskins PR, Routh HF and Davidson F, Ultrasound in medicine & biology, 1999, 25, 105–110. [DOI] [PubMed] [Google Scholar]
- 140.Brindise MC, Chiastra C, Burzotta F, Migliavacca F and Vlachos PP, Annals of biomedical engineering, 2017, 45, 542–553. [DOI] [PubMed] [Google Scholar]
- 141.Geoghegan PH, Jermy MC and Nobes DS, Journal of Mechanics in Medicine and Biology, 2017, 17, 1750041. [Google Scholar]
- 142.Rathod M, Ahn J, Jeon N and Lee J, Lab on a Chip, 2017, 17, 2508–2516. [DOI] [PubMed] [Google Scholar]
- 143.Montini-Ballarin F, Calvo D, Caracciolo PC, Rojo F, Frontini PM, Abraham GA and Guinea GV, Journal of the mechanical behavior of biomedical materials, 2016, 60, 220–233. [DOI] [PubMed] [Google Scholar]
- 144.Rizwan M, Yao Y, Gorbet M, Tse J, Anderson D, Hinds MT and Yim EK, ACS Applied Bio Materials, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Polanczyk A, Klinger M, Nanobachvili J, Huk I and Neumayer C, Applied Sciences, 2018, 8, 1017. [Google Scholar]
- 146.Song G, Bai X, Zhang Z, Wang X, Long L, Yongjie M, Ren J and Jiao L, Chinese Journal of Cerebrovascular Diseases, 2017, 14, 193–196. [Google Scholar]
- 147.Byrom MJ, Bannon PG, White GH and Ng MK, Journal of vascular surgery, 2010, 52, 176–195. [DOI] [PubMed] [Google Scholar]
- 148.Tseng YC, Roan JN, Ho YC, Lin CC and Yeh ML, Journal of Materials Science: Materials in Medicine, 2017, 28, 166. [DOI] [PubMed] [Google Scholar]
- 149.Sharath U, Shwetha C, Anand K and Asokan S, Journal of Human Hypertension, 2014, 28, 736–742. [DOI] [PubMed] [Google Scholar]
- 150.Lehmann ED, Hopkins KD and Gosling RG, Ultrasound in medicine & biology, 1993, 19, 683–710. [DOI] [PubMed] [Google Scholar]
- 151.Chirinos JA, Journal of Cardiovascular Translational Research, 2012, 5, 243–255. [DOI] [PubMed] [Google Scholar]
- 152.Standard AN, 2010, 2008.
- 153.Lovett M, Eng G, Kluge J, Cannizzaro C, Vunjak-Novakovic G and Kaplan DL, Organogenesis, 2010, 6, 217–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Colombo A, Guha S, Mackle JN, Cahill PA and Lally C, Biomechanics and modeling in mechanobiology, 2013, 12, 671–683. [DOI] [PubMed] [Google Scholar]
- 155.Lehoux S. p. and Tedgui A, Hypertension, 1998, 32, 338–345. [DOI] [PubMed] [Google Scholar]
- 156.Potter CM, Schobesberger S, Lundberg MH, Weinberg PD, Mitchell JA and Gorelik J, PloS one, 2012, 7, e31228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Lemson M, Tordoir J, Daemen M and Kitslaar P, European Journal of Vascular and Endovascular Surgery, 2000, 19, 336–350. [DOI] [PubMed] [Google Scholar]
- 158.Fillinger MF, O’Connor SE, Wagner RJ and Cronenwett JL, Journal of vascular surgery, 1993, 17, 1058–1068. [PubMed] [Google Scholar]
- 159.Golledge J, European journal of vascular and endovascular surgery, 1997, 14, 333–343. [DOI] [PubMed] [Google Scholar]
- 160.Tsaousi A, Williams H, Lyon CA, Taylor V, Swain A, Johnson JL and George SJ, Circulation research, 2011, 108, 427–436. [DOI] [PubMed] [Google Scholar]
- 161.Soletti L, Hong Y, Guan J, Stankus JJ, El-Kurdi MS, Wagner WR and Vorp DA, Acta Biomaterialia, 2010, 6, 110–122. [DOI] [PMC free article] [PubMed] [Google Scholar]


