An Artificial Intelligence Approach to Assess Spatial Patterns of Retinal Nerve Fiber Layer Thickness Maps in Glaucoma

Abstract

Purpose

The purpose of this study was to classify the spatial patterns of retinal nerve fiber layer thickness (RNFLT) and assess their associations with visual field (VF) loss in glaucoma.

Methods

We used paired reliable 24-2 VFs and optical coherence tomography scans of 691 eyes from 691 patients. The RNFLT maps were used to determine the RNFLT patterns (RPs) by non-negative matrix factorization (NMF). The RPs were correlated with mean deviation (MD), spherical equivalent (SE), and major blood vessel locations. The RPs were further used to predict the 52 total deviation (TD) values by linear regression compared with models using 24 15-degree sectors. Last, we associated the RPs with average TDs of the central upper two locations (C2-TD). Stepwise regression was applied to remove redundant features.

Results

NMF highlighted 16 distinct RPs. Twelve RPs had arcuate-like informative zones (iZones): six with superior iZones, five with inferior iZones, and one RP with a bi-hemifield iZone, and four with non-arcuate-like temporal or nasal iZones. Twelve, nine, nine, and nine RPs were significantly (P < 0.05) correlated to MD, SE, and superior and inferior artery locations, respectively. Using RPs significantly (P < 0.05) improved the prediction of 52 TDs compared with using 24 15-degree sectors. Using RPs significantly (P < 0.001) improved the C2-TD prediction related to thinning in the inferior vulnerability zone compared with using the 24 sectoral RNFLTs.

Conclusions

Using RPs improved the VF prediction compared with using sectoral RNFLTs.

Translational Relevance

The RPs characterizing both pathological and anatomical variations can potentially assist clinicians better assess RNFLT loss.

Introduction

The measurement of retinal nerve fiber layer (RNFL) thickness (RNFLT) by optical coherence tomography (OCT) is widely used to diagnose and monitor glaucoma in clinical practice. Numerous studies indicate that RNFLT measurements facilitate glaucoma diagnosis, correlate with visual field (VF) loss, and have utility in detecting glaucoma progression.^1–9

In many prior studies, RNFLT measurements from the circle scan of 3.46 mm diameter were used to study glaucoma due to its simplicity and the reported optimal reproducibility of these measuresments.^10,11 However, the 6 mm by 6 mm RNFLT map contains more complete information regarding peripapillary RNFLT integrity, and has shown great potential to improve glaucoma detection accuracy as well as inform structure-function relationships.^12–15 To quantitatively assess the high dimensional RNFLT map data (e.g. 225 by 225 pixels for Cirrus OCT), various artificial intelligence (AI) techniques^14–17 have been developed.¹² For example, principal component analysis (PCA), a classical unsupervised AI method for data dimensionality reduction,^18,19 has been applied to determine 10 RNFLT patterns from the RNFLT maps. These PCA RNFLT patterns improved glaucoma detection and progression prediction compared with using circumpapillary RNFLT, with increase in the area under the receiver operating curve from 0.55 to 0.74 for progression detection.¹⁵ However, although the PCA technique reduced the data dimensionality of the RNFLT map, the PCA RNFLT patterns were not intuitive for clinical interpretation because they contained both positive and negative regions, whereas RNLFT maps contain solely positive data. More recently, a deep learning model has been developed to use the RNFLT maps to predict VF sensitivities and the presence of VF defects with high accuracy.¹⁶ Despite the high accuracy achieved, the “black box” nature of the model detracts from its clinical utility.

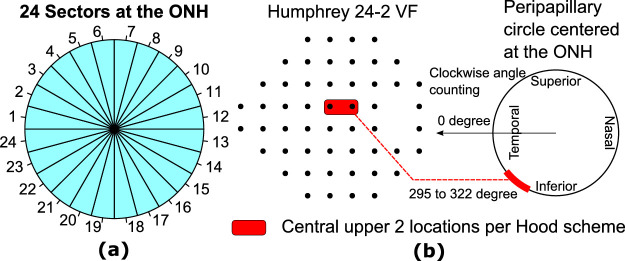
In this work, we propose to reduce the high dimensional RNFLT map data into representative RNFLT patterns determined by an unsupervised AI method termed non-negative matrix factorization (NMF). The NMF method is specialized to learn sparse and part-based non-negative representation of non-negative data,^20,21 theoretically making them more clinically useful to assess the non-negative RNFLT map data. First, the NMF was applied to determine the RNFLT patterns, and 10-fold cross-validation was used to determine the optimal number of patterns. Second, we associated the RNFLT patterns with mean deviation (MD), spherical equivalent, and major blood vessel locations on the circumpapillary circle of 3.46 mm diameter. Third, the RNFLT patterns were used to predict the total deviation (TD) values at each of the 52 VF locations by linear regression, which were compared with the models using 24 sectors of 15 degrees (Fig. 1a) to illustrate the efficacy of using NMF for data dimensionality reduction. Last, the RNFLT patterns that correspond to superior paracentral VF loss at the central upper two locations (the most common type of glaucomatous central vision loss) popularized by Hood and coworkers^22,23 were detailed to demonstrate the potential clinical utility of our NMF pattern models.

Figure 1.

(a) Twenty-four angular sectors of 15 degrees centered at the optic nerve head (ONH), and (b) a schematic of the central upper 2 locations on the 24-2 visual field (VF) per the Hood scheme.^22,23

Methods

The institutional review board (IRB) of Massachusetts Eye and Ear (MEE) approved this retrospective study. Because of the retrospective nature of the study, the IRB waived the need for informed consent of patients. The study complies with the Declaration of Helsinki as well as all federal and state laws.

Participants and Data Preprocessing

There were 2161 eyes from 2161 patients visiting the MEE glaucoma service between 2011 and 2014 meeting the following data selection criteria that were initially included: (1) VF reliability criteria: fixation loss ≤ 33%, false negative rates ≤ 20%, and false positive rates ≤ 20%; (2) OCT reliability criteria: Cirrus optic nerve head (ONH) OCT scan (Optic Disc Cube protocol with A-scan resolution 200 by 200 within an area of 6 mm by 6 mm) with signal strength ≥ 6; and (3) test dates of OCT scans within 1 year from the closest VF measurements. If more than one pair of OCT and VF measurements per eye met the criteria, the most recent measurement was selected. If both eyes of a patient met the selection criteria, only one eye was included randomly to avoid potential bias of inter-eye correlation.

Cirrus ONH OCT scans with an area of 6 mm by 6 mm were used for this analysis. The ONH center was determined by the Cirrus machine as the centroid of Bruch's membrane opening. OCT scans with ONH centers that deviated more than 0.3 mm in horizontal or vertical direction from the fundus image center were excluded. Thereafter, the RNFLT maps and the corresponding fundus images of each eye were centered based on the ONH center. To ensure the availability of data over the complete area for each centered scan, 0.3 mm of the edges were removed, resulting in a 5.4 mm by 5.4 mm scan region for each image. All fundus images were manually examined by a trained observer to exclude OCT scans with missing RNFLT measurements (black pixels on RNFLT maps within the region of 5.4 × 5.4 mm) and motion artifacts (defined as vessel shifts of more than one vessel diameter or a visible shift within ONH on fundus image). The region with a radius of 1.25 mm were excluded from data analyses to ensure RNFLT values are available for all eyes regardless of disc size as well as to avoid determining patterns only reflecting variation in disc size.

The major artery locations on four concentric circles with diameters of 2.46, 3.46, 4.46, and 5.40 mm were tracked by a trained observer on each fundus image with a custom software we developed. We used the coordinate system of the Cirrus device, which defines the angular position of zero as the horizontal line toward the temporal direction and calculates angles clockwise and counterclockwise for the right and left eyes, respectively, as described in our prior publications.^24–26

Electronic medical records were used to ascertain demographic and ophthalmic features for all patients, including glaucoma diagnostics and spherical equivalent.

Statistical Analyses

An unsupervised AI method, NMF, was applied to determine the RNFLT patterns. Compared with axis-learning (e.g. PCA and independent component analysis),^15,18,27 center-learning (e.g. k-means and Gaussian mixture modeling),^28,29 and corner learning (i.e. archetypal analysis)^30,31 methods, the NMF is a boundary learning method and specialized to learn non-negative focal patterns that remove redundant information for clearer clinical interpretation. The optimal number of patterns was determined by 10-fold cross validation based on minimization of mean squared error.³² The data were randomly partitioned into 10 subsets. Each of the 10 subsets was used as a test subset once with the remaining 9 subsets serving as a training set. The RNFLT map reconstruction errors were calculated on the test subsets for the number of patterns (k) from 2 to 20. The RNFLT map reconstruction errors were calculated as the differences between the original RNFLT maps and the reconstructed RNFLT maps. The reconstructed RNFLT maps were calculated as the sum of the RNFLT patterns multiplied by their pattern decomposition coefficients. The optimal pattern number k_o was determined by the following criteria: the minimum k with reconstruction errors that are not statistically different (i.e. Bayes factor < 3.0)³³ from the k that produced the smallest average reconstruction error.

The properties of the RNFLT patterns were subsequently examined by correlating with MD, spherical equivalent, and major retinal artery locations on the standard scan circle of 3.46 mm diameter. To demonstrate the clinical utility of using NMF for data dimensionality reduction, multivariable linear regression was applied to predict the 52 VF TD values from the RNFLT patterns. These models were compared with those using a naive dimensionality reduction scheme: 24 sectors of 15 degrees as shown in Figure 1a.^34,35 The zero angular position was defined as the horizontal line toward the temporal direction. The angle was counted clockwise for the left eyes and counterclockwise for the right eyes. Furthermore, we used the RNFLT patterns with multivariable linear regression to predict superior paracentral VF loss at the central upper two locations (the most common type of glaucomatous central vision loss) according to the Hood schemes (Fig. 1b) to illustrate the potential clinical utility of our NMF pattern model compared with the model using 24 sectoral RNFLTs. The average TD value for the central upper two locations was calculated to measure the degree of superior paracentral VF loss. Stepwise regression with Bayesian information criterion (BIC) was used to select the optimal features to predict VF sensitivities and paracentral VF loss for fair comparison purpose. The performance of the linear models was measured by adjusted multiple correlation (adjusted r_m), which was the square root of R-squared that has been adjusted for the number of predictors in the models to avoid overfitting. We applied the bootstrapping procedure^36,37 to obtain the distributions of the adjusted r_m for the optimal models using RNFLT patterns and the optimal models using 24 sectors of 15 degrees. The t-test was used to compare whether the RNFLT patterns were more significantly associated with VF loss compared with the average RNFLTs of the 24 15-degree sectors.

We also compared the RNFLT pattern model for predicting 52 TD values with the models using the 4 sectors (temporal, superior, nasal, and inferior sectors) and 6 sectors (temporal, temporal-superior, nasal-superior, nasal, nasal-inferior, and temporal-inferior sectors) used in OCT software as well the model using PCA patterns. For predicting the superior paracentral loss, we also compared the RNFLT pattern model with the model using the average RNFLTs in the macular vulnerability zone (295 to 322 degrees) around the ONH proposed by Hood and coworkers.^22,23

Results

Patient Characteristics

Of the initially selected 2161 eyes with OCT signal strength ≥ 6, there were 1082 eyes that were excluded due to motion artifacts. In addition, 221 eyes were excluded due to decentered OCT scans and 167 eyes were excluded due to missing RNFLT measurements, leaving 691 eyes from 691 patients for data analyses. The Table summarizes the demographic and ophthalmic data for patients included in the study. Of 691 patients (age: 60.9 ± 14.6 years; MD: -3.7 ± 5.1 dB), 569 patients had spherical equivalent (SE: 1.0 ± 2.8 diopters) information in the electronic medical records.

Table.

Demographic and Ocular Characteristics of Patients Included in this Study (n = 691 Patients)

Race	Glaucoma Diagnosis	Patient Statistics
European: 74.0%	Open angle glaucoma: 45.7%	Female: 55.3%
African: 6.6%	Angle closure glaucoma: 2.2%	Age: 60.9 ± 14.6 years
Asian: 10.3%	Mixed mechanism glaucoma: 2.5%	MD: -3.7 ± 5.1 dB
Hispanic: 4.9%	Glaucoma suspect: 42.1%	SE: 1.0 ± 2.8 diopters
Mixed/other: 4.2%	Normal: 7.5%

The RNFLT Patterns, Eye Anatomy, and Visual Field Loss

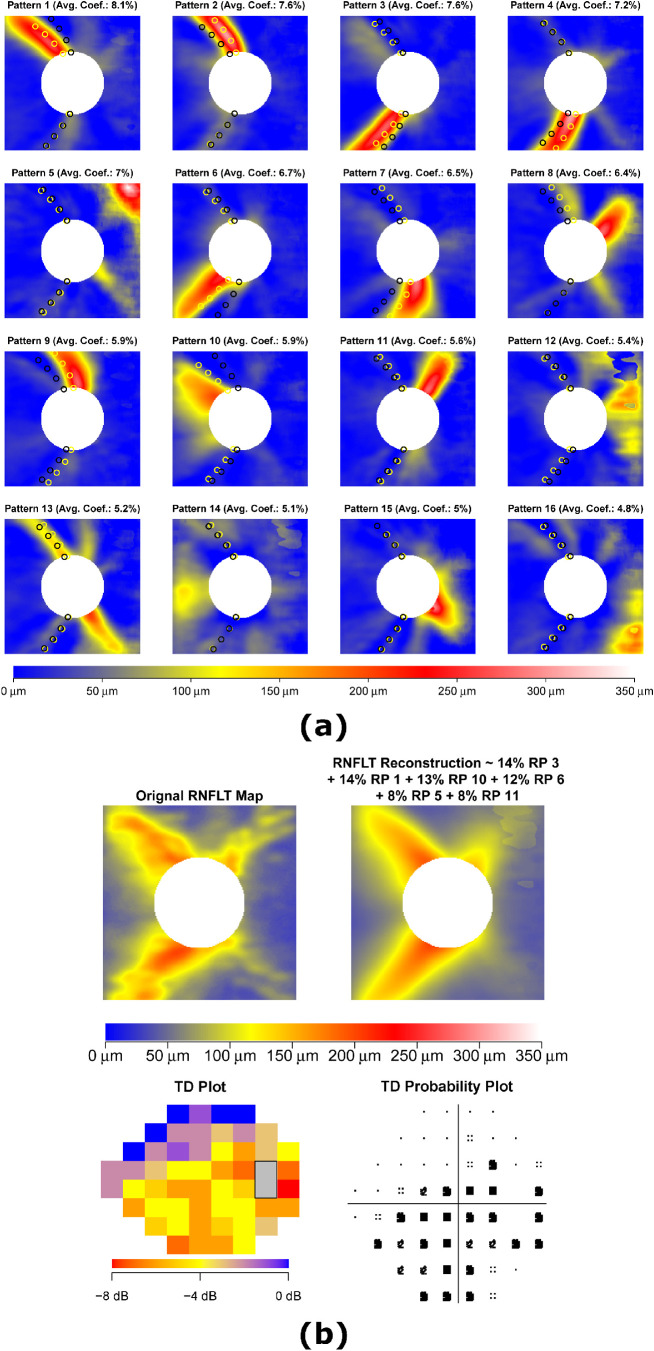
We determined 16 RNFLT patterns (RPs) by the NMF method (Fig. 2a). The yellow and red regions indicate where the RNFL was thicker and large variations existed among different eyes, and were therefore considered to be the relatively informative zones (iZones) on the RNFLT map. By contrast, the blue regions represent where the RNFL was thinner and minimal variations existed among different eyes, and were therefore considered to be the relatively non-informative zones (non-iZones). There were 12 RPs with arcuate-like iZones: 6 RPs with superior iZones (RPs 1, 2, 8, 9, 10, and 11), 5 RPs with inferior iZones (RPs 3, 4, 6, 7, and 15), and 1 RP with a bi-hemifield iZone (RP 13), and 4 RPs with non-arcuate-like iZones: 1 RP with temporal iZone (RP 14) and 3 RPs with nasal iZones (RPs 5, 12, and 16). The RPs were ordered by their respective average decomposition weights over all 691 OCT scans from 691 eyes. In general, a higher RP coefficient implied thicker RNFL in the iZone and vice versa. Yellow/black circles denote average major artery locations on four concentric circles with diameters of 2.46, 3.46, 4.46, and 5.40 mm for eyes with the highest/lowest 10% RP coefficients. Based on visual observation, the average major artery locations for eyes with the highest 10% RP coefficients were closer to the iZone centers of multiple RPs (e.g. RPs 1, 2, 3, 4, 6, 7, 9, and 10) compared with eyes with the lowest 10% RP coefficients, which suggested these RPs were anatomically related to blood vessel locations. Figure 2b shows an example of the RNFLT map decomposition into the RNFLT patterns with at least 5% weights along with the corresponding VF of TD and TD probability plots. The pattern decomposition coefficients of the RNFLT map sum to 100%.

Figure 2.

(a) The 16 RNFLT patterns determined by non-negative matrix factorization (NMF), and (b) an example of RNFLT map decomposition into its respective RNFLT patterns with at least 5% weights alongside the corresponding visual field (VF) of total deviation (TD) and TD probability plots. The yellow and red regions indicate where the RNFL was thicker and large variations existed among different eyes, and were therefore considered relatively informative zones (iZones) on the RNFLT map. In contrast, the blue regions represent where the RNFL was thinner and minimal variations existed among different eyes, and were therefore considered relatively non-informative zones (non-iZone). For any RNFLT map, the decomposition coefficients sum to 100%. Yellow/black circles in a: average major artery locations at 4 circumpapillary radii for eyes with the highest/lowest 10% RP coefficients. RNFLT = retinal nerve fiber layer thickness; RP = retinal nerve fiber layer thickness pattern.

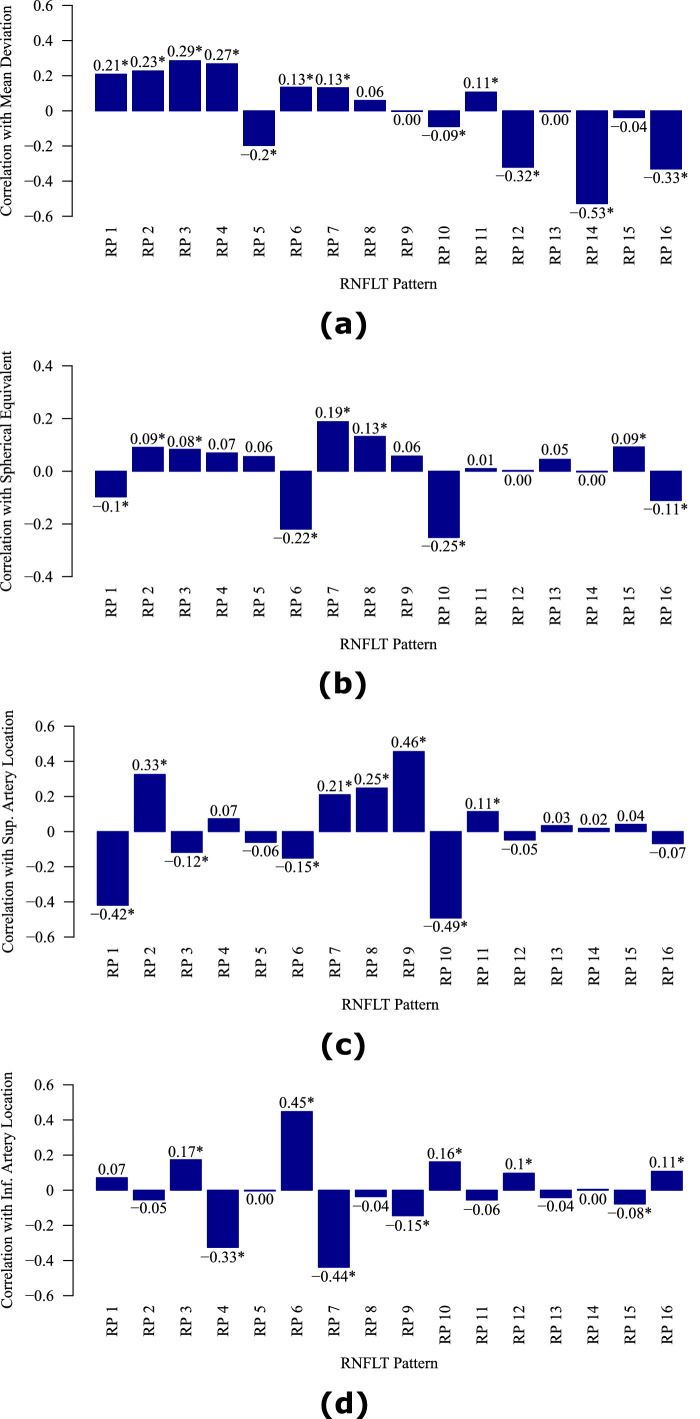
Figure 3 shows the correlations between the decomposition coefficients of the RNFLT patterns and (a) MD, (b) spherical equivalent, (c) superior artery location on the circumpapillary circle of 3.46 mm diameter, and (d) inferior artery location on the circumpapillary circle of 3.46 mm diameter. Various RPs were significantly (P < 0.05) correlated with MD (12 patterns with Pearson correlations ranging from -0.53 to 0.29 [absolute range: 0.09 to 0.53]; the 3 most correlated RPs: RPs 12, 14, and 16), spherical equivalent (9 patterns with Pearson correlations ranging from -0.25 to 0.19 [absolute range: 0.08 to 0.25]; the 3 most correlated RPs: RPs 6, 7, and 10), superior retinal artery location (9 patterns with Pearson correlations ranging from -0.49 to 0.46 [absolute range: 0.11 to 0.49]; the 3 most correlated RPs: RPs 1, 9, and 10), and inferior retinal artery location (9 patterns with Pearson correlations ranging from -0.44 to 0.45 [absolute range: 0.08 to 0.45]; the 3 most correlated RPs: RPs 4, 6, and 7). The RPs encoded not only the effect of pathological RNFLT thinning (evidenced by their correlations with MD) but also the anatomic RNFLT variation (evidenced by their correlations with spherical equivalent and major blood vessel locations) related to myopia and blood vessel locations.

Figure 3.

The correlations between the decomposition coefficients of RNFLT patterns and the (a) mean deviation, (b) spherical equivalent, (c) superior artery location on the circle of 3.46 mm diameter, and (d) inferior artery location on the circle of 3.46 mm diameter. RP = retinal nerve fiber layer thickness pattern. *Denotes significant (P < 0.05) correlations.

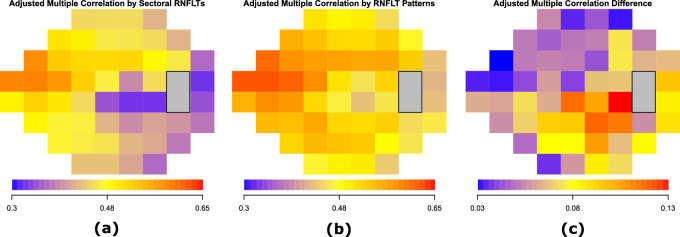
Figure 4 shows the adjusted multiple correlations r_m of the optimal models to predict TD values at each of the 52 VF locations, using (a) the average RNFLTs of the 24 sectors of 15 degrees, and (b) the RNFLT patterns. The adjusted r_m for the optimal model using the average RNFLTs of the 24 sectors ranged from 0.32 to 0.59 with a median of 0.45. The adjusted r_m for the optimal model using the RNFLT patterns ranged from 0.42 to 0.62 with a median of 0.51. For both models, the superior nasal VF region was more associated with the RNFLT measurements, whereas the inferior paracentral and temporal regions were less associated with the RNFLT measurements. Figure 4c shows the improvement in adjusted r_m by the optimal models using RNFLT patterns compared with the optimal models using the 24 sectoral average RNFLTs. The improvement in adjusted r_m was statistically significant (P < 0.05, t-test with bootstrapping) at all 52 locations, ranging from 0.03 and 0.13 with a median of 0.06. The improvement was more substantial in the inferior paracentral and temporal VF regions, and less substantial in the superior nasal VF regions. Furthermore, using the RNFLT patterns (adjusted r_m: 0.63) significantly (P <0.001, t-test with bootstrapping) improved the prediction of MD compared with using the average RNFLTs of the 24 sectors (adjusted r_m: 0.55). In predicting 52 TD values, the RNFLT pattern model largely outperformed the models using the 4 and 6 sectors used in OCT software as well as the models using 16 PCA patterns (encoding at least 80% data variance) and 14 PCA patterns (each pattern encoded as least 1% data variance) in terms of r_m and BIC comparisons. See more details in Supplementary Figures.

Figure 4.

The adjusted multiple correlations r_m of the optimal models to predict the total deviation value at each of the 52 VF locations using (a) the average RNFLTs of the 24 sectors of 15 degrees, and (b) the RNFLT patterns. (c) The improvement in r_m by the optimal models using RNFLT patterns compared with the optimal models using the 24 sectoral average RNFLTs. The improvement at all 52 locations was statistically significant (P < 0.05) by t-test with bootstrapping.

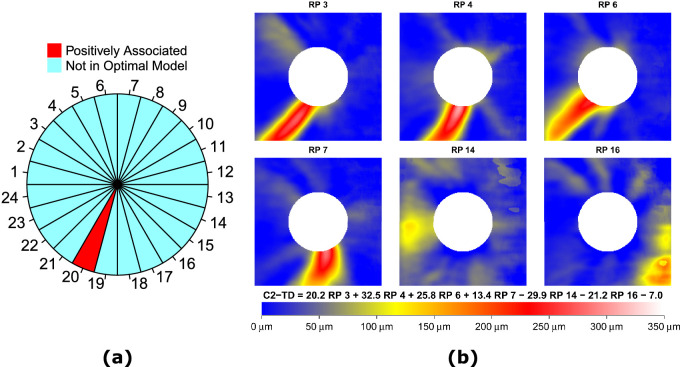
Figure 5a shows the specific sector in the optimal model that was associated with the average TD value at the central upper 2 locations (C2-TD) according to the Hood scheme (see Fig. 1b).^22,23 Among the 24 sectors, only the average RNFLT of sector 20 (285 to 300 degrees) remained in the optimal model and was positively associated with C2-TD, whereas RNFLT in the macular vulnerability zone around ONH from 295 to 322 degrees was expected to best predict C2-TD per the Hood scheme.^22,23 Figure 5b shows the 6 RNFLT patterns in the optimal model that were associated with C2-TD. Lower coefficients for four RPs with inferior iZones (RPs 3, 4, 6, and 7) were associated with worse C2-TD, implying that thinning in the inferior iZones was associated with worse C2-TD. On the other hand, higher coefficients for RPs 14 (an RP with temporal iZone) and 16 (an RP with inferior nasal iZone) were also correlated with worse C2-TD, suggesting that unusual thickening in the temporal and inferior nasal iZones and lack of the typical superior and inferior RNFLT bundles were associated with worse C2-TD. The adjusted multiple correlation r_m to predict C2-TD for the optimal model using the 6 RNFLT patterns was 0.52, which was significantly (P < 0.001, t-test with bootstrapping) higher than that of the optimal model using sector 20 (adjusted r_m = 0.47) and the model using the average RNFLT in the macular vulnerability zone (adjusted r_m = 0.37).

Figure 5.

(a) Sector 20 (marked as red) out of 24 sectors, and (b) the RNFLT patterns (RPs), in the respective optimal models that were significantly (P < 0.05) associated with the average total deviation value at the central upper 2 locations (C2-TD) according to the Hood scheme.

Discussion

In this work, 16 RNFLT patterns were determined by an unsupervised AI method termed NMF. The RNFLT patterns highlight regions that varied greatly between eyes from different patients, which we designate as the relatively informative zone (iZone) colored by yellow and red; in contrast, the remaining regions had minimal variation among eyes and are considered the relatively uninformative zone (non-iZone) colored by blue. There were 12 RPs with arcuate-like iZones (6 RPs with superior iZones, 5 RPs with inferior iZones, and 1 RP with bi-hemifield iZone) and 4 RPs with non-arcuate-like iZones. Using the RNFLT patterns significantly improved the prediction of TD values at each of the 52 VF locations compared with a naive dimensionality reduction scheme of 24 15-degree sectors. The improvement was more substantial in the inferior paracentral and temporal regions of the VF, and less substantial in the superior nasal regions. Furthermore, the correlation of the RNFLT patterns with superior paracentral loss per the Hood scheme^22,23 was greater than that of the model using 24 sectors. We also compared the RNFLT pattern model with the models using the four sectors (temporal, superior, nasal, and inferior sectors) and six sectors (temporal, temporal-superior, nasal-superior, nasal, nasal-inferior, and temporal-inferior sectors) used in OCT software. In predicting VF loss at the 52 VF locations, the RNFLT pattern model outperformed the models using 4 sectors and 6 sectors. Furthermore, the NMF RNFLT pattern model outperformed the PCA pattern models in predicting VF loss at most of the 52 VF locations. See Supplementary Figures for more details.

Various RNFLT patterns were significantly correlated to MD (12 patterns), spherical equivalent (9 patterns), and superior (9 patterns) and inferior retinal artery (9 patterns) locations on the circle of 3.46 mm diameter, respectively. The RNFLT patterns not only encode the variance of pathological RNFLT thinning (evidenced by the correlations between the RNFLT patterns and MD) but also the anatomic RNFLT variation related to myopia and blood vessel locations. For example, RPs 6 and 10 were most strongly correlated with myopia as the arcuate-like iZones in these 2 RPs lie closer to the fovea and RP 7 was most strongly correlated with hyperopia as the arcuate-like iZone in RP 7 lies farther from the fovea. For example, the arcuate-like iZone in RP 6 lies closer to the temporal horizontal direction, and, therefore, RP 6 was also related to inferior artery locations closer to the temporal horizontal direction; conversely, the arcuate-like iZone in RP 7 lies farther from the temporal horizontal direction, and, therefore, RP 7 was also related to inferior artery locations farther from the temporal horizontal direction. Prior studies suggested that anatomic factors, such as spherical equivalent and blood vessel locations, should be considered for assessing structure-function relationships.^25,26,38,39 The RNFLT patterns determined by unsupervised AI automatically accounted for the impact of anatomic factors in structure-function relationships. Furthermore, RP 3 with inferior iZone was more strongly (bootstrapping, P < 0.001) related to MD than RP 1 with superior iZone, which was consistent with existing knowledge that inferior RNFLT damages are more frequent in glaucoma.¹²

The RNFLT measured on the circle of 3.46 mm diameter has been predominantly used for glaucoma diagnosis for its simplicity and documented reproducibility.¹⁰ However, using the RNFLT information only on this standard circle can often miss RNFLT damages,⁴⁰ as it disregards the abundant information contained in the 2D RNFLT map. On the other hand, it is challenging for clinicians to accurately and sufficiently assess the high dimensional data in the 2D RNFLT map by visual inspection. Our work provides a unique tool to decompose any RNFLT map into a linear combination of 16 RNFLT patterns that characterize RNFLT variations among different subjects (either due to glaucomatous damage or anatomic factors). This tool can lessen the burden clinicians may face in manually and visually assessing RNFLT maps. Furthermore, the decomposition coefficients of an RNLFT map sum to 100% and are, therefore, intuitive for clinical interpretation.

In addition, our RNFLT patterns showed high correlation with VF measurements. Compared with the model using the average RNFLTs of the 24 15-degree sectors, a naive data dimensionality reduction scheme, the model using 16 RNLFT patterns significantly improved the prediction of MD (adjusted r_m 0.63 vs. 0.55) as well as TD values at all 52 VF locations. The improvement was greater in the inferior paracentral and temporal regions of the VF, and less in the superior nasal regions of the VF.

Hood and co-workers proposed the macular vulnerability zone from 295 to 322 degrees around the ONH for central vision loss (the central upper 2 locations, see Fig. 1b).^22,23 Our results found that thinner RNFLT in sector 20 (285 to 300 degrees) was specifically associated with worse TD values at the central upper two locations (see Fig. 5a), consistent with the Hood scheme. Furthermore, Figure 5b shows that lower coefficients for 4 RPs with inferior iZones (RPs 3, 4, 6, and 7) were associated with worse C2-TD, indicating that thinning in the inferior iZones was associated with worse C2-TD. These inferior iZones overlap with the Hood vulnerability zone for central vision as well. More recently, Hood and colleagues further proposed a model describing the superior (45 to 90 degrees) and inferior (270 to 315 degrees) vulnerability zones, which are more susceptible to RNFLT damages.⁷ Among the 12 RNFLT patterns with arcuate-like iZones, there were 9 patterns involving iZones in the superior and inferior vulnerability zones: 4 patterns with superior iZones (RPs 1, 2, 9, and 10), 4 patterns with inferior iZones (RPs 3, 4, 6, and 7), and 1 bi-hemifield iZone (RP 13). Our AI-based RNLFT patterns highlighted similar regions related to pathological changes and anatomic variations as the superior and inferior vulnerability zones proposed by Hood and colleagues.⁷

Several studies have used deep learning techniques (i.e. deep neural network)^14,16,17 and a classical unsupervised AI method termed PCA¹⁵ to quantitatively assess the high dimensional RNFLT map data. Compared with the “black box” deep learning approaches, the unsupervised AI methods typically aim to determine representative patterns from the data with reduced dimensionality to facilitate clinical assessment. In a recent study, PCA was applied to determine the RNLFT patterns,¹⁵ which were associated with MD. However, the RNFLT patterns determined by PCA contained both positive and negative values, which were not amenable for meaningful clinical interpretations. Compared with the RNFLT patterns by PCA, the RNFLT patterns by NMF are more intuitive for clinical assessment due to the properties of non-negativity and feature sparsity. The data dimensionality reduction in our analysis leaves 16 patterns, which admittedly can still be difficult for clinicians to track, but this is likely because our model also accounts for variable retinal vessel positions.

This study has limitations. First, it was observed in Figure 3a that higher coefficients for the 4 RPs (RP 5, 12, 14, and 16) with non-arcuate-like temporal/nasal iZones were associated with worse MD. This finding would indicate that thicker RNFL in non-arcuate-like temporal/nasal iZones were related to worse visual function, which is not intuitive to understand. An alternative interpretation is that the lack of arcuate-like iZones was related to more severe glaucoma. Nevertheless, more data with longitudinal measurements are needed to improve our understanding of these non-arcuate-like patterns. Second, given the high dimensionality of the RNFLT map data, a larger sample size would help to better quantify the RNFLT patterns, particularly for stratifying RNFLT patterns by glaucoma severity stage. Third, because we use the full dataset to both determine the RNFLT patterns and assess structure-function relationships by multivariable linear regression, the prediction performance of the linear model can be inflated due to potential model overfitting. However, as we applied the cross-validation procedure for determining RNFLT patterns and the BIC model selection for assessing structure-function relationship to alleviate the potential model overfitting, we expect the prediction performance inflation issue has been mitigated. Furthermore, even if there is model overfitting due to various model comparisons, the prediction performance of the models using sectoral RNFLTs and PCA patterns should also be inflated. Our results have shown that the RNFLT pattern model is better associated with visual function even subject to the common issue of performance inflation. Fourth, our analysis was based only on the Cirrus OCT measurements. In future studies, we would like to determine the RNFLT patterns with OCT scans from other devices, such as Spectralis and Topcon as well, to make our findings more generalizable. Last, further work is needed to demonstrate the utility of NMF in decomposing RNFL loss in glaucoma through more extensive prediction of functional loss and assessment of glaucoma progression with change in RNFL patterns over time.

In summary, 16 representative RNFLT patterns were determined by an unsupervised AI method termed NMF. These patterns highlighted the relatively informative zones (iZones) of the RNFLT map, and characterized both pathological changes and anatomic variation in glaucoma. Furthermore, using the RNFLT patterns significantly improved the prediction of VF sensitivities. The AI-based RNFLT patterns have potential to assist clinicians in better assessing and interpreting the RNFLT maps. Compared with the traditional way to quantify regional RNFLTs by circular sectors^34,35 and superpixels^12,41 that are manually specified, our unsupervised AI model provides an alternative objective way to quantify regional RNFLTs to potentially improve the assessment of structure-function relationship and structural progression.