Standard Practices of Reticular Chemistry

Short abstract

Reticular chemistry is a growing field of science with a multitude of practitioners with diverse frames of thinking, making the need for standard practices and quality indicators ever more compelling.

Introduction

Reticular chemistry, the linking of molecular building blocks by strong bonds into crystalline extended structures, is one of the fastest growing fields of science.^1,2 In metal–organic frameworks (MOFs), the strong bonds are metal to charged ligand rather than the weaker metal to neutral ligand-type bonds of coordination networks (or polymers),³ and in covalent organic frameworks (COFs) the strong bonds are covalent bonds. There are many distinguishing features of reticular chemistry, which stand out from the usual practice of chemists—a practice that has been largely focused on the study of discrete organic compounds, metal complexes, supramolecular compounds, and polymers, with the occasional foray into solid-state materials such as metal oxides. Although coordination networks have been reported since 1959,⁴⁻¹¹ little effort was applied in developing the strong bond approach using charge-assisted coordination and covalent bonds to produce crystalline, infinite two- and three-dimensional metal–organic and organic structures.¹² One of us (O.M.Y.) recalls that as a student in the mid-1980s, chemists deemed the building of crystalline extended structures by strong bonds an unlikely objective because it was expected to yield amorphous solids (due to the crystallization problem).¹³ The lack of attention to this subject is indicated by its near absence from common inorganic and organic textbooks.^14,15 The discovery and development of permanently porous crystalline frameworks, such as MOFs¹⁶⁻²⁵ and COFs,²⁶⁻³⁰ two areas of reticular chemistry, are changing this state of affairs in a foundational way.

In this context and in the spirit of this article, we wish to point out that it is inaccurate to refer, as sometimes found in the literature, to MOFs and COFs as supramolecular frameworks (or solids). We make a distinction here that supramolecular chemistry is the chemistry of controlling noncovalent interactions, and its outcome is molecules held together by such weak bonds to make larger assemblages.³¹ These entities often find their inspiration from biology. In contrast, MOFs and COFs are held together by strong bonds between metal ions and charged linkers, and covalent bonds between light elements (e.g., B, C, N, O), respectively. The shift from the weak to the strong bond energy landscape comes with new challenges (such as achieving reversibility) that chemists have to overcome in order to make reticular structures in crystalline form. Thereby, chemical structures with distinguished physical and chemical properties become accessible, as manifested by their architectural and chemical stabilities. As such, reticular frameworks can withstand a wide range of chemical reactions without loss of their porous backbone. This has opened up many opportunities for chemists to practice precision reactions on infinite two- and three-dimensional (2D and 3D) extended chemical structures.³²

The reticular synthesis of MOFs and COFs uses molecular building blocks and covalent linking reactions emanating from inorganic and organic chemistry. The study of their porosity and molecular confinement properties requires the practitioner to be well-versed in physical chemistry. Recently, the success of incorporating these materials into devices and their field testing required chemistry researchers to extend their skills to engineering.³³⁻³⁷ It is becoming increasingly evident that the reticular chemist par excellence is one who is not just grounded in chemistry, but also has the ability to develop skills in other fields as the task at hand may require. Indeed, taking one’s basic research all the way to applications should include demonstrating its use in society or at least making credible attempts to take it “outside” the laboratory. This approach is fruitful when the basic science is done rigorously, and the applications are pursued under conditions relevant to those required for their deployment in industry and society. We are not advocating that societal needs necessarily have to dictate the basic research; rather, we wish to emphasize the importance of independent fundamental research and, at the same time, encourage scientists to pursue emerging opportunities to apply their findings toward technologies that address societal problems. This is the spirit with which reticular chemistry was founded and is being developed, and among the reasons for the current excitement and expansion of the field over the last 25 years.

With the increasing number of reticular researchers worldwide of varying backgrounds and interests comes the need for systematizing knowledge and providing guidelines for what constitutes acceptable standards of reporting scientific findings. Every mature field has such standards, although often not formally agreed upon, but they are part of the commonly accepted practice. The introduction of such guidelines for reticular chemistry is needed in light of its rapid development that involves making and predicting new compounds. This would set the tone for incoming researchers and enhance the quality of the science for those who already practice it routinely, not to mention others who might occasionally venture into it in the hope of finding answers to questions raised in their own research.

One of the principal difficulties in reticular chemistry deals with the fact that the results of synthesis are solids having strongly bonded extended structures. As such, they are insoluble in aqueous and nonaqueous media, and therefore the usual protocols and techniques practiced in molecular chemistry rarely provide definitive answers. Evaluation of yield and achieving molecular-level characterization of such reticular solids are much more arduous than for their molecular, soluble counterparts. Despite the constantly evolving crystallographic methods, most importantly X-ray and electron diffraction, a single technique to fully characterize extended structures in their numerous relevant properties is still absent; thus, many different characterization methods are needed for one to achieve the same level of precision commonly realized for discrete molecules. Accordingly, the question of providing guidelines for quality becomes more relevant as is the adherence to the basic chemistry principles on what constitutes a pure compound. As we strive to bring higher precision to the characterization of reticular solids, one must not neglect the power of making meaningful comparisons between results and developing trends in the course of evaluating quality. As in many thriving endeavors, a multitude of practitioners with diverse frames of thinking have entered reticular chemistry, making the need for recalling essential principles and standards (discussed in many other contributions)³⁸ ever more compelling (Figure 1, see Supporting Information). We note that a major turning point came in 1995 when it was first demonstrated that a charged organic molecule could be linked to a transitions metal-ion and produce a crystalline extended structure, termed a metal–organic framework (Figure 1).¹⁶ This was a departure from the plethora of coordination networks reported up to that point, wherein the linkages are based on metal-neutral ligands. It was the MOFs made from charged linkers (carboxylates) that were later proven to be architecturally robust and to have permanent porosity,¹⁷ making them objects of extensive study until today (Figure 1).

Figure 1.

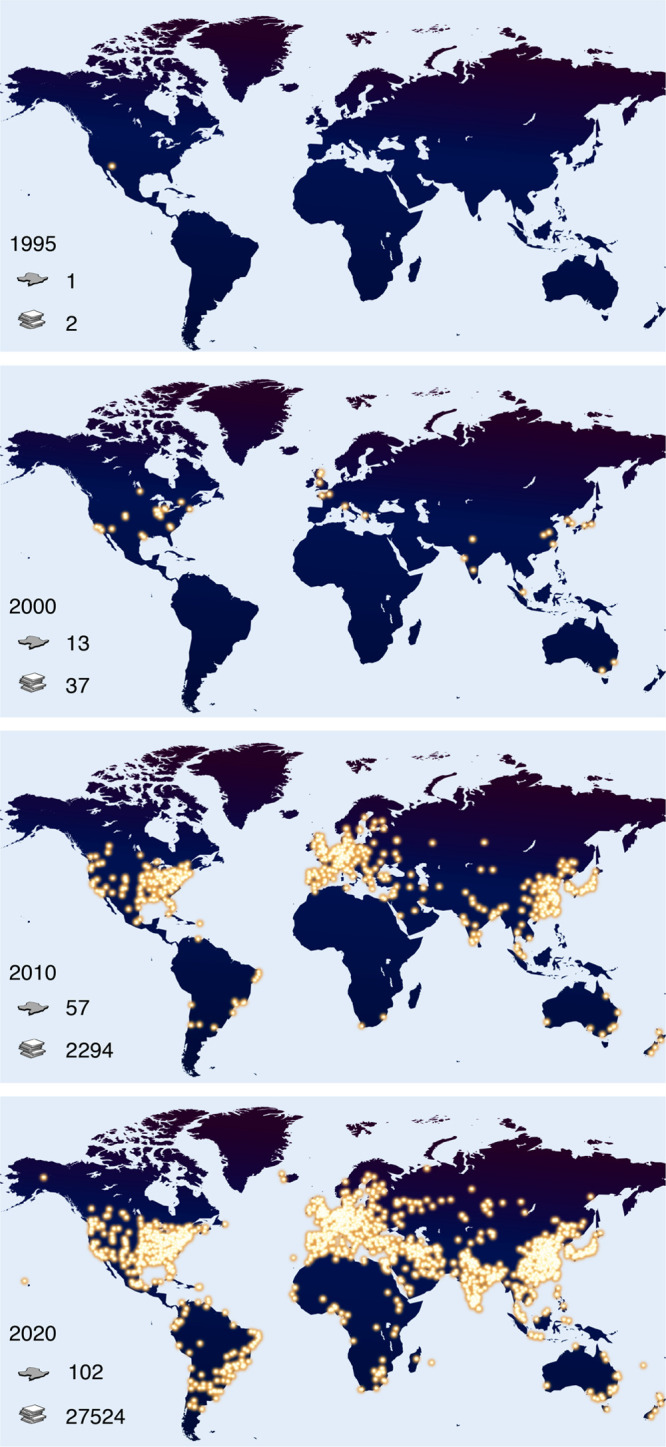
Expansion of reticular chemistry from 1995–2020. The bright yellow dots represent the institutes actively working on MOFs, COFs, and ZIFs. The search was restricted to the terms MOF, COF, and ZIF in original articles and reviews, and the affiliations were counted only for the corresponding authors. In total, as of the day of the search May 4, 2020, researchers in 5102 institutes and 102 countries (country icon) have published a total of 27,524 papers (manuscript icon).

In addition to the points presented above, we wish to outline the goals of this contribution. First, we wish to enumerate the common parameters in the practice of reticular chemistry that define the system under study in its operation, sets of conditions, and results.

Second, we wish to layout guidelines and recommendations for what hopefully would become standards of quality and clarity to be used in reporting scientific data related to these parameters. Our intent is not to give a blueprint for how one achieves such “standards” in the laboratory, but rather to share with the community what we think would strengthen the routine practice of standards. In addition, we offer scientific motivation for closely considering what we call “quality indicators” when reporting research results. We deliberately do not attempt to be prescriptive or comprehensive but instead wish to invoke some deeper thought about this topic and bring awareness to it as we pursue our respective endeavors under the expanding field of reticular chemistry.

Workflow in the Practice of Reticular Chemistry

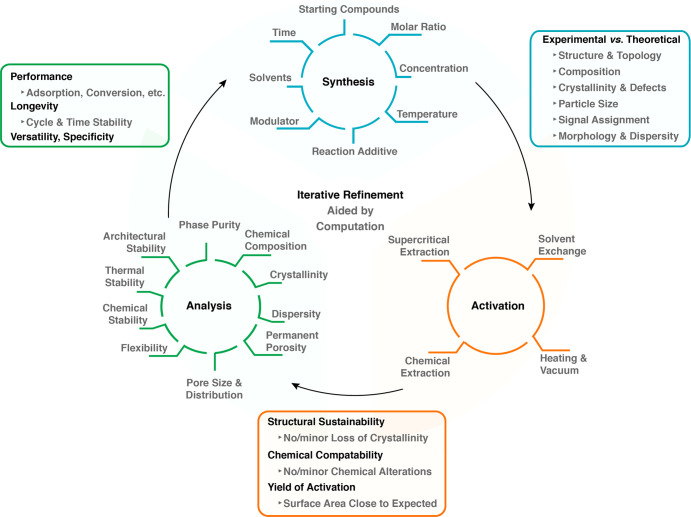
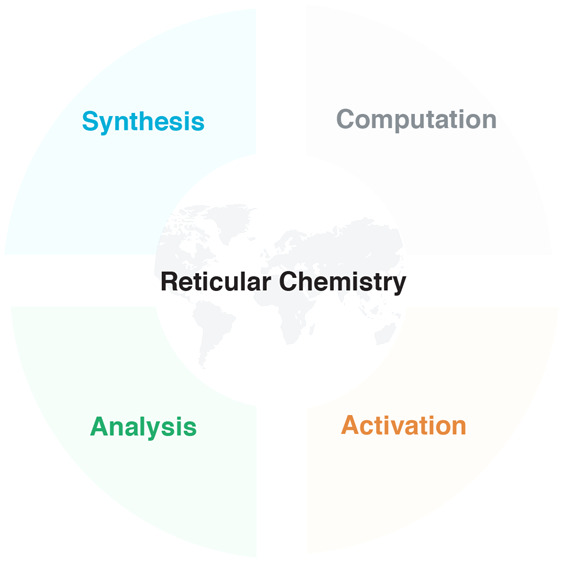
At the heart of reticular chemistry and the impetus for its rapid growth is the creation of new structures, where increasingly these are being used to address societal problems. While it has not been and it should not be an objective to have all researchers follow a specific scheme of activities, inevitably patterns in conducting research emerge, and thus a general workflow can be articulated (Figure 2). Such workflow facilitates the research and enhances its replicability and reproducibility. In this regard, we identified three key steps in the practice of reticular chemistry: The synthesis, activation, and analysis of the products (blue, orange, and green cycles in Figure 2). Ideally, the process of venturing from one step to the next should be considered as an iteration for the purpose of refinement (iterative refinement) and ultimate optimization of properties. This iterative process, best aided by computations, implies that each key step is revisited until the compound at hand complies with the quality standards necessary to make the findings valuable to the wider scientific community. Analytical tools and techniques enabling the researcher to examine the outcome of each step are central to the optimization process. It is essential that the assessment of the outcome of each cycle adheres to common quality indicators (bordered by blue, orange, and green squares in Figure 2).

Figure 2.

A workflow illustration of the most common scientific activities and related parameters (blue, brown, and green cycles), which reticular researchers follow in their synthesis and characterization of solids. This includes the quality indicators (correspondingly colored squares), which should be carefully considered in reporting of results.

Specifically, every discovery of an extended structure, be it a MOF or a COF, starts with its synthesis (Figure 2, Synthesis). Here, the most commonly considered parameters—and there are arguably many more—are starting compounds, molar ratios, temperature, concentration, reaction additives such as acid or base, modulators (small molecules influencing the reticulation process), solvents, and reaction time. Depending on the experience and persistence of the researcher, one or more of these parameters are varied to obtain the desired crystalline product (noting that in some cases noncrystalline forms, such as glassy materials are targeted).³⁹⁻⁴¹ The experimental process can be accelerated by high-throughput synthesis⁴² or screening by the aid of computational techniques.⁴³

A primary quality indicator that allows the researcher to evaluate the outcome of the synthesis is the validation of the atomic structure of the products, as determined by powder or single-crystal X-ray diffraction. The experimental diffraction pattern should match the calculated one, and all reflections that do not match should be assigned to contaminants, unreacted starting compound(s) or byproduct(s), whose structure ideally should be identified. Microscopy techniques are valuable additions, through which the purity of the newly made compound can be evaluated by scrutinizing the shape and elementary composition of the crystals. Particularly for COFs, microscopy techniques are essential to investigating the structural aspects that cannot be probed only by diffraction due to their lower crystallinity relative to MOFs. Finally, chemical group analysis, most importantly done by spectroscopic techniques, should be employed to monitor functional group conversions, compositional heterogeneities, and defects.

Following the initial synthesis, the permanent porosity and architectural stability of the compound at hand are assessed by initially carrying out a process called activation (Figure 2, Activation). Activation describes the practice of removing all guest molecules (including solvent) from the pores of the framework without causing collapse of its structure. This step should be undertaken thoughtfully in that one needs to consider the possible guest-framework interactions and the impact their disruption might make on the overall structure of the framework. Thus, initially the activation of a new framework must be delicately examined to understand the conditions under which permanent porosity and architectural stability can be achieved for that framework. We liken the process of activation to that of separation in molecular chemistry, where a target molecule is isolated from others through separation methods. In the present context of reticular structures, one might consider the activation as a separation of the guests from the framework.

The methods for activation are comprised of conventional heating and vacuum drying, chemical extractions, supercritical CO₂ extraction, and solvent exchange. For a detailed discussion on the advantages or disadvantages of each technique, the reader is referred to recent literature reviews.⁴⁴⁻⁴⁶ An important quality indicator for the success of activation is the measurement of a nitrogen or argon adsorption isotherm (at subatmospheric pressure and below their respective boiling point), followed by analysis of the specific surface area.^1,17 We note that measurements done at room temperature and high pressure are not proof of permanent porosity because under pressure gases are “forced” to permeate through a substance porous and nonporous alike. It is only through measurement of gas adsorption isotherms that pore volume and surface area values are obtained, and any distortions in the framework structure are manifested in the shape of the isotherm.^17,18

The surface area is routinely obtained from the isotherm and compared to the value calculated from the theoretical model. After activation, it should be verified by atomic structure analysis that no detectable loss in crystallinity occurred. Re-examination of the molecular composition and chemical group analysis will indicate the induced chemical alterations (if any) to the framework.

Next comes the study of the identity and character of the compound (Figure 2, Analysis). This process describes the identification and characterization of the physical and chemical properties of the compounds, thereby allowing the researcher to identify what elevates them from an exercise of scientific curiosity to a meaningful advance in technology. Among those unique identifiers of a compound are phase purity, proving that the compound is free of contaminants. Here, the researcher will have to resort to analytical and computational techniques used to study the atomic structure of the compounds. Finding the chemical composition includes the analysis of the atomic content of the metals and light elements, as well as chemical group analysis. NMR spectroscopy on the digested compound provides valuable information on the composition and stoichiometry by analyzing its molecular organic components.

Crystallinity describes the degree of structural order, which is defined primarily by mosaicity, defects, and disorder, and ultimately encompasses the crystal size and morphology (Figure 2, Analysis). This information is best acquired by combining diffraction and microscopy techniques. Nitrogen or argon isotherms confirm the permanent porosity of the framework and are used to calculate the surface area and pore volume. The pore size and its distribution are experimentally deduced from the isotherm based on its type and profile features. It is important to note that the theoretical models, which are used to calculate the discrete pore size from the isotherms, were originally developed for porous inorganic compounds, such as carbon and zeolites. Therefore, the transferability of these models to MOFs and COFs should be carefully evaluated.

Flexibility, or lack of rigidity, describes the reversible motion or switching of a framework’s backbone while maintaining its permanent porosity.⁴⁷⁻⁵² It is not to be confused with architectural instability, which is due to the irreversible change of the framework conformation or its loss of structural integrity.⁵³ For example, indicative of a framework’s flexibility is sometimes the observation of a hysteresis in the nitrogen or argon isotherm, and this behavior can be further examined by in situ/operando spectroscopic and X-ray scattering techniques, and computational simulations. The stability of a framework is indicated by its ability to withstand chemical and/or thermal strain. It is a requirement that the atomic structure and architectural integrity of the compound be preserved after such strain assessment. Architectural stability is undeniably one of the most important features of the framework as it leads to permanent porosity, which is the accessible surface area, and this lays the foundation for most applications.

The main quality indicators at this third stage (Figure 2, Analysis) are relative to the applications of the compounds. These are expressed in terms of performance, longevity, versatility, and specificity. Performance is the efficacy of a compound to execute the designated task. In catalysis for instance, this can be identified by the turnover frequency, while in gas sorption it can be either the capacity or the kinetics of the uptake and release. Longevity is a measure of the long-term performance of the compound and more specifically consists of its ability to maintain the observed performance over time. Versatility is the capability of a compound to carry out more than one function, while the specificity describes how selective the compound is toward one or a group of chemicals.

We recognize that through the application of this iterative refinement researchers can convince themselves that the results are reproducible, but we recommend in addition that such reproducibility be independently confirmed by others in the laboratory. In general, researchers should endeavor to report detailed description of their synthesis procedures to the level that a newcomer to the field with little experience can reproduce it. We provide below what we believe are “best practices” for the correct execution of the analysis and a thorough description of the results.

Characterization Techniques for Reticular Compounds

The complete characterization of reticular compounds, such as MOFs and COFs, is only achieved through the combination of multiple techniques. Here, we provide a description of the most relevant characterization techniques in support of steps articulated above for the practice of reticular chemistry. For every type of analysis, we clarify which kind of information can be reliably obtained, and the cases where the data should not be overinterpreted but need to be complemented with the results from other techniques. Our purpose here is to provide guidelines to avoid common pitfalls during the characterization process, and to report results and necessary information in a useful and sensible manner. Before discussing the details of single techniques, a few general requirements for the experimental methods description are listed below. These must be supplemented with other essential information, which is specific to each characterization method and will be specified in each dedicated paragraph.

The instrument’s model is an important piece of information as it defines the kind, precision, and accuracy of the resulting analytical information. These details must also comprise the most important components, such as, for spectroscopic and scattering techniques, source type and detector model. A description of the sample holder is also necessary, when its features are not unique and obvious from the instrumentation. The software (and version) used for the data processing, often provided with the instrument, must always be clarified, as well as additional software used for further data treatment, as for instance structure solution and refinement programs for crystal structure determination.

The description of the sample preparation must include all the treatments performed after the synthesis until the start of the data collection. Finally, the conditions that the sample is subjected to during the data acquisition must be described. These include temperature, pressure, and chemical environment such as gas mixture or solvent. This last piece of information can be excluded when it is obvious, for instance, in the case of measurements normally conducted in high vacuum as in scanning and transmission electron microscopies (SEM and TEM).

Single-Crystal X-ray Diffraction (SCXRD)

SCXRD provides evidence for the structural features of any crystalline compound at the atomic level. It allows the determination of the framework atomic positions, and the corresponding bond lengths and angles, with subangstrom precision. Widely used and developed for decades, SCXRD is the preferred technique for the determination of any new crystal structure. Moreover, SCXRD also allows the study of guest–framework interactions resulting from sorption processes,^54,55 structural changes after postsynthetic modifications,⁵⁶ or structural determination of molecules included or generated inside the framework pores,^57,58 provided these processes occur while maintaining the single-crystal nature of the reticular compounds.

Results of the SCXRD experiments provide a picture of the average structure of the crystals. Because of their porous nature, MOF crystals are usually comprised of well-ordered atoms belonging to the framework, and other atoms with a higher degree of disorder, usually belonging to guest molecules located in the pores. Furthermore, even for framework atoms, differences are also commonly found for the different building units, namely, inorganic secondary building units (SBU) and organic linkers. Terminal ligands or chemical functionalities pointing into the pores might also exhibit positional disorder. In these situations, the resulting atomic anisotropic displacement parameters (ADPs) will show these differences, which should be carefully inspected during the refinement. Whenever possible, a disorder model should be attempted to explain otherwise unusually large ADPs. In this regard, the display of difference Fourier maps can highlight whether the regions covered by the large ADPs clearly contain more than one electron density maximum. In such cases, the modeling of multiple atomic positions should be attempted, assisted by the careful use of chemically sound crystallographic restraints/constraints. The large contrast in electron density between framework and pores in the unit cell could make it difficult to locate solvent molecules, or counterions in the case of charged frameworks. This effect is even more pronounced for MOFs made of heavy metal elements. Here, some of the lighter atoms might not be easily evident in the difference Fourier maps, where only areas with small values of electron density are discernible. The presence of atoms with partial occupancies (either not present in every single unit cell, or having split positions) is also common, most particularly for atoms belonging to adsorbed guests, or products of postsynthetic modifications. In these cases, the quantification of the atomic composition or reaction yield should always be corroborated with additional analysis.

Similarly, in the case of structures that contain metal elements with close atomic numbers, and therefore similar scattering factors, X-ray diffraction will not straightforwardly provide a definitive assignment of the atomic species. The use of solvent mask procedures⁵⁹ should be opted for critically and only when, in the latest steps of the refinement, every attempt to locate the atomic positions of the molecules in the pores has failed. In any event, the provided crystallographic files should incorporate details of the solvent mask procedure. We also recommend including the refinement indicators obtained before and after applying the solvent mask in the reported crystallographic tables. When dealing with limited data quality as in the cases of crystals that only diffract to limited resolution, the use of restraints/constraints during the refinements is helpful, for example, to refine some molecules as rigid bodies. Whenever used, details on the employed restraints and constraints must be clearly explained and justified in the experimental methods description.

Any newly disclosed crystal structure should adhere to International Union of Crystallography (IUCr) recommendations regarding data reporting in the form of crystallographic information files (CIFs). The provided CIFs must include the experimental structure factors and refinement instructions, which can be easily implemented with modern refinement programs. They must be validated accordingly by the unified CheckCIF procedure (https://checkcif.iucr.org/). When discussing any value obtained from SCXRD, such as distances or angles, their corresponding estimated standard deviations (esd) must be given. Main data collection and refinement indicators should be clearly accessible to the readers. This includes wavelength, source type, maximum resolution reached for I/σ > 2, temperature, atmosphere, instrument with source and detector, unit cell parameters, cell volume, space group, R₁, wR₂, GOF, largest diffraction peak and hole, and Flack parameter in the case of a non-centrosymmetric structure. When using a solvent mask, the refinement indicator values obtained before and after applying the mask should be given for comparison. Researchers using SCXRD can find further detailed guidelines on structure optimization, validation, and avoidance of common pitfalls in recent crystallographic educational articles.⁶⁰⁻⁶²

Finally, the interpretation of a refined crystal structure involves a process we call “reading a crystal structure”. This is the examination of directly bonded and nonbonded distances, and angles to determine whether they are reasonable and precedented. This process of familiarizing oneself with the structure uncovers any unusual findings if indeed they exist in the crystal. Often, a model can be helpful during this process.

Powder X-ray Diffraction (PXRD)

According to the basic postulate of structural crystallography, “only one single chemically sound crystal structure exists that is compatible with the observed diffraction data”.⁶³ PXRD is thus invaluable in providing the unique footprint of any crystalline material. The identification of any reticular compound with PXRD is made by comparison of experimental and calculated PXRD patterns, and it is vital for the identification of any crystal phase in the sample, ensuring that no other crystalline solid is present in the bulk. Through the analysis of the diffraction profiles, PXRD also provides information on crystal size, as well as on the degree of crystallinity of the samples, or presence of partial disorder. PXRD can be also applied for structural elucidation when access to single crystals is not possible. Variable temperature PXRD is often used in the study of dynamic reticular structures and in the study of phase change. The interpretation of PXRD data can be rather challenging, and different approaches are possible for structure solution from powder diffraction data. The reader is referred to the specific literature on this topic.⁶⁴

Acquisition and interpretation of PXRD data must be made considering the holistic nature of X-ray diffraction. Sample preparation might have a dramatic impact on the obtained pattern. When using a reflection configuration, the sample must be placed on a flat surface, and a sufficiently large amount must be used to decrease background contribution from the sample holder. When this is made challenging by the small amount of available sample, the use of low-background silicon holders is preferable, as well as, when available, the use of beam-limiting slits to reduce the illuminated area to the one covered by the sample. We recommend grinding the sample prior to depositing it on the holder, to homogenize particle sizes, thus reducing to some extent possible preferred orientation effects. The preparation of a fine powder is also crucial to ensure that the sample is properly flattened on the holder, so that its surface roughness is minimized to limit its contribution to the peak broadening when using a reflection configuration. The user also must be aware that an imprecise sample height introduces errors in the position of the peaks in the final diffractograms.

For air-stable MOFs or COFs, we strongly recommend collection of PXRD patterns on well-dried samples, and preferably after activation to facilitate the comparison with the calculated pattern, which often does not account for guest species in the pores. When dealing with air-sensitive samples, we recommend using sample holders specially designed for this purpose, to avoid any structural changes during the pattern acquisition. In these cases, the use of transmission geometries combined with the sample preparation in glass capillaries (Debye–Scherrer configuration) minimizes the exposure of the sample to the external environment, while also decreasing preferred orientation phenomena induced by the powder flattening during the sample preparation. The 2θ range for acquisition of PXRD patterns should be sufficiently large to cover a significant number of diffraction peaks. The lower limit should be in accordance with the expected position of the first diffraction peak. On the higher end, the 2θ range should be large enough to cover the possible presence of impurities with dense crystal structures and small lattices, such as metals or metal oxides. Keep in mind that the lattice parameters ultimately determine the position of the first diffraction peak, and thus a recommended range for the most widely used Cu Kα radiation is between 3° and 50° (corresponding to d = 29.45 and 1.82 Å, respectively). The experimental step size during the acquisition should be small enough to properly describe the shape of the diffraction peaks and disfavor overlap of different reflections having very similar d values. The instrumental set up greatly influences peak profile, and we therefore recommend a step size no larger than 0.03°. The acquisition time is surely influenced by the sample amount and its intrinsic diffractive power, but it is also largely dependent on the instrument source intensity and the quality of the detector. Generally speaking, acquisition time should be sufficiently large to properly resolve from the background all the peaks in the selected range.

Because of their structural features, most MOF and COF PXRD patterns show a large difference in intensities between low and high angle peaks. We advise not to report patterns where the first most intense peaks are evident, but the signal-to-noise ratio in high-angle areas is such that weaker peaks are not clearly resolved. We strongly advise against performing a background subtraction after data collection. If a large background contribution is present in the PXRD pattern due to the presence of solvent, this must avoided by using a dry sample, when possible. If the background contribution is still obvious with the dry sample, this could be indicative of the presence of an amorphous phase, or of limited sample crystallinity, and accordingly this information should not be removed from the pattern. The plot of the experimental pattern must allow the identification of diffraction lines that have close positions (avoid thick lines, see Figure 3). The origin of the structure taken for the calculation of the simulated powder pattern must be clearly specified with its corresponding database reference code and the bibliographic reference of its original journal article. In addition to the entire simulated pattern, the comparison graph should also include position marks for every Miller plane in the plotted range, demonstrating that every single peak in the experimental pattern is indexed.

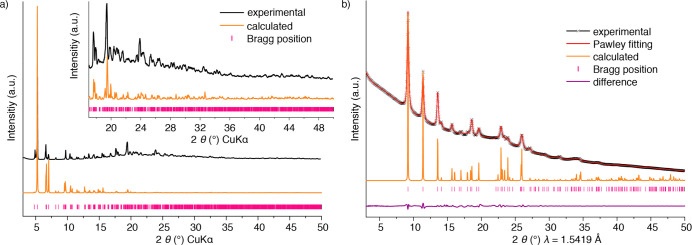
Figure 3.

Representation of PXRD patterns for MOFs and COFs. Comparison between the experimental and simulated patterns of MOF-520 (a).⁶⁵ Because of the large difference in relative intensities in different 2θ regions, a blown up area is required. A synchrotron collected (wavelength indicated) PXRD pattern of COF-112 (b).⁶⁶ In this case, a Pawley refinement can be made, since there are enough experimentally observed reflections. The nature of the refinement is indicated in the figure legend, and the image includes the calculated pattern for the corresponding model, for visual comparison of the expected relative intensities.

Since the relative intensities of the diffraction patterns are influenced by the presence of guest molecules, it should be clearly stated whether these are included in the model used for the pattern simulation. If noteworthy differences in relative intensities are attributed to the occurrence of preferred orientation, this hypothesis should be commented on and corroborated by microscopy measurements to show the relevant features of crystal morphology and size. Moreover, many programs used for simulating PXRD patterns allow the introduction of a preferred orientation factor. In these cases, calculated patterns with and without preferred orientation effects should be provided.

COF Structural Simulations

Although 3D COF crystals suitable for SCXRD have been obtained,⁶⁷ and structure solutions using electron diffraction data have also proved feasible,^68,69 these techniques are not yet always possible. Structural elucidation of most new COFs therefore strongly relies on a combination of computer simulation and powder X-ray diffraction analysis. Structural simulation of COFs (and for microcrystalline MOFs) is typically accomplished by following a topological approach.⁷⁰ Here, crystal models are generated by placing the selected organic linkers at the position of the nodes and edges of the possible networks resulting from the geometry and connectivity of the building units. The models are geometrically optimized, and their PXRD patterns are thus calculated, and compared with the experimental ones.⁷⁰

This approach exploits the unique features of reticular chemistry, namely, the formation of extended networks by strong bonds between selected building units, and it has been extremely successful in elucidating the structure of numerous COFs with a limited number of observable diffraction peaks. However, one must remember that during the structural simulation process several assumptions are made, such as the completeness of the bond formation reaction between linkers, or that the organic linkers do not undergo any fundamental geometrical alterations during the COF formation process. These points must consequently be corroborated with spectroscopic techniques, and all characterization results must be consistent with the features of the proposed crystal models. Moreover, one must ensure that after generation and optimization of models, these do not contain abnormal values of atomic bond lengths and angles, which could result from the incorrect assignment of unit cell parameters or space group.

Regarding the interpretation and comparison of the diffraction pattern calculated from the models, cell-restrained whole powder pattern decomposition (WPPD) refinements are commonly performed. Pawley and Le Bail are two variations of cell-restrained WPPD,⁷¹ which were originally developed to extract peak intensities from powder diffraction patterns and subsequently to be used for structure solution. They require knowledge of the lattice parameters and space group to calculate the diffraction peak positions, information that for COFs is usually obtained from the computer-generated models. The pattern refinement process is thus applied to refine the initially proposed unit cell parameters. However, Pawley or Le-Bail methods do not consider atomic coordinates, and there is no structural information in these refinements. The results are only indicative of the validity of the lattice parameters, and they must not be taken as a measure of the quality of the proposed crystal structure. Moreover, because of the nature of these refinements, for those patterns with a small number of observable diffraction peaks, similarly good refinement values can be reached for different unit cells. Consequently, applying a Pawley or Le-Bail refinement is not informative, as low residual values are always obtained due to the dominating contribution of the background. In these cases of less than 10 diffraction lines, we discourage reporting Pawley or Le-Bail fittings, as they do not sufficiently support the correctness of the chosen unit cell and space group. The validation of a crystal structure determined by means of powder diffraction is made with the completion of a Rietveld refinement.⁷² With the Rietveld method, atomic coordinates and other structural and profile variables are used to calculate the intensities of the simulated patterns. These atomic and profile variables are adjusted together to fit calculated and experimental whole patterns. Note that performing a meaningful Rietveld refinement requires a sufficient number of observable, well-defined diffraction peaks, which is not always feasible for many COFs.

In the report of any computer-generated COF crystal model, its three-letter code topology for which the model is based on should be indicated.^73,74 The crystal system, space group, and lattice parameters of the final model must be clearly specified. Models should be completed within a space group compatible with the symmetry of the selected framework topology, and organic linkers, avoiding the report of P1 models unless justified by the actual lack of symmetry on them. Entire structure data including atomic coordinates should be given in electronic format (such as cif). The comparison between experimental and calculated patterns should be made to facilitate the visual comparison of the relative intensity distribution. Considering that experimental diffraction peaks might be contributed to by more than one diffraction plane, instead of adding a single set of Miller indexes on top of an observed reflection, it is recommended that positions of the Miller planes be marked, and the calculated positions and relative intensities of the Miller indexes be given, preferably in a tabulated form.

The simulated pattern should be calculated in the absence of guest molecules and compared with an experimental pattern that equally corresponds to an activated sample. If guest species are part of the model (counterions, or other molecules determined to be present with other techniques), it must be clearly indicated. In the particular case of 2D COFs, the structural model of a layer can be accomplished in a straightforward manner following reticular chemistry principles. However, the determination of the stacking sequence (if any) is not evident, since there are only weak interactions between the layers. For these cases, it is necessary to complete multiple models with a different stacking sequence, such as staggered (AB) or eclipsed (AA) configurations, but also other intermediate cases. Including a third layer in the stacking sequence (i.e., ABC) might result in substantially different distribution of relative intensities. Multiple models should thus be considered during the structural analysis, with their corresponding comparison of calculated diffraction patterns. If two models present only small differences in the relative intensities, the assignment to one or another stacking sequence cannot be made with just PXRD analysis, and it must be supported by additional characterization results, such as thorough sorption studies. Having said this, it is important to recognize that deciphering stacking sequences in 2D COFs is an ongoing challenge, because of the inherent disorder along the stacking axis.

Scanning Electron Microscopy (SEM)

SEM is widely used in reticular chemistry to investigate size, morphology, and surface elemental composition.⁷⁵ As far as the morphological analysis is concerned, conventional SEM analysis generally has a resolution down to a few tens of nanometers, which largely suffices for a reliable assessment of morphology and size in most cases. Concerning the elemental composition analysis, this relies on the detection of characteristic X-rays emitted from the superficial layers of the sample, known as energy-dispersive X-ray analysis (EDX). Although the thickness of the layer probed by EDX can vary depending on various sample and instrumental parameters, this analysis remains mostly limited to the surface, and it is semiquantitative. Therefore, its results should not be considered meaningful concerning the overall composition of the bulk material, for which inductively coupled plasma-optical emission spectroscopy (ICP-OES) or mass spectrometry (ICP-MS) and elemental analysis are more suited.

Before performing an SEM analysis on MOFs or COFs, two sample preparation steps must be followed: Sample drying and sample sputtering. The use of dry sample is essential as most SEM instruments operate in high vacuum conditions and must be protected against chemical contaminations. For this reason, special attention should be paid to the stability of the framework in such low pressures, which should be assessed by exposing the material to analogous conditions and verified by PXRD that no irreversible collapse occurred. Another essential step in the preparation of framework samples for SEM analysis is sputtering the sample with a conductive metallic or carbon film. This is made necessary by the commonly poor electron conductivity of porous materials, resulting in the accumulation of electrons on the sample surface due to their hampered discharge along the sample holder. These excessive charges can be easily recognized as excessively bright regions of the crystals compromising the resolution of the picture. There are, however, two cases when the sputtering treatment can compromise the entire analysis, and its use can be reasonably discarded. The first case is when the sample consists of small nanoparticles. Since the sputtered coating is usually between 5 and 10 nm thick, morphological features close to this range are unavoidably lost. A second case is when SEM is used to investigate the elemental composition by EDX analysis, and the emission signals of the analytes are overlapping with those of the conductive layer. In these cases, the resulting chemical information must be discarded and the sample reprepared for purely elementary examinations using either a different coating element or, in case this is unavailable, by avoiding the sputtering treatment.

Specific information needed for a meaningful report of SEM analysis must include acceleration voltage used for imaging and the one used for EDX. In case nonroutine conditions allowed on specifically designed instruments are used, such as mild pressures or high/low temperatures, their description must be added as well. As far as the data display is concerned, all SEM micrographs must include scale bars, possibly introduced automatically with the raw data reduction software. In any case, all the collected pictures must be included unedited, in full resolution, and with automatically generated scale bars in the Supporting Information file. When displaying any type of size comparison between different samples it is appropriate, scientifically expected, and intellectually honest to use pictures with identical scale bars (Figure 4).

Figure 4.

(a–d) Four different types of pure-metal and mixed-metal ZIF-8 samples are shown with good clarity and information completeness. This is achieved by presenting several crystals and, when necessary, magnifications highlighting the morphology of single specimens. Note that each set of high- and low-magnification pictures has identical scale bar length (0.1 and 1 μm, respectively) to facilitate the comparison between different samples. Reproduced from ref (76) with permission from the Royal Society of Chemistry.

As for EDX maps and spectra, their use must be accompanied by the raw data in the Supporting Information file. Finally, local morphology and compositional analysis must be complemented with the same kind of information from a reasonably larger sample, which is therefore more representative of the bulk product. For instance, exemplary images of a few single crystals need to be compared with one or more pictures displaying a large multitude of crystals (a few tens at least) to show how the local information relates to the general characteristics of the sample.

Transmission Electron Microscopy (TEM)

TEM is one of the most versatile techniques for the analysis of reticular frameworks as it can be used to obtain atomically resolved morphological, compositional, and crystallographic information in a single measurement session. Additionally, TEM instruments can also be employed to investigate particle density heterogeneity, bonding energies, and many other features whose analysis is not considered part of the routine practice. For these more advanced applications, readers can find valuable information in recent bibliography in the field.⁷⁷

The exceptional precision of TEM analysis is balanced by its lack of representativeness of the bulk sample. This is due to the small amount of sample used for an analysis, usually a few micrograms, and the high probability of sample contamination, which is strongly influenced by how the sample preparation is conducted. Below, we are not covering the many important aspects of this step, as we assume every TEM user is thoroughly trained on, but we instead comment on some issues that are more specifically encountered in the analysis of reticular frameworks. In standard sample preparation protocols, the sample is crushed in an agate mortar with the aid of a few droplets of solvent. When this preparation procedure is planned, the chemical and architectural stability of the sample to such solvent-assisted grinding should be proven by comparing its PXRD profiles before and after the treatment. In cases where damage is certain or suspected, the sample should be deposited on the TEM grid by simple mechanical contact, for instance, by rubbing the grid gently on some powder lying on a cleaned glass slide. Concerning the TEM analysis, a distinctive trait of MOFs and COFs is their high beam sensitivity. This often causes sample amorphization and loss of morphological details within a few seconds of illumination. Current instrumentations are usually equipped with highly sensitive detectors, which when combined with low electron doses allow for the analysis of reticular solids without considerable damage. Nevertheless, while collecting images on particles, their diffraction must always be checked and documented, and in case no diffraction is observed, the pre-existing amorphous state of the sample must be confirmed by PXRD analysis. If the amorphization is induced by the electron beam, the significance of the morphological information must be commented on during the interpretation of the results. Beam damage can be minimized not only by decreasing the intensity of the beam, but also by selecting its energy.⁷⁸ In this respect, high energies, achieved by using a high acceleration voltage like 300 kV, can be used to minimize the probability of electron-matter inelastic scattering and the resulting ionization damage (radiolysis). However, high energy electrons can cause knock-on damage where atoms are extracted from the sample generating chemical and structural rearrangements. In general, molecular frameworks suffer mainly from radiolysis damage, so that higher energies might be preferable, but these aspects can differ from sample to sample and should be considered when choosing a specific acceleration voltage.

As far as the display of TEM images is concerned, the same general criteria outlined for SEM apply. This also transfers to the importance of reporting the high-tension value used for the analysis, the environmental conditions of the sample and the type of grid and sample holder that have been used. In general, EDX analyses should be considered indicative and not a reliable source of quantitative information for the elementary composition of the sample. In-zone diffraction patterns accompanying the images should contain the reciprocal lattice axes and/or the assignment of some relevant reflections to support the identification of the crystal orientation. In case a selected area aperture or other beam-limiting means is used, the portion of the sample that has been probed by diffraction must be highlighted in its picture (Figure 5).

Figure 5.

Exemplary display of TEM imaging data of a reticular structure, UiO-66. The transmission image of the selected crystal (a) is accompanied by a further magnifications (b–c) of an highlighted area of (a), the diffraction pattern of the entire crystal with indexed reflections (d), and the FFT (e) of the high-resolution image shown in (b). Reproduced from ref (79) with permission from the Royal Society of Chemistry.⁷⁹

Surface Area and Pore Size Distribution

Permanent porosity is one of the intrinsic properties of reticular compounds, and measuring adsorption isotherms is the standard practice to confirm their porosity. On the basis of the adsorption isotherms of MOFs and COFs, the surface area, pore size distribution, and pore volume can be obtained. Before adsorption studies on other gases and kinetic breakthrough measurements, N₂ or Ar adsorption should be run at low pressure and low temperature to provide a basic porosity profile of the compound.^1,17 Reporting the surface area and pore volume of structures based on structure modeling should not replace the experimental gas adsorption studies (Figure 6).

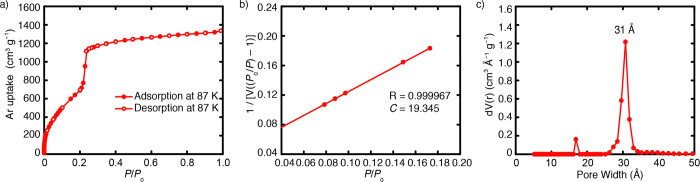
Figure 6.

Low-pressure Ar adsorption isotherm of IRMOF-74-IV at 87 K (a).⁸⁰ 65 adsorption data points (P/P₀ from 1.3 × 10^–5 to 0.99) and 15 desorption data points were collected. Five continual points at the P/P₀ range from 7.85 × 10^–2 to 1.73 × 10^–1 were used for BET surface area calculation (b). The specific BET surface area of IRMOF-74-IV is 2516 m² g^–1, with a correlation coefficient R being 0.999967. The C constant in the BET equation is 19.345. Pore distribution profile of IRMOF-74-IV using the NLDFT model from the Ar adsorption data (P/P₀ from 10^–5 to 0.99) at 87 K (calculation model: Ar at 87 K zeolites/silica based on a cylindrical pore model; (c)). The fitting error between experimental isotherm and that based on NLDFT model is 0.819%.

A good adsorption isotherm on reticular structures requires enough sample loading and complete sample activation. By evaluating the PXRD pattern of materials after activation and its preliminary adsorption data, the activation method should be optimized to obtain frameworks with preserved integrity and surface area comparable to the calculated value from the structural model. It is worthy of note that for the N₂ or Ar adsorption isotherm at 77 or 87 K, data points at P/P₀ as low as 10^–7 or 10^–5, respectively, are necessary for surface area and pore size distribution analysis in high quality. This is the gold standard for measuring permanent porosity on microporous structures. MOFs with dynamic structural change require a longer equilibration time, and the data collection strategy should be reported.

A comprehensive description of the physisorption isotherm type and hysteresis feature (if any) is indispensable. When the Brunauer–Emmett–Teller (BET) method is used to report the surface area, the limitation of the model should be understood.^81,82 For most structures with micropores, data from low pressure range (P/P₀ < 0.1) in which the term V(1 – P/P₀) continuously increases with P/P₀, rather than the classical range (P/P₀ = 0.05–0.3), should be used in the BET equation. A correlation coefficient greater than 0.995 and a positive C value are the gold standards for the multipoints BET method, and they should be reported along with the data point range and the corresponding BET surface area.

Authors should be aware that the pore distribution analysis results are strongly influenced by the model selection and accuracy of the parameters (pore shape, size, and the main interactions between adsorbent and adsorbate).⁸³ We advise listing the full information on the pore distribution analysis, including calculation methods, application pore size range, adsorbate, pressure range used, and fitting error. For example, a proper description reads: “The pore size distribution from 0.35 to 100 nm of MOF-A was analyzed by the non-local density functional theory (NLDFT) model from the Ar adsorption data (P/P₀ from 10^–5 to 0.995) at 87 K (calculation model: Ar at 87 K zeolites/silica based on a cylindrical pore model). The fitting error between experimental isotherm and that based on NLDFT model is 0.189%.” The criteria to choose a proper model is not how your pore distribution analysis fit the new crystal structure, since the material may have a different pore distribution due to model limitation, potential structural change, or unsuccessful activation. NLDFT and grand canonical Monte Carlo (GCMC) models are believed to describe the fluid state in the micropores of MOFs and COFs better than classical methods, such as the Barrett–Joyner–Halenda (BJH) method. While there is no kernel developed specifically for reticular structures yet, multiple models need to be investigated, and a comparison between the measured isotherm and the modeled isotherm is important to judge the confidence of the pore distribution result. A fitting error as low as 1% is considered acceptable, and special attention should be paid to the isotherm in the low P range for microporous samples.

The pore volume in framework structures is calculated from the total adsorbed gas volume when P/P₀ approaches 1.0. Micrometer sized crystals usually have negligible external surface areas, and typically a P/P₀ of 0.90–0.95 is used for the pore volume calculation. Some reticular structures and their composites feature very large macropores and interparticle pores, and the uptake curve goes up vertically at the tail end of the isotherm. In this case, the total volume calculation may not be accurate since the uptake value at this range tends to be arbitrary.

Thermogravimetric Analysis (TGA)

TGA is used to measure mass loss in a sample over time as a result of temperature changes in a controlled and stable atmosphere. This method helps to quantitatively examine many processes, including the loss of water or solvent, decarboxylation, pyrolysis, oxidation, or other types of decomposition, and even evaporation and sublimation. Linear fits can be applied to the thermogravimetric thermal curve to extrapolate the temperatures of weight loss onset.^84,85

At least two characteristic weight loss steps are observed in reticular structures. The first occurs at relatively low temperatures (ca. < 300 °C): This is the desorption of guest molecules inside the porous structure. The second step occurring at a higher temperature indicates framework degradation. This temperature is used as an indication of the thermal stability of the framework, but stability measurements must be confirmed by PXRD. The mass of the framework after combustion is also important, and finding the ratio between the weight loss due to the linker and the weight of the inorganic residue can be used to calculate the composition of the framework. When the ratio is compared to the ideal composition, in principle the number of defects (missing linkers and SBUs) can be determined.

Liquid and Solid-State Nuclear Magnetic Resonance (NMR)

NMR spectroscopy is used to detect and quantify impurities incorporated in MOFs and COFs that might occur due to side reactions during their synthesis. For example, the commonly used solvent N,N-dimethylformamide (DMF) can formylate amino-functionalized linker molecules at elevated temperatures as was shown for UiO-66(Zr)-NH₂ and MIL-101(Al)-NH₂.⁸⁶ Furthermore, NMR spectroscopy is the method of choice to quantify the degree of postsynthetic modification or to evaluate the efficacy of purification. For application of liquid NMR spectroscopy, the framework needs to be digested. Usually, acidic solutions, such as D₂SO₄, DCl, or DF are used to digest the frameworks,⁸⁷ some of which require digestion by acid-free mixtures without causing damage to sensitive functionalities or mask hydrolyzable impurities.⁸⁵ It is often more difficult to find methods to appropriately digest those chemically robust COFs.

If for some reason a particular linkage (bonds forming between atoms of adjacent building units) is not decipherable by solution NMR of the digested frameworks, solid-state NMR provides a powerful tool not only to identify but also to quantify the organic components in MOFs and COFs. Detailed experimental parameters in cross-polarization magic angle spinning (CP-MAS) spectroscopy, such as spinning rate, pulse angle and width, contact time, and recycle delays, are essential for the reproducibility of solid-state NMR data. Authors are recommended to provide this information when publishing their results. Apart from the main and satellite peaks attributed to the product, any other peaks should be identified and discussed. The assignment of NMR peaks needs to be validated as the resonance signals for solids often deviate from those in solution. When the spectrum is compared to a simulation, modeling details should be specified. When the spectrum intensity is too weak due to low natural abundance of the nuclei of interest, isotope labeling is recommended. CP-MAS should be applied to both pristine reticular structures and those subjected to postsynthetic modifications. This analysis provides a quantitative measure of conversion,⁸⁸ which becomes very important in the case where the functional groups do not survive in acids and could not be quantified using solution NMR on the acid-digested frameworks.

Elemental Analysis

The weight percent of metal, carbon, hydrogen, nitrogen, and sulfur should be provided using chemical analysis and ICP-OES/MS. The values should be reported along with those calculated from an accurate formula. The elemental composition obtained from the surface using X-ray photoelectron spectroscopy (XPS) and EDX are not quantitatively reliable as the elemental information does not come equally from all regions of the sample, hence limiting the accuracy of these techniques, which should not replace the standard elemental analysis methods. We suggest measurement of the CHNS percentages should be within 0.40% (absolute) of the calculated values as has been commonly practiced and recommended in organic chemistry. If the deviation value exceeds the limit, a formula reflecting another possible structure should be proposed

Considering the porous nature of MOFs and COFs, measurements should be performed on the fully activated sample, with no guests remaining in the pores. Otherwise, a large degree of inaccuracy is introduced in the found formula. For instance, a sample based on MOF-5¹⁸ [found (%): C, 38.50; H, 2.28; N, 1.71; Zn, 31.56] could be interpreted as MOF-5 containing 0.9 DMF per formula unit [Zn₄O(O₂C−C₆H₄−CO₂)₃]·0.9{CHO−N(CH₃)₂}, Calc. (%): C, 38.37; H, 2.21; N, 1.51; Zn, 31.31], or MOF-5 with ∼3.3% linker vacancy and 1.1 DMF per formula unit [Zn₄O(O₂C−C₆H₄−CO₂)_2.9]·1.1{CHO−N(CH₃)₂}, Calc. (%): C, 38.16; H, 2.33; N, 1.85; Zn, 31.37]. Coordinated solvent (such as H₂O and C₂H₅OH) can be removed by activation, thus creating open metal sites in the framework. The uncoordinated metal sites may be saturated with moisture captured from the air, in which case sample handling should be done under inert atmosphere (e.g., glovebox). Given that reticular structures contain many different elements common between the framework and the guest molecules, we caution against the tendency to derive an empirical formula from elemental analysis that incorporates guest molecules. This aspect comes with the need to make sure that the sample analysis is performed on the fully activated framework.

Chemical Stability

It is crucial to list the details of chemical stability measurements when performed in moisture (temperature, humidity, time), or in any liquid environment (media, pH, temperature, time). Some parameters, such as the amount of sample in certain amount of liquid, with or without guests in the pores, and the time interval between the media exchange, may profoundly affect the results. When setting up a standard chemical stability study, we strongly suggest that it involves the conditions that are required by the intended application of the framework.

We propose the use of three different quality indicators to support the stability of reticular structures. First, crystallinity retention: the PXRD pattern of the sample before and after exposure to chemical agents should be carefully compared under similar data collection conditions to make sure the intensity of the peaks is maintained and no new peaks emerge. Alteration in peak intensity and width could indicate amorphization and, possibly, destruction of the framework, and it should be discussed accordingly. Second, porosity retention: A precise description of any change in surface area, pore size distribution, and pore volume should be made as this indicates compromised porosity and framework integrity. Third, weight retention: For measurements done in liquid media, weight loss of the sample could be obtained by measuring the concentration of metal and/or linker in the supernatant. Considering the structural diversity and complexity of reticular solids, a quantitative evaluation of these three indicators is highly recommended. When possible, the mechanism of degradation or reasons for the stability of the examined frameworks should be discussed.⁸⁹

Computational Modeling of Reticular Frameworks

Computational modeling of reticular structures has been usefully employed in the last 10–15 years.⁹⁰⁻⁹³ Multiscalar levels of simulations are employed ranging from quantum chemical calculations to explore catalysis in MOFs⁹⁴ and their conductive and magnetic properties, to classical simulations based on force fields⁹⁵⁻⁹⁷ to investigate gas storage, adsorption, separation, and transport. These simulations are very useful because they allow the community to predict novel compounds, their properties, and reactivity before they have been made in the laboratory, but they also pose a challenge because of the complexity of these systems and related phenomena. As was stated recently: “Electronic structure calculations have become ubiquitous, with much of the work published in the field (chemistry) today making use of theoretical results. [···] We find ourselves at a perceived turning point where quantum chemical calculations are believed by many to be on par with experimental methods.”⁹⁸

To make progress in computational and theoretical studies, it is important that the protocols of the simulations fulfill quality indicators and can be reproduced by different research groups. It is a best practice in computational chemistry, both in electronic structure theory and classical simulations, to benchmark methods. In order for these calculations to be reliable, a systematic validation has to be performed, and the limitations of the methods and models should be disclosed. Researchers should not only report results that agree with experiments as this will not necessarily be a quality indicator for the calculations. In the spirit of this article, we encourage both reviewers and editors to appreciate and value the challenges involved with calculations.

In the following, some examples will be presented on how to implement best practices in reticular systems. Let us start with an example of catalysis in MOFs. One should carefully describe their models and methods. It is a good practice to provide in the Supporting Information of a journal article one or more examples of relevant inputs/outputs of the calculations and the structural information on all the species investigated, i.e., coordinate files. When reporting the results one should always keep in mind the scenario in which someone from a different group would like to replicate them and should provide all the necessary information to do so. It is important to discuss the motivation for the choice of a model (for example, did you set up a finite cluster model or a periodic one of a MOF or COF, and why did you do so?) as well as the motivation for the choice of a level of theory, and one should not just state “that was used in previous studies”.⁹⁹ A best practice would be to compare different models (cluster vs periodic) and different methods (for example, different density functionals and different basis sets). Validation against existing experimental data is also a useful approach for assessing the quality of a given model and method. However, one should bear in mind that experiments and calculations may be carried out under different conditions. The main goal of theory is to make predictions, provide reasonable explanations, and inspire new thinking.

When one studies reactivity, the spin states of the species involved along the reaction should be reported together with relevant thermochemical quantities, e.g., enthalpies and free energies. One should be careful in describing the conditions in which the various thermodynamic contributions have been calculated (for example, temperature, pressure, and how vibrational frequencies have been accounted for to compute the vibrational partition function). The code used for these calculations and its version should be reported so that it can be replicated by others. The hardware such as type of processor and amount of RAM should also be described to give researchers an idea of the necessary amount of computational resources.

If one wishes to compute macroscopic properties, e.g., adsorption isotherms or other averaged properties in a MOF or COF, Monte Carlo or molecular dynamics simulations are usually performed. Force field development for reticular structures is an active area of research, and inconsistency issues among force fields may emerge. The force field employed in the simulations should be described, and all the relevant input and output files should be provided so that the calculations can be replicated. It is not uncommon that two different Monte Carlo codes, even using the same force field, give different results, depending on the specific sampling schemes used. Once a force field has been developed, it should be broadly tested with different codes to show that there is uniformity in the results. For the calculations to be fully reproducible, it is not enough to cite the reference of the force field, but rather all parameter values that are not part of the accepted standard should be reported in the Supporting Information. It is not uncommon that a small change in a parameter of a force field makes a result irreproducible, and this should be avoided.

Generally, it would be helpful if researchers create a repository with more information than what can be reported in the Supporting Information of a journal article. This repository should be made accessible to the community, especially when the research is conducted as part of a joint center involving many institutions and groups, where data sharing is particularly important.

Finally, it is a best practice to have more than one person working together on a computational project, if the project allows for such collaboration. The reason is that if two or more people work on the same project, even if from different angles, there will be more discussion and validation of the results. Moreover, this will foster collaboration and hopefully advance the level of the discovery. The emerging area of big data science, machine learning, and artificial intelligence in general is changing the way we make, analyze, and study reticular frameworks.¹⁰⁰ We expect that, in light of these developments, further elaboration on our standard practices will be made in due course.

Practice in Reporting Chemical Formulas

The preparation of a new reticular compound comes with the task of assigning a term of identification for easy reference. Ideally, the identification should be unique and concise, and give justice to the complexity of the newly made structure. Finding the right balance between clarity and brevity is especially challenging for reticular structures, where identifiers should not only give information concerning the chemical composition, but also the connectivity of the constituents. In addition, identifiers have to account for structural complexities, such as heterogeneity and postsynthetic modifications.

In reticular chemistry, the naming of a compound starts with the chemical formula (Table 1), which describes the chemical composition of the structure at hand. The analytical techniques necessary to obtain the accurate chemical formula were treated in the sections above; we emphasize once more that the chemical formula should reflect the experimentally obtained chemical composition and not the “ideal” expected one. For example, the reaction of Zn(NO₃)₂·4H₂O with benzene dicarboxylic acid under the reported reaction conditions gives Zn₄N₂O₁₅C₃₀H₂₆. This chemical formula gives the exact composition of the framework structure. However, it provides the reader with little information on the molecular composition and connectivity of the reported structure.

Table 1. Examples of Chemical Formula, Molecular Formula, Reticular Formula, and Trivial Names for MOF-5·2DMF and COF-300^18,101.

MOFs
chemical formula	Zn4N2O15C30H26
molecular formula	[Zn4O(O2C−C6H4−CO2)3]·2{CHO−N(CH3)2}
reticular formula	[(Zn4O)(BDC)3]·2DMF
trivial name	MOF−5·2DMF

COFs
chemical formula	C41H28N4
molecular formula	[C−(C6H4−NCH)4][(−C6H4−)]2
reticular formula	[(TAM)(BDA)2]imine
trivial name	COF-300

For this reason, we recommend a molecular formula [Zn₄O(O₂C−C₆H₄−CO₂)₃]·{2CHO−N(CH₃)₂}, which clarifies the nature of the building units making up the structure. Since the molecular formula can become elaborate, the reticular chemistry community has practiced writing a reticular formula [(Zn₄O)(BDC)₃]·2DMF, where the building units and guests are abbreviated for clarity. Generally, we recommend that the multimetallic SBU be distinguished from the organic linker and from any guests that might occupy the pores of the framework.

Note that when the framework contains guests, such as DMF, it is preceded by a dot in both the molecular and the reticular formulas. If the structure contains terminal ligands (such as H₂O) bound to the backbone, as in HKUST-1, this is accounted for in the formula before the dot: [Cu₃(BTC)₂(H₂O)₃]·xG, where G stands for guest.¹⁹ In the case of charged frameworks, the formula must also incorporate the counterions following the same convention, might they be ligands or guests.

For COFs, to specify the connectivity of the organic linkers, the reticular formula includes the type of linkage in the subscript. For example, the condensation of benzene dialdehyde (BDA) with tetra-(4-aminophenyl)-methane (TAM) affords the chemical formula C₄₁H₂₈N₄, which corresponds to the molecular formula [C−(C₆H₄−NCH)₄][(−C₆H₄−)]₂ and the reticular formula of [(TAM)(BDA)₂]_imine. Again, solvent or guest molecules that are part of the chemical formula should be specified as is the case for MOFs.

In addition to the molecular and reticular formula, a trivial name is assigned to each compound. In the case of [(Zn₄O)(BDC)₃], it is MOF-5, and for [(TAM)(BDA)₂]_imine, it is COF-300. We recommend that these trivial names refer to the framework structure for easy reference, and in the case that any variations are made on the backbone, such as metalation and covalent functionalization, these should be appropriately appended to the trivial name. For example, MOF-5 was originally assigned to the zinc-containing structure, but recently a cobalt substituted derivative was reported. This is preferably referred to as Co-MOF-5. If its partial substitution, then the molar ratio should be indicated as a subscript x, Co_x-MOF-5.¹⁰²

Framework Components

For reticular structures, it is useful to make the following distinctions to have consistency in reporting. We observed that these, on occasions, have been used interchangeably, and this has obscured their accurate meaning. First, linker/linkage/ligand: Linkers are organic components bearing strongly coordinating functional groups, such as carboxylates, azolates, phosphates, and catecholates, which are used to connect the inorganic SBUs into extended structures. Linkages are defined as the atoms involved in linking the binding groups from the linkers to the metals in the SBUs. For example, in MOF-74,¹⁰³ the linker is dihydroxyterepthalic acid, and the linkages are the Zn–O bonds made to the hydroxyls and carboxylates. Any solvent molecules bound to Zn, such as DMF, are ligands.

Second, COFs and porous polymers: COFs are defined as crystalline extended solids realized by linking only organic building units through covalent bonds between light elements (e.g., B, C, N, O, and Si).¹ Here, crystalline, covalently bonded, and extended are the three main prerequisites. The term “porous polymers” is usually used to refer to amorphous organic solids.

Third, MTV and solid solutions: Multivariate (MTV) frameworks have multiple types of functional groups and/or mixed metal components in the same structure.¹⁰⁴ The introduction of multiple functionalities and metals do not alter the connectivity (topology) of the underlying backbone structure. Multivariate components are thus occupying topologically equivalent positions. MTV frameworks should not be confused with solid solutions. The formation of solid solution requires the two constituents similar in size and shape, and partial or limited ranges of the constituents is far more common. A solid solution requires mutual solubility between the components, which implies exchangeability between them (as different metal atoms in alloys).¹⁰⁵ In a substitutional solid solution, the components are usually randomly distributed at sites, or ordered in a form of a supercell in some cases. On the other hand, in MTV frameworks, functionalities and metals with very different sizes and charges have proven to be compatible within one framework. The functional groups and metals are fixed at crystallographic positions by strong bonds, and the place swap is less likely.

Special Consideration in the Area of MTV-MOF

The continuing intense interest in MTV frameworks has motivated us to suggest a standard practice in characterizing and reporting them. We use here MTV-MOFs as an illustrative example. Assessing bulk purity and homogeneity is not straightforward since MTV-MOFs share the same backbone with the simple component MOFs. It is extremely difficult, when not impossible to differentiate a pure phase MTV-MOF from a physical mixture of its corresponding simple component MOFs using only PXRD. The difficulty is to determine whether one obtains a MOF of many different kinds of linkers or a physical mixture of many MOFs, each of which is composed of only one kind of linker. The authors should perform high resolution elemental mapping on many different fragments of crystals. When advanced solid-state NMR and advanced fluorescent spectroscopic techniques are possible, mapping of organic linkers should be provided by analyzing the interactions between different functionalities to ensure both the bulk purity and the homogeneity (or heterogeneity) of the MTV-MOFs.^106,107 The nomenclature of MTV-MOFs should reflect the composition of different metals and linkers in the structure, rather than the input ratio of different metals and linkers used in the synthesis. For example, the ratio of Mg/Mn (45:55) in MTV-MOF-74 structure deviates from the input ratio of Mg/Mn (30:70), and the suggested formula and name for this MOF should be stated as (Mg_xMn_1–x)₂(DOBDC) (x = 0.45, DOBDC = 2,5-dioxidotere-phthalate) and Mg_0.45Mn_0.55-MOF-74.

Illustration of Frameworks

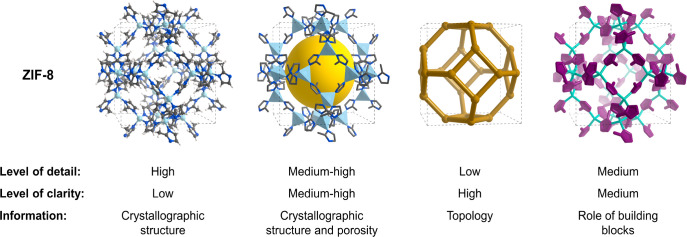
The proverbial phrase “a picture is worth a thousand words” holds particularly true in reticular chemistry, where illustrations are essential to visualize the extension of a structure into 2D and 3D space. Reticular frameworks—and illustrations thereof—are typically founded in crystal structures obtained by diffraction techniques. Finding the right balance between detail and clarity is challenging, and we wish to take this opportunity to discuss the different illustration techniques that are available for MOFs and COFs.

First, it should be specified whether the structure is based on experimental data or theoretical models. Artistic modifications of the experimentally found crystal structure are discouraged, as it may detract from the power of data. The depiction of a reticular structure ideally contains three components (such as in Figure 7). First, the molecular building units of the MOF or COF are presented. For MOFs, the SBUs should be illustrated in a stick-and-ball representation, accompanied by a polyhedral model, and highlighted throughout the figure. The organic units in MOFs and COFs are illustrated in a ChemDraw-style¹⁰⁸ representation.^101,109 It is worthwhile to specify the linkage of the COF structures. Second, for both MOFs and COFs, it is advisable to give an intermediate illustration, emphasizing the first sphere connectivity of the building blocks (SBUs and organic linkers). Third, we recommend providing an overall representation of the repeating unit (unit cell) of the crystal structure with special attention given to clarity. Depending on the focus of the framework representation, different graphical choices may be required to enhance the effectiveness of the illustration. Figure 8 provides the reader with some examples of how the same structure can be represented differently to highlight different aspects of the framework architecture, while achieving different degrees of clarity and level of detail. We recommend that the name and version of the program used to make the illustration be indicated in the figure caption or as a citation.^110−112 When a sphere (yellow in Figure 7–8) is placed in the pore of an illustrated framework, its size should be that of the largest sphere that can fit in that pore without touching the van der Waals radii of the framework atoms. A more detailed description of the graphical choices and technical guidelines for their use is provided in the Supporting Information. The underlying net of the MOF or COF, usually found in structural databases, such as the RCSR, should be given in a three-letter symbol (bold, lowercase).^{73,74,113−115}

Figure 7.

Example of a MOF and a COF depicted in three building-up stages (specified in the section above).^{101,109−111} The unit cell is highlighted in dashed gray lines. Only one of the interpenetrated networks of COF-300 is shown.

Figure 8.

Structure of ZIF-8 (sod) is used to show how different graphical options can enhance clarity while highlighting the type of information that the figure aims to provide.^112,115 The unit cell is highlighted in dashed black lines.

Scholarly Practice of Citations

Scientists are arguably motivated by the thrill of discovery and to a certain extent by gaining credit for those discoveries. Nowhere more than in an emerging field is the need more pressing for authors to provide scholarly citations and comparisons of relevant work done by others. This topic has been discussed and presented in cogent articles over the years.¹¹⁶ The recent rapid rise in the number of publications and the speed with which these are being communicated make it necessary to adhere to high standards of acknowledging others’ work. Here, we wish to encourage practices in citations that will enhance the quality of scientific reports. First, original citations: It is a scholarly practice to cite the work that influenced researchers’ thinking and their study. The practice of “political citations” is considered highly undesirable since it detracts from the scholarship of the scientific contribution. Second, reference “38(d)”: Key earlier contribution should be cited up front and not buried deeply in the reference list or not cited at all. Third, even comparisons: When comparisons are made to preceding work, it is fair and honest to make relevant and even comparisons. For example, if compound X’s performance is not as good as that of the tenth generation of compound Y (made by others), let us call it Y10; X should be compared to Y10 not the performance of the original version of Y. Fourth, early steps: In our eagerness to elevate our work, we unintentionally demote the importance and relevance of others’ work by not acknowledging it as an important “first” or “essential” step. Fifth, start from the same: When reproducing others’ work, it is necessary to start from their reported starting points and to follow closely their procedures before their results are deemed “irreproducible”. Sixth, substantiating claims by data: For example, we have heard it said, and occasionally seen it written, that “MOFs or COFs are expensive” or “unstable” without actual data (or citations) to support these generalizations. There is a wide range of variations of MOFs made from almost every metal in the periodic table, and many of which are made from inexpensive organic linkers (some of these linkers also form the basis for COFs). Which ones are expensive and, more to the point, how much do they cost? The answer almost always depends on the application of the reticular structure in question, its production scale, and many would argue, market forces.

Concerning stability, we all know examples of MOFs and more recently COFs exhibiting extraordinary thermal and chemical stability and that reticular structures have long moved beyond this question.^1,117 We note that stability or lack thereof find equally important utility as the intended function may require. Thus, we recommend that a MOF or COF be specified in the discussions concerning cost and stability, or any other attribute, and that it be backed by data.

Closing Remarks

In this contribution, we briefly outlined some of what we think are worthwhile considerations concerning standard practices and quality indicators in the field of reticular chemistry. We are all “guilty” on occasion to have overlooked some of these points in our own work and publications, but certainly we all endeavor to continue to improve and build on such standard “best” practices as the field evolves. In no way does our presentation mean that this is the first and last word on this topic, but we sincerely and in good faith attempted to remind, inform, and hopefully inspire serious thinking around these important considerations for the ultimate objective of improving our way of acquiring and presenting data. With this contribution, each one of us has the opportunity to share it with potential authors and researchers embarking on presenting their work to the wider community.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.0c00592.

• Description of data search for Figure 1; detailed description of graphical illustrations; color codes and settings for Figure 7 (PDF)

Author Contributions

^‡ C.G. and S.C. share equal contribution.

C.G., Leopoldina postdoctoral fellow of the German National Academy of Science (LPDS 2019-02), acknowledges the receipt of a fellowship of the Swiss National Science Foundation (P2EZP2-184380). S.C. acknowledges the Research Foundation Flanders (FWO) for supporting his research (Project 12ZV120N). S.W. acknowledges funding from the Basque Government Industry Department under ELKARTEK and HAZITEK programs. F.G. acknowledges funding from the Spanish Research Agency (AEI, CTQ2017-87262-R, EUR2019-103824), and Ramón y Cajal program (RyC-2015-18384). Q.L. acknowledges the National Natural Science Foundation of China (21922103 and 21961132003) for supporting his research. L.G. acknowledges the Inorganometallic Catalyst Design Center, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences (DE-SC0012702), and the Nanoporous Materials Genome Center, funded by the U.S. Department of Energy, Office of Basic Energy Sciences, under Award DE-FG02-17ER16362, as part of the Computational Chemical Sciences Program. O.M.Y. acknowledges the support and collaboration as part of UC Berkeley-KACST Joint Center of Excellence for Nanomaterials for Clean Energy Applications, King Abdulaziz City for Science and Technology, Riyadh 11442, Saudi Arabia.

The authors declare no competing financial interest.