Predicting short-range order and correlated phenomena in disordered crystalline materials

Short-range structure in disordered materials can be predicted by application of Pauling’s rules.

Abstract

Disordered crystalline materials are used in a wide variety of energy-related technologies. Recent results from neutron total scattering experiments have shown that the atomic arrangements of many disordered crystalline materials are not random nor are they represented by the long-range structure observed from diffraction experiments. Despite the importance of disordered materials and the impact of disorder on the expression of physical properties, the underlying fundamental atomic-scale rules of disordering are not currently well understood. Here, we report that heterogeneous disordering (and associated structural distortions) can be understood by the straightforward application of Pauling’s rules (1929). This insight, corroborated by first principles calculations, can be used to predict the short-range, atomic-scale changes that result from structural disordering induced by extreme conditions associated with energy-related applications, such as high temperature, high pressure, and intense radiation fields.

INTRODUCTION

Structural disorder in crystalline materials can be engineered for specific functionalities, such as increasing conductivity via chemical doping in semiconductors (1), enhancing flux pinning in high-temperature superconductors (2), and optimizing electrical properties of PZT (lead zirconate titanate perovskite) (3). In these materials, structural properties are commonly studied with techniques that probe the translational periodicity of the atomic constituents over repeating unit cell length scales, such as by x-ray diffraction, and modeled as though atoms may be randomly distributed across their atomic sites. Recently, however, with the development of experimental techniques capable of probing subnanometer length scales, there has been an increased interest in disordered materials for which the actual atomic arrangement is not represented by the periodic structure identified from a diffraction experiment (4). In some disordered oxides, it has been shown that atomic distributions only appear random when sampled over long length scales but are, in fact, ordered at the nanoscale (5, 6). Thus, there is a decoupling of the local symmetry of atomic configurations from the symmetry of the global, long-range structure.

Although discrepancies between short- and long-range structures (7, 8) and a locally ordered distribution of atoms (or vacancies) (9–11) have been reported for disordered crystalline materials, the challenge has been to characterize these materials over multiple length scales. For instance, Shamblin et al. (5) investigated a disordered fluorite structure formed by Ho₂Zr₂O₇, similar to the structure adopted by yttria-stabilized zirconia (Y_xZr_1−xO_2−0.5x) and nuclear fuel uranium dioxide (UO_2+x + fission products). Using the neutron total scattering method (12), they showed that the local atomic distribution in Ho₂Zr₂O₇ is not represented by a disordered fluorite structure but instead is better explained by a lower-symmetry superstructure of the fluorite structure in which cations and oxygen ions are distributed in a nonrandom manner with concomitant structural distortions. The origin of this short-range ordering is not understood nor is the relation between the short- and long-range atomic configurations. Here, we demonstrate that such heterogeneous structural disorder can be understood by application of Pauling’s rules (13, 14). These rules were established on the basis of ordered crystalline structures with atoms placed at ideal positions, in agreement with x-ray diffraction experiments. The same rules, which include a powerful electrostatic principle dictating charge balance, can be applied to predict the intricate short-range atomic ordering schemes and correlated phenomena observed in disordered crystalline materials. This approach advances the current understanding of disordered crystalline materials, as the principle governing balance of ionic charges applies to second nearest neighbor interactions, and Pauling’s rules are used in a predictive manner. These predictions are corroborated by neutron total scattering experiments, sensitive to both cation and anion behavior across all spatial scales, and first principles calculations.

RESULTS AND DISCUSSION

To construct an atomic-scale understanding of heterogeneous disorder, we have focused on the complex oxide structures of spinel (rock salt derivative, general formula AB₂O₄, Fd-3m) and pyrochlore (fluorite derivative, general formula A₂B₂O₇, Fd-3m) as model systems because of their inherent structural disorder (15, 16), a reported discrepancy between the long- and short-range behavior (5, 6), and their importance to many energy-related applications (17, 18). Spinel oxides are isostructural with natural magnesium aluminate (MgAl₂O₄) and are conventionally described by three structural parameters: the isometric unit cell parameter (a), the position of the oxygen anion along the unit cell body diagonal (u), and the inversion parameter (i). Many members of this structural family are disordered, where the two cations are distributed across four-coordinated tetrahedral sites and six-coordinated octahedral sites; the inversion parameter quantifies the fraction of tetrahedral sites occupied by the B cation. Each oxygen is crystallographically equivalent (Wyckoff equipoint 32e), bonded to one tetrahedrally coordinated cation and three octahedrally coordinated cations. This structure is indicated by the Bragg peaks in the neutron diffraction pattern (Fig. 1A) with this specific MgAl₂O₄ sample exhibiting an inversion parameter of 38%. According to this structural model, the cation tetrahedra are identical in all ways (i.e., volume, bond lengths, and bond angles), regardless of whether they are occupied by the larger Mg²⁺ (ionic radius^IV = 0.57 Å) (19) or smaller Al³⁺ (ionic radius^IV = 0.39 Å).

Fig. 1. Neutron total scattering data collected from disordered MgAl₂O₄.

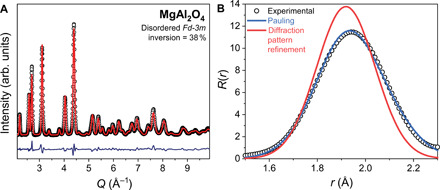
(A) Experimental neutron diffraction pattern (black circles) of MgAl₂O₄ modeled with the disordered spinel structure (red line). (B) Experimental pair distribution function (PDF; black circles) of MgAl₂O₄ compared with a simulated PDF calculated from the model refined from the diffraction pattern (red) and one simulated directly from application of Pauling’s first rule (blue) with Shannon’s ionic radii.

To probe the atomic-scale structure of MgAl₂O₄, we analyzed the pair distribution function (PDF) collected from a neutron total scattering experiment (Fig. 1B). This experimental approach is well suited for heterogeneously disordered oxides because (i) neutrons scatter strongly from oxygen and generally provide contrast between elements of similar atomic number (e.g., Mg and Al), and (ii) diffuse scattering that arises due to local deviations from the global space group symmetry (12) can be analyzed in real space. The PDF of MgAl₂O₄ is a histogram of atom-atom distances (20). There is an obvious discrepancy between the experimental PDF (Fig. 1B, black circles) and the one simulated from the long-range disordered spinel structural model (Fd-3m) obtained from analysis of the neutron diffraction pattern (Fig. 1B, red line) (6). The long-range structural model creates Mg─O and Al─O bond distances (d_A−O = 3a(u − 1/4), d_B−O = a [2(u − 3/8)² + (5/8 − u)²]^1/2) (15) that are too short to accurately reproduce the actual interatomic distances observed in the experimental data. This implies that the local atomic arrangement of MgAl₂O₄ is not represented by the disordered, long-range structure. This discrepancy, however, can be reconciled by extending Pauling’s rules to disordered spinel. A straightforward application of Pauling’s first rule, which states that the cation-anion distance is the sum of the cationic and anionic radii, indicates that the polyhedra in each case should be much different. When the Mg²⁺ occupies the tetrahedral site, the sum of the ionic radii (O^2−,IV + Mg^2+,IV) is 1.95 Å and when Al³⁺ occupies the tetrahedral site, the sum is 1.77 Å. A hypothetical PDF can be constructed using only Pauling’s first rule (Fig. 1B, blue line) that more accurately reproduces the experimental PDF than the long-range disordered spinel model. In this representation, the structural distortion associated with cation inversion is better accounted for by the incorporation of bond lengths predicted by the first rule.

Cation inversion also leads to complex charge balance schemes. The disordered structure, according to the diffraction pattern analysis, has cations randomly distributed on the cation sublattice, but in reality, each cation polyhedra must be occupied either by Mg²⁺ or by Al³⁺. When an oxygen is bonded to Mg²⁺ in tetrahedral coordination, then it can also be bonded with zero, one, two, or three other Mg²⁺ in octahedral coordination, and the same four octahedral combinations are available when Al³⁺ is in tetrahedral coordination. Therefore, disordering of the cation sublattice results in eight unique local oxygen environments (Fig. 2). The bond strength (charge divided by coordination number) sum of each of these environments, governed by Pauling’s second rule, provides further insight into the local atomic configuration of the disordered phase. When Mg²⁺ occupies the tetrahedral site (∼62% occurrence), there is a unique way to locally satisfy this rule: by filling the octahedral sites with Al³⁺, which is the conventional, “normal” spinel arrangement. When Al³⁺ occupies the tetrahedral site (∼38%), there is no way to exactly satisfy the second rule. Pauling gives a prescription for this problem by stating that, while this rule may not be “rigorously satisfied...it should, however, be always satisfied approximately.” The most straightforward solution to this problem in a disordered spinel is a simple mixture of the motifs in which the electrostatic valence bond strengths are 2.083 and 1.917, which average to 2. In this scheme, when an oxygen is bonded to an Al³⁺ tetrahedra, it will prefer to be coordinated to two Mg²⁺ and one Al³⁺ octahedra and be nearest neighbors with an oxygen that bonded with an Al³⁺ tetrahedra, one Mg²⁺, and two Al³⁺ octahedra. This valence consideration explains the atomic arrangement that was revealed by O’Quinn et al. (6), in which the local structure around a cation antisite in Mg_1−xNi_xAl₂O₄ was best modeled with a tetragonal unit cell and three unique oxygen positions (Pauling bond strength sums of 2, 2.083, and 1.917). In this case, the lower-symmetry “local phase” contained the necessary short-range atomic ordering and associated relaxations required to satisfy Pauling’s rules. Therefore, the PDF of this disordered material is reproduced correctly by accounting for Pauling’s first and second rules: The size mismatch of the ions dictates a specific structural distortion away from the long-range symmetry (Fig. 1B), and local charge balance dictates a specific distribution of ions within a lower-symmetry structural motif (Fig. 2). The question arises whether Pauling’s rules are only useful to understand the local atomic arrangements within a disordered material or whether they can also give fundamental insight into the underlying mechanisms that govern the actual disordering process itself.

Fig. 2. Schematic representation of the eight possible combinations of oxygen environments in the A²⁺B³⁺₂O⁻⁴₂ spinel structure with their electrostatic valence bond strengths calculated from Pauling’s second rule.

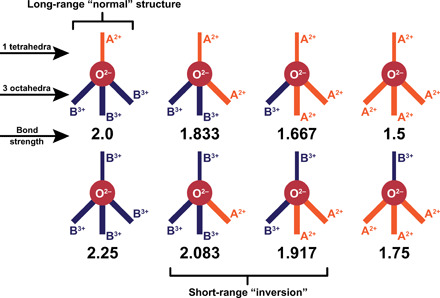
In this representation, the thinner solid line above the oxygen anion (symbolized as solid red circle) represents the single bond with the tetrahedral site, and the three thicker solid lines below oxygen represent the bonds with the octahedral sites. The orange and dark blue bonds are with A²⁺ and B³⁺ cations, respectively. Only one of the eight possible arrangements produce an electrostatic valence bond strength equal and opposed to that of the oxygen anion satisfying Pauling’s valence rule (the normal spinel arrangement, top left).

To answer this question, we have investigated the pyrochlore-to-fluorite transformation (general formula A₂B₂O₇), a classical example of a disordering process. Whereas fluorite oxides (AO₂) contain large, tetravalent cations, there are two cation sites in the pyrochlore structure: an eight-coordinated A site generally occupied by a trivalent rare-earth cation and a six-coordinated B site generally occupied by a tetravalent group 4 element (Fig. 3A) (21); the stability field of the pyrochlore structure has been generally correlated with the cationic radius ratio (1.46 < r_A^VIII/r_B^VI < 1.78). The ordered pyrochlore structure can be driven by irradiation, temperature, pressure, or chemical doping into a disordered state (22, 23), with a disordering process proposed to be driven by cation exchange (24, 25), by randomization of vacancies on the oxygen sublattice (26, 27), or by simultaneous rearrangements on both sublattices (28). Sufficient disordering of the pyrochlore structure ultimately triggers a long-range order-disorder transformation to a fully disordered, anion-deficient fluorite structure (“defect fluorite,” Fm-3m) (22, 29). The preference of the cations for specific local environments, given by Pauling’s rules, helps to identify the atomic-scale disordering sequence, as well as the final atomic arrangement, which is not random but retains some level of predictable order, similar to the behavior observed in spinel. While the disordering of a pyrochlore structure does involve both cation antisite and anion Frenkel defects (22), it can be surmised by application of Pauling’s first rule that cation sublattice disorder is driven by an anion sublattice disordering mechanism (fluorite-related structures are generally oxygen ion conductors) (18). Without a precursor oxygen defect, the sizes of the cation coordination polyhedra are simply too large (or small) to accommodate a stable cation antisite defect. In contrast, the motion of the 48f oxygen to the previously vacant 8a site creates a distinct pattern of cation coordination geometries in the local environment around the Frenkel defect (an “8-7-6-7” arrangement; Fig. 3B). Whereas, previously, the tri- and tetravalent cations had a preference for occupying the large, eight-coordinate and small, six-coordinate sites, respectively, newly created seven-coordinate sites (more appropriate in size for both A³⁺ and B⁴⁺) become available for the formation of cation antisite defects via the motion of the oxygen anion. This scenario is in excellent agreement with previous ab initio studies on pyrochlore oxides that showed that oxygen migration facilitates the disordering process (30, 31). However, in contrast to the traditional long-range picture of a complete cation randomization into only seven-coordinated polyhedra, part of the initial coordination polyhedra are retained in the local structure of the disordered phase. In the traditional structural approach, it is not easy to unambiguously determine how many of the original polyhedra are retained in the new structural motif or how far this motif extends into the ordered matrix. This can be better conceptualized in the framework of the structural building blocks that form the ordered structure and their change through the motion of oxygen into the vacant site. The pyrochlore structure can be built using a layer stacking model (32) that consists of an A₃B layer, a Kagome lattice of A^VIII cations with B^VI cations occupying the interstices (Fig. 4A), and an AB₃ layer, a Kagome lattice of B^VI cations with A^VIII cations occupying the interstices (Fig. 4B). The building blocks that produce these layers (33) are arrangements of A₃B (8-8-8-6 motif) and AB₃ (6-6-6-8 motif) polyhedra (Fig. 4C). These blocks can be understood in terms of Pauling’s rules as fundamental units with particularly stable polyhedral configurations. The disordering process induced by movement of the 48f oxygen into the vacant 8a site now changes the polyhedra and cation coordination scheme of the building blocks to an 8-7-7-6 motif in the A₃B layer and a 6-7-7-8 motif in the AB₃ layer (Fig. 4D). Thus, the six-coordinated sites are now highly distorted, ideally prompting a subsequent relaxation of other oxygen. Interestingly, the 8-7-7-6 motif of coordination polyhedra is characteristic for weberite-type Y₃TaO₇ (C222₁). This explains why a weberite-type structure has been previously shown to accurately model the local structure of a material that adopts the disordered, anion-deficient fluorite structure (5). The C222₁ space group, in particular, best describes the experimental neutron PDF of the disordered, anion-deficient fluorite Ho₂Zr₂O₇ (fig. S1) with the difference that the seven-coordinated polyhedra are populated by both Ho³⁺ and Zr⁴⁺ cations (only Y³⁺ for Y₃TaO₇). This Pauling-inspired building block approach also has practical applications. Using the fundamental building blocks of the pyrochlore and weberite-type structure, we constructed primitive cells for first principles calculations, which reveal that a local structure containing weberite-type building blocks (Fig. 4E) is a lower-energy configuration for Ho₂Zr₂O₇ than a local structure containing pyrochlore building blocks with only eight and six coordination; the reverse is true for Ho₂Ti₂O₇ (table S1). Even after removing the constraints of the weberite-type symmetry on Ho₂Zr₂O₇, the relaxation of this atomic arrangement converges to the same energy (−198.811 eV) with a nearly identical configuration. The density functional theory (DFT) calculations also show how the previously distorted six-coordinated octahedra that are distorted by the oxygen motion are now relaxed such that the two polar oxygen form a ∼180° angle (as was the case with ordered pyrochlore). With the application of Pauling’s rules to the disordering process of pyrochlore, the local weberite-type polyhedral motif can be fully explained.

Fig. 3. Schematic illustration of cation coordination.

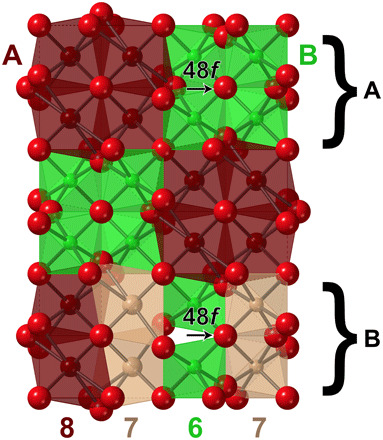
(A) before and (B) after the motion of an oxygen anion from the 48f to the 8a Wyckoff equipoint in the pyrochlore structure. The dark brown polyhedra are eight-coordinated, the light brown polyhedra are seven-coordinated, and the green polyhedra are six-coordinated. The viewing direction is [100]_Fd-3m.

Fig. 4. Two cation layers comprise the layer stacking model (32) that describes the pyrochlore structure.

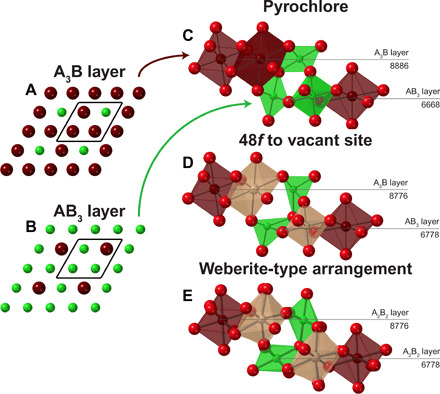
The fundamental building blocks contained within these two layers comprising the layer stacking model, (A) an A₃B layer and an (B) AB₃ layer, are shown (C) before and (D) after the motion of an oxygen anion from the 48f to the 8a Wyckoff equipoint. The cation coordination scheme is compared with (E) the DFT-relaxed weberite-type arrangement of Ho₂Zr₂O₇. The dark brown polyhedra are eight coordinated, the light brown polyhedra are seven coordinated, and the green polyhedra are six coordinated. The viewing directions for (A) and (B) are [1 1 1]_Fd-3m, [0 −1 1]_Fd-3m for (C) and (D), and [0 1 0]_C21/m for (E).

What remains to be understood for a full description of the heterogeneous disorder in pyrochlore oxides is the relation between the weberite-type local structural motifs and the long-range disordered, anion-deficient fluorite structure. While the weberite-type structural motifs are induced over a subnanometer length scale, they still scatter neutrons (or x-rays) coherently. A crystallographic approach developed by Neder et al. (34) considers these structural motifs as ordered variants inserted in a host crystal that is the configuration average of all possible orientations (phases) of the domains. One can show with a detailed crystallographic analysis that the sharp Bragg intensities correspond to the reciprocal lattice points of the host crystal, while diffuse scattering is induced by the correlated differences between each domain structure and the average host crystal structure. This approach explains, based on group theory, that an ensemble of subnanoscale weberite structural motifs (C222₁) with all possible orientations (formed by random movement of different 48f oxygens into vacant 8a sites) will become, on average, an anion-deficient fluorite structure (Fm-3m) over longer length scales, resulting in the extinction of all superstructure peaks (Supplementary Materials). Thus, the disordering process in pyrochlore can be understood as an accumulation of local weberite-type structural motifs that form a long-range anion-deficient fluorite structure, yielding the observed heterogeneous structure over different length scales. Through a solid-solution series that covers the entire order-disorder space from fully ordered pyrochlore (Ho₂Ti₂O₇) to fully disordered, anion-deficient fluorite (Ho₂Zr₂O₇), we have investigated whether the order-to-disorder transformation proceeds over different length scales simultaneously. Neutron total scattering experiments were performed on intermediate members of the solid solution binary Ho₂(Ti_1−xZr_x)₂O₇. The neutron diffraction data reveal that there is a narrow compositional range over which the series transforms from the pyrochlore structure to the disordered, anion-deficient fluorite structure (Fig. 5, black line). By contrast, the local weberite-type phase forms immediately upon substitution of Zr for Ti, and the fraction increases nearly linearly with the amount of Zr across the series (Fig. 5, red line). Thus, there is an apparent decoupling of the local weberite-type formation in Ho₂(Ti_1−xZr_x)₂O₇ that proceeds gradually upon substitution for Ti⁴⁺ with Zr⁴⁺, while the long-range anion-deficient fluorite phase forms only within a narrow compositional range of about ∼60% substitution. Again, Pauling’s rules are key to explain this complex and intriguing disordering scheme. Once an oxygen is moved into a vacant site and a sevenfold Zr⁴⁺ site is created, this limits the movement of other nearby oxygens; another oxygen must not move to be also coordinated with this newly created sevenfold Zr⁴⁺ site. Thus, the newly formed local environment dictates how the construction of the material must proceed over longer length scales. To obey Pauling’s rules, the local weberite domains will maintain a critical distance until a certain critical density is reached, which triggers a long-range phase transformation. A similar behavior has been observed in phase transformations induced by heavy ion irradiation of A₂O₃ oxides (35) in which oxygen vacancies are created and arrange themselves as far away from one another as possible until saturation triggers a global phase transformation. The present data can be interpreted in the same way, particularly as the fundamental weberite-type structural motif is just, in principle, the short-range ordering and structural relaxations associated with an anion Frenkel defect (Fig. 4E).

Fig. 5. The locally ordered weberite-type (red diamonds) versus global, disordered, anion-deficient fluorite phase fractions (black squares), obtained from small-box and Rietveld refinements of neutron total scattering data, respectively, from Ho₂Ti_2−xZr_xO₇ pyrochlore.

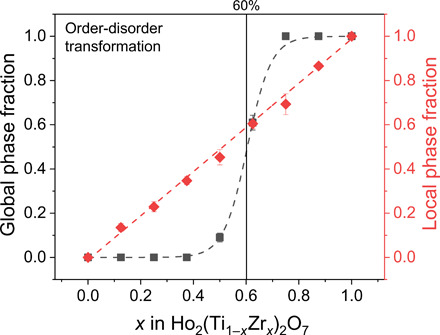
Dashed lines are included to guide the eye.

As structural disorder is highly correlated with the expression of physical properties, this new insight has implications for engineering materials over different length scales to obtain the desired physical properties for technologically important applications. The promise of manipulating the specific local environment of a material that appears randomly disordered can be appreciated with the example of PZT perovskite. The origin of enhanced piezoelectricity in PZT has remained largely a mystery since the 1950s due to the complex phase diagram of the material (36). Recent work has suggested that piezoelectricity in PZT may be explained by the growth of nanoscale low-symmetry domains that average to a different higher-symmetry structure over longer length scales (37). Within a certain compositional range, the substitution of Zr⁴⁺ for Ti⁴⁺ modifies local cation environments and increases the piezoelectric response without altering the observed long-range symmetry (7). The fact that the local structure of such a disordered material can now be interpreted as a result of fundamental known chemical rules is relevant for next-generation materials engineering. In pyrochlore oxides, the propensity of the structure to disorder has been linked with increased oxygen conductivity (38), improved performance in radiation fields (39), and the emergence of exotic magnetic properties such as spin ice behavior (40). This study has provided the basis not only to understand these phenomena in terms of the underlying atomic arrangement but also how to manipulate the structure across different length scales to induce desired material properties.

Pauling’s original formulations were based on the nature of chemical bonds between ions (41), a very short-range interaction dictated by quantum mechanics (42). Thus, it is therefore not unexpected that a disordering mechanism will not violate these fundamental chemical rules. Once disorder is induced via some internal (e.g., doping) or external (e.g., irradiation, pressure, and mechanical action) mechanism, the atomic structure will rearrange itself to a specific configuration that is a direct consequence of Pauling’s rules. For example, inversion in spinel or cation antisite defects in pyrochlore is not just simply switching atoms, which would violate these rules, but instead new sites are created that accommodate the size and charge of the cations. Thus, this rearrangement and its consequences for both the short- and long-range structures can be correctly predicted by Pauling’s rules: Rule 1 determines how far apart atoms are and how many neighbors atoms have, rule 2 determines how unlike ions balance charge with one another, rules 3 and 4 determine how like ions repel charges from one another, and rule 5 is a restatement of Occam’s razor—the complexity of the structure should be a minimum. The examples discussed in this study were predominately explained with Pauling’s first and second rules, which describe highly local phenomena: the distances between ions, the coordination polyhedra they form, and the way that unlike ions balance charges. Rules 3 to 5 were used to verify the obtained structural models. While we have shown the examples of the behavior of spinel and pyrochlore structures, we have experimental data that show the same behavior for doped ThO₂, A₂BO₅ oxides, and A₃BO₇ oxides. Furthermore, this complexity has been observed in materials disordered by nonstoichiometry (43), intense radiation (10), mechanochemical synthesis (44), or temperature exposure (45). This demonstrates that the new disordering concept presented in this study is, as Pauling’s rules were for ordered ionic compounds, a general phenomenon for a wide range of disordered materials independent on how the disorder is introduced. This knowledge is important, as the specific short-range atomic configurations in these materials are no longer represented by the observable long-range structure. If disorder occurs in a crystalline material, then Pauling’s rules can be used to predict which atoms move from their ideal positions to their final arrangement within the disordered phase (Fig. 6). This atomic-scale process is not random, as would be suggested by the structural behavior over longer length scales, but involves a high level of order that must be considered when designing materials for energy-related applications.

Fig. 6. Schematic illustration of atomic arrangements in ordered (left) and disordered (right) ionic materials.

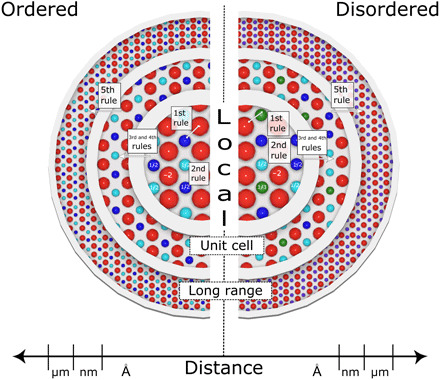
The red circles represent anions, and the different blue and green circles represent unique cation species. When a material that appears structurally disordered over longer length scales is studied at the atomic-scale, the actual atomic configuration and accompanying structural distortions obey Pauling’s rules. The rules are labeled for the length scales over which they are primarily applicable.

MATERIALS AND METHODS

Neutron total scattering

Oxide materials for this study were prepared via conventional solid-state methods. Structural characterization was performed at the Nanoscale-Ordered Materials Diffractometer (NOMAD) beamline (46) of Oak Ridge National Laboratory’s Spallation Neutron Source. Polycrystalline powders (100 to 150 mg) of each sample were placed in quartz capillaries and exposed to the thermal neutron beam. Scattering background was accounted for by subtracting the scattering data collected from an empty quartz capillary of identical dimension measured for an identical length of time to the sample of interest. The total scattering structure function, S(Q), was produced by normalizing the background-corrected scattering data to neutron scattering from vanadium (to account for the neutron spectrum). Using STOG (47), the PDF, G(r), was obtained from the structure function, S(Q), via Fourier transform

$$G(r)=4\mathrm{\pi }r{\mathrm{\rho }}_0[g(r)-1]=\frac{2}{\mathrm{\pi }}\int Q[S(Q)-1]\text{sin}(\mathit{Qr})\mathit{dQ}$$ (1)

where the integral was carried out over a Q range of 0.2 to 31.4 Å⁻¹. The magnitude of the scattering vector, Q, is given by

$$Q=\frac{4\mathrm{\pi } \text{sin}\mathrm{\theta }}{\mathrm{\lambda }}$$ (2)

where λ is the neutron wavelength. The PDF, g(r), is related to the radial distribution function (RDF), R(r) (20), by

$$R(r)=4\mathrm{\pi }{r}^2{\mathrm{\rho }}_{0}g(r)$$ (3)

where ρ₀ is the sample atomic density.

X-ray total scattering

X-ray total scattering was performed at the 28-ID-2 X-ray Powder Diffraction (XPD) beamline at the National Synchrotron Light Source-II (48) at Brookhaven National Laboratory. Ho₂Zr₂O₇ powder was investigated at room temperature in a Kapton tube capillary with an exposure time of 10 s and photon wavelength of 0.18754 Å (~66.1 keV). An empty Kapton tube and a LaB₆ standard were measured to correctly subtract the capillary’s scattering as background, scale the sample’s scattering intensity correctly, and determine the instrument parameters for use in structural refinement software. The scattering from the sample was recorded as a two-dimensional (2D) diffractogram gathered using a PerkinElmer XRD 1621 digital imaging detector. The structure function S(Q) was extracted from the resulting 2D diffraction image, with the scattering vector Q varying from Q_min = 0.5 Å⁻¹ to Q_max = 25.0 Å⁻¹. The PDF, G(r), was obtained using the software PDFgetX3 (49) via the relation

$$G(r)=r(A{\displaystyle {\int }_{Q_{\text{min}}}^{Q_{\text{max}}}}Q[S(Q)-1]\text{sin}(\mathit{Qr})\mathit{dQ})$$ (4)

Total scattering data were analyzed by a variety of methods including Rietveld and small-box refinement. General Structure Analysis System (GSAS) I (50) and GSAS II (51) were used to perform Rietveld refinement of the diffraction patterns, in which refined parameters included vertical scale, unit cell parameters, atomic positions, atomic displacement parameters, and site occupancies when appropriate. PDFgui (52) was used to perform small-box refinements of the PDFs; in addition to the same parameters that are refined during Rietveld refinements, another parameter was refined to account for correlated atomic motion that has the effect of sharpening the peaks in low r. Additional details concerning the small-box refinement of disordered spinel and fluorite oxides can be found elsewhere (5, 6). Simulated RDFs were calculated using the relation

$$\text{Coordination number}=\int R(r)\mathit{dr}$$ (5)

accounting for the fact that the total RDF is composed of contributions from partial pair correlations, which are weighted by the product of the neutron scattering lengths and concentrations of the atoms that comprise the pair.

First principles calculations

To identify the thermodynamically stable forms of Ho₂Zr₂O₇ and Ho₂Ti₂O₇ and the different atomic arrangements, we calculated the relative stabilities of four different phases by first principles calculations: pyrochlore, weberite (Imma), and two weberite-type arrangements derived by the C222₁ structure of Y₃TaO₇. The electronic structure calculations are performed within the DFT framework using the projector augmented wave approach (53) for the core-valence interaction and the general gradient approximation with Perdew-Burke-Ernzerhof (PBE)–generalized gradient approximation (CGA) (54) for the exchange-correlation functional as implemented in the Vienna Ab initio Simulation Package (VASP) code (55).

The potentials use 9 valence electrons for Ho, 12 for Ti, 12 for Zr, and 6 for O. A plane wave kinetic energy cutoff was determined at 520 eV, with a uniform k-point mesh for Brillouin zone sampling, adapted to each specific symmetry, based on the Monkhorst-Pack scheme (56) that was found to be sufficient to achieve well-converged energies. Electronic self-consistency was considered achieved when the total energy change between electronic steps is less than ≤1 μeV. The lattice metric was relaxed for all crystal symmetries, and the internal structural parameters were relaxed until all Hellmann-Feynman forces on each ion were ≤2 meV/Å.

After the initial structural optimizations using the PBE GGA functionals, calculations were performed using GGA + U functionals within the simplified rotationally invariant approach introduced by Dudarev et al. (57) to take into account the strongly correlated nature of the f-states of Holmium. In those calculations, we used a Ho potential with 21 valence electrons. A (U-J) value of 5.4 eV was found to be a good compromise for all structures. The value was obtained using the linear response ansatz (58) and is in good agreement with previous reports in the literature for lanthanide systems (43, 59, 60).

The primitive structure of the weberite-type structure can be used as a starting point for modeling the A₂B₂O₇ compounds. Obviously, the change of stoichiometry from A₃BO₇ to A₂B₂O₇ destroys part of the symmetries of the structure. In the weberite-type A₃BO₇ structures, a quarter of the cations occupy the B site and are bonded to six O atoms, forming an octahedron. Another quarter of the cations occupy an A-type site and are bonded to eight O atoms, a polyhedron that can be described as a distorted cube. The remaining half of the A-type cations occupy the remaining A-type sites that are bonded to seven O atoms. A reasonable choice is to use half of the sevenfold-bonded A-type site to accommodate the surplus of B cations of the A₂B₂O₇ compound. There are two simple nonequivalent choices for distributing the B cations onto the sevenfold coordinated sites in an ordered way.

The first type of weberite-type structure corresponds to filling M1 and M2 sites with B-type ions. The other type of structure is created by filling M1 and M3 sites with B-type ions. The resulting symmetries in the conventional orthorhombic lattices are quite different. The DFT calculations were performed in primitive structures containing two chemical formulas of the compound. A uniform k-point mesh (6 × 6 × 5) for Brillouin zone sampling based on the Monkhorst-Pack scheme (56), corresponding to 54 irreducible points for the type 1 structure and to 36 points for the type 2 structure, was found to be sufficient to achieve well-converged energies. The space group of the type 1 structure is monoclinic C21/m. Unfortunately, this group does not exist in the International Tables of Crystallography (ITC), so we can only use the simple monoclinic subgroup P21/m to describe the type 1 structure in a standard way. The direct consequence of this choice is that the list of independent atoms doubles, because each atom in the structure is duplicated by the explicit expression of the C-centering. The space group of the type 2 structure, obtained transforming the primitive lattice back to the conventional representation of weberite-type structures, is orthorhombic C2mm (group number 38 in ITC) but with an origin shift (0 0 1).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/35/eabc2758/DC1