Increasing Muscle Speed Drives Changes in the Neuromuscular Transform of Motor Commands during Postnatal Development in Songbirds

Abstract

Progressive changes in vocal behavior over the course of vocal imitation leaning are often attributed exclusively to developing neural circuits, but the effects of postnatal body changes remain unknown. In songbirds, the syrinx transforms song system motor commands into sound and exhibits changes during song learning. Here we test the hypothesis that the transformation from motor commands to force trajectories by syringeal muscles functionally changes over vocal development in zebra finches. Our data collected in both sexes show that, only in males, muscle speed significantly increases and that supralinear summation occurs and increases with muscle contraction speed. Furthermore, we show that previously reported submillisecond spike timing in the avian cortex can be resolved by superfast syringeal muscles and that the sensitivity to spike timing increases with speed. Because motor neuron and muscle properties are tightly linked, we make predictions on the boundaries of the yet unknown motor code that correspond well with cortical activity. Together, we show that syringeal muscles undergo essential transformations during song learning that drastically change how neural commands are translated into force profiles and thereby acoustic features. We propose that the song system motor code must compensate for these changes to achieve its acoustic targets. Our data thus support the hypothesis that the neuromuscular transformation changes over vocal development and emphasizes the need for an embodied view of song motor learning.

SIGNIFICANCE STATEMENT Fine motor skill learning typically occurs in a postnatal period when the brain is learning to control a body that is changing dramatically due to growth and development. How the developing body influences motor code formation and vice versa remains largely unknown. Here we show that vocal muscles in songbirds undergo critical transformations during song learning that drastically change how neural commands are translated into force profiles and thereby acoustic features. We propose that the motor code must compensate for these changes to achieve its acoustic targets. Our data thus support the hypothesis that the neuromuscular transformation changes over vocal development and emphasizes the need for an embodied view of song motor learning.

Introduction

Animal behavior results from system-wide interactions among nervous system, muscles, body, and the surrounding environment (Chiel and Beer, 1997; Nishikawa et al., 2007). During motor skill learning, the brain generates activation patterns causing behaviors with increasing reliability, while the body exhibits large changes due to growth and training (Adam and Elemans, 2019). Because of the long extent (months to years) of fine motor skill learning, little is known about how motor code changes and how the developing body contributes to behavioral changes. Recent work shows that small changes in biomechanics can cause behavioral state changes previously attributed to neural drive alone (Zhang et al., 2019). It is thus essential to include biomechanics when studying motor control (Nishikawa et al., 2007; Tytell et al., 2011) and especially over developmental timescales (Zhang and Ghazanfar, 2018).

An excellent model to study motor skill learning is vocal imitation learning in songbirds. In zebra finches, males learn how to sing early in life by first memorizing a tutor song, which they match acoustically through trial-and-error learning over 60 days (Tchernichovski et al., 2001). Vocal output is controlled by well characterized neural circuitry (i.e., the song system) that consists of the following two main pathways: (1) the anterior forebrain pathway (AFP), which is necessary to learn and maintain song (Scharff and Nottebohm, 1991); and (2) the motor pathway, which encodes the learned vocalizations and is needed throughout life to produce them. In the avian cortex, the motor pathway produces millisecond-scale, precisely timed complex sequences of motor commands (Chi and Margoliash, 2001; Hahnloser et al., 2002) that result in force trajectories by respiratory and superfast vocal muscles (Elemans et al., 2008; Elemans, 2014). The transform from spikes to force is often referred to as the neuromuscular transform (NMT; Zhurov and Brezina, 2006). During song, these force trajectories modulate pressure in the respiratory system (Srivastava et al., 2017) and the position and tension of vibrating structures in the sound-producing organ, the syrinx, thereby altering the vocal output (Riede and Goller, 2010; Elemans, 2014). Thus, via the NMT, motor commands of the song system directly drive the acoustic features of song.

The changes in song observed over the course of vocal imitation learning are typically attributed to changes in neural drive (Jarvis, 2004; Fitch et al., 2010). However, in this same period the syrinx and particularly the syringeal muscles that execute motor commands from the song system are also undergoing significant changes (Adam and Elemans, 2019). One change directly influencing the NMT is that force responses of syringeal muscles double in speed when stimulated by single spikes (Mead et al., 2017). The observed changes seem driven predominantly by use, suggesting that extensive training of syringeal muscles is essential to achieve their maximal speed (Adam and Elemans, 2019). However, in vivo muscle contractions underlying behavior are never elicited by single spikes, but by spike trains with variable interspike intervals (ISIs), and it remains unknown whether the observed changes in muscle speed over development functionally alter force profiles and thereby behavioral output.

Here we test the hypothesis that muscle properties relevant to the NMT change over vocal development in male songbirds. We investigated three critical NMT features related to activation by spike trains. First, we show that all speed parameters of twitch and tetanic contractions significantly increase over vocal development. Second, we show that forces are higher than expected by linear summation (i.e., supralinear summation) and that this effect increases over development. Third, we show that submillisecond spike timing can be resolved by syringeal muscles and that spike timing sensitivity increases with speed. Together, our data show conclusively that the NMT changes over vocal development. We propose that the song system must compensate for NMT changes to achieve correct song targets, such as pitch trajectories over syllables. Because motor neuron (MN) and muscle properties are tightly linked, our data allow for predictions on the boundaries of the yet unknown motor code that correspond well to cortical activity.

Materials and Methods

Experimental animals

All data presented here were collected in zebra finches (Taeniopygia guttata). Birds were raised in individual breeding cages together with their biological parents and siblings. In total, 80 zebra finches were used in this study (males, 55; females, 25). All animals were kept on a 12h light/dark cycle and provided with food and water ad libitum. All experiments and procedures were performed in accordance with the Danish Animal Experiments Inspectorate (Copenhagen, Denmark).

To quantify speed-related contraction parameters of syringeal muscles over the course of vocal development, we extracted muscle fiber bundles from musculus tracheobronchialis dorsalis (DTB) of male syrinxes at the following four time points: at 25 d posthatch (DPH), right before the start of the sensorimotor phase (Roper and Zann, 2006); at 50 DPH, during plastic song; at 75 DPH, after the sensory phase has ended; and at 100 DPH, when song is crystalized and the birds are considered adults (Immelmann, 1984). We included a cohort of age-matched females for comparison. Sex was determined by dissection postmortem (25 DPH) or plumage (all other ages).

In vitro muscle physiology

Muscle fiber bundles were prepared and stimulated in vitro to record isometric force responses as previously described (Elemans et al., 2008; Srivastava et al., 2017). In brief, birds were killed by an isoflurane overdose, and the syrinx was exposed, isolated, and pinned down on SYLGARD-covered Petri dishes in cold, oxygenated Ringer's solution. Fiber bundles were obtained randomly from the left or right DTB. Depending on whether the tissue originated from males (>30 DPH) or juveniles and adult females, fiber bundles consisted of a subsection of or the entire DTB. Muscle preparations were mounted in a temperature-controlled bath, which was continuously supplied with oxygenated Ringer's solution. The rostral end of the preparation was fixed to a force transducer (model 400A, Aurora Scientific) and the caudal end to a micromanipulator, which was used to control the length of the preparation (Fig. 1A). After mounting the muscle preparation in the bath chamber, it was allowed to rest for 20 min. Muscle fibers were stimulated through the bath solution by a high-power follow stimulator (model 701C, Aurora Scientific) at constant voltage using platinum electrodes. This stimulator is designed for muscle work, and, with an output ranging from 0.4 mA to 1 A, it guarantees we are stimulating muscle membranes directly and before activating the neuromuscular junction. Force and stimulation signals were low-pass filtered at 10 kHz (EF120 BNC throughfeed low-pass filter, Thorlabs) and digitized at 20 or 40 kHz (NI DAQ Board PCI-MIO-16E4, National Instruments). All stimulations were conducted at 39.0 ± 0.1°C, which is within the body temperature range of 38–44°C in zebra finches (Zann, 1996). As muscle contraction speed increases with temperature (Mead et al., 2017), we are thus slightly underestimating the speed of the muscle and all correlated parameters. All software to control the setup and record data were written in MATLAB (MathWorks; RRID:SCR_001622).

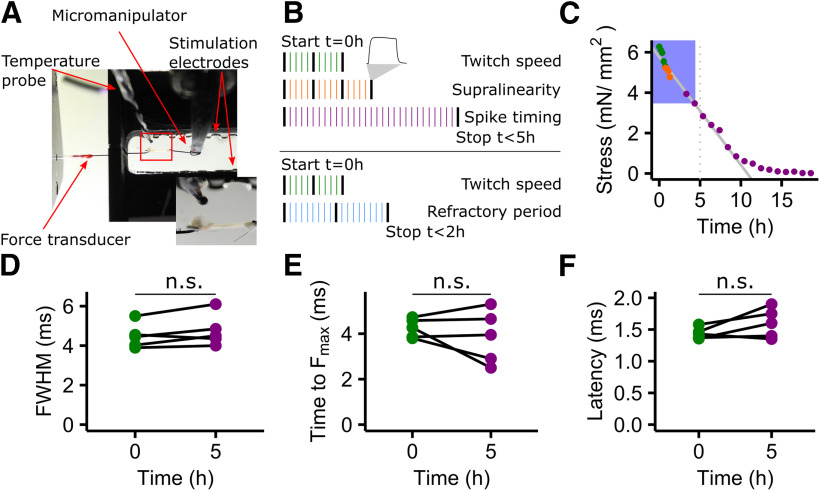
Figure 1.

Muscle speed does not change over experimental time. A, In vitro muscle physiology setup. Muscle fiber bundles were fixed to a force transducer (left) on the rostral end and to a motorized micromanipulator (right) on the caudal end. The bath chamber (black) was continuously supplied with fresh oxygenated Ringer's solution. The red box indicates the inset showing a closeup of a muscle fiber bundle in the setup. B, Schematic of the experimental timeline and design. Two sets of experiments (1 − 3 and 1 + 4) were run on two different groups of animals. One iteration consisted of a 50 ms high-frequency control stimulation (black bars) and several different stimulation patterns (colored bars). Stimulation patterns were assigned randomly within each iteration. C, Maximal tetanic force declines over time. Depicted is an example of one muscle preparation. The decline is linear (solid gray line) over >5 h (dotted vertical line). D–F, Data included in this study were all acquired within 5 h (blue box), and over this time twitch kinematics did not change significantly (paired t test; FWHM: t = −1.917, df = 4, p = 0.13, time to F_max: t = 0.920, df = 4, p = 0.41; latency: t = −1.805, df = 4, p = 0.15). The coloring of all dots is according to B.

Stimulation protocols

First, we optimized stimulation amplitude (pulse width, 300 µs) for maximal force production. The typical stimulation amplitude in our setup was 16 V. Second, we applied 100 ms pulse trains ranging from 100 to 800 Hz in 100 Hz steps, to determine the force frequency curve and the stimulus frequency at which maximal tetanic force was produced. Last, muscle length was optimized for maximal force for each preparation. The optimal length of fiber bundles was 4.55 ± 0.45 mm (median = 4.5 mm, N = 45) and the cross-sectional area (CSA) was 0.10 ± 0.16 mm² (median = 0.05 mm², N = 28). CSA was calculated from dry weight, optimal length and density (Mendez and Keys, 1960). Combining our CSAs with published fiber densities in syringeal muscles (Christensen et al., 2017; Adam et al., 2020), our preparations consisted of ∼68 muscle fibers. Assuming a constant distribution of superfast/fast fibers between muscles (Christensen et al., 2017), suggests our preparations consisted of 60 superfast and 8 fast oxidative fibers. Pulse width and optimal stimulation amplitude were kept constant for all stimulations within one animal.

A critical gap in our knowledge of the song system is that virtually no information is available about firing characteristics of the MNs during song. The output nucleus of both the AFP and motor pathway is the robust nucleus of the arcopallium (RA), which sends direct projections to the MNs located in the hypoglossal nucleus nXII (Nottebohm et al., 1976; Wild, 1993a, b). MNs in the tracheosyringeal part of nXII (nXIIts) innervate the syringeal muscles (Wild, 1997). Although multiunit recordings of nXIIts have been reported (Williams and Nottebohm, 1985; Otchy et al., 2019), no firing characteristics of single units in nXIIts that comprise the actual motor code exist, to the best of our knowledge. Thus, while neural coding in the song system upstream of the MNs is well described, virtually no information is available on the motor code controlling the vocal organ. High-quality neural data have been obtained from single units in the motor cortex (i.e., nucleus RA), which is directly driving the syrinx MNs in nXIIts, and we therefore used RA firing statistics to design our stimulation patterns. Over song development, RA firing activity develops from variable firing with a wide ISI distribution to sparse, bursty firing, that is precisely locked to song and has a very narrow ISI distribution (Leonardo and Fee, 2005; Ölveczky et al., 2011).

For each muscle preparation, we performed several stimulation experiments in series in the order described below (Fig. 1B). Each experiment consisted of several stimulation patterns (described in the section below for each experiment). Each iteration was started by a tetanic pulse train (100 for experiment 1 and 50 ms for other experiments) followed by 3 min of rest. Subsequently, all stimulation patterns of one experiment were applied in random order with a 2 min rest in between. Each experiment was then repeated for several iterations (specified below for each experiment) and patterns were rerandomized within each iteration.

Experiment 1: isometric stress and muscle speed.

Each iteration consisted of a 100 ms stimulation at the frequency producing maximal force followed by four single twitches. The experiment was run for at least two iterations.

Experiment 2: supralinear force summation.

We used four stimulation patterns consisting of two spike patterns with ISIs of 2, 4, 6, and 8 ms, covering the range of ISIs most commonly observed in RA (Ölveczky et al., 2011). The experiment was run for at least three iterations.

Experiment 3: spike timing.

To investigate the effect of spike timing on force responses, we designed a three-spike stimulation paradigm (based on the study by Srivastava et al., 2017), consisting of 29 stimulation patterns based on four different frequencies (200, 400, 600, and 800 Hz). To introduce spike-timing changes without changing the overall rate, the middle spike was moved in small increments (range, 0.1–1 ms) from its centered position toward the first or last spike. The stimulation patterns by frequency were as follows: at 200 Hz, we used 11 stimulation patterns with ISIs between the first and second spike (ISI1) of 0.4, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9 ms. At 400 Hz, we used seven stimulation patterns with ISI1s of 0.4, 0.5, 1, 2, 2.5, 3, and 4 ms. At 600 ms, we used six stimulation patterns with ISI1s of 0.4, 0.5, 1, 1.66, 2, and 3 ms. At 800 ms, we used five stimulation patterns with ISI1s of 0.4, 0.5, 1, 1.25, and 2 ms. The experiment was run for one iteration.

Experiment 4: refractory period.

Stimulation patterns consisted of eight two spike patterns with ISIs ranging from 0.3 to 1.5 ms in 0.2 ms steps, and a single-pulse stimulation as control. The experiment was run for at least two iterations. Data were acquired on 13 additional animals and acquired directly after experiment 1.

Data analysis

All data analysis was conducted in R (R Project for Statistical Computing; RRID:SCR_001905).

Force decrease correction.

During the experiments, the force output of the preparations decreased linearly due to dying muscle fibers. The above-described experiments took 3.71 ± 0.57 h (maximally, 4.5 h) and 1.2 ± 0.39 h, and the force decrease at the end of all experiments was 55.8 ± 27.2% and 75.1 ± 26.9%, for experiment 1 − experiment 3 and experiment 1 + experiment 4, respectively. To correct for this force decrease, we normalized all force data from our stimulation patterns over all experiments. For normalization, we used the linear regression between the maximal force of the 50 ms tetanic contractions, which were part of each iteration, and the experimental time. Typically, the force decrease over time was linear until force reached 15% compared with the start of the experiment (Fig. 1C), which was well past the end of the experiments included in this study.

Isometric stress.

Stress was calculated as F/CSA of the muscle, where F is the force. The cross-sectional area CSA was estimated from the optimal (resting) length L₀, the dry weight (dry–wet conversion factor: 5) and density [1060 kg/m³ (from the study by Mendez and Keys, 1960)] of the muscle fibers.

Muscle speed, single stimulations.

The full-width at half-maximal (FWHM) force of single twitches was defined as the time from crossing 50% force increase to decrease, and is the same parameter as previously reported (t_50-50; Elemans et al., 2004; Srivastava et al., 2017). The time to maximal force (F_max) was defined as the time from stimulation to reaching the peak of the twitch. Latency was defined as the time from stimulation to the force signal crossing the mean plus five times the SD of a 50 ms segment of the force before stimulation. All values reported are the average of seven twitch contractions. The FWHM of two other syrinx muscles, VTB (ventral tracheobronchial) and musculus syringealis ventralis (VS), was extracted using previously published data from 12 (Mead et al., 2017) and 5 (Adam et al., 2020) additional animals, respectively.

Muscle speed, tetanic contractions.

We fitted a mathematical model (Watanabe et al., 2010) to the fusion index–frequency curve (FFC) and force–frequency relation (FFR) using the nls function in R to extract the frequencies corresponding to 10% fusion (start of summed responses), 90% fusion (f_fused), and 90% of maximal tetanic force (f_Tet).

Supralinearity.

We normalized the maximal force amplitude of all force traces to the F_max of the first peak of the 8 ms pattern within each iteration. A twitch model (Raikova and Aladjov, 2002) was fitted and used to calculate linear summations by adding two modeled twitches offset by the ISIs used for stimulation. Supralinearity was quantified as the ratio between the normalized and modeled F_max values as well as the ratio of the area under the curve (AUC) of the normalized force data and the summation model. The AUC was calculated using the AUC function from the DescTools package (Signorell, 2019).

Spike timing.

To quantify the variability introduced by changing spike timing, the coefficient of variation (CV) was calculated for the timing (CV_Timing) as well as for the amplitude (CV_Amplitude) of F_max per stimulation frequency and animal for one iteration of the protocol.

Estimation of pitch changes.

The fundamental frequency of sound is often called “pitch.” Although pitch is a perceptual measure that is not always equivalent to fundamental frequency, we will refer to the fundamental frequency as pitch to avoid confusion between stimulation and sound frequencies. To illustrate the effect of spike-timing manipulations on sound production, we estimated the pitch changes that would occur if the entire VS would be stimulated simultaneously with the three-pulse patterns during sound production. We focused on VS, as it is well established that VS controls pitch (Goller and Suthers, 1996; Elemans et al., 2015; Srivastava et al., 2015). VS force was calculated for each animal by dividing the stress data by the CSA of VS (1.05 mm²; Adam et al., 2020). Pitch was calculated from force data using the force–pitch transformation (pitch = 26.6*F_VS) of the VS (Adam et al., 2020). The average pitch difference per animal was calculated as the difference between the minimal and maximal pitch values per bird across all stimulation patterns of the spike-timing protocol. Translating our results acquired on DTB to VS is valid if stress and speed do not differ between the two muscles. We recently reported that stress generated by DTB and VS is not significantly different (Adam et al., 2020). Additionally, the FWHM ranges of DTB and VS are overlapping. We can thus interpret spike-timing results from DTB to VS.

Refractory period.

F_max values were extracted from all force responses and normalized to F_max of the control twitch within each iteration. To estimate the refractory period (t_Ref), we fitted a log-logistic model to the normalized F_max values using the drm function of the drc package (Ritz et al., 2015), as follows:

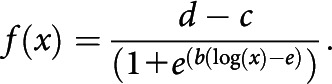The t_Ref was estimated as the ISI, where the normalized maximal force was 10% higher than of a single-twitch response using linear interpolation (Boërio et al., 2005).

Change of contraction speed over experimental time.

Over the time needed to acquire all data for one preparation, muscle fibers were dying. To exclude that this decrease differentially affected different fiber types (Christensen et al., 2017; Mead et al., 2017) with potentially different contraction speeds, we tested whether speed changed between the start of the experiment and 5 h of experimental time. We included data of preparations from adult males that was acquired between 4.5 and 5.5 h after the start of the experiment (Fig. 1D–F). The latency, FWHM and the time to reach F_max did not change significantly over 5 h. We thus conclude that overall contraction kinematics are not affected by dying muscle fibers within the preparation.

Experimental design and statistical analyses

All data are reported as the average ± SD; N refers to individual animals. Statistical significance was accepted for p < 0.05.

Statistical tests

Linear mixed-effects models with subsequent Tukey's post hoc comparison were used to assess statistical difference in the FWHM (Fig. 2B), F_max (Fig. 3B), and supralinearity (Fig. 3E) datasets. Statistical design for each dataset can be found in the respective figure captions. ANOVA with subsequent Tukey's post hoc test was used to detect significant differences between age groups in the f_fused (Fig. 2F), f_max (Fig. 2G), time to F_max (Fig. 2C), and latency (Fig. 2D) datasets, and between stimulation frequencies and CV_Amplitude and CV_Timing (Fig. 4B). Linear models were used to test the correlation with f_fused for FWHM (Fig. 2H), supralinearity (Fig. 3F,G), and CV_Amplitude and CV_Timing (Fig. 4C). Welch's t test was used to test for sex differences in t_Ref (Fig. 5C), and paired t tests were applied to test changes in contraction speed over experimental time (Fig. 1D–F).

Figure 2.

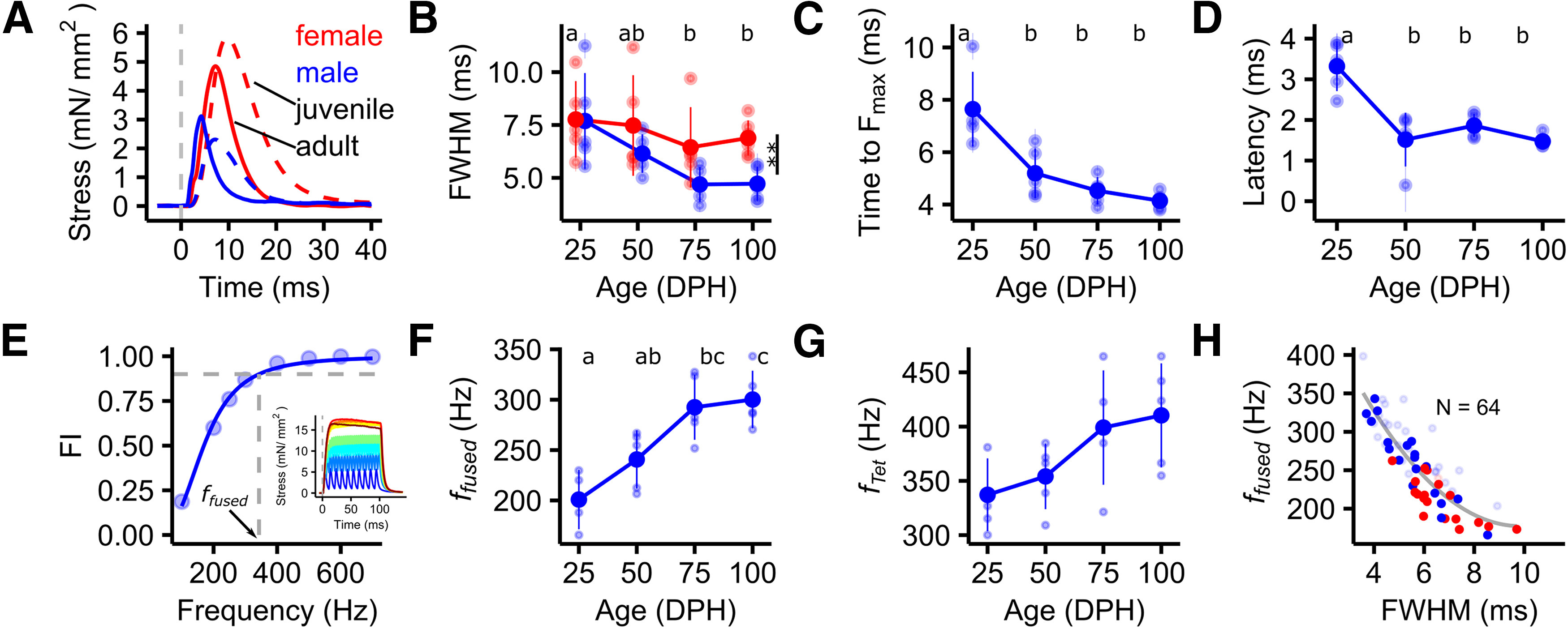
Contraction speed increases over development in male songbirds. A, Twitch contraction speed was higher in adult males compared with juveniles or adult females, as illustrated by the narrower force peak. Examples of twitch responses of juvenile and adult male (blue) and female (red) zebra finch syrinx muscles. The dashed, vertical, gray line indicates the time point of stimulation. B, FWHM force decreased over vocal development in males, but not in females [linear mixed-effects model (LMM): FWHM ∼ sex + age + (1|animal); sex: df(1), F = 7.5, p < 0.01; age: df(3), F = 3.9, p < 0.05; animal: df(1), likelihood-ratio test (LRT) = 835, p < 0.001]. C, D, Time to F_max decreased significantly between 25 and 50 DPH (C; ANOVA: Fs = 14.98, df(3,16), relative SE (RSE) = 0.91, p < 0.001), as did the latency from stimulation to the force onset (D; ANOVA: F = 16.5, df(3,16), RSE = 0.48, p < 0.001). E, A mathematical model was fitted to the FFC and the FFR to extract the frequency when responses start to fuse [fusion index (FI) = 0.1], reach f_fused and f_Tet, respectively. Depicted is an example of an FFC of an adult male. Crossing of the gray dashed line with the x-axis indicates f_fused. The inset depicts the force responses to stimulation with spike trains from 100 to 700 Hz (encoded by color) used to calculate FI. F, G, f_fused (F) and f_tet (G) both increased significantly over vocal development (f_fused: ANOVA: F = 10.91, df(3,15), RSE = 29.84, p < 0.001; f_Tet: ANOVA: F = 3.48, df(3,16), RSE = 42.14, p = 0.041). H, FWHM and f_fused are highly correlated [N = 64; LM: f_fused ∼ FWHM, p < 0.001, RSE = 51.66, df(63)]. Solid points indicate data from preparations depicted in B, C, D, F, and G, while transparent points are derived from additional preparations of other syringeal muscles, partially published in the study by Mead et al. (2017). Unshared lower case letters above plots indicate post hoc differences with a significance level p < 0.05. **p < 0.01. A horizontal jitter was applied to data points in B for clarity.

Figure 3.

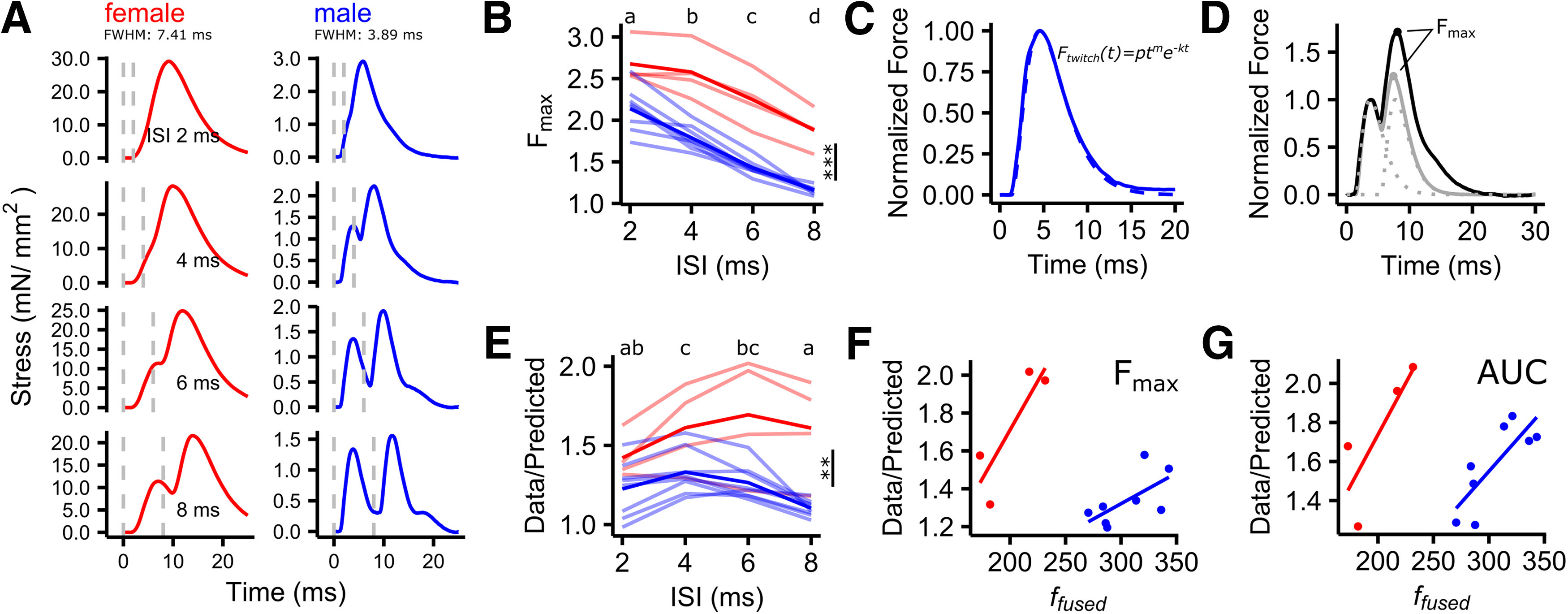
Force summation is supralinear and depends on contraction speed. A, The shape of force trajectories changed dramatically with muscle contraction speed (male vs female) when driven by identical stimulation patterns. This is illustrated by examples of force responses of a female (red) and a male (blue) syrinx muscle to stimulations with two pulses with ISIs of 2, 4, 6, and 8 ms. The dashed, vertical, gray lines indicate the time points of stimulation. B, Maximal force relative to a single twitch decreased with increasing ISI and was higher in males compared with females [linear mixed-effects model (LMM): normalized F_max ∼ sex + ISI + (1 | animal); sex: df(1), F = 45.4, p < 0.001; ISI: df(3), F = 102.3, p < 0.001; animal: df(1), likelihood-ratio test (LRT) = 16.3, p < 0.001]. Transparent lines represent individual preparations, and solid lines represent means. C, Twitch responses were fitted to a phenomenological model (Raikova and Aladjov, 2002). D, Recorded force responses (black) were compared with the summation model (gray) derived by summing two twitch models (dashed line). The amount of supralinearity was defined as the ratio between F_max or the AUC of the measured data and the summation model. E, The amount of supralinearity depended on ISI and was higher in females compared with males (LMM: supralinearity ∼ sex + ISI + (1 | animal); sex: df(1), F = 11.5, p < 0.01; ISI: df(3), F = 5.2, p < 0.01; animal: df(1), LRT = 21, p < 0.001). On average, the maximum occurred at a lower ISI in males (4 ms) compared with females (6 ms). F, G, Maximal supralinearity increased with f_fused, for both F_max (LM: ratio F_max ∼ f_fused + sex; f_fused: df(2), t = 3, p < 0.01; sex: df(9), t = −4.3, p < 0.01) and AUC (LM: Ratio AUC∼ f_fused + sex, f_fused: df(2), t = 3.8, p < 0.01, sex: df(9), t = −4.1, p < 0.01). Unshared lower case letters above plots indicate post hoc differences with significance level at p < 0.05. **p < 0.01, ***p < 0.001.

Figure 4.

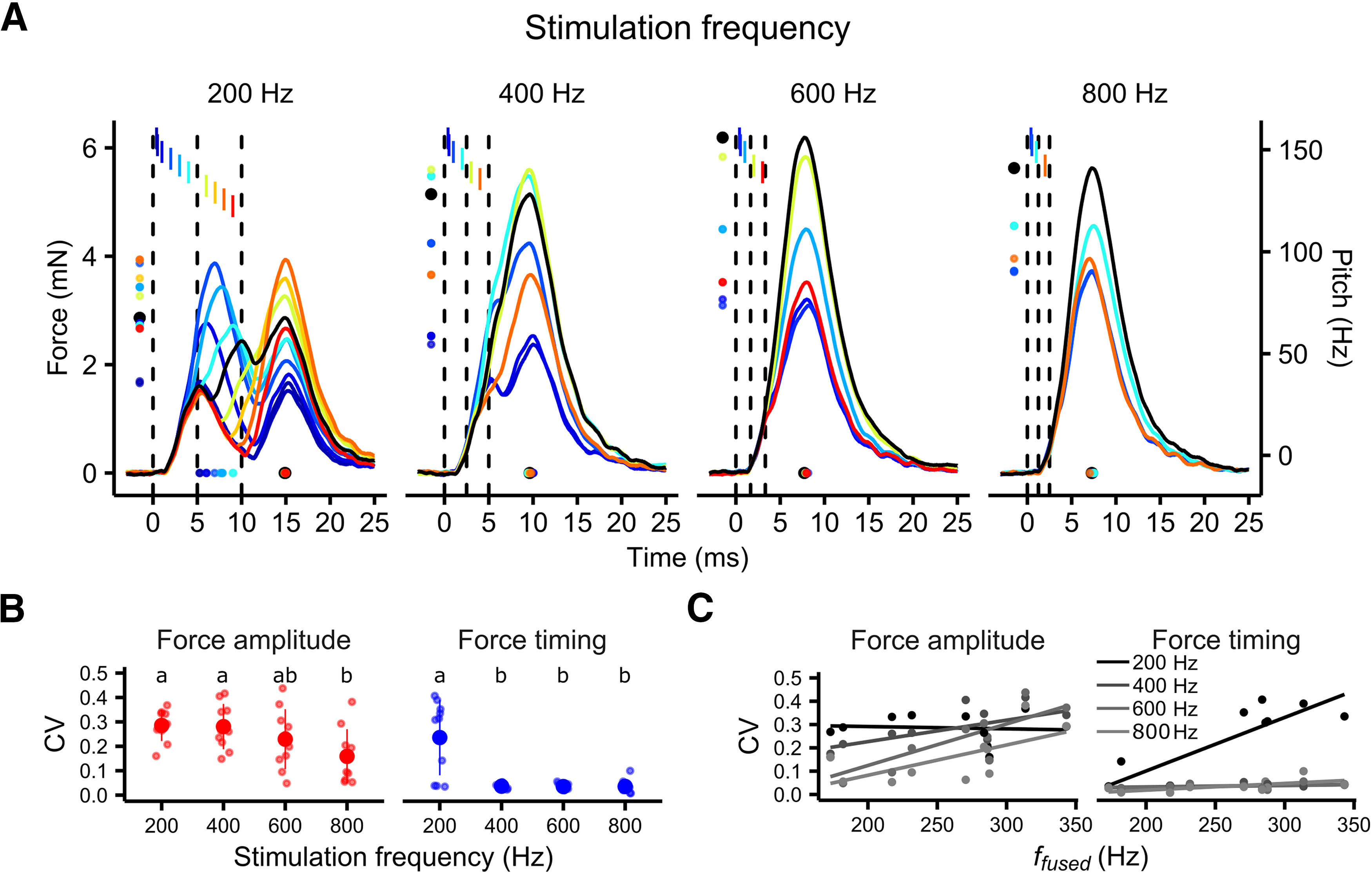
Submillisecond changes in spike timing affect the magnitude and timing of maximal force development in superfast syrinx muscles. A, Three-spike patterns with timing changes to the middle spike cause changes in both the timing and amplitude of force profiles as illustrated by example raw data of a male syrinx muscle (FWHM, 4.45 ms; f_fused, 284 Hz). Lines depict the normalized force response. Indicated are the timing (dots at bottom) and amplitude (left) of F_max. Vertical dashed bars indicate the timepoints of stimulation with regular ISIs, and the colored bars indicate the stimulation time point of the middle spike when offset from the centered position. Color encodes the relative offset of the middle spike from its regular position. B, The variability introduced by changes to spike timing depended on the base stimulation frequency and was generally higher at 200 Hz (CV_Amplitude, 0.29 ± 0.06; CV_Timing, 0.24 ± 0.15) compared with 800 Hz (CV_Amplitude, 0.16 ± 0.11; CV_Timing, 0.04 ± 0.03; CV_Amplitude: ANOVA, F = 3.47, df(3,36), RSE = 0.100, p < 0.05, CV_Timing: ANOVA, F = 16.14, df(3,36), RSE = 0.079, p < 0.001). C, CV_Amplitude significantly depended on muscle speed (f_fused) at base stimulation frequencies of 600 and 800 Hz (600 Hz: N = 10, LM: CV_Amplitude ∼ f_fused, p = 0.004, F = 15.41; 800 Hz, N = 10; LM: CV_Amplitude ∼ f_fused, p = 0.04, F = 5.96), while CV_Timing did so at 200 Hz (N = 10; LM: CV_Timing ∼ f_fused, p = 0.003, F = 17.92). A horizontal jitter was applied to data points in B for clarity. Unshared lowercase letters above plots indicate post-hoc differences with significance level p < 0.05.

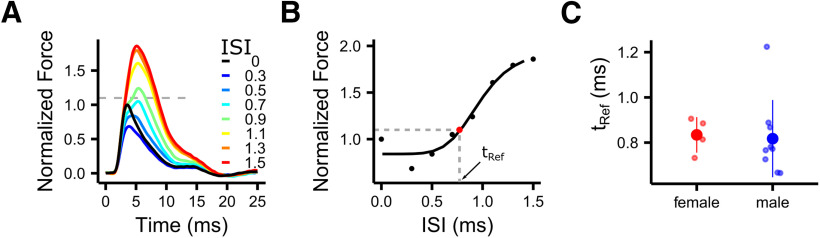
Figure 5.

The refractory period of syringeal muscle fibers is submillisecond. A, Force summation decreases with ISIs <1 ms and eventually disappears completely as shown by example force traces of stimulations with short ISIs of a male syrinx muscle. Color encodes the ISI, and the dashed gray line indicates the threshold used to estimate t_Ref. B, t_Ref was calculated by fitting a log-logistic model and was defined as the ISI between two spikes, where the F_max is 10% higher than F_max of a single twitch. C, t_Ref of male and female DTB was not significantly different between males and females (Welch's t test: t = 0.242, df = 10.87, p = 0.81).

As the FWHM did not change significantly with developmental age in females, we did not analyze the female data for all further measures of muscle speed in the developmental dataset. To increase the range of muscle speed in our dataset quantifying supralinearity and the influence of spike timing, we included data from female DTB preparations.

All statistical comparisons were conducted in R (R Project for Statistical Computing; RRID:SCR_001905).

Results

Contraction speed of syringeal muscles increases over vocal development in male songbirds

We measured isometric contraction speed of vocal muscles over song learning using the following two commonly applied stimulation paradigms: (1) single stimulations yielding a single twitch contraction; and (2) stimulations with equidistant trains of spikes with varying frequencies (100–800 Hz), resulting in summed force responses (Fig. 2). At 25 DPH, FWHM of single twitches did not differ significantly between males and females and was 7.7 ± 2.2 ms (N = 5) and 7.8 ± 1.8 ms (N = 5), respectively. Over development, the speed of female DTB muscles did not change significantly and FWHM values stayed similar until 100 DPH (6.9 ± 0.8 ms, N = 6; Fig. 2B). However, in strong contrast, male DTB muscles became steadily faster and finally doubled in speed with force FWHM almost halved to 4.7 ± 0.8 ms (N = 5) at 100 DPH, corroborating previous findings in another syringeal muscle (Mead et al., 2017). The time from stimulation to F_max (Fig. 2C) and latency from stimulation to force onset (Fig. 2D) also steadily increased over development but were already significantly different between 25 and 50 DPH.

We measured three other muscle speed parameters by applying multiple equidistant stimulation trains, as follows: the stimulation frequency at which the force response (1) starts to summate, (2) is fully fused (i.e., f_fused), and (3) reaches f_Tet (see Materials and Methods). The frequency at which twitches start to summate increased from 65.43 ± 6.24 Hz at 25 DPH (N = 4) to 75.26 ± 11.24 Hz in adult animals (N = 5). f_fused increased steadily and significantly from 25 DPH (201 ± 29 Hz, N = 4) to 100 DPH, reaching its maximum at 300 ± 29 Hz (N = 5; Fig. 2F). Likewise, f_Tet increased from 337 ± 34 Hz at 25 DPH (N = 5) to 410 ± 48 Hz at 100 DPH (N = 5; Fig. 2G). The f_Tet was higher than f_fused in all groups (seen by higher values in Fig. 2F compared with Fig. 2G). This means that force still increased as a function of stimulation frequency even after the force responses were fully fused. This has also been reported in other motor systems (Kernell, 1995; Orizio et al., 2004). Interestingly, in our large dataset of 64 animals we found that force FWHM accurately predicted the stimulation frequency at which fused tetanic contractions occurred, independent of age, sex, and muscle (Fig. 2H). Together, all isometric twitch and tetanic speed parameters steadily and significantly increased over vocal development in male songbirds.

Supralinear force summation increases with muscle speed

Activating muscle fibers with multiple spikes at sufficiently small ISIs leads to summed force responses that are larger than expected from simple algebraic summation of single twitches (Kernell, 1995), which is an intrinsic property of the NMT, often referred to as supralinear or nonlinear force summation. If supralinear force summation occurs, the force–ISI relationship cannot be described by a simple linear regression (Kernell, 1995; Binder et al., 2011; Srivastava et al., 2017). In the songbird respiratory system, millisecond changes in spike timing can cause significant behavioral changes, that reflect4 and potentially even exploit these nonlinear properties of muscles (Srivastava et al., 2017). The same could be true in syrinx muscles, but we do not know whether they also exhibit supralinear summation to begin with and whether its magnitude changes depending on muscle speed. Therefore, we quantified the magnitude of supralinear force summation in syringeal muscles (see Materials and Methods).

First, when driven by identical stimulation patterns, the shape of force trajectories changed dramatically with muscle contraction speed (Fig. 3A). F_max decreased significantly with increasing ISIs (Fig. 3B) in all preparations and was significantly higher in females than in males for all ISIs tested (females: 2.3 ± 0.4, N = 4; males: 1.6 ± 0.4, N = 8). Second, force summation was supralinear in all preparations, as the observed force response had a higher F_max than expected from a summation model (Fig. 3E; see Materials and Methods). The magnitude of supralinear summation significantly depended on spike timing (Fig. 3E), corroborating previous findings in songbird respiratory muscles (Srivastava et al., 2017). Third, the maximal magnitude of supralinear summation increased with muscle speed, regardless of whether it was calculated from F_max (Fig. 3F) or AUC (Fig. 3G). Thus, together, the maximal magnitude of supralinear summation increases with speed and can thus also be expected to increase over development.

Submillisecond changes in spike timing affect magnitude and timing of maximal force development

The timing of spikes relative to a behavior usually exhibits variability (Stein et al., 2005; Lisberger and Medina, 2015), and it has recently become apparent that the exact timing carries information (Stein et al., 2005; Sober et al., 2018). In songbirds, variability in RA indeed correlates to acoustic variability down to the millisecond scale (Sober et al., 2008; Tang et al., 2014). However, in RA firing precision is even higher and is reported as 0.2 ms (Chi and Margoliash, 2001), but it is unknown whether submillisecond precision spike timing can pass through the syringeal muscle NMT and cause changes in force trajectories.

To address this question, we performed muscle stimulations with three-spike patterns introducing timing changes to the middle spike in steps from 1 to 0.1 ms (see Materials and Methods). These timing manipulations evoked changes in both the timing and amplitude of force profiles, and the effect differed between stimulation frequencies (Fig. 4A). To quantify the amount of variability introduced by the timing manipulations, we calculated the CV_Timing and CV_Amplitude of F_max. Both CV_Timing and CV_Amplitude were significantly higher at a stimulation frequency of 200 Hz compared with 800 Hz (Fig. 4B,C). While 200 Hz stimulation patterns caused variability in both the timing and magnitude of F_max, higher stimulation frequencies almost exclusively affected F_max amplitude (Fig. 4B), but not its timing (Fig. 4C).

Because the variability of force timing and amplitude introduced by changes in spike timing showed a wide variation between animals, we hypothesized that the effects could depend on muscle speed. To assess this hypothesis, we tested for the dependency of CV_Timing and CV_Amplitude on f_fused, representing the intrinsic contraction speed of each animal. Overall, CV_Amplitude and CV_Timing increased significantly with f_fused (Fig. 4B). However, as the stimulation frequency clearly influenced the magnitude of the CVs as well as the dependency on f_fused, we calculated linear models for each stimulation frequency separately. CV_Amplitude significantly depended on f_fused at 600 and 800 Hz, and on CV_Timing at 200 Hz (Fig. 4C). These results mean that the quality of the effect of changes in spike timing are set by the relationship between stimulation frequency and muscle speed (i.e., f_fused): force timing is affected at stimulation frequencies below the f_fused of adult male muscles (range, 173–343 Hz; median, 277 Hz), while force amplitude is affected at all stimulation frequencies. The quality of the effect on the other hand is set by muscle speed confirming our hypothesis, that the variability introduced by spike-timing changes depends on the contraction speed of the muscle. Together, our results show that submillisecond spike timing affects the shape of force profiles. Syringeal muscles can thus resolve spike timing in the submillisecond range. Additionally, muscle speed sets the sensitivity of the muscle to changes in force timing, as illustrated by the increase in variability with increasing muscle speed.

Although spike-timing changes in the submillisecond range affected F_max of force profiles, it is not given that these force changes result in changes in sound production within the physiologically relevant range. For illustration, we estimated the maximal pitch difference caused by stimulating VS with our three pulse patterns (Fig. 4A; see Materials and Methods). We can apply our interpretation from DTB to VS, because both muscles produce similar stress (Adam et al., 2020) and the FWHM ranges of VS (4.3–6.6 ms, N = 5; see Materials and Methods) and DTB (3.9–5.6 ms; Fig. 2B) overlap. We estimated an average force difference of 8.15 ± 6.02 mN (N = 10) between the minimal and maximal F_max across all spike-timing stimulation patterns (see Materials and Methods). Based on in vitro measurements of the VS force-to-pitch transform (Adam et al., 2020), this translates into an estimated pitch difference of 217 ± 160 Hz. Because zebra finch females can detect changes in pitch <1 Hz (Lohr and Dooling, 1998), this difference is well within the detectable range. Therefore, we conclude that spike-timing changes in the range of submilliseconds might have behavioral correlates.

Changing spike timing in the high-frequency stimulation patterns (600 and 800 Hz) always resulted in a reduction of maximal force compared with the regular stimulation pattern (Fig. 4A). We hypothesized that this decrease was caused by moving spikes into the t_Ref of the muscle, which is 2–5 ms for most skeletal muscles (Farmer et al., 1960). To estimate the unknown t_Ref of syringeal muscles, we stimulated with two pulses with very short ISIs (Fig. 5A; see Materials and Methods). The t_Ref was extremely short, with 0.83 ± 0.08 ms for female syrinx muscle and 0.82 ± 0.17 ms for male syrinx muscle (females, N = 4; males, N = 9), and was three to seven times faster than regular skeletal muscle (Fig. 5C). Thus, despite the extremely short t_Ref, we confirmed our hypothesis that the reduction of maximal force due to spike-timing changes at 600 and 800 Hz is caused by moving spikes into the refractory period of the muscle.

Discussion

We show that the songbird syrinx undergoes essential transformations during song learning that drastically change how neural commands are translated into force profiles and thereby acoustic features. All isometric contraction speed-related features of male syrinx muscles, such as FWHM, f_fused, and f_Tet, significantly increased over development. Interestingly, the latency from stimulus to force production also significantly decreased. Furthermore, we show that two additional NMT features change significantly with muscle speed. First, we establish that supralinear summation of twitch force occurs in syrinx muscles at ISIs in the millisecond range and that its magnitude increases with muscle speeds. Second, we show that spike timing in the submillisecond range can be resolved by syringeal muscles. Force amplitude was affected at all spike rates tested, while changes in peak force timing were only evoked at spike rates below f_fused. Furthermore, the sensitivity to changes in spike timing was set by muscle speed. Together, our data provide strong support for our hypothesis that muscle properties relevant to the NMT change over vocal development. The observed NMT changes are driven by syringeal muscle speed as it increases over vocal development. Furthermore, our data show that the extreme speed of adult muscles is not available to juveniles during song learning.

Several mechanisms could underlie the increasing scontraction speed over development in males. First, the speed increase correlates with a shift in myosin heavy chain isoform composition within the entire muscle toward increased expression of the isoform known as superfast myosin, encoded by the MYH13 gene (Mead et al., 2017). Second, the speed increase over development in males could be caused by a change in fiber type, as described in many other systems (Schiaffino and Reggiani, 2011). Syrinx muscles contain two distinct fiber types (fast and superfast) that are present at different ratios in males and females (Christensen et al., 2017). In adult male zebra finches, syrinx muscles have four times more superfast fibers (up to 87%) and four times fewer fast oxidative fibers than in females (Christensen et al., 2017; Mead et al., 2017). Furthermore, syringeal muscles of adult female zebra finches contract slower (Elemans et al., 2008) and express less MYH13 (Mead et al., 2017). Our data show that at 25 DPH male and female muscle performance was indistinguishable and female muscle speed did not change over development. Together, these findings strongly suggest that myosin genesis underlies the increase in contraction speed, but the causal relationship remains to be established. Furthermore, it remains unknown whether myosin composition changes occur within muscle fibers or between fiber types.

In other motor systems, MYH13 expression is driven by innervation. Experimental transnervation with faster spiking nerves increases muscle speed (Paniello et al., 2001), and increased use is associated with higher MYH13 expression in extraocular muscles (Brueckner et al., 1999; Moncman et al., 2011). Thus, an increase in MN discharge rate might be driving the upregulation of MYH13 and consequently the increase in contraction speed in syringeal muscles (Adam and Elemans, 2019). Whether this is only due to the increase in high-frequency input to the MNs (Ölveczky et al., 2011) or also because their intrinsic properties change over development is unknown. Understanding what drives the increase in contraction speed thus requires knowing the motor code over development.

The song template is assumed to be fixed during song learning (Mooney, 2009), and individuals are trying to minimize perceptual error in trial-to-trial renditions (Fee and Scharff, 2010). The increasing syringeal muscle speed over development has the consequence that identical motor commands result in distinct force trajectories, depending on postnatal age, and thus alter behavioral output. If birds aim to produce the same force trajectory during song development, we propose they must dynamically alter their motor code to correct for NMT changes when trying to sing target syllables.

Although the song system neurocircuitry is well studied, the actual motor code, the firing patterns of single units in nXIIts, during singing is unknown (Williams and Nottebohm, 1985; Otchy et al., 2019). In many motor systems, the intrinsic properties of MNs and the biomechanical properties of the innervated muscle fibers are highly tuned (Zhurov and Brezina, 2006; Manuel et al., 2019). For example, the discharge rates of MNs typically fall within the range of frequencies required to generate summed force responses. This is reflected by matching between the firing characteristics of the MN and its muscle FFR, so that the observed range of firing rates modulates forces along the steepest portion of the FFR (Kernell, 1995). This phenomenon is called speed matching. Reversely, speed properties of muscles thus set boundaries within which the motor code is operating. The FFR of a muscle thus allows prediction of the firing rates of the MNs innervating it.

Using our characterization of the biomechanical properties of syringeal muscles, we make three predictions for the nXIIts MN firing frequencies during singing in adult males. First, force summation begins at ISIs >13.3 ms (i.e., 75 Hz). Thus, to activate syrinx muscles to produce summed force responses, firing rates have to be >75 Hz. Second, spikes arriving at the NMJ during the refractory period of the muscle will not activate the muscle and are thus lost. To avoid losing spikes, instantaneous firing rates must stay below frequencies leading to lost spikes. Because the refractory period of male syrinx muscles ranges from 0.7 to 1.2 ms, MNs must fire <1000 Hz. Together, these two predictions set the outer boundaries for motor code spike rates. Last, we predict the peak of the distribution of nXIIts firing frequencies, as follows: force increase by skeletal muscles can be achieved by increasing the number of recruited MNs and thus connected muscle fibers (recruitment), and by increasing the firing rate of MNs (rate coding). Rate coding is most effective on the steep slope of the FFR (Fuglevand et al., 2015; Enoka and Duchateau, 2017). Additionally, to achieve unmodulated force increases, frequencies should be above f_fused. Therefore, we predict ISIs between 3.4 ms (average f_fused, 290 Hz) and 2.5 ms (average f_Tet, 413 Hz) to be most suited to change the force output of syrinx muscles in adult males.

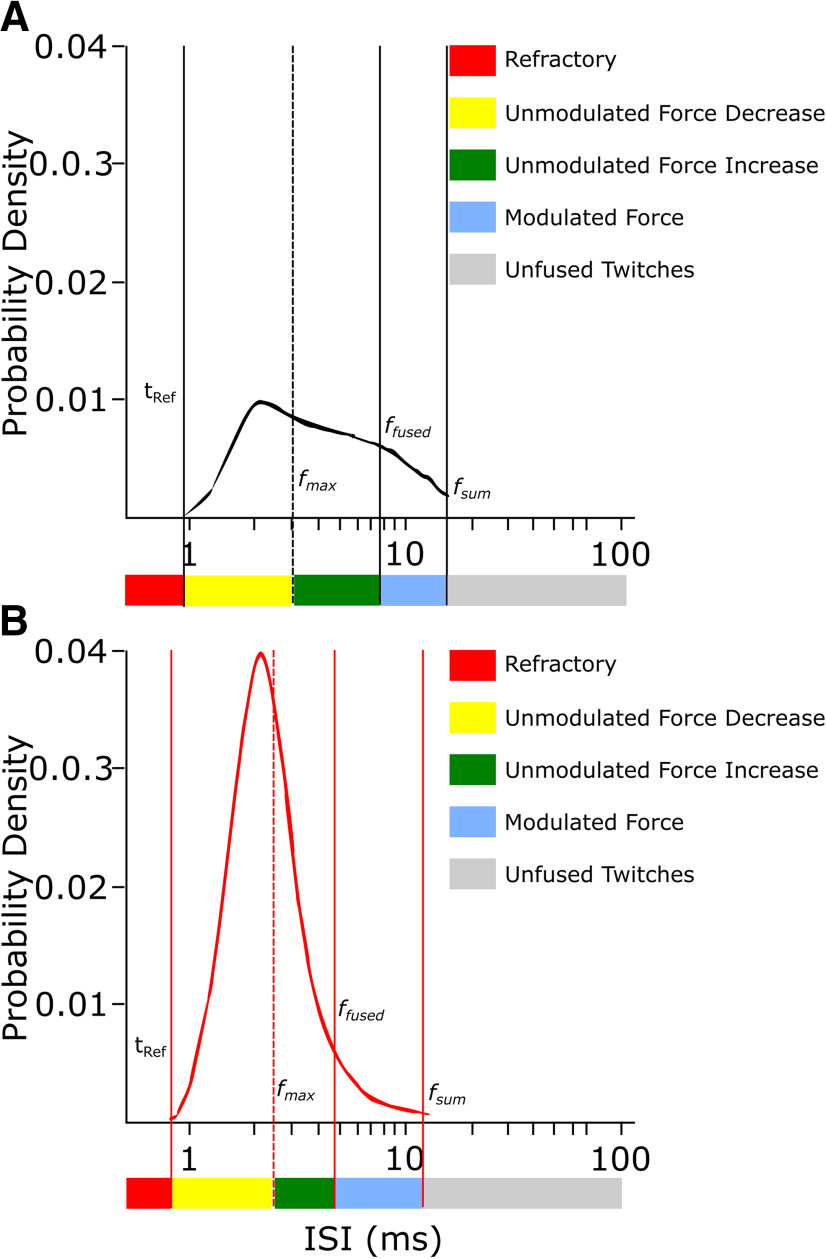
If speed matching occurs during the process of vocal development, the ISI distribution of MNs in juveniles should be shifted toward higher ISIs to match the slower speed of the juvenile syringeal muscles. Because of the lack of data on MN firing, we cannot test this hypothesis directly. However, the firing characteristics of the cortical premotor neurons projecting to the MNs in nXIIts (namely RA_nXIIts) have been characterized over development (Ölveczky et al., 2011). Interestingly, the refractory period, f_Tet, f_fused, and the frequency when force responses start to sum before and after song learning align well with the ISI distributions of age-matched RA_nXIIts neurons during singing (Fig. 6). The ISI distribution of spikes in RA becomes narrower from subsong (Fig. 6A) to adult song (Fig. 6B), and the boundaries are perfectly demarcated by t_Ref and the frequency when force responses start to sum. The majority of RA_nXIIts ISIs lie between t_Ref and f_fused for both age groups. Together, RA activity supports the notion that nXIIts MNs and syrinx muscles are speed matched over development.

Figure 6.

Biomechanical properties of syrinx muscles match the ISI distribution of the last premotor neurons driving them. A, B, The t_Ref and summation threshold (f_sum) of syrinx muscles match the boundaries of the RA–ISI distribution before the start of song learning (A) as well as after crystallization (B). The majority of ISIs lie between t_Ref and f_fused. The ISI probability density plots are modified from the study by Ölveczky et al. (2011).

Interestingly, the refractory period of syrinx muscles (<1 ms) is shorter than the t_Ref of normal skeletal muscles and within the range of refractory times typically found in MNs (Boërio et al., 2005). We show that syringeal muscle is able to support instantaneous firing rates up to 1000 Hz, while normal skeletal muscles are typically driven by <50 Hz (Enoka and Duchateau, 2017). The only muscle activation rates we are aware of that are higher are found in the electric organ of weakly electric fish (Apteronotus leptorhynchus). The electrical organ contains heavily modified myofibers that do not contract, and spinal neurons innervating them can reach brief bursts >1100 Hz (Dunlap et al., 2010). Thus, in addition to speed-limiting fundamental architectural constraints of skeletal muscle (Mead et al., 2017), extreme speed in songbird syrinx muscles may additionally be limited by another hard constraint: the refractory time of the CNS.

Our results support the idea that it is critical to include body biomechanics when interpreting motor commands (Nishikawa et al., 2007; Tytell et al., 2011) and emphasize the need for an embodied view of song motor learning (Düring and Elemans, 2016; Zhang and Ghazanfar, 2018). The increased higher variability of juvenile vocalizations (Tchernichovski et al., 2001; Ölveczky et al., 2011) could for example be partially explained by a mismatch between contraction speed and neural firing characteristics during the process of vocal development (Adam and Elemans, 2019; Kollmorgen et al., 2020). Which mechanisms drive muscle speed changes over developmental timescales remain unknown, but we recently argued it may be driven predominantly by use (Adam and Elemans, 2019). This implies that extensive training of syringeal muscles is required to achieve maximal speed, and that the total duration and trajectory of song learning may not just be set by neural circuit formation but is also required for extensive muscle training.