The Topography of Visually Guided Grasping in the Premotor Cortex: A Dense-Transcranial Magnetic Stimulation (TMS) Mapping Study

Abstract

Visuomotor transformations at the cortical level occur along a network where posterior parietal regions are connected to homologous premotor regions. Grasping-related activity is represented in a diffuse, ventral and dorsal system in the posterior parietal regions, but no systematic causal description of a premotor counterpart of a similar diffuse grasping representation is available. To fill this gap, we measured the kinematics of right finger movements in 17 male and female human participants during grasping of three objects of different sizes. Single-pulse transcranial magnetic stimulation was applied 100 ms after visual presentation of the object over a regular grid of 8 spots covering the left premotor cortex (PMC) and 2 Sham stimulations. Maximum finger aperture during reach was used as the feature to classify object size in different types of classifiers. Classification accuracy was taken as a measure of the efficiency of visuomotor transformations for grasping. Results showed that transcranial magnetic stimulation reduced classification accuracy compared with Sham stimulation when it was applied to 2 spots in the ventral PMC and 1 spot in the medial PMC, corresponding approximately to the ventral PMC and the dorsal portion of the supplementary motor area. Our results indicate a multifocal representation of object geometry for grasping in the PMC that matches the known multifocal parietal maps of grasping representations. Additionally, we confirm that, by applying a uniform spatial sampling procedure, transcranial magnetic stimulation can produce cortical functional maps independent of a priori spatial assumptions.

SIGNIFICANCE STATEMENT Visually guided actions activate a large frontoparietal network. Here, we used a dense grid of transcranial magnetic stimulation spots covering the whole premotor cortex (PMC), to identify with accurate spatial mapping the functional specialization of the human PMC during grasping movement. Results corroborate previous findings about the role of the ventral PMC in preshaping the fingers according to the size of the target. Crucially, we found that the medial part of PMC, putatively covering the supplementary motor area, plays a direct role in object grasping. In concert with findings in nonhuman primates, these results indicate a multifocal representation of object geometry for grasping in the PMC and expand our understanding of how our brain integrates visual and motor information to perform visually guided actions.

Introduction

Visually guided hand-object interactions are a fundamental component of primate behavior. Such behavior is modular, including several main dissociable components, from transporting the hand toward the object (reaching component) to shaping the hand according to it (grip component) (Turella and Lingnau, 2014). The present work focuses on how the brain uses visual information on object geometrical properties to guide hand-shape while reaching for the object itself.

Converging neurophysiological and neuroimaging studies in primates indicate that the different subcomponents that underlie visually guided hand-object interactions are mediated by a specific neural substrate, linking the posterior parietal cortexto frontal regions, mainly to the premotor cortex (PMC) (Jeannerod et al., 1995; Wise et al., 1997; Turella and Lingnau, 2014; Caminiti et al., 2015; Borra et al., 2017). In particular, human parietofrontal networks for upper limb movements are classified into two main systems, referred to as the dorsomedial and dorsolateral systems, on account of being both embedded in the dorsal visual stream (Rizzolatti and Matelli, 2003; Turella and Lingnau, 2014; Caminiti et al., 2015; Gallivan and Culham, 2015; Borra et al., 2017; Monaco et al., 2017; Cavina-Pratesi et al., 2018). The dorsomedial pathway, which includes superior parieto-occipital cortex (SPOC), the medial part of the intraparietal sulcus and dorsal PMC, is classically considered to contain maps of the space around us, associated with reaching movements for controlling the upper limb position (Connolly et al., 2003; Prado et al., 2005; Filimon et al., 2007, 2009; Cavina-Pratesi et al., 2010; Turella and Lingnau, 2014). The dorsolateral pathway connects the anterior part of the intraparietal sulcus with the ventral PMC (PMv). This pathway is coding grasping, and it is responsible for the transformation of the properties of the object (e.g., shape and size) into the appropriate motor command (Culham et al., 2003; Frey et al., 2005; Cavina-Pratesi et al., 2010). However, much evidence is not entirely compatible with the notion of independent neural coding for grasp and reach movements, and recent findings in humans (Gallivan et al., 2011, 2013; Verhagen et al., 2012; Fabbri et al., 2014; Turella and Lingnau, 2014; Monaco et al., 2015; Turella et al., 2016) suggested that both the dorsolateral and the dorsomedial pathways could code for grasping information. Such observations of object- and grasping-related activity in the dorsomedial pathway are inspired and supported by findings in nonhuman primates, which demonstrated grasping-relevant information both in the medial occipito-parietal cortex (Fattori et al., 2010, 2012) and medial PMC (Lanzilotto et al., 2016; Bonini, 2017; Gerbella et al., 2017; Livi et al., 2019).

In human, there is growing evidence indicating that parietal activity within the dorsomedial pathway encodes grasp-related parameters. Gallivan et al. (2011, 2013) demonstrated that preparatory activity along the dorsomedial circuit, in particular SPOC, decodes reach-to-touch versus reach-to-grasp movements. A recent transcranial magnetic stimulation (TMS) study (Vesia et al., 2017) directly demonstrated a crucial role of SPOC in encoding handgrip formation during action preparation. In general, while accumulating evidence shows that that grasping representations in the posterior parietal cortex are distributed between the dorsolateral and the dorsomedial systems, the representation of grasping in the PMC is still incompletely understood. In particular, an important, yet unresolved, question is whether grasping information represented in the medial parietal regions (Gallivan et al., 2011; Vesia et al., 2017) has a counterpart in the medial premotor regions. Neuroimaging studies demonstrated that both visually guided (Gallivan et al., 2011, 2013) and nonvisually guided (Fabbri et al., 2014) reach-to-grasp actions activated not only the PMv, but also a more medial-dorsal part of the PMC (Turella and Lingnau, 2014). However, functional neuroimaging lacks the temporal resolution to investigate the neural correlates of ongoing movements, and most fMRI studies focus on the preparatory phase before the actual voluntary movement (Medendorp et al., 2005; Beurze et al., 2007, 2009). Therefore, from a functional perspective, the specificity of premotor activity can be difficult to interpret because these approaches cannot determine whether this neural activation reflects neural processing that is critical for grasping movements. TMS does not suffer from these limitations and can provide more accurate information about where and when grasping movements are coded. However, most TMS studies on voluntary actions explored single foci that were chosen a priori within the PM cortex: therefore, they yielded limited spatial information on the overall functional organization of the PM region.

In the present study, we explored the topographic distribution of goal-directed sensorimotor functions in healthy volunteers performing grasping movements toward cylindrical objects of three different sizes. Event-related TMS was applied to single spots of a dense grid of 8 points on the participants' left hemi-scalp, putatively covering the whole of PM. Single-pulse TMS was applied at 100 ms after the Go signal, a time window that has been previously demonstrated critical for hand movement preparation and visuomotor transformations (Davare et al., 2006). This approach has a double advantage: On the one hand, dense mapping with TMS (i.e., stimulating the cortex across a uniform array of adjacent target foci) allows the detailed functional cartography of the PMC. On the other hand, it allows to generate spatially unbiased data in a relatively hypothesis-independent way (Cattaneo, 2018; Lega et al., 2019). In support of this approach, data-driven classification algorithms were used to classify the kinematic parameters as belonging to the small, medium, or large object, and to compare the classification accuracy between active and sham spots.

Materials and Methods

Participants

Seventeen participants took part in the experiment (10 females and 7 males; mean age: 26 years; SD: 4.15 years). All participants were right-handed and with normal or corrected-to-normal visual acuity and normal color vision. Before the TMS experiment, each subject filled in a questionnaire to evaluate eligibility for TMS. None of the participants reported any contraindications for TMS use (Rossi et al., 2009). Written informed consent was obtained from all participants before the beginning of the experiment. The study protocol was approved by the local ethical committee, and the experiment was conducted in accordance with the Declaration of Helsinki.

Experimental design

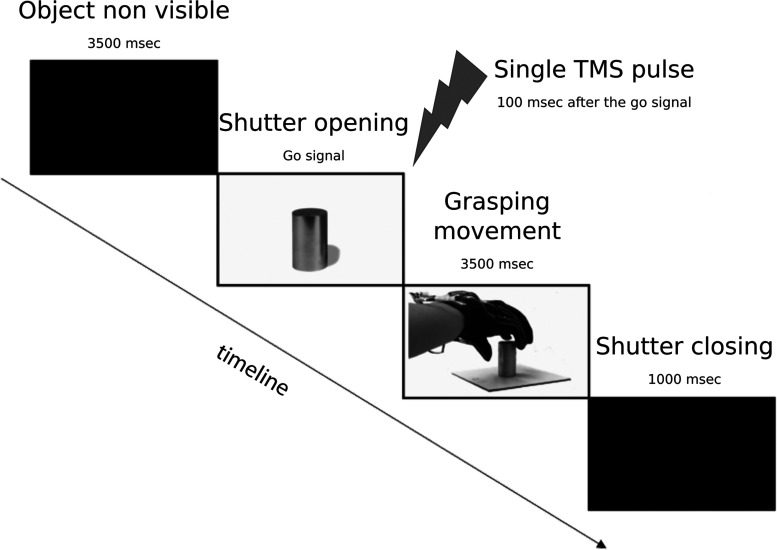
The timeline of an experimental trial is shown in Figure 1. Participants performed a grasping movement while we measured the grip aperture of their right hand by a glove equipped with flexible sensors strategically put to detect fingers' movements (Gentner and Classen, 2009). The whole experiment was conducted in the semidark condition. Participants had to grasp a cylindric object of three possible sizes (diameter: 1, 3, and 5 cm). Participants wore glasses with LCD shutter lenses, controlled by a specific voltage that makes them opaque or transparent, so that subjects could see the object to grasp only from the “go” signal just before the beginning of the grasping movement. The “go” was represented by three different signals that happened simultaneously: (1) the glass became transparent; (2) participants heard a “beep” sound; and (3) a flexible mini LED USB light was fixed over the object and lit up the object to be grasped. Participants were instructed to maintain their right hand over a response button and to keep it pressed. After the Go signal, they were required to grasp the object and leave their right hand over the object until the light went out and the glass became opaque (3500 ms). After that, participants were instructed to come back and again press the response button. The subsequent trial started after 4500 ms. At 100 ms after the Go signals, online single-pulse TMS was applied over 8 different sites of left PM and 2 sham sites, for a total of 10 sites of stimulation. Participants performed 20 blocks (2 blocks for each stimulation sites; see below). In each block, participants performed 27 grasping (9 small object, 9 medium object, and 9 large object). This led to a total of 54 grasping movement (18 for each object size) for each stimulated site. The order of the first 10 blocks (one for each stimulation site) was pseudo-randomized so that the TMS conditions were equally distributed across participants. After performing the first 10 blocks, the order of the remaining 10 blocks was reversed relative to the first part. This was done to minimize any carryover effects related to stimulation site. Each experimental session lasted ∼3 h. The software Open-Sesame (Mathôt et al., 2012) was used for stimulus presentation, data collection, and TMS triggering.

Figure 1.

Schematic representation of the trial sequence. The object remains invisible for 3500 ms. Each movement started with the shutter opening, indicating the Go signal. Participants were instructed to grasp the object and to keep the hand on the object until shutter closing (3500 ms). The following trial started after 4500 ms.

Sensor glove

Kinematic information on finger movements was acquired by means of a glove in which flexion sensors were embedded. This technique is widely used to record finger dynamics (see, e.g., Gentner and Classen, 2006; Kumar et al., 2012; Cattaneo et al., 2015; Fricke et al., 2019), and instructions for its realization have been published by Gentner and Classen (2009). Three commercial right-hand gloves of a stretchable grade of Lycra, of three different sizes (small, medium, and large hand size) were modified to accommodate four 114-mm-long flexion sensors (flexsensors 4.5 inch, Spectrasymbol) over the metacarpophalangeal and proximal interphalangeal joints of the thumb, index, and little fingers (1 sensor for each finger). The ring finger was not recorded because of its high covariance with little finger activity (Hager-Ross and Schieber, 2000).

Neuronavigation

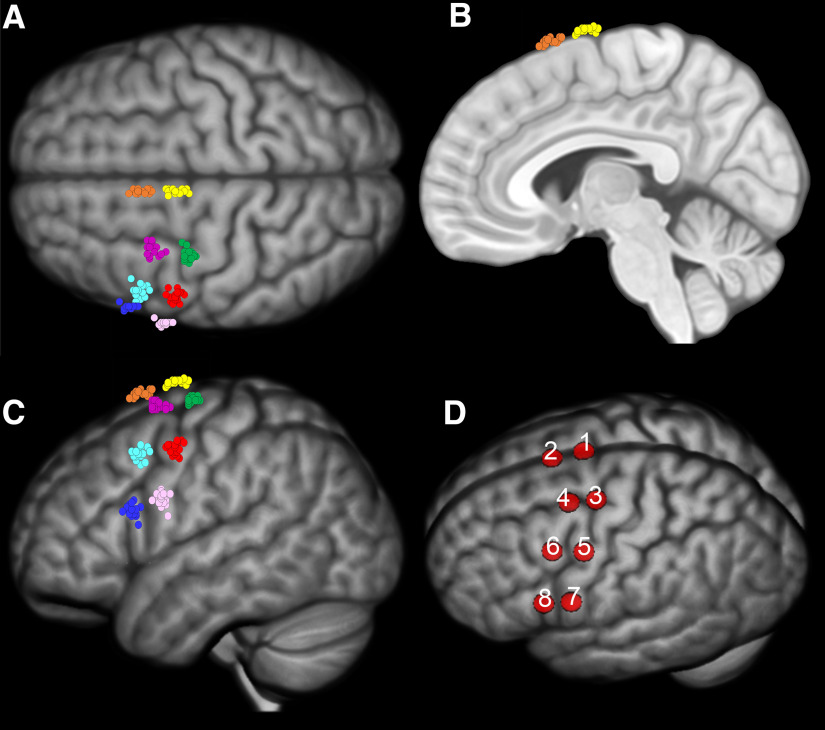
All participants underwent high-resolution MP-RAGE anatomic MRI scans. Individual anatomic scans were converted to the nifti format and loaded on a neuronavigation software (SofTaxic, E.MS). Surface renderings of the brain surfaces were used to mark an 8-spot grid covering the premotor region. The grid had a 2 × 4 structure, with the long side extending along the mediolateral dimension, form the midline to the ventral premotor region and the short side extending along the caudal-cranial direction (Fig. 2). The spots were localized according to individual anatomic landmarks. First, we localized the 4 spots of the posterior row (Spots 1, 3, 5, and 7) in the following way: Spot 1 was localized 5 mm lateral to the midline, 5 mm anterior to the end of the paracentral lobule. Spot 4 was localized in the apex of the crown of the precentral gyrus, 10 mm inferior to the junction between the precentral sulcus and the inferior frontal sulcus. Spots 2 and 3 were localized along an imaginary line connecting Spots 1 and 4, at equal spacings. The anterior row was set by simply moving 2 cm cranial from the 4 spots of the posterior row. While images in native space were used for actual neuronavigation, all individual brains and grids were also normalized to MNI space to allow for interindividual comparisons and group analysis. Mean MNI coordinates of the 8 stimulated points are reported in Table 1. Coordinates of all 17 subjects are available online (https://osf.io/2rdzk/?view_only=bf4172e9ee5640fa84764e3ecf691637; stored on the Open Science Framework data sharing platform). Furthermore, 2 spots (Sham 1 and Sham 2) where sham stimulation was to be applied, were localized in the dorsal and ventral part of the PMC as control condition. A 3D optical digitizer (Polaris Vicra, NDI) was used in combination with the SoftTAxic neuronavigation software to coregister in the same virtual space the participant's head, the digitizer pen, and the TMS coil throughout the whole experiment to monitor coil position on every spot of the grid.

Figure 2.

The 8-spot grid covering the PMC. Each spot for each participant is visualized in MNI space in the superior (A), medial (B), and lateral (C) view. D, A schematic illustration of the eight stimulation sites.

Table 1.

Mean MNI coordinates of the eight stimulated target points

Spots	x	y	z
1	−7.9	−1.4	80.2
2	−8	13.8	75.3
3	−36.1	−7.2	72.4
4	−34.9	6.3	69.4
5	−53.5	−1.2	50.4
6	−51.1	14.3	47.9
7	−68.2	4.8	27.6
8	−64.2	17.8	22.5

TMS

Single-pulse TMSs were delivered at 100 ms after the Go signal. A 70 mm figure-of-eight stimulation coil was placed over the stimulation sites tangentially to the skull, with the handle pointing backward at a 45° angle from the midsagittal line. For the two sham points, the coil was held at a 90° position to ensure that the magnetic field did not stimulate the target area. Indeed, this sham condition has been proven to be ineffective in producing an electric field capable of changing neuronal excitability (Lisanby et al., 2001). TMS was applied with a Super Rapid2 system (Magstim). The intensity of the magnetic stimulation was set separately for each participant 120% of the individual motor threshold and was kept constant between sessions. The mean stimulating intensity was 58% of the maximum stimulator output. We checked in each participant whether stimulation over the defined 8 premotor spots evoked any motor-evoked potentials and reassessed the grid spots if this was the case. The resting motor threshold was determined using the software Motor Threshold Assessment Tool, version 2.0 (http://www.clinicalresearcher.org/software.htm) that uses an adaptive threshold tracking algorithm (Awiszus, 2003) instead of the canonical “relative frequency” method. A motor-evoked potential ≥ 50 μV peak-to-peak amplitude was fed back to the software as valid response. EMG recordings were made with 10 mm Ag/AgCl surface cup electrodes. The active electrode was placed over the first dorsal interosseous muscle of the right hand and the reference electrode over the metacarpophalangeal joint of the index finger. The EMG signal was sampled and amplified 1000× by using a Digitimer D360 amplifier (Digitimer) and digitized by an analog-digital converter (Power 1401, Cambridge Electronic Design) at 5 kHz sampling rate, bandpass filtered 10 Hz to 2 kHz, and then stored using the Signal software (Cambridge Electronic Design).

Statistical analysis

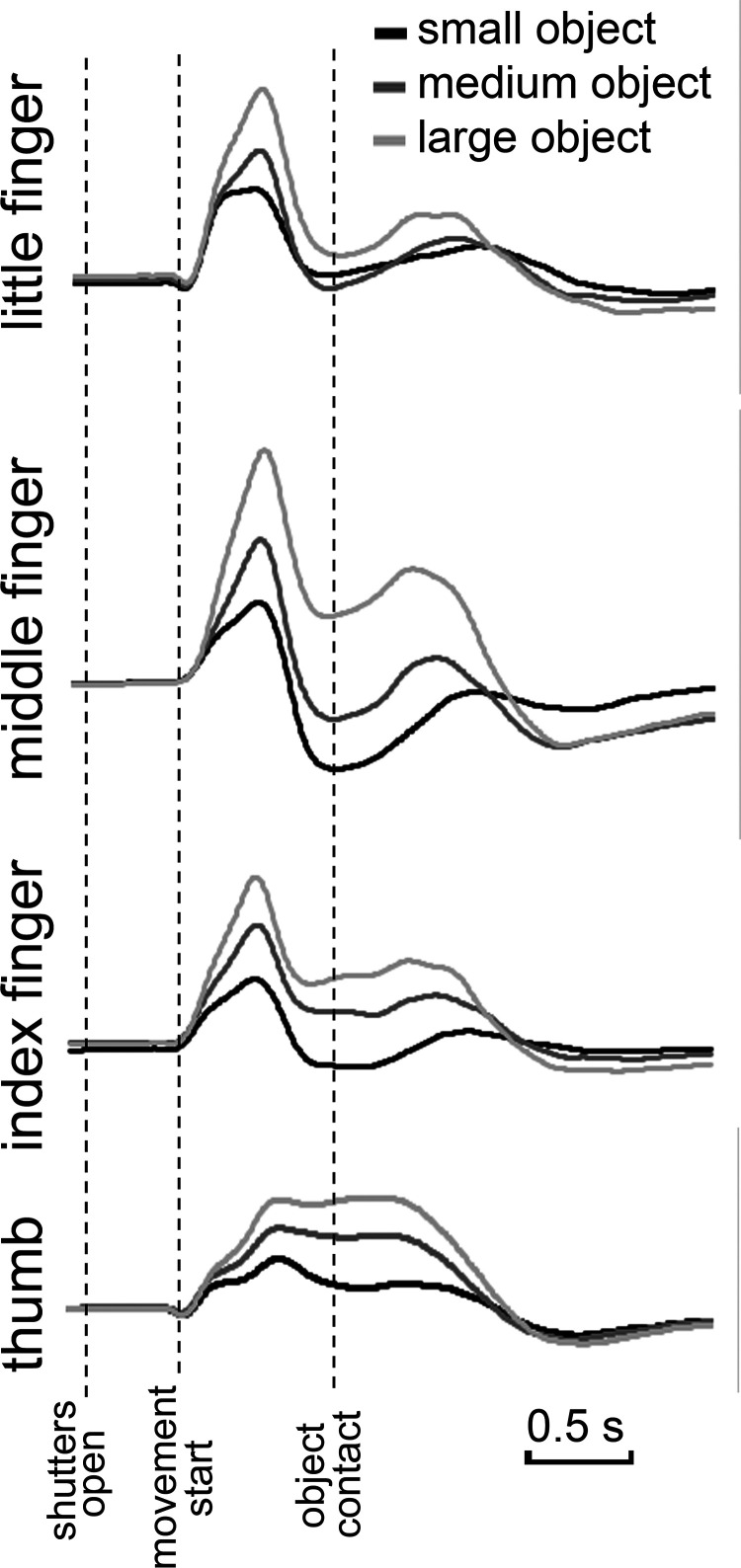
The output of each trial was the raw recordings from each of the four flexion sensors, starting in the resting position (baseline level), opening during reaching, and closing on the object (for an example of recording, see Fig. 3). We extracted from the raw signal the following data: (1) The flex-sensor values corresponding to the peak finger aperture, defined as the difference between initial baseline flex-sensor values and maximum peak value during reaching. This value is indicative of the maximum angle that the phalanxes form with respect to each other. We will refer to these as “peak aperture.” (2) The peak velocity of flex-sensor signal while reaching peak aperture. We will refer to this value as “peak angular velocity.” (3) The time of movement onset, corresponding to the time between the opening of the shutter lenses and the release from the response button. We will refer to this value as “reaction time.” Peak aperture and peak angular velocity were analyzed by means of a classification procedure, which is aimed at building a model able to predict the category of an unknown object (among a set of prespecified categories) (Duda et al., 2001; Bishop, 2006; Rajkomar et al., 2019). In particular, in our study, for a given subject (and a given stimulation), we measure the capability of a classifier in discriminating between the three different cylinders (small vs medium vs large), based on finger openings. The idea is that we can assess the impact of the stimulation on the subject by measuring the decrease in classification accuracy (i.e., if the task becomes more difficult for the classifier when the subject is stimulated). More in detail, we adopted the following strategy:

Figure 3.

Example of recording of the first participant: the figure represents the four flexion sensor traces (thumb, index finger, middle finger, and little finger) as a function of the three object sizes (small, medium, and large).

Step 1. For a given subject Sub_i and a given state Stat_j (i.e., stimulation site), we define a classification problem in which every object is a single repetition of the given task (i.e., grasping the cylinder) done by the subject Sub_i who has been stimulated in the state Stat_j. Every experiment is described with the four opening values, and has associated the label 1, 2, or 3 according to the grasped cylinder, as shown in Table 2.

Table 2.

Structure of experimental variables for the classification procedures

Repetition	Opening	Labels
1	x1 = [x11, x12, x13, x14]	c1 (1,2, or 3)
2	x2 = [x21, x22, x33, x24]	c2 (1,2, or 3)
N	xN = [xN1, xN2, xN3, xN4]	cN (1,2, or 3)

Step 2. For every classification problem (i.e., for every subject-state), we chose a classifier, and calculate its classification accuracy with a cross-validation strategy, that is, a mechanism that permits to test the classifier using objects not present in the training set (the set of objects used to learn the classifier). This ensures to estimate the generalization capability of the given classifier, that is, its capability in classifying also objects not present in the training set (Duda et al., 2001). We used the variant called leave-one-out (Bramer, 2016), a variant that should be preferred when the number of instances in a dataset is small (Wong, 2015). The procedure is as follows: in the first step, the classifier is trained with all the objects, except the first, which is then used for testing; if the label predicted by the classifier is different from the true label of the testing object, then an error occurred. We then repeat the scheme by leaving out the second object and so on, until all objects have been tested. The final classification accuracy is measured as the number of the objects that have been correctly predicted by the classifier, divided by the total number of objects. Using this scheme, the testing set is always separated from the training set (this permits to measure generalization capabilities), whereas the size of the training set is maximized (this permits to have good estimates of the classifiers). An additional advantage of the leave-one-out is that it does not involve a randomness mechanism; and therefore, research reproducibility is allowed. In order to increase the significance of the results, we used different classifiers (Duda et al., 2001; Bishop, 2006), which ranged from the simple Nearest Neighbor up to more complex classifiers, such as Support Vector Machines or Random Forests. More in details we used:

• (1nn): The classic Nearest Neighbor rule, in which the testing object is assigned to the class of its most similar training object (i.e. the nearest object of the training set). Here we used the Euclidean distance as proximity measure, using the MATLAB prtools library (http://prtools.tudelft.nl/) (Duin et al., 2000) implementation knnc.

• (knn(opt K)): The K-Nearest Neighbor rule, which generalizes the nearest neighbor by assigning an unknown object to the class most frequent inside its K most similar points of the training set (the K nearest neighbors of the testing object). Also, in this case, we used the Euclidean distance, and we found the optimal K using another leave-one-out strategy on the training set (as provided in the knnc routine of the prtools library).

• (ldc): The Linear Discriminant Classifier, a probabilistic classifier that implements the Bayes decision rule: in this case, every class is modeled with a different Gaussian distribution, and the covariance matrix is shared among the different classes. In particular, the joint covariance matrix is the average of the class-specific covariance matrices, each one weighted by the a priori probability (function ldc of prtools).

• (qdc): The Quadratic Discriminant Classifier, which is similar to ldc but the covariance matrix is different for every class (function qdc of prtools).

• (svm): The Support Vector Machine (Cristianini and Shawe-Taylor, 2000), a classifier based on the statistical learning theory. Here we used the rbf kernel with the scale parameter automatically estimated on the training set (as provided in the MATLAB Statistics and Machine Learning toolbox routine fitcsvm).

• (RF-100): The Random Forest classifier, an effective classifier (Breiman, 2001), based on an ensemble of decision trees. Here we used the routine TreeBagger from the Statistics and Machine Learning toolbox, using 100 trees.

Step 3. At the end of the previous step, we have computed 17 accuracies (corresponding to the 17 subjects involved in the study) for every state stimulation and for every classifier. In order to see the impact of the stimulation in a given state Stat_j, we can compare the accuracy obtained in such state with the accuracy obtained in the Sham state. In order to have a more robust estimation of the Sham(i.e., the baseline accuracy), we averaged the accuracies obtained in the Sham 1 and Sham 2.

Step 4. Moreover, to have a statistical significance, we performed a paired t test to compare the 17 accuracies obtained by a given classifier in a given state with the accuracies obtained by the same classifier in the sham state, with the hypothesis that the two matched samples come from distributions with equal means (i.e., the difference between them is assumed to come from a normal distribution with unknown variance). We used a significance level of 0.05, corrected by the Bonferroni rule for multiple tests.

The effect of TMS on reaction time was tested using a linear mixed model using R (R Core Team, 2016) and the lme4 package (version 1.1-12) (Bates et al., 2015). Statistical significance was tested with the F test with Satterthwaite approximation of degrees of freedom. The experimental factor TMS (the 8 active spots and the collapsed sham spots), size (small vs medium vs large), and their interaction were entered as fixed-effect factors in a linear mixed model that predict reaction times (the sham condition was the reference level for all comparisons). Random coefficients across participants were estimated for intercept and for the factor TMS.

Data visualization

Data of Subject 1 are visualized in Figure 4 for illustration purposes. The plots represent the first two principal components of each set of experiments. More in details, we projected each flexor sensor (represented with 4 values) in a bidimensional space, using a classic and well-known linear transformation, the Principal Component Analysis (Jolliffe, 2002) (in particular, we used the MATLAB prtools library [prtools] (Duin et al., 2000) implementation pcam).

Figure 4.

First two principle components (PCA) extracted from the four flexion sensors data of the first participant.

Results

Peak aperture

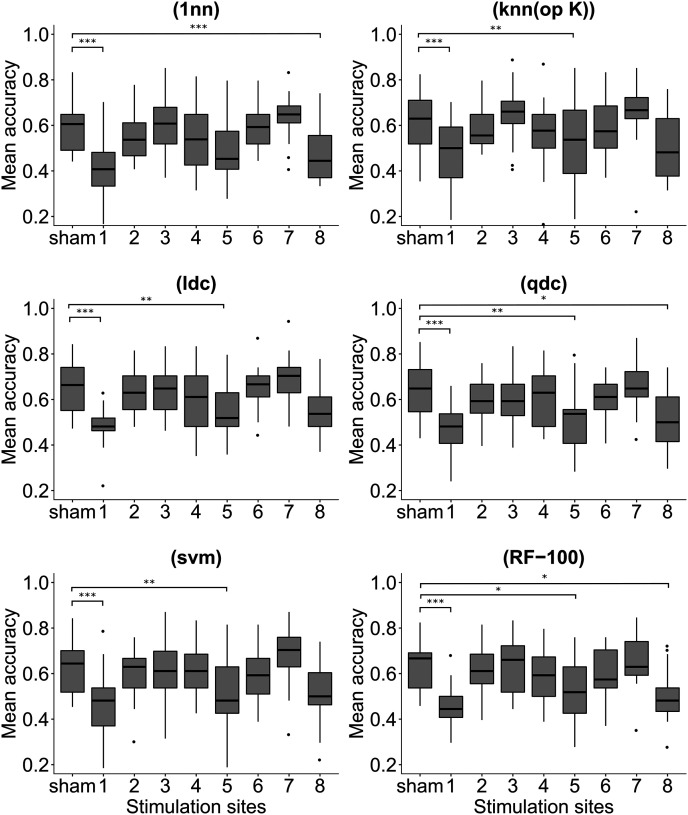
Mean accuracy and statistics for the six different classifiers, as a function of the 8 premotor stimulation sites are indicated in Table 3. Results indicated that overall the accuracy of the six classifiers under the sham conditions is 63%, which is significantly higher compared with a random classifier (random classifier accuracy = 33%, p < 0.01). Overall, results consistently indicated that the accuracy of the classifiers under the stimulation of the Site 1 (mean accuracy = 46%) is significantly reduced compared with sham stimulation (mean accuracy = 63%). More specifically, analysis indicated that the accuracy is significantly reduced after the stimulation of the Site 1 in the medial part of the PMC, for all the six classifiers considered ((1nn): t₍₁₆₎ = 6.39, p < 0.001; (knn (opt K)): t₍₁₆₎ = 5.41, p < 0.001; (ldc): t₍₁₆₎ = 6.38, p < 0.001; (qdc): t₍₁₆₎ = 6.53, p < 0.001; (svm): t₍₁₆₎ = 6.39, p < 0.001; (RF-100): t₍₁₆₎ = 6.72, p < 0.001) (Fig. 5). Furthermore, analysis also demonstrates that overall the six classifiers are less accurate in discriminating the three cylinders after stimulation of Site 5 in the PMv (mean accuracy = 52%), compared with the sham stimulation (mean accuracy = 63%). Five of six classifiers showed significantly lower accuracy compared with the sham conditions ((1nn): t₍₁₆₎ = 2.94, p = 0.07; (knn (opt K)): t₍₁₆₎ = 3.91, p = 0.009; (ldc): t₍₁₆₎ = 4.22, p = 0.005; (qdc): t₍₁₆₎ = 4.43, p = 0.003; (svm): t₍₁₆₎ = 3.68, p = 0.01; (RF-100): t₍₁₆₎ = 3.35, p = 0.003). Finally, the overall accuracy was also reduced after stimulation of the lateral part of the PMv, Site 8 (mean accuracy = 52%), compared with the sham control conditions. For Site 8, analysis demonstrated that three of six classifiers are significantly less able to discriminate the movements toward the three different objects, compared with the sham ((1nn): t₍₁₆₎ = 3.78, p = 0.01; (knn (opt K)): t₍₁₆₎ = 2.63, p = 0.14; (ldc): t₍₁₆₎ = 2.81, p = 1.0; (qdc): t₍₁₆₎ = 3.17, p = 0.04; (svm): t₍₁₆₎ = 2.57, p = 0.16; (RF-100): t₍₁₆₎ = 3.89, p = 0.001). Results indicated that the accuracy of the all six classifiers were comparable between the sham and the stimulation site number 2 (all p values = 1.0), number 3 (all p values = 1.0), number 4 (all p values > 0.51), number 6 (all p values = 1.0), and number 7 (all p values > 0.90) (for details, see Figs. 5, 6; Table 3).

Table 3.

Maximum finger aperture^a

Stimulation sites	(1nn)			(Knn (opt K))			(ldc)			(qdc)			(svm)			(RF-100)
	Mean	t	p	Mean	t	p	Mean	t	p	Mean	t	p	Mean	t	p	Mean	t	p
1	41.9*	6.39*	<0.001*	47.5*	5.41*	<0.001*	47.5*	6.38*	<0.001*	47.2*	6.53*	<0.001*	46.2*	6.39*	<0.001*	46.6*	6.72*	<0.001*
2	56.1	1.61	1.0	59.5	0.57	1.0	63.5	0.87	1.0	60.2	1.42	1.0	58.7	1.56	1.0	61.7	0.84	1.0
3	61.0	0.25	1.0	64.6	1.19	1.0	63.2	0.90	1.0	60.1	1.36	1.0	61.7	0.26	1.0	63.2	0.17	1.0
4	53.6	1.98	0.51	55.1	1.81	0.71	60.6	1.98	0.51	60.5	1.01	1.0	59.7	1.17	1.0	58.1	1.86	0.65
5	49.2	2.94	0.07	50.5*	3.91*	0.009*	55.4*	4.22*	0.005*	51.1*	4.43*	0.003*	51.2*	3.68*	0.01*	52.7*	3.35*	0.03*
6	59.3	0.28	1.0	58.5	1.17	1.0	64.5	0.52	1.0	60.0	1.37	1.0	59.1	1.49	1.0	60.0	1.48	1.0
7	63.3	1.44	1.0	64.6	1.60	1.0	69.3	1.67	0.90	65.5	0.69	1.0	66.3	1.58	1.0	65.2	0.51	1.0
8	47.3*	3.78*	0.01*	52.2	2.63	0.14	55.9	2.81	0.10	52.0*	3.17*	0.04*	52.2	2.57	0.16	50.7*	3.89*	0.01*
Sham	60.1			61.0			65.7			63.8			62.6			63.9

^aMean accuracy and statistics (t values, p values, Bonferroni correction) for the six different classifiers, as a function of the eight premotor stimulation sites. Degrees of freedom for all tests are 16.

*Significant.

Figure 5.

Mean classification accuracy for the six different classifiers as a function of the 9 stimulation sites (8 + sham). Significant contrasts between sham and the active spots: ***p < 0.001; **p < 0.01; *p < 0.05.

Figure 6.

Statistical map projected on the brain of the average t values per site across the six classifiers. Negative t values indicate a better ability of the classifiers to discriminate the three objects compared with the sham control condition. Positive t values indicate a worse ability of the classifiers to discriminate the three objects compared with the sham control condition.

In order to further inspect what specifically drove the reduced classifiability of movement kinematics after TMS stimulation, we plotted the difference between the mean peak aperture in each active spot and the sham control condition, as a function of sensors, objects, and stimulation sites (Fig. 7). Positive values of such difference indicate a greater mean aperture compared with the sham condition and negative values smaller mean aperture compared with the sham in the same condition. Therefore, the visual inspection of the data consistently shows that, under the stimulation of Spots 1, 5, and 8, participants tended to overestimate the size of the smaller object and to underestimate the size of the larger object compared with the sham control condition, a pattern that is likely the basis of the reduced capacity of the classifiers to correctly discriminate the three objects.

Figure 7.

The difference between peak aperture values in the active condition minus the peak aperture in the sham condition is shown separately for each sensor (thumb, index, middle, and little finger), for each object (small, medium, and large), and for each stimulation site. Positive values indicate that active TMS is associated with a greater mean aperture compared with the sham condition. Vice versa, negative values indicate that TMS is associated with smaller mean apertures compared with the sham condition. Dashed lines indicate Spots 1, 5, and 8 in which TMS reduced classifiability of object in the main analysis.

Peak angular velocity

Following the same logic of the peak aperture analysis, for a given subject (and a given stimulation), we measure the capability of a classifier in discriminating between the three different cylinders (small vs medium vs large), based on maximum finger opening velocity. Mean accuracy and statistics for the six different classifiers, as a function of the 8 premotor stimulation sites, are indicated in Table 4. Overall, the results corroborated and strengthened the results concerning the peak aperture. Indeed, analysis consistently indicated that the accuracy of the classifiers under the stimulation of the Site 1 (mean accuracy = 35%) is significantly reduced compared with sham stimulation (mean accuracy = 57%). More in details, analysis indicated that the accuracy is significantly reduced after the stimulation of the Site 1 in the medial part of the PMC, for all the six classifiers considered ((1nn): t₍₁₆₎ = 4.46, p < 0.001; (knn (opt K)): t₍₁₆₎ = 5.42, p < 0.001; (ldc): t₍₁₆₎ = 7.60, p < 0.001; (qdc): t₍₁₆₎ = 7.57, p < 0.001; (svm): t₍₁₆₎ = 5.67, p < 0.001; (RF-100): t₍₁₆₎ = 6.71, p < 0.001). Furthermore, analysis also demonstrates that overall the six classifiers are less accurate in discriminating the three cylinders after stimulation of Site 5 in the PMv (mean accuracy = 36%), compared with the sham stimulation (mean accuracy = 57%). All the six classifiers showed significantly lower accuracy compared with the sham conditions ((1nn): t₍₁₆₎ = 7.58, p < 0.001; (knn (opt K)): t₍₁₆₎ = 6.04, p < 0.001; (ldc): t₍₁₆₎ = 6.20, p < 0.001; (qdc): t₍₁₆₎ = 7.57, p < 0.001; (svm): t₍₁₆₎ = 9.91, p < 0.001; (RF-100): t₍₁₆₎ = 8.46, p < 0.001). Finally, the overall accuracy was also reduced after stimulation of the lateral part of the PMv, Site 8 (mean accuracy = 36%), compared with the sham control conditions. Also for Site 8, all the six classifiers are significantly less able to discriminate the movements toward the three different objects, compared with the sham ((1nn): t₍₁₆₎ = 5.23, p < 0.001; (knn (opt K)): t₍₁₆₎ = 4.25, p = 0.004; (ldc): t₍₁₆₎ = 7.20, p < 0.001; (qdc): t₍₁₆₎ = 6.11, p < 0.001; (svm): t₍₁₆₎ = 6.20, p < 0.001; (RF-100): t₍₁₆₎ = 6.43, p < 0.001).

Table 4.

Peak angular velocity^a

Stimulation sites	(1nn)			(Knn (opt K))			(ldc)			(qdc)			(svm)			(RF-100)
	Mean	t	p	Mean	t	p	Mean	t	p	Mean	t	p	Mean	t	p	Mean	t	p
1	37.8*	4.46*	<0.001*	33.8*	5.42*	<0.001*	36.6*	7.60*	<0.001*	34.3*	7.57*	<0.001*	34.2*	5.67*	<0.001*	34.6*	6.71*	<0.001*
2	53.2	0.28	1.0	53.8	0.66	1.0	55.6	1.65	0.93	53.6	1.93	0.56	54.0	0.96	1.0	54.0	0.74	1.0
3	53.2	0.24	1.0	55.0	0.19	1.0	56.5	1.17	1.0	52.9	2.58	0.15	52.7	1.60	1.0	53.8	0.91	1.0
4	49.7	1.12	1.0	54.5	0.36	1.0	56.6	0.91	1.0	54.2	1.76	0.77	52.0	1.94	0.55	56.6	0.21	1.0
5	36.0*	7.58*	<0.001*	30.1*	6.04*	<0.001*	40.2*	6.20*	<0.001*	39.1*	7.57*	<0.001*	33.4*	9.91*	<0.001*	37.2*	8.46*	<0.001*
6	56.0	1.50	1.0	55.2	0.16	1.0	60.8	0.73	1.0	57.5	0.73	1.0	55.8	0.58	1.0	55.3	0.42	1.0
7	56.3	1.68	0.89	54.0	0.40	1.0	60.0	0.25	1.0	59.1	0.22	1.0	57.1	0.14	1.0	59.1	1.14	1.0
8	34.5*	5.23*	<0.001*	36.0*	4.25*	0.004*	38.1*	7.20*	<0.001*	35.1*	6.11*	<0.001*	34.3*	6.20*	<0.001*	35.1*	6.43*	<0.001*
Sham	52.5			55.6			59.4			58.6			56.9			56.0

^aMean accuracy and statistics (t values, p values, Bonferroni correction) for the six different classifiers, as a function of the eight premotor stimulation sites. Degrees of freedom for all tests are 16.

*Significant.

Reaction time

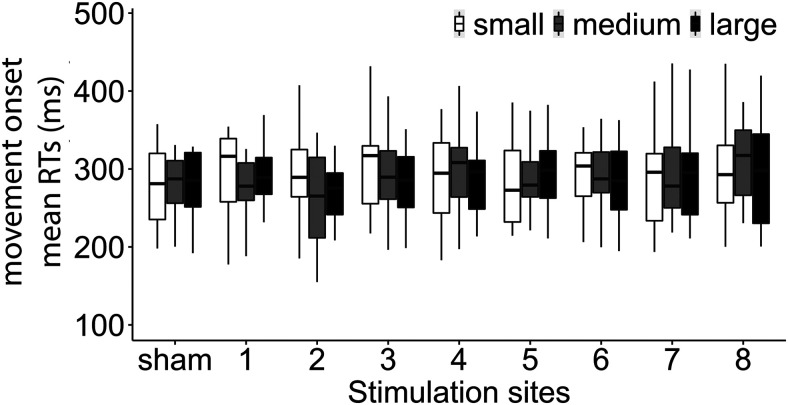
Overall mean reaction time was 299 ms, and median reaction time was 281 ms (SD = 111 ms). The analysis revealed a nonsignificant main effect of TMS (F_(8,15.3) < 1, p = 0.92), indicating that overall TMS did not significantly affect the start of the movement (all contrasts, p > 0.39), as well as a nonsignificant main effect of size (F_(2,5830.3) < 1, p = 0.55). The interaction between TMS and size was also nonsignificant (F_(16,5827.8) < 1, p = 0.49) (Fig. 8).

Figure 8.

Mean reaction times (ms) of movement onset as a function of the 9 stimulation sites (8 + sham) and the three different objects (small, medium, and large).

Discussion

The ability to reach and grasp objects is at the basis of our daily interaction with the external world. At the neural level, the information relative to the grip component (i.e., the posture of the hand to anticipate the shape, size, and orientation of the object) has been classically attributed to the dorsolateral pathway, connecting the anterior part of the intraparietal sulcus with the PMv. Recent neuroimaging studies in human (Gallivan et al., 2011, 2013; Verhagen et al., 2012; Fabbri et al., 2014; Monaco et al., 2015; Turella et al., 2016) did not support this functional exclusivity of the human frontoparietal dorsolateral circuit, demonstrating grasp-related activity within the dorsomedial pathway as well (Grafton et al., 1996; Culham et al., 2003; Grol et al., 2007; Turella and Lingnau, 2014; Vesia et al., 2018). This is particularly evident in the parietal cortex, where both neuroimaging (Gallivan et al., 2011, 2013; Turella and Lingnau, 2014; Gallivan and Culham, 2015) and neuromodulation studies (Vesia et al., 2017) have shown that a component of the dorsomedial system in the parietal lobe (in particular the SPOC) is involved in encoding grasping information. On the contrary, the functional representation of grasping in the PMC is still incompletely understood. In particular, clear-cut causal evidence on which regions within the PMC mediate reach-to-grasp behaviors is still missing. Here, we used a dense TMS approach to map the role of the entire PM in producing visually guided grasping in healthy human volunteers. Using a hypothesis-free data analysis approach, our study indicated that TMS altered finger joint motion when applied over spots located in the PMv and a spot located near the midline, putatively corresponding to the supplementary motor area (SMA). Importantly, in accordance with previous findings (Davare et al., 2006), TMS did not affect the time to movement onset but did affect the kinematic parameters associated to the correct hand posture configuration, therefore indicating a selective role of those spots in direct visuomotor transformation. The present findings corroborate a robust body of evidence showing hand-related information in the ventral part of the PMC. More interestingly, the present study is the first to directly indicate a causal involvement of the medial part of the PMC in mediating grip information during a visually guided grasping movement. The present findings are discussed in relation to the nonhuman literature.

Grasp information within the PMv

The present study demonstrated that stimulation of 2 different spots within the PMv directly interfere with the hand preshaping. Indeed, the classifiers consistently indicated a lower accuracy in discriminating the size of the three different objects when TMS was applied in the medial PMv and partly in the lateral-anterior PMv compared with a control sham condition. This result is in line with a considerable amount of evidence both in human (Grol et al., 2007; Cavina-Pratesi et al., 2010; Filimon, 2010; Turella and Lingnau, 2014; Vesia et al., 2017) and nonhuman primates (Jeannerod et al., 1995; Tanné-Gariépy et al., 2002; Brochier and Umiltà, 2007), indicating the PMv as a crucial node in encoding the visuomotor transformation for grasp movements. Electrophysiological studies in monkeys demonstrated that PMv neurons show a strict congruency between the coded grip and the intrinsic properties of the object, thus confirming the role of PMv in shaping the hand posture appropriately to grasp object (Murata et al., 1997; Rizzolatti and Luppino, 2001; Raos et al., 2006). Ventral premotor sector F5 contains visuomotor neurons (“canonical” neurons), which are active both when the monkey is performing grasping movement and when observing graspable objects (Bonini et al., 2014). Furthermore, selective inactivation of the monkey PMv leads to severe deficits in the grasping component of hand movements, keeping the reach component unaffected (Fogassi et al., 2001). Congruently, TMS studies in humans demonstrated that stimulation of both the left and the right PMv (but not of dorsal PMC) interferes with the hand preshaping, a crucial prerequisite for a well-planned grasping movement (Davare et al., 2006). Importantly, this effect was selectively observed when the TMS was delivered at 50 and 100 ms after the Go signal, but not at later timing, therefore suggesting an early involvement of the PMv during hand movement preparation. By unveiling a decrease in the classification accuracy of the three different objects after early PMv stimulation, the present findings are therefore in line with those of Davare et al. (2006), both in terms of behavioral outcomes and timing of stimulation. Indeed, the fact that the classifier is less able to discriminate whether the movement is associated to a big, small, or medium object is direct evidence that the PMv stimulation interferes with the hand configuration during the grasping movement. Although the present findings significantly expand our understanding of the premotor involvement during grasping movement, it would be important for future investigation to explore the temporal dynamics of both dorsal and ventral premotor spots in object-oriented behaviors and to test the TMS effect in early versus later phases of movement preparation.

Grasp information within the SMA

To the best of our knowledge, this is the first causal evidence in human showing the involvement of the SMA in coding the grasping components of goal-directed hand behaviors. Crucially, this finding is corroborated by recent studies in nonhuman primates, showing that neurons within the SMA (F6 sector) play a role in the integration of visuomotor transformation and sensorimotor association for grasping (Lanzilotto et al., 2016; Gerbella et al., 2017; Livi et al., 2019). Lanzilotto et al. (2016) showed that motor and visuomotor neurons of area F6 shared common features with neurons in sector F5 within the ventral PM, supporting a functional interplay between these two areas and suggesting to consider area F6 as a crucial additional node of the brain circuit for object grasping (Lanzilotto et al., 2016; Bonini, 2017; Gerbella et al., 2017; Livi et al., 2019). Area F6 is anatomically connected to the crucial premotor and parietal areas of the grasping network (Luppino et al., 1993, 2003; Rozzi et al., 2006; Gamberini et al., 2009; Gerbella et al., 2011). Furthermore, tracing studies directly show that the dorsomedial and the dorsolateral pathways are not completely anatomically segregated (e.g., Gharbawie et al., 2011; Janssen et al., 2018; Livi et al., 2019). Together, these findings suggested that the SMA may play a pivotal role in coding the grasping component, by integrating information coming from crucial regions of the grasping network. Importantly, the evidence from the medial PMC is not surprising if we consider that it nicely parallels the results already observed in the parietal cortex, where grasping neurons in the medial occipito-parietal cortex (V6A) of the macaque monkey have been consistently reported (Fattori et al., 2010, 2012). Likewise, neuroimaging studies in human demonstrated that preparatory activity in the medial parietal cortex (SPOC, the putative homolog of area V6A) accurately predicted upcoming grasping movement (Gallivan et al., 2011, 2013). These results were recently corroborated by a TMS experiment (Vesia et al., 2017), showing that the dorsomedial SPOC-M1 pathway encodes handgrip formation during reach-to-grasp movement preparation. By unveiling a causal involvement of the SMA in visuomotor transformation for grasping, the present findings suggested a similar counterpart of grasping representation within the PMC. These results are in line with a growing body of evidence demonstrating that the hand-related information is coded within both the dorsolateral and the dorsomedial pathways, comprising the PMv, but also a more medial-dorsal part of the PMC (Gallivan et al., 2011, 2013; Verhagen et al., 2012; Fabbri et al., 2014; Monaco et al., 2015; Turella et al., 2016). In human, the SMA is part of the network associated with the control of hand posture (Rizzolatti et al., 2014) and is classically known to be involved in the planning and execution of goal-directed behaviors (Nachev et al., 2008; Rauch et al., 2013) and in motor sequence learning (Sakai et al., 1999). Nonetheless, its specific involvement in grasping movements has been observed, especially for precision grip movements (for review, see King et al., 2014). The present study corroborates and extends these findings, first demonstrating a direct involvement of the medial part of the PMC in visuomotor transformation necessary for a correct visually guided grasping. This result is congruent with recent evidence in monkeys, thus suggesting that the functional neuroanatomy of sensorimotor transformation needed to preshape the hand correctly may be similar between human and nonhuman primates. Future investigations are needed to better clarify the role of the pre-SMA in coding grasping information and its temporal dynamic compared with the PMv. For instance, once the critical role of PMv and SMA in grasping movement is identified, TMS stimulation at different time points will reveal the temporal unfolding of the mechanisms that are implemented in the targeted areas during the course of grasping movement. Furthermore, one limitation of the current study is that the data-glove adopted here just allowed to record and analyze finger joint motion (which indeed was our main interest). Nonetheless, combining TMS with kinematic tracking will allow to directly test whether the stimulation of SMA and/or PMv causally influence other kinematic parameters.

TMS statistical mapping

Finally, the present study adopted a cutting-edge methodological approach to shed light on the functional role of the entire PMC in visually guided grasping movement. First, we used the dense sampling TMS approach, which ultimately allows to map the functional role of the left PMC with a reliable spatial information. Dense TMS spatial mapping gives more detailed information compared with TMS studies adopting the a priori localization of coil positioning and has already been demonstrated successful in mapping different cognitive functions (Ellison et al., 2004; Stoeckel et al., 2009; Cattaneo and Barchiesi, 2011; Finocchiaro et al., 2015; Maule et al., 2015; Parmigiani et al., 2015; Schaeffner and Welchman, 2017; Cattaneo, 2018; Lega et al., 2019). Second, the analysis approach went in the same direction, since data-driven classification algorithms allow to describe the data in a relatively hypothesis-independent way. Furthermore, to increase the significance of the results, we used different classifiers (Duda et al., 2001; Bishop, 2006). Importantly, these methods allowed to substantiate previous TMS studies on the crucial role of PMv in visuomotor transformation (Davare et al., 2006), therefore confirming the validity of our approach. In addition, they allowed to draw a more detailed functional cartography of the human PMC, revealing a direct involvement of SMA in object grasping, a clear-cur causal evidence that has never been described in human literature.

In conclusion, using a dense TMS spatial mapping approach, the present findings showed a detailed functional cartography of the entire PMC, consistently indicating a multifocal representation of object geometry for grasping. More specifically, we demonstrated that information about the preshaping of the hand with respect to the object's intrinsic properties is coded in the human PMv. More interestingly, the present study also indicated the human SMA as causally involved in visuomotor transformation for grasping. In accordance with monkey literature (Lanzilotto et al., 2016; Gerbella et al., 2017), we suggested inclusion of the SMA as a crucial node of the human cortical grasping network.