A simple approach to optimum pool size for pooled SARS-CoV-2 testing

Abstract

Systematic, large-scale testing of asymptomatic subjects is an important strategy in the management of the SARS-CoV-2 pandemic. In order to increase the capacity of laboratory-based molecular SARS-CoV-2 testing, it has been suggested to combine several samples and jointly measure them in a sample pool. While saving cost and labour at first sight, pooling efficiency depends on the pool size and the presently experienced prevalence of positive samples. Here we address the question of the optimum pool size at a given prevalence. We demonstrate the relation between analytical effort and pool size and delineate the effects of the target prevalence on the optimum pool size. Finally, we derive a simple-to-use formula and table that allow laboratories performing sample pooling to assess the optimum pool size at the currently experienced target prevalence rate.

Introduction

An efficient diagnostic pipeline is crucial in the management of the present SARS-CoV-2 pandemic and of great value for society returning back to normality with confidence (Koo et al., 2020). Recently, Hogan et al. (2020) demonstrated sample pooling in SARS-CoV2-testing to increase capacities of RT-PCR, which remains the gold standard for testing. Despite compromised sensitivity, pooling may be particularly suited for testing of asymptomatic carriers with high viral load, who likely contribute most to the spread of the disease (Wolfel et al., 2020, Zou et al., 2020). However, the decision to setup a pooling strategy with possibly compromising sensitivity must be rational and the benefits must be significant to justify the procedure of sample pooling. Several critical aspects such as the setting (e.g. hot spot screening), purpose (e.g. risk assessment), availability of equipment and materials, and local statutory provisions may affect the individual decision of a laboratory to set up a pooling strategy.

On the other hand, the success of pooling depends on the frequency of positive samples, which also determines the optimum pool size for a pooling strategy. Positives pools must eventually be resolved, which brings about additional workload. This study provides a simple strategy to estimate the optimum pool size for two-staged pooling based on a known target prevalence.

Methods

All calculations, including deriving the function that defines the required tests at a given prevalence, generation of data matrices and preparation of contour plots were performed using Matlab 2019, Ver. 9.7.0 (MathWorks Inc.). While the mathematical relation between a target prevalence and the resulting total number of tests required to resolve all positive subjects in a two-step pooling procedure is described in the results section, the differentiation was accomplished using the Matlab “diff” function, which can be used to approximate partial derivatives. Plotting of the results was achieved by generating grid coordinates as required using the Matlab “meshgrid” function, then generating a matrix by applying the grid coordinates to the respective equation and eventually plotting isolines using the Matlab “contour” function. Intersections of the isolines of the derivative with the x-axis were used for curve fitting using the Matlab curve fitting toolbox and the “power” fit algorithm.

Results

The most important factor for determining the efficiency of a pooling strategy is the net analyses required per specimen (θ), which may also be considered a proxy of associated analytical efforts and cost. While the probability Pn of a pool of size ps being negative at target prevalence (p) can be described as $Pn={\left(1-p\right)}^{ps}$, the probability of a pool being positive (Pp) can be described as $Pp=1-{\left(1-p\right)}^{ps}$, with p always being in the format of the decimal value of the ratio of positives/total samples. To determine the required analyses per specimen (θ), the total analyses (At) per total specimens (S) can be calculated by adding the number of subjects from positive pools to the number of total pools (Pt), divided by total specimens (S):

$$\theta =\frac{At}{S}=\frac{\left(Pt+\left(Pp*Pt*ps\right)\right)}{S}=\frac{\left(\frac{S}{ps}+\left(\left(1-{\left(1-p\right)}^{ps}\right)*Pt*ps\right)\right)}{S}$$

This simplifies as:

$$\theta =\frac{1}{ps}-{\left(1-p\right)}^{ps}+1$$ (1)

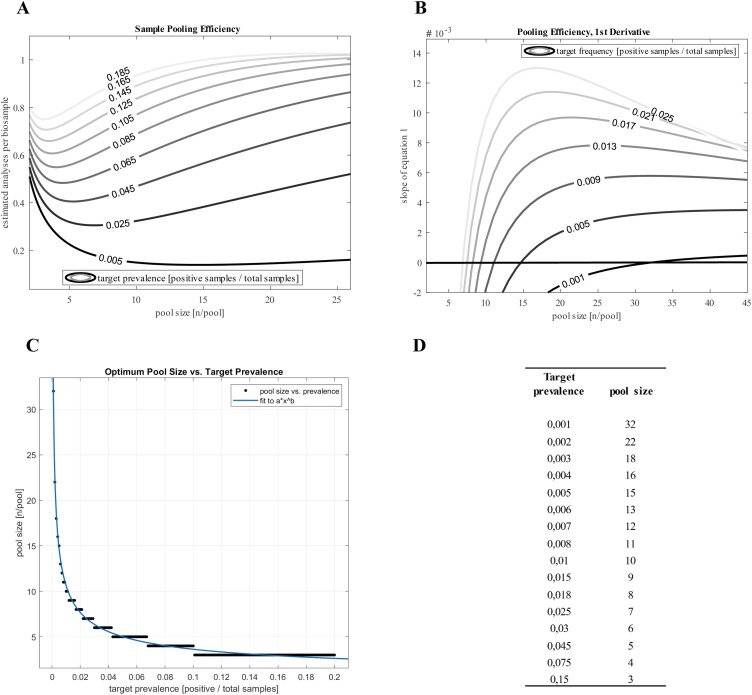
The optimum pool size for a given frequency is defined by the local minima of the isolines in Figure 1 A and can be more precisely determined by the first derivative of Eq. (1) (Figure 1B):

$$d\theta =-\frac{1}{p{s}^2}-\text{log}\left(1-p\right)*{\left(1-p\right)}^{ps}$$

Figure 1.

The relation between the estimated analyses per specimen and a pool size are given for various target prevalence rates as defined by Eq. (1) (isolines; A). Local minima suggest optimum pool sizes at the respective target prevalence rate (isolines; A). The first derivative of Eq. (1) allows precise determination of optimum pool sizes from the intersections of the isolines with the x-axis (B). Optimum pool sizes associated with a given target prevalence are summarized for select target prevalence rates (D). The association between prevalence and optimum pool size closely follows a power function $y=a{x}^b$ with sufficient precision (R² >0.99) and a = 1.24 and b = –0.466, allowing to estimate the optimum pool size by the formula $poolsize=1.24*prevalenc{e}^{-0.466}$.

The intersections of the isolines of the derivative with the x-axis yield the optimum pool sizes (Figures 1B and D). The association between prevalence and optimum pool size (Figure 1C) fits to a simple power function in the format $y=a{x}^b$ (Eq. (2)), allowing to approximate optimum pool size with the formula:

$$poolsize=1.24*prevalenc{e}^{-0.466}$$ (2)

To rapidly identify the optimum pool size at a given prevalence, the prevalence has to be entered into the formula (Eq. (2)) in the format of a ratio (positives/total samples), resulting in the optimum pool size (n). For a target prevalence of 2/100 = 0.02, the optimum pool size would be $1.24\times {0.02}^{-0.466}=8(roundedup)$ and for a target prevalence of 2/1000 = 0.002 it would be $1.24\times {0.002}^{-0.466}=22$.

Discussion

The results from this analysis clearly demonstrate the relation between target prevalence rates and optimum pool sizes in a two-staged pooling strategy. The power function (Eq. (2)) derived from the relation between prevalence and optimum pool size (Figure 1D) provides a simple tool to calculate the optimum pool size at an expected prevalence. The results suggest that at high target prevalence rates (>0.1), sample pooling can marginally improve testing capacities, whereas pooling at rather low target frequencies, as observed by Hogan et al. (2020), may substantially enhance sample throughput and thus lower the effort and cost associated with RT-PCR-based testing strategies. Rational pooling may thus provide the basis to overcome a shortage of reagents or help with otherwise limited testing capacities, even with larger pool sizes when used in combination with sensitive assay procedures (Lohse et al., 2020). While sample pooling can generally increase throughput, reduce analysis time and cost, it may compromise sensitivity for samples with low viral loads. On the other hand, it is widely accepted that subjects with high viral loads contribute most to the spread of the disease. This suggests pooling as a strategy towards a fast and efficient testing procedure of asymptomatic cohorts, and highlights the need to adjust the pool size to an individual testing environment. While this approach can help to determine the most economical pool size at a given prevalence, there are other important aspects including, but not limited to, reagent availability, local regulations, sampling options, and available extraction strategies that may significantly affect the decision to perform pooling in general.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Funding sources

We acknowledge support from the German Research Foundation (DFG) and the Open Access Publication Funds of Charité – Universitätsmedizin Berlin.

Ethical approval

Not applicable.