Abstract
The magnitudes by which aberration and incoherent noise sources, such as diffuse reverberation and thermal noise, contribute to degradations in image quality in medical ultrasound are not well understood. Theory predicting degradations in spatial coherence and contrast in response to combinations of incoherent noise and aberration levels is presented, and the theoretical values are compared to those from simulation across a range of magnitudes. A method to separate the contributions of incoherent noise and aberration in the spatial coherence domain is also presented and applied to predictions for losses in contrast. Results indicate excellent agreement between theory and simulations for beamformer gain and expected contrast loss due to incoherent noise and aberration. Error between coherence-predicted aberration contrast loss and measured contrast loss differs by less than 1.5 dB on average, for a −20 dB native contrast target and aberrators with a range of root-mean-square time delay errors. Results also indicate in the same native contrast target the contribution of aberration to contrast loss varies with channel signal-to-noise ratio (SNR), peaking around 0 dB SNR. The proposed framework shows promise to improve the standard by which clutter reduction strategies are evaluated.
I. INTRODUCTION
Medical ultrasound imaging faces many challenges to image quality in clinical settings. A combination of inadequate acoustic windows, errors in focusing through complex tissue, and large patient body habitus, especially in abdominal imaging, can result in high levels of acoustic noise. The noise is manifested in the form of clutter, a temporally stable haze resembling speckle, which reduces target conspicuity by decreasing contrast and obscuring details. In abdominal imaging, it has been shown that clutter is largely produced by phase aberration and reverberation originating from the abdominal wall.1,2 This work presents methods to separate the individual contributions of phase aberration and incoherent noise sources, such as reverberation, to degradations in contrast and beamformer gain by means of spatial coherence, a well-validated measure of ultrasonic noise. Such separation will inform new methods to evaluate novel beamforming and adaptive imaging strategies.
Phase aberration describes distortions in the ballistic acoustic wave caused by local variations in sound speed due to tissue heterogeneity. These distortions introduce focusing errors on transmit and receive and, depending on the severity, create broader beams than those predicted by diffraction physics.3 Furthermore, the energy from the main lobe is shifted to the side lobes,4 decreasing the relative energy of the main lobe, and increasing off-axis scattering. An extensive simulation study using six digitized human abdominal walls found a wide range of arrival time errors, distribution of energy levels, and waveform similarities;5 those results were in concordance with in vivo arrival time errors using cross-correlation methods, where a broad range of arrival time errors was also found.6–10 These studies also found a similar range of spatial frequencies present in the time error profile.
Reverberation clutter is generated when the acoustic wave is subject to multiple scattering and reflection events in near-field tissue layers. These deviations from the ballistic path trap a fraction of the acoustic energy in these near-field layers and propagate the captured energy back to the transducer face at a later time than the ballistic wave. This produces a signal overlaying that of the tissue deep to the reverberant layers. In some cases, the layers are normal to the direction of acoustic propagation, and repetitions of the layered structure appear in the B-mode image. Otherwise, the reverberations produce a diffuse haze with a short autocorrelation full-width half maximum, often modeled as incoherent in the aperture domain.11–13 The diffuse case may be more prevalent in patients with thicker or more complex abdominal walls, which may contain several layers of connective tissue. An additional source of incoherent noise in the received signal is thermal noise, which is inherent to the electrical and mechanical properties of the transducer itself.14–16 Thermal noise is prevalent in scenarios where the signal received is significantly weakened, such as the case of high thermoviscous attenuation when imaging at depth and tissue harmonic imaging.17 The different types of image degradation are briefly summarized in Table I.
TABLE I.
Types of image degradation in medical ultrasound.
| Type | Spatial coherence | Description |
|---|---|---|
| Phase aberration | Partially coherent18 | Speed of sound heterogeneities result in broadened acoustic beams and increased side lobe energy.3–10 |
| Reverberation | Incoherent11–13 | Random noise generated by system electronics.1,2,11–13 |
| Thermal noise | Incoherent13 | Loss of signal due to attenuation and transducer properties amplify electronic noise.14–17 |
There exists an abundance of clutter reduction techniques, but each type comes with associated limitations.6,19–30 Motion-based filters19,20 are limited to removing reverberation clutter and require some degree of tissue motion to extract stationary clutter components; as a result, they see wide use in Doppler applications but not B-mode imaging. Phase aberration correction has been widely explored,6,21–24 and while improvements in image quality have been well documented for simulation and phantom cases, evidence for robust improvements remains elusive in clinical settings. Model-based approaches to clutter reduction, though they show marked improvement over previously mentioned methods, rely on simple models of scattering that result in errors in estimation of the inherent tissue signal.25,26 Likewise, spatial coherence techniques, which measure the similarity of backscattered echoes in the aperture domain, remain limited by their respective assumptions about the origin of clutter and thus utilize overly broad generalizations about clutter27,28 or seek to address only one source.29,30
Absent in these existing methods is the interplay between incoherent and partially coherent sources of clutter. Some methods seek to correct one type while the other is often ignored or assumed to be negligible, but this is not indicative of the clinical experience. Other methods assume all sources of clutter behave similarly and attempt to remove clutter in an inefficient, non-targeted fashion. Therefore, effective clutter quantification, specifically, the separation of aberration and incoherent sources of clutter, is needed to rigorously evaluate methods for clutter reduction, a conclusion supported by previous efforts.1,2 The reduction of singular sources of clutter can be quantified, while simultaneously assessing potential undesired amplifications of other sources of clutter. Such characterization can be extended to adaptive imaging applications, by which transmit parameters can be adjusted to minimize clutter before acquiring data.
This paper is organized as follows: Sec. II outlines the theory behind a coherence-based separation scheme. Section III describes the simulation methods used to acquire data and model clutter. Section IV compares simulation results to the theory presented in Sec. II, and Sec. V discusses the implications and limitations of this framework.
II. THEORY
A. Spatial coherence
The spatial coherence of backscattered ultrasound echoes is sensitive to all major forms of ultrasonic noise. For an M-element array (with M − m pairs of elements with lag, i.e., element separation, m), the normalized spatial coherence function, , for two spatially separated signals, si and , can be calculated as
| (1) |
where M is the number of transmit elements, m is the lag in terms of element separation, and n1 and n2 are the sampling bounds of the axial kernel.31
From this, a coherence function across the aperture domain can be constructed by calculating the correlation for all lag pairs in the active aperture. For a focused transmit pulse into diffuse scattering media, this coherence function is predicted by the van Cittert-Zernike (VCZ) theorem as the autocorrelation of the aperture function,31 which, for a rectangular aperture, is a triangle function whose base is twice the width of the aperture.
The addition of various sources of noise cause the coherence curve to deviate from the predicted triangle. Consider the case of linearly additive spatially incoherent noise, which is present in forms of diffuse reverberation and thermal noise and approximated as a δ function in coherence space.11–13 Through superposition, the resultant coherence curve, , which incorporates both signal and noise, appears as the weighted combination of the incoherent components () and the inherent noise-free target coherence curve (),
| (2) |
where , and the relative values of w1 and w2 change with the level of clutter.
Because the level of incoherent noise is encoded in this weighted sum, the level of clutter due to such sources can be estimated by taking the value of the coherence curve at m = 1, i.e., the average correlation between nearest-neighbor channels. This value, lag-one coherence (LOC), has been shown by Long et al. to be predictive of channel signal-to-noise ratio (SNR) and contrast in the presence of incoherent noise.13 If the channel SNR is known, the expected LOC, henceforth denoted as to indicate its relation to the spatial coherence curve, due to the measured level of noise can be calculated as
| (3) |
where the approximation can be made for large, clinically relevant, apertures, i.e., large M.
However, the noise component in this formulation is indicative of incoherent sources only. In this case, it is useful to note that the described SNR is due to incoherent sources, denoted as χ, alone. We can rewrite the description of as ,
| (4) |
Aberration, a partially coherent source, operates beyond the first lag. A thorough review of the effects of aberration on spatial coherence can be found in the work of Walker and Trahey.18 First, consider the spatial autocorrelation of an aberrator, , of known full-width half maximum, Γ,
| (5) |
| (6) |
where m is again the distance described in terms of element separation. The multiplicative effect of the aberrator, , on the noise-free coherence curve is then described as
| (7) |
| (8) |
where is a dimensionless variable describing the aberrator severity in terms of the acoustic frequency, f, and the root-mean-square (rms) time delay error, η. can also be described as the time delay error as a fraction of the wavelength. For example, a time delay error that is 50% of the wavelength in the time domain is described as . For a fixed time delay error, increases with frequency.
The effect of the aberrator is a Gaussian weighting of the noise-free coherence curve that scales in magnitude and width with and Γ, respectively. For aberrators with time delay errors approaching 0, , and becomes the identity for all lags. Likewise, in the presence of slow-varying aberrators in space, , and approaches the identity again. The effect of aberration can be combined with incoherent sources to rewrite Eq. (4),
| (9) |
More complex formulations of the coherence curve can be derived to include other sources of clutter, such as bright off-axis scattering resulting from non-uniform scattering functions; these manipulations are beyond the scope of this work.
B. Beamformer gain
The receive beamformer gain, G, is defined as the ratio of the beamformed SNR (SNRbf) to the channel SNR (SNRc),
| (10) |
Bamber et al.32 present an elegant method to calculate the beamformer gain with the spatial coherence function,
| (11) |
This formulation shows beamformer gain as a weighted integral of the spatial coherence function, where lower lags are weighted more heavily than higher lags, and the relative contribution decreases linearly with lag. Based on the spatial coherence function estimated by the VCZ theorem for ideal imaging conditions, there is a theoretical limit on realizable gain in a diffuse, speckle-generating target. Substituting the triangle function for , we can see that
| (12) |
where the approximation holds for large element counts, i.e., large M. This solution states that in ideal conditions and for large element counts, as is typically found in conventional pulse-echo ultrasound, the beamformer gain is roughly two-thirds of the number of elements in the active aperture.
An overview of Eq. (9) and its applications to Eq. (11) is visualized in Fig. 1. Spatial coherence curves showing contributions of incoherent clutter (S+χ), aberration (S + A), and their combination (S+χ+A) are shown in blue, red, and yellow lines, with the ideal coherence curve (S) shown in black in Fig. 1(a). Incoherent clutter is 0 dB relative to signal power in the channel domain, and the aberrator is defined as and Γ = 5 mm. Note the scaling effects of both clutter components. The δ function, representing the incoherent component, is evident in both S+χ and S+χ+A models, and the characteristic Gaussian of the partial decorrelation due to aberration is present in the S + A and S+χ+A models. The width of the Gaussian is unchanged in the presence of incoherent noise.
FIG. 1.
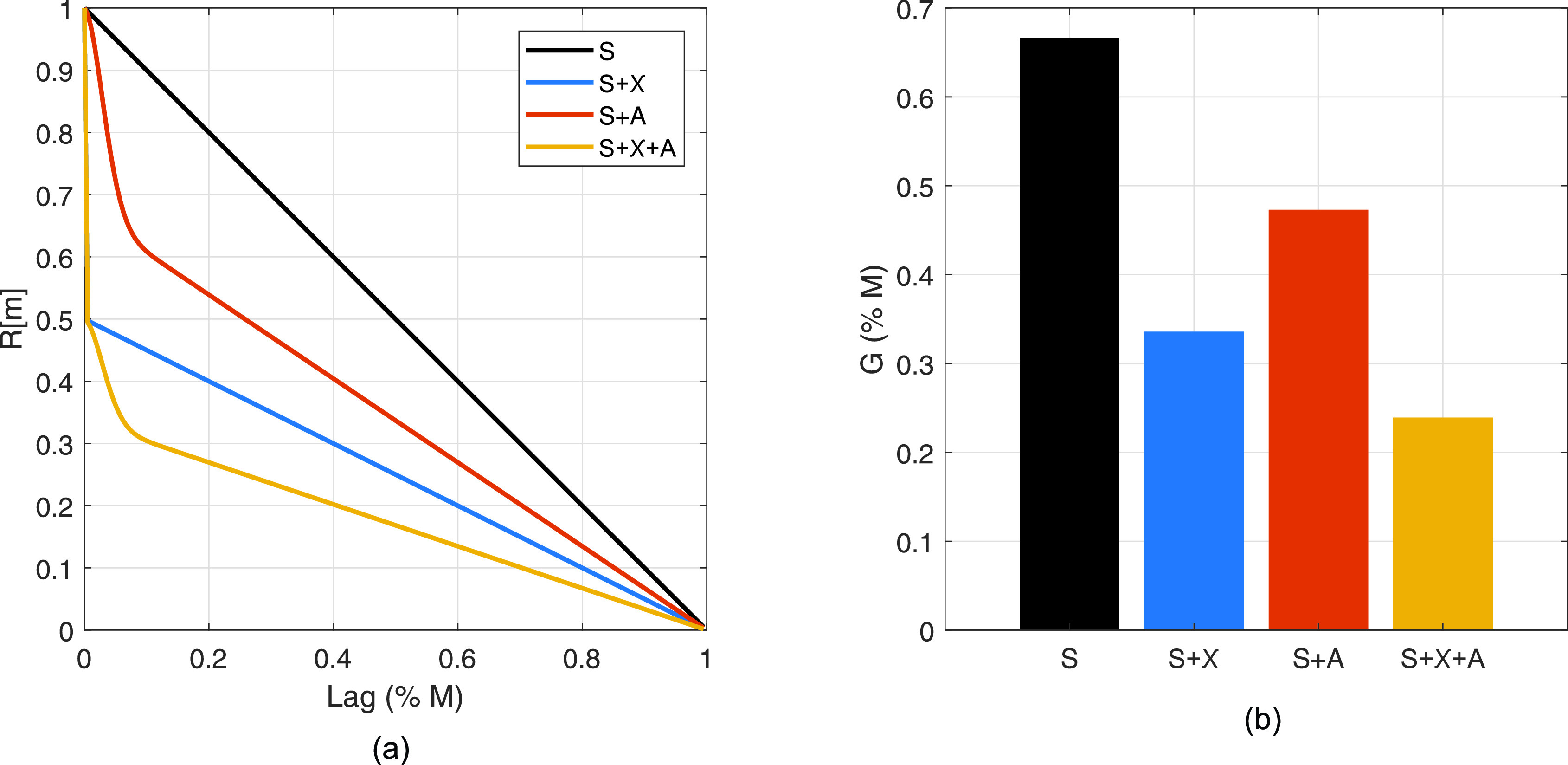
Spatial coherence curves (a) and calculated beamformer gain (b) for manipulations of ideal speckle coherence (S) due to incoherent clutter (S+χ), aberration (S + A), and their combination (S+χ+A). Modeled aperture is a continuously defined linear array with a 2.2 cm active aperture width. Incoherent clutter is 0 dB relative to signal power. Aberration is defined as and Γ = 5 mm.
The beamformer gain for each of the modifications to the ideal coherence curve is shown in Fig. 1(b). First, it is clear that for incoherent clutter 0 dB relative to channel signal power, the beamformer gain is reduced by a factor of 2, as predicted by Eq. (4). The relationship holds for cases with aberration when comparing the values for S + A and S+χ+A. Likewise, aberration has a similar multiplicative effect as predicted in Eq. (9). For this particular aberrator, regardless of the presence of incoherent clutter, the difference between the aberrated and unaberrated beamformer gain is roughly a factor of 1.4. Hence, beamformer gain captures the contributions of both incoherent clutter and aberration; in Secs. II C and II D, we will use it to estimate contrast and parse contributions of incoherent noise and aberration to contrast losses.
C. Estimated contrast
Long et al.13 derived an expression for expected contrast in the presence of incoherent noise, in terms of signal intensity, based on the beamformer gain, channel SNR in a background region, and native contrast (C0),
| (13) |
where SNRχ is calculated from LOC in a uniform scattering region according to the inverse of Eq. (3). This formulation shows that in low-noise conditions, i.e., high SNRχ, the first term in the numerator dominates. Conversely, in high-noise conditions, the second terms in the numerator and denominator dominate, causing the expected contrast to approach 0 dB, i.e., no perceptible contrast.
However, the work assumes a constant value for beamformer gain in using Gmax, rather than using Eq. (11) to capture potential losses in the beamforming gain. Though this is a good approximation in the case of incoherent noise, where SNR is well-captured in LOC, the presence of partially coherent noise complicates the estimation. To address this, we relax the use of Gmax in Eq. (13) to incorporate the use of a calculated, rather than assumed, beamformer gain degraded solely by aberration, while using the LOC, i.e., , to predict the SNR. A slight modification to Eq. (11) is needed to correct the coherence curve for the purposes of incoherent noise compensation and reflect the degradation in gain due to aberration alone, as is proposed by Long et al.,30
| (14) |
where the subscript A indicates degradation due to aberration alone. Note that in the absence of aberration, GA reduces to Gmax. This value can be substituted into Eq. (13) as follows:
| (15) |
The effects of aberration and incoherent noise on the expected contrast for a −6 and −20 dB target are shown in Fig. 2. Incoherent noise is varied −20 to 20 dB in the channel domain, and aberration is defined as 0 to 0.5 for a fixed Γ (5 mm). Increases in aberration and incoherent noise both decrease the expected contrast. High levels of incoherent noise ( dB) render the target nearly undetectable, with contrast values below 3 dB even in the aberration-free case. On the other hand, severe aberrators () do not have quite as perceptible an effect for the range of incoherent noise selected, but still reduce contrast for all values of SNRχ. For the same range of clutter parameters, the expected contrast deviates more for the more hypoechoic target. This is seen by the larger area of white-yellow for the −6 dB target, indicating better stability at the native contrast, compared to the −20 dB target.
FIG. 2.
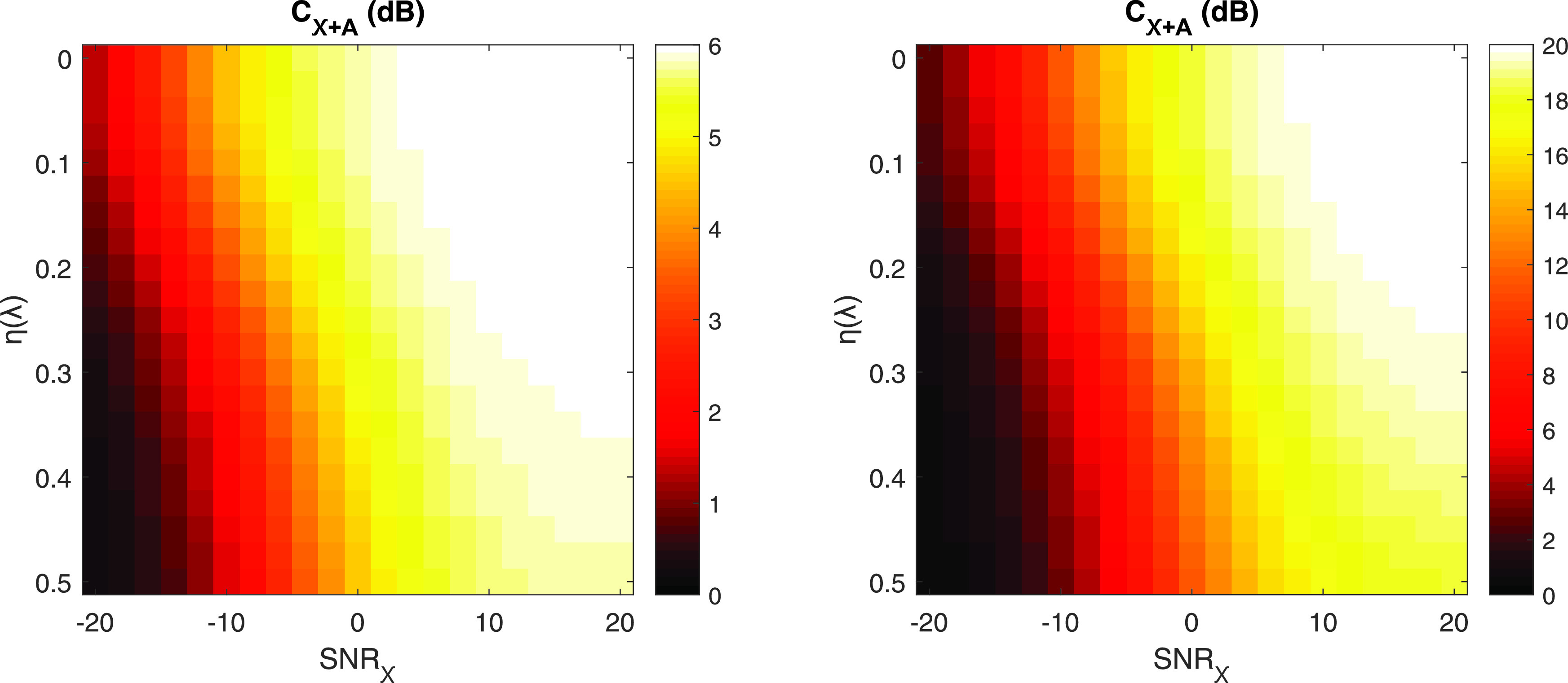
Expected contrast, calculated in Eq. (15), for various combinations of incoherent noise (x axis) and aberrator strengths (y axis). Incoherent noise is added to produce channel SNRχ from −20 to 20 dB. Aberrators vary from 0 to 0.5 for fixed Γ = 5 mm. Native contrasts presented are −6 (a) and −20 dB (b) to portray low and high contrast clinical targets, respectively, and the modeled aperture is a continuously defined linear array with a 2.2 cm active aperture. Note the differing color axes.
D. Quantification of clutter sources
Contributions to losses in beamformer gain and contrast can be decomposed into incoherent noise-only and aberration-only components if the full coherence curve, , is known. Returning to Eq. (13), we can estimate the contrast as predicted by incoherent noise.
This formulation can be modified slightly to describe the calculated Cχ in terms of contrast loss, rather than a contrast value. For the remainder of this section and the work, variables referring to contrast will refer to values in dB. The calculation is as follows:
| (16) |
where CdB,0 is the native contrast in dB. For hypoechoic targets, i.e., , this loss is described as a positive value to indicate movement away from the native contrast.
To isolate the contribution of aberration, the difference between the contrast value, in dB, measured by and that by can be taken to extract the remaining loss in contrast,
| (17) |
where CdB,χ+A is the expected contrast as calculated by Eq. (15) in dB. Again, note that CdB,loss,A does not describe the observable contrast in the presence of aberration alone, but rather the loss in contrast due to the contribution of aberration. A similar separation can be achieved with beamformer gain, though results in Sec. IV show the applications of this separation for contrast in order to focus on conventional image quality metrics.
A brief description of the presented metrics, as well as other intermediate variables, can be found in Table II.
TABLE II.
Description of presented variables.
| Variable | Description |
|---|---|
| Measured spatial coherence | |
| Theoretical noise-free spatial coherence | |
| with incoherent noise | |
| with incoherent noise and aberration | |
| SNRχ | SNR due to incoherent noise |
| Γ | Aberrator spatial autocorrelation FWHM |
| Aberrator rms as fraction of wavelength | |
| η | Aberrator rms in time |
| C0 | Native contrast |
| C | Contrast in terms of signal intensity |
| CdB | Contrast in dB |
| G | Beamformer gain |
| GA | Aberration-specific beamformer gain |
| Closs,χ | Contrast loss due to incoherent noise |
| Closs,A | Contrast loss due to aberration |
III. METHODS
A. Field II simulations
In order to validate the theory presented in Sec. II, Field II33,34 was used to simulate radio frequency (RF) channel data for a transducer with parameters summarized in Table III. Field II calculates a linear description of ultrasound fields using spatial impulse responses based on the inherent transducer properties, focusing geometry, and spatial locations of the scatterers. Each simulation was performed in 40 independent realizations of uniform scattering of size 10 × 10 × 0.5 cm in axial by lateral by elevation, with 30 scatterers per resolution cell in order to satisfy requirements for fully developed speckle.14 These uniform phantoms were used to measure spatial coherence, which was then used to predict contrast, as per Eq. (15).
TABLE III.
Transducer parameters.
| Parameter | Value |
|---|---|
| Geometry | Linear |
| Element pitch | 0.3 mm |
| Element count | 64 |
| fc | 5 MHz |
| Fractional bandwidth | 0.9 |
| Focal depth | 6.5 cm |
| Apodization | Rectangle |
Simulations were also performed for a series of hypoechoic inclusions ( 5 mm) with from −30 to −6 dB native contrast to model cysts. To create the inclusions, randomly distributed scatterers were placed in the inclusion volume with the same scatterers per resolution but with scattering amplitude according to the desired echogenicity. A similar method for varying the contrast was used to simulate layered phantoms with the same range of native contrast. In these phantoms, one side of the phantom was kept at constant echogenicity while the other varied to produce vertically-oriented layers; such phantoms minimize off-axis scattering from the boundary and thus provide a controlled environment to which measurable off-axis scattering in the cyst phantoms can be compared. For both the cyst phantom and the layer phantom, 40 realizations were simulated for four different native contrasts. The contrast measured in both cyst and layer phantoms was then compared to the predicted contrast from uniform phantoms under similar conditions of clutter. An example of the simulated phantom geometries is shown in Fig. 3.
FIG. 3.
Example geometries for uniform (a), cyst (b), and layer (c) phantoms. Note the hypoechoic regions, shown with darker scatterers, in the cyst and layer phantom examples.
B. Addition of clutter
For all phantoms, clutter was added post-simulation to introduce incoherent clutter, modeling diffuse reverberation and thermal noise, and aberration. Incoherent clutter was simulated by adding Gaussian white noise filtered to the bandwidth of the transducer to the receive channel data. Noise power was scaled relative to the noise-free channel signal power, over the range from −20 to 20 dB, to encompass the range of noise levels found in vivo.13 Aberration was introduced by means of a randomly generated thin phase screen on receive, for an aberrator with 5 mm and 0 to 0.5λ, following methods presented in Walker and Trahey.18 Though aberrators in tissue are more complex than simple phase screens, literature has demonstrated success in modeling higher order, distributed aberrators as an effective phase screen.35,36 Each independent scatterer realization was paired with an independent aberrator and incoherent noise realization.
Measurements of coherence were calculated according to Eq. (1) using 10λ axial kernels within the depth of field in the uniform phantoms. These large kernels were used to achieve the spatial averaging necessary for good estimates in the mid-to-high lag region of the coherence curve in order to match theory conditions as closely as possible. From these measurements of the full coherence curve, the beamformer gain was calculated according to Eq. (11). These values were compared to values calculated according to theoretical coherence curves predicted by Eq. (9) for matched incoherent noise and aberration parameters.
Contrast was calculated as the ratio of the mean delay-and-sum (DAS) signal in target (μT) and background regions (μB) in envelope-detected images for the cyst and layer phantoms. For the same range of clutter parameters, matched predictions of contrast were performed in the uniform phantom using measurements of beamforming gain and Eq. (15). The theoretical comparison value was calculated by combining Eqs. (9) and (15), using theory-derived coherence curves in matched clutter parameters and native contrast.
IV. RESULTS
A. Spatial coherence and beamformer gain
Spatial coherence curves for three different aberrator strengths (η = 0 to ) are shown in Fig. 4 for incoherent noise levels of 20 dB [Fig. 4(a)] and 0 dB [Fig. 4(b)] in channel. Line style indicates the data type, with theory shown in solid lines and simulation shown in dashed lines with error bars indicating standard deviation over speckle realizations. Line color indicates the degree of aberration. Theory and simulation show good agreement in both cases, with slight deviation in the mid-lag region (). Note the almost total decorrelation beyond the short-lag region () for both levels of incoherent noise in the presence of severe aberration ().
FIG. 4.
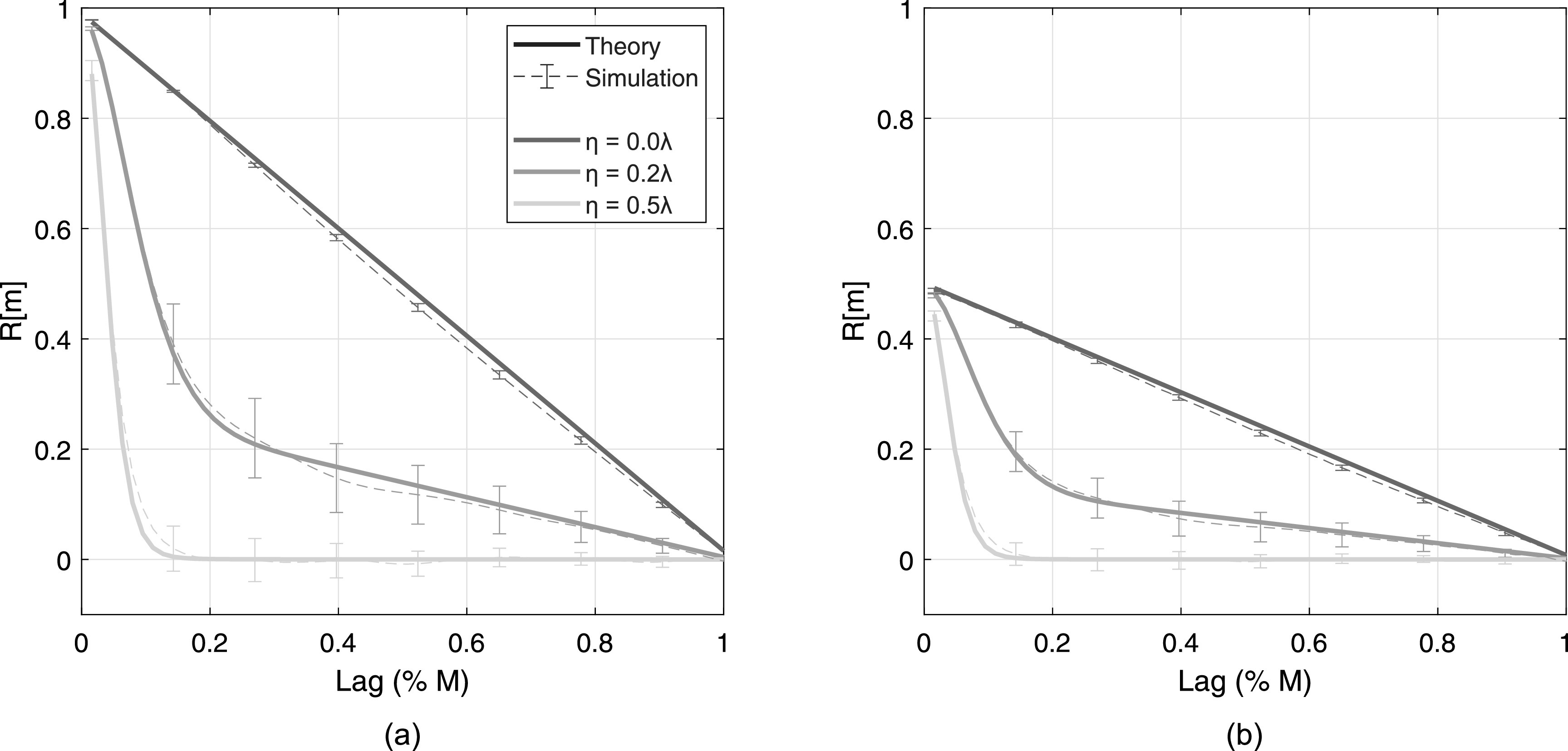
Spatial coherence curves in the presence of aberration for dB (a) and dB (b). Aberrators vary from for fixed Γ = 5 mm. Theory is shown in thick solid lines and simulation is shown in thin dashed lines with error bars indicating standard deviation over 40 speckle realizations. For readability, error bars are not shown for all lags.
The multiplicative effects of aberration and incoherent noise shown in Fig. 1 are present here as well. Line style indicates the data type and line color indicates the degree of aberration. The addition of 0 dB channel noise, which is expected to scale the coherence curves by a factor of 0.5 per Eq. (3), is visible in Fig. 4(b). The Gaussian multiplicative factor is seen when comparing η = 0.2 and 0.5λ cases to the η = 0λ case [Fig. 4(a)]; this factor is maintained with increases in incoherent noise. The severity of aberration, i.e., η, its temporal magnitude, does not appear to change the width of the Gaussian weighting in simulation, as predicted by Eq. (7) and corroborating the claim made by Walker and Trahey.18
The congruence between theory and simulation for beamformer gain and LOC is shown in Fig. 5. Theory and simulation are shown with solid and dashed lines, respectively, with error bars indicating standard deviation for simulation results across speckle realizations. Line colors indicate varying levels of aberration, from η = 0 to . Like the spatial coherence curves shown in Fig. 4, good agreement is found between theory and simulation, with only slight deviation in the mean gain value across simulations for the most severe aberrator in Fig. 5(a). Beamformer gain increases with SNRχ and decreases with η, corresponding to the trend predicted by Eq. (9). Although the most severe aberrator results in almost total decorrelation beyond the short-lag region, the partial correlation present within the short-lag is adequate for measurable beamformer gain. Recall that the theoretical maximum gain for a rectangular aperture, Gmax, is , or roughly 0.66 in Figs. 5(a) and 5(b).
FIG. 5.
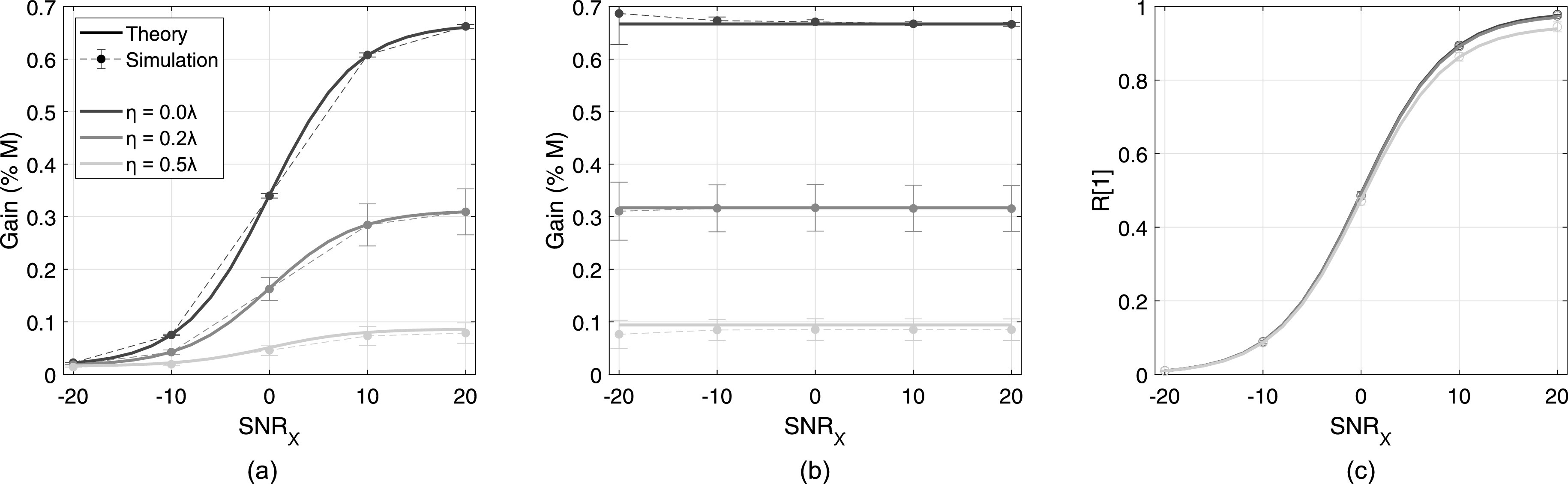
Total beamformer gain (a), aberration-specific gain (b), and LOC, (c), in the presence of three aberrator strengths (η = 0 to , shown in gray scale) and incoherent noise from −20 to 20 dB in channel. Theory is shown in thick solid lines and simulation is shown in thin dashed lines with error bars indicating standard deviation over speckle realizations.
The adjustment detailed in Eq. (14) is applied to the spatial coherence curves shown in Fig. 4 to produce gain values in Fig. 5(b). Values are consistent across a range of SNRχ within each aberrator strength, indicating consistent correction to the incoherent noise-free condition. In the aberration-free case, values are close to Gmax, with slight overestimation at SNRχ = –20 dB; this is likely due to the small LOC values measured at low SNRχ, where minor fluctuations result in substantial differences in the corrective factor in Eq. (14).
LOC, shown in Fig. 5(c), also increases with SNRχ, but unlike beamformer gain, minor differences are seen between aberrator strengths. For the largest η, the mean LOC measured in simulation at SNRχ = 20 dB is 96% of the theoretical maximum (0.945 vs 0.984). Larger variation in LOC is seen in the dimension of SNRχ, rather than η.
B. Estimated contrast
The measurements of adjusted beamformer gain, theoretical and simulated, are extended to Eq. (15) to estimate contrast, which is compared to the measured contrast of layer and cyst phantoms of variable echogenicity in Fig. 6. Results are shown for aberrators of strength η = 0 [Fig. 6(a)], 0.2 [Fig. 6(b)], and 0.5λ [Fig. 6(c)] for native contrasts from −30 to −6 dB and SNRχ from −20 to 20 dB. Solid lines indicate the theoretical prediction derived from the coherence curve described by Eq. (9). Thick dashed lines indicate the contrast as estimated by the measured beamformer gain in a uniform simulation. Layer and cyst simulation data is shown in thin dashed lines with filled and unfilled markers, respectively. Error bars indicate standard deviation over independent speckle realizations. Across theory and all simulations, contrast increases with SNRχ and decreases with aberrator strength, both monotonically in a similar fashion to beamformer gain.
FIG. 6.
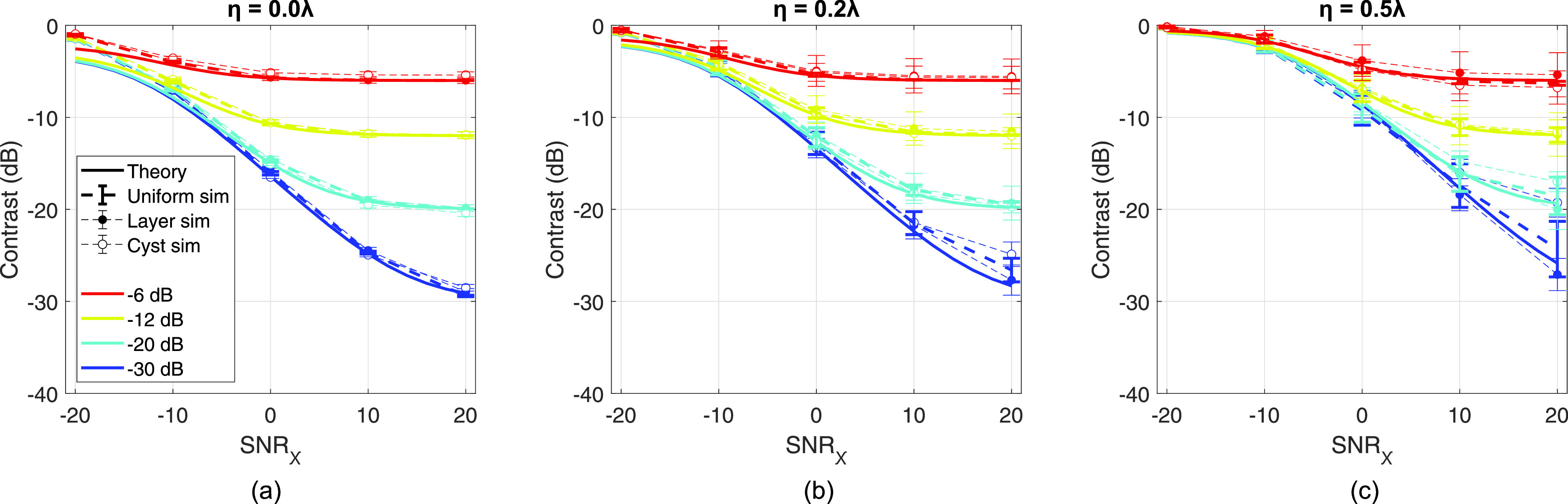
Contrast predicted by theory in Eq. (15) and measured contrast in simulation for aberrators of η = 0 (a), 0.2 (b), and 0.5λ (c) and fixed Γ = 5 mm, across SNRχ from −20 to 20 dB. Solid lines indicate theoretical prediction and thick dashed lines indicate uniform phantom simulation results. Thin dashed lines with filled markers and unfilled markers indicate layer and cyst phantom simulation results. Error bars indicate standard deviation over speckle realizations. Native contrasts of −6, −12, −20, and −30 dB are shown in red, yellow, cyan, and blue, respectively.
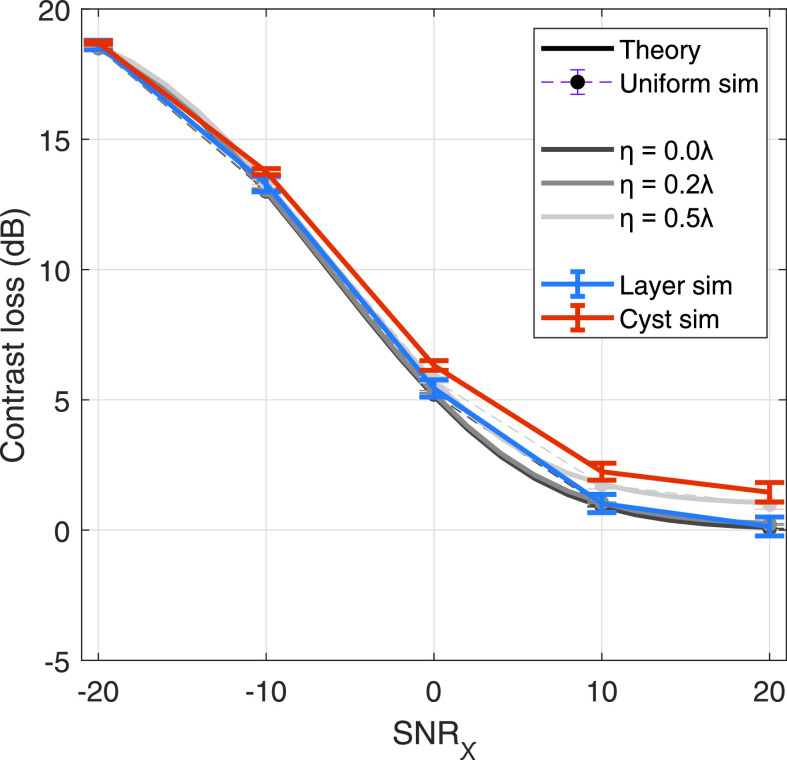
The predicted contrast from beamformer gain, measured in uniform scattering phantoms, shows good agreement with theory over the range of SNRχ and aberrator strengths interrogated for all native contrast values. These findings are further corroborated with agreement from layer simulations. Cyst simulations also show adequate agreement, with notable exceptions in the −30 dB native contrast simulations for dB, at all aberrator strengths. The cyst simulations show slight underestimation of contrast, i.e., less negative values, compared to the layer or uniform simulation analogues. However, outside these exceptions, deviation from theory does not appear to trend with native contrast, SNRχ, or aberrator strength. The relatively tight error bars, which indicate small fluctuations in simulation contrast, suggest the effect of phase screen aberrators on contrast is well predicted by theory.
C. Quantification of clutter sources
The results of assuming a fixed beamformer gain to describe contrast losses due to incoherent noise alone (CdB,loss,χ) are shown in Fig. 7. Theory and uniform simulation results are shown in solid and dashed gray scale lines, for three different aberrator strengths (η = 0 to ). We see that, regardless of aberrator strength, correction of the coherence curve collapses all measurements of contrast to the aberration-free case, i.e., . These results are compared to aberration-free layer and cyst simulations, shown in blue and red lines, respectively, and good congruence is found between all cases. This provides evidence that the theory presented appropriately models the separability of incoherent noise from aberration.
FIG. 7.
Incoherent noise-only contrast loss measurements (CdB,loss,χ), as calculated by Eqs. (13) and (16), for a −20 dB native contrast target. Solid and thin dashed lines over gray scale indicate theory and uniform simulation results over three aberrator strengths (η = 0 to ). Aberration-free, i.e., , contrast values for layer and cyst simulations are shown in blue and red lines, respectively.
The application of Cχ to calculate aberration-only contrast, Closs,A, is shown in Fig. 8. Theory is shown in solid gray scale lines, and uniform simulation results are shown in thick unmarked lines. Layer and cyst simulation values, calculated by subtracting the known aberration-free values, are shown in thin dashed lines with filled and unfilled markers, respectively. Note that layer and cyst simulation values are not shown for because Cχ is identical to the measured value.
FIG. 8.
Calculated and measured aberration-only contrast loss (CdB,loss,A), as calculated by Eq. (17), for a −20 dB native contrast target. Line style indicates data type: solid line and thick dashed lines indicate theory and uniform simulation results, respectively, and thin dashed lines with filled and unfilled markers indicate layer and cyst simulation results, respectively. Line color indicates aberration severity.
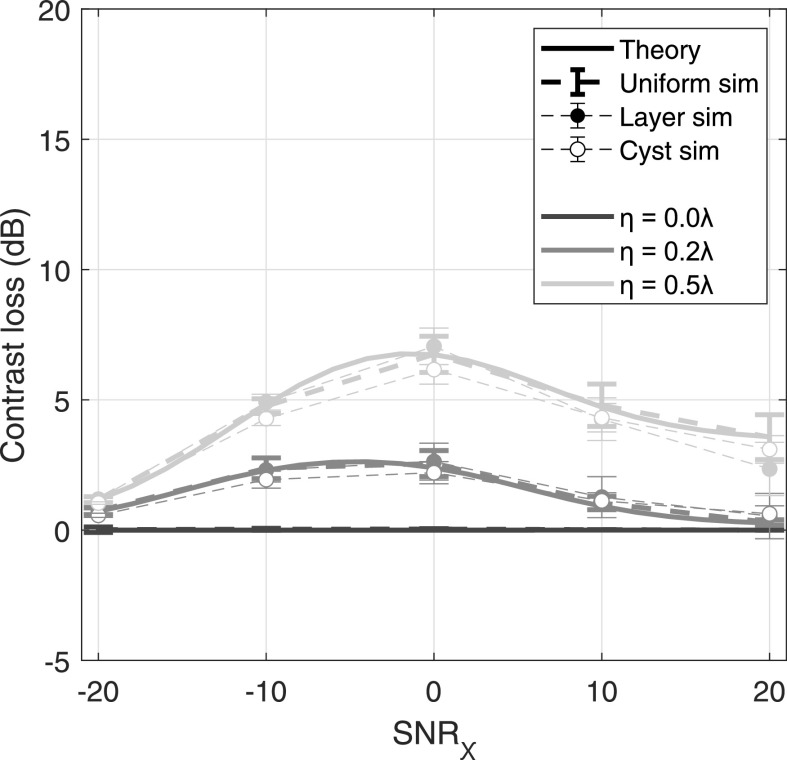
Again, we find good agreement between theory and all simulation cases, with only slight deviation in the most severe aberrator case. As expected, in the case of no aberration, the calculated contrast loss is 0 in both theory and uniform simulations. The contribution of aberration to contrast loss does not appear to trend monotonically with SNRχ. For very low and high values of SNRχ, aberration contributes minimally to contrast loss, with less than 5 dB loss in even the most severe aberrator case. There is a range of SNRχ values, between −10 and 10 dB, where aberration appears to affect contrast most, peaking around 7.5 dB of loss for the most severe aberrator.
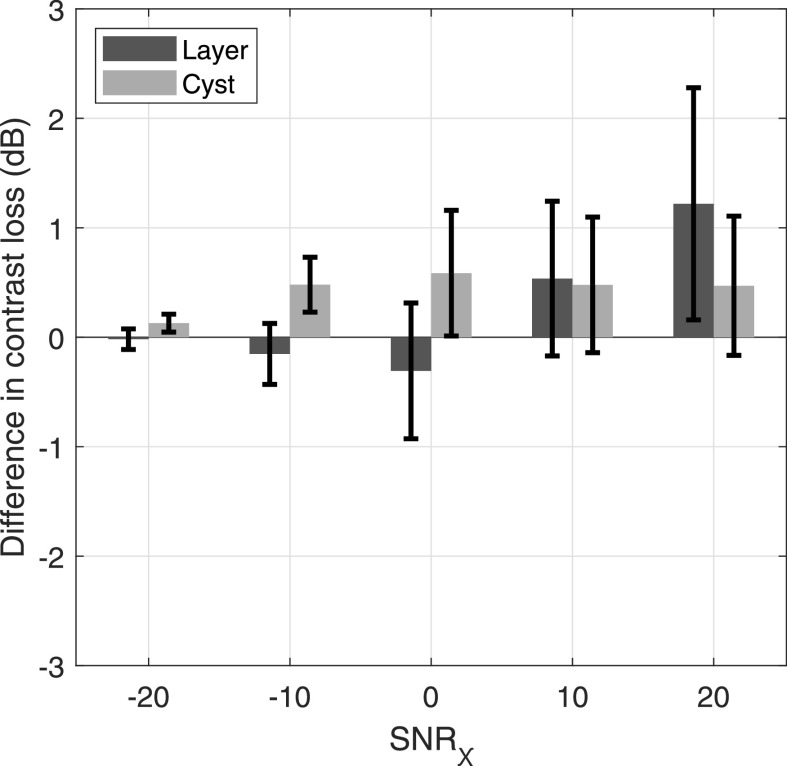
Figure 9 shows the difference in aberration contrast loss between the prediction made in the uniform simulation and the measurements made in the layer (dark gray) and cyst simulations (light gray) for a −20 dB native contrast target and . Error bars indicate the standard deviation over speckle realization pairs. The largest aberrator interrogated is plotted to show the largest discrepancies present. Though the error bars are large relative to the differences, the mean and standard deviation of the differences are overall small relative to the native contrast (–20 dB).
FIG. 9.
Difference between aberration-only contrast loss predicted from coherence measured in a uniform scattering simulation and measured contrast loss in layer (dark gray) and cyst (light gray) simulations, over a range of SNRχ in a −20 dB native contrast target for . Error bars indicate standard deviation over speckle realization pairs.
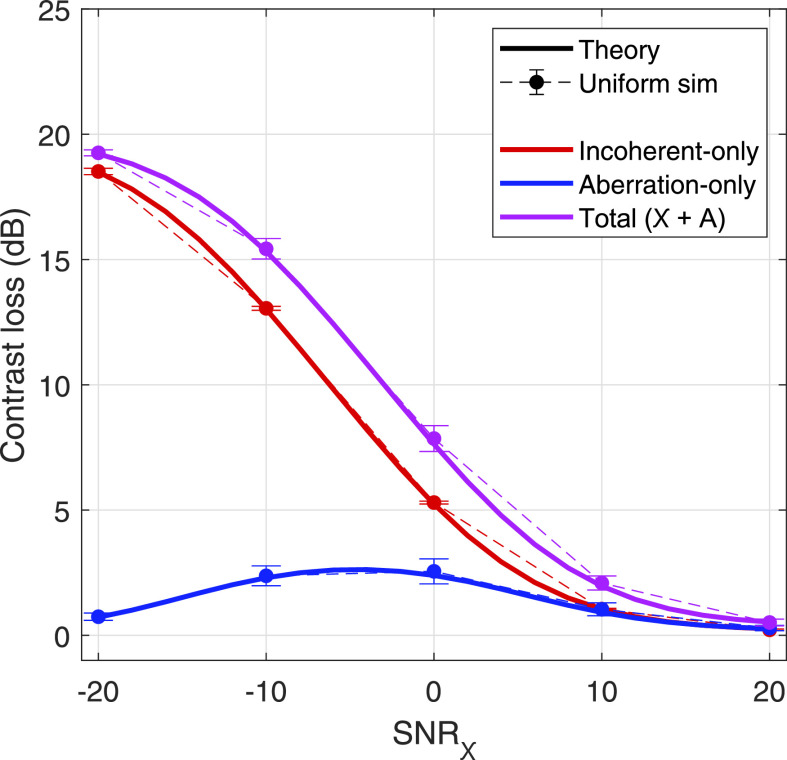
Last, this separability can be illustrated in the specific case of an assumed native contrast target of −20 dB for an aberrator of η = 0.2λ in Fig. 10. The same range of SNRχ is presented for contrast values predicted by theory and simulation shown in solid line and markers with error bars, respectively. The incoherent-only, aberration-only, and total contrast loss is shown in red, blue, and purple lines, respectively. Total contrast loss is described as the gap in dB between the expected contrast, predicted by Eq. (15), and the native contrast. The increase in the contribution of aberration, shown in Fig. 8 and replotted in blue in Fig. 10, is reflected in the deviation between red and purple lines. The gap is largest around −5 dB, indicating the regime over which aberration contributes maximally, and decreases at low and high values of SNRχ.
FIG. 10.
Separability of incoherent noise and aberration-dependent losses in contrast in an assumed −20 dB native contrast target, illustrated with incoherent-only (red), aberration-only (blue), and total contrast loss (purple) for an intermediate level of aberration (η = 0.2λ) over a previously swept range of SNRχ. Theory is shown in solid lines, and contrast predicted by the uniform simulation is shown with circle markers and error bars, which indicate standard deviation over speckle realizations.
V. DISCUSSION
A. Coherence and beamformer gain
The results presented herein validate the theory presented in Sec. II, by which a spatial coherence curve degraded by aberration and incoherent noise can be translated to an estimated contrast value. This congruence is rooted in the similarity between spatial coherence curves measured in simulation and those predicted by theory (Fig. 4). Even in the presence of severe aberration, exceeding that reported in literature,6,7,9 Eq. (9) is a good predictor of spatial coherence. The agreement between simulation and theory is extended to measurements of beamformer gain [Fig. 5(a)], where minimal differences are found for all interrogated levels of incoherent noise and aberration. Significant degradation of gain is observed for high levels of clutter, and values for just an intermediate level of aberration () fall below half the maximum theoretical value ().
Figure 5(b), which shows stable GA, the adjusted gain removing incoherent noise, over a range of SNRχ for a given aberrator strength, validates the use of the corrective factor present in Eq. (14). Due to the length of Γ, which is based on the range present in literature,7,9,37 relative to the modeled element pitch, the majority of degradation in coherence seen at lag-one is due to incoherent noise [Fig. 5(c)], allowing us to confidently remove such contributions and recover degradations due to aberration alone. The use of GA allows for the original derivation of contrast, presented by Long et al.,13 to be modified to reflect the intuition that phase errors in the received speckle signal weaken the beamformed signal power. Bamber et al.,32 who first derived the transformation of coherence to gain, alluded to this by relating variations in calculated gain to variations in target echo strength in cardiac imaging. This effect is similar to beamforming in the presence of additive, uncorrelated channel noise; Bottenus and Trahey38 confirmed the equivalence of the two sources of noise with phase apodizations to model time domain decorrelation.
The flexibility of beamformer gain to describe losses in image quality due to incoherent and partially coherent sources of noise motivates its future use as an image quality metric. Additionally, though not explicitly explored in this work, the framework is extendable to variations in element apodization and focusing schema. Related fields in beamformation, such as radar and sonar, implement variants of gain to assess array performance and signal quality.4,39,40 Recently, novel ultrasonic clutter suppression methods have utilized beamformer gain to estimate SNR.30
B. Expected contrast and separation of clutter sources
The predictions of contrast from beamformer gain show good agreement with layer simulations, but deviate slightly from cyst simulations for high native contrast (C0 = –30 dB) and increasing levels of aberration (Fig. 6). The discrepancy between the measured contrasts of layer and cyst simulations reflects a limitation introduced in Sec. II: the lack of modeling of off-axis scattering. Due to the lateral extent of the point spread function (PSF), write-in is observed for high native contrast, from high-scattering regions to low-scattering regions, as the magnitude of the PSF lateral “tails” become comparable to the scattering strength within the cyst itself. The discrepancy is barely present for native contrasts equal to and above −20 dB, indicating the PSF tails are at least below −20 dB relative to the main lobe.
Furthermore, the increase in the discrepancy with aberrator severity, seen particularly in Fig. 6(c) for the −30 dB contrast target, aligns with the notion that aberration redistributes energy in the main lobe to the side lobes.4 Proper correction of any off-axis component requires a priori information of the target scattering function,31 which is not present in vivo. However, the error shown herein is only present for high contrast and high aberration cases, which are rare in vivo.6,7,9 Additionally, for particular scattering functions where the off-axis component is manifested as a source of partial decorrelation, decreases in image quality will be present in degradations in beamformer gain. In these cases, the framework for separation can be relaxed to separating incoherent sources from partially coherent sources, and other parameter spaces, such as imaging frequency, are needed to differentiate between off-axis scattering and aberration.
The ability of the separation framework to accurately isolate the contribution of incoherent noise (Fig. 7) follows the agreement seen in a previous utilization incoherent noise-only gain to estimate contrast from increasing thermal noise.13 The extension of this theory to isolate aberration with little deviation from a simulation control (Figs. 8 and 9) reveals that Closs,A is neither monotonic nor stable with respect to SNRχ. This is an interesting finding when juxtaposed to Closs,χ, which is stable with respect to η. The lack of a clear trend indicates that the contribution of aberration is dependent on the incoherent noise level, whereas the contribution of incoherent noise is independent of aberration. This can be related back to Eq. (15): in the aberration-free case, GA is approximated by Gmax, but SNRχ is able to affect the estimated contrast value. Conversely, when , i.e., no incoherent noise, the predicted contrast equals the native contrast term regardless of GA. This is a shortcoming of the framework related to off-axis scattering as discussed previously. The contribution of aberration is solely captured in its degradation of beamformer gain, which describes the reduction in noise components upon coherent summation. In the incoherent noise-free case, beamformer gain reduces to a measure of main lobe reduction, which can be considered irrelevant for this perfect detection scenario.
Still, the framework is useful for the range of clutter seen in clinical environments, where aberration and incoherent noise are perceptible. The theory presented herein may be used to comment on the dynamics between the relative contributions of incoherent noise and aberration in a variety of tissue environments, an example visualization of which is shown in Fig. 10. In a simulation study, Pinton et al.1 concluded that reverberation is the dominant source of clutter in fundamental imaging, whereas aberration is much more prevalent in harmonic imaging. Fatemi et al.41 challenge this broad categorization for cardiac imaging, and instead argue that the contribution of clutter, specifically reverberation, is spatially varying.41 This framework address both points, motivating the need for high-resolution coherence mapping to robustly evaluate clutter.
As alluded to in Sec. I, separation of clutter sources will allow for improved assessment of beamforming and filtering methods to reduce clutter, if access to channel RF data is preserved. This has the opportunity to provide insight into how aberration affects not only the PSF, but also the contribution of noise to pixels. For example, it may be useful to know that an aberration correction scheme improves aberration-specific contrast loss by 10 dB, but worsens thermal noise-specific contrast loss by 5 dB. In the current standard of evaluating improvements of image quality, this improvement is seen as 5 dB, but the separation of clutter sources reveals that improvement could be at least as high as 10 dB if the “off-target” effect is removed.
C. Other limitations
Another limiting factor of this theoretical framework is the complex nature of tissue aberration. An assumption in the proposed clutter separation is that aberration has a small effect at lag one in the aperture domain, relative to the effects at higher lags. This is based on the Gaussian model of coherence introduced in Eq. (7) for a phase screen aberrator; because of the shape of the multiplicative factor, the degradation at lag one is negligible if Γ, the aberrator FWHM, is considerably larger than the element pitch. Published literature values for Γ, which range from 2 to 10 mm,7,9,37 exceed the element pitch of nearly all commercial arrays used for common diagnostic tasks.
Other studies propose that a spatially distributed model of phase errors is required to describe aberration.42 To address this, locally adaptive phase aberration correction (LAPAC) calculates a phase screen at each beamformed pixel in a synthetic aperture sequence, though major recovery of contrast remains elusive for experimental data.43 Recent approaches to speed of sound mapping suggest that the spatial distribution of aberrators follows the spatial distribution of speed of sound in near-field abdominal layer,44 and this practice can be translated to direct aberration correction by means of estimating propagation-related time delays.45 However, Berkhoff and Thijssen35 show that an optimal phase screen for correction can be calculated, and although its performance depends on the spatial location of the correction, results indicate that a bulk phase screen is an adequate approximation for the distorting effects of aberration. Recent efforts assuming a optimal phase screen for clutter reduction in plane wave imaging have also shown promising results.36
Though this work uses thin phase screens to validate theory, the literature suggests the findings can be extended to spatially distributed aberrators. The averaging kernel may exceed the isoplanatic extent of a single phase screen, but the spatial averaging required to calculate a coherence curve produces measurements indicative of a bulk phase screen. Furthermore, rejection of high lag-information, due to their drastically lower contributions to the final value of beamformer gain, may allow for smaller averaging kernels for more local characterization, though evaluation of the threshold of rejection is needed. The challenge, instead, is the distribution of Γ in a distributed aberrator. Due to the spatial variation of aberrator, there is likely a “bandwidth” of Γ, the lower end of which may lie within the lag one region of an array. In this particular case, the assumptions inherent in the framework become invalid. A similar problem is the issue of partially coherent reverberation, which may result from placing the transducer normal to reverberant layers or a consequence of long propagation distances.11
VI. CONCLUSION
A novel coherence-based quantification of acoustic clutter was presented to evaluate degradations in image quality resulting from phase aberration and incoherent noise. Beamformer gain, a multi-lag description of spatial coherence, can be calculated in uniform scattering regions to provide an estimate of the loss in signal quality over a clinically-relevant range of incoherent noise and aberrator severity. Measurements of beamformer gain and channel SNR can then be adapted to predict the measured contrast, as well as attribute the loss in contrast to incoherent noise-only and aberration-only mechanisms.
Simulation results show good agreement with theoretical calculations, motivating the use of the separation scheme for future work in experimental data. The findings indicate that off-axis scattering, which is not explicitly modeled in the framework, does not significantly contribute to contrast loss for small cylindrical targets (r = 5 mm) of native contrast less than −20 dB. The contribution of aberration to contrast loss was also found to be dependent on the SNR with respect to incoherent noise. The proposed quantification of individual clutter sources shows promise to facilitate novel clutter reduction strategies.
Future work will extend this framework to non-linear, propagation-based simulations to evaluate the robustness of the separation in the presence of distributed aberrators and reverberation from validated tissue maps.1,5,46 Exploration of various transmit frequencies and filtering bandwidths will also be explored to elucidate the dynamics between frequency and clutter. In vivo acquisitions will also be used to assess the clutter mapping capabilities of the separation scheme, in addition to observing dynamics in tissue harmonic imaging. Extensions of this framework can also be applied to adaptive imaging strategies to make informed decisions regarding the automated selection of transmit parameters, such as imaging frequency and element apodization.
ACKNOWLEDGMENTS
This work was funded by NIH R01-EB017711 and R01- EB026574 from the National Institute of Biomedical Imaging and Bioengineering, and the National Science Foundation Graduate Research Fellowship Program.
References
- 1. Pinton G. F., Trahey G. E., and Dahl J. J., “ Sources of image degradation in fundamental and harmonic ultrasound imaging using nonlinear, full-wave simulations,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58(4), 754–765 (2011). 10.1109/TUFFC.2011.1868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Lediju M. A., Pihl M. J., Dahl J. J., and Trahey G. E., “ Quantitative assessment of the magnitude, impact and spatial extent of ultrasonic clutter,” Ultrason. Imag. 30(3), 151–168 (2008). 10.1177/016173460803000302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Smith S. W., Trahey G. E., Hubbard S. M., and Wagner R. F., “ Properties of acoustical speckle in the presence of phase aberration part II: Correlation lengths,” Ultrason. Imag. 10(1), 29–51 (1988). 10.1177/016173468801000103 [DOI] [PubMed] [Google Scholar]
- 4. Steinberg B. D., Principles of Aperture and Array System Design ( Wiley-Interscience, New York, 1976). [Google Scholar]
- 5. Mast T. D., Hinkelman L. M., Orr M. J., and Waag R. C., “ The effect of abdominal wall morphology on ultrasonic pulse distortion. Part II. Simulations,” J. Acoust. Soc. Am. 104(6), 3651–3664 (1998). 10.1121/1.423947 [DOI] [PubMed] [Google Scholar]
- 6. O'Donnell M. and Flax S. W., “ Phase aberration measurements in medical ultrasound: Human studies,” Ultrason. Imag. 10(1), 1–11 (1988). 10.1177/016173468801000101 [DOI] [PubMed] [Google Scholar]
- 7. Freiburger P. D., Sullivan D. C., LeBlanc B. H., Smith S. W., and Trahey G. E., “ Two dimensional ultrasonic beam distortion in the breast: In vivo measurements and effects,” Ultrason. Imag. 14(4), 398–414 (1992). 10.1177/016173469201400406 [DOI] [PubMed] [Google Scholar]
- 8. Sumino Y. and Waag R. C., “ Measurements of ultrasonic pulse arrival time differences produced by abdominal wall specimens,” J. Acoust. Soc. Am. 90(6), 2924–2930 (1991). 10.1121/1.401766 [DOI] [PubMed] [Google Scholar]
- 9. Hinkelman L. M., Liu D., Metlay L. A., and Waag R. C., “ Measurements of ultrasonic pulse arrival time and energy level variations produced by propagation through abdominal wall,” J. Acoust. Soc. Am. 95(1), 530–541 (1994). 10.1121/1.408347 [DOI] [PubMed] [Google Scholar]
- 10. Hinkelman L. M., Mast T. D., Metlay L. A., and Waag R. C., “ The effect of abdominal wall morphology on ultrasonic pulse distortion. Part I. Measurements,” J. Acoust. Soc. Am. 104(6), 3635–3649 (1998). 10.1121/1.423946 [DOI] [PubMed] [Google Scholar]
- 11. Pinton G. F., Trahey G. E., and Dahl J. J., “ Spatial coherence in human tissue: Implications for imaging and measurement,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61(12), 1976–1987 (2014). 10.1109/TUFFC.2014.006362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Dahl J. J., Jakovljevic M., Pinton G. F., and Trahey G. E., “ Harmonic spatial coherence imaging: An ultrasonic imaging method based on backscatter coherence,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 59(4), 648–659 (2012). 10.1109/TUFFC.2012.2243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Long W., Bottenus N., and Trahey G. E., “ Lag-one coherence as a metric for ultrasonic image quality,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 65(10), 1768–1780 (2018). 10.1109/TUFFC.2018.2855653 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Cobbold R. S., “ Ultrasound transducers,” in Foundations of Biomedical Ultrasound ( Oxford University Press, New York, 2007), pp. 329–412. [Google Scholar]
- 15. Goldberg R. L. and Smith S. W., “ Optimization of signal-to-noise ratio for multilayer PZT transducers,” Ultrason. Imag. 17(2), 95–113 (1995). 10.1177/016173469501700202 [DOI] [PubMed] [Google Scholar]
- 16. Oakley C. G., “ Calculation of ultrasonic transducer signal-to-noise ratios using the KLM model,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 44(5), 1018–1026 (1997). 10.1109/58.655627 [DOI] [Google Scholar]
- 17. Lencioni R., Cioni D., and Bartolozzi C., “ Tissue harmonic and contrast-specific imaging: Back to gray scale in ultrasound,” Eur. Radiol. 12(1), 151–165 (2002). 10.1007/s003300101022 [DOI] [PubMed] [Google Scholar]
- 18. Walker W. F. and Trahey G. E., “ Speckle coherence and implications for adaptive imaging,” J. Acoust. Soc. Am. 101(4), 1847–1858 (1997). 10.1121/1.418235 [DOI] [PubMed] [Google Scholar]
- 19. Lediju M. A., Pihl M. J., Hsu S. J., Dahl J. J., Gallippi C. M., and Trahey G. E., “ A motion-based approach to abdominal clutter reduction,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56(11), 2437–2449 (2009). 10.1109/TUFFc.2009.1331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Mauldin F. W., Lin D., and Hossack J. A., “ The singular value filter: A general filter design strategy for PCA-based signal separation in medical ultrasound imaging,” IEEE Trans. Med. Imag. 30(11), 1951–1964 (2011). 10.1109/TMI.2011.2160075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Nock L., Trahey G. E., and Smith S. W., “ Phase aberration correction in medical ultrasound using speckle brightness as a quality factor,” J. Acoust. Soc. Am. 85(5), 1819–1833 (1989). 10.1121/1.397889 [DOI] [PubMed] [Google Scholar]
- 22. Fink M., “ Time reversal of ultrasonic fields. I. Basic principles,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 39(5), 555–566 (1992). 10.1109/58.156174 [DOI] [PubMed] [Google Scholar]
- 23. Krishnan S., Li P.-C., and O'Donnell M., “ Adaptive compensation of phase and magnitude aberrations,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 43(1), 44–55 (1996). 10.1109/58.484462 [DOI] [Google Scholar]
- 24. Shin J., Huang L., and Yen J. T., “ Spatial prediction filtering for medical ultrasound in aberration and random noise,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 65(10), 1845–1856 (2018). 10.1109/TUFFC.2018.2860962 [DOI] [PubMed] [Google Scholar]
- 25. Byram B., Dei K., Tierney J., and Dumont D., “ A model and regularization scheme for ultrasonic beamforming clutter reduction,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 62(11), 1913–1927 (2015). 10.1109/TUFFC.2015.007004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Morgan M. R., Trahey G. E., and Walker W. F., “ Multi-covariate imaging of sub-resolution targets,” IEEE Trans. Med. Imag. 38(7), 1690–1700 (2019). 10.1109/TMI.2019.2917021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Lediju M. A., Trahey G. E., Byram B. C., and Dahl J. J., “ Short-lag spatial coherence of backscattered echoes: Imaging characteristics,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58(7), 1377–1388 (2011). 10.1109/TUFFC.2011.1957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Li P.-C. and Li M.-L., “ Adaptive imaging using the generalized coherence factor,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 50(2), 128–141 (2003). 10.1109/TUFFC.2003.1182117 [DOI] [PubMed] [Google Scholar]
- 29. Camacho J., Parrilla M., and Fritsch C., “ Phase coherence imaging,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56(5), 958–974 (2009). 10.1109/TUFFC.2009.1128 [DOI] [PubMed] [Google Scholar]
- 30. Long W., Bottenus N., and Trahey G. E., “ Incoherent clutter suppression using lag-one coherence,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1, 1544 (2020). 10.1109/TUFFC.2020.2977200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Mallart R. and Fink M., “ The van Cittert-Zernike theorem in pulse echo measurements,” J. Acoust. Soc. Am. 90(5), 2718–2727 (1991). 10.1121/1.401867 [DOI] [Google Scholar]
- 32. Bamber J. C., Mucci R. A., and Orofino D. P., “ Spatial coherence and beamformer gain,” Acoust. Imag. 24, 43–48 (2002). 10.1007/b117447 [DOI] [Google Scholar]
- 33. Jensen J. A., “ Field: A program for simulating ultrasound systems,” Med. Biol. Eng. Comput. 34, 351–354 (1996).8945858 [Google Scholar]
- 34. Jensen J. A., “ A multi-threaded version of Field II,” in Proceedings of the 2014 IEEE International Ultrasonics Symposium, Chicago, IL (September 3–6, 2014), pp. 2229–2232. [Google Scholar]
- 35. Berkhoff A. P. and Thijssen J. M., “ Correction of concentrated and distributed aberrations in medical ultrasound imaging,” in Proceedings of the 1996 IEEE Ultrasonics Symposium, San Antonio, TX (November 3–6, 1996), pp. 1405–1410. [Google Scholar]
- 36. Bendjador H., Deffieux T., and Tanter M., “ The SVD beamformer: Physical principles and application to ultrafast adaptive ultrasound,” IEEE Trans. Med. Imag. (published online 2020). [DOI] [PubMed] [Google Scholar]
- 37. Hinkelman L. M., Liu D., Waag R. C., Zhu Q., and Steinberg B. D., “ Measurement and correction of ultrasonic pulse distortion produced by the human breast,” J. Acoust. Soc. Am. 97(3), 1958–1969 (1995). 10.1121/1.412069 [DOI] [PubMed] [Google Scholar]
- 38. Bottenus N. B. and Trahey G. E., “ Equivalence of time and aperture domain additive noise in ultrasound coherence,” J. Acoust. Soc. Am. 137(1), 132–138 (2015). 10.1121/1.4904530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. D'Spain G. L., Luby J. C., Wilson G. R., and Gramann R. A., “ Vector sensors and vector sensor line arrays: Comments on optimal array gain and detection,” J. Acoust. Soc. Am. 120(1), 171–185 (2006). 10.1121/1.2207573 [DOI] [Google Scholar]
- 40. Li J., Zhang X., and Gao X., “ A joint scheme for angle and array gain-phase error estimation in bistatic MIMO radar,” IEEE Geosci. Remote Sens. Lett. 10(6), 1478–1482 (2013). 10.1109/LGRS.2013.2260526 [DOI] [Google Scholar]
- 41. Fatemi A., Berg E. A. R., and Rodriguez-Molares A., “ Studying the origin of reverberation clutter in echocardiography: In vitro experiments and in vivo demonstrations,” Ultrasound Med. Biol. 45(7), 1799–1813 (2019). 10.1016/j.ultrasmedbio.2019.01.010 [DOI] [PubMed] [Google Scholar]
- 42. Ng G. C., Worrell S. S., Freiburger P. D., and Trahey G. E., “ A comparative evaluation of several algorithms for phase aberration correction,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 41(5), 631–643 (1994). 10.1109/58.308498 [DOI] [Google Scholar]
- 43. Chau G., Jakovljevic M., Lavarello R., and Dahl J., “ A locally adaptive phase aberration correction (LAPAC) method for synthetic aperture sequences,” Ultrason. Imag. 41(1), 3–16 (2018). 10.1177/0161734618796556 [DOI] [PubMed] [Google Scholar]
- 44. Jakovljevic M., Hsieh S., Ali R., Chau Loo Kung G., Hyun D., and Dahl J. J., “ Local speed of sound estimation in tissue using pulse-echo ultrasound: Model-based approach,” J. Acoust. Soc. Am. 144(1), 254–266 (2018). 10.1121/1.5043402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Ali R. and Dahl J. J., “ Distributed phase aberration correction techniques based on local sound speed estimates,” in Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan (October 22–25, 2018), pp. 1–4. [Google Scholar]
- 46. Pinton G. F., Dahl J., Rosenzweig S., and Trahey G. E., “ A heterogeneous nonlinear attenuating full-wave model of ultrasound,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56(3), 474–488 (2009). 10.1109/TUFFC.2009.1066 [DOI] [PMC free article] [PubMed] [Google Scholar]