Abstract
COVID-19 has killed more than 500,000 people worldwide and more than 60,000 in Brazil. Since there are no specific drugs or vaccines, the available tools against COVID-19 are preventive, such as the use of personal protective equipment, social distancing, lockdowns, and mass testing. Such measures are hindered in Brazil due to a restrict budget, low educational level of the population, and misleading attitudes from the federal authorities. Predictions for COVID-19 are of pivotal importance to subsidize and mobilize health authorities’ efforts in applying the necessary preventive strategies. The Weibull distribution was used to model the forecast prediction of COVID-19, in four scenarios, based on the curve of daily new deaths as a function of time. The date in which the number of daily new deaths will fall below the rate of 3 deaths per million — the average level in which some countries start to relax the stay-at-home measures — was estimated. If the daily new deaths curve was bending today (i.e., about 1250 deaths per day), the predicted date would be on July 5. Forecast predictions allowed the estimation of overall death toll at the end of the outbreak. Our results suggest that each additional day that lasts to bend the daily new deaths curve may correspond to additional 1685 deaths at the end of COVID-19 outbreak in Brazil (R2 = 0.9890). Predictions of the outbreak can be used to guide Brazilian health authorities in the decision-making to properly fight COVID-19 pandemic.
Keywords: COVID-19, Forecast predictions, Weibull distribution, Brazil, Death toll
Introduction
Since the World Health Organization declared the COVID-19 outbreak a Public Health Emergency of International Concern, in January 30, 2020, more than ten million cases of the disease and more than 600,000 deaths related with the infection by SARS-CoV2 virus were registered worldwide. The impacts of COVID-19 in low- and middle-income countries (LMICs) are of great concern [1, 2], since these countries present a large percentage of the population living in overcrowded conditions, with deficient access to clean water and sanitizers, among other factors that limit people living in LMICs to follow the public health advices on how to reduce the spread of the virus [3]. Although Brazil has the World ninth larger gross domestic product [4], 42% of the Brazilian population live with less than 10 USD per day and more than ten million Brazilians live in extreme poverty [5]. As in other countries, poverty and social inequality are being aggravated by the COVID-19 pandemic in Brazil. Brazil occupies now the second place in number of registered COVID-19 cases [6]. Forecast predictions made by the Imperial College (London, UK) present Brazil as the country with the highest rate of transmission and one of the countries where a large number of deaths are expected from, on next weeks [7]. The health crisis is sharpened by a political crisis, depicted by two changes of the Health Minister in less than 1 month [8], and by Federal government authorities constantly denying the severity of COVID-19 pandemic and the scientific consensus on the lockdown and social distancing measures [9].
Forecast predictions configure a pivotal strategy for decision-making in the evaluation of measures against COVID-19 [10–13] and should be closely considered by governments and health authorities. In this work, we have used the Weibull distribution on the number of daily new cases and deaths data of COVID-19 to predict the evolution of the pandemic [12]. The Weibull distribution is one of the most commonly used parametric lifetime models [14], mostly for its parsimony, its ability to satisfactorily model data which are commonly encountered in survival analysis, and its availability in statistical software packages [15, 16]. A parameter called Diagnostic-Death lag (DDlag), given by the temporal distance, in days, between the peak of daily new cases and the peak of daily new deaths, which strongly correlates with the lethality rate (LR) of COVID-19, was calculated for Brazil’s official data. DDlag represents the average time between the diagnostic of new infections and patient deaths due to the diagnosed disease. Intuitively, one could suppose that the more efficient are the detection and the health care delivered to patients, the larger DDlag would be. DDlag can be used to predict COVID-19 evolution and to evaluate its LR, as well as to infer the level of underreported cases of COVID-19 [12]. We took in account four distinct scenarios based in the daily number of new deaths, considering the maximum of 1250, 1500, 1750, and 2000 daily new deaths at the maximum turning point of the curve. Because our predictions are based in the number of daily new deaths, it can be daily reviewed aiming to evaluate the measures further taken to fight the COVID-19 pandemic in Brazil, such as lockdowns and mass testing and, also, when these measures should be reformulated.
Material and methods
Data on Brazil’s daily and total number of confirmed cases and deaths were obtained from the Our World in Data Project [6] as comma-spaced values (CSV) files, processed in MS Excel 2019 and exported to Sigma Plot 14.0, with the aim to build scatter and regression plots. Data fitting was performed by non-linear regression through SigmaPlot, using the Dynamic Fit Wizard Tool. The curve fitter uses the Marquardt-Levenberg algorithm to fit the data by the least squares method [17]. The following starting values were used for the fit calculations: t0 = 100, β = 200, η = 100, step = 1, and tolerance = 10−10, using the built-in 4-parameter Weibull distribution (Eq. 1), described as:
| 1 |
where t is the time in days; f(t) is the number of new cases or new deaths as a function of t; t0 is the time where the maximum of the projected peak is observed (maximum number of daily cases or deaths, or maximum turning point); α is the value of f(t) at t0; β and η are Weibull’s shape and scale parameters, respectively. Values of α, t0, β and η were calculated in order to find the best fit to t and f(t) data. Although this is a built-in SigmaPlot equation named by the software as 4-parameter Weibull peak equation, it is, indeed, derived from the Weibull 4-parameter density function in which the location parameter was substituted by in order to put the parameters α and t0 in evidence.
Since the Diagnostic-Death lag (DDlag) expresses the temporal distance between the peak of daily new diagnosed cases and the peak of daily new deaths, it could be calculated by the difference of the Weibull t0 parameter computed from cases and death curves, determined as [12]:
| 2 |
where Δt0 = DDlag, is the value of t on the maximum turning point of the daily new cases curve, and is the value of t on the maximum turning point of daily new deaths curve (mode). The correlation between DDlag and LR was determined by the analysis of Weibull projections on daily new cases and daily new deaths of COVID-19 in many countries, as shown in a previous work [12]. This correlation responds to a logarithm function given by:
| 3 |
As the curves for daily new cases and daily new deaths of COVID-19 in Brazil are still in the exponential growth phase, it was not possible to determine when— and how much cases and deaths with — the maximum turning point will be reached (data not shown). Thus, the forecast predictions in this work were performed in four distinct prospective scenarios, based on the maximum number of daily new deaths for COVID-19 registered at the peak (maximum turning point). Such scenarios were arbitrarily chosen taking into account the actual number of daily deaths and possible worsening situations for near future: scenario a: 1250, scenario b: 1500; scenario c: 1750, and scenario d: 2000 deaths per day at a maximum turning point. Data of daily new cases and daily new deaths for COVID-19 in Brazil were fit as described above. Calculations for each scenario were performed with addition of constrains for the values of α in Eq. 1, corresponding to the number of daily new deaths at the maximum turning point for each scenario.
The lethality rate (LR) of COVID-19 was calculated as the relation between the cumulative number of cases and deaths, as:
| 4 |
where αC is the total number of cases and αD is the total number of deaths.
The estimation of the safe date to start relaxing lockdown measures in Brazil was done empirically, based on the observation of the relaxing measures in other countries, indexed by the Oxford COVID-19 Government Response Tracker (OxCGRT). OxCGRT systematically collects information on several different common policy responses that governments have taken to respond to the pandemic on 17 indicators such as school closures and travel restrictions [6]. Most of the countries that faced COVID-19 epidemic on January or on early February start to ease lockdown measures in the beginning of May. For instance, Spain, Italy, and Germany presented the first easing measures on May 3; Portugal and Belgium on May 4; France, Netherlands, and Canada on May 10; and so on. The numbers of daily new cases and daily new deaths in some of those countries (Belgium, Canada, France, Germany, Italy, Netherlands, Portugal, and Spain) when they start to ease the lockdown measures — evaluated by the decrease of the OxCGRT index — were around 20 cases per million habitants and 3 deaths per million habitants in average, respectively (precisely 21 ± 11 daily cases/million and 3.3 ± 1.8 daily deaths/million), as extracted from data in Oxford’s Our World in Data Project [6].
In Brazil, with actual population of 209.5 million habitants, if one considers that 20 cases per million habitants and/or 3 daily deaths per million habitants as a threshold to start easing stay-at-home requirements, it would correspond to 628 deaths and 4190 cases, respectively. We do not have theoretical fundaments to evaluate if this number can be safely considered a base for health measures against COVID-19 pandemics. However, purely based on the examples previously described for other countries, we used these numbers in this work to project dates to start easing the stay-at-home requirements in Brazil. The dates in which Brazil will present less than 628 daily new deaths and/or less than 4190 daily new cases can be estimated by calculating the value of t that gives these value as f(t) in Eq. 1, with the respective constants for each scenario.
Errors presented here were calculated from asymptotic errors and from coefficients of determination (R2) given by the software fitter. Error propagation was done as by regular rules [18].
Results
Data on cases and deaths of COVID-19 in Brazil were extracted from Our World in Data Project on Coronavirus [6] and used to perform forecast prediction of the COVID-19 epidemics in Brazil. Analysis of the epidemic data in many countries displays that the LR of COVID-19 evolves following a common behavior. LR of COVID-19 in Brazil was calculated using the number of cumulative deaths divided by the number of cumulative cases, as shown in “Material and methods.” The first case in Brazil was registered on February 26. Since then, the LR for COVID-19 in Brazil has grown until it reaches a constant value around May 13, when it displayed a slight decrease (Fig. 1). This behavior of the LR is similar to those observed for most countries, in which the LR raises up to the peak of the epidemic and then maintain stable or with a slight decrease (data not shown). Figure 1 shows that percent LR for COVID-19 in Brazil reached 4.68 ± 0.01%. This value was used to estimate the maximum number of daily new cases at the peak of the COVID-19 epidemic curve from the number of daily new deaths chosen for each scenario by applying Eq. 4 (see “Material and methods”).
Fig. 1.
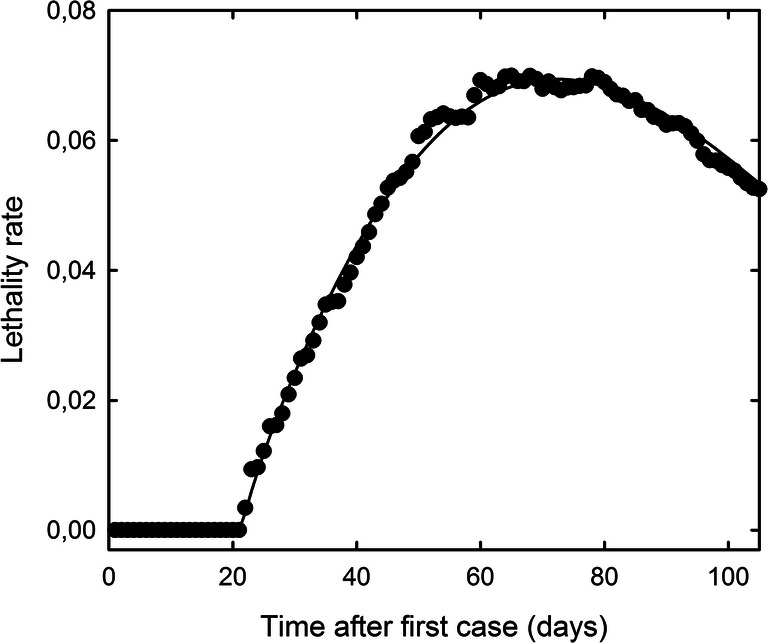
Evolution of the lethality rate (LR) during the COVID-19 pandemic in Brazil. LR is given by the number of cumulative deaths divided by the number of cumulative cases. Points were fit within Weibull’s density function equation
Brazil is still facing an exponential growth of daily new deaths and cases, what does not permit acceptable predictions on when the curve is going to bend. However, taking into account four distinct scenarios based on the maximum turning point of the Weibull prediction curve of daily new deaths for COVID-19 in Brazil, it was possible to draw non-linear regression curves depicting the forecast predictions on the number of daily new deaths in every day, until the end of the epidemic. Figure 2 shows the plots of the number of daily new deaths and cases as a function of time, in days. Values of the number of daily new cases at the maximum turning points for each scenario were calculated with Eq. 4 from the LR observed in Fig. 1 (0.468). Thus, panels a to d show scatter plots based on data for daily new cases and deaths, and line plots based on the results of the Weibull predictions of these data for each scenario, being the scenario a the most optimistic and the scenario d the most pessimistic. Numbers of daily new deaths and daily new cases at the maximum turning points, calculated with Eq. 4 for each scenario, are as follows: panel a, 1250 daily deaths and 26,709 daily cases; panel b, 1500 daily deaths and 32,051 daily cases; panel c, 1750 daily deaths and 37,393 daily cases; and panel d, 2000 daily deaths and 42,735 daily cases (parameter α at Eq. 1).
Fig. 2.
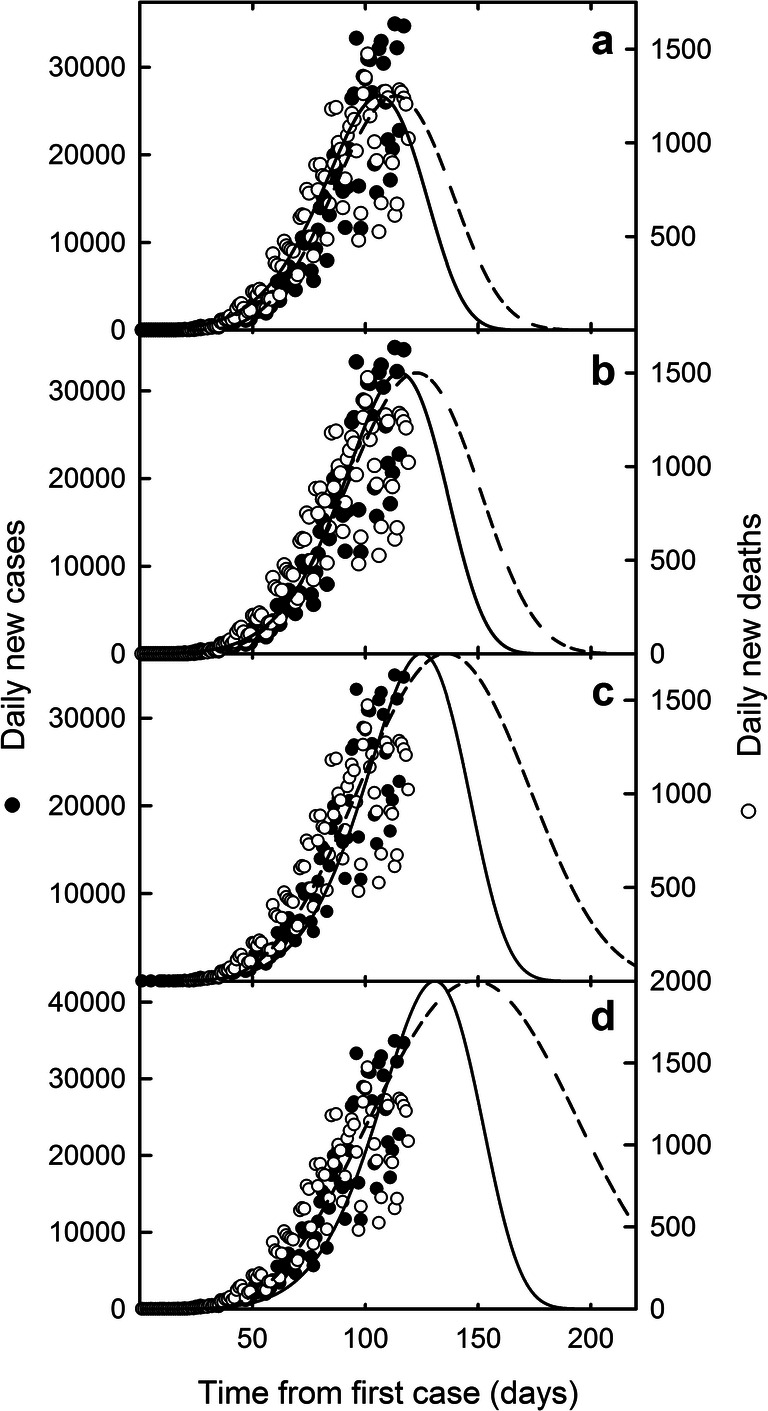
Weibull distribution on daily new cases and deaths as a function of time. Data on daily new cases (closed circles) and daily new deaths (open circles) were fit within the Weibull distribution (solid lines for deaths, traced line for cases). Four scenarios with distinct maximum rates at the peak top are shown: a 1250 deaths per day; b 1500 deaths per day; c 1750 deaths per day; and d 2000 deaths per day
The forecast projections were done by using the Weibull distribution to fit the number of daily new cases and deaths for COVID-19 in Brazil. Each panel in Fig. 2 shows projections for the number of daily new cases in traced lines and for the number of daily new deaths in solid lines. It was possible, from fit curves and from β and η parameters, to predict the date at the maximum turning points of the curves, given by t0 in Eq. 1. Thus, the total number of deaths and cases at the end of pandemic could be determined by the areas under the fit curves, as well as the predicted numbers of daily new cases and deaths at a forward day in the future, by the value of f(t) for such day (t).
As shown in Fig. 2, as we move to more pessimistic scenarios (from panel a to panel d), not only the heights of the peaks increase, and the dates at the maximum turning points tend to shift to latter times, but also the lasting of the peak tails becomes longer. Both the increase of the height of the peak and the elongation of the peak tail would contribute to the raise of the overall death toll for COVID-19 in Brazil. The y-axis scales of the plots in Fig. 2 were calibrated to match the number of new daily cases (left y-axis) and the number of daily new deaths (right y-axis) at the turning points of the regression curves (traced lines for daily cases and solid lines for daily deaths). With this view, plots in Fig. 2 visually reflect DDlag as the distance between the solid and the traced lines.
DDlag could be calculated from curve fit parameters in Fig. 2 by applying Eq. 2, as well as the overall death toll of COVID-19 from the area under the curve. Table 1 summarizes the main results estimated from Fig. 2. As shown, DDlag for COVID-19 epidemic in Brazil varies from 7.3 to 17.5 days from the most optimistic scenario (a) to the most pessimistic scenario (d), respectively. Additionally, the overall death toll of COVID-19 in the most optimistic scenario (a) is 78,347 deaths, though it increases successively up to 176,757 deaths in the most pessimistic scenario (d). Yet, it was possible to estimate, from fit curves in Fig. 2, the date in which the number of daily new deaths would decrease to less than 3 new daily deaths and/or 20 new daily cases per million habitant (i.e., less than 628 and 4190 deaths and cases per day, respectively, for the population of Brazil). These values were arbitrary taken as examples from other countries that started to relax the lockdown measures when they presented, in average, about 3 new deaths and 20 new cases per million habitants per day (see “Material and methods”). As displayed in Table 1, the forecast predictions presented here estimate that Brazil would present less than 3 deaths per million habitants per day, in the most optimistic scenario (a), on July 5. However, if the curve for daily number of new deaths is not going to bend soon, i.e., if the country would present an increase in the number of new daily deaths in the next days, that date might be shifted up to August 29 in the most pessimistic scenario (d). At last, predictions for the date in which Brazil may present less than 20 cases per million habitants per day are presented in Table 1. These predictions are quite distinct from those estimated by the number of daily new deaths. We believe that it is due to the decrease of the LR of COVID-19 in Brazil observed since May 22 (Fig. 1), what will be further discussed below.
Table 1.
Forecast projection parameters from modeled curves shown in Fig. 2
| Scenario (deaths/day) | Max. registered cases/day | Overall death toll | Model DDlag (days) | Less than 626 deaths/dayb | Less than 4190 cases/dayb |
|---|---|---|---|---|---|
| 1250 | 26,709 ± 3 | 70,664 ± 5584 | 7.3 ± 0.3 | July 5 ± 10.3 | August 3 ± 11.8 |
| 1500 | 32,051 ± 3 | 85,172 ± 12,536 | 7.4 ± 0.3 | July 16 ± 20.8 | August 19 ± 11.7 |
| 1750 | 37,393 ± 4 | 99,370 ± 20,836 | 10.9 ± 0.5 | August 14 ± 32.1 | August 30 ± 12.3 |
| 2000 | 42,735 ± 4 | 113,566 ± 23,813 | 17.5 ± 0.9 | August 29 ± 33.5 | October 19 ± 15.9 |
aErrors propagated from standard errors and R2 given by fit software
bErrors are presented in days
Discussion
COVID-19 is a global health emergency that is going to change the way in which people, institutions, and governments manage their lives and duties. The fact that there is no known specific drugs or vaccines for COVID-19 until now raises the importance of behavioral strategies, such as social distancing, lockdowns [19–23], and mass testing [24–27] in the fight against the pandemic. Data analysis can be of outstanding importance during disease outbreaks, mainly if fast decision-making is crucial to slow down the spread of the disease. The prediction of the course of COVID-19 pandemic in highly affected countries is considered a live-saving demand [28, 29].
Our results show that the LR of COVID-19 in Brazil rose since the beginning of pandemic and reached 0.070 (or 7.0%) on May 22. After that, the LR starts to decrease until it reaches 0.0468 (or 4.68%) on June 21. This decrease was due to a rapid growth in the number of daily new cases, mainly after June 1. In almost every country, the LR of COVID-19 tends to remain constant toward the epidemic peak (data not shown). Thus, this decrease of LR observed in Brazil could be indicative that an increase of daily new deaths might be observed in the next days, following the rapid increase of the number of daily new registered cases.
It has been previously demonstrated that there is a correlation between LR and DDlag for many countries in which the COVID-19 pandemic is become controlled. Those countries are already experiencing the descendent phase of the curve for daily new cases and daily new deaths. DDlag has been shown to be an efficient, empiric parameter to evaluate the overall results of several factors that may affect the spread of COVID-19. As DDlag displayed a strong correlation with the LR, it can be used as a tool to evaluate the level of sub-notification, as well as the efficacy of measures taken in response to the epidemic [12]. This correlation is represented by Eq. 3 and can be used to estimate DDlag from LR and vice versa. Actually (June 21), the LR of COVID-19 in Brazil is 0.0468 (Fig. 1). This LR value would correspond, second Eq. 3, to a DDlag of 14.1 days. This value of DDlag is compatible with, in average, those ones calculated for scenarios c (1750 deaths per day) and d (2000 deaths per day) (Table 1).
Figure 2 shows predictions for the course of COVID-19 pandemic in Brazil in four prospective scenarios based on the number of daily new deaths. Although the number of daily deaths is around 1200, while these lines are written (June 21), the rapid increase in the number of daily new cases on last weeks made the first — and more optimistic scenario (a) — to be less probable, since the number of daily new cases today is already out of the fit curve (Fig. 2a, black circles). Weibull distribution fits the actual data for daily new cases with similar precision in scenarios b and c (R2 = 0.87), what prevents a precise prediction on which scenario is the most probable. However, DDlag value, estimated by applying LR in Eq. 3, points to a prospective scenario that lies between 1750 and 2000 daily new deaths (scenarios c and d, respectively).
In this work, we based on the measures taken by the governments of countries that faced the COVID-19 pandemic on January or early February to estimate criteria for suggesting the easing of stay-at-home measures in Brazil. The countries that were selected for this sample already started to relax restriction measures, what could be monitored by the OxCGRT index [6]. The day in which the first decrease in the OxCGRT index was observed, in such countries, was used as a landmark for the starting date of relaxing restriction measures (see “Material and methods”). Based on this, it was possible to determine, from Weibull fit curves in Fig. 2, the date in which it would be registered less than 628 deaths per day (3 deaths per million habitants) and/or less than 1490 cases per day (20 cases per million habitants) of COVID-19 in Brazil. Table 1 displays the estimated dates in which Brazil would present less than 628 daily deaths and less than 1490 daily cases, as well as the total death toll at the end of COVID-19 pandemics, for each scenario. As shown, considering the criteria described above, Brazil would present conditions for start to ease restriction measures on July 5, in the most optimistic scenario (a). This prediction date may be extended up to August 29 as the epidemic scenario is changed to the most pessimistic one (d).
As shown in Table 1, the higher the number of daily new deaths at the turning point of the peak, the longer it will last for Brazil to register less than 3 deaths per million habitants per day and to safely relax the stay-at-home measures. Consequently, the higher will be the death toll at the end of pandemic. Measuring the correlation between t0 values for the number of daily new deaths (open circles) and the overall death tall (Table 1), it is possible to estimate that each additional day that Brazil takes to bend the daily new deaths curve adds more 1685 deaths to the overall death toll of COVID-19 in Brazil (R2 = 0.9890). Many papers have been published on the importance of lockdown measure, but little effort has been dedicated to what are the best criteria to be taken into account to decide the right moment of relaxing quarantine, lockdown, and social isolation measures. There is no consensus on the right time to ease, or finish, the lockdown measures toward COVID-19 pandemic. Indeed, each country responds in a particular way, taking into account many subjective criteria. Rawson and coworkers have used a Susceptible-Exposure-Infection-Recovery (SEIR) model to evaluate two potential lockdown release strategies, as well as the best moment to apply them, in order to limit recurrent spread of the disease [30]. In that work, it has been suggested that the first relaxing measures should be taken 2 weeks after the end of the infection peak, what may occur even months after the maximum turning point of new deaths and new cases. In the present work, we did not use scientific or technical criteria to determine the conditions in which the relaxation of stay-at-home measures can safely begin. Criteria adopted here were merely based on the example of selected countries measures and, thus, may be carefully evaluated and, also, equalized with other criteria, before to be considered by health authorities and decision-makers.
Weibull distribution showed to be very reliable for data analysis on COVID-19 epidemics, mainly when applied in daily new cases and deaths. Predictions based on daily data are especially efficient because they can be continuously revised, offering to governments and to health authorities the opportunity of re-conducting their decisions as new data become available. We believe that such predictions can be used by decision-makers in order to define strategies to fight COVID-19, both in the present days and in the near future. Still more, these results depict the primal importance of reinforcing the strict surveillance measures in Brazil, such as hardening lockdown measures, increasing the number of performed tests, and improving the quality of health services and work conditions of health professionals. These measures might be taken in order to flat the infection curve, i.e., the curves for daily new deaths and cases in view to mitigate the social and economic impact of COVID-19 outbreak in Brazil.
Acknowledgments
Thanks are due to Dr. Ricardo Portela for the critical reading of the manuscript and to Dr. Gilson Carvalho for valuable discussions of the theme.
Author contributions
The author has gained full consent from the responsible authorities at the institute/organization where the work has been carried out.
Funding information
This work was supported by the author’s own resources.
Compliance with ethical standards
Conflict of interest
The author declares that there is no conflict of interest.
Ethical approval
Not applicable
Consent to participate
Not applicable. VHM is the only author of this MS.
Consent for publication
Not applicable. VHM is the only author of this MS.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Hopman J, Allegranzi B, Mehtar S. Managing COVID-19 in low- and middle-income countries. JAMA. 2020;323(16):1549. doi: 10.1001/jama.2020.4169. [DOI] [PubMed] [Google Scholar]
- 2.Burki T. COVID-19 in Latin America. Lancet Infect Dis. 2020;20(5):547–548. doi: 10.1016/s1473-3099(20)30303-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bong C-L, Brasher C, Chikumba E, McDougall R, Mellin-Olsen J, Enright A. The COVID-19 pandemic. Anesth Analg. 2020;131:86–92. doi: 10.1213/ane.0000000000004846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.IMF (2020) IMF Data [Internet]. World Economic Databases, April 2020. https://www.imf.org/external/pubs/ft/weo/2020/01/weodata/index.aspx. Accessed May 25
- 5.Beltekian D, Ortiz-Ospina E (2018) Extreme poverty is falling: how is poverty changing for higher poverty lines? [Internet]. Our World in Data. https://ourworldindata.org/poverty-at-higher-poverty-lines. Accessed 2020 May 19
- 6.Roser M, Ritchie H, Ortiz-Ospina E, Hasel J (2020) Coronavirus pandemic (COVID-19) [Internet]. https://ourworldindata.org/coronavirus. Accessed 2020 May 15
- 7.Bhatia S, Cori A, Parag K V, Mishra S, Cooper L V, Ainslie KEC, et al. (2020) Short-term forecasts of COVID-19 deaths in multiple countries [Internet]. Imperial College Lodon. https://mrc-ide.github.io/covid19-short-term-forecasts/index.html. Accessed 2020 May 23
- 8.Phillips D (2020) Brazil loses second health minister in less than a month as Covid-19 deaths rise [Internet]. The Guardian. Rio de Janeiro; https://www.theguardian.com/world/2020/may/15/brazil-health-minister-nelson-teich-resigns. Accessed 2020 May 23
- 9.Londoño E, Andreoni A, Casado L (2020) Bolsonaro, isolated and defiant, dismisses coronavirus threat to Brazil [Internet]. The New York Times. https://www.nytimes.com/2020/04/01/world/americas/brazil-bolsonaro-coronavirus.html. Accessed 2020 May 23
- 10.Ciufolini I, Paolozzi A. Mathematical prediction of the time evolution of the COVID-19 pandemic in Italy by a Gauss error function and Monte Carlo simulations. Eur Phys J Plus. 2020;135(4):355. doi: 10.1140/epjp/s13360-020-00383-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gupta S, Raghuwanshi GS, Chanda A. Effect of weather on COVID-19 spread in the US: a prediction model for India in 2020. Sci Total Environ. 2020;728:138860. doi: 10.1016/j.scitotenv.2020.138860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kim S, Bin SY, Jung E. Prediction of COVID-19 transmission dynamics using a mathematical model considering behavior changes. Epidemiol Health. 2020;42:e2020026. doi: 10.4178/epih.e2020026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li L, Yang Z, Dang Z, Meng C, Huang J, Meng H, et al. Propagation analysis and prediction of the COVID-19. Infect Dis Model. 2020;5:282–292. doi: 10.1016/j.idm.2020.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Moreau VH (2020) Projection of daily new cases and deaths of COVID-19 by Weibull distribution. Submited
- 15.Lawless JF (2003) Basic concepts and models 1.1. In: statistical models and methods for lifetime data, second edition. p. 1–47
- 16.Khan SA. Exponentiated Weibull regression for time-to-event data. Lifetime Data Anal. 2018;24(2):328–354. doi: 10.1007/s10985-017-9394-3. [DOI] [PubMed] [Google Scholar]
- 17.Marquardt DW. An algorithm for least-squares estimation of nonlinear parameters. Soc Ind Appl Math. 1963;11:431–441. doi: 10.1126/science.151.3712.859-b. [DOI] [Google Scholar]
- 18.Toginho Filho DO, Andrello AC. Medição e propagação de erros [Internet]. Catálogo de Experimentos do Laboratório Integrado de Física Geral. PR: Londrina; 2009. [Google Scholar]
- 19.Saez M, Tobias A, Varga D, Barceló MA. Effectiveness of the measures to flatten the epidemic curve of COVID-19. The case of Spain. Sci Total Environ. 2020;727:138761. doi: 10.1016/j.scitotenv.2020.138761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sjödin H, Wilder-Smith A, Osman S, Farooq Z, Rocklöv J. Only strict quarantine measures can curb the coronavirus disease (COVID-19) outbreak in Italy, 2020. Eurosurveillance. 2020;25(13):1–6. doi: 10.2807/1560-7917.es.2020.25.13.2000280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wilder-Smith A, Freedman DO. Isolation, quarantine, social distancing and community containment: pivotal role for old-style public health measures in the novel coronavirus (2019-nCoV) outbreak. J Travel Med. 2020;27(2):1–4. doi: 10.1093/jtm/taaa020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mitjà O, Arenas À, Rodó X, Tobias A, Brew J, Benlloch JM. Experts’ request to the Spanish government: move Spain towards complete lockdown. Lancet. 2020;395(10231):1193–1194. doi: 10.1016/s0140-6736(20)30753-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lau H, Khosrawipour V, Kocbach P, Mikolajczyk A, Schubert J, Bania J et al (2020) The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. J Travel Med 27(3). 10.1093/jtm/taaa037 [DOI] [PMC free article] [PubMed]
- 24.Anderson RM, Heesterbeek H, Klinkenberg D, Hollingsworth TD. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet. 2020;395(10228):931–934. doi: 10.1016/s0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Choi JY (2020) Covid-19 in South Korea. Postgr Med J. 10.1136/postgradmedj-2020-137738
- 26.Salath M, Althaus CL, Neher R, Stringhini S, Hodcroft E, Fellay J et al (2020) COVID-19 epidemic in Switzerland: on the importance of testing, contact tracing and isolation. Swiss Med Wkly. 10.4414/smw.2020.20225 [DOI] [PubMed]
- 27.Peto J (2020) Covid-19 mass testing facilities could end the epidemic rapidly. BMJ:m1163. 10.1136/bmj.m1163 [DOI] [PubMed]
- 28.Remuzzi A, Remuzzi G. COVID-19 and Italy: what next? Lancet. 2020;395(10231):1225–1228. doi: 10.1016/s0140-6736(20)30627-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Verma V, Vishwakarma RK, Verma A, Nath DC, Khan HTA (2020) Time-to-death approach in revealing chronicity and severity of COVID-19 across the world. Navaneetham K, editor. PLoS One. 15(5):e0233074 10.1371/journal.pone.0233074 [DOI] [PMC free article] [PubMed]
- 30.Rawson T, Brewer T, Veltcheva D, Huntingford C, Bonsall MB. How and when to end the COVID-19 lockdown: an optimisation approach. medRxiv. 2020;8(June):2020.04.29.20084517. doi: 10.1101/2020.04.29.20084517. [DOI] [PMC free article] [PubMed] [Google Scholar]


